Beim browsen stieß ich zufällig auf diesen Beitrag:
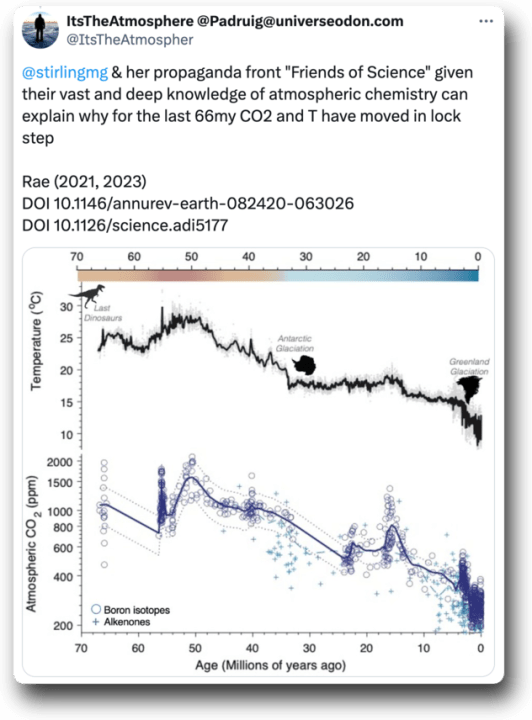
Abbildung 1. Beitrag auf X mit einer gekürzten Version der ursprünglichen Abbildung 6 aus der weiter unten verlinkten Studie.
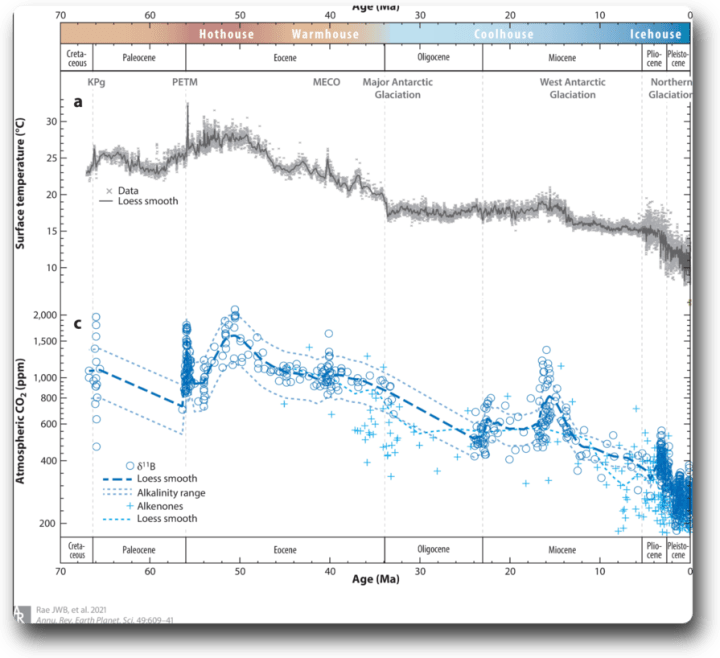
Das sieht nach einer interessanten Studie aus. Paläo-CO₂-Werte bis vor etwa 65 Millionen Jahren, die bei etwa 2000 ppmv ihren Höhepunkt erreichten.
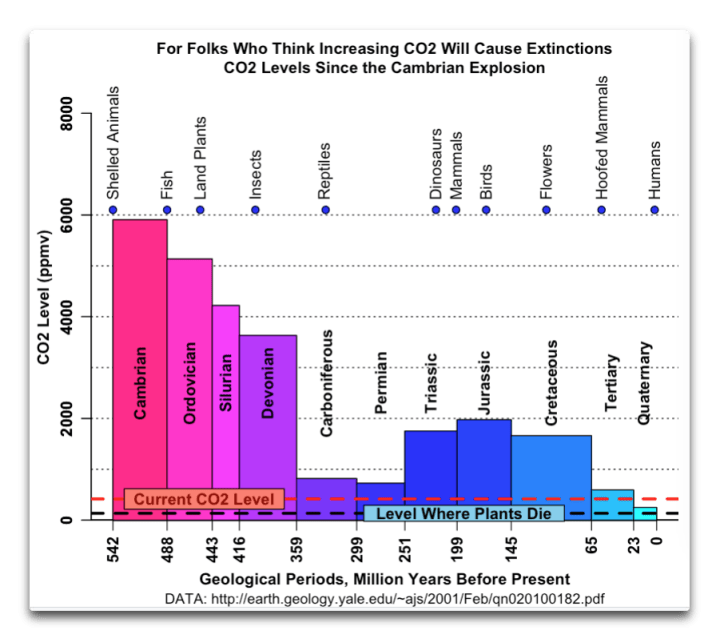
Das erinnerte mich an eine frühere Grafik von mir, welche die Paläo-CO₂-Werte über eine viel längere Zeitspanne zeigte. Die obige Abbildung 1 deckt nur die Zeitalter des Tertiärs und des Quartärs ab, also die beiden Kästchen ganz rechts in Abbildung 2 unten:
Also ging ich zu der in Abbildung 1 genannten Quelle, einer Studie mit dem Titel „Atmospheric CO₂ over the Past 66 Million Years from Marine Archives“ von Rae et al. Die folgende Grafik ist eine gekürzte Version von Abbildung 6 der Studie von Rae et al:
Die Autoren haben sich voll und ganz auf die „CO₂-Roolz-Klima“-Theorie eingelassen und sagen u.a.:
Veränderte CO₂-Konzentrationen in der Atmosphäre werden seit langem mit der gut dokumentierten Abkühlung des Klimas im Känozoikum in Verbindung gebracht; abgesehen von einer Handvoll gut untersuchter Klimaübergänge war es jedoch schwierig, eine enge Verbindung zwischen CO₂ und Klima herzustellen. Unsere neue kombinierte CO₂-Zusammenstellung auf Meeresbasis zeigt deutlicher als in früheren Studien eine enge Korrelation zwischen CO₂ und Aufzeichnungen der globalen Temperatur (entweder auf der Grundlage geochemischer Rekonstruktionen und/oder des Zustands der Kryosphäre) während des gesamten Känozoikums (Abbildung 6).
…
Nichtsdestotrotz ist es trotz dieser Vorbehalte klar, dass atmosphärisches CO₂ und Temperatur eng miteinander gekoppelt sind, sowohl im gesamten Datensatz als auch in kürzeren Zeitfenstern. Während der Datensatz als Ganzes auf eine relativ hohe Klimasensitivität hindeutet, wird ein Großteil dieser Temperaturänderung offenbar durch Sprünge zwischen verschiedenen Klimazuständen erreicht.
Ich habe mich gefragt, warum sie nicht den Wert der, wie sie behaupten, „relativ hohen Klimasensitivität“ für den Datensatz als Ganzes erwähnt haben. Also schaute ich mir die Daten an.
Bei den CO₂-Daten war das ganz einfach. Die Daten werden in einer Excel-Datei im Zusatzmaterial zur Verfügung gestellt.
Bei den Temperaturdaten ist das Gegenteil der Fall. Sie sagen „Temperatur geschätzt aus dem benthischen δ18O-Stapel von Westerhold et al. (2020), unter Verwendung des Algorithmus‘ von Hansen et al. (2013)“ … nur dass sie nicht die entsprechenden Links zu den Daten oder dem Algorithmus angeben.
Grrr. Ich habe das getan, Westerholds Daten ausgegraben, den Hansen-Algorithmus gefunden und angewandt, Links oben – und das hat eine ganze Weile gedauert.
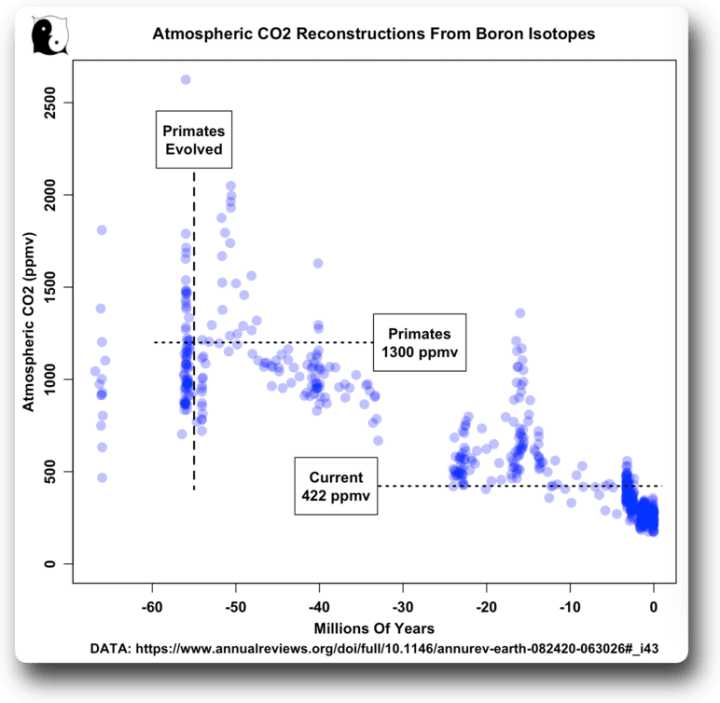
Auf jeden Fall sind hier ihre CO₂-Daten:
Unsere heutigen Werte sind weit entfernt von den höchsten Werten der letzten 5 Millionen Jahre, geschweige denn von 60 Millionen Jahren. (Bitte beachten Sie, dass ich keine LOWESS-Glättung der Daten vorgenommen habe, da dies die Daten von zig Millionen Jahren quasi erfinden würde).
Meine nächste Frage war natürlich, wie gut die Temperatur mit dem Logarithmus der CO₂-Werte übereinstimmt. Abbildung 5 zeigt diese Beziehung:
Ich muss sagen, dass dies eine sehr gute Übereinstimmung für Klima- und Paläo-Standards ist, wo Messungen immer unsicher sind.
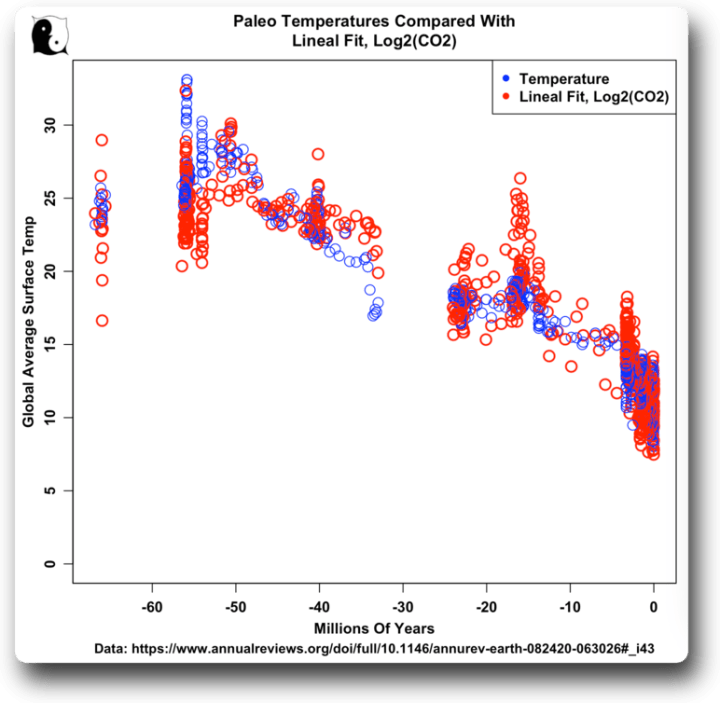
Als nächstes habe ich mir den unübersichtlichen Bereich unten rechts genauer angesehen. Das ist die Zeit der „Eiszeiten“, also Perioden der Vergletscherung, gefolgt von Wärmeperioden. Abbildung 6 zeigt die Eiszeiten:
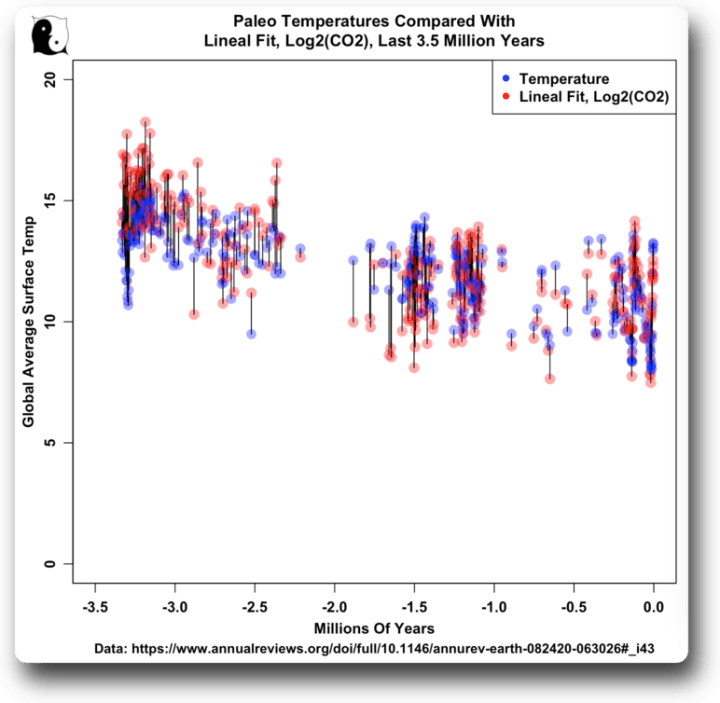
Abbildung 6. Paleo-Temperaturen und lineare Anpassung des Logarithmus‘ zur Basis 2 der CO₂-Werte. Ich habe Linien zwischen der Temperatur und den angepassten CO₂-Werten für jeden Messzeitpunkt eingezeichnet.
Noch einmal: Nach den Maßstäben von Paläo und Klima sind dies gute Anpassungen.
Also … was gibt es daran nicht zu mögen? Zeigt dies tatsächlich, dass CO₂ in Höhe von 0,04 % der Atmosphäre wirklich der geheime globale Temperaturregler ist, wie die Autoren behaupten?
Vielleicht nicht.
Schauen wir uns zunächst einmal die Berechnungen an. Ich werde die Mathematik aufteilen, um Leute, die Mathe nicht mögen, nicht zu stören … für Sie, überspringen Sie einfach diesen Abschnitt. Hier ist die Zusammenfassung der linearen Anpassung von log2(CO₂) und Temperatur:
Koeffizienten:
„log2_CO₂“ ist der Logarithmus zur Basis 2 der Veränderung von CO₂. Der oben fettgedruckte „Schätzwert“ von 6,3 ist die Klimasensitivität, die Schätzung der Temperaturänderung, die einer Verdoppelung des CO₂ entspricht.
Also ja, wie die Autoren oben sagen, zeigt dies eine „relativ hohe Klimasensitivität“. Die Klimasensitivität von 6,3 ist die dritthöchste von 172 verschiedenen früheren Schätzungen der Klimasensitivität. Hier ist ein Blick auf frühere Schätzungen:
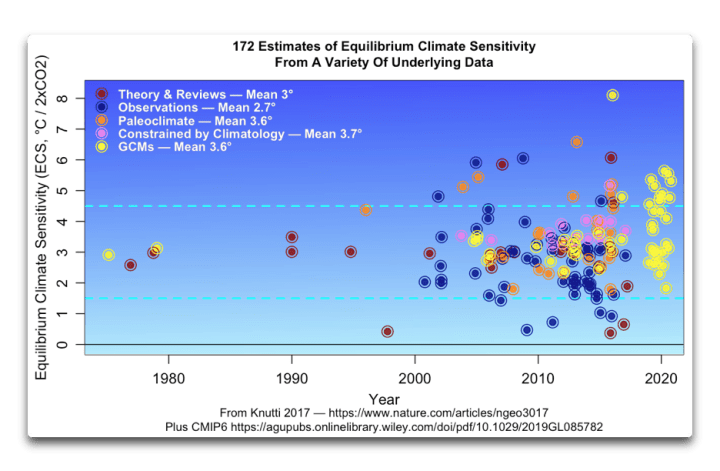
Abbildung 7. Schätzungen der Klimasensitivität aus Theorie und Übersichten, Beobachtungen, Paläoklima, Klimatologie und GCMs.
Ein weiteres Problem, abgesehen davon, dass die Klimasensitivität eine der höchsten der 173 Schätzungen ist, sind die in Abbildung 2 dargestellten viel höheren CO₂-Werte in der Vergangenheit. Wenn die Klimasensitivität bei 6,3 °C pro Verdopplung liegt, würde das bedeuten, dass die globale durchschnittliche Temperatur im Kambrium bei etwa 40 °C und im Devon bei etwa 36 °C lag … das erscheint unwahrscheinlich.
Es gibt jedoch ein größeres Problem. Die CO₂-Theorie besagt, dass ein Anstieg des CO₂ mehr aufsteigende langwellige Strahlung absorbiert. Dies führt zu einem Ungleichgewicht in der Nettostrahlung am oberen Rand der Atmosphäre, da ein Teil der aufsteigenden langwelligen Strahlung zurück an die Oberfläche geleitet wird. Der Betrag dieser erhöhten abwärts gerichteten Strahlung wird als CO₂-Antrieb bezeichnet.
Die Temperatur steigt daraufhin und erhöht die aufsteigende langwellige Oberflächenstrahlung, um das Gleichgewicht wiederherzustellen.
Abbildung 8 unten zeigt den Schwierigkeitsfaktor. Wenn sich die Erdoberfläche erwärmt, gibt sie gemäß der so genannten Stefan-Boltzmann-Gleichung mehr Strahlung ab. Die folgende Abbildung 8 zeigt den erhöhten Treibhauseffekt aufgrund der gestiegenen CO₂-Konzentration in der Vergangenheit und den entsprechenden Anstieg der aufsteigenden langwelligen Oberflächenstrahlung aufgrund des Temperaturanstiegs:
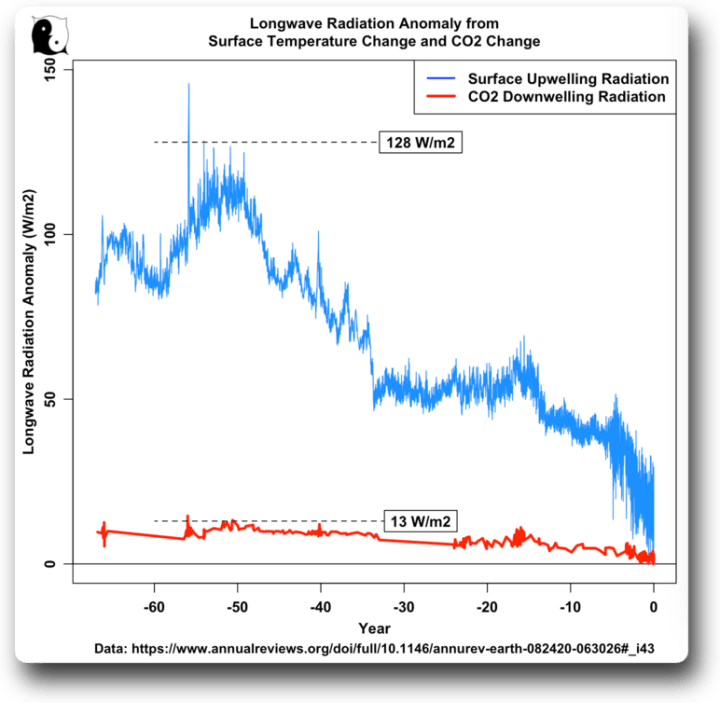
Abbildung 8. Veränderungen der aufsteigenden langwelligen Oberflächenstrahlung und der absteigenden atmosphärischen langwelligen Strahlung aufgrund von CO₂.
Aha! Das ist also die Perplexität – wir sollen glauben, dass eine Änderung des CO₂-Antriebs von 13 W/m² eine entsprechende Änderung der aufsteigenden langwelligen Oberflächenstrahlung um 128 W/m² verursacht.
Aber woher kommt die zusätzliche Energie? Es scheint, als ob der Schwanz mit dem Hund wedelt. Nach Berücksichtigung der 13 W/m² CO₂-Antrieb gibt es weitere 115 W/m² an zusätzlicher Energie, welche die Oberfläche verlässt … aber woher kommt das alles?
Zum Vergleich: Die von der Oberfläche absorbierte Sonnenenergie beträgt 164 W/m². Die Oberfläche muss also weitere drei Viertel der Energie einer Sonne von … irgendwoher bekommen…
Es müsste sich um eine außerordentlich große Rückkopplung zur Erwärmung handeln, wenn dies die Ursache für die weitere Erwärmung wäre. Der Rückkopplungsfaktor müsste ~ 0,9 sein … und wenn der Rückkopplungsfaktor größer als 1,0 ist, wächst er ohne Ende. Und das würde bedeuten, dass die natürlichen Schwankungen dieser Rückkopplung irgendwann in der Vergangenheit zu einem endlosen Wachstum geführt hätten.
Und es ist schwierig, sich einen physikalischen Prozess vorzustellen, welcher der Oberfläche diese 115 W/m² zuführen würde. Beispielsweise reflektiert die Albedo der Wolken insgesamt etwa 75 W/m² zurück ins All. Wenn also die positive Wolkenrückkopplung zum vollständigen Verschwinden der Wolken führen würde, würde dies die von der Oberfläche absorbierte Sonnenstrahlung nur um 66 W/m² erhöhen, wenn man die erhöhte Oberflächenreflexion berücksichtigt … und wir suchen nach 115 W/m².
Das Gleiche gilt für die positive Wasserdampf-Rückkopplung. Die Zahlen sind nicht groß genug. Der IPCC AR6 WG1 Kapitel 7 Abschnitt 7.4.2.2 schätzt die kombinierte Rückkopplung von Wasserdampf und Lapse-Rate auf 1,12 W/m² pro °C Erwärmung. Die Erwärmung bis vor 60 Millionen Jahren beträgt etwa 15 °C. Die Rückkopplung von Wasserdampf und Sturzgeschwindigkeit würde also in der Größenordnung von 15°C * 1,12 W/m² pro °C = 17 W/m² liegen … und wir suchen nach 115 W/m².
Was sonst … die Paläo-Temperatur oder das Paläo-CO₂ könnten falsch berechnet worden sein, in diesem Fall zeigt das alles nichts.
Eine letzte Möglichkeit ist natürlich, dass die Erwärmung wenig mit CO₂ zu tun hat und dass die CO₂-Werte eine Funktion der Temperatur sind und nicht umgekehrt …
Ich habe diesen Beitrag mit „Ein seltsames Paleo-Puzzle“ betitelt. Und das hier ist das Rätsel: Wie kann ein Anstieg des CO₂-Antriebs um 13 W/m² einen Anstieg der aufsteigenden langwelligen Oberflächenstrahlung um 115 W/m² verursachen?
Alle Vorschläge sind willkommen.
Daten: Ich habe zwei CSV-Dateien mit den in dieser Analyse verwendeten Daten erstellt, damit sie in Excel oder einer Computersprache Ihrer Wahl verwendet werden können. Die eine enthält die Temperaturen, 23.722 verschiedene Paläo-Messungen.
Die andere enthält die Paläo-CO₂-Daten, 646 Messungen. Diese enthält auch die Temperaturen aus dem anderen Datensatz, interpoliert zu den Daten der CO₂-Messungen. Dies ermöglicht die Berechnung und grafische Darstellung der Beziehung zwischen den Datensätzen.
Die Datensätze: „Rae CO₂ and Interpolated Temps.csv“ und „Rae Temperatures.csv“.
Link: https://wattsupwiththat.com/2024/02/23/a-curious-paleo-puzzle/
Übersetzt von Christian Freuer für das EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Ist man sich bewußt, dass auch die x Millionen von Jahren der 1. Graphik nur Hilfskonstrukte sind um die Hypothese der Evolution zu stützen. Mit Wissenschaft, also einem Nachweis im Experiment, hat das also so von garnix zu tun. Man braucht es halt um seine Weltsicht aufrecht zu halten. Vor kurzem auf Youtube den Film „Plasmaversum“ gesehen. Auch ein Ansatz. Der wiederum zu ganz eigenen Aussagen hinsichtlich des Universums, seiner Größe, seines Alters kommt. Vernünftig begründet. Daß aufgrund der Aussagen der Bibel nur ca. 6000 Jahre als Alter des Universums in Frage kommen, wird hier wahrscheinlich nur ein mitleidiges Lächeln hervorrufen. Begründung: „Millionen von „Wissenschaftlern“ können sich nicht irren.“ Kennt noch jemand den ähnlichen Spruch bezogen auf die Bild-Zeitung?
Fakten:
Warum CO2 das Klima kühlt und andere nützliche Informationen.
Die Jährliche Emissionen von CO2 durch die Kunststoff Produzenten ist mindestens 1.000 mal so hoch, wie die CO 2 Erzeugung durch sämtliche Bauern weltweit. Dabei ist die Speicherung von CO2 durch landwirtschaftliche Flächen ein zusätzlicher Faktor zur CO2 Reduzierung.
Eine flächendeckende Versorgung landwirtschaftlicher Betriebe mit Biogasanlagen wäre zudem in der Lage, die Methan Erzeugung und den durch Energie Verbrauch erzeugten CO2 Anteil der Bauern beziehungsweise sämtliche Treibhausgasemissionen landwirtschaftlicher Betriebe auf nahezu Null zu reduzieren und durch die Einspeisung der überschüssigen sauberen Energie in das Netz etwa 13 Prozent der russischen Gas Importe zu ersetzen.
Quelle:
https://www.srf.ch/play/tv/10-vor-10/video/kuhmist-bietet-ungenutztes-potenzial-fuer-biogas?urn=urn:srf:video:8e338971-7164-4ad6-b253-b3e583f2cb11
Und:
https://www.axpo.com/de/de/ueber-uns/medien-und-politik/medienmitteilungen.detail.html/medienmitteilungen/2022/Axpo-Iberia-Biomethan-aus-Viehmist.html
Anstatt die Fleisch und Milchproduktion aus ideologischen Gründen zu verbieten und Steuergelder sinnlos zu verplempern, sollten die verantwortlichen Politiker die Alternativen diskutieren und in Biogasanlagen investieren. Die Förderung von landwirtschaftlichen Biogasanlagen wäre eine Investition in eine nachhaltige und saubere Landwirtschaft. Die Kosten für eine Biogasanlage zur Stromerzeugung durch Kuhmist für einen mittleren Betrieb belaufen sich auf etwa 200.00 Euro. Der Bau einer landwirtschaftlichen Biogasanlage dauert nur 2 bis 3 Wochen. Das aus Methan erzeugte Gas ist komplett emissionsfrei. Die Einspeisung der erzeugten Energie durch eine Biogasanlage in das Stromnetz reduziert die Anschaffungskosten innerhalb weniger Jahre und sorgt für zusätzliche Einnahmen für landwirtschaftliche Betriebe. Die Abhängigkeit von Gas Exporten kann durch landwirtschaftliche Biogas Anlagen durch eine Erhöhung des Viehbestands sogar noch zusätzlich verringert werden, während der Methan Ausstoß und der CO2 Verbrauch landwirtschaftlicher Betriebe auf Null sinkt. Tatsache ist, dass die Landwirtschaft dank ihres Viehbestands in der Lage ist einen entscheidenden Teil zur zur Klima Rettung zu leisten. Dazu muss Herr Habeck nur die Voraussetzungen von günstigen Krediten für den Bau von landwirtschaftlichen Biogasanlagen schaffen. Das ist die Realität, die leider nirgendwo diskutiert wird.
Obwohl die Kunststoff Industrie nach der Ölindustrie der größte Produzent von CO2 ist, scheint die Politik nicht daran interessiert zu sein, dieses Problem zu thematisieren.
Allein die Herstellung von 3 Zahnbürsten erzeugt 3.000 Gramm CO2 und verbraucht 600 ml Öl.
Bericht aus dem Jahr 2019.
Im Jahr 2019 wird die Herstellung und Verbrennung von Kunststoff mehr als 850 Millionen Tonnen Treibhausgase erzeugen –
das entspricht den Emissionen von :
189 500-Megawatt- Kohlekraftwerken.
Das ist die tausendfache Menge an CO2 ,die sämtliche Landwirtschaftlichen Betriebe weltweit zusammen erzeugen.
Quelle:
https://www.boell.de/sites/default/files/2019-10/ciel-ES-GHG-German-10.19.pdf
Warum CO2 das Klima kühlt.
Man muss sich nicht ernsthaft mit den staatlich vorgegebenen, verlogenen und faktenfreien emotionalen Scheißhausparolen einer angeblichen Klimaveränderung auseinandersetzen, wenn man die wissenschaftlich bewiesenen Fakten zum frei erfundenen Klimawandel kennt.
Tatsache ist zum einen, dass CO 2 in Wahrheit das Klima abkühlt.
Hier sind einige Quellenangaben mit wissenschaftlichen Fakten. Darunter sind auch 2 Artikel, die sich mit den Ursachen der globalen Erwärmung vom 10 bis zum 14 Jahrhundert befassen. Zwischen dem zehnten und dem vierzehnten Jahrhundert war die Erderwärmung deutlich höher als heute.
Außerdem werden darin auch die Ursachen für die Entstehung der kleinen Eiszeit, die vom 15 bis zum 18 Jahrhundert andauerte exakt beschrieben.
Title: Why CO2 cools the Surface of the Earth.
https://gerhard.stehlik-online.de/
https://arcticportal.org/ap-library/news/600-little-ice-age-was-caused-by-volcanic-eruptions
Climate scientists now understand that the Medieval Warm Period was caused by an increase in solar radiation and a decrease in volcanic activity.
https://news.utexas.edu/2010/11/11/medieval-warm-period-not-so-random/
http://www.co2science.org/subject/g/summaries/globalmwp.php
Schon das erste Bild zeigt den ganzen Irrsinn der CO2- Diskussion und des Klimawahns.
Die detaillierten, interessanten Aussagen im Text und den Kommentaren sind das eine. Mir geht es mehr um die Grundaussage, die aus dem Bild ohne Fachkenntnisse für jeden erkennbar ist: in allen Zeiten vor uns war der CO2-Anteil größer als heute, 6000ppm( 0,6%) sagen die einen, 16% andere. Würde das CO2 steigen, kämen wir also in Bereiche, die wir alle schon mal hatten und die wir kennen.
Uns wird eingeredet, dass ein CO2-Anstieg zur Katastrophe führen wird, 2° mehr und die Erde brennt (Schellnhuber) und die Meere kochen (Umweltministerin Lemke). 1,5 Grad hatten wir vor einigen Wochen schon für einige Tage .Doch heben wir im Geiste die eingezeichnete 420 ppm-Gerade auf die doppelte Höhe. Wir sehen dann , dass es in den vergangenen 500 Mio Jahren immer höhere CO2-Werte gab und trotzdem Tiere und Pflanzen massenhaft existierten und bestens gedeihen konnten.Warum also jetzt die ganze Panik und die Einleitung von gesetzlichen Konsequenzen?
Eine ganze Regierung , das Volk im Schlepptau, macht aus normalem Klimawandel eine Religion, dazu gehört natürlich eine Kirchensteuer. Nur heißt die jetzt CO2-Steuer. EDENHOFER (PIK) hat schon 2011 erklärt, dass es gar nicht ums Klima geht. Welch ein Zufall: heute lese ich, dass er sich jetzt noch eine METHAN-Steuer ausgedacht hat.
Wie wäre es mit einer ATEM-Steuer?
Dr.-Ing. Gerhard Kühn
leicht abgewandeltes Zitat vom GRÖKLAZ (größter Klimamini aller Zeiten) „Dem Klima gehts SCHLECHT, nur die Zahlen sind PRIMA!“… 😉
Oder umgekehrt.
Sehr geehrter Herr Dr. Roland Ullrich
„Der Artikel erinnert mich an mein Problem mit der Venus, wo offenbar viele, auch Ganteför, dem CO2, dass dort 100.000 mal konzentrierter ist als auf der Erde, eine Temperaturerhöhung um ca. 500 Grad zuschreiben. Die CO2-Klimasensitivität gibt aber bestenfalls 18 Grad her“
Der Grund für die hohen Bodentemperaturen ist ein ganz anderer: Es liegt daran, daß sich die oberste Wolkendecke auf der Venus in etwa 61 km Höhe befindet. Dort ist die bei Atmosphärenphysikern bekannte sogenannte „Emissionshöhe“, ab der ein Strahlungsaustausch mit dem Weltraum stattfindet und die einfallende Leistung der Sonnenstrahlung der abgestrahlten Wärmeleistung des Planeten entsprechen sollte. (Bei der Erde liegt sie bei grob 5 km.) In dieser Emissionshöhe auf der Venus herrscht eine Temperatur von ca. -13 C und ein Druck von 0.2 bar, also fast irdische Verhältnisse.
Unter dieser Höhe liegt eine sehr dicke und schwere Atmosphäre. Der Temperaturgradient über der Höhe h, dT/dh, hängt direkt am Druckgefälle dp/dh und bestimmt sich nur über Gaseigenschaften der Atmosphäre, und das dp/dh hängt nur an der Gravitation und der Atmosphärendichte. Bei der Venusatmosphäre, einer fast reinen CO2-Atmosphäre, beträgt der Zusammenhang etwa (dT/dh = 0.14 dp/dh), was bedeutet, daß bei einer großen Emissionshöhe und schwerer Atmosphäre die Bodentemperatur gar nicht anders kann als sehr hoch zu sein. Das hat zunächst einmal mit Treibhauseffekten gar nichts zu tun.
MfG
G.Wedekind
Herr Wedekind, das Problem ist nur: Stationärer Gasdruck führt zu keiner Temperaturerhöhung! Es muss von irgendwoher geheizt werden – von unten? Beispiel: Wenn Sie eine Gasflasche oder einen Autoreifen befüllen und der Druck steigt, dann steigt nur kurzzeitig die Temperatur – nach den adiabatischen Gasgesetzen. Wenn der gewünschte Gleichgewichtsdruck erreicht ist, also keine Druckänderung mehr (wie in der Venus-Atmosphäre), dann stellt nach kurzer die Umgebungstemperatur ein – bei der Venus die Nullgrad-Weltraumtemperatur. Es sei denn, es wird von irgendwoher Heizenergie zugeführt.
Sehr geehrter Herr Dr. Roland Ullrich
„Es muss von irgendwoher geheizt werden – von unten?“
Nein! Man kann es auch so sehen: Es kommt nicht auf die Temperatur an, sondern auf die Totalenergie: Diese hängt bei Gasen in einem Schwerefeld – vergessen wir mal die geringen Geschwindigkeiten, magnetische Kräfte usw. – von Temperatur, Druck und Höhenlage ab.
Sinkt ein Luftpaket nach unten, dann verliert es an Höhenenergie (Gravitationsenergie). Um die Totalenergie zu halten, muß, da „adiabat“ Druck und Temperatur mit dT/T = 0.14 dP/P zusammenhängen, Druck und Temperatur notwendigerweise steigen. Steigt das Paket, dann gewinnt es Höhenenergie, und Druck und Temperatur sinken. So funktioniert Konvektion und Wolkenbildung und so stellen sich die Temperaturverläufe in einer Atmosphäre ein.
Daß Energie über Strahlung, Leitung usw. in der Atmosphäre ausgetauscht werden, steht auf einem anderen Blatt. Diese Austauschformen sind sehr viel langsamer als die Konvektion und spielen bei den atmosphärischen Temperaturgradienten kaum eine Rolle.
Bei den Planeten stellt sich auf die Dauer natürlich keine Weltraumtemperatur ein, weil die Sonne nachheizt. Erst, wenn die Sonne nicht mehr heizen würde, würden sie auf Wlrtraumtemperatur abkühlen.
Übrigens ist mir in meinem Kommentar ein Fehler unterlaufen:
Es muß heißen: dT/T = 0.14 dP/P und dT/dh = 0.14 T/p dp/dh
MfG
G.Wedekind
„Der Temperaturgradient über der Höhe h, dT/dh, hängt direkt am Druckgefälle dp/dh und bestimmt sich nur über Gaseigenschaften der Atmosphäre, und das dp/dh hängt nur an der Gravitation und der Atmosphärendichte. Bei der Venusatmosphäre, einer fast reinen CO2-Atmosphäre, beträgt der Zusammenhang etwa (dT/dh = 0.14 dp/dh), was bedeutet, daß bei einer großen Emissionshöhe und schwerer Atmosphäre die Bodentemperatur gar nicht anders kann als sehr hoch zu sein. Das hat zunächst einmal mit Treibhauseffekten gar nichts zu tun.“
So ist das!
Werden die AGW-Propagandafuzzies aber nie zugeben wollen…
Wenn man seinen Blickwinkel öfters mal „verwässern“ würde, dann käme man vielleicht darauf das CO2 nur marginalen Einfluss hat und wohl eher wegen eines Temperaturanstieges ebenfalls ansteigt und nicht umgekehrt.
“
Elektromagnetische Wellen werden in erster Linie durch schwingende elektrische Dipole erzeugt. Folglich kann eine Schwingung nur dann Strahlung (d.h. elektromagnetische Wellen) erzeugen, wenn mit ihr in irgendeiner Form ein schwingendes elektrisches Dipolmoment verbunden ist. Und andersherum kann die Schwingung auch nur dann durch Strahlung beeinflusst werden, wenn sich durch die Schwingungsbewegung das elektrische Dipolmoment periodisch ändert.
Abb.2 Der grüne Pfeil zeigt das oszillierende Dipolmoment
Die Energien, die mit Schwingungen verbunden sind, entsprechen Strahlung im infraroten Spektralbereich (IR). Wenn durch eine Schwingung ein schwingendes Dipolmoment entsteht, kann sie Infrarotstrahlung erzeugen. Mann nennt sie dann IR-aktiv. Alle gezeigten Schwingungen des H2O sind IR-aktiv. Das liegt daran, dass H2O von sich aus bereits ein Dipolmoment besitzt und jede Änderung der Geometrie dieses Dipolmoment verändert.
Das muss aber nicht generell so sein. Wenn ein Molekül von sich aus kein Dipolmoment besitzt, wie z. B. CO2, dann führen nicht alle Schwingungen zwingend auch zu einem schwingenden Dipolmoment. Als Beispiel sind die Schwingungen des CO2 in einer Animation rechts gezeigt. Bei der symmetrischen Streckschwingung (oben) bleibt das Dipolmoment stets null. Diese Schwingung kann keine Strahlung erzeugen und nicht durch Strahlung beeinflusst werden. Sie ist nicht IR-aktiv. Die beiden anderen Schwingungen erzeugen ein oszillierendes Dipolmoment: Bei der asymmetrischen Streckschwiingung (mitte) ist es entlang der Molekülachse orientiert. Daher ist die erzeugte Strahlung auch parallel zur Molekülachse polarisiert. Bei der Biegeschwingung (unten) ist das Dipolmoment senkrecht zur langen Achse orientiert. Folglich ist die erzeugte Strahlung auch so polarisiert.
Im infraroten Schwingungsspektrum eines Moleküls treten nur Spektrallinien auf, die zu IR-aktiven Schwingungen gehören.“
und dazu passend diese Studie mit ähnlicher Begründung aufgrund desselben ursächlichen Parameters, der übrigens in keiner! Paläoklimatischen Studie berücksichtigt wird, vielleicht weil er nicht berücksichtigt werden kann mangels spezifischer Proxis?
https://setpublisher.com/index.php/jbas/article/view/2488/2250
Die darin geäußerten Gründe beschäftigen mich schon sehr lange, nur ist dazu wenig verwertbares zu finden.
interessanter Link – DANKE!
Es geht mir ehrlich gesagt schon lange auf den Keks(Sorry :-D) das in allen Diskussionen zum THE nur über den zweiten Schritt gestritten wird und die „Formelgläubigen“ dabei ihren Streit austragen. Zweiter Schritt deshalb, weil die Quantifizierung erst nach der Qualifizierung, Wirkungsanalyse, erfolgen kann. Zu vorderst gilt es zu analysieren welche atmosphärischen Komponenten entfalten genau welche Wirkung und unter welchen Bedingungen in der realen Welt. Schon dabei fällt geneigten Streitern auf, das CO2 gegenüber dem sich in den Strahlungsbanden teilweise überlappenden H2O-Wasserdampfmolekülen, somit mindestens annähernd gleich wirksamen „Wärmereflektor“ um etwa den Faktor 100 im Nachteil ist. Man stelle sich vereinfacht die atmosphärische Gase dergestalt vor, das jedes Gasmolekül beispielsweise 1cm groß ist, dann finden sich jeweils im Abstand, Gasgemische sind Homogen, von 23m eines von CO2 und dazwischen allerlei Gewusel sonstiger Gasmoleküle und Aerosolpartikel nebst dem hundertfachem an H2O-Molekülen. Die vom Boden abgehenden Infrarotstrahlen treffen somit eher zufällig auf ein IR-aktives Molekül der CO2-Steuerklasse, aber um ettliches häufiger auf die Wasserdampfköpfchen. Hinzu kommt, das H2O in allen Schwingungszuständen IR-Rückstrahlung abgeben kann und CO2 wie beschrieben eben nicht. Für alle anderen, nicht IR-aktiven Gase gilt nach Einstein dennoch ein „Strahlungsdurchgang“ mit Absorption, Emission und Impuls, nur ist dieser eher dem Prinzip der Transmmission, Durchgang ohne Energieabgabe/-wirkung, ähnlich, ohne aktive Emission wie bei den IR-Gasen. Klingt stark vereinfachtund abstrahiert, ist es sicher auch, aber zum prinzipiellen Verständnis denke ich vielleicht hilfreich. Wenn ich diesen, ersten Schritt, gegangen bin und mir über die grundlegenden qualitativen Anteile der atmosphärischen Gase im klaren bin, dann kann ich mich schwungvoll zu Schritt 2 bewegen und dem Formelwahn frönen um quantitative Aussagen zu treffen. Wohlwissend natürlich das dies auch längst nicht zu eindeutigen Aussagen führt aber näher an der Realität sein wird als die leider am häufigsten praktizierte „Wissenschaft des zweiten Schrittes“, weil ich wesentliche Faktoren, wie Druckverhältnisse, Albedo, etc. und vieles Andere außer acht gelassen habe. Das ist die übliche herangehensweise in vielen anderen Wissenschaften, nur die Klimapropagandisten scheinen diesbezüglich abstinent zu sein.
👍. „Selbstverständliches“ wird bewußt vermieden. Gedacht wird, wenn überhaupt, immer vom gewünschten Ergebnis her…..THE und CO2-Dämonisierung sind bewußt erfundene Konstrukte raffgieriger Wirtschaftsinteressen. Deshalb d a r f nicht widersprochen werden. Für kleines Geld wird der kleine Verstand fanatisiert.
Mittels irrelevanter Informationen aus der IPCC-Haltungsecke soll durch eine desavouierende, emotionale Bewertung ein bestimmtes Verhalten erzwungen und freie Meinungsäußerung eingeschränkt werden. Eine oktroyierte, schreckliche Infantilisierung der Gesellschaft soll Eigenverantwortung, Selbstdenken, Freiheit und UNABHÄNGIGKEIT ständig latent abbauen und kritisieren. Behaviorismus von und für geistig Arme. Jetzt im Cannabis-TRAN.
Ein Kommentator erzählt heute einen wirklich guten Witz mit einer Wette zwischen Klimakterischen und einem Jäger. Eine kleine Episode, die nebenbei noch die Realität widerspiegelt; so treffend, daß Heinimann direkt in seine übliche Beleidigungskaskade verfällt…..😂🤣😂🤣 Volltreffer. Schiff versenkt.
Liegen wir nicht mit der dauernd diskutierten Abhängigkeit von Temperatur und CO2 in geologischen Zeiten völlig daneben? Spielt nicht ein anderer Faktor gewaltig mit und treibt sowohl Temperatur als auch den atmosphärischen CO2-Gehalt? Es ist die Plattentektonik!
Seit der Kreidezeit passen nämlich Meeresspiegelhöhe, Temperatur und CO2-Gehalt überraschend gut bis in Einzelheiten überein, siehe z.B. Frisch, W., Meschede, M. „Plattentektonik“, Primus-Verlag, 2005 fig 6.20.
So war der Meeresspiegel in der Kreidezeit um bis zu 250 m höher als heute. Der Grund dafür ist in der Bildung von Basaltprovinzen – besonders in der Kreidezeit – zu suchen. Allgemein bekannt sind die außermeerischen Dekkantraps in Indien, die aus dieser Zeit stammen, aber es entstanden damals auch untermeerische Provinzen wie u.a. das Kerguelen-Plateau oder das Onton-Java-Plateau, das in der Kreidezeit ein Volumen von 30 Millionen Kubikkilometern(!) gehabt haben soll. Solche vulkanischen Provinzen verdrängen beim Entstehen das Wasser und fallen später, wie an den Hawaii-Inseln zu beobachten, wieder in sich zusammen. Abhängig davon steigt und fällt der Meeresspiegel.
Heute ist die Erde zu etwa 70% mit Wasser bedeckt, und damals muß es bis zu 80% gewesen sein. Vor allem in den nördlichen Breiten standen große Teile der Kontinente unter Wasser. (Deswegen gibt es ja auch die Kreidefelsen von Dover und Rügen). Dieser hohe Meeresspiegel muß die Ursache sowohl für die hohen Temperaturen in der Kreidezeit und danach gewesen sein – und für den hohen CO2-Gehalt der Atmosphäre, denn wärmere Ozeane verschieben das CO2-Gleichgewicht in Richtung Atmosphäre.
Seit dieser Zeit sinken sowohl der Meeresspiegel als auch die Temperaturen und der CO2-Gehalt wieder ab.
Ist also die ganze Diskussion nicht irrelevant? Es scheint so, daß Temperatur und CO2 beide gleichzeitig von einer anderen Größe getrieben werden und nicht oder nur wenig voneinander abhängig sind.
MfG
G.Wedekind
Sehr guter Einwand.
Interessante Aspekte! Aber was sagt Korrelation über Ursachen aus? Meeresspiegel als Treiber für Temperaturen und weshalb? oder umgekehrt? oder ganz andere Ursachen? Und schließlich, wie für die Zwischeneizeiten erwiesen: die Temperaturen treiben das CO2 (in der Atmosphäre) und nicht umgekehrt! andererseits fällt in der Gegenwart der CO2-Anstieg fünf bis zehnmal zu groß aus, um von den Temperaturen getrieben zu sein. Und wo war der CO2-Anstieg während der zurückliegenden Warmzeiten?
Dennoch: In letzter Zeit ist auffallend viel von Korrelation des CO2 mit den Temperaturen in den (in Abb. 2 dargestellten) weit zurückliegenden Zeiträumen die Rede – z.B. auch bei Ganteför. Früher, zumindest nach den EIKE-Veröffentlichungen, stellte man eine solche Korrelation in Abrede.
Aber auch bei Willis Eschenbach habe ich ein Problem: Nach dem T hoch 4 -Gesetz von SB erhält man bei ca. 7 % Temperaturerhöhung (etwa 20 Grad mehr) in Kelvin 30 % mehr Abstrahlung – sicherlich weniger als 128 W/m2. Wo liegt der Fehler?
Der Artikel erinnert mich an mein Problem mit der Venus, wo offenbar viele, auch Ganteför, dem CO2, dass dort 100.000 mal konzentrierter ist als auf der Erde, eine Temperaturerhöhung um ca, 500 Grad zuschreiben. Die CO2-Klimasensitivität gibt aber bestenfalls 18 Grad her…
„Die CO2-Klimasensitivität gibt aber bestenfalls 18 Grad her…“
Verstehe nicht, wie der Begriff KLIMASENSITIVITÄT überhaupt ernst genommen werden kann.
„Klimasensitivität“ als ein Maß dafür, wie sensibel die global gemittelte bodennahe Lufttemperatur auf der Erde auf Änderungen der Kohlendioxid-Konzentration reagiert.
Das ist genauso willkürlich geschätztes Pille-Palle, wie die globale Durchschnittstemperatur. Ein geschaffenes IPCC-Hilfsmittel, um gewünschte Ergebnisse in gefakte, ungenaue Parameter zu interpretieren. Wie alt ist dieser Begriff und wie lange existiert Klima ?
Nicht zufällig waren es „Rahmshuber und Schellntorf“, die diesen Begriff Arrhenius in den Mund legten, einem genialen Forscher, dessen Erkenntnisse aber längst nicht alle bis heute Bestand haben.
Die errechnete geringe, weitgehend gesättigte spektrale Erwärmung durch CO2 (CO2-Klimasensitivität) dürfte stimmen, da steckt glaubwürdige Physik dahinter. Auch bestätigt durch Spektralmessungen aus dem Weltraum. Und die Venus-Atmosphäre soll ja praktisch nur aus CO2 bestehen. Konvektionskühlung gibt es dort sicherlich auch. Aber ganz bestimmt keine 500 Grad spektrale Erwärmung durch CO2, obwohl das (im Vergleich zur Erde noch stärker gesättigte) CO2 überreichlich vorhanden ist. Auf der Erde gibt es zusätzlich den dominierenden Wasserdampf samt seiner Aggregatzuständen, der auch sehr effektiv kühlt – eine komplizierte Gemengelage! Deshalb gehen die Klimamodelle auseinander wie ein Gamsbart und übertreiben in aller Regel – dem Alarm zuliebe…
Schätze Ihre Beiträge sehr, aber allein der Satz, 👉 – „Die errechnete geringe, weitgehend gesättigte spektrale Erwärmung durch CO2 (CO2-Klimasensitivität) dürfte stimmen, da steckt glaubwürdige Physik dahinter..“ – …könnte auch von Müller stammen. Was in aller Welt soll „glaubwürdige Physik“ sein ? ✌️
Gemittelte, halb vermutete Werte, 👉 eine gemittelte, globale, bodennahe Lufttemperatur haben ungefähr so viel Aussagekraft, wie Umfragewerte zur politischen Lage aus dem Mainstream.
KEINE. Und diese Parameter potenzieren sich in den Modellberechnungen millionenfach….
Wer sich mit solchen Werten aufs Glatteis des IPCC begibt, betritt rutschigen Boden und schlittert mit den ideologisierten, hysterischen Klimakterischen immer hin und her…..
thatˋs my opinion. 😎