EINFÜHRUNG
Meine beiden letzten Beiträge haben eine neue Methode beschrieben, um den durchschnittlichen Wärmeinsel-Effekt als eine Funktion der Bevölkerungsdichte zu quantifizieren, indem Tausende von Paaren von Temperatur-Messstationen benutzt wurden, die im Abstand von 150 Km zueinander lagen. Die Ergebnisse stützen frühere Arbeiten, die gezeigt haben, dass die Wärmeinsel-Erwärmung logarithmisch mit der Bevölkerung steigt, wobei die größte Rate der Wärmezunahme dort ist, wo der Anstieg von der niedrigsten Bevölkerungsdichte stattfindet.
Doch wie hilft uns das bei der Entscheidung, ob die globalen Erwärmungstrends auf fehlerhafte Weise durch Effekte verstärkt wurden, die in den führenden Oberflächentemperaturdaten-Reihen liegen, wie sie beispielsweise von Phil Jones (CRU) und Jim Hansen (NASA/GISS) erzeugt wurden.
Wenn auch meine Quantifizierungen des Wärmeinsel-Effekts eine interessante Übung sind, so beweist das Vorhandensein dieses Effekts auf den Raum bezogen (für Stationen mit räumlicher Entfernung) nicht notwendigerweise, dass es auch einen Erwärmungsfehler bei den Temperaturdatenim zeitlichen Verlauf gegeben hätte. Der Grund dafür liegt darin, dass, soweit die Bevölkerungsdichte [in der Umgebung] einer Messstation sich nicht über die Zeit verändert, die unterschiedlichen Maße des Wärmeinsel-Einflusses bei unterschiedlichen Messstationen wahrscheinlich geringen Einfluss auf die Langzeit-Temperatur-Trends haben. Städtische Stationen werden tatsächlich wärmer als der Durchschnitt sein, aber die „globale Erwärmung“ wird sie in etwa genau so beeinflussen wie die eher ländlichen Stationen.
Diese hypothetische Annahme scheint trotzdem unwahrscheinlich zu sein, weil die Bevölkerung doch tatsächlich mit der Zeit zunimmt. Wenn wir uns auf genug ländliche Stationen verlassen könnten, könnten wir alle anderen Wärmeinsel-verseuchten Daten wegwerfen. Unglücklicherweise gibt es nur sehr wenige Langzeit-Messungen von Thermometern, die keinerlei Veränderungen in ihrer Umgebung ausgesetzt waren … normalerweise sind es die menschlichen Bauwerke und Bodenabdeckungen, die zu fehlerhafter Erwärmung führen.
Deshalb müssen wir Daten von Stationen mit wenigstens geringer Wärmeinsel-Kontaminierung benutzen. Und damit erhebt sich die Frage, wie berücksichtigt man derartige Effekte?
Als Lieferant der offiziell abgesegneten GHCN – Temperatur-Reihen, auf die sich Hansen und Jones stützen, hat die NOAA einen ziemlich mühsamen Ansatz gewählt, bei dem die Langzeit-Temperaturdatenreihen von den einzelnen Messstationen Homogenitäts-„Korrekturen“ unterzogen werden, die auf (vermutlich fehlerhaften) abrupten Temperaturänderungen über der Zeit beruhten. Das Entstehen und Vergehen von Messstationen im Verlauf der Jahre verkompliziert weiterhin die Erstellung von Temperaturdatenreihen für Zeiträume bis zu 100 Jahren oder mehr zurück.
Das alles (und noch mehr) hat zu einem Mischmasch von komplexen Anpassungen geführt.
EINE EINFACHERE TECHNIK ZUM AUFSPÜREN VON FEHLERHAFTER ERWÄRMUNG
Bei der Analyse bevorzuge ich stets die Einfachheit – wo immer möglich. Komplexität bei der Daten-Analyse sollte nur eingeführt werden, wenn dies zur Aufklärung eines Sachverhalts nötig ist, der mithilfe einfacherer Analyse nicht erklärbar ist. Und so zeigt sich, dass die einfache Analyse der öffentlich zugänglichen Rohdaten der NOAA/NCDC von den jeweiligen Messstationen zusammen mit hoch aufgelösten Bevölkerungsdichte-Daten klare Belege dafür liefert, dass die GHCN-Daten für die Vereinigten Staaten Wärmeinsel-verseucht sind.
Ich begrenze die Analyse auf 1973 und nachfolgend, weil dies (1.) die primäre Erwärmungsperiode ist, die den menschlichen Treibhausgas-Emissionen zugeschrieben wird, und (2.) dies die Periode mit der höchsten Anzahl von Überwachungsstationen seit 1973 ist; und (3.), weil eine relativ kurze 37-Jahre-Historie die Anzahl der fortwährend arbeitenden Stationen maximiert. Dabei entfällt die Notwendigkeit, Übergänge zu behandeln, wenn ältere Stationen außer Betrieb gehen und neue hinzukommen.
Wie ich schon früher dargelegt habe: Ich bilde für vier Temperaturmessungen pro Tag (00, 06, 12, 18 Uhr UTC) für jede U.S.-Messstation einen Mittelwert (GHCN benutzt tägliche max/min-Werte) zur Errechnung eines Tagesmittels. Für eine monatsbezogene Durchschnittsbildung braucht man Messungen für wenigstens 20 Tage. Dann nehme ich nur diejenigen Stationen, die wenigstens 90% vollständige monatliche Daten von 1973 – 2009 haben. Die jährlichen Verläufe der Temperaturen und der Anomalien werden von jeder Station getrennt berechnet.
Dann errechne ich Multi-Stations-Anomalie-Durchschnitte für Quadrate mit der Größe von 5×5 Grad Breite/Länge, die ich dann mit den Temperatur-Trends der jeweiligen Region im CRUTem3-Datenbestand (das ist der Datenbestand von Phil Jones) vergleiche. Um aber zu erkennen, ob der CRUTem3–Datenbestand irgendwelche Fehler-Trends hat, teile ich meine Durchschnittswerte in 4 Klassen unterschiedlicher Bevölkerungsdichte: 0 – 25; 25 – 100; 100 – 400; mehr als 400 Menschen pro qkm. Die Bevölkerungsdichte ist auf eine nominale 1 km Auflösung eingestellt, die für 1990 bis 2000 erhältlich ist. Ich benutze die Daten von 2000.
Aus allen diesen Einschränkungen ergeben sich 24 bis 26 Fünf-Grad-Kästchen, verteilt über die Vereinigten Staaten mit allen Bevölkerungsdichteklassen in der 37-Jahre-Aufzeichnung. Zum Vergleich: Die gesamten Vereinigten Staaten überdecken ca. 40 Gitterkästchen im CRUTem3-Datenbestand. Weil die nachfolgend dargestellten Ergebnisse einen regionalen Subset (mindestens 60%) der USA darstellen, werden wir erkennen, dass die CRUTem3–Temperaturänderungen für die gesamten Vereinigten Staaten sich nicht substanziell ändern, wenn alle 40 Kästchen in die CRUTem3–Durchschnittsbildung einbezogen werden.
BELEG FÜR GROSSEN FEHLERHAFTEN ERWÄRMUNGSTREND IN DEN U.S. – GHCN-DATEN
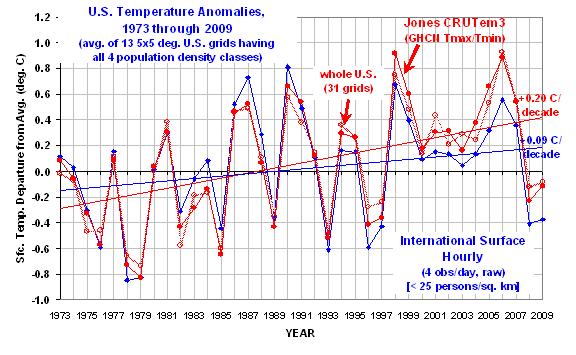
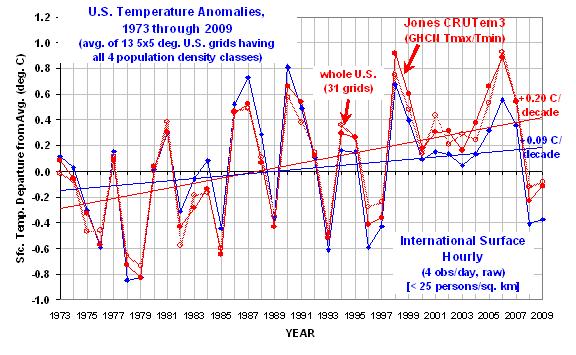
Die dicke rote Linie ist vom CRUTem3 Datenbestand und kann so als die „offizielle“ Abschätzung gelten. Die dicke blaue Kurve gilt für die Klasse der niedrigsten Bevölkerungsdichte. (Die übrigen drei Bevölkerungsdichteklassen würden die Grafik so unkenntlich machen, dass sie weggelassen sind, aber wir werden die Ergebnisse unten in brauchbarer Form sehen.)
Die folgende Grafik zeigt die jährlichen gebietsgemittelten Temperatur-Anomalien von 1973 – 2009 für die 24 bis 26 über die Vereinigten Staaten verteilten 5-Grad-Kästchen mit allen vier Bevölkerungsdichte-Klassen (wie auch eine CRUTem3-Durchschnittstemperaturmessung). Alle Anomalien sind rückgerechnet auf die 30-Jahr-Periode von 1973-2002.
Der Erwärmungstrend in der niedrigsten Bevölkerungsdichte-Klasse ist um 47% signifikant geringer als der CRUTem3-Trend. Ein Unterschied um den Faktor 2.
Interessant ist auch, dass in den CRUTem3-Daten 1998 und 2006 die beiden wärmsten Jahre der Aufzeichnungsperiode sind. Aber in der niedrigsten Bevölkerungsdichte-Klasse sind die beiden wärmsten Jahre 1987 und 1990. Bei der Analyse der CRUTem3-Daten für die gesamten Vereinigten Staaten (die hellrote Linie) sind die beiden wärmsten Jahre vertauscht, 2006 steht an erster, 1998 an zweiter Stelle.
Wenn man sich die wärmsten Jahre im CRUTem3-Datenbestand ansieht, gewinnt man den Eindruck, dass jedes Hochtemperatur-Jahr das vorhergehende an Intensität übertrifft. Doch die Stationen aus dem Niedrig-Bevölkerungsdichte-Gebiet zeigen das Umgekehrte: die Intensität der wärmsten Jahre nimmt tatsächlich ab im Verlauf der Zeit.
Zur besseren Vorstellung, wie der errechnete Erwärmungstrend von der Bevölkerungsdichte in allen 4 Klassen abhängt, zeigt die folgende Grafik – wie ich schon früher über den räumlichen Wärmeinsel-Effekt berichtet habe –, dass der Erwärmungstrend nichtlinear mit der Abnahme der Bevölkerungsdichte einhergeht. Tatsächlich würde die Extrapolation dieser Ergebnisse auf Null-Bevölkerungsdichte-Wachstum kaum Erwärmung zeigen:
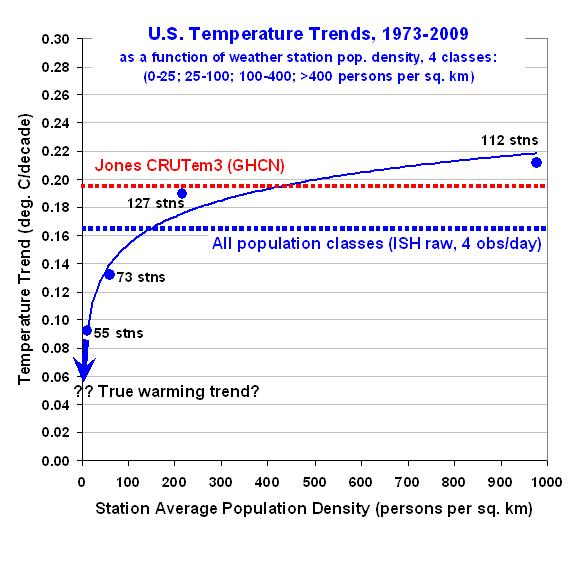
Das ist ein sehr signifikantes Ergebnis. Es deutet die Möglichkeit an, dass überhaupt keine Erwärmung in den Vereinigten Staaten seit den 1970er Jahren stattfand.
Man beachte auch, dass sich in der höchsten Bevölkerungsdichte-Klasse eine leicht erhöhte Erwärmung zeigt im Vergleich zu den CRUTem3-Daten. Das stützt das Vertrauen, dass die hier gezeigten Effekte real existieren.
Zum Schluss zeigt die nächste Grafik den Unterschied zwischen der niedrigsten Bevölkerungsdichte-Klasse im Vergleich zur ersten Grafik oben. Hier gewinnt man eine bessere Vorstellung davon, welche Jahre zur großen Differenz bei den Erwärmungstrends beigetragen haben.
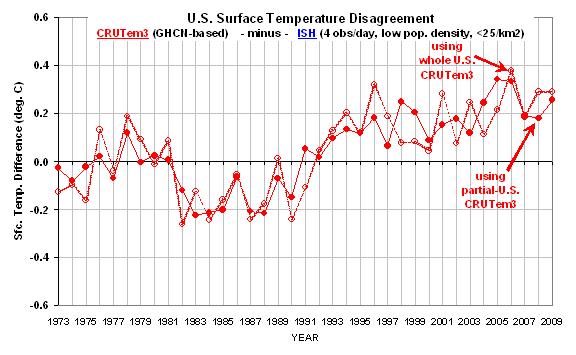
In der Zusammenschau glaube ich, dass diese Ergebnisse einen starken und direkten Beleg für die substanzielle Fehlerhaftigkeit der Erwärmungskomponente in den GHCN-Daten darstellen, zumindest für die hier angesprochene Periode (seit 1973) und Region (U.S.).
Wir brauchen wirklich neue und unabhängige Analysen der globalen Temperatur-Daten… der Rohdaten. Wie ich schon früher gesagt habe, brauchen wir unabhängige Gruppen zur unabhängigen Analyse der Globaltemperaturen – keine internationalen Gremien von Nobelpreisträgern, die Meinungen auf steinernen Gebotstafeln herunterreichen.
Aber wie immer wird diese Untersuchung präsentiert, um die Gedanken und die Diskussion anzuregen. Sie ist kein peer-reviewed Papier.
CAVEAT EMPTOR.
Roy Spencer (Original hier)
Die Übersetzung besorgte dankenswerterweise Hellmut Jäger für EIKE
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Lieber Herr NB,
vielen Dank für Ihre Antwort. Ich hatte mir schon gedacht, gass gerade Sie ordentlich auf meine Fragen usw. antworten können. Ihre Antworten haben mich beruhigt und wieder einmal gezeigt, dass man einen Fehler begeht, wenn man die Fachwelt (welche auch immer) unterschätzt. Wie sollte es auch anders sein, Gott sei Dank!
Bernd Hartmann
Lieber Herr Hartmann,
Zu 1*: In Mitteleuropa bekommen Sie typischerweise folgende Abweichungen in den Temperaturmitteln durch verschiedene Mittelungen gegenüber einer kontinuierlichen Ablesung und dem Zeitintegral darüber:
Monatsmittel Mittlere Abweichung Standardabweichung
24 Werte zur vollen Stunde: -0,002 °C 0,007 °C
Mannheimer Stunden
(7h+14h+2*21h)/4: -0.02 °C 0,13 °C
(Max+Min)/2: +0.2 °C 0,23 °C
Tagesmittel Mittlere Abweichung Standardabweichung
24 Werte zur vollen Stunde: -0,002 °C 0,06 °C
Mannheimer Stunden
(7h+14h+2*21h)/4: -0.02 °C 0,6 °C
(Max+Min)/2: +0.2 °C 0,7 °C
Sie sehen, dass die Max-Min-Methode zu nicht mehr vernachläsigbaren Abweichungen in Monats- (und Jahres)mitteln führt (im einzelnen Tagesmittel sogar bis 3°C Abweichung), was man durch Homogenisierung korrigieren muss. Auch der Übergang von Mannheimer Stunden zu 24-Std bewirkt eine in klimatologischen Reihen im Homogenitätstest auffallende Abweichung (im einzelnen Tagesmittel sogar bis 2°C Abweichung). Wie in den wissenschaftlichen papern nachlesen kann, werden die verschiedenen Tagesmittelmethoden soweit möglich durch Korrekturen berücksichtigt. 24-Std Werte liefern Tagesmittel, die von der kontinuierlichen Ablesung nicht zu unterscheiden sind, im Extremfall 0.2 °C im einzelnen Tagesmittel.
Lieber Herr Hoffmann,
das von Ihnen geschilderte Polygon-Verfahren wurde in der Klimatologie auch zur Berechnung von Flächenmitteln verwendet. Der DWD macht dies seit Jahren jedoch nicht mehr, sondern benutzt ein Rasterverfahren. Die Verfahren zur Berechnung der hier diskutierten und kritisierten globalen und regionalen Temperaturanomalien können Sie bei CRU bzw. GISS nachlesen.
Zur Fehlerbestrachtung:
zu *1: Die Fehlerintervalle für verschiedenen Mittelwerte (Jahr, Monat, Tag, und diese noch flächig gemittelt), die durch unterschiedliche Methoden zur Berechnung des Tagesmittels entstehen, können Sie selber ausprobieren, indem Sie das anhand von Zeitreihen (es gibt genug online Wetterdaten im Netz) durchrechnen.
Zu *2): Da man Anomalien berechnet, spielt der Höheneffekt nicht die große Rolle, aber bei den Klimakarten wird dies entsprechend wie in der Fläche durch Regressionen interpoliert. Das klappt ausgezeichnet. Könne Sie ebenfalls selber ausprobieren.
*2 & 3)Wie gesagt, das Polygonverfahren wird nicht generell verwendet, daher gibt es dieses Repräsentanz- bzw. Gewichtuungproblem in der beschriebenen Form nicht allgemein. Dafür gibt es andere, wie z.B. bei Hansen/Lebedeff 1987/GISS beschrieben. Auch dies könne Sie ausprobieren, die Stationsdaten sind bei GISS verfügbar.
„Bei näherer Betrachtung kann man sehen, dass die Bestimmung von Mittelwerten geschweige denn auch noch globaler, objektiv gesehen, ein gar nicht so triviales „Ding“ ist.„
Wenn Sie sauber arbeiten und die Fehler quantifizieren, ist das Problem machbar und vergleichsweise trivial.
„Ich habe das Gefühl, dass in der Wissenschaft über die Art und Weise der Bestimmung, über den Sinn und Unsinn der Bestimmung solcher Werte bei weitem noch nicht das letzte Wort gesprochen wurde, oder?“
Das es Sinn macht, ist keine Frage, schließlich haben Atlanten Ihren Sinn. Dass das letzte Wort nicht gesprochen ist, gilt für jede wissenschaftliche Arbeit. Fest steht auch, dass es „die“ Lösung nicht gibt, denn man hat nun mal kein kontinuierliches Feld gemessen. Vielmehr muss man ein Verfahren verwenden, das einen Fehler gegenüber der theoretischen Lösung (das Flächenintegral über die kontinuierliche Feldgröße) aufweist, die klein gegenüber anderen Fehlern sind (insb. den Mess- oder Repräsentationsfehlern der Punktdaten). Denn Fehler durch die Berechnungsmethode lassen sich einfacher reduzieren als Fehler, die in den Messdaten stecken.
Ja, wenn ich mir das alles so auf der Zunge zergehen lasse, was so diskutiert wird über die Ermittlung von mittleren und globalen Temperaturen, dann beschleichen mich auch angesichts der Geschehnisse und „Offenbarungen“ der letzten Monate wie jeden normalen halbwegs interessierten Bürger allmählich auch Zweifel an der Richtigkeit der Mittelwertbestimmung. Allein deshalb schon, dass es zum Thema Ansatzpunkte gibt, die diskussionswürdig sind. Aber nicht nur das – wenn ich lese, dass bei die Temperaturbestimmung bzw. Interpolation „kästchenweise“ vorgegangen wird, kann ich das höchstens so verstehen, dass die benutzte entsprechende Software das so ausgibt. Bleibt man aber an diesen „Kästchen“ kleben, so zeugt das m. E. von „Softwareblindheit“ und dem Unvermögen der Beherrschung des Handwerks. Software anzuwenden ist nur dem „erlaubt“, der auch das „Handwerk“ beherrscht. Ich befürchte, dass letzteres oft der Fall ist. Hoffentlich irre ich mich da!
Fiele ich gerade vom Himmel und erhielte die Aufgabe eine Aufgabenstellung für die Entwicklung einer Software für die letztendliche Bestimmung der konkreten globalen Temperatur zu formulieren, so würde ich folgendes Grundschema bzw. Algorithmus vorgeben:
1. Ausgangssituation/Grundlagen
– unregelmäßiges Messnetz, d. h. unregelmäßige Verteilung (bzw. inhomogene Dichte) von Messpunkten in der Fläche
– Anzahl und Zeitpunkt der Messungen für jeden Messpunkt sind gleich
– Datenbank mit:
folgende konstante Daten für jeden Punkt:
Koordinaten jedes Messpunkts (Flächenkoordinate – x, y; absolute Höhe des Messpunktes bzw. der Ausführung der Messung -z);Zeitpunkt der Messung – absolute Uhrzeit, Datum
Variable bzw. zu messende Parameter:
Temperatur, Luftdruck, Feuchtigkeit usw. (bin kein Meteorolge)
2. Auswertung
Phase 1 – Berechnung der messpunktbezogenen Tagesmittelwerte, daraus Mittelwertberechnung(*1) für gewünschte Zeitintervalle (z. B. Monat, Quartal, Halbjahr, Jahr, Jahrzehnte usw.)
*1)darauf komme ich noch zu sprechen
Phase 2 –
Da ein unregelmäiges Netz vorliegt, muss die „Einflussfläche“ für jeden Messpunkt individuell bestimmt werden (*2). Diese Flächen können nur in höchst seltenen Fällen 4-Ecke („Kästchen“) sein. Bei diesen Flächen handelt es sich um Vielecke, bei denen die Anzahl ihrer Ecken von der Anzahl der zum Messpunkt am nächsten gelegenen Nachbarmesspunkte vorgegeben ist.
Bestimmung der Größe der „Einflussfläche“ (z. B. neues Feld in der o. g. Datenbank, dessen Wert so lange konstant bleibt, wie sich die Lage und Anzahl der sich in der Messpunktumgebung befindenden Nachbarmesspunkte nicht ändert);
Berechnung des globalen Wertes der Temperatur über ein bestimmtes Zeitintervall als über die Größe der „Einflussflächen“ aller Messpunkte gewichteten Mittelwertes (*3)
3. Produkte/Ausgabe der Software
Hauptprodukt – globaler Mittelwert der globalen Temperatur und der anderen Messwerte für einen gewünschten Zeitabschnitt
weiter Produkte – globale Isoliniendarstellungen für alle Messparameter über einen bestimmten Zeitabschnitt
Verarbeitung der Daten aus der Datenbank nach allen „Regeln der Kunst“ d. h. hinsichtlich mathematischer Statistik (deskriptive und fortgeschrittene Methoden)
So ungefähr müsste nach meiner Auffassung das Grundgerüst einer Bestimmung der globalen Temperaturwerte für ein bestimmtes Zeitintervall. Dass das prinzipielle Herangehen so sein müsste, darüber bin ich mir ziemlich sicher. Vielleicht habe ich hier das Fahrrad auch neu erfunden…?
*) mögliche Fehlerquellen:
zu *1 – da die Änderung der Wetterdaten im Tagesverlauf nicht linear ist, kann die Bildung von arithmetischen Mittelwerten über den Tag, ganz streng gesehen, zu nicht ganz genauen Ergebnissen führen. In wie weit was, wie gehandhabt wird bzw. ob der dabei entstehende Fehler vernachlässigbar ist oder nicht, kann ich als Meteorologielaie natürlich nicht beurteilen.
*2)Wo zieht man die Grenze des Einflusses beispielsweise zwischen zwei benachbarten Punkten die einmal auf der Zugspitze und zum anderen in der Nähe von München liegen? Ich könnte mir vorstellen, dass hier eine Quelle für subjektive Fehler lägen. Inwieweit wird bei einer Mittelwertberechnung für eine Fläche der höhenabhängige Temperaturgradient berücksichtigt? Inwieweit kann das überhaupt „automatisiert“ werden. Wenn ja, dann müsste für die rechnergestützte Auswertung ein digitales Höhenmodell zu Grunde liegen oder?
Für Messpunkte im Bereich der Verbreitung der Meere wäre die wahrscheinlich nicht das Problem, ungeachtet dessen, dass hier Lage der messpunkt wahrscheinlich nicht konstant ist. Aber hier gibt es sicher auch noch ein anderes Problem – wie wird die Verteilung und Menge der Messpunkte in Abhängigkeit ihrer Lage zu Meeresströmungen unterschiedliche Wärme berücksichtigt usw.?
Diese Fragen kann ich mir natürlich nicht selbst beantworten! Auch kann ich die Wichtung meiner Fragen nicht beurteilen.
*3) Wäre es statthaft für die Wichtung der Temperaturwerte die Größe von für die Messpunkte repräsentativen Flächensegmenten zu verwenden. Die Verewendung von Raumsegmenten mit definierter Höhe (eigentlich mit sphärischen Grund- und Oberflächen sowie trapezähnlichen Seitenflächen mit gekrümmten Grundlinien) würde wahrscheinlich zu genaueren Ergebnissen führen. Auch hier kann ich nicht beurteilen, in wie weit das vernachlässigbar ist usw.
Bei näherer Betrachtung kann man sehen, dass die Bestimmung von Mittelwerten geschweige denn auch noch globaler, objektiv gesehen, ein gar nicht so triviales „Ding“ ist. Ich habe das Gefühl, dass in der Wissenschaft über die Art und Weise der Bestimmung, über den Sinn und Unsinn der Bestimmung solcher Werte bei weitem noch nicht das letzte Wort gesprochen wurde, oder?
Also, könnte mir jemand helfen, meine hier geschilderten Befürchtungen zu zerstreuen und ernsthaft und kompetent die von mir aufgeworfenen Fragen zu beantworten? Ich würde mir in diesem Zusammenhang auch wirklich gefallen lassen, dass mir jemand glaubhaft klarmachte, dass ich überhaupt spinne.
Mit freundlichem Gruß an alle
B. Hartmann
Lieber Herr Jahn #5,
ihre Anmerkung gilt ja auch für die Kurve mit der das IPCC das radiative Forcing von CO2 anfittet.
RF = 5.35 * Log( x/280).
Mit freundlichen Grüßen
Günter Heß
#4: P Gosselin sagt am Dienstag, 23.03.2010, 21:18:
„http://www.youtube.com/watch?v=mV-j4cB8qmg“
Naja, genau genommen sagt P. Gosslin ja nicht, aber im Link gehts wieder mal um die aufgewärmte Geschichte mit mit der falschen/gefälschten/whatever Latif-Aussage über 30 Jahre Abkühlung. bei jemandem, der so aktiv in der Blog-Scene ist, wie P.Gosselin kann man da kaum noch Unwissenheit unterstellen, das grenzt schon an böse Absicht. Egal, die Diskussion gabs hier schon mehrmals, auch bei Accuweather gibts einen Thread dazu: http://preview.tinyurl.com/ygzjx9s
Dort gibts auch nochmal einen Link darauf, was Latif wirklich gesagt hat und um was es in seiner Arbeit wirklich geht – im Gegensatz zu dem, was im Video behauptet wird: http://preview.tinyurl.com/yhsjfg8
Die logarithmische Interpolation des Temperaturtrends als Funktion der Bevölkerungsdichte ist etwas fragwürdig. Für eine Bevölkerungsdichte gegen 0 konvergiert der Trend gegen minus unendlich (!), siehe zweite Grafik.
http://www.youtube.com/watch?v=mV-j4cB8qmg
Wie ich es mir gedacht hatte. Die Jahresmittel für die USA schwanken von Jahr zu Jahr so stark (wie man sieht), dass der lineare Trend ein nicht zu vernachlässigbares Fehlerintervall hat. Ich habe mir die Mühe gemacht, die CRUtem3-Daten ähnlich wie Spencer für die USA-Fläche zu extrahieren. Ich bekomme auch in etwa die rot mit offenen Punkten markierte Zeitreihe in Spencer’s erster Abb. hin, aber da ich nicht weiß, welche 31 gridboxes Spencer genommen hat, habe ich alle 36 im Intervall 30° bis 50°N und 120°W bis 75°W genommen. Dann ergibt sich als Trend von 01/1973 bis 12/2009 wie bei Spencer +0.2 °C/Dekade. Da die Daten ziemlich zappeln, umfasst das Fehlerintervall des Trends +0.09 °C/Dekade und 0.32°C/Dekade (90%-Kondidenzintervall). Es macht also wenig Sinn, den linearen Trend der USA von 1973 bis 2009 genauer als +/- 0.1°C/Dekade anzugeben. Den von Spencer gefundenen Zusammenhang zwischen Trend mit der Bevölkerungdichte halte ich für echt, aber schwer zu quantifizieren.
Denn andererseits ist es auch klar (und dies wird von GISS/CRU auch betont), dass regionale Trends eben nicht besonders signifikant genau angegeben werden können und Spencers Untersuchung bestätigt das nur wieder mal.
Spencers Fehler ist nun, dass er die Fehlerintervalle nicht konsequent angibt. Denn diese müssten auch in Abb. 2 übertragen werden. Dort suggeriert er, dass die Trends in Abhängigkeit von der Bevölkerungsdichte einen kurvigen (logarithmisch-ähnlichen) Verlauf implizieren.
Dies ist jedoch eine Irreführung. Denn wenn man die Fehlerintervalle des Trend einträgt, so überlappen die sich für verschiedene Bevölkerungsdichten, sodass auch der konstante Verlauf (also keine Abhängigkeit) NICHT ausgeschlossen werden kann! Die Extrapolation zu Trend= Null ist unter Berücksichtigung dieses Hinweises schon ein starkeres Stück, und eigentlich weiß Spencer selbst, dass es falsch ist (siehe Satellitendaten)..
Die Spencer-Beitrag ist wirklich gut. Mich würde nun noch interessieren, ob der Trend von +0.1°C/Dekade (Spencers ISH der geringsten Bevölkerungsklasse) signifikant verschieden von den +0.2°C/Dekade vom CRU sind. Also, wie genau kann man für die USA alleine überhaupt den Trend angeben?
Lieber Herr reinhard, (#1)
„Hier mal die neueste Bildmeldung!“
Wo?
„Soviel zur Klimaerwärmung! Wenn denen keine Paroli geboten wird lachen die sich nur schlapp über uns!“
Wer sind „die“?
Ich lache mich gerne übers Paroli schlapp. Was soll also an den WMO-Aussagen falsch sein?
Hier mal die neueste Bildmeldung! Soviel zur Klimaerwärmung! Wenn denen keine Paroli geboten wird lachen die sich nur schlapp über uns!
2009 war nach Angaben der UN-Wetterbehörde das fünftwärmste seit Beginn der Aufzeichnungen 1850. Die Auswertung der letzten beiden Monate des vergangenen Jahres habe eine entsprechende Prognose vom Dezember bestätigt, erklärte die Weltorganisation für Meteorologie (WMO) am Dienstag in Genf. Die Landtemperaturen hätten 2009 um 0,34 bis 0,56 Grad über dem Durchschnitt der Jahre 1961 bis 1990 gelegen, der als Vergleichswert genommen wird. Außerdem sei das Jahrzehnt von 2000 bis 2009 das wärmste seit Beginn der Aufzeichnungen gewesen.