[Originaltitel: „As Above, So Below“]
Ich habe den besten Wissenschaftsjob der Welt. Ich kann forschen, was ich will, wann ich will, so lange ich will, und ich bekomme keinen Cent, egal wie hart ich arbeite. Was kann man daran nicht mögen?
Auf jeden Fall habe ich mir überlegt, wie viele Temperaturstationen wir brauchen, um eine genaue Vorstellung von der Durchschnittstemperatur der Erde zu bekommen. Da ich eher ein Datenmensch, denn ein Theoretiker bin, dachte ich mir, dass ich den CERES-Datensatz verwenden könnte, um einen ersten Versuch zu wagen, diese Frage zu beantworten.
Vorab möchte ich den Temperaturdatensatz erläutern, den ich für meine Analysen verwende. Die CERES-Strahlungsdatensätze enthalten keinen Temperaturdatensatz. Sie enthalten jedoch einen Datensatz für die aufsteigende langwellige (thermische) Strahlung an der Oberfläche. Da viele meiner Analysen den CERES-Datensatz verwenden, habe ich den CERES-Datensatz für die Oberflächenstrahlung benutzt, um einen Datensatz für die Temperatur zu erstellen. Für die Berechnung habe ich die Stefan-Boltzmann-Gleichung verwendet und den gerasterten Oberflächen-Emissionsgrad von hier genutzt.
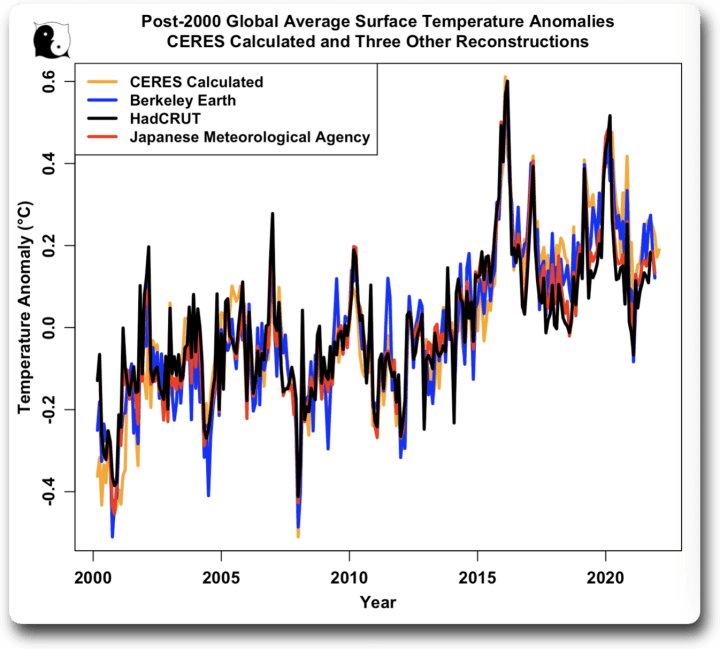
Wie gut ist der mit CERES berechnete Temperaturdatensatz? Hier ist ein Vergleich mit den Datensätzen von Berkeley Earth, HadCRUT und der Japanischen Meteorologischen Agentur. Saisonale Schwankungen wurden aus allen Datensätzen entfernt:
Wie man sieht, stimmt die berechnete CERES-Temperatur mit den anderen drei Daten überein, und sie stimmen auch untereinander überein. Es stellt sich heraus, dass sie auch besser mit dem Berkeley Earth-Datensatz übereinstimmt als der HadCRUT- oder der JMA-Datensatz… daher verwende ich die CERES-Daten in dieser und meinen anderen Analysen. Wie aus dem obigen Diagramm hervorgeht, macht es jedoch keinen praktischen Unterschied, welcher Datensatz verwendet wird. Wenn man die folgende Analyse mit dem Berkeley-Earth-Temperaturdatensatz durchführt, erhält man im Wesentlichen die gleichen Ergebnisse wie mit dem CERES-Datensatz.
Nach diesem Prolog bestand mein Plan darin, zufällig eine Teilmenge der 64 800 Gitterzellen mit 1° Breitengrad und 1° Längengrad auszuwählen, aus denen die Erdoberfläche besteht, und zu sehen, was diese Teilmenge als Durchschnittstemperatur ergab.
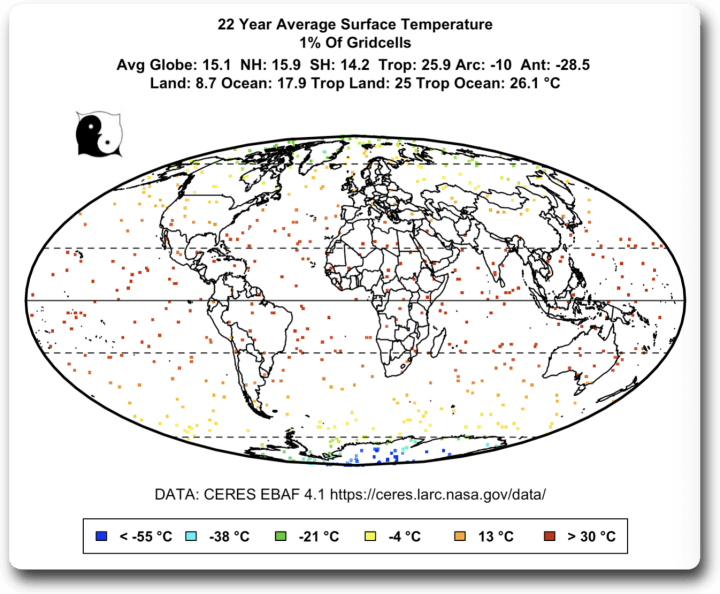
Die interessantesten Ergebnisse ergaben sich, wenn ich nur ein Prozent der Gitterzellen (n = 648) verwendete. Hier ist ein Beispiel für eine zufällige Auswahl von 1 % der Gitterzellen:
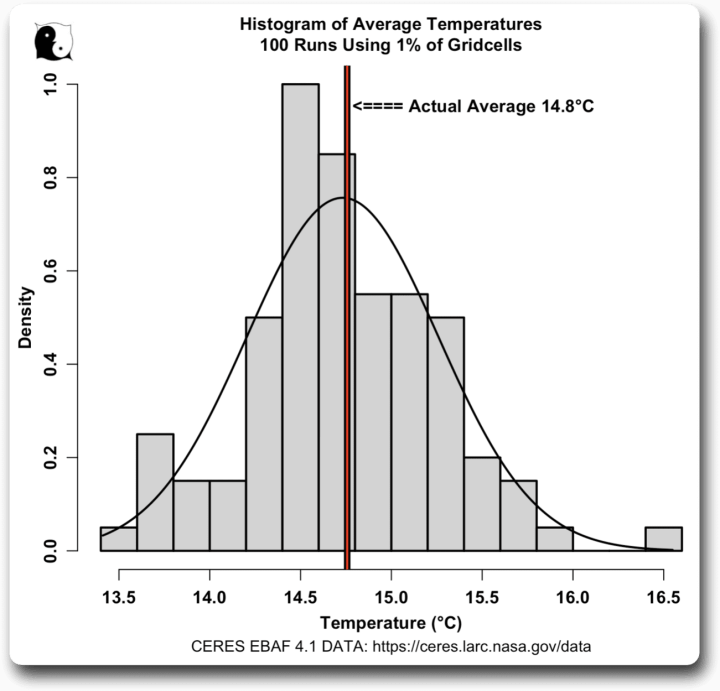
Wie man sich vorstellen kann, ergaben sich bei mehrmaliger Ausführung des Zufallsbeispiels sehr unterschiedliche Durchschnittstemperaturen aus verschiedenen zufälligen Teilmengen von 1 % der Gitterzellen. Hier ist ein Histogramm der Durchschnittstemperaturen eines typischen Laufs von 100 Versuchen mit nur 1 % der Gitterzellen:
Die Durchschnittstemperaturen liegen zwischen 13,5 und 16,5 Grad, so dass es kaum Übereinstimmungen zwischen den Teilmengen gibt. Keine Überraschung, wie ich sagte.
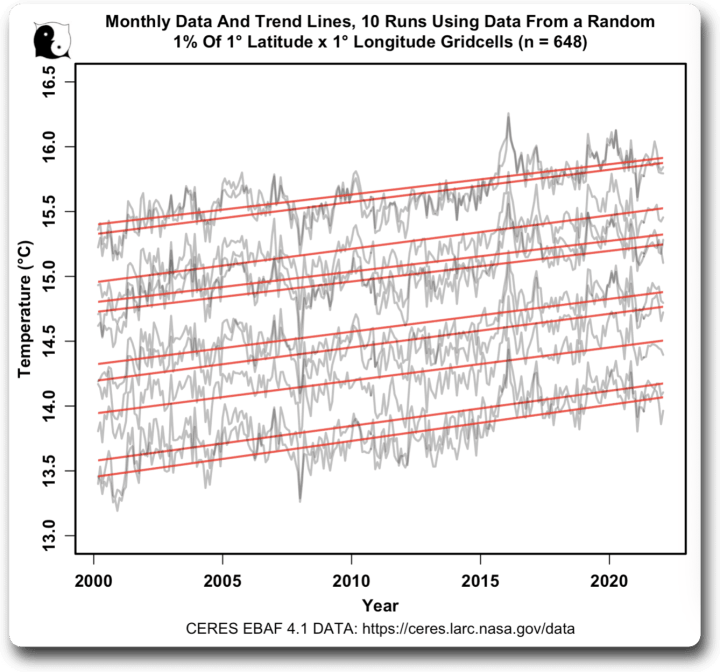
Aber meine nächste Grafik war eine Überraschung. Ich beschloss, die monatlichen Daten für einige der einzelnen Läufe aufzuzeichnen. Hier ist ein Beispiel von zehn Läufen, einschließlich der linearen Trendlinien. Ich habe die saisonalen Schwankungen aus den einzelnen Datensätzen entfernt:
Zwei Dinge waren dabei überraschend. Zum einen waren die Trends alle ziemlich identisch. Ich hatte viel größere Unterschiede erwartet, wenn man nur 1 % der Daten verwendet.
Die andere war, dass die tatsächlichen monatlichen Ergebnisse alle so ähnlich waren, mit der gleichen Gesamtform, nur mit einer anderen Durchschnittstemperatur.
Um das weiter zu untersuchen, habe ich die Anomalien für jeden der Läufe aufgezeichnet. Ich erstellte die Anomalien, indem ich den Durchschnitt eines jeden Laufs von den Werten des jeweiligen Laufs subtrahierte. Hier sind die Ergebnisse:
Faszinierend. Obwohl wir aus 1 % der Daten nicht viel Klarheit über die absolute globale Durchschnittstemperatur gewinnen können, können wir das gleiche 1 % der Daten verwenden, um eine ziemlich gute Vorstellung vom Gesamttrend und den monatlichen Schwankungen der globalen Durchschnittsdaten zu bekommen. Keiner der einzelnen 1 %-Läufe weicht wesentlich vom globalen Durchschnitt ab, und ihre Trends liegen eng beieinander. Das hatte ich überhaupt nicht erwartet.
Als Nächstes dachte ich über die oft wiederholten Behauptungen nach, dass die Kleine Eiszeit in den Jahren 1600 bis 1700 nur ein Phänomen der nördlichen Hemisphäre war oder dass sie nur auf Aufzeichnungen vom Festland basierte, oder beides. Also warf ich einen Blick auf die Landdaten der nördlichen Hemisphäre, um zu sehen, wie zufällige Teilmengen von Landdaten der nördlichen Hemisphäre mit den globalen Daten übereinstimmen. Da die Landfläche der Nordhemisphäre viel kleiner ist als die der Erde und es sich um Land und nicht um Ozean handelt, sind die Temperaturschwankungen der durchschnittlichen Landtemperatur in der Nordhemisphäre natürlich größer als die Schwankungen des gesamten globalen Durchschnitts. Um einen Vergleich zu ermöglichen, habe ich dies in der folgenden Grafik berücksichtigt:
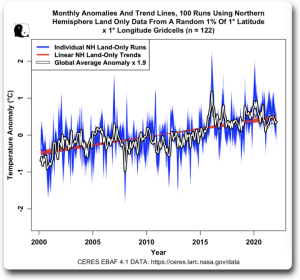
Auch das ist höchst interessant. Mit der Kenntnis der Temperatur in etwa hundertzwanzig zufällig ausgewählten Gitterzellen der insgesamt 64.800 Gitterzellen, wobei sich die bekannten Gitterzellen nur auf dem Land befinden und weniger als ein Viertel eines Prozents der Erdoberfläche abdecken, können wir sowohl die globale Temperaturanomalie als auch den globalen Temperaturtrend genau annähern.
Jeder einzelne Durchlauf mag eine exakte Übereinstimmung mit dem gesamten Globus sein oder auch nicht, aber keiner von ihnen unterscheidet sich wesentlich, und ihre Trends variieren nur geringfügig … was mich an dem Gedanken zweifeln lässt, dass die Kleine Eiszeit ein lokales Phänomen war.
Es scheint eine Bestätigung dessen zu sein, was ich bescheiden „Willis‘ erste Klimaregel“ nenne, die besagt:
„Im Klima hängt alles mit allem zusammen, was wiederum mit allem zusammenhängt … außer wenn das nicht der Fall ist.“
Link: https://wattsupwiththat.com/2023/10/21/as-above-so-below/
Übersetzt von Christian Freuer für das EIKE
Anmerkung der Redaktion:
Bevor nun jemand in Freudentränen darüber ausbricht, wie präzise doch CERES Strahlungsdaten und Thermometwermessungen übereinstimmen, sei etwas Wasser in den Wein der Freude geschüttet.
Erstens: Willis‘ Datensatz beginnt erst im Jahr 2000. Die Hinweise bswp von Pat Fank und M. Limburg aber auch andere beziehen sich auf Daten für Temperaturen und Sensoren des 19./20. Jahrhunderts. Vor dem Satelliteneinsatz.
Zweitens: Die drei Oberflächentemperaturtrends sind keine Rohdaten. Es sind angepasste und damit manipulierte Daten. Niemand weiß, was sie tun, um ihre Rohdaten in endgültige Daten umzuwandeln. Möglicherweise gibt es sogar Anpassungen, die die Rohdaten mit den TOA-Emissionen in Einklang bringen. Wir wissen es nicht.
Außerdem handelt es sich bei CERES auch nicht um reine Daten. Auf dieser Seite, https://ceres.larc.nasa.gov/science/, heißt es zum Beispiel in der Abbildung „CERES-Messungen der planetaren Wärmeaufnahme“ darunter: „Kumulative planetarische Wärmeaufnahme von CERES. Eine einmalige Anpassung an CERES.“ Der globale mittlere Netto-TOA-Fluss für den Zeitraum 07/2005–06/2015 wurde angewendet, um die Konsistenz mit dem In-situ-EEI im gleichen Zeitraum sicherzustellen.“ Eine einmalige Anpassung, um zwei Datensätze in Übereinstimmung zu bringen! Dies bedeutet wahrscheinlich, dass ein Versatz nach oben oder unten angewendet wurde. Woher weiß man, dass sie die richtige Entscheidung getroffen haben?

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"@Werner Schulz am 27. Oktober 2023 um 10:27
Wie soll das CO2 bei höherer Stoffmengenkonzentration mehr strahlen? Bei höherer Konzentration ist die mittl. Höhe ab welcher das CO2 final ins All abstrahlt auch höher und damit der Temperaturunterschied zur Erdoberfläche. Für 1 °C Temperaturabsenkung des CO2 aufgrund der Konzentrationserhöhung, erhöht sich die Bodentemperatur um etwa 0.1 °C.
MODTRAN zeigt bei mir nicht, dass sich die aufintegrierte Wärmeleistungsdichte im CO2 Trichter erhöht.. Im Gegenteil: der Trichter wird breiter. Was geben Sie dort an Daten ein?
Genau aus dem gleichen Grund warum es mehr absorbieren soll. Wie soll eine waermere Atmosphaere mehr Waerme aus der Bodenstrahlung absorbieren? Wollen sie sagen das ist gar nicht so?
Wie wird denn die mittlere Hoehe festgelegt? Spielen da werte wie Dichte, Temperatur, Druck eine Rolle? Wie legen sie den Temperaturunterschied zue Erdoberflaeche fest?
Sie meinen die Temperaturabsenkung erhoeht die Temperatur? Klingt wie ein Perpetuum Mobile. Beim Kuehlschrank muss ich dafuer Arbeit reinstecken. UNd wie wird die Temperatur durch Konzentrationserhoehung abgesenkt? Ist es durch mehr Strahlung, die sie aber gerade verneint haben?
Wann wird der Trichter breiter und was bedeutet das? Wollen sie sagen, das atm. Fenster wird groesser wenn sie die Konzentration erhoehen? Oder wollen sie feststellen, das das Fenster schmaler wird? Erhoeht sich die Temperatur der Atmosphaere, wenn sich die Bodentemperatur erhoeht? Wird die Atmosphaere auf der mittleren Abstrahlhoehe waermer oder kaelter, falls sie einen konstanten Gradienten als Modell annehmen wollen?
Es gibt nicht die „eine Temperatur“ bei der die Atmosphäre ins das All und auf die Erdoberfläche zurückstrahlt. Das wissen Sie auch: da ist der atm. Temp.Gradient dazwischen. „Wollen sie sagen das ist gar nicht so?“
Auch das hatten wir schon: die Höhe, bei der die THGe eine spezielle Wellenlänge final ins All abstrahlen, ist festgelegt durch die Menge an absorbierfähigen THGe-Molekülen von dieser Höhe auf dem Weg bis ins All. Diese Höhe erhöht sich mit höherer Konzentration, da mit höherer Konzentration auch die Menge an absorbierfähigen THGe-Molekülen von dieser Höhe auf dem Weg bis ins All größer wird.
Auch das hatten wir schon, am 1. September 2023 um 21:54 (https://eike-klima-energie.eu/2023/08/16/buchvorstellung-es-existiert-kein-natuerlicher-treibhauseffekt/ ):
Die Erde muss im Mittel den gleichen Leistungsdichte abstrahlen, wie sie absorbiert. Wenn nun weniger Leistung im Spektrum durch das CO2 final ins All abgegeben wird (weil sich von diesem die ERL erhöht und damit die Umgebungstemp. sinkt), muss dies durch das restliche Spektrum ausgeglichen werden.
Da durch die THGe die Oberfläche „am Kuehlen [ge]hinder[t]“ wird, erhöht sich ihre Temperatur, wie am 1. November 2023 um ca 17:30 erklärt (https://eike-klima-energie.eu/2023/10/26/nachts-ist-es-kuehler-als-draussen-oder-warum-macht-die-klimaerhitzung-gruensprech-so-einen-riesenbogen-um-deutschland/ )
Der Bereich im Spektrum, auf denen das CO2 ins All emittiert, wird breiter, wenn ich statt 400ppm 800ppm vorgebe. Die Temperatur der Atmosphäre erhöht sich in Bodennähe und die mittlere Umgebungstemperatur des CO2 fällt.
Gerne beantworte ich auch weiterhin Ihre Fragen, es wäre aber schon schön, wenn sie auch meine Fragen beantworten könnten: Was geben Sie in MODTRAN für Daten ein?
„… was mich an dem Gedanken zweifeln lässt, dass die Kleine Eiszeit ein lokales Phänomen war“
Der Artikel belegt m.E. nur, dass es in den letzten Jahrzehnten keine lokalen Klimaereignisse gab, die durch das gröbere Temperatur-Messraster fallen. Aber Rückschlüsse auf die Kleine Eiszeit, die mindestens 100 Jahre früher endete, und ihre Ausdehnung? Bei damals nur wenigen Temperatur-Messdaten? Die Aussage wäre: Weil es heute keine lokal begrenzten Klimaereignisse gibt, gab es damals auch keine. Gott sei Dank gibt es noch andere Nachweise für die Existenz der Kleinen Eiszeit.
Herr Kowatsch, in der Grafik sehen Sie einen beobachteten Anstieg von etwa 0,4 Grad in 20 Jahren. Gemäss dem CO2-Anstieg um etwa 40 ppm müssten es mit ECS transient gemäß 0,6•0,69•ln(420/380)/ln(2) nur 0,06 Grad sein. Die Beobachtung liefert also das 6,7fache. Wie wollen Sie damit zur CO2-Sensitivität (Sie nannten ja „allerhöchstens homöopathische Dosen“) eine brauchbare Aussage machen?
Peter Dietze schrieb am 24/10/2023, 10:21:13 in 344025
Ist mir ein Kommentar von Herrn Kowatsch entgangen?
Aber ich kann den Kommentar gut verstehen. In den Artikeln von Herrn Kowatsch fehlt ja immer, welche Erwärmung eigentlich zu erwarten wären, wenn man die Aussagen des IPCC zugrunde legt. Und wenn man aus dem kurzen Zeitraum auf die Sensitivität schlussfolgern könnte, dann wäre das ja ein Wert um 0.4/(0.69 * ln(420/380)/ln(2)) = 4.01, also sogar eher im hohen Sensitivitätsbereich. Man sähe also genau das Gegenteil dessen, was Herr Kowatsch schreibt …
@M.Müller, Sie schreiben: „…In den Artikeln von Herrn Kowatsch fehlt ja immer, welche Erwärmung eigentlich zu erwarten wäre, wenn man die Aussagen des IPCC zugrunde legt…“ Antwort: Das tun Sie selbst auch nicht. Sie haben noch niemals geantwortet auf meine Frage, von welcher CO2-Sensitivität Sie ausgehen.
Lieber Herr Müller. Schauen Sie sich den mainstream in Deutschland an. Jeder warme Sommer, jeder Starkregen, jede Überschwemmung wird als ein Beweis der menschengemachten CO2-Klimaerwärmung genommen. Wir wehren wir uns gegen die Panikmache und Verteuflung des Kohlendioxids. Die Grafiken des DWD geben das nicht her, da ist überhaupt keine CO2-Erwärmung für uns erkennbar. Falls Sie eine erkennen sollten, dann äußern Sie sich bei unserem Artikel. Falls Sie keine oder kaum eine CO2-Erwärmung erkennen, dann tun Sie dies bitte genauso kundt.
Es wäre schön, wenn Sie gemeinsam mit uns diese Panikmache einer Erdüberhitzung a la Grüne und letzte Generation aufgrund der CO2-Zunahme bekämpfen würden. Herr Dietze äußert sich deutlichst. Das tun Sie leider nicht.
Es ist immer wieder erstaunlich wie über die „Temperatursensitivität“ des CO2 gestritten wird obgleich es keine physikalisch plausible Begründung für eine Klimaerwärmung durch ir-anregbare Spurengase gibt – im Gegenteil. Das erinnert mich an den Theologenstreit über das Wesen Gottes ohne dass die Grundsatzfrage,nämlich die Existenz Gottes, überhaupt gestellt wird. Die Klimakirche hat eine Klimaerwärmung durch CO2 postuliert und die Theologen (heissen hier „Klimatologen“) streiten jetzt darüber wie hoch diese ausfällt…. 🤦♂️
Wenn man einen globalen Temperatur-Mittelwert bildet, muss man doch, egal wie falsch und unsinnig das ist, mindestens angeben können, welchen Ansatz und welche Rechenschritte das beinhaltet.
Was da gemacht wird und womit Großrechner gefüttert werden, muss man doch irgendwie verständlich beschreiben können. Wer z. B. in Potsdam kann es?
Für BEST findet man die Beschreibung der Methode z. B. in http://dx.doi.org/10.4172/gigs.1000103 und https://doi.org/10.5194/essd-12-3469-2020.
Peter Puschner, Prof. Dr.-Ing. schrieb am 23/10/2023, 21:05:10 in 343979
Ein wenig Literaturrechserche würde Antworten auf diese Fragen liefern.
Diese Frage müßte man auch beantworten können, wenn man – statt Literaturrecherche zu betreiben – nur Eike liest. Man wählt sich einen Referenzzeitraum, mittelt die Temperatur einer Station für diesen Zeitraum und zieht diesen Wert von allen gemessenen Temperaturen ab. Dann hat man die Anomalie – die Abweichung vom Referenzzeitraum – für diese Station. Damit rechnet man dann weiter …
#Marvin Müller am 24. Oktober 2023 um 12:42
Und wenn man 2 oder 3 unterschiedliche Referenzzeiträume bildet, die zu 2 oder 3 unterschiedlichen Ergebnissen führen, kann man sich den darüber gebildeten „Anomaliewert“ passend zum Narrativ aussuchen.
Hervorragend, das ist mal echte Wissenschaft!!!
Bin gespannt auf die Literaturstelle, die die zusätzliche Adjustierung liefert. Wie man da als Referenz mit einer einzigen Messstelle hinkommen will, obwohl der Rest „global“ gedacht wird, bleibt ein Rätsel. Aber vielleicht hilft da auch statt einer Antwort ebenfalls ein Hinweis auf Literatur-Recherchen. Jedenfalls muss die Antwort so kompliziert sein, dass man auf Literatur-Recherchen verweisen muss, da man sie selbst nicht geben kann oder will.
Peter Puschner, Prof. Dr.-Ing. schrieb am 24.10.2023, 19:57:24 in 344086
Ja, verschiedene Referenzperioden können zu Verwirrung führen, wenn man die Zusammenhänge nicht kennt. Allerdings müssen Sie schon genau hinsehen, wer mit der Auswahl geeigneter Referenzperioden spielt. Die Anomaliewerte sind geringer, je näher die Referenzperiode an der Gegenwart liegt …
Das wird bei jeder Station gemacht – die Referenz für die einzelne Station ist der Mittelwert dieser Station für den Referenzzeitraum. Dann mit den Anomalien der einzelnen Stationen weitergerechnet. Habe ich nicht deutlich genug hingeschrieben.
Musste man früher nicht Literatur lesen, wenn man eine Dr. oder gar Professor-Titel bekommen wollte? Verlernt man das mit der Zeit und glaubt dann eher einem Kommentator in einem Blog im Internet?
Warum referenziert man nicht einfach die physikalisch zu erwartende Mitteltemperatur anstatt Rechenwerte mit Rechenwerten zu vergleichen?
Man koennte ja auch alles auf die Wohlfuehltemperatur der Erdoberflaeche beziehen. Wie hoch ist die noch mal? 14 Grad C oder 15 Grad C?
Dann umschifft man das Problem der Referezperiode oder the Willkuerlichkeit der Auswahl.
Mit ein bisschen Normung kann man da was machen, aber will man das?
#mARVIN mÜLLER am 24. Oktober 2023 um 23:29
Mich interessiert nicht die gesamte Literatur von Mann bis Rahmstorf und Schellnhuber, sondern die verdrehte Physik. Egal, was in der Literatur zu Temperaturmittelwertem oder gar globalen Temperaturmittelwerten von wem auch immer geschrieben wird, eine gemittelte Größe kann nicht mehr als Einganggröße bei weiteren Berechnungen mit physikalischen Gesetzen herangezogen werden. Physikalische Gesetze, in denen Globaltemperaturen verwendet werden, können zwar von eitlen Personen mit einer Vielzahl von Adjustierungen neu gebildet werden, sie werden dennoch nie aussagefähig und verwertbar sein.
Und deshalb frönen die 99% der Konsens-Wissenschaftler lediglich einer Religion, aber auf keinen Fall der „Wissenschaft“.
Und nebenbei, Herr Müller, sparen Sie sich Ihre Anzüglichkeiten, bevor Sie sich nicht die Mühe gemacht haben, herauszufinden, was der oder diejenige geleistet hat, denen Ihre Bloßstellungen gelten sollen. So gut und erhaben stehen auch Sie sicher nicht über den Dingen dieser Welt, wie Sie es gern zu formulieren belieben!
Peter Puschner, Prof. Dr.-Ing. schrieb am 25/10/2023, 11:30:39 in 344146
Global gemittelte Werte werden lediglich in einfachen Erklärungen der Prinzipien verwendet. Richtige Wetter- und Klimamodelle arbeiten nicht mit global gemittelten Größen, sondern mit den Größen für die konkrete Zelle entsprechend der Auflösung des Modells (momentan 100km soweit ich weiss).
Herr Müller, sehr gut dass hier mal demonstriert wird dass der minimale CO2-Verdoppelungseffekt ECS wegen vieler deutlich größerer Einflüssene keinesfalls aus lokalen Temperaturverläufen (D hat z.B. nur 0,7 Promille der Erdoberfläche), aus Wetterbeobachtungen abgeleitet werden kann. Es wird Zeit dass ECS (etwa 0,6 Grad am Boden, wie auch all inclusive von MODTRAN strahlungsphysikalisch berechnet, basiert auf höchstpräzisen Labormessungen) zur Kenntnis genommen wird. Insbesondere sollten jene Wissenschaftler ihre Aussagen revidieren, die noch nicht wissen dass CO2 unterhalb von Wolken die Gegenstrahlung kaum erhöhen kann und der Feedbackfaktor 2,7 welcher fälschlich aus Eisbohrkernen abgeleitet wurde (also aus solar-ozeanischer Ausgasung), ein Märchen ist. Fälschlich wird auch angenommen, CO2 habe statt nur etwa 22% sogar 50-100% Anteil an der bisher beobachteten globalen Erwärmung, und „IPCC/2“ (also etwa 1,5 statt 3 Grad) sei doch schon eine beachtliche Verbesserung.
@Dietze, @Müller, finden Sie nicht auch, daß Sie sich hier, gegenseitig befruchtend, nur lächerlich machen ? Sie jonglieren im Brustton der Überzeugung mit wagen Behauptungen mit ECS, 😂, mit „deutlich größeren Einflüssen“, 😂🤣😂, auf „hochpräzisen Labormessungen“, 😂🤣😂🤣😂, (wer legt das fest ? ), Gegenstrahlung und Bohrlöchern……👎🏽 Kurzum, spekulatives Aufblasen mit viel Gedöns….dazwischen ein bißchen Beschimpfung und ein paar Unverschämtheiten, um den eigenen Quatsch aufzuwerten….traurig. Früher rühmte eine fundierte Erkenntnis den verantwortlichen Menschen. Heute rühmt der verantwortliche Mensch seine eigene Erkenntnis u n d desavouiert den Diskussionspartner. Ein ganz mieses Zeugnis.
Peter Dietze schrieb am 25/10/2023, 07:37:29 in 344122
Wie soll das zur Kenntnis genommen werden, wenn das nicht in einer Form veröffentlicht wird, in der es überhaupt diskutiert werden kann? Eine Veröffentlichung in Deutsch in der Zeitschrift Fusion wird doch niemand zur Kenntnis nehmen. Oder haben Sie das auch schon irgendwo anders veröffentlicht?
Herr Müller, da sind Sie auf dem Holzweg. MODTRAN ist ein wiss. anerkanntes Berechnungstool das nicht von mir stammt und wofür ich keinen Artikel in einer Review-Fachzeitschrift veröffentlichen muss. Dokumentation dazu existiert bereits. Ich fordere nur dazu auf, das Ergebnis für ECS (welches u.a. auch von Prof. Harde und mir verifiziert wurde) zu beachten. Weiter habe ich auf mehrere essentielle Fehler von IPCC hingewiesen, die wohl der Grund dafür sind dass dort MODTRAN ignoriert und ein 5fach (!) zu hohes ECS angenommen wird. Herrn Pesch, der meint, man könne doch garnicht über die Grösse des CO2-Effekts diskutieren wenn man (wegen des 2.HS) noch nichtmal geklärt hat ob die (gemessene!) IR-Gegenstrahlung überhaupt eine Erwärmung am Boden bewirkt, können wir aussen vor lassen.
Peter Dietze schrieb am 25/10/2023, 17:44:03 in 344192
Ich habe ja nicht gesagt, dass Sie einen Artikel über Modtran veröffentlichen sollen, sondern über Ihre Anwendung von Modtran zur Ermittlung der Sensitivität. In dem Fusion Artikel stehen einige Behauptungen ohne Belege drin – die müßte man in einer richtigen Veröffentlichung entsprechend untermauern. Und offensichtlich ist nicht bekannt, dass man Modtran dafür benutzen kann, da alle Welt komplizierte Modelle baut. Eine überzeugende Veröffentlichung könnte daran was ändern…
Aber die größte Frage, die bei mir beim Lesen entsteht, ist folgende: Sie ermitteln, dass sich der Boden um 0,6°C erwärmen müßte, um das Ungleichgewicht von 3,28 W/m² am Boden auszugleichen. Allerdings muß doch eigentlich die Abstrahlung im atmosphärischen Fenster um diesen Betrag steigen, da nur dort ein Ausgleich der reduzierten Abstrahlung erreicht werden kann. Sie müßten also eigentlich prüfen, um wieviel die Temperatur am Boden steigen muss, damit in diesem Fenster 3,28W/m² mehr abgegeben werden. Das sehe ich nicht bzw. übersehe es oder mir fehlt eine Erklärung, warum das nicht so sein muss. auch das würde IMHO im rahmen eines Veröffentlichungsversuches geklärt werden.
Herr Müller, die 3,28 W/m² müssen nur zwischen Boden und unterer Atmosphäre (wo eine Hin- und Herstrahlung stattfindet) ausgeglichen werden. Die kommen NICHT durch das Fenster nach oben raus, denn dort bleibt es ja bei 240 W/m². Ihr Argument würde fälschlich zu einem erheblich höheren ECS führen. Die 3,28 W/m², wo mit mehreren Korrekturen der IPCC-Strahlungsantrieb für clear sky und ohne Wasserdampf an TOA auf den Boden herunter gerechnet wurde, hatte ich in einem gesonderten Paper ermittelt, was den Rahmen des FUSION-Artikels https://www.fachinfo.eu/dietze2018.pdf gesprengt hätte.
Sie wissen doch dass eine IPCC ad absurdum führende Veröffentlichung (insbesondere zum real um etwa den Faktor 5 (!!) geringeren CO2-ECS, der Grundlage aller Modellrechnungen) in einem Fachjournal durch Mainstream-Reviewer verhindert und deshalb auch MODTRAN ignoriert wird. CO2 unterhalb von Wolken (IR-Schwarzstrahler) ist ja fast wirkungslos und der Fake-Feedbackfaktor 2,7 liegt real nur bei etwa 1,4. Mein Ergebnis wird nicht nur durch MODTRAN, sondern z.B. auch durch Prof. Harde sowie etliche Fachleute des MIT welche Trump zum Ausstieg von Paris geraten haben, bestätigt. Und auch durch die Berechnung mit dem transienten Temperaturanstieg von 1,1 Grad seit vorindustriell wenn der realistische Anteil von nur 22% für CO2 eingesetzt wird: 1,1•0,22=0,6•0,69•ln(420/380)/ln(2).
Sorry, Tippfehler. Es muss heissen 1,1•0,22=0,6•0,69•ln(420/280)/ln(2)
Peter Dietze schrieb am 27/10/2023, 07:17:03 in 344373
Die 3,7W/m² werden aber als Differenz für TOA bestimmt, sie müssen also dort ausgeglichen werden. Der „CO2-Trichter“, auf den Sie auch immer verweisen, wird ja dort sichtbar und damit gibt es dort die Differenz zwischen ein- und ausgehender Strahlung. Und damit sich dort wieder 240W/m² ergeben, muss mehr durch das atmosphärische Fenster kommen. Falls mir hier etwas entgeht, wäre ich für Hinweise dankbar.
Nein, das ist mir neu. Kann man das irgendwo nachlesen? Evtl. inklusive der Reviews?
#344397
Herr Mueller,
sie sagen:
Es ist falsch anzunehmen, das der Ausgleich nur im Atm. Fenster erreicht werden kann. Es kann auch gut sein, das mehr CO2 mehr strahlt und mehr Strahlung aus der Atmosphaere kommt. Dann kommt der Ausgleich aus der Atmosphaere.
Modtran zeigt auch, das wenn die Tempertur steigt, die Strahlung in und aus der Atmosphaere zunimmt.
Herr Müller, bei jeder CO2-Verdoppelung (mit Albedo, aber ohne Wolken und Wasserdampf) werden bei IPCC 7,4 W/m² von der Bodenabstrahlung mehr absorbiert und 3,7 W/m² zurückgestrahlt. Daher würde der Boden im Strahlungsmodell erstmal um 0,68 Grad wärmer bis oben wieder 240 W/m² herauskommen. Aber durch die Hin- und Herstrahlung tritt der Faktor 1/EPS=391/240 auf, so dass daraus 1,11 Grad werden. Daraus werden dann durch den Fake-Feedbackfaktor 2,7 die 3 Grad des IPCC bei einer Ein- und Abstrahlung am Boden von 16,3 W/m².
Nach meiner Rechnung sind erstmal die 7,4 W/m² um 46% zu hoch (die Absorption ist nicht proportional zur Bodenemission, sondern zur Nettodurchstrahlung). Weiter reduziert sich der CO2-Effekt durch die Wolkenbedeckung, die Wasserdampfüberlappung und Feuchtkonvektion auf 41%. Dann kommt noch der Faktor 1/EPS und wegen Feedback und Schrägstrahlung (längerer Absorptionsweg) noch der Faktor 1,95 dazu. Damit werden aus 3,7 W/m² dann die 3,28 W/m² und mit S-B wird ECS 0,6 statt 3 Grad.
Für Sie ist die von uns Kritikern mehrfach festgestellte Tatsache neu dass in Fachjournalen durch Mainstream-Reviewer entsprechende Veröffentlichungen verhindert werden und in der IPCC-Literatur MODTRAN nicht existiert weil damit CO2 ja zum Scheinproblem wird und es keine Klimakatastrophe gibt. Von IPCC und Politik wird auch das Badewannenmodell mit heute bereits 50% (oder schon 60%) und weiter ansteigendem Senkenfluss ignoriert, weshalb es garkein Restbudget gibt und eine CO2-Halbierung ausreicht wenn man einen weiteren ppm-Anstieg verhindern möchte. Wo wollen Sie das nachlesen – wenn nicht hier bei EIKE?
👏👏👏👏👏, welch unsinniges Vorhaben, das auf multifaktoriellen Unsicherheiten, ungeahnten Wechselwirkungen, ausschließlich bekannten Parametern und jede Menge SPEKULATION beruht. Gut, daß der Autor sein Geld nicht damit verdienen m u ß ….😄👍😎🤝✌️
Ich muss ihnen widersprechen:
mit „multifaktoriellen Unsicherheiten, ungeahnten Wechselwirkungen, ausschließlich bekannten Parametern und jede Menge SPEKULATION“
kann man sehr gut Geld verdienen!
Wie recht Sie doch haben!
All Ihre Frage zeigen manigfaltige Manipulationsmöglichkeiten auf. Sammle ich in den Temperaturauswertungen entsprechend nur die Daten ein, die meine vorgefasste These stützen, dann werde ich meine These am Ende „wissentschaftlich“ stützen können (Hereuka [ich habe gefunden], oder, ich hab es ja schon vorher gewußt). Das ist der Geschäftskern des Geschäfts!
Und genauso arbeitet doch der politische IPCC, zwar nicht wissenschaftlich, aber dumm ist das nicht, oder?
Mein Vorschlag: diskutieren Sie das doch mit Willis bei WUWT.