Wie das so geht bei derartigen Untersuchungen, wurde das Thema unserer Diskussion und Untersuchung bald zu einer größeren und noch interessantesten Frage – welcher der vielen natürlichen Datensätze (Temperatur, Regenmenge, Ausbrüche, Druck usw.) und/oder korrespondierende Klimamodelle sind chaotisch?
Natürlich muss ich mit der offensichtlichen Frage anfangen: was ist mit „chaotisch“ gemeint? Ein chaotisches System ist eines, in dem ähnliche Ausgangsbedingungen exponentiell entweder konvergieren oder divergieren. Ein Beispiel ist die Meeresoberfläche. Falls man zwei versiegelte leere Flaschen von einem Schiff mitten in einem Ozean ins Wasser wirft, je eine auf jeder Seite des Schiffes, werden sie mit der Zeit auseinanderdriften. Dieser Vorgang wird zunächst langsam ablaufen, dann aber schneller und immer schneller, wenn die Flaschen nämlich von verschiedenen Strömungen und Winden in verschiedenen Gebieten erfasst werden.
Ob ein Datesatz chaotisch ist oder nicht, wird allgemein mit Hilfe des Lyapunov-Exponenten [?] festgestellt. Dabei handelt es sich um eine Maßzahl des „Dehnungsfaktors“ [stretching factor]. In unserem Beispiel mit den Ozeanen misst der Dehnungsfaktor, wie schnell sich die beiden Punkte mit der Zeit auseinander bewegen. In einem chaotischen Datensatz nimmt der Dehnungsfaktor allgemein mit der Zeit zu oder ab. In nicht-chaotischen Datensätzen andererseits bleibt der Dehnungsfaktor mit der Zeit konstant. Die folgende Abbildung zeigt die „Lyanupov-Kurven“ der Evolution des Dehnungsfaktors mit der Zeit bei einigen natürlichen und berechneten Datensätzen.

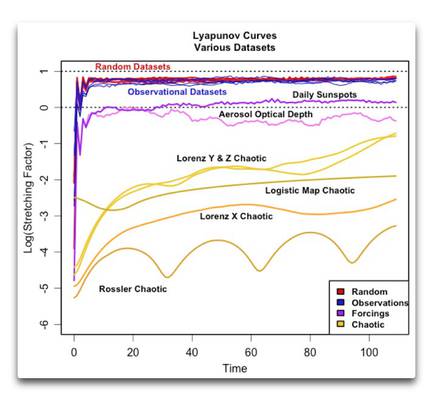
Abbildung 1: Lyanupov-Kurven für einige Datensätze. Alle Datensätze sind vor der Analyse trendbereinigt und standardisiert worden.
Nun habe ich vier Arten von Datensätzen graphisch dargestellt, gekennzeichnet durch die vier Farben. Der erste Typ (rot), meist überdeckt von den blauen Linien, zeigt eine Auswahl von vier verschiedenen Zufalls-Datensätzen – normal, gleichmäßig, eine Poisson-Verteilung [?] und ein hoher Hurst-Exponent, teils Gauss’sche Zufallszahlen. Im Grunde liegen die Lyanupov-Kurven von Datensätzen mit Zufallszahlen ziemlich genau übereinander. Beginnend am Zeitpunkt 0 erreichen sie sehr schnell ihren maximalen Wert und verharren dann dabei. Wie zu erwarten war gibt es in den Zufallsdaten keinen Trend des Dehnungsfaktors mit der Zeit.
[Dieser Abschnitt enthält einige Fachbegriffe, die ich noch nie gehört habe. Um sicherzustellen, dass die Übersetzung korrekt ist, folgt hier das Original: Now, I’ve graphed four types of datasets above, indicated by the four colors. The first type, shown in red and mostly obscured by the blue lines, shows four different varieties of random numbers—normal, uniform, poisson, and high Hurst exponent fractional Gaussian random numbers. Basically the Lyapunov curves of the random number datasets are all plotting right on top of each other. Starting from time = 0, they climb rapidly to their maximum value and then just stay there. As we would expect from random data, there’s no trend in the stretching factor over time.]
Die nächste Gruppe in blau zeigt die Lyanupov-Kurven für ein halbes Dutzend klimabezogener Datensätze, nämlich:
● HadCRUT4 monatliche mittlere Lufttemperatur 1850 bis 2015
● Jährlichen Minimal-Wasserstand im Nil 622 bis 1284 [ Annual Nilometer Minimum River Height]
● Monatliche Gezeiten in Stockholm 1801 bis 2001
● Tägliche Maximum-Temperatur der Aufzeichnung in Central England 1878 bis 2015
● Tägliche mittlere Temperatur in Armagh, Irland, 1865 bis 2001
● Jährliche mittlere Durchflussmenge des Nils in m³ pro Sekunde, 1870 bis 1944
Wie man sieht, sind hinsichtlich der Lyanupov-Analyse alle sechs dieser klimabezogenen Datensätze (blaue Linien) nicht unterscheidbar von den vier Zufallsdatensätzen (rote Linien), welche wiederum untereinander ununterscheidbar sind. Keiner zeigt irgendwelche Spuren chaotischen Verhaltens.
Eine weitere Gruppe von Datensätzen, und zwar jene unten in gelben Farben, unterscheiden sich ziemlich von den Zufalls- und den Beobachtungs-Datensätzen. Bei ihnen handelt es sich um einige chaotische Datensätze. Man beachte, dass sie alle eines gemeinsam haben – wie oben erwähnt, nimmt die Entfernung voneinander (bestimmt nach dem „Dehnungsfaktor“) mit der Zeit zu. Die Rate des Auseinanderdriftens erreicht einfach nicht einen höchsten Punkt und bleibt dort, wie es bei den anderen beiden Datensätzen der Fall war. Die Rate des Auseinanderdriftens in chaotischen Datensätzen nimmt mit der Zeit unverändert weiter zu.
Schließlich sind noch ein paar andere Datensätze in violett gezeigt. Diese zeigen Beobachtungen von Phänomenen, die man gewöhnlich als „Treiber“ [forcings] betrachtet. Eine davon zeigt die Änderungen der Sonnenaktivität mit den täglichen Sonnenflecken als Proxy für die Aktivität von 1880 bis 2005. Die andere ist die jährliche optische Tiefe [Dichte?] von Aerosolen von 800 bis 2000, welche normalerweise eine Funktion vulkanischer Aktivität ist und aus Eisbohrkernen berechnet wurde. Komischerweise liegen diese beiden Datensätze irgendwo zwischen den Zufalls-Beobachtungen oben und den chaotischen Datensätzen unten. Zusätzlich zeigen beide eine signifikante Variation des Dehnungsfaktors mit der Zeit. Die Sonnenflecken zeigen einen leichten, wenngleich signifikanten Anstieg. Die optische Tiefe der Aerosole geht zurück, und es sieht so aus, als würde sie danach wieder steigen. Es scheint also, dass diese beiden Datensätze schwach chaotisch sind.
Diese Ergebnisse waren für mich sehr überraschend. Ich habe lange gedacht, ohne dies nachzuprüfen, dass das Klima chaotisch ist … allerdings zeigt diese Analyse, dass zumindest jene sechs Beobachtungs-Datensätze, die ich oben analysiert habe, nicht im Mindesten chaotisch sind. Aber was weiß ich schon … ich bin von gestern.
Gibt es überhaupt irgendwelche Klima-Datensätze, die chaotisch sind, und sei es auch nur schwach chaotisch? Ich denke schon. Es scheint, dass die Wassertemperatur tropischer Ozeane leicht chaotisch ist … aber dieser Frage werde ich im nächsten Beitrag nachgehen, in dem es um den Gedanken von Dan Hughes geht hinsichtlich der Hurst-Analyse, um zwischen chaotischen und nicht-chaotischen Datensätzen zu unterscheiden.
CODE: To calculate the Lyapunov exponent I’ve used the lyap_k function from the R package tseriesChaos. Here are the functions I used to make Figure 1:

Link: http://wattsupwiththat.com/2015/10/22/is-the-climate-chaotic/
Übersetzt von Chris Frey EIKE
Anmerkungen von Prof. Dr. Horst-Joachim Lüdecke:
Der Aufsatz von Willis Eschenbach verwirrt, denn ihm sind unsere nachfolgend aufgeführten Arbeiten, die alle den Hurst-Exponenten als maßgebende Größe berücksichtigen, eigentlich bekannt, wurden aber weder erwähnt noch berücksichtigt. Zumindest bei einer Blogdiskussion (Judith Curry) über eine dieser Arbeiten war Eschenbach sogar mit dabei, ohne allerdings dabei tiefere Kenntnis über autokorrelierte Zeitreihen an den Tag zu legen, was seinen Aufsatz in WUWT verständlicher macht. Ich hatte in einem E-Mail-Verkehr mit ihm damals versucht, ihm die Grundzüge der DFA-Analyse zu erklären. Ob mit Erfolg, weiß ich nicht. (US-Kollegen haben oft die für mich oft befremdliche Art, wenn sie an einer Information interessiert sind, unglaublich nett und höflich um diese zu bitten und zu kommunizieren. Ist das Thema abgeschlossen oder kann man die Info nicht zufriedenstellend erbringen, wird der Austausch dann kommentarlos und abrupt abgebrochen, kein Dankeschön, nichts).
Der Blog "kalte Sonne" und die ersten beiden der unten aufgeführten Publikationen belegen, dass das Klima sehr wohl maßgebende zyklische Eigenschaften auf Zeitskalen von mehreren 100.000 Jahren (Milankovitch) bis zumindest herunter von 200 Jahren (de Vries / Suess Zyklus) aufweist. Chaotische Eigenschaften hat es überdies. Das Klima ist anscheinend beides, geforscht wird heute, wie sich die Anteile auswirken bzw. wie stark sie sind.

H.-J. Lüdecke, A. Hempelmann, and C.O. Weiss: Paleoclimate forcing by the solar de Vries / Suess cycle, Clim. Past Discuss 11, 279-305, 2015
http://www.clim-past-discuss.net/11/279/2015/cpd-11-279-2015.pdf

H.-J. Lüdecke, A. Hempelmann, and C.O. Weiss: Multi-periodic climate dynamics: spectral analysis of long-term instrumental and proxy temperature records,
Clim. Past. 9, 447-452 (2013), http://www.clim-past.net/9/447/2013/cp-9-447-2013.pdf 

H.-J. Lüdecke, R. Link, F.-K. Ewert: How Natural is the Recent Centennial Warming? An Analysis of 2249 Surface Temperature Records, Int. J. Mod. Phys. C, Vol. 22, No. 10 (2011), http://www.eike-klima-energie.eu/uploads/media/How_natural.pdf
Bei einem Vergleich von natürlichen Zeitreihen mit den Ergebnissen aus Klimamodellen auf der Basis von Hurst Exponenten kann kaum Sinnvolles herauskommen. Für eine Hurst-Analysyse (mindestens 500 Datenpunkte) sind Messdaten erforderlich – Temperaturzeitreihen in aller Regel – aber auch Niederschlagsreihen. Solche Messdaten sind stets zufällig + autokorreliert. Nebenbei: Niederschlagsdaten sind nach bisherigen Untersuchungen nicht autokorreliert, also offenbar rein zufällig, hier.
Die Eigenschaft "zufällig + autokorreliert" weisen aber in aller Regel die Ergebnisse von Klimamodellen nicht auf, weil die Algorithmen in Klimamodellen den Hurst-Exponenten H auf unnatürliche Werte weit über 1 treiben (Natürliche Temperaturzeitreihen liegen um 0,5 < H < 0,9, der Wert H = 1 entspricht schon rotem Rauschen usw. Eine Zeitreihe mit H > 1 entfernt sich mit zunehmender Zeit beliebig weit vom Ausgangswert, ist also chaotisch, offenbar liefert hier auch der Ljyapunov Exponent ein ähnliches Werkzeug wie die Autokorrelationsanalyse DFA).
Jeder Algorithmus erhöht den Hurst-Exponent unnatürlich und verfälscht ihn, und Klimamodelle enthalten nun einmal Algorithmen. Man kann es auch von folgender Seite sehen: Es ist nicht einfach, zufällige Zeitreihen mit einer vorgegebenen Autokorrelation künstlich zu erzeugen. Ich bezweifle stark, dass es Zeitreihen von Klimamodellen gibt, die zufällige Ergebnisse liefern und dabei realistische Autokorrelationswerte (H < 1) aufweisen. Aber man weiß ja nie was den "Modellieren" noch so alles einfällt. Ein Vergleich von Messdaten mit Klimamodellergebnissen, der auf unterschiedliche Autokorrelation (Hurst-Exponenten) abzielt, erscheint mir daher sinnlos. Man vergleicht Äpfel mit Birnen.
Die physikalische Ursache für die Autokorrelation von realen Temperaturzeitreihen ist übrigens unbekannt. Es könnten in den Reihen steckende Zyklen sein, es kann aber auch etwas anderes sein. Um Zyklen zu entdecken oder gar näher zu analysieren ist die Autokorrelationsanalyse (DFA) leider nicht geeignet. Sie ist aber für vieles andere geeignet (s.o. unsere Arbeiten), näheres dazu würde hier zu weit führen.

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken