Oder wie es diese Gelehrten es ausdrücken:

Temperaturänderung (∆T) = Klimasensitivität ( λ ) mal erzwungene Änderung durch Antriebe (∆F).

Oder als Gleichung:

∆T = λ  ∆F.

Das Problem dabei ist Folgendes: Nach dreißig Jahren von Versuchen, die natürliche Welt in diese Zwangsjacke zu stecken, ist es ihnen bis heute nicht gelungen, diese Zahlen festzumachen. Meine Theorie lautet, dass die Ursache hierfür ein theoretisches Missverständnis ist. Der Fehler liegt in der Behauptung, dass Temperaturänderung gleich den Änderungen der Antriebe mal irgendeiner Konstante ist.

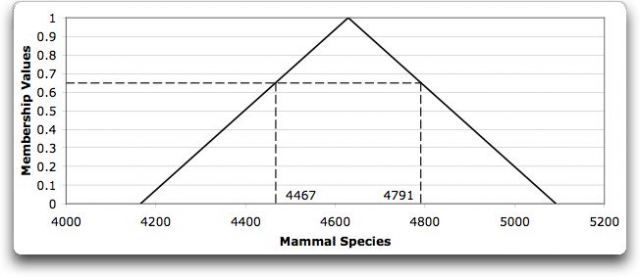
Bild rechts: Die unscharfe Dreieckszahl für die Anzahl der Säugetierarten [4166,  4629, 5092]wird repräsentiert durch die durchgezogene Linie. Die Spitze liegt bei der besten Schätzung, 4629. Die oberen und unteren Begrenzungen der vermuteten Anzahl der Arten variieren mit dem Wert der Zugehörigkeit [membership value]. Für einen Wert der Zugehörigkeit von 0,65 (gepunktete Linien) liegt die untere Grenze bei 4467Arten und die obere Grenze bei 4791Arten (IUCN 2000)

Was sind also unscharfe Dreieckszahlen, und wie können sie uns helfen zu verstehen, warum die Behauptungen des IPCC bedeutungslos sind?

Eine unscharfe Dreieckszahl setzt sich aus drei Schätzungen irgendwie unbekannter Variablen zusammen – die niedrigste, die höchste und die beste Schätzung. Um mit diesen ungewissen Angaben Berechnungen anzustellen, ist es nützlich, „unscharfe Mengen“ zu verwenden. Die traditionelle Mengenlehre enthält die Entscheidung, ob etwas exklusiv Teil der Menge ist oder nicht. Zum Beispiel ist ein Tier entweder lebendig oder tot. Allerdings kann für eine Anzahl von Mengen keine klare Mitgliedschaft bestimmt werden. Zum Beispiel, ist eine Person mit 55 Jahren „alt“?

Während man keine klare ja/nein-Antwort geben kann, können wir unscharfe Mengen nutzen, um die Größenordnungen dieser Art von Werten zu bestimmen. Anstelle von 0 oder 1, die die Mitgliedschaft in traditionellen Mengen festlegen, verwenden unscharfe Mengen eine Zahl zwischen 0 und 1, um eine teilweise Mitgliedschaft in der Menge zu kennzeichnen.

Unscharfe Mengen können auch verwendet werden, um Grenzen um ungewisse Werte zu ziehen. Zusätzlich zu höheren und niedrigeren Werten können diese Grenzen auch beste Schätzungen enthalten. Es ist eine Möglichkeit, Sensitivitätsanalysen durchzuführen, wenn man wenig Informationen über die tatsächlichen Fehlerquellen und die Größe der Fehler hat. Am einfachsten wäre Folgendes: Alles, was wir brauchen, sind Werte, von denen wir es für sehr unwahrscheinlich erachten, größer oder kleiner als * zu sein. Diese niedrigeren und höheren Begrenzungen plus die beste Schätzung bilden eine Dreieckszahl. Eine Dreieckszahl wird geschrieben als (niedrigster vermuteter Wert, beste Schätzung, höchster vermuteter Wert).

*Man vergleiche mit dem Original. Das steht dort wirklich so! Wenn da etwas fehlt, weiß ich nicht, was. A. d. Übers.

Zum Beispiel wird die Anzahl der Säugetierarten durch die Rote Liste der IUCN mit 4629 Arten angegeben. Allerdings ist dieser Wert bekannt dafür, ein Gegenstand geschätzter Fehler zu sein, der normalerweise mit ± 10% angegeben wird.

Diese Bandbreite von Schätzungen der Anzahl der Säugetierarten kann durch eine unscharfe Dreieckszahl repräsentiert werden. Für die Anzahl der Arten lautet diese (4166, 4629, 5092), um die unteren und oberen Grenzen ebenso wie die beste Schätzung in der Mitte zu beschreiben. Die Abbildung oben rechts zeigt die unscharfe Zahl, die die Zählung aller Säugetierarten repräsentiert.

Alle normalen mathematischen Operationen können unter Verwendung von Dreieckszahlen durchgeführt werden. Das Endergebnis der Operation zeigt den wahrscheinlichsten Wert zusammen mit den zu erwartenden maximalen und minimalen Werten. Für die Prozedur von Additionen, Subtraktionen und Multiplikationen werden der niedrigste, der beste und der höchste Wert einfach addiert, subtrahiert oder multipliziert. Nehmen wir zwei unscharfe Zahlen, die Dreieckszahl

T1 = [L1,  B1,  H1]

und die Dreieckszahl

T2 = [L2,  B2,  H2],

wobei „L“, „B“ und „H“ der niedrigste [lowest], der beste und der höchste Wert sind. Die Regeln sind Folgende:

T1 + T2  =  [L1 + L2,  B1 + B2,  H1 + H2]

T1 – T2  =  [L1 – L2,  B1 – B2,  H1 – H2]  (Nicht korrekt ausgeführt, siehe unten. Zu schnell).

T1 * T2  =  [L1 * L2,  B1 * B2,  H1 * H2]

Dieser Teil ist also einfach. Für Subtraktion und Division ist es etwas anders. Der niedrigste mögliche Wert wird die niedrige Schätzung im Zähler und die hohe Schätzung im Nenner sein, und umgekehrt für den höchsten möglichen Wert. Also sieht die Division folgendermaßen aus:

T1 / T2 = [L1 / H2,  B1 / B2,  L2 / H1]

Und für die Subtraktion so:

T1 – T2  =  [L1 – H2,  B1 – B2,  H1 – L2]

Wie können wir nun unscharfe Dreieckszahlen anwenden, um zu sehen, was das IPCC macht?

Nun, die Klimasensitivität (in °C pro W/m²) oben in der magischen Formel des IPCC besteht aus zwei Zahlen – die durch eine Verdoppelung des CO2-Gehaltes erwartete Temperaturänderung und der dadurch erwartete zunehmende Antrieb. Für jede haben wir Schätzungen der wahrscheinlichen Bandbreite der Werte.

Von der ersten Zahl, also dem Antrieb durch eine Verdoppelung des CO2-Gehaltes, sagt das IPCC, dass sich ein zusätzlicher Antrieb von 3,7 W/m² ergibt. Die Endpunkte dieses Wertes sind wahrscheinlich 3,5 für den niedrigeren und 4,1 für den höheren Wert (Hansen 2005). Dies ergibt eine Dreieckszahl von (3,5; 3,7; 4,0) W/m² für die Änderung des Antriebs durch den doppelten CO2-Gehalt.

Die zweite Zahl, die Temperaturänderung durch die Verdoppelung des CO2-Gehaltes wird vom IPCC hier als die Dreieckszahl (2,0; 3,0; 4,5) °C angegeben.

Dividiert man die Sensitivität durch Verdoppelung durch die Änderung des Antriebs durch Verdoppelung, ergibt sich ein Wert der Temperaturänderung (∆T, °C) aus einer gegebenen Änderung des Antriebs (∆F, W/m²). Dies wiederum ist ebenfalls eine Dreieckszahl, und nach den Gesetzen der Division ergibt sie sich zu:

T1 / T2 = [L1 / H2, B1 / B2, L2 / H1] = [2.0 / 4.0,   3.0 / 3.7,   4.5 / 3.5]

also eine Klimasensitivität von (0,5; 0,8; 1,28) °C Temperaturänderung für jede Änderung des Antriebs in W/m². Man beachte, dass der zentrale Wert wie erwartet der autorisierte Wert von 3°C durch Verdoppelung des CO2-Gehaltes ist.

Betrachten wir jetzt, was dies in der realen Welt bedeutet. Das IPCC vergleicht die Änderung des Antriebs seit der „vorindustriellen Zeit“, die sie mit [dem Jahr] 1750 festlegen. Die Änderung des Antriebs seit 1750, ∆F, legt das IPCC hier mit einer Zunahme um (0,6; 1,6; 2,4) W/m² fest.

Die Multiplikation der Dreieckszahl für die Änderung des Antriebs (0,6; 1,6; 2,4) W/m² mit der Dreieckszahl der Sensitivität (0,5; 0,8; 1,28) °C pro W/m² ergibt die IPCC-Schätzung der Temperaturänderung, die man seit 1750 erwarten dürfte. Natürlich ist auch das eine Dreieckszahl, die wie folgt berechnet wurde:

T1 * T2 = [L1 * L2, B1 * B2, H1 * H2] = [0.5 * 0.6,  0.8 * 1.6,  2.4 *1.28]

Die endgültige Zahl, die IPCC-Schätzung der Erwärmung seit 1750 vorhergesagt durch ihre magische Formel liegt bei einer Erwärmung von (0,3; 1,3; 3,1) °C.

Lassen Sie mich das anders ausdrücken, es ist wichtig. Ein Vierteljahrhundert lang haben die AGW-Befürworter Millionen Stunden und Millionen Dollar in Studien und Computermodelle gesteckt. Außerdem knirscht und kracht es im Gebälk des gesamten IPCC-Apparates seit nunmehr fünfzehn Jahren, und das ist das Beste, was sie uns sagen können, für all das Geld und all die Studien und all die Modelle?

Der Berg kreißte und schlussfolgerte, dass wir seit 1750 eine Erwärmung irgendwo zwischen einem Drittel Grad und drei Grad gehabt haben… Das ist wirklich ein eindrucksvolles Stück Detektivarbeit, Lou…

Im Ernst? Das ist das Beste, was sie tun können, nach dreißig Jahren Studium? Eine Erwärmung zwischen einem Drittel Grad und drei Grad? Ich kann mir keine weniger falsifizierbare Behauptung vorstellen. Jede Erwärmung lässt sich mühelos in dieses Intervall einpassen. Egal, was passiert, sie werden immer den Erfolg für sich in Anspruch nehmen. Und das ist Nachhersage, nicht einmal Vorhersage. Huch!

Ich sage noch einmal, dass das Gebiet der Klimawissenschaft mit der Übernahme der durch nichts gestützten Behauptung in die falsche Richtung abgebogen ist, nämlich dass bei einem so gewaltig komplexen System wie dem Klima eine lineare Beziehung besteht zwischen der Änderung des Inputs und der Änderung der Operationsbedingungen. Die fundamentale Gleichung des konventionellen Paradigmas, ∆T = λ ∆F; die Grundbehauptung, dass die Temperaturänderung eine lineare Funktion der Änderung des Antriebs ist, stimmt einfach nicht.

Willis Eschenbach

Link: http://wattsupwiththat.com/2012/02/07/triangular-fuzzy-numbers-and-the-ipcc/

Übersetzt von Chris Frey

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken