aktualisiert am 23.10.18

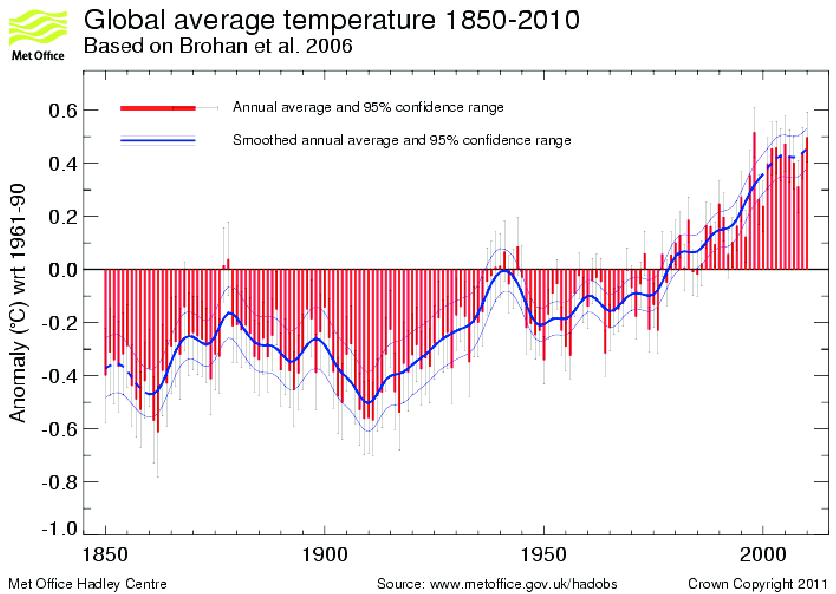
Die Quelle der ursprünglichen Grafik (hier wird die aktualisierte Version von Juli 2010 gezeigt) ist ein Aufsatz der IPCC Leitautoren Brohan und Jones[1] (hier mit Brohan et al 2006 genannt) indem detailliert beschrieben wird, wie man die unterschiedlichsten Temperaturdaten weltweit zusammenfasst und wie man dabei versucht allfällige Fehler, die diese Daten haben, zu kompensieren. Besonders schwierig ist das mit sog. systematischen Fehlern. Geht eine Uhr z.B. ständig 5 Minuten nach, dann nützt auch ein häufigeres Ablesen der Uhrzeit nicht weiter, die abgelesene Zeit ist immer um 5 Minuten falsch. Erst ein Vergleich mit einer genauen Referenzuhr erlaubt den Fehler zu erkennen und dann – als Korrrektur- von der abgelesenen Zeit einfach 5 Minuten hinzuzählen. Damit wäre der Fehler korrigiert. Diese einfache Methode ist natürlich bei den Temperaturdaten der Vergangenheit so gut wie nie anwendbar. Deswegen versucht man es dort u.a. mit der Bildung von Differenztemperaturen, in der Hoffnung dass sich dadurch die systematischen Fehler gegenseitig zum Verschwinden bringen.

Viele Klimatologen weltweit glauben nämlich fest daran [2], dass, wenn sie für die Trendbestimmung von Temperaturen, Differenzen aus bestimmten Temperatur-Variablen bilden würden, diese Differenzen (Anomalien) von allen systematische Fehlern befreit seien. Ein bekannter IPCC Leitautor gab mir auf Anfrage (wie man denn Seewassertemperaturen mit Lufttemperaturen mischen könne, wo doch beide Medien völlig unterschiedlich auf Wärme reagieren) vor einiger Zeit dazu diesen guten Rat:: „…… Think in ANOMALIES and not absolute temperatures.“ Diesen Rat befolgend, denke ich nun in Anomalien und schaue mir deren Verhalten in den offiziellen Temperaturganglinien an.

Anomalienbildung und Fehlerkorrektur

Das Verfahren der Differenzen- oder Anomalienbildung wird von allen Klimatologen umfassend eingesetzt, um die Trendverläufe stark unterschiedlicher Temperaturgänge vom Äquator bis zu den Polen vergleichbar machen zu können. Nun sind die gemessenen absoluten Temperaturen immer mit zahllosen Fehlern behaftet. Auch die daraus gebildeten  Tages- Monats- oder Jahresmittelwerte enthalten diese Fehler. Und es kommen neue Fehler hinzu, die durch den verwendeten Algorithmus der zur Durchschnittsbildung verwendet wird, entstehen. Näheres dazu hier. Nach der Fehlertheorie unterscheidet man dabei zwischen zufälligen,  groben, und systematischen Fehlern. Für diese Betrachtung sollen uns nur die systematischen Fehler interessieren.

In der Klimatologie werden zur Bestimmung des Referenzwertes, die errechneten Monatsmittel oder Jahrsmittel der gemessenen Temperatur einer Station, über den Zeitraum von 1961 bis 1990 aufaddiert und durch die Anzahl aller Monats- oder Jahresmittel dieses Zeitraumes geteilt. Der so enthaltene Wert entspricht einer Geraden gleicher „Temperatur“ über den Referenz-Zeitraum von 1961 bis 1990. (Es kann im Prinzip aber auch jeder andere Zeitraum sein.) Der zugehörige Referenz-Wert wird oft das Stationsnormal genannt. Folgerichtig heißen die Abweichungen vom (Stations)-Normal Anomalien.

Nun bildet man die Differenz aus allen absoluten Jahresmitteln Tx der Zeitreihe und dem Stationsnormal Tref und ermittelt auf diese Weise eine neue Zeitreihe der Anomalien eben dieser Station.  Dabei geht man von der Annahme aus, dass diese, wenn sie einen Fehler C enthalten, dieser auch im Stationsnormal vorhanden ist. Ferner unterstellt man, dass C eine konstante Größe hat. Bspw. Brohan und Jones[3] formulieren diese Annahme (in Bezug auf die Fehler durch unterschiedliche Mittelwertbildung) so:

„..There will be a difference between the true mean monthly temperature (i.e. from 1 minute averages) and the average calculated by each station from measurements made less often; but this difference will also be present in the station normal and will cancel in the anomaly.

Berechnet man jetzt die Anomalie Ax = (Tx+C) –(Tref+ C), dann hebt sich C auf. Das ist schlichte Algebra. So weit so gut! Die große Frage ist nun, funktioniert das bei Zeitreihen auch so? Warum denn nicht, wird mancher vorschnell antworten. Die Algebra ist schließlich immer gleich! Oder?

Es zeigt sich sehr schnell, dass die Idee der Fehlerkompensation, die hinter dieser einfachen Methode steckt, ebenso plausibel wie falsch ist, bzw. sie stimmt nur innerhalb ganz enger Randbedingungen, die in der hier interessierenden Praxis nicht eintreten.

Anomalien und sprunghafter Fehler

Machen wir dazu die Probe aufs Exempel, indem wir einen Anomalienverlauf aus einem (künstlichen) sinusförmigen Temperaturverlauf von 1850 bis 2009 erzeugen. Blau sei der Anomalienverlauf ohne Fehler. Die Anomalie verläuft fast gradlinig, wie die blaue Trendlinie anzeigt. Ab 1940 wird nun ein Fehler von + 1 K eingefügt. Gemäß Rechenanweisung w.o. wird dann aus beiden Werten für alle Jahre (x) die Differenz gebildet. Ab 1940 hebt sich der Fehler auf. Beide Verläufe gehen ineinander über. Vor 1940 jedoch wird allein durch den Rechenprozess die Temperaturanomalie um 1 k abgesenkt. Wir sehen, die Annahme von vorhin gilt nur für die Zeit nach 1940. Vorher nicht.  Lässt man Excel eine Trendgerade durch diese Werte legen, dann sehen wir, dass sich beide erheblich unterscheiden.

Daran ändert sich auch nichts, wenn wir den Eintritt des Fehler auf später verlegen. Wie das nächste Bild zeigt. Dort werden die Kurven Anomalie 1 und 3 genannt.

Auch hier hebt sich der Fehler nicht auf, sondern ist weiter voll vorhanden und wirksam, natürlich erst, nachdem er auftritt. Der Unterschied zum ersten Beispiel ist, dass nun überhaupt keine „wahre“ Temperaturanomalie mehr gezeigt wird, sondern nur noch die fehlerbehaftete Summe.

Schleichender Fehler

Genauso entwickelt sich das Ergebnis, wenn man anstatt (oder zusätzlich) einen schleichenden Fehler in den zuvor fehlerfreien Verlauf einbringt.  Ich habe das in der folgenden Abbildung getan. Dort wurde von Anfang an ein schleichender systematischer Fehler von +0,1 K/Dekade eingebracht, wie er z.B. vom städtischen Wärmeinseleffekt hervorgerufen werden kann.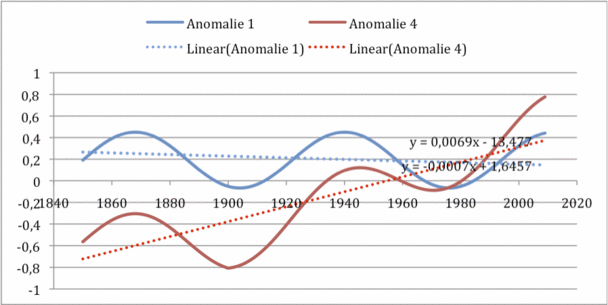

Wir sehen einen schön ansteigenden Verlauf (zuvor war er fast gerade) – verursacht allein durch den schleichenden systematischen Fehler- z.B den UHI. Nur kann jetzt überhaupt nicht unterschieden werden, ob ein systematischer Fehler vorliegt, oder ob sich die Umgebungstemperatur z.B. durch den Treibhauseffekt erhöht hat.

Man könnte nun beanstanden, dass die Fehlergröße in diesen Beispielen etwas hoch gewählt wurde. Dem ist aber nicht so, wie die zahlreichen Untersuchungen z.B. von Watts (http://www.surfacestations.org/) zeigen. Denn Fehler dieser Art gab und gibt es zahlreich. Sie werden durch Stationsverlegungen, Thermometertausch, Änderung der Farbbeschichtung der Station, Änderung des Algorithmus für die Berechnung des Mittelwertes u.v.a. mehr eingebracht. Es wäre nun vielleicht möglich den Anstieg im obigen Beispiel als Ausreißer zu erkennen, weil er einmalig und sprunghaft  -wenn auch konstant- auftritt, und ihn durch entsprechende Rechnungen zu kompensieren. Das geschieht aber nur sehr, sehr selten, weil sich bei den abertausenden von Datensätzen der Vergangenheit kaum jemand diese Mühe macht, bzw. machen kann

Kein Fehlerausgleich möglich

Eine Korrektur unterbleibt hauptsächlich deswegen, weil man die Binsenweisheit (siehe Brohan et al 2006) von zuvor glaubt, dass sich der Fehler bei Anomalienbildung von selbst ausgleicht.  Das ist aber, wie wir gesehen haben, grottenfalsch!

Eine Korrektur unterbleibt aber auch in den allermeisten Fällen deshalb, weil die dazu erforderlichen sog. „Metadaten“ fehlen und auch nicht mehr herbeigeschafft werden können. Diese beschreiben die Umgebungsbedingungen, Maßnahmen, Algorithmen und vieles anderes, was in und um die Station über den Zeitraum passiert ist. (Siehe dazu bspw. Harrys Read Me Files des Meteorologen und Programmierers bei der CRU Harry: „HARRY_READ_Me.txt.“ z.B. hier http://www.anenglishmanscastle.com/HARRY_READ_ME.txt. Diese ist 274 Seiten lang. Die dazugehörige Datenbasis enthält über 11.000 Dateien aus den Jahren 2006 bis 2009[4])

Allgemein gilt daher, die Annahme, dass sich bei Anomalienbildung die Fehler aufheben, ist nur dann richtig, wenn der gemeinsame, gleich große und richtungsgleiche Fehler vor dem Beginn der untersuchten Zeitspanne eintritt und dann so bleibt. In unserem Falle also vor 1850. Das liegt jedoch weder in unserem Ermessen, noch haben wir davon Kenntnis, sondern es wird allein durch die Realität bestimmt. Deshalb kann festgehalten werden, dass diese simple Fehlerkorrekturmethode in aller Regel nicht anwendbar ist. Angewendet wird sie aber von sehr vielen -auch IPCC- Klimatologen trotzdem.

Zusammenfassung

In der Statistik ist es eine gängige Methode Werte von div. Variablen mit Referenzwerten eben dieser Variablen zu vergleichen, um auf diese Weise bei eventuellen Abweichungen u.U. Ähnlichkeiten im Verlauf oder sogar Hinweise auf mögliche Ursache und Wirkungsbeziehungen zu bekommen. Allerdings muss man sich immer im Klaren darüber sein, wie sehr diese Methode von den Randbedingungen abhängt. Es wird gezeigt, dass eine schlichte Anomalienbildung keineswegs ausreichend ist, um schwer bestimmbare variable oder konstante systematische Fehler herauszurechnen. Im Gegenteil, man müsste in jedem Fall diese Fehler bestimmen, sie quantifizieren und einordnen, um sie dann evtl. mehr oder weniger gut rechnerisch ausgleichen zu können. In der Klimatologie ist diese Einschränkung in Bezug auf die Schwächen der Anomalienbildung offensichtlich nicht überall bekannt. Nur so lässt sich erklären, dass auch hochangesehene Forscher diese simplen Zusammenhänge oft nicht beachten. Ihre Ergebnisse sind dadurch entsprechend falsch und damit unbrauchbar, bzw. mit wesentlich größeren Fehlern (Unsicherheiten) behaftet als angegeben.

Michael Limburg EIKE

[1] Brohan, PK,J. J. Harris, I., Tett S. F. B.; & Jones, P. D. (2006) Uncertainty estimates in regional and global observed temperature changes: a new dataset from 1850. HadCRUT 3 HadCRUT 3:1 to 35.

[2] Brohan et. al 2006 geben auf Seite 6 den allgemeinen Glauben an die Fehlerfreiheit der Anomalien wider, in dem sie schreiben: „..There will be a di?erence between the true mean monthly temperature (i.e. from 1 minute averages) and the average calculated by each station from measurements made less often; but this di?erence will also be present in the station normal and will cancel in the anomaly. So this doesn’t contribute to the measurement error. Im Folgenden beschreiben die Autoren wie die Anforderungen an die Bildung der „station normals“ also der Referenzwerte (lt. WMO der Mittelwert jeder Station über die Jahre 1961-1990) aufgeweicht (relaxed) wurden. Die durchgeführte Re­duk­ti­on der An­for­de­run­gen zur Bildung des Referenzwertes (Station Normal) auf nur noch 15 Jah­re und da­raus 3 x 4 Jah­re in je­der De­ka­de, er­höht den Feh­ler, der schon in der Ver­wen­dung des Sta­ti­on Nor­mals steckt, wei­ter

[3] Brohan, PK,J. J. Harris, I., Tett S. F. B.; & Jones, P. D. (2006) Uncertainty estimates in regional and global observed temperature changes: a new dataset from 1850. HadCRUT 3 HadCRUT 3:1 to 35.

[4] Details entnommen aus ‚Botch after botch after botch‘ Leaked ‚climategate‘ documents show huge flaws in the backbone of climate change science By LORRIE GOLDSTEIN

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken