Von Henri Masson, Professor (emeritus) an der University of Antwerp (Belgium) und Michael Limburg Dipl. Ing.

Dieser Artikel wiederholt weitgehend einen Teil des Vortrags, den der Autor Henri Masson auf der 12. jährlichen EIKE-Konferenz (München 2018) gehalten hat. Der Text, der die PowerPoint-Folien der Präsentation umgibt, ist jedoch unveröffentlicht, ebenso wie das, was den Kern dieser Studie ausmacht: die Analyse der Anpassungs-Residuen von Hadcrut 5.0.1.0-Daten durch eine Summe von Sinuskurven oder eine lineare Regressionslinie.

Der Beitrag wurde aus praktischen Gründen in 4 Teile aufgeteilt

Das Video dazu findet man hier.

Teil 3

Messungen der Temperatur über dem Meer

Sie wurden nach und nach durch Messungen der Wassertemperatur am Eingang der Kühlkreisläufe der Motoren und in jüngerer Zeit durch ein Netz von Tauchbojen ersetzt, welche die Temperatur an der Oberfläche sowie in verschiedenen Tiefen der Ozeane messen. Die meisten Messungen vor der Inbetriebnahme der Bojen wurden daher entlang der am stärksten befahrenen Handelsrouten durchgeführt, was ein Problem der Repräsentativität darstellt, und mit zwei verschiedenen Verfahren, was ein Problem der Kalibrierung und des Anschlusses beim Wechsel von einem Messverfahren zum anderen darstellt (Abbildungen 16 und 17):

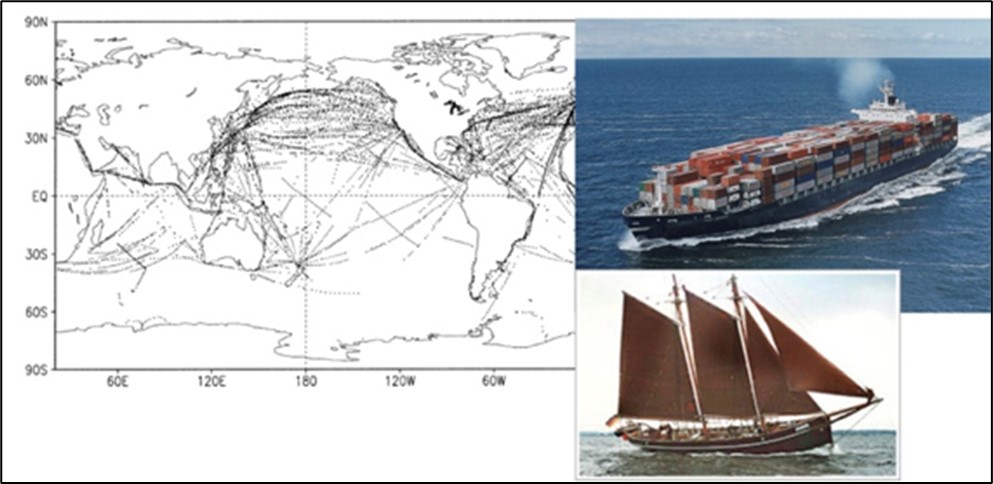
Abbildung 16: Die kleinen Punkte auf der Karte links stellen die Standorte der Messungen der Meerestemperatur dar, die in der ersten Januarwoche 2000, auf dem Höhepunkt der Entwicklung des Schiffsverkehrs, durchgeführt wurden. Die meisten Messungen wurden entlang der am stärksten befahrenen Schifffahrtsrouten durchgeführt, was die räumliche Repräsentativität der Messungen in Frage stellt. Das obere Bild rechts zeigt ein Containerschiff, dessen Gangway sich 25 m über der Meeresoberfläche befindet und dessen Rumpf 10 bis 15 m tief getaucht ist. Die Kühlwasser-Entnahmestelle liegt etwa 5 m unter der Meeresoberfläche. Das Bild in der unteren rechten Ecke (um 1900 aufgenommen) zeigt das deutsche Schiff Atalanta, dessen Deck 1,5 m über der Meeresoberfläche liegt.

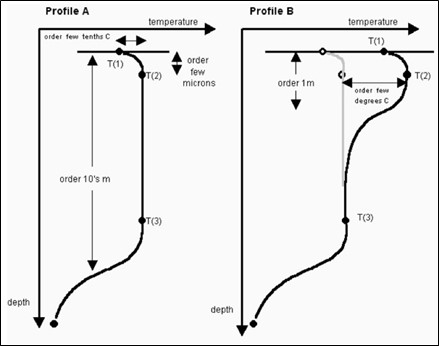
Abbildung 17: Typische Temperaturprofile im oberen Ozean. Die Temperaturen an der Oberfläche sowie die in zehn Metern Tiefe gemessenen Temperaturen können um mehrere Grad Celsius voneinander abweichen, allerdings auf unsystematische und daher nicht korrigierbare Weise.

Bei diesen Messungen handelt es sich um Messungen der Meerestemperatur (SST), die nicht genau mit den Lufttemperaturen übereinstimmen, solange sich das System Ozean-Atmosphäre nicht im Gleichgewicht befindet, was nie der Fall ist.

Bojen hingegen treiben frei entlang der Oberflächenströmungen und füllen die Ozeane allmählich auf relativ einheitliche Weise, was eine bessere räumliche Repräsentativität der Messungen ergibt, aber die Länge der gesammelten Zeitreihen überschreitet im besten Fall nicht einige Jahrzehnte, was zu kurz ist, um in der Klimadebatte von Nutzen zu sein.

Der Abgleich der mit verschiedenen Verfahren gewonnenen OSH-Messungen ist schwierig, weil der Anteil der verwendeten Techniken im Laufe der Zeit stark variiert hat und vor allem, weil für viele von ihnen die Messmethode nicht einmal identifiziert wurde (Abbildung 18):

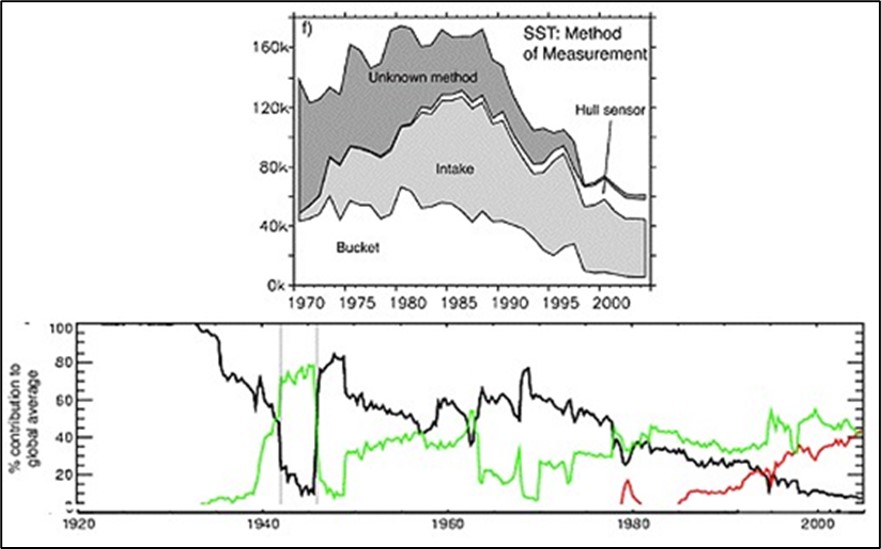Abbildung 18: Verfahren zur Messung der Wassertemperatur in Abhängigkeit von der Zeit. Die vertikale Achse stellt die Anzahl der Messungen in der oberen Abbildung dar, und die Prozentsätze in der unteren Abbildung, wobei die rote Linie den Prozentsatz der Messungen durch Bojen darstellt, die grüne Linie die Anzahl der Messungen am Einlass des Motorkühlsystems (ERI), und die schwarze Linie die Messungen durch Tanks.

Satellitenmessungen

Satellitenmessungen haben den Vorteil einer einheitlichen und repräsentativen räumlichen Abdeckung. Sie haben jedoch das Problem, dass die Umlaufbahn im Laufe der Zeit abweicht oder sogar ein Satellit durch einen anderen ersetzt wird, was Probleme bei der Kalibrierung und Verbindung mit sich bringt. Schätzungen der Temperatur an Land und in den Ozeanen beruhen auf komplexen Algorithmen, die ebenfalls durch Kalibrierungsfehler beeinträchtigt werden. Im Gegensatz zu Oberflächenmessungen, bei denen die Temperatur der Luft- oder Meeresoberfläche direkt gemessen wird, beruhen Satellitenmessungen auf der Interpretation der vom Boden oder der Meeresoberfläche ausgesandten Strahlung und leiten die entsprechenden Temperaturen ab; dabei kommen komplexe Kalibrierungsverfahren zum Einsatz, die ebenfalls mit erheblichen Fehlern behaftet sind (Abbildung 19):

Abbildung 19: Kalibrierung von Satellitenmessungen (Berkeley-Datensatz). Von einer auf der Ordinate (vertikale Achse) angegebenen Messung muss ein auf der x-Achse (horizontale Achse) abgelesener Wert abgeleitet werden. Bei einem TOA-Wert von 238, der in der Mitte des Messbereichs liegt, reicht der Unsicherheitsbereich auf der horizontalen Achse von 13,8°C bis 15,0°C, wobei der wahrscheinlichste Wert bei 14,5°C liegt.

Satelliten, Bojen und Thermometer messen nicht das Gleiche. Die Unterschiede sind gering, aber vergleichbar mit den Trends des Klimawandels, die der IPCC über ein Jahrzehnt hinweg zu erkennen behauptet.

Folgen wir immer noch dem IPCC?

Lassen wir diese Unzulänglichkeiten zu, um nicht zu sagen grundlegende experimentelle, mathematische oder algorithmische Fehler, und konzentrieren wir uns daher wie das IPCC auf globale Temperaturanomalien und deren Interpretation.

Das IPCC stützt sich bei seiner Arbeit hauptsächlich auf die Temperaturanomalien von 1980-2022 und behauptet, dies sei das einzige Zeitfenster, in dem zuverlässige, repräsentative und räumlich zufriedenstellend verteilte Messungen verfügbar sind. Das IPCC präsentiert seine Schlussfolgerungen auch in Form einer Regressionslinie, die die berechneten Temperaturanomalien am besten linear anpasst, und leitet aus der Steigung dieser Regressionslinie einen jährlichen, dekadischen oder hundertjährigen Temperaturanstieg ab, der für Schlagzeilen sorgt und die politischen Entscheidungsträger dazu veranlasst, dringend eine Anti-Kohlenstoff-Politik zu verabschieden, die enorme Kosten verursacht, um (angeblich) den Planeten zu retten.

Am Rande sei bemerkt, dass eine Änderung des Beginns und der Länge dieses Messfensters zu radikal anderen Ergebnissen führt, wie das folgende Beispiel zeigt:

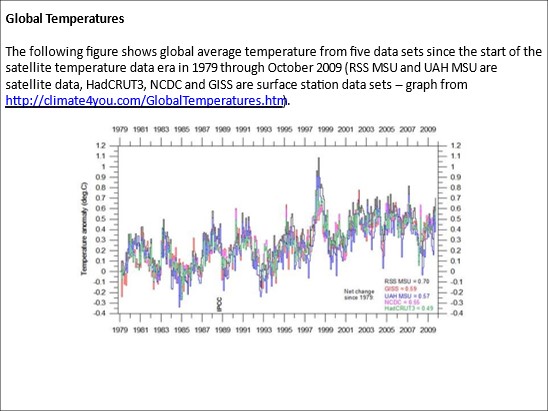Abbildung 20: Daten zur Veranschaulichung der Auswirkungen der Länge des Messfensters und seiner Anfangszeit.

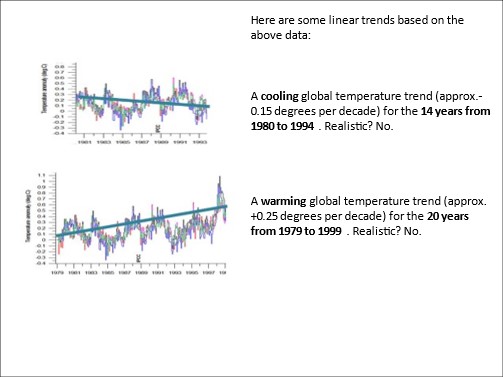
Abbildung 21: Regressionslinien, die mit Messfenstern erhalten wurden, die zu unterschiedlichen Zeiten beginnen und unterschiedlich lang sind. Das Ergebnis ist unsinnig…

Ein unbedarfter Mensch könnte meinen, dass das Datum 1980, mit dem das vom IPCC verwendete Messfenster beginnt, nicht zufällig gewählt wurde. Es entspricht einem Temperaturminimum in längeren Temperaturmessungen.

Wie dem auch sei, aber zurück zu einigen grundlegenderen Überlegungen. Es sei darauf hingewiesen, dass der Vergleich der Dauer des Messfensters mit den Perioden der zyklischen Komponenten zu den Vorarbeiten jeder ernsthaften Analyse von Zeitreihen gehört. Um seine Bedeutung zu veranschaulichen, können wir eine einfache Sinuskurve mit einer Periode betrachten, die mit dem Messfenster vergleichbar ist, und die Regressionslinien zeichnen, die verschiedenen Phasenverschiebungen der Sinuskurve in Bezug auf das Messfenster entsprechen, um zu erkennen, dass wir als Ergebnis alles und jedes erhalten, während die Steigung Null sein sollte, eine um eine Horizontale oszillierende Sinuskurve. In der Praxis hat es sich bewährt, dass das Messfenster mehr als das 6-fache der Sinusoid-Periode beträgt, um diese „Randeffekte“ zu eliminieren.

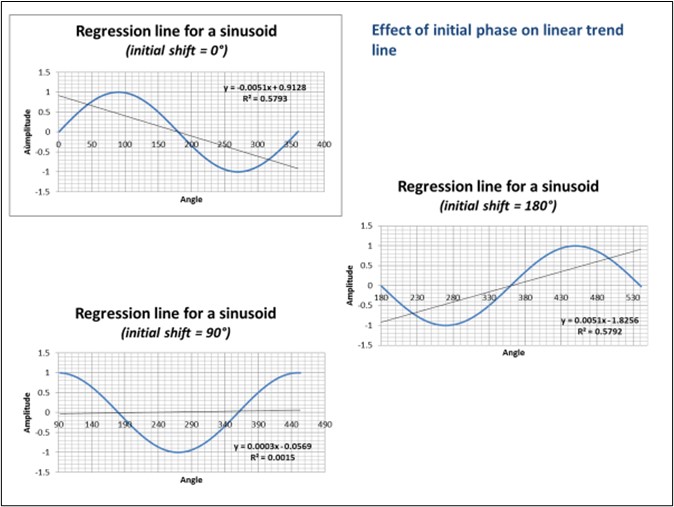
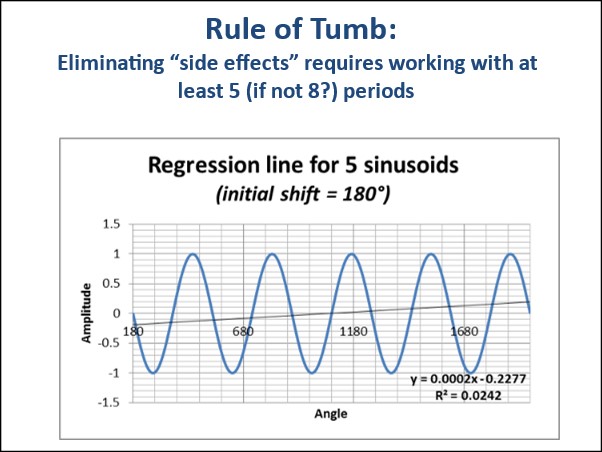Abbildung 22: Sinuskurven und Regressionsgeraden. 22a: Auswirkung der Anfangsposition des Messfensters (mit einer Länge, die der Periode der Sinuskurve entspricht); die Steigung variiert von +1 bis -1 je nach der Position des Anfangszeitpunkts des Messfensters im Verhältnis zur Sinuskurve. 22b: Regressionslinie über mehrere Sinuswellenperioden. Die Steigung wird sehr gering.

Abbildung 23: Maximale Steigung (anfängliche Phasenverschiebung um 180°) einer über mehrere Perioden berechneten Regressionslinie. Über 6 Perioden hinaus ist die Steigung vernachlässigbar.

Zum Leidwesen des IPCC gibt es, wie in Tabelle 2 erwähnt, eine Vielzahl von zyklischen Komponenten in den Temperaturaufzeichnungen, deren Perioden von einem Tag bis zu mehreren hunderttausend Jahren reichen, wie eine Analyse des Leistungsspektrums (Fourier-Transformation der Autokorrelationsfunktion) oder die Untersuchung von Skalogrammen deutlich zeigen. Und da das IPCC ein Messfenster ab 1980 verwendet, also ein Fenster, das sich über vierzig Jahre erstreckt, ist die Einhaltung der oben erwähnten „6-Perioden-Regel“ völlig unmöglich. Alle „Projektionen“, die der Weltklimarat verkündet, ausgedrückt als Temperaturanstieg pro Jahrzehnt oder pro Jahrhundert (d.h. in Form der geraden Steigung der Regression der Temperaturanomalie), sind daher mit einem „Randeffekt“ behaftet, der es ermöglicht, sie je nach Beginn und Länge des berücksichtigten Messfensters so zu gestalten, wie wir es wollen, also völlig willkürlich.

Darüber hinaus ist zu beachten, dass diese natürlichen Zyklen nicht exakt periodisch sind, was einen leicht chaotischen Charakter des Klimasystems widerspiegelt, der ihre vollständige Eliminierung durch Filterung verhindert. Es ist daher physikalisch unmöglich, mit einem Messfenster zu arbeiten, das die „6-Perioden-Regel“ einhält. Es ist daher mathematisch nicht korrekt, unter diesen Bedingungen eine Regressionslinie zu zeichnen, deren Steigung je nach Wahl des Anfangszeitpunkts und der Länge des Messfensters variiert. Und dennoch leitet der IPCC aus der Steigung einer solchen Regressionsgeraden die „Projektionen“ des „höchstwahrscheinlichen“ (sic) Temperaturanstiegs über das kommende Jahrzehnt oder gar Jahrhundert ab.

Es ist völlig unverantwortlich, eine Klimapolitik, die ebenso entbehrlich wie schädlich für die Wirtschaft und das Wohlergehen der Bevölkerung ist, die ihr unterworfen ist, weil sie furchtbar teuer ist, auf der Grundlage der Steigung einer solchen Regressionslinie zu entwickeln, die letztlich völlig willkürlich ist. Und doch …

Lineare Regression der globalen Temperaturanomalien?

Trotz allem, was soeben in Erinnerung gerufen wurde, wird die Aufzeichnung der globalen Temperaturanomalien, die von der amerikanischen NOAA herausgegeben und vom IPCC übernommen wurde, durch eine Regressionslinie angenähert, die nichts aussagt (oder die dazu gebracht wird, das zu sagen, was wir wollen, mit einigen vernünftigen Anpassungen der Länge oder des Anfangszeitpunkts des Messfensters, wie wir gezeigt haben).

Zunächst ist festzustellen, dass der aufsteigende Zweig einer Sinuskurve mit einer Periode von 84 Jahren, die mit dem Messfenster synchronisiert ist, die Temperaturanomalien genauso gut, wenn nicht sogar etwas besser anpasst als die Regressionslinie; eine Sinuskurve hat jedoch den Vorteil, dass sie realistischer in die Vergangenheit und damit wahrscheinlich auch in die Zukunft extrapoliert werden kann als eine Regressionslinie (siehe Abbildung unten).

Tatsächlich offensichtlich: ein Blick in die Vergangenheit zeigt, dass die Temperatur nicht gleichmäßig gesunken ist, sondern dass es eine Abfolge von kalten und warmen Episoden gegeben hat. Jeder kennt das römische und das mittelalterliche Optimum sowie die Maunder-Mini-Eiszeiten (während derer die zugefrorene Themse begangen wurde) und das Dalton-Minimum zu Beginn des 19. Jahrhunderts. Symmetrisch, mit Blick auf die Zukunft, können wir feststellen, dass die „Pause“ (oder „Lücke“), die beim Anstieg der globalen Temperaturanomalien seit fast 20 Jahren beobachtet wird, ganz einfach damit erklärt werden kann, dass die Sinuskurve ihr Maximum überschritten hat, was bedeutet, dass wir uns nicht auf eine Erwärmung, sondern auf einen Temperaturrückgang zubewegen, dessen Anfänge also bereits anhand der wichtigsten Daten zu beobachten sind. Zuletzt.

Abbildung 24: Anpassung der Temperaturanomalien durch eine Regressionslinie und durch den aufsteigenden Ast einer Sinuskurve. Die Sinuskurve hat einen R²-Wert = 0,549 und erklärt damit 55 % der Gesamtvarianz, während die Regressionsgerade ein R² = 0,48 aufweist. Die Sinuskurve passt sich also besser an als die Linie, insbesondere zu Beginn und am Ende des Messfensters. Es ist richtig, dass sie drei Parameter (Amplitude, Frequenz und Anfangsphase) verwendet, während die Regressionsgerade nur zwei verwendet.

Schließlich ist zu beachten, dass die Krümmung, die einem aufsteigenden Zweig der Sinuskurve eigen ist, in Verbindung mit einer nicht trivialen Wahl der Länge und des Anfangszeitpunkts des Messfensters zu der falschen Annahme führen kann, dass sich die globale Erwärmung beschleunigt (wenn darauf geachtet wird, die Analyse vor dem Beginn der „Pause“ zu unterbrechen), wie unten dargestellt (Abbildung 25 ). Das IPCC ist in diese Falle getappt oder nutzt sie vielleicht sogar wissentlich, indem es den Eindruck erweckt, dass sich der Klimawandel beschleunigt und daher dringend kontrolliert werden (muss), indem er ihn einerseits mit großen Schüben mehr oder weniger verdeckter und so genannter tugendhafter Steuern und andererseits mit großzügigen Subventionen für „Dienstleistungen“ und kolossalen Finanztransfers an Entwicklungsländer finanziert.

Abbildung 25: Anpassung der Temperaturanomalien über einen Zeitraum von zwei Jahrhunderten durch Regressionslinien. Das Erscheinungsbild in Form eines aufsteigenden Sinuszweiges (mit einer Periode von etwa 360 Jahren) ist in dieser Abbildung, die mit dem Dalton-Minimum beginnt, deutlicher zu erkennen. Die über immer kürzere Zeiträume berechneten Regressionslinien (mit Anfangszeitpunkten, die immer näher am heutigen Zeitpunkt liegen) weisen immer stärkere Steigungen auf, was auf eine Beschleunigung der globalen Erwärmung hindeutet, während wir diese Abbildung genauso gut als aufsteigenden Zweig einer Sinuskurve interpretieren können, die bald ihr Maximum durchlaufen wird (tatsächlich endet diese Grafik im Jahr 2000, und seither wurde das Maximum erreicht), bevor sie wieder abnimmt.

Wird fortgesetzt.

Wer den gesamten Bericht sofort lesen will kann das hier tun.IPCC has it all wrong Li-Edition Deutsch