Ich hasse Statistiken, wie viele von Ihnen wissen. Manche Leute glauben, dass Statistiken und/oder statistische Modelle, welche die üblichen statistischen Kriterien erfüllen, Fakten sind. Der IPCC kann so sein. Sie erstellen statistische Modelle der globalen Temperaturen mit Modellen vulkanischer und anthropogener Antriebe und vergleichen das Modell mit einem Modell, das nur vulkanische Antriebe berücksichtigt. Dann wenden sie sich mit ernster Miene an uns und sagen, der Vergleich zeige, dass der anthropogene Antrieb für die gesamte Erwärmung verantwortlich sei. Was ist mit der Sonneneinstrahlung? Oh, das haben sie berücksichtigt, sagen sie, die Sonne macht keinen Unterschied, siehe ihr Diagramm in Abbildung 1 des AR6. [1] Es wird angenommen, dass der solare Antrieb gleich Null und der Vulkanismus gering ist, so dass das Modell davon ausgeht, dass die gesamte jüngste Erwärmung auf den Menschen zurückzuführen ist, und dann in einem perfekten Beispiel für einen Zirkelschluss dieselbe Schlussfolgerung zieht. Aber was ist, wenn der solare Antrieb nicht gleich Null ist? Welchen Unterschied macht das?

Abbildung 1. Die vom IPCC AR6 angenommenen, die globale Erwärmung beeinflussenden Kräfte, umgerechnet in Grad C. Aus AR6 WG1, Seite 961.
Es wurden zahlreiche Arbeiten veröffentlicht, die zeigen, dass die Sonne einen größeren Einfluss auf die globalen Temperaturen und den Klimawandel haben könnte als vom IPCC angenommen.[2] Wir dürfen nicht vergessen, dass statistische Modelle keine Beweise oder Theorien sind, sie sind nicht einmal richtige Hypothesen. Sie sind lediglich ein Instrument, um die Gültigkeit von Ideen zu testen, und aus einem statistischen Modell kann eine Hypothese hervorgehen, aber ein Beweis wird es nie. Wenn ein Modell die Zukunft wiederholt genau vorhersagt, dann ist das ein Beweis für die Richtigkeit der Hypothese, aber kein Beweis. Der IPCC präsentiert sein statistisches Klimamodell mit den in Abbildung 2 dargestellten Diagrammen.
Abbildung 2 ist recht umfangreich, aber sie besagt kurz und bündig, dass der IPCC davon ausgeht, dass die natürliche Erwärmung (dicke grüne Linie) gleich Null ist, so dass nach seinen Annahmen die gesamte Erwärmung auf menschliche Aktivitäten zurückzuführen ist. Der Bericht der WG1 AR6 ist 2391 Seiten stark, aber Abbildung 2, die gegenüber der Darstellung auf Seite 441 leicht verändert wurde, fasst wirklich alles zusammen, was darin vorgeschlagen wird. Der Rest ist Füllmaterial.
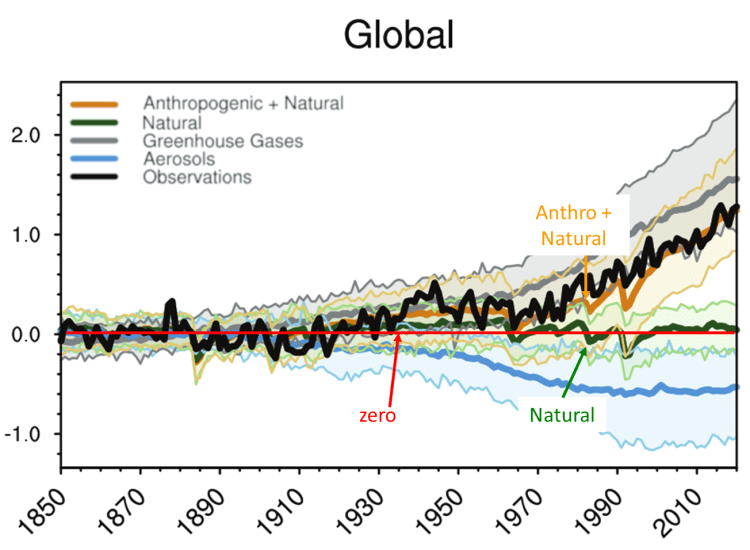
Abbildung 2. Das IPCC-Modell zeigt seine Treibhausgas-Erwärmungshypothese mit dieser Grafik. Dies ist nach IPCC AR6 WG1 Abbildung 3.9b (Seite 441). Die vertikale Achse ist die Temperaturanomalie im Vergleich zu 1850-1900.
Es gibt zahlreiche Probleme mit Abbildung 2, aber wir werden uns auf den Vergleich zwischen den anthropogenen + natürlichen Modellen, in orange, und den Beobachtungen in schwarz konzentrieren. Zunächst einmal ist das Orange nicht ein einziges Modell, sondern der Durchschnitt vieler ausgewählter Modelle. Die Spanne der Modellberechnungen (5. bis 95. Perzentil) ist hellorange schattiert dargestellt. Die Spanne ist ziemlich groß. Wenn sie Vertrauen in ihre Modelle hätten, würden sie dann nicht das beste Modell auswählen und verwenden? Wenn sie den Modellen nicht trauen, warum versuchen sie dann, sie als Beweis dafür zu verwenden, dass die Sonne keinen Einfluss hat und die gesamte Erwärmung auf menschliche Aktivitäten zurückzuführen ist? Warum verwenden sie die Modelle, um eine vom Menschen verursachte Klimakatastrophe vorauszusagen?
In der Zusammenfassung der AR6 WGII für politische Entscheidungsträger (S. 12-20) wird auf der Grundlage von Modellergebnissen ein hohes Vertrauen in viele zukünftige Katastrophen berichtet. Warum ein hohes Vertrauen, wenn die Modelle so ungenau sind, dass sie gemittelt werden müssen? Zweitens werden dicke Linien verwendet, um die Unterschiede zwischen den schwarzen und orangefarbenen Linien zu verschleiern, aber die Unterschiede sind erheblich, insbesondere zwischen 1935 und 1976 sowie 1980 und 2000. Der Modell-Durchschnitt zwischen 1920 und 1960 sieht fast wie von Hand gezeichnet aus, weil er im Verhältnis zu den steigenden Temperaturen bis 1944 und den fallenden Temperaturen danach so gerade ist.
Wählen wir also einen anderen Ansatz. In der klassischen Paläoklimaliteratur vor dem IPCC wurde meist davon ausgegangen, dass die Sonnenvariabilität den Klimawandel dominiert.[3] Im Laufe der Zeit hat die Untersuchung der kosmogenen Isotope ¹⁴C [4] in Baumringen und ¹⁰Be [5] in Eiskernen zu anerkannten Proxy-Aufzeichnungen der Sonnenleistung geführt, die Tausende von Jahren zurückreichen (siehe die Erörterung von Kohlenstoff¹⁴ und Beryllium¹⁰ hier). [6] Diese Isotope entstehen in der Atmosphäre, wenn galaktische kosmische Strahlung das Magnetfeld der Sonne durchdringt und auf die Atmosphäre trifft. Wenn die Sonnenleistung hoch ist, ist das Magnetfeld stärker als bei geringer Sonnenleistung. Daher deuten niedrige Konzentrationen von ¹⁴C [7] und ¹⁰Be [8] auf eine starke Sonnenleistung hin und umgekehrt. Seit 1700 bieten Sonnenfleckenaufzeichnungen ein genaueres Bild der Sonnenaktivität [9].
Untersuchungen von ¹⁴C-, ¹⁰Be- und Sonnenfleckenaufzeichnungen haben vier große langfristige Sonnenzyklen aufgedeckt. Dabei handelt es sich um den Hallstatt-Zyklus (oder Bray-Zyklus) mit einer Dauer von etwa 2 400 Jahren, [10] den Eddy-Zyklus mit einer Dauer von etwa 1 000 Jahren, [11] den de Vries-Zyklus (oder Suess-Zyklus) mit einer Dauer von etwa 210 Jahren, den Feynman-Zyklus (oder Gleissberg-Zyklus) mit einer Dauer von etwa 105 Jahren, [12] und den Pentadecadal-Zyklus mit einer Dauer von etwa 50 Jahren. [13] Alle Zyklusperioden sind ungefähre Angaben, außerdem können sie im Laufe der geologischen Zeit variieren [14]. Manchen mag es nicht gefallen, dass ich den Begriff „Zyklen“ verwende, da unser Verständnis der Zyklusperioden und der Stärke oder Kraft der einzelnen Zyklen gering ist. Vielleicht wäre der Begriff „Oszillation“ besser, aber ich bin mir darüber im Klaren, dass wir diese Zyklen nur unzureichend verstehen, und verwende den Begriff nur der Einfachheit halber und nicht unbedingt im Sinne der genauen Definition des Wortes.
Die Sonne ist ein Dynamo und erzeugt ein Magnetfeld, das die Schwankungen ihrer Leistung im Laufe der Zeit steuert. Ein solcher Dynamo hat Zyklen, und wir haben gezeigt, dass es sie gibt und dass sie das Klima der Erde beeinflussen, aber die Details sind nur skizzenhaft. Astrophysiker und Paläoklimatologen haben die Sonne und die Auswirkungen der Sonne auf das Klima der Erde beobachtet und phasengleiche Muster der Sonnenaktivität und der Klimaauswirkungen erkannt. Wir erörtern diese beobachteten (aber nur ungefähren) Muster in diesem Beitrag und setzen sie in Beziehung zu HadCRUT5. Zyklen werden auch bei anderen Sternen beobachtet, die unserer Sonne ähnlich sind[15].
Es gibt auch kürzere Perioden solarer Variabilität, wie den Sonnenfleckenzyklus, der eine schwankende Periode und eine asymmetrische Form hat, die im Durchschnitt etwa 11 Jahre beträgt. [16] Schließlich gibt es noch den ENSO-Zyklus, der ebenfalls eine schwankende Periode hat und zum Teil durch die Sonnenaktivität angetrieben wird. [17] Um die kürzeren Sonnenzyklen abzudecken, beziehen wir die SILSO-Sonnenfleckenaufzeichnung [18] und die ERSST-Niño-3.4-Aufzeichnung (ENSO) von KNMI ein. [19]
Falls wir die Annahme des IPCC ignorieren, dass die Sonnenaktivität seit 1750 keine Rolle für den Klimawandel gespielt hat, wie in Abbildung 1 vorgeschlagen, ist es möglich, die Korrelation dieser gut etablierten Zyklen oder Oszillationen und einer der im AR6 verwendeten Aufzeichnungen der globalen Temperatur, der HadCRUT5[20], zu untersuchen. Leider reicht der HadCRUT5-Datensatz für die globale Temperatur nur bis 1850 zurück, aber es handelt sich um einen instrumentellen Datensatz, der den Proxies vorzuziehen ist. Die zur Erstellung von HadCRUT5 verwendeten Daten sind vor 1958 unzureichend, [21] daher werden wir auch den noch kürzeren Zeitraum der genaueren Daten von 1958 bis 2023 untersuchen.
Wir haben eine statistische Mehrfachregression verwendet, um zu sehen, wie gut diese Zyklen und Daten HadCRUT5 vorhersagen können. Uns ist klar, dass wir, selbst wenn wir ein multiples Regressionsmodell mit einem hohen R² (Bestimmtheitsmaß oder das Quadrat des Korrelationskoeffizienten) erstellen können, noch nichts bewiesen haben. Wir wissen auch, dass die globale durchschnittliche Temperatur zwar eine wichtige, aber nicht die einzigee Messgröße für den Klimawandel ist. Andere Messgrößen wie die Windgeschwindigkeit und -richtung in den mittleren Breiten sowie die Entwicklung der Temperatur an den Polen und in den Tropen (insbesondere in der mittleren Troposphäre [22]) sind ebenfalls wichtig. Mit diesem Beitrag soll lediglich gezeigt werden, dass die Entscheidung des IPCC, die Korrelation zwischen den Trends des Logarithmus der CO₂-Konzentration und der globalen durchschnittlichen Temperatur als „Beweis“ oder „Beleg“ dafür zu bezeichnen, dass CO₂ und andere menschliche Treibhausgasemissionen den Klimawandel antreiben, nicht sehr solide ist. In der Tat ist es wahrscheinlich falsch. Andere vernünftige Korrelationen sind möglich und wohl auch besser.
Abbildung 3 ist eine Darstellung der unabhängigen oder prädiktiven Variablen, die in unserer Regressionsstudie verwendet wurden. Sie wurden auf Skalen von -3 bis +3 normalisiert, indem die größeren Variablen (Log(CO₂) und Sonnenflecken) durch ihren Mittelwert geteilt wurden, um die Variablen besser miteinander vergleichen zu können. Darüber hinaus haben wir die Sonnenfleckenzahl durch ihre Standardabweichung geteilt, um sie mit den anderen Variablen vergleichbar zu machen.
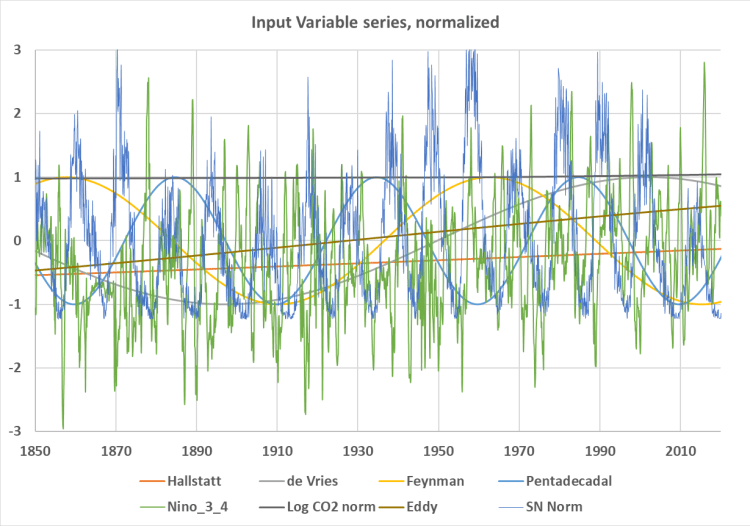
Abbildung 3. Die in dieser Studie zur multiplen Regression verwendeten Eingangsreihen. Die Skala der y-Achse ist ein Index, und die Kurven können nicht quantitativ verglichen werden.
Leider ist unser Zeitraum zu kurz, um einige der stärkeren Klimazyklen, wie den Hallstatt- (hellblau) und den Eddy-Zyklus (orange), richtig zu bewerten. Diese beiden Zyklen erreichten ihren Tiefpunkt in der Kleinen Eiszeit und ihre Zeiträume sind so lang, dass sie fast wie gerade Linien erscheinen, aber sie steigen wie die HadCRUT5-Aufzeichnung. Der Logarithmus von CO₂ [23] ist ebenfalls fast eine gerade Linie und steigt nur sehr leicht an. Bei den CO₂-Daten handelt es sich um interpolierte Jahresdurchschnittswerte, um saisonale Schwankungen zu vermeiden.
Die in der Studie verwendeten ENSO 3.4, Sonnenflecken (SN Norm) und CO₂ (Log CO₂ Norm) Daten stammen aus bekannten Datensätzen. [24] Die längerfristigen Sonnenzyklen werden mit einer Sinusfunktion [25] der folgenden Form erstellt:
● Zyklus (t) = cos(2πft – Offset)
Dabei ist das Cosinus-Argument im Bogenmaß, f=Frequenz, t=Zeit, und der Offset wird verwendet, um die Sinuswelle mit den von Ilja Usoskin [26] und Joan Feynman angenommenen Zyklus-Minima (Kaltzeiten) in Einklang zu bringen. [27] Weitere Informationen zu dieser Transformation, die in der Fourier-Analyse verwendet wird, finden Sie in der Arbeit von David Evans hier. [28] Diese Tiefstwerte sind nicht genau und müssen anhand der verfügbaren Daten geschätzt werden. Die tatsächlich verwendeten Werte und die genauen Funktionen findet man in den am Ende dieses Beitrags verlinkten zusätzlichen Materialien.
Das Modell der multiplen Regression
Ich habe eine Reihe von Regressionen mit den in Abbildung 3 dargestellten Variablen und verschiedenen Untergruppen davon durchgeführt. In allen Fällen, in denen ich dies feststellen konnte, war der Logarithmus von CO₂ die statistisch wichtigste Einzelvariable, wie aus AIC, [29] Summe der Quadrate und R² hervorgeht. Allerdings waren alle Variablen signifikant, und CO₂ war im Vergleich zu den Auswirkungen aller anderen Variablen zusammengenommen gering, wie wir sehen werden. AIC stuft die Input-Prädiktoren für den Fall von 1958 wie folgt ein: Log_CO₂, Nino_3_4, Hallstatt, Eddy, Pentadecadal, Sonnenflecken und schließlich de Vries. Der AIC basiert auf der Summe der Quadrate und kann daher bei autokorrelierten Reihen [30] wie diesen problematisch sein. Die nachstehenden Diagramme vermitteln ein Gefühl für die relative Bedeutung der wichtigsten Variablen, die statistisch nur schwer (vielleicht gar nicht) genau zu berechnen ist, vor allem aufgrund der kurzen Zeitspanne unserer instrumentellen Daten und der langen Perioden der wichtigen Sonnenzyklen. Die nächsten vier Diagramme beziehen sich auf die gesamte instrumentelle Aufzeichnung von 1850 bis 2023. In Abbildung 4 sind alle Variablen der Studie enthalten:
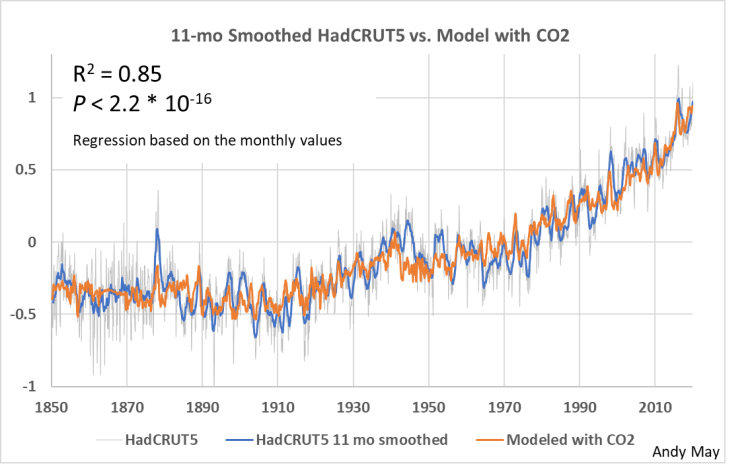
Abbildung 4. Ein Modell mit allen Reihen, einschließlich log(CO₂). Die feine graue Linie sind die monatlichen HadCRUT5-Daten, und die blaue Linie ist mit einem 11-jährigen gleitenden Durchschnitt geglättet. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, bezogen auf den Zeitraum 1961-1990. Die orangefarbene Linie ist das Modell.
In Abbildung 5 werden alle Variablen außer Log_CO₂ verwendet. In beiden Abbildungen ist die blaue Linie der geglättete HadCRUT5-Datensatz, und die feine graue Linie sind die monatlichen HadCRUT5-Daten. Die orangefarbene Linie ist das Modell. Wir können sehen, dass Log_CO₂ visuell wenig zur Übereinstimmung zwischen Beobachtungen und Modell beiträgt. Eine signifikante Verbesserung ist um 1940 herum zu erkennen, ansonsten sind die beiden Modelle in etwa gleich.

Abbildung 5. Darstellung der Regression, wenn log(CO₂) aus der Liste der Prädiktoren entfernt wird. Das R² sinkt auf 0,84, und zwischen 1935 und 1947 ist eine deutliche Verschlechterung der Anpassung festzustellen. Die feine graue Linie und die blaue Linie sind wie zuvor. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, bezogen auf 1961-1990.
Abbildung 6 vergleicht das Modell, das Log_CO₂ verwendet, mit dem Modell, das nur die solarbezogenen Variablen verwendet. Die beiden Modelle sind ähnlich. Die einzigen auffälligen Unterschiede liegen vor 1940, als CO₂ vermutlich keine große Rolle spielte. Es ist möglich, dass die Unterschiede auf die Datenqualität zurückzuführen sind. Wie wir sehen werden, waren die Daten vor 1958 von geringerer Qualität als die Daten nach diesem Datum.

Abbildung 6. Ein Vergleich zwischen den Modellen „ohne CO₂“ und „mit CO₂“. Alle anderen Prädiktoren sind in beiden Modellen enthalten. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, relativ zu 1961-1990.
In Abbildung 7 modellieren wir HadCRUT5 nur mit CO₂. Obwohl das R² 0,8 beträgt und das Modell im Allgemeinen HadCRUT5 folgt, fehlt dem Modell die in den Abbildungen 5 und 6 zu erkennenden Granularität und Detailgenauigkeit. Der IPCC bezeichnet die Granularität als natürliche Variabilität und tut sie als statistisches „Rauschen“ ab, das zufällig ist. Man beachte, dass sich der P-Wert nicht ändert. Der P-Wert ist bei Modellen wie diesem, die viele Beobachtungen haben und gute Übereinstimmungen liefern, von geringem Nutzen. Er ist kein gutes Maß für die Qualität des Modells.
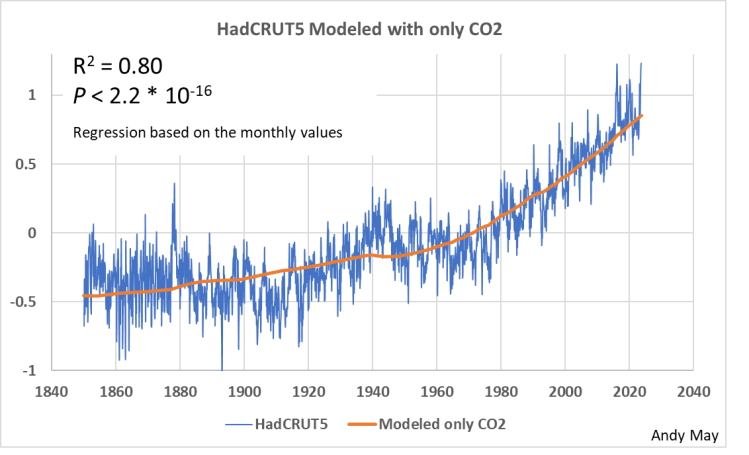
Abbildung 7. HadCRUT5 wird nur mit CO₂ modelliert. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, bezogen auf 1961-1990.
Als Nächstes wiederholen wir die obigen vier Diagramme unter Verwendung eines neuen Modells, das nur die Daten zwischen 1958 und dem heutigen Tag verwendet. Dies ist der größtmögliche Zeitraum mit guten Daten. Um eine weitere Verbesserung der Datenqualität zu erreichen, müssten wir bis zum Jahr 2005 gehen, als das ARGO-Netz groß genug wurde, um bessere Daten über die Temperaturen der Ozeane zu liefern, als wir sie von Schiffen erhalten können. Aber nur 17 Jahre mit guten Ozeandaten sind nicht lang genug, um den Einfluss der längeren Sonnenzyklen zu beurteilen.
Abbildung 8 zeigt eine gute visuelle Übereinstimmung zwischen den Beobachtungen und einem Modell mit allen Variablen. Es hat auch ein R² von 0,9, was beeindruckend wäre, wenn die Variablen unabhängig und nicht autokorreliert wären. Die Nichtübereinstimmung zwischen 1992 und 1995 ist wahrscheinlich auf den Ausbruch des Pinatubo im Jahr 1991 zurückzuführen, der nicht in dieses Modell aufgenommen wurde.
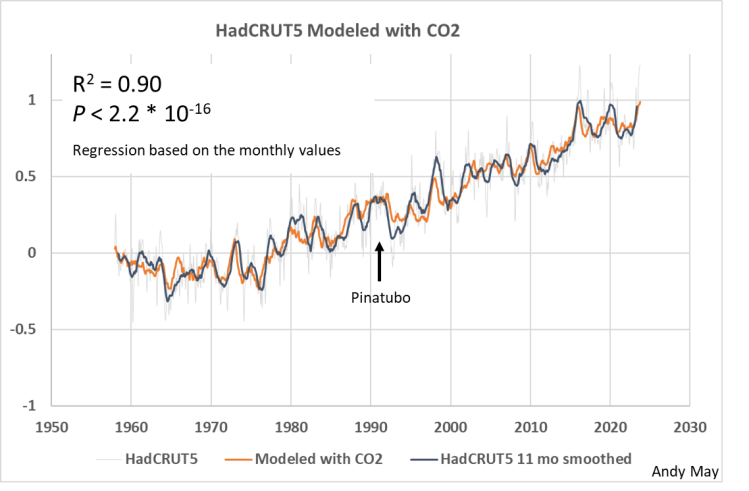
Abbildung 8. Ein Modell mit allen Prädiktoren, einschließlich CO₂, von 1958 bis zum heutigen Tag. Die Eruption des Pinatubo ist gekennzeichnet. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, bezogen auf 1961-1990.
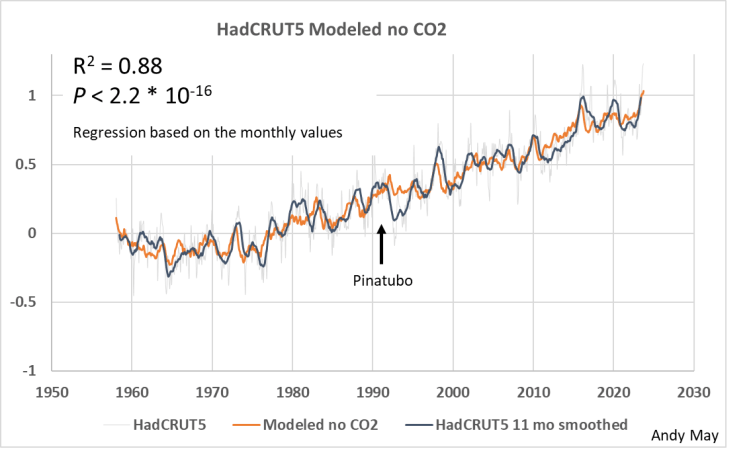
Abbildung 9. Ein Modell von 1958 mit allen Prädiktoren außer CO₂. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, bezogen auf 1961-1990.
Abbildung 9 zeigt das Modell mit allen Variablen außer CO₂. Die Übereinstimmung ist immer noch gut, aber es gibt Unterschiede im Detail, die darauf hindeuten, dass das Hinzufügen von CO₂ einen Unterschied macht. Der große Unterschied kurz nach 1992 ist wahrscheinlich auf den Einfluss des Ausbruchs des Pinatubo im Sommer 1991 zurückzuführen. Die Auswirkungen des Ausbruchs dauerten mehrere Jahre an. Mit Ausnahme des Pinatubo-Ausbruchs ist das Modell fast so gut wie das Modell, das CO₂ enthält, zumindest visuell.
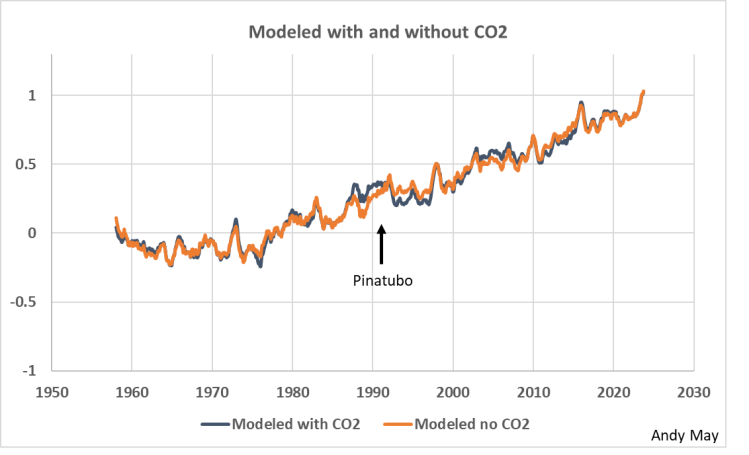
Abbildung 10. Modelle mit und ohne CO₂ über den Zeitraum von 1958 bis heute. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, bezogen auf 1961-1990.
In Abbildung 10 werden die Modelle mit und ohne CO₂ direkt miteinander verglichen, und mit Ausnahme des Zeitraums um den Ausbruch des Pinatubo ist die Übereinstimmung hervorragend. Ich will damit nicht sagen, dass Pinatubo vor seinem Ausbruch eine Wirkung hatte, sondern nur, dass die großen Auswirkungen des Ausbruchs auf die HadCRUT5-Aufzeichnung (siehe Abbildung 11) die beiden Regressionen in diesem Zeitraum unterschiedlich verzerrt haben könnten. Möglicherweise macht die Hinzufügung von CO₂ einen kleinen Unterschied, aber er ist in diesem Diagramm nirgends sichtbar, außer um den Ausbruch herum.

Abbildung 11. Ein Modell mit nur CO₂ als Prädiktor von 1958 bis heute. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, bezogen auf 1961-1990.
Abbildung 11 zeigt ein Modell, das nur den Logarithmus von CO₂ verwendet. Es gibt eine allgemeine Übereinstimmung von Temperatur und CO₂, aber es fehlen viele Details, die wir in den anderen Modellen sehen. Wir können argumentieren, dass die Schwankungen des HadCRUT5-Datensatzes um das orangefarbene Modell in Abbildung 11 kein zufälliges Rauschen sind, wenn sie mit Sonnenzyklen modelliert werden können.
Ein Wort zur Statistik
Das Risiko bei der Bewertung von Regressionsstatistiken von Modellen autokorrelierter Reihen lässt sich am einfachsten erkennen, wenn man bedenkt, dass zwei monoton ansteigende Zeitreihen, z. B. CO₂ und Temperatur seit 1850, zu korrelieren scheinen, auch wenn sie nicht miteinander verbunden sind. Das ist der Grund, warum ich Statistiken oft hasse. Zu oft werden statistische Anpassungsmaße wie R² oder berechnete statistische Wahrscheinlichkeiten verwendet, um den Lesern etwas vorzugaukeln, was nicht wahr ist. Die erste Beurteilung einer Korrelation sollte anhand einer Darstellung der Daten im Vergleich zum Modell erfolgen, die zweite sollte eine Darstellung der Residuen sein. Schwanken die Residuen gleichmäßig um den Wert Null, oder haben sie einen Trend? Alle Residuen-Diagramme für die Top-Modelle in diesem Beitrag weisen keinen Trend auf, was auch so sein sollte.
Das Wichtigste ist, dass Sie Ihren Augen trauen, nicht den statistischen Messungen der Anpassungen, die sind zweitrangig. Manchmal ist das Offensichtliche richtig. Um diesen Punkt zu veranschaulichen, habe ich eine schrittweise Regression verwendet, um die Modelle zu ordnen. Um diese vier Modelle zu erstellen, entfernte ich die oberste Variable (entsprechend ihrem AIC) und wiederholte die Regression mit den verbleibenden Variablen, bis das visuelle Modell nicht mehr sehr gut zu HadCRUT5 passte. Das Verfahren legt nahe, dass die wichtigsten Variablen Log_CO₂, Hallstatt und Eddy sind. Die vier akzeptablen schrittweisen Regressionsmodelle sind in Abbildung 12 dargestellt.
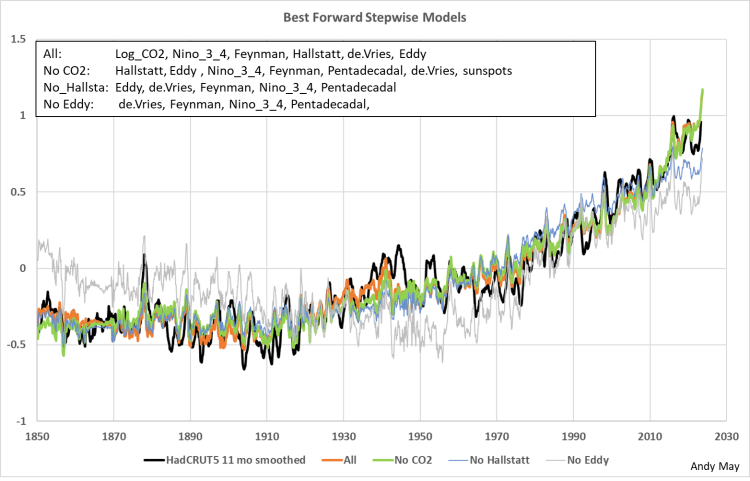
Abbildung 12. Die vier besten schrittweisen Vorwärts-Regressionsmodelle. Die vertikale Skala ist die HadCRUT5-Temperaturanomalie in Grad Celsius, relativ zu 1961-1990.
Das erste schrittweise Modell (Alle) wählte die in der Abbildung aufgeführten Variablen. Die Variablen sind in der Reihenfolge ihrer Wichtigkeit entsprechend ihrer AIC-Werte aufgeführt. Die visuell besten Modelle sind „Alle“ und „kein CO₂“, und es ist schwer, den Unterschied zwischen den beiden Modellen zu erkennen. Zu beachten ist, dass mehr Variablen ausgewählt wurden, als CO₂ aus der Auswahlliste entfernt wurde.
Nachdem Hallstatt entfernt wurde, schrumpft die Liste der ausgewählten Variablen, aber das Modell verschlechtert sich visuell stark. Nachdem Eddy entfernt wurde, wird das Modell sehr schlecht. Die beste Variable nach AIC ist Log_CO₂, aber wenn Log_CO₂ aus dem Modell entfernt wird (die grüne Kurve), ist die Übereinstimmung mit HadCRUT5 immer noch gut. Andere Modelle wurden ebenfalls auf diese Weise bewertet, aber diese drei sind die besten.
Die Variablen, die laut AIC durchweg am unteren Ende lagen, waren der Pentadekadenzyklus und die Sonnenflecken. Das Entfernen dieser Variablen führte jedoch immer zu einer visuellen Verschlechterung des Modells, die nicht akzeptabel war. Daher ist AIC zwar nützlich, aber kein alleiniges Kriterium für den Wert von Variablen oder Modellen. Man muss immer die Diagramme anschauen.
Schlussfolgerungen
Aus dieser Studie ergeben sich mehrere logische Schlussfolgerungen:
1. Ein erfolgreiches Modell kann nur mit Hilfe von Sonnenzyklen, ENSO und der Sonnenfleckenaufzeichnung erstellt werden.
2. Die Hinzufügung von CO₂ zu dem in (1) beschriebenen Modell trägt ein wenig zur Anpassung bei, vor allem in kurzen Intervallen, wie von 1935 bis 1940 und in der Mitte der 1990er Jahre um den Pinatubo-Ausbruch.
3. Statistische Standardmaße wie AIC, R² oder der P-Test können nicht als alleiniges Maß für den Erfolg des Modells verwendet werden. Die Auswertung der Diagramme ist entscheidend.
Diese Studie zeigt, dass die Sonnenvariabilität, zumindest statistisch gesehen, mindestens genauso gut mit HadCRUT5 korreliert wie CO₂. Da HadCRUT5 eine der wichtigsten Aufzeichnungen der globalen durchschnittlichen Temperatur ist, die vom IPCC zur Messung des Klimawandels verwendet wird, lautet ihre Schlussfolgerung, wie in der technischen Zusammenfassung des AR6 angegeben:
„Zusammen mit zahlreichen formalen Zuordnungsstudien über ein noch breiteres Spektrum von Indikatoren und theoretischen Erkenntnissen untermauert dies die eindeutige Zuordnung der beobachteten Erwärmung von Atmosphäre, Ozean und Land zum menschlichen Einfluss.“ – AR6 TS, Seite 63, Hervorhebung [vom Autor] hinzugefügt.
Dies ist falsch und das Ergebnis ihrer nicht belegten Behauptung, dass die Sonne keinen Einfluss auf das Klima hat. Sie sollten ernsthaft den Einfluss der Sonnenvariabilität auf den Klimawandel untersuchen. Ich habe erwartet, dass ich mich in dieser Studie mit verzögerten Sonneneffekten auf das Klima befassen muss. Mögliche mehrjährige Verzögerungen zwischen solaren Ereignissen und den damit verbundenen Klimaeffekten werden in vielen Veröffentlichungen erwähnt (Beispiel hier, andere Beispiele werden in Eichler et al. zitiert), aber die Beobachtungen bzw. Modellübereinstimmungen in diesem Beitrag wurden alle ohne Verzögerungen erzielt.
I would like to thank Charley May and David Evans for their help with this post, although if there are any errors, they are mine alone.
Download the bibliography here.
Download the supplementary material here. You will find the R code to create all the models and Excel code to make the main models, not all the R models can be made in Excel. To run the models in Excel you will need to the “Analysis ToolPak” and the “Solver” Add-in. These are found under File/Options/Add-ins.
- (IPCC, 2021, p. 961) ↑
- See especially: (Connolly et al., 2021), (Hoyt & Schatten, 1997), (Soon, Connolly, & Connolly, 2015), (Usoskin I. , 2017), (Usoskin, Gallet, Lopes, Kovaltsov, & Hulot, 2016), (Scafetta N. , 2023), (Vahrenholt & Lüning, 2015), and (Judge, Egeland, & Henry, 2020). ↑
- (Hoyt & Schatten, 1997) and (Bray, 1968) ↑
- 14C is the Carbon-14 isotope, except for nuclear bombs it is only created in the atmosphere by galactic cosmic rays, which increase when the Sun is less active. It has been used a proxy for solar activity for many decades. It is stored in tree rings, which provide a convenient and accurate date for each 14C concentration. (Cain & Suess, 1976) and (Cain W. , 1975). ↑
- 10Be is an isotope of Beryllium that is created by cosmic rays and is also inversely correlated with solar activity. It is stored in ice cores. (Beer, Blinov, Bonani, & al., 1990). ↑
- (Beer, Blinov, Bonani, & al., 1990) and (Hoyt & Schatten, 1997, p. 174) ↑
- (Bray, 1968) ↑
- (Delaygue & Bard, 2011) ↑
- https://www.sidc.be/SILSO/datafiles ↑
- (Bray, 1968) ↑
- (Abreu, Beer, & Ferriz-Mas, 2010) ↑
- Joan Feynman studied this centennial cycle and the pentadecadal cycle for many years. She called it the Gleissberg cycle, but since many have used the name Feynman cycle, we continue with that name here (Feynman & Ruzmaikin, 2014). See also (Peristykh & Damon, 2003). ↑
- The Pentadecadal cycle was first recognized by Rudolf Wolf in 1862 (Peristykh & Damon, 2003). He recognized that two or three high cycles were often followed by two or three low cycles. More formal recognition of the cycle was made by (Feynman & Ruzmaikin, 2014) and (Clilverd, Clarke, Ulich, Rishbeth, & Jarvis, 2006). ↑
- (Peristykh & Damon, 2003) ↑
- (Judge, Egeland, & Henry, 2020) and (Baliunas, et al., 1995) ↑
- (Peristykh & Damon, 2003) ↑
- (Roy, 2014) ↑
- https://www.sidc.be/SILSO/datafiles ↑
- https://climexp.knmi.nl/getindices.cgi?WMO=NCDCData/ersst_nino3.4a&STATION=NINO3.4&TYPE=i&id=someone@somewhere ↑
- https://www.metoffice.gov.uk/hadobs/hadcrut5/ ↑
- 1958 was the International Geophysical Year (IGY), which led to gathering much higher quality climate and climate-related data. It is notable that the late S. Fred Singer was one of the organizers of this project and that it was organized in James Van Allen’s living room in 1950. According to Van Allen, it was his wife’s (Abigail) chocolate cake that sealed the deal that day. (Korsmo, 2007). ↑
- (McKitrick & Christy, 2018) and (McKitrick & Christy, 2020) ↑
- CO₂ concentration varies as the logarithm to the base 2 with temperature, which means as CO₂ doubles, temperature increases linearly. As CO₂ concentration increases, its effect on surface temperature decreases. (Romps, Seeley, & Edman, 2022) and (Wijngaarden & Happer, 2020) ↑
- ENSO 3.4 is from ERSST, which only goes back to 1854. 1850 through 1853 are filled in with the Webb, 2022 ONI. The sunspot number is from SILSO, and the CO₂ concentration data are from NASA and NOAA. The CO₂ record is interpolated yearly averages to avoid the seasonal changes. ↑
- (Evans, 2013) ↑
- (Usoskin, Gallet, Lopes, Kovaltsov, & Hulot, 2016) and (Usoskin I. , 2017) ↑
- (Feynman & Ruzmaikin, 2014) ↑
- (Evans, 2013) ↑
- AIC stands for Akaike Information Criterion. It estimates the information lost by using the regression model in the place of the measurements. Like R2, it is based on the sum of squares and is susceptible to inflation (making variables and models look better than they actually are) due to autocorrelation. The Wikipedia article on this metric is helpful, see here. The lower the AIC value the better the model. ↑
- All the input time series used in these multiple regression models are autocorrelated, which simply means each value in the series is highly dependent on its previous values not independent of one another as required by the rules of regression. This artificially inflates the statistical measures often used to evaluate the quality of a regression, such as the R2 value shown in some of the plots. ↑
Link: https://andymaypetrophysicist.com/2023/11/16/modeling-hadcrut5-with-CO₂-and-without-CO₂/
Übersetzt von Christian Freuer für das EIKE
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Man sollte nicht «Statistiken hassen», sondern die dilettantische Auswertung von Daten, die elementare Prinzipien der mathematischen Statistik missachten. Eine Welt-Durchschnitts-Temperatur auf ein halbes Grad C genau ist zwar Teil der Weltklima-Religion, zugleich aber dilettantischer Unfug.
Klimamodelle, Korrelationen mit Sonnenschwankungen – offenbar sind die Ozeanischen Oszillationen nicht berücksichtigt. Gott sei Dank steigt das segensreiche CO2 nicht ewig. Erst dann werden die monokausalen CO2-Hysteriker von ihrem Wahn ablassen. Egal, was die Temperaturen machen.
Doch bis dahin haben die Vorreiter vorauseilend ihr Land samt Zukunft ruiniert. Auch ist die Gefahr groß, dass der Klimawahn mit immer neuen menschengemachten „Katastrophen“ samt Kipppunkten weiter befeuert wird. Der Wahn funktioniert einfach zu gut. Von diesem Irrsinn kann uns nur eine andere Politik befreien. So, wie fünf Jahre lang die USA unter Trump, der sich von Prof. Happer überzeugen ließ.
Wenn man glaubt eine Katastrophe zu brauchen um seine ideologische Agenda durchzudrücken, dann macht man sich halt eine bzw. behauptet halt dergleichen. Könnte irgendjemand einen für jedermann leicht einsichtigen BEWEIS liefern, dass CO2 nicht zu der proklamierten Klimakatastrophe führen wird, wäre das vollkommen egal. Dieselben Leute würden dann ziemlich schnell einfach eine neue Katastrophe konstruieren um ihre Agenda eben damit weiter verfolgen zu können.
Nicht CO2 muss ausgeschaltet werde. Die Katastrophen-Konstrukteure müssen das.
Ich mag ja vielleicht zu blöd sein, um den Text zu verstehen, aber wenn ich das richtig verstanden habe, zeigt Abb. 10 die Temperaturentwicklung der Modelle mit und ohne Einfluß von CO2. Da kein oder nur ein unwesentlicher Unterschied des Kurvenverlaufs besteht, heißt das für mich, dass die Software auch ohne irgendeinen Beitrag von CO2 die gleiche Erwärmung errechnet. Also kann man ansetzen was man will, es kommt immer eine Erwärmung heraus? Garbage in, Garbage out?
Sollte das tatsächlich so sein, muss diese Abbildung überall verbreitet werden. Sollte ich falsch liegen, erklärt mir bitte, wo mein Denkfehler ist.
Recent research: SIM-movments, barycenter, variations of Solar irradiance and the suns movments, bringing the sun closer to earth in spring equinox. Read more :
„It clearly shows that the shifts in the S-E distances are reduced more in April – September and increase more in October-February of each year of millennium M2.
This means that the input of solar irradiance to the Earth is not evenly distributed over the time of the Earth revolution, or over the Earth’s location in the orbit.“
https://www.scirp.org/journal/paperinformation.aspx?paperid=124007
Modell-Simulationen HadCRUT5 mit CO₂ und ohne CO₂
„Sie (Statistiken) sind lediglich ein Instrument, um die Gültigkeit von Ideen zu testen.“
Da kann man testen bis zum Abwinken, solange HadCRUT5 und Ableger mit gemittelten Global-Temperaturen arbeiten und schöne Bildchen produzieren, ist der Output bestenfalls HadCRUT5-Shit, auch wenn viele Wissenschaftler und Scheinwissenschaftler damit ihr Geld verdienen. Dem CO2 ist es ohnehin egal, was bei dem im Nanosekundenbereich ablaufenden Gewürfel mit Nullen und Einsen dann schließlich als Wissenschaft verkauft wird. Falsche Ansätze bei einem hochkomplexen Gebilde kann der beste Rechner der Welt nicht selbst korrigieren, auch wenn man das Ergebnis mit einem Namen HadCRUT5 adelt.
Wenn die von aller Komplexität befreite Idee dahinter nur darin besteht, dass CO2 allein das Klima mit seinen höchst komplexen Ausgleichprozessen von Tausenden Parametern bestimmt, dann können noch so viele Instrumente zu HadCRUT748204854….54367836 gefahren werden und die Rechner unter der Wärme dank ihrer Verluste in den arithmetischen Einheiten zusammenbrechen, von den Gültigkeit von Ideen werden die so erzeugten Ergebnisse dennoch befreit sein.
Die Ideengeber nutzen es weidlich aus, dass nur wenige Menschen zum Klima überhaupt bescheidene Denkansätze haben und der übrige Anteil der Menschen umso mehr in den damit gebildeten Medien-Katastrophen erstarrt und nur noch Windräder, Solarfelder, E-Autos und Wärmepumpen bauen will oder dies zumindest mit Gesetzeskraft aufgezwungen bekommt. Daneben gibt es ein paar Großverdiener, die sich vor Freude auf die Schenkel klopfen und das Kapital der zu Sündenböcken markierten Erdenbürger auf sich konzentrieren. Die brauchen natürlich HadCRUT5 und was da noch alles so geboren wird.
Lang lebe die globale Temperatur-Mittelwert-Bildung, die ist doch einfach nur genial, auch wenn sie mit Physik rein gar nichts zu tun hat! – Hauptsache das Geschäft läuft weiter und aus dem Lebensgas CO2 kann man Geldströme ableiten.
Und wenn der Himmel auf die Erde fällt, sind alle Vögel platt (…. ist nur eine These). Um die Gültigkeit dieser Idee zu testen, habe ich in meinem Computer-Modell vereinfachend die Erde ohne CO2, angenommen, und tatsächlich, praktisch alle Vögel sind platt (Ergebnis mit hohem Vertrauen)! Daraus kann man dann messerscharf folgern: Keine Vögel bei einer Atmosphäre ohne CO2. (Oder ist da vielleicht doch irgendwo ein Denkfehler enthalten? Nicht bei den platten Vögeln, sondern HadCRUT5?)
Dass die globale mittlere Temperatur Unfug ist, darüber sind wir uns einig. Mich würde interessieren, wann Sie eine Mittelwertbildung akzeptieren. Lehnen Sie generell Mittelwerte ab? Wenn ja, wie soll man gewisse Vergleiche führen? Eine Antwort würde mich sehr freuen.
#Dr. Konrad VOGE am 18. November 2023 um 12:51
Sehr geehrter Herr Voge,
natürlich arbeite ich auch mit Mittelwerten, das aber bezogen auf einzelne Messgrößen von einzelnen Sensoren, die entweder selbst stochastische Störungen erzeugen oder auf die auf dem Weg zur Erfassung der Messgrößen stochastische Störgrößen einwirken. Störgrößeneinwirkungen auf Messleitungen bleiben ohne Gleichanteil, da sie in der Regel kapazitiv oder induktiv einwirken.
Mittelungen mit den Relaxationszeiten der zu erfassenden Größen angepassten Zeitkonstanten helfen der digitalen Wandlung, nicht auf Spitzen und Ausreißer zurück zu greifen. Mit derart gemittelten Messgrößen kann mach auch gut mit bekannten physikalischen Gesetzen weiter rechnen.
Messwerte unterschiedlicher Sensoren an unterschiedlichen Orten zu mitteln, macht keinen Sinn, weil sie auf unterschiedliche Werte von Quellen zurückgreifen, wobei die Quellen sich untereinander nicht kennen und deren Größen durch unterschiedliche Einwirkarten gestört werden. Ganz schlimm sind natürlich Temperaturen rund um den Globus, auch wenn man zum Mittel der Anomaliebestimmung greift. Der Bezug für eine Anomalie ist von Ort zu Ort völlig unterschiedlichen Störgrößen ausgesetzt. Wenn man so gemittelte Temperaturen noch in die 4. Potenz setzt, ist der Unsinn perfekt. Letztlich kann aus gemittelten Anomalien keine sog. „eindimensionale“ Global-Temperatur abgeleitet werden, die ist nämlich auf wundersame Weise wieder von der Anomalie zu einer absoluten Temperatur gewandelt worden, was gar nicht geht. Bestenfalls kann man eine Anomalie mitteln, welchen Sinn soll die haben?
Solange ein Integral über einen Messwert einen physikalischen Sinn ergibt, darf man nach Division durch die Integrationszeit auch einen sinnvollen gemittelten Wert erwarten.
Nur, wie bildet man ein Integral über die Messwerte von Tausenden Sensoren an Tausenden unterschiedlichen Messorten mit weit auseinander liegenden Messgrößen, die untereinander völlig unabhängig sind? Mit den einzelnen Skalaren kann das jeder Digitalrechner vollziehen. Nur, wer zieht danach die Dimension Temperatur, zwischendurch aufbewahrt an einem sicheren Ort wieder aus der Tasche und hängt sie dann einfach an das eindimensionale Ergebnis wieder dran?
Als Schüler, der gerade Mathematik und Physik entdeckt, ist das ein verzeihlicher Fehler. Aber nur da!
Das Ganze hat so etwas, wie wenn man die von Mikrofonen aufgenommenen Signale verschiedener Konzerte an verschiedenen Orten mittelt und dann glaubt, auch das wäre nach der Wiedergabe noch Musik.