Willis Eschenbach

ERSTER TEIL – REALE WELT

Ich fing an, über die Beziehung zwischen der Absorption der Sonnenstrahlen an der Oberfläche und der Temperatur nachzudenken. Hier sind die CERES-Satellitendaten, die diese Beziehung zeigen:

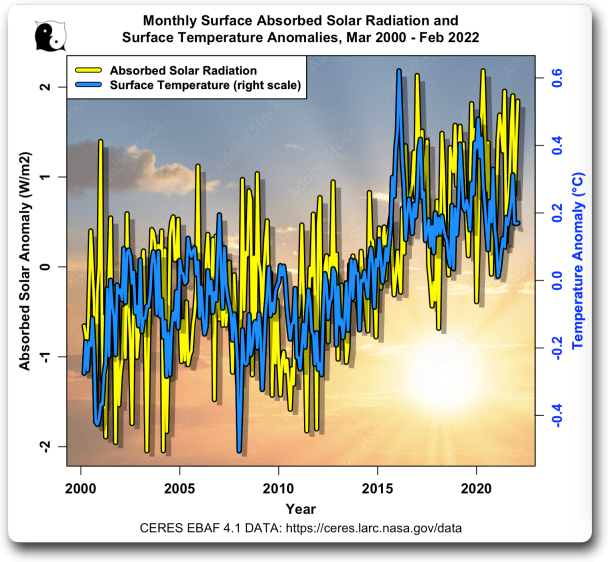
Abbildung 1. Temperatur und Absorptionsgrad der Sonnenstrahlung an der Oberfläche. Die Strahlung wird in Watt pro Quadratmeter (W/m²) angegeben.

Wie wir aufgrund unserer täglichen Erfahrung erwarten würden, steigt die Temperatur bei mehr Sonnenschein und sinkt sie bei weniger Sonnenschein.

Es stellt sich natürlich die Frage, um wie viel die Oberflächentemperatur für jedes zusätzliche W/m² an absorbierter Strahlung an der Oberfläche steigt.

Wir können uns dieser Frage auf drei verschiedene Arten nähern. Erstens, ein Streudiagramm der in Abbildung 1 gezeigten monatlichen Werte, zusammen mit der Trendlinie:

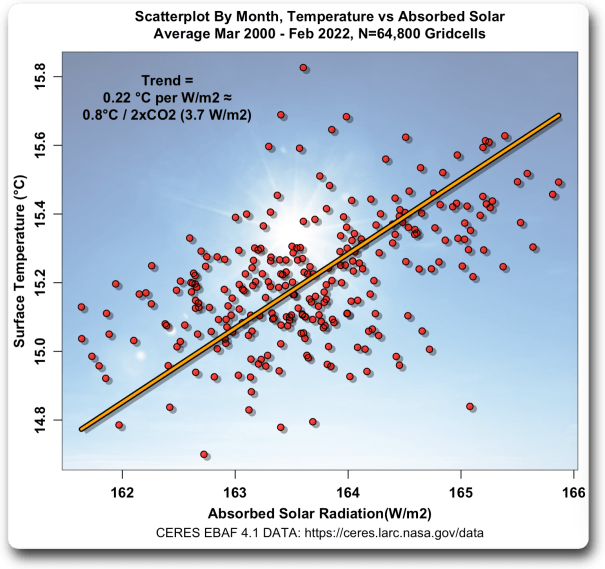
Abbildung 2. Streudiagramm, monatliche Temperatur im Vergleich zum Anteil der Sonnenstrahlung, der an der Oberfläche absorbiert wird. Da die monatlichen Durchschnittswerte mit Unsicherheit behaftet sind, habe ich die Deming-Regression und nicht die lineare Standardregression verwendet.

Die zweite Möglichkeit, die Beziehung zwischen der Oberflächentemperatur und der absorbierten Sonneneinstrahlung zu berechnen, ist eine lineare Regression auf der Basis von Gitterzellen, gewichtet nach der Fläche der Gitterzellen. Dies ergibt die gleiche Antwort, nämlich 0,22 °C pro zusätzlichem W/m² absorbierter Sonnenstrahlung.

Die dritte Möglichkeit, die Beziehung zu untersuchen, besteht darin, die langfristigen Durchschnittswerte von Temperatur und absorbierter Sonnenstrahlung als Streudiagramm für jede einzelne Gitterzelle zu betrachten. So können wir sehen, was bei unterschiedlichen Temperaturen passiert:

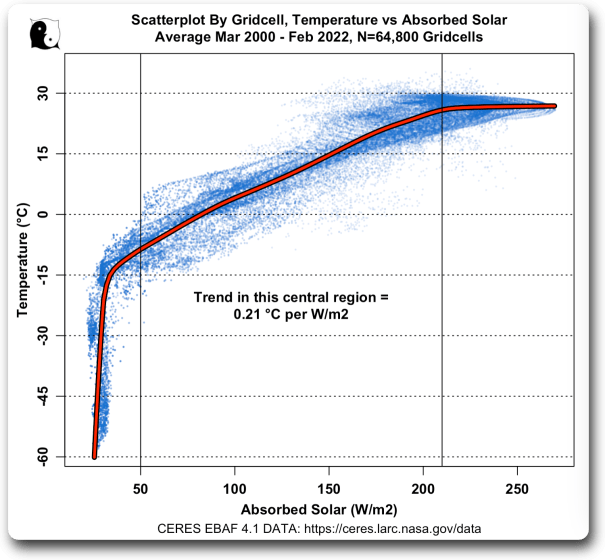
Abbildung 3. Streudiagramm, Mittelwerte der Gitterzellen, Temperatur gegenüber der durchschnittlichen absorbierten Sonnenstrahlung. Die Steigung der roten Linie zeigt den Trend der Temperatur im Verhältnis zur absorbierten Sonnenstrahlung bei verschiedenen Temperaturen.

An diesem Diagramm sind mehrere Dinge interessant. Erstens ist die Beziehung zwischen der absorbierten Sonnenstrahlung und der Temperatur über den größten Teil der Erde (zentrale Region oben) ziemlich linear, mit einem durchschnittlichen Trend (Steigung der roten Linie) von 0,21 °C pro W/m².

Um dies besser zu verstehen, ist hier eine Grafik, die zeigt, wie viel Sonnenstrahlung an der Oberfläche absorbiert wird:

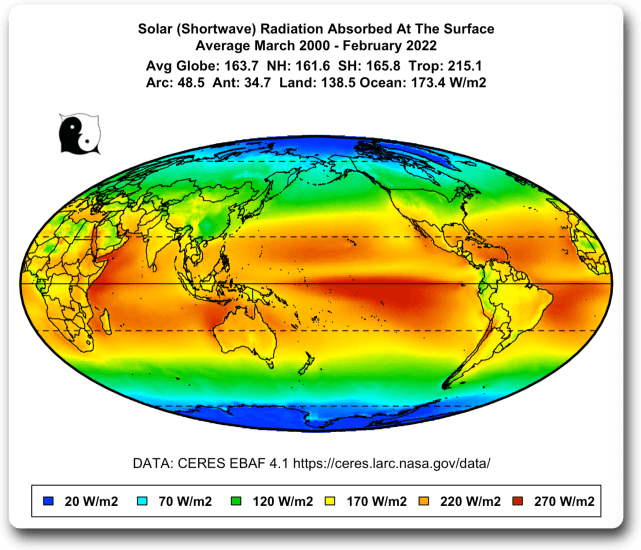
Abbildung 4. Von der Oberfläche absorbierte Sonnenstrahlung (abwärts gerichtete Strahlung minus reflektierte Strahlung)

Die Auswirkung der fast durchgängigen Bewölkung an der intertropischen Konvergenzzone (ITCZ) ist als gelber Streifen knapp über dem Äquator zu erkennen.

Um auf Abbildung 3 zurückzukommen: In den Gebieten mit geringer Sonneneinstrahlung steigt die Temperatur mit zunehmender Sonneneinstrahlung sehr schnell an. Die folgende Karte zeigt, wo sich diese Gebiete befinden:

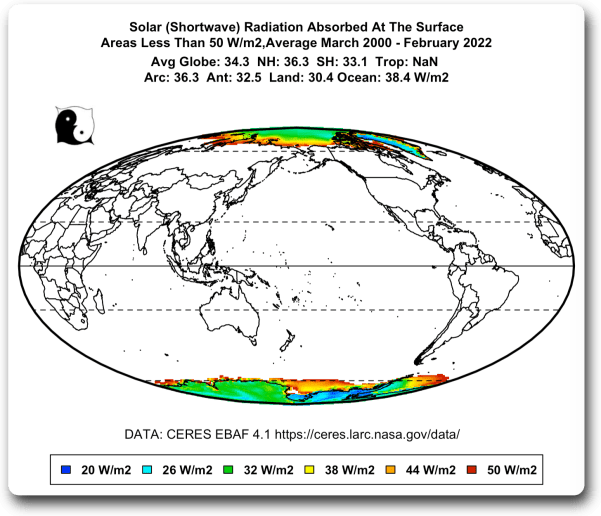
Abbildung 5. Teile der Welt, in denen die absorbierte Sonnenstrahlung im Jahresdurchschnitt weniger als fünfzig Watt pro Quadratmeter beträgt.

Und am rechten Ende der Skala in Abbildung 3 erwärmt sich die Oberfläche in Gebieten, in denen die durchschnittliche absorbierte Sonnenstrahlung über 210 W/m² liegt, überraschenderweise gar nicht so sehr. Die durchschnittliche Reaktion in den unten dargestellten farbigen Gebieten beträgt 0,03 °C pro W/m². Hier sind diese Gebiete:

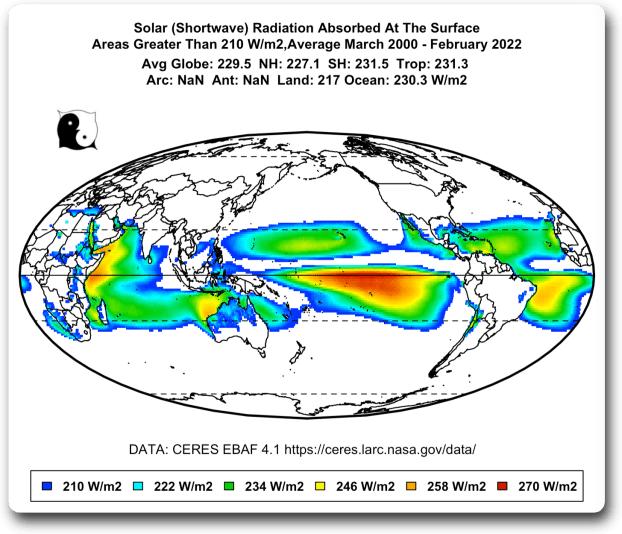
Abbildung 6. Teile der Welt, in denen die absorbierte Sonnenstrahlung im Jahresdurchschnitt mehr als zweihundertzehn Watt pro Quadratmeter beträgt.

Die horizontalen gepunkteten Linien über und unter dem Äquator auf der Karte in Abbildung 6 zeigen die Grenzen der Tropen. Man beachte, dass sich die meisten tropischen Ozeane nicht weiter erwärmen, wenn die absorbierte Sonnenstrahlung über 210 W/m² ansteigt.

Und am Ende haben wir drei verschiedene Schätzungen, wie stark die Temperaturen steigen, wenn die Sonneneinstrahlung zunimmt, und wie stark sie sinken, wenn die Sonneneinstrahlung abnimmt. Alle drei Schätzungen liegen in der Größenordnung einer Temperaturänderung von 0,2 °C je 1 W/m² Änderung der absorbierten Sonnenstrahlung. Und alle drei zeigen, dass die Temperatur mit der absorbierten Sonneneinstrahlung variiert, d. h. mit mehr Sonnenschein steigt sie an und mit weniger Sonnenschein sinkt sie, so wie wir es jeden Tag beobachten.

ZWEITER TEIL – MODELLWELT

Nachdem ich mir angesehen habe, was tatsächlich passiert, warf ich einen Blick darauf, was die Modelle sagen. Die Modelldaten sind auf der wunderbaren KNMI-Website verfügbar, indem man „Monthly CMIP5 scenario runs“ auswählt. Diese stammen aus dem Fifth Computer Model Intercomparison Project (CMIP5). Die Lufttemperatur an der Oberfläche wird als „TAS“ (Temperature Air Surface) bezeichnet. Die abwärts gerichtete Sonneneinstrahlung an der Oberfläche wird als „RSDS“ (radiation shortwave downwelling surface) bezeichnet, die reflektierte Sonneneinstrahlung an der Oberfläche als RSUS (radiation shortwave upwelling surface). Die absorbierte Strahlung ist die absteigende Sonnenstrahlung minus die reflektierte Sonnenstrahlung.

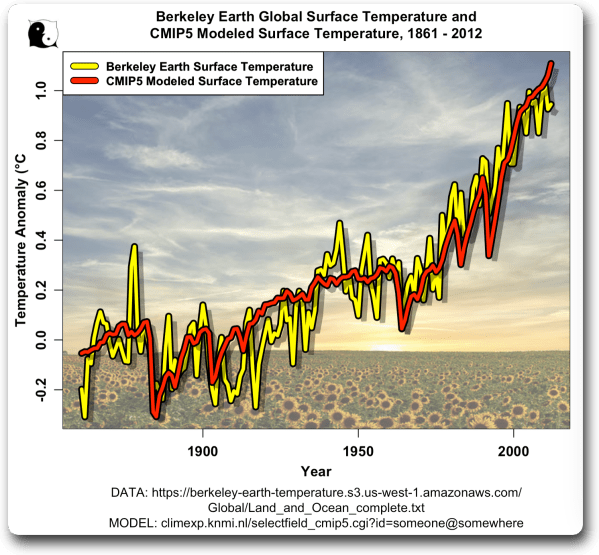
Ich habe mit den Temperaturdaten begonnen. Ich interessierte mich für die historischen Daten, die für die vier „Szenarien“, yclept RCP26, RCP45, RCP60 und RCP85, im Wesentlichen identisch sind. Ich verwendete die RCP26-Daten. Die historischen Daten enden im Jahr 2012. Hier die CMIP5-Rekonstruktion der mittleren globalen historischen Temperatur im Vergleich zur globalen Temperatur von Berkeley Earth:

Abbildung 7. Berkeley Earth und CMIP5-Modelltemperaturen im Vergleich.

Nun, das ist ziemlich respektabel. Die Modelle haben die wichtigsten Veränderungen der historischen Temperaturen gut nachgebildet. (Das wirft die Frage auf, wie verschiedene Modelle mit sehr unterschiedlichen Klimaempfindlichkeiten die Temperatur so gut nachbilden können, eine Frage, die ich in „Dr. Kiehl’s Paradox“ erörtert habe … aber ich schweife ab.)

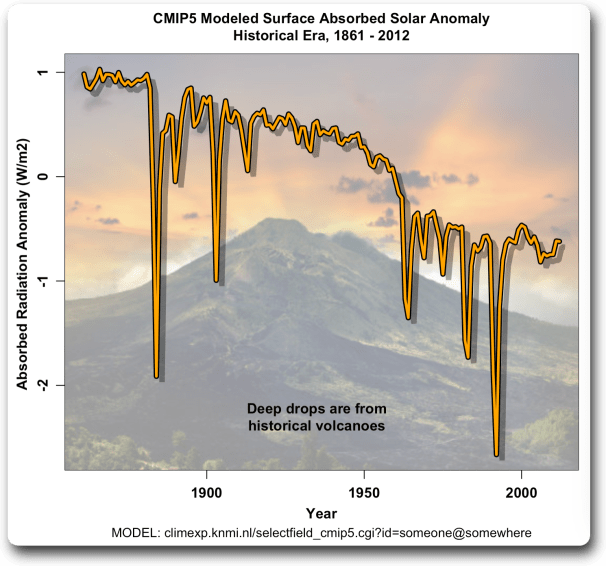
Nachdem ich all das getan hatte, schaute ich mir die modellierte absorbierte Sonnenstrahlung an … und mir fielen die Augen aus dem Kopf. Hier ist das modellierte Ergebnis. Wie bei der Temperatur sind die Ergebnisse für die Sonneneinstrahlung in den vier Szenarien im Wesentlichen identisch, daher zeige ich RCP26:

Abbildung 8. CMIP5 RCP26 historische Anomalie der absorbierten Oberflächen-Sonnenstrahlung.

Huch? Die Temperaturen steigen und die absorbierte Sonneneinstrahlung sinkt? Wie bitte? Wie unglaublich ist das denn?

Aber moment da ist noch mehr! Hier sind die gleichen RCP26-Solardaten, diesmal einschließlich der Projektion der absorbierten Sonnenstrahlung an der Oberfläche bis zum Jahr 2100:

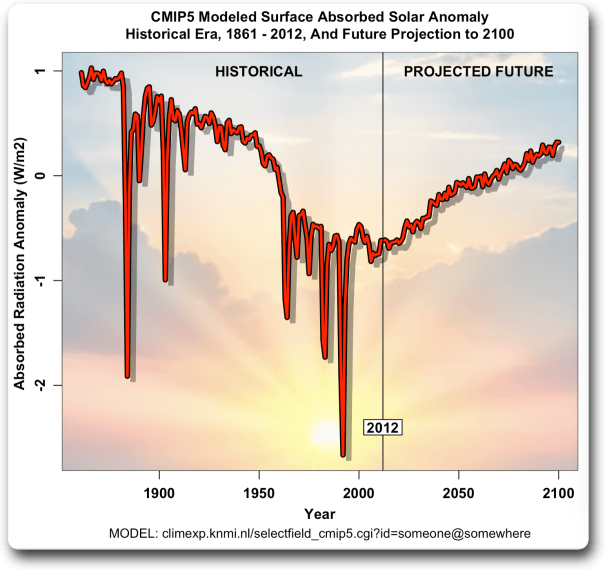
Abbildung 9. CMIP5 RCP26 historische und projizierte Anomalie der absorbierten Oberflächen-Sonnenstrahlung.

Das ist … merkwürdig. Die modellierte absorbierte Sonnenstrahlung an der Oberfläche nimmt über den gesamten historischen Zeitraum bis 2012 ab, um dann sofort wieder zu steigen.

Wahrscheinlich ist das nur ein Zufall.

Aber bedenken Sie … wenn sie irgendwie steigende historische Temperaturen bei sinkender historischer absorbierter Sonnenstrahlung erhalten, stellen Sie sich vor, wie hoch ihre zukünftigen Prognosen bei steigender absorbierter Sonnenstrahlung sein werden. Das ist eine Win-Win-Situation für die Alarmisten!

Und wie kommt es, dass ich derjenige bin, dem diese Dinge auffallen, und nicht die guten Leute, die die Modelle betreiben, oder die Leute von CMIP5?

Immer wieder neue Fragen.

Link: https://wattsupwiththat.com/2023/06/19/sun-temperatures-and-models/

Übersetzt von Christian Freuer für das EIKE

 

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken