Von Henri Masson, Professor (emeritus) an der University of Antwerp (Belgium) und Michael Limburg Dipl. Ing.

Dieser Artikel wiederholt weitgehend einen Teil des Vortrags, den der Autor Henri Masson auf der 12. jährlichen EIKE-Konferenz (München 2018) gehalten hat. Der Text, der die PowerPoint-Folien der Präsentation umgibt, ist jedoch unveröffentlicht, ebenso wie das, was den Kern dieser Studie ausmacht: die Analyse der Anpassungs-Residuen von Hadcrut 5.0.1.0-Daten durch eine Summe von Sinuskurven oder eine lineare Regressionslinie.

Das Video dazu findet man hier.

Teil 4

Der richtige Weg zur Vorgehensweise

Die Anpassung von Zeitreihen, sei es durch eine Linie, eine oder mehrere Sinuskurven oder eine andere Funktion, muss bestimmten, oft vernachlässigten Bedingungen genügen, um statistisch gültig zu sein. Eine dieser Bedingungen betrifft das Residuum der Anpassung. Dieser muss:

● keine Informationen mehr enthalten

● ● stationär sein: (nicht mit der Zeit wachsen oder abnehmen)

● ● keine signifikanten periodischen Komponenten mehr enthalten

● mit weißem Rauschen vergleichbar sein

● ● um die Regressionskurve herum gemäß einer Normalverteilung verteilt sein

● ● eine Autokorrelationsfunktion haben, die mit der von weißem Rauschen vergleichbar ist

● die Homoskedastizität einhalten (eine homogene Streuung über die Regressionskurve aufweisen).

Der Sache zuliebe und trotz aller Kritik, die in dieser Arbeit an den globalen Temperaturanomalien geübt wird, wollen wir diese Kriterien auf die Anpassung der jährlichen HADCRUT 5.0.1.0-Daten anwenden, die vom englischen Wetterdienst zusammengestellt wurden, eben weil sie vom IPCC verwendet werden; und wir wollen diese Daten verwenden, um die Qualität ihrer Anpassung durch eine Regressionslinie zu bewerten (wie es das IPCC tut, wenn es von einem globalen durchschnittlichen Temperaturanstieg von einigen Grad pro Jahrhundert spricht). Zum Vergleich wollen wir auch die Qualität der Anpassung bewerten, die mit einer Summe von Sinuskurven erzielt wird, deren Bedeutung sich im Laufe der folgenden Analyse zeigen wird.

Hadcrut-5-Daten und ihre Anpassung

Die jährlichen Hadcrut-5.0-Daten seit 1850 sind unten dargestellt (Abbildung 26). Es handelt sich dabei um die neuesten Daten, die bisher verfügbar sind:

Abbildung 26. Jährliche globale Temperaturanomalien (Hadcrut 5.0-Daten).

Im Prinzip ist diese Abbildung identisch mit Abbildung 25, die mit Daten von 2001 erstellt wurde. Der Leser wird das Ausmaß der an den vergangenen Temperaturen vorgenommenen Anpassungen zu schätzen wissen, Anpassungen, die nicht immer ordnungsgemäß dokumentiert und noch weniger überzeugend begründet sind (Abbildung 27):

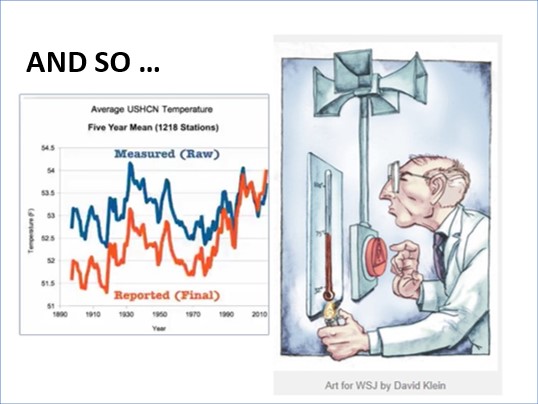
Abbildung 27 Nicht immer harmlose Anpassungen der Daten. Um 2010, während einer Episode dessen, was seither als Climategate bezeichnet wird, enthüllten Whistleblower die Existenz kompromittierender E-Mails von Met-Beamten, die über Datenmanipulationen für die „Bedürfnisse der Klimasache“ berichteten, d. h. die Menschen über die Medien zu alarmieren und die politischen Entscheidungsträger zu dringendem Handeln zu bewegen. Dies sind bekannte Bestandteile des Social Engineering (eine elegantere Formel als „Massenmanipulation“, um diese Art von Verhalten zu beschreiben), die ein fester Bestandteil des Medienarsenals von Umweltschützern und Klimaalarmisten sind. Das Bedürfnis von Wissenschaftlern und Aktivisten, die Risiken und die Dringlichkeit ihrer Beseitigung zu übertreiben, ist leider zum Mainstream geworden, zum Nachteil der intellektuellen Integrität, die jede wissenschaftliche Arbeit begleiten sollte, die diesen Namen verdient.

Das Leistungsspektrum (Fourier-Transformation der Autokorrelationsfunktion) dieser Daten zeigt das Vorhandensein einer kontinuierlichen Komponente (Frequenz Null) und einiger Periodizitäten, die größer sind als die der kontinuierlichen Komponente. Diese Beobachtung rechtfertigte die Entscheidung, die empirische Kurve durch eine Summe von Sinuskurven zu beschreiben.

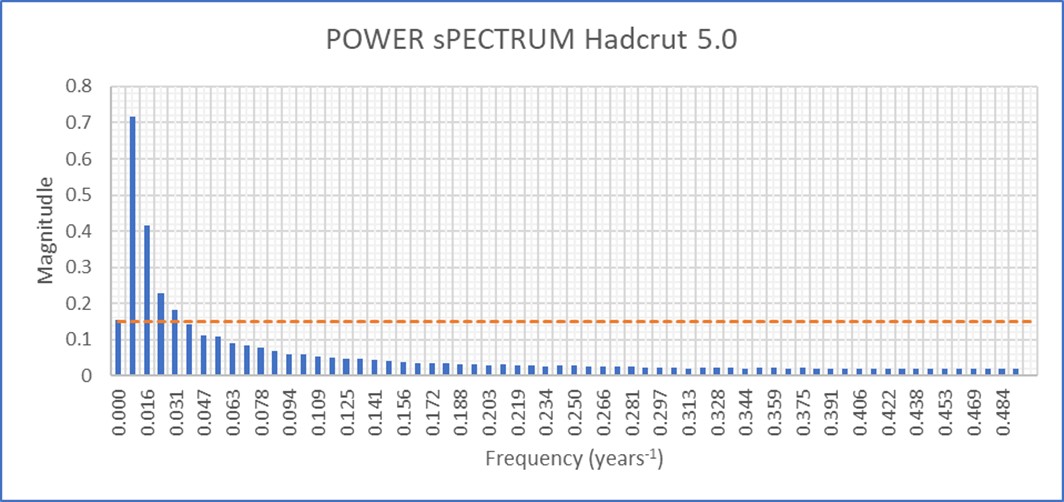Abbildung 28. Leistungsspektrum der Hadcrut 5.0.1-Daten. Die gestrichelte rote Linie entspricht dem Betrag der kontinuierlichen Komponente (Nullfrequenz). Diese Frequenzen sind Näherungswerte, da sie (algorithmisch) einem Vielfachen der Abtastfrequenz geteilt durch die Länge der Datenreihe entsprechen. Diese Länge muss (algorithmisch) immer ein Exponent von 2 sein. In diesem Fall bedeutet dies 256 Messpunkte und eine Zerlegung des Leistungsspektrums in 128 Punkte (das Ergebnis einer Fourier-Analyse nach dem FFT-Verfahren ist symmetrisch, was die Anzahl der Punkte durch zwei teilt). Die maximale Frequenz beträgt 0,5 Jahre (die halbe Abtastrate nach dem Shannon-Theorem), die minimale Frequenz beträgt 1/128.

Anpassung der Hadcrut 5.0-Daten

Die folgende Abbildung 29 zeigt die jährlichen HADCRUT 5.0.1-Daten seit 1850 und ihre Anpassung durch eine Regressionslinie und eine Summe von 4 Sinuskurven, deren Parameter in der folgenden Tabelle angegeben sind. Diese Parameter wurden (Tabelle 3) durch nichtlineare Optimierung der Summe der Quadrate der Abweichungen (SSE) definiert, die minimiert werden sollten.

Abbildung 29. Anpassung der Hadcrut 5.0.1-Daten durch die Regressionsgerade (schwarz gestrichelte Linien) und eine Summe von 4 Sinuskurven (rote Kurve)

Tabelle 3. Optimierte Parameter der 4 Anpassungs-Sinusoide. Die optimalen Frequenzen unterscheiden sich von den per Leistungsspektrum erhaltenen, da letztere eine Reihe von diskreten Werten sind (Vielfache der Abtastfrequenz geteilt durch die Länge der nutzbaren Daten). Die Perioden von 22 Jahren, 60 Jahren, 120 Jahren (unter der Harmonischen von 60 Jahren) und die von etwa 300 Jahren wurden in der Literatur mit natürlichen Zyklen in Verbindung gebracht. Die Sinuskurve von 300 Jahren ist im Leistungsspektrum einer (abgeschnittenen) Zeitreihe von 256 Jahren nicht als solche zu erkennen. Sie verschmilzt mit der kontinuierlichen Komponente.

Am Rande sei bemerkt, dass die Extrapolation des sinusförmigen Ansatzes eine Stagnation der Temperaturen voraussagt, die zwei bis drei Jahrzehnte lang leicht um den aktuellen Wert schwanken, bevor sie ab 2050 wieder sinken, und dies ohne jegliches menschliches Eingreifen. Die lineare Regression sagt einen kontinuierlichen Temperaturanstieg in der Größenordnung von 0,5 °C pro Jahrhundert voraus, ohne dass der Mensch eingreift; damit würden noch vier Jahrhunderte verbleiben, bevor die verhängnisvollen zwei Grad erreicht werden, bei deren Überschreitung die Alarmisten (ohne rationale Begründung) irreversible Klimakatastrophen vorhersagen.

Es gäbe also keinen Klimanotstand, unabhängig davon, welcher Ansatz gewählt wird.

Qualität der Anpassung

Die Qualität einer Zeitreihenanpassung wird in der Regel durch den Vergleich der Quadratsummen der Anpassungsresiduen (SSE Sum of Squared Errors) bestimmt, die minimiert werden sollten. Da diese Summe von der Anzahl der Messpunkte abhängt, wird, wenn die zu vergleichenden Zeitreihen unterschiedlich lang sind, vorzugsweise das Bestimmtheitsmaß R² verwendet, berechnet mit der folgenden Formel:

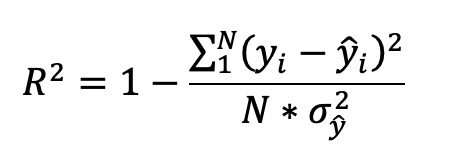
In dieser Formel:

N ist die Anzahl der Punkte in der Zeitreihe

yi die in der Zeitreihe enthaltenen Werte

ŷ die entsprechenden bereinigten Werte

σ² die Varianz der in der Zeitreihe enthaltenen Daten

R² misst den Prozentsatz der Gesamtvarianz der Daten, der durch ihre Anpassung erklärt wird. Wie aus der nachstehenden Tabelle hervorgeht, führt in diesem Fall die Anpassung durch 4 Sinuskurven zu einem Wert von R² = 0,91, der der linearen Regression = 0,65.

Tabelle 4. Bewertung der Anpassungsqualität von Hadcrut 5.0-Daten durch 4 Sinuskurven und eine lineare Regression. Die 4 Sinuskurven erklären 91 % der Gesamtvarianz, während die lineare Regression 64 % erklärt.

Dieses Ergebnis ist nicht überraschend, da bei der Anpassung durch 4 Sinuskurven 12 Parameter verwendet werden (viermal eine Amplitude, eine Frequenz und eine anfängliche Phasenverschiebung), während die lineare Regression nur zwei verwendet. Es ist anzumerken, dass die Hinzufügung einer fünften Sinuskurve zum Sinusmodell nur einen marginalen Qualitätsgewinn bedeuten würde. Dies würde man als parametrische Überdimensionierung bezeichnen.

Überprüfung der Anwendungsbedingungen der Anpassungsverfahren.

Die erste Überprüfung ist rein visuell und besteht darin, die Entwicklung der Residuen in Abhängigkeit von der Zeit zu untersuchen. Beachten Sie, dass diese folgende Bedingungen erfüllen müssen:

● stationär, ohne zunehmende, abnehmende oder schwankende Tendenz mit der Zeit

● symmetrisch um den Nullpunkt verteilt, sonst führt die Anpassung zu einer Verzerrung

● Homogen (ohne Streuungsschwankung) um ihren Mittelwert Null über die Zeit verteilt

Abbildung 30 zeigt, dass die Residuen, die der Anpassung durch 4 Sinuskurven entsprechen, diese drei Bedingungen in etwa erfüllen; dies ist bei den Residuen der linearen Regression nicht der Fall:

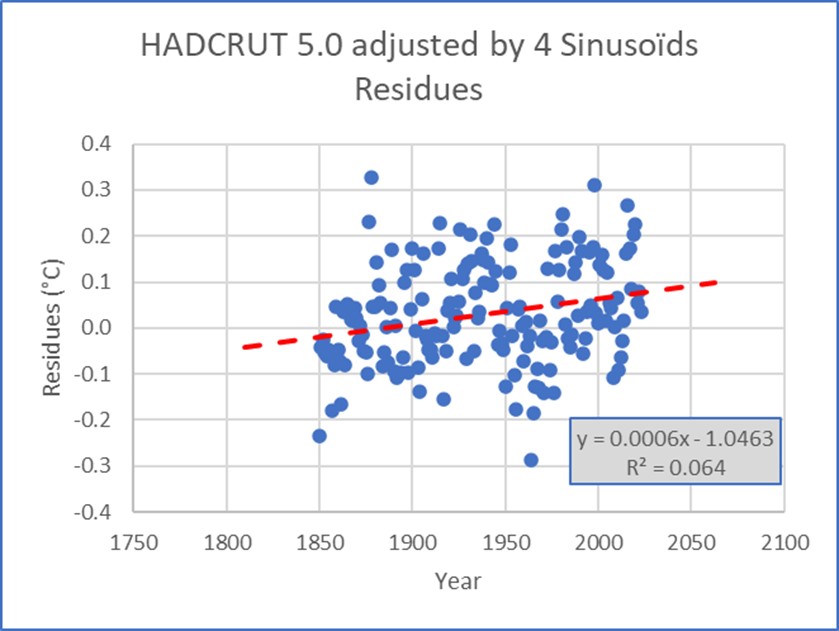
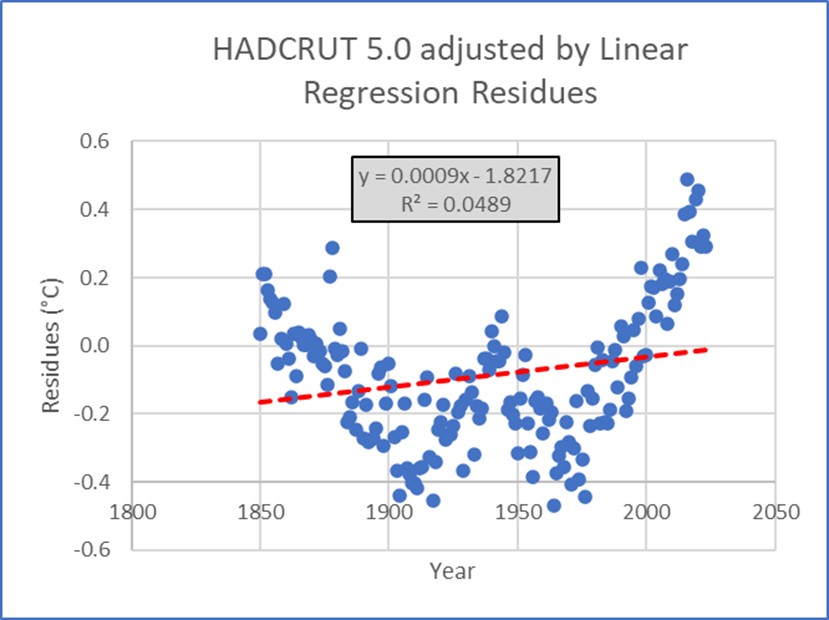
Abbildung 30. Entwicklung der Residuen der Anpassung der Hadcrut 5.0-Daten. Oben die Anpassung durch 4 Sinuskurven, unten die Anpassung durch die Regressionsgerade. Die Sinusoid-Anpassung führt zu Residuen, die zwar nicht exakt qualifiziert sind, aber viel näher an den Residuen liegen, die sich aus der linearen Regressionsanpassung ergeben.

Das zweite Kriterium der Anpassungsqualität bezieht sich auf die Amplitudenverteilung der Residuen, die im Idealfall einer Normalverteilung folgen sollte. Dies lässt sich visuell beurteilen, wie in der nachstehenden Abbildung dargestellt, indem man ein Diagramm erstellt, das dem Histogramm der Residuen eine Normalverteilung mit demselben Mittelwert und derselben Standardabweichung überlagert. Auch hier ist zu erkennen, dass die Verteilung der Residuen der Sinusanpassung näher an der theoretischen Kurve liegt als die Verteilung der Residuen der linearen Regression, die auch in diesem Fall eindeutig bimodal ist.

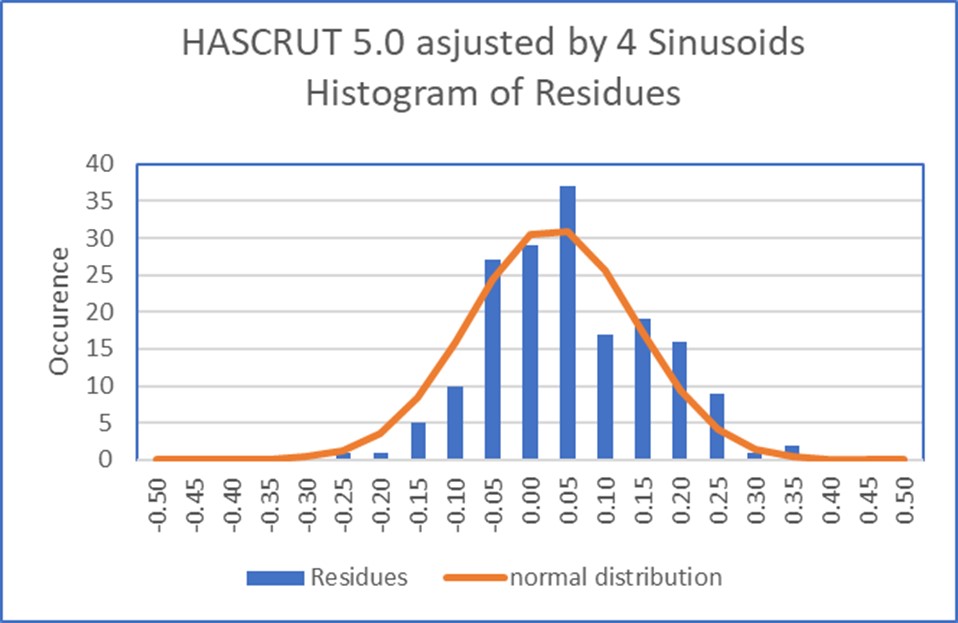
Abbildung 31. Histogramm der Residuen im Vergleich zu einer Normalverteilung. Oben für die sinusförmige Anpassung, unten für die lineare Regression.

Ein anderer visueller Ansatz ist die Erstellung eines QQ-Diagramms, in dem die Dezile oder Perzentile (Unterteilung der Punktpopulation in 10 bzw. 100 gleiche Teile) der Normalverteilung auf der Abszisse und die der Residuen-Verteilung auf der Ordinate aufgetragen werden. Im Idealfall sollten die Punkte genau mit der aufsteigenden Diagonale der Abbildung übereinstimmen.

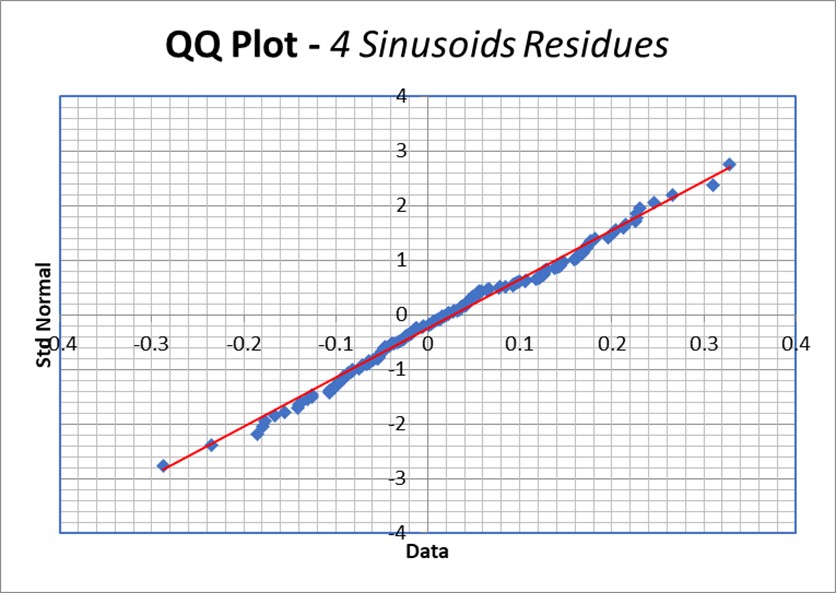
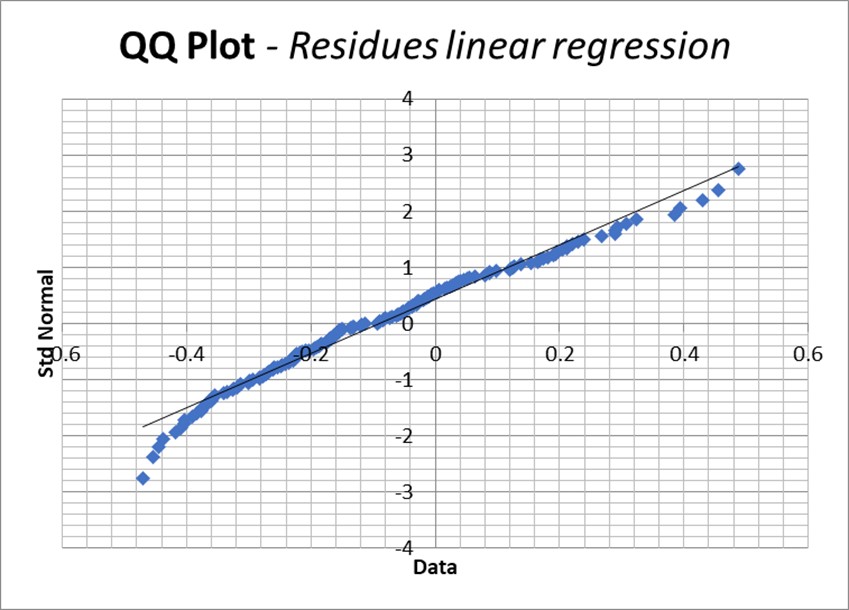
Abbildung 32. QQ-Diagramm der Residuen im Vergleich zu einer Normalverteilung. Oben: Sinusförmige Anpassung. Unten, lineare Regression. Im Idealfall sollten die Punkte auf die Diagonale fallen. Es ist zu erkennen, dass die Residuen der linearen Regressionsanpassung weiter und an den Enden sogar erheblich abweichen.

Mit einem der zahlreichen Hypothesentests kann auch die Übereinstimmung mit einer Normalverteilung geprüft werden. Unter diesen Tests gehören die Tests von Shapiro-Wilkinson und Agostino-Pearson zu den effizientesten. Die sinusförmige Anpassung besteht beide Tests, während die lineare Regressionsanpassung beide Tests nicht besteht (Tabelle 5):

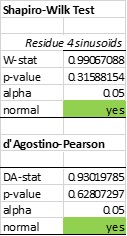
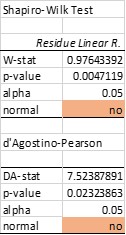
Tabelle 5. Zwei Konformitätstests mit einer Normalverteilung. Links die Verteilung der Residuen einer sinusförmigen Anpassung. Rechts ist die Verteilung der Residuen einer linearen Regression zu sehen. Die sinusförmigen Anpassungsresiduen der Hadcrut-Daten bestehen beide Tests, im Gegensatz zu den linearen Anpassungsresiduen.

Der letzte Punkt ist zu prüfen, ob die Residuen mit weißem Rauschen vergleichbar sind. Eine gängige Methode zur Durchführung dieser Prüfung ist die Untersuchung der Autokorrelations- und partiellen Autokorrelationsfunktionen der Anpassungsresiduen und der Vergleich der Ergebnisse mit den 95 %-Konfidenzintervallen von weißem Rauschen (siehe Abbildung 33 unten).

Zur Erinnerung: Die Autokorrelationsfunktion entspricht der folgenden Formel:

Wobei N die Anzahl der Daten x der Zeitreihe, τ der Offset und σ² die Varianz ist.

Auch hier besteht die Anpassung durch 4 Sinuskurven den Test mehr oder weniger gut, während die Residuen der linearen Anpassung weitgehend versagen.

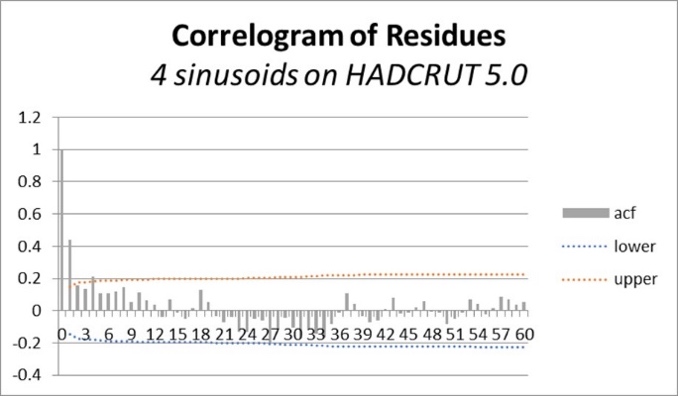
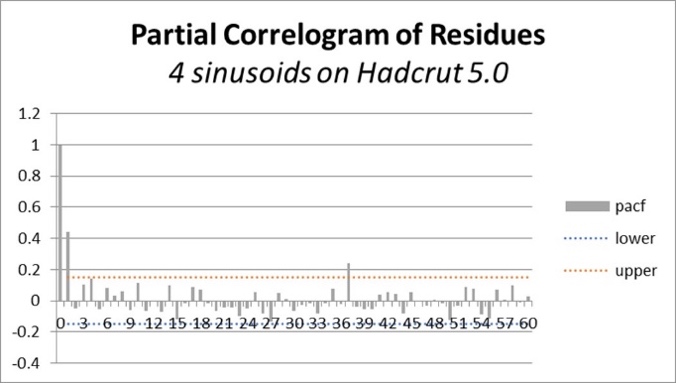
Abbildung 33. Autokorrelationsfunktionen und partielle Autokorrelation der Residuen. „4 Sinuskurven“ bedeutet sinusförmige Anpassungsresiduen; „Linear“ die einer linearen Regression, „Korrelationsdiagramm“ die Autokorrelationsfunktionen und „Partielles Korrelationsdiagramm“ die partiellen Autokorrelationsfunktionen. Bei letzteren handelt es sich um Autokorrelationsfunktionen, die um die Auswirkungen der Spitzenwerte, die kleineren Verschiebungen entsprechen, „bereinigt“ sind. Weißes Rauschen ergibt eine Autokorrelationsfunktion mit einer anfänglichen Spitze bei Nullverschiebung und dann unbedeutenden Schwankungen, die dem Rauschen entsprechen. In den Abbildungen geben die schraffierten Bereiche die Grenzen des 95%-Konfidenzintervalls an. Damit eine Anpassung gültig ist, müssen die Autokorrelationsfunktionen ihrer Residuen innerhalb der Grenzen dieses Konfidenzintervalls für weißes Rauschen bleiben. Bei der Anpassung durch 4 Sinuskurven wird dies mit zwei Spitzenwerten erreicht. Die Regressionsgeraden-Anpassung scheitert weitgehend, da die Autokorrelationsfunktion typisch für nicht-stationäre Daten ist. Die partiellen Autokorrelationsfunktionen sind sehr ähnlich; sie haben beide eine leicht signifikante Spitze für eine 38-jährige Verzögerung. Und signifikante Spitzen für 1-Jahres-Verzögerungen; diese Spitze hat die doppelte Amplitude im Fall der linearen Anpassung.

Die Ergebnisse der durchgeführten Residuen-Analyse sind in der nachstehenden Tabelle zusammengefasst:

Tabelle 6. Zusammenfassung der Übereinstimmungsanalyse

Das Urteil ist endgültig: Keine der Bedingungen für die Gültigkeit einer Zeitreihenanpassung wird durch eine auf Hadcrut 5.0-Daten angewandte Regressionslinie erfüllt. Diese Feststellung bedeutet auch und vor allem, dass jede Extrapolation einer linearen Regression, die auf Hadcrut 5.0-Daten angewendet wird, statistisch unzulässig ist. Und dennoch…

Bevor wir zum Schluss kommen und um das Konzept der Temperaturanomalien endgültig zu desakralisieren, können wir sehen, dass sie in der Tat nichts anderes sind als das Ergebnis der Anpassung der Temperaturdaten durch ein Verfahren der „wirklich rudimentären Projektion“: Wir untersuchen das Ergebnis einer Anpassung der Daten durch den Durchschnitt, der über einen festen Zeitraum von 30 Jahren berechnet wird, der am Anfang des Messfensters endet, das sich selbst über einen Zeitraum von 30 Jahren entwickelt, bevor es zurückgesetzt wird. Es handelt sich nicht einmal um ein einfaches Verfahren des gleitenden Durchschnitts, da der Bezugszeitraum nicht dem Messpunkt „folgt“. Und natürlich erfüllt dieser Rückstand nicht die oben beschriebenen Bedingungen. Daraus lässt sich nur ableiten, dass die Verwendung von Temperaturanomalien eine schlechte, statistisch nicht abgesicherte Technik zur Temperaturanpassung ist, mehr nicht.

Schlussfolgerungen

Lokale Daten von Wetterstationen, Messungen der Meerestemperatur (sei es durch Versenkung, Kühlwasser-Temperaturmessung oder Bojen) oder Satelliten unterliegen Mess- und Kalibrierungsfehlern, die sie nicht vollständig miteinander kompatibel machen, und sind noch weniger in der Lage, kleinste Temperaturschwankungen von Jahr zu Jahr zu erkennen, die sich mit experimentellen Fehlerkreuzungen vermischen.

Das Konzept der globalen Temperaturanomalie hat nicht nur keine physikalische oder geografische Bedeutung, sondern leidet auch unter einem Mangel an räumlicher und zeitlicher Repräsentativität und erzeugt falsche Trends und Verzerrungen bei Vorhandensein zyklischer Komponenten in den Rohdaten. Es wird daher dringend davon abgeraten, Temperaturanomalien zur Rechtfertigung klimapolitischer Maßnahmen zu verwenden.

Andererseits sind die klimatischen Folgen lokal. Das IPCC stützt seine die Empfehlungen rechtfertigenden Projektionen auf globale Zirkulationsmodelle, die mit globalen Temperaturanomalien kalibriert sind. Diese Modelle sind nicht in der Lage, lokale, ja sogar regionale Temperaturschwankungen zu beschreiben, und zwar beim derzeitigen Stand ihrer Entwicklung und den Fähigkeiten der Supercomputer, die für die Durchführung der nötigen langen und komplexen Berechnungen erforderlich sind.

Trotz dieser Kritikpunkte und um die Analyse der IPCC-Praktiken zu vervollständigen, wurde die Zeitreihe HADCRUT 5.0.1 der globalen Temperaturanomalien analysiert, die vom British Met entwickelt wurde und vom IPCC weitgehend zur Kalibrierung seiner Modelle verwendet wird.

Diese Analyse zeigt deutlich die statistische Legitimität der Annäherung an die jährlichen Klimadaten HADCRUT 5.0.1 durch eine Summe von 4 Sinuskurven, im Gegensatz zu einer linearen Regression, die die meisten Bedingungen ihrer Anwendbarkeit in diesem Fall verletzt und die daher zu Schlussfolgerungen führt, die sicherlich alarmierend, aber vollkommen unbegründet sind.

Es sei daran erinnert, dass, auch wenn dies gängige Praxis ist, nicht besagt, dass die beste Anpassung der vorhandenen Daten auch die beste Projektion in die Zukunft ergibt.

Die Extrapolation lokaler Klimadaten, der Vergleich der verschiedenen Anpassungs- und Projektionsmethoden, die dem „Stand der Technik“ entsprechen (multiple Regressionen, Dekomposition, Arima, neuronale Netze usw.), die Definition der Konfidenzintervalle dieser Projektionen unter Berücksichtigung der Fehlerfortpflanzung, die Erkennung einer möglichen chaotischen Signatur (durch die so genannte nichtlineare Analyse) und in einigen Fällen sogar die Grenzen des Vorhersagehorizonts (durch die Sichtbarkeitskarte) werden in den kommenden Monaten erneut veröffentlicht werden.

Jedem seine Wahrheit, wir wollen Sie nicht überzeugen, sondern Ihnen helfen, das, was man Ihnen über das Klima erzählt, auf der Grundlage einiger elementarer mathematischer Überlegungen kritisch zu reflektieren.

Ende

Wer den ganzen Bericht lesen will hier ist er als pdfIPCC has it all wrong Li-Edition Deutsch

Beitrag als PDF speichernBeitrag drucken