Durch eine für mich typische Reihe von Missverständnissen und Zufällen bin ich dazu gekommen, mir die durchschnittlichen Modellergebnisse des Climate Model Intercomparison Project 5 (CMIP5) anzusehen. Ich habe die Durchschnittswerte der einzelnen Modelle für jedes der vier Szenarien verwendet, insgesamt also 38 Ergebnisse. Der gemeinsame Zeitraum für diese Ergebnisse ist 1860 bis 2100 oder eine ähnliche Zahl. Ich habe die Ergebnisse von 1860 bis 2020 verwendet, damit ich sehen konnte, wie die Modelle abschneiden, ohne eine imaginäre Zukunft zu betrachten. Die CMIP5-Analyse wurde vor ein paar Jahren durchgeführt, so dass für alle Jahre bis 2012 aktuelle Daten vorlagen. Die 163 Jahre von 1860 bis 2012 waren also eine „Nachhersage“ unter Verwendung tatsächlicher Treibhausdaten, und die acht Jahre von 2013 bis 2020 waren Prognosen.
Abbildung 1. Durchschnittswerte der CMIP5-Szenarien nach Modell sowie der Gesamtdurchschnitt.
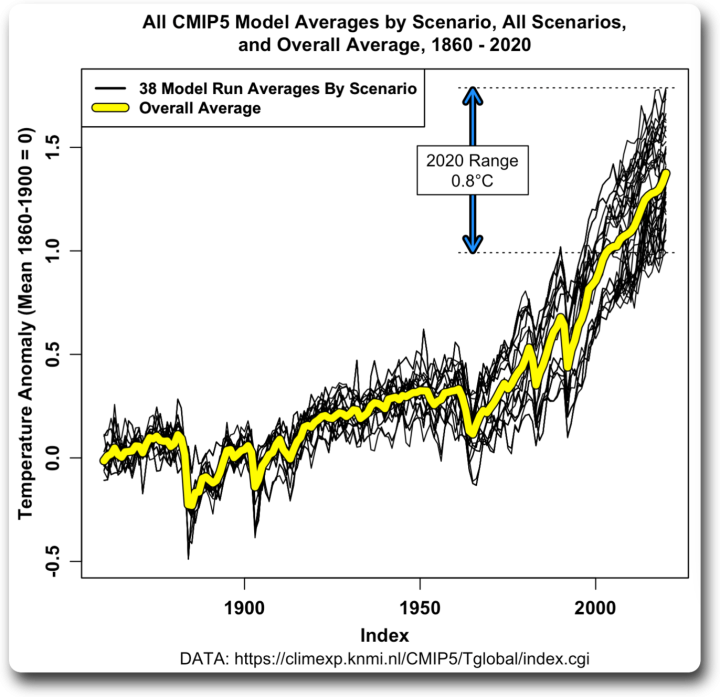
An Abbildung 1 waren für mich mehrere Dinge interessant. Erstens die große Spanne. Ausgehend von einer gemeinsamen Basislinie reichten die Modellergebnisse bis 2020 von einer Erwärmung von 1°C bis zu einer Erwärmung von 1,8°C…
In Anbetracht dieser schrecklichen Temperaturstreuung zwischen den Modellen in einem Hindcast bis 2012 plus acht Jahre Vorhersage, warum sollte jemand den Modellen für das Jahr 2100 vertrauen?
Die andere Sache, die mich interessierte, war die gelbe Linie, die mich an meinen Beitrag mit dem Titel [übersetzt] „Das Leben ist wie eine schwarze Schachtel Pralinen“ erinnerte. In diesem Beitrag habe ich die Idee einer „Black Box“-Analyse erörtert. Das Grundkonzept besteht darin, dass man eine Blackbox mit Eingängen und Ausgängen hat und die Aufgabe darin besteht, ein einfaches oder komplexes Verfahren zu finden, um den Eingang in den Ausgang zu verwandeln. Im vorliegenden Fall ist die „Black Box“ ein Klimamodell, die Eingaben sind die jährlichen „Strahlungsantriebe“ durch Aerosole, CO2, Vulkane und dergleichen, und die Ausgaben sind die jährlichen globalen Durchschnittstemperaturwerte.
Im gleichen Beitrag wird auch gezeigt, dass die Ergebnisse des Modells extrem genau nachgebildet werden können, indem die Eingaben einfach verzögert und neu skaliert werden. Hier ein Beispiel aus dem Beitrag, wie gut das funktioniert:
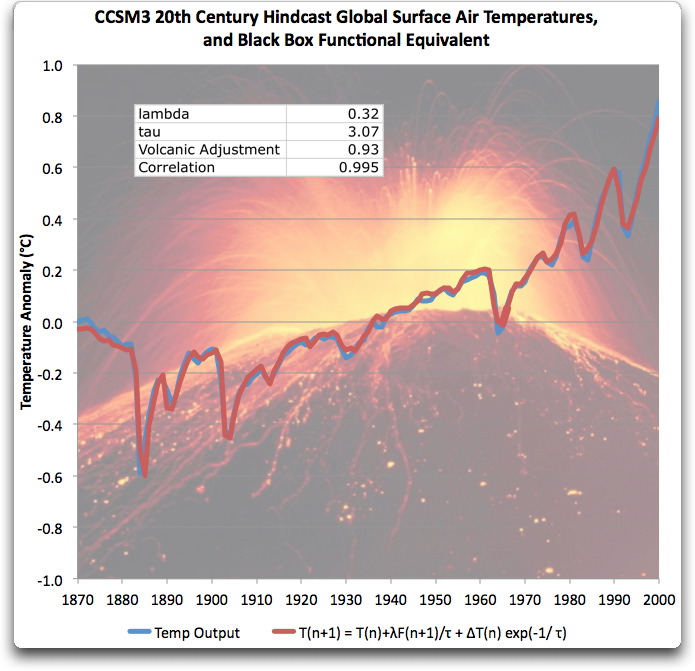
Abbildung 2. Original Bildunterschrift: „Funktionale Äquivalenzgleichung des CCSM3-Modells, verglichen mit der tatsächlichen CCSM3-Ausgabe. Die beiden sind fast identisch.“
Ich besorgte mir also eine Reihe von CMIP5-Forcings und verwendete sie, um den Durchschnitt der CMIP5-Modelle zu emulieren (Links zu den Modellen und Forcings in den technischen Anmerkungen am Ende). Abbildung 3 zeigt das Ergebnis:
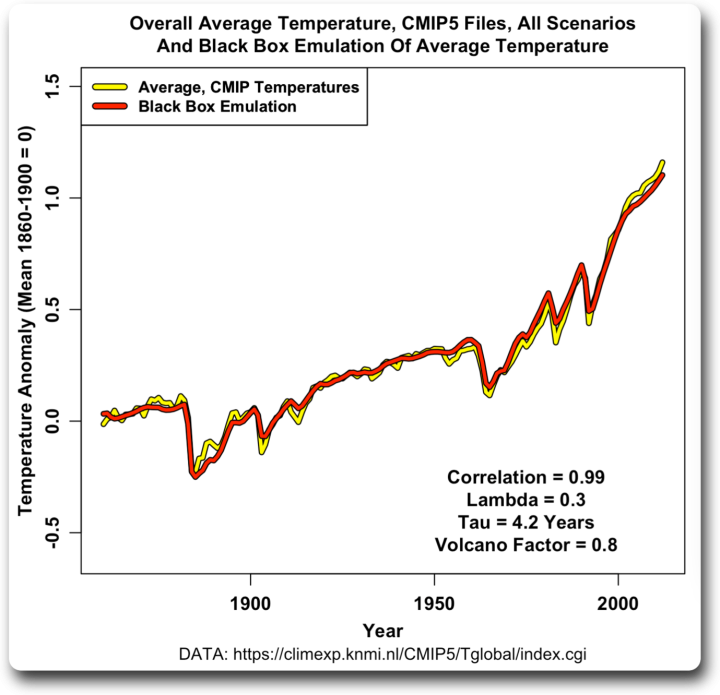
Abbildung 3. Durchschnitt der CMIP5-Dateien wie in Abbildung 1, zusammen mit der Black-Box-Emulation.
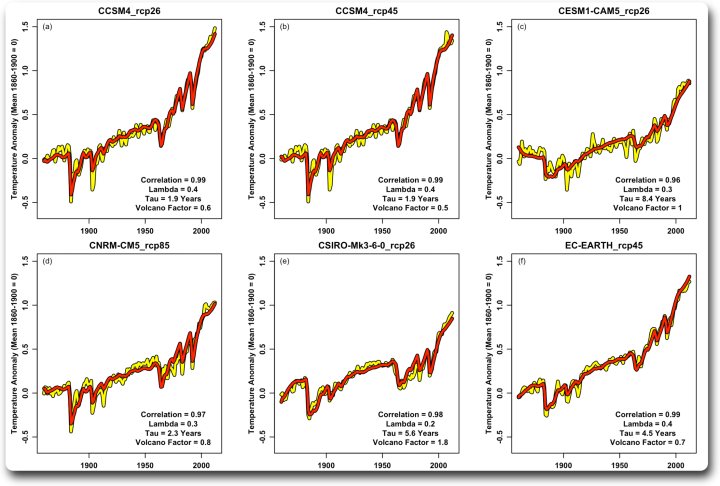
Auch hier ist die Übereinstimmung sehr gut. Nachdem ich das gesehen habe, wollte ich mir einige Einzelergebnisse ansehen. Hier ist der erste Satz:
Abbildung 4. Durchschnittswerte für sechs Szenarien aus verschiedenen Modellen.
Ein interessanter Aspekt dabei ist die Variation des Vulkanfaktors. Die Modelle scheinen mit dem Antrieb durch kurzfristige Ereignisse wie Vulkane anders umzugehen als mit dem allmählichen Anstieg des Gesamtantriebs. Und die einzelnen Modelle unterscheiden sich voneinander, wobei der Faktor in dieser Gruppe von 0,5 (halber vulkanischer Faktor) bis 1,8 (80 % zusätzlicher vulkanischer Faktor) reicht. Die Korrelationen sind alle recht hoch und reichen von 0,96 bis 0,99. Hier ist eine zweite Gruppe:
Abbildung 5. Sechs weitere Szenario-Durchschnittswerte aus verschiedenen Modellen.
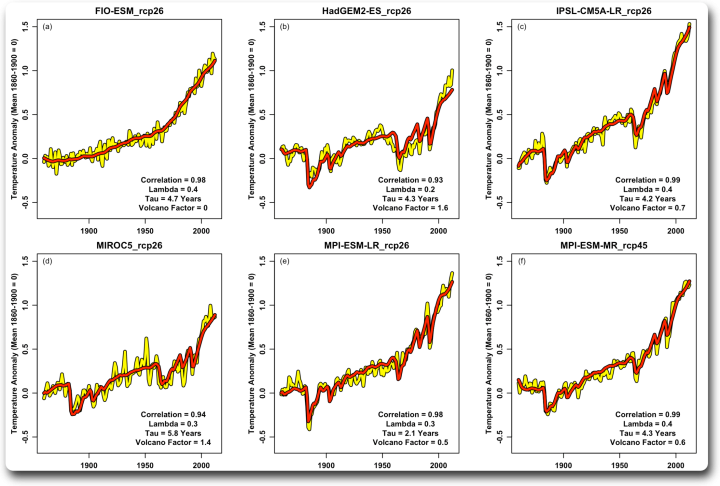
Panel (a) oben links ist insofern interessant, als dass die Vulkane offensichtlich nicht in den Antrieb für dieses Modell einbezogen wurden. Infolgedessen ist der Faktor für den vulkanischen Antrieb gleich Null … und die Korrelation beträgt immer noch 0,98.
Dies zeigt, dass trotz der unglaublichen Komplexität und der Tausenden und Abertausenden von Codezeilen und der 20.000 2D-Gitterzellen mal 60 Schichten gleich 1,2 Millionen 3D-Gitterzellen … die Ergebnisse in einer einzigen Codezeile nachgebildet werden können, und zwar:
[Die Hoch- und Tiefstellungen in den folgenden Abschnitten lassen sich in den eingeschränkten Möglichkeiten des Editors nicht abbilden. Daher sind diese Absätze hier in einer Graphik-Darstellung zusammen gefasst. A. d. Übers.]
Seltsam, nicht wahr? Millionen von Gitterzellen, Hunderttausende von Codezeilen, ein Supercomputer, der sie verarbeitet … und es stellt sich heraus, dass die Ausgabe nichts anderes ist als eine verzögerte (tau) und neu skalierte (lambda) Version der Eingabe.
Nachdem ich das gesehen hatte, dachte ich, ich wende das gleiche Verfahren auf die aktuellen Temperaturdaten an. Ich habe den Berkeley Earth Datensatz für die globale durchschnittliche Temperatur verwendet, obwohl die Ergebnisse bei Verwendung anderer Temperaturdatensätze sehr ähnlich sind. Abbildung 6 zeigt das Ergebnis:
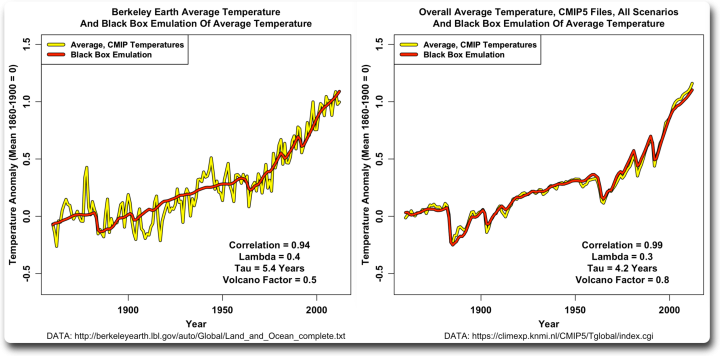
Abbildung 6. Die Temperaturaufzeichnung von Berkeley Earth und die Emulation unter Verwendung der gleichen Antriebsfaktoren wie in den vorherigen Abbildungen. Zum Vergleich habe ich Abbildung 3 auf der rechten Seite eingefügt.
Es zeigt sich, dass der Modelldurchschnitt viel empfindlicher auf den vulkanischen Antrieb reagiert und eine kürzere Zeitkonstante tau hat. Und da es sich bei der Erde um ein einzelnes Beispiel und nicht um einen Durchschnitt handelt, enthält sie natürlich viel mehr Schwankungen und hat daher eine etwas geringere Korrelation mit der Emulation (0,94 gegenüber 0,99).
Zeigt dies also, dass die Einflüsse tatsächlich die Temperatur bestimmen? Nun … nein, aus einem einfachen Grund. Die Treibhausgase wurden im Laufe der Jahre so ausgewählt und verfeinert, dass sie gut zur Temperatur passen … die Tatsache, dass sie passen, hat also keinerlei Aussagekraft.
Eine letzte Sache, die wir tun können. FALLS die Temperatur tatsächlich ein Ergebnis der Treibhausgase ist, können wir die oben genannten Faktoren verwenden, um die langfristigen Auswirkungen einer plötzlichen Verdopplung des CO2 zu schätzen. Der IPCC sagt, dass dies den Treibhauseffekt um 3,7 Watt pro Quadratmeter (W/m²) erhöhen wird. Wir verwenden einfach eine Stufenfunktion für den Treibhauseffekt mit einem Sprung von 3,7 W/m² zu einem bestimmten Zeitpunkt. Hier ist das Ergebnis, mit einem Sprung von 3,7 W/m² im Modelljahr 1900:
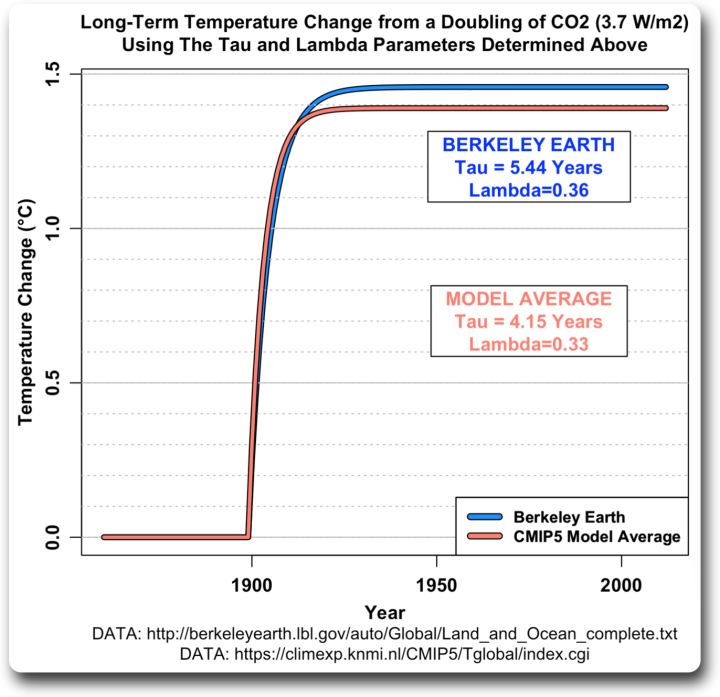
Abbildung 7. Langfristige Temperaturveränderung bei einer Verdoppelung des CO2-Ausstoßes unter Verwendung von 3,7 W/m² als Anstieg des Antriebs und berechnet mit den Lambda- und Tau-Werten für die Berkeley Earth und den CMIP5-Modelldurchschnitt wie in Abbildung 6 gezeigt.
Man beachte, dass die reale Erde (blaue Linie) mit der größeren Zeitkonstante Tau länger braucht, um das Gleichgewicht zu erreichen, etwa 40 Jahre, als wenn man den Durchschnittswert des CMIP5-Modells verwendet. Und da die reale Erde einen größeren Skalenfaktor Lambda hat, ist das Endergebnis etwas größer.
Ist dies also die geheimnisvolle Gleichgewichts-Klimasensitivität (ECS), über die wir so viel gelesen haben? Kommt darauf an. FALLS die Werte für den Treibhauseffekt genau sind und FALLS der Treibhauseffekt die Temperatur beeinflusst … dann sind sie vielleicht richtig.
Oder auch nicht. Das Klima ist ungeheuer komplex. Was ich bescheiden „Willis‘ erstes Klimagesetz“ nenne, besagt:
Alles im Klima ist mit allem anderen verbunden … was wiederum mit allem anderen verbunden ist … außer wenn dem nicht so ist.
Im Original folgen jetzt noch diverse technische Angaben, die in dieser Übersetzung nicht genannt werden.
Link: https://wattsupwiththat.com/2022/02/03/into-the-black-box/
Übersetzt von Christian Freuer für das EIKE
„Dies zeigt, dass trotz der unglaublichen Komplexität und der Tausenden und Abertausenden von Codezeilen und der 20.000 2D-Gitterzellen mal 60 Schichten gleich 1,2 Millionen 3D-Gitterzellen … die Ergebnisse in einer einzigen Codezeile nachgebildet werden können, und zwar:“
Mittelwert der Global-Temperatur (NCEP-Reanlayse)
1962-1991;13,79°C
1992-2021;14,25°C
Differenz 0,46°C
Mittelwert der CO2-Konzentration (Mauna Loa)
1962-1991 334,79 ppm
1992-2021 383,95 ppm
dT= 3,7*ln(383,95/334,79)= 0,51 °C
Es gibt im Originalartikel eine Diskussion zwischen Willis Eschenbach und Nick Stokes, die ein wenig Licht auf die Ursachen für dieses Verhalten werfen könnte. Die Kurzform des Arguments wäre etwa: Die Modelle berechnnen temperaturverläufe und leiten daraus die Forcings ab. Wenn man dann aus den Forcings wieder Temperaturen ableitet ist das lediglich eine Umkehrung der Rechnung und daher nicht sonderlich überraschend.
Es ist mathematisch nicht erlaubt, nur das CO2 zu berücksichtigen, und das H2O nicht beachten. Wenn ich auch das atmosphärishce Wasser beachte, komme ich auf folgende Werte:
Wenn sich die CO2-Konzentration verdopppelt, erhöht sich die Konzentration der IR-aktiven Gase (vulgo Treibhausgase) um 1 %. Wobei die Wasserkonzentration – im Gegensatz zur CO2-Konzentration – in einem sehr breiten Bereich schwankt je nach Tageszeit, geografischer Lage, Jahreszeit. Diese Schwankung ist aber in den meteorologischen Daten nicht bemerkbar. Die durchschnittliche Konzentartion der IR-aktiven Gase beträgt in der Sahara 0,81 Vol-% (bei 24 °C), in Bangkok 3,24 Vol-%. D.h. die Differenz von 2,44 % ist 188-mal mehr, als die Konzentrationsänderung von CO2 von 0,028 Vol-% auf 0,041 Vol-% von 1958 bis 2021. Daher ist die Herstellung jeder künstlichen Beziehung zwischen Klimaänderung und CO2-Konzentration unwissenschaftlich, sinnlos.
Übrigens sinkt seit 6 Jahren die Durchschnittstemperatur der Erde, trotz ständig steigender CO2-Konzentration.
„Daher ist die Herstellung jeder künstlichen Beziehung zwischen Klimaänderung und CO2-Konzentration unwissenschaftlich, sinnlos.“
Da stimme ich Ihnen vorbehaltlos zu. Man kann die Resultate der Klima-Alarmforschung allenfalls als Worstcase benutzen. Und selbst da zeigt sich, dass es einen weiteren 50%-Anstieg des CO2 (mit schlimmstenfalls nochmals 1 Grad Temperaturanstieg) nicht geben wird, weil die CO2-Abgabe an Pflanzen und Ozeanen mit dem CO2-Partialdruck steigt. Von der segensreichen Wirkung des CO2 auf Pflanzenwuchs und Welternährung ganz zu schweigen.
Während unglaublich dumme Klima-Politiker vor allem im Vorreiterland alle Dekarbonisierungs-Anstrengungen unternehmen (Gott sei Dank vergeblich), durch Ölverknappung und Verteuerung sowie Dekarbonisierung das Land zu ruinieren. Und fanatisch und Ideologie-getrieben damit auch den Welthunger ankurbeln und möglichst die ganze Menschheit schädigen – elend dumme deutsche Politiker schon wieder.
Vorreiterland lebt nur noch von den vielen tüchtigen und fleißigen Menschen, die täglich ihre Arbeit verrichten – wie lange noch? Unsere Polit-Versager hingegen geben sich jede Mühe, dies alles kaputt zu machen und zu ruinieren, aus nicht zu übertreffender Unfähigkeit und unendlicher Klima-Verdummung. Der Oppositionsführer ist nicht besser – ein Jurist, der sich zur Klima-Sicht von Luisa bekennt („die größte Herausforderung des 21. Jahrhunderts“- das Credo aller Klima-Verdummten).
Genauso dumm, wie grün-verdummte Verfassungsrichter, erbärmliche Einfaltspinsel, die sie sind. Die offenbar nur noch ein Ziel vereint, nämlich das Land zu ruinieren – aus unendlicher Klima-Dummheit. So wie die Weichen heute gestellt sind, hat das Klima-dauer-hirngewaschene Absurdistan keine Zukunft mehr – die grünen Klima-Trottel haben es geschafft und uns dazu. Unter tatkräftiger Mithilfe unserer grünen Scheuklappen-Medien, die sich als Parteiorgane der grünen Partei verstehen.
Man halte sich vor Augen, es war die Politik, die die Alarmforschung gegründet hat, um zu alarmieren. Und elend dumme Politiker sind die ersten, die auf den bestellten Klima-Dauer-Alarm hereinfallen. Die Alarmforscher leben gut von der Alarm-Verdummung. Was geht nur in den Hirnen von so dummen und unfähigen Klima-Trotteln vor, die aus unendlicher Dummheit das Land und die Menschheit ruinieren – es ist nicht zu fassen!