Der Originaltitel ist als Wortspiel nur schwer übersetzbar: Do not smooth times series, you hockey puck!
Der Ratschlag, der den Titel dieses Beitrags bildet, wäre der eines Statistikers, wie man keine Zeitreihenanalyse durchführt. Nach den Methoden zu urteilen, die ich regelmäßig auf Daten dieser Art angewendet sehe, ist diese Zurechtweisung dringend nötig.
Der Ratschlag ist jetzt besonders relevant, weil sich eine neue Hockeystick-Kontroverse zusammenbraut. Mann und andere haben eine neue Studie veröffentlicht, in der viele Daten zusammengeführt wurden, und sie behaupten, erneut gezeigt zu haben, dass das Hier und Jetzt heißer ist als das Damals und Dort. Man gehe zu climateaudit.org und lese alles darüber. Ich kann es nicht besser machen als Steve, also werde ich es nicht versuchen. Was ich tun kann, ist zu zeigen, wie man es nicht tun soll. Ich werde es auch schreien, denn ich möchte sicher sein, dass jeder es hört.
Mann stellt auf dieser Site eine große Anzahl von Temperatur-Proxy-Datenreihen zur Verfügung. Hier ist eine von ihnen mit der Bezeichnung wy026.ppd (ich habe einfach eine aus dem Haufen herausgegriffen). Hier ist das Bild dieser Daten:
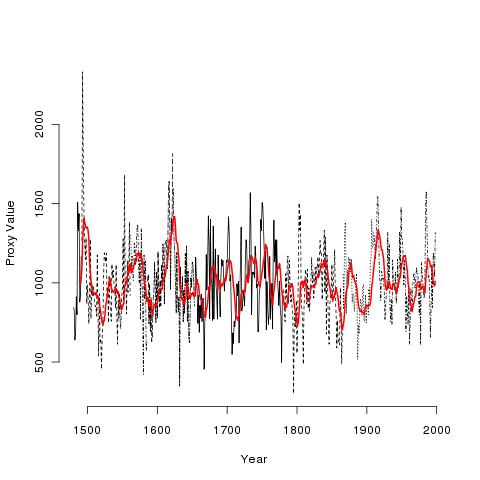Die verschiedenen schwarzen Linien sind die tatsächlichen Daten! Die rote Linie ist ein geglätteter 10-Jahres-Mittelwert! Ich nenne die schwarzen Daten die realen Daten, und die geglätteten Daten die fiktiven Daten. Mann hat einen „Tiefpassfilter“ verwendet, der sich vom laufenden Mittelwert unterscheidet, um seine fiktiven Daten zu erzeugen, aber eine Glättung ist eine Glättung, und was ich jetzt sage, ändert sich kein bisschen, je nachdem, welche Glättung man verwendet.
Jetzt werde ich die große Wahrheit der Zeitreihenanalyse verkünden. Solange die Daten nicht mit Fehlern gemessen werden, glätte man nie, niemals, aus keinem Grund, unter keiner Drohung, die Reihe! Und wenn man sie aus irgendeinem bizarren Grund doch glättet, verwende man die geglättete Reihe AUF KEINEN FALL als Input für andere Analysen! Wenn die Daten mit Fehlern gemessen werden, kann man versuchen, sie zu modellieren (was bedeutet, sie zu glätten), um den Messfehler abzuschätzen, aber selbst in diesen seltenen Fällen muss man eine externe (das gelehrte Wort ist „exogene“) Schätzung dieses Fehlers haben, d.h. eine, die nicht auf den aktuellen Daten basiert.
[Alle Hervorhebungen im Original]
Wenn man in einem Moment des Wahnsinns Zeitreihendaten glättet und sie als Eingabe für andere Analysen verwendet, erhöht man dramatisch die Wahrscheinlichkeit, sich selbst zu täuschen! Das liegt daran, dass die Glättung Störsignale hervorruft – Signale, die für andere Analysemethoden echt aussehen. Egal wie, man wird sich seiner Endergebnisse zu sicher sein! Mann et al. haben ihre Reihen erst dramatisch geglättet und dann separat analysiert. Unabhängig davon, ob ihre These stimmt – ob es wirklich einen dramatischen Temperaturanstieg in letzter Zeit gibt – sind sie sich ihrer Schlussfolgerung nun garantiert zu sicher.
Und jetzt zu einigen Details:
● Ein Wahrscheinlichkeitsmodell sollte nur für eine Sache verwendet werden: um die Unsicherheit von noch nicht gesehenen Daten zu quantifizieren. Ich gehe immer wieder darauf ein, weil diese einfache Tatsache aus unerfindlichen Gründen offenbar schwer zu merken ist.
● Die logische Folge dieser Wahrheit ist, dass die Daten in einer Zeitreihenanalyse die Daten sind. Diese Tautologie ist dazu da, um zum Nachdenken anzuregen. Die Daten sind die Daten! Die Daten sind nicht irgendein Modell derselben. Die realen, tatsächlichen Daten sind die realen, tatsächlichen Daten. Es gibt keinen geheimen, versteckten „zugrundeliegenden Prozess“, den man mit irgendeiner statistischen Methode herauskitzeln kann und der die „echten Daten“ zeigen wird. Wir kennen die Daten bereits und sie sind da. Wir glätten sie nicht, um uns zu sagen, was es „wirklich ist“, weil wir bereits wissen, was es „wirklich ist“.
● Es gibt also nur zwei Gründe (abgesehen von Messfehlern), jemals Zeitreihendaten zu modellieren:
1. Um die Zeitreihe mit externen Faktoren in Verbindung zu bringen. Dies ist das Standard-Paradigma für 99 % aller statistischen Analysen. Man nehme mehrere Variablen und versuche, die Korrelation usw. zu quantifizieren, aber nur mit dem Gedanken, den nächsten Schritt zu tun.
2. Um zukünftige Daten vorherzusagen. Wir brauchen die Daten, die wir bereits haben, nicht vorherzusagen. Wir können nur vorhersagen, was wir nicht wissen, nämlich zukünftige Daten. So brauchen wir die Baumring-Proxydaten nicht vorherzusagen, weil wir sie bereits kennen.
● Die Baumringdaten sind nicht die Temperatur! Deshalb werden sie Proxy-Daten genannt. Ist es ein perfekter Proxy? War die letzte Frage eine rhetorische Frage? War das auch eine? Weil es ein Proxy ist, muss die Unsicherheit seiner Fähigkeit, die Temperatur vorherzusagen, in den Endergebnissen berücksichtigt werden. Hat Mann das getan? Und was genau ist eine rhetorische Frage?
● Es gibt Hunderte von Zeitreihen-Analysemethoden, die meisten mit dem Ziel, die Unsicherheit des Prozesses zu verstehen, damit zukünftige Daten vorhergesagt werden können und die Unsicherheit dieser Vorhersagen quantifiziert werden kann (dies ist aus gutem Grund ein riesiges Studiengebiet, z. B. auf den Finanzmärkten). Dies ist eine legitime Verwendung von Glättung und Modellierung.
● Wir sollten sicherlich die Beziehung zwischen dem Proxy und der Temperatur modellieren und dabei die sich im Laufe der Zeit verändernde Natur des Proxys berücksichtigen, die unterschiedlichen physikalischen Prozesse, die dazu führen, dass sich der Proxy unabhängig von der Temperatur verändert, oder wie die Temperatur diese Prozesse verstärkt oder auslöscht, und so weiter und so fort. Aber wir sollten nicht damit aufhören, wie es alle getan haben, etwas über die Parameter der Wahrscheinlichkeitsmodelle zu sagen, die zur Quantifizierung dieser Beziehungen verwendet werden. Dadurch wird man sich der Endergebnisse wieder einmal viel zu sicher. Uns interessiert nicht, wie der Proxy die mittlere Temperatur vorhersagt, uns interessiert, wie der Proxy die Temperatur vorhersagt.
● Wir brauchen keinen statistischen Test, um zu sagen, ob eine bestimmte Zeitreihe seit einem bestimmten Zeitpunkt gestiegen ist. Warum? Wenn man es nicht weiß, gehe man zurück und lese diese Punkte von Anfang an. Es liegt daran, dass wir uns nur die Daten ansehen müssen: wenn sie einen Anstieg zeigen, dürfen wir sagen: „Sie [die Zeitreihe] hat zugenommen.“ Wenn sie nicht gestiegen sind oder gar abgenommen haben, dann dürfen wir nicht sagen: „sie hat zugenommen.“ So einfach ist es wirklich.
● Man kann mir jetzt sagen: „OK, Herr Neunmalklug. Was wäre, wenn wir mehrere verschiedene Zeitreihen von verschiedenen Orten hätten? Wie können wir feststellen, ob es einen generellen Anstieg bei allen gibt? Wir brauchen sicherlich Statistiken und p-Werte und Monte-Carlo-Berechnungen, um uns zu sagen, dass sie zugenommen haben oder dass die ‚Nullhypothese‘ von keiner Zunahme wahr ist.“ Erstens hat mich niemand schon lange „Herr Neunmalklug“ genannt, also sollten Sie sich Ihre Sprache besser überlegen. Zweitens: Haben Sie nicht aufgepasst? Wenn Sie sagen wollen, dass 52 von 413 Zeitreihen seit einem bestimmten Zeitpunkt gestiegen sind, dann schauen Sie sich die Zeitreihen an und zählen Sie! Wenn 52 von 413 Zeitreihen gestiegen sind, dann können Sie sagen „52 von 413 Zeitreihen sind gestiegen.“ Wenn mehr oder weniger als 52 von 413 Zeitreihen gestiegen sind, dann können Sie nicht sagen, dass „52 von 413 Zeitreihen gestiegen sind.“ Sie können es zwar sagen, aber Sie würden lügen. Es gibt absolut keinen Grund, über Nullhypothesen usw. zu schwätzen.
Wenn Ihnen die Punkte – es ist wirklich nur ein Punkt – die ich anspreche, langweilig erscheinen, dann habe ich es geschafft. Die einzige faire Art, über vergangene, bekannte Daten in der Statistik zu sprechen, ist, sie einfach zu betrachten. Es ist wahr, dass das Betrachten von massiven Datensätzen schwierig ist und immer noch eine Art Kunst darstellt. Aber Schauen ist Schauen und es ist völlig gleichberechtigt. Wenn Sie sagen wollen, wie Ihre Daten mit anderen Daten in Beziehung standen, dann müssen Sie wiederum nur schauen.
Der einzige Grund, ein statistisches Modell zu erstellen, ist die Vorhersage von Daten, die man nicht gesehen hat. Im Fall der Proxy-/Temperaturdaten haben wir die Proxies, aber wir haben nicht die Temperatur, so dass wir sicherlich ein Wahrscheinlichkeitsmodell verwenden können, um unsere Unsicherheit in Bezug auf die nicht gesehenen Temperaturen zu quantifizieren. Aber wir können diese Modelle nur erstellen, wenn wir gleichzeitige Messungen der Proxies und der Temperatur haben. Nachdem diese Modelle erstellt sind, gehen wir wieder zu dem Punkt zurück, an dem wir die Temperatur nicht haben, und können sie vorhersagen (wobei wir daran denken müssen, dass wir nicht ihren Mittelwert, sondern die tatsächlichen Werte vorhersagen müssen; außerdem müssen wir berücksichtigen, wie die Beziehung zwischen Temperatur und Proxy in der Vergangenheit anders gewesen sein könnte, und wie die anderen vorhandenen Bedingungen diese Beziehung verändert haben könnten, und so weiter und so fort).
Was man nicht tun kann oder sollte ist, zuerst die Proxydaten zu modellieren/glätten, um fiktive Daten zu erzeugen und dann zu versuchen, die fiktiven Daten und die Temperatur zu modellieren. Dieser Trick wird einen immer – einfach immer – zu sicher machen und in die Irre führen. Man beachte, wie die gelesenen fiktiven Daten viel strukturierter aussehen als die realen Daten und es wird verständlich.
Der nächste Schritt ist, mit den Proxydaten selbst zu spielen und zu sehen, was zu sehen ist. Sobald mir der Wunsch erfüllt wird, jeden Tag mit 48 Stunden zu füllen, werde ich das tun können.
Link: https://wmbriggs.com/post/195/
Übersetzt von Chris Frey EIKE
Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Mal ein paar ganz allgemeine Bemerkungen zum Thema:Mein „tägliches Brot“ sind Widerstands- Temperaturbeziehungen bei Widerstandsthermometern aller möglicher Kennlinien. Die erforderlichen Temperaturreferenzen werden dazu bei mehreren Temperaturen kalibriert, Zwischenwerte entstehen durch (Jahrzehnte erprobte!) Interpolationsverfahren. Der grundlegende Kennlinienverlauf ist also gut bekannt.Grundlage der „Kurvenbildung“ sind mind 3 Wertepaare (drei sinnvoll abgestufte Temperaturen und die zugehörigen Widerstände bei diesen Temperaturen). Damit geht es in die Mathematik (Regression). Beim Platin z.B. ist die Kennlinie immer ein Parabelast einer nach unten geöffneten Parabel, also Polynomregression als math. Methode. Man kann natürlich viel mehr Wertepaare nutzen und trotzdem „nur“ eine quadratische Gleichung daraus machen. Im Ergebnis kann man über den Korrelationskoeffizienten abschätzen, wie „gut“ Fühler bzw. die Kalibrierung sind.Man kann für die gleichen Wertepaare natürlich auch völlig andere Regressionsarten vorgeben. Eine „Ergebniskennlinie“ gibt es meistens, die aber praktisch völlig unbrauchbar ist.Bei den o.g. Zeitreihen haben wir sehr viele Wertepaare, die für eine „Aussage“ benutzt werden sollen. Im einfachsten Falle wird für die „Trendermittlung“ meist irgendwie eine Gerade hindurchgezimmert. Was sind diese Ergebnisse real Wert??? Mathematisch NICHTS, denn wir wissen nicht, welche „Grundkurve“ dem Ganzen wirklich zu Grunde liegt. Im „schlimmsten Fall“ ist es eine Sinuskurve unbekannter Periodendauer oder Überlagerungen mehrerer zyklischer Einflüsse und man „rechnet“ da auf einem kurzen Zeitabschnitt der Periode herum.Diese Tatsachen betreffen allerdings sowohl die Alarmisten als auch die „Skeptiker“. Ich bekomme deshalb auch immer Stirnfalten, wenn unsere „EIKE-Meteorologen“ viele bunte Diagramme posten mit vielen Geraden als Trendlinien. Die sind in der Interpretation genauso „gefährlich“ wie die der Alarmisten, zumal der „Datenpool“ für alle schon lange nicht mehr ganz „koscher“ ist, sich mathematisch also bestimmte Ableitungen verbieten, worauf hier im Faden schon Kommentare hingewiesen haben.Ich verweise an dieser Stelle auf einen sehr guten Artikel hier bei EIKE zur Signalanalyse …..
Ich habe den Artikel ein wenig strukturierter in diesem Editor verfasst…..
Schuldfrage?
Sobald ein über der Zeit sich verändernder Parameter über ein Filter oder Integration mit Division durch die Integrationszeit gemittelt wird, darf die so errechnete Größe für weitere rechnerische Verwertung nicht mehr herangezogen werden. Das gilt insbesondere für Leistungs- oder Energiegrößen.***** Eine sog. globale Erwärmung bedeutet immer das Feststellen einer Veränderung von Wärmeenergie (genauer: thermische Energie). Zur Ermittlung von Wärmeenergie gehört jedoch immer auch die mathematische Verknüpfung mit denjenigen Massen und zuzuordnenden spezifischen Wärmekapazitäten, bei denen die gemessenen Temperaturen zu deren Energiebestimmung herangezogen werden. Die Massen, auch die von Luft und deren Dichte, als auch die zuzuordnenden spezifischen Wärmekapazitäten sind jedoch unterschiedlich und zusätzlich von den momentan dort vorgefundenen Temperaturen abhängig. Für das Bilden einer globalen Erwärmung ist also die Summe unzählig vieler Einzelenergien von unzählig vielen unterschiedlichen Massen und zuzuordnenden Temperaturen und spezifischen Wärmekapazitäten erforderlich. Wer diese Prozedur scheut und lediglich viele Temperaturen zu einer globalen Temperatur mittelt, kann daraus keine Energie-Veränderung mehr berechnen. Tut er es dennoch, verstößt er gegen grundlegende physikalische Gesetze, da hilft es auch nicht, dass man Temperaturen ja global mitteln kann. Mathematik lässt grundsätzlich auch deren physikalisch falsche Anwendung zu. Wäre sie ein Lebewesen, würde sie aufgrund dessen, was Ihnen Klimafolgenforscher zufügen, vor lauter Schmerzen nur noch ununterbrochen schreien. ***** Operative Fehler mitteln sich nicht dadurch heraus, dass man immer wieder die gleichen operativen Fehler macht, auch wenn viele das glauben. In der Wissenschaft zur Elektrotechnik weiß man, dass man aus den gemittelten Werten von Spannung und Strom keine Leistungs- oder Energiegrößen mehr berechnen kann, sondern nur durch die fortlaufende Multiplikation der Momentanwerte und deren Summation. Vielleicht sollten Klimafolgenforscher einmal einen Grundkurs in Elektrotechnik belegen, damit sie nicht leichtfertig von globaler Temperatur-Mittelung auf globale Erwärmung oder globale Abkühlung schließen.
Da fallen mir aus Nachbarfäden hier bei EIKE schlagartig mehrere „Physiker“ ein.
Temperatur-Unterschiede sind die Ursache von Wärmeleitung, Konvektion und thermischer Strahlung. Die Stärke der Flüsse ist natürlich auch von den Wärmekapazitäten abhängig. Aber ohne Temperatur-Unterschiede gibt es keine (Netto-)Flüsse. Deshalb ist es wichtig das horizontale und vertikale Temperatur-Profil der Erde zu kennen.
Oder kurz: Zitat von Sokrates: „Ich weiß dass ich nicht weiß.“
Naja, NICHTS wissen wir nicht, aber nicht viel …..
Allerdings: Dieser Zustand läßt sich auch nicht mit Brechstangen ändern …..
Wissen ist Macht,
nichts wissen macht auch nichts.
Diesen sehr richtigen Text sollte man bestimmten Leuten Tag und Nacht um die Ohren hauen!!!
Deswegen haben wir ihn wieder aus der Versenkung geholt.
Es gibt nur einen zugriffsfähigen Temperaturmeßdatensatz in der nötigen Auflösung von TMAX und TMIN für jeden Tag und der geringen horizontalen Auflösung von weniger als 100 km, der fernab der Ozeane zustande gekommen ist, den der USA. Alle anderen Datensätze sind unbrauchbar, da viel zu kurz oder eben von den Ozeanen beeinflußt. Man sollte nie übersehen, daß nördlich von Island irgendwo die Oberflächenwassermenge nach unten absackt, dann zurück gen Süden wandert und ein Teil irgendwo westlich von Afrika wieder nach oben kommt. Und das erst Jahre später. Ein anderer Teil wandert am Nordkap Norwegens vorbei und sorgt dafür, daß es da bis Spitzbergen und Nowaja Semlja das ganze Jahr eisfrei bleibt.Ein anderer Teil des abgesackten Wassers östlich von Grönland wandert ganz bis nach Süden fast bis zur Antarktis und wandert da dann um die Antaktis rum und kommt dann irgendwo da, in der Gegend von Südwestafrika, im Pazifik oder Indischen Ozean wieder nach oben. All das hat Auswirkungen auf den globalen Temperaturverlauf, und das mit erheblichem Zeitverzug.Desweiteren hängt das Alles auch noch von der Sonnenfleckenanzahl ab. Wenn die im ca. 11-Jahresrhythmus gen null gehen, sacken auch irgendwann die gesamten Oberflächentemperaturen ab. Und es wird dann nördlich des Polarkreises richtig kalt.Nur diese wissenschaftlichen Kenntnisse stören die Politbonzen bei ihren Menschenunterdrückungszielen. Fakt ist: Mit sinkenden Temperaturen sacken die Pflanzenwüchse ab und die gigantische Menschheit, die ja extrem unkontrolliert wächst, wird extrem vom Hunger getroffen werden.
Ein bitteres Beispiel wie man es in 2020 mit Regressionen geglätteter Daten und anderen Datenmanipulationen bis in „Nature“ schaffen kann: https://judithcurry.com/2020/11/17/slower-decay-of-landfalling-hurricanes-in-a-warmer-world-really/
Die meisten Messgeräte mitteln zeitlich und räumlich. Das muss man bei der Interpretation von Mess-Daten immer beachten.
???
Was meinen sie?
Naja, in meiner Firma wird täglich tausendfach Widerstand gemessen (hochauflösende Digitalmultimeter). Den Meßgeräten gibt man sinnvolle Meßzeiten für die Digitalisierung vor, meist als Anzahl von Netzzyklen (Verminderung von Netzeinflüssen), über die eine Meßwertgewinnung ablaufen soll. Bei allen Meßgeschwindigkeiten, die heute möglich sind, eine gute Umsetzung braucht ihre Zeit, und das schon von Anbeginn der Digitalisierung im Messen an.
Dieses Verfahren hat natürlich automatisch und zwangsläufig eine „mittelwertbildende“ Komponente, hat aber wohl mit dem Fadenthema überhaupt nichts zu tun.
Ihre Fragezeichen sind also berechtigt.
Ich bin Physiker und habe oftmals Daten geglättet. Dafür gibt es zwei Gründe:1. Die Daten sind mit statistischen Fehlern behaftet, die dann durch die Glättung gedämpft werden.2. Die Daten sebst sind statistischer Natur, z. B. quantenmechanische Effekte, Zufallsexperimente, …Im Fall 1, der am häufigsten auftritt, muss man beachten, dass die Mittelung genügend Rauschen dämpft, aber die Zeitabhängigkeit des Nutzsignals nicht verfälscht. Da beides unabhängig voneinander ist, sollte das immer möglich sein.Der Fall 2 ist sehr viel schwieriger, da die statistischen Variationen inhärent mit dem Messsignal verbunden sind. Genau dieser Fall liegt aber bei den Klimadaten vor, zumal Klima ja gerade als zeitlich gemitteltes Wetter definiert ist. Hier muss man beachten, dass die Mittelung hochfrequentes Rauschen eliminiert, nicht jedoch niederfrequentes Rauschen. Ein großes Problem sind dabei gleitende Mittelwerte. Sie täuschen vor, dass sehr viele Daten vorliegen, die sich auf einer mehr oder weniger glatten Kurve befinden. Hier muss man beachten, dass tatsächlich nicht mehr Daten vorliegen, als der Gesamtzeit geteilt durch die Mittelungsbreite entspricht. Das niederfrequente Rauschen, welches noch in den gemitelten Daten vorhanden ist, kann nur mit Zeitperioden betrachtet werden, die größer sind als die Mittelungsbreite. Deshalb ist es besser, nach der Mittelung eines z. B. 10 Jahre breiten Datenbereichs für diesen Mittelwert nur eienne Datenpunkt einzuzeichnen und für 10 Jahre später den nächsten Datenpunkt. Dann erkennt man deutlicher, ob die Veränderung der gemittelten Daten echt oder statistischer Natur sind.Das Problem beim IPCC ist dann aber, dass man tatsächlich von der gesamten Erde nur ganze ZWEI Datenpunkte für das Klima hat. Das ist für Auswertungen und Vorhersagen recht dürftig. Mit dem gleitenden Mittel werden dagegen mehr Daten vorgetäuscht als existieren.