Der allgemeine Treibhauseffekt (GHE) wird häufig als der Unterschied zwischen der durchschnittlichen globalen Temperatur der Erde ohne Treibhausgase (THG) und mit ihnen definiert. Treibhausgase sind alle Gase, die einen Teil der von der Erdoberfläche abgegebenen Wärmeenergie absorbieren. Das wichtigste dieser Gase ist Wasserdampf, aber es gibt auch geringer wirkende Treibhausgase wie CO₂, Ozon und Methan.
Zur Berechnung der Erdtemperatur ohne Treibhausgase wird normalerweise die Planetenkugel ausgepackt und im Weltraum in der durchschnittlichen Entfernung der Erde von der Sonne platziert, wobei die gesamte Erdoberfläche von der Sonne mit einem Viertel der Sonnenleistung beleuchtet wird, um der kugelförmigen Erde und der Tatsache Rechnung zu tragen, dass die Hälfte der Erde immer dunkel ist. Diese imaginäre flache Erde dreht sich nicht, und kein Teil der Erde ist jemals dunkel. Eine Beschreibung der Berechnung kann in Benestad (2017) nachgelesen werden. Die mit diesem Szenario berechnete globale Durchschnittstemperatur beträgt etwa 255 K (-18 °C), und da dies etwa 33 °C niedriger ist als die aktuelle globale Durchschnittstemperatur von 15 °C, wird der gesamte Treibhauseffekt mit etwa 33 °C angenommen. Weitere Erläuterungen zu dieser Definition findet man hier.
In diesem Beitrag werde ich zunächst die Probleme mit dem GHE-Modell der „flachen Erde“ auflisten und dann ein Modell einer neuen, treibhausgasfreien, kugelförmigen, rotierenden Erde vorstellen. Danach werde ich die Annahmen auflisten, die zur Erstellung des Modells der kugelförmigen Erde verwendet wurden, sowie die Probleme, die damit verbunden sind, und schließlich diskutieren, was wir bei der Erstellung des Modells gelernt haben. Computermodelle sind Lernwerkzeuge, sie geben nie eine richtige Antwort, aber sie helfen dabei, etwas über die Probleme zu erfahren, zu deren Untersuchung sie entwickelt worden sind.
Probleme mit dem Flache-Erde-Modell
Das Modell der flachen Erde ohne Treibhausgase ignoriert die Tatsache, dass die Erde eine rotierende Kugel ist und dass die Hälfte der Erde immer im Dunkeln liegt. Die dunkle Seite strahlt immer Energie ab, empfängt aber keine. Das ist ein großer Unterschied zu dem Modell, bei dem die Sonne 24 Stunden am Tag mit überall gleicher Intensität direkt auf die Erde scheint. Die Befürworter des Modells der flachen Erde begründen dies damit, dass die Temperatur der satellitengestützten Treibhausgasemissionen der Erde ebenfalls 255 K beträgt (Benestad, 2017), was unter Verwendung einer Tabelle mit der durchschnittlichen Temperatur im Verhältnis zur Höhe (der US-amerikanischen oder internationalen Standardatmosphäre) eine durchschnittliche Emissionshöhe von etwa fünf Kilometer ergibt. Es wird wenig darüber diskutiert, wie die Energie von der Oberfläche, wo die meiste Sonnenenergie absorbiert wird, in fünf Kilometer Höhe gelangt. Der Transport erfolgt jedoch größtenteils durch Konvektion, und der größte Teil der von den Treibhausgasen emittierten Energie wird bis zu einer Höhe von fünf Kilometern als latente Wärme im Wasserdampf gespeichert. Oberhalb von 5 km wird sie hauptsächlich in den Weltraum abgestrahlt, da der Wasserdampf in der kälteren mittleren bis oberen Troposphäre zu Wassertröpfchen kondensiert und/oder immer geringer wird.
Wenn man sich nur mit Durchschnittswerten befasst, d. h. mit dem durchschnittlichen atmosphärischen Temperaturprofil, der durchschnittlichen Temperatur, der durchschnittlichen Emissionshöhe, dem durchschnittlichen Emissions-Intensitäts-Spektrum usw., kann das Modell der flachen Erde genau erscheinen und mit der Realität übereinstimmen. Die Treibhausgasemissionen in den Weltraum entstehen jedoch in einer troposphärischen Schicht von etwa zwei bis zehn Kilometern, je nach atmosphärischen und Bewölkungs-Bedingungen. Außerdem gibt es keine einheitliche Beziehung zwischen der Oberflächentemperatur und der Temperatur in der atmosphärischen Treibhausgas-Emissionsschicht, sondern sie variiert je nach Wetterbedingungen, Bewölkung, Jahreszeit und Tageszeit. Die Oberfläche funktioniert weitgehend unabhängig von der Emissionsschicht, beide sind durch Konvektion und Wetter getrennt.
In der Astronomie wird oft angenommen, dass die Emissionsfrequenz und -intensität eines Planeten das „Schwarzkörper“-Frequenzspektrum des Planeten ist, das nach dem Stefan-Boltzmann-Gesetz eine Schwarzkörpertemperatur definiert. Dabei handelt es sich nicht um die tatsächliche Temperatur der Planetenoberfläche, sondern nur um eine grobe Schätzung. Planeten sind keine perfekten schwarzen Körper. Sie sind „graue Körper“. Ein Schwarzkörper strahlt die gesamte Energie ab, die er absorbiert, und da er per Definition eine konstante Temperatur hat, strahlt er die gesamte einfallende Energie mit einem Frequenzspektrum ab, das durch seine Temperatur bestimmt wird. Am wichtigsten ist, dass ein schwarzer Körper keine Energiespeicherkapazität hat oder dass sein Gesamtenergiespeicher konstant ist und sich nie ändert.
Graukörper hingegen geben nicht die gesamte Energie ab, die sie aufnehmen; sie speichern einen Teil der Energie und geben den Rest ab. Die Ozeane der Erde haben eine enorme Wärmekapazität und speichern mehr Energie als die Oberfläche der Venus, aber während die Venusoberfläche eine Temperatur von 464 °C hat, beträgt die Oberflächentemperatur der Erde nur etwa 15 °C. Das liegt daran, dass die Ozeane der Erde eine Wärmekapazität von 5,4 x 1024 Joule/K haben und die Venus keine Ozeane besitzt. Das Fehlen von Ozeanen und atmosphärischem Wasserdampf in Verbindung mit dicken Schwefelsäurewolken und einer sehr dichten Atmosphäre führt zu der hohen Temperatur der Venusoberfläche.
Ein rotierendes Erde-Modell frei von Treibhausgasen
Ziel des Modells der flachen Erde ist es, den Einfluss der Treibhausgase auf die Temperatur der Erdoberfläche zu berechnen. Dies erfordert eine Schätzung dieser Temperatur ohne Treibhausgase. Das ist schwierig, denn das bedeutet, dass es kein Wasser, keine Wolken und keinen Wasserdampf gibt, und das sind entscheidende Merkmale der Erde. Das klassische Modell der flachen Erde geht davon aus, dass der Planet seine derzeitige Albedo (Reflexionsvermögen) von 0,3 beibehält, was bedeutet, dass 30 % der einfallenden Sonnenenergie reflektiert wird. Die Hälfte oder mehr dieser Albedo ist jedoch auf die Wolken zurückzuführen. Ohne Wasser gäbe es keine Wolken und die Albedo der Erde wäre eher mit der des Mondes vergleichbar, der eine Albedo von 12 % hat. Wir untersuchen beide Albedo-Schätzungen mit dem Modell.
Ein weiterer wichtiger Aspekt ist die Tatsache, dass Treibhausgase Energie in den Weltraum abgeben. Wenn die Atmosphäre keine Treibhausgase enthält, gibt sie nur wenig Energie in den Weltraum ab und wirkt wie ein Isolator. Während jedoch die Treibhausgase die von der Oberfläche unserer Atmosphäre abgegebene Strahlung einfangen, ist die Atmosphäre ohne Treibhausgase transparent, und alle Oberflächenemissionen gelangen direkt in den Weltraum; die Erde speichert nur die von der felsigen Oberfläche absorbierte Sonnenenergie.
Das häufigste Gestein auf der Erdoberfläche ist Basalt. Auf unserer Erde gibt es viel Wasser, das den Basalt chemisch in Schlamm oder Schmutz verwandelt. Auf der treibhausgasfreien Erde gibt es kein Wasser, daher nehme ich an, dass die Oberfläche aus blankem Basalt besteht. Er wird durch Meteoriten etwas aufgebrochen, aber das ignorieren wir für dieses Modell. Felsen haben eine höhere thermische Trägheit als Erde oder Schlamm und halten die aufgenommene Wärme länger fest.
Wie die meisten Gesteine ist Basalt ein ziemlich guter Isolator, aber er hat eine Temperaturleitfähigkeit, d. h. die Geschwindigkeit, mit der er Wärme durch sein Inneres leitet. Der Wärmedurchgangskoeffizient wird in m²/Sekunde angegeben. Jeder, der schon einmal an einem warmen Tag in einer alten mittelalterlichen Kirche war, weiß, dass der Wärmedurchgangskoeffizient von Gestein gering ist. Wenn also Sonnenlicht auf Basalt trifft und ihn erwärmt, dringt ein Teil der Wärme in den Basalt ein, wo sie eine Zeit lang gespeichert wird, und der Basalt gibt den Rest der Sonnenenergie durch die treibhausgasfreie, transparente Atmosphäre in den Weltraum ab. Mein treibhausgasfreies Modell berücksichtigt ausdrücklich die thermische Diffusivität.
Darüber hinaus gibt der warme Basalt durch Wärmeleitung auch etwas Wärme an die Atmosphäre ab. Die Atmosphäre ist frei von Treibhausgasen und gibt daher nur sehr wenig Energie direkt in den Weltraum ab, so dass wir sie für unser Modell ignorieren können. Allerdings ist die Tagseite des rotierenden Planeten etwa 170°C wärmer als die Nachtseite, so dass die Winde überschüssige Wärmeenergie als fühlbare Wärme von der Tagseite zur Nachtseite oder von den Tropen zu den Polen transportieren werden. So erreichen die Windgeschwindigkeiten in der wasserfreien Atmosphäre der Venus 700 km/h (430 mph). Die Winde transportieren überschüssige Wärme aus den heißeren Gebieten in die kühleren Gebiete und leiten dann einen Teil der Wärme an die Oberfläche, wo sie ins All abgegeben oder absorbiert wird. Aus diesem Grund wird davon ausgegangen, dass die Erwärmung der Atmosphäre auf unserem treibhausgasfreien Planeten durch die Erwärmung der Oberfläche seitens der Atmosphäre genau ausgeglichen wird.

Abbildung 1. Das treibhausgasfreie Modell der Temperatur der rotierenden Erdoberfläche in Kelvin. Die Tages- und Nachtseite des Modells sind markiert. Die Ost-West-Lage ist willkürlich, der lokale Mittag liegt willkürlich bei null Grad Länge und Breite und die angenommene axiale Neigung ist Null. Dies ist das Ergebnis eines Modelllaufs, bei dem eine Albedo von 0,12 und eine thermische Trägheit im Basalt von 0,1 angenommen wurde.
Das Modell geht davon aus, dass die Atmosphäre für das einfallende Sonnenlicht völlig transparent ist und die gesamte Energie von der Basaltoberfläche absorbiert wird, die sich entsprechend dem Einfallswinkel des Sonnenlichts auf die Tageshälfte der Kugeloberfläche erwärmt. Zwar wird ein Teil des Sonnenlichts von der Atmosphäre gestreut, doch wird dieser Effekt im Modell ignoriert. Abbildung 1 zeigt die Temperatur nach einem Tag auf der treibhausgasfreien Erde gemäß dem Modell. Die Ost-West-Positionen sind willkürlich auf den Äquator auf dem Längengrad Null zentriert und sind aufgrund der konstanten Rotation der THG-Erde bedeutungslos. Die Nord-Süd-Positionen sind aussagekräftig und repräsentieren eine Erde ohne axiale Neigung. Das Fehlen einer axialen Neigung bedeutet, dass die THG-freie Erde keine Jahreszeiten hat.
Abbildung 1 veranschaulicht, dass sich die Oberfläche in direktem Verhältnis zur empfangenen Strahlung erwärmt und die maximale Strahlung empfangen wird, wenn die Sonne direkt über uns steht. Die maximale Sonneneinstrahlung beträgt nach Korrektur um die Mondalbedo von 12 % 1198 W/m² und tritt für einige Minuten am Äquator zur lokalen Mittagszeit auf. In Abbildung 1 ist dies bei Längengrad = 0 und Breitengrad = 0, also am Äquator direkt südlich von Greenwich England, wo die Temperatur zur Mittagszeit 381K (108°C) erreicht. Die Erde dreht sich von West nach Ost, weshalb die Temperatur auf der Nachtseite am östlichen Ende der Nachtseite (rechts in Abbildung 1) höher ist als auf der Westseite (links in Abbildung 1).
Da die thermische Diffusionsfähigkeit von Basalt sehr gering ist, etwa 9 x 10↑-⁷ m²/sec (Robertson, 1988), dauert es eine Weile, bis sich die oberen Schichten der Gesteinsoberfläche erwärmen und in diesem Modell eine Art Gleichgewicht der globalen durchschnittlichen Basalttemperatur erreicht wird. Die Tagseite absorbiert die Sonnenstrahlung und gibt Wärmeenergie ab. Die Nachtseite hingegen empfängt nichts, gibt aber aufgrund ihrer gespeicherten Wärmeenergie dennoch Strahlung ab. Die Nachtseite gibt aufgrund ihrer niedrigeren Oberflächentemperatur weniger Energie ab als die Tagseite.
Wie viel genau tagsüber im Basalt gespeichert ist und wie viel später am Tag, wenn die Oberflächentemperatur kühler ist, abgegeben wird, ist nicht bekannt, kann aber anhand der Temperaturleitfähigkeit des Basalts geschätzt werden. Die Diffusivität variiert mit der Temperatur ungefähr entsprechend der in Abbildung 2 dargestellten Funktion.
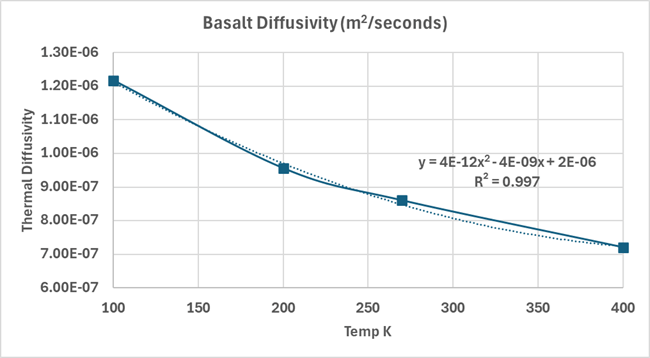
Abbildung 2. Thermische Diffusivität von Basalt als Funktion der Temperatur. Daten hauptsächlich aus Robertson, 1988, (Hartlieb, Toifl, Kuchar, Meisels, & Antretter, 2015), (Halbert & Parnell, 2022) und (Sabol, Gillespie, McDonald, & Danillina, 2006).
Obwohl die Diffusivität bei höheren Temperaturen geringer ist, speichert der Basalt tagsüber zunächst mehr Energie als er nachts abgibt. Dem Modell zufolge wird auf der Tagseite mehr Gesamtenergie emittiert als auf der Nachtseite, was jedoch auf die höhere Temperatur der Tagesoberfläche zurückzuführen ist. Das Modell besagt also, dass ein Teil der Energie, die tagsüber in den Basalt diffundiert, auf die Nachtseite gelangt, der Rest wird tagsüber bei niedrigeren Tagestemperaturen emittiert, die bei der Rotation des Planeten näher an den Rändern der Tagseite auftreten.
Auf der Nachtseite steigt ein Teil der tagsüber gespeicherten Energie auf, um die Oberfläche zu erwärmen, und wird in den Weltraum abgestrahlt. Auf der Nachtseite sind zwei entgegengesetzte Kräfte am Werk. Die thermische Diffusionsfähigkeit von Basalt nimmt bei niedrigeren Temperaturen zu, aber die niedrigeren nächtlichen Temperaturen führen zu einer geringeren Energieabgabe an den Weltraum. Es besteht also ein Missverhältnis zwischen der Speicherung am Tag und den nächtlichen Emissionen. Das bedeutet nicht, dass die Oberfläche auf den absoluten Nullpunkt abkühlt, denn das wird nicht passieren, weil die thermische Trägheit des Basalts zu groß und die Diffusivität zu gering ist, aber es bedeutet, dass es eine Weile dauert, bis eine stabile Temperatur an der Oberfläche erreicht wird. Ich habe dieses Modell für 36 500 Iterationen oder etwa 100 Jahre laufen lassen. Die durchschnittliche globale Temperatur an der Oberfläche entwickelte sich wie in Abbildung 3 dargestellt:
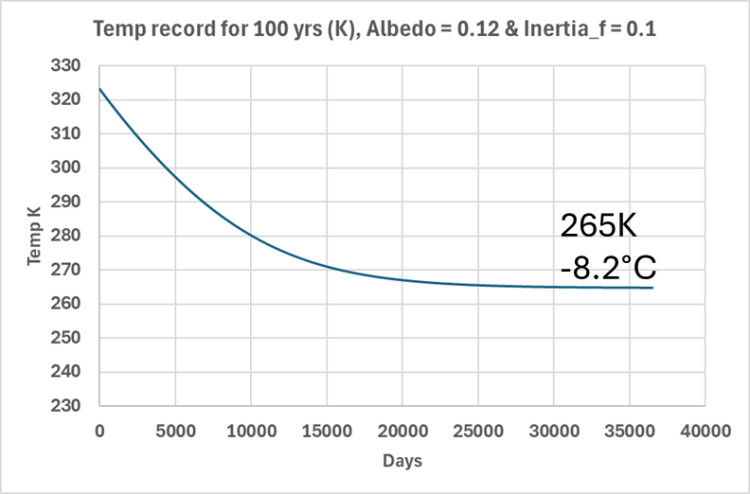
Abbildung 3. Globale durchschnittliche Temperatur des treibhausgasfreien Modells in den ersten 100 Jahren. Die weitgehend stabilisierte globale Durchschnittstemperatur nach 100 Jahren liegt bei 265 K oder -8 °C.
Wie aus Abbildung 3 hervorgeht, stabilisiert sich die durchschnittliche Temperatur unter Verwendung der in mein Modell eingebauten Annahmen schließlich auf eine solche, die niedriger ist als die heutige Temperatur. Bei diesem Ergebnis wird die Albedo des Mondes zugrunde gelegt, die der Albedo der Erde ohne Wasser oder Wasserdampf ähnlich ist. Außerdem wird ein Ausweichfaktor für die thermische Trägheit von 0,1 angenommen. Ich habe verschiedene Schätzungen der thermischen Trägheit ausprobiert, darunter den Wärmedurchgangskoeffizienten (Sabol, Gillespie, McDonald, & Danillina, 2006) und den „R“-Isolationsfaktor, und keine davon hat aus verschiedenen Gründen gut funktioniert. Es gibt viele Möglichkeiten der Wärmeübertragung, Leitung, Konvektion und Strahlung, und diese variieren je nach den örtlichen Gegebenheiten, so dass es keine allgemeine Definition der Wärmeträgheit gibt. Alle vernünftigen Annahmen zeigen jedoch einen hohen Wert der thermischen Trägheit im Basalt, der dazu führt, dass die Temperatur nach der Initialisierung des Modells sinkt.
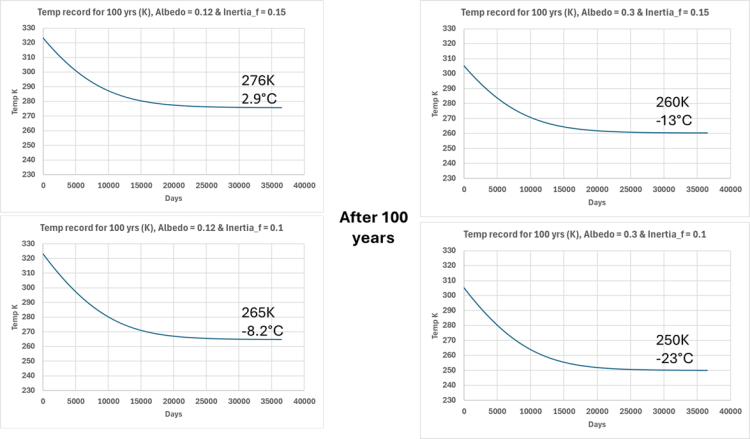
Obwohl unterschiedliche Annahmen die endgültige globale Gleichgewichtstemperatur verändern, führen alle vernünftigen Werte für die thermische Trägheit zu einer niedrigeren globalen durchschnittlichen Temperatur als heute. Abbildung 4 vergleicht einige der von mir untersuchten Szenarien nach 100-Jahre-Durchläufen. Das Modell wurde sowohl mit der Albedo des Mondes von 0,12 als auch mit der aktuellen Albedo der Erde (einschließlich der nicht vorhandenen Wolken) von 0,3 durchgeführt. Ohne Treibhausgase würde die Erde ihre derzeitige Albedo nicht beibehalten, aber dies ist der übliche Wert, den ich zu Vergleichszwecken verwendet habe. Die beiden diskutierten Werte für die thermische Trägheit (0,1 und 0,15) sind vernünftige Annahmen, da die tatsächliche thermische Trägheit von Basalt recht hoch ist, aber selbst diese Werte könnten ein wenig zu hoch sein. Höhere Werte dieses Faktors bedeuten eine geringere Trägheit und niedrigere Werte eine höhere Trägheit. Andere Werte für die Trägheit wurden untersucht, aber als unwahrscheinlich angesehen.
Die thermische Trägheit ist der Widerstand eines Materials gegenüber Temperaturänderungen. Es gibt keine formale oder allgemeine Methode zur Beschreibung der thermischen Trägheit, da sie sehr situationsabhängig ist. Das Newton’sche Kühlungsgesetz gilt für kleine Temperaturunterschiede, versagt aber in Situationen, wie ich sie hier modelliert habe. Der Wärmewirkungsgrad, auch thermisches Reaktionsvermögen genannt, der die Quadratwurzel aus dem Produkt von Wärmeleitfähigkeit, Dichte und spezifischer Wärmekapazität ist, funktionierte ebenfalls nicht. Mein letzter Versuch war die Verwendung des „R“-Isolationsfaktors, aber auch dieser Versuch schlug fehl.
Meine Analyse dieser verschiedenen Trägheitsfaktoren ist als Tabellenkalkulation beigefügt, ein Link zum Herunterladen befindet sich am Ende des Beitrags. Eine Art neues Maß für den Wärmewiderstand (Trägheit) muss für die von mir modellierte Situation entwickelt werden. Für den Moment habe ich einen angenommenen Faktor erstellt, der den Anteil der im Basalt gespeicherten Wärmeenergie darstellt, der innerhalb von 12 Stunden an die Oberfläche gelangen und als Strahlung abgegeben werden kann. Im Modell wird dies „inertia_f“ genannt. Die Werte 0,1 und 0,15 sind vernünftig, wenn man die etablierten Werte der Wärmeleitfähigkeit, Dichte und spezifischen Wärmekapazität durchschnittlichen Basalts berücksichtigt.
Man beachte, dass alle nach 100 Jahren berechneten Temperaturen niedriger sind als die derzeitige globale Temperatur. In Anbetracht der großen Unsicherheit des Modells sind Werte, die über der derzeitigen globalen Temperatur liegen, möglich, aber Werte von mehr als 300 K gelten als äußerst unwahrscheinlich. Außerdem wird der Temperaturunterschied zwischen der Tagseite der treibhausgasfreien rotierenden Erde und der Nachtseite niemals verschwinden, wie Abbildung 5 nach 100 Jahren zeigt:
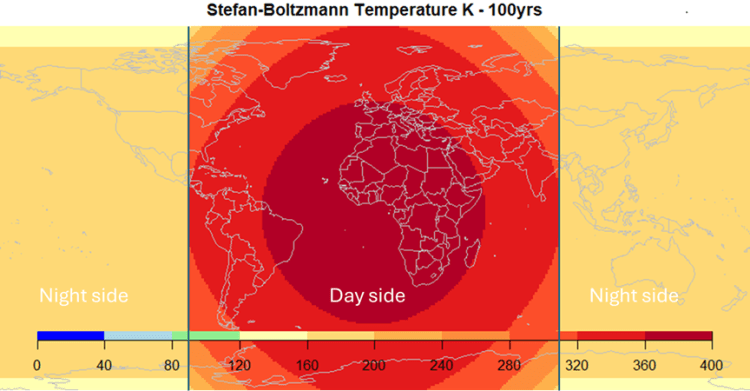
Abbildung 5. Temperaturverteilung auf dem treibhausgasfreien Planeten nach 100 Jahren. Sie stammt aus einem Modelllauf, der eine Albedo von 0,12 und eine thermische Trägheit im Basalt von 0,1 verwendet. Aufgrund der Rotationsgeschwindigkeit der Erde ist die Grenze zwischen der Tages- und der Nachtseite schärfer als bei einem tatsächlich rotierenden treibhausgasfreien Planeten.
Die im Modell eingehenden Annahmen
Das Modell geht davon aus, dass die einzigen nennenswerten Energieverluste von der Oberfläche ausgehen, obwohl die Atmosphäre eine geringe Menge an Energie in den Weltraum abgibt. Diese atmosphärischen Emissionen werden in dem Modell ignoriert.
Das Modell geht von keiner axialen Neigung aus.
Das Modell geht von einer kreisförmigen Umlaufbahn aus.
Das Modell berücksichtigt keine Konvektion, außer dass es davon ausgeht, dass sie in Bezug auf die Emissionen in den Weltraum gleich Null ist. Dies ist vernünftig, da wir auch davon ausgehen, dass die Atmosphäre für Oberflächen-Emissionen transparent ist.
Das Modell geht davon aus, dass die Topographie (Berge, Täler usw.) den Wärmetransport durch die Atmosphäre netto nicht beeinflusst.
Das Modell geht davon aus, dass die thermische Diffusivität des Oberflächenbasalts einer Funktion der Temperatur folgt, wie in Robertson, 1988, beschrieben. Die Funktion ist in Abbildung 2 eingezeichnet. Die Wärmedurchlässigkeit (α) folgt der Formel in Gleichung 1:
Gleichung 1: α = wobei: k= Wärmeleitfähigkeit, ρ= Dichte und cp die spezifische Wärmekapazität ist.
[Eine explizite Gleichung ist im Original nicht angegeben. A. d. Übers.]
Die Temperaturleitfähigkeit nimmt bei niedrigeren Temperaturen zu, was mit der abnehmenden spezifischen Wärmekapazität des Gesteins und der zunehmenden Wärmeleitfähigkeit übereinstimmt (Einzelheiten und Einheiten siehe beigefügtes Arbeitsblatt). Die für die Wärmeleitfähigkeit und die spezifische Wärmekapazität von Basalt verfügbaren Daten reichen nicht bis zu den niedrigen Temperaturen, die auf der Nachtseite auftreten, so dass die im Modell verwendeten Werte extrapoliert werden mussten.
Die Wärmeleitfähigkeit von trockener Luft ist bei den in diesem Modell betrachteten Temperaturen 6 bis 38 Mal höher als die von Basalt. Daher wird der Wärmestrom an der Oberfläche normalerweise vom Basalt zur Luft fließen, wenn die Temperaturen ähnlich sind. Der niedrigere Wert von sechs tritt jedoch bei niedrigeren nächtlichen Temperaturen auf, und wenn die darüber liegende Luft ausreichend wärmer ist als der Basalt, kommt es zu einem Fluss von der Luft zum Basalt. Die erwarteten starken Winde von der Tages- zur Nachtseite spielen also eine Rolle und transportieren Wärmeenergie zum nächtlichen Basalt, die in den Weltraum abgestrahlt wird.
Die wichtigste Annahme in dem Modell ist die angenommene thermische Trägheit, die eine wichtige Rolle für die Temperatur der Nachtseite spielt. Meine Berechnung der von der Tagseite auf die Nachtseite übertragenen gespeicherten Wärme ist vernünftig und vertretbar, aber die Geschwindigkeit, mit der sie auf der Nachtseite in den Weltraum abgestrahlt wird, ist etwas spekulativ.
Die Probleme mit diesem Modell
Die berechnete Absorption von Wärmeenergie durch die Oberfläche auf der Tagseite ist sehr grob. Ich habe bei der Berechnung die thermische Diffusivität von Basalt verwendet und angenommen, dass der Rest der Energie in den Weltraum abgestrahlt wird.
Der Einfachheit halber wurde eine gleichmäßige und glatte Felsoberfläche angenommen, was jedoch unwahrscheinlich ist. Ohne Ozeane ist eine zerklüftete Topographie wahrscheinlich, welche die zu erwartenden Winde mit sehr hoher Geschwindigkeit in einer Atmosphäre ohne Wasserdampf leiten wird. Dies wird zu einer komplizierteren und ungleichmäßigeren Temperatur führen als in den Abbildungen 1 und 5 dargestellt. Unabhängig von der Komplexität der Konvektion kann jedoch davon ausgegangen werden, dass der atmosphärische Nettotransport von Wärmeenergie nahe Null liegt. Die Energie, die in die Atmosphäre gelangt, kommt aus dem Basalt, und die Energie aus der Atmosphäre geht in den Basalt. Die reale Erde hat mehr Kontrolle, da sie durch die Energiespeicherung in Wasser und Wasserdampf sowohl die Emissionen als auch die Sonneneinstrahlung in gewissem Maße steuern kann, indem sie die Wolkenbedeckung, den gesamten atmosphärischen Wasserdampf und die Speicherung in den Ozeanen variiert, aber das gilt nicht für eine Erde ohne Treibhausgase.
Diskussion
Meiner Meinung nach hat das THG-freie Modell eine ziemlich enge Bandbreite plausibler Ergebnisse. Einige Modellläufe (es werden nicht alle Läufe gezeigt) führen zu globalen Durchschnittstemperaturen knapp über dem Gefrierpunkt, aber globale durchschnittliche Temperaturen höher als heute werden als unwahrscheinlich angesehen. Temperaturen, die deutlich unter 235 K liegen (Albedo=0,3 und Trägheit_f=0,05), sind ebenfalls unwahrscheinlich. Nach diesem Modell liegt der gesamte Treibhauseffekt wahrscheinlich zwischen 15 und 53°C. Somit liegt der gesamte Treibhauseffekt der flachen Erde innerhalb des plausiblen Bereichs, der mit diesem Modell der rotierenden kugelförmigen Erde ermittelt wurde. Während der Einfluss von Wasserdampf, Eis und Wasser auf das Klima der Erde leicht zu erkennen ist, ist der Einfluss der anderen Treibhausgase schwieriger zu ermitteln.
Das Modell des Treibhauseffekts der flachen Erde ist so konzipiert, dass es einfach die Differenz zwischen der scheinbaren Schwarzkörpertemperatur der Erde, wie sie vom Weltraum aus gesehen wird, und der aktuellen globalen durchschnittlichen Temperatur berechnet. Die Erde ist jedoch eindeutig kein Schwarzkörper, und die vom Weltraum aus gesehene Schwarzkörpertemperatur ist keine Oberflächentemperatur. Die aus dem Weltraum festgestellte Treibhausgasstrahlung wird hauptsächlich von Wasserdampf aus 2 bis 10 km Höhe in der Atmosphäre emittiert (siehe Abbildung 4), hinzu kommen einige geringfügige Emissionen anderer Treibhausgase aus verschiedenen anderen Höhenlagen. Oberflächenstrahlung in den THG-Frequenzen kann nicht den ganzen Weg von der Oberfläche ins All zurücklegen. Auf Meereshöhe ist es 50.000-mal wahrscheinlicher, dass ein Treibhausgas die Energie eines absorbierten Photons durch Zusammenstöße mit anderen Molekülen abgibt, als dass es sie wieder emittiert, so dass die Konvektion die Wärmeenergie zunächst von der Oberfläche in eine Höhe transportieren muss, in der sie in den Weltraum abgestrahlt werden kann.
Das in diesem Beitrag beschriebene Modell der rotierenden kugelförmigen Erde ohne Treibhausgase ist realistischer als das Modell der flachen Erde, hat aber immer noch Probleme. Wie George Box 1976 schrieb, sind „alle Modelle falsch“. Das Modell ist nicht endgültig, aber mein bevorzugter Modelllauf hat eine Albedo von 0,12 und eine Trägheit_f von 0,1; das Ergebnis dieses Laufs ist in Abbildung 3 dargestellt. Er führt zu einer THG-freien Temperatur von 265 K (-8 °C), die geringer ist als beim Modell der flachen Erde und einen geringeren Gesamteffekt der Treibhausgase zeigt. Allerdings ist dieses Ergebnis immer noch unsicher. Die Hauptunsicherheit des Modells liegt in den thermischen Eigenschaften des Gesteins auf der Oberfläche, insbesondere in der schlecht definierten „thermischen Trägheit“, die angenommen worden war.
Zukunft
Es handelt sich um ein sehr einfaches Modell, das eher ein Proof of Concept als ein echtes Modell ist. Es kann verbessert werden. Die Hinzufügung einer axialen Neigung, so dass die treibhausgasfreie Erde Jahreszeiten hat, könnte interessant sein, ebenso wie die Hinzufügung einer gewissen orbitalen Exzentrizität. Die wichtigste Ergänzung wäre jedoch eine gut definierte und geeignete Funktion für die thermische Trägheit von Basalt. Vielleicht hat ja ein Petrophysiker eine Idee, wie man das machen könnte? Wir können es nur hoffen. Kommentare zur Angemessenheit der Annahme, dass die Atmosphäre thermisch neutral ist, wären interessant zu lesen. Auf jeden Fall ist dies eine Verbesserung gegenüber der einfachen Subtraktion der von Satelliten gemessenen durchschnittlichen Temperatur des schwarzen Körpers von der aktuellen durchschnittlichen Temperatur zur Berechnung eines möglichen Treibhauseffekts.
Ein weiterer Punkt: Mir missfällt die Tendenz der Klimamodellierer, die thermischen Eigenschaften der Oberfläche bei der Modellierung des Erdklimas zu ignorieren. Die Oberfläche, ob Ozean oder Land oder eine Kombination davon, ist keine thermisch statische „Platte“. In der realen Erde verfügt die Oberfläche, sowohl der Ozean als auch das Land, über einen großen Vorrat an thermischer Energie, und dieser Vorrat ändert sich mit der Zeit (May & Crok, 2024) & (Crok & May, 2023), er spielt definitiv eine Rolle im langfristigen Klima und sollte berücksichtigt werden.
To download the model, which is written in R, click here.
To download the thermal diffusivity spreadsheet click here.
Bibliography
Benestad, R. E. (2017, May). A mental picture of the greenhouse effect. Theoretical and Applied Climatology, 128, 679-688. Retrieved from https://link.springer.com/article/10.1007/s00704-016-1732-y
Box, G. E. (1976). Science and Statistics. Journal of the American Statistical Association, 71(356), 791-799. Retrieved from http://www-sop.inria.fr/members/Ian.Jermyn/philosophy/writings/Boxonmaths.pdf
Crok, M., & May, A. (2023). The Frozen Climate Views of the IPCC, An Analysis of AR6. Andy May Petrophysicist LLC.
Halbert, D., & Parnell, J. (2022). Thermal conductivity of basalt between 225 and 290 K. Meteorit Planet Sci, 57, 1617-1626. doi:10.1111/maps.13829
Hartlieb, P., Toifl, M., Kuchar, F., Meisels, R., & Antretter, T. (2015). Thermo-physical properties of selected hard rocks and their relation to microwave-assisted comminution. Minerals Engineering, 91, 34-41. doi:10.1016/j.mineng.2015.11.008
May, A., & Crok, M. (2024, May 29). Carbon dioxide and a warming climate are not problems. American Journal of Economics and Sociology, 1-15. doi:10.1111/ajes.12579
Robertson, E. C. (1988). Thermal Properties of Rocks. Reston: USGS. Retrieved from https://pubs.usgs.gov/of/1988/0441/report.pdf
Sabol, D. E., Gillespie, A. R., McDonald, E., & Danillina, I. (2006). Differential thermal inertia of geological surfaces. Proceedings of the 2nd annual international symposium of recent advances in quantitative remote sensing, torrent, Spain, (pp. 25-29
Link: https://andymaypetrophysicist.com/2025/03/12/the-earth-without-greenhouse-gases/
Übersetzt von Christian Freuer für das EIKE-Website
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Hurra, wir retten die Eiszeit….
https://www.achgut.com/artikel/hurra_wir_retten_die_eiszeit
Zu Glück gibt es ja die wärmenden CO2 Moleküle die wie eine Bettdecke die Erde warm halten…. 😁😁🤦♂️
Da es aber unter dieser Decke immer unchristlicher zugeht droht der Hitzetod, so zu sagen als Strafe des Klimagottes für das sündige Treiben der Menschen…
Wer den Klimaquatsch noch ernst nimmt ist eh nicht mehr zu retten… 🤦♂️
Ich frage mich, warum immer wieder neue komplizierte Rechnungen mit Tausenden Annahmen.
Es geht doch ganz einfach mit der Hölderschen Ungleichung: Der Mittelwert der Temperaturen über eine beliebige Fläche ist kleiner als die vierte Wurzel aus dem Mittelwert der vierten vierten Potenzen der Temperaturen. Der Term T^4 wird mit sigma erweitert und sigma T^4 ist das Stefan-Boltzmann-Gesetz.
Wie die Temperaturen und Strahlungen lokal verteilt sind, ist für die Mittelwerte unerheblich (z.B Tag und Nacht, Äquator und Pole). Der Mittelwert der Abstrahlung muß gleich der absorbierten Solarstrahlung sein.
Daraus folgt, daß der Durchschnittswert der Temperatur deutlich unter -18°C liegen muß, d.h. der Treibhauseffekt ist deutlich größer als 33 K.
Vielleicht können Sie bei der Gelegenheit mal eine physikalisch saubere Definition der THE liefern? Gemäß IPCC: „The greenhouse effect is the infrared radiative effect of all infrared-absorbing constituents in the atmosphere.„
Simmen Sie dem zu?
Henry Schau 17. März 2025 12:19
„Stimmen Sie dem zu?“
Ich finde es immer mangelhaft, das fast immer nur von Absorption gesprochen wird. Einen wesentlichen Anteil am THE hat die Emission. Insofern ist schon die Beschreibung des THE durch Fourier 1824 besser, der von Behinderung des Transports dunkler Wärme gesprochen hat.Heute heißt die dunkle Wärme Infrarot. Nach Fourier sorgt diese Behinderung dafür, daß die Oberflächentemperatur höher ist als ohne diese Behinderung.
Außerdem stellte Fourier fest, daß ohne die Beweglichkeit der Luft (Konvektion) die Oberflächentemperatur noch höher wäre.
Im Laufe der Zeit ist die Konvektion besser spezifiziert. Die Konvektion trifft nur für die Troposphäre zu, in der Stratosphäre ist kaum Konvektion.
In der Stratosphäre ist der Temperaturgradient proportional dem Produkt von Wärmestrom und Treibhausgaskonzentration. Das Kriterium für den Übergang Stratosphäre in die Troposphäre beschreibt Schwarzschild 1906.
Henry Schau 17. März 2025 12:19
„Stimmen Sie dem zu?“
Auch die Behinderung der Wärmeausbreitung ist heute deutlicher erklärbar. Fast allgemein akzeptiert ist die Tatsache der Absorption – aber leider haben nicht alle den Wissensstand seit 1861 (Kirchhoff): Dort wo stark absorbiert wird, wird auch stark emittiert.
Die Behinderung könnte man so ausdrücken: Es findet immer ein Wechsel Absorption/Emission statt. Dort wo die Absorptionslänge kurz ist (Lambert-Beer-Gesetz) ist dieses Wechselspiel in dem Abstand Erdoberfläche/Weltraum sehr häufig, also große Behinderung.
Das Lambert-Beer-Gesetz hat einen großen Mangel, der aber bei vielen Anwendungen vernachlässigt werden kann: Das Gesetz macht keine Aussage, was mit der absorbierten Energie geschieht, sondern beschreibt nur die Energieabnahme des einfallenden Strahls. Es gilt aber der Energieerhaltungssatz, so daß die absorbierte Energie nicht ins Nirwana verschwindet.
In einem isothermen Hohlraum wird lokal die gleiche Strahlung aus allen Richtungen absorbiert und gleichzeitig in alle Richtungen emittiert. Dadurch bleibt das Gas isotherm.
Wenn durch das Gas Strahlungswärme von einem Ort zum anderen transportiert wird, sind nicht mehr alle Richtungen gleichberechtigt. Bei der Erde: Die Strahlung nach oben hat eine größere Intensität als die Strahlung nach unten (Gegenstrahlung). Die Differenz zwischen Aufwärts- und Abwärtsstrahlung ist gleich der transportierten Strahlungswärme.
Auch die Absorption/Emission kann spätestens seit Einstein 1917 erklärt werden. Die Moleküle können durch Absorption (und ggf. auch durch Zusammenstöße) in einen angeregten Zustand versetzt werden, den sie durch spontane Emission (und ggf. auch durch Zusammenstöße – Thermalisierung) wieder verlassen.
Im Infrarotbereich sind bei den Atmosphärentemperaturen weniger als 1% der Moleküle im angeregten Zustand, so daß Absorption und Emission diesen Anteil nur unwesentlich verändern. Durch sehr starke Bestrahlung (z.B. mit einem leistungsstarken Laser) kann man den Anteil signifikant verändern (Sättigungsspektroskopie): Da weniger nicht angeregte Moleküle vorhanden sind, nimmt die Absorption ab (Lamb-Dip).
Wie berechnet man die Oberflächentemperatur ohne Wirkung der Treibhausgase?
Hierzu muss erst einmal der THE definiert werden. Gemäß IPCC:
Der Treibhauseffekt ist die Infrarot-Strahlungseffekt aller infrarotabsorbierenden Bestandteile der Atmosphäre.
Der THE ist also nicht einfach die Wirkung der Atmosphäre oder der Wolken, sondern nur der Effekt der infraroten Strahlung. Damit hat die Reflexion/Streuung der (kurzwelligen) Sonnenstrahlung an den Wolken, auch wenn sie durch Wasserdampf erfolgt, nichts mit dem THE zu tun. Auch der Energietransport durch Wärmeleitung, Konvektion und Evapotranspiration (Verdunstung) ist kein Bestandteil der THE. Das heißt, bei der Berechnung der Oberflächentemperatur sind diese Effekte sehr wohl zu berücksichtigen. Das einfache Strahlungsmodell mit dem Albedo der Erde setzt Reflexion und Absorption an der Oberfläche an. Tatsächlich erfolgt die Reflexion und auch die Absorption der Sonnenstrahlung teilweise an/in der Atmosphäre. Welche Auswirkungen hat der nicht durch Strahlung bedingte Energietransport? Ich kenne keine Aussagen dazu und keine Berechnung des THE auf Basis aller nicht ir-bedingten Effekte. Kann man dies überhaupt (einfach) berechnen? Was ist mit den 33 K? Oder wirft man doch besser die Definition über Bord und betrachtet den Atmosphäreneffekt? Wie quantifiziert man dann aber die Wirkung der Treibhausgase? Alles Fragen über Fragen, die ich erst einmal nicht beantworten kann.
Aus dieser Sicht hilft der Artikel nicht weiter und die Art der Berechnung ist keineswegs neu. Nebenbei ergibt sich die Frage, warum umständlich eine thermische Trägheit berechnet wird, wenn diese in Lösung der Wärmeleitungsgleichung quasi automatisch eingeht? Weitere Punkte wurden bereits genannt.
Kann man zum Vergleich auch gleich den Mond nehmen.
Ein Mondtag dauert einen Monat.
Mit der Sonne im Zenit steigt die Temperatur auf etwa 130 °C und fällt in der Nacht auf etwa −160 °C. Die Durchschnittstemperatur über die gesamte Oberfläche beträgt 218 K = −55 °C.
Herr Krüger, hab ich mir spontan auch gedacht. zu bedenken ist aber die viel kleinere Mondoberfläche und die viel langsamere Rotation des Mondes.
In die Berechnungen geht nicht die absolute Größe der Oberfläche sondern das Verhältnis der Querschnittsfläche pi x R^2 zu der Oberfläche 4 x pi x R^2 ein. Die Strahlungs-/Energiebilanz hängt daher nicht vom Radius ab.
Eigentlich sehr einfach. Die auf eine ebene Scheibe einfallende Leistung L= pi* r2 * S (r hoch2) gleich der auf eine Kugel mit gleichem Radius (hier der Erdradius) einfallenden Leistung. Teilt man nun L einfach durch die Kugelfläche L/4*pi*r2 = S/4 so ergibt das die mittlere Einstrahlung auf die Erdkugel pro qm. Das ist ein Mittelwert! Es ist dabei egal, ob sich die Erdkugel dreht und wie schnell sie sich dreht. Das ändert nur die Verteilung und nicht den Mittelwert. Allerdings treten enorme Unterschiede in der aufgenommen Leistung vom Äquator zu den Polen auf. Also auch enorme Temperaturunterschiede. Berechnet man nun abzüglich der Albedo durch Umkehrung des Stefan Boltzmann T hoch 4 Gesetzes eine Temperatur aus diesem Mittelwert, dem ja eine Temperaturverteilung zugrunde liegt, so gilt mathematisch korrekt, dass die mittlere Temperatur sehr viel kleiner als 255K sein muss. Mathematisch leitet sich das aus dem Hölder´schen Mittelwertsatz ab. Bekannt ist vielleicht eher, dass die Wurzel aus dem quadratischen Mittel immer größer ist als der arithmetische Mittelwert. Das kann man sich leicht selbst ohne höhere Mathematik ableiten. Das gilt aber auch für die vierte Potenz. Gerlich und Tscheuschner haben das einmal für die Erdkugel berechnet und erhalten -129°C. Für den Mond wird das recht gut bestätigt. An sich ist das alles sehr einfach. Die Modellrechnung, dass der THE die Temperatur im Mittel um 33°C erhöht, ist schlichtweg unbrauchbar um nicht zu sagen mathematisch falsch. Einfacher gesagt, aus einem Mittelwert kann man über eine physikalische Gleichung keinen weiteren Mittelwert berechnen. Die atmosphärische „Gegenstrahlung“ und die Ausstrahlung in den Weltraum ist allein eine Funktion der Temperatur. Durch diese Strahlung kühlt sich die Atmosphäre ab. Die Atmosphäre erwärmt sich im Wesentlichen durch Konvektion über den Kontinenten und Verdunstung über den Meeren (latente Wärme). Die Erwärmung durch IR Absorption ist dabei sehr gering.
Das halte ich fuer falsch.
Geben sie den Mittelwert an, wenn sich die Erde einmal in der Sekunde um sich selbst dreht.
Geben sie den Mittelwert an, wenn sich die Erde gar nicht dreht.
Kann man eine auf eine Flaeche bezogene Einheit uener eine Flaeche mitteln, auf der sie nicht wirkt?
Die Leistung L oben in Watt ist nicht auf eine Fläche bezogen! In der einfachen Modellrechnung wird die Rotation der Erde gar nicht berücksichtigt, man sagt nur, im Mittel ist die Intensität der Einstrahlung gleich der Ausstrahlung und berechnet daraus (aus der Einstrahlung!) eine Temperatur. Also aus einen Mittelwert für die Ausstrahlung, der sich aus einer Temperaturverteilung ergibt. Herr Edel weiter oben hat das auch sehr richtig beschrieben. Gerlich und Tscheuschner haben das den Kardinalfehler der Klimatologie genannt. Erstaunlich ist, dass die Intensität der Strahlung oftmals mit einer Energie verwechselt wird.
Dann darf die Leistung nur auf eine Hemisphaere bezogen werden!
Dann sind die Flaechen fuer Abstrahlung und Einstrahlung im Verhaeltnis 2 zu 1.
Herr Ebel hat aber nicht die Bedingungen angewendet, wie sie sie formulieren. Und wenn sie Gerlich und Tscheuschner erwaehnen, die kommen nich auf -18 Grad C.
Etwas stimmt hier nicht.
Kohl 16. März 2025 17:00
„Die Erwärmung durch IR Absorption ist dabei sehr gering.“
Wenn Sie nicht die Zweiteilung der Atmosphäre in Troposphäre und Stratosphäre berücksichtigen kommt Kohl raus. In der Stratosphäre wird der Temperaturgradient durch den Strahlungstransport des IR bestimmt.
In der Darstellung (weiter oben) sind wir uns ja völlig einig. Worin besteht dann ihr Problem? Die Gegenstrahlung entspringt der Troposphäre. Sie haben bereits den Einwand von Herrn Schulz geklärt. Sehr schön. Das Problem sind die ständigen Mittelwerte. Die Natur berechnet keine Mittelwerte und stört sich an solchen auch nicht. So gibt es zu keinem Zeitpunkt und nirgendwo ein Strahlungsgleichgewicht. Das gilt dann für zeitliche Mittelwerte über mindestens ein Jahr. Ich freue mich, dass auch einmal jemand anders bei Fourier nachgelesen hat. Das kann man hier leider nicht sinnvoll diskutieren.
Herr Kohl,
der Treibhauseffekt existiert auch ohne Mittelwertbildung. Stimmen Sie dem zu?
Zum Thema der Erde ohne Treibhauseffekt: Es ist natürlich unsinnig, die Temperatur zu mitteln, die sich aus lokalen Strahlungsgleichgewichten am Boden ergibt. Denn auch ohne Treibhausgasatmosphäre wäre die Erdoberfläche nicht im lokalen Strahlungsgleichgewicht. Die so gemittelte Strahlungstemperatur ist ja – wie Sie schrieben (Gerlich et al.) geringer als die Strahlungstemperatur einer atmosphärenlosen Erde am Boden, wenn man die absorbierte Sonneneinstrahlung gleichmäßig über die gesamten Erdkugel verteilt und die dem entsprechende Strahlungstemperatur von -18°C berechnet. Letzeres ist aber realitätsnäher als Gerlichs Vergleich mit lokalen Strahlungsgleichgewichten.
Die korrekte Rechnung einer atmosphärenlosen Erde würde zonal von einem leichten Tagesgang der Temperatur ausgehen, während die Temperatur zu den Polen hin abnimmt. Das Temperaturniveau (bemessen mit z.B. dem globalen Mittel darüber) der Erde wäre wieder durch die Energiebilanz determiniert. Es wäre freilich immer noch kälter als mit Treibhausatmosphäre.
Thomas Heinemann 18. März 2025 9:12
„Denn auch ohne Treibhausgasatmosphäre wäre die Erdoberfläche nicht im lokalen Strahlungsgleichgewicht.“
Jein. Durch die Speicherwirkung des Erdrandes stimmen lokal und aktuell Emission und Absorption nicht überein. Aber über einen Zyklus müssen die Mittelwerte fast übereinstimmen, sonst würde sich die mittlere Temperatur ändern – was sie aber voraussetzungsgemäß nicht tun soll. Die globalen Mittelwerte der Temperaturen und der globalen Mittelwerte der emittierten Strahlung (gemäß dem lokal gültigen Stefan-Boltzmann-Gesetz) sind über die Höldersche Ungleichung verbunden (G&T zeigen das an einem Beispiel).
Danach sind die -18°C ein theoretischer Höchstwert bei Gleichheit aller Temperaturen (aus der Ungleichung wird eine Gleichung), der aber bei der Erde nie erreicht werden kann. Deshalb ist der Treibhauseffekt deutlich größer als 33 K.
Dr. rer. nat. W Kohl 18. März 2025 8:31
„Die Gegenstrahlung entspringt der Troposphäre.“
Der Satz ist etwas zu ergänzen:
Die Gegenstrahlung, die die Erdoberfläche erreicht, entspringt weitgehend der Troposphäre.
„So gibt es zu keinem Zeitpunkt und nirgendwo ein Strahlungsgleichgewicht.“
Das trifft nicht zu, besonders in der Stratosphäre. Durch die lokale Speicherwirkung können Absorption und Emission etwas differieren, so kommt z.B. der Tagesgang der Temperatur zu Stande. Wenn die absorbierte Strahlungsintensität zu einer Temperatur gehört, die niedriger ist als die aktuelle Temperatur, dann wird die höhere Emission aus der gespeicherten Wärme gespeist (bzw. umgekehrt) bis Absorption und Emission gleichen Wert haben. Das geht recht schnell und zu den Zeiten hat schon Natanson 1888 geschrieben.
„jemand anders bei Fourier nachgelesen hat.“
Fourier hat ja in französisch geschrieben. Das macht es nicht einfach. Ich habe das mal übersetzt mit Kommentaren:
https://www.ing-buero-ebel.de/Treib/Fourier.pdf
Dr. rer. nat. W Kohl 18. März 2025 8:31
Ergänzung:
Die Gegenstrahlung existiert natürlich in der ganzen Atmosphäre.
Herr Dr. Kohl, koennen sie bitte verlinken oder zitieren, wo Herr Ebel meinen (welchen?) Einwand geklaert hat?
Also,
Ich würde ja sagen, dass die Temperatur der Atmosphäre hauptsächlich vom Stickstoff bestimmt wird!
Immerhin zu 78% in der Atmosphäre vertreten und sehr träge was das halten der Temperatur anbetrifft.
Welches er übrigen Gase hat diese Eigenschaft?
Es ist sogar so, das 78% der Atmosphaere Stickstoff ist und dieser eine Temperatur hat.
Ich denke sie haben nicht ganz unrecht!
Alleine dieser Absatz schon steckt so voller Fehler, dass man den Autor zurück in die Grundschule versetzen möchte.
„…während die Venusoberfläche eine Temperatur von 464 °C hat, beträgt die Oberflächentemperatur der Erde nur etwa 15 °C. Das liegt daran, dass die Ozeane der Erde eine Wärmekapazität von 5,4 x 1024 Joule/K haben und die Venus keine Ozeane besitzt. Das Fehlen von Ozeanen und atmosphärischem Wasserdampf in Verbindung mit dicken Schwefelsäurewolken und einer sehr dichten Atmosphäre führt zu der hohen Temperatur der Venusoberfläche.“
Richtig ist es auch nach meiner Überzeugung, dass es nicht die CO2-Atmosphäre ist (wie es z.B. Ganteför meint), die zu den hohen Oberflächentemperaturen (464 Grad C) der Venus führt. So oft verdoppeln, wie dazu notwendig wäre, lässt sich die CO2-Konzentration auch auf der Venus nicht. Auch die Wärmekapazität der Ozeane spielt im stationären Gleichgewicht keine Rolle. Verdunstungskühlung, Kühlung durch Niederschläge und Transport von latenter Wärme hingegen schon.
Mir fehlt die Berücksichtigung der Wärme aufgrund von Reibung (z.B. durch Ebbe und Flut, tektonische Plattenverschiebung, Wind) sowie die Wärmeleitung aus dem heissen Erdinneren und zwar nicht nur durch Vulkanismus. Man reibe mal seine Hände an einander, um die Bedeutung der Reibung zu erkennen.
Die aktuelle globale Durchschnittstemperatur von 15°C/288K ist die Lufttemperatur nahe der Oberfläche (Surface Air Temperature). Niemand misst die Temperatur der Erdoberfläche.
Die hypothetische effektive Emissionshöhe soll sich in der Höhe befinden in der die Temperatur -18°C/255K beträgt – diese Temperatur findet man in 5.1km, entnommen aus der Standardatmosphäre. Nutzt man nun den durchschnittlichen (feucht adiabatischen) Temperaturgradienten der Standardatmosphäre vom 6.5°C pro 1000m so wird die Luftsäule am Boden 5.1×6.5= 33.15K wärmer sein, man erhält eine SAT von 288.15K.
Hätte die Erde ohne Atmosphäre eine durchschnittliche Oberflächentemperatur von 255K so würde, im Durchschnitt, die 288.15K warme Luft die kältere Oberfläche um jene 33.15K erwärmen – durch Wärmeleitung, nicht durch Strahlung! Das ist was man auch auf der Venus, hier aber real beobachten kann. Auf der Erde kühlt die Luft die Oberfläche am Tag und wirkt über Nacht wie eine Wärmedämmung; Wasserdampf sorgt dafür dass die Oberfläche nicht so stark auskühlt wie es z.B an sehr trockenen Orten geschieht, er schließt sozusagen das atmosphärische Fenster.
Die Modellierer nehmen nun das Schichtenmodell der Standardatmosphäre und simulieren einen Energieaustausch zwischen diesen Schichten, man hat sich die lapse rate „ausgeliehen“ und offensichtlich haben sich die Strahlungsenthusiasten hier komplett verrannt; man glaubt nun dass Strahlung maßgeblich ist und dass diese eben nur von IR-aktive Gasen kommt.
Irgendwie scheint sich der Irrglaube eingebürgert zu haben die Erde hätte ein Problem damit nicht zu überhitzen, in der Realität sind es die Luft, das Wasser und die großräumige Verteilung der Wärme durch beide welche die (Luft)Temperaturen habitabel halten, so zwischen -90°C und +50°C SAT.
Die Oberflächentemperatur ist komplett irrelevant. Arrhenius ging einfach davon aus dass Luft- und Bodentemperatur identisch sind, und diese Temperatur war 1896 auch 15°C. Damit ist der GHE widerlegt, in den letzten 129 Jahren hat die Lufttemperatur um die 15°C herum geschwankt und ist quasi gleich geblieben währen der CO2 Gehalt angestiegen ist. Die Manipulationen der Temperaturaufzeichnungen dienen einzig und allein dem Zweck die Menschen an der Nase herumzuführen, ihnne Angst zu machen und das Geld aus den Taschen zu leiern. Es ist auf Deutsch gesagt: Beschiss.
So, und jetzt warten wir auf die Spezialisten die uns erkälren werden dass man das ideale Gasgesetz und die Gravitation (barometrische Formel) nicht in einem Modell anwenden kann während das Strahlungsmodell genau die Realiät widergibt, dessen Zahlen aber vom Standardmodell „geklaut“ sind. „Experten“…
Weart: This was a radiative convective model, so where’s the convective part come in. Again, are you using somebody else’s…
Hansen: That’s trivial. You just put in…
Weart: … a lapse rate…
Hansen: Yes. So it’s a fudge. That’s why you have to have a 3-D model to do it properly. In the 1-D model, it’s just a fudge, and you can choose different lapse rates and you get somewhat different answers. So you try to pick something that has some physical justification.
Man muß schon ein echter „Spezialist“ sein, um anzunehmen, daß eine Atmosphärenschicht, die irgendwo zufällig auch ca. -18°C hat, ein alles zudeckender „schwarzer Strahler“ wäre, der statt der Erdobefläche, egal welche Temperatur diese hat, eben rundherum mit ca. 239 W/m² ≈ -18°C strahlt.
Diese sog. „Abstrahlhöhe“ ist ein oft benutztes Gaunerwort, mit dem sich die „Spezialisten“ die Welt richten wollen, wie sie sie brauchen …
When madmen lead the blind …
Betriebsblindheit ist tatsächlich die beste Beschreibung für das was die „Spezialisten“ hier zeigen, man hat den Bezug zur Realität verloren.
Also mal Fragen aus meinem beschränkten Denken als Maschinenbauer.
1. Was nützt es, wenn ich weiß, ohne Lufthülle wäre die “ Erdtemperatur“ ( die es so nicht gibt) sound so hoch.
2. Wenn die empfangene Energie und die selbsterzeugte Energie nicht in ungefähren Gleichgewicht stehen würden ( es gibt ja Kalt- und Warmzeiten), wären wir tatsächlich entweder erfroren oder, wie jetzt, verglüht.
3. Das Wort „Treibhaus“ sollte weder für Gase noch für etwas Anderes als wirklich Treibhäuser verwendet werden.
4. Welche Aktionen sind erforderlich, wenn die „Erdtemperatur“ modelliert werden kann? Verbrennerverbot? Kraftwerke sprengen,?
Die Erde ist eine Scheibe. Und Wolken, Wasserdampf, etc. spielen keine Rolle. Noch besser als im Tagerdemodell.
Übertrifft noch das Tagerdemodell von Herrn Weber. Ein Flacherdemodell, wo Atmosphäre, Wolken und THG keine Wärme ins All abstrahlen.
Richtig bist: Es kommt darauf an, ob ein Himmelskörper eine Gashülle hat oder nicht. Was passiert, wenn er keine hat: Siehe Mond. Kosmisch so nahe bei uns, dass alle Einflüsse von außen gleich sind wie bei der Erde. So ist ein direkter Vergleich möglich. Die Zusammensetzung der Gashülle ist ebenfalls wichtig, das Wärmerückhaltungsvermögen bestimmt die Temperatur der Gashülle, s. „Schneeballerde“ und „Sauerstoffkatastrophe“ bei wiki. Wer das einmal begriffen hat, der sieht die Dinge realistisch/er.
Wieder ein Beitrag aus der Rubrik „Pippi Langstrumpf“ – Ich mach‘ mir die Welt Widdewidde wie sie mir gefällt.
Wenn die gut bezahlten Pipi Langstrumpf-Erzähler schon nix auf die Reihe bekommen um ihre Katastrophenmeldungen zu begründen, warum soll man dann nicht selbst darüber nachdenken was wirklich sein könnte. Ist zumindest ein Ansatz der logisch aufgebaut ist und Aspekte enthält die den Allarmisten immer im Wege stehen.
Sinn und Zweck sollte aber sein es besser als die, und nicht noch viel schlechter zu machen. Das ganze Thema Klimawandel existiert nur deshalb noch, weil die „kritische Seite“ so verdammt inkompetent ist.
Nach meinem Kenntnisstand ist der THE die Wirkung der ir-aktiven Gase (Gegenstrahlung). In dem Artikel wird aber ein Planet ohne Atmosphäre mit einem mit Atmosphäre und THE verglichen. Die Wolken und übrigens auch Aerosole reflektieren (streuen, rückstreuen) kurzwellige Strahlung, daher ist Albedo-Effekt der Wolken keine Wirkung der ir-aktiven bzw. im langwelligen Bereich wirksamen Gase und darf nicht den THE zugeordnet werden. Das Albedo ist das Rückstrahlvermögen diffus reflektierender (aber nicht spiegelnder) Oberflächen, angegeben als Verhältnis von reflektierter zu einfallender kurzwelliger Strahlung (Definition des DWD).
Alle Modellvorstellungen, die in so gut wie allen Parametern nicht mit der Wirklichkeit übereinstimmen, wie das Modell über 33°C „natürlicher THE“, sind falsch.
Man sollte daher die Hauptenergie dorthin legen, verstehen zu versuchen, wieso dieses Modell falsch ist.
Diesbezügliche Tips: der Zusammenhang zwischen Temperatur und Strahlungsleistung ist nicht linear, sondern eine 4. Potenz. Nur bei linearem Zusammenhang wäre eine Viertelung physikalisch erlaubt möglich. Und – Wärme ist Energie und Energie kommt in der üblicherweise verwendeten Formel von Stefan-Boltzmann nicht vor. Dager kann man mit dieser Formel auch keine auf Energie beruhenden Erwärmungen berechnen.
Daß solche grundsätzliche Zusammenhänge von der „Klimawissenschaft“ nicht verstanden oder ignoriert werden, zeugt von deren pseudophysikalischer „Desorientiertheit“!
Was stimmt denn nicht mit der Wirklichkeit überein? Bzw. wer bestimmt denn was die Wirklichkeit ist? Es werden soviele reale Wirklichkeits-Elemente parametrisiert ohne vorher hinlänglich zu klären von welcher Qualität deren Einfluss auf das System tatsächlich ist.
Was die Wirklichkeit ist, bestimmen Meßwerte. Und es gibt keinen Meßwert, der eine konstante Bestrahlung der Erde rundherum senkrecht mit 341 W/m² belegt und auch keinen, der eine konstante Oberflächentemperatur rundherum von -18°C belegt. Es gibt natürlich auch keine, die eine konstante Oberflächentemperatur rundherum von +15°C belegt. Es soll sich um einen sog. „stationären“ Fall handeln, der hier modelliert wird. Unter stationär versteht man örtlich und zeitlich nicht verändert bzw.unverändert.
stefan strasser 17. März 2025 11:49
„konstante Bestrahlung der Erde …“ usw.
Sie haben Probleme mit Mittelwerten. Ein Mittelwert von 341 W/m² bedeutet eben keinen konstanten Wert von 341 W/m² sondern wie der Name sagt: Mittelwert.
Informieren Sie sich mal über Mittelwerte. Ein Beispiel für Mittelwerte ist die Bevölkerungsdichte, z.B.:
https://de.wikipedia.org/wiki/Liste_der_deutschen_Bundesl%C3%A4nder_nach_Bev%C3%B6lkerungsdichte
Wollen Sie das „stationäre Modell“ der Klimatologie umdefinieren in nicht stationär?
Zur Erinnerung, es geht um meinen Initialsatz:
„Alle Modellvorstellungen, die in so gut wie allen Parametern nicht mit der Wirklichkeit übereinstimmen, wie das Modell über 33°C „natürlicher THE“, sind falsch.“
Natürlich ist die Wirklichkeit nicht stationär. Aber das ist es ja genau, daher ist so eine Modellvorstellung absurde Pseudophysik!
Wo sehen Sie hier Korrelationen zu einer Bevölkerungsdichte?
stefan strasser 18. März 2025 0:28
„Wo sehen Sie hier Korrelationen zu einer Bevölkerungsdichte?“
Ich sehe keine Korrelationen zur Bevölkerungsdichte und habe das auch nicht geschrieben. Das Aufzeigen eines Beispiels sollte helfen, daß Sie Mittelwerte besser verstehen.
Da gibt es noch schönere Beispiele zwischen örtlicher Realisierung und möglichen Realisierungen: https://www.leifiphysik.de/quantenphysik/quantenobjekt-photon/versuche/doppelspaltversuch-mit-einzelphotonen-simulation
Es kommt immer auf die Zusammenhänge an. Zum Verständnis der Zusammenhänge beim Treibhauseffekt ist es sinnvoll die Beschreibung anhand der Durchschnittswerte zu machen, kein Fachmann behauptet, das lokal die Durchschnittswerte zutreffen.
Wieso nehmen Sie an, ich verstehe Mittelwerte nicht?
Ich rede, wie mehrfach nachlesbar, vom „stationären Modell“ der Klimatologie. Diese Bezeichnung stammt nicht von mir, sondern von denen. Unter stationär versteht man gem. Duden örtlich und zeitlich nicht verändert bzw. unverändert.
Genau das trifft aber in der Wirklichkeit weder zu, noch kann es durch „berechnete“ Mittelwerte simuliert werden. Oder wollen Sie das etwa behaupten?
Erdmodell mit Luft, aber ohne Treibhausgase, interessanter Artikel, wo sich nun Physiker austoben können. Was fehlt bei diesem Modell gegenüber der Realität nach dem ersten Durchlesen? 4 Punkte.
1) Die Erde ist zu 70% mit Wasser bedeckt und nicht zu 100% aus (Basalt)gestein
2) Die 30% Landmasse ist mit einer Flora – kleine und große Pflanzen, ganz Wälder- überzogen und ist nicht kahl wie die Mondoberfläche.
3) Das Weltall hat keine – 273C oder 0 K, diese Temperatur liegt allen Rechnungen zugrunde
4) Die Erde hätte ohne Sonne und ohne Lufthülle auch keine -273 C, aber auch nicht weltraumkalt mit 4 K, sondern sie besitzt eine radiogene Eigenwärme. A.Agerius schätzt diese Eigenwärme in seinem neuen Buch auf 30 bis 40°C.
Auf die ersten beiden Punkte wird in diesem Aufsatz wenigstens am Schluß hingewiesen und auch auf deren mögliche Bedeutung/Abweichungen bei den Modellrechungen.
Realität. Und die (grünen) Regierungen nehmen alles wohlwollend zur Kenntnis und machen damit Politik. Alles und jeder hilft, was ihrem Geschäftsmodell zuarbeitet. Seriöse Menschen haben diese linksgrüne Politik jetzt doch endgültig satt.
Was aber grundsätzlich in allen gängigen Modellen ausgeblendet wird, ist der Einfluss der Konduktion auf den zeitlichen Versatz der Energieabstrahlung ohne Einstrahlung. Findet in den Alarmmodellen garnicht statt und wird im obigen Modell wenigstens als Diffussion angedacht.
Wie hoch ist die CO2-KLimasensitivität und wie stark erwärmend wirken Treibhausgase?
Das weiß niemand!
Fakt ist lediglich, dass die Sonne die Erdoberflälche zu 100% über Strahlung erwärmt, aber die Lufthülle über dem Boden nicht zu 100% Strahlung allein aus Strahlung rückerwärmt wird und auf dieser Falschaussage baut der gesamte Treibhauseffekt auf, indem behauptet wird: würde die Lufthülle kein CO2 enthalten, dann würde laut Stefan Boltzmann die Luft -18 C kalt sein. Nach meiner Überzeugung würde sie genauso warm sein, weil die Strahlungserwärmung über CO2 nur einen sehr geringen Anteil ausmacht, den wir in den DWD-Temperaturreihen nicht finden können.
„nach meiner Überzeugung“, ich selbst weiß es auch nicht. Wie hoch die Klimasensitivität von CO2 nun tatsächlich ist, darüber kann ich gar nichts aussagen und will auch nichts berechnen, im Gegensatz zu Leuten, die sich für qualilfizierte Physiker halten, weil sie ein paar Formeln beherrschen und kunterbunt Zahlen einsetzen können.
Wie gehen nun alle Physiker der Welt vor?: Sie geben eine ECS-Glaubenzahl vom Gefühl her für sich vor – möglichst eine, die auch Geld bringt- und versuchen dann ein Rechen-Modell zu entwickeln, dass diesen angenommenen Glaubenswert bestätigt. Um so mehr, wenn das Ergebnis zugleich ein Arbeitsnachweis für deren Monatsgehalt ist, und der errechnete Wert dem Geschäftsmodell Klimakatastrophe zuarbeitet.
Das richtige geldbringende Ergebnis lautet dann: Natürlicher Treibhauseffekt 33 Grad, Klimasensitivität zwischen 2 und 5 Grad. Dann fließt das Geld weiter und das Einkommen bleibt bis zur Rente gesichert.
Aber so haben die Physiker auch schon bei den Nazis gearbeitet. „Deutsche Physik“
Bitte keinen Rundschlag gegen Physiker! „Staatstreue“ Wissenschaftler gab und gibt es in allen Bereichen. Das Problem ist meines Erachtens die Verquickung von Politik/Ideologie und Wissenschaft. Noch schlimmer sind zudem die Medienvertreter, die keine Fachwissen oder gefährliches Halbwissen haben und den Weltuntergang verkünden. Hinzu kommen die „Gutgläubigen“, die denken, die öffentlichen Medien verkünden die reine Wahrheit.
Genau wie bei Herrn Weber.
Beide sind Geophysiker. Soweit ich weiß. Würde mich mal interessieren, wer da wessen Theorie aufgegriffen hat?
Josef Kowatsch 16. März 2025 9:56
„Das weiß niemand!“
… von den Klimaleugnern. Die machen die Augen zu und sagen ich sehe nichts.
Es gibt ganz viele Messungen sowohl der Oberflächentemperatur als auch der CO2-Konzentration. Da mit großen Listen kaum etwas anzufangen ist, faßt man die Meßergebnisse zu Durchschnittswerten zusammen. Und da ist es ganz eindeutig:
Fast genau 1 K Temperaturerhöhung bei einer Konzentrationserhöhung des CO2 um 100 ppmV. Und diese Meßergebnisse sind konstant seit über 100 Jahren.
Für das reale Erde-Atmosphäre-System ist die Fiktion einer CO2-getriebenen Atmosphärentemperaturveränderung widerlegt. (Auch) in den letzten 60 Jahren mit detaillierten Temperatur- und CO2-Aufzeichnungen war die atm. CO2-Konzentration Folge, nicht Ursache für atm. Temperaturänderungen!  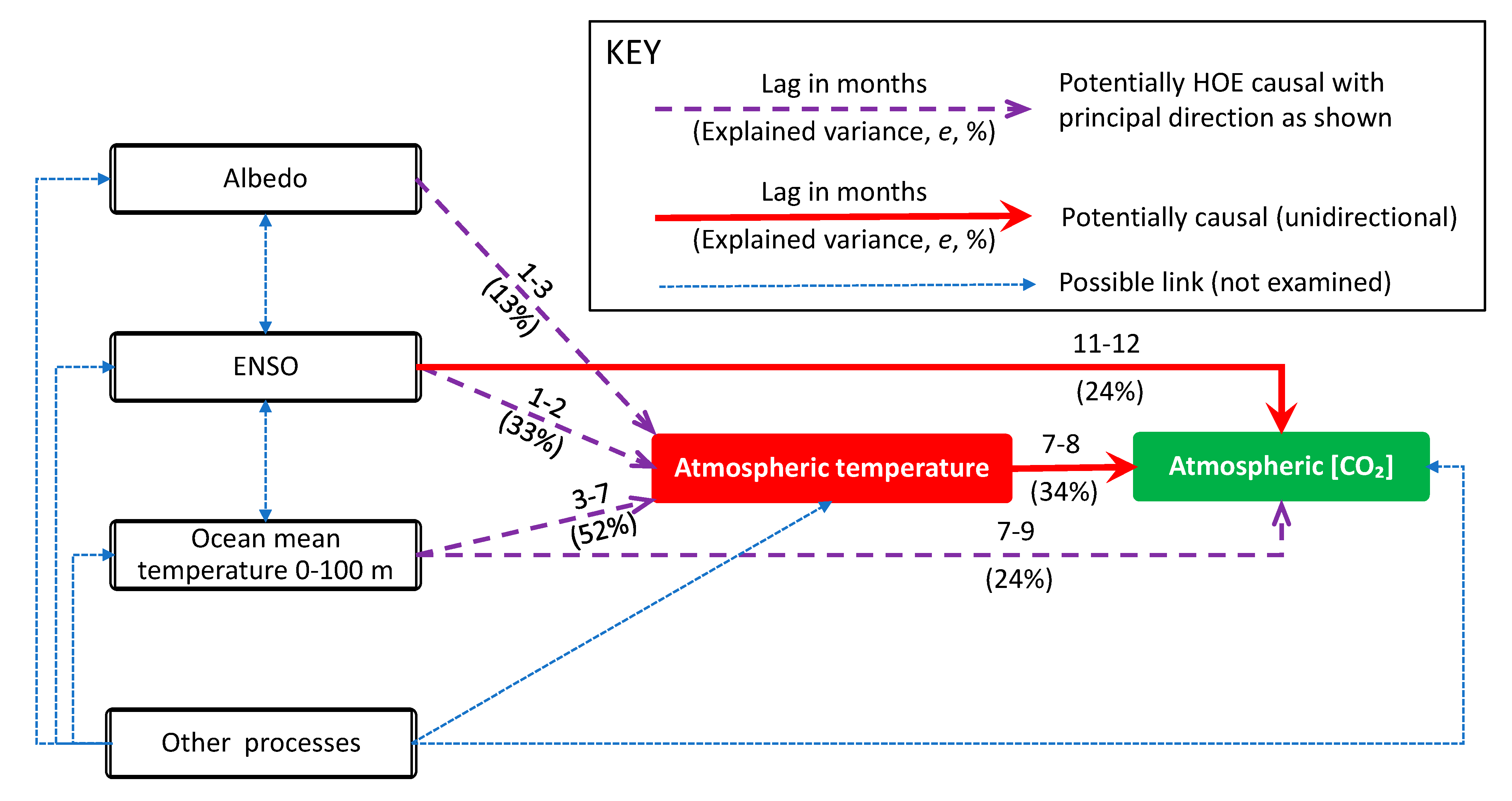 .
.