Dieses geometrische Verhältnis der Division durch 4 für die Einstrahlungsenergie erzeugt das absurde Paradoxon, dass die Sonne nachts direkt auf die Erdoberfläche scheinen muss. Die korrekte Aussage hingegen ist, dass die Intensität der Sonnenenergie über die gesamte Oberfläche einer beleuchteten Hemisphäre gesammelt wird (durch 2 dividieren) und dass es der abgehende Wärmestrahlungsenergiefluss ist, der von der gesamten Erdoberfläche ausgeht (durch 4 dividieren).
Zwischen diesen beiden geometrischen Beziehungen der Einstrahlung und der Ausstrahlung zurück in den Weltraum liegt das atmosphärische Reservoir, die gasförmige Hülle der Erde, in der alle Klimaprozesse ablaufen. Die folgende Tabelle und Abbildung, die aus dem kanonischen Modell von Kiehl und Trenberth (1997) übernommen wurden, dienen der Veranschaulichung eines Modells, in dem die grundlegenden Realitäten einer beleuchteten (Tag) also Hell- und unbeleuchteten (Nacht) Halbkugel als irreduzibles logisches geometrisches Minimum für den Energiehaushalt des Erdklimas beibehalten werden.
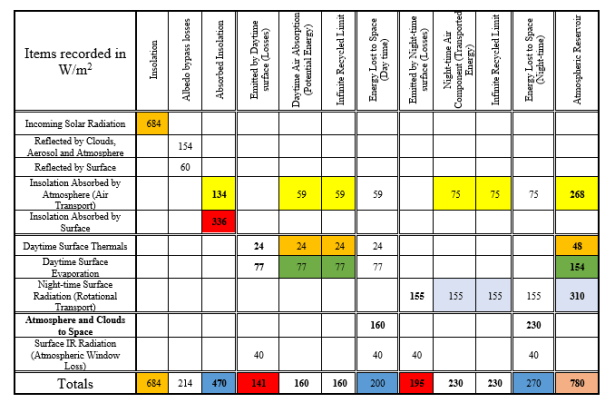
Tabelle 1: Der Prozess der Energierückgewinnung aus atmosphärischen Reservoiren für ein Hell-Hemisphärenmodell.
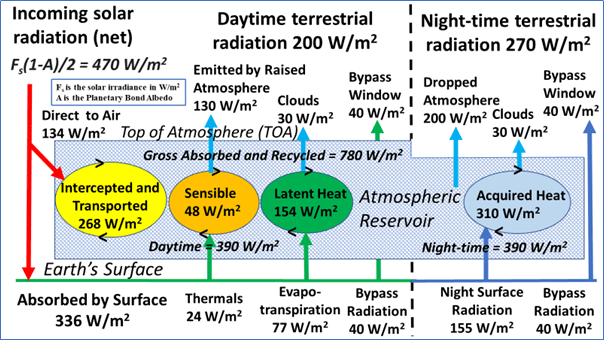
In der folgenden Abbildung wurden die Parameter unter Verwendung halbkugelabhängiger thermischer Energieabflusswerte von 200 W/m² (Tag) und 270 W/m² (Nacht) auf der Grundlage eines dynamischen atmosphärischen Energietransportmodells des Erdklimas (Wilde und Mulholland, 2020b) angepasst.
Haupt-Erkenntnisse aus dem Diagramm:
-
Es zeigt, dass das Konzept des atmosphärischen Reservoirs für eine Hell – Halbkugel (durch 2 teilen) Sonneneinstrahlung anwendbar ist.
-
Es zeigt, wie sich das atmosphärische Reservoir sowohl als Energiespeicher als auch als Energietransporter verhält.
-
Alle eingefangenen Energie-Flüsse werden durch den Prozess des unendlichen geometrischen Recyclings verdoppelt (die Hälfte geht verloren; die Hälfte wird zurückgehalten, wodurch sich eine unendliche Reihe von Hälften von Hälften zu einer Hälfte summiert).
-
Tagsüber dehnt sich die Troposphäre aus, da sie potentielle Energie mit der gegen die Schwerkraft geleisteten Arbeit speichert.
-
Potenzielle Energie kann nicht weggestrahlt werden, so dass der Tagesverlust am oberen Ende der Atmosphäre (TOA) mit der Ausdehnung der Atmosphäre verringert wird.
-
Während der Nacht zieht sich die Troposphäre bei ihrer Abkühlung zusammen, wodurch potenzielle Energie wieder in kinetische Energie umgewandelt wird, die für den erhöhten nächtlichen Energieverlust an den Weltraum verantwortlich ist.
-
Der Bruttowert des atmosphärischen Reservoirs von 780 W/m2 wird auf den kanonischen Wert von 390 W/m2 halbiert, weil die Oberfläche des emittierenden Globus doppelt so groß ist wie die der Sonnenkollektor-Halbkugel.
-
Die Tagesprozesse der Thermik und der Evapotranspiration werden in erster Linie durch direkte Sonnenenergie angetrieben und finden daher nachts nicht statt (viele Vorbehalte hier: wenn die Oberfläche feucht ist, kann der Verdunstungsprozess auch nachts stattfinden, z.B. Land gegen Meer, feuchter Tropenwald gegen trockene Wüste, Advektion von Wettersystemen usw.).
-
Die Erdoberfläche ist ein riesiger, langsam freigesetzter Speicherstrahler, der seine eingefangene Sonnenenergie auch nachts und im Winter abgibt.
-
Die Bypass-Strahlung tritt sowohl am Tag als auch in der Nacht mit der gleichen Rate (40 W/m²) auf wie im kanonischen Modell, weil die gleiche Flächenproblematik der Sammlung gegenüber der Emission wie in Punkt 7 aufgeführt ist.
Die Lungen von Gaia
Man könnte den Prozess des Einfangens von Sonnenenergie am Tag, der die Atmosphäre zur Ausdehnung bringt, gefolgt von der nächtlichen Kontraktion der Atmosphäre beim Abkühlen, mit dem „Atmen“ der Erde vergleichen. Die Atmosphäre ist die Lunge unseres Planeten, die sich im Laufe eines 24-Stunden-Zyklus ausdehnt und zusammenzieht und dabei die Zufuhr potenzieller Energie an die Oberfläche variiert. Dieser rhythmische Prozess sorgt für die Aufrechterhaltung des hydrostatischen Gleichgewichts der gesamten Atmosphäre, indem die thermische Strahlungsenergie in den Weltraum mit der hochfrequenten Strahlungsenergie der Sonne in Einklang gebracht wird.
References
Kiehl, J.T and K.E. Trenberth, 1997. Earth’s Annual Global Mean Energy Budget. Bulletin of the American Meteorological Society, Vol. 78 (2), 197-208
Wilde, S.P.R. and Mulholland, P., 2020a. An Analysis of the Earth’s Energy Budget. International Journal of Atmospheric and Oceanic Sciences. Vol. 4, No. 2, 2020, pp. 54-64. doi: 10.11648/j.ijaos.20200402.12
https://www.researchgate.net/publication/344539740_An_Analysis_of_the_Earth’s_Energy_Budget
Wilde, S.P.R. and Mulholland, P., 2020b. Return to Earth: A New Mathematical Model of the Earth’s Climate. International Journal of Atmospheric and Oceanic Sciences. Vol. 4, No. 2, 2020, pp. 36-53. doi: 10.11648/j.ijaos.20200402.11
Link: https://wattsupwiththat.com/2020/10/22/the-lungs-of-gaia/
Übersetzt von Chris Frey EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"#Herr Müller,
zu inneren Widersprüchen in KT97:
KT 97 vergleicht sich mit den Mittelwerten der Messwerte (ERBE).
Fall 1: 235W/m² sollen 243W/m² (bewölkt) entsprechen. 30 W/m² in FIG.7. KT97 Einfluss der Wolken mit 31 net cloud forcing Messwert passen zusammen. Denn dann sind 235 W/m² die maximal mögliche, durchschnittliche Abstrahlung im Modell KT97. 107 im Modell (Albedo = shortwave radiation, aber Messwert 101 W/m²), Abweichung 6 W/m². Dann wäre 205W/m², über 200W/m² für sich genommen ein Modellwert für klaren Himmel. Mit der Differenz von 30 W/m² wäre zumindest auch das net cloud focing berücksichtig, aber in der falschen Richtung. Der Messwert für klaren Himmel clear sky longwave radiation ist 276 W/m² #205 W/m², und damit logischer Widerspruch.
Fall 2: 235 W/m² sollen im Modell KT97 dem (klaren) Himmel entsprechen. Dann wäre analog zu den Messwerten 243 W/m² + 31W/m² = 274 W/m², was dem Messwert von 276 W/m² nahekommt. (net jetzt in der richtigen Richtung.) Eine 2 W/m² Abweichung zwischen Modellwert und Messwert und den Messwerten untereinander erscheint als Modelltoleranz gerechtfertigt. 276 W/m² müssten ebenfalls im Modell KT97 abgebildet werden, da es sich mit den durchschnittlichen Messwerten vergleicht. 1368W/m²/4 – 107 W/m² (Albedo) = 235 W/m² kleiner 276 W/m². Der Messwert kann nicht dargestellt werden. Logischer Widerspruch.
Fall 3. KT97 zeigt mit einem Atmosphärischen Fenster von 40 W/m² eine durchschnittliche Bewölkung von 62%. Dann stimmen die Werte für LH 78 W/m² und SH = 24 W/m² nicht, da das atmosphärische Fenster falsch berechnet wurde. 38% klar = 62% bedeckt. 38% klar befindet sich zwischen klarem und bedecktem Himmel. Nach KT97, S205, Abschnitt 5 letzte Zeile, clear sky case atmospheric window 99 W/m², cloudy 80 W/m². Für 37,6 W/m² 0der gerundet 40 W/m² ergeben sich aber nur, wenn man für die Interpolation den bedeckten Himmel für das Fenster mit 0 W/m² annimmt. Das ist falsch, somit beträgt das atmosphärische Fenster 87.2 W/m² = 80 + 38/100 x 19. Bsp. schon mit SH = 20 < 24 und LH = 68 < 78, gibt es nun von der Erdoberfläche keine langwellige Abstrahlung, da 168 – 20 – 68- 80 = 0 Und 168 = 342 -107 – 67 (Satm). 24 und 78 sind in KT97 somit falsch. Konvektion SH und Wärmeleitung LH sind keine Strahlungen. Die langwellige Strahlung 80W/m² entschwindet durchs Atmosphärische Fenster. Mit 0W/m² kann CO2 nicht angeregt werden. Dies war aber das Ziel der Studie KT97. Logischer Widerspruch. Folge, andere Interpretation der Messwerte, in dem man sich eine halbseitige Beleuchtung der Kugel betrachtet.
Albert Agerius schrieb am6. November 2020 um 16:45
Wärmestrahlung geht im Bereich des atmosphärischen Fensters durch Wolken durch, ohne absorbiert zu werden? Woher nehmen Sie das? Bisher habe ich immer gelesen, dass Wolken über den kompletten Infrarotbereich absorbieren …
LH bzw latent heat ist keine Wärmeleitung…
Herr Mueller,
ihre frei-falsche Interpretation vom Gesagten wird nur noch von ihrer falsch-selektiven Zitierungen übertroffen.
Alles in Allem nichts neues von Ihnen.
Wolken absorbieren nicht nur, sondern strahlen auch noch in allen Wellenlängen ab. Etwas was sie von CO2 nicht sagen können.
Aber das sie erkannt haben, das Latent Heat keine Wärmeleitung ist, ist fortschrittlich.
Bitte bestätigen auch sie, das die Erde nicht flach ist, und das die Sonne immer nur eine Hemisphäre bestrahlt.
# Marvin Müller
Herr Müller, zu Ihren Fragen (was kurzzeitig weg war):
bei den Net- Strahlungswerten handelt es sich um gefunkte Messwerte. Im EIKE Beitrag“ Umgebungsgleichung (Stefan-Boltzmann-Gesetz)…./ Mittelwertbildung“ zeige ich eine Anordnung in drei Gruppen Longwave-, Net-, Shortwave- für eine Trennung von clear und cloudy Werten. Ich arbeite mit dem Durchschnitt der Jahre 1985-1989. Für den Wert von clear sky shortwave cloud forcing man schafft die exakte Trennung nicht ganz, es entsteht hierbei eine Abweichung von 11.5% =48/(276+42+48+50)x100. Man erkennt aber dann, dass sich einerseits jeweils immer zwei Werte zu einem Dritten in jeder Dreiergruppe sehr genau ergänzen. Anderseits entspricht sich annähernd die Summe clear sky = 416 W/m² mit der Summe cloudy sky 413 W/m². Der Mittelwert ergibt 414.5 W/m². Für das Modell wird hier um 2 W/m² gerundet. Deshalb habe ich in FIG.8. clear sky statt 50 auf 48 abgerundet und von net cloud forcing von 18 auf 19 aufgerundet 0der 3W/m²/2 =1.5 oder 2 W/m² und 1W/m². 414 + 69 (LH) + 17 (SH) + 184 (Albedo) =684 und 184/684= 0.269 = ist dann exakt der gefunkte Messwert im fünfjährigen Mittel der Albedo, Streuung der gefunkten Albedo von 0.268 bis 0.271.
Eine Frage an die Administration: Ich hatte Herrn Agerius relativ ausführlich geantwortet (heute, 13:58, Kommentar 265799). Gibt es einen speziellen Grund, diesen Kommentar nicht zu veröffentlichen? Wird die Diskussion über die Ideen von Herrn Agerius hier nicht gewünscht?
Zu lang. Kürzer fassen. Oder eigenen Blog aufmachen.
Sehr geehrter Herr Müller,
Textblöcke werden schnell zu lang, mir geht es ähnlich. Falls Sie wollen, senden Sie sie mir ihren Text direkt an: aulus-agerius@gmx.de
Albert Agerius schrieb am 6. November 2020 um 16:38
(Die Kurzform meines Kommenatrs reduziert auf ein offensichtliches Problem in der Summe).
Die kurzwellige Strahlung, die von Erbe und Ceres ausgewiesen wird, ist die aufgrund des Albedos reflektierte Sonnenstrahlung. Die Summe von langwelliger, kurzwelliger und net Radiation entspricht der Einstrahlung (siehe Net Radiation).
Für 1987 wäre das P_l = 243.1 + 100.8 + 19.9 = 363.8 bzw. für kurzwellig P_s = 276.5 + 50.5 + 41.1 = 368.1.
Berechnet man das rückwärts aus Albedo und kurzwelliger Einstrahlung erhält man P_l = shortwave/albedo * 100= 100.8/26.9 * 100 = 374, P_s = 50.5/13.6*100 = 371. Das ist eher in der Nähe von 340W/m² als 680W/m².
In der von Herrn Agerius angegebenen Summe steckt die kurzwellige Abstrahlung jetzt zweimal drin, einmal in den aus Sattelitendaten berechneten 414W/m² und dann nochmal in den 184W/m² = 684 * 0.269. Hier wird also versehentlich die Energiemenge erhöht, indem man zweimal einen Term für die auf Albedo basierende kurzwellige Rückstrahlung aufführt.
Die Argumentation für die anderen fälschlicherweise in den Summen enthaltenen Terme (cloud forcing, latent heat, sensitive heat) entfällt, um den Kommentar kurz zu halten.
Zu Herrn Müller vom 9.11.2020 um 9:17 Uhr
KT97 verwendet ein mehr planes, ebenes Modell mit geometrischem Ansatz der Albedo, vergleichbar einem Lambertschen Stahler. Einstrahlung, Reflektion, Absorption und Abstrahlung liegen in einer Wirkungslinie. Die kurzwellige Strahlung 101 wird als Albedo mit 107 gleichgesetzt. Achtung Modellunterschied. Bei hemispherischem Ansatz kann die Albedo als bondsche oder sphärische Albedo interpretiert werden. Beispiel: Mücke (Satellit) fliegt wenige cm um eine seitlich, extern beleuchtete Diskokugel (Erde). Die sphärische Albedo ist die allseitig durch die Krümmung in den Raum weggestreute Strahlung. Der Teil, 184 W/m², der an der Mücke „vorbei“ geworfen wird, ist somit auch für den Satelliten verloren. 184 müssen aber dennoch in der Bilanzierung erscheinen. Vielleicht wird es hierdurch etwas besser verständlich.
Albert Agerius schrieb am 9. NOVEMBER 2020 UM 17:27
Ich rede über Ihre Argumentation, die auf Satellitendaten basiert. Warum weichen Sie immer auf KT97 aus? Sie haben sich die Erbe-Daten genommen und mit einer Interpretation unterlegt, die IMHO falsch ist. Ich habe Ihnen die Beschreibungen von Ceres gezeigt, die mit denen von Erbe übereinstimmen sollten. Denken Sie, dass die von mir verwendeten Begriffsbestimmungen/Zusammenhänge falsch sind? Dann verweisen Sie bitte auf die Beschreibungen, auf die Sie sich stützen. Oder sagen Sie klar, dass das Ihre eigenen Annahmen sind, die von denen der Wissenschaftler abweichen, die die Daten erhoben haben.
Der Kommentar, auf den Sie geantwortet haben, bezog sich rein auf die von Ihnen verwendeten Erbe-Daten. Er hatte nichts mit KT97 zu tun und Sie sind auf keinen meiner Punkte eingegangen – zumindest war es für mich nicht zu erkennen. Oder sollte die Behauptung, es gäbe 184W/m^2, die einfach unerkannt am Satelliten vorbeigehen, eine Antwort auf meine Anmerkung sein, dass Sie die kurzwellige Strahlung zweimal in die Summe aufgenommen haben?
Ich warte auch immer noch auf eine Erklärung, warum Sie einfach die Abbildung der Einstrahlung auf eine Halbkugel ignorieren können, was die Energiemenge mal eben verdoppelt …
Die Energiemenge ist nicht verdoppelt.
Rein mathematisch ist S2/A2 das Gleiche wie S4/A.
Falls sie das nicht so sehen, spezifizieren sie bitte die mathematische Regel die das nicht zulässt!
Werner Schulz schrieb am 10. November 2020 um 13:35
Seufz … Wie wäre es denn, wenn Sie erst mal lesen würden, worum es geht?
Angenommen Sie haben eine Einstrahlung S in W/m² und lassen die auf die Oberfläche einer Kugel einwirken. Wie gross ist die mittlere Einstrahlung?
a) S
b) S/2
c) S/4
Wenn Sie die Texte von Herrn Agerius lesen, werden Sie sehen, dass er für die Abbildung der Satellitenwerte a) annimt. Das habe ich angemerkt und um eine Erklärung gebeten, warum er denkt, das wäre korrekt …
Weil sich die Strahlstärke der Einstrahlung nicht durch die Geometrie der Oberfläche ändert.
Der selbe Grund warum sie auch noch in der Polarregion einen Sonnenbrand holen können und weil man auch noch an den Polen S als messwert feststellen kann, wenn man senkrecht zur Einstrahlrichtung misst.
Werner Schulz schrieb am 11. November 2020 um 5:38
Warum rechnen Sie dann mit S/2 für die Einstrahlstärke auf der beleuchteten Hemnisphäre, die ja eine Halbkugel und keine Ebene ist?
Das ist echt lustig, die ganze Zeit argumentieren Sie, dass man mit S/2 statt mit S/4 rechnen muss, da nur eine Halbkugel bestrahlt wird und nun argumentieren Sie, dass man doch einfach S nehmen kann. Die Beliebigkeit Ihrer Argumentation ist echt erstaunlich.
Herr Mueller,
Was misst man also ihrer Meinung nach senkrecht zur Einstrahlung der Sonne?
Die Frage „Warum rechnen Sie dann mit S/2 für die Einstrahlstärke auf der beleuchteten Hemnisphäre, die ja eine Halbkugel und keine Ebene ist?“
Lässt sich einfach beantworten! Weil eben die Fläche, die die Strahlung erhält keine Ebene sondern eine Halbkugel ist.
Und falls sie das Argument nicht verstehen, hier noch mal:
Die Strahlstärke der Einstrahlung ändert sich nicht durch die Geometrie der Oberfläche.
Sie müssen schon unterscheiden zwischen gemittelter Leistung pro Fläche und Strahlstärke.
„Angenommen Sie haben eine Einstrahlung S in W/m² und lassen die auf die Oberfläche einer Kugel einwirken. Wie gross ist die mittlere Einstrahlung?“
Soll das das Beispiel Erde Sonne sein? Also nur eine Quelle die immer nur eine Hemisphäre bestrahlt? Die Antwort ist Leistung pro m2 S/2.
Die Strahlstärke ist S.
S/4 ist falsch für die Einstrahlung.
Werner Schulz schrieb am 11. November 2020 um 14:10
Das weiss ich. Daher kritisiere ich ja, dass Herr Agerius den Faktor 1/2 einfach wegläßt. Lesen Sie doch einfach mal, was er schreibt, statt mir immer irgendwelche abstrusen Dinge zu unterstellen …
Sehr geehrter Herr Müller,
Also wieder ein Fehler, der zeigt, dass Herr Agerius Probleme mit dem Aufstellen einer einfachen Bilanz hst.
Herr Petersen,
Sie würden nicht mal einen Fehler entdecken wenn da einer wäre.
Erklären sie mal den Lesern warum die Eingangs und Ausgangsleistung, angegeben als Strahlstärke, gleich sein sollen, wenn die Ausstrahlfläche doppelt so gross ist wie die Einstrahlfläche.
Die Energiebilanz stimmt wenn man mit S2 rechnet.
Herr Schulz, ihre Annahme (Ausstrahlfläche doppelt so gross ist wie die Einstrahlfläche.) ist falsch, die Erde rotiert!
Ich bin es etwas leid, extrem triviale Zusammenhänge zu erklären.
Herr Petersen,
ihre Erde ist flach und ich kann nichts mehr fuer sie tun.
Zur Abwechslung der Argumentation die Rotation der Erde hat nichts damit zu tun, das die Einstrahlfläche nur halb so gross ist, wie die Abstrahlfläche der Erde. Das ist eine geometrische Realität, die durch die Fast-Kugelgestalt der Erde gegeben ist.
Haben sie schon den Versuch mit der Taschenlampe und dem Fußball gemacht. Wenn sie mit einer Lampe ohne andere Hilfsmittel den gesamten Fußball ausleuchten können, sagen sie Bescheid.
Albert Agerius schrieb am 4. NOVEMBER 2020 UM 18:10:
Um sicherzugehen, dass ich Sie richtig verstehe:
* die 9 „Messwerte“ sind {long wave, short wave, netto} für clear sky und cloudy sky und {long wave, short wave, netto} cloud forcing
* die aufgeführten Summen sind (mit den Werten, die ich für 1987 aus den GIFs entnommen habe)
** 5 Messwerte cloudy Sky = cloudy long wave + cloudy short wave + cloudy net + long wave cloud forcing + net cloud forcing = 243 + 100,8 + 19,9 + 30,9 + 18,3
** 4 Messwerte clear Sky = clear sky long wave + clear sky short wave + clear sky net + ? = 276,5 + 50,5 + 41,1 + ? (die zweite 48 konnte ich nicht zuordnen, in Ihrem anderen Artikel hatten Sie für klaren Himmel ein short wave cloud forcing angesetzt, ist das hier auch gemeint?)
Habe ich das so richtig verstanden?
Dann wäre meine erste Frage, warum Sie in die Summen die Netto Werte mit einfliessen lassen. Das sind doch keine Messwerte, sondern Differenzen aus Messwerten, z.B. net = Einstrahlung – (long wave + short wave) wenn ich das richtig verstanden habe.
Die nächste Frage wäre, warum Sie das Cloud forcing einfach hinzuaddieren. das long wave cloud forcing wirkt nicht in die gleich Richtung wie die kurz und lagwellige Abstrahlung, im Gegenteil.
Und warum wirkt bei Ihnen bei klarem Himmel ein short wave cloud forcing?
Und zu guter letzt: Das sind globale Mittelwerte. Diese setzen Sie in Beziehung zu einem Wert, der nur für eine Hemnisphäre, also nur für die Hälfte der Erdoberfläche gilt. Das ist schon beim ersten Hinkucken falsch, da die Bezugsflächen flasch sind. Der eine Wert gilt für eine halbe Fläche, die anderen Werte für die ganze Fläche …
Herr Agerius hatte auf meinen Kommentar geantwortet, ist aber nicht auf meine (relativ konkreten) Fragen eingegangen. Der kommentar ist versehentlich gelöscht worden. Daher einfach einige weitere Anmerkungen zu den aufgestellten Summen in der Hoffnung, dass dann die Anworten konkreter werden.
Die von Erbe bereitgestellten „Meßwerte“ sind
3 SHORTWAVE RADIATION
4 LONGWAVE RADIATION
5 NET RADIATION
6 ALBEDO
7 CLEAR-SKY SHORTWAVE RADIATION
8 CLEAR-SKY LONGWAVE RADIATION
9 CLEAR-SKY NET RADIATION
10 CLEAR-SKY ALBEDO
11 LONGWAVE CLOUD FORCING
12 SHORTWAVE CLOUD FORCING
13 NET CLOUD FORCING
Gemessen sind dabei Longwave Radiation, Shortwave Radiation, und Albedo – jeweils als clear sky und komplett. Die anderen Werte sind berechnet, z.B. Longwave cloud forcing = Clear sky longwave radiation – Long wave radiation.
Die Gleichung für ein und ausgehende Energie ist Einstrahlung = Langwellige Abstrahlung + Kurzwellige Abstrahlung. Sie blasen die rechte Seite jetzt auf, indem Sie noch Longwave cloud forcing, Net cloud forcing und Net radiation hinzufügen. Aber das sind nur Differenzen der drei anderen Energieflüsse – die kann man doch nicht einfach nochmal draufaddieren und damit Energieflüsse erzeugen, die es so gar nicht gibt.
Könnte das sein, dass Sie die dargestellten Werte einfach missverstanden haben? Oder könnten Sie mir erklären, was ich an den Werten falsch verstehe?
Ich schrieb am 5. November 2020 um 22:25
Hier muss ich mich selber korrigieren. Da Net radiation als Differenz zwischen eingehender Strahlung und ausgehender kurz und langwelliger Strahlung definiert ist, ist es natürlich OK, die zu ausgehender kurz- und langwelliger Strahlung hinzuzuaddieren und mit der eingehenden Strahlung gleichzusetzen. Die Satellitendaten, auf denen dieser Wert beruht, gehen nur von 60°N-60°S geht. Da kann ein Überchusss entstehen, der an den Polen ausgeglichen wird.
Cloud forcing hat dort jedoch nichts zu suchen …
# zu Herrn Müller vom 6.11.2020 um 10:33 Uhr
In Fall 3 habe ich versucht, Sie etwas aus der Reserve zu locken. Bei 62% Bedeckung passt die verbliebene Strahlung von 66 W/m² auch komplett ins atmos. Fenster von 87 W/m² und kann mit geringster Anregung von CO2 ins Orbit entschwinden. CO2 strahlt meiner Meinung nach wirklich, aber nur unwesentlich marginal.:
Gefunkte Albedo 1987 = 0.269 ist gleich 100.8/(100.8+276.5) = 0.267 aus gefunkten Messwerten errechnete Albedo von 1987.
Für 62% Bedeckung oder 38% klar wären in FIG.7., mit Zahlen in W/m² und Werte von 1987, aus Strahlung bei 100% klar = 276.5 (long-) und 100% klar = 50.5 (shortwave), etc.
shortwave radiation = 50.5+0.62 (100.8-50.5) = 81.7
longwave radiation = 276.5-0.62 x (276.5-243.1) = 255.8
Albedo 100% klar oder 0% bedeckt = klar = 0.136 (1987) und 100% bedeckt = 0.269 (1987) aus Messwerten
Albedo 62% =81.7/(81.7+255.8)=82/337.5=0.24 0der 0.135+0.62 x(0.269-0.135) = 0.22, dh. zwischen 0.22 und 0.24
Würde KT97 62% darstellen, müsste in Kiehl und Trenberth FIG.7. abgebildet sein: shortwave radiation = 82 W/m² statt 107 W/m² outgoing longwave radiation 256 W/m2 statt 235 W/m² und die Albedo betrüge ca. 0.23 statt 0.32 (107/342) Damit stellt KT97 nicht 62% dar, logischer Widerspruch.
Anmerkung: clear sky net radiation plus clear sky shortwave radiation ergibt shortwave radiation. Die drei net– Strahlungenmessungen stehen auch selbst in innerem Zusammenhang. Net cloud forcing und net radiation ergeben die clear sky net radiation. Wären diese drei Null, müsste man sie nicht berücksichtigen. (Auch diese Variante, alle drei net = 0 für die Trennung von clear und cloudy , habe ich gerechnet. Es ändern sich der Absorptionsanteil der Atmosphäre und die Werte für Konvektion und Wärmeleitung, aber 390 W/m² als langwellige Abstrahlung bleiben erhalten).
Albert Agerius schrieb am 7. November 2020 um 18:28
Hmm … Zahlen für 1987
* clear sky net: 41.1
* clear sky short wave: 50.5
* short wave: 100.8
100.8 – (50.5 + 41.1) = 9.2. Das ist eine ziemlich grosse Differenz.
Und warum sollte das so sein? Das ergibt keinen Sinn. Net radiation ist definiert als Incoming radiation – (long wave radiation + short wave radiation). Warum sollte Incoming radiation – (clear sky long wave radiation + clear sky short wave radiation) + clear sky short wave = Incoming radiation – clear sky long wave radiation das gleiche sein wie short wave radiation? Welchen physikalischen Zusammenhang vermuten Sie da?
Sehr geehrter Herr Müller,
Scheint, dass Herr Agerius noch dickere Eier gelegt hat (frei nach W. Pauli) als alleine schon mit dem Eingangswert für die langfristig gemittelte solare Einstrahlung ins Klimasystem.
Daher habe ich mich erstmal aufs Einfachste beschränkt. Wenn er daran schon scheitert, wird der Rest wohl aufgrund von ähnlich grundlegenden Verständnisproblemen ebenfalls massiv fehlerdurchsetzt sein.
#Marvin Müller 5.11.2020 um 22:25 Uhr
#Fortsetzung zu Herrn Marvin Müller 5.11.2020 um 22.25 Uhr
4.Warum in Bezug setzen zur Hemisphäre:
Die Trennung in clear und cloudy erfolgt, weil die Messwerte einschließlich der net- als Energiebeträge betrachtet werden. Nun fällt auf, dass sich die als Energiebeträge net cloud forcing und net radiation zu clear sky net radiation ergänzen. Wie sich 684W/m² für die Hemisphäre als modellierte durchschnittliche Einstrahlung für den Satellit im Modell errechnen, hatte ich bereits begründet. Durch den Energieerhaltungssatz kann keine Energie verloren gehen. Dies ist von der Strahlungsaufteilung 1368 W/m² auf eine Kugel oder 1368W/m² auf zwei halbe Kugeln unabhängig. Deshalb hatten beide Modelle 1.507 E +22 J Energie in 24 h. Die Fallunterscheidung in clear und cloudy, siehe Schaubilder aus dem EIKE Beitrag „Umgebungsgleichung (Stefan Boltzman…), liefert 684 W/m² mit 4 bzw. 5 Strahlungsmesswerten aus Tag- und Nachtmittel, was dem Satelliten aus Tag- und Nachtmittel auf Grund der Energieerhaltung entsprechen muss. Deshalb sind die net- Messwerte keine bloßen mathematischen Differenzen, sondern echte Energiebeträge. Ohne net- Beträge gäbe es keine 1.507 E +22 J im Hemisphären Modell = Energie in KT97.
5. 60 Grad
Der Satelliten NOAA-9 geht über die Pole und liefert ähnliche Werte, z.B. NOAA-9 albedo 1986 a = 0.269 und ERBS albedo 1986 a = 0.267. Die Datenlage bei ERBS ist aber in Summe erheblich besser. Für NOAA9 Werte siehe CEDA.
#Marvin Müller 5.11.2020 um 22:25 Uhr
Sehr geehrter Herr Müller,
1, ich hatte auf Ihre Fragen z. B. „48“, „shortwave am klaren Himmel“ „Richtung der Strahlung“ ausführlich geantwortet, ist momentan nicht sichtbar.
2, wir sprechen von den gleichen Werten (CEDA, Oxford,). Fünfjähriger Durchschnitt und Werte von 1987 unterscheiden sich nur sehr geringfügig.
3,warum net:
In KT97 erreichen 342 W/m² modellierte „Incoming Solar Radiation“ die Erde sowohl für den klaren, wolkenlosen Himmel und gleichzeitig bei bewölktem Himmel. Alle vom Satelliten gefunkten Strahlungs- Albedo Datensätze sind mit aus Scannern gewonnene Messwerte. Messwerte mit der Bezeichnung Net- sind ebenfalls clear- und cloudy zugeordnet. Als Strahlungen müssen sie in einem Bilanzschema mitberücksichtigt werden.
[Einschub] Für Strahlungen gibt es kein Subtraktionsgesetz. Bsp. Sie haben in einem dunklen Keller 6 Kerzen, drei links und drei rechts. Die zünden Sie an. In der Mitte entsteht kein dunkler Fleck. Sie verschieben die Kerzen zu 2 links und 4 rechts. Die rechten vier Kerzen schwächen nicht die linken zwei. Für Strahlung gibt es nur ein Additionsgesetz. Auf dem einen m² einer Sekunde wirkt als Einheit: 1 m² x W/m² x sec = 1 m² x J sec /m² x sec = J. Man kann die Energie als Beträge betrachten. Es folgt eine Fortsetzung.
1 Grill, 1 Hähnchen, 1 Spieß, 1 Leistung P.
A) Grill an, auf Stufe I Oberhitze. Hähnchen aufgespießt ohne Rotation. Annahme: Hähnchenoberseite ist nach 15 Minuten knackig gar. Hmmmm. Die untere Seite lassen wir lieber außer Acht, da sicher noch schwabbelig.
B) Gleiches Experiment, neues Hähnchen, Stufe 1 Leistung P Oberhitze, aber jetzt mit Rotation!
Nach 15 Minuten ist das Hähnchen mit Sicherheit noch nicht gar wie in Fall A)
Theoretisch müssten es 30 Minuten sein, um ein vergleichbares Ergebnis zu erlangen, weil es auf die Fläche ankommt, die der (direkten) Strahlung durch die Heizstäbe ausgesetzt ist.
Fazit: 1/2 S ist richtig und 1/4 S falsch. (Frag den Koch!!)
Super Vergleich!
Herr Agerius,
schön, dass Sie die Diskrepanz doch noch klären wollen.
Schritt 1 ist korrekt. Bei Schritt 2 machen Sie den bekannten Fehler.
Vielleicht hilft es Ihnen, wenn ich Ihr Analogon mit dem Auto mitbenutze. Sonne = Heizstrahler liefert eine konstante Leistung. Auto = Erdoberfläche…? Aber welche Erdoberfläche?
Bei Schritt 1 ist das einfach, da ist Auto = eine feste Hemisphäre, nämlich die, die konstant beleuchtet wird. Denken Sie, dass Sie letztlich die Bilanz an jedem Punkt der Erdoberfläche betrachten müssen, denn
Bei Schritt 2 dreht sich die Sonne um die Erde. Die Fläche, die in einem Zeitintervall zumindest zeitweise beleuchtet wird, wächst mit der Zeit. Neue Punkte am Westrand bekommen dann Sonnenstrahlung, während Punkte am Ostrand keine Sonne mehr bekommen. Nun betrachten wir die Energie, die in einem Zeitintervall durch die Sonne zurgeführt wurde. Ein Teil der Energie erreichte noch Punkte am Ostrand, ein Teil der Energie zum Schluß auch neue Punkte am Westrand. Aber weder die im Zeitintervall neu aufgetauchten noch die verschwundenen Punkte bekamen über die gesamte Zeitspanne einen Energiebetrag, der in Summe von 12 Stunden zu einem räumlichen Mittel von 684 W/m2 führen. Es ist weniger (!!!), denn diesen Mittelwert über die beleuchtete Hemisphäre bekommen Sie nur hin, wenn wie in Schritt 1 die Punkte über 12h immer die gleichen sind und konstant beleuchtet werden.
Analogie zu Ihrem Auto: das Auto hat keine konstanter Leistung, sondern benötigt mehr Leistung mit der Zeit (die Zahl beleuchteter Punkte, die in einem Zeitintervall einmal beleuchtet wurden, bzw. die insgesamt einmal zumindest zeitweise beleuchteten Flächen in diesem Zeitintervall nimmt mit der Zeit zu). Da aber die Sonne konstante Leistung liefert, ist der Mittelwert der Leistung auf die in einem Zeitintervall beleuchteten Fläche bei einer rotierenden Sonne (Schritt 2) gegenüber dem Fall der ruhenden (Schritt 1) geringer! Über 24 h gemittelt kommt dann genau die Hälfte heraus, denn die in 24 h zumindest zeitweise beleuchtete beleuchtete Fläche ist doppelt so groß wie eine Hemisphäre! Schritt 3 geht von den falschen Voraussetzungen Ihrers Schritts 2 aus.
Das Paradoxon der „Nachts scheint die Sonne“ gibt es nicht. Sie machen den Fehler, die am Boden zur Absorption gegelieferte Sonnenenergie zeitlich gleichzusetzten mit der Abstrahlung derselben (synchrone Umwandlung). Das ist aber falsch. Bei der Absorption geht die Energie ja erstmal großteils in thermische Energie des Bodens über. Die „Freisetzung“ dieser ist ein physikalisch anderer Vorgang , der z.B. Zeitkonstanten entsprechend der Wärmekapazitäten etc. hat.
Ich habe schon geschrieben: „ist hier egal“, da ich erstmal Ihren grundlegenden Fehler in der Sonnenenergie, der gleich bei den Eingangsdaten der Bilanz passiert, klären möchte und erst alleine diesen Punkt klar machen möchte.
Langfristig gilt im stationären Mittel, dass absorbierte Leistung gleich abgestrahlter Leistung sein muss, aber nicht instantan, denn die Wärmereservoire „puffern“ zwichendurch und führen zu einer Differenz zwischen in einem Zeitintervall absorbierter Energie und gleichzeitig darin abgestrahlter Energie (stationär im langfristigen Mittel ändern die ihren Wärmeinhalt natürlich per Voraussetzung nicht, die Differenz ist langfristig Null).
Es gibt keine Bilanz von Leistungen.
Das Konzept Leistung und Energie nicht verstanden.
Sechs, setzen!
„Langfristig gilt im stationären Mittel, dass absorbierte Leistung gleich abgestrahlter Leistung sein muss…“
Ja, aber wir wissen nicht, ob wir in einem „stationären Mittel“ leben!!!
Siehe G/T, Wärmekapazität der Erde ff. (hat nichts mit der hier in diesem Thread diskutierte Fragestellung zu tun, ist aber dennoch insgesamt von Bedeutung)
Der Unterschied ist, das die Leistung nicht gleich sein muss, sondern die Energiemenge.
Wer versucht an dieser Stelle Leistungen zu bilanzieren muss sich gefallen lassen, das man ihm sagt, das er Leistung und Energie nicht auseinanderhalten kann.
Oder einfach mal den Koch fragen!
Zwei ausführlichere Antworten durchs Raster – jetzt mag ich nicht mehr.
Kurz: wenn Leistungen zeitlich konstant sind ergibt sich immer die selbe konstante Energiemenge. In diesem Fall nehme ich Leistung als Synonym für Energiemenge,
da es ja auch nicht um die Menge an sich, sondern um das Gleichheitszeichen ging
Ich weiss zwar nicht was sie ansonsten schreiben wollten.
Aber sie haben ja sicher mitbekommen, das die Frage ist auf welcher Flaeche die Energie ankommt.
Damit gibt es bei der Angabe der Leistung nur eine physikalisch richtige Antwort und das ist S/2. Da sich Einstrahlflaeche und Abstrahlflaeche genau um den Faktor 2 untersccheiden.
Energie ist gleich.
Mathematisch ist S/4 auch moeglich. erlaubt aber keine sinnvollen fuer die Einstrahlleistung.
Teil 2/3 Erläuterung zu Hemisphärenmodell
Schritt 1:
Die Erde stünde 24h still. Die Strahlungsleistung pHem erfolge einseitig auf S/2, flächenbezogene, also zeitlose Leistung für die Einstrahlung auf den Körper im Mittel: [Oder welche Leistung müsste ein Heizstrahler als Äquvalent für diesen durchschnittlichen m² haben?]
pHem = 8208 h S W/m² / [S / 2] / 24 h = 684 W/m²
684 W/m² -> Erde „die Erde stünde still“
24 h
Schritt 2:
Die Erde sei halbseitig beleuchtet stünde still. Nun bewege sich – nur zur anschaulicheren Erklärung der Modellierung – die Sonne „geozentrisch“ um die Erde. Die flächenbezogene, zeitlose Leistung in Watt der Einstrahlung im Modell errechnet sich [NL1] für auf die beleuchtete halbe Kugel im Mittel: [Oder welche Leistung müsste dieser Heizstrahler haben, wenn man ihn jetzt geozentrisch um die nicht rotierende Erde trägt ?]
684 W/m² -> Erde „die Erde steht still“
[Oder Ihr PKW hat 100 PS = 74KW = 74000Watt. Sie fahren um den Telegrafenberg herum im Kreis mit 45 Km/h. Ihr Auto hat 74KW auch an der roten Ampel. Die Leistung Watt ist unabhängig von der Winkelgeschwindigkeit. Für den „Heizstrahler“ Sonne gilt dies ebenso.]
Teil 3/3 Erläuterung zu Hemisphärenmodell
Da Erde und Sonne eine Relativbewegung zueinander vollführen,
Schritt 3: ist dies identisch mit: Die Sonne ist nun wieder heliozentrisch beleuchtet eine rotierende Erde halbseitig.
Hemisphärenmodell 684 W/m² -> Erde „die Erde rotiert“
Sonne 24 h
Die auf einen m² bezogene Einstrahleistung pHem = 684 W/m² liefert so eine langwellige Abstrahlungsleistung der Erdoberfläche von 390 W/m², was der gemessenen Globaltemperatur von ca. 15 °C entspricht und das Paradox „Nachts scheint Sonne“ verschwindet. Der beleuchtete Teil wandert in den Schatten. Der Unbeleuchtete kehrt in die Sonne. Alle Messwerte bilden sich ab.
Im Gegensatz hierzu:
Ergänzung KT97: 342 W/m² -> Erde <- 342 W/m²
24 h
siehe Fall 1 Erde rotiert
Sonne 1 Erde Sonne 2
1 Paradoxon 9 Strahlungsmesswerte 414 W/m² >342 W/m²
2 Paradoxon „Nachts scheint die Sonne“
3 Paradoxon „System von 2 Sonnen“, KT97 ist ein falsches Modell q.e.d.
Albert Agerius schrieb am 2. November 2020 um 18:28 :
Wenn ich da einfach die Probe mache und Ein- und Ausstrahlung gegenüberstelle, sehe ich folgendes: A/2 * 684 W/m² * 24h = A * 342 W/m² * 24h < A * 390 W/m² * 24h
Da ist also ohne Berücksichtigung von Albedo schon ein Defizit von 48W/m², bei Berücksichtigung von Aldo erhöht sich das auf 150W/m².
# Marvin Müller vom 3.11.20 um 13:30 Uhr
„Wenn ich da einfach die Probe mache und Ein- und Ausstrahlung gegenüberstelle, sehe ich folgendes: A/2 * 684 W/m² * 24h = A * 342 W/m² * 24h < A * 390 W/m² * 24h“
Sehr geehrter Herr Müller,
die Kugel bei KT 97 besteht im Modell nur aus Durchschnittsquadratmetern, hierin steht die Strahlung senkrecht zur Oberfläche, d.h. an den Polen und am Äquator genauso mit 342 W/m² für jeden der 360 Meridiane. Im Hemisphärenmodell ist dies genauso. Würden Sie das Hemisphären Modell genauer betrachten, sehen Sie, wie sich die 684 W/m² zusammensetzen. Es addieren sich zu 390 W/m² (ca. 15°C) LH, SH, Satm (Absorbiert und wieder abgegeben von der Atmosphäre) und der Albedoanteil auf Basis des ERBS Satelliten mit 5 jährigem Durchschnitt a = 0.269 ( 684W/m² x 0,269 = 184 W/m²), wie folgt:
Bezogen, wie in KT97, auf den Durchschnittsquadratmeter
684 W/m² = 390 W/m² + 69 W/m² + 17 W/m² + 24 W/m² +184 W/m²
Einstrahlung = Abstrahlung + LH +SH + Satm + Reflektion
oder umformuliert
Einstrahlung = Satellitenmesswerte + LH + SH + Reflektion
684 W/m² = 414 W/m² + 69 W/m² + 17 W/m² +184 W/m² mit
414 W/m² = 5 Messwerte cloudy Sky = 101 +19+20+243+31
= 4 Messwerte clear Sky = 48 +48 +42 + 276
NASA-Messwerte, siehe CEDA, Server Oxford, England, EEBEDATA/ERBS und hierin im Reiter global mean, für 1985- 1989. Im Hemisphärenmodell bilden sich diese Werte dann auf 2 Watt/m² genau ab.
Würde etwas fehlen, ergäbe das Modell nicht 1.507 J E14m².
Sehr geehrter Herr Müller, Sehr geehrter Herr Petersen,
ich richte diese Frage an Sie beide: Wo finden Sie jeden einzelnen dieser 9 Strahlungsmesswerte in der FIG.7. von Kiehl und Trenberth 1997 wieder?
Warum ist es Ihrer Meinung nicht falsch, dass das gemessene Strahlungsprofil mit 414 W/m² erheblich größer ist als die rechnerischen 342 W/m² ?
PS: Teil 1/3 mit Erläuterung zum Hemisphärenmodell und Schritt 0, konnte ich aus unbekannten Gründen bisher nicht hochlanden.
„Sehr geehrter Herr Müller, Sehr geehrter Herr Petersen, ich richte diese Frage an Sie beide: Wo finden Sie jeden einzelnen dieser 9 Strahlungsmesswerte in der FIG.7. von Kiehl und Trenberth 1997 wieder?“
Sehr geehrter Herr Agerius,
ich kann leider dazu nichts sagen. Um die technischen Details zu KT kümmere ich mich nicht. Ich erkläre nur Ihren Fehler in der Berechnung des globalen Mittelwerts über die Erdkugel der eingestrahlten Leistungsdichte bzw. der dafür zugrundeliegenden über ein Zeitintervall eingestrahlten Sonnenenergie.
Die resultierenden S/4 und die zugehörige Erklärung, die ich hier mehrmals in meinen Worten, schrittweise und detailliert darstellte, findet sich verkürzt in jedem Lehrbuch und ist viel älter als KT. Daher ist KT und wie und was sie gemessen haben, hier nicht wesentlich, letztlich bestätigen sie S/4 und damit das, was man eh schon vor rund 100 Jahren ermittelt hat.
Albert Agerius schrieb am 3. NOVEMBER 2020 UM 16:38
Wenn Sie so nett wären, mal einen genauen Verweis auf die Quelle der Daten zur Verfügung zu stellen, würde ich mir die mal ansehen. Vielleicht habe ich an der falschen Stelle gekuckt, aber ich habe auf http://dap.ceda.ac.uk/badc/CDs/erbe/erbedata/erbs/ keine Mittelwerte gefunden.
Zu Sverre Petersen vom 30.10.2020 um 1:08 Uhr
Herr Petersen,
Sie schrieben, Zitat:“…Der Mittelwert ist überhaupt keinem Zeitpunkt zugeordnet.“ Dies ist eine gemeinsame Basis. Der Mittelwert 342W/m² bei KT97 oder 684 W/m² beim Hemisphären Ansatz multipliziert mit 1 m² ergibt als Einheit Watt. Als Watt ist der Mittelwert eine physikalische Größe der Leistung. Sie schreiben im Anschluss: „Der Mittelwert ist nur die gesamte auf die Erdkugel in 24 h eingestrahlte Energie durch Oberfläche und 24 h geteilt – fertig.“
Wenn Sie eine Leistung, hier die solare Einstrahlung [ W/m²], mit dem Kreisquerschnitt der Erde [m²], nun mit 24 Stunden multiplizieren – (somit diese Produkte als Energie formulieren), anschließend gleich durch 24 Stunden dividieren und dann auf eine Oberfläche [m²] verteilen, fällt sofort die Zeit komponente 24 h heraus.
Die Größe des Mittelwertes erfolgt als reine Leistungsbetrachtung. Sie ist gesteuert über die Größe der hierzu betrachteten Oberflächen. Genau das mache ich im hemisphärischen Ansatz. Statt der Vollkugel, verteile ich auf die halbe Kugel. Damit habe ich die doppelte Leistung auf der halben Fläche.
Sie führten fort: „Ob das physikalisch Sinn macht, ist hier egal.“
Sie zeigen, es fällt der Tag mit 24 Stunden heraus. Es ist aber nicht egal, wie die Beleuchtung erfolgt. Für jede Stunde, Sekunde, Millisekunde ist unbeleuchtete Erdhälfte nicht bestrahlt. Wenn es egal ist, was physikalisch Sinn macht, frage ich mich, warum beschäftigen Sie sich mit Physik des Klimas? Durch den zu niedrigen Durchschnitt von 342 W/m² ist es nicht mehr möglich alle 11 Messwerte der Strahlung/Albedo siehe NASA- ERBE für klare und bedeckten Himmel im Modell von KT97 darzustellen. Die möglichst genaue Abbildung der Wirklichkeit muss doch das Ziel einer physikalischen Modellierung sein. Bei gleicher Energie von 1.507 E+22 J im Modell schafft dies der hemisphärische Ansatz und das Paradoxon „Nachts scheint Sonne“ verschwindet.
Werner Schulz
2. NOVEMBER 2020 UM 2:20
„Mathematisch und physikalisch ist die Energieerhaltung bewahrt, wenn man fuer die Einstrahlung A/2 und S2 annimmt und für die Abstrahlung A und S/4.“
Lesen Sie. Der Fehler, auf den ich hier hinweise, bezieht sich ausschliesslich auf die Einstrahlung.
Das habe ich bereits mehrmals geschrieben. Was ich bewiesen und mehrmals erklärt habe, ist die Tatsache, dass die Energieerhaltung für die Einstrahlung NICHT bewahrt ist.
Denn es gibt bei der Agerius/Weber Argumentation keine fix beleuchtete Hemisphäre H1 oder S2, die 684 W/m2 im langzeitlichen und räumlichen Mittelwert erreicht.
Ihre 12 h Mittelung über die beleuchtete Hemisphäre trifft alle Punkte der Erde und und nicht nur eine Hälfte, denn die Erde hat sich in den 12 h um eine Hemisphäre weiterbewegt.
Es kann doch nicht so schwer vorstellbar sein, dass eine Hemisphäre nur zu dem Zeitpunkt, zu dem sie voll beleuchtet wird, diesen Mittelwert hat, aber zu jedem anderen Zeitpunkt eine kleinere momentane hemisphärisch gemittelte Leistungsdichte hat.
Im zeitlichen Mittel kommt dann 342 W/m2 raus. Meine Graphik umzeigt dies doch auch anschaulich genug, wie sich der Mittelwert über einen Streifen zeitlich entwickelt. Die gesamte Oberfläche hat natürlich den gleichen Langzeitmittelwert wie ein beliebig gewählter Streifen, denn sie lässt sich ja aus solchen N-S-Streifen zusammengesetzt denken.
„Koennen sie mal bestaetigen, das die Sonne immer nur eine Hemisphäre bestrahlt?“
Momentan immer eine Hälfte, die sich zeitlich stets aus neuen Punkten zusammensetzt, aber in 24 Stunden werden offensichtlich alle Punkte der Erde bestrahlt, denn die Erde dreht sich, siehe meine Rechnung. Ihre Frage ist etwas zu simple. Haben Sie was interessanteres?
„Oder welche wirren Annahmen ihrerseits führen dazu anzunehmen, das die Sonne die gesamte Erdoberfläche in einer Sekunde bestrahlt?“
Das nehme ich offensichtlich nicht an, wie Sie sehen würden, wenn Sie meine Rechnung verstanden hätten. Wenn Sie überfordert sind, lassen Sie es einfach mit diesem Thema.
Herr Petersen,
sie machen einen grossen Fehler. Sie denken nicht nach.
Allein ihre Aussage das sich die Erde in 12h um eine Hemisphaere weiterbewegt hat, zeugt von ihrer Vorstellungslosigkeit.
Sie reden von Punkten und machen keinen, da die Einstrahlflaeche immer eine Hemisphaere ist. IN JEDER SEKUNDE. Kriegen sie das irgendwann noch mit.
Und in geschätzten 10 Beiträgen habe ich ihnen erklärt das aufgrund der Schiefstellung der Erdachse eben nicht in 24 h die gesamte Erdoberfläche beschienen wird.
Denken sie doch bitte einmal mal nach. Die Hälfte der Oberfläche wird in der ersten Sekunde bestrahlt! Und dann haben sie ungefähr 24 Stunden für die nächste Hälfte.
Wissen sie wie warm diese zweite Hälfte wird? In Ihrem Beispiel behaupten sie, dreht sich die Erde, aber wenn ich S/4 sehe, dann weiss ich das sie flach ist. Das hemisphärische Model für die Einstrahlung ist physikalische Realität. Und die Erde kann sich drehen oder nicht.
Versuchen sie mal ihr vier Minute Beispiel oder die sich nicht drehende Erde.
Im vier Minuten Beispiel brauchen wir die Fläche damit wir die Lösung in W/m2 rauskriegen. Wenn ihre Rechnung fuer die Einstrahlleistung stimmt dann kriegen sie Ihren Wert raus oder nicht?
Werner Schulz schrieb am 3. November 2020 um 1:16
Wenn man sich die Formulierung von Herrn Agerius ansieht mit S/2 und 12h und Ihre Logik darauf anwendet … Dann würde man da eine flache Erde mit 2 Seiten sehen, die alle 12h gewendet wird. Warum das korrekter sein soll, wird sich mir wohl nie erschliessen.
Sicherlich nicht, da sie verstehen muessen das 12 Stunden nicht gleichbedeutend ist mit A/2.
A/2 stimmt schon fuer eine Sekunde. Daher kann man das auch nutzen um fuer jedweden Zeitpunkt unter Einbeziehung von A/2 die Energie, die auf der Erde von der Sonne ankommt zu bestimmen.
Die Leistung bei der das passiert ist S/2.
Werden sie nie verstehen!
Die Wirklichkeit beweist, daß die 342 W/m² Rechnung falsch ist!
Rechnet man mit vollen 342 W/m², ergeben sich nach S.B. ca. 5,7°C Durchschnitt, mit 30% Albedo kommt man auf ca. 240 W/m², was die berühmten -18°C ergibt, und rechnet man mit 161 W/m², die gem. Trenberth/Kiehl nur die Oberfläche erreichen, dann sind es gar nur -42°C Oberflächentemperatur.
Ein Treibhauseffekt müßte nach diesen Rechnungen also eine konstant angenommene Basiseinstrahlungsleistung kumulativ – also wirkungsadditiv – mehrfachausnutzen, etwas, das es in der Realität aber nicht geben kann, weil es einem energieerzeugenden Perpetuum Mobile gleich käme.
Zwei Dinge sind an dieser populär behaupteten Temperaturberechnung falsch:
erstens die Rechnung mit gemittelten Werten und
zweitens die Annahme, man könnte mit Stefan-Boltzmann Temperaturen von real existierender massebehafteter, also Energie speichernder, Materie berechnen.
So einfach ist das …
Zur Ergänzung zu meiner Antwort auf M. Müller vom 30.10.20 20:15 Uhr:
Energie Hemisphärenmodell an einem Tag:
Erdoberfläche A = 5.1 E14 m² und mit 1 h = 60 min x 60 sec = 3600 sec
Energie in J = 8208 W/m² x h x A = 8208 W/m² x 3600 sec x 5,1 E14 m²
=1.507 E+ 22 J
Energie im Standartmodel KT97 an einem Tag:
Energie in Joule = 1.507 E +22 J „gesamte Energie auf die Erde innerhalb von 24 Stunden“, abgeleitet mit dem sehr anschaulichen Beispiels des Strahlenbündels siehe Blogbeitrag von Herrn S. Petersen vom 31.10.2020 um 11:02 Uhr
Herr Agerius, schön, dass Sie nun wenigtens für die Energie über 24 h auf den korrekten Wert kommen, die in Ihrem Modell allerdings nur für eine Hemisphäre reicht, während für die andere Null Energie übrigbleibt.
Das mit den festen Punkten für die beiden Hemisphären müssen Sie verstehen, sonst kommen Sie nicht hinter Ihren Fehler.
Herr Petersen,
es gibt keinen Fehler in der Rechnung von Herrn Agerius da es nie die Frage war, wieviel Energie auf der Oberfläche ankommt.
Die Frage ist und bleibt mit welcher Leistung die Einstrahlung erfolgt.
Und die ist im Flächenmittel S/2.
Es ist nun mal so das die Sonne immer nur eine Hemisphäre bescheint.
Sie scheinen das nicht wahrhaben zu wollen. Warum? Gibt es bei ihnen kein Tag und Nacht?
@Sverre Petersen
ich argumentiere jetzt mal bewusst provokativ im Stil des PIK. Wenn ich mir hier alle Kommentare zu diesem Thema (1/4 oder 1/2 und T Mittel) anschaue und dazu auch noch die Kommentare der zum Teil verlinkten Hinweise auf frühere Artikel zum gleichen Thema, dann stelle ich fest, dass Sie mit Ihrer Sichtweise ziemlich alleine oder in der deutlichen Minderheit dastehen. Die meisten (Natur)Wissenschaftler, die hier mit Ihnen fachlich diskutieren sind der Ansicht, dass Ihre Sichtweise falsch ist. Dann muss sie doch auch falsch sein, wenn so viele das sagen, oder? Das war jetzt eine Retour Kutsche an die pseudowissenschaftliche Argumentation des PIK zum menschengemachten TE.
# Marvin Müller vom 30.10. 2020 um 11:01
Teil 3)
Sehr geehrter Herr M. Müller,
zur Ergänzung KT97: 342 W/m² x 24 h x A = 8208 W/m² x h x A
zur Ergänzung Hemisphären Modell mit A = Oberfläche der Vollkugel und H = Halbe Kugel in 24 h:
A/2 x 12 h x 684 W/m² + A/2 x 12 h x 0 W/m²
H1 (hell) H2 (dunkel)
A/2 x 0 h x 684 W/m² + A/2 x 12 h x 684 W/m²
H1 (dunkel) H2 (hell)
Summe H1 + H2 = A x 12 h x 684 W/m² = 8208 W/m² x h x A
Zu Frage 3)
Bezüglich Energieüberschuss der Tagseite. Dieser wird gespeichert und nachts abgegeben. Hätte wir keine Ozeane und keine Atmosphäre, etc., sondern eine Mondlandschlaft, würde die Nachtemperatur schnell und extrem abfallen.
Herr Agerius,
„A/2 x 12 h x 684 W/m² + A/2 x 12 h x 0 W/m² H1 (hell) H2 (dunkel“
Diese Formeln sind falsch, da H1 und H2 über die 12 h ständig wechselne physikalische Orte bilden. Sie sehen in meinem Bild des Leistungsverlaufs eines N-S- Streifens fester Orte, dass die mittlere Leistung nie 684 erreicht, sondern sich mit der Mittelungszeit auf 342 einstellt.
https://share-your-photo.com/0bbfae1c0c
Herr Petersen,
das sind alles wunderschöne thermische Nicht-Gleichgewichtszustände.
Da können Sie mit S-B keine sinnvolle mittlere Temperatur draus ableiten. Das ist und bleibt völliger Unsinn!
Albert Agerius schrieb am 30. Oktober 2020 um 20:15
Die Summe ist nicht ganz korrekt, es fehlt ein Summand, das müßte H1 + H2 = A * 12h * 684 W/m² + A * 12h * 0W/m² sein. Sie wollen schließlich eine ganze Erdumdrehung beschreiben und können dabei nicht einfach die unbeschienene Hälfte weglassen oder gar so tun, als würden in den nächsten 12h auch 8208 W/m² x h x A auf die Erdoberfläche einwirken. Alternativ könnten Sie auch schreiben H1 + H2 = A/2 * 24h * 684 W/m², was eher zu Ihrer Betonung passen würde, dass immer nur eine Hemnisphere beschienen wird.
Falls Sie mir hier zustimmen sollten: Sie erhalten also für eine Erdumdrehung genausoviel ankommende Energie wie K&T. Wie lösen Sie dann den offensichtlichen Widerspruch auf, dass H1 + H2 = A/2 * 24h * 684 W/m² * (1 – Albedo) < A * 24h * 390W/m² ist?
Ich schrieb:
Das sollte ein „H1 + H2 = A/2 * 24h * 684 W/m² * (1 – Albedo) < A * 24h * 390W/m²“, mit war nicht bewusst, dass man neuerdings ein „kleiner als“-Zeichen schrieben kann …
Herr Müller,
„Die Summe ist nicht ganz korrekt, es fehlt ein Summand, das müßte H1 + H2 = A * 12h * 684 W/m² + A * 12h * 0W/m² sein.“
genau, die Mogeleien des Herrn sind unglaublich. Es ist unfassbar, wie hier trickreich versucht wird, um den heißen Brei herumzureden und eine tote Theorie aufrechtzuerhalten. Aber nun scheint er aufgegeben zu haben und meldet sich nicht mehr.
Sie haben also nicht mal Ahnung von Mathematik?
Muliplikation mit Null ist nun mal Null. Genau wie die Einstrahlung auf einer Fläche auf der sie gerade nicht erfolgt völlig unbedeutend ist.
Nehmen sie den Term mit 4 Minuten und sie kriegen sogar die Richtige Energiemenge raus die in der Zeit von der Sonne kommt.
Nur die Einstrahlflaeche unter demW in W/m2 muss man kennen.
Wissen sie schon die fuer 4 Minuten? 12 Stunden wäre ja auch ein gute Frage.
Zur Erinnerung in der ersten Sekunde wird schon die Hälfte der Erde beschienen. Was blos passiert in 12 Stunden? So viel Zeit und so wenig Fläche.
# Marvin Müller vom 30.10. 2020 um 11:01
Teil 2)
Sehr geehrter Herr M. Müller,
zu Frage 3) hinsichtlich Bild clear sky und cloudy sky von Modell 5
Ca. 15°C sind das globale Messwertmittel aus Tag- und Nacht Temperaturmessungen. Die Satellitenmesswerte selbst sind die Mittelwerte aus mehrfachen Erdumläufen in 24h über die Tag- und Nachtseite. Der Wert von 684 W/m² berücksichtigt den Satellitendurchgang durch Nacht und Tag, deshalb muss nun die Modellierung ebenfalls auf 15° C bezogen werden. Die Ursache der Temperaturwirkung ist die Einstrahlung der Sonne auf eine halbe Kugel in jeder Sekunde. 1 Joule/sec = 1 Watt. Die Erde selbst gibt auf der beleuchteten Seite Heizleistung X (W/m²) im globalen Mittel ab. Dieser globale Mittelwert Wert X ist tags genauso groß, wie nachts. Dieser Leistungswert geht in das S-B Gesetz ein.
Von lediglich theoretischem Interesse wäre im Modell zusätzlich eine Unterscheidung in Tag- und Nacht Strahlungswerten. Man würde dann eine höhere Tages- und eine niedrigere Nachttemperatur bezogen auf 15° angesetzten. Hierzu sind mir weder Temperaturwerte noch Strahlungswerte bekannt. Eine weitere Unterscheidung gibt es nur für clear- und cloudy Werte, die ich abbilde.
Herr Agerius, wie schon bewiesen, ist Ihre Betrachtung auf Basis der Hemisphären falsch, denn die Hemisphären drehen sich in Wirklichkeit und damit bekommt eine Hemisphäre mit definierten Orten nicht im Mittel 684 W/m2 Sonnenleistungsdichte, weil sie sich kontinuierlich aus dem beleuchteten Teil wegdreht. Man will je die Energie für physikalische Orte auf der Sphäre berechnen.
Ihre 684 W/m2 im Mittel der beleuchteten Hemisphäre stimmen nur für den Fall, wenn sich die Erde nicht drehen würde, und damit dann aber ebenfalls nicht für die gesamte Erde.
Sie können es betrachen wie Sie wollen, die Physik können Sie nicht betrügen. Ausserdem sehen Sie ja auch, dass Sie die doppelte Leistung „verbrauchen“ als von der Sonne angeliefert wird.
Der einzige der die Physik nicht versteht sind sie.
Leistung in W = J/s
Augenblickliche Einwirkung von Energie.
Die wirksam bestrahlte Fläche eine Hemisphäre.
Jede einzelne Sekunde ist das so.
Die Berechnung der Energie kann man mathematisch so oder so machen.
Die Einstrahlleistung funktioniert nur mit der Hemisphäre.
Herr Schulz, ihre Verständnisprobleme müssen Sie selber lösen, sie sind für die hier behandelte Verletzung des Energieerhaltungssatzes, welche Herr Agerius für sein Modell – bewußt oder unbewußt – voraussetzen muß, irrelevant.
Lesen sie überhaupt was geschrieben wird?
Mathematisch und physikalisch ist die Energieerhaltung bewahrt, wenn man fuer die Einstrahlung A/2 und S2 annimmt und für die Abstrahlung A und S/4.
Koennen sie mal bestaetigen, das die Sonne immer nur eine Hemisphäre bestrahlt? Oder welche wirren Annahmen ihrerseits führen dazu anzunehmen, das die Sonne die gesamte Erdoberfläche in einer Sekunde bestrahlt?
# Marvin Müller vom 30.10. 2020 um 11:01
Teil 1)
Sehr geehrter Herr M. Müller,
zu Frage 1) und 2)
Sie halten den Wert 684 W/m² für „korrekt“ berechnet, dann haben wir eine gemeinsame Basis.
Zu Frage 1 zu Wert 684 W/m², ob ich den Wert benutze. Ja, 684 W/m² sind Ausgangspunkt der Modellierung, analog wie bei KT97, die mit 342 W/m² beginnt.
Zu Frage 2: a) KT 97 stellt in einem Referenz Quadratmeter den Durchschnitt des Ein- und Aus- bzw. Abstrahlungsveralten der Erde dar. Ich verfahre analog, nur mit einem anderen Wert für die Einstrahlung. So, wie bei Kiehl und Trenberth, ist die Strahlung als Pfeil zur Vergleichbarkeit dargestellt und damit bei mir ebenfalls senkrecht zur Oberfläche. b) Auch teilen durch 2? Nein, da, im Vergleich zu KT97, der Nachtteil, der dort 342 W/m² beträgt, nun beim Hemisphären Modell in den Tagteil zurückgeschoben wird. Der Tagteil, bei KT97 342 W/m², wird damit im Hemisphären Modell auf 684 W/m² erhöht. Dadurch hat der Nachtteil keine Einstrahlung.
Albert Agerius schrieb am 30. Oktober 2020 um 20:11
Die Zahlen bei KT97 sind die Zahlen nach der Abbildung des TSI auf die Erdoberfläche und Mittelung über längere Zeiträume. Bei Ihnen ist es die Zahl nach der Mittelung über die Zeit aber vor der Abbildung auf die beleuchtete Hemnisphere. Sie lassen die aufgrund der Geometrie erforderliche Abbildung einfach weg, weil das einen Effekt hat, den Sie nicht haben wollen. Dadurch kommen Sie dann zu einem falschen Ergebnis.
Falls ich mich irren sollte und es doch einen plausiblen Grund gibt, die geometrische Abbildung weglassen zu können, würde ich den gerne hören.
PS: Sie schrieben: „der Nachtteil, der dort 342 W/m² beträgt, nun beim Hemisphären Modell in den Tagteil zurückgeschoben wird.“ Das ist bereits passiert, als Sie das TSI_{im Mittel} bestimmt haben. Und dass Sie diesen Wert korrekt bestimmt haben, darüber sind wir uns ja anscheinend einig.
Hier einmal für die, die sich Forneln nicht vorstellen können, die mittlere eingestrahlte Solarleistung über die Zeit für einen Streifen Erdoberfläche von Pol zu Pol, in Abhängigkeit von der Zeit, ab der mit der Energiesummation angefangen wird und die Summationsdauer.
https://share-your-photo.com/0bbfae1c0c
Wenn man mittags anfängt, ist die mittlere Leistung hoch und entspricht dem Momentanwert zum Sonnenhöchststand, fängt man abends zum Sonnenuntergang an, kommt die Nacht bis zum Sonnenaufgang erstmal nichts und erst dann beginnt mit Sonnenaufgang auch die mittlere Leistung zu steigen.
Der Punkt ist, dass die Kurven alle mit der Zeit den Wert S/4 annehmen (nur mal die ersten 2 Tage gezeigt), was trivial-geometrisch eh das physikalisch korrekte Ergebnis ist.
Herr Petersen,
wenn ihre Kurven den Wert S/4 annehmen, dann deshalb, weil sie S/4 in ihrer Berechnung haben.
Wenn sie mit S/2 rechnen dann nimmt die Kurve den Wert S/2.
Was sie sicherlich nicht angegeben haben ist die Flaeche die von der Sonne beschienen wird.
Zur Erinnerung das ist eine Hemisphaere. Nennt sich auch Tagseite.
Auf der Nachtseite scheint keine Sonne, ausser vielleicht bei Ihnen.
Herr Schulz, ich habe kein S/4 in der Rechnung und S/2 kann auch nicht das Ergebnis werden, woher sollte diese Freiheit kommen?
Das Ergebnis ist S/2 wenn man die Solarkonstante über die Einstrahlfläche mittelt.
# Sverre Petersen zu 29.10.2020 9.29 Uhr
Sehr geehrter Herr Petersen,
Ihr Oberflächenintegral ist natürlich nur mathematisch richtig ausgerechnet, es bildet die tatsächlichen, physikalischen Verhältnisse nicht ab:
In jeder Sekunde von T = 0 sec bis T = 60 x 60 x 24 = 86400 sec wird hierin mathematisch die solare Einstrahlung mit der Abstrahlung gekoppelt und gleichzeitig – sozusagen im Umkehrschluss – auch die Abstrahlung mit der Einstrahlung gekoppelt. Genauso machen es ja Kiehl und Trenberth. Die Abstrahlung in 24 h entspricht damit in jeder Sekunde der Einstrahlung, siehe FIG. 7. Earth ´s Annual Global Mean Budget, AMSOG, Vol. 78, No.2, 1997, S. 197 – 208. (KT97)
Unberücksichtigt bleibt hierbei, dass im Augenblick der Einstrahlung nur die halbe Erde beleuchtet wird, bzw. der Zeitversatz zwischen beleuchteter und unbeleuchteter Erdhälfte. Der Strahlungsmittelwert über 24 h und der damit errechnete Faktor ¼ wird der Wirklichkeit nur nicht gerecht. Die Satellitenmesswerten (ERBS) beweisen es:
Messwerte (ERBS) des fünfjährigen Mittels im Hemisphären Modell siehe Artikel: „Umgebungsgleichung (Stefan- Boltzmann- Gesetz) / ungerechtfertigte Kritik an Ulrich O. Weber /…., vom 27. Juli 2020 veröffentlicht auf EIKE, siehe auch ERBS Satellit auf dem CEDA Server, United Kingdom, Oxford.
http://data.ceda.ac.uk/badc/CDs/erbe/erbedata/erbs
cloudy sky (W/m²): 101+19+20+234+31 = 414 W/m² > 342 = 1368 /4
clear sky (W/m²): 48+48+42+276 = 414 W/m² > 342 = 1368 W/m²/4
Obige Messwerte bilden jeweils in Summe das Strahlungsprofil der Erde ab. Sie bestehen aus langwelligen und kurzwelligen Strahlungen. Mit 414 W/m² als langjähriges Mittel über den Globus übertreffen sie die 342 W/m² bei weitem. Die Messwerte 19, 20, 48,48,42 und 276 kommen in KT97 gar nicht vor, Sie fehlen und warum? Da bei KT97 die Summe der gemessenen Strahlung mehr liefert als das ¼. Deshalb vermieden Kiehl und Trenberth in KT97 einen Vergleich von Modellwert und Messwert. Beide wollten einen Treibhauseffekt faktisch erzwingen. Wie die Messwerte zeigen, ist KT97 aber mit 1/4 falsch . Q.e.d.
Für weitere Fehler in KT97 und Fehler in der Vorstudie zu KT97 von B. Barkstrom verweise ich auf „Kritische Analyse zur globalen Klimatheorie“.
Nur mit dem Faktor ½ lassen sich der 12 h stündige Zeitversatz und alle 9 Strahlungswerte Messwerte und 2 Albedos auf 2 W/m² genau abbilden. Es entfällt aber so der Treibhauseffekt von 33K, da die Gegenstrahlung dann gegen Null läuft. Das CO2-Dogma wäre tot. Mir ist klar, dass dies Ihnen, Herr S. Petersen, missfällt.
Ihre Formulierungen hier vom 24.10.2020 18:46 Uhr „physikalische Zeit, …, zeittranslationsinvariantes, also stationär […], etc., lassen für mich die Überlegung zu: Sie haben vermutlich auch eine Arbeit zur Relativitätstheorie veröffentlicht, neben Veröffentlichungen zum Klima. An anderer Stelle auf dem EIKE Kommentarbereich ließen Sie tieferes Hintergrundwissen zum ERBE Programm der NASA aufblitzen. Sollte ich Sie vielleicht doch besser mit Prof. Stefan Rahmstorf ansprechen? Es könnte gut möglich sein, aber Sie würden es sicherlich nicht sagen.
Herr Albert Agerius
29. OKTOBER 2020 UM 18:24
„Ihr Oberflächenintegral ist natürlich nur mathematisch richtig ausgerechnet, es bildet die tatsächlichen, physikalischen Verhältnisse nicht ab: In jeder Sekunde von T = 0 sec bis T = 60 x 60 x 24 = 86400 sec wird hierin mathematisch die solare Einstrahlung mit der Abstrahlung gekoppelt“
Falsch, zeigen Sie mir, wo ich irgendeine Abstrahlung berechnet oder an irgendwas gekoppelt hätte. Mit meiner Rechnung wird lediglich die Energie, die von der Sonne auf die Erdkugel fällt, bestimmt.
Nichts weiter! Steht dort auch mehrmals. Also bitte nochmal genau lesen statt Unzutreffendes einfach zu unterstellen! Das ist kein guter Stil.
Wie schon mehrmals erklärt, und Sie haben es immer noch nicht hinbekommen: Auf die Erdkugel trifft in 24 Stunden 1368*pi*R^2*86400 = 1,507e+22 Joule Sonnenenergie (R Erdradius in Metern).
Nämlich genau die, die in dieser Zeit aus dem Strahlenbündel durch den Erdquerschnitt herausgenommen wird (diese Energie – ein 24 Lichtstunden langer Zylinder fehlenden Sonnenlichts- fehlt im direkten Schatten hinter der Erdkugel).
Das ist die Menge, die dem Klimasystem in 24 Stunden zur Verfügung gestellt wird. Und genau diese Menge habe ich nachgerechnet. Davon wird der Albedo-Anteil von etwa 30% „ungenutzt“ reflektiert, der Rest im Klimasystem „verwurstet“.
Mehr habe ich nicht überprüft. Wenn Sie nun behaupten, auf die Erdkugel würde in 24 Stunden die doppelte Menge von 1,507e+22 Joule Sonnenenergie treffen, holen Sie damit also Energie aus dem Nichts. Ihre Eingangsgröße ist also schon falsch.
Voellig uninteressant.
Die Frage bleibt, was ist die Einstrahlleistung pro Fläche.
Sie haben immer noch nicht den Unterschied zwischen Leistung und Energie verstanden.
Es gibt auch im Original-Artikel auf Wattsup interessante Kommentare dazu, z.B. von Roy Spencer (durch google translate gejagt und die wichtigen Begriffe im orignal englisch ergänzt):
Die folgenden Kommentare sind dann auch interessant (speziell die Überraschung von Philip Mulholland, dass die Modelle einen vollständigen Tag-Nacht- und saisonalen Zyklus verwenden …)
Die Frage die man Herrn Spencer stellen muss ist, warum erkennt er das es nicht *instantaneous* ist, er aber weiterhin die Einheit Watt verwendet, in der es um die augenblickliche „Anwendung“ von Energie geht.
Damit widerspricht er sich selber.
Unter bezugnahme der hemisphärischen Fläche kann man die Einstrahlleistung darstellen. Wenn man die gesamte Erdoberfläche verwendet, kann man keinen Temperaturbezug fuer die Einstrahlung herstellen. Schon gar nicht mit SB.
Werner Schulz schrieb am 30. Oktober 2020 um 1:41
Das gleiche gilt auch für S/2, der auch nicht *instantaneous* ist, sondern ein Mittelwert über die beleuchtete Hemnisphäre. *instantaneous* wäre der winkelabhängige Einstrahlungswert für den konkreten Zeitpunkt.
Das wichtigere an Spencers Aussage ist, dass richtige Modelle nicht mit Mittelwerten, sondern mit der winkelabhängigen Einstrahlung rechnen. Was dabei für ein einfaches Modell rauskommt, hat Spencer gezeigt.
Das ist falsch, weil die Mittelung ueber die augenblickliche Einstrahlleistung, also pro Sekunde, was in einem Watt nun mal drinnen steckt, mit der Hemisphaere funktioniert.
Aber wenn sie denken das Herr Spencer diese Aussage macht, weil die Modelle so arbeiten, dann bitte schoen, das waere nicht falsch oder? Das KT Diagram wird deshalb trotzdem nicht richtig.
„Die Frage die man Herrn Spencer stellen muss ist, warum erkennt er das es nicht *instantaneous* ist, er aber weiterhin die Einheit Watt verwendet, in der es um die augenblickliche „Anwendung“ von Energie geht.“
Verwenden Sie auch eine andere Einheit für eine Durchschnittsgeschwindigkeit als für eine Momentangeschwindigkeit? Instantaneous wird die Sonnenenergie sowieso nicht wieder abgegeben, was soll also diese Frage?
Ja Herr Petersen, was soll die Frage?
Was wollen sie denn jetzt mit Geschwindigkeiten?
Sie werfen gleich mehrere Dunstgranaten weil sie nicht mehr durchblicken wollen.
Weder sage ich das man nicht W/m2 nehmen kann, sondern es geht um die Flaeche auf die sich das bezieht.
Weiterhin geht es immer noch um die Einstrahlung nicht um die Abstahlung. Die erfolgt von der gesamten Erdoberflaeche, und auch aus der Atmosphaere, von den Wolken usw.
Noch Fragen?
Herr Petersen,
weder sage ich das man die Einheit W/m2 nicht benutzen darf, sondern es geht darum, das man diese Einheit auf die richtige Flaeche, bei der Erde und Sonneneinstrahlung auf die Hemisphaere beziehen muss.
Zweitens Geht es hier um die Sonneneinstrahlung nicht um die Abstrahlung. Bleiben sie beim Thema!
Es geht nicht um Energie es geht um Leistung.
#Marvin Müller am 28.10.2020 um 10.31
Herr Müller schrieb, Zitat: „Nimmt man dieses TSI im Mittel und läßt es auf die beleuchtete Halbkugel wirken, kommt man wie jeder andere auf TSI/4 = 342 W/m² als mittlere Einstrahlung.“
Hierzu zitierten Sie meinen auf EIKE veröffentlichten Artikel mit:
„In der Perspektive des Satelliten: TSI im Mittel = (1368 W/m² + 0) / 2 = 684W/m²“
Sehr geehrter Herr Müller,
mit 1368W/m² steht der Satellit in der Achse Sonne – Satellit – Erde,
mit 0 W/m² steht der Satellit in der Achse Sonne – Erde – Satellit, also im Erdschatten.
Die modellierte Strahlung im Hemisphären Modell aus der Perspektive des Satelliten berücksichtigt dies mit TSI im Mittel = (1368 W/m² + 0) / 2 =684W/m². Die Messwerte des Satelliten sind aber ebenfalls Mittelwerte aus Tag- und Nachtmessungen. 684 W/m² beleuchten im Modell lokal von 6 Uhr bis 18 Uhr die Hemisphärenhälfte H1, während H2 in der Dunkelheit liegt. Hemisphäre H2 wird lokal von 6 Uhr bis 18 Uhr beleuchtet, während H1 in der Dunkelheit liegt. Zwischen H1 und H2 ist ein Zeitversatz von 12 h.
Damit beleuchten 684 W/m² beide Hemisphären aber in Zeitversatz. Aus diesem Grund dürfen Sie 684 W/m² nicht erneut durch 2 teilen, sonst verschieben Sie Sonnenschein in die Nachthälfte. Nachts scheint keine Sonne. Deshalb ist die Mittelung über 24h falsch.
„684 W/m² beleuchten im Modell lokal von 6 Uhr bis 18 Uhr die Hemisphärenhälfte H1, während H2 in der Dunkelheit liegt. Hemisphäre H2 wird lokal von 6 Uhr bis 18 Uhr beleuchtet, während H1 in der Dunkelheit liegt.“
Da ist ein Denkfehler drin. Wenn schon so, so müssen Sie zur Bilanz die beiden Hemisphären fix halten, also feste Orte zuordnen, z.B. von 90 W bis 90 Grad O geographische Länge die eine Hemisphäre (HS) und die andere von 90 grad W bis 90 Grad O. Bei den Hemisphären werden in der Zeit von 6 bis 18 Uhr wechselnde Orte beleuchtet und in den 12 h hat sich die eine gegen die andere HS ausgewechselt.
„Zwischen H1 und H2 ist ein Zeitversatz von 12 h.“
Nein, wenn H1 jetzt voll beleuchtet wird, so ist in der nächsten Sekunde am Westrand ein Stück von H1 im Dunklen verschwunden, während am Ostrand ein gleich großes Stück von H2 beschienen wird. Der Übergang ist also kontinuierlich. In meiner Rechnung läuft das genau so und damit kommen Sie auch zum korrekten Ergebnis und keiner falschen Verdopplung.
„Damit beleuchten 684 W/m² beide Hemisphären aber in Zeitversatz.“
Falsch, H1 bekommt in der nächsten Sekunde weniger Leistung als 684 W/m2 im räumlichen Mittel, während H2 mit der Energiesammlung anfängt, indem das erste Stück beleuchtet wird. Wenn Sie das korrekt aufsummieren bekommen beide HS im Mittel 342 W/m2. Die mittlere räumliche Leistung nimmt für H1 in den 12h ab jetzt ja von 684 auf 0 ab, indem in den 12 h immer mehr Fläche von H1 auf die unbeleuchtete Seite verschwindet.
“ Aus diesem Grund dürfen Sie 684 W/m² nicht erneut durch 2 teilen, sonst verschieben Sie Sonnenschein in die Nachthälfte.“
Das wird so sowieso nicht gerechnet.
„Nachts scheint keine Sonne. Deshalb ist die Mittelung über 24h falsch.“
Das ist unlogisch. Der Mittelwert ist überhaupt keinem Zeitpunkt zugeordnet. Der Mittelwert ist nur die gesamte auf die Erdkugel in 24 h eingestrahlte Energie durch die Oberfläche und 24 h geteilt – fertig. Ob das physikalisch Sinn macht, ist hier egal. Und ob Sie glauben, dieser Mittelwert hätte etwas mit dem Treibhausefekt zu tun, erst recht. Hat er nicht, das Postulat brauchen nur Sie, weil Sie mit der Physik strahlender Gase ein Problem haben. Wichtig ist, dass der Wert stimmt, nur 342 W/m2 mal Erdoberfläche mal 24 h ist identisch mit der in dieser Zeit eingestrahlten Sonnenenergie. Bingo.
Bitte kürzer fassen.
So ist es. Deswegen verwenden ihn ja die Klimaforscher so gern. Und die Politik macht ihn sogar zum Ankerpunkt internationaler Verträge.
Albert Agerius schrieb am29. Oktober 2020 um 11:30
Sehr geehrter Herr Agerius,
ich habe diese Rechnung nicht in Frage gestellt, sie ist aus meiner Sicht korrekt. Daher nur einige Fragen dazu, da mir dann ihre weiteren Schritte nicht klar sind.
1. Warum berechnen Sie diesen Wert, wenn Sie ihn im weiteren nicht benutzen?
2. Falls Sie ihn doch benutzen (In Bildnachweis, A. Agerius FIG8 b Modell 5 clear sky) : Dieser Wert gilt nur, wenn er senkrecht auf die Erdoberfläche fällt. Warum müssen Sie ihn nicht durch 2 teilen, um die Abbildung auf die Halbkugel durchzuführen?
3. Falls Sie in „Bildnachweis, A. Agerius FIG8 b Modell 5 clear sky“ doch wieder nur die Verhältnisse auf der beleuchteten Hemnisphäre darstellen – müßten Sie dann nicht ein zweites Bild danebenstellen, dass die Verhältnisse auf der unbeleuchteten Hemnisphäre darstellt? Und müßte dann nicht auf der beleuchteten Hemnisphäre ein Energieüberschuss ausgewiesen werden, der das Energiedefizit auf der unbeleuchteten ausgleicht?
# Eugen Ordowski vom 24.10.20 um 9:41
Sehr geehrter Herr Ordowski,
Ihr Beispiel zur Leistung eines Pkw Motors ist sehr anschaulich und gut gewählt. Den Ansatz der Leistung möchte ich auf die Klima Modellierung übertragen.
Ziel des Modells von Bruce Barkstorm und seiner Weiterentwicklung von Kiehl und Trenberth war aus den Satellitenmesswerten eine Aussage zur Globaltemperatur machen zu können, bzw. diese mit über den Globus gemittelten Temperaturmessungen vergleichen zu können. Aus der langwelligen Abstrahlung, Messwert in Watt/m², kann, wie bekannt, über das S-B Gesetz eine Temperatur ermittelt werden. Watt ist ein Begriff der Leistung und kann auf eine Fläche als W/m² bezogen werden.
Leistung und Energie, genau wie Sie sagen, müssen getrennt werden, deshalb nun ein Leistungsvergleich des Modells von Kiehl und Trenberth bezeichnet als (Modell 4 oder Index´) mit dem Hemisphären Modell (5 oder Index´´). A ist die Erdkugeloberfläche und Isr sei die modellierte Bestrahlstärke der Sonne in W/m2.
Leistungsvergleich
Leistung gemessen in Watt, bzw. bezogen auf eine Fläche.
mit Isr ´= 342 W/m², gemäß Modell 4
mit Isr´´= 684 W/m², gemäß Modell 5 und Isr´´= 2.0 x Isr´
Bestrahlstärke Isr´x (0,5 A (Tagseite) + 0,5 A (Nachtseite)) = L4= Leistung Modell 4 = Isr´x A
Bestrahlstärke Isr´´x 0,5 A (Tagseite) = Leistung Modell 5
2.0 Bestrahlstärke Isr´ x 0,5 A (Tagseite) = L5 = Leistung Modell 5 = Isr´ x A
L4 (Kiehl und Trenberth) = L5 (Hemisphärenmodell) = Isr´ x A
Beide Modelle werden mit der gleichen Leistung beaufschlagt.
Die willkürliche – weil der Beobachtung widersprechend – Verteilung von Sonnenschein in die Nacht in KT97, analog zu Ihrem Pkw in der Garage, berechnet die Wärmewirkung der Sonne in diesem Modell deshalb falsch. Bei KT97 verbleiben nach Abzug von Albedo, Satm, LH und SH nur 66 W/m² Wärmewirkung für das S-B Gesetz. Der Treibhauseffekt aus Aufspaltung aus einer Null (0 = + 324 W/m² – 324 W/m²) erzeugt heizt das KT97 Modell nun aus sich selbst heraus. Man kann dies rechnen, aber es ist physikalisch falsch. So wie sich Münchhausen mit seinem Haarschopf aus dem Sumpf zieht. Man kann dies als Bild zeichnen oder auf dem Computer als Standbild darstellen, aber es ist nicht wahr, weil physikalisch falsch. In KT97 wird aus der Null eine eigenständige Energiequelle. Dies ist falsch.
„Sehr geehrter Herr Ordowski, Ihr Beispiel zur Leistung eines Pkw Motors ist sehr anschaulich und gut gewählt. Den Ansatz der Leistung möchte ich auf die Klima Modellierung übertragen.“
Dieses Beispiel demonstriert das Missverständnis, welches hier herrscht und welches dazu führt, dass man glaubt, die Zeiten mit Null-Leistung bei der Mittelwertberechnung ausschliessen zu können. Um die mittlere Leistung eines Verbrauchers zu bestimmen, ist es natürlich unsinnig, die Zeiten des micht Gebrauchs einzurechnen. Aber das Beispiel taugt nicht.
Die beim Klimasystem hier relevante Frage ist, wieviel Energie dem Klimasystem zugeführt wird. Und da diese akkumulativ anwachsend ist, rechnet man dies zur Einfachheit in einen Mittelwert pro Zeiteinheit um. Fertig.
Das ist so, als wenn Sie nach 3 Jahren den Spritverbrauch des Autos aufsummieren und berechnen, wieviel Sie im Schnitt im Monat verbraucht oder gezahlt haben. Da interessiert dann nur, wieviel Sie pro Monat zahlen und nicht pro tatsächlich genutzter Fahrzeit im Monat.
Man fragt sich warum sie nach dieser Erkenntnis:
hier noch weiter diskutieren.
Beim Klimasystem ist es interessant mit welcher Leistung die Sonne einstrahlt. Wieviel Energie ankommt ist sogar fast uninteressant, da wir aufgrund der Energieerhaltung davon ausgehen, das genausoviel Energie ankommt wie wieder weggeht.
Was viel interessanter ist, ist wieviel Energie zu jedem bestimmten Zeitraum im System vorhanden ist, weil das die Temperatur bestimmt.
Können sie den Lesern hier erklären wie ein Schweißbrenner funktioniert?
Sehr geehrter Herr Agerius,
„Ziel des Modells von Bruce Barkstorm und seiner Weiterentwicklung von Kiehl und Trenberth war aus den Satellitenmesswerten eine Aussage zur Globaltemperatur machen zu können, bzw. diese mit über den Globus gemittelten Temperaturmessungen vergleichen zu können“
Das ist wieder eine Unterstellung, die nicht belegt ist. Kiehl und Trenberth haben mit KT97 nur die Mittelwerte der Leistungsdichten, die u.a. durch ERBE genauere Zahlen als die vorher lieferten, neu ermittelt und in dem seit 100 Jahren bekannten Schema eingezeichnet. Das war’s. Das KT97 Diagramm ist kein Modell, was igendwas erklären will, es ist nur eine Zusammenfassung von Messungen.
Daher ist KT auch kein schlechtes oder unzureichendes Modell, welches Sie oder andere weiterentwickeln möchten, es ist KEIN Modell, klar?
Ein Klimamodell ist ein Modell, weil dort Wetter aus physikalischen Gleichungen berechnet wird.
# S. Petersen vom 5.11.2020 um 22:04 Uhr
Sehr geehrter Herr Petersen,
zu Ihrer Aussage, Zitat: “Das KT97 Diagramm ist kein Klimamodell,…“
KT97 ist die Weiterentwicklung der Modellierung von B.Barkstorm, Climate and Erath´s Radiation Budget, Mai 1989, in PHYSICS TODAY, American Institute of Physics, S.22 f. Hierin schreibt Barkstorm et alt.:
„The simplest zero-dimensional model of climate considers the long-term average (on a time scale greater than a year) of the long-term average and annual mean temperature. […] We can write this symabiolically as H = S0 /4 / (1-α) – σ T4 =0 […] Let us turn to a one dimensional model. The atmosphere constantly loses energy (see figure 1).
Figure 1 von Barkstorm entspricht dem Bild Fig. 7. von KT97 mit geringfügig abgeänderten Werten ohne Klammer, KT97 Werte in runden Klammern.
LH = 90 (78) [85], SH = 16 (24) [20], Gegenstrahlung = 327 (324) [342], Albedo = 0.307 (0.313) [0.294], Reflected solar Radiation = 105 (107) [100], Outgoing Longwave Radiation = 237 (235) [239], Satm 68 (79)
Deshalb stellt KT97, FIG.7. ein Klimamodell erster Ordnung dar.
Norman Loeb et alt in 2012 “The global energy balance from a surface perspective”, FIG.1, doi 10.1007/s0000382-012-1569-8 macht in der Darstellungsstruktur eines eindimensionalen Klimamodels den Vergleich von 22 CMIP5/IPCC AR5 Klimamodellen, Werte in eckigen Klammern als Durchschitt der 22.
„Ein Klimamodell ist ein Modell, weil dort Wetter aus physikalischen Gleichungen berechnet wird.“
Die Vorhersagegüte von höher dimensionalen Klimamodellen und ihre Modellierung als solche wird vielfach im Langzeitbereich angezweifelt. Hierzu können Sie sich auf EIKE sehr gut informieren. Wie gut Wetter (Regen, Winde, Wolken etc.,) in Grids global abgebildet werden können, ist eine ganz andere Frage.
Sehr geehrter Herr Agerius,
6. NOVEMBER 2020 UM 12:23
„KT97 ist die Weiterentwicklung der Modellierung von B.Barkstorm, Climate and Erath´s Radiation Budget, Mai 1989, in PHYSICS TODAY, American Institute of Physics“
Woran machen Sie nun genau fest, dass KT97 ein einfaches 1D Energiebilanzmodell wie das von Ihnen hier zitierte in Ramanathan, Barkstrom, Harrison sein soll? Für mich ist KT97 eine Bilanz mit fixen Werten. Denn KT beantwortet ja z.B. gar nicht die Frage, wie sich ihre Bilanzwerte ändern, wenn H aus der ersten Gleichung in Ihrem zitierten Ramanathan et al. paper ungleich Null wird oder was sich durch 4 W/m2 radiative forcing bei CO2-Verdopplung ändert. KT97 hat überhaupt keine dynamische Klimaphysik implementiert.
Mit solchen einfachen 1D Energiebilanzmodelle wie in Ramanathan, Barkstrom, Harrison begann in den späten 50igern die Klimasystemforschung. Wenn ich von Klimamodell schreibe, meine ich die heutigen GCMs (3D mit Ozeanankopplung und Wechselwirkung mit anderen Geosphären etc.). Auch die einfachsten 3D Modell gab es 1989 schon. Im paper wird ja auf die hingewiesen (Outstanding problems): „The fundamental limitation of the models described above [1D Modelle] is that they lack explicit formulations for the interaction between … . The GCMs were developed initially for forecasting weather. Such models lead to significant insights into the causes of important climatological phenomena, such as… .” Sag ich doch. Dass GCMs genauer sind als 1D Modelle, ist offensichtlich.
„Figure 1 von Barkstorm entspricht dem Bild Fig. 7. von KT97 mit geringfügig abgeänderten Werten ohne Klammer, KT97 Werte in runden Klammern.“
Wen wundert das, Barkstrom hat sein 1D Modell mit den aktuellen Randbedingungen aus den ERBE-Messungen „gefüttert“.
„Deshalb stellt KT97, FIG.7. ein Klimamodell erster Ordnung dar.“
Was soll ein „Klimamodell erster Ordnung“ sein?
„Norman Loeb et al in 2012 “The global energy balance from a surface perspective…”
In diesem paper geht es darum, die Modellresulte von GCMs wie CMIP5 mit lokalen Bodenmessungen und Satellitenmessungen zu kombinieren und daraus eine globale Bilanz (Fig 1) abzuleiten. Das GCMs liefert die grid interpolation, die Messungen die Zielwerte.
Wenn Sie nun selber ein 1D Modell machen wollen, so sorgen Sie erstmal für die korrekten Randbedingungen. Denken Sie daran, dass ein 1D Modell nicht zwischen Tag und Nacht unterscheiden kann (es gibt keine Tagesperiode), sondern die 24 Stundenmittel nehmen muss. Ihre Bilanz der Sonneneinstrahlung ist mit 684 W/m2 fürs 24h Mittel immer noch falsch.
„Ihre Bilanz der Sonneneinstrahlung ist mit 684 W/m2 fürs 24h Mittel immer noch falsch.“
Diese ist nicht mal mathematisch falsch. Der einzige Diskussionspunkt der besteht ist der, auf welcher Flaeche die Sonnenenergie pro Sekunde einwirkt.
Und das ist die Hemisphaere. Ihre Loesung ist zwar mathematisch machbar, stellt aber keine physikalische Realitaet dar.
In jeder Sekunde ist immer nur eine Hemisphaere der Erde beleuchtet.
Sehr geehrter Herr Petersen,
ich habe die originale Text und Bild Quellen zitiert und zu mir die Arbeit gemacht diese für zur Überprüfung exakt angeben. Da Sie meinen Text offensichtlich nicht lesen, ‚ woran machen Sie das fest‘, ist jegliche Kommunikation mit Ihnen blanke Zeitverschwendung.
Sehr geehrter Herr Agerius,
Sie meinen dieses fett?
„The simplest zero-dimensional model of climate“
Lesen sie lieber mal meinen Text, ich schrieb schon, dass Ihr Zitat explizit das Barkstrom Modell meint . Das Kiehl Trenberth Diagramm ist kein modell. Das kann ja wohl nicht so schwer zu begreifen sein. Lesen sie auch den rest von mir. Das ist wichtig.
„Das Kiehl Trenberth Diagramm ist kein Modell.“
Man fragt sich wirklich warum Sie, Herr Petersen ueberhaupt noch diskutieren!
Falls es ihnen um eine Energiebilanz geht, dann nehmen sie zur Kenntnis, das man diese mit S/2 darstellen kann.
In dem Zusammenhang verweise ich noch mal auf die Grafik im Hauptartikel. Abbildung 1
Aus dieser koennen sie die richtige Energiebilanz mit korrekt gemittelten Leistungen ersehen.
Was sie nicht begreifen ist, das sie voellig aberwitzig gegen die physikalische Realitaet diskutieren, naemlich das die Sonne immer nur eine Hemisphaere bescheint.
Das koennen sie nur bestreiten, wenn sie denken die Erde waere flach.
Ihre favorisierte mathematischen Loesung bildet die physikalische Realitaet der Einstrahlleistung nicht richtig wider.
Bitte bestaetigen sie das sie verstehen, das die Sonne immer nur eine Hemisphaere bescheint!
mfg
Werner
Herr Agerius,
machen Sie doch einfach die folgende Rechnung:
a) Auf einem Quadratmeter ebene Fläche, die senkrecht zu den Sonnenstrahlen steht, fallen pro Sekunde 1368 Joule Sonnenstrahlung ein (S = 1368 W/m2).
b) Auf einem Quadratmeter ebene Fläche, die tangential zur Kugeloberfläche am Ort mit den geographischen Koordinaten x (W-O) und y (S-N) liegt, fallen pro Sekunde 1368 × cos(x) × cos(y) Joule Sonnenstrahlung ein (I= S × cos(x) × cos(y)), wenn x auf der Tagseite liegt, bzw. I= 0 (null), wenn x auf der Nachtseite liegt.
c) Die Leistung der Sonnenstrahlung L(x), die auf einen Meridianstreifen mit der Winkelbreite Dx in W-O-Richtung bei der geographischen Länge x (Orte mit gleicher Zeit nach einer Sonnenuhr) von y=-90 grad (Südpol) bis y=+90 grad (Nordpol) einfällt, ergibt sich aus der Summe von I längs Y (Integral über I dY), indem man die geographische Breite y in Länge in Metern Y ausdrückt Y = y × R × pi/180°, R Erdradius.
L(x) = R^2 dx int I(x,y) cos y dy
von Südpol zum Nordpol in rad. L in W. Der cos y ergibt sich aus der Verkürzung der Breitenkreislänge in Meter mit Winkellänge Dx zu den Polen hin.
Ergebnis für die Tagseite L(x) = pi × R^2/2 × S × cos x × Dx
Ergebnis für die Nachtseite L(x) = 0
d) Auf den Streifen fällt entsprechend seiner Position zur Sonne nun L(x). Die auf den Streifen einfallende Energie E ergibt sich aus der Summe über L(x) über die Zeit.
Nun lassen wir diesen Streifen mit der Erdkugel rotieren und berechnen, wieviel Energie in T = 24 Stunden – einer vollen Umdrehung- auf den Streifen einfallen. Der W-O-Winkel relativ zur Sonne x wandert mit der Winkelgeschwindigkeit der Erdkugel dx=(2pi/T) × dt, T = 86400 s= 24 h.
Ergebnis E = pi × R^2 × S × T × Dx/(2 pi) in Joule
Der Streifen hat eine Fläche von A = 2 × R^2 × Dx in Quadratmeter
Damit ist die Energiedichte der in T eingefallenen Sonnenenergie in J/m2 E/A = S/4 × T
Die mittlere in T eingefallene Leistungsdichte ist dann
P = E/A/T = S/4 = 342 W/m2 q.e.d.
Es ist keine Frage der Berechnungsmethode, sondern schlicht eine der Betrachtung der Realität. Und nur das ist Physik.
Admin, ich stimme Ihnen zu, das gleiche (Lehrbuch)Ergebnis bekommt man ja auch durch eine simple geometrische Überlegung. Die Physik fügt sich natürlich der Mathematik, wenn diese auf korrekte physikalische Gesetze und Zusammenhänge angewandt wird.
Umgekehrt wird ein Schuh draus:
Die Mathematik fügt sich natürlich der Physik, wenn sie korrekt auf physikalische Zusammenhänge angewandt wird. Dann und nur dann entsteht daraus „a law“ wie Richard Feynman sagte. Und dies muss mit den Beobachtungen übereinstimmen.Wenn nicht, dann ist es „wrong“. Wieder Feynman.
Mein Physikprofessor bläute un ein: „Die Mathematik ist die Kammerzofe der Physik“ Sie ist ein mächtiges Werkzeug um in komplexe reale Prozesse etwas begreif- und berechenbare Ordnung reinzubringen. Nicht mehr und nicht weniger.
Feynman kann man nur zustimmen und Ihrem Physiklehrer auch. In meinem Fall kommt auch nur das raus, was ohnehin physikalisch klar war.
Wenigstens darin sind wir einig. Auch wenn meine Zitate das komplette Gegenteil von dem sind, was Sie geschrieben haben. Nur in der Anwendung nicht.
„In meinem Fall kommt auch nur das raus, was ohnehin physikalisch klar war.“
Physikalisch klar ist, was meßtechnisch bestätigt ist.
Physikalisch klar ist nicht, wenn eine Gleichung richtig gelöst wird.
Die Gleichung muß auch die Realität abbilden.
Letztere wird durch Messung definiert!
„Die Physik fügt sich natürlich der Mathematik…“
…und daraus resultieren dann Erfindungen wie schwarze Locher, Wurmlöcher usw.
Mit Einstein ist die Physik zu einer Unterdisziplin der Mathematik verkommen.
Physik sollte aber die Beschreibung und Erklärung des Beobachteten sein, Mathematik ein Instrument hierfür.
Hier wedelt der Schwanz mit dem Hund!
Herr Keks, schon wieder Dank an Sie. Werfe meinen vorbereiteten Kommentar gerne in den Kübel.
Statt „verkommen“ würde ich allerdings „gekommen“ vorschlagen.
Und der Professor hatte mit der Kammerzofe gar nicht so unrecht! Die waren damals nämlich „Herr“ im Haus! Das hat unser @Admin vielleicht vergessen.
Mathematik braucht keine Physik, einzig und allein sich selbst! Aber: Physik ohne Mathematik? Mathematik: Die schönste und unbestechlichste aller Künste!
Unsereiner mußte bis zum Physik-Vordiplom 4 Semester Mathe besuchen und dann ne Prüfung ablegen. Und da also 4 Semester Mathe reichen ist Mathe ein Unterfach für Physiker.
Und anders sieht das in der Ökonomie auch nicht aus.
„Statt „verkommen“ würde ich allerdings „gekommen“ vorschlagen.“
Herr Suntinger,
ich habe nichts gegen die Mathematik, auch wenn vieles dabei völlig ohne Nutzen ist.
Ich meine aber – und darum habe ich das Wort gewählt – daß Physiker heutzutage ihre Aufgabe darin sehen wilde , auf den Regeln der Mathematik basierende Theorien aufzustellen anstatt mit Beobachtungen als Basis Erklärungen für diese Beobachtungen zu liefern.
Niemand beobachtet schwarze Löcher, Wurmlöcher, schwarze Materie usw.
Damit hat sich die Logik der Wissenschaft umgedreht:
es wird nicht mehr beobachtet und erklärt, sondern behauptet und nach Beweisen gesucht.
Das meinte ich mit verkommen (=degeneriert)
MfG
Herr Keks, haben Sie, wie Einstein, eine physikalische Theorie auf der Basis von Mathematik entworfen, deren Plausibilität erst Jahrzehnte später mit der dann zur Verfügung stehenden Technik überprüft werden konnte? Einstein hat die Krümmung des Raumes beschrieben und postuliert, dass es in Folge der Ablenkung der Lichtstrahlen Gravitationslinsen geben müsste. Inzwischen beobachtet. Einstein hat postuliert, dass verringerte Gravitation und hohe Geschwindigkeiten den Lauf der Zeit verlangsamen. Gemessen und bestätigt. Einstein hat die Existenz von Gravitationswellen postuliert. Gemessen und bestätigt. Damit sind Einsteins Theorien nicht bewiesen, so wie keine naturwissenschaftliche Theorie letztlich endgültig beweisbar ist. Niemand verbietet Keks et al, eine bessere Theorie vorzulegen. Nur sollte man das, was den eigen Horizont übersteigt, nicht pauschal verdammen. Damit verhält man sich unwissenschaftlich.
@Werner Burger
30. OKTOBER 2020 UM 9:59
Lieber Herr Burger,
es gibt andere, sehr einfache und naheliegende Erklärungen für einige der von Ihnen genannten Phänomene.
Den „Nachweis“ von Gravitationswellen würde ich unter „Showbusiness“ abspeichern.
Bitte beschäftigen Sie sich mal mit der Theorie des Plasma-Universums.
Starten Sie dabei unbedingt mit den Primerfield-Videos 1-3 von David LaPoint,
dann https://youtu.be/5AUA7XS0TvA und die weiteren Videos auf
https://www.thunderbolts.info/wp/
bzw. deren Youtube-Kanal ThunderboltsProject.
Sie werden staunen – versprochen!
Herr Petersen glaubt halt daran, dass sein Auto nicht schneller als eine Schnecke sein kann je länger er es in der Garage stehen lässt.
Bleiben Sie beim konkreten Thema, ich sehe keinen Bezug zwischen der Geschwindigkeit einer Schnecke und der Strahlungsenergie der Sonne.
Zum Thema dann also.
Sie können eine Einstrahlleistung nicht auf eine Fläche verteilen die gar nicht bestrahlt wird.
Sie können gerne die Energie auf die Fläche verteilen die im Laufe der Zeit bestrahlt wird.
Sie können nicht aus mit der Energiemenge eine Einstrahlleistung für die gesamte Fläche berechnen und dann physikalische Schluesse daraus ziehen.
Sonst landen sie wieder bei ihrem langsam beschleunigten Auto.
Nur weil sie den Bezug nicht sehen, heisst es nicht, das es ihn gibt.
Ich sage nur noch Schweissbrenner!
Das ist derselbe Fehler, wie die Angabe der Nennleistung von Windkraftanlagen und der Ableitung daraus, wieviele Haushalte daraus „versorgt“ werden können. Der Vergleich von Äpfeln mit Birnen.
Admin:
„Das ist derselbe Fehler, wie die Angabe der Nennleistung von Windkraftanlagen und der Ableitung daraus, wieviele Haushalte daraus „versorgt“ werden können. „
Genau so ist das!
„Das ist derselbe Fehler, wie die Angabe der Nennleistung von Windkraftanlagen und der Ableitung daraus, wieviele Haushalte daraus „versorgt“ werden können. Der Vergleich von Äpfeln mit Birnen.“
Genau!
Die AGW.Bande macht hier genau den gleichen Fehler wie die EE-Mafia.
Sie stellen eine Energiebilanz über ein Jahr auf und meinen damit wäre was zu beweisen.
Sie vergessen im EE-Fall, daß das Angebotsleistung und Nachfrageleistung zu jedem Zeitpunkt und nicht übers Jahr ausgeglichen werden müssen.
Und im TH-Fall will man nicht wahrhaben, daß S-B auch nur auf aktuelle Leistungsflüsse und nicht auf Bilanzen anwendbar ist.
In beiden Fällen mangelt es an physikalischem Verständnis
Admin schrieb am 29. Oktober 2020 um 9:55 :
Die Realität kann man ja beobachten. Mal angenommen, man würde zur Tag/Nachtgleiche am Äquator ein Messgerät aufstellen und die einfallende Sonnenstrahlung messen. Was wäre der zu erwartetende Wert für die mittlere Einstrahlung über eine Erdumdrehung in W/m²?
Bestrahlung wird in Joule pro m2 gemessen.
Werner Schulz schrieb am 29. OKTOBER 2020 UM 11:25
Sie können sie auch gern in J/m^2 angeben. Interessant wäre nur mal eine konkrete Zahl statt allgemeinem Rumeinern.
Na bringen sie mal eine Zahl. Herr Petersen hat es doch schon fuer sie ausgerechnet. In Joule. Braucht man nur noch durch die Flaeche teilen, dann haben sie Joule/m2.
Gehen sie doch mal konkret auf die Kommentare ein.
Sind sie echt der Meinung, das die Sonne nur -18 Grad C erzeugen kann?
Klar, gibt es Messungen, die die Rechnung und das Lehrbuch bestätigen. Ich messe das selber und bekomme es dadurch mit Hilfe von Messungen bestätigt, wenn auch eben nur bei mir. 2×342 W/m2 als jährliches 24 Stundenmittel ist sowohl analytisch, wie auch geometrisch wie auch gemessen falsch. Und die Fehler von Agerius und anderen wurde ja auch erklärt.
Sverre Petersen schrieb am 29. OKTOBER 2020 UM 11:34:
Die Frage richtete sich an den Admin …
Wen wollen Sie eigentlich mit diesen ganzen Wurmfortsätzen an Formeln und Fachbegriffen erreichen? Die etablierte Wissenschaft sicher nicht, den Otto Normalbürger und Laien? Oder politische Entscheider?
Oder nichts von alledem weil man hier am liebsten im geschlossenen Zirkel debattiert wie am Stammtisch?
Mir hat ein Prof. mal ein 15seitiges Manuskript für ein Referat um die Ohren gehaut: Wenn Sie es auf einer Seite nicht verständlich darlegen können, sind die 13 anderen Seiten für den Müll.
Sie müssen ja hier nicht mitlesen.
Dann bitte ich um eine kurze Erklärung. All die vielen Formeln sollen offenbar berechnen helfen, wie viel Sonnenenergie zum Zeitpunkt x auf der Oberfläche der Kugel Erde ankommt. Kann man das überhaupt berechnen? Wird nicht ein Teil der Sonnenenergie von der Atmosphäre bereits ins Weltall reflektiert, an den Polen mehr, am Äquator weniger (Einfallswinkel der Strahlung)? Gibt es nicht ebenso ein stärkere oder schwächere „Abschirmung “ der Sonneneinstrahlung je nach Art und Ausdehnung der Wolkendecke?
Richtig ist in jedem Fall das: Die Erde erhält die Energiemenge x von der Sonne und gibt die gleiche Energiemenge y wieder ab, dadurch ist die Temperatur im Gleichgewicht, stabil über lange Zeiträume mit im Verhältnis zu den möglichen Extremwerten (Erdmond ohne Atmosphäre) vergleichsweise moderaten Schwankungen, immerhin zwischen Tropenklima und Eiszeit. Stabil sind bemerkenswerte Weise auch andere uns bekannte Himmelskörper mit Atmosphäre wie Venus, Mars oder Titan – wenngleich auf völlig anderem Temperaturniveau. Man kann davon ausgehen, dass Himmelskörper, auf denen sich ein Atmosphärischer Gleichgewichtszustand nicht eingestellt hat oder verloren ging, sich von ihrer Atmosphäre verabschieden mussten. Deshalb gibt es blanke Planeten wie Merkur (Atmosphäre verdampft?) und etliche mit dickem Eis bedeckte Monde (Atmosphäre eingefroren?)
Fazit: Sind wir mal froh dass wir uns überhaupt Gedanken machen können über den Zustand unserer blauen Murmel ….
Da offensichtlich einigen die Mathematik zu unheimlich ist und die Physik dahinter nicht mehr sehen, kurze Erläuterungen:
a) die S=1368 W/m2 sind messtechnisch validiert, vielleicht nicht auf das letzte W/m2, aber darauf kommt es hier nicht an. Das ist auch der einzig notwendige Messwert, der erforderlich ist, um zu bestimmen, wieviel Energie die Erdkugel von der Sonnen innerhalb eines Zeitraumes bekommt. Wenn nun andere Messungen zu gegenteiligen Messergebnissen käme, so hätte man ein messtechnisches Problem oder die Erde wäre alles andere als kugelförmig. Dass S aber zwischen 1300 und 1400 W/m2 liegt, besteht seit Jahrzehnten kein Zweifel, dazu gilt es dutzende von verschiedenen Messungen.
b) dass die einfallende Leistungsdichte auf eine zur Normalen schräg stehenden Ebene mit dem cos des Winkels abnimmt, ist pure Geometrie. Dies dedarf keiner Messung. Dass dies in Kugelkoordinaten ausgedrückt für tags so aussieht S × cos(x) × cos(y), ist sphärische Geometrie und bedarf keiner Messung, solche Abhängigkeiten haben die Nautiker der letzten Jahrhunderte genug verifiziert. Das es nachts Null ist, ist definitionsgemäß so, denn dann ist Nacht.
c) Zur Berechnung der Leistung der Sonnenstrahlung L(x), die auf einen Meridianstreifen fällt, muss man die Integralrechnung beherrschen, eine simple Aufsummierung der Leistungsdichte über die Flächenelemente eines Meridianstreifens von z.B. 1° Längenweite in Excel liefert korrespondierende Resultate.
d) Auch die Energiesumme kann mit Excel überprüft werden, indem man die Sonnenenergie aufsummiert, die den Streifen bei seiner Erddrehung erreicht, dabei muss man nur berücksichtigen, dass die Sonne um 1° pro 4 min weiterwandert und die durch die sich ändernde Schrägstellung Leistungsdichte einrechnen. Somit bekommt man die Sonnenenergie, die den Streifen in 24 h erreicht. Die Hälfte der Zeit kam nachts hinzu, wenn der Streifen da auf der Nachtseite war, am Mittag war die Leistungsdichte maximal (1070 W/m2 im meridionalem Mittel), vorher und nachher reduziert sie sich mit den cos des Stundenwinkels der Sonne, um gegen Abend und Morgen Null zu erreichen.
Das, was für den beliebigen Streifen gilt, gilt zeitversetzt für jeden gleichbreiten Streifen längs einer anderen Geograph. Länge, in 24 Stunden sammelt jedoch jeder Streifen dieselbe Energiemenge auf. Wenn man diese durch 24 Stunden und die Streifenfläche teilt, kommt S/4 raus.
Bei jeder Messung von S müssen übrigens solche geometrischen Überlegungen für die Auswertung der Messungen angestellt werden, selbst Pouillet hat das 1838 gemacht. Denn man misst i.a. immer gekippt zu den Sonnenstrahlen.
Herr Petersen,
einer ihrer besseren Beitraege,
Es waere interessant zu hoeren, was sie fuer eine Mittelung der Einstrahlleistung auf ihrem Streifen rausbekommen.
Laut ihrer eigenen Logik, gilt diese Einstrahlleistung fuer jeden einzelnen Streifen. Das heisst es gilt auch fuer die bestrahlte Flaeche.
Bin auf ihr Ergebnis gespannt und vor allem wie sie die unbeleuchtete Flaeche mit einbeziehen wollen.
„Es waere interessant zu hoeren, was sie fuer eine Mittelung der Einstrahlleistung auf ihrem Streifen rausbekommen.“
siehe Sverre Petersen 30. OKTOBER 2020 UM 16:07 und link dort
Und die Nummer ist?
Können Sie nicht lesen?
1,507e+22 Joule = 86400 sec (die Länge eines vollen Tag-Nachtzyklusses = 24 Stunden) * 5,1e+14 m2 (die Erdoberfläche) * 1368/4 W/m2 (= S/4=342 W/m2)
ist die gesamte eingestrahlte Energie auf die Erde innerhalb von 24 Stunden. Äquivalent zu dem zeitlichen und räumlichen Mittel 342 W/m2
Ganz einfach.
Ah ich sehe ihr Streifen ist 24 Stunden breit. Doch nicht nur vier Minuten.
Ich hätte schon gerne eine Lösung in W/ m2 für die von Ihnen vorgeschlagene Zeit.
Für welches Datum stimmt ihre Rechnung eigentlich?
Die Annahme der gesamten Erdoberfläche über 24 Stunden ist auf Grund der Schiefstellung der Erdachse falsch. Ohne Angabe von Datum natürlich.
Bisher nichts neues von Ihnen.
Anstatt S zu vierteln kann man auch die Fläche physikalisch richtig halbieren. Und S halbieren. Dann stimmt alles auch ohne Datumsangabe, in jeder Sekunde, für vier Minuten wie sie wollen.
Also Meine Lösung oder eine Flächenangaben für vier Minuten von Ihnen.
Kommt da noch was von Ihnen Herr Petersen?
a) die S=1368 W/m2 sind messtechnisch validiert, vielleicht nicht auf das letzte W/m2, aber darauf kommt es hier nicht an. Das ist auch der einzig notwendige Messwert, der erforderlich ist, um zu bestimmen, wieviel Energie die Erdkugel von der Sonnen innerhalb eines Zeitraumes bekommt.
Albedo???
Die Albedo ist auch seit Jahrzehnten auf genauer als 10% bekannt.
Dann sind es schon 2 Meßwerte und +/-10% Albedo ist ne ganze Menge im Vergleich zum angeblichen THE
Zu all dem: Die Sonne macht das Wetter, sie ist nicht ganz unbeeinflußt und „die Wissenschaft“ soll uns in Ruhe lassen. Sie hat uns in X Fällen bewiesen, daß sie von >>>Menschen betrieben wird. Fehler und Fälschungen sind der Beweis.
Natürlich gibt es Klimawandel, ich bin doch nicht blöd. Aber an den vom Menschen gemachten Klimawandel glauben, bin ich blöd?
CO2, als Spurengas in die Atmosphäre eingefügt, ermöglicht überhaupt erst das Leben als Nahrung für die Grünpflanzen. Es ist nie eine Gefahr, außer man vergißt im Gärkeller einer kleinen Brauerei die Entlüftungsanlage umzuschalten, was mir einmal passiert ist. (60 Jahre her). Nur ein Temperaturanstieg erhöht die Prozesse und damit eine CO2-Zunahme.
ER hat abiotisches Erdöl in die Erde eingelagert, damit wir nicht unsere Wälder verheizen müssen. Die sind als CO2-Senken gedacht.
# Sverre Petersen zu # 27.10.20 um 19:39
„Soso, Ihr [Agerius] Fehler liegt daran, dass Sie die 0 Einstrahlung in der gleichzeitig unbeleuchteten Fläche ignorieren und nur die positivbeträge der beleuchteten Hemisphäte summieren.“
Fall 1:
„o“ meint tatsächlich „Null“ Einstrahlung [von der Sonne] in der gleichzeitig unbeleuchteten Fläche. Die unbeleuchtete Fläche hat von der Sonne keine oder „0“ Einstrahlung. Deshalb gibt es eine dunkle Hemisphäre. Diese bildet sich in den Modellen von Philipp Mulholland und mir ab. Damit ignorieren wir aber nicht „0“ Einstrahlung, sondern berücksichtigen gerade „zero“.
Zu „nur positivbeträge“: Negativbeträge der Einstrahlung sind mir nicht bekannt. Falls Sie mit Negativbeträge der Einstrahlung die Albedo meinen, das Reflektionsvermögen bzw. die zurückgeworfene Sonneneinstrahlung wird von uns selbstverständlich berücksichtigt.
Fall 2:
„o“ ist ebenfalls ein Tippfehler. Statt „o“ wollten Sie möglicherweise einen von Null verschiedenen Zahlenwert schreiben, den ich dann ignorieren würde. Rechnet man im Augenblick der Einstrahlung der Sonne, solare Einstrahlung größer Null in die dunkle, lichtabgewandte Erdschattenseite, begeht man einen Logikfehler: Die dunkle Hälfte bleibt nicht dunkel. Natürlich können Sie das auf dem Papier rechnen, aber es entspricht nicht der Beobachtung, ist deshalb sinnlos.
Fall 3:
Mit Einstrahlung meinen Sie nicht die solare Einstrahlung, sondern möglicherweise die ominöse „Gegenstrahlung“. Im # zu diesem Artikel vom 26.10.20 um 22:18 Uhr habe ich dargelegt, dass mit der ½ Verteilung sich 390 W/m² langwellige Abstrahlung mit Zeitversatz zur Einstrahlung an der Erdkugel bilden. Die Globaltemperatur von 15° C entsteht so von selbst ohne Gegenstrahlung, die bei Kiehl und Trenberth 1997 324 W/m² beträgt.
Mulholland zeigt mit obigem Hemisphären Modell, Ulrich O. Weber mit seinem Hemisphären Modell aus der Perspektive der Kugeloberfläche und ich mit dem Hemisphären Modell aus der Perspektive der Satelliten Messwerte, dass es die Gegenstrahlung mit mehreren Hundert Watt/m² nicht gibt.
Die 24 h Mittelung schiebt über den Verteilungsfaktor 1/4 die Hälfte der Sonneneinstrahlung direkt in die Nachtseite der Erde. Der so betrachtete Durchschnitt der solaren Einstrahlung im Modell von Kiehl und Trenberth wird so um die Hälfte zu gering berechnet, statt 684 W/m² (korrekte Verteilung mit 1/2), 342 W/m² (falsche Verteilung mit 1/4). Diesen Fehler soll dann die Gegenstrahlung heilen, die aus einer Null entsteht und bilanzneutral ist. Deshalb muss die Gegenstrahlung eine Größenordnung von über 300 W/m² haben. Zum hemisphärischen Modell (1/2) habe ich mich erschöpfend erklärt, im Übrigen bin ich nicht Ihr Schuljunge.
Herr Agerius,
Mit 0 meine ich die Zahl Null. Mit Einstrahlung die solare Einstrahlung, nicht die durch Albedo reduziere Sonnenstrahlung, die vom Erdsystem absorbiert wird. Positiv sind in der Mathematik die Zahlen, die echt grösser Null sind. Da es keine negative Einstrahlung gibt, meinte ich damit die Situationen, in der die Sonne unter dem Horizont ist, die Einstrahlung am betrachteten Ort also Null ist. Das globale Mittel der solaren Einstrahlung beträgt dann S/4 = 342 W/m2.
Ihr doppelter Wert ist falsch, weil Sie ihn doppelt rechnen, indem Sie argumentieren, die unbeleuchtete Hemisphäre würde 12 Stunden später beleuchtet. Aber wir betrachten den momentanen (und hier zeitlich konstanten) Mittelwert, Sie müssen also die momentane Leistung an jedem Ort der Erdoberfläche simultan betrachten und dann global mitteln.
Nochmal einfach die Frage an Sie, wieviel Energie die Erdkugel nach Ihrer Rechnung in 24 Stunden an Sonnenstrahlung eingestrahlt bekommt und wieviel die Sonne in der gleichen Zeit durch die Querschnittsfläche der Erdkugel strahlt.
Logik ist nicht ihre Stärke Herr Petersen.
Aber die Unbeleuchtete Hemisphäre bleibt immer die unbeleuchtete Hemisphäre.
Falls sie das nicht verstehen, es ist genau das selbe als wenn man sagt, das es eine Tag und eine Nachtseite gibt.
Falls es sie stoert, das die Erde sich unter der Beleuchtung wegdreht, dann rechnen sie einfach mit einer nicht drehenden Erde.
Und noch mal als Hinweis, sie fragen nach ENERGIE. Die Antwort darauf hat die Einheit Joule. Nicht Watt.
Simple Fragestellung zur Logik: Die Sonne scheint durch einen Baum, so dass auf dem Bodenbelag zum Teil der Schatten der Blätter zu sehen ist und zum Teil der direkt bestrahlte Boden.
Wie bestimme ich die Temperatur der von der Sonne beschienen Teile des Bodenbelags mit Hilfe des S-B Gesetzes? Eine Flächeneinheit im Schatten der Blätter wird mir wohl kaum die Temperatur des der Sonne ausgesetzten Bodenbelags liefern, oder? Ich darf m.E. nur Fläche wählen, die von der Sonne bestrahlt wird, nicht aber einfach nur 1 Quadratmeter mit Sonne und Schatten-Partien. Damit kommt über S-B niemals die T des Bodenbelags heraus. Oder habe ich S-B nicht verstanden?
Ja, Sie haben SB nicht verstanden.
Sie haben völlig Recht Herr Greiner.
Es ist unmöglich, mit dem SB Gesetz eine Oberflächentemperatur zu berechnen. Abgesehen von Ihrem Beispiel mit der ungleichmässigen Bestrahlung kommen noch zig andere Faktoren dazu. Schon die Farbe spielt eine Rolle, weiß strahlt zurück, schwarz erwärmt sich mehr. Dann benötigen Stoffe unterschiedliche Energiemengen , um sich zu erwärmen. Es spüren alle, der Rasen ist kühl, der Asphalt daneben heiß…
Es gibt aber hier SB Fetischisten, sie nehmen nicht das Fieberthermometer sondern berechnen ihre Temperatur nach SB.
Muss man nicht weiter beachten.
100%
# Sehr geehrter Herr Sverre Petersen # zum 27. Oktober um 12:54
Die beleuchtete Hemisphäre (halbe Kugel) dreht sich mit einer Geschwindigkeit von 15° Längengraden pro Stunde. In 24 Stunden ergibt dies 24h x 15°/h = 360° = Kugel. Die unbeleuchtete Hemisphäre dreht sich genauso schnell und liegt der Beleuchteten gegenüber. Diese beiden halben Kugeln oder Hemisphären bilden eine gemeinsame Kugel. Die Einstrahlung erfolgt an der halben Kugel. Die Abstrahlung erfolgt sowohl an der beleuchteten Hälfte sofort und auch zeitversetzt als auch an der Unbeleuchteten durch Zeitversatz zur Einstrahlung.
Dies führt zum Verteilungsfaktor ½ für die Einstrahlung und damit zu 1368 W/m² / 2 = 684 W/m². Schaut man sich die Bahn des Satelliten z.B. ERBS an, der die Erde 7-mal am Tag die Erde umkreiste, kommt man auf die identische Mittelung 1368 W/m² / 2. Dies ist von mir beschrieben in Artikel „Umgebungsgleichung (Stefan- Boltzmann- Gesetz) / ungerechtfertigte Kritik an Ulrich O. Weber /…., vom 27. Juli 2020 veröffentlicht auf EIKE, dort im Abschnitt D. Mittelwertbildung.
Ich verweise für die nun verwendeten Zahlenwerte auf diesen Artikel. Vom Satelliten ERBS wurde die Albedo zu 0.269 im 5- jährigen Mittel gemessen. Wenn man die hierzu gehörenden 5 Messwerte für cloudy sky + Konvektion + Wärmeleitung und den Betrag der Albedo aus dem hemisphärischen Ansatz aufaddiert, Zahlen in W/m²: 101 + 19 + 20 + 243 + 31 + 17 + 69+ 184 = 684 W/m², liefert dies sehr exakt die Einstrahlung an der Hemisphäre bei bedeckten Verhältnissen. Bei clear sky: 4 Messwerte + Konvektion + Wärmeleitung + Reflektion aus Albedo = 48 + 48 + 42 + 276 + 17 + 69 + 184 = 684 W/m² = Einstrahlung an der Hemisphäre für klare Himmelsverhältnisse. Diese 9 Satellitenmesswerte zuzüglich der gemessenen Albedo rechtfertigen oder beweisen den Strahlungsverteilungsfaktor ½. Die Erdkugel aus zwei Halbkugeln zusammengesetzt mit v = 15°/h als Rotationsgeschwindigkeit in 24 h hat im Modell einen Kreisquerschnitt.
„Die Einstrahlung erfolgt an der halben Kugel.[] Dies führt zum Verteilungsfaktor ½ für die Einstrahlung und damit zu 1368 W/m² / 2 = 684 W/m².“
Soso, Ihr Fehler liegt daran, dass Sie die 0 Einstrahlung in der gleichzeitig unbeleuchteten Fläche ignorieren und nur die positivbeträge der beleuchteten Hemisphäte summieren.
Die korrekte mittlere Leistungsdichte von S/4 bekommt man auch durch Berechnung der an jedem Punkt der Kugel in 24 Stunden eingestrahlten Sonnenenergie und Aufsummation hin. Die Formel habe ich beim letzten Disput, dem Sie ausgewichen sind, hingeschrieben. Wenn Sie nun nicht mehr ausweichen und Ihren Denkfehler erkennen wollen, so knüpfen Sie da an.
Zum Aufwärmen einfach die Frage an Sie, wieviel Energie die Erdkugel nach Ihrer Rechnung in 24 Stunden an Sonnenstrahlung bekommt und wieviel die Sonne in der gleichen Zeit durch die Querschnittsfläche der Erdkugel strahlt (richtig für letzteres ist 1368 W/m2 * pi*R*R*24 h, sollte klar sein. Ihren Lösungsvorschlag für ersteres werden Sie dann angeben).
Wie schon im Beitrag unten von Herrn Ordowski gesagt wurde, kann man die Leistung nicht mitteln fuer Zeiten in denen sie nicht erbracht wurde, wenn man gleichzeitig versucht eine physikalische Wirkung daraus abzuleiten.
Die Null Einstrahlung der Sonne muss man ignorieren, wenn man die Einstrahlleistung mittelt.
Sie muessen Physik und seine Einheit schon ordentlich anwenden. Und Leistung mit 24 Stunden in Zusammenhang zu bringen heisst sie arbeiten mit Energie und nicht mit Leistung. Fuer die physikalische Wirkung der Erwaermung guckt man auf die Leistung. Und die ist nun mal hoeher wenn man ueber die reale Einstrahlflaeche mittelt. Das waere die Hemisphaere und das aender sich nicht.
Die Frage wieviel Energie von der Sonne kommt, kann man mit dieser Formel einfach berechnene fuer jedwede Zeit x:
Q=x h *1/2 S(1-A)*Erdoberfläche/2
Der physikalisch richtige Zusammenhang in der Formel legt dar, das in jedem Augenblicht die Hemisphaere (A/2) beschienen ist. Und die Solarkonstante sich ueber die Kruemmung der Erdoberflaeche im Mittel halbiert.
Und wie schon gesagt ist die Flaechenbestimmung in ihrer Formel fuer 24 Stunden oder irgendeine andere Zeit vom Datum und Anfangszustand der Drehung abhaengig.
Solche Abhaengigkeit kennt man nur von betruegerischen Buchhaltern und hat mit realer Physik nichts zu tun.
„Wie schon im Beitrag unten von Herrn Ordowski gesagt wurde, kann man die Leistung nicht mitteln fuer Zeiten in denen sie nicht erbracht wurde, wenn man gleichzeitig versucht eine physikalische Wirkung daraus abzuleiten.“
Nun, aber in unserem Fall ersteckt sich die Wirkung auf die gesamte Zeit, also lückenlos Tag und Nacht. Wenn die Energie auch nur am Tag bereitgestellt wird, so wird sie kontinuierlich (Tag und Nacht) im System verarbeitet, das Klimasystem funktioniert ja auch bei Nacht. Die mittlere Leistungsdichte von 342 W/m2 ist ja nichts anderes als ein Maß für die Energie E, die in 24 Stunden auf die gesamte Erdoberfläche einstrahlt.
E = 86400 s * 342 W/m2 * 5,10 e+14 m2.
Dabei ist erstmal egal, wie diese über die Oberfläche verteilt wird, der Anteil A wir md reflektiert, der Rest absorbiert, umgewandelt, verströmt, abgestrahlt etc.
@ Sverre Petersen
„Wenn die Energie auch nur am Tag bereitgestellt wird, so wird sie kontinuierlich (Tag und Nacht) im System verarbeitet, das Klimasystem funktioniert ja auch bei Nacht.“
Daran sehen Sie doch, dass wir es in diesem Zeitraum keinesfalls mehr mit einem thermodynamischen Gleichgewichtszustand zu tun haben. Natürlich können Sie T mitteln, aber dann bitte nicht auf Gesetze anwenden und Schlüsse daraus ziehen, für die ein thermisches Gleichgewicht Voraussetzung ist. (S-B).
Da vergewaltigen Sie die Physik.
Genau, die Sonne scheint auf eine Hemisphäre.
Es geht nicht um Zeit, es geht nicht um Energie sondern um Leistung pro Fläche! Weil sie davon auf eine Temperatur schließen wollen.
Aber wenn es ihnen egal ist, was diskutieren sie dann?
Geben sie doch mal die wirksam beschienenen Fläche an?
Zeitunabhängig ist das die Hemisphaere.
Können sie das bestätigen oder leugnen sie Tag und Nacht?
Albert Agerius schrieb am 27. Oktober 2020 um 18:22 :
In dem Artikel kann man folgendes lesen:
Nimmt man dieses TSI im Mittel und läßt es auf die beleuchtete Halbkugel wirken, kommt man wie jeder andere auf TSI/4 = 342W/m² als mittlere Einstrahlung.
Herr Mueller,
die Aussage der Mittelung des TSI wurde schon für die Halbkugel gemacht !
Eine weitere Mittelung der Leistung auf der Hemisphäre ist unzulässig.
Sie haben aber immer noch nicht verstanden worum es geht.
Die Annahme das die Sonne eine Temperaturquelle von nur -18 Grad C ist, ist falsch.
Die Sonne ist eine Temperaturquelle von fast 120 Grad C (TSI). Das kann man auf der Sonnen beschienenen Seite flaechenmaessig mitteln und dann kommt man eben auf
30 Grad C (nach abzug der atmosphärischen Absorption und Reflection) = 479 W/m2.
Sie betrachten doch die Atmosphäre als Isolation. Eine Isolation erhöht jedoch nicht das Wärmepotential der Wärmequelle. Mit Ihrer Sonneneinstrahlung von -18 Grad C kann die Atmosphäre die Erde nicht auf 15 Grad C erwärmen.
Wenn sie jedoch eingestehen, das am Tage die Temperatur der Erde durch die Sonne auf 30 Grad C erwärmt werden kann, dann wird sich herausstellen, das einen geringere Abkühlung durchaus die gemittelte Temperatur der Erde von 15 Grad C darstellen kann.
Wie sie sehen ist die Angabe der korrekten Leistung bei Berücksichtigung der wirklich angestrahlten Fläche wichtig das ihr Model funktioniert.
Die Viertelung von TSI ist ein Mathematisches Konstrukt fuer die Berechnung der Effektiven Temperatur eines Planeten, da die Abstrahlung von der gesamten Oberfläche ausgeht. Wenn man den Eingang der solaren Energie mit der Abstrahlung gleichsetzt, dann kann man eine Halbierung fuer die TSI machen und die Viertelung für die Abstrahlung. Damit erfasst man physikalisch die wirksamen Flächen richtig.
Die Viertelung über die Hemisphaere so wie sie sie darstellen ist grundsätzlich falsch.
Falls sie hier gelesen haben https://en.wikipedia.org/wiki/Planetary_equilibrium_temperature
The factor of 1/4 in the above formula comes from the fact that only a single hemisphere is lit at any moment in time (creates a factor of 1/2), and from integrating over angles of incident sunlight on the lit hemisphere (creating another factor of 1/2).[6]
Dann sind sie leider einer Falschinformation aufgesessen.
Werner Schulz schrieb am 29. Oktober 2020 um 2:38
Sie sehen im Zitat, wie der Wert ermittelt wurde. Sie können auch gern im Originalartikel nachlesen. Der Wert ist der Mittelwert zwischen den Messungen in der Sonne und im Erdschatten. Ich zitiers einfach nochmal:
Und das ist eigentlich total trivial. Bei Solarpanels wissen das auch alle, da wird immer betont, dass die Nachts keine Energie liefern können, da die Sonne nicht scheint. Bei der mittleren Einstrahlung wird das dann plötzlich nicht berücksichtigt, da scheint anscheinend auch Nachts die Sonne …
Na und wie warm werden Solarpanele? Es geht um die Temperatur und die temperaturwirksame Leistung.
Nicht um wieviel Energie ankommt.
Ein errechneter Temperaturmittelwert aus Einstrahlung und Abstrahlung mag genauso wie ein Klimamittelwert für hochtrabende Wissenschaftsdiskusionen interessant sein, hat aber keinerlei praktischen Nutzen für Flora und Fauna der unterschiedlichen Erdregionen. Was sagen uns 30°C in den Tropen im Vergleich zu 50°C in den Wüsten bezüglich Energieinhalt der Atmosphäre? Nicht die Temperatur ist das Maß der Dinge, sondern die Energie die sich in der regionalen Atmosphäre befindet.
Nur so bringt man einige wenige Menschen zum Nachdenken.
# Sverre Petersen vom 24.10.2020 18:46 Uhr
„Wenn man nur die absorbierte Sonnenenergie am Boden betrachtet, so reicht diese allein nicht aus, um die beobachtbaren Temperaturen zu erklären…“
Diese Aussage ist schlichtweg falsch, da sie auf einem falschen Modell der Strahlungsverteilung, der Viertelverteilung der Einstrahlung, beruht. Im Augenblick der Einstrahlung wird hierin die Sonne auf die dunkle Nachtseite mit verteilt und die helle Seite der beleuchteten Erde sofort zu gering berechnet.
Wir beobachten aber, dass nachts die Sonne nicht scheint. In 24 Stunden ist stets in jeder Sekunde nur eine halbe Kugel beleuchtet. Deshalb darf auch nur die halbe Kugel im Vorgang der Einstrahlung betrachten werden.
Die Einstrahlung der Sonne auf die halbe Erde als hemisphärisches Modell mit Strahlungsverteilungsfaktor ½ reicht aus, um eine langwellige Abstrahlung im globalen Mittel von 390 W/m² mit rund 15 °C zu erzielen. Dies beweisen gerade die Satellitenmesswerte, die gemessene Albedo. Hierin müssen aber alle Satellitenmesswerte (in Summe 11) des gesamten Strahlungsprofil verwenden werden und beide Albedo Werte.
Der Leser kann es direkt nachprüfen im Artikel „Umgebungsgleichung (Stefan-Boltzmann-Gesetz) / ungerechtfertigte Kritik an Ulrich O. Weber / Strahlungsgleichgewicht / Mittelwertbildung“ von Agerius vom 27. Juli auf der EIKE Interseite, hierin siehe Abschnitt D. Mittelwertbildung, Bild Modell 5 clear sky bzw. cloudy sky.
Aus diesem Bild des hemisphärischen Modells entnommene Werte:
Einstrahlung auf halbe Erdkugel: 1368 W/m² / 2 = 684 W/m²
abzüglich des Albedo Anteils: – 184 W/m²
abzüglich Satm: – 24 W/m²
abzüglich Sensible Heat (d.h. Konvektion): -17 W/m²
abzüglich Latent Heat (d.h. Wärmeleitung): -69 W/m²
verbleiben als langwellige Abstrahlung der Erdoberfläche: 390 W/m².
Dies entspricht 15 °C Globaltemperatur und „reicht so alleine aus, um die beobachteten Temperaturen zu erklären.“ Die 1/4 Verteilung ist damit nachgewiesen falsch.
„Die 1/4 Verteilung ist damit nachgewiesen falsch.“
Da stimme ich Ihnen voll zu. Aber nicht nur die ist falsch, sondern auch die Anwendung des Stefan-Boltzmann Gesetzes. Was sind das nur für sog. Experten beim PIK, die so einen Bockmist verzapfen. Das Stefan-Boltzmann Gesetz sagt etwas über den Zusammenhang einer bestrahlten Fläche und der damit verbundenen Temperaturveränderung DIESER Fläche aus. Wer diesen Zusammenhang dazu verwendet, um eine NICHT bestrahlte Fläche (wegen notwendiger Mittelung für irgendwelche Zellen in Klimamodellen benötigt) für eine Temperaturberechnung der bestrahlten Fläche mit zu verwenden, hat schlichtweg keine Ahnung von Physik bzw. dieses Gesetz nicht verstanden oder er will uns etwas vorgaukeln. Außerdem werden dabei Ergebnisse aus der Gleichgewichtsthemodynamik auf instationäre und sich zeitlich verändernde Größen übertragen, was völliger Unsinn ist. Das S-B Gesetz gilt für thermisches Gleichgewicht und abheschlossenes System! Das ist Grundvoraussetzung für seine Anwendung. Liebes PIK und liebe Klima-Alarmisten, schaut Euch noch einmal die Herleitung des S-B Gesetzes über die Thermodynamik an und dann, was Ihr daraus in Euren Klimamodellen macht. Das ist Pfusch hoch vier!
Herr Probst
„Stefan-Boltzmann Gesetz sagt etwas über den Zusammenhang einer bestrahlten Fläche und der damit verbundenen Temperaturveränderung DIESER Fläche aus.“
Das ist falsch. Das Stefan-Boltzmann-Gesetz sagt nichts über die EINSTRAHLUNG und der TemperaturÄNDERUNG der bestrahlten Fläche aus, sondern über den Zusammenhang zwischen der Temperatur und der thermischen Abstrahlung derselben.
„Das S-B Gesetz gilt für thermisches Gleichgewicht und abheschlossenes System! “
Abgeschlossen muss es nicht sein, aber natürlich müssen die Subsysteme eine definierte Temperatur haben, dann lässt sich das SB gesetz für die Subsysteme entsprechend ihrer Temperatur anwenden.
Auch für Sie Herr Agerius nochmal der Hinweis, Ihren Rechenfehler nachzuvollziehen.
In Lehrbüchern der Klimatologie finden sich Zahlenwerte, die Ihren widersprechen. Wenn Sie da etwas entdeckt hätten, was zehntausende Wissenschaft über hundert Jahre verpennt hätten und simple Geometrie bei Klimafragen nicht greift, Gratulation, Sie haben ein neues Universum erschaffen.
Herr Petersen sitzt, ich sehe ihn geradezu auf seinem Spazierstockhocker, am Waldrand und blickt vergnügt auf eine sonnenbestrahlte Wiese, blinzelt auch ab und zu gen Himmel! Und als Akademiker hat er natürlich die Brille auf und liest in den Memoiren vom Aristoteles.
Man kann sich auch an der Natur erfreuen ohne sie zu verstehen.
Aristoteles ist übrigens für Naturwissenschaftler nur von historischem Interesse.
# Bluecher
Die Vorgehensweisen von Mr. Philip Mulholland kann ich bestätigten – die Sonne beim Sonnenschein auf die Erde mit dem Faktor 1/2 zu modellieren. Der Faktor 1/4 ist für die Einstrahlung falsch. Kiehl und Trenberth – unter Verwendung von 1/4 in KT97 – schreiben, dass ihr Modell auf den ERBS/ERBE-Satellitendaten basiert. Ich überprüfte KT97 mit den Original- Satellitendaten, die erst seit kurzem auch einer breiteren Öffentlichkeit zugänglich sind. Es gibt beispielsweise beim ERBS Satelliten (NASA ERBE Programm), 9 Strahlungs- und 2 Albedomessungen, die ich in meiner Studie, Kritische Analyse zur globalen Klimatheorie, Agerius, 2019, Tredition, veröffentlicht habe. Dort gebe ich die exakten Links zur Quelle für Überprüfbarkeit der hierzu verwendeten Satelliten Daten an.
Kiehl und Trenberth sagten in KT97 dagegen nichts über die Anzahl dieser verschiedenen 11 Datenreihen. Nur alle 9 Strahlungsmessungen gemeinsam bilden das Abstrahlungsprofil der Erde komplett und korrekt ab, den so wurde ja auch gemessen. Kiehl und Trenberth verwenden jedoch nur 5 von 11 Satellitenwerten. Sie unterschlagen den Rest, erwähnen die Existenz der übrigen, nicht benutzten Strahlungsmessreihen nicht einmal!!!
Nur deshalb kann in KT97 Modell mit 1/4 überhaupt gerechnet und mit den 5 Datenreihen des ERBE Satelliten Programm verglichen werden. Mit den 5 verwendeten Werten gibt es darüber hinaus eine große Abweichung zwischen von Kiehl und Trenberth errechneten Modellwert und dem verwendeten Satelliten Vergleichs Messwerten. Ich kann anhand des Verteilungsfaktors 1/2 in einem Modell, das dem von Mulholland sehr ähnlich ist, zeigen, dass die Abweichung zwischen Meß- und Modellwert der Strahlung mit Verteilungsfaktor 1/2 a) weniger als 2 Watt / m² beträgt und b) alle 11 Messwerte in diesem neuen Modell mit Faktor 1/2 dann auch aufpoppen.
Damit wird beweisen, dass die grobe Mittelung über 24 Stunden mit Strahlungsverteilungsfaktor von 1/4 falsch ist. Im Augenblick der Einstrahlung wird nur die halbe Kugel beleuchtet und dies beweisen nun auch alle 11 Satelliten Messreihen!
Und der einfache Test ist ein Fussball und eine Taschenlampe.
Die Ausleuchtung des gesamten Fußballs mit einer Taschenlampe geht nicht. Man kann die Haelfte des Balles ausleuchten. Der Rest liegt im Schatten.
Die Erfahrung von Tag und Nacht bestätigt ebenfalls, das der Faktor 1/4 falsch sein muss.
Mal sehen wann die Trolle auftauchen und es wieder besser wissen.
Ihr Modell wird realitätsnäher, wenn Sie die Energien betrachten, die ein rotierender Fussball in seiner Rotationsperiode absorbiert. Die Erde rotiert in knapp 24 h einmal um ihre N-S-Achse müssen Sie wissen.
Herr Petersen,
was sie nicht sagen. Und augenblicklich bestrahlte Flaeche wird deswegen immer noch nicht groesser!
Ich sage augenblicklich, weil in Watt steckt eine SEKUNDE drin.
Falls sie die Bestrahlung meinen, die wird in Joule pro Quadratmeter angegeben.
Um das Model fuer sie verstaednlicher zu machen, neigen sie die Drehachse. An einem Pol gibt es ein Gebiet das nicht bestrahlt wird. Sowas aber auch. Mit 24 Stunden stimmt ihr Model nicht, so wie sie behaupten.
Wenn sich der Fußball schnell genug dreht, was nimmt der Beobachter der Lichtquelle auf dem Fußball dann wahr? Nur noch Licht oder nur Dunkelheit oder eine Mischung?
Sie meinen so 50 mal in der Sekunde? Das ist in der Tat eine gute Frage!
Frage auch was sieht ein Beobachter von draussen?
Grau?
Auch das „1/2-Faktor Modell“ ist falsch oder Unsinn. Das kann man an den Messwerten der ERBE Mission erkennen.
Aus den Messungen der ERBE Mission wurden folgende Werte ermittelt:
+ Mittlere solare Einstrahlung (22 Jahre 1983-2005): 8,195 kWh/m^2/day (341,4 W/m^2) -> hemisphärischer Wert: 1365 W/m^2
+ Mittlere solare Einstrahlung (All-Sky) auf die Oberfläche (22 Jahre 1983-2005): 4,526 kWh/m^2/day (188,6 W/m^2) -> hemisphärischer Wert: 755 W/m^2
+ Mittlere solare Einstrahlung (Clear-Sky) auf die Oberfläche (22 Jahre 1983-2005): 5,932 kWh/m^2/day (247,2 W/m^2) -> hemisphärischer Wert: 989 W/m^2
Die solare Einstrahlung auf die Oberfläche der Hemisphäre muss nach den ERBE Messungen logischerweise bei ungefähr 755 W/m^2 liegen. Die 470 W/m^2 aus den „1/2-Faktor Modell“ sind also nicht korrekt.
Wie ich bereits schrieb: Den Fehler, den alle Theorien oder deren Modelle zu diesem Thema machen ist, ein geometrisches Flächen-Verhältnis auf eine Eingangsgröße anzuwenden, statt auf die wirksame Bezugseinheit der Eingangsgröße.
Die Zeit und die Oberfläche bilden eine Bezugseinheit [(O*t)]. Man muss sich immer auf die Gesamtheit eines Körpers beziehen, um Teile zu spezifizieren.
Kugel (Gesamtheit vom Körper): O – [Oberfläche], t – [Rotationsperiode] und zusammengesetzt die Ot = [(O*t)] [Periodenoberfläche]
Für die halbe Gesamtheit gilt: O/2 – [halbe Oberfläche] , t/2 – [halbe Rotationsperiode] und für die halbe Periodenoberfläche ergibt sich Ot/2 = [(O*t)]/2
Einstrahlung am Erd-Hemisphärenrand: Q_a = S * [(O*t)]/2
Einstrahlung am TOA der Erd-Hemisphäre: Q_i = M(i) * [(O*t)]/2
Ausstrahlung der sphärischen Oberfläche: Q_s = M(s) * [(O*t)]
Ausstrahlung am TOA der Erd-Sphäre: Q_p = M(p) * [(O*t)]
Mit den bekannten Werten (gerundet) aus den Messungen (ERBE, CERES und SORCE):
Q_a = 1361 W/m^2 * [(5,1*10^14 m^2 * 24h)]/2 = 8,3*10^18 Wh = 3*10^22 J/d
Q_i = 1361 W/m^2 * (1 – 0,3) * [(5,1*10^14 m^2 * 24h)]/2 = 5,8*10^18 Wh = 2,1*10^22 J/d
Q_s = 378 W/m^2 * [(5,1*10^14 m^2 * 24h)] = 4,6*10^18 Wh = 1,7*10^22 J/d
Q_p = 238 W/m^2 * [(5,1*10^14 m^2 * 24h)] = 2,9*10^18 Wh = 1*10^22 J/d
Die Energiebilanz am TOA Q_i/2 = Q_p muss ungefähr ausgeglichen sein, damit der Erhaltungssatz der Energie für das System erfüllt wird. Damit hat sich jedweder „atmosphärische Treibhauseffekt“ ins Nirwana verabschiedet. Hieraus erklärt sich auch der Faktor 1/4, der nur an der Grenze TOA (System/Umgebung) anwendbar und gültig ist.
Mfg
Werner Holtz
@ Herrn Werner Holtz
Sie haben bei Ihrem Kommentar, „Auch das „1/2-Faktor Modell“ ist falsch oder Unsinn“, einen Faktor-2-Fehler fabriziert:
Einstrahlung am TOA der Erd-Hemisphäre: Q_i = 2,1*10^22 J/d
Anmerkung: Einstrahlung am TOA mit (1-ALBEDO) halte ich für gewagt
Ausstrahlung am TOA der Erd-Sphäre: Q_p = 1*10^22 J/d
Diesen Faktor-2-Fehler heilen Sie dann durch einen unkommentierten Faktor-2-Eingriff, indem Sie die hemisphärische „Einstrahlung am TOA“ einfach noch mal halbieren, Zitat:
„Die Energiebilanz am TOA Q_i/2 = Q_p muss ungefähr ausgeglichen sein, damit der Erhaltungssatz der Energie für das System erfüllt wird.“
Vielleicht sollten Sie Sich Ihre Faktor-2×2-Berechnungen doch noch einmal ganz genau anschauen, denn eigentlich fordert der Energieerhaltungssatz ja, dass Einstrahlung und Abstrahlung gleich groß sein müssen. Bei der Frage „falsch oder Unsinn“ möge der geschätzte Herr Holtz also erst mal vor seiner eigenen Tür kehren; ich verweise höflich auf den Fußball von Herrn Schulz im Kommentar darüber als Anschauungsobjekt.
Zitat: Einstrahlung am TOA mit (1-ALBEDO) halte ich für gewagt
Was halten Sie daran gewagt?
Sie können sich ja mal mit der Frage beschäftigen – Was die sphärische Albedo ist, dann kommen Sie vielleicht darauf.
Zitat: Vielleicht sollten Sie Sich Ihre Faktor-2×2-Berechnungen doch noch einmal ganz genau anschauen, denn eigentlich fordert der Energieerhaltungssatz ja, dass Einstrahlung und Abstrahlung gleich groß sein müssen.
Nein, werde ich nicht! Die Werte sind Messwerte aus den Missionen ERBE, CERES und SORCE. Dann wären die Messwerte falsch. Und der Erhaltungssatz der Energie für ein offenes (fast passives) System wie die Erde lautet: Systemenergie = Austauschenergie.
Aber irgendwann werden Sie es auch noch lernen.
Mfg
Werner Holtz
@ Herrn Werner Holtz,
Es ist schon sehr erstaunlich, bei Ihnen wirkt die sphärische Albedo also zwischen „Einstrahlung am Erd-Hemisphärenrand“ und der „Einstrahlung am TOA der Erd-Hemisphäre“. Vielleicht überlegen Sie sich das doch noch mal.
PREISFRAGE: Was wäre eigentlich, wenn bei richtigen Satellitenmesswerten Ihre Faktor-2×2-Berechnungen trotzdem falsch sind? – Der Hauptgewinn ist Erkenntnis.
Schaunmeralsomal: Die solare Einstrahlung erfolgt auf einer KREISFLÄCHE (PI R²) und Ihre Messwerte beziehen sich auf Schnittpunkte solcher EINSTRAHLUNGSFLÄCHEN mit der jeweiligen Satellitenbahn auf der tagseitigen HEMISPHÄRE (@2 PI R²). Diese Messwerte können also die Erdkrümmung gar nicht berücksichtigen, und deren unkorrigierte Übernahme ergibt dann Ihre fehlerhafte Verdoppelung. Es ist also keineswegs so, dass die Solarkonstante auf der gesamten Tagseite der Erde die gleiche, von Satelliten gemessene spezifische Strahlungsleistung „auf den Boden bringt“, wie das in Ihren Faktor-2×2-Berechnungen unterstellt wird. Bei Ihnen fehlt vielmehr der Cosinus des örtlichen Zenitwinkels. Schaun Sie doch einfach mal auf das Berechnungsschema für meinen hemisphärischen S-B-Ansatz, da werden Sie geholfen…
@ U. Weber
Zitat: PREISFRAGE: Was wäre eigentlich, wenn bei richtigen Satellitenmesswerten Ihre Faktor-2×2-Berechnungen trotzdem falsch sind?
Ist sie nicht, weil mit drei alternativen winkel-treuen Modellen verifiziert.
Zitat: Die solare Einstrahlung erfolgt auf einer KREISFLÄCHE (PI R²) …
Nein, die solare Einstrahlung wirkt auf die Hemisphärenfläche.
Zitat: Diese Messwerte können also die Erdkrümmung gar nicht berücksichtigen, und deren unkorrigierte Übernahme ergibt dann Ihre fehlerhafte Verdoppelung.
Nein, Sie wollen und können es nicht verstehen.
Jeder Punkt auf der Hemisphäre wird im Idealfall mit 1361 W/m^2 bestrahlt (Einstrahlung am Erd-Hemisphärenrand). Bei einer Kugel muss die Krümmung berücksichtigt werden. Die Berücksichtigung der Krümmung erfolgt in der sphärischen Albedo vom Himmelskörper (Einstrahlung am TOA der Erd-Hemisphäre).
Sie haben sich gar nicht die Mühe gemacht, trotz meines Rates, nachzuforschen, was die sphärische Albedo im Grunde beschreibt. Und ihren hemisphärischen S-B-Ansatz halte ich für ziemlich unausgegoren.
Mfg
Werner Holtz
@ Herrn Werner Holtz
1. Ihr Zitat: „Sie haben sich gar nicht die Mühe gemacht, trotz meines Rates, nachzuforschen, was die sphärische Albedo im Grunde beschreibt.“
Um es ganz deutlich zu sagen: Bei Ihnen wirkt die sphärische Albedo zwischen „Einstrahlung am Erd-Hemisphärenrand“ (Q_a = 3*10^22 J/d) und der „Einstrahlung am TOA der Erd-Hemisphäre“ (Q_i = 2,1*10^22 J/d) immer noch in der falschen Richtung.
ERGO: Bei Ihnen ist die „Einstrahlung am Erd-Hemisphärenrand“ GRÖSSER ALS die „Einstrahlung am TOA der Erd-Hemisphäre“.
2. Sie haben Ihren Faktor2-Gedankensprung noch immer nicht erklärt, Ihr Zitat: „Die Energiebilanz am TOA Q_i/2 = Q_p muss ungefähr ausgeglichen sein“, also:
„(Einstrahlung am TOA der Erd-Hemisphäre=Q_i)/2“ = (Ausstrahlung am TOA der Erd-Sphäre = Q_p)
ERGO: Nach Ihren Angaben soll die Ausstrahlung @TOA der HALBEN Einstrahlung @TOA entsprechen
3. Ihr Zitat: „Jeder Punkt auf der Hemisphäre wird im Idealfall mit 1361 W/m^2 bestrahlt (Einstrahlung am Erd-Hemisphärenrand)…“.
Aber auf dem Mond ist das offenbar ganz anders: Abbildung Kombination der beiden vorherigen Abbildungen WUWT/Weber
Oberflächentemperatur auf dem Mond am Landeplatz von Apollo 15
(Originalabbildung aus einem Artikel von Willis Eschenbach auf EIKE, Primärquelle WUWT)
Llila/blau: Gemessene Oberflächentemperatur auf dem Mond am Landeplatz von Apollo 15
Rot: Hemisphärische S-B-Inversion für das S-B-Temperaturäquivalent aus der solaren Einstrahlung am Landeplatz von Apollo 15 über den Höhenwinkel des Sonnenstandes ohne Berücksichtigung der Ekliptik
ERGO: Wie erklären Sie den WIDERSPRUCH zwischen Ihrer unter (3.) zitierten Aussage und der Übereinstimmung von gemessener und hemisphärisch modellierter Temperatur auf der Tagseite des Mondes, die eindeutig dem Höhenwinkel (SIN) oder Azimut(COS) der Sonne folgt?
@ U. Weber
Zitat: Sie haben Ihren Faktor2-Gedankensprung noch immer nicht erklärt, Zitat: „Die Energiebilanz am TOA Q_i/2 = Q_p muss ungefähr ausgeglichen sein“
Das sollte doch logisch sein!? Die Energiezufuhr bezieht sich auf die halbe Gesamtheit [G/2] und die Energieabgabe auf die Gesamtheit 2*[G/2]: E(in,TOA)*[G/2] = 2*[G/2]*E(out,TOA) -> E(out,TOA) = E(in,TOA)/2.
Die sphärische (planetare) Albedo gilt nur für eine sphärische Objektoberfläche. Die sphärische Albedo darf man nicht auf eine planare Kreisfläche anwenden, weil das Reflexionsverhalten der Oberfläche von der Objektform abhängig ist.
++ Akademisches Beispiel zur Veranschaulichung: Wenn die Sonne eine Kreisfläche im Winkel α = 0° und β = 0° (x,y)-Richtung bestrahlt, dann erhält die Kreisfläche einen Energiestromdichte von j(0°,0°) = S*cos(0°)*cos(0°) = 1361 W/m^2. Wenn die gleiche Kreisfläche um einen Winkel α = 45° in x-Richtung neigt wird, dann erhält die Kreisfläche eine Energiestromdichte von j(45°,0°) = S*cos(45°)*cos(0°) = S/√(2) = 1361/√(2) = 962 W/m^2. Neigt man diese Kreisfläche nochmals um den Winkel β = 45° in y-Richtung, dann ergibt sich j(45°,45°) = S*cos(45°)*cos(45°) = S/2 = 1361/2 = 680,5 W/m^2. Der Flächenanteil bezogen auf eine Hemisphäre zwischen den Winkel α = ±45° und β = ±45° betreffen rund 71% der Gesamtoberfläche der Hemisphäre. Daraus ergibt sich nach Abschätzung, dass die mittlere Energiestromdichte der Einstrahlung für die Hemisphäre größer als 680,5 W/m^2 sein muss. Aus diesem Grund sind die Modelle, die mit S/4 oder S/2 für eine mittlere hemisphärische Einstrahlung von der Sonne arbeiten, nicht korrekt.
Als Anschauungs-Beispiel sei die Abbildung von Diviner Lunar Radiometer Experiment (Bild rechts) verwiesen:
https://imagebank.osa.org/getImage.xqy?img=M3cubGFyZ2UsYW8tNTQtNC1CNjQtZzAwNQ
+ Diese Abbildung kann näherungsweise durch das statische Modell mit Zentral-Solarpunkt beschrieben werden.
Bei der Temperaturverteilung auf einer nicht-rotierenden Kugeloberfläche (Hemisphäre) bei Gültigkeit vom Lambertschen Kosinussatz und des Stefan-Boltzmann-Gesetz bilden sich isotherme konzentrische Kreisbänder um den Zentral-Solarpunkt T0, wobei T0 = [(1-A)*S/(ε*σ)]^0,25 ist. Wenn man den Zentral-Solarpunkt T0 als thermischen Pol definiert, dann ergibt sich die Temperatur beim thermischen Breitengrad β nach: T(β) = T0*cos(β)^0,25.
A) Der mittlere Temperaturwert über die scheinbare Hemisphäre der Erde ergibt T(β,avg) = 306K, wobei dies einer mittleren Energiestromdichte von j = ε*σ*T(β,avg)^4 = 0,96*5,67*10^-8*306^4 = 478 W/m^2 entspricht.
B) Der flächen-gewichtete Temperaturwert über die Hemisphäre der Erde ergibt T(β,wavg) = 330K, wobei dies einer mittleren Energiestromdichte von j = ε*σ*T(β,wavg)^4 = 0,96*5,67*10^-8*330^4 = 646 W/m^2 entspricht.
C) Beachtet man noch, dass die Sonnenscheibe den Zentral-Solarpunkt T0 in 32 Bogenminuten überstreift, dann ergibt sich für die flächen-gewichtete Temperatur über die Hemisphäre der Erde der Wert von T(β,wavg,32′) = 341K. Mit diesem Temperaturwert erhält man eine mittlere Energiestromdichte von j = ε*σ*T(β,wavg,32′)^4 = 0,96*5,67*10^-8*341^4 = 734 W/m^2.
+ Eine alternative Mittelung für den Fall A
Das Kreisflächen-Mittel (Fall A) ist nicht das Gleiche wie das Kugeloberflächen-Mittel einer Hemisphäre (Fall C). Man kann dies erkennen (Beispiel: Randverdunkelung der Sonne), indem man die Fläche von den Regionen eines Kreises und einer Halbkugel mit |x| ≤ 1/2*r bestimmt. Für die Kreisfläche ergibt sich [π/3 + √(3)/2]*r^2, welches ca. 61% von der Gesamtkreisfläche ausmacht. Für eine Halbkugeloberfläche (Hemisphäre) ergibt sich π*r^2, also genau 50% der Gesamtoberfläche der Halbkugel. Tatsächlich sind beim Kreisflächen-Mittel die Pol-Regionen übergewichtet und die äquatorialen Regionen der Hemisphäre untergewichtet.
Man muss mit einem Gewichtungsfaktor von π/[π/3 + √(3)/2] rechnen, um ein Kreisflächen-Mittel auf einer Hemisphäre abzubilden. Damit würde sich eine Energiestromdichte für die Hemisphäre von 478 [W/m^2] * π/[π/3 + √(3)/2] = 785 W/m^2 ergeben.
Mfg
Werner Holtz
@ Herrn Werner Holtz
Sie haben Sich sehr bemüht, aber:
1. Irgendwie haben Sie meinen hemisphärischen S-B-Ansatz über den örtlichen Azimutwinkel der Sonne nicht verstanden und kaprizieren sich noch immer auf den Ausdruck „Faktor 2“, der den diametralen Gegensatz zum herkömmlichen „Faktor 4“-Ansatz hervorhebt und lediglich einen anschaulichen Durchschnittswert liefert.
2. Zu Ihrem E(out,TOA) = E(in,TOA)/2: Sie beziehen die ENERGIE auf das Flächenverhältnis (OUT@4PIR²:IN@2PIR²). Bei (nahezu) konstanter „gemessener Globaltemperatur NST“ sollten hemisphärisch eingestrahlte Energie (Ein) und global abgestrahlte Energie Eout in [Ws=Joule] für gleiche Zeiträume aber in etwa gleich sein:
(Ein @ 2PIR²= Einstrahlung auf der Tageshemisphäre) = (Eout @ 4PIR²=Abstrahlung von der gesamten Erdoberfläche)
Möglicherweise meinen Sie ja die spezifische STRAHLUNGSLEISTUNG [W/m²]?
3. Den tieferen Sinn für Ihre Mittelwertberechnungen der durchschnittlichen spezifischen Strahlungsleistung über Durchschnittstemperaturen (A-C) habe ich nicht verstanden. Das ist m. E. eine Rekursion zu viel, schließlich ist bei einer S-B-INVERSION die örtliche Strahlungsleistung primär und die Ortstemperatur sekundär. Was soll also eine aus der gemittelten Temperatur (sekundär) zurückgerechnete spezifische Strahlungsleistung (primär) aussagen? Meine hemisphärische Berechnung über konzentrische 1° Segmente ergibt übrigens ca. 14°C und konvergiert bei ca. 15°C (=2xLösungG&T).
4. Und auf die Übereinstimmung meiner hemisphärischen Berechnungen mit originalen Meßwerten von der Mondoberfläche sind Sie erst gar nicht eingegangen. Sie kennen sich offenbar auch mit den Mond-Temperaturen aus, haben sich aber bisher um eine konkrete Antwort gedrückt. Da warte ich also immer noch auf eine qualifizierte Rückäußerung.
Das war der Ursprung unserer Diskussion.
@ Herrn Werner Holtz (27. Oktober 2020 um 11:41): Sie haben bei Ihrem Kommentar, „Auch das „1/2-Faktor Modell“ ist falsch oder Unsinn“, einen Faktor-2-Fehler fabriziert.
Ihre Behauptungen haben sich also ins Nirwana verflüchtigt.
Ihr hemisphärischer S-B-Ansatz soll sich auf eine Kreisfläche beziehen, was aber physikalisch völlig sinnfrei ist. Wie kommen Sie den auf die 940 W/m^2 in ihrem Modell? Korrekt berechnet erhält 962 W/m^2 für die Einstrahlung auf der Hemisphäre (ideale Kugel).
Zitat: Den tieferen Sinn für Ihre Mittelwertberechnungen der durchschnittlichen spezifischen Strahlungsleistung über Durchschnittstemperaturen (A-C) habe ich nicht verstanden.
Das war für ihre mathematischen und physikalischen Fähigkeiten wahrscheinlich etwas zu viel.
Zitat: Da warte ich also immer noch auf eine qualifizierte Rückäußerung.
Und den Mond haben Sie ins Spiel gebracht, nicht ich. Deshalb sehe ich auch keinen Grund mich dazu zu äußern. War nicht Kern der Diskussion. Wenn man Mond und Erde beschreiben will, muss man eine Dämpfungsanalyse machen.
Mfg
Werner Holtz
@ Herrn Werner Holtz
Es geht Ihnen hier offenbar längst nicht mehr um eine diskursive Wahrheitsfindung, sondern nur noch ums krampfhafte Recht behalten wollen. Den strittigen Satz aus Ihrem Eingangskommentar hatten Sie ja noch richtig zitiert, aber anstatt jetzt endlich zu liefern, weichen Sie auf ad hominem und Nebenschauplätze aus. SIE haben also wieder einmal die Kontenance verloren und sind auf einem guten Weg nach Alaska.
Die folgenden Diskussionspunkte müssen daher offen bleiben:
1. Sie kaprizieren Ihre Kritik inzwischen lediglich auf den Unterschied zwischen 940 W/m^2 und 962 W/m^2. Die wirkliche Diskrepanz besteht aber zwischen hemisphärischen 940 W/m²*COS(Azimut) ohne THE und globalen 235 W/m² mit THE.
2. Ihr Faktor-2-Fehler hat sich keineswegs ins „Nirwana“ verflüchtigt: Ihre FAKTOR-2-UNGLEICHUNG (E(out,TOA) = E(in,TOA)/2) widerspricht dem Energieerhaltungssatz und würde die sogenannte „gemessene globale Durchschnittstemperatur“ apokalyptisch steigen lassen.
3. Sie kompensieren IHRE EIGENE Unfähigkeit, die Bedeutung Ihrer komischen Durchschnittstemperaturen (A=306K=33°C, B=330K=57°C und C=341K=68°C) für unsere reale Erde zu begründen, indem Sie MIR mindere fachliche Fähigkeiten unterstellen.
4. Die von IHNEN SELBST verlinkten Mondbildchen kommen zum gleichen Ergebnis wie meine hemisphärischen Mond-Berechnungen – und um das nicht zugeben zu müssen, machen SIE SICH jetzt einfach mal einen schlanken Fuß…
Für mich sind Sie kein seriöser Diskussionspartner mehr, Herr Holtz, schämen Sie Sich reichlich!
Herr Agerius, die Erdkugel absorbiert deswegen in 24 Stunden 24h*1/4 S(1-A)*Erdoberfläche=24h* S(1-A)*Erdquerschnitt weil die eine Kugel mit kreisförmigem Querschnitt ist. Wenn Sie das bei Ihrer Auswertung nicht berücksichtigen, wird es falsch.
Herr Petersen,
Und was wollen sie mit dieser Rechnung?
Die richtige Aussage muss lauten: x h *1/2 S(1-A)*Erdoberfläche/2 =x h * S(1-A)*Erdquerschnitt.
Sie koennen jetzt eine Angabe in W/m2 fuer jeden beliebigen Zeitpunkt treffen.
Wenn sie 24 h nehmen, haben sie bei der realexistierenden Erde ein Problem, da durch die Schiefstellung der Erdachse an den meisten Tagen im Jahr nicht die gesamte Erdoberlfläche bestrahlt wird.
Kommentar von A. Agerius aus The Lungs of Gaia
„Der Faktor von 1/2 , Sonneneinstrahlung 1368 / 2, wird auch in “ Kritische Analyse der globalen Klimatheorie, Disproof of basic study of IPCC greenhouse effect, Kiehl und Trenberth 1997, mit Messwerten des ERBS-Satelliten auf einem neuen Modell diskutiert. „, 2019, Verfügbar als eBook bei amazon in USA und Europa. Damit kann die beobachtete globale Erwärmung von ca. 1,2 Kelvin zwischen 1850 und 2018 ohne den Einfluss von CO2 durch langfristige Wolkenveränderung (Albedoveränderung) erklärt werden. Durch die Verwendung von 1/2 in diesem neuen Modell kann nachgewiesen werden, dass ein Treibhauseffekt für unsere Erde mit Messwerten der Satelliten ERBS, TERRA und AQUA CERES) nicht existiert.“
Übersetzt mit http://www.DeepL.com/Translator (kostenlose Version)
Jetzt sollten dann wirklich mal unsere Weltuntergangs Klima Gurus vom PIK um Stellungnahme gebeten werden.
@Petersen
„der Boden mehr Energie in Summe der 24 h abgibt als er nur durch die Sonne bekommt“.
Dann müssten wir alle schon längst am Kältetod gestorben sein und der Erdkern würde auskühlen.
Ihrer Erklärung kann ich nicht folgen.
Herr Petersen kann leider nicht zwischen Energie und Wärme unterscheiden. Ein wichtiger Unterschied wenn man sich mit Thermodynamik auseinandersetzt.
Gucken Sie sich einmal im Lehrbuch die Energiebilanz des Klimasystems an und darin die Energieabgabe des Bodens und wieviel er direkt von der Sonne bekommt.
Empfehle ein Buch der Thermodynamik, das gerade bei Strahlung zwischen Energie und Wärme unterscheidet.
Die Frage die sie sich stellen müssen ist, verliert der Erdboden genausoviel Wärme wie er abstrahlt oder nicht?
Sverre Petersen
19. OKTOBER 2020 UM 14:35
Das ist ja wirklich lustig, dass Sie und Schulz glauben, im KT97 Diagramm Erwärmung zu sehen. Sie können dann ja auch sicher sagen, welche Zahlen welche Erwärmungsrate determinieren, also welche W/m2 Angabe(n) dort führt nach Ihrer Vorstellung zu wieviel Kelvin/Jahr.
Alle, die das Diagramm kapiert haben, sehen, dass die Erwärmungsrate anhand dieser KT97 Werte offensichtlich Null ist (stationär).
Ich habe keine Fragen. Für Sie die Frage wieviel Wärme zwischen Boden und Atmosphäre im KT97 übertragen wird. Nun, das mit dem stätionären Verhältnissen dort müssen Sie vorher noch begreifen, dann kriegen Sie diese Frage vielleicht auch hin. Damit beantwortet sich auch Ihre Frage. Die Antwort ist ganz einfach, wenn man das KT97 kapiert, ich habs auch schon früher erklärt.
Herr Petersen,
wovon reden sie bitte? Sie haben das KT Diagram verstanden? Gut! Geben sie die Wärmeflüsse an!
Wie hoch ist denn der Wärmefluss durch Strahlung von der Atmosphäre in Richtung Oberfläche?
Hier ein schönes Diagram das die Energieflüsse von der Sonne besser als KT darstellt:

Ich habe was gegen Modelle, welche dazu dienen sollen, Zahlenwerte herzustellen. Man kann damit billig und nach Belieben inflationäre Mengen solcher Werte herstellen, eben wie Inflationsgeld.
Das einzige, was taugt, sind wirkliche Meßwerte. Die sind aufwendig, selten und teuer – wie Gold.
@ F. Bluecher
Zitat: Das einzige, was taugt, sind wirkliche Meßwerte. Die sind aufwendig, selten und teuer – wie Gold.
Da haben Sie recht und eine Theorie, die die Messwerte nicht abbilden kann, ist nutzlos. Den Fehler, den alle Theorien oder deren Modelle zu diesem Thema machen ist, ein geometrisches Flächen-Verhältnis auf eine Eingangsgröße anzuwenden, statt auf die wirksame Bezugseinheit der Eingangsgröße.
Es gibt übrigens Messwerte zu diesem Thema.
Mfg
Werner Holtz
Mann oh Mann, was wird in „Return to Earth: A New Mathematical Model of the Earth’s Climate“ nur für ein Unsinn berechnet
Die Kreisflächen-Mittelung ist nicht das Gleiche wie die Kugeloberflächen-Mittelung einer Hemisphäre. Man kann dies erkennen (Beispiel: Randverdunkelung der Sonne), indem man die Fläche von den Regionen eines Kreises und einer Halbkugel mit |x| ≤ 1/2*r bestimmt. Für die Kreisfläche ergibt sich [π/3 + √(3)/2]*r^2, welches ca. 61% vom der Gesamtkreisfläche ausmacht. Für eine Halbkugeloberfläche (Hemisphäre) ergibt sich π*r^2, also genau 50% der Gesamtoberfläche der Halbkugel. Tatsächlich sind bei der Kreisflächen-Mittelung die Pol-Regionen übergewichtet und die äquatorialen Regionen untergewichtet.
Man muss also mit einem Gewichtungsfaktor von π/[π/3 + √(3)/2] rechnen, um eine Kreisflächen-Mittelung auf einer Hemisphäre abzubilden. Damit wurde sich eine Energiestromdichte für die Hemisphäre von 472,27 [W/m^2] * π/[π/3 + √(3)/2] = 775,5 W/m^2 ergeben.
Mfg
Werner Holtz
Das ist zu speziell. Man sollte erst mal beim Fussball bleiben.
Zum Verständnis sehr interessant sind die sich entwickelten, absolut fairen und emotionslosen Diskussionen zu diesem Artikel
https://wattsupwiththat.com/2020/10/22/the-lungs-of-gaia/
(Allerdings auf Englisch)
Verstehen dieser Thematik, oder besser, das Interesse daran sie verstehen zu wollen, von – vorsichtig ausgedrückt – der Mehrzahl der Grünen zu erwarten, halte ich für gleichbedeutend damit, von Affen Verständnis für die Ursachen von Tag und Nacht zu erwarten.
Bitte anderen Texteditor verwenden.
willco – will comply
„Während der Nacht zieht sich die Troposphäre bei ihrer Abkühlung zusammen, wodurch potenzielle Energie wieder in kinetische Energie umgewandelt wird, die für den erhöhten nächtlichen Energieverlust an den Weltraum verantwortlich ist.“
Dieses und die zwei Punkte vorher müsste mir mal jemand genauer erklären.
Erklärt sich doch von selbst: Die Erde atmet. Dann hoffen wir mal, dass sie sich kein Coronavirus und keine Lungenentzündung einfängt.
Am ehesten sollte sie sich mit der Adiabatic auseinandersetzen.
Vorher noch anschauen welche Energieformen es gibt.
Dann noch etwas Theorie der Temperatur.
Die Grundaussage ist, das potentielle Energie der Molekuele die in der Atmosphäre aufsteigen, sich als verringerte kinetische Energie = verringerte Temperatur bemerkbar macht.
Potentielle Energie hat damit keinen Anteil an der abgestrahlten Energie. Insofern wird die Energie gespeichert. Beim Absteigen der Moleküle wird potentielle Energie in kinetische Energie umgewandelt.
Dadurch ist die Temperatur der Atmosphäre beständiger als die einfache Abstrahlungstheorie der Klimaunwissenschaften uns glauben machen wollen.
mfg Werner
ÄÄääähhmmm — Satire?
Nach meinen Insiderinformationen ist das PIK bereits dabei, die für’s bedrohte „Erdatmen“ notwendigen Intensivstationen zu bauen!
Bitte Herr Thumulla, greifen sie zu einem Radiergummi, entfernen sie das Fragezeichen hinter „Satire“ und ersetzen sie dasselbige durch ein !
!SATIRE!
Hier kann man nicht korrigieren.
Im Prinzip alles ganz einfach.
kein mensch kommt af die Idee, für die Berechnung der durchschnittlich gelieferten leistung seines PKW Motors auch die Stunden anzusetzen, in denen der PKW in der Garage stand und der Motor keine Leistung abgab!
Für die Theorie des „Treibhauseffektes“ wird aber genau das getan, man betrachtet einen Zeitraum, in dem die Sonne die eine hälfte der Erde nicht bescheint, als Berechnungsgrundlage uns stellt lapidar fest, die Sonne ist nicht in der Lage, die Erde auf durchschnittlich 15 Grad C zu erwärmen!
Genaugenommen, ergibt dann die Leistungsberechnung für den PKW Motor, dass er überhaupt nicht in de lage ist diesen 2 Tonner auf 200 Km/Stunde zu beschleunigen! Warum kann ich trotzdem über 200 Km/h schnell fahren???
Weil es den“ Autobahnenergie-effekt“ gibt, der für zusätzlich Energie des PKW`S sorgt, nun wer glaubt so etwas – alle Treibhausgläubigen!
Ihre Begründung mittels des Autos ist falsch.
Die Berechnungsgrundlage für das Energiebudget des Klimasystems ist die physikalische Zeit. Die läuft in einem gewählten Inertialsystem streng monoton stetig und linear ab.
Da aber ein zeittranslationsinvariantes, also stationäres, Klimasystem aber Periodizitäten hat, kann man sich auf diese Periode beschränken.
In den Fall hier vernachlässigt man längerperiodische Driften durch Jahresgang und die säkularen Trends durch Klimaänderungen bzw. rezentem Klimawandel und betrachtet das Energiebudget über die Grundperiode 24h.
Wenn man nur die absorbierte Sonnenenergie am Boden betrachtet, so reicht diese allein nicht aus, um die beobachtbare Temperturen zu erklären, bzw. den Tagesgang. Die Diskrepanz findet man, indem der Boden mehr Energie in Summe der 24 h abgibt als er nur durch die Sonne bekommt.
Herr Petersen,
bitte definieren sie „physikalische Zeit“
Welche Periodizität der Temperatur gibt es im Klimasystem und wo befinden wir uns gerade in der Periode?
Können sie die Einstrahlleistung ausserhalb der 24 h berechnen? Eine Periode von 12 h bietet sich an!
Ansonsten erklären sie bitte die Diskrepanz bei der der Boden mehr Energie in Summe der 24 h abgibt als er nur durch die Sonne bekommt. Leugnen sie jetzt also auch die Gegenstrahlung?
Sehr verbunden!
mfg Werner
Genau so ist das!
Den Schweißbrenner versteht Herr Petersen auch nicht.
Aber so sind sie die Akademiker.
Sitzen im Wald und sehen die Bäume nicht und erklären uns den Himmel!