Was soll das alles nun? Ein Tweet über das, was Strogatz „mathematisches Twitter“ nennt. Das Tweet lautete:
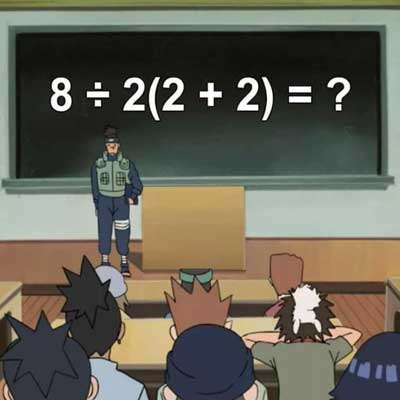
em ♥︎ (@pjmdolI) 28. Juli 2019
Das ist einfach: Die korrekte Antwort lautet:
Jawohl, das stimmt! Die korrekte Antwort lautet: entweder 16 oder 1, abhängig von einem interessanten Aspekt der Mathematik. Das vorgestellte Image vermittelt uns ein paar Einsichten darüber, was hier los ist. Strogatz erklärt es so:
Obige Frage hat eine eindeutige und definitive Antwort – vorausgesetzt, wir richten uns alle nach den gleichen Regeln, welche die „Reihenfolge der Operationen“ vorgeben. Stehen wir wie in diesem Fall davor, verschiedene mathematische Operationen durchzuführen – um Ausdrücke in Klammern zu evaluieren, um Multiplikationen und Divisionen durchzuführen oder Additionen und Subtraktionen – die Reihenfolge der Durchführung dieser Operationen kann einen gewaltigen Unterschied ausmachen.
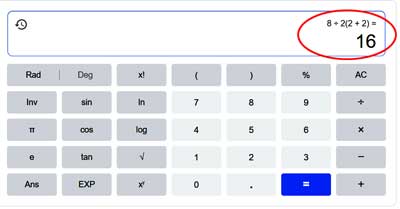
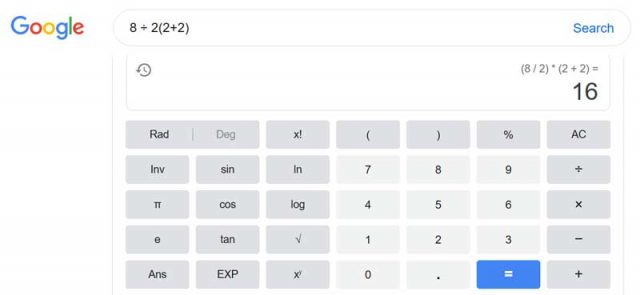
Wenn wir die Taschenrechner heranziehen, zeigt sich, dass meine Antwort absolut korrekt ist:
Der TI-84Plus C von Texas Instruments zeigt das Ergebnis „16”, während der Casio fx-115MS das Ergebnis „1” zeigt.
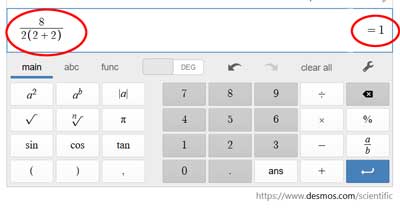
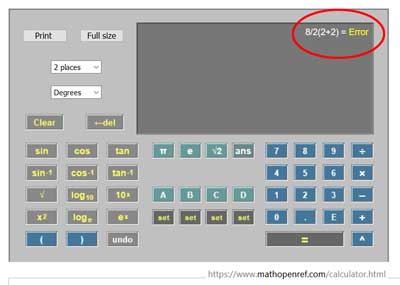
Auch eine rasche Durchsicht des Online-Taschenrechners ergibt gemischte Ergebnisse:
Und vielleicht etwas genauer:
Mathe-Freaks wissen, dass das Problem in der Reihenfolge der Operationen liegt, und es gibt Konventionen hinsichtlich dieser Reihenfolge. In der Schule haben wir eine der folgenden Konventionen gelernt:
BODMAS ist eine Abkürzung. Sie steht für Bracket, Of, Division, Multiplication, Addition und Subtraction. In manchen Regionen ist PEDMAS (Parentheses, Exponents, Division, Multiplication, Addition und Subtraction) das Synonym für BODMAS.
PEMDAS ist eine Abkürzung für die Begriffe Klammern (Parenthesis), Exponenten, Multiplikation, Division, Addition, Subtraktion. Finden sich zwei oder mehr Operationen in einer einzigen Gleichung, gibt die Reihenfolge der Buchstaben in PEMDAS vor, was zuerst berechnet werden muss, was als zweites usw. bis die Rechnung vollständig ist. Falls es Klammern in der Gleichung gibt, sagt PEMDAS, zuerst die Berechnungen innerhalb der Klammern durchzuführen.
Strogatz sagt: „Die strikte Antwort zu dieser elementaren PEMDAS-Konvention ergibt nur eine Antwort: „16“. Oh, aber sein Eingabefeld (his editor) und viele Leser „…bestanden darauf, dass die richtige Antwort ,1′ sei“.
Um Strogatz‘ Ergebnis „16“ zu erhalten, muss man Folgendes machen: 8/2 = 4, dann 4 x (2+2) oder 4 x 4 = 16.
Wie man das Ergebnis „1“ bekommt, erklärt Strogatz so:
Was war da los? Nach der Lektüre der vielen Kommentare zu dem Beitrag erkannte ich, dass die meisten Kommentatoren eine andere (und anspruchsvollere) Konvention als die elementare PEMDAS-Konvention bemühen, die ich in dem Artikel beschrieben habe.
In dieser anspruchsvolleren Konvention, die oftmals in der Algebra Anwendung findet, wird einer impliziten Multiplikation höhere Priorität eingeräumt als einer expliziten Multiplikation oder expliziten Division, in welchen jene Operatoren aus Symbolen bestehen wie x; *; / oder ÷. Unter dieser anspruchsvolleren Version wird der impliziten Multiplikation in 2(2+2) höhere Priorität eingeräumt als in der expliziten Division in 8÷2(2+2). Mit anderen Worten, 2(2+2) sollte zuerst evaluiert werden. Dann ergibt sich 8÷2(2+2) = 8÷8 = 1. Nach der gleichen Regel, so argumentierten viele Kommentatoren, ist der Term 8÷2(4) nicht synonym mit 8÷2×4, weil die Klammern die sofortige Berechnung verlangen, was wiederum 8÷8 = 1 ergibt.
Falls also jedermann den gleichen Konventionen folgt, und zwar sowohl bei der Konstruktion von Gleichungen als auch bei deren Lösung, wäre alles in Ordnung und wir würden alle die von uns erwartete Antwort bekommen.
Aber…:
Diese (anspruchsvollere) Konvention ist sehr vernünftig, und ich stimme zu, dass die Antwort dann ,1′ ist, falls wir alle dieser Konvention folgen. Aber das ist eben allgemein nicht der Fall. Die Taschenrechner von Google und WolframAlpha benutzen die elementarere Konvention und unterscheiden nicht zwischen impliziter und expliziter Multiplikation, wenn sie darauf programmiert werden, einfache arithmetische Terme zu berechnen.
Und außerdem, nachdem Google und WolframAlpha evaluierten, was immer in Klammern steht, löschen sie diese Klammern effektiv und stellen deren Inhalt nicht höher in der Priorität. Im Einzelnen interpretieren sie 8÷2(2+2) als 8÷2x(2+2) und behandeln dies synonym mit 8÷2×4. Dann haben gemäß PEMDAS Division und Multiplikation die gleiche Priorität. Also rechnet man von links nach rechts und erhält 8÷2×4 = 4×4 und kommt zum Ergebnis 16. Für meinen Beitrag habe ich mich entschieden, mich auf diese einfachere Konvention zu konzentrieren.
Unser werter Mathematiker folgert:
Genauso ist es wesentlich, dass jeder, der Software für Computer, Tabellen und Taschenrechner schreibt, die Regeln der Reihenfolge von Operationen kennt und diesen folgt.
Aber ich habe schon gezeigt, dass die Software-Schreiber nicht alle den gleichen Konventionen folgen … Strogatz weist darauf hin, dass selbst anspruchsvolle Software wie WolframAlpha und Google nicht den anspruchsvollen Regeln folgen und „16“ erhalten.
Das finale Statement von Strogatz lautet: „Einige Tabellen-Kalkulationen und Software-Systeme weigern sich schlicht und ergreifend, die Frage zu beantworten – sie schrecken vor der verstümmelten Natur zurück. Das ist auch mein Gefühl sowie das Gefühl der meisten Mathematiker, mit denen ich gesprochen habe. Falls man eine eindeutigere Antwort haben will, dann stelle man eine eindeutigere Frage.
Kenneth Change von der NY Times schrieb jüngst dazu den Beitrag „Essay: Why Mathematicians Hate That Viral Equation“.
—————————
Vielleicht findet der eine oder andere diesen Beitrag instruktiv oder erheiternd. Die wirkliche Krux des Ganzen ist, dass der ursprüngliche Term „8÷2(2+2) absichtlich so schlecht formuliert worden ist, damit er unklar bleibt.
Aber was soll das Ganze jetzt? Nun, es erhebt sich eine sehr ernste Frage: Falls einfache mathematische Gleichungen mit verschiedenen Antworten interpretiert werden können oder verschiedene Lösungen ergeben, abhängig von der Reihenfolge der Operationen und unter der Vorgabe, dass selbst ernste mathematische Software verschiedenen Konventionen folgt – welches der sehr anspruchsvollen mathematischen Modelle, in denen die Variablen alle voneinander abhängig sind, muss iterativ gelöst werden?
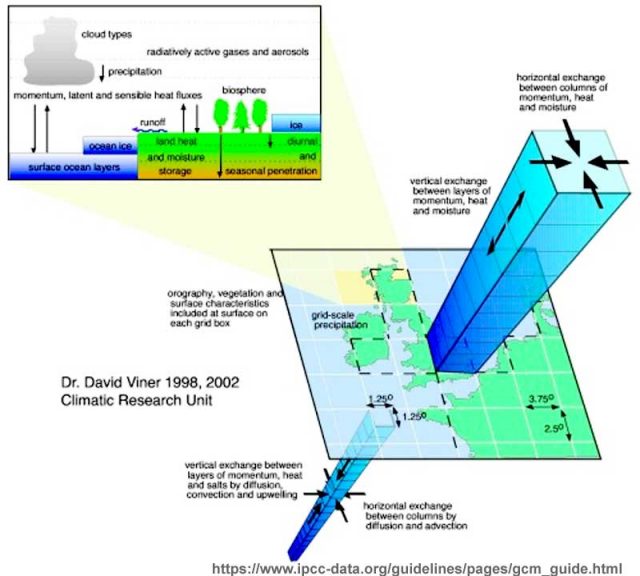
Was die Klimawissenschaft betrifft – werden unterschiedliche zukünftige Klima-Szenarien simuliert, falls jemand die Reihenfolge der Berechnung ändert? Nicht in dem einfachen Sinn dieser viralen Twitty-Gleichung, sondern in einem erheblich ernsteren Zusammenhang: Sollte ein Klimamodell, ein General Circulation Model, erst nach Temperatur auflösen? Oder nach Luftdruck? Oder zunächst die einfallende Strahlung berücksichtigen? Das IPCC-Diagramm sieht so aus:
Ich versuchte, die Anzahl der Variablen zu zählen, die in diesem vereinfachten Diagramm auftauchen, und kam auf ein paar Dutzend – bevor ich erkannte, dass es zu vereinfacht war, um eine reale Anzahl zu liefern. Wo beginnt das Modell mit jeder Iteration? Spielt es eine Rolle, mit welcher Variablen es anfängt? Ergibt die Reihenfolge der Berechnungen vereinfachter Versionen der nicht-linearen Gleichungen einen Unterschied hinsichtlich der Ergebnisse?
Das muss es – würde ich denken.
Rechnen alle GCMs der westlichen Welt in der gleichen Reihenfolge? Was ist mit den zumeist unabhängigen russischen Modellen (INM-CM4 and 5)? Ergeben die russischen Modelle realistischere Ergebnisse, weil sie die mathematischen Operationen mit einer anderen Reihenfolge durchführen?
Ich weiß es nicht – aber es ist eine schreckliche Frage.
Link: https://wattsupwiththat.com/2019/08/07/howd-they-calculate-that/
Übersetzt von Chris Frey EIKE
Bemerkung des Übersetzers: Mit der einfachen Gleichung oben werde ich mal „hausieren“ gehen, mal sehen, was so kommt. Aber mir kam ein ganz anderer Gedanke: Da die CO2-Geschichte ja rein politischer Propaganda-Natur ist, wird man sicher die Reihenfolge der Rechnungen so gewählt haben, dass das Gewünschte herauskommt. Wie ist das eigentlich bei den kurz- und mittelfristigen Wettervorhersagemodellen (GFS, EZMW, ICON usw.)?



















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"„Peter Puschner, Prof. Dr.-Ing.
Das Problem liegt einfach in der unbestimmten Gleichung, welche den Term „2“ nicht eindeutig der Operation als Divisor der 8 oder als Faktor der Klammer (2+2) zuweist.“
Das sehe ich nicht so.
Das Fehlen eines Operators vor der Klammer weist die 2 eindeutig als Faktor des Klammerausdrucks aus.
Bei einer Gleichung wie y = 4 ÷ 2x kommt ja auch niemand auf die Idee, die 2 als Divisor der 4 zu behandeln.
In Memoriam „Josef Filser“, literarische Figur von Ludwig Thoma (bayerischer Dichter):
oiso – des is ganz oafch, da nimmt ma d Finga und zoit zamma no kimmt zehne raus und des is z vui. Wenn ma de Damma (Daumen) weglast bleim Achte üba. Jetzat werds kompliziert. Do san zwoa Zeigefinga, zwoa Middlfinga, zwoa Ringfinga und zwoa kloane Finga. Mir ham zwoa Hend und wann ma obzät san des wirkli 10 Finga.
Beim Jagaloisl stimmt des net, der hat si an linka Damma wegschnin beim brotscheidn. Wamma na mit da rechtn Hand e linkn Finga zait ohne Damma kimmt fiere raus und bei da rechtn hand des gleiche. Jetzat is scho oafacha. Denn ma hot zwoamoi viere und des gibt wahrscheinli achte.I hob unsan hochwürn Herrn Pfarrer gfrogt und de sogts gleiche – dann muas stimma.
Robert Kümmel
Passend dazu folgende Aufgabe:
230-220*1/2=?
Die Antwort lautet 5! Warum das trotz Punkt-vor-Strich-Regel richtig ist:
https://www.spektrum.de/kolumne/das-versteckte-mathematische-zeichen/1667294
Hinter der 5! (5Fakultät) fehlt im Text der Punkt.
Lustig. Erinnert mich an einen vor langer Zeit gelesenen Witz mit Physiker und Mathematiker, die irgendwie Wasser zum Kochen bringen sollen, aber irgendwas Entscheidendes fehlt. Das Wasser ist kalt und das Feuer brennt nicht. Keiner schafft die Aufgabe, aber der Mathematiker stellt den Wassertopf auf die kalte Feuerstelle und hat damit zumindest mal zwei Probleme auf eines reduziert.
Wir wissen doch alle, dass diese ganze Computerrechnerei für die Katz ist, weil das CO2 nichts für‘s Klima kann. Mir ist es, ehrlich gesagt, völlig wurscht, welchen Term die mit ihrer geballten Rechnerkapazität (die jede Menge Energie vergeudet!) zuerst nicht sinnvoll auflösen. Iterieren ist menschlich?
Alles falsch!
8:2(2+2) = 8:2*(2+2) = 8:(2+2)*2 = 8:4*2 = 2*2 = 4
… also weder 16 noch 1.
(Faktoren eines Produkts sind in der Reihenfolge der Berechnung beliebig!)
Das Problem liegt einfach in der unbestimmten Gleichung, welche den Term „2“ nicht eindeutig der Operation als Divisor der 8 oder als Faktor der Klammer (2+2) zuweist.
…. 😉 … und ich hatte Mathe bisher für das „interpretationsfreieste“ Fach gehalten …., aber mit der entsprechenden „Hinterfotzigkeit“ kann man der Mathematik auch karnevalistische Züge verleihen. .. wenn es nicht so ernst wäre ….
Ach du meine Güte, wieder so ein Rummel um simple Arithmetik. Es sind hier drei einfache Regeln (ich glaube, 3. Klasse in der DDR-Schule) anzuwenden. Erstens Strichrechnung geht vor Punktrechnung. Zweitens in Klammer Gesetztes zuerst auflösen. Drittens bei gleichen Rechenzeichen (Punkte oder Striche) gilt von links nach rechts rechnen. Also: zuerst Klammer: 2 plus 2 ist 4. Dann steht dort: 8 : 2 . 4 = (Punkt vor Strich fällt weg), dann von links nach rechts rechnen. 8 durch 2 ist 4 mal 4 ist 16. Ganz einfach.
So und nicht anders. Daraus einen langen Artikel zu machen, um Zweifel an Mathematik und darauf basierenden Berechnungen zu streuen, sagt alles über EIKE. Man diskutiert selbst über eindeutig belegtes, um Zweifel am menschgemachten Klimawandel unter der einfachen Bevölkerung zu streuen.
Nichts ist belegt!
„So und nicht anders.“
Das stimmt zwar nicht, aber Sie hören sich ganz wichtig an.
„… unter der einfachen Bevölkerung zu streuen.“
Noch einfacher als Sie? Bitte, bitte versuchen Sie zu denken und plappern Sie nichts nach, nur weil es Ihnen gerade in den Kram passt!
Sie haben die Klammer aufgelöst und dann von links nach rechts gerechnet. Ganz toll. Das, was Sie davor geschrieben haben, stimmt nicht.
Warum wohl?
„Erstens Strichrechnung geht vor Punktrechnung.“
Aua, aua!
Ersetzt man das Divisionszeichen durch einen Bruchstrich, ist der Lösungsweg eindeutig.
Wenn die Aufgabe so gelöst wird wie sie zu sehen ist, ist die Lösung ist 16.
Man löst die Klammer auf und da es sich um gleichwertige Rechenzeichen handelt rechnet man von links nach rechts.
Richtig. In der Technik (Divisionszeichen gibt es in keiner Formelsammlung) arbeitet man nur mit Bruchstrichen dadurch ist der Rechenweg eindeutig definiert. Als Techniker gibt es nur eine Lösung = 1
Super!
Wenn man die m.E. falsche oder zumindest unklare Schreibweise verwendet, kann das Ergebnis auch nicht eindeutig sein. Bei eindeutiger Schreibweise wären alle Unklarheiten beseitigt.
8:2x(2+2)=16
8:(2x(2+2))=1
untere Version ist identisch mit der Darstellung des *durch* als Bruchstrich.
Unsinn, manche Systeme setzen ein * (mal, x), wenn es fehlt. Man kann es nicht immer weglassen! Man sollte IMMER vollständig hinschreiben, was man will, um Fehlinterpretationen zu vermeiden und die Lesbarkeit zu erhalten. Übrigens wird von links nach rechts gerechnet, ansonsten wären zusätzliche Klammern zu setzen, 8/(2*(2+2)) — aber das steht eben nicht da.
Fehlende Rechenzeichen und fehlende Klammern — keine Ausrede. Kein Wunder, daß der Parser da Mist versteht.
Aber wenn die (Klima)Modelle an so etwas scheitern…
Nein, das tun sie nicht. Funktionen und Module werden geprüft, getestet, freigegeben, im größeren Rahmen getestet, wieder freigegeben…
Wir sind nicht mehr im Zeitalter des Pentiumfehlers — oder doch?
Im Zeitalter des Klimawahns sind wir jetzt!.
Faule Ausrede! Andere Berechnungen scheitern ja auch nicht.
Carsten
—
Demagogie schlägt Demokratie
Ich habe Probleme, das Problem zu verstehen: Nach den Regeln aller (höheren) Computersprachen, die ich kenne, ist das Ergebnis eindeutig:
8/2*(2+2) = 16
8/(2*(2+2)) = 1
Die schlecht, weil bewußt irreführende, Aufgabe taugt nicht zur Illustration der (gegenwärtigen) Unmöglichkeit von Klimaprognosen. So, als ob man einen Kinderroller zu Rate zieht hinsicht von Wurmloch-Reisen.
Genau so ist es! Treffer und versenkt.