Wie haben sie das berechnet?
Was soll das alles nun? Ein Tweet über das, was Strogatz „mathematisches Twitter“ nennt. Das Tweet lautete:
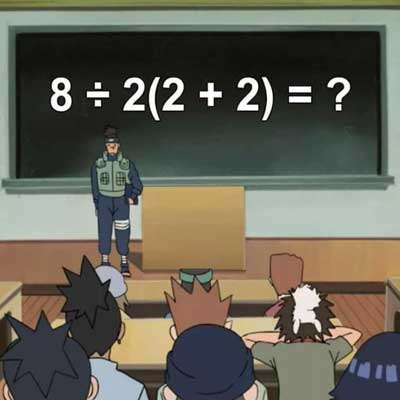
em ♥︎ (@pjmdolI) 28. Juli 2019
Das ist einfach: Die korrekte Antwort lautet:
Jawohl, das stimmt! Die korrekte Antwort lautet: entweder 16 oder 1, abhängig von einem interessanten Aspekt der Mathematik. Das vorgestellte Image vermittelt uns ein paar Einsichten darüber, was hier los ist. Strogatz erklärt es so:
Obige Frage hat eine eindeutige und definitive Antwort – vorausgesetzt, wir richten uns alle nach den gleichen Regeln, welche die „Reihenfolge der Operationen“ vorgeben. Stehen wir wie in diesem Fall davor, verschiedene mathematische Operationen durchzuführen – um Ausdrücke in Klammern zu evaluieren, um Multiplikationen und Divisionen durchzuführen oder Additionen und Subtraktionen – die Reihenfolge der Durchführung dieser Operationen kann einen gewaltigen Unterschied ausmachen.
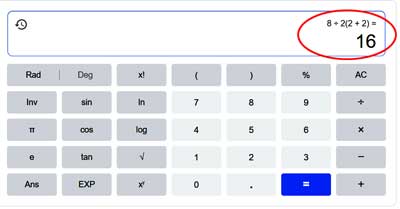
Wenn wir die Taschenrechner heranziehen, zeigt sich, dass meine Antwort absolut korrekt ist:
Der TI-84Plus C von Texas Instruments zeigt das Ergebnis „16”, während der Casio fx-115MS das Ergebnis „1” zeigt.
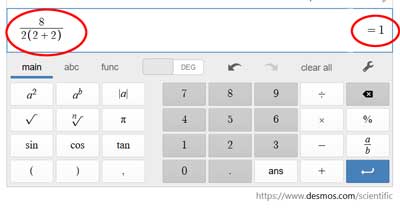
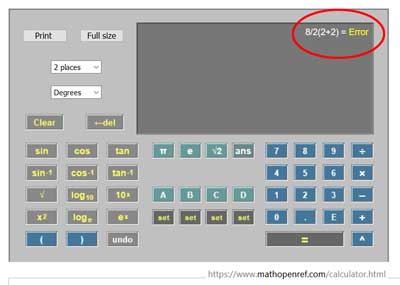
Auch eine rasche Durchsicht des Online-Taschenrechners ergibt gemischte Ergebnisse:
Und vielleicht etwas genauer:
Mathe-Freaks wissen, dass das Problem in der Reihenfolge der Operationen liegt, und es gibt Konventionen hinsichtlich dieser Reihenfolge. In der Schule haben wir eine der folgenden Konventionen gelernt:
BODMAS ist eine Abkürzung. Sie steht für Bracket, Of, Division, Multiplication, Addition und Subtraction. In manchen Regionen ist PEDMAS (Parentheses, Exponents, Division, Multiplication, Addition und Subtraction) das Synonym für BODMAS.
PEMDAS ist eine Abkürzung für die Begriffe Klammern (Parenthesis), Exponenten, Multiplikation, Division, Addition, Subtraktion. Finden sich zwei oder mehr Operationen in einer einzigen Gleichung, gibt die Reihenfolge der Buchstaben in PEMDAS vor, was zuerst berechnet werden muss, was als zweites usw. bis die Rechnung vollständig ist. Falls es Klammern in der Gleichung gibt, sagt PEMDAS, zuerst die Berechnungen innerhalb der Klammern durchzuführen.
Strogatz sagt: „Die strikte Antwort zu dieser elementaren PEMDAS-Konvention ergibt nur eine Antwort: „16“. Oh, aber sein Eingabefeld (his editor) und viele Leser „…bestanden darauf, dass die richtige Antwort ,1′ sei“.
Um Strogatz‘ Ergebnis „16“ zu erhalten, muss man Folgendes machen: 8/2 = 4, dann 4 x (2+2) oder 4 x 4 = 16.
Wie man das Ergebnis „1“ bekommt, erklärt Strogatz so:
Was war da los? Nach der Lektüre der vielen Kommentare zu dem Beitrag erkannte ich, dass die meisten Kommentatoren eine andere (und anspruchsvollere) Konvention als die elementare PEMDAS-Konvention bemühen, die ich in dem Artikel beschrieben habe.
In dieser anspruchsvolleren Konvention, die oftmals in der Algebra Anwendung findet, wird einer impliziten Multiplikation höhere Priorität eingeräumt als einer expliziten Multiplikation oder expliziten Division, in welchen jene Operatoren aus Symbolen bestehen wie x; *; / oder ÷. Unter dieser anspruchsvolleren Version wird der impliziten Multiplikation in 2(2+2) höhere Priorität eingeräumt als in der expliziten Division in 8÷2(2+2). Mit anderen Worten, 2(2+2) sollte zuerst evaluiert werden. Dann ergibt sich 8÷2(2+2) = 8÷8 = 1. Nach der gleichen Regel, so argumentierten viele Kommentatoren, ist der Term 8÷2(4) nicht synonym mit 8÷2×4, weil die Klammern die sofortige Berechnung verlangen, was wiederum 8÷8 = 1 ergibt.
Falls also jedermann den gleichen Konventionen folgt, und zwar sowohl bei der Konstruktion von Gleichungen als auch bei deren Lösung, wäre alles in Ordnung und wir würden alle die von uns erwartete Antwort bekommen.
Aber…:
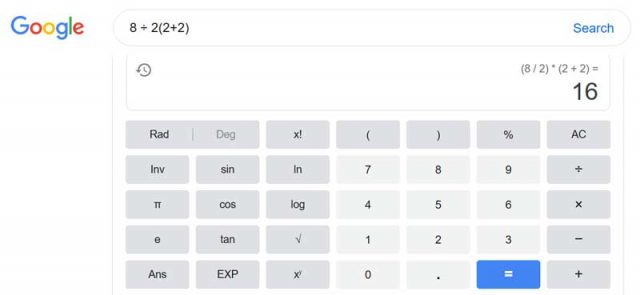
Diese (anspruchsvollere) Konvention ist sehr vernünftig, und ich stimme zu, dass die Antwort dann ,1′ ist, falls wir alle dieser Konvention folgen. Aber das ist eben allgemein nicht der Fall. Die Taschenrechner von Google und WolframAlpha benutzen die elementarere Konvention und unterscheiden nicht zwischen impliziter und expliziter Multiplikation, wenn sie darauf programmiert werden, einfache arithmetische Terme zu berechnen.
Und außerdem, nachdem Google und WolframAlpha evaluierten, was immer in Klammern steht, löschen sie diese Klammern effektiv und stellen deren Inhalt nicht höher in der Priorität. Im Einzelnen interpretieren sie 8÷2(2+2) als 8÷2x(2+2) und behandeln dies synonym mit 8÷2×4. Dann haben gemäß PEMDAS Division und Multiplikation die gleiche Priorität. Also rechnet man von links nach rechts und erhält 8÷2×4 = 4×4 und kommt zum Ergebnis 16. Für meinen Beitrag habe ich mich entschieden, mich auf diese einfachere Konvention zu konzentrieren.
Unser werter Mathematiker folgert:
Genauso ist es wesentlich, dass jeder, der Software für Computer, Tabellen und Taschenrechner schreibt, die Regeln der Reihenfolge von Operationen kennt und diesen folgt.
Aber ich habe schon gezeigt, dass die Software-Schreiber nicht alle den gleichen Konventionen folgen … Strogatz weist darauf hin, dass selbst anspruchsvolle Software wie WolframAlpha und Google nicht den anspruchsvollen Regeln folgen und „16“ erhalten.
Das finale Statement von Strogatz lautet: „Einige Tabellen-Kalkulationen und Software-Systeme weigern sich schlicht und ergreifend, die Frage zu beantworten – sie schrecken vor der verstümmelten Natur zurück. Das ist auch mein Gefühl sowie das Gefühl der meisten Mathematiker, mit denen ich gesprochen habe. Falls man eine eindeutigere Antwort haben will, dann stelle man eine eindeutigere Frage.
Kenneth Change von der NY Times schrieb jüngst dazu den Beitrag „Essay: Why Mathematicians Hate That Viral Equation“.
—————————
Vielleicht findet der eine oder andere diesen Beitrag instruktiv oder erheiternd. Die wirkliche Krux des Ganzen ist, dass der ursprüngliche Term „8÷2(2+2) absichtlich so schlecht formuliert worden ist, damit er unklar bleibt.
Aber was soll das Ganze jetzt? Nun, es erhebt sich eine sehr ernste Frage: Falls einfache mathematische Gleichungen mit verschiedenen Antworten interpretiert werden können oder verschiedene Lösungen ergeben, abhängig von der Reihenfolge der Operationen und unter der Vorgabe, dass selbst ernste mathematische Software verschiedenen Konventionen folgt – welches der sehr anspruchsvollen mathematischen Modelle, in denen die Variablen alle voneinander abhängig sind, muss iterativ gelöst werden?
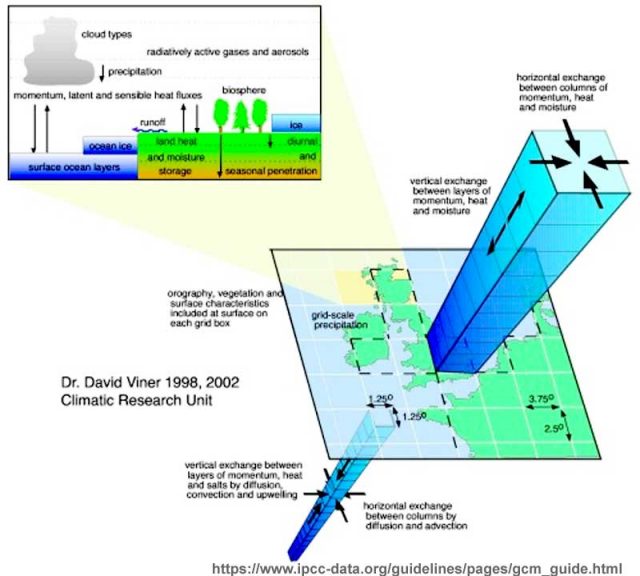
Was die Klimawissenschaft betrifft – werden unterschiedliche zukünftige Klima-Szenarien simuliert, falls jemand die Reihenfolge der Berechnung ändert? Nicht in dem einfachen Sinn dieser viralen Twitty-Gleichung, sondern in einem erheblich ernsteren Zusammenhang: Sollte ein Klimamodell, ein General Circulation Model, erst nach Temperatur auflösen? Oder nach Luftdruck? Oder zunächst die einfallende Strahlung berücksichtigen? Das IPCC-Diagramm sieht so aus:
Ich versuchte, die Anzahl der Variablen zu zählen, die in diesem vereinfachten Diagramm auftauchen, und kam auf ein paar Dutzend – bevor ich erkannte, dass es zu vereinfacht war, um eine reale Anzahl zu liefern. Wo beginnt das Modell mit jeder Iteration? Spielt es eine Rolle, mit welcher Variablen es anfängt? Ergibt die Reihenfolge der Berechnungen vereinfachter Versionen der nicht-linearen Gleichungen einen Unterschied hinsichtlich der Ergebnisse?
Das muss es – würde ich denken.
Rechnen alle GCMs der westlichen Welt in der gleichen Reihenfolge? Was ist mit den zumeist unabhängigen russischen Modellen (INM-CM4 and 5)? Ergeben die russischen Modelle realistischere Ergebnisse, weil sie die mathematischen Operationen mit einer anderen Reihenfolge durchführen?
Ich weiß es nicht – aber es ist eine schreckliche Frage.
Link: https://wattsupwiththat.com/2019/08/07/howd-they-calculate-that/
Übersetzt von Chris Frey EIKE
Bemerkung des Übersetzers: Mit der einfachen Gleichung oben werde ich mal „hausieren“ gehen, mal sehen, was so kommt. Aber mir kam ein ganz anderer Gedanke: Da die CO2-Geschichte ja rein politischer Propaganda-Natur ist, wird man sicher die Reihenfolge der Rechnungen so gewählt haben, dass das Gewünschte herauskommt. Wie ist das eigentlich bei den kurz- und mittelfristigen Wettervorhersagemodellen (GFS, EZMW, ICON usw.)?