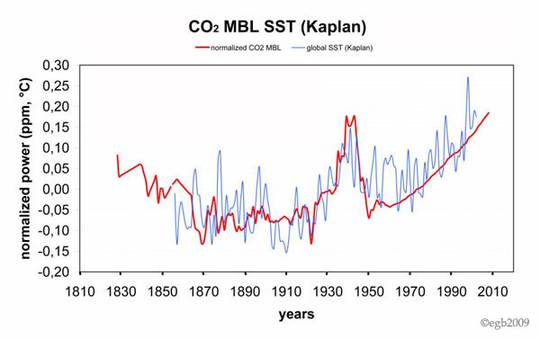
Mit ein paar bemerkenswerten Ausnahmen sind die Schlussfolgerungen in nahezu allen Studien ähnlich derjenigen von Liu und Rodriguez (2005) aus ihrem Abstract:
Mit der Anwendung ökonometrischer Verfahren zur Auswahl von I(1) und I(2)-Trends fanden wir das Vorhandensein von statischen, langfristigen Steady-State- und dynamischen langfristigen Steady-State-Beziehungen zwischen Temperatur und Strahlungsantrieb durch die Sonneneinstrahlung sowie einen Satz von drei Treibhausgas-Reihen.
Vielen WUWT-Lesern werden die von mir angesprochenen Probleme der CO2-Daten vor 1958 kennen. Ziel dieses Essays ist es zu erklären, wie die Datenprobleme vieles der statistischen Forschung hinfällig machen, die hinsichtlich einer Beziehung zwischen atmosphärischen CO2-Konzentrationen und der globalen mittleren Temperatur durchgeführt worden sind. Ich vermute, dass viele der in diese Forschungen involvierten Ökonomen nicht in vollem Umfang die Natur der Daten ermessen können, mit denen sie umgegangen sind.
Die üblichen Quellen atmosphärischer CO2-Daten seit 1958 sind Messungen des Scripps Institute of Oceanography und der NOAA am Mauna Loa, der Antarktis und anderswo. Diese Daten wurden auf monatlicher Basis erstellt, manchmal häufiger, und stellen so ein gutes Niveau zeitlicher Genauigkeit her zum Vergleich der jährlichen mittleren CO2-Konzentrationen mit den globalen mittleren Temperaturen.
Unglücklicherweise gab es vor 1958 nur sporadisch direkte Messungen der atmosphärischen CO2-Konzentrationen. Ernst-Georg Beck sammelte viele der Daten vor 1958 und hat sie auf seiner Website veröffentlicht.

Die meisten Forscher, die die Beziehungen zwischen Treibhausgasen und Temperatur vor 1958 untersucht haben, griffen auf antarktische Eisbohrkerne zurück, die Etheridge et al. (1966) zur Verfügung gestellt hatten. Etheridge maß die CO2-Konzentration der im Bohrkern eingeschlossenen Luftbläschen, und zwar in drei Bohrkernen am Law Dome, die bis zu einer Tiefe von 200 bis 2000 Metern reichten.
Es gab viele veröffentlichte Studien durch verschiedene Forscher, die die CO2-Konzentrationen vor 1958 von Etheridge verwendet haben. Unter jüngeren statistischen Studien auf der Basis der Etheridge-Daten finden sich Liu & Rodriguez (2005), Kaufmann, Kauppi & Stock (2006a), Kaufman, Kauppi, & Stock (2006b), Kaufmann, Kauppi, & Stock (2010), Beenstock, Reingewertz, & Paldor (2012), Kaufmann, Kauppi, Mann, & Stock (2013) und Pretis & Hendry (2013). In jeder einzelnen dieser Studien werden die Etheridge-Daten vor 1958 so behandelt, als seien sie jährliche Angaben zu der atmosphärischen CO2-Konzentration.
Eine Untersuchung von Etheridges Studie enthüllt, dass die Daten nur 26 Messungen von Luftbläschen umfassen, genommen zu verschiedenen Zeiten in der relevanten Periode von 1850 bis 1957. Außerdem stellt Etheridge in seiner Studie eindeutig fest, dass die Luftbläschen aus den Eisbohrkernen ein Altersbereich haben, der mindesten 10 bis 15 Jahre umfasst. Man hat den zeitlichen Rahmen weiter vergrößert durch das Einpassen eines „Glättungsprofils“ mit einem Zeitfenster von 20 Jahren. So geschehen mit Daten aus zwei der Bohrkerne, um jährliche Schätzungen des atmosphärischen CO2 zu erhalten. Diese Jahresschätzungen, die die Grundlage bilden für die Daten von 1850 bis 1957 auf der GISS-Website, können brauchbar gewesen sein für jede Absicht, die Etheridge verfolgt hat, sind aber total ungeeignet für Tests statistischer Zeitreihen, die in den o. g. Studien durchgeführt worden waren. Die Ergebnisse der Tests mit den Daten vor 1958 sind fast mit Sicherheit falsch.

Details der Daten aus den Eisbohrkernen nach Etheridge et al. (1996)

Etheridge hat an der Stelle Law Dome in der Ostantarktis zwischen 1987 und 1993 drei Bohrkerne gezogen. Die Kerne wurden gekennzeichnet als DE08 (bis zu einer Tiefe von 234 Metern), DE08-2 (243 Meter) und DSS (1200 Meter). Dann nahmen sie sich die in den Bohrkernen in verschiedenen Tiefen eingeschlossenen Luftbläschen vor, um zu bestimmen, wie viel CO2 sich in der Atmosphäre befand zu verschiedenen Zeitpunkten in der Vergangenheit. Sie bestimmten das Alter des Eises und dann dasjenige der im Eis eingeschlossenen Luftbläschen. Etheridge schreibt:
Die vom Eis eingeschlossene Luft weist eine Alters-Spannbreite auf infolge diffuser Durchmischung und nur allmählichem Einschluss des Bläschens … Die Mehrheit der Luftbläschen findet sich bei größerer Dichte und Tiefe. Schwander und Stauffer (1984) stellten fest, dass etwa 80% aller Blaseneinschlüsse bei Firndichten zwischen 795 und 830 kg/m³ erfolgten. Messungen der Durchlässigkeit im DE08-2 zeigen eine Bandbreite von 790 und 825 kg/m³, was mit einer Dauer von 8 Jahren korrespondiert in den Bohrkernen DE08 und DE08-2 und etwa 21 Jahre bei DSS. Falls sich nach dem Einschluss keine Luft mehr in die Tiefe mischt, ergibt sich die Altersbandbreite hauptsächlich aus der Diffusion, geschätzt aus Diffusionsmodellen etwa 10 bis 15 Jahre. Falls sich eine kleine Menge Luft nach dem Einschluss in die Tiefe mischt, würde die Dauer des Einschluss der Blase eine größere Rolle spielen bei der Ausweitung der Altersbandbreite. Man kann unten sehen, dass allein durch Diffusion eine größere Altersbandbreite als erwartet erforderlich ist, um die beobachteten CO2-Differenzen zwischen den Bohrkernen zu erklären.
Mit anderen Worten, Etheridge ist sich nicht sicher hinsichtlich der genauen Datierung der Luftbläschen in den Bohrkernen. Der graduelle Einschluss der Luftbläschen hat eine Altersbandbreite von 8 Jahren verursacht bei den Bohrkernen DE08 und DE08-2, und Diffusion sorgte für eine Altersbandbreite zwischen 10 und 15 Jahren. Die Ergebnisse von Etheridge aus den Bohrkernen DE08 und DE08-2 folgen hier (aus ihrer Tabelle 4):
Etheridge Tabelle 4: Bohrkern DE08

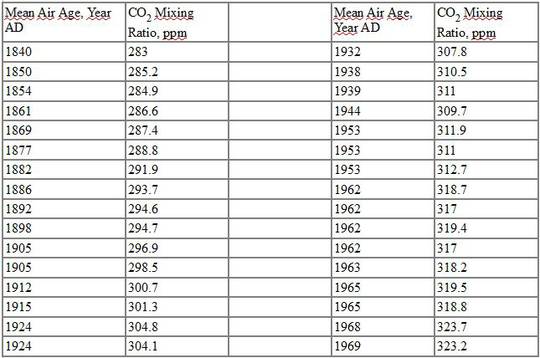
Bohrkern DE08-2

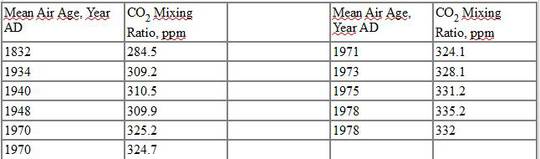
Wegen der Problematik von diffuser Durchmischung und graduellem Einschluss der Luftbläschen zeigen alle diese Zahlen lediglich eine Schätzung der mittleren CO2-Konzentration über einen Zeitraum, der 15 Jahre oder länger sein kann. Falls die Verteilung des Alters der Luft symmetrisch um dieses mittlere Alter verteilt ist, kann der Schätzwert von 310,5 ppm aus dem Bohrkern DE08 für den Zeitpunkt 1938 auch Luft enthalten aus den Jahren 1930 bzw. 1946.
Etheridge kombinierte die Schätzungen aus den Bohrkernen DE08 und DE08-2 und passte eine 20-jährige Glättungskurve an die Daten an, um jährliche Schätzungen der CO2-Konzentrationen zu erhalten. Diese können hier betrachtet werden. Diese jährlichen Schätzungen, die tatsächlich gleitende Mittelwerte über 20 Jahre oder mehr sind, wurden von Dr. Makiko Sato verwendet, der damals für NASA-GISS gearbeitet hatte, um eine jährliche Zeitreihe der CO2-Konzentrationen zusammenzustellen für den Zeitraum von 1850 bis 1957. Dr. Sato nutzte direkte Messungen des CO2 vom Mauna Loa und anderswo für den Zeitraum von 1958 bis heute. Er bezieht sich auf die Eisbohrkern-Daten von Etheridge auf jener Website und fügt hinzu, dass sie „für ein globales Mittel adjustiert worden sind“. Einige der Studien, die sich auf die Daten der Website von GISS beziehen, findet man hier.
Ich habe Dr. Sato (der jetzt an der Columbia University tätig ist) eine E-Mail geschrieben und ihn gefragt, ob er die Zahlen aus der 20-jährigen Glättungskurve von Etheridge genommen hatte und was genau er gemacht hat, um die Werte für ein globales Mittel zu adjustieren. Er antwortete, dass er sich nicht daran erinnern könne, was er gemacht hatte, aber jetzt präsentiert er die gleichen Daten vor dem Jahr 1958 auf der Website der Columbia University hier.
Ich glaube, dass Dr. Satos Daten aus den Zahlen von der 20-jährigen Glättungskurve von Etheridge abgeleitet sind. Für jedes Jahr von 1850 bis 1957 liegen sie weniger als 1 ppm auseinander. Wegen der großen zeitlichen Ungenauigkeit der CO2-Schätzungen in den vom Eis eingeschlossenen Luftbläschen, die durch die Verwendung der 20-jährigen Glättungskurve noch verschlimmert wurde, haben wir nur grobe gleitende Mittelwert-Schätzungen der CO2-Konzentration in der Luft für jedes Jahr und eben keine präzisen jährlichen Schätzungen. Der Schätzwert von 311,3 ppm für das Jahr 1950, der auf den Websites von GISS und Columbia angegeben wird, kann beispielsweise Luft aus dem Jahr 1922 bzw. aus dem Jahr 1978 enthalten. Das Anpassen der Glättungskurve kann für die Ziele von Etheridge absolut akzeptabel sein, aber wie wir sehen werden, ist es vollständig inakzeptabel für die Verwendung in den zuvor erwähnten Tests statistischer Zeitreihen.

Empirische Studien, die die Etheridge’schen Eiskerndaten vor 1958 verwenden

Wie in der Einführung erklärt, gibt es eine Anzahl statistischer Studien, die versuchen, eine Relation zwischen Treibhausgasen und globaler mittlerer Temperatur herzustellen. Unter diesen Forschern befanden sich Klimatologen, Ökonomen und oftmals eine Mischung der beiden Gruppen.
Liu and Rodriguez (2005), Beenstock et al (2012) und Pretis & Hendry (2013) verwenden die jährlichen Daten aus der Etheridge’schen Glättungskurve für den Zeitraum von 1850 bis 1957 von der GISS-Website, wie sie von Sato für das globale Mittel adjustiert worden sind.
Kaufmann, Kauppi, & Stock (2006a), (2006b), and (2010) und Kaufmann, Kauppi, Mann, & Stock (2013) verwenden ebenfalls die Etheridge-Daten vor 1958 und ihre eigene Interpolationsmethode. Ihre Datenquelle für CO2 wird beschrieben im Anhang zu Stern & Kaufmann (2000):
Vor 1958 verwendeten wir Daten der Eisbohrkerne DE08 und DE08-2 aus Law Dome (Etheridge et al. 1996). Wir interpolierten die fehlenden Jahre mittels eines natürlichen kubischen Profils und Daten vom Mauna Loa aus zwei Jahren (Keeling und Whorf 1994), um einen Endpunkt zu nennen.
Die Forschungen von Liu und Rodriguez (2005), Beenstock et al (2012), Pretis & Hendry (2013) sowie die vier Studien von Kaufmann et al. verwenden ein Paar allgemeiner statistischer Methoden, die von Ökonomen entwickelt worden waren. Ihr erster Schritt war das Austesten von Treibhausgas-Zeitreihen einschließlich CO2 für Stationarität. Man nennt dies auch das Testen einer unit root [?], und es gibt eine Reihe von Tests zu diesem Zweck. Laut Kaufmann et al (2006a) lautet der mathematische Ausdruck für eine Zeitreihe mit einer Einheitswurzel (Unit Root):

        (1)

Dabei ist ɛ der Term des Zufalls-Fehlers [random error term], der Schocks oder Innovationen auf die Variable Y repräsentiert. Der Parameter λ ist gleich eins, falls die Zeitreihe eine Einheitswurzel aufweist. In solch einem Falle wird jeder Schock auf Y dauerhaft bleiben, und Y wird eine nicht stationäre Verteilung aufweisen. Falls λ kleiner als eins ist, werden die ɛ-Schocks eventuell verschwinden, und Y wird eine stationäre Verteilung aufweisen, die auf ein gegebenes Mittel zurückgreift, auf Varianz und anderes. Der von Kaufmann et al. (2006a) durchgeführte statistische Test ist ein erweiterter Dickey-Fuller-Test (ADF), der von Dickey und Fuller (1979) entwickelt worden ist und mit dem sie die folgende Regression jährlicher Zeitreihen-Daten von CO2 und Temperatur haben laufen lassen:

        (2)

Hierbei ist ∆ der erste Unterschieds-Operator, t ist ein linearer Zeittrend, ɛ ist ein Zufalls-Fehler-Term und γ = λ – 1. Der ADF-Test gilt für die Null-Hypothese, dass γ = 0 und daher λ = 1 ist, und Y ist eine nicht stationäre Variable mit einer Unit Root, ebenfalls als I(1) bezeichnet.
Es gibt noch viele andere Tests für Einheitswurzeln, die von vielen Forschern verwendet werden, darunter Phillips & Perron (1988), Kwiatkowski, Phillips, Schmidt, & Shin (1992) und Elliott, Rothenberg, & Stock (1996). Sie alle haben eines gemeinsam: eine Art der Regression einer Zeitreihen-Variablen auf verzögerte Werte derselben wie in Gleichung 2.
Eine Regression nach Art von Gleichung 2 kann ordentlich nur mit sich nicht überlappenden Daten durchgeführt werden. Wie zuvor erklärt, können die Eiskerndaten von Etheridge vor 1958 Luft von 20 Jahren vor bzw. nach dem gegebenen Zeitpunkt enthalten. Das Problem wird noch gravierender durch die Tatsache, dass sich Etheridge nicht sicher ist hinsichtlich der Stärke der Diffusion. Auch kennen wir nicht die Verteilung, wie viel Luft aus jedem Jahr sich in jedem Bläschen befindet. Folglich legen diese Forscher eine Regression nicht durch die jährlichen CO2-Konzentrationen aus der Vergangenheit (wie 1935 auf 1934, 1934 auf 1933 usw.), sondern durch einige Mittelwerte von 1914 bis 1954 auf 1913 auf 1953 und so weiter. Dies kann nur zu falschen Ergebnissen führen, weil der Test zumeist darin besteht, eine Regression der CO2-Daten für einen Zeitraum auf sich selbst durchzuführen.
Die zweite von den Forschern verwendete statistische Methode ist es, eine Integration der Treibhausgase (konvertiert zu Strahlungsantrieb) und den Temperaturdaten zu testen. Damit soll bestimmt werden, ob es eine Gleichgewichts-Beziehung zwischen Treibhausgasen und Temperatur gibt. Das Konzept der Integration wurde zuerst von Engle & Granger (1987) durchgeführt, um dem Problem der Erkennung einer Relation zwischen nicht stationären Variablen zu begegnen. Das traditionelle Verfahren kleinster Quadrate der Regression von nicht stationären Zeitreihen-Variablen führt oft zu falschen Ergebnissen. Integrationstests wurden erstmals mit makroökonomischen Zeitreihen-Daten durchgeführt wie das Bruttoinlandsprodukt, Geldmengen und Zinsraten.
In den meisten Studien werden die Strahlungsantriebe der verschiedenen Treibhausgase addiert und kombiniert mit Schätzungen der solaren Einstrahlung. Aerosole und Schwefel werden in einigen Studien auch berücksichtigt. Dann wird ein Test dieser Messungen durchgeführt, um zu bestimmen, ob sie mit jährlichen Temperaturdaten passend sind (wobei üblicherweise die jährlichen Mittelwerte der GISS-Zeitreihen Verwendung finden). Der Integrations-Test involviert das Auffinden eines linearen Vektors auf eine Weise, dass eine Kombination der nicht stationären Variablen mit diesem Vektor selbst stationär ist.
Ein Integrationstest kann nur gültig sein, falls die Datenserie ein hohes Maß zeitlicher Genauigkeit aufweist und auf geeignete Weise aufbereitet wird. Die Temperaturdaten weisen wahrscheinlich eine gute zeitliche Genauigkeit auf, aber die Etheridge’schen CO2-Daten vor 1958, aus denen die Daten des Strahlungsantriebs abgeleitet sind, sind gleitende Mittel über 20 Jahre oder mehr mit unbekannter Länge und Verteilung. Sie können nicht angemessen getestet werden auf eine Integration mit jährlichen Temperaturdaten, ohne falsche Ergebnisse zu liefern. Beispiel: Anstatt die CO2-Konzentration von 1935 mit der Temperatur von 1935 zu vergleichen, würde der Integrationstest einen Mittelwert der CO2-Konzentration über den Zeitraum 1915 bis 1955 mit der Temperatur von 1935 vergleichen.
Zur Verteidigung von Beenstock et al. (2012) muss gesagt werden, dass es das primäre Ziel ihrer Studie war zu zeigen, dass die CO2-Daten, die sie und die anderen Forscher als I(2) (zwei Unit Roots) ermittelten, nicht mit den I(1)-Temperaturdaten verglichen werden können, solange sie nicht polynomisch integriert werden. Sie behaupten nicht, eine Beziehung zu finden zwischen den CO2-Daten vor 1958 und den Temperaturreihen.
Schlussfolgerung von Kaufmann, Kauppi, & Stock (2006a) aus ihrem Abstract:
Regressionsergebnisse bieten direkte Beweise für eine statistisch bedeutsame Relation zwischen Strahlungsantrieb und globaler Temperatur. Ein einfaches, auf diesen Ergebnissen basierendes Modell zeigt, dass Treibhausgase und anthropogene Schwefelemissionen zum größten Teil verantwortlich sind für die Temperaturänderung der letzten 130 Jahre.
Die anderen in diesem Essay erwähnten Studien, außer Beenstock et al. (2012), kommen zu ähnlichen Ergebnissen. Wegen des geringen Niveaus der zeitlichen Genauigkeit der CO2-Daten vor 1958 können ihre Ergebnisse für diese Zeit nicht gültig sein. Der einzige angemessene Weg, mit diesen Daten zu arbeiten wäre es, eine obere Grenze der Zeit-Bandbreite festzulegen, die durch die Länge des Blaseneinschlusses und der Diffusion von Gasen durch das Eis bestimmt werden könnten. Beispiel: falls eine obere Grenze von 20 Jahren eingeführt werden könnte, dann könnten die Forscher eine mittlere CO2-Konzentration für sich nicht überlappende Zeiträume von 20 Jahren berechnen und dann die Unit Root- und Integrations-Tests durchführen. Unglücklicherweise würde der Zeitraum 1850 bis 1957 nur fünf vollständige 20-Jahres-Perioden umfassen. Eine so kleine Datenmenge ist nutzlos. Bis man eine Quelle findet, die CO2-Daten vor 1958 mit besserer zeitlicher Genauigkeit ermittelt, macht es keinen Sinn, Integrations-Tests mit Temperaturdaten für jenen Zeitraum durchzuführen. (Hervorhebungen von der Redaktion)

References

Beenstock, M., Y. Reingewertz, and N. Paldor (2012). Polynomial cointegration tests of anthropogenic impact on global warming. Earth Syst. Dynam., 3, 173–188.
Dickey, D. A. and Fuller, W. A.: 1979, ‘Distribution of the estimators for autoregressive time series with a unit root’, J. Am. Stat. Assoc. 74, 427–431.
Elliott, G., Rothenberg, T. J., and Stock, J. H.: Efficient tests for an autoregressive unit root, Econometrica, 64, 813–836, 1996.
Engle, R. F. and Granger, C. W. J.: Co-integration and error correction: representation, estimation and testing, Econometrica, 55, 251–276, 1987.
Etheridge, D. M., Steele, L. P., Langenfelds, L. P., and Francey, R. J.: 1996, ‘Natural and anthropogenic changes in atmospheric CO2 over the last 1000 years from air in Antarctic ice and firn’, J. Geophys. Res. 101, 4115–4128.
Kaufmann, R. K., Kauppi, H., Mann, M. L., and Stock, J. H.: Does temperature contain a stochastic trend: linking statistical results to physical mechanisms, Climatic Change, 118, 729–743, 2013.
Kaufmann, R., Kauppi, H., and Stock, J. H.: Emissions, concentrations and temperature: a time series analysis, Climatic Change, 77, 248–278, 2006a.
Kaufmann, R., Kauppi, H., and Stock J. H.: The relationship between radiative forcing and temperature: what do statistical analyses of the instrumental temperature record measure?, Climatic Change, 77, 279–289, 2006b.
Kaufmann, R., H. Kauppi, and J. H. Stock, (2010) Does temperature contain a
stochastic trend? Evaluating Conflicting Statistical Results, Climatic Change, 101, 395-405.
Kwiatkowski, D., Phillips, P. C. B., Schmidt, P., and Shin, Y.: Testing the null hypothesis of stationarity against the alternative of a unit root, J. Economet., 54, 159–178, 1992.
Liu, H. and G. Rodriguez (2006), Human activities and global warming: a cointegration analysis. Environmental Modelling & Software 20: 761 – 773.
Phillips, P. C. B. and Perron, P.: Testing for a unit root in time series regression, Biometrika, 75, 335–346, 1988.
Pretis, F. and D. F. Hendry (2013). Comment on “Polynomial cointegration tests of anthropogenic impact on global warming” by Beenstock et al. (2012) – some hazards in econometric modelling of climate change. Earth Syst. Dynam., 4, 375–384.
Stern, D. I., and R. K. Kaufmann, Detecting a global warming signal in hemispheric temperature series: A structural time series analysis, Clim. Change, 47, 411 –438, 2000.
Übersetzt von Chris Frey EIKE, der einige Fachbegriffe hier nicht verstanden und daher möglicherweise falsch übersetzt hat.

Beitrag als PDF speichernBeitrag drucken