Vom Prinzip her – und man muss unterstellen, sogar mit voller Absicht – wird dabei außen vor gelassen, dass es diese Größe in der Natur nicht gibt. Sie ist weder physikalisch an Hand der Realität definierbar, noch ist sie messtechnisch erfassbar. Wenn man nämlich versucht, sie sauber zu definieren, so bleibt nichts weiter als eine nach subjektiven Kriterien berechnete Zahl. Man könnte annehmen, dass sie eine Art Index ist. Aber auch das trifft nicht nicht zu, weil ihre Bezugsgrundlagen über der Zeit ständig variieren. Von einem aussagefähigen Index – wie z.B. dem Aktienindex DAX- verlangt man, dass die Zahl der Aktienwerte immer gleich ist. In diesem Falle sind es immer 30 DAX-Werte. Nicht immer dieselben, aber immer gleich viel. Das trifft aber für die per Thermometer bestimmten globale Mitteltemperatur nicht zu. Die Zahl der einbezogenenen Messstationen änderte sich permanent, auch deren Position im Kleinen wie im Großen, aber auch die Zeitpunkte an denen abgelesen wurde. Die Anforderungen die an einen Index gestellt werden, erfüllt sie also auch nicht.
Trotzdem kann man mit ihr und ihrem errechneten Trend viele kluge aber noch viel zahlreichere weniger kluge Sachen anstellen, über die sich trefflich und ausgiebig streiten lässt. Und gerade weil das so ist, wird der Streit darüber mit erbitterter Härte geführt und erinnert den geschichtsbewussten Beobachter immer mehr an den unendlichen Streit der mittelalterlichen Scholastiker über die Frage, wieviele Engel wohl auf eine Nadelspitze passen. Dieser Streit ist – weil völlig irreal – bis heute nicht entschieden, ebenso wenig wie der Streit darüber, was eine globale Mitteltemperatur eigentlich ist. Daher ist es gut, sich die physikalischen Realitäten zunächst einmal vor Augen zu führen.
Abbildung 1: Linkes Bild-Die Fragezeichen symbolisieren die verschiedenen Messorte von Messungen zur Bestimmung einer Durchschnittsstemperatur in einem Haus. Rechtes Bild- dasselbe Problem dargestellt an einem KfZ. In beiden Fällen wäre die Bestimmung einer Mitteltemperatur selbst wenn die Einzelwerte zur gleichen Zeit gemessen würden, sinnlos.
Die Physik definiert Temperatur in Anlehnung z.B. an Gehrtsen [Meschede, 2003] wie folgt als:
(Wärmezustand eines Körpers (nicht Wärmeenergie ))….und dann unter „Statistische Theorie der Wärme“: je Freiheitsgrad der sich in ungeordneter Wärmebewegung befindlichen Atome (L. Boltzmann 1890, Wien) gültig für Gase , Festkörper und Flüssigkeiten.
Anders ausgedrückt bedeutet dies: Die Temperatur ist eine physikalische, thermodynamische Zustandsgröße der Materie am Ort der Messung. Die physikalischen Eigenschaften der Temperatur werden in der Lehre von der Thermodynamik behandelt. Man bezeichnet dort die Temperatur als eine systemeigene, intensive Zustandsgröße.
Was ist eine „globale Erwärmung“?
In der Klimatologie wird diese Definition allerdings nicht verwendet. Welche Probleme man sich damit einhandelt, beschreiben z.B. Essex et. al [Essex, 2006] ausführlich in ihrer Arbeit. Darin zeigen sie, dass die in der Global-Klimatologie übliche Definition zu Problemen führt. Dort wird die von einer fiktiven Mitteltemperatur abhängige Temperaturabweichung Ξ(tM) (leider bildet der Zeichenvorrat des typo3 Editors mathematische Sonderzeichen nur unzreichend ab, ich bitte um Nachsicht) zur Zeit tM:
![]()
Ξ(tM) gebildet, indem von jeder Ortstemperatur ein gleitender Durchschnitt der Vergangenheit (2-ter Term in der Klammer) abgezogen wird. Ξ(tM) wird zutreffend als Temperaturanomalie bezeichnet. Die Summierung (Index i) erfordert im Prinzip eine räumliche Integration des Temperaturfeldes über die gesamte Oberfläche der Erde, wobei ![]() die Lufttemperatur an der Position ri und zur Zeit tM ist und die Summierung über j für einen passenden Zeitraum (üblich sind 30 Jahre) durchgeführt wird. Die Anomalie Ξ ist also eine Funktion von
die Lufttemperatur an der Position ri und zur Zeit tM ist und die Summierung über j für einen passenden Zeitraum (üblich sind 30 Jahre) durchgeführt wird. Die Anomalie Ξ ist also eine Funktion von ![]() für alle Ortsvektoren ri. Im Gegensatz dazu sind lokale (thermodynamische – Anm. des Verfassers -) Gleichgewichtszustände in einem Feld nur für einen besonderen Ort r definiert. Andere Orte, sofern sie sich nicht in infinitesimaler Nachbarschaft befinden, sind davon unberührt. Die statistische Größe Ξ hat dieselbe Eigenschaft wie ein arithmetischer Durchschnitt von unterschiedlichen Temperaturen zwischen räumlich voneinander entfernten Systemen. Sie hängt daher von den Zuständen aller räumlich getrennten Subsysteme ab.
für alle Ortsvektoren ri. Im Gegensatz dazu sind lokale (thermodynamische – Anm. des Verfassers -) Gleichgewichtszustände in einem Feld nur für einen besonderen Ort r definiert. Andere Orte, sofern sie sich nicht in infinitesimaler Nachbarschaft befinden, sind davon unberührt. Die statistische Größe Ξ hat dieselbe Eigenschaft wie ein arithmetischer Durchschnitt von unterschiedlichen Temperaturen zwischen räumlich voneinander entfernten Systemen. Sie hängt daher von den Zuständen aller räumlich getrennten Subsysteme ab.
Damit entsteht ein Paradox. Ξ am Ort r hängt auch von den Zuständen an allen entfernten Positionen {rk} ab. Jedoch sind chemische, physikalische oder biologische Prozesse, die durch die Temperatur am Ort r gesteuert werden, keine Funktionen der Temperaturen außerhalb von r. Wenn man in Klimamodellen darauf besteht, dass Ξ Prozesse auslöst, wie z.B. das Schmelzen von Gletschern, dann ist dieser Vorgang zwangsläufig eine Funktion von Temperaturen anderswo auf dem Planeten. Dies ist physikalisch unhaltbar. Fernwirkende Mechanismen für thermodynamische Prozesse gibt es nicht.
Mit der genauen Ermittlung der Kennziffer „Globaltemperatur“ T und ihres Verlaufes über der Zeit sollen u.a. Rückschlüsse auf eventuelle klimatisch relevante Einflussgrößen („Antriebe“ oder Forcings) ermöglicht werden. Namentlich ist hier der Einfluss des Spurengases CO2 gemeint, das gemeinhin als Treibhausgas bezeichnet wird. Durch die vielfältige statistische Behandlung wird jedoch aus dem ursprünglich physikalischen Wert der Temperatur T des Messortes und der Zeit nur noch eine fiktive Zahl T*. Sie hat keinen physikalischen Inhalt mehr, obwohl sie in der Literatur mit der Dimension °C oder K bezeichnet wird. Somit verliert die berechnete Größe „mittlere Globaltemperatur“ als Durchschnittswert aller gemessenen lokalen Temperaturwerte ihren physikalischen Bezug. Sie unterliegt in ihrer Bestimmung nicht mehr den allgemein gültigen physikalischen Gesetzen, sondern den zwar ausgefeilten, in wesentlichen Teilen jedoch willkürlich definierten statistisch-mathematischen Regeln und Konventionen. Jeder Versuch, ein Feld aus unterschiedlichsten lokalen Temperaturen über willkürliche Rechenregeln zusammenzuführen (es gibt z.B. – streng genommen – unendlich viele Methoden der Mittelwertbildung. Welche ist hier die „Richtige“?), liefert lediglich eine neue Zahl, die alle ihre physikalisch bestimmenden Eigenschaften verloren hat. Sie erhält dafür neue Eigenschaften, die sich primär aus den verwendeten Rechenregeln und den verabredeten (für den ursprünglichen Zweck möglicherweise sinnvollen, aber willkürlichen) Konventionen ergeben.
Der klimatologische Begriff der Lufttemperatur und die Messmethoden
Im Bericht des National Research CouncilXE „National Research Council“ [NRC, 2005] wird die mittlere Globaltemperatur T als “heat content”, also – im Gegensatz zur Auffassung von Gehrtsen- als Wärmeenergieinhalt, wie folgt definiert: ‘‘According to the radiative-convective equilibrium concept, the equation for determining global average surface temperature of the planet is
![]()
where H. . .. . .is the heat content of the land-ocean-atmosphere system. . … Equation (1) describes the change in the heat content where f is the radiative forcing at the tropopause, T´ is the change in surface temperature in response to a change in heat content, and λ is the climate feedback parameter (Schneider and Dickinson, 1974), also known as the climate sensitivity parameter, which denotes the rate at which the climate system returns the added forcing to space as infrared radiation or as reflected solar radiation (by changes in clouds, ice and snow, etc.).’’
Danach ist T die mittlere Globaltemperatur und T´ die Abweichung von dieser Temperatur, hervorgerufen durch die Strahlungs-Antriebe (radiative forcings) f. Diese Definition erleichtert zwar u. U. die Zuordnung einzelner Antriebe zur gemessenen oder gerechneten Veränderung T´, hilft aber bei der eigentlichen Ermittlung der Globaltemperatur T nicht weiter. Überdies unterstellt diese Definition eine reine Strahlungstemperatur, was der beobachteten Vielfalt der Temperaturquellen, zusätzlich zur Strahlungstemperatur, nicht gerecht wird.
Widersprüchliche Definitionen
Die klassische Meteorologie war sich schon lange des Widerspruchs bewusst, der sich aus der Ermittlung der lokalen wahren Lufttemperatur T und ihrer Verwendung als statistischem Mittelwert T* ergab. So erläutert R. Assmann, der Erfinder des heute noch vielfach verwendeten Aspirationspsychrometers, in seinem umfangreichen Aufsatz „Das Aspirations-Psychrometer; Ein Apparat zur Ermittlung der wahren Temperatur und Feuchtigkeit der Luft“ auf Seite 120 (6)[Assmann, 1892] Original-Zitat (alle Hervorhebungen vom Autor, die alte Schreibweise bitte zu entschuldigen):
„1. Begriff der Lufttemperatur. Sprung definiert in seinem Lehrbuche der Meteorologie auf S. 307 den Begriff der Lufttemperatur, wie man denselben in der Meteorologie schlechtweg gebraucht, als »diejenige Temperatur, welche der über betreffende Gegend hinwegstreichende Luftstrom in einer Höhe‘ von 1-2 m über der Erdoberfläche wirklich besitzt.
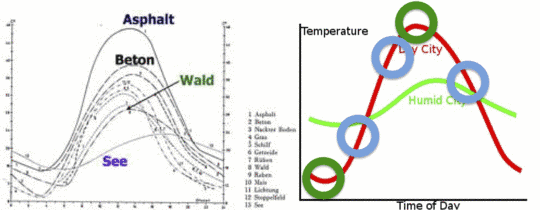
Abbildung 2: Das linke Bild zeigt den Temperaturverlauf an einem sonnigen Tag in Deutschland über verschiedenen Bodenarten. Die Temperaturskala links fängt bei 0°C an und endet bei 48 °C. Das rechte Bild zeigt den Temperaturverlauf symbolisch über einen Tag in feuchter Umgebung und in trockener Umgebung, sowie die Messwerte bei gleichem Verlauf aber zu verschiedenen Zeiten zur Berechnung des Tagesmittels.
Koeppen [Köppen, 1913] dagegen sagt in seiner Abhandlung »Studien über die Bestimmung der Lufttemperatur und des Luftdrucks« auf S. I: »Was ist Lufttemperatur ? Die Antwort lautet einfach: Die Temperatur der Luft, zunächst derjenigen, welche wir unmittelbar der Prüfung unterwerfen und weiterhin die Temperatur anderer, größerer Luftmassen, als deren Repräsentantin die erstere dienen kann«. Wie man sieht, ist Koeppens Definition die weitere, von einer Höhenangabe über dem Erdboden gänzlich absehende, während Sprung’s Definition dem für die beobachtende Meteorologie allerdings wesentlich maßgebenden Begriffe der »klimatischen Temperatur« nahe kommt.
Koeppen unterscheidet aber ferner gewissermaßen zwei verschiedene Arten der Lufttemperatur, deren erste man die physikalische nennen könnte, während die letztere auf das praktische Bedürfnis klimatologischer Untersuchungen Rücksicht nimmt. Für unsern Zweck, ….. ebenso auch im Innern eines von der Lufttemperatur abhängigen physikalischen Apparates so ermitteln, wie sie unter dem Zusammenwirken aller für den speciellen Fall wirksamen Faktoren thatsächlich vorhanden ist. Man könnte deshalb vielleicht auch sagen, dass wir als Lufttemperatur diejenige Temperatur anzusehen haben, welche eine beliebige, der Untersuchung unterworfene Luftmenge unter dem Zusammenwirken der jeweiligen sie treffenden Einflüsse der Ein- und Ausstrahlung direkter wie reflektirter Wärme jeder Wellenlänge, ferner der Leitung und Konvektion von Wärme wirklich besitzt.
Eine verschleppte „Erbkrankheit“ der Meteorologie
Damit umgeht Koeppen jede physikalische Definition der Größe, die er beobachten will, was aber bis zur Erfindung der Treibhaustheorie eigentlich niemanden störte.
Dieses klar erkannte Dilemma wurde aber in den letzten 120 Jahren nicht nur nicht ausgeräumt, sondern im Gegenteil weiter verfestigt und führt daher, auch weiter bei Klimawissenschaftlern jeglicher Provenienz zu munterer Begriffsverwirrung. An dieser „Erbkrankheit“ leidet die Meteorologie sowie die mit ihr verknüpfte Klimaforschung bis heute. Anschaulich unterstreicht dies eine aktuelle, leicht verständlich gehaltene Darstellung auf der Webseite des Goddard Institute for Space Studies, GISS) der NASA, das in den USA auch für Belange der Meteorologie und Klimaforschung zuständig ist. Dort wird das „kleine“ Problem, wie die alles entscheidende Ursprungs-Größe, die Basis aller Globaltemperaturen, nämlich die lokale bodennahe Lufttemperatur und ihr Tagesdurchschnitt zu ermitteln ist, mit Hilfe eines kurzen Frage- und Antwortspiels wie folgt beschrieben:
Boden-Temperaturanalyse nach GISS/ Die schwer fassbare Absolute Boden-Temperatur (SAT)
Frage: Was genau ist mit SAT (Absolute Surface Air Temperature) gemeint?
Antwort: Ich bezweifle, dass es eine allgemeine Übereinstimmung gibt, wie man diese Frage beantworten kann. Selbst an ein und demselben Ort kann sich die Temperatur in Bodennähe sehr von der Temperatur in einer Höhe von 5 Fuß [ca. 1,5 m] über dem Boden unterscheiden und diese wiederum von der Temperatur in 10 oder 50 Fuß [ca. 3 m bzw. 15 m] über Grund. Vor allem beim Vorhandensein von Vegetation (sagen wir mal im Regenwald) kann sich die Temperatur oberhalb der Vegetation sehr stark von der Temperatur unter dem Blätterdach unterscheiden. Ein vernünftiger Vorschlag könnte es sein, die mittlere Temperatur der ersten 50 Fuß entweder über dem Boden oder über der Vegetation zu verwenden. Um SAT zu messen, müssten wir übereinstimmend feststellen, was damit gemeint ist, und so weit ich weiß, ist bis heute ein solcher Standard nicht vorgeschlagen oder allgemein übernommen worden. Selbst wenn man den 50-Fuß-Standard übernimmt, kann ich mir nicht vorstellen, dass man an einer Wetterstation einen 50 Fuß hohen Turm mit einer Anzahl Thermometer errichtet, um die wirkliche SAT an dieser Stelle zu ermitteln.
Frage: Was meinen wir mit dem täglichen Mittel von SAT?
Antwort: Noch einmal, da gibt es keine universell korrekte Antwort. Sollten wir die Temperatur alle 6 Stunden messen und mitteln, oder sollten wir es alle zwei Stunden tun, stündlich oder mit Hilfe einer Maschine jede Sekunde, oder sollten wir einfach das Tagesmaximum und –minimum nehmen und die Summe durch zwei dividieren? An einigen Tagen werden die verschiedenen Methoden zu drastisch unterschiedlichen Ergebnissen führen.
Frage: Über welche SAT berichten die lokalen Medien?
Antwort: Die Medien melden die Messungen an einem bestimmten Thermometer einer nahe gelegenen Wetterstation. Diese Temperatur kann von der wirklichen SAT selbst an dieser Stelle sehr unterschiedlich sein und hat mit Sicherheit nichts zu tun mit der wirklichen regionalen SAT. Um die wirkliche regionale SAT zu messen, müssten wir viele 50 Fuß hohe Thermometersäulen verwenden, die gleichmäßig über das ganze Gebiet verteilt sind, eine offensichtlich praktische Unmöglichkeit.
Frage: Wenn die gemeldeten SATs nicht die wirklichen SATs sind, warum sind sie dennoch nützlich?
Antwort: Die gemeldete Temperatur ist wahrhaftig nur für jene Person von Bedeutung, die die Wetterstation zufällig in genau dem Moment aufsucht, zu dem die gemeldete Temperatur gemessen wird – mit anderen Worten also für niemanden. Allerdings fügen die Medien zusätzlich zu der gemeldeten SAT auch hinzu, ob diese Temperatur ungewöhnlich hoch oder niedrig liegt, um wie viel sie von der Normaltemperatur abweicht, und diese Information (diese Anomalie) ist für die ganze Region bedeutsam. Außerdem, wenn wir von einer bestimmten Temperatur hören (z. B. 70°F [ca. 21°C]), übertragen wir diesen Wert instinktiv in heiß oder kalt, aber der Schlüssel für diese Übertragung hängt von der Jahreszeit und dem Gebiet ab. Der gleiche Temperaturwert kann im Juli ‚kalt’ und im Januar ‚warm’ sein, da wir mit ‚warm’ immer wärmer als normal meinen. Das heißt, wir übertragen alle Temperaturwerte automatisch in Anomalien, ob wir das nun merken oder nicht.
Frage: Falls man die SATs nicht messen kann, wie werden dann Karten mit der Temperaturverteilung erzeugt?
Antwort: Das kann man nur mit Hilfe von Computermodellen, den gleichen Modellen, die verwendet werden, um die tägliche Wettervorhersage zu erstellen. Wir können die Modellrechnung mit einigen wenigen gemessenen und verfügbaren Daten füttern und den Rest mit Vermutungen (auch Extrapolationen genannt) füllen. Danach lassen wir das Modell so lange laufen, dass die Eingangs-Annahmen keine Rolle mehr spielen, aber nicht zu lange, um die zunehmenden Ungenauigkeiten des Modells mit der Zeit zu vermeiden. Man kann auch als Anfangszustand die mittleren Bedingungen mehrere Jahre nehmen, so dass das Mittel (eine ‚Klimatologie’ genannt) hoffentlich eine typische Karte für einen bestimmten Monat oder ein bestimmtes Jahr repräsentiert.
Frage: Was muss ich tun, wenn ich absolute SATs brauche und nicht Anomalien?
Antwort: In 99,9% aller Fälle wird man finden, dass Anomalien genau das sind, was man braucht, nicht absolute Temperaturen. In den übrigen Fällen muss man sich eine der verfügbaren Klimatologien heraussuchen und die Anomalien hinzufügen (unter Berücksichtigung einer geeigneten Bezugsperiode). Als globales Mittel erzeugen die Modelle, denen man am meisten vertraut, einen Wert von etwa 14°C, aber es kann gut irgendwo zwischen 13°C und 15°C liegen, und regional, geschweige denn lokal, ist die Lage sogar noch schlimmer.
Ich bin mir sicher dass die o.a. Ausführungen zu reger Diskussion führen werden. Daher eine Bitte: Bleiben Sie in Ihren Kommentaren sachlich.
Michael Limburg
Die GISS Darstellung wurde von von Chris Frey EIKE übersetzt.
Kommentar hierzu von Dipl.-Met. Hans-Dieter Schmidt:
Als mir dieser Text des GISS gezeigt wurde, habe ich mich schon im ersten Moment ertappt gefühlt – dieses unbewusste Übertragen in Anomalien, von dem in diesem Text die Rede ist, passiert mir nämlich auch – im privaten Bereich. Als Meteorologe im Vorhersagedienst (oder besser gesagt während der Arbeit) sind mir die absoluten Werte dagegen relativ egal – die Vorhersage von Wettererscheinungen ist wichtiger und schwieriger.
Dennoch, um auf die Problematik von „globalen Temperaturen“ hinzuweisen, kann dieser Artikel gar nicht hoch genug einschätzt werden. Und wenn mich mein Nachbar fragt, wie lange ‚es noch so heiß bleibe’, gebe ich gerne die Antwort: ‚Es war doch schon mal noch heißer um diese Jahreszeit!’
‚Hitze’ und ‚Kälte’ betrachte ich als Wettererscheinungen. Auch privat – ich leide unter der Hitze – und nicht unter 32°C oder 35°C. Schon während meiner Ausbildung (vor rund 40 Jahren) habe ich gelernt, Wertungen strikt aus der Formulierung von Vorhersagen herauszuhalten. Dieser Artikel liefert mir selbst nach so langer Zeit den klaren Grund für diese Anweisung.
Hans-Dieter Schmidt
Literatur in der Reihenfolge ihrer Erwähnung
Meschede, D (2003) Gehrtsen Physik. J. Springer, Berlin Heidelberg
Essex, C, Mc Kittrick, R. Andresen, B. (2006) Does A Global Temperature Exist? Non-Equilibrium Thermodynamics
NRC (2005) Radiative Forcing of Climate Change: Expanding the Concept and Addressing Uncertainties, 207 pp.,. 207 pp.
Assmann, R (1892) Das Aspirations-Psychrometer; Ein Apparat zur Ermittlung der wahren Temperatur und Feuchtigkeit der Luft.
Köppen, W (1913) Einheitliche Thermometeraufstellungen für meteorologische Stationen zur Bestimmung der Lufttemperatur und der Luftfeuchtigkeit Meteorologische Zeitschrift 30
GISS Surface Temperature Analysis The Elusive Absolute Surface Air Temperature (SAT)
http://data.giss.nasa.gov/gistemp/abs_temp.html














„Und zu den Randbedingungen gehört selbstverständlich die mittlere Temperatur des Mediums dessen Strahlung sie daraus berechnen wollen.“
Wie sich schon oben schrieb: der Sinn eines Klimamodell ist es gerade, das Klima aus externen Randbedingungen mittels der physikalischen Gesetze zu bestimmen.
Dies umfasst auch, die Temperatur im Klimasystem nur durch externe Randbedingungen (solare Einstrahlung, chemische Zusammensetzung der Atmosphäre, Vulkanausbrüche, anthropogene Faktoren) und konstante Systemeigenschaften (Land-Meer-Verteilung, Topographie, physikalische und chemische Eigenschaften der Substanzen im Klimasystem, Erdbahnparameter,…) zu determinieren.
Also ist die Temperaturverteilung im Klimasystem eine Funktion der externen Randbedingungen und damit wie jeder Klimaparameter eine von den externen Randbedingungen abhängige Variable. Ebenso ist natürlich die thermische Abstrahlung der Atmosphäre oder des Bodens eine abhängige Variable des Klimasystems, die zwar explizit auch von der Temperatur abhängt aber natürlich letztlich wiederum von den externen Randbedingungen anhängt.
Nur anhand der physikalischen Abhängigkeit von Temperatur und der entsprechenden thermischen Strahlung der temperierten Medien alleine werden dessen Werte ja nicht festgelegt.
„Wie wollen Sie Energieflüsse berechnen, wenn Sie die Anfangsenergie mit ihrem Hauptparameter Temperatur nicht berücksichtigen. Schöpfen Sie die Energie, die da fließen solle zuvor aus dem Nichts?“
Nein, selbstverstaendlich aus der externen Randbedingung, der angelieferten Energie von der Sonne.
Das Klimasystem berechnet sich dann aus den physikalischen, chemischen und geometrischen Verhaeltnissen auf der Erde mit Hilfe der physikalischen Gesetze.
„Wenn Sie die Energiebilanz rechnen wollen, was die Modelle tun, ist die Temperatur ein unverzichtbarer Input.“
Dazu wird aber die Temperatur aber erstmal berechnet und das geschieht lokal ueber die progostische Gleichung fuer die Temperatur, diese wiederum enthaelt die lokalen Energiefluesse… das ist also ein rekursives Verfahren.
Mit input-Parameter meine ich extern vorgegebene Randbedingungen wie die solare Einstrahlung, die Topographie oder die chemische Zusammensetzung der Atmosphaere und nicht ein Zwischenergebnis wie die Energiefluesse oder die Temperatur, deren Zeitentwicklung ist Modelloutput. Die Lösung des Gleichungssatzes des Klimamodells erfüllt dann zu einem Zeitpunkt synchron die Energieflüsse und die zugehörigen Temperaturen bei den gegebenen Randbedingungen.
„Ich habe nicht die Mittelwertbildung bezweifelt, sondern die Behauptung, dass es sich dabei um eine Temperatur im physikalischen Sinne handelt.“
Das wird von den Klimatologen aber auch nicht behauptet.
„Und weil das so ist, kann man den ermittelten Mittelwert auch schlecht z.B. als bestimmenden Parameter in Klimamodellen einsetzen.“
Das ist ebenfalls eine falsche Annahme. Die Temperatur ist ein Modelloutput, nicht ein Input. Außerdem geben die heute üblichen 3 D Modelle 3 D Temperaturverteilungen aus.
am Montag, 19.08.2013, 10:15
#24: S.Hader
Interessanter Vergleich, insbesondere aufgrund eines offensichtlichen Fehlschlusses.
Kommentar:
Bitte nur unter vollem Klarnamen posten. Siehe Regeln.
mfG
Admin
———
Hallo, admin
warum gilt Ihre Aussage oben nicht für „Ebel“?
Nur `ne Frage- muss nicht in den blog.
Antwort an Web- Adresse wäre nett.
Alles Gute
K.L.
„@ #73: J. Ehlig sagt am Mittwoch, 21.08.2013, 01:10
Komisch – der Eine überliest die Abkühlung, der Andere die Erwärmung.“
Ist „kaputtmachen“ Erwärmung oder Abkühlung? Paßt wohl eher zum neuen Jargon „Klimawandel“.
Hallo Herr Ebel,
im Großen und Ganzen stimme ich Ihrem Kommentar zu!
Das gilt sehr weitgehend auch für Ihren Satz:
„Ist zwar alles hypothetisch, aber verständlich – und entspricht auch heutigen Verhältnissen.“
Allerdings geht aus der teilweise sehr guten Überlieferungslage aus dem römischen Imperium auch hervor, das selbst diese insgesamt wesentlich weiter entwickelte Zivilisation relativ schnell vor Problemen stand, wenn die Versorgung der Bevölkerung mit Lebensmitteln nicht funktionierte – gleich aus welchen Gründen. Zwar kann man wohl von einer entwickelteren Vorratswirtschaft ausgehen, ob die aber stets die Ernährungsbedürfnisse stützte, ist zweifelhaft.
„Hartz IV“ war unbekannt. Von einem System sozialer Abfederung kann nicht gesprochen werden.
Die politisch stärksten Kaiser mußten auf der Hut sein, wenn sich in ihrem Imperium Unmut im Volk wegen schlechter Versorgungslage und Teuerung breitmachte. Häufig wurde eine solche Situation von anderen Playern (Senatoren, Militärs)zum oft auch unmittelbar für den Herrscher tödlichen Staatsstreich genutzt. Ich empfehle Ihnen, die Geschichte des 3. Jahrhunderts zu lesen, in dessen letztes Drittel nach Proxydaten auch eine gewisse Abkühlung fällt.
Tja, Ursachen und Wirkungen sind auch auf diesem Themenfeld schwer abzuschätzen. Neben klimatischen Veränderungen, spielen auch Bevölkerungswachstum (und Abnahme), inneres Chaos, militärische Auseinandersetzungen, Seuchen u.v.m. eine Rolle.
Nach den Proxydaten aus den Baumringen sieht es so aus, als wenn eine tatsächlich durchgreifende Abkühlung erst um 600 n.Chr. ihren Tiefpunkt erreichte. Da waren die großräumigen Wanderungsbewegungen soeben zum Ende gekommen.
Ob die letze Bewegung (die Langobarden nahmen weite Teile Italiens um 568 ein) damit zusammenhängt, ist unklar, für mich aber denkbar. Es wäre diesen aber sehr wahrscheinlich nicht möglich gewesen, dort ein eigenständiges Reich zu errichten, wenn dort nicht zuvor ein verheerender 20-jähriger Krieg zwischen dem byzantischen Reich und dem in Italien bis dahin existierenden Ostgotenreich getobt hätte. Letzteres verschwand von der politischen Bildfläche, während die Sieger – vielleicht auch aus Gründen der Erschöpfung – ihren Sieg nicht mehr nutzen konnten. In das „Vakuum“ wanderten die Langobarden ein, könnte vermutet werden. Sicher war es in Italien wärmer als in den nördlichen Herkunftsgebieten, aber andererseits soll Italien verwüstet gewesen sein. Wir denken heute oft, ein verwüstetes Land sei kein Magnet für Einwanderung. Wie sahen die Langobarden dies?
Wir wissen zuwenig. Und das gilt offensichtlich nicht nur für die menschliche Historie.
Das sollten wir alle auch hier im Blog immer ein wenig im Hinterkopf haben.
In der Erwartung weiteren guten Dialogs, auch auf dem Gebiet, dass von Ihnen hier oft „beackert“ wird. Ihre Kommentare sind immer interessant, Herr Ebel. Und ich bin kein Physiker.
mit freundlichen Grüssen
Dirk Weißenborn
„Sie hätten sich auch aus ganz anderen Gründen diesem Heer anschließen können, z.B. Habgier, Neid auf den römischen Reichtum und Karrierestreben.“
Natürlich spielen solche Beiträge auch mit eine Rolle – aber auch diese Beiträge hängen vom Gefälle ab. Die Römer konnten Änderungen besser abfangen – die Germanen weniger, d.h. das Gefälle vergrößerte sich. Solange sich die Germanen wohl gefühlt haben, ist auch ein Wohlstandsgefälle kein großer Nährboden für Neid.
Ist zwar alles hypothetisch, aber verständlich – und entspricht auch heutigen Verhältnissen.
MfG
Berichtigung
Ups, Standardabweichung sollte das naturlich heißen. Vielleicht habe ich zu intensiv an Freud gedacht.
@ #73: J. Ehlig sagt am Mittwoch, 21.08.2013, 01:10
Komisch – der Eine überliest die Abkühlung, der Andere die Erwärmung.
MfG
„hat denn bislang noch niemand die Standardverteilung eines dermaßen wichtigen Mittelwertes bestimmt?“
Klar doch, gucken Sie sich die Graphik im Artikel oben an. Die jährlichen Temperaturanomalie hat ein 95%-Konfidenzintervall des Fehlers zwischen ca. +/- 0,2 (zu frühen Jahren) und +/- 0,1 °C (bis heute). Wenn man die Fehler gaußverteilt annimmt, so ist der Faktor zwischen der 2,5% bzw. 97,5%-Quantile (2*2,5% langen ja oberhalb und unterhalb der Intervallgrenzen raus) und der Standardabweichung (Sigma) 1,96. D.h. die Standardabweichung der jährlichen global gemittelten Temperaturanomalie beträgt zwischen 0,1 bis 0,05 °C für die letzten 100 Jahre.
„Sie muß ja da sein, denn mal wird er mit +14 °C, mal mit +15 °C angegeben.“
Vorsicht, diese unterschiedlichen Angaben des globalen und jährlichen Mittelwertes der absoluten bodennahen Temperatur sind nicht durch Meßfehler in den Ausgangsdaten bedingt. Die obige Streuung der Anomalie-Mittelwerte ist deswegen geringer, weil Anomalien eine geringere räumliche Variabilität zeigen als absolute Temperaturen. Wenn Sie die 2m-Temperatur benachbarter Stationen in verschiedenen Höhen über NN vergleichen, so verlaufen die Monats- und Jahresmitteltemperaturen weitgehend parallel aber zeigen natürlichen einen offset, der durch die unterschiedliche Höhe bedingt ist. Es macht also keinen Sinn, die absoluten Temperaturen ohne Berücksichtigung der Höhe global zu mitteln! Denn da würde nur die Streuung dominieren, die durch die Höhenverteilung bedingt ist. Dies ist aber kein Meßfehler. Um eine Man muß also die absoluten Temperaturen entweder auf ein einheitliches Referenzniveaus reduzieren (z.B. Meereshöhe), dann auf dem Referenzniveau zu mappen und mitteln. Oder man versucht, über die Topographie 2m über dem Boden zu mappen und dann zu mitteln. Da das mittlere Höhenniveau der Erde rd. 800 m über NN beträgt (http://tinyurl.com/Hypsometrie) und die mittlere Temperaturabnahme mit der Höhe in Bodennähe rund 0,5 °C/100 m beträgt, ist alleine schon ein Unterschied in der absoluten globalen mittleren Temperatur von 4 °C zwischen dem Referenzniveau Meeresspiegel und mittleren topographischen Höhenlage zu erwarten. Ich kann mir also vorstellen, daß die Unterschiede von 1°C durch entweder unterschiedliche verwendete Referenzniveaus (das müßten Sie an Ihren Daten klären) oder daß bei gleichem Referenzniveau die Höhenabhängigkeit statistisch so ungenau zu erfassen ist, daß eben je nach Methode Unterschiede von 1 °C rauskommen. Das wäre dann eben tatsächlich ein Fehlerintervall, welches man einrechnen muß. Aufgrund dieser topographisch bedingten Zusatzprobleme, die man bei der absoluten Temperatur hat, macht man globale Trends ja auch mit den globalen Anomaliemitteln, denn diese verschleiern nicht klimatische Effekte mit topographischen.
Herr Hader,
Sie schreiben:
„Seltsam Herr Weißenborn, ich verstehe den Artikel von Herrn Limburg anders.“
Wie Sie die schriftlichen Darlegungen von Herrn Limburg auffassen, ist mir völlig schnuppe.
mfG
Dirk Weißenborn
Hallo Herr Ebel,
Sie schreiben:
„Was meine Sie, was sich alles ändert, wenn z.B. der Supervulkan „Yellowstone“ ausbricht.“
Genau, Herr Ebel, wenn der Supervulkan ausbricht, erledigen sich sofort alle weiteren Diskussionen über die Reduktionen der anthropogenen CO2-Emmisionen.
Dann haben wir alle, auch Sie, ganz andere Probleme. Ihnen wird z.B. überhaupt keiner mehr zuhören.
„Was meinen Sie, warum es trotz relativ kleiner Temperturschwankungen die Völkerwanderung gab. Auch die durch geringe Klimaänderungen ausgelöste Hungersnot ist mit „Schuld“ an der französischen Revolution.“
Was verstehen Sie eigentlich unter (der) „Völkerwanderung“? Selbst „mitgewandert“?
Als Angehöriger eines alemannischen „Kommandos“, welches den Rhein um 275n.Chr.überquerte und u.a. Augusta Treverorum, das heutige Trier, plünderte und brandschatzte, müssen Sie und Ihre Stammesgenossen nicht unbedingt hungrig wegen kältebedingter Ernteausfälle gewesen sein – auch wenn Baumringdaten von Arven und Lärchen aus den Alpen einen – zeitlich eher begrenzten Temperaturrückgang just um 270n.Chr. nahelegen.
Sie hätten sich auch aus ganz anderen Gründen diesem Heer anschließen können, z.B. Habgier, Neid auf den römischen Reichtum und Karrierestreben.
Diese Stadt wurde schon ca. 80 Jahre vorher von „germanischen“ Kriegern angegriffen, als die Temperaturen (nach eben diesen Baumringdaten)noch höher lagen.
Gleiches gilt für die sogenannten Markomannenkriege (um 167 – 182n.Chr.) in Norditalien, der Donau und auf dem Balkan.
Monokausalität ist hier fehl am Platze. Immerhin haben Sie im Fall der Französischen Revolution von „mit Schuld“ gesprochen und sich die Hintertür offengelassen.
Die schlechten gesellschaftlichen Verhältnisse am Vorabend der französischen Revolution hatten sicher mehrere Gründe. Da wären auch die Mißwirtschaft, Verschwendung (denken wir an den Hof in Versailles), Korruption und Ausgaben für die militärischen Operationen in Amerika (unter LaFayette) einige Jahre vorher zu nennen.
Es wundert mich, dass gerade Sie dieses Versagen der Herrschenden in Frankreich nicht mehr herausstellen.
Immer nur wie es gerade paßt.
Haben die leicht höher liegenden Temperaturen bis ca. 1945 den allierten Nachschub auf dem atlantischen Ozean (Geleitzüge) durch fehlende Eisberge (Prof. Heinz Haber, 1989) auf den Hauptrouten unterstützt? Vielleicht. Daraus aber gleich den Hauptgrund für den Ausgang des II.Weltkriegs zu machen, wäre sicher auch übertrieben.
mfG
Dirk Weißenborn
am Mittwoch, 21.08.2013, 11:06
#69: NicoBaecker
Hallo Herr Baecker,
hat denn bislang noch niemand die Standardverteilung eines dermaßen wichtigen Mittelwertes bestimmt?
Sie muß ja da sein, denn mal wird er mit +14 °C, mal mit +15 °C angegeben.
Da ich nicht vom Fach bin, kann ich Ihnen die Sets leider nicht liefern. Ich könnte mir auch vorstellen, dass das – global gesehen – eine ganze Menge sind.
#####
Möglicherweise finden Sie hier was Sie suchen:
http://data.giss.nasa.gov/gistemp/2011/
ich kann die Zweifel an einer Mittelwertbildung der Hütten-Lufttemperaturen (Vereinbarung: 2m über Grund) nicht verstehen, vorausgesetzt, man verwendet nicht die Temperatur-Anomalien, wie Sie sie in der Grafik „Globale Mitteltemperatur von 1850 bis 2012 Met-Office“ dargestellt haben. Danach werden die heutigen Temperaturen auf den vorangegangenen Klimaabschnitt vor 30 Jahren bezogen (etwa 1960 – 1990), als wir eine kalte Phase hatten und die Presse von einer neuen Eiszeit sprach. Diese (falsche) Betrachtung suggeriert z.B. einen globalen Temperaturanstieg von 0,9 °C in den vergangenen 100 Jahren, obwohl dieser real nur 0,6 °C beträgt, wenn man 100 Jahre wirklich betrachtet, indem man von dem letzten Tiefpunkt der Kleinen Eiszeit im Jahre 1911 ausgeht. Dieser Wert wird auch allgemein bei einschlägigen (seriösen) Diskussionen zugrunde gelegt.
In meiner Untersuchung „Gibt es eine anthropogen verursachte Klimaerwärmung?“ (Status April 2013) habe ich die vom Deutschen Wetterdienst gemessenen und veröffentlichten Lufttemperaturen seit 1881 mit den seit 1843 gemessenen Meeresspiegel-Höhen in der Deutschen Bucht verglichen.
Die Veränderungen der Meeresspiegel-Höhen sind dabei der verlässlichste Indikator, weil hierbei wie bei den Flüssigkeitsthermometern (Quecksilber oder Alkohol) die Längenänderungen der Flüssigkeitssäulen proportional zu der aufgenommenen Wärmeenergie sind (bei Wasser gilt diese Proportionalität allerdings erst einige Grade oberhalb von +4°C. Siehe hierzu Nachtrag 2 in meinem Bericht).
Beim Vergleich der Verläufe der linear gemittelten Mittelwerte von Lufttemperaturen und Wasserspiegelhöhen zeigt sich, dass diese gleich sind und selbst Extremereignisse in bestimmten Jahren gleich abgebildet werden. Damit dürfte bewiesen sein, dass die in den veröffentlichten Grafiken Verläufe der jährlich gemittelten Lufttemperaturen diese durchaus richtig wiedergeben. Hierbei ist ihre absolute Höhe, regional abhängig, in diesem Falle sogar noch als genauer zu bewerten als die Wassertemperatur, die erst mit Hilfe von Annahmen errechnet werden muss.
Aus der bisherigen Diskussion entnehme ich, dass meine Untersuchung, die ich mit großem Verteiler verbreitet hatte, nicht gelesen wurde, auch von Ihnen nicht, Herr Limburg.
Mit freundlichen Grüßen, Gerd Zelck
Hallo Herr Baecker,
hat denn bislang noch niemand die Standardverteilung eines dermaßen wichtigen Mittelwertes bestimmt?
Sie muß ja da sein, denn mal wird er mit +14 °C, mal mit +15 °C angegeben.
Da ich nicht vom Fach bin, kann ich Ihnen die Sets leider nicht liefern. Ich könnte mir auch vorstellen, dass das – global gesehen – eine ganze Menge sind.
„Bei der durch Klimaänderungen ausgelösten Völkerwanderung, wanderten Viele. Heute soll durch Zäune, Ersaufenlassen im Meer usw. eine Völkerwanderung verhindert werden, weil die Hochtechnologieländer zwar alle mitleiden lassen, aber selber das etwas kompensieren können.“
Sieh an, da glaubt doch einer, daß wir (die reichen Länder) das Klima in den armen Ländern kaputtmachen.
Wahrscheinlich macht dann Bayern auch das Klima in Mecklenburg kaputt – der „Flüchtlingstrom“ ist da prozentual größer als der potenzielle weltweite in die reichen Gut-Klima-Länder.
Ich hätte auf die Realität zurückgreifen können. Stichwort: Waldsterben. Aber das beschränkte sich ja lediglich auf Deutschland. Über unsere offensichtlich sehr widerstandsfähigen Grenzen kam „Le Waldsterben“ ja nicht hinweg.
Also sehen sie mir doch nach, wenn mein Beispiel nicht zu 100% den Unsinn des AGW-Klimawahns trifft.
„Was meinen Sie, warum es trotz relativ kleiner Temperturschwankungen die Völkerwanderung gab. Auch die durch geringe Klimaänderungen ausgelöste Hungersnot ist mit „Schuld“ an der französischen Revolution.“
Ebel, bei Ihrem Geschwätz fangen Steine zum Weinen an:
Alles was Sie an Beispielen bringen sind Klimaänderungen hin zu KÄLTEREN Temperaturen.
Wir sollen uns aber wegen ein paar Zentel ERWÄRMUNG fürchten.
Verstehen Sie den Unterschied?
Ne? Dachte ich mir!
P.S.: was ist mit dem einen KW?
„Die Kausalität zwischen mehr CO2 und höheren globalen Durchschnittstemperaturen ist in der Wissenschaft bekannt und wird auch vom EIKE-Fachbeirat nicht abgestritten.“
Schmarrn bleibt Schmarrn.
Das wird auch durch hundertfaches runterbeten nicht anders.
Oder haben Sie eine Korrelation über einen relevant
langen Zeitraum anzubieten?
Ich weiß,haben Sie leider nicht…
„Trotzdem würde mich die Standardabweichung der mittleren Globaltemperatur (oder globalen Mitteltemperatur) von 15 °C interessieren, so es sie gibt.“
Wenn Sie mir die Sets von Verteilungen schicken die Sie interessieren, kann ich Ihnen die Standardverteilung der daraus ergebenden verschiedenen Mittelwerte berechnen. Koennen Sie aber auch selber machen, einfach die Formel nehmen.
“ Es scheint sich ja dabei um einen Mittelwert zu handeln.“
Sicher, was denn sonst?
Beide haben sich einen willkürlichen Zeitraum ausgesucht.“
Lieber Herr Jensen, bis hier hin, haben Sie noch keinen Fehler gemacht. 🙂
„Der „Klimawissenschaftler hat als Grund für diesen Anstieg das CO2 ermittelt und mit diesem die Politik aufgeschreckt (2-Grad-Ziel).
Der „Wissenschaftler“ in meinem Beispiel hat auch irgendeinen Grund gefunden. Welcher das ist, können sie sich aussuchen. Ich schlage dann einfach mal den Zuwachs an Fahrrädern in Deutschland in den letzten zwei Jahren vor. Die Politik setzt daraufhin ein „Nur-noch-halb-so-viele-Fahrräder-Ziel“ in die Welt.“
Um überhaupt Vorhersagen in die Zukunft hinein machen zu können, muss man Kausalitäten kennen. Irgendwelche statistischen Korrelationen helfen da nicht weiter. Die Kausalität zwischen mehr CO2 und höheren globalen Durchschnittstemperaturen ist in der Wissenschaft bekannt und wird auch vom EIKE-Fachbeirat nicht abgestritten. Streitpunkt ist da nur das quantitative Wirksamkeit dieser Kausalität. Der Zuwachs an Fahrrädern bzgl. der Körpergröße ist vielleicht gut genug, um eine Korrelation anzubieten. Aber von einem kausalen Zusammenhang ist nicht auszugehen. Eine Reduzierung des Fahrradbestandes hätte auf die zukünftige Größenentwicklung hätte dann genauso viel Einfluss, wie die verstärkte Ansiedlung des Klapperstorchs an der Geburtenrate.
„Der „Klimawissenschaftler“ rechnet den Anstieg für die nächsten Jahre fort und warnt vor höheren Durchschnittstemperaturen.
Der „Wissenschaftler“ in meinem Beispiel rechnet das Wachstum der letzten zwei Jahre fort und kommt auf eine höhere Durchschnittsgröße des Menschen von 9m.“
Das was Sie beschreiben ist eine lineare Extrapolation. Das findet aber in der Klimawissenschaft nicht statt. Zur Klarstellung, eine lineare Trendberechnung der Durchschnittstemperaturen wird nicht deshalb gemacht, um zukünftige Temperaturen linear zu extrapolieren. Es geht darum, aus einem vergangenen Zeitintervall festzustellen, ob ein Anstieg stattgefunden hat und wie stark dieser war und wie unsicher im statistischen Sinne diese Angaben sind.
Hallo Herr Baecker,
ja, war mein Fehler.
Trotzdem würde mich die Standardabweichung der mittleren Globaltemperatur (oder globalen Mitteltemperatur) von 15 °C interessieren, so es sie gibt. Es scheint sich ja dabei um einen Mittelwert zu handeln.
Falls nicht, dann sollte man das Dingens dringend umbenennen und ganz klar deutlich machen, dass es sich dabei um einen fiktiven Wert handelt
„Kann mir mal jemand die Standardabweichung für diese mittlere Globaltemperatur von +15 °C nennen?…Ich schätze mal (ganz grob): 15 °C +40 / -70.“
Mit dem Intervall geben Sie doch nicht die Standardabweichung der global gemittelten Temperatur („Globaltemperatur“) an, sondern den Wertebereich der Temperaturen auf der Erde, aus dem dieser Mittelwert berechnet wird.
Meinen Sie die Standardabweichung des Mittelwertes oder der Verteilung? Die Standardabweichung eines Mittelwertes berechnet sich, aus der Verteilung der Mittelwerte (!!) verschiedener Verteilungen aus derselben Grundgesamtheit.
„Aber was hat sich in unserem betrachteten Zeitraum von 100000 Jahren nicht alles geändert, nicht nur beim „Klima“?“
Was meine Sie, was sich alles ändert, wenn z.B. der Supervulkan „Yellowstone“ ausbricht.
Was meinen Sie, warum es trotz relativ kleiner Temperturschwankungen die Völkerwanderung gab. Auch die durch geringe Klimaänderungen ausgelöste Hungersnot ist mit „Schuld“ an der französischen Revolution.
Bei der durch Klimaänderungen ausgelösten Völkerwanderung, wanderten Viele. Heute soll durch Zäune, Ersaufenlassen im Meer usw. eine Völkerwanderung verhindert werden, weil die Hochtechnologieländer zwar alle mitleiden lassen, aber selber das etwas kompensieren können.
MfG
Mein fiktives Beispiel passt schon.
Die „Klimaforscher“ haben den Anstieg der Temperatur seit 1860 errechnet. Der „Wissenschaftler“ in meinem Beispiel hat den Anstieg der Körpergröße zwischen dem 12. und 14. Lebensjahr errechnet.
Beide haben sich einen willkürlichen Zeitraum ausgesucht.
Der „Klimawissenschaftler hat als Grund für diesen Anstieg das CO2 ermittelt und mit diesem die Politik aufgeschreckt (2-Grad-Ziel).
Der „Wissenschaftler“ in meinem Beispiel hat auch irgendeinen Grund gefunden. Welcher das ist, können sie sich aussuchen. Ich schlage dann einfach mal den Zuwachs an Fahrrädern in Deutschland in den letzten zwei Jahren vor. Die Politik setzt daraufhin ein „Nur-noch-halb-so-viele-Fahrräder-Ziel“ in die Welt.
Beide werfen Dinge in einen Topf, die offensichtlich nichts miteinander zu tun haben.
Der „Klimawissenschaftler“ rechnet den Anstieg für die nächsten Jahre fort und warnt vor höheren Durchschnittstemperaturen.
Der „Wissenschaftler“ in meinem Beispiel rechnet das Wachstum der letzten zwei Jahre fort und kommt auf eine höhere Durchschnittsgröße des Menschen von 9m.
Beide ziehen völlig unsinnige und übertriebene Schlussfolgerungen draus.
Die „Klimapolitik“ will den CO2-Ausstoß begrenzen, in meinem Beispiel werden eben Fahrräder reduziert.
Und dann stellt sich nach ein paar Jahren heraus, dass sich die durchschnittliche Körpergröße der Menschen gar nicht erhöht hat, obwohl die Anzahl der Fahhräder noch weiter zugenommen hat. Und dann kommt der „Wissenschaftler“ mit der Botschaft, dass sich wohl die Zunahme der Körpergröße der Menschen in der Anzahl der Insekten „versteckt“ hat. Etwas, was kein Mensch nachprüfen kann, so wie die Zunahme der Ozean-Temperatur in Tiefen von 4000m, wo sich ja die Erderwärmung „verstecken“ soll.
Seltsam Herr Weißenborn, ich verstehe den Artikel von Herrn Limburg anders. Hauptpunkt ist, ob eine globale Durchschnittstemperatur (egal wie sie nun bestimmt wurde) eine physikalische Relevanz hat. Ich zitiere: „Durch die vielfältige statistische Behandlung wird jedoch aus dem ursprünglich physikalischen Wert der Temperatur T des Messortes und der Zeit nur noch eine fiktive Zahl T*. Sie hat keinen physikalischen Inhalt mehr, obwohl sie in der Literatur mit der Dimension °C oder K bezeichnet wird. Somit verliert die berechnete Größe „mittlere Globaltemperatur“ als Durchschnittswert aller gemessenen lokalen Temperaturwerte ihren physikalischen Bezug.“
Übrigens, das hier ist ja ein offenes Forum. Da sollte es auch erlaubt sein, dass User auf Fragen eingehen, die nicht explizit an sie gerichtet wurden. Oder was denken Sie, Herr Weißenborn?
Stimmt, Herr Ketterer.
Wie hoch ist dann das Sigma?
Hallo Herr Ebel,
es läßt schon tief blicken, dass Sie jetzt die Fragen beantworten, die ich an Herrn Hader gerichtet habe. Sind Sie sein Sprachrohr?
Wer hat eigentlich behauptet, dass „Durchschnittstemperaturen“ (prinzipiell) nicht bestimmbar wären, zumindest in der Gegenwart?
Es geht hier doch wohl eher um die Genauigkeit. Und die spielt bei Temperaturniveaus, welche sich nicht annähernd so unterschiedlich darstellen, wie zwischen Holstein-Interglazial und Drenthe 1 Stadial prinzipiell eine größere Rolle, vor allem für die Beantwortung wichtiger Fragen wie
1. Steigen die (gleichgültig wie)gemittelten Globaltemperaturen oder fallen sie?
2. Welche weiteren Schlußfolgerungen lassen sich unter Einbeziehung weiterer Parameter, wie z.B. des Gehaltes an atmosphärischen Spurengasen, Aerosolen (und mehr) aus der Steigung der entsprechenden Ausgleichsgerade tatsächlich ziehen?
3.Welche politisch-gesellschaftlichen Schlußfolgerungen können daraus belastbar gezogen werden? Dies ist übrigens eine Frage, um deren Beantwortung Sie sich grundsätzlich herumdrücken.
Im Fall des Holstein-Interglazials und des anschließenden Drenthe 1 Stadials spielt die Genauigkeit der Durchschnitts-Temperaturbestimmung keine so entscheidende Rolle, weil die Faktenlage aus den Geowissenschaften (Transgression, Regression, Moränenablagerungen, Verbreitung, von Schmelzwasserablagerugnen usw.)in jedem Fall einen, verglichen mit rezenten Verhältnissen, enormen Unterschied zwischen den beiden Zeitabschnitten zwingend nahelegt.
Und es gibt natürlich auch die Proxydaten, wie z.B. Delta O18/O16 – Werte. Letztere sind sehr wahrscheinlich einer akribischen Messung der Temperaturen (die wir ja rückwirkend gar nicht durchführen können) unterlegen.
Nur mal hypothetisch: Die Menschen der Holsteinzeit beschließen, ein meteorologisches Meßnetz heutiger Technologie aufzubauen, weil Sie enorme, zukünftige, klimatische Veränderungen befürchten und sich darauf einrichten wollen.
Sie führen Messungen (und Wartung sowie die Auswertungen) über sagen wir 5000 Generationen akribisch und ohne ideologische Scheuklappen sowie Denkverbote fort.
Wieviele Meßstationen richten Sie im Gebiet, sagen wir Mitteleuropas, ein?
Welche Einzelparameter bestimmen sie neben der Lufttemperatur?
Wo errichten Sie die Meßstationen? Kann es nicht sein, dass im Laufe des Zurückweichens des Holstein-Meeres und des anschließenden Vorrückens des nordischen Inlandeises Meßstationen allein schon deshalb versetzt werden müßten?
Betrachten wir einen Meßpunkt. Er wird in der Nähe der heutigen Unterelbe auf dem Meerespiegel des Holstein-Meeres eingerichtet. Allein schon die nachfolgende langsame Regression des Holsteinmeeres mit beginnender Kaltzeit ändert die „Höhenlage“.
Irgendwann liegt die Meßstation auf einem tonigen Thundrenboden.
Dann wird sie von Schmelzwassersanden überschüttet und mußt natürlich neu aufgebaut werden.
Schließlich „überfährt“ das Inlandeis seine eigenen Schmelzwassersande. Das Höheniveau der (ständig in Betrieb gehaltenen) steigt um einige hundert Meter. Die Station befindet sich auf dem Inlandeis mit nun wieder ganz anderen Verhältnissen (Albedo, etc.)
Kann es ein, dass irgendwann einmal Meßstationen unter solchen Bedingungen gar nicht mehr betrieben werden können oder sie werden „versetzt“? Ändert sich die Anzahl?
Um nun zum Schluß zu kommen:
„Durchschnittstemperaturen“ und ihre zeitlichen Verläufe hätten unsere Vorfahren geinnen können, Aber was hat sich in unserem betrachteten Zeitraum von 100000 Jahren nicht alles geändert, nicht nur beim „Klima“? Die ganze Meßeinrichtung und Positionierung wahrscheinlich auch.
Sind die Vorfahren der „wahren“ Durchschnittstemperatur damit nähergekommen?
Zum anderen, von Herrn Limburg aufgeworfenen Thema, ob es sich bei der globalen Durchschnittstemperatur nun um eine physikalische Größe handelt oder nicht, mögen Sie mit den anderen Experten der Atmosphärenphysik hier trefflich streiten. Ich bin sicher, Ihnen fällt aufgrund Ihrer Fachkompetenz einiges dazu ein.
mit freundlichen Grüssen
Dirk Weißenborn
am Montag, 19.08.2013, 13:48
Kann mir mal jemand die Standardabweichung für diese mittlere Globaltemperatur von +15 °C nennen?
Ist so etwas überhaupt in der Literatur irgendwo angegeben?
Ich schätze mal (ganz grob): 15 °C +40 / -70.
Was sagt uns das?
########
Was Sie schreiben sagt uns, dass Sie offensichtlich von statistischen Grundwissen unbelastet sind. Ein keiner Hinweis: sigma wird nicht als Intervall angegeben.
„Wenn die Durchschnittsgeschwindigkeit höher ist, haben Sie die Strecke in kürzerer Zeit zurückgelegt…“
Lieber Herr Ebel,
Ich glaube ich brauche Ihre Unterstützung.
Ich habe vor kurzen mein altes Auto verkauft. 13 J alt, 350 000 km gelaufen. Mein Bordcomputer zeigte eine Durchschnittsgeschwindigkeit über die gesamte Laufzeit von 42,6 km/h an.
Ich habe mir mehrere Wochen den Kopf zerbrochen, wozu muss ich das wissen?
Jetzt, dank Ihnen weiß ich, dass ich die Strecke von 350 000 km schneller gefahren bin. Danke.
Nun jetzt quält mich die Frage – als was? Können sie mir da ein wenig helfen? Sind Sie sicher, dass es schneller und nicht langsamer war?
MfG
„Im Ernst, nach meiner Meinung ist die einzig vernünftige Methodik die u.a. k.F. Ewert verwendet, in dem er sich die Trends aller Stationen ansieht, die nach steigend, fallend, stagnierend, gruppiert und dann bestimmt, wieiviele (z.B. in %) davon fallen, steigen oder stagnieren. Da kommt Erstaunliches heraus. “
Da wird erstaunlicher Unsinn rauskommen; das wäre etwa so, als wenn man 20 Stationen in Berlin und eine auf der Zugspitze nimmt.
Wenn man diese Methode anwenden will, müssen die Stationen so verteilt sein, dass immer exakt eine Station repräsentativ für ihr Gebiet ist.
200 km² geschlossener Nadelwald ohne nennenswerten Relief kann mit einer Station repräsentativ erfasst werden. 200 km² mit mehreren Seen, Städten und starkem Relief benötigren mehrere Stationen, die repräsentativ für je ein Teilgebiet der 200 km² sind.
Die heutige Verteilung der Messstationen ist meiner Meinung global nicht repräsentativ.
Eine globale Auswertung der Atmosphärentemperatur ist meiner Meinung nach nur mit Statelliten möglich.
„Genauso wie man sich die Zeit zwischen 12 und 14 Jahren eines Kindes rauspicken kann und die Entwicklung dann für den Rest des Lebens fortschreibt.“
Um Prognosen zu machen, muß man für die Prognose wissenschaftliche Grundlagen verwenden.
Für die Größenentwicklung ist es die Biologie und auch da wird auf die zu erwartende Größe extrapoliert – zwar nicht linear, sondern auf der Basis des Wissens.
Genau so ist es bei Klima- und Wetterprognosen. Grundlage dafür ist die Physik. Und den Unterschied an Kurzzeit- (Wetter) und Langzeit- (Wetter)Prognose sehen Sie durch Anwendung der Physik bei der Gasbetrachtung:
– kurzzeitig ist die Bewegung der Gasteilchen angebbar
– langfristig gelten die Gasgesetze.
MfG
Dann gebt mir mal die Durchschnitts Temperatur der Erde an. Und zwar über die letzten 4,5 Millarden Jahre! Die Zeit, meine Herren, ist der Feind JEDER MESSUNG!
Wenn ich über das Klima forschen will, dann komme ich nicht darum herum mich mit dem Thema Zeit und Raum auseinander zu setzen.
Solange ihr aber immer noch beim CO2 Gas, dass einen Anteil von 0,039% an der Atmosphäre hat rum jammert, solange werdet ihr NIE eine wahrheitsfindende Wissenschaft betreiben.
Das Klima kennt keine festen Werte, weil das Klima den Raum und die Zeit des Menschen (menschliche Epoche der Erde) sprengt. Und damit ist jede Bestimmung und Berechnung einer Durchschnittstemperatur, die weltweit gelten soll, reine Willkür und dient der Verblödung der Menschheit!
„im Prinzip stimme ich Ihnen zu – Aber wie bestimmen Sie denn die Differenz der Durchschnittstemperaturen“
Wenn Sie bestreiten, daß eine Durchschnittstemperatur bestimmt werden kann, dann können Sie sich auch nicht auf Veränderungen der Durchschnittstemperaturen berufen – machen das aber mit
@ #46: Dirk Weißenborn sagt am Montag, 19.08.2013, 21:02
„die Differenz der Durchschnittstemperaturen zwischen dem Holstein-Interglazial und dem älteren Drenthestadial“
Wenn keine Durchschnittstemperaturen bestimmbar sind, wie definieren Sie dann einen Unterschied „zwischen dem Holstein-Interglazial und dem … Drenthestadial“. Haben Sie sich irgend etwas aus den Fingern gesaugt?
MfG
Lieber Herr Jensen, nix für ungut, aber ich bezweifle ernsthaft, dass Sie mit Ihrem Hintergrundwissen und Ihrer Ausbildung wesentliches über die Arbeitsweise in der Klimawissenschaft berichten können. Wenn Sie meinen, dass man Klimaprognosen durch Extrapolationen von gemessenen Werten betreibt, dann können Sie das von mir aus gerne weiter glauben, hat aber sehr wenig mit dem State-of-the-art zu tun.
„Beispiel: Ein Auto hat einen Bordcomputer. Der zeigt u.a. Durchschnittsgeschwindigkeit aller gefahrenen km an (wenn man kein reset macht). Nur, der „Wert“ ist wertlos.“
Nicht ganz. Wenn die Durchschnittsgeschwindigkeit höher ist, haben Sie die Strecke in kürzerer Zeit zurückgelegt – ganz gleich wie die Verteilung über Bleifuß und Stau war.
Bloß in der Regel wird man nicht über die Durchschnittsgeschwindigkeit gehen, sondern einfacher über die Fahrzeit.
MfG
„Analog: Es gibt keine Durchschnittstemperatur“
Der Zweifel an der Durchschnittstemperatur kam von Ihnen – nicht von mir.
MfG
„Zur Frage, ob aufgrund der möglichen Mangelhaftigkeit in der Erfassung und Auswertung von Temperaturdaten eine solide Basis für weitreichende Maßnahmen von Regierungen gegeben sind,haben Sie sich leider nicht geäußert.“
Wenn Sie eine mangelnde Erfassung behaupten, die die Daten wertlos machen würde, dann können Sie sich auch nicht auf Daten berufen, die angeblich keine Temperatursteigerung begründen würde.
Wenn Sie dagegen nur die Grundlagen der Physik anerkennen wollen, dann ergibt sich daraus die Zunahme der Oberflächentemperatur – ist schon seit 1906 bekannt: http://tinyurl.com/schwara
MfG
=================================
Das stimmt nicht so ganz. Die AGW-„Klimawissenschaft“ arbeitet mit 2 Fiktionen, nämlich mit der „globalen Erwärmung“ und dem „Treibhauseffekt“, und behauptet, dass CO2 eine Erwärmung verursachen muss, und zwar durch Gegenstrahlung.
Um diesen Quatsch zu widerlegen reicht es schon zu demonstrieren, dass physikalisch keine Erwärmung durch Gegenstrahlung möglich ist, aber die andere Fiktion ist auch nicht uninteressant.
Es gibt da auch andere Hilfsfiktionen, wie z.B. „weltweite Gletscherschmelze“, angeblicher Eisverlust auf Greenland und vieles mehr, aber man sollte sich in erste Linie mit der Hauptfiktion „Treibhauseffekt“ auseinandersetzen.
Genauso wie man sich die Zeit zwischen 12 und 14 Jahren eines Kindes rauspicken kann und die Entwicklung dann für den Rest des Lebens fortschreibt.
Sie können auch gern die Wachstumsrate aller Kinder zwischen 12 und 14 Jahren nehmen, daraus einen Mittelwert bilden und den dann fortschreiben.
Das ist das, was die AGW-„Klimawissenschaft“ macht.
„Nur, der „Wert“ ist wertlos.“
In der Tat.
Angenommen, man könnte es nicht reseten, wäre es ein sehr interessanter Ansatz zur Bestimmung des Fußabdruckes des Fahrers und damit der Ermittlung des Wertes des Gebrauchtwagens.
Selbstverständlich durch Erstellung eines Fahrmodells und darauf folgenden Projektionen (keine Vorhersagen – wohlgemerkt) der verbliebenen Langlebigkeit des Motors. 🙂
Leider hat die Sache einen Fehler. 😮
Wir wissen nicht ob er ein notorischer Bleifuß war, oder das Glück hatte überwiegend auf Autobahnen und Schnellstraßen unterwegs zu sein. Also wertlos 🙁
MfG
Herr Hader,
im Prinzip stimme ich Ihnen zu.
Aber wie bestimmen Sie denn die Differenz der Durchschnittstemperaturen zwischen dem Holstein-Interglazial und dem älteren Drenthestadial (für Mitteleuropa)?
Sind die beiden Zeitspannen gleich lang?
Wo befinden sich ihre Meßpunkte? Wieviele Meßpunkte mit den jeweiligen Ergebnissen ziehen Sie heran?
Befinden sich Ihre Meßpunkte während des Gesamtzeitraums an ein und demselben jeweiligen Ort?
mfG
Dirk Weißenborn
Lieber Herr Jensen, was Sie machen ist eine Extrapolation eines Durchschnittwertes. Davon war in dem Artikel von Herrn Limburg nicht die Rede.
Beispiel: Ein Auto hat einen Bordcomputer. Der zeigt u.a. Durchschnittsgeschwindigkeit aller gefahrenen km an (wenn man kein reset macht). Nur, der „Wert“ ist wertlos.
„Es gibt extensive („äußere“) und intensive („innere“) Eigenschaften eines Systems. …Über extensive Größen darf man mitteln, über intensive nicht.“
Verwechseln Sie das nicht mit nominalen vs. metrischen Größen? Über nominale (Augenfarbe) kann man nicht mitteln, über metrische (Körpergröße) schon.
„Nun ist die Problematik einer „mittleren globalen Temperatur“ einfach die, daß der Wärmegehalt eines Systems eine extensive Größe ist, die Temperatur aber nicht.“
Wenn Sie die Masse, Teilchenzahl, oder sonstige Bezugsgröße, auf die sich die extensive Größe bezieht, nicht kennen, ist tatsächlich nicht auszurechnen, welche thermische Energie ein System unbekannter Menge hat, welches die Temperatur 20°C hat.
Wenn Sie aber wissen, daß das System eine Temperatur T hat und die Abhängigkeit zwischen Temperatur, anderen Größen und der betrachteten extensiven Größe besteht, so ist es kein Problem, die Änderung der extensiven Größe mit der Temperatur zu bestimmen. Ein Beispiel aus dem Lehrbuch: Das Volumen V eines idealen Gases ist eine extensive Größe, Temperatur T und Druck p intensive. Für ein ideales Gas der Teilchenzahl N besteht der Zusammenhang p*V = N*k*T (bzw. = m*R0/M*T, mit R0 universelle Gaskonstante, M Molmasse, m Masse des Gases). Wenn p fix bleibt und N bekannt ist, so ist der Zusammenhang zwischen der extensiven Größe V und der intensiven Größe Temperatur eindeutig (Gesetz von Gay-Lussac, Prinzip des Gasthermometers). Auch die Änderung der extensive Größe innere Energie U ist durch eine Zustandsgleichung eindeutig mit der Temperatur bestimmt. dU = m*cv*dT.
„Man kann also über den mittleren Wärmegehalt der bodennahen Luftschichten mit Hilfe der Zustandsgleichung auf die mittlere Temperatur schließen. Dies ist der einzig physikalisch zulässige Weg. Den mittleren Wärmegehalt kann man aber nicht bestimmen. Schließlich ist die Atmosphäre eben genau nicht im thermodynamischen Gleichgewicht. “
Das liegt aber nicht an der Mittelung selber, sondern an der in der Klimatologie verwendeten. Wenn man n Pakete i=1,…n mit trockener Luft mit den Temperaturänderungen dTi und Masse mi hat, so ist die Änderung der innere Energie der Summe dU = cv*Summe mi*dTi = cv*dTm*m, wobei m = Summe mi ist und Tm die massen(bzw. dichte)gewichtete mittlere Temperatur ist. Wenn man das für die bodennahe Luft einer definierten Schichtdicke global macht, so bekommt man den Anteil der inneren Energie trockener Luft raus (man muß noch die latente addieren). Sinnvollerweise benutzt man dafür aber nicht die global geometrisch gemittelte Temperatur, sondern die global dichtegewichtete gemittelte Temperatur, wobei die Unterschiede marginal sind, wie Sie selber ausprobieren können.
„Wenn ich mich richtig erinnere, behaupteten Klimaforscher in Replik auf Essex, die an den Stationen tatsächlich gemessenen Temperaturen bzw. deren Mittelwerte wären eine lineare Funktion dieser thermodynamischen mittleren Temperatur.“
Empirisch aus den Modellen schon. In erster Näherung läßt sich sicherlich der lokale Temperaturtrend mit dem globalen in einer linearen Beziehung nähern, zumindest die langfristigen über mehrere Dekaden. Nur gibt es keine mittlere Temperatur, die thermodynamisch wäre und es gibt kein thermodynamisches Gleichgewicht des Klimasystems in sich. Das ist klimatisch wie meteorologisch wie physikalisch klar und das Essex paper stellt dies ja auch noch mal raus. Da haben Sie die Replik sicher missverstanden.
„Analog: Es gibt keine Durchschnittstemperatur – aber das die seit 1998 konstant ist, ist sicher.“
Analog:
Herr Ebel und Herr Limburg sind noch Kinder und spielen mit anderen Kindern im Hoff mit einem Ball (egal was).
Herr Ebel stellt Regeln auf, wann ein Tor gefallen ist und gilt.
Herr Limburg weist darauf hin, dass nach diesen Regeln man nie weiß ob ein Tor überhaupt gefallen ist.
Herr Ebel rückt nicht ab. Die Kinder spielen.
Herr Ebel verbucht ein Tor nach dem anderen. Der Abstand zu Limburg wächst.
Plötzlich wächst der Abstand nicht mehr, er schrumpft sogar ein wenig, weil Herr Limburg entweder Tore schießt oder aus der Spielsituation heraus nach den Ebelschen Regel zählen sie obwohl kein Ball im Tor.
Normalfall: die Kinder analysieren die Regeln und machen Korrekturen.
AGW-ler Fall: Herr Ebel beklagt sich bei Herr Limburg, das auch Tore zählen die gar nicht gefallen sind obwohl er mit den Regeln nicht eiverstanden war.
Mache ich hier einen Denkfehler, oder lässt sich tatsächlich die Ganze AGW-Lehre in 5 Sätzen beschreiben?
MfG
Und nun stellen Sie sich mal einen „Wissenschaftler“ vor, der sich ein 14jähriges Kind ansieht und die Wachstumsrate der letzten 2 Jahre. Sagen wir, das Kind ist in der Zeit von 1,30m auf 1,50m gewachsen. Das sind 20cm in den letzten zwei Jahren. Und nun geht dieser Wissenschaftler an die Öffentlichkeit und warnt davor, dass wenn es mit dieser Anstiegsrate so weitergeht, dann werden die Menschen im Schnitt 9 Meter groß!
Und er findet auch gleich noch eine Ursache für diesen rasanten Anstieg und die Politik wird aufgeschreckt und ergreift Maßnahmen, um die Größe des Menschen wenigstens auf 3 Meter zu begrenzen.
Und damit hätten wir ihr schönes Beispiel rund.
Ist so etwas überhaupt in der Literatur irgendwo angegeben?
Ich schätze mal (ganz grob): 15 °C +40 / -70.
Was sagt uns das?
„““Ich würde gern dafür eine Beweis sehen. Den gibt es aber nicht. Deswegen ist das nur eine plausible These, nicht mal eine Theorie, aber mehr nicht.“““
eine „plausible These“ also, na immerhin. Was genau ist ihnen plausibel dabei?
„““Selbst eine bewiesene Theorie wird durch einen einzigen Gegenbeweis falsifiziert. Siehe Stillstand der „Globaltemperatur“ bei gleichzeitigem Anstieg der CO2 Konzentration. Inzwischen müsste diese Zahl um 0,3 K höher sein, nach den Modellen. Ist sie aber nicht“““
Herr Limburg, dass ist falsch und sie wissen es. Denn, wenn man nur mal grob annimmt, dass diese ca. +1°C für eine Verdopplung von CO2 gelten mögen und das wird sogar von den meisten EIKE „Experten“ so gehandhabt, dann darf man die folgende Milchmädirechnung aufstellen: von 300 auf 600 also ca. 1°C dazu. Wir halten bei knapp 400, also sagen wir mal gut 0,3°C dazu, dass aber bitte über 100a gerechnet und mit etwas „Nachhinken“ in Folge der trägen Ozeane vielleicht nur so 0,2-0,3°C an anthropogenem Anteil an der gesamten Erwärmung der letzten 100a bis heute (rein CO2).
Ich bin seit jeher der Ansicht, dass nicht viel mehr dem anthropogenen Anteil zuzuschreiben ist, bis heute wohlgemerkt! Damit wird auch klar, dass natürliche, dekadische Variationen diesem noch deutlich kleinerem „AGW Signal“ weit überlegen sind und somit kann es auch in Zukunft mit der T in Wellen rauf und runter gehen, ohne das damit irgendeine „Theorie“ bestätigt oder falsifiziert wird!
Recht kann man ihnen nur geben, wenn sie sagen, die Klimamodelle sind falsch. Das zeigt sich mittlerweile doch sehr deutlich, wir „bräuchten“ die kommenden 5-10 Jahre eine globale Erwärmung von ca. zusätzlich 0,5°C um knapp ins Ensemblemittel der GCM`s zu gelangen und das ist nicht möglich.
Aber, nur weil hier offensichtlich zu starke positives Feedbacks eingehen, bzw. zu wenig von den negativen od. auch die natürlichen Variationen unterschätzt werden, ist der THE noch lange nicht ein „Phantom“ od. wie auch immer sie meinen mögen, es zeigt sich nur, dass der Alarmismus stark übertrieben scheint, nicht mehr und nicht weniger und das wissen wir aber schon sehr lange, od. etwa nicht?
mfg
Gunnar
Ich fand auf http://www.wetter24.de das die höchste Temperatur in Death Valley gemessen wurde und zwar im Jahre 1913. 100 Jahre später und man muss sich schon wundern das nicht mal 0.1 Grad Celsius mehr gemessen wurde.
http://www.ecad.eu zeigt mir für die Zeit von 1900 bis jetzt etwa 1.5 Grad Celsius mehr für Berlin-Mitte. Was bleibt übrig wenn man jetzt das abzieht was Berlin selbst verursacht? Die Hitzerekorde für Berlin waren in 1992 bei 38,6 Grad und 38,1 Grad im Sommer 1959. Auch hier muss man fragen wieviel Berlin selbst dazu beigetragen hat . Wie war das nochmal, Berlin hatte letzten Winter die Schlagzeile “Berlin friert im Jahrhundertwinter”. Das wiederum zeigt das alles möglich ist.
Man muss es kalibrieren, aber wie?
Ich lebe in Irland und habe mal die Daten für Juli 2012 und 2013 verglichen. Dieses Jahr hatten wir sehr viele schöne Tage. Der Himmel war meistens Wolkenfrei und kaum Regen. Letztes Jahr war es genau umgekehr. Viele Wolken und auch viel Regen. Was ich in den Daten sehe ist das die Wolken und der Regen einen Temperaturunterschied ca. 8 Grad bewirken. Also kann man nicht nur von der Temperatur ausgehen, da die Wolken und der Regen abkühlen. Ist jetzt 2012 oder 2013 ein typisches Jahr?
Interessanter Vergleich, insbesondere aufgrund eines offensichtlichen Fehlschlusses.
Hallo Herr Ebel,
Sie schreiben:
„Wie kann man bei etwas, was „nicht existiert“ eine Veränderung feststellen?“
In diesem Zusammenhang weise ich auf die Anführungszeichen vor und nach dem Wort „Durchschnittstemperatur“ hin.
Sie schreiben weiterhin:
„Also gehen Sie davon aus, daß doch eine Durchschnittstemperatur existiert – und wenn diese existiert, kann man auch deren Veränderung feststellen und ggf. beeinflussen, da ja die Durchschnittstemperatur von Einflüssen abhängt.“
Vergleichen Sie bitte mal die „Feststellung“ einer „Durchschnittstemperatur“ – von der ich schrieb – mit der Feststellung der Zahl der TATSÄCHLICH erwerbslosen BürgerInnen im erwerbsfähigen Alter.
Bei letzterer wird staatlicherseits auch „gemessen“. Aber erstens bleibt die Frage der Ungenauigkeit dieser „Messung“ (Stichtagszählung, etc.)und zweitens kommt die Anlegung gewisser Kriterien hinzu, bevor schließlich eine (Prozent-) Zahl öffentlich genannt wird.
Zur Frage, ob aufgrund der möglichen Mangelhaftigkeit in der Erfassung und Auswertung von Temperaturdaten eine solide Basis für weitreichende Maßnahmen von Regierungen gegeben sind,haben Sie sich leider nicht geäußert.
Schade!
Dennoch:
mit freundlichen Grüssen
Dirk Weißenborn
„Da haben Sie recht. Gleichgültig auf welche Weise die „Durchschnittstemperatur“ ermittelt wurde, könnte diese sowohl angestiegen als auch gesunken sein.“
Wie kann man bei etwas, was „nicht existiert“ eine Veränderung feststellen?
@ #31: Dirk Weißenborn sagt am Montag, 19.08.2013, 09:45
„Welche weitreichenden Maßnahmen von Regierungen könnte man also mit der „Feststellung“ der „Durchschnittstemperatur“ begründen?“
Also gehen Sie davon aus, daß doch eine Durchschnittstemperatur existiert – und wenn diese existiert, kann man auch deren Veränderung feststellen und ggf. beeinflussen, da ja die Durchschnittstemperatur von Einflüssen abhängt.
MfG
Man könnte auch sagen, daß intensive Größen bei der Mittelung ihren Bezug verlieren. Der Mittelwert von zwei Massen bspw. ist wieder eine Masse, der Mittelwert von zwei Temperaturen aber ist irgendwas nicht näher definiertes, nur eben keine Temperatur.
Nun ist die Problematik einer „mittleren globalen Temperatur“ einfach die, daß der Wärmegehalt eines Systems eine extensive Größe ist, die Temperatur aber nicht.
Man kann also über den mittleren Wärmegehalt der bodennahen Luftschichten mithilfe der Zustandsgleichung auf die mittlere Temperatur schließen. Dies ist der einzig physikalisch zulässige Weg. Den mittleren Wärmegehalt kann man aber nicht bestimmen. Schließlich ist die Atmosphäre eben genau nicht im thermodynamischen Gleichgewicht.
Anders ausgedrückt: Die mittlere globale Temperatur der bodennahen Luftschichten wäre diejenige, die sich einstellen würde, wäre die in den bodennahen Luftschichten gespeicherte Wärme überall gleich verteilt.
Hier setzen die oben zitierten Essex et. al. zu Recht an. Wenn ich mich richtig erinnere, behaupteten Klimaforscher in Replik auf Essex, die an den Stationen tatsächlich gemessenen Temperaturen bzw. deren Mittelwerte wären eine lineare Funktion dieser thermodynamischen mittleren Temperatur. Dann könnte man die Messungen tatsächlich als Maß für die Abweichung von der thermodynamischen Gleichgewichtstemperatur verwenden. Insbesondere bei der Bildung von Anomalien würden diese dann den Abweichungen von der thermodynamischen Gleichgewichtstemperatur entsprechen.
Nur habe ich für diese lineare Abhängigkeit noch nirgends einen Beweis gesehen. Essex wohl auch nicht. Letztendlich ist das nur eine Annahme der Klimaforschung, die berühmte Art des Physikers „in erster Näherung“ zu arbeiten, wenn man es nicht besser weiß.
„Haben Sie das wirklich noch nicht gemerkt? Egal, welcher „Denkschule“ wir innerhalb EIKE anhängen, sind wir einig darin, dass die Klimapanik, die geschürt wird, totaler Unsinn ist, “
Ja, das ist der gemeinsamer Nenner. Aber in der Begründung Ihrer gemeinsamer Position widersprechen Sie sich diametral. Das ist nicht überzeugend und wissenschaftlich sowiso nicht.
Hallo Herr Ebel,
Sie schreiben:
„Analog: Es gibt keine Durchschnittstemperatur – aber das die seit 1998 konstant ist, ist sicher.“
Da haben Sie recht. Gleichgültig auf welche Weise die „Durchschnittstemperatur“ ermittelt wurde, könnte diese sowohl angestiegen als auch gesunken sein.
Welche weitreichenden Maßnahmen von Regierungen könnte man also mit der „Feststellung“ der „Durchschnittstemperatur“ begründen?
mit freundlichen Grüssen
Dirk Weißenborn
Daß der Mittelwert einer Verteilung nicht selbst in der Verteilung vorkommen muß und daß im Speziellen das Mittel der Temperaturverteilung selbst nicht zwingend die Temperatur eines thermodynamischen Ensembles beschreibt und weder ein größeres Teilsystem des Klimasystems noch das Klimasystem als Ganzes, ist trivial und das weiß jeder, der sich mit Meteorologie und Klima beschäftigt.
Da man das Klimasystem quantitativ durch 3D-Klimamodelle basierend auf den Gleichungen der Physik beschreiben kann (also inklusive der der Thermodynamik), kann man auch erforschen, wie sich die Änderungen der Randbedingungen des Klimasystems auf die lokale Temperatur auswirkt. Dann kann man diese Ergebnisse mit den lokal beobachtbaren Trends vergleichen. Analog zu den Beobachtungsdaten kann man dann die lokal berechneten Temperaturen global mitteln und mit dem Beobachtungswert vergleichen. Letzeres passt erwartungsgemäß viel besser mit den Beobachtungen zusammen als die lokalen Werte. Denn das Klima hat nun mal eine räumliche Variabilität, die das 3D-Modell nicht in allen Details widergeben kann.
Damit ist jedoch nicht alles berücksichtigt. Um eine genaue Aussage zu treffen, müsste die Umlaufbahn der Erde um die Sonne und die unterschiedlichen Erdachsenneigungen der Erde über die 4,5 Mrd. Jahre noch mit einberechnet werden. Weiterhin haben auch die anderen Planetenstellungen im Sonnensystem einen Einfluss über das Erdklima in den vergangen 4,5 Mrd. Jahre.
Somit kann der Mensch weder für die Vergangenheit, noch für die Gegenwart und erst recht nicht für die Zukunft eine Erd-Mittel-Temperatur ermitteln.
Dazu hat der Mensch und wird der Mensch IMMER zu wenig Wissen haben. Die Vergangenheit wie auch die Zukunft des Erdklima bauen auf Glauben und Simulationen. Mit wahren Wissen hat das NICHTS zu tun! Spekulation nichts als Spekulationen und manipulierbare Interpretatioen bestimmen die AGW Szene. Das gegenwertige Wetter/Klima wird mal so und dann mal wieder anders interpretiert. Gerade so wie es einen in den Kramm passt. Mit Wissen hat das sehr wenig zu tun.
Das erinnert mich an
„Ob Tell gelebt hat, weiß man nicht – aber das er Geßler erschossen hat, ist sicher.“
Analog: Es gibt keine Durchschnittstemperatur – aber das die seit 1998 konstant ist, ist sicher.
MfG
Sie sind ein gutes Beispiel für jemanden, der kristalline und dynamische Intelligenz verwechselt. Mit kristallin intelligenten Kollegen, deren Wissen manchmal sehr beeindruckend ist (den „Hans-Joachim“ ordne ich in diese Kategorie ein), habe ich regelmßig zu tun – und nehme dann Reißaus, um mich nicht zu Tode zu langweilen. Die ganzen kristallin intelligenten Kollegen gehen mir gehörig auf den Senkel, weil sie nicht einmal in der Lage sind, sich zu reflektieren oder gar um die Ecke zu denken. Aber so ist das an den Universitäten, wo zweitklassige Forscher drittklassige berufen und diese wiederum viertklassige – der peak-IQ wurde eben schon vor vielen vielen Jahren überschritten, und jetzt geht es eben nur noch abwärts. Ich kann mir gut vorstellen, bei Ihnen in einer Prüfung durchzufallen, ich gehe aber auch jede Wette ein, dass Sie bei mir keine Prüfung bestehen würden. Es war eine meiner bittersten Erfahrungen, dass viele Lehrstühle mit „Nieten in Nadelstreifen“ besetzt sind. Das wollte ich anfangs nicht wahr haben, habe es nach beinahe 15 Jahren aber akzeptiert.
Außerdem habe ich doch nur, ich sage es zum letzten mal, meinen – Gott hab ihn selig – Geographie-Lehrer zitiert. Ich habe doch mit keinem Wort gesagt, dass das meine Meinung ist, obwohl ich „was Gescheits“ studiert habe. Und bzgl. der Klimawissenschaften bestätigen Sie doch, was ich gesagt habe.
„Nehmen wir einmal an, dass es eine globale Temperatur gibt, dann können wir, so wie es die Klimamodelle besagen, der Erde eine Temperatur T(Erde) zuschreiben.“
Was veranlasst Sie zu glauben, dass Klimamodelle der Erde mit nur einem Temperaturwert beschrieben? Das ist fuer die Klimamodell mir mehr als Null Dimensionen nicht der Fall. Die modernen Modelle modellieren in drei Dimensionen und damit die raeumliche Temperaturverteilung. Ist Ihnen das bislang nicht bekannt gewesen?
Sehr geehrter Herr M.L., sicher wird über die ganze Erdkugel und das ganze Jahr gemittelt, um einen globalen Mittelwert für ein ganzes Jahr zu errechnen.
Mir ist nicht klar, was Sie daran stört und wie Sie es anders machen würden.
Ich verstehe auch nicht, warum man die zur Verfügung stehenden Seewassertemperaturen nicht verwenden sollte.
Das dies angeblich „willkürlich“ geschieht, ist eine Unterstellung ihrerseits.
Falls Sie tatsächlich Zweifel an den terrestrisch erhobenen Daten haben sollten, vergleichen Sie diese doch einfach mit Satellitendaten. Sie weisen fast exakt den gleichen Trend auf.
Gruß
Hans Jung
Bemerkenswert ist aus meiner Sicht, dass argumentativ „der Feind meines Feindes ist mein Freund“ wichtiger als eine solide wissenschaftliche Basis ist. Solange die politische Grundausrichtung stimmt, ist alles okay. So wie es in vielen öffentlichen Einrichtungen und Institutionen wichtig war (und ist) das richtige Parteibuch zu haben, so ist hier nur entscheidend wie man es mit der „Klimapanik“ und der Energiewende hält. Schade.
Ich meine, wer einer Lufttemperaturänderung eine Änderung des Wärmeinhalts zuordnet, ist ja schon unglaubwürdig.
Wenn dann noch ein Temperatur-Mittelwert (der abstrakt ist, wie im Artikel sehr richtig erläutert also keine physikalische Größe eines Objektes darstellt) von verschiedenen Orten verwendet wird, ist das nur eine Potenzierung der Unglaubwürdigkeit.
Ich habe den Eindruck, daß Klimatologen mit der Thermodynamik nicht viel am Hut haben oder bewußt haben wollen.
====================================
Das glaube ich Ihnen gerne, Herr Innerhofer, und kann deshalb nur wiederholen: das Geschäft „Klimawissenschaft“ muss dringend geschlossen werden, da es mit den Klimaprofis nie klappen könnte.
Sie können natürlich einen Mittelwert zwischen Erde und Mars definieren. Ob dieser Mittelwert nun besonders aussagekräftig ist, bezweifle ich, aber das ist dann ihr Problem.
Mitteltemperaturen von Planeten sind dagegen durchaus aussagekräftig, nicht umsonst finden sie in jedem Lexikon solche Tabellen.
Oder noch einfacher: Lesen Sie doch einfach mal die letzten 10 Artikel hier bei EIKE und die Kommentare dazu. Wenn ich betrachte, dass jeder hier die Metrik „mittlere Globaltemperatur“ benutzt, dann ist sie ja offensichtlich nützlich.
„Ein simples Beispiel. Nehmen wir einmal an, dass es eine globale Temperatur gibt, dann können wir, so wie es die Klimamodelle besagen, der Erde eine Temperatur T(Erde) zuschreiben.“
Wenn Sie die Erde als 0 dimensional beschreiben, waere das sogar exakt. Aber beim 0D Klimamodell fehlen natuerlich viele Feinheiten. Daher gibt es ja heute auch 3 D Klimamodelle mit einer 3 D Temperaturverteilung.
Unabhaendig davon laesst sich natuerlich auch bei der 2 D Temperaturverteilung ein globaler Mittelwert bilden, mehr als der Mittelwert ist dies aber nicht. Nur Mittelwerte und andere Verteilungsmomente sind nunmal bekanntlich die statistischen Kenngroessen einer Verteilung. Das ist so ublich in der Statistik.
ein 0D Modell eines Erdemarsmixplaneten halte ich fuer unsinnig. Was wollen Sie damit?
„Sie weichen aus! Meine zentrale Aussage war, dass die mittlere Globaltemperatur nur so heißt, aber keine Temperatur mehr ist, sondern nach mehr oder weniger willkürlichen Regeln ermittelte Zahl.“
a) der globalen Mittelwert der Temperatur gibt nicht die Temperatur eines Koerpers an. Das ist doch wohl trivial und offensichtlich.
b) Die Regeln sind nicht so willkuerlich wie Sie glauben, es gibt zwar verschiedene Rechnungsmethoden, aber das Ziel ist immer, das Integral der bodennahen Temperatur ueber die Erdsphaere zu berechnen. Dazu gilt es verschiene Approximationen. Geteilt durch die Oberflaeche ergibt dies den globalen Mittelwert. Das ist uebliche Mittelwertbildung.
PS es gibt beliebig viele andere Beispiele, bei denen der Mittelwert einer Verteilung nicht als Wert in der Verteilung vorkommt.
Ein simples Beispiel. Nehmen wir einmal an, dass es eine globale Temperatur gibt, dann können wir, so wie es die Klimamodelle besagen, der Erde eine Temperatur T(Erde) zuschreiben. Dies ist dann natürlich auch für den Mars mit T(Mars) möglich. Die gemeinsame Temperatur von Erde und Mars könnten wir dann als T(Mittel)=0.5(T(Erde)+T(Mars)) definieren. Welchen Sinn soll diese Temperatur haben? Sie besagt nichts über die Erde, nichts über den Mars und auch nichts über das Gebiet dazwischen aus. Falls ihnen das Beispiel zu simpel ist, dann lesen sie doch einfach den Artikel von Essex et al. im J. of Non-Equilibrium Thermodynamics und beweisen, wo der Fehler der Autoren liegt. Wenn sie dies nicht können, dann schweigen sie einfach einmal, auch wenn es einen Kernpunkt ihrer Philosophie oder ihres Glaubens betrifft.
die meisten Definitionen und Beschreibungen eines atmosphaerischen Treibhauseffekts beruhen auf der global gemittelten oberflaechennahen Lufttemperatur sowie einer fiktiven Temperatur, die man als effektive Strahlungstemperatur bezeichnet. Das kann man auch in dem Beitrag von Luedecke & Link, „Der Treibhauseffekt – wie funktioniert er?“ von 2010 zu finden, der hier immer noch als EIKE-Publikation aufgelistet wird. Von daher ist Ihr Angriff auf die globale Mitteltemperatur zumindest als merkwuerdig einzuordnen. Haben Sie keine Angst davor, als Nestbeschmutzer bezeichnet zu werden?
Was diese effektive Strahlungstemperatur aus physikalischer Sicht wert ist, haben mein Ko-Author Dr. habil. Dlugi und ich in Arbeiten von 2010 und 2011. dargelegt, naemlich nichts. Also braucht niemand diese global gemittelte oberflaechennahe Lufttemperatur, ausgenommen natuerlich diejenigen, die sich mit einem „globalen“ Klima beschaeftigen, was nach der Bedeutung des Wortes „Klima“ nicht existiert.
Nun hat vor zwei Jahren mein Fachkollege Dr. Thuene einen Artikel, „Statistiken vernebeln zunehmend die Realität“, in der Preussischen Allgemeinen Zeitung publiziert, in dem er u.a. schrieb:
„Der Treibhauseffekt ist eine simple Behauptung, die noch nie wirklich nachgewiesen werden konnte. Bevor sich ein Effekt, die Abhängigkeit der Temperatur vom Kohlenstoffdioxidgehalt der Luft, im globalen Maßstab zeigt, müsste er tatsächlich gemessen und gezeigt werden können.“
Damit sprach er die Problematik des Begriffs „Treibhauseffekt“ zielgerecht an. In einem offenen Brief, der hier auf der Webseite von EIKE zu lesen war, erwiderte der EIKE-Hausphysiker:
„Dieses Argument verfehlt den Punkt. Ein hoher Prozentsatz von Phänomenen und Effekten der Physik, die zudem Basis technischer Anwendungen sind, können nicht direkt gemessen werden. Nur ein stellvertretendes Beispiel – Druck und Temperatur im Sonneninneren. Der Bethe-Weizsäcker-Zyklus, der die Arbeitsweise des Fusionsofens „Sonne“ beschreibt, ist eine kernphysikalische Theorie, von der immer nur Details hier auf der Erde und im Labor gemessen werden können. Diese Theorie trifft zu.“
Er verglich also den auf vielfache Weise definierten und beschriebenen Treibhauseffekt mit einer physikalischen Theorie wie dem Bethe-Weizsaecker-Zyklus, was nur bedeuten kann, dass er nicht weiss, was eine physikalische Theorie ist, denn der atmospaherische Treibhauseffekt ist keine Theorie, sondern, wenn man all die verschiedenen Definitionen und Deutungen heranzieht, eine laengst als falsch widerlegte Hypothese.
Sie muessen endlich darlegen, was EIKE eigentlich zum Ziel hat.
MfG
sie sprechen zum Teil ja wirklich nennenswerte Probleme der sg. Klimawissenschaft an. Auch diese Definition bzw. Messung und dann Berechnung der globalen Mitteltemperatur ist, auch wenn die Problemchen längst bekannt, nennenswert.
Wir wollen aber mehr wissen. Was darf man zB. von ihren Aussagen halten wie hier:
„““Seit die Idee vom menschgemachten Klimawandel in die Köpfe der Menschen Einzug gehalten hat“““
sie denken, Treibhausgasemissionen hätten KEINEN Einfluss aufs Klima?
„““Namentlich ist hier der Einfluss des Spurengases CO2 gemeint, das gemeinhin als Treibhausgas bezeichnet wird“““
-gemeinhin-? sie meinen status quo der Wissenschaft?
Sind sie eigentlich mit Herrn Lüdecke einig, was sie hier so darstellen wollen? Ist ihnen einfach alles recht, was nur irgendwie gegen den IPCC Alarmismus steht, oder versuchen sie, totalen Quatsch von guter Kritik zu trennen? ich bin mir nicht so sicher, mir scheint eher, bevor sie die wirklichen Fakten realisieren, ist es ihnen lieber, wenn Leute gar G&T zitieren, oder den alten Woods hervorkramen um damit reinsten Unsinn in Foren zu laden, einfach um „gegen alles“ zu sein.
Glauben sie nicht, auch wir Skeptiker und ja, ich bin einer, haben keinen Anspruch auf Qualität?
Es gäbe genügend gute Ansätze, die Alarmisten zu bekämpfen, aber nicht mit Kellerniveau. Damit macht man denen höchstens eine Freude, ich hoffe, sie werden das bald mal einsehen.
Wenn sie heute hergehen und Pyrgeometer als was der Teufel will darstellen versuchen, die Mittelung der Globaltemperatur als Unsinn hinstellen usw, ja dann sollten sie schon mal mit besseren Ideen daherkommen und überhaupt mal überlegen ob es sein kann, dass wir vom Fach alles Trottel sind und nur sie od. Herr Paul, Herr Keks und Konsorten die wenigen sind, die alles besser verstanden haben.
MfG
Gunnar
am Sonntag, 18.08.2013, 12:26
Ich erinnere mich hier an den Rat unseres Erdkunde/Geographie-Lehrers auf dem Gymnasium aus den 1970er Jahren: „Komm mir bloß keiner auf die Idee, Meteorologie zu studieren. Das ist Dilettantismus auf allen Ebenen !“ Das habe ich dann zum Glück auch nicht studiert. Heute würde er, Gott hab ihn selig, wohl sagen: „Komm mir bloß keiner auf die Idee, Klimawissenschaften zu studieren. Das ist Dilettantismus auf allen Ebenen !“
Herr Schlohr,
offenbar wissen Sie und Ihr Geographielehrer ueberhaupt nicht, was Meteorologie ist. Nur so kann man diesen Quatsch kommentieren, den Sie hier zum besten geben.
Fur Sie zum mitschreiben: Gegenstand der Meteorologie ist die Physik und Chemie der Atmosphaere. Klimatologie, die von Herrn Limburg angesprochen wurde, ist nur ein kleiner Teilaspekt. In den 1970er Jahren haben wir als Studenten die Klimatologie als gesellschaftswissenschaftlichen Teil der Meteorologie bezeichnet, zu der wir auch die Wetterprognose zugerechnet haben.
Was an der Universitaet zu Koeln von der Diplom- und Studienordnung als Vorlesungen zur Meteorologie vorgeschrieben wurde, war bis zum Vordiplom nahezu identisch mit dem Studium in der Physik. Der einzige Unterschied bestand darin, dass an Stelle einer Vorlesung zur Chemie die Einfuehrung in die Meteorologie genommen werden musste. Nach dem Vordiplom standen weitere Vorlesungen der Theoretiscen Physik an, naemlich Thermodynamik und Statistik sowie Quantenmechanik. Hinzu kamen vier Theorievorlesungen der Meteorologie sowie diverse Spezialvorlesungen, z.B. Physik der planetarischen Grenzschicht, atmosphaerische Strahlung etc. In meinem Falle hatte ich noch Geophysik als weiteres Nebenfach, so das auch die Theorievorlesungen der Geophysik zu hoeren und Leistungenachweise zu erbringen waren.
Aus Ihren Beitraegen, die Sie hier zum besten geben, darf ich nur anmerken, dass Sie aller Wahrscheinlichkeit nach nicht einen einzigen Leistungsnachweis in einer meiner Vorlesungen (Dynamik, Physik der atmosphaerischen Grenzschicht, Strahlung und Turbulenz) erhalten wuerden.
Noch eine Anmerkung: Nach meinem Wissensstand existierte bis vor ein paar Jahren in Deutschland nirgendwo ein eigenstaendiger Diplomstudiengang Klimatologie. In der Schweiz ist offenbar ein solcher Studiengang eingerichtet worden. Mag sein, dass mittlerweile auch in Deutschland dieser Unfug Nachahmung gefunden hat.
Zu ihren Anmerkungen in meinem #1:
„“Mit welcher Metrik würden Sie den entscheiden, wie gut oder schlecht Klimamodelle der Realität entsprechen?“
Dieselbe Frage könnten Sie dem Besucher auf dem Rummelplatz stellen, der sich von einer Wahrsagerin mit Kristallkugel die Zukunft vorhersagen lässt.
Versuchen Sie es mal!
Im Ernst, nach meiner Meinung ist die einzig vernünftige Methodik die u.a. k.F. Ewert verwendet, in dem er sich die Trends aller Stationen ansieht, die nach steigend, fallend, stagnierend, gruppiert und dann bestimmt, wieiviele (z.B. in %) davon fallen, steigen oder stagnieren. Da kommt Erstaunliches heraus.“
Das könnte man tun. Ob man damit aber die Stagnation der letzten 15 Jahre überhaupt bemerkt hätte? GISS z.B. nennt +0,06° für diesen Zeitraum.
Es wären aber noch Probleme zu lösen:
1.) Unterschiedliche Verteilungsdichte der Stationen
100 Stationen in der Schweiz können nicht dasselbe Gewicht haben wie 100 Stationen für ganz Afrika. Mir fällt da als Lösung nur eine Rastereinteilung des Globus ein und Mittelwertbildung für jede Rasterzelle.
2) Vergleich der Stationentrends
Eine Einteilung in steigend oder fallende Trends ist viel zu grob: Eine Zunahme von +5° kann nicht dasselbe Gewicht haben wie eine Abnahme von -0,5°. Mir fällt als Lösung nur Mittelwertbildung.
Und dann sieht man, dass man im Prinzip genau das tut, was derzeit zur Ermittlung der globalen Mitteltemperatur getan wird.
Noch etwas:
Abgesehen davon, dass mit ihrer vorgeschlagenen Methode man die Stagnation kaum entdeckt hätte, gibt es noch ein anderes Problem: Ohne globale Temperatur kann es logischerweise auch keine Stagnation derselben geben.
Es scheint bei EIKE aber auch nicht jeder ihre Einwände zu teilen. Wenn Sie in das letzte Paper von Herrn Lüdecke blicken, werden Sie erkennen, dass von der ersten bis zur letzten Seite Temperaturmittel gebildet und interpretiert werden. Ohne diesen Begriff wäre die Arbeit gar nicht möglich gewesen.
MfG
Kommentar:
Elusive lt. Leo „schwer fassbar“. Dass damit die Lufttemperatur gemeint ist, weiß jeder, der sich hier tummelt.
### ######################
Ja und genau das ist der Grund weswegen EIKE hier von BODENtemperaturen spricht.
„Boden-Temperaturanalyse nach GISS/ Die schwer fassbare Absolute Boden-Temperatur (SAT)“
Leider fehlen der Klimawissenschaftl klar definierten Vorgehensweisen in Veröffentlichungen insbesondere historisch gewachsener, aus welchen sich jedermann einen klaren Zusammenhang eben dieses Maßes “Welt-Temperatur“ Wertes erklären und auch folgerichtig wissenschaftlich kritisch argumentieren kann.
Wenigstens für seines Steuer-Gelder in Anspruch zu nehmen um zu kontrollieren und auf Unzulängliches überhaupt hinweisen zu können.
Hinzu genommen sollte werden: die Signifikanz (des Maß genau sein) eines jeden einzelnen Messwertes:, um die Aussagekraft der Messungen in physikalisch nachvollziehbaren Vorgängen zu haben.
Insbesondere jedoch ist in der Physik (beispielsweise Wolkenbildung) um Vorgänge zur Energie Übertragung tunzu können Kenntnis erforderlich um die Statistik für Klima-Änderungs-Analysen-Vorhersagen überhaupt heranziehen zu können: was im Wesentlichen vom Transport der Wärme(Energie) per Strahlung( von der Sonne), Leitung und Konvektion hier via Wasser(dampf) bestimmt wird.
Den Trend des Maßes “Temperatur“ aus : fallend, stagnierend, steigend: Häufungen zu erörtern gibt den Temperaturgang, doch dieser bestimmt in bekannter Weise nicht alleine das Klima auf Erden, wie selbe Werte an Temperatur jedoch unterschiedlich vorkommend: beispielsweise Vegetation aufzeigen, usw. usw.
ZUERST MAL VIELEN DANK FÜRS ÜBERSETZEN!!!!.
Einem Laien kann‘s passieren, aber Herrn Limburg hätte das nicht durchgehen dürfen:
GISS: The Elusive Absolute Surface Air Temperature (SAT)
Wird bei Eike zur Die schwer fassbare Absolute Boden-Temperatur (SAT)
Zum einen ist es falsch weil die Bodennahe Lufttemperatur gemeint ist (alos je nach Meteorologischem Dienst zwischen 1,2m und 2m gemessen).
Zum andern ist es falsch wie gerade die Bodentemperatur sehr gut erfassbar ist.
Bitte verbessern
MfG
Ketterer
Sehr geehrter M.L., der Mittelwert nach einer räumlichen Interpolation sagt aus, ob und wie sich der Mittelwert der globalen Temperaturen verändert.
Gruß
Hans Jung
Meteorologen sind also Dilettanten, hmm.
Das sagt einer der was studiert hat?“
Sie haben mich völlig missverstanden. Ich habe doch nur meinen – Gott hab ihn selig – Geographie-Lehrer zitiert und spekuliert, was er heute sagen würde 🙂 . Ich habe doch gar nicht gesagt, dass Meteorologen Dilettanten sind, und ganz sicher gibt es sehr helle Köpfe bei den Meteorologen.
Und zu Ihren Ausführungen bzgl. der Klimawissenschaften: Sie sagen doch selber, dass man dieses Fach nicht „richtig“ studieren kann.
„Damit entsteht ein Paradox. ? am Ort r hängt auch von den Zuständen an allen entfernten Positionen {rk} ab. Jedoch sind chemische, physikalische oder biologische Prozesse, die durch die Temperatur am Ort r gesteuert werden, keine Funktionen der Temperaturen außerhalb von r“
Xi ist aber per Definition keine vom Ort abhaengige Funktion, genauso wenig wie die absolute Globaltemperatur. Wenn Sie ein Mittel ueber eine Kugel bilden, so ist dieser Wert natuerluch nicht von den Koordianten auf der Kugel abhaengig. In Ihrer zitierten Formel von Essex ist Xi ja auch nur von der Zeit tM abhanegig, aber nicht von ri.
Meteorologen sind also Dilettanten, hmm.
Das sagt einer der was studiert hat?
Wahsrcheinlich gar nichts und so haben sie nicht die geringste Ahnung, wie ein Studienplan der Meteorologie aufgebaut ist und sie wissen ja nicht mal, dass man „Klimawissenschaften“ nicht als Studiengang findet. Mit dem Klima beschäftigen sich in erster Linie Meteorologen, Physiker, Geologen und andere Naturwissenschafter.
Nur Laien sehen in der gloablen T Bestimmung ein „Phantom“. Es gibt Schwierigkeiten, die sind aber längst bekannt und die möglichen Fehler liegen im unteren 1/10 Berreich. Das reicht!
Sehr geehrter Herr M.L., da kann alles mögliche herauskommen. Nur nichts Brauchbares zur Beantwortung der Frage, ob und wie sich die globale Durchschnittstemperatur ändert.
Auch ohne besondere mathematische Kenntnisse ist klar, man braucht hierfür zuallermindest:
1. Eine Quantifizierung des Temperaturtrends jeder Station.
2. Eine räumliche Interpolation dieser Werte.
Gruß
Hans Jung
zur Definition der globalen Mitteltemperatur und ihrer Bestimmung wurde ja schon in der Vergangenheit alles gesagt, daher bringe ich mal einen pragmatischen Aspekt ins Spiel:
Mit welcher Metrik würden Sie den entscheiden, wie gut oder schlecht Klimamodelle der Realität entsprechen?
Mit welcher Metrik würden Sie bestimmen, ob die global warming (der Einfachheit halber jetzt mal reduziert auf die Atmosphäre)im letzten Jahrzehnt stagnierte oder nicht?