Kritik an Trenberth‘ Energiefluss

Das Trenberth/IPCC “Earth’s Energy Budget Diagram”

(2. Entwurf vom 25. 10.2011 von Bob Fernley-Jones, genannt Bob_FJ)

Die nachfolgende Grafik stammt aus einem Trenberth –  Papier von 2009. Sie ist eine Aktualisierung der Grafik aus dem IPCC-Bericht von 2007 (war auch schon im 2001er Bericht):

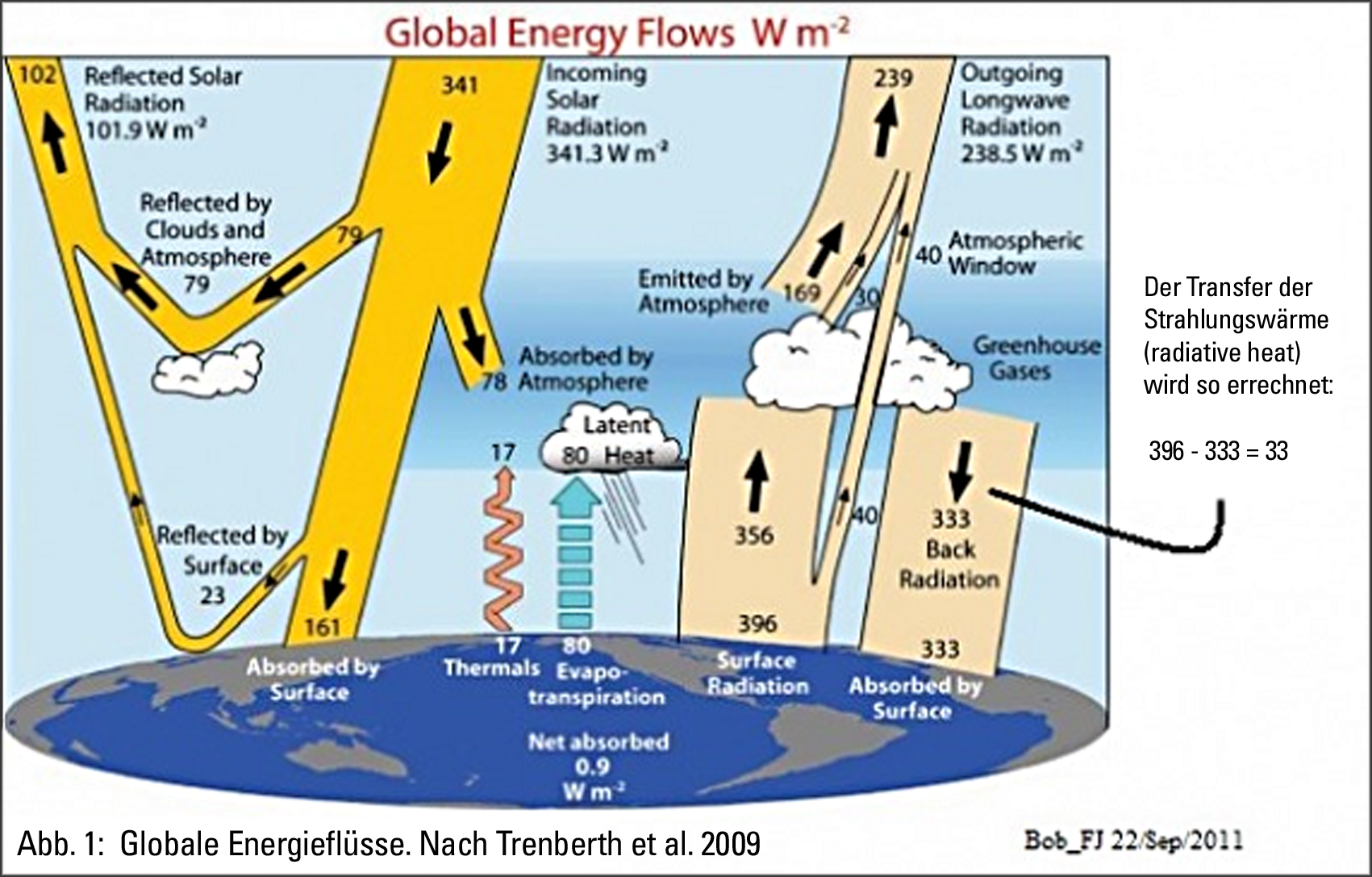
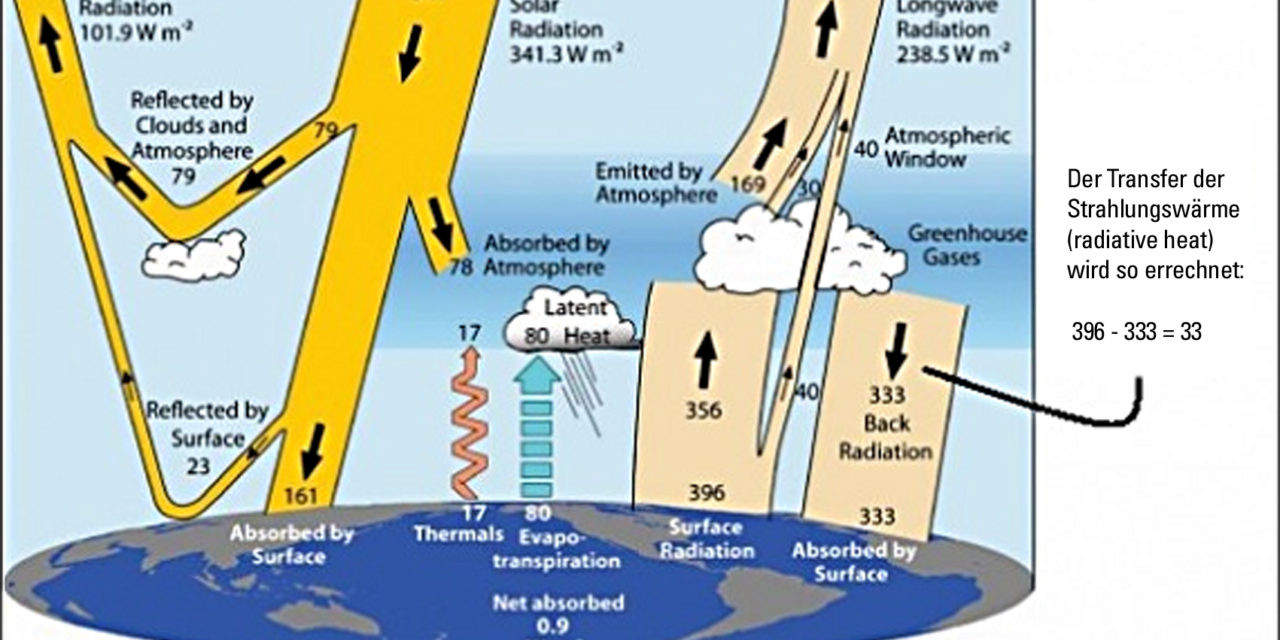
Das Ungewöhnliche an dieser Grafik ist: Sie zeigt nicht den Wärmetransfer durch Abstrahlung von der Erdoberfläche. Stattdessen beschreibt sie den Treibhauseffekt in Form eines Strahlungsflusses, so wie die Autoren ihn sehen. Anders gesagt, als elektromagnetische Strahlung. Dazu enthält sie weitere Beschreibungen, mit denen Naturwissenschaftler auf dem Kriegsfuß stehen. Die elektromagnetische Strahlung ist eine Energieform, die häufig mit Wärme verwechselt wird. Später wird gezeigt, dass die oben dargestellte Oberflächenabstrahlung (Surface Radiation) von 396 W/m2 sich ganz anders als Wärme verhält. Auch kann eine Temperaturänderung in Materie nur stattfinden, wenn es Wärmeaustausch gibt, ganz gleich, wie viel elektromagnetische Strahlung in der Atmosphäre herumsaust.

Die nachfolgende Abb. 2 ist ein leichter verständliches Schema. Es stammt von der NASA und aus Wikipedia. Dieses Schema vermeidet die oben angesprochene Problematik.

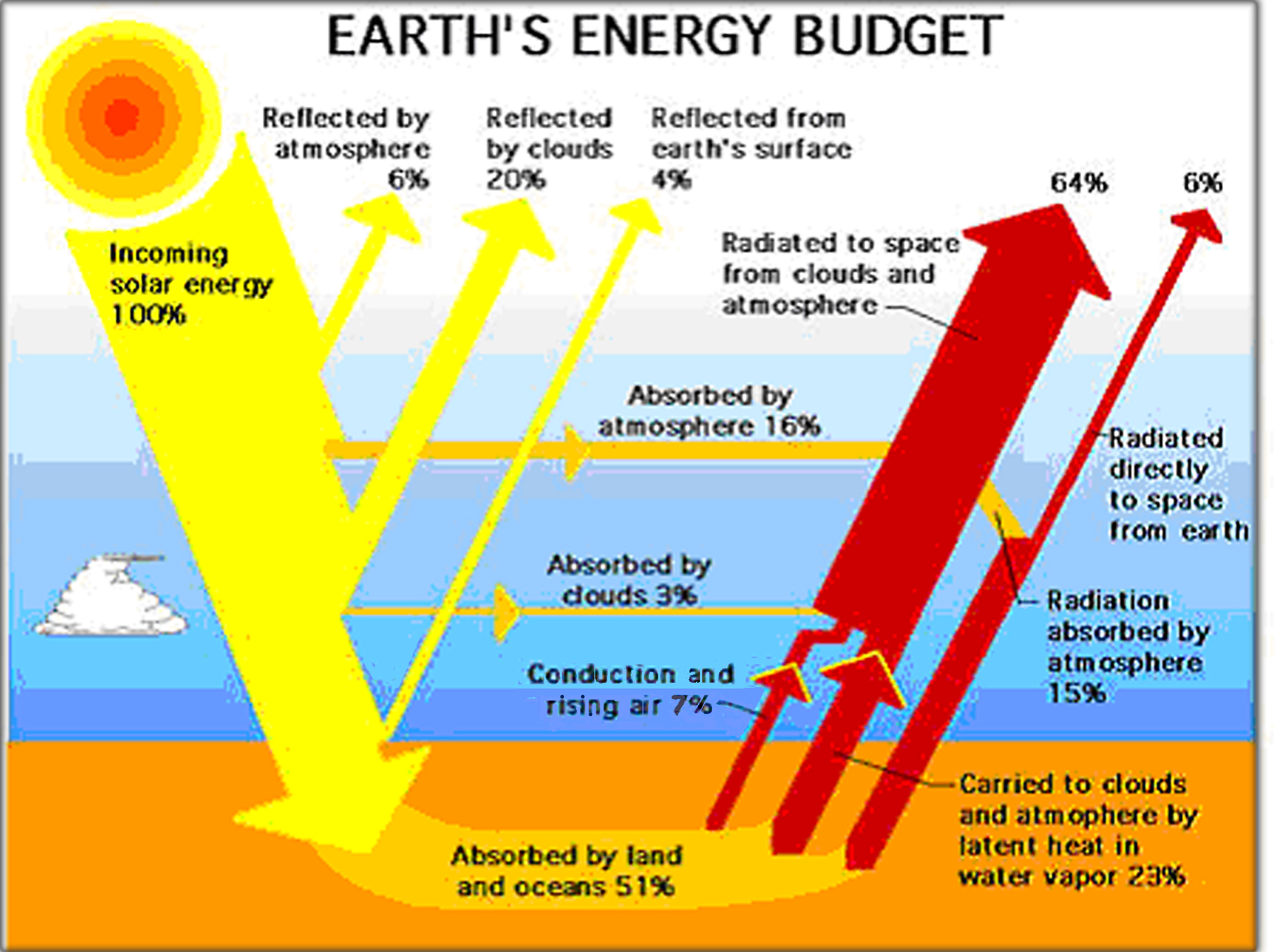
Abb. 2                                                     (NASA)

Im zitierten Trenberth et al. Papier wird gesagt, dass die in der Grafik mit 396 W/m2 angegebene emittierte Elektromagnetischen Strahlung nach dem Stefan-Boltzmann-Gesetz abgeleitet wurde, unter Annahme von durchschnittlichen jährlichen Bedingungen. Unter Hintanstellung einiger untergeordneter, aber dennoch wichtiger Fragen, sollte man sich vor Augen halten:

1) Das Stefan-Boltzmann’sche Gesetz beschreibt die Gesamtemission von einer flachen Oberfläche, die gleichmäßig in alle Richtungen abgeht (isotropisch/hemisphärisch). Stefan hat das experimentell entdeckt, sein Schüler Boltzmann hat es mathematisch abgeleitet. 

2) Die gleichmäßige halbkugelförmige elektromagnetischen Abstrahlung wird durch die Sonne unter Beweis gestellt. Sie erscheint bei bloßer Betrachtung mit dem Auge als flache Scheibe gleichmäßiger Helligkeit, sie ist aber in Wirklichkeit eine Kugel.
Von ihrem Außenrand geht die Strahlung tangential zur Erde ab, nicht senkrecht. Das Beispiel ist nicht ganz treffend wegen der Besonderheit der solaren Randverdunkelung. Diese rührt daher, dass die Oberfläche der Sonne nicht fest, sonder aus Plasma mit Verdunkelungseffekten besteht. Das sieht man aber nicht.
(Bei direkter Sonnenbeobachtung immer geschwärzte Gläser benutzen!)

3) Stefan benutzte bei seinem Laborexperiment einen kleinen flachen Körper, der in eine Halbkugel abstrahlte, die Ergebnisse können auf größere Bereiche übertragen werden, indem man viele flache Körper zu einer flachen Gesamtheit zusammensetzt, weil elektromagnetischen Strahlung einander durchdringt. Man denke dabei an nächtliche Autoscheinwerfer: Die Helligkeit der Scheinwerfer entgegenkommender Autos verändert sich nicht, wenn das eigene helle Licht darauf trifft. (Nicht zu verwechseln mit Blendwirkung oder Streulicht!)

4) Die nachfolgende Zeichnung zeigt, warum die Abstrahlung in seitliche Richtungen am größten ist. Das gilt [in der Atmosphäre] sowohl für die anfängliche Stefan-Boltzmann’sche halbkugelförmige Bodenabstrahlung, wie auch für die nachfolgende kugelförmige Abstrahlung aus der Atmosphäre.

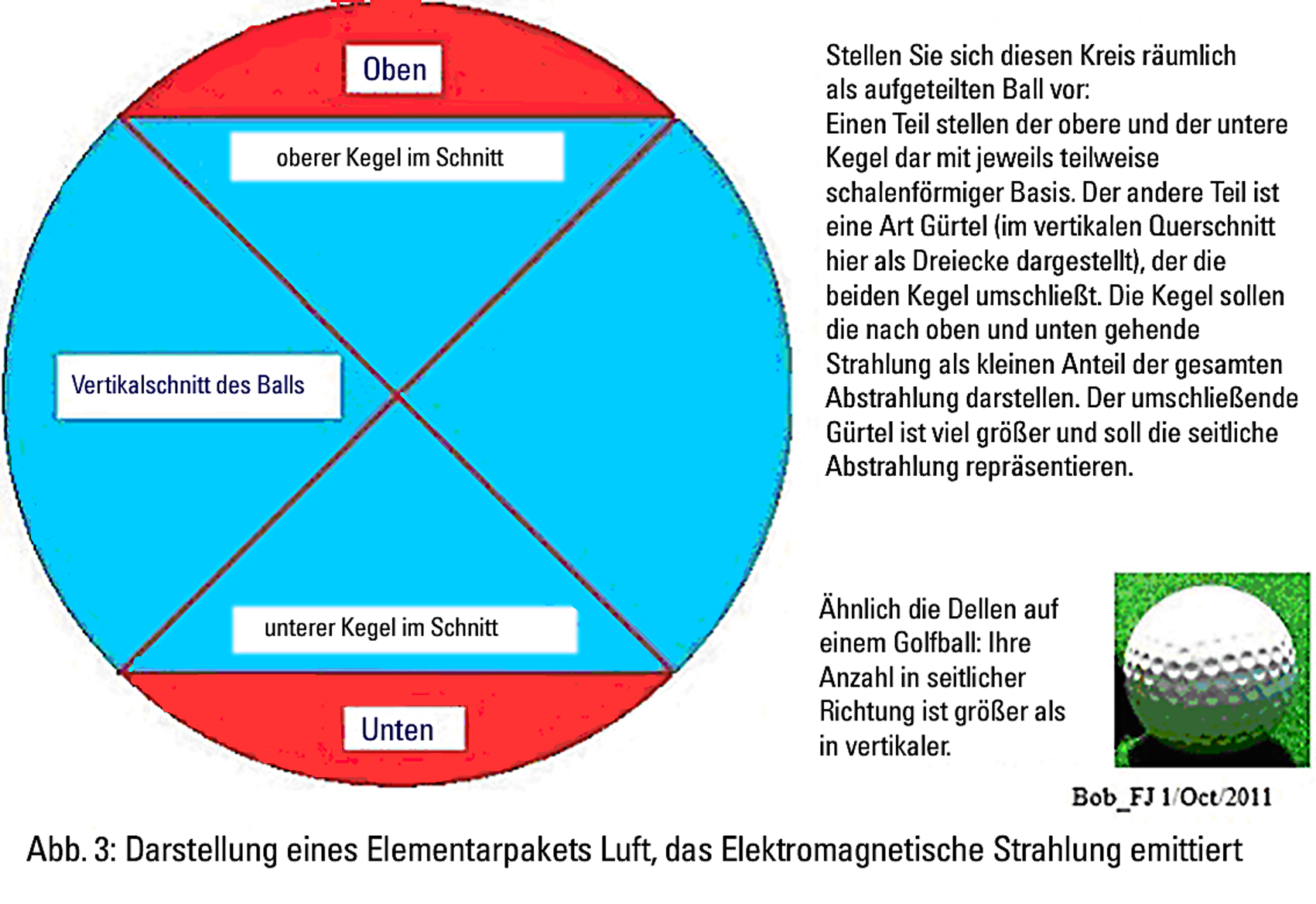
5) Zur Erläuterung der Abb. 3:  Die Lufttemperatur sinkt mit der Höhe (mit dem Gradienten). Wenn wir uns aber eine dünne Luftschicht mit geringer Turbulenz über einem kleinen Gebiet in einem kleinen Zeitintervall vorstellen, dann können wir die Temperatur in der Schicht als konstant betrachten. Die am stärksten konzentrierte Strahlung innerhalb der Schicht geht horizontal in alle Richtungen. Der Netto-Wärmeaustausch dabei ist Null. Wo die Abstrahlung nicht genau horizontal ist, wird sie von benachbarten Schichten abgefangen.

Die zutreffendere Art der Beschreibung ist die vektorielle. Eine vektorielle Beschreibung ist eine mathematische Methode zur Behandlung von Parametern, die Richtungsinformationen enthalten.

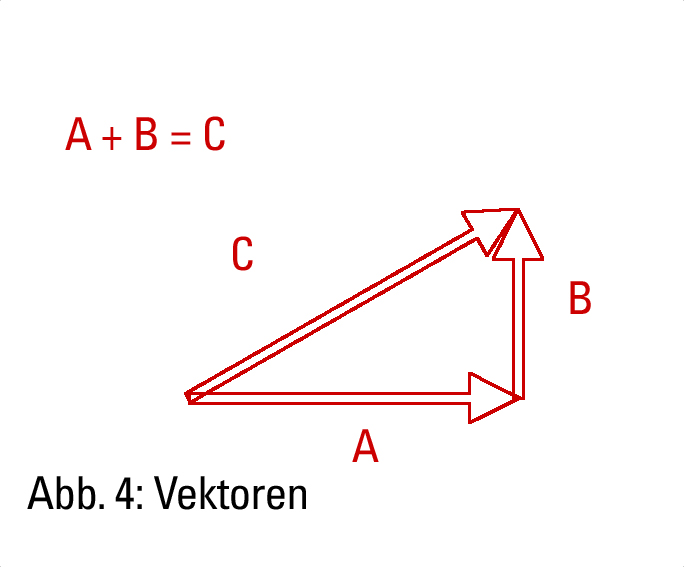
In Abb. 4 geht man von einer beliebigen elektromagnetischen Abstrahlung (C) mit recht flachem Winkel aus und betrachtet deren vertikale und horizontale Vektorbestandteile. Die Länge jedes Vektors ist proportional der Stärke des Strahls in seiner Richtung: A + B = C.  Die Abbildung stellt den Sachverhalt nur zweidimensional dar, bei dreidimensionaler Betrachtung gibt es unzählige ungerichtete Strahlen. Die Mehrzahl konzentriert sich in der horizontalen Ebene in alle Richtungen, dort nähern sich die vertikalen Vektorbestandteile dem Wert Null an.

6) Trenberths Abb. 1 geht von 65% Wärmeverlust an der Erdoberfläche durch Konvektion und Kondensations/Verdampfung aus. Dabei wird nicht erwähnt, dass infolge des Wärmeaustauschs nach oben zusätzliche IR-Abstrahlung in der Luftsäule stattfindet, weil sie erwärmt wird. Es fängt zunächst mit sphärischer Abstrahlung und Absorption an, aber mit zunehmender Höhe und Verdünnung der Luft wird die Absorption geringer, schließlich geht nur noch Strahlung in den Weltraum. Deswegen hat die aus dem Weltraum beobachtete IR-Abstrahlung der Erde komplexe Quellen aus vielen Höhen. Man weiß aber nie genau, woher sie kommt. Daher sind viele Zuschreibungen der Quellen „schwierig“.

Was heißt das nun?

Die anfänglich isotrope Stefan-Boltzmann’sche Emission (Trenberths globale 396 W/m2) wird zum größten Teil von den Treibhausgasen nahe der Oberfläche sofort eingefangen (lassen wir mal außer acht, dass ein Teil auch direkt in den Weltraum durch das sogenannte “atmosphärische Fenster” geht). Dennoch ist der größere Anteil der anfänglichen Stefan-Boltzmann’schen 396-Watt-Oberflächen-Abstrahlung durchgängig lateral, wenn man die von Trenberth angenommen konstanten Bedingungen unterstellt. Es findet überhaupt kein Wärmeaustausch statt, die horizontalen Strahlungsvektoren können nicht im behaupteten 396er Senkrechtfluss enthalten sein, weil sie außerhalb der vertikalen Sicht sind.

Nachdem die anfänglichen atmosphärischen Absorptionen stattgefunden haben, kann das nur für die Oberflächenluft gültige Stefan-Boltzmann’sche Gesetz nicht mehr angewandt werden. (Obschon einige Wolken zuweilen fast wie Schwarze Körper betrachtet werden.) Der Großteil der anfänglichen Absorption/Emission der Luft findet in Bodennähe statt, aber die vertikale Verteilung ist hoch, wegen erheblicher Variation in den Pfadlängen der Photonen. Sie unterscheiden sich unter dem Einfluss vieler Faktoren, ein großer Faktor ist die regionale und sehr viel stärkere Verteilung der Konzentration des Treibhausgases Wasserdampf. Sie beträgt in globaler Betrachtung ~0 bis ~4 %. Im Vergleich dazu: Die CO2-Konzentration ist mit ~0.04 % in etwa konstant. Beim Versuch der Modellierung der möglichen Wirkungen trifft man auf eine sehr hohe Gesamtkomplexität. Das soll hier nicht weiter betrachtet werden. Wichtig ist nur, dass alle Luftschichten mit zunehmender Höhe ständig eine ganze Menge an seitlicher Abstrahlung besitzen, die teilweise von den Stefan-Boltzmann’schen hemisphärischen 396 Watt angetrieben wird und daher keinen Anteil an den in Abb. 1 behaupteten vertikalen 396 Watt haben kann.

Ergebnis:

Der von  Trenberth et al. als 396 W/m2 dargestellte vertikale Strahlungsfluss von der Erdoberfläche bis in die hohen Wolkenschichten wird auch von prinzipiellen Überlegungen nicht gestützt. Die Stefan-Boltzmann’schen 396 W/m2 sind definitionsgemäß isotropisch, wie auch deren Abklingen mit aufsteigender Höhe. Dabei überwiegen stets die horizontalen Vektoranteile, die bei vertikaler Betrachtung keine Rolle spielen. Die verbleibenden vertikalen Komponenten der elektromagnetischen Abstrahlung aus dieser Quelle sind deshalb geringer als die behaupteten 396 W/m2.

Es ist offensichtlich, dass der durch Konvektion und Verdampfung verursachte Wärmeverlust an der Oberfläche sich zum tatsächlichen vertikalen Verlust durch elektromagnetischen Abstrahlung addiert. Das wird auch vom Weltraum her beobachtet. Dieser Verlust kann sehr wohl in der Größenordnung von 396 W/m2 liegen. Das ist aber nicht der von Trenberth beschriebene Stefan-Boltzmann’sche Abstrahlungsprozess.

Autor Bob Fernley-Jones

ist ein pensionierter Maschinenbauingenieur und lebt in Australien

Der Originalbeitrag erschien hier

(Die Übersetzung besorgte Helmut Jäger, EIKE)

###############################################

Zusatz für besonders Interessierte

Wer weiß mehr? :

In der Abb. 5 unten stellen die links angegebenen NIMBUS 4 Satellitendaten alle Strahlungsquellen dar, wie sie vom Weltraum her beobachtet werden. In unserem Falle von einem Punkt über dem tropischen Pazifik. Die gesamte Abstrahlungsmenge wäre das Integral unter der Kurve. Es wird leider nicht angegeben. Für Vergleichszwecke gibt ein MODTRAN Kalkulator für eine Beobachtungshöhe von 100 km eine interessante Information zu dieser Abbildung. Sie wird in der Tabelle darunter detailliert. Leider gibt der Kalkulator keine globalen Daten oder durchschnittliche Bewölkungsbedingungen an. Wir vergleichen also Äpfel mit Birnen. Das tun wir nicht nur bei NIMBUS sondern auch bei Trenberth. Allerdings scheinen sie alle von gleicher Größenordnung, wie aus den zusätzlichen Tabellenwerten ersichtlich.

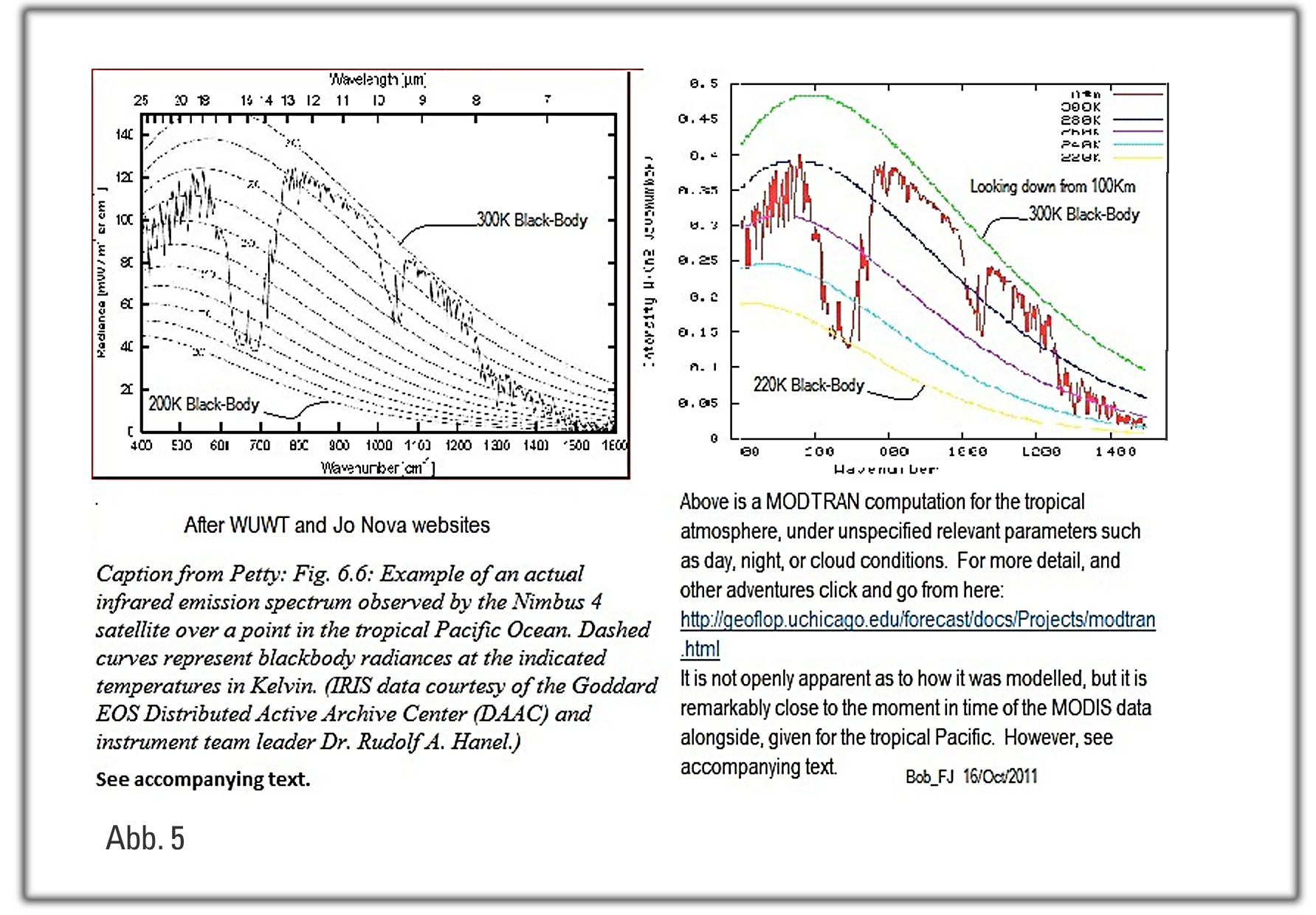
Vergleich MODTRAN & “Trenberth” aus zwei Höhen, dazu die Oberflächentemperatur
Ort	Kelvin	10 Meter	100 Km.	(Zentigrad)
Tropische Atmosphäre	300K	419 W/m^2	288 W/m^2	(27C)
Mittlere Breiten Sommer	294K	391 W/m^2	280 W/m^2	(21C)
Mittlere Breiten Winter	272K	291 W/m^2	228 W/m^2	(-1C)
Sub-Arktischer Winter	257K	235 W/m^2	196 W/m^2	(-16C)
Trenberth Global	288K ?	396  W/m^2	239 W/m^2	(15C ?)

Vergleich MODTRAN & “Trenberth” aus vier Höhen:  W/m^2
Ort	Aus 10 m	Aus 2 Km	Aus 4Km	Aus 6Km
Tropische Atmosphäre	348	252	181	125
Mittlere Breiten Sommer	310	232	168	118
Mittlere Breiten Winter	206	161	115	75
Sub-Arktischer Winter	162	132	94	58
Trenberth Global	333   Von hoher Bewölkung herrührend (= Stefan-Boltzmann lt. MODTRAN)