Zusammenfassung
Das Carbon Dioxide Information Analysis Center (CDIAC) stellt Messdaten des CO2 Zyklus zur Verfügung, die mit dem Jahre 1959 beginnen und eingeschränkt bis 1850 zurückreichen. Die geringen Mengen von anthropogenem CO2 um das Jahr 1750, welche durch erste Anfänge der Industrialisierung und stärkere Holzverbrennung erzeugt wurden, gelangten noch vollständig in die Atmosphäre. Die heute emittierten CO2 Mengen, die inzwischen den CO2 Gehalt der Luft um 100 ppm erhöht haben, gehen aber nur noch zur Hälfte in die Atmosphäre. Die andere Hälfte wird etwa zu gleichen Teilen vom Ozean und der Biosphäre aufgenommen. Diese Verschiebung wird bei starken anthropogenen CO2 Emissionen der weiteren Zukunft in einen Zustand übergehen, bei dem alles anthropogene CO2 nur noch vom Ozean aufgenommen wird und damit der CO2 Anstieg in der Atmosphäre zum Stillstand kommt.
Unser Modell gibt den globalen CO2 Zyklus in guter Übereinstimmung mit den CDIAC Messungen über mehr als 160 Jahre wieder. Es handelt sich um die CO2 Konzentration der Atmosphäre und die jährlichen CO2 Flüsse in die Atmosphäre, den Ozean und die Biosphäre. Gleiches leisten die bisher veröffentlichten Modelle trotz größerer Komplexität nicht. Unsere Modellvorhersage für die nächsten 100 Jahre lässt auf Grund dieser langfristigen Übereinstimmung mit den Messungen Verlässlichkeit auch für die Zukunft erwarten. Als wesentliches Ergebnis wird die ansteigende CO2 Konzentration in der Atmosphäre zum Stillstand kommen und unter keinen Umständen ca. 800 ppm übersteigen. Dies ergibt auch eine Grenze für einen durch CO2 bewirkten Anstieg der Erdtemperatur. Da in den Arbeiten der Literatur der letzten Jahre die Klimasensitivität (Anstieg der Temperatur bei Verdopplung der CO2 Konzentration) auf unter 1 °C beziffert wird (hier), kann die Erdtemperatur selbst bei beliebig großen anthropogenen CO2 Emissionen nur um weniger als 1 °C ansteigen. Eine gefährliche Erderwärmung durch CO2, wie beispielsweise vom „Wissenschaftlichen Beirat der Bundesregierung Globale Umweltveränderungen“ (WBGU) aktuell behauptet, stellt sich hiermit erneut – wie in vielen schon existierenden Arbeiten – als falsche Hypothese heraus.
Der CO2 Zyklus und seine Messung
Seit 1850 liegen Schätzungen der anthropogenen CO2 Emissionen vor, die auf den weltweit verbrannten Mengen an Kohle und Holz beruhen. Ferner ist die CO2 Konzentration der Luft aus Eisbohrkernanalysen bekannt. Ab 1959, dem Beginn der berühmten CO2 Messkurve von C.D. Keeling auf dem Mauna Loa (Hawaii), wurden dann erhebliche Anstrengungen zur Vermessung des globalen CO2 Zyklus unternommen. Zu den Messungen des CO2 in der Luft kamen Messungen des CO2 Austauschs zwischen Atmosphäre, Ozean und Biosphäre hinzu. Das Carbon Doixide Information Analysis Center (CDIAC) veröffentlicht diese Messungen seit vielen Jahren regelmäßig in Rahmen seines Carbon Budget Projekts [4] (die in eckigen Klammern angegebenen Zitate sind hier generell die Zitate der Originalarbeit), die hierzu gehörende jüngste Fachveröffentlichung von Le Quéré (hier). Gleichzeitig erfuhr auch die Modellierung des CO2 Zyklus einen Aufschwung. Erstaunlicherweise wurde aber in der Fachliteratur bis heute kein Versuch unternommen, die von CDIAC zur Verfügung gestellten Messungen der Komponenten des CO2 Zyklus durch ein Modell zu beschreiben. Dies erfolgte (begutachtet) erstmalig mit der hier besprochenen Arbeit der Autoren. Das Journal der Veröffentlichung verfolgt die „Open“-Linie, d.h. die Publikation ist frei verteilbar.
Grundlegendes zum CO2 Zyklus
In der Fachliteratur wird Kohlenstoff (C) an Stelle von CO2 verwendet. Die Äquivalenz ist wie folgt: 1 ppm CO2 in der Luft entspricht 2,12 Gigatonnen Kohlenstoff (GtC) [2]. So ist z.B. die aktuelle atmosphärische CO2 Konzentration von 400 ppm dem Wert von 848 GtC in der Atmosphäre äquivalent. Hier wird im Folgenden sowohl CO2 als auch C verwendet. CO2 ist zwar schwerer als Luft, aber nur ein Spurengas, so dass es sich nicht am Boden anreichert sondern bis etwa 15 km Höhe homogen verteilt ist. Nur tausendfach höhere CO2 Konzentrationen reichern sich am Boden an und können z.B. bei Vulkanausbrüchen gefährlich werden.
Der Kohlenstoffgehalt der Weltmeere beträgt 37000 GtC [3], also mehr als das Vierzigfache der Luft mit ihren aktuell 848 GtC. Zwischen Luft, Ozean und Biosphäre findet ein ununterbrochener starker CO2 Austausch statt (CO2 Bruttoflüsse). Dieser verschob aber vor 1750, abgesehen von kleineren Schwankungen, nicht das natürliche Gleichgewicht. So flossen und fließen nach wie vor jährlich etwa 80 GtC zwischen Ozean und Luft sowie 120 GtC zwischen Biosphäre und Luft hin- und her, ohne dass dies vor 1850 wesentlich veränderte Kohlenstoffinhalte von Ozean, Luft oder Biosphäre verursachte. Ein informative Abbildung aller beteiligten Kohlenstoff-Flüsse zeigt die Grafik von Bild 1, die noch zum Jahr 2012 gehört. In dieser Grafik sind die natürlichen Flüsse schwarz, die anthropogenen rot. Alle anderen Flüsse sind dagegen vernachlässigbar, insbesondere auch der Vulkanismus von nur 0,1 GtC pro Jahr, der immer wieder von Laien irrtümlich als entscheidender „Zyklus-Joker“ ins Spiel gebracht wird.

Bild 1: Jährliche Kohlenstoffbrutto-Flüsse in GtC/a, Quelle IPCC, WG1AR5, Chapter 06 final, S. 471
Der industrialisierte Mensch begann ab etwa 1750 zum erstenmal in das natürliche CO2 Gleichgewicht einzugreifen, ab 1850 wurde dieser Eingriff dann spürbar. So emittiert der Mensch aktuell (2015) rund 11 GtC pro Jahr, wovon, wie schon erwähnt, grob die Hälfte in die Atmosphäre geht und die andere Hälfte zu etwa gleichen Teilen vom Ozean und der Biosphäre aufgenommen wird. Der hierdurch bewirkte stärkere Pflanzenwuchs der Erde, der die Welternährungslage signifikant verbesserte, ist inzwischen gut bekannt [14, 15, 16]. Es ist klar, dass die anthropogenen CO2 Mengen als Nettoflüsse das natürliche Gleichgewicht des globalen CO2 Zyklus verändern. Der steigende CO2 Gehalt der Luft zeigt es.
Unser Modell des anthropogen geprägten CO2 Zyklus
Die entscheidende Eigenschaft unseres Modells, mit der es sich von den bisher bekannten Modellen unterscheidet, besteht darin, dass es nur die Netto-Flüsse von CO2 betrachtet. Nur diese verändern das Gleichgewicht des CO2 Zyklus. Diese Beschränkung hat den entscheidenden Vorteil, ohne Daten der Ozeanchemie oder Messungen des Brutto-CO2-Austauschs auszukommen.
Das Modell ist einfach und bringt dennoch die maßgebenden Zyklusbestandteile in beste Übereinstimmung mit den Messungen. Sogar die spärlichen und weniger genauen Messwerte der Periode von 1850 bis 1959 werden noch befriedigend wiedergegeben. Somit liegt nunmehr eine erstaunlich gute Übereinstimmung über mehr als 160 Jahre vor. Unser Modell ist kein empirischer Fit sondern aus physikalischen Gesetzmäßigkeiten hergeleitet. Man darf aus diesem Grunde sowie wegen der guten Wiedergabe der Messungen erwarten, dass das Modell auch noch die nächsten 100 Jahre seine Gültigkeit beibehält. Unter dieser Prämisse und mit allen Kaveats ergeben sich mit unserem Modell Obergrenzen des CO2 in der Atmosphäre, die in keinem Fall – auch bei Verbrennen aller verfügbaren Kohlereserven der Menschheit – überschritten werden. Das Modell erlaubt ferner die Aussage, wie lange es dauert, bis eine Störung des natürlichen CO2 Zyklus, wie sie aktuell durch anthropogenen CO2 Emissionen entsteht, von der Natur wieder ausgeglichen wird.
Die erste physikalische Gesetzmäßigkeit des Modells entspricht dem Massenwirkungsgesetz der Chemie. Ihr liegt die Näherung zugrunde, dass sich durch menschgemachte CO2 Emissionen zwar der CO2 Partialdruck der Atmosphäre ändert, praktisch nicht aber der des Ozeans – was am sehr viel höheren CO2 Inhalt des Ozean liegt. Der in den Ozean hineingedrückte Kohlenstoff-Nettofluss ist proportional zur Partialdruckdifferenz von Luft und Ozean und wird durch die lineare Gleichung (2.1) ausgedrückt. „Tau“ in (2.1) ist ein Modellparameter, der unabhängig von den CDIAC Daten bereits von anderer Seite grob bekannt ist [13]. Die zweite Grundannahme fordert einen CO2 Nettofluss in die Biosphäre, proportional zum entsprechenden Nettofluss in die Atmosphäre. Diese Annahme ist sinnvoll, weil höhere CO2 Konzentrationen der Luft in linearer Näherung höheres Pflanzenwachstum bewirken. Die Annahme wird durch zahlreiche Veröffentlichungen gestützt wie z.B. [14, 15, 16] und ist in Gleichung (2.2) mit „b“ als zweitem Modellparameter formuliert. Über „b“ kann ohne weiteres allenfalls nur eine extrem grobe Schätzung abgegeben werden. Zu (2.1) und (2.2) kommt schließlich noch das Gesetz der Massenerhaltung der Gleichungen (2.3) und (2.4) hinzu.
Aus den Gleichungen (2.1)-(2.4) folgt durch einfache Umformung die Differentialgleichung (2.7) (DGL). Der in (2.7) versuchsweise noch zusätzlich eingeführte Term der Meerestemperatur S_a(t) hat später praktisch keinen Einfluss auf die Ergebnisse und kann daher entfallen. Die Ableitung der integrierten Größe N_a(t) in (2.7) ist der jährliche Netto-Kohlenstoff-Fluss in die Atmosphäre. Die numerische Lösung ist in den Abschnitten 4. und 5. der Arbeit beschrieben.
Das Modell benötigt als einzige Eingangsgröße die anthropogenen jährlichen Kohlenstoffemissionen. Ferner ist zur Lösung der Modell-DGL (2.7) ein Anfangswert der atmosphärischen CO2 Konzentration erforderlich. Für die Lösung der DGL werden als Zeitschritte Jahre verwendet. Die Lösung liefert als Ergebnisse den jährlichen Netto-Kohlenstoffeintrag in die Atmosphäre, den Ozean und die Biosphäre. Diese Werte integriert liefern die CO2 Mengen, die in die genannten Senken über viele Jahre gehen. Von den integrierten Größen ist insbesondere der CO2 Gehalt der Atmosphäre interessant.
Die Werte der zwei Modellparameter werden in unserer Arbeit mit der nichtlinearen SIMPLEX-Methode nach dem Kriterium der besten Anpassung an die CDIAC Messwerte berechnet. Wir betonen, dass die Parameter nur aus den Messwerten des Zeitraums 1959 bis 2013 ermittelt werden und dennoch das Modell auch den Zeitraum von 1850 bis 1959 gut wiedergibt. Dies zeigt, dass eine Einbeziehung der vielen möglichen Detailprozesse unnötig ist und zur Beschreibung und Voraussagbarkeit nichts beitragen kann.
Ergebnisse für den CO2 Zyklus von 1850 bis heute
Sie finden sich in Fig. 1 und Fig. 2 der Arbeit (die Messwerte stets in rot). In Fig. 1 oben stellt die schwarze Line den berechneten CO2 Gehalt der Atmosphäre dar, die grüne Kurve die jährlichen anthropogenen Kohlenstoff-Emissionen. Da die optimalen Parameter aus dem Vergleich mit den Messwerten über den Zeitbereich 1959- 2013 ermittelt wurden, sind die Ergebnisse der frühen Periode 1850 – 1959 nicht ganz so gut wie für 1959 – 2013. Fig. 1 unten zeigt die Airborne Fraction (AF) als den Bruchteil der anthropogenen Kohlenstoff- Emissionen, der in die Atmosphäre geht. Da es sich bei der AF nicht um eine integrierte Größe handelt, ist insbesondere die Schwankung ihrer Messwerte beträchtlich. Dennoch sind auch über 160 Jahre keine längerfristigen Änderungen der AF zu erkennen.
Fig. 2 zeigt die Ergebnisse der integrierten Größen, für den Kohlenstoffgehalt der Luft N_a, für den CO2 Gehalt des Ozeans N_s und für den der BiosphäreN_b. Da für N_s und N_b keine Anfangswerte bekannt sind, wurden diese beliebig festgelegt. Es kommt nur auf den Zeitverlauf dieser Größen an. Die anderen Teilbilder zeigen die jährlichen CO2 Netto-Zuwächse, die heftig schwanken. Diese Schwankungen sind vermutlich von jahreszeitlich bedingtem unterschiedlichen Pflanzenwuchs und weiteren Faktoren verursacht. Die integrierten Größen werden dagegen praktisch perfekt wiedergegeben.
Ergebnisse für den zukünftigen Zyklus bis 2100
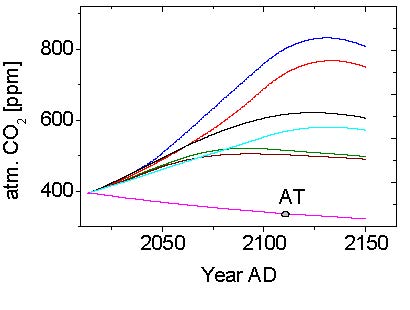
In der Literatur sind Emissionsszenarien bis zum Jahre 2100 veröffentlicht. Wir verwendeten die in [20] zur Verfügung gestellten sechs Szenarien. Um das Modell zu testen, verlängerten wir sie bis zum Jahre 2150 mit der etwas willkürlichen Annahme einer linearen Abnahme auf den jeweils halben Wert des Jahres 2100. Die Szenarien und ihre zugehörigen Modellergebnisse sind in Fig. 3. gezeigt. Interessant ist dabei, dass das ungünstigste Szenario A1Fi schon weit mehr Kohlenstoffverbrennung erfordert als es alle Kohlenstoffreserven der Erde zusammen. Dennoch erreicht der CO2 Gehalt der Luft nur im Jahre nur einen Maximalwert von weniger als 800 ppm. Der Grund dafür wird im rechten unteren Teilbild der Airborne Fraction AF deutlich. Die AF beginnt abzunehmen und wird irgendwann Null – danach sogar negativ, wenn die anthropogene CO2 Zufuhr schwächer wird. Mit anderen Worten: es kommt ein Zeitpunkt, an dem die Partialdruckdifferenz zwischen Atmosphäre und Ozean so groß geworden ist, dass kein menschgemachtes CO2 mehr in die Luft sondern in Ozean und Biosphäre geht.
Vergleich mit Teilergebnissen anderer Modelle
In der Literatur findet sich ein Vergleich für ein numerisch-theoretisches „Experiment“ [7]. In diesem wird im Jahre 2010 ein Impuls von 100 GtC den anthropogenen Emissionen hinzuzugefügt und danach die anthropogenen Emissionen konstant auf 10 GtC pro Jahr festgehalten. In Fig. 4, oberes Teilbild, gibt die graue Zone den Ergebnisbereich der in [7] verwendeten 15 Modelle an. Die blaue Kurve ist das Ergebnis unseres Modells. Das untere Teilbild von Fig. 3 zeigt den Modellvergleich bis zum Jahre 3000.
Die Diskrepanz zwischen unserem Modell und den 15 anderen Modellen rührt im Wesentlichen von unserer Nichtberücksichtigung des Revelle-Effekts (hier) her. Dieser Effekt wird mit Ozeanchemie begründet und fordert eine verminderte CO2 Aufnahmefähigkeit bei steigender CO2 Konzentration der Luft. Der Revelle-Effekt zeigt sich aber bisher nicht in den Messungen (s. Fig. 1 unteres Teilbild). Dieser Mangel wird auch in einer weiteren Arbeit betont [13]. Solange der Revelle-Effekt in der globalen Natur nicht gemessen wird, ist er hypothetisch. Mögliche Gründe, warum er sich nicht zeigt, werden in unserer Publikation erwähnt.
Die Modelle in [7] und unsere Arbeit zeigen gleichermaßen ein recht langes Abklingen des 100 GtC – Impulses. Die Halbwertszeit dieses Abklingens AT beträgt in unserem Modell etwa 100 Jahre und wird von einem eigenen weiteren numerischen „Experiment“ bestätigt (Fig. 3 unteres linkes Teilbild, rote Kurve). AT ist die Anpassungs-Halbzeit, die die Natur benötigt, um eine Störung des natürlichen Kohlenstoffzyklus zur Hälfte zu beseitigen. Davon zu unterscheiden ist die Verweilzeit RT eines CO2 Moleküls in der Atmosphäre, die nur etwa 5 Jahre beträgt [8]. Der Grund für den extrem kleinen Wert der RT verglichen mit dem sehr großen Wert der AT ist der bereits beschriebene, um mehr als eine Größenordnung höhere Bruttoaustausch von CO2 zwischen Atmosphäre, Ozean und Biosphäre verglichen mit den CO2 Netto-Flüssen.
Die Historie unserer Arbeit
Die Grundzüge des Modells hat Prof. Werner Weber von der theoretischen Physik an der Universität Dortmund anlässlich eines gemeinsamen Kolloquiums des Potsdamer Instituts für Klimafolgenforschung (PIK) und EIKE in Potsdam im Oktober 2010 vorgetragen. Weil W. Weber sein Modell nicht weiterverfolgte, kontaktierte ich (Lüdecke) ihn und schlug eine Zusammenarbeit vor. Diese zog sich mit langen Unterbrechungen über mehrere Jahre hin und hatte als schönstes Resultat das Entstehen einer intensiven persönlichen Freundschaft. Wir telefonierten nicht selten oft mehrere Stunden wöchentlich – nicht nur über Physik. In den letzten Monaten dieser Zeit schloss sich Prof. Carl Otto Weiss unserem Team an. Während des Entwurfs einer gemeinsamen Veröffentlichung im Jahre 2014 verstarb Weber unerwartet. Eine erste Version der Arbeit erschien in „Earth System Dynamics Discussion“ (ESDD) (hier), wurde aber für ESD nicht angenommen. Die hier vorgestellte Publikation ist eine verbesserte Version der abgelehnten Einreichung.
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Wichtiger als Modellieren erscheint mir das Abklären der Grundlagen. Zum Beispiel, woher kommt denn die seltsame Annahme, der CO2-Gehalt der Luft habe sich um 100 ppm = 0,01 % angereichert? Der Vergleich mit über hundert Jahre alten Naturlehre-Büchern zeigt, dass die Luft damals wie heute denselben Kohlendioxidgehalt aufweist.
@Dirk Weissenborn: „Eine interessante Arbeit! Diese allein reicht schon, den Alarmismus in seine Schranken zu weisen“
Leider kaum, da Prof. Lüdecke durch seinen Modellfehler in Glg 2.5 mit einer real 2,6-fach zu hohen Zeitkonstanten deutlich zu hohe Konzentrationsverläufe berechnet hat. Ich empfahl ihm daher bereits zu seiner ersten (abgelehnten) Fassung bei ESDD dringend ein Korrigendum. Hierzu war er jedoch nicht bereit, da er keinen Fehler finden konnte. Ich schlug – vergeblich – vor, wenigstens ein Stabilisierungsszenario nachzurechnen, z.B. WRE 550 von IPCC oder besser das welches Prof. Weber anhand seines Modells im April 2011 beim PIK vorgestellt hatte.
Es ging dort um eine Konstant-Emission von 8,5 GtC/a welche im Endzustand eine Konzentrationserhöhung um 220 ppm, also von 280 auf 500 ppm bewirken würde. Da der Senkenfluß (der proportional zum Konzentrationszuwachs angenommen wird) von 8,5 GtC/a =Pufferüberschuß/Zeitkonstante ist, ergibt sich mit 220*2,123 Gt in der Atmosphäre die 1/e-Zeitkonstante Tau zu 55 Jahren – und nicht zu etwa 100/ln(2) =144 Jahren. Ca. 100 Jahre ist die fälschlich berechnete „adjustment time“ AT (Halbwertszeit), mit der Prof. Lüdecke einen ppm-Anstieg um 592 auf 872 ppm (!) statt 500 berechnet hätte und sofort erkannt hätte daß er das Weber-Modell falsch implementiert hat.
Zum Revelle-Faktor, der bei knapp 10 liegt, ist zu sagen dass Prof. Lüdecke meint, dieser sei nur hypothetisch da er sich in den Messungen (noch) nicht manifestiert. Das ist ein großer Irrtum, denn ohne den Revelle-Faktor würde sich der C-Gehalt der oberen Mischungsschicht der Ozeane (etwa im Gleichschritt mit der Atmosphäre) um denselben Prozentsatz erhöhen. Tatsache ist aber daß die Erhöhung dort nur etwa 1/10 davon beträgt (was in Bild 1 unzutreffend, da nur für den Gesamtozean dargestellt ist). Weil die obere Mischungsschicht einen erweiterten Atmosphärenpuffer darstellt, steigt dessen gesamter C-Inhalt nicht um etwa 29% wie in Bild 1, sondern deutlich weniger, und damit wird auch die Zeitkonstante Tau geringer als die etwa 81 Jahre.
Erwähnt werden muß noch dass die CO2-Senkenfunktion der Biomasse im Lüdecke-Modell dynamisch völlig falsch implementiert ist. Diese wird als atmosphärischer Zusatzpuffer von 66,8 % angenommen so daß deren CO2-Absorption stets proportional zur Aufnahme der Atmosphäre ist (Glg 2.2). Angenommen, wir befänden uns am Beginn der Industrialisierung wo die Konzentration kaum gegenüber 280 ppm erhöht ist und die Atmosphäre fast sämtliche Emission aufnimmt. Dann agiert die Bio-Senke äußertst aktiv, obwohl sie real noch keinerlei Reaktion zeigt. Umgekehrt sieht es bei Sättigung nach langer Konstantemission aus. Dann ist die CO2-Konzentration maximal und die ‚airborne fraction‘ wird Null. Damit wird auch die Bio-Senke zu Null – obwohl sie dann maximal aktiv ist.
Allerdings hat Prof. Lüdecke durch den Fehler in der Modellgleichung versehentlich den Senkenfluß seiner Biomasse eliminiert (!) indem er die Zeitkonstante (die ja den Senkenfluß bestimmt) in Glg 2.5 mit 1,668 multipliziert hat (81,7*1,668 =136 Jahre). Dadurch werden die berechneten Konzentrationsverläufe – und damit auch die vermeintlich erforderlichen CO2-Reduktionen – deutlich zu hoch (was natürlich nicht der Grund der Ablehnung durch IPCC-nahe Reviewer war). Aber gegen den EIKE-Beitrag des ‚Geophysikers‘ Uli Weber, der den (real vermeintlich nicht extstenten) Treibhauseffekt nur auf eine falsche Anwendung des Stefan-Boltzmann-Gesetzes zurückführt, erscheint solch ein Fehler eher harmlos…
Die Autoren schätzen die gegenwärtige Gesamtmenge an Kohlendioxid (im Maß C) auf 37.000 GtC + 848 GtC = 37.848 GtC. Die Flora hat bisher etwa 1,215 x 10^15 t Sauerstoff freigesetzt und dabei das Kohlendioxid Inventar von Ozeanen und Atmosphäre um etwa 450.000 GtC reduziert. – Offenbar legt nicht nur das Aussterben der Dinosaurier nahe, dass die Spezies Mensch wohl eher die Nahrungsgrundlage der Flora als ein „Klimagespenst“ im Auge behalten sollte! Modell hin, Modell her, sicher ist, dass die Flora weiter tätig bleibt
Ausnahmslos sämtliche Aussagen bezüglich sowohl des derzeitigen als auch des zukünftigen Einflusses von CO2 auf das Klima beruhen auf sogenannten Modellen. Die einzig zur Verfügung stehenden Messdaten sind eine zunehmende CO2-Konzentration der Atmosphäre und eine Zunahme der „Temperatur des Klimas“. Da die vielfältigen gegenseitigen Einflussgrößen dieser beiden messbaren Werte nicht bekannt sind, werden rein hypothetische Annahmen in die Modellrechnungen auf die Weise eingeführt, dass der Verlauf des Klimas der letzten 150 Jahre wiedergegeben wird. Die in dem Modell verwendeten Annahmen und Rechenverfahren sollen dann eine Aussage für das Klima der Zukunft erlauben. Eine solche Art von Aussagen ist nach den Regularien der Naturwissenschaften prinzipiell nicht möglich, da diese Aussagen durch Messungen nicht überprüfbar und damit nicht falsifizierbar sind. Darüber hinaus sind chaotische Systeme wie das Wettergeschehen aufgrund der enthaltenen Rückkopplungen selbst dann nicht prognostizierbar, wenn sämtliche Einflussgrößen messbar und damit bekannt wären. Das ist Standardwissen in Lehrbüchern der Mathematik und müsste damit auch Physikern bekannt sein.
Da ich hier nichts Neues in die Welt gesetzt habe und die obigen Zusammenhänge wohl bekannt sind, werden diese Modellrechnungen von allen Fachleuten prinzipiell abgelehnt, wie man es auch im EIKE-Blog in Hunderten von zitierten Veröffentlichungen und Kommentaren verfolgen konnte. Ich bin deshalb etwas verwirrt, von EIKE-Mitgliedern eine auf Modellrechnungen beruhende Aussage zu zukünftigen CO2-Werten und Temperaturen zu erfahren.
Dr. Heinz Schütte
Wir sollten uns nochmal darüber unterhalten, was man eigentlich unter dem „Natürlichen Gleichgewicht“ bezogen auf diesen Absatz…
So emittiert der Mensch aktuell (2015) rund 11 GtC pro Jahr, wovon, wie schon erwähnt, grob die Hälfte in die Atmosphäre geht und die andere Hälfte zu etwa gleichen Teilen vom Ozean und der Biosphäre aufgenommen wird. Der hierdurch bewirkte stärkere Pflanzenwuchs der Erde, der die Welternährungslage signifikant verbesserte, ist inzwischen gut bekannt [14, 15, 16]. Es ist klar, dass die anthropogenen CO2 Mengen als Nettoflüsse das natürliche Gleichgewicht des globalen CO2 Zyklus verändern. Der steigende CO2 Gehalt der Luft zeigt es.
…..verstehen will.
Auch der Mensch ist ein Teil der Natur, der Evoltion, des Leben auf der Erde in unseren Sonnensystem. Ich kann das Lebenwesen Mensch nicht als etwas „künstliches“ bzw. nicht von dieser Erde stammendes Etwas sehen. Der Mensch nutzt die Rohstoffe, die auf dieser Erde vorhanden und immer wieder in einen Kreislauf wiederverwertbar sind. Der Mensch ist kein Außerirdischer, der der Erde etwas wegnimmt oder ihr hinzufügt. Das einzige, was der Mensch macht….er setzt sein Wissen und seinen Geist ein um aus den vorhandenen Rohstoffen und Materialien, was ihm die Erde so anbietet ein Lebensumfeld nach seinen Vorstellung zu gestalten. Der Mensch bringt Ordnung und Struktur in das Chaos der Naturlandschaften. Der Mensch kann also nur für seine Zeit der Anwesenheit auf dieser Erde für sich ein Lebensumfeld schaffen in dem er vom Überleben zum Leben sein Wisssen und seinen Geist zum Einsatz bringt. Das bringt weder die Erde noch die Natur aus den Gleichgewicht noch wird hier der Erde bzw. Natur etwas genommen. Es ist nur ein kurzes Gastspiel für den Menschen auf dieser Erde, die ihm von der Evolution zugestanden wird. Das Gastspiel der Menschen wird sich mit dem Gastspiel der Dinosauerier nicht messen können. Wir haben heute schon einen zu niedrigen CO2 Wert auf der Erde und der wird sich trotz der menschlichen CO2 Förderung weiter und weiter nach unten fortsetzen. Und zwar aus dem einfachen logischen Grund…weil sich der CO2 Anteil der Atmosphäre seit seiner Hochzeit nicht mehr an diese Hochzeit herangekommen ist. Der CO2 Anteil ist weiter und weiter gesunken und mit ihm sind dann die großen Lebewesen (Dinosauerer und Große Pflanzen) zurückgegangen. Die Erde war in ihrer Hochzeit des CO2 ein „offener Planet“ mit vielen Vulkanen und einer zum Teil flüssigen Magmaoberfläche. Die Erde hat in dieser Zeit soviel Eigenwärme abgestrahlt…die hätte die Sonne gar nicht gebraucht um kuschelig Warm zu sein. Seit dieser Hochzeit kühlte aber die Erde auch immer mehr und mehr ab. Die Eigenwärme der Erde spüren wir heute somit kaum mehr an der Erdoberfläche. Die einzige Wärmequelle ist somit für unser Leben die Sonne. Wer jetzt eins und eins zusammenzählen kann. der wird erkennen, dass wir Menschen in Zukunft mehr ein Problem mit der „KÄLTE“ als mit der „WÄRME“ bekommen werden. Und das CO2…ist und bleibt was es schon immer war…ein Pflanzendünger und die Basis für das Leben bzw. für das moderne Leben des Menschen. Die Erde kühlt sich ab und dies erst nicht seit heute oder gestern schon seit über Millionen von Jahren. Die Erde wird somit immer mehr auf die Sonnen-Energie-Wärme angewiesen sein. Wobei man auch noch berücksichtigen soll, dass die Sonne natürlich auch immer mehr schwächelt und abbaut. Und das sich die Erde seit Millionen von Jahren nicht nur ihren Mond beim Entfernen zusehen muss sondern die Erde selbst sich auch von der Sonne entfernt. Da kommt dann schon so einiges Zusammen in den letzten Millionen von Jahren und den nächsten Millionen Jahren, dass unseren Leben auf der Erde mehr die „Kälte“ als die „Wärme“ bringen wird.
Volle Zustimmung.
„Da kommt dann schon so einiges Zusammen in den letzten Millionen von Jahren und den nächsten Millionen Jahren, dass unseren Leben auf der Erde mehr die „Kälte“ als die „Wärme“ bringen wird.“
„Volle Zustimmung.“
Man muß gar nicht in Zeiträumen von Millionen von Jahren denken.
Die nächste Eiszeit steht vor der Türe.
Ob in 50, in 200 oder 2000 Jahren, die Menschheit wird es schwer haben diese zu überleben.
Allein aus diesem Grund ist diese alberne CO2-Diskussion so notwendig wie ein Kropf.
Man kann es auch so sagen…die Menschen sind die Endstation der „Säuger Evolution“. Der Endpunkt und zu gleich der Höhepunkt der Spezies der Säugetiere. Das Leben hängt immer vom Umfeld ab. Und Säugetiere brauchen nun mal den Sauerstoff der sich aber nur mit dem CO2 erzeugen lässt. Was bleibt also übrig, wenn das CO2 komplett aus der Atmosphäre getilgt ist und sich im Gestein/Ozean gebunden hat….Sauerstoff?….wohl eher nur Stickstoff…bin für Vorschläge offen…
Vielleicht entwickelt sich das Leben dann wieder in die Meere (Wasser) zurück. Aus dem Wasser stammt das Leben auf der Erde und zum Wasser kehrt das Leben wieder zurück. Zurück bis zu den Mikroben. Es sind Mikroben die in einen noch so „Lebensfeindlichen Umfeld“ (aus Sicht der Menschen) zurecht kommen.
Sind nur so einige Gedanken….das Thema kann man ja bei Gelegenheit etwas vertiefen.
Hallo Herr Ketterer,
vielen Dank für die (nochmalige) Aufführung des Links zur Diskussionsseite.
Nach Sichtung der Definition des Revelle-Effektes komme ich zu dem Ergebnis, dass dieser Effekt nur die Lösung bis hin zum Carbonat-Ion (CO3–) bzw. das Verschieben des Gleichgewichtes in diese Richtung betrachtet, jedoch nicht die Abscheidung des Calciumcarbonates in Form von Aragonit und Calcit durch und in marinen Organismen.
Das macht aber wieder „Platz“ in der Lösung. Die Frage, ob der Revelle-Effekt nun überhaupt (gut) beobachtbar sein kann, ist von daher offen.
MfG
Horst-Joachim Lüdecke und Carl Otto Weiss stellen in der neuen Fachpublikation wieder ihr
bereits beim ESDD-Review abgelehntes – weil zu einfaches – Modell vor, das durch einen Fehler in der Modellgleichung 2.5 (auf den ich längst, aber leider ohne Erfolg, hingewiesen habe) mit einer „Halbwertszeit“ von etwa 100 Jahren – statt real mit etwa nur 40 – viel zu hohe Konzentrationsanstiege berechnet. Hier liegt sogar ein Widerspruch zu den IPCC-nahen CDIAC-Daten vor, die nach Bild 1 eine 1/e-Zeitkonstante (Tau) von etwa 80 Jahren ergeben und mit ln(2) eine Halbwertszeit von 55 Jahren. Originalarbeit: http://tinyurl.com/j9qgq6h
Durch die fehlerhaften Modellrechnungen wird letztlich – ausgerechnet von EIKE – die Zurückweisung von Forderungen nach CO2-Reduktionen und Dekarbonisierung konterkariert, denn schließlich fehlt auch jeglicher Hinweis auf die von IPCC benutzte 5-fach zu hohe Klimasensitivität von 3 Grad pro Verdoppelung welche für das 2-Grad-Ziel einen maximalen CO2-Anstieg auf nur 445 anstatt auf 2820 (!!) ppm ergibt.
Sehr geehrter Herr Dietze,
Unser Modell geht von den zwei physikalischen Grundannahmen Glg.(2.1, 2.2) aus, wobei jede einen Parameter enthält- Glg.(2.1) „tau“und Glg.(2.2) „b“. Diese beiden Grundannahmen führen durch einfache mathematische Umformung zur Modellgleichung Glg.(2.7). Die Wertezuweisungen für „tau“ und „b“ könnten prinzipiell mit bereits bekannten Werten aus der Literatur erfolgen. Die gibt es leider nur für „tau“, s. Gloor et al. mit tau = 81,4 yr, nicht aber für „b“.
Die Wertzuweisungen erfolgen daher bei uns mit Hilfe der nichtlinearen Optimierung, wobei das Verfahren numerisch-mathematisch diejenigen Parameterwerte ermittelt, die die beste Übereinstimmung des Modells mit den Messungen liefern. Das ist übliches Vorgehen in der Physik. Das Modell muss die Natur wiedergeben, nicht umgekehrt. Unsere so erhaltenen 80,4 yr (mit Meerestemperaturterm) bzw. 84 yr ohne diesen Term stimmen mit dem von Gloor angegebenen Wert exzellent überein.
Im Übrigen weisen wir darauf hin, dass die Modellösung für (Glg.(2.7) im Gegensatz zu Ihrer Spekulation keine Exponentialfunktion ist. Es steht Ihnen frei, ein anderes Modell in einem Fachjournal einzureichen. Wir wünschen viel Erfolg.
MfG
Horst-Joachim Lüdecke
Carl Otto Weiss
Meine Fragen an die Autoren:
Wie sieht der DeltaC13 -Wert dieses Modells aus. Der, welcher sich aus den IPCC-Annahmen ergibt, stimmt ja überhaupt nicht mit dem gemessenen überein.
Welche Aufenthaltsdauer haben die Autoren bei Ihrem Modell für das aus der Veerbrennung der Kohlenwasserstoffe stammenden CO2 angenommen.
Gratulation: Ein wirklich erfreulich interessantes Papier.
Herr Weissenborn, die Diskussion um das paper ist (wie oben schon angegeben) hier verlinkt:
http://www.earth-syst-dynam-discuss.net/esd-2015-63/
Tab „Discussion“
Eine interessante Arbeit! Diese allein reicht schon, den Alarmismus in seine Schranken zu weisen.
Bezieht sich der Revelle-Effekt nur allein auf die „Lösung Ozeanwasser“ oder auf das Gesamtsystem „Ozean“? Dieser Punkt ist m.E. nicht ganz unwichtig. Immerhin wäre es möglich, dass das Ozeanwasser mit steigenden CO2-Partialdrücken in der Atmosphäre zwar tendenziell weniger CO2 aufnimmt, jedoch andererseits das Gesamtsystem „Ozean“ mittels Karbonatabscheidung, welche fast immer an Organismen (vor allem Planktion, wie Globigerinen, Coccolithen, Foraminiferen und auch höhere Lebewesen wie Korallen und Schwämme) geknüpft ist, seine Senkenfunktion für C bzw. CO2 dennoch fortsetzt.
Ein Grund, warum die Ozeane zumindest während des Phanerozoikums nicht versauert (unter ph 7) sind.
Diese Aussage bestreite ich insgesamt nicht, Herr Lüdecke (Herr Weiss)! Jedoch sollte man sich klarmachen, dass der Begriff „Vulkanismus“ sowohl von „Laien“ als auch von Nicht-Geowissenschaftlern oft unscharf gebraucht wird. Das deutet sich u.U. schon in der Grafik der C-Flüsse an. Dort wird der Vukanismus bildlich mit einem Kegelvulkan dargestellt, was eine enorme Verengung in Bezug auf seine CO2-Emissionen darstellt. Es existieren in dieser Hinsicht nur für eine Minderzahl dieser Vulkane glaubwürdige Abschätzungen und Messungen. Dass „vukanische“, besser „magmatische“ CO2-Freisetzungen darüber hinaus an eienr Vielzahl weiterer Quellen, stattfinden, dürfte unbestritten sein. Dazu gehören Fumarolen, Geysire, Spaltensysteme und Tiefenbrüche in der Erdrinde und vor allem – Sie erinnern sich, wir sprachen schon einmal darüber, Herr Lüdecke – sämtliche Riftzonen einschließlich der mittelozeanischen.
Da besteht aus naheliegenden Gründen Erkenntnismangel.
Jedoch kann ich daraus für die von Ihnen und Ihrem Kollegen betrachtete Zeitspanne keine deutlich erhöhte CO2-Zufuhr geogener Art ableiten. Kleinere Inputschwankungen sind jedoch möglich.
Noch etwas: warum wurde die Vorläuferarbeit abgelehnt?
MfG
Dirk Weißenborn