Wenn der zeitliche Verlauf globaler Temperaturen graphisch dargestellt wird, so z. B. von dem NASA Goddard Institut for Space Studies (GISS), werden meist Temperaturanomalien gezeigt. (Abb. 1 nebenstehend) Dabei handelt es sich z. B. um Jahresmittelwerte, die ihrerseits auf einen Mittelwert über ein definiertes Zeitintervall bezogen werden, z. B. 1961 – 1990. Man muss sich darüber im Klaren sein, dass es sich bei Mittelwerten um Schätzungen handelt, die letztendlich auf einer für repräsentativ gehaltenen Auswahl von Einzelmessungen beruhen.
Die zulässigen Methoden der Mittelwertbildung unter Berücksichtigung der Schätzfehler von den Messdaten bis zur globalen Jahresmitteltemperatur soll im Folgenden dargestellt werden. Darauf aufbauend werden für ausgewählte Temperaturreihen die Mittelwerte auf signifikante Unterschiede analysiert.
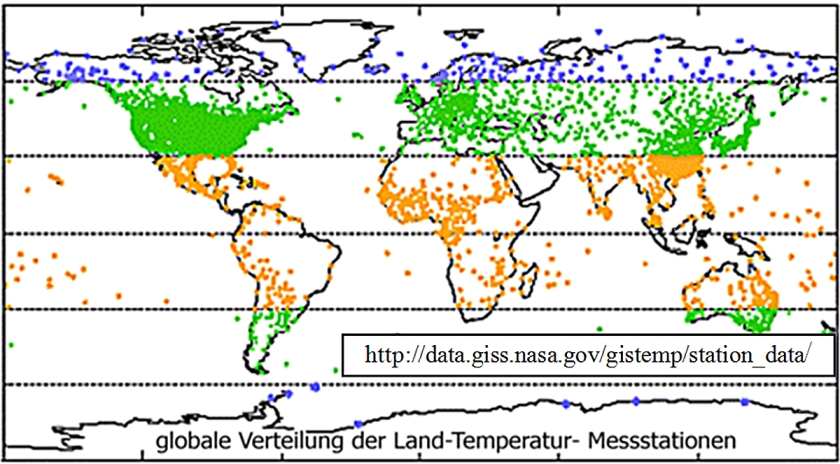
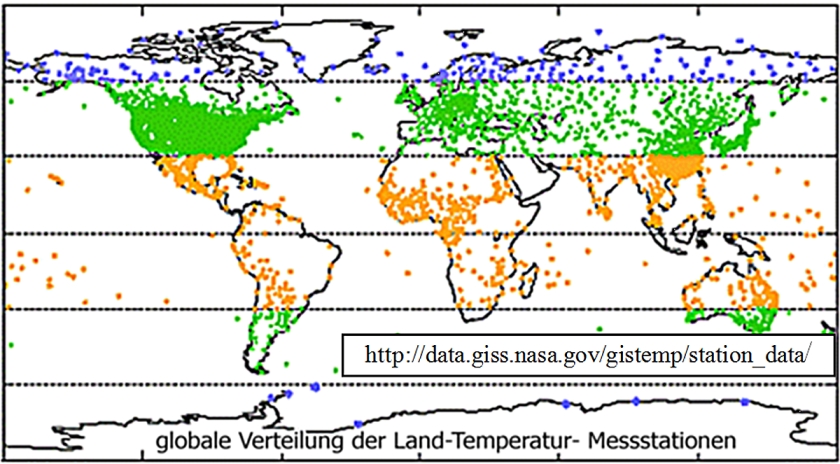
Abb. 2
Es existieren weltweit ca. 39.000 meteorologische Stationen, die neben der Registrierung anderen Wetterdaten die bodennahen (2m) Lufttemperatur messen. Wie Abb. 2 zu entnehmen, sind diese Stationen sind nicht homogen über die Landfläche der Erde verteilt (die Markierungen in den Meeren beziehen sich auf Inseln).
Zwischen 1000 und 3000 von ihnen werden mit z. T. unterschiedlicher Gewichtung zur Berechnung der Globaltemperatur-Reihen der verschiedenen Institutionen herangezogen. Die bodennahen Lufttemperaturen werden auch von einem Satelliten (TIROS-N ) erfasst und können u. a. als globale Verteilungen dargestellt werden.
So wurden von der NOAA (National Oceanic and Atmospheric Administration, USA) z. B. für den 2. März 2012 die folgenden ”Momentaufnahmen” (Abb. 3)veröffentlicht:
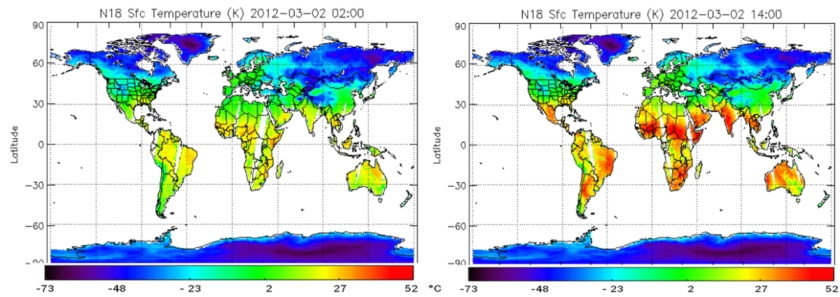
Abb. 3
Die riesige geographische Variabilität der bodennahen Landtemperaturen durch einen einzigen Mittelwert charakterisieren zu wollen, erscheint sehr ehrgeizig. Die ständigen täglichen, wie auch jahreszeitlichen Temperaturänderungen erschweren dieses Vorhaben zusätzlich.
Betrachtet man zunächst einmal nur eine einzige Station. Die allgemein vorgeschriebenen Bedingungen zur Messung der bodennahen Temperatur verlangen, dass ein geeichtes Thermometer in einem als ”englische Hütte” bezeichneten Kasten zwei Meter über dem Erdboden untergebracht ist (Abb. 4).

Abb. 4
Der weiße Anstrich und die Belüftungslamellen sollen gewährleisten, dass die Lufttemperatur ungestört (im Gleichgewicht mit der Umgebung) gemessen werden kann. Tagesmittelwerte werden weltweit nach verschiedenen Methoden gebildet
In Deutschland wird traditionell das arithmetische Mittel aus den 7 Uhr, 14 Uhr und 21 Uhr Temperaturen berechnet, wobei der 21 Uhr Wert doppelt gewichtet wird.
Nach Umstellung auf elektronische Datenerfassung sind auch andere Mittelwertbildungen gebräuchlich.
Der Tagesmittelwert ist in jedem Fall eine Schätzung, die als verbindlich betrachtet wird, ohne mögliche Fehlerquellen der Station (Ablesefehler, Aufbau und Anstrich der ”englischen Hütte”, Beeinflussung der Umgebung durch lokale Wärmequellen) zu berücksichtigen.
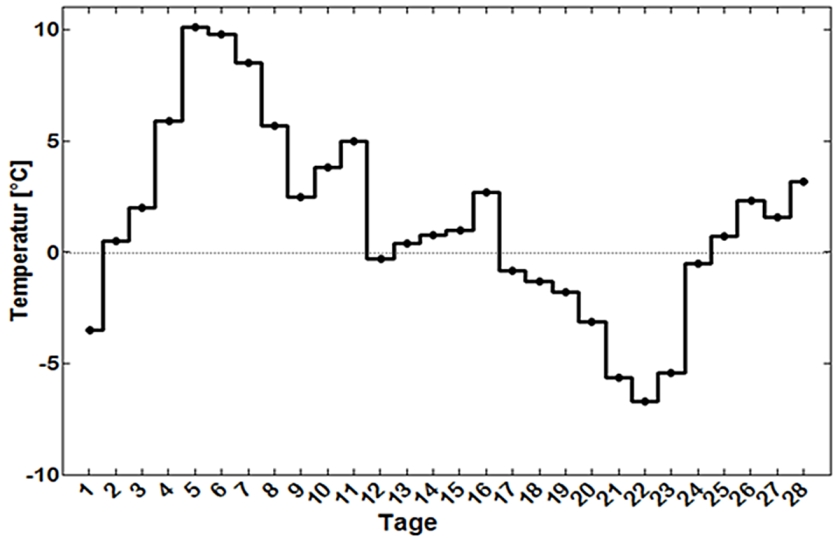
Abb. 5 zeigt die Tagesmittelwerte der Station Braunschweig Völkenrode des Deutschen Wetterdienstes (DWD) für Februar 2011 dargestellt. Wenn daraus ein Monatsmittelwert gebildet werden soll, muss man aus statistischer Sicht erst einmal untersuchen, welche Art der Mittelwertbildung für diese Grundgesamtheit, wie eine solche Ansammlung von Werten genannt wird, zulässig ist. Das arithmetische Mittel, also die durch ihre Anzahl dividierte Summe aller Werte, ist nur dann sinnvoll (zulässig), wenn sie einer definierten Verteilung unterliegen. Dazu werden die Tagesmitteltemperaturen in Größenklassen unterteilt und als Histogramm dargestellt:
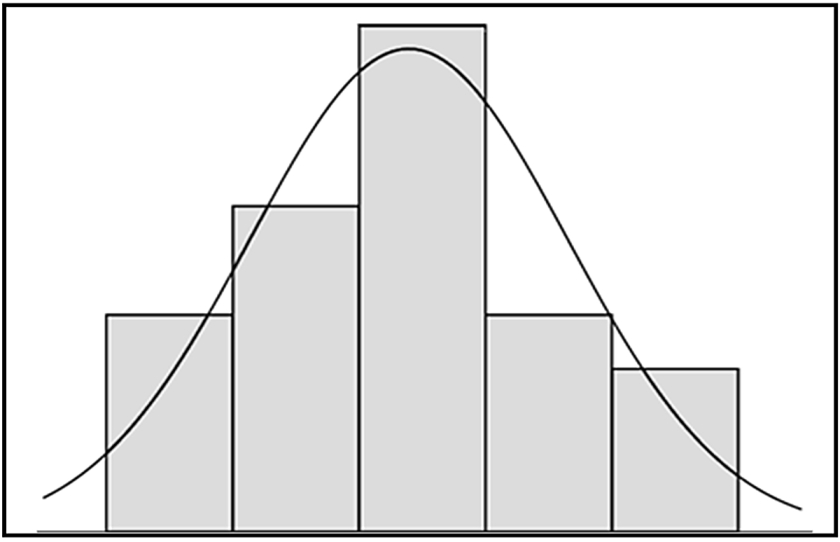
Abb. 6
Wenn die Flächen der Klassen annähernd die Fläche unter der Kurve, die einer Normalverteilung nach Gauss entspricht, ausfüllen, kann die Grundgesamtheit als normalverteilt betrachtet werden (Abb.6). Dies zu entscheiden gibt es statistische Testverfahren, die in der Wissenschaft routinemäßig am Beginn einer statistischen Auswertung stehen. Für die gezeigten Tagesmittelwerte ist die Bildung eines arithmetischen Mittels demnach zulässig. Hätte der Test das Vorliegen einer normalverteilten Grundgesamtheit abgelehnt, wäre der Median zur Beschreibung der Monatsmitteltemperatur sinnvoll (erlaubt) und ein besserer Repräsentant für den Monatsmittelwert. Aus der aufsteigend angeordneten Einzelwerten wird der Wert bei der halben Anzahl ausgewählt und als Median bezeichnet.
Genau dieser Fall tritt für die Oktober-Temperaturen 2011 ein.
In Abb. 7 sind die Verteilungen der Einzelwerte als schwarze Punkte als sogenannte Jitterplots dargestellt. -Die Februarwerte streuen symmetrisch um das blau eingezeichnete arithmetische Mittel herum, während die Oktoberwerte unsymmetrisch mit einer Tendenz zu höheren Temperaturen um das das arithmetische Mittel verteilt sind. 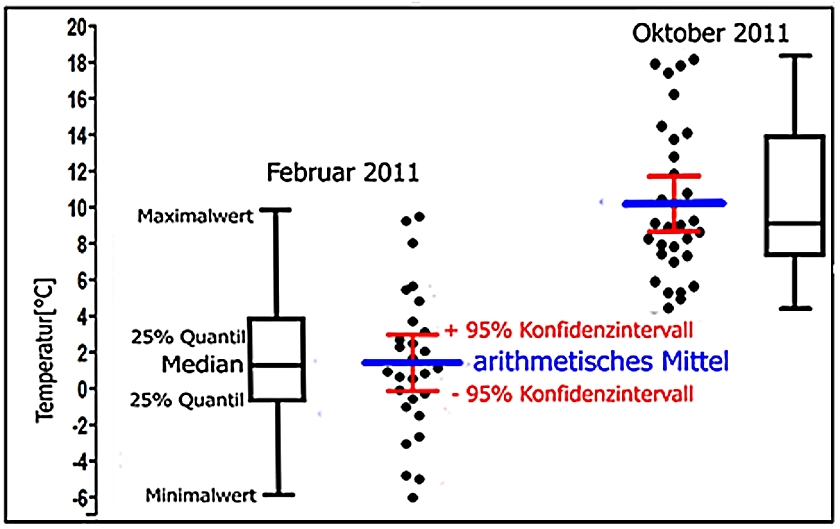
Abb. 7
Von diesem weicht der Median deutlich ab, da er sich an der Lage der meisten Einzelwerte orientiert. Die Kästchen über und unter dem Median repräsentieren die Lage von jeweils 25% der Einzelwerte (25% Quantile) und sind für den Oktober 2011 sehr unterschiedlich, während sie für den Februar fast gleich groß ausfallen. Auch sind die Werte für Median und arithmetisches Mittel fast identisch. Dies ergibt sich bei normalverteilten Grundgesamtheiten, bei denen zusätzlich Kenngrößen für die Streuung berechnet werden können.
Die rot eingezeichneten Vertrauensbereiche (Konfidenzintervalle) weisen aus, dass der zutreffende Mittelwert unter Berücksichtigung der Verteilung der Einzelwerte mit einer Wahrscheinlichkeit von 95% (95% Konfidenzniveau) in diesem Bereich liegt.
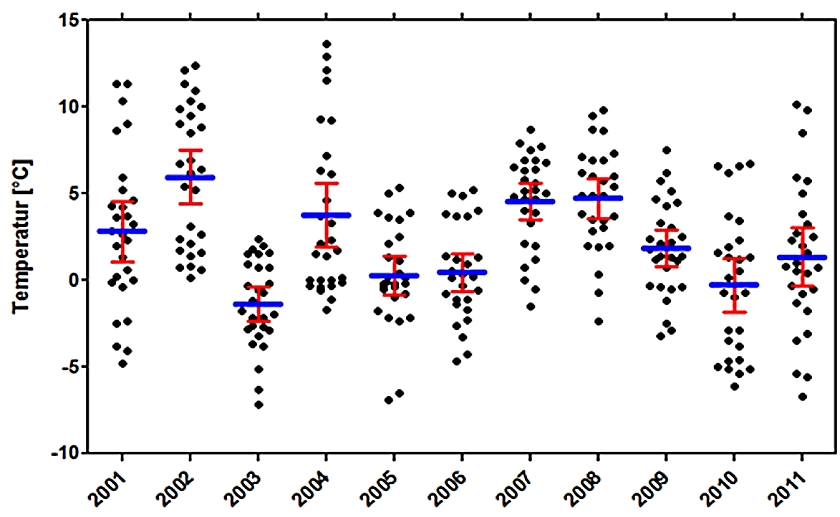
Abb. 8
Da jede Mittelwertbildung eine Schätzung darstellt, ist ihr eine von der Anzahl der Einzelwerte und deren Verteilung (eben der Grundgesamtheit) abhängiges Streuungsmaß sozusagen aufgeprägt.
Dies erlaubt die Anwendung von Signifikanztests, mittels derer zum Beispiel für ein vorgegebenes Konfidenzniveau entschieden werden kann, ob sich Mittelwerte signifikant voneinander unterscheiden. Für normalverteilte Grundgesamtheiten werden dabei andere Tests (Varianzanalyse) als für beliebige (nicht parametrische) Verteilungen angewandt, z. B. der Kruskal-Wallis Test.
Für den Vergleich der Februar-Mitteltemperaturen von 2001 bis 2011 der DWD Station Braunschweig (Abb. 8) können die arithmetischen Mittel der Tagesmittelwerte verglichen werden, da für jedes Jahr eine Normalverteilung vorliegt. Die darauf angewandte Varianzanalyse kommt zu dem Ergebnis, dass sich die Mittelwerte insgesamt auf einem Konfidenzniveau von 95% unterscheiden.
Um Jahresmittelwerte zu bilden, kann man die Tagesmittelwerte direkt verrechnen oder nach Bildung von Monats-mitteln, diese zur Mittelwertbildung verwenden.
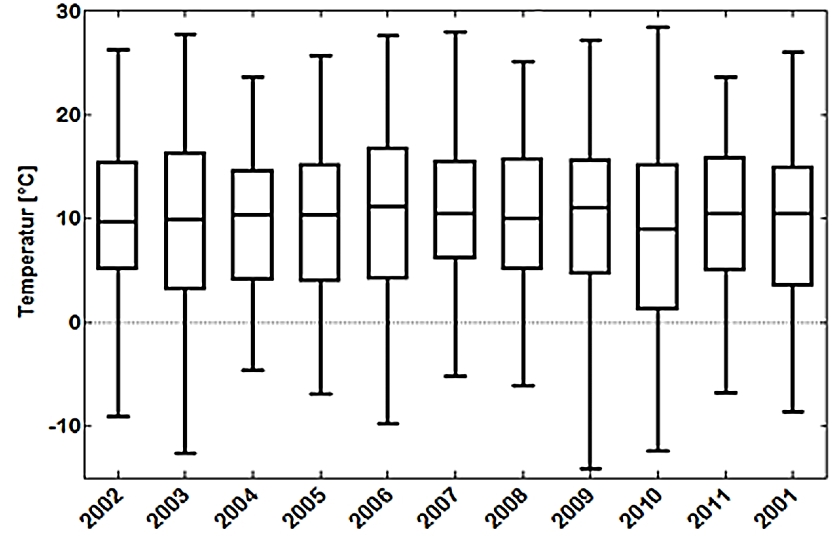
Abb. 9
Da für die DWD Station Braunschweig die Jahresverteilungen der Tagesmittel die Normalitätskriterien nicht erfüllen, müssen die Mediane benutzt werden (Abb. 9).
Zur Entscheidung, ob sich die Jahres-Mediane signifikant voneinander unterscheiden, wird der Kruskal-Wallis Test angewandt, der zu dem Ergebnis gelangt, dass insgesamt kein signifikanter Unterschied zwischen ihnen vorliegt.
In der Praxis weren jedoch die Jahresmittelwerte aus den Monatsmittelwerten gebildet, wobei einfach vorausgesetzt wird, dass die Tageswerte der Monate jeweils normalverteilt sind. Das trifft auch meistens zu, da Mittelwerte, auch wenn sie aus nicht normalverteilten Grundgesamtheiten gebildet werden, tendenziell dazu neigen, eine Normalverteilung anzunehmen.
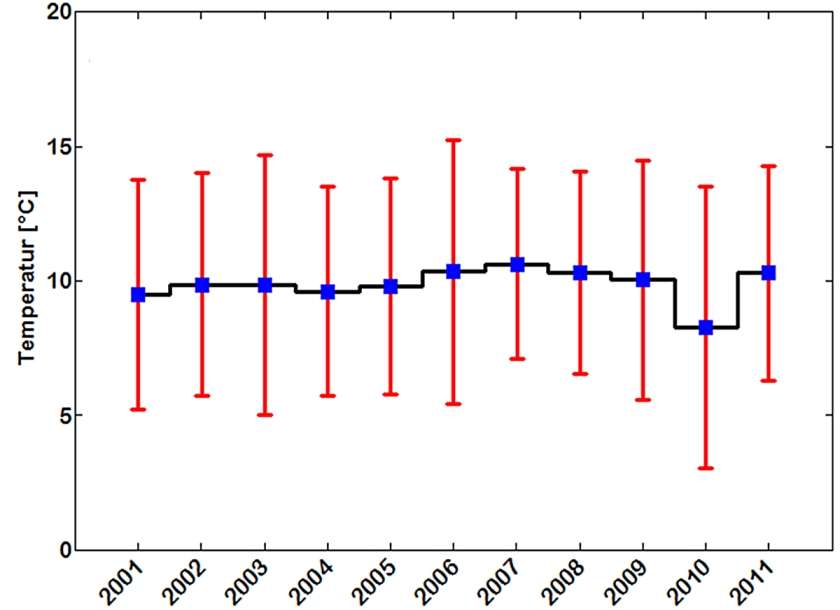
Abb. 10
Die Streungsmaße der Monatsmittel werden in den öffentlich zugänglichen Datensätzen nicht weiter berücksichtigt, was jedoch aufgrund der Fehlerfortpflanzungsregeln nach Gauss geboten ist.
Somit stehen nur solch Streuungsparameter, die sich bei der Bildung von Jahresmittelwerten aus den veröffentlichten Monatswerten ergeben, für Signifikanztests zur Verfügung.
In die Berechnung von Konfidenzintervallen geht die Anzahl der Einzelwerte als Divisor ein. Daher fallen sie für Jahresmittelwerte relativ groß aus, da diese jeweils nur aus 12 Werten (Monaten) gebildet werden (Abb. 10). Die Varianzanalyse sagt aus, dass sich die Jahresmittelwerte nicht signifikant voneinander unterscheiden und gelangt damit zum gleichen Ergebnis wie der vorige Vergleich der Mediane aus Tagesmittelwerten geführt. 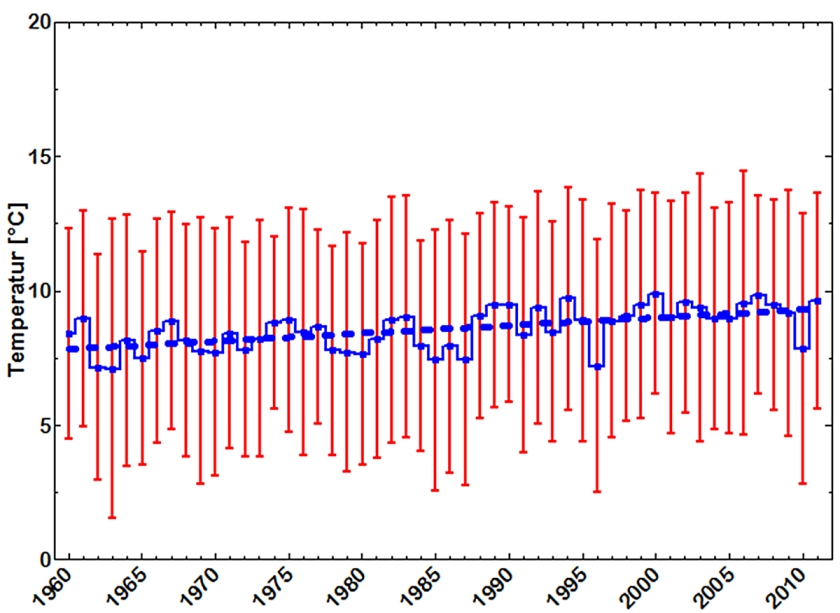
Abb. 11
Im nächsten Schritt, werden aus den Monatsmitteln einzelner Stationen Gebietsmittel gebildet. Der Deutsche Wetterdienst berücksichtigt z. Zt. 264 Stationen, die zur Berechnung einer für Deutschland relevanten Mitteltemperatur herangezogen werden. Die Monatswerte sind normalverteilt, so dass die Jahresmittelwerte durch arithmetische Mittel und ihre Konfidenzintervalle repräsentiert werden können. Eine Varianzanalyse weist keine signifikanten Unterschiede zwischen den Jahresmittelwerten seit 1960 aus (Abb. 11).
Dennoch läßt sich ein Trend berechnen, der durch eine Steigung von 0,03 ± 0,006 °C/Jahr der Regressionsgeraden charakterisiert wird, für die mit einem Bestimmtheitsmaß von R2 = 0,33 eine beträchtliche Unsicherheit besteht.
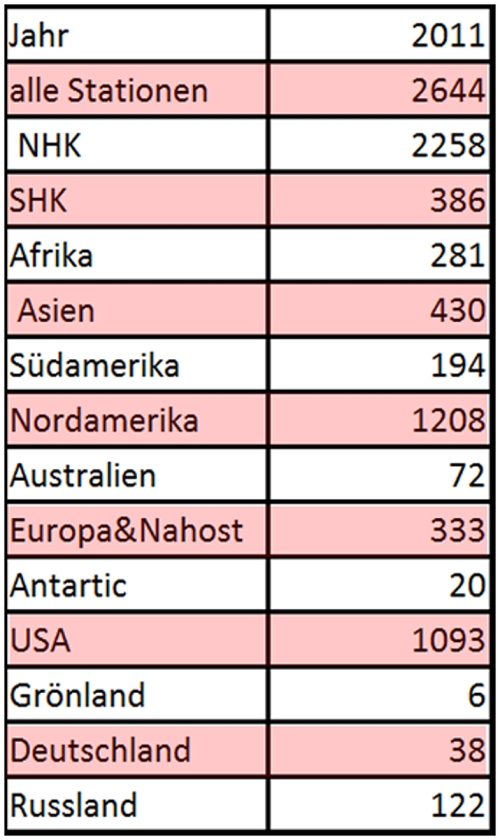
Tab. 1
Nach Angaben des Global Historical Climatology Network (GHCN), bei dem die Temperaturen der weltweit verteilten Stationen gesammelt werden, wurden 2011 zur Ermittlung der globalen mittleren Landtemperatur die Daten von 2644 Stationen berücksichtigt. Anzahl und Verteilung ist der Tabelle 1 zu entnehmen. Wie schon aus der oben gezeigten Karte hervorging, sind die Stationen nicht homogen über die Landfläche verteilt.
Temperatur – Zeit – Reihen werden im Wesentlichen von 3 von Institutionen mit unterschiedlichen Gewichtungen der Werte erstellt und publiziert.


Laure M. Montandon et al. haben die unterschiedliche Berücksichtigung der vom GHCN nach Oberflächentypen differenzierten Landstationen tabelliert (Tab. 2). Auffällig sind die hohen Anteile der urbanen Stationen.
In jüngster Zeit haben Überarbeitungen der Zeitreihen dazu geführt, dass sich die Ergebnisse weitestgehend angenähert haben. Dies gilt auch für die beiden Reihen, in denen die Messungen des TIROS-N Satelliten auswertet werden.
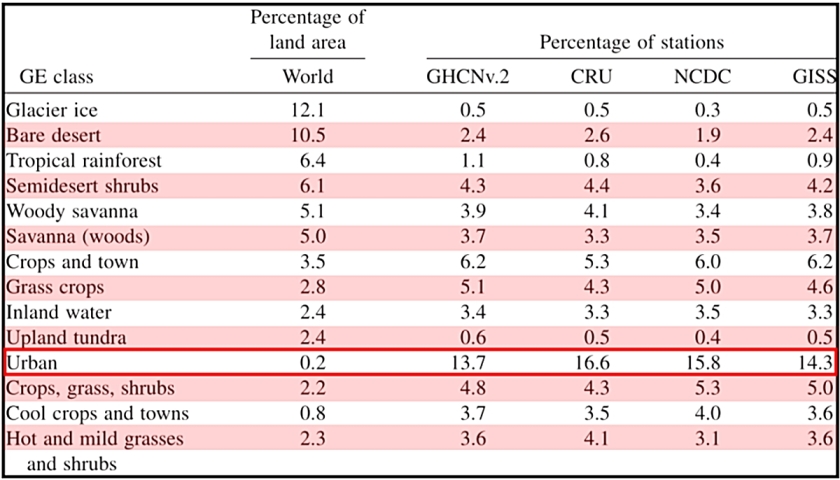
Tab. 2
Diese Daten basieren auf der Reflexion von ausgesandten Mikrowellensignalen und liefern relative Werte, die mithilfe der landgestützten Auswertungen kalibriert werden müssen, um sie in Temperaturwerte umrechnen zu können.
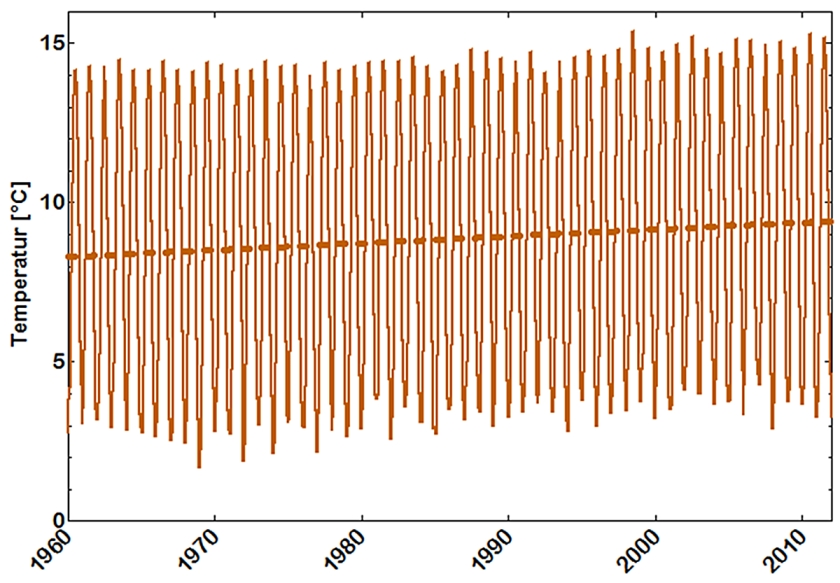
Abb. 12 stellt die Zeitreihe der globalen monatlichen Mitteltemperaturen dar, wie sie vom NCDC (National Climate Data Center) bereitgestellt wird. Es sei darauf hingewiesen, dass keine Streuungsmaße mitgeteilt werden und daher auch nicht eingezeichnet sind.
Die die Regressionsgerade weist eine Steigung von 0,022 mit einem Konfidenzintervall von ± 0,01 °C/Jahr auf und hat ein äusserst geringes Bestimmtheitsmaß von R2 = 0,006 so dass der Trend als sehr unsicher angesehen werden muss.
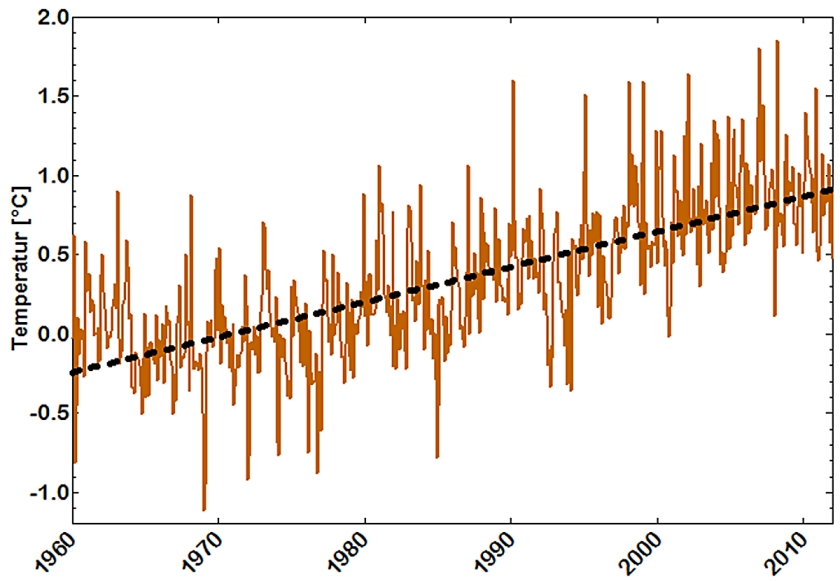
In Abb. 13 sind die Temperaturanomalien, bezogen auf die Referenzperiode von 1960 bis 1990, zu sehen.
Auch hier fehlen Streuungsmaße, die aufgrund der Subtraktion der Mittelwerte der Referenz-Monatsmittemittel von den jeweiligen monatlichen Mittelwerten nach dem Fehlerfortpflanzungsgesetz sehr beträchtlich ausfallen.
Da diese nicht berücksichtigt werden, d. h. weniger Information über die Ausgangsdaten für weitere Berechnungen vorliegt, erhält man mit R2 = 0,5 nur ein scheinbar größeres Bestimmtheitsmass für die Regressionsgerade.
Ihre Steigung unterscheidet sich mit 0,022 ± 0,001 ebenfalls nur durch ein augenscheinlich um den Faktor 10 verringertes Konfidenzintervall von der obigen.
Da die Erdoberfläche nur zu angenähert einem knappen Drittel (29 %) aus Land, zu gut zwei Ditteln (71%) aber aus Ozeanen besteht, erscheint es sinnvoll, deren Temperaturen zur Berechnung einer Global-Mitteltemperatur einzubeziehen. Früher wurde dazu eine Wasserprobe mit einem Schöpfeimer (Pütz oder Bucket) genommen und die Temperatur des Wassers darin gemessen. Deren Schöpftiefe sollte 1 m betragen. Das wurde aber aus praktischen Gründen selten eingehalten. Man kann unterstellen, dass sie je nach Geschwindigkeit des Schiffes und Sorgfalt der beauftragten Person, diese irgendwo zwischen wenigen Zentimetern und max 1 bis 1,5 m lag. Heute wird die Wassertemperatur im Kühlwassereintritt der Schiffe in 3m bis 15 m Tiefe bestimmt. Stationäre Bojen messen die Wassertemperatur in 2m Tiefe (nach Mitteilungen von M. Limburg).
Die solchermaßen gewonnenen Wassertemperaturen werden als SST (Sea Surface Temperatures) bezeichnet.
In Abb. 14 sind die NCDC Zeitreihen für die SST Monatsmittel-Temperaturen und Anomalien abgebildet:
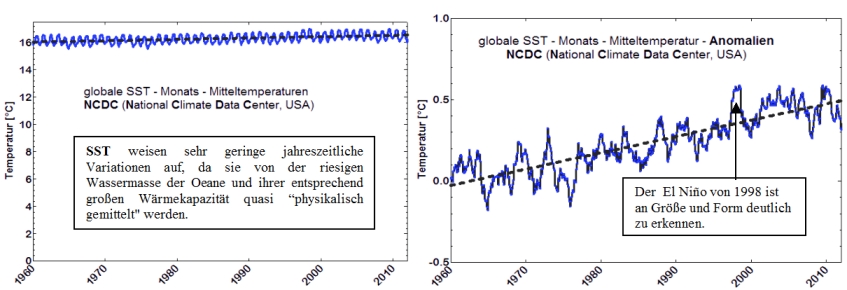
Abb. 14
Die Steigungen der Regressionsgeraden sind mit 0,009 ± 0,001 und 0,01 ± 0,0002 nahezu identisch. Für die Anomalien ergibt sich ein R2 = 0,7, das aber auf dem Hintergrund fehlender Fehlerfortpflanzung kritisch zu betrachten ist.
Die Kombination von Land- und Ozeanberflächentemperaturen wird in Abb. 15 gezeigt:
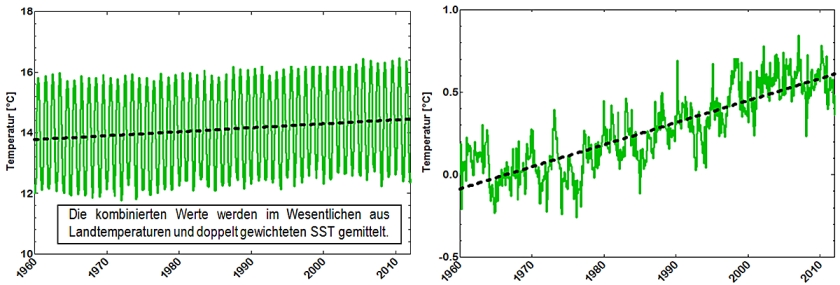
Abb. 15
Die Steigungen der Regressionsgeraden fallen mit 0,013 ± 0,004 bzw. 0,013 ± 0,0004 auch hier praktisch gleich aus. Das Bestimmtheitsmaß ist mit R2 = 0,7 für die Mittelwert-Anomalien größer als für die Mitteltemperaturen mit R2 = 0,02.
Zwar ist es bemerkenswert, dass die Steigung für die Landwerte rund doppelt so hoch wie für SST und Land + SST Werte, jedoch sollte immer bedacht werden, dass die Bestimmtheitsmaße recht gering sind, bzw. für die Anomalien wegen der nicht berücksichtigten Fehlerfortpflanzung nur gesteigert erscheinen.
Werden aus den Monatsmittelwerten Jahresmittel gebildet und die Signifikanzintervalle berechnet und dargestellt, ergibt sich die Abb. 16 für Landtemperaturen der NCDC Reihe. 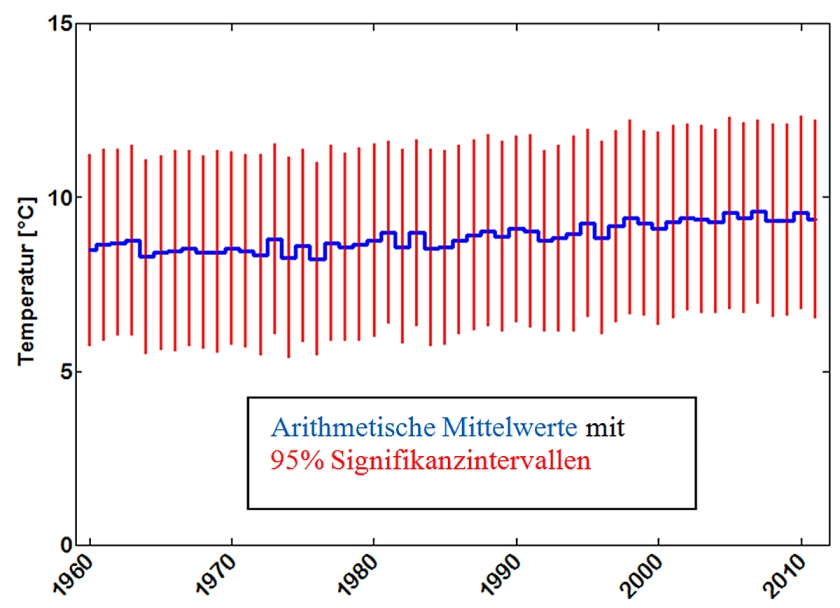
Abb. 16
Für die normalverteilten Werte der globalen Monatsmittel ergibt eine Varianzanalyse, dass sich zwischen den arithmetischen Jahresmitteln keine signifikanten Unterschiede nachweisen lassen.
Hierbei wird deutlich, dass bei der üblichen Darstellung von Temperaturreihen als Anomalien ohne Angabe von Streuungsparametern wichtige Informationen unterdrückt werden und dadurch ungesicherten Spekulationen über Temperaturunterschiede und -trends Vorschub geleistet wird.
Die Angabe einer globalen Mitteltemperatur bzw. der Veränderung einer globalen Mittelwertanomalie (z. B. um 2°C gegenüber einem definierten Zeitpunkt) ist daher unter Beachtung statistischer Gesetzmäßigkeiten, ohne Angabe von Konfindenzintervallen als sinnlos zu betrachten.
Autor: PD Dr. habil Dr. Eckhard Schulze < eckhard.schulze@gmx.org >
Quellen:
zu Tab. 1 http://fzuber.bplaced.net/NOAA-GHCN-Stations-E.pdf
zu Tab. 2 Laure M. Montandon et al. Earth Interactions Volume 15 (2011) Paper No. 6
zu Abb.1 http://cdiac.ornl.gov/trends/temp/hansen/graphics/gl_land.gif
zu Abb.2 http://data.giss.nasa.gov/gistemp/station_data/
zu Abb.3 http://www.osdpd.noaa.gov/ml/mspps/surftprd.html
zu Abb.4 http://imk-msa.fzk.de/Wettervorhersage/images/Huette.jpg
zu Abb. 5 bis 10 avacon.com/cms/ContentFiles/Internet/Downloads/Netze_SN_unterbrVerbrauchseinr_Tagesmitteltemp_2012.xls
zu Abb.11 http://www.dwd.de/bvbw/generator/DWDWWW/Content/Oeffentlichkeit/KU/KU2/KU21/klimadaten/german/download__gebietsmittel__temp,templateId=raw,property=publicationFile.xls/download_gebietsmittel_temp.xls
zu Abb.12 u. 13 http://junksciencearchive.com/MSU_Temps/NCDCabsLand.csv bzw. http://junksciencearchive.com/MSU_Temps/NCDCanomLand.csv
zu Abb.14 a u.b http://junksciencearchive.com/MSU_Temps/NCDCabsOcean.csv bzw. http://junksciencearchive.com/MSU_Temps/NCDCanomOcean.csv
zu Abb.15 a u. b http://junksciencearchive.com/MSU_Temps/NCDCabs.csv bzw. http://junksciencearchive.com/MSU Temps/NCDCanom.csv
Der gesamte Text kann als pdf im Anhang herunter geladen werden
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Dieser Diskurs ist liegt schon eine Weile zurück. Ich kann die statistische Argumentation absolut nachvollziehen. Mich interessieren Quellen, die folgende Fragen adressieren:
– wie genau sind die Temperaturdaten überhaupt. Digitale Daten gibt es erst seit 30-40 Jahren. Die normalen Thermometer haben doch sicher schon Streuungen von +/- 0.5 °C
– wie realistisch ist die Zunahme des Abschmelzens der Antarktis? Gibt es wärmere Strömungen, die den Gegendruck des Packeises mindern und zu höheren Fliessgeschwindigkeiten führen? Passt dies zu dem Pufferargument der Ozeane?
– Wie genau sind die Messungen der Höhe des Meeresspiegels. Im cm-Bereich p.a. gibt es hier doch bei Tidehubhöhen im Meterbereich die gleichen Probleme wie mit T-Messungen
– Rückgang der Gletscher in Grönland – welche Rolle spielen Staub und Ruß
– Energiebilanz: Wenn Gigatonnen Fossiles verbrannt werden, muss doch Energie auch durch die Landmasse gespeichert werden. Wie ist die Absorption hier erklärt.
Bei der -18°C und +15°C Diskussion wird diese Differenz nur den Treibhausgasen zugeschrieben. Welche Rolle spielen Lava, Radioaktivität etc. Die -18°C erklären sich nur aus der Sonnenein- und abstrahlung im Gleichgewicht.
Lieber Herr Schulze,
haben Sie die vergangenen Tage genutzt, um zu verstehen, warum die Streuung eines Jahresmittels eines bestimmten Jahres nicht aus
den Messdaten dieses Jahres berechnet? Die Streuung kennzeichnet selbstverstaendlich nur die Statistik von Jahresmitteln, die mehrere
Jahre umfassen, die Streuung der Daten fuer die Berechnung des Einzelwertes spielt dabei gar keine Rolle!
DrPaul,
eben, da die Streuung wichtig ist, sollte man sie auch kennen. Aber falsch berechnen, ist keine Lösung 😉
Herr Schulze geht von der falschen Vorstellung aus, dass ein Jahresmittel einen Erwartungswert für jeden Monat des Jahres darstellt. Aber nur weil Erwartungswerte bei Normalverteilungen gleich dem arithmetischen Mittelwert sind und dies die gleiche Formel wäre, wie fürs Jahrsmittel, wenn denn die Temperaturen übers JAhr normalverteilt wären, so ist das Jahresmittel NICHT der Erwartungswert. Das Jahresmittel charakterisiert nur das Jahr als kleinste Klasse, aber nicht die Unterklassen wie Monate oder Tage.
Deutlicher kann man sich dies machen (wenn man für eine sachgerechte Aufklärung aufgeschlossen ist), wenn man mal dieses 1:1 Analogon (die Übertragung ist offensichtlich) klarmacht:
man misst eine Länge L durch Hintereinanderlegen von verschiedenen kürzeren Masstäben der Längen Xi unterschiedlicher Genauigkeit. Wie groß ist die Genauigkeit der Längenmessung?
Definiert man eine Größe Y = Länge/Anzahl der Masstäbe, so ist diese Größe Y exakt analog dem Jahresmittel.
Klar ist, dass die Genauigkeit von L (bzw. Y) NICHT durch über die SD = wurzel(1/(N-1) Summe Xi^2) der Teilstückwerte Xi zu berechnen ist!
#64: „Das soll ein weiterer dezenter Hinweis für die Unterstützung von Herrn Dr. Schütze sein,
dass die Definition einer „globalen Mitteltemperatur“ ohne Angabe von Konfidenzintervallen sinnlos ist.“
Vollkommene Zustimmung bei der letzten Aussage. Soweit ich das sehe, werden in Fachpublikationen über Globaltemperaturen entsprechende Konfidenzintervalle mit angegeben.
Ach übrigens Herr Paul, wenn man schon jemanden unterstützen möchte, dann sollte man wenigstens dessen Familiennamen richtig schreiben. Ich hatte vorsorgehalber beim Autor mich dafür entschuldigt, evtl. seinen Vornamen beim ersten Posting nicht richtig zu schreiben.
#62: NicoBaecker falsch,
es ist gerade klimatisch wichtig, wie groß die Streuung, also der Maximal und der Minimalwert der Temperatur ist.
Ein Kontinentalklima mit extremen Schwankungen kann den gleichen Jahresmittelwert haben, wie ein Seeklima mit geringen Schwankungen.
Das gleiche gilt doch für die Tag- und Nachtdifferenzen. Sie können sehr gering (Äquator) und sehr groß (Sahara) sein.
Das soll ein weiterer dezenter Hinweis für die Unterstützung von Herrn Dr. Schütze sein,
dass die Definition einer „globalen Mitteltemperatur“ ohne Angabe von Konfidenzintervallen sinnlos ist.
Freundlichen Gruß
Lieber Herr Schulze,
ich habe ihn oben oefter einen Test vorgeschlagen, wie Sie die SEM des Jahresmittels anhand der Daten ueberpruefen koennen. Warum machen Sie das nicht?
Lieber Herr Schulze, #61
„Ansonsten wird mir die Diskussion mit Ihnen zu spitzfindig “
Das ist nicht spitzfindig, sondern der entscheidende Punkt!
Geben Sie mir bitte mal ein Argument, warum meine Schlußfolgerung aus #57, wo ich Ihre Gleichungen für die Berechnung der SEMref (dort korrekten) auf das SEM des Jahresmittel für n=1 anwende, nicht richtig wäre. Referenzzeitraum n = 30 Jahre, ein Jahr n = 1. Ist doch völlig klar!
Ich komme immer aufs Gleiche zurück und habe Ihnen schon ganz zu Anfang gesagt: Sie berechnen das SEM eines Jahresmittels FALSCH! Das Jahresmittel des Jahres X ist nur ein Messpunkt (oder ein Zug aus der Lottokugel) und zu dem gibt es keine Streuung, machen Sie sich das klar!
Sinnvoll ist nur die Frage, wie Jahresmittel (also mehrere Jahre aufeinander) streuuen. Dies wird z.B. durch Ihre SEMref Berechnung gezeigt. Wenn Sie annehmen, dass alle 30 Jahre des Referenzzeitraumes das gleiche Klima herrschte, so sind dies 30 „Züge aus der Lottokugel“ und damit können Sie den klimatischen Mittelwert und seine Streuung quantifizieren. Aber die Streuung eines einzelnen Jahresmittels berechnet sich nicht aus der Streuung der 12 Monatsmittel wie Sie es abgeben, denn diese sind nicht aus der gleichen „Lottokugel“, denn es sind ja 12 verschiedene Monate, klar nun?
zu # 54
Lieber Herr Bäcker.
Sie schreiben. „Dann hatte ich in #50 gefragt:
„Wenn ich nun Ihre Konfidenzintervalle (CL) der Jahresmittel basierend auf Monatsanomalien angucke, die Sie mir schickten, so beträgt das 95%-CL ca. plus minus 2 C. Das bedeutet, dass SEM ca. = 0,9 C sein muß, und damit SD ca. 3 C. Ist das richtig so? “
Darauf sind Sie leider noch gar nicht eingegangen. Können Sie das bestätigen?
Ich kann Ihnen bestätigen, dass ich darauf nicht eingegangen bin und es auch nicht weiter tun werde, da ich alles dazu schon in # 47 geschrieben haben. Wenn Sie das auf ein konkretes Zahlenbeispiel anwenden, traue ich Ihnen schon zu, dass Sie es richtig umgesetzt haben.
Ansonsten wird mir die Diskussion mit Ihnen zu spitzfindig und ich teile mittlerweile Dr. Pauls Eindruck (#59), dass Sie sich über mich lustig machen wollen. Ihr Satz “ Ein einzelnes Jahresmittel hat gar keine Standardabweichung, da es nur einen Wert gibt.“ den Sie ausdrücklich bestätigt haben, lässt mich in der Tat an der Ernsthaftigkeit Ihrer Kommentare (ver)zweifeln.
Sehr geehrter Dr. Eckhard Schulze,
der Hinweis von Ihnen auf die konkreten Temperaturdaten zu gehen, war sehr
gut. Ich habe wirklich nochmal einige Zeit in die Daten und Formeln
investiert und muss einiges von meinen bisherigen Aussagen revidieren. Ich
habe bewusst versucht, die Ergebnisse auf zwei verschiedene Rechenwegen
nachzuvollziehen, um eine höhere Kontrolle bei der Vergleichbarkeit zu
bekommen. Einmal bin ich möglist streng nach der Formel zur
Fehlerfortpflanzung gegangen. Als zweiten Weg wählte ich einen eher intuitiven Ansatz.
Zunächst zur Fehlerfortpflanzung. Allgemeinen geht man von einer
multivariaten Funktion y= f(x1,x2,…) aus. Die Zielgröße y setzt sich
dementsprechend aus den verschiedenen Teilgrößen xi zusammen. Wenn sigma
(y) die Streuung der Zielgröße ist, dann ist
sigma(y)= sqrt(sigma(x1)^2*(part(f)/part(x1))^2+sigma(x1)^2*(part(f)/part
(x1))^2+…)
wobei part(f)/part(xi) für die partielle Ableitung der Funktion f an der
Variable xi steht.
Wenn der Jahresmittelwert j = (m1+m2+…+m12)/12 ist, dann ist
sigma(j)= sqrt(sigma(m1)^2*(1/12)^2+sigma(m2)^2*(1/12)^2+…+sigma(m12)^2*
(1/12)^2)
sigma(j)= (1/12)*sqrt(sigma(m1)^2+sigma(m2)^2+…+sigma(m12)^2)
Für den Referenzzeitraum 1961-1990 erhält man einen Standardfehler(Streuung) von einem einzelnen(!) Jahresmittelwert von 0,5168°C.
Ein alternativer Weg auf diesen wert zu kommen, ist die Anwendung der
Formeln a^2*sigma(x)= sigma(a*x) und sigma(y)^2= sigma(x1)^2+sigma(x2)^2
als Addition der Varianzen, wenn y=x1+x2.
Dann ergibt sich aus der Jahresmittelwertformel ebenfalls
sigma(j)= (1/12)*sqrt(sigma(m1)^2+sigma(m2)^2+…+sigma(m12)^2).
Nun war ja die Frage auch, wie es sich mit den Temperaturanomalien
verhält. Dazu braucht man die Streuung des 30-Jahres-Durchschnitts. Wenn
die Streuung für ein Jahresmittelwert 0,5168°C beträgt, dann ist entsprechend sigma(j30)= 0,5168°C/sqrt(30)= 0,0944°C
Durch die Subtraktion von j und j30 addieren sich die Varianzen.
sigma(j-j30)= sqrt(0,5168°C^2+0,0944°C^2)= 0,5254°C
Bei einem 95%-Konfidenzintervall bedeutet das eine Spanne von +/-
1,96*0,5254°C= +/-1,0297°C. D.h. die tatsächliche Temperatoranomalie
befindet sich in einem etwa 2°C großem Intervall mit 95%iger Sicherheit.
Bei diesem Unsicherheitsfaktor kann man sich schon die Frage stellen, ob
man einen realen Trend überhaupt erkennen kann bzw. ob ein beobachteter Trend überhaupt real vorliegt. Mindestens zwei Punkte sind hier
wichtig. Zum einen macht die Anwendung der Fehlerfortpflanzungsformel nur
dann wirklich Sinn, wenn das Meßsystem für die beobachteten Fehler
verantwortlich ist. Zum Beispiel liegen die Standardabweichungen für die
12 verschiedenen Monate zwischen 0,9°C und 3,0°C. Die Ursache liegt aber
nicht am Meßsystem alleine. Selbst wenn man die perfektesten Thermometer
besitzen würde, damit ganz Deutschland vollständig zupflastert und jede
Sekunde misst und alles mittelt, würden die Streuungen der
Monatsmittelwerte immer noch in dieser Größenordnung liegen. Es liegt
einfach am Wetter, dass die Maitemperatur einige Grad wärmer oder kälter
als die vom Vorjahr sein kann. Von daher kann die Fehlerfortpflanzung uns nicht wirklich sagen, wie weit unsere errechneter Jahresmittelwert vom
tatsächlichen Wert entfernt liegt. In der Regel wird man die Meßtoleranz
zu groß abstecken.
Jedoch selbst wenn man ein großes Rauschen auf seinen Daten hat und ein
schwaches Signal, sprich einen steigenden Trend, kann man bei einem
genügend großen Zeitintervall das Signal detektieren. Man kann ja mal
folgendes Experiment machen. Angenommen man hat eine 100-Jahre-Zeitreihe
und jedes Jahr würde die Temperatur um 0,01°C steigen. Gleichzeitig hat man jedes Jahr ein gaußsches Rauschen von sigma= 0,5°C, wie stark würde die gemessene Steigung (die man mit einer Regressionsgeraden bestimmt) schwanken? Ich war jetzt zu faul, dass händisch auszurechnen, obwohl das bestimmt ohen größere Aufwände machbar wäre. Wenn es schnell gehen muss, tut es auch eine Monte-Carlo-Simulation. Nach 10.000 Durchläufen befanden sich 95% aller Steigungen zwischen 0,0066°C und 0,0133°C pro Jahr. D.h. bei einem 100-Jahres-Trend würde man den Temperaturanstieg trotz Rauschen gut wahrnehmen. Wenn man nur eine 30-Jahre-Zeitreihe nimmt, dann liegen die Steigungen zwischen -0,0107°C und 0,0305°C. Da wäre es nur in wenigen Fällen möglich, den Trend zweifelsfrei zu detektieren. Allerdings wäre ein Meßrauschen von 0,5°C bei einer Vielzahl von gemittelten Meßstationen schon recht groß. Letztlich sollen diese Beispiele nur zur Veranschaulichung dienen.
@NicoBaecker, #57: „Nach den Lehrbüchern der Statistik ist dann die Varianz von Y (dem Jahresmittel) (siehe #45):
V_Y = (1/12)^2 (VJan + … VDez)
Damit ist die SD (= stdv) des Jahresmittels Y
SD = wurzel (V_Y) = 1/12 * wurzel(VJan + … VDez) oder 1/12 wurzel (SDJan^2+…+ SDDez^2)“
Ich denke das war der Knackpunkt in den Berechnungen. Statt 1/12 zu rechnen, wurde 1/sqrt(12) genommen. Dieser Fehler kann passieren, weil man durch die ganzen Standardabweichungen, Varianzen und Quadrate schnell durcheinanderkommt. Dieser Fehler ist mir beim händischen Umstellen der Gleichungen auch mind. einmal passiert, aber zum Glück kann man Kontrollrechnungen durchführen. :o) Im Prinzip sind unsere Erklärungen mit anderen Worten formuliert in vielen Dingen deckungsgleich.
„Ich nehme an, Sie haben die stdv eines Jahres nun aus den 12 Monatsanomalien nach der Formel
stdv = sqrt(sum(Xi-Xmean)^2)/n-1) berechnet, mit n =12, Xi als Monatsanomalien und Xmean als Jahresanomalie. Stimmt das? Das wäre wie oben und schon öfter gesagt falsch.“
Ich denke schon, dass Herr Schulze die Formeln vom Prinzip richtig aufgestellt hat, und nur einmal 1/sqrt(12) statt 1/12 als Vorfaktor verwendet hat. Ich bin jetzt aber echt zu müde, um das alles nochmal aufzudröseln.
Guts Nächtle
S.Hader
#58: NicoBaecker Sind Sie auf einmal dumm geworden,
oder wollen Sie sich über Herrn Schulze lustig machen?
Zu jedem Referenzintervall gehört eine Standardabweichung, das sollte reichen.
Leider haben wir aber nicht nur eine einzige Globaltemperatur,
sondern deren mindestens 6
UAH temperatures
RSS temperatures
HadCRUT3 temperatures
NCDC temperatures
GISS temperatures
AMSU temperatures
Wir leben also sozusagen auf 6 verschiedenen Erden,
den Inseleffekt haben wir noch gar nicht mitberücksichtigt,
was schehrt meinen Garten z.B. der Anstieg des Flugverkehrs am Frankfurter Flughafen, den der DWD uns immer als Wetterkatastrophe mitteilt.
Was meinen Sie also Baecker,
wie sich das alles auf die Standardabweichung auswirkt?
Ich muss jetzt einfach diese ungeheuer schwierige Frage stellen, die natürlich ein wenig aus den von Ihnen immer beklagten pädagogischen Vereinfachungen herausfällt:
Wird die Standartabweichung dann
a) größer
oder
b) kleiner
Herr Schulze kann sich inzwischen als Statistiker etwas erholen,
Baecker wird die Antwort so schnell nicht finden,
wirklich vielleicht ein ganz kleines bischen unfair,
so weit abseits der pädagogischen Vereinfachung.
a) oder b) ?
mfG
Lieber Herr Schulze, #54
könnten Sie mir auch noch mitteilen, ob ich in #54 Ihre Formeln korrekt interpretiert habe und sich damit tatsächlich ein Fehler in Ihrer Notation steckt (SEM ist nicht gleich SEM bei Ihnen).
Dann hatte ich in #50 gefragt:
„Wenn ich nun Ihre Konfidenzintervalle (CL) der Jahresmittel basierend auf Monatsanomalien angucke, die Sie mir schickten, so beträgt das 95%-CL ca. plus minus 2 C. Das bedeutet, dass SEM ca. = 0,9 C sein muß, und damit SD ca. 3 C. Ist das richtig so? “
Darauf sind Sie leider noch gar nicht eingegangen. Können Sie das bestätigen?
Lieber Herr Schulze,#56
„Ein Jahresmittelwert repäsentiert somit die Verteilung von 12 Monatswerten und weist somit einen SEM von stdv/sqrt(12)auf“
Eben das ist falsch! Das Jahresmittel Y repräsentiert eben NICHT die Verteilung der Monatsmittel (und die Jahresanomalie auch nicht die Monatsanomalien des gleichen Jahres), sondern ergibt sich als abgeleitete Zufallsvariable nach der Gleichung in #43
Y = 1/12(X1 + … + X12)
Dabei sind die Xi die Monatsmittel des betreffenden Jahres (1 = Jan, …12 = Dez).
Wenn man alles auf Anomalien bezieht wird es klarer. Dann sind im Idealfall X1, …, X12 unkorrelierte Zufallsvariable mit Erwartungswert Null mit den Varianzen V1…V12.
Nach den Lehrbüchern der Statistik ist dann die Varianz von Y (dem Jahresmittel) (siehe #45):
V_Y = (1/12)^2 (VJan + … VDez)
Damit ist die SD (= stdv) des Jahresmittels Y
SD = wurzel (V_Y) = 1/12 * wurzel(VJan + … VDez) oder 1/12 wurzel (SDJan^2+…+ SDDez^2)
Wenn alle Monate etwa die gleiche Standardabweichung SDm haben, so ist die des Jahresmittels:
SD = 1/12 wurzel(12*SDm^2) = SDm/wurzel (12)
Die Rechnung zur Bestimmung der Konfidenzintervalle des Jahresmittels einen bestimmten Jahres (bzw. Referenzzeitraumes) läuft also darauf hinaus, die SD’s der einzelnen Monate des Jahres (bzw. Referenzzeitraumes) zu berechnen!
Und dies war kein Flüchtigkeitsfehler von mir, denn die SD z.B. des Monats Januar, SDJan, lässt sich für ein bestimmtes Jahr gar nicht angeben, das Jahr nur einen Januar hat und für das Januarmittel damit nur ein Wert vorliegt. Deshalb gibt es auch kein SD für das Jahresmittel eines Jahres!
Anders ist es beim Referenzzeitraum (oder einem anderen Zeitraum). Da errechnet sich das SDJan =
= stdvJan = sqrt(sum(XJan_i-XJan mean)^2)/n-1), XJan mean = sum(XJan_i)/n mit i = 1 bis n, wobei n die Zahl der Jahre im Referenzzeitraum ist (das ist Ihre Formel aus #52)!
Wie man leicht sieht, ist diese Formel nicht anwendbar, wenn n = 1 ist, also der Zeitraum nur 1 Jahr beträgt, und damit gibt es auch keine Standardabweichung eines Jahresmittels eines einzelnen Jahres!
Ich nehme an, Sie haben die stdv eines Jahres nun aus den 12 Monatsanomalien nach der Formel
stdv = sqrt(sum(Xi-Xmean)^2)/n-1) berechnet, mit n =12, Xi als Monatsanomalien und Xmean als Jahresanomalie. Stimmt das? Das wäre wie oben und schon öfter gesagt falsch.
Lieber Herr Baeker,
Sie schrieben bereits in #48 „Ein einzelnes Jahresmittel hat gar keine Standardabweichung, da es nur einen Wert gibt.“
Diese Aussage konnte ich gar nicht fassen und habe angenommen, dass Sie einen Flüchtigkeitsfehler gemacht hatten.
In # 54 wiederholen Sie diese Aussage, so dass ich meinerseits noch einmal wiederhole, was ich in meinem Artikel ausführlich erläutert habe.
Ein Jahresmittel für ein bestimmtes Jahr bildet der DWD aus den Monatsmittel Temperaturen bzw. Monatsmittel Anomalien dieses Jahres, wie Sie unmittelbar nachrechnen können, wenn Sie sich die Mühe machten, die EXCEL Tabelle
http://tinyurl.com/7jrduqg
herunterzuladen, wie ich es Ihnen schon mehrere Male anempfohlen habe.
Ein Jahresmittelwert repäsentiert somit die Verteilung von 12 Monatswerten und weist somit einen SEM von stdv/sqrt(12)auf.
Worauf ich in meinem Artikel nicht explizit eingegangen bin, ist die Berechnung der Fehlerfortpflanzung, die ich aber in # 47 beschrieben habe. Wie bei Herrn Hader hatte ich auch bei Ihnen aufgrund Ihres Kommentars # 50 den Eindruck gewonnen, dass Sie die Rechnung nachvollzogen hatten:
Für jeden Monat wird ein Mittelwert mit zugehöriger SD (=stdv) über das Referenzintervall (n=30) gebildet, woraus für jeden Monat ein SEM resultiert, den ich in # 47 SEMmon genannt habe. Daraus wird entsprechend den Fehlerfortpflanzungsregeln ein SEM für alle 12 Monatswerte des Referenzintervalls gebildet den ich SEMref genannt habe. Dem SEM für individuelle Jahre (z. B. 2010), den ich entsprechend SEM2010 nennen würde und der sich von Jahr zu Jahr ändert, wird SEMref zugerechnet, der konstant bleibt, solange ich kein anderes Referenzintervall wähle.
Sehr geehrter Herr Hader,
die Definitionen gelten ersteinmal ganz allgemein. Bezogen auf die Berechnung von Monatsmittel Anomalien werden für jeden Monat getrennt die Monatsmitteltemperaturen über das Referenzintervall gemittelt. Zu jedem dieser 12 Referenzwerte gehört natürlich eine Standardabweichung.
Bitte tun Sie sich und mir den Gefallen und schauen sich die Datensammlung des DWD (im EXCEL-Format) an, in der diese Werte für verschiedene Referenzintervalle aufgeführt sind:
http://tinyurl.com/7jrduqg
Die weitere Vorgehensweise habe ich in # 47 erläutert und ich hatte aufgrund Ihres Kommentars # 49 den Eindruck gewonnen, dass Sie diese nachvollzogen haben
Lieber Herr Schulze, #52
„stdv = sqrt(sum(Xi-Xmean)^2)/n-1)
Xmean = sum(Xi)/n mit i = 1 bis n
SEM = stdv/sqrt(n)
d.h für das Intervall 1961 bis 1990 ist n = 30“
Das wäre aber die Formel zur Berechnung von SEMref (Notation nach Ihrem #47)
Nun geben Sie aber den SEM von einzelnen Jahresmitteln an, also z.B. 2010. Welche Daten benutzen Sie für diese Berechnung, da wäre n = 1 statt 30?
In #47 geben Sie aber an SD/sqrt(12) = SEM, also n =12 und berechnen SD wohl aus den Monatsmitteln. Sie haben also etwas falsch gemacht bzw. sind in Ihrer Notation inkonsistent.
Also nochmal zur endgültigen Klärung:
Welche Daten (und wie wird das SD daraus berechnet) werden konkret für Ihr SEM [(SD/sqrt(12) = SEM] des Jahresmittel eines Jahres verwendet, welche fürs SEMref eines Mittels der Jahresmittel über 30 Jahre (z.B. 1961-1990)?
Sehr geehrter Herr Dr.Eckhard Schulze, entschuldigen Sie bitte, wenn ich noch mal nachfrage, aber um #52 zu verstehen, müsste man auch wissen, für was Xi steht. Sind das alle Monatswerte aus dem Referenzzeitraum 1961-1990? Oder sind das die Monatswerte nach den konkreten Monaten aufgeschlüsselt, als Januar, Februar usw.? Wenn letzteres zutrifft, hätte man 12 verschiedene stdv und entsprechend 12 verschiedene SEM. Wie werden diese dann zusammengefasst?
Zu # 49 und # 50
Herr Baecker fragt, wie ich die SD berechnet habe, Herr Hader möchte wissen, wie ich die SEM berechnet habe.
Die Antwort ist: mit EXCEL.
Die SD wird mit dem Befehl stdv berechnet hinter dem der folgender Algorythmus steht:
stdv = sqrt(sum(Xi-Xmean)^2)/n-1)
Xmean = sum(Xi)/n mit i = 1 bis n
SEM = stdv/sqrt(n)
d.h für das Intervall 1961 bis 1990 ist n = 30 und nicht wie ich geschrieben hatte 29. Sorry, da hatte ich wohl noch die Freiheitsgrade im Kopf. Gerechnet habe ich aber mit 30.
Hallo Statistiker,
Ein interessanter Beitrag (Ist zwar schon ein bißchen älter, aber hat seine Bedeutung nicht vorloren): http://tinyurl.com/43wd5vu
MfG
W. Kinder
Lieber Herr Schulze, #47
Ihre 95%-Konfidenzintervalle des Jahresmittels berechnet aus Monatsanomalien zeigten etwa plus minus 2 Grad C. Ihre Gleichungen in #47
SEM = SD/sqrt(12)
und
95%-Konfidenzintervall = 2,2 * SEM
sind soweit korrekt, und die SEM-Gleichung für unkorrelierte Monatsmittel entspricht den Gln. von Herrn Hader und mir in #45.
Auch die Gl.
SEMref=sqrt(SEMJan*SEMjan+…………+ SEMdez*SEMdez)/sqrt(12)
und damit das Gesamtergebnis:
SEMges=sqrt(SEM*SEM + SEMref* SEMref)
sind richtig, sofern Unkorreliertheit vorausgesetzt werden kann.
Wenn ich nun Ihre Konfidenzintervalle (CL) der Jahresmittel basierend auf Monatsanomalien angucke, die Sie mir schickten, so beträgt das 95%-CL ca. plus minus 2 C. Das bedeutet, dass SEM ca. = 0,9 C sein muß, und damit SD ca. 3 C. Ist das richtig so?
Können Sie mir also noch erklären, wie Sie auf die SD’s gekommen sind?
Sehr geehrter Dr.Eckhard Schulze,
gut das Sie nochmal vorbeigeschaut haben. Was Sie schreiben, hat nochmal einige Klarheit (zumindest auf meiner Seite) gebracht:
„Auch wenn Sie und Herr Harder so argumentieren, dass die Voraussetzungen für die Gaussschen Fehlerfortpflanzunggesetze nicht erfüllt sind, bleibt es dennoch eine Tatsache, dass bei Mittelung der Monatsmittel über das Referenzintervall Fehler für den Mittelwert auftreten.“
In dem Punkt muss ich Sie korrigieren. Ich sage nicht, dass man das Gesetz nicht anwenden kann, sondern dass man dazu auch die richtigen Standardabweichungen einsetzen muss.
„In der DWD Datensammlung sind die SD der Refernz-Monatsmittelwerte für unterschiedliche Intervalle daher auch angegeben.
Wenn man daraus für jeden Monat den SEM (SEMmon) bildet ( also z. B. SDmon /sqrt(29) für das Referenzintervall 1961-1990) und aus diesen mittels Fehlerfortpflanzung ein SEM für das Referenzintervall (SEM ref), erhält man einen zusätzlichen Fehler, der zu dem SEM hinzukommt, der bei der Berechnung von Jahresittelwerten aus Monatsmittel Anomalien auftritt.
SEMref=sqrt(SEMJan*SEMjan+…………+ SEMdez*SEMdez)/sqrt(12)
Damit ergibt sich ein Gesamtfehler (SEMges) für die Jahresmittel Anomalien aus Monatsmittelanomalien zu:
SEMges=sqrt(SEM*SEM + SEMref* SEMref)“
Okay, versuchen wir es nochmal auseinander zu dröseln, denn das ist wirklich interessant. Sie wollen das Konfidenzintervall der Temperaturanomalien bestimmen. Für die Anomalie selbst rechnet man den Jahresmittelwert eines bestimmten Jahres minus dem Jahresmittelwert des Referenzzeitraumes 1961-1990. Bei einer Subtraktion werden die Varianzen der beiden Größen aufaddiert. Daraus ergibt sich wie oben beschrieben:
SEMges=sqrt(SEM*SEM + SEMref*SEMref)
Weiter oben wird angegeben, wie man zu SEMref kommt.
SEMref=sqrt(SEMjan*SEMjan+…………+ SEMdez*SEMdez)/sqrt(12)
Da bin ich auch voll bei Ihnen. Für jeden Monat muss man individuell einen eigenen SEM berechnen. Weiter oben wird beschrieben, wie man zu einem SEM-Monatswert kommt.
SEMmon= SDmon/sqrt(29)
Eigentlich muss es sqrt(30) heissen, denn der Referenzzeitraum enthält 30 einzelne Jahre und nicht 29, aber das ist jetzt nicht entscheidend. Viel wichtiger ist, wie man zu SDmon kommt, also die Standardabweichung vom jeweiligen Monat. Dazu kann man den Referenzzeitraum nehmen und ausrechnen, wie stark jeder einzelne Monat in den 30 Jahren geschwankt ist. Wie haben Sie die Werte berechnet?
Jetzt zu dem Punkt, wie man das SEM in der SEMges-Gleichung berechnet. Leider geht das aus Ihren bisherigen Ausführungen der Rechenweg nicht eindeutig hervor. Prinzipiell sehe ich da zwei Möglichkeiten sich diesem Wert anzunähern. Man kann zum einen wieder den Weg der Monatsmittel wie oben gehen. Dazu müsste man SDjan, SDfeb usw. ebenfalls über einen Referenzzeitraum schätzen. Man müsste sich überlegen, welcher am geeignetsten ist. Das Problem dabei ist, um beispielsweise SDjan gut schätzen zu müssen, bräuchte man einen langen Zeitraum, der klimatisch stabil geblieben ist und repräsentativ für das jeweilige Jahr ist. Man kann aber auch einfachhalthalber dieselben SD-Werte wie aus dem Zeitraum 1961-1990 heranziehen, in der Annahme, dass die sich auf die heutige Zeit kaum geändert haben. Demzufolge wäre
SEM= sqrt(SDjan*SDjan+…………+ SDdez*SDdez)/sqrt(12).
SEM ist auch deutlich größer als SEMref, weil dort keine Mittelung über 30 Jahre stattfand.
Man kann aber nach meinen Dafürhalten auch als zweiten Weg über die Tagesmittelwerte gehen. Dabei braucht man zu jedem einzelnen Tag die Standardabweichung, die man empirisch ermitteln würde, analog wie bei den Monaten. Dann ergibt sich
SEM= sqrt(SD(1.Jan)*SD(1.Jan)+SD(2.Jan)*SD(2.Jan)+…+SD(31.Dez)*SD(31.Dez))/sqrt(365)
Es wäre wirklich interessant von Ihnen zu hören, wie sie den Wert SEM konkret berechnet haben.
Zur Anwendung des Gauß’schen Fehlergesetzes muss man eine Sache noch erwähnen. Eigentlich nutzt man dieses Gesetz, um Auswirkungen von verschiedenen Meßfehlern besser abschätzen zu können. Wenn man beispielsweise die Standardabweichung der Durchschnittstemperatur vom 14.Mai schätzt, dann spielt der Meßfehler des Thermometers nur eine begrenzte Rolle. Selbst wenn der Thermometer fehlerfrei messen würde, wäre die Standardabweichung > 0, weil jedes Jahr am selben Tag ein etwas anderes Wetter vorherrscht. D.h. SD(14.Mai) wird deshalb relativ groß sein, weil es permanente Wetterschwankungen gibt. Von daher ist es ein fraglicher Weg, wenn man Meßfehler dadurch ermitteln will, wie stark das Wetter jeweils am 14.Mai geschwankt ist. Der verwendete Thermometer dürfte darauf kaum Einfluss haben. Wenn es dazu noch eine Klimaerwärmung gibt, dann nimmt SD ebenfalls zu. Deshalb gehe ich davon aus, dass man mit der oben beschriebenen Methode eher zu große Fehlerbalken bekommt.
Lieber Herr Schulze,
wie aber eigentlich schon von Herrn Hader und mir erklärt wurde, berechnen Sie aber den Standard Error of Mean (SEM) des Jahresmittels falsch, denn Sie verwenden NICHT die Standardabweichung (SD) der Jahresmittel, sondern (in Ihrer Rechnung) die von Monatsmitteln. Ein einzelnes Jahresmittel hat gar keine Standardabweichung, da es nur einen Wert gibt.
Wenn Sie es nicht glauben, so testen Sie doch einfach wie ich schon angeregt hatte Ihrer Konfidenzintervalle der Jahresmittel anhand der Daten. Es müssen bei 95%-Konfintervalle ja 5% außerhalb liegen, bei 67%-Konfintervalle eben 33% etc.
Ich denke, Sie hat etwas durcheinander gebracht, dass das Jahresmittel die Summe (Integral) von diskreten Größen ist, welches dann durch die summierte Anzahl geteilt wird. Ich habe es eigentlich in #45 schon erklärt, aber denken Sie mal daran, wie man die SD einer Summe von N stochastischen Grössen bestimmt. Wenn man diese Summe durch N teilt, ist die SD von diesem Mittelwert auch durch N zu teilen. Siemüssen einfach die Formel in #45 verwenden, steht in jedem Statistikbuch.
Zu #46
Lieber Herr Baeker,
ich habe die Deutschlandmittel so wie sie vom DWD publiziert wurden, als gegeben angenommen ohne an dieser Stelle weitere Streufehler zu berücksichtigen. Wenn ich in #20 gegenüber Herr Harder angemerkt habe, dass sie auf den Mittelwerten (Tagesmw., Monatsmw.) von 264 Stationen beruhen, so bleibt das ersteinmal richtig, habe ich mich doch überhaupt nicht zu dem Algorithmus der Gebietsmittelberechnung geäußert. Meine Bemerkung zielte daraufhin, dass die publizierten Monatsmittel für Deutschland normalverteteilt seien, wozu Mittelwertbildungen aus Mittelwerten neigen und es somit zulässig (sinnvoll) sei, den arihmetischen Mittelwert (ohne von mir an dieser Stelle erwähnt), natürlich auch die SD (Standard Deviation) zu bilden.
Die Zeitreihen Diagramme in meinem Beitrag wie auch die, die ich Ihnen per e-mail zugeschickt habe, enthalten als Streuungsmaß das +/- 95% Konfidezintervall für den Mittelwert, das folgendermaßen berechnet wird:
SD/sqrt(12) = SEM (Standard Error of Mean ~ 67% Konfidenzniveau))
Um Konfidenzintervalle zu berechnen, muss man bei kleinen, normalverteilten Grundgesamtheiten, wie den Jahresmittelwerten oder den Jahresmittel Anomalien, eine Studentverteilung annehmen.
Um das Konfidenzintervall für 95% Konfidenzniveau zu berechnen, wird der SEM mit dem t –Wert für (n-1) Freiheitsgrade multipliziert.
Im Fall der Jahresmittelwerte aus Monatsmitteln bzw. Monatsmittel Anomalien ist der t-Wert für 11 Freiheitsgrade (2,201) zu verwenden.
Der Fehler für die Jahresmittel Anomalien aus Monatsmittel Anomalien bleibt dabei weiterhin unterschätzt, da die Monatsrefernzen natürlich auch streuen. Das habe ich in meinem Text mehrmals angemerkt und eine Berücksichtigung dieser Tatsache mittels Fehlerfortpflanzung vorgeschlagen. Auch wenn Sie und Herr Harder so argumentieren, dass die Voraussetzungen für die Gaussschen Fehlerfortpflanzunggesetze nicht erfüllt sind, bleibt es dennoch eine Tatsache, dass bei Mittelung der Monatsmittel über das Referenzintervall Fehler für den Mittelwert auftreten.
In der DWD Datensammlung sind die SD der Refernz-Monatsmittelwerte für unterschiedliche Intervalle daher auch angegeben.
Wenn man daraus für jeden Monat den SEM (SEMmon) bildet ( also z. B. SDmon /sqrt(29) für das Referenzintervall 1961-1990) und aus diesen mittels Fehlerfortpflanzung ein SEM für das Referenzintervall (SEM ref), erhält man einen zusätzlichen Fehler, der zu dem SEM hinzukommt, der bei der Berechnung von Jahresittelwerten aus Monatsmittel Anomalien auftritt.
SEMref=sqrt(SEMJan*SEMjan+…………+ SEMdez*SEMdez)/sqrt(12)
Damit ergibt sich ein Gesamtfehler (SEMges) für die Jahresmittel Anomalien aus Monatsmittelanomalien zu:
SEMges=sqrt(SEM*SEM + SEMref* SEMref)
Diese Fehler liegen in der Größenordnung der SEM für Jahresmittelwerte aus Monatsmittel Temperaturen, wie Sie selbst nachrechnen können. Zum Vergleich müssen Sie letztere natürlich relativieren, d. h. durch den Mittelwert dividieren.
Wie gesagt, auch wenn die Voraussetzungen für die Gaussschen Regeln nicht vollständig erfüllt sein mögen, darf eine Fehlerfortpflanzung nicht ignoriert werden, die in jedem Fall zu gesteigerten Streuungen führt!
Lieber Herr Schulze,
mein Beitrag #45 erklaert im Prinzip dasselbe wie Herr Hader bereits schon in #12 beschrieben hat. Ihr Fehler ist vermutlich, dass Sie die Division durch wurzel 12 beim SEM nicht machen. Zumindest wuerde dies in etwa klaeren, wie Sie auf die zu grossen Konfidenzintervalle in der Jahresmittelanomalie aus den Monatsmittelanomalien berechnet bekommen, die Sie mir als Graphen mit 3 unterschiedlichen Bezugsintervallen (1961-1990, 1961-2010, 1981-2010) fuer die Referenzbezuege der Anomalien zuschickten.
Koenne Sie einfach mal die Gleichung, die Ihrer Berechnung der Konfidenzintervalle zugrundeliegt hier veroeffentlichen, dann laesst sich gleich der Fehler sehen?
Noch etwas zu den Flaechenmitteln Deutschland des DWD. Sie schrieben in #26
„es sich um die Mittelung der Monatstemperaturen von z.Zt.. 264 DWD Stationen handelt und Mittelwertbildung aus Mittelwerten tendenziell zu Normalverteilungen neigt. “
Der DWD ermittelt das Deutschlandmittel so aber nicht. Lesen Sie mal auf den DWD Seiten nach, wie er das macht. Am wichtigsten ist selbstverstaendlich den Hoeheneffekt zunaechst rauszurechnen (sozusagen raeumliche Anomaliebildung), dann eine Kartierung der auf Meereshoehe reduzierten Stationstemperaturen vorzunehmen und ueber das Gelaendemodell wieder auf die wahre Topographie Deutschlands hochzurechnen und dann auf dem Raster (ich glaube 1 km Raster) das Oberflaechempnmittel zu integrieren.
Hier die Loesung von # 43 (siehe Lehrbuecher der Statistik unter n-dim Zufallsvariable)
Die Varianz V1 von Y1 ist natuerlich V, die von Y2 ist jedoch V2 = (1/12)^2 * 12*V = V/12. Damit ist also die Standardabweichung (Konfidenzintervalle) von Y2 1/wurzel 12 mal der von Y1. Dies liegt daran, dass die Zufallsvariable Xn in Y2 sich unabhaengig voneinander (unkorreliert) addieren und damit Y2 weniger schwankt als Y1.
Wenn die Monatsmittel aufeinanderfolgender
Monate ebenfalls unkorreliert sind, so ist die SD des Jahresmittels 1/wurzel 12 der Monatsmittel. In Praxis verhaelt sich dies etwa wie 1:2 statt 1:3,5.
Sind die Zufallsvariable korreliert, wird die Varianz um Summanden mit den Kovarianzen vergroessert. Im Falle der strikten Kovarianz aller Monatsmittelanomalien (die Korrelationskoeffizienten aller Kombinationen der 12 Monatsmittel waeren gleich 1) waere die
Varianz des Jahresmittelanomalie gleich der der mOnatsmittelanomalie. Diesen Fall haben Sie in Ihrer Rechnung irrtuemlich angenommen.
#42: „Genau das fehlt bei der AGW Forschung: die Herrschaften haben nicht die geringsten Zweifel, niemals. Al Gore sagt ja so überzeugend: „I invite you to have courage to join the consensus“. Merkwürdiges Verständnis von Wissenschaft!“
Ich wusste gar nicht, dass Al Gore Klimawissenschaftler ist, Herr Zuber. Da Sie selbst nicht in der Wissenschaft gearbeitet haben, ist es wohl verzeihlich, dass Sie nicht wissen, dass man dort in der täglichen Arbeit seine Thesen, Experimente und Rechnungen mehrfach hinterfragt und sie auch mit anderen Kollegen diskutiert.
Lieber Herr Schulze,
ueberlegen Se sich nochmal grundsaetzlich, wie der Zusammenahng zwischen den Varianzen (und damit Den Konfidenzintervallen) folgender zwei Zufallsvariable Y1 und Y2 ist:
Y1 = X1
Y2 = 1/12(X1 + … + X12)
wenn X1, …, X12 unkorrelierte Zufallsvariable mit Erwartungswert Null und gleicher Varianz V sind.
@41 Herr Rabich „..dass am Anfang jeder Forschung fruchtbringend der Zweifel steht…“
Genau das fehlt bei der AGW Forschung: die Herrschaften haben nicht die geringsten Zweifel, niemals. Al Gore sagt ja so überzeugend: „I invite you to have courage to join the consensus“. Merkwürdiges Verständnis von Wissenschaft!
Sehr geehrter Herr Hader,
natürlich kann man die Statistik auch für ein ausgewähltes Ensemble heranziehen, aber dann muss man die Anomalitäten der lokalen Mess-Stationen kennen und angeben. Wenn Sie Schadstoff-Spuren in Fabrik-Hinterlassenschaften untersuchen, gehört das zum unerläßlichen Vorgehen.
Tatsächlich, ich habe bislang gerade auf die Frage nach der Repräsentativität der bislang herangezogenen CO2-Daten auch von den hierzu berufenen Fachleuten keine Antwort erhalten. Sie können sich selbst überzeugen, wenn Sie die CDIAC-Datenbank heranziehen.
Modelle üben – wenn man sie eingeführt hat – einen unheimlichen Sog aus, ehe man sie als unbefriedigend aufgibt. Es ist eine erprobte Kunst, nach Vorurteilsfreiheit zu streben, aber selbst in Gerichtsprozessen hat der Richter oft Mühe, das zu verwirklichen, im Notfall schlägt er einen Vergleich vor.
Klima-Skeptiker werden schon wegen der gemeinschaftlichen Skepsis oft leider klassifiziert als „Völkchen“, aber das wußten schon die Philosophen, dass am Anfang jeder Forschung fruchtbringend der Zweifel steht.
Lieber Herr Prof.Kramm,
ich finde die Klima-Definition der WMO sehr gut und akzeptiere sie seit Anbeginnn. Wie Sie bemerkt haben sollten, spielt diese Definition jedoch keine Rolle, wenn ich mich mit Herrn Schulze ueber die statistische Analyse von Temperaturdaten auseinandersetze, denn wie Sie sicherlich in Ihrer Statisrikbibliothek nachlesen koennten, sind die statistischen Methoden nicht davon abhaengig, um welche physikalischen Groesse es sich handelt und wie und wo sie gemessen wurde, sondern ausschliesslich von der Statsitik der Daten selber.
#34: „Der Autor des zu kommentierenden Artikels hat sich nur mit der statistischen Auswertung befaßt und der Frage, ob die Mittelwerte hinreichend aussagekräftig und vertrauenswürdig sind, aber leider nicht mit den Fragen, ob die jetzige Ermittlungsmethode mit anschließenden Rechenverfahren datenmäßig wissenschaftlich verwertbar sind.“
Hallo Adalbert Rabich,
Das ist meist in der Wissenschaft so, dass man sich einem Gesamtproblem immer nur stücklesweise annähern kann. Es macht schon Sinn, sich mit konkreten, abgerenzten Teilproblemen zu befassen, so wie es der Autor mit der statistischen Auswertung von Temperatur-Zeitreihen gemacht hat.
„Bei kritischer Sicht ist schon ein Mittelwert innerhalb einer begrenzten Zahl von Meßstationen für ein Ensemble fragwürdig, denn lokale Abweichungen auf kurzer Distanz werden uns täglich vorgeführt.“
Einen Mittelwert aus verschiedenen Meßstationen zu ermitteln, halte ich erstmal nicht für fragwürdig. Wichtig ist, dass man abschätzen kann, wie weit man im Schnitt vom wahren Ergebnis entfernt liegt, dazu hat uns die Statistik Werkzeuge bereitgestellt.
„Noch trauriger stimmt es mich, wenn ich ein weiteres klimarelevantes Datum, die CO2-Emmission anschaue – unabhängig von der Frage vom “Treibhaus-Effekt” -, es gibt faktisch nur Hochrechnungen aus Produktionsdaten gewisser Quellen. Aber die Hypothese wird nicht an globaler Steigerung von CO2 in der Atmosphäre geprüft?“
Wieso denken Sie, dass das nicht gemacht wurde? Kennen Sie die Arbeiten, die sich genau mit dieser Fragestellung beschäftigen? Die Keeling-Kurve wird auch von denen weitgehend akzeptiert, die nicht im Verdacht stehen, AGW-Anhänger zu sein. Das allein ist noch keine Bestätigung dieser These, aber zeigt ja doch, dass diese zumindest kritisch hinterfragt wurde.
„Aber “Vernünftige” lassen sich niemals von Wünschen und angeblichen Trends leiten, das gilt in der Wissenschaft als unwürdig.“
Da stimme ich Ihnen zu, dass man im Idealfall ergebnisoffen forschen sollte und sich nicht von eigenen Wünschen bzgl. dem Ergebnis beeinflussen lassen darf. Aber nun frage ich Sie mal, finden Sie, dass viele sogenannte Klima-Skeptiker in ihrer Arbeit vollkommen ergebnisoffen in alle Richtungen forschen? Oder ist es da nicht auch eher so, dass man zunächst von seiner Vorstellung überzeugt ist und nun nach guten Argumenten für die Bestätigung der eigenen These sucht? Ich meine jeder Wissenschaftlicher muss sich hinterfragen, ob nicht seine Wünsche seine Ergebnisse beeinflusst haben. Aber häufig habe ich beim Lesen im Forum den Eindruck, als wenn sich viele Klima-Skeptiker dieser Frage nicht unterziehen wollen und das immer nur von der Gegenseite einfordern.
MfG
S.Hader
#33: E.Teufel ich denke, dass man keineswegs „alles“ damit anstellen kann.
Dabei ist Ihre „Methode des scharfen Hinsehens“ für einfache Erkenntnisse durchaus zu gebrauchen.
Z.B. um zu erkennen ob ein Wert (Temperatur) nun steigt oder fällt,
oder ob zwischen 2 Werten (Temperatur und CO2) ein Zusammenhang besteht oder nicht.
Hier geht es lediglich darum, dass bei den „Rohdaten“ nur bei der „Erdtemperatus“ mit der „Methode des scharfen Hinsehens“ ein Trend NICHT zu erkennen ist und die „Statistik“ erst durch „Glättung“ und „Mittelung“ etc. diese Rohdaten soweit „bearbeitet“ werden müssen, bis eine bescheidene Trendbeurteilung möglich wird.
Für mich ist schwer nachvollziehbar, dass man sich über eine so minimale Temperaturerhöhung überhaupt streitet.
Noch viel weniger um einen statistisch ÜBERHAUPT NICHT NACHWEISBAREN Einfluss von CO2 auf die Temperatur trotz aller Tricks
und die Krönung natürlich speziell der gar nicht bekannte Anteil, den der Mensch dazu beiträgt.
Sehr sehr unseriös!
mfG
#32,
Herr Baecker,
wenn Sie die Definition der WMO nicht akzeptieren wollen, dann ist das Ihr Bier, aber das hat dann nichts mit Klima zu tun. Eine Vegleichbarkeit der Ergebnisse ist dann nicht mehr gegeben. Sie vergleichen dann Aepfel mit Birnen.
Dass eine Klimaperiode zumindest eine Zeitspanne von 30 Jahren umfassen muss, ist wohlbegruendet. Zu diesen Gruenden zaehlen die quasi-Zufaelligkeit des Auftretens von Wetterereignissen, eine Anforderung der Statistik, und typische Zyklen, wie sie im System Erde-Atmosphaere infolge der astronomischen Bedingungen auftreten.
Sie gehoeren offenbar zu den biederen Handwerkern, die glauben, die Definition einer Methode anpassen zu muessen, weil sie diese Methode irgend wann gelernt haben. Das hat nichts mehr mit einer exakten Wissenschaft zu tun , sondern nur noch mit dem Versuch, diese zu ruinieren.
Was Leute wie Sie bereits angerichtet haben, zeigt das Beispiel der sog. alternativen Massenbilanzgleichung, die im Jahre 2003 von Finnigan et al. publiziert wurde. Obwohl diese alternative Massenbilanzgleichung erstens unvereinbar ist mit dem Satz von der Erhaltung der Masse und zweitens unvereinbar ist mit den mathematischen Gesetzmaessigkeiten zur Behandlung der delta-Distribution, haben wissenschaftliche Blindgaenger diesen Schrott schon 200 mal zitiert, wobei nur ganz wenige Zitate als Kritik an diesem physikalischen und mathematischen Schrott zu werten sind. Mit dieser Arbeit wollten Finnigan et al. nachweisen, dass eine Aenderung der Emission z.B. von CO2 direkt zu einer Aenderung der Konzentration beitraegt, was kompletter Bloedsinn ist. Mit dieser Arbeit hat diese Bande die Mikrometeorologie auf Jahrzehnte hin zerstoert; denn dieser Bloedsinn schlug sich auch noch in dem Handbuch der Mikrometeorologie nieder.
Ein anderes Beispiel beschreibt das Vorgehen der sog. Klimamodellierer. So schrieb Hasselmann in einer Arbeit von 2002:
„Prior to the modern view of climate as a dynamic rather than a static system, climate was defined in terms of 30 yr averages. This had the conceptual disadvantage of introducing a spectral gap between weather and climate prediction.“
Mittlerweile sprechen die Klimamodellierer schon gar nicht mehr von „prediction“, weil naemlich klar ist, dass das Klima nicht „predictable“ ist. Trotzdem wird dieser bluehende Unsinn weiterhin von den Klimamodellierern gepraedigt.
Wir haben das bereits vor 3 Jahren in einem Bericht kommentiert. Wir schrieben:
„This means that this spectral gap between weather and climate predictions, i.e., two forms of applications of atmospheric modeling, served to redefine the statistical basis of climate from a set of about 11,000 daily weather states observed at each location of a network to a set of 20 or somewhat more ones. Note that in practice we are glad to predict the weather for the next 5 or 6 days with a sufficient degree of accuracy. This strong deviation from the theoretical limit is not only affected by imperfect balance equations, but also by imperfect initial and boundary conditions.“
Sie, Herr Baecker, und viele der ‚Global Warming“-Aktivisten werden anscheinend von wissenschaftlichem Sektierertum geleitet, was allerdings mit einer exakten Wissenschaft nichts gemein hat.
Lieber Herr Schulze,
ichbhabe Ihnen per email mal den Test Ihrer Konfidenzintervalle des Jahresmittels ohne beruecksichtigung, dass eine Teil der Varianz nicht- stochastisch, sondern saisonal bedingt ist vorgeschlagen. Bitte pruefen Sie ernsthaft anhand der Zeitreihe der Jahresmittel der (oder einer anderen Station) der Vergangenheit, ob die Konfidenzintervall (Sie geben fuers 95% Niveaus ca. 5 bzw 15 C an) so stimmen, also die Jahresmittel beim 95% Niveau ca. 5% der Jahre ausserhalb liegen, bzw fuer geringere Kondidenz zB 80% entsprechen 20% ausserhalb liegen etc.
Die Schweizer sind mal wieder anderen voraus. Nachfolgend ein Link zur Euro-Climhist (Mit Euro-Climhist werden witterungs- und klimageschichtliche Daten für die Schweiz im Zeitraum zwischen 1550 und 1999 mit einer benutzerfreundlichen Suche zugänglich gemacht).
Quelle: http://tinyurl.com/7zu4n4g
Der Autor des zu kommentierenden Artikels hat sich nur mit der statistischen Auswertung befaßt und der Frage, ob die Mittelwerte hinreichend aussagekräftig und vertrauenswürdig sind, aber leider nicht mit den Fragen, ob die jetzige Ermittlungsmethode mit anschließenden Rechenverfahren datenmäßig wissenschaftlich verwertbar sind. Allein eine Diskussion über WMO und die long-term statistic mit 30 Jahren zeigt, dass man „gesetzte Daten“ mit 30 Jahren als rechtfertigbar akzeptiert, aber das Verheddern in Definitions-Interpretationen bringt uns in der Erkenntnis nicht weiter. Bei kritischer Sicht ist schon ein Mittelwert innerhalb einer begrenzten Zahl von Meßstationen für ein Ensemble fragwürdig, denn lokale Abweichungen auf kurzer Distanz werden uns täglich vorgeführt. Wieweit eine Globale Temperatur überhaupt qualifiziert machbar und gleichwertig über der Zeit ist, scheint abgehakt, sollte aber eher zur Kritik herausfordern.
Noch trauriger stimmt es mich, wenn ich ein weiteres klimarelevantes Datum, die CO2-Emmission anschaue – unabhängig von der Frage vom „Treibhaus-Effekt“-, es gibt faktisch nur Hochrechnungen aus Produktionsdaten gewisser Quellen. Aber die Hypothese wird nicht an globaler Steigerung von CO2 in der Atmosphäre geprüft; die wenigen Meßstationen und ihre nicht sicher vergleichbaren Daten werden als Bestätigungen von vielen hingenommen (Keeling-Kurve), gerade wohl von Klima-Katsstrophen-Positivisten. Aber „Vernünftige“ lassen sich niemals von Wünschen und angeblichen Trends leiten, das gilt in der Wissenschaft als unwürdig.
@Admin #27
„Was man mit Statistik in verrauschten Signalen alles so anstellen kann.“
Damit kann man so ziemlich alles anstellen. Deswegen -denke ich- sind die Diskussionen um das Klima ja auch unendlich.
Übrigens: Mit der Methode des scharfen Hinsehens kann ich noch einen Sprung so etwa 2003 bis 2004 erkennen. Also gibt es jetzt aller 26 Jahre so einen Temperatursprung? Wann kommt der Nächste? Nie, oder in 26 Jahren oder viel eher, in 20 Jahren (wegen noch mehr CO2)?
mfg
E.T.
Lieber Herr Prof.Kramm,
so schwer ist das eigentlich nicht, wenn Sie erst einmal lesen wuerden. Ich schieb nicht, dass ich einen anderen Begriff des Klimas als die WMO verwende. Wenn Sie nun meinen, aus der Klimadefinition der WMO wuerde explizit folgen, dass man immer nur Datenstrings ueber mindestens je 30 Jahre vergleichen darf, und nur bei statistisch signifikanten Unterschieden der beiden zeitlich separierten Ensembles von Aenderungen im Klimazustand sprechen darf, so zeigen Sie kir explizit, wo dies die WMO definiert hat. Wenn dies so waere, so waeren viele auch unter der WMO durchgefuehrten Untersuchungen, die zum Schluss kommen, dass das Untersuchungsergebnis zeigen wuerde, dass sich das Klima aendern wuerde, hinfaellig waeren.
Ich habe ausserdem schon geschrieben, dass ich den Begriff „Klimaaenderung“ fuer problematisch halte, wenn die Nachweisebene nur auf einzelnen Parameters beruht und es weder einen einzelnen Parameter gibt, der das Klima misst, noch eine Vorschrift existiert, wie ein Buendel von meteorologischen Messgroessen zusammen den Klimazustand quantifizieren. Es gibt dies nicht. Daher gibt es keine physikalisch strikte Ableitung, wie aus der nachgewiesenen Aenderung von einzelnen Parametern auf eine Aenderung des Klimas geschlossen werden kann. Und da diese Diskussion muessig ist und an dieser Stelle gar nicht thematisch ansteht, bleibe ich da, wo ich war und was das Thema des Herr Schulze ist, naemlich bei dem Nachweis der Aenderungen von Temperaturen.
Um dort siginifikante Aenderungen nachzuweisen, genuegt es vollkommen, die ueblichen Methoden der Statistik anzuwenden, und die schreiben keine allg. Regel ueber Datenlaengen vor, sondern der noetige Mengenumfang ergibt sich aus der Statistik des Ensembles selber.
#28:Sehr geehrter Herr Pof. Gerhard Kramm,
lassen Sie sich nicht durch diesen Beckehr ärgern,
dieser Mensch glaubt an der Hockeystick und an das tolle Trenberth-Chema also an die Energieentstehung aus dem NICHTS.
Dazu muss er auch noch die Sonneneinstrahlung verstümmeln und terrestrische Strahlung zu CO2-Strahlung umwandeln.
Und er glaubt an diesen Rammsdorf.
mfG
#27: Peter Jensen, diese statistische Betrachtung ist mathematisch völlig korrekt.
Möglich ist sie durch die große Schwankungsbreite im Grad-Bereich und die geringe Gesamterhöhung im 1/10 Gradbereich.
Wenn jetzt noch die Kritik an Messfehler und Wärmeinseleffekt dazukommt, wissen Sie was dann übrig bleibt.
Die absolute Krönung des Allarmismus ist aber die Behauptung, dass eine Erwärmung die wir bereits mehrmals in historischen Zeiten hatten,
eine Katastrophe wäre, statt das genaue Gegenteil,
ein Segen.
In diesem Winter gab es z.B. rel. viele Frostschäden einschließlich Tote durch Erfrierung.
mfG
#26: „Indem man die Tagesmittel (Stundenmittel) eines Monats zu einen einzigen Wert zusammenfaßt, d. h. durch einen Mittelwert repräsentiert, nimmt die Information über die Verteilung drastisch ab.
Bildet man aus diesen Monatsmittelwerten wiederum einen Jahresmittelwert, schlägt sich das in einem vergrößerten SEM nieder.“
Sehr geehrter Dr.Eckhard Schulze,
ob man aus den Tagesmitteln zuerst die Monatsmittel berechnet und daraus anschliessend das Jahresmittel, oder gleich von den Tageswerten auf den Jahreswert geht, ändert kaum etwas am numerischen Ergebnis. Durch die unterschiedlich langen Monate gibt es leichte Veränderungen in der Gewichtung im Jahresmittel, aber die Genauigkeit bleibt fast dieselbe. Das ist auch logisch, warum soll genau dasselbe Ergebnis einmal eine hohe und dann einmal eine geringe Unsicherheit besitzen?
Wenn Sie das Gauß’sche Fehlerfortpflanzungsgesetz anwenden wollen, dann ist doch die Frage, welche Fehlerwerte für m1, m2, … m12 anzuwenden sind. Wenn ich Sie richtig verstanden habe, dann wollen Sie für den Fehler die Standardabweichung von der Gesamtheit aller Monatswerte heranziehen. Aber genau das wäre falsch, weil m1 eben nicht diesselbe Verteilung wie m2 usw. besitzt. Man muss die empirischen Standardabweichungen von jeden einzelnen Monat, also m1, m2 bis m12 berechnen. Dann kann man auch nach dem Gauß’schen Fehlerfortpflanzungsgesetz die 12 Einzelsummenden berechnen.
Um es auf einen Satz zu reduzieren, Sie setzen für den mittleren Fehler des Mittelwertes bei den Monatswerten zu hohe Werte an und bekommen deshalb riesige Konfidenzintervalle heraus.
MfG
S.Hader
#21,
Herr Baecker,
es wird immer lustiger mit Ihnen. Offenbar wissen Sie nicht, dass eines meiner Hauptarbeitsgebiete die atmosphaerische Turbulenz ist. Um dieses Stroemungsphaenomen zu erfassen, sind umfangreiche Kenntnisse in der Statistik erforderlich. Von daher habe ich die Statistikkenntnisse, die ich mir schon waehrend des Ingenieursstudium angeeignet hatte, erst recht waehrend meines Meteorologiestudiums verfeinert. Klassische Lehrbuecher der Statistik, die in deutsch und englisch verfasst wurden, gehoeren zu meiner privaten Lehrbuchsammlung. Hinzu kommen noch die Statistik-Lehrbuecher unserer Bibliothek, die sich nur ein Stockwerk tiefer befindet. Glauben Sie allen Ernstes, ich muesste also auf etwas zurueckgreifen, was Sie hier irgendwo verfasst haben? Es waere doch viel zeitsparender, eines der Lehrbuecher aufzuschlagen, um Sinn und Zweck des Konfidenzintervalls nachzulesen, als hier in diesem Weblog zu suchen, ob der Baecker hierzu was geschrieben hat.
Wenn Sie behaupten:
„Nochmals, die 30 Jahre sind der Zeitraum zur Bestimmung von Referenzdaten, aber nicht eine universelle Periode, ueber die generell Daten zu ermitteln sind. Die notwendige Datenmenge und damit implizit auch Zeitintervalle haengen vom statistischen Test ab, der eine Hypothese testet. Wenn ich z.B. Trends hier angebe liefere ich die Konfidenzintervalle immer mit, egal, wie lang das Zeitintervall ist. Der Leser kann selber sehen, ob das Ergebnis signifikant ist oder nicht, und fuer die, die die Daten nicht verstehen, schreibe ich dazu, welches Testergebnis signifikant ist und welches nicht. Recherchieren Sie mal im Archiv ueber meinen Stil. Wenn Sie etwas daran auszusetzen haben, koennen wir dies konkret am Fall ausdiskutieren.‘
so kann ich nur sagen, dass Sie nicht wissen, wovon Sie reden. Der Begriff „long-term statistics“, der in der WMO-Definition des Klimas auftritt, erfordert ein grosse Zeitspanne, weil sonst die Zahl der Wetterereignisse ,die als zufaellig betrachtet werden muessen, zu klein ist. Dass Klimastatistiker, die etwas mehr davon verstanden, als Sie je verstehen werden, 30 Jahre als alsreichend lange empfahlen, wollen Sie nicht wahrnehmen.
Schon wieder versuchen Sie mit sinnlosem Stoerfeuer, jede sachliche Diskussion im Keim zu ersticken. Was soll das eigentlich? Sind Sie unfaehig, sich auf die Aussagen anderer zu konzentrieren? Offenbar verstehen Sie nicht, dass jede Aenderung des Zustands in einem System grundsaetzlich einen Referenzzustand erfordert. Das hat ueberhaupt nichts mit Klima oder statistischen Methoden zu tun. Im Falle des Klimas ist eine Aenderung allerdings nur dann diagnostizierbar, wenn zwei sich nicht ueberlappende Klimaperioden betrachtet werden. Noch spielt die Definition, was Klima ist, die Hauptrolle dabei, egal welche statistischen Verfahren dann angewendet werden. Anderenfalls werden Aepfel mit Birnen verglichen.
Eigentlich muessten Sie doch darin trainiert sein, wie Definitionen in der Mathematik gehandhabt werden. Wenn von einer Ableitung einer Funktion in der Analysis die Rede ist, dann ist doch auf Grund der Definition der Ableitung klar, was damit gemeint ist. Mit welcher Methode dann im speziellen Falle die Ableitung bestimmt wird, haengt von der Funktion ab. So ist das auch mit der Definition des Klimas. Wenn Sie diese Definition nicht moegen, dann suchen Sie sich ein anderes Gebiet, in dem Sie Ihre „Weisheiten“ verbreiten koennen.
Sie erinnern mich an einen frueheren Nachbarn. Der war nicht faehig zu begreifen, dass Ozon ein dreiatomiges Sauerstoffmolekuel ist, und fuehlte sich im Recht, weil er als Chemielaborant arbeitete.
Interessant! Die globale Erwärmung, also genauer gesagt der Trend der Erwärmung in den letzten 50 Jahren könnte auf nur einem extremen Sprung auf ein höheres Temperaturniveau im Jahre 1977 beruhen. Davor und danach ergibt sich auf jeweils unterschiedlichem Temperaturniveau so gut wie überhaupt kein Trend.
Kann dazu jemand was Erhellendes beitragen?
http://tinyurl.com/cnjbt8x
(Wieder mal sorry Admin, aber von meinem Firmenrechner funktionieren die URL-Verkürzer nicht)
Sehr geehrter Herr Harder,
je mehr Einzelwerte sie zur Mittelwertbildung heranziehen um so größer ist die Information über die Verteilung und desto zutreffender ist der geschätzte Mittelwert. Wenn N –> ? , dann SEM –> 0.
Indem man die Tagesmittel (Stundenmittel) eines Monats zu einen einzigen Wert zusammenfaßt, d. h. durch einen Mittelwert repräsentiert, nimmt die Information über die Verteilung drastisch ab.
Bildet man aus diesen Monatsmittelwerten wiederum einen Jahresmittelwert, schlägt sich das in einem vergrößerten SEM nieder.
Unter Berücksichtigung der Fehlerfortplanzung geht mehr Information über Verteilung der Tagesmittel in die Mittelwertbildung ein und die SEM wird geringer. Im Idealfall, d. h. bei exakter Normalverteilung der Tagesmittel werden die SEM identisch.
Zu ihrem Pferdefuss kann ich nur auf Ihre Feststellung in #1 verweisen: „Ob nun letztlich das arithmetische Mittel oder doch eher der Median besser geeignet wäre die Jahrestemperatur zu umschreiben, müssen wohl die Experten in der Meteorologie entscheiden.“
Nun, zumindest die Experten des DWD haben sich entschieden. In der umfangreichen Sammlung von Monatsmittelwerten für Deutschland, deren link ich in # 10 bereits mitgeteilt hatte < http://tinyurl.com/7jrduqg>, sind die Jahresmittel nach der von Ihnen monierten Formel aus Monatsmitteln gebildet und als offizielle DWD Daten publiziert.
Da ich davon ausgehe, dass die Fachleute die Voraussetzungen für (sinnvolle) arithmetischer Mittelwertbildung beachtet haben, muss ich annehmen, dass die Monatsmittel von ihnen als normalverteilt und unabhängig betrachtet werden, was darauf beruht, dass es sich um die Mittelung der Monatstemperaturen von z.Zt.. 264 DWD Stationen handelt und Mittelwertbildung aus Mittelwerten tendenziell zu Normalverteilungen neigt.
Hierauf stütze ich meine Streuungsbetrachtung bei der Bildung von Jahresmittelwerten aus Monatsmitteln.
Da für die DWD Station Braunschweig Völkenrode die Tagesmittel publiziert sind, konnte ich selbst überprüfen, ob die Tagesmittel für einzelne Monate normalverteilt sind. Das trifft nicht für alle Monate eines Jahres zu und
spiegelt sich auch in den Jahresverteilungen der Tagesmittel wider, für die keine Normmalverteilung abzusichern ist.
In diesem Fall ist es durchaus sinnvoll, eine mittlere Temperatur durch den Median zu repräsentiern. Die in Abb. 9 gewählte box and whiskers Darstellung beinhaltet im Vergleich der Boxengrößen oberhalb und unterhalb des Medians (25% Quntile bzw. 2. Und 3. Quartil) das nichtparametrische Analogon der Skewness und im Verhältnis der zentralen Quantile zur Spannweite (Länge der whiskers) das Analogon zur Kurtosis.
Im betrachteten Fall der der Abb. 9 braucht man eigentlich keinen Signifikanztest, um festzustellen dass sich die einzelnen box and whiskers plots sich kaum (signifikant) unterscheiden. Diese visuelle Beurteilung setzt übrigens nicht voraus, dass die Einzelwerte der so dargestellten (deskribierten) Verteilung unabhängig voneinander sein müssen.
Wie auch immer dürfte deutlich geworden sein, dass mit welcher Mittelungsmethode und welchen Streungsmaß auch immer es unsinnig ist, eine mittlere Globaltemperaturen zu ermitteln und diese zudem durch einen einzigen Zahlenwert zu beschreiben von der Absicherung signifikanter Unterschiede zwischen den globalen Mittelwerten verschiedener Jahre.
Herr Baecker, wieso schaffen Sie es nicht auf den Hauptpunkt von Prof. Kramm einzugehen, nämlich dass die „Globaltemperatur“ physikalisch vollkommen wertlos ist.
Aus Ihrem Schweigen zu diesem Punkt entnehme ich nun, dass Sie mit dieser Bewertung der „Globaltemperatur“ einverstanden sind.
# 17
Da Sie formale Anrede downgegradet haben, begrüße ich Sie auch als lieber Herr Baecker!
„Den Satz habe ich nicht verstanden: „kausale Verknüpfung von sequentiellen Meßdaten hinweisen“ sagt mir nichts, wo soll ich auf welche Kausalitäten zwischen was hinweisen?
Ich habe mich auf ihre Forderung in #6 bezogen: „Bessere Modelle muessen den Saisoneffekt und die Kurzfristpersistenz, also die Korrelation aufeinanderfolgernder Tage beruecksichtigen“
Bevor wir uns nun über die Bedeutung von “Korrelation“ streiten: Ich verstehe diesen Begriff immer im Zusammenhang zwischen einer unabhängigen und einer davon kausalen abhängigen Variabelen.
„Man vergleicht in der Klimatologie also nicht z.B. das Tagesmittel vom 7. Mai 2012 mit dem Monatsmittel vom Mai 2012, sondern immer nur auf gleichem Zeitmaß, also z.B. Monatsmittel vom Mai 2012 mit Mai 2011, etc.“
????? Das ist ja wohl völlig selbstverständlich, hier verstehe ich Ihre Intention nicht, so etwas anzumerken.
Ebenso ist mir nach folgenden Sätzen, in der Sie mir die unterschiedliche Definition von arithmetischen Mittelwerten im mathematischen und klimatologischen Sinn erläutern: „Da die Klimatologie diese Mittelwerte nicht als Schätzungen für Erwartungswerte der statistischen Verteilung nutzt, ….“
nicht verständlich, dass Sie mich darauf hinweisen ich : „müsse(n Sie) eben darauf achten, ob auch eine Normalverteilung vorliegt, bei der können Sie nämlich sicher sein, dass der arithmetische Mittelwert auch der beste Schätzwert des Erwartungswertes der Normalverteilung ist.“
Ich habe in meinem Beitrag (Abb. 4 bis 9) dezidiert auf diese Problematik hingewiesen und bei nicht möglicher Absicherung einer Normalverteilung (z. B. mit dem heute bevorzugten d’Agostino and Pearson Test) eine nichtparametrische Signifikanzentscheidung vorgeschlagen und durchgeführt (s. meine letzte Antwort auf # 12 an Herrn Harder).
Interessanter finde ich Ihren Vorschlag, saisonale Anteile durch Anomaliebildung zu eliminieren.
Ihre Argumentation leuchtet auf den ersten Blick auch erst einmal ein. Ich gebe aber zu bedenken, dass bei der Bildung der Referenzmittelwerte (z. B. über jeweils 30 Monate) Streuungen entstehen, die bei der Differenzbildung mit jeweils aktuellen Monatsmittel zu berücksichtigen sind. Außerdem darf, wenn nur die saisonalen Beiträge unterdrückt werden sollen, kein ansteigender oder absteigender Trend im ausgewählten Referenzintervall vorliegen, d. h. praktisch ein 30-järiges Temperaturplateau gewählt werden. Ob letztendlich durch die Benutzung von Monats-Mittel-Anomolien eine Reduzierung der Jahresmittel Konfidenzintervalle erzielt wird, vermag ich nicht so klar wie sie zu sehen.
„Das stimmt nicht, es werden auch Weltkarten der Temperaturverteilung publiziert.“
Siehe Abb. 2 meines Beitrags, zu der ich anmerke, dass ich es als ein sehr ehrgeiziges Vorhaben ansehe, diese geographische Variabilität durch einen einzigen Wert repräsentieren zu wollen. Diese Unmöglichkeit haben andere, z. B.
Gerlich&Tscheuschner oder Kramm& Dlugi nachgewiesen.
Ihrer vorletzten Anmerkung, dass : „Die Wahrscheinlichkeit, einen bestimmten Wert in Ihrer Gesamtverteilung anzunehmen, ist nicht unabhängig vom Monat.“ ist , stimme ich ausdrücklich zu und habe deshalb stellvertretend für die anderen Monate den Vergleich der Februar Mittelwerte aus Tagesmittelwerten (Braunschweig, Abb.8) durchgeführt.
Wenn ich solche Signifikanztests auch auf Jahresmittel anwende, orientiere ich mich letztendlich an der weitverbreiteten Fixierung auf globale Jahresmittelwerte ( 20xx war das wärmste Jahr seit Einführung der Temperaturmessung) und möchte die Insignifikanz solcher Statements nachweisen.
Lieber Herr Rabich,
“ sondern dieses System selbst ist abhängig von übergeordneten Einflüssen, die es zu klären gilt.“
Meinen Sie damit natuerliche oder „uebernatuerliche“ Einfluesse, wie z.B. Faelschung der Daten?
@20 Herr Rabich „Aber die Meßdaten an sich müssen erst einmal vertrauenswürdig sein – und das ist nicht nachgewiesen.“
Ganz genau!! Genau das sage ich auch schon seit Jahren! Was für ein Datensalat geht überhaupt ein in die GHCN Datenbank von NOAA/NCDC? Wer überprüft die Vergleichbarkeit der Daten. Angeblich ist die Homogenisierung der Daten sakrosankt und über jeden Zweifel erhaben. Ich habe da so meine Zweifel. Wenn man sich nur schon auf http://www.surfacestations.org ansieht, wie es um die Qualität der US Temperaturmessstandorte aussieht (Wärmeinseleffekte, viele Standorte auf Flughäfen, systematische Elimination ruraler Standorte zugunsten „wärmerer“ urbaner Standorte, etc. etc.), kann man sich leicht vorstellen, wie es auch anderorts zugehen mag.
Dazu kommt: von den Meeren gibt es gar keine Lufttemperaturmessungen in 2 Meter über der Wasseroberfläche (ausser von Inseln), sondern man misst sehr unvollständig Wassertemperaturen und tut dann quasi so, als wären das Lufttemperaturen. Aber auch nur in einem verschwindend kleinen Bereich der Ozeane.
Also, selbst wenn die „Globaltemperatur“ auch nur irgendeinen physikalischen Sinn haben sollte (was sie ja gar nicht hat, gemäss den überzeugenden Ausführungen von Prof. Kramm) ist nur schon auf Grund der Datenqualität eine darauf gründende mittlere Temperatur der reine Unfug (man würde besser von einer mittleren „Meerwassertemperatur korrigiert um Landfaktoren“ sprechen).
Lächerliche „Klimawissenschaft“!! Und unsere Politiker und Medien fallen gerne darauf herein!! Wie lange können die sich das noch erlauben?
Lieber Herr Prof.Kramm, #15
„die Definition, was Klima ist, und die Festlegung, wie gross das Beobachtungsingtervall sein muss, stammen nicht von mir. “
Das weiss ich selbstverstaendlich.
“ warum versuchen Sie mir etwas unterzujubeln, was nicht von mir stammt.“
Sie bilden sich etwas ein, ich habe Ihnen nichts untergejubelt.
„Der Begriff des Konfidenzintervalls hat etwas mit der zuvor festgelegten Wahrscheinlichkeit zu tun, dass ein gewisser Wert (z.B. der Mittelwert) innerhalb dieses Konfidenzintervall zu finden ist. Das Konfidenzintervall sollte nicht mit dem Erwartungsintervall verwechselt werden.“
Das Satz koennte von mir stammen, haben Sie das aus einem meiner Texte hier bei Eike kopiert 😉 ? Sie scheinen immer erst Dinge, die anderen Ihnen sagen, in eigene Worte fassen zu muessen, schoen,dass wir beide wissen, was Konfidenzintervalle sind. Da sind wir einigen meilenweit voraus.
„Statt staendig dagegen zu verstossen, sollten Sie eine begruendete Kritik an der Laenge einer solchen Klimaperiode liefern. Koennen Sie da nicht, dann haben Sie diese Empfehlung zu akzeptieren“
Nochmals, die 30 Jahre sind der Zeitraum zur Bestimmung von Referenzdaten, aber nicht eine universelle Periode, ueber die generell Daten zu ermitteln sind. Die notwendige Datenmenge und damit implizit auch Zeitintervalle haengen vom statistischen Test ab, der eine Hypothese testet. Wenn ich z.B. Trends hier angebe liefere ich die Konfidenzintervalle immer mit, egal, wie lang das Zeitintervall ist. Der Leser kann selber sehen, ob das Ergebnis signifikant ist oder nicht, und fuer die, die die Daten nicht verstehen, schreibe ich dazu, welches Testergebnis signifikant ist und welches nicht. Recherchieren Sie mal im Archiv ueber meinen Stil. Wenn Sie etwas daran auszusetzen haben, koennen wir dies konkret am Fall ausdiskutieren.
„Ihre Bemerkung hinsichlich des Referenzzustandes zeigt, wie wenig Sie verstanden haben. Eine Aenderung des Zustands in einem beliebigen System kann nur dann diagnostiziert werden, wenn ein Referenzzustand existiert.“
Die Feststellung statistisch signifikanter Aenderung haengt allgemein nicht an einer 30 Jahresperiode, sondern haengt wie gesagt, von der statistischen Untersuchung an der Datenmenge ab. Selbst bei lokalen Temperaturdaten kann die 30 Jahresperiode u.U. nicht ausreichend sein. Mal ein ganz einfaches und unmittelbar einleuchtendes Beispiel: wenn Sie die 99% Quantile eines absoluten Temperaturtagesmaximums eines Monats bestimmen wollen, so bekommen Sie ja nur 30mal 30 (31) Tagesmaxima an Daten in den 30 Jahren, also wird die 99% Quantile nur durch von der Groessenordnung einer Messung determiniert, viel zu wenig fuer befriedigende Konfidenzgrenzen dieser Klimakennzahl. Umgekehrt kann eine Klimaanomalie auch ueber kuerzere Zeitraeume als signifikant (und damit erst als Anomalie bezeichnet werden) angesehen werden, wenn sie nur ausgepraegt genug ist. Ist eben alles nur Mathematik.
Wie ich schon schrieb, testet man zwei Datenensembles auf Grundgesamtheit durch stat. Tests. Eine Aenderung liegt dann vor, wenn das eine Ensemble getestet mutmasslich einer anderen Grundgesamtheit zugehoert als das erste Ensemble. Die (i.a. nur naeherungsweise bekannte) Grundgesamtheit ist der Referenzzustand. Um statistisch nachzuweisen, dass zwei Ensemble signifikant mutmasslich zum gleichen oder zu verschiedenen Grundgesamtheiten gehoeren, muss man die Grundgesamtheit aber nicht kennen. Sind wir uns in diesem Punkt einig?
es sind in den Kommentaren immer die Voraussetzungen für aussagefähige Daten die Rede, von Unabhängigkeit, von Zufälligkeit usw. Aber die Meßdaten an sich müssen erst einmal vertrauenswürdig sein – und das ist nicht nachgewiesen. Wir haben es nicht nur mit einem dynamischen Sysstem zu tun, sondern dieses System selbst ist abhängig von übergeordneten Einflüssen, die es zu klären gilt.
Wenn man die Beiträge von Prof. Kramm und Herrn Bäcker liest versteht man sofort, warum jemand Professor an einer renommierten Universität ist und der andere bloss ein fanatischer AGW Anhänger eines minderen akademischen Ranges, der dem Herrn Professor in überhaupt gar keiner Hinsicht das Wasser reichen kann.
Empfehlung an den Wichtigtuer und CO2 Polit-Talker NicoBaecker:
Studieren Sie mal gaaanz genau, was der Herr Professor hier doziert hat, und versuchen doch mal freundlicherweise auch das Wesentlichste daraus zu kapieren: NÄMLICH, DASS DIE GLOBALTEMPERATUR EINE ABSOLUT NICHTSNUTZIGE RECHENGRÖSSE IST, DIE NUR DEN ZWECK VERFOLGT, EINFÄLTIGEN LAIEN VORZUGAUKELN, DASS MAN DAS KLIMA GANZ EINFACH VERSTEHEN KANN. EIN MANIPULATIONSMITTEL FÜR MEDIEN, POLITIK UND BEVÖLKERUNG SEITENS EINER POLITISIERTEN PSEUDO-KLIMAWISSENSCHAFT. DAZU ZÄHLEN SICH JA DIE CO2 POLITIKER BÄCKER, FISCHER, KETTERER, MENDEL, HADER ETC.