Wie kann man eine mittlere Globaltemperatur ermitteln? Was die Statistik verlangt und erlaubt
Wenn der zeitliche Verlauf globaler Temperaturen graphisch dargestellt wird, so z. B. von dem NASA Goddard Institut for Space Studies (GISS), werden meist Temperaturanomalien gezeigt. (Abb. 1 nebenstehend) Dabei handelt es sich z. B. um Jahresmittelwerte, die ihrerseits auf einen Mittelwert über ein definiertes Zeitintervall bezogen werden, z. B. 1961 – 1990. Man muss sich darüber im Klaren sein, dass es sich bei Mittelwerten um Schätzungen handelt, die letztendlich auf einer für repräsentativ gehaltenen Auswahl von Einzelmessungen beruhen.
Die zulässigen Methoden der Mittelwertbildung unter Berücksichtigung der Schätzfehler von den Messdaten bis zur globalen Jahresmitteltemperatur soll im Folgenden dargestellt werden. Darauf aufbauend werden für ausgewählte Temperaturreihen die Mittelwerte auf signifikante Unterschiede analysiert.
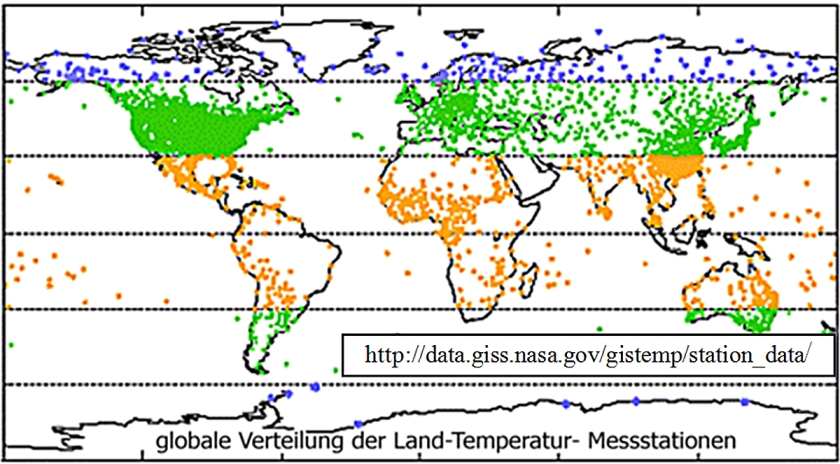
Abb. 2
Es existieren weltweit ca. 39.000 meteorologische Stationen, die neben der Registrierung anderen Wetterdaten die bodennahen (2m) Lufttemperatur messen. Wie Abb. 2 zu entnehmen, sind diese Stationen sind nicht homogen über die Landfläche der Erde verteilt (die Markierungen in den Meeren beziehen sich auf Inseln).
Zwischen 1000 und 3000 von ihnen werden mit z. T. unterschiedlicher Gewichtung zur Berechnung der Globaltemperatur-Reihen der verschiedenen Institutionen herangezogen. Die bodennahen Lufttemperaturen werden auch von einem Satelliten (TIROS-N ) erfasst und können u. a. als globale Verteilungen dargestellt werden.
So wurden von der NOAA (National Oceanic and Atmospheric Administration, USA) z. B. für den 2. März 2012 die folgenden ”Momentaufnahmen” (Abb. 3)veröffentlicht:
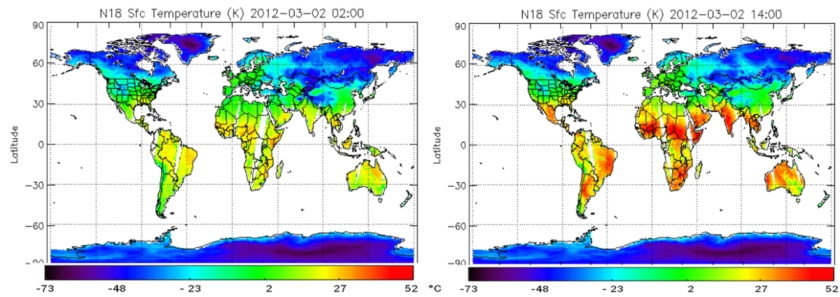
Abb. 3
Die riesige geographische Variabilität der bodennahen Landtemperaturen durch einen einzigen Mittelwert charakterisieren zu wollen, erscheint sehr ehrgeizig. Die ständigen täglichen, wie auch jahreszeitlichen Temperaturänderungen erschweren dieses Vorhaben zusätzlich.
Betrachtet man zunächst einmal nur eine einzige Station. Die allgemein vorgeschriebenen Bedingungen zur Messung der bodennahen Temperatur verlangen, dass ein geeichtes Thermometer in einem als ”englische Hütte” bezeichneten Kasten zwei Meter über dem Erdboden untergebracht ist (Abb. 4).

Abb. 4
Der weiße Anstrich und die Belüftungslamellen sollen gewährleisten, dass die Lufttemperatur ungestört (im Gleichgewicht mit der Umgebung) gemessen werden kann. Tagesmittelwerte werden weltweit nach verschiedenen Methoden gebildet
In Deutschland wird traditionell das arithmetische Mittel aus den 7 Uhr, 14 Uhr und 21 Uhr Temperaturen berechnet, wobei der 21 Uhr Wert doppelt gewichtet wird.
Nach Umstellung auf elektronische Datenerfassung sind auch andere Mittelwertbildungen gebräuchlich.
Der Tagesmittelwert ist in jedem Fall eine Schätzung, die als verbindlich betrachtet wird, ohne mögliche Fehlerquellen der Station (Ablesefehler, Aufbau und Anstrich der ”englischen Hütte”, Beeinflussung der Umgebung durch lokale Wärmequellen) zu berücksichtigen.
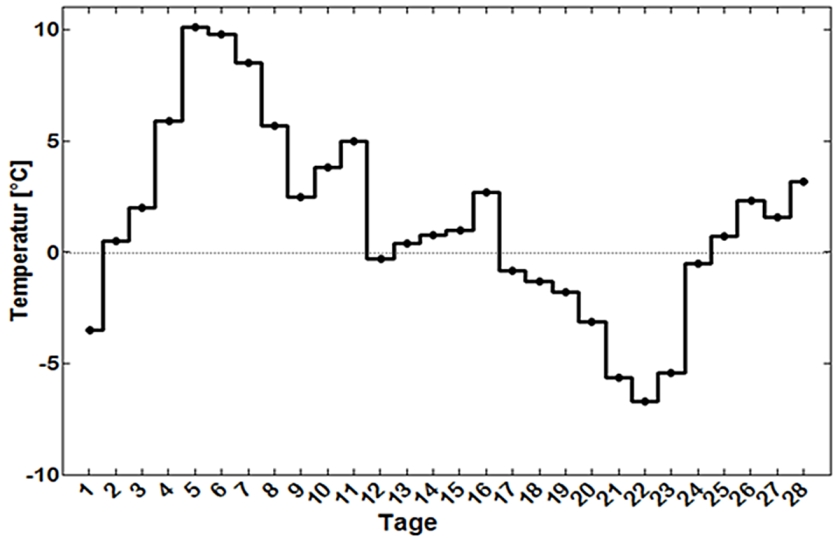
Abb. 5 zeigt die Tagesmittelwerte der Station Braunschweig Völkenrode des Deutschen Wetterdienstes (DWD) für Februar 2011 dargestellt. Wenn daraus ein Monatsmittelwert gebildet werden soll, muss man aus statistischer Sicht erst einmal untersuchen, welche Art der Mittelwertbildung für diese Grundgesamtheit, wie eine solche Ansammlung von Werten genannt wird, zulässig ist. Das arithmetische Mittel, also die durch ihre Anzahl dividierte Summe aller Werte, ist nur dann sinnvoll (zulässig), wenn sie einer definierten Verteilung unterliegen. Dazu werden die Tagesmitteltemperaturen in Größenklassen unterteilt und als Histogramm dargestellt:
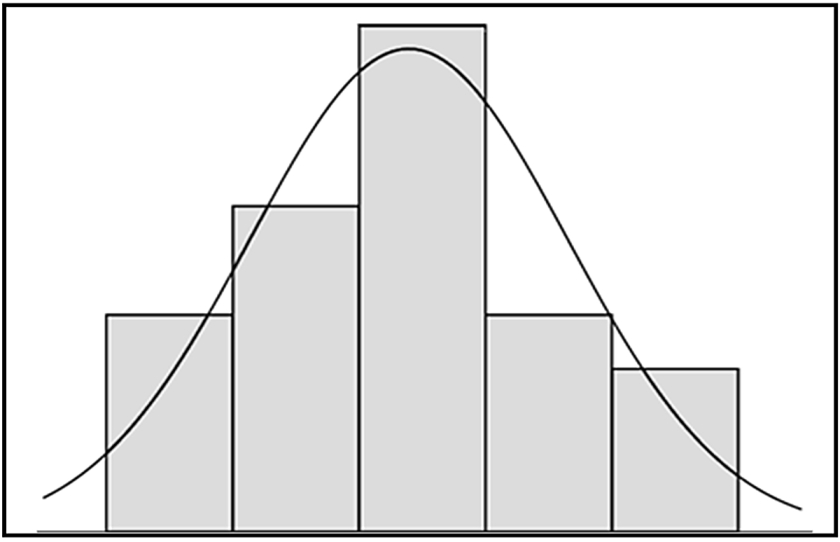
Abb. 6
Wenn die Flächen der Klassen annähernd die Fläche unter der Kurve, die einer Normalverteilung nach Gauss entspricht, ausfüllen, kann die Grundgesamtheit als normalverteilt betrachtet werden (Abb.6). Dies zu entscheiden gibt es statistische Testverfahren, die in der Wissenschaft routinemäßig am Beginn einer statistischen Auswertung stehen. Für die gezeigten Tagesmittelwerte ist die Bildung eines arithmetischen Mittels demnach zulässig. Hätte der Test das Vorliegen einer normalverteilten Grundgesamtheit abgelehnt, wäre der Median zur Beschreibung der Monatsmitteltemperatur sinnvoll (erlaubt) und ein besserer Repräsentant für den Monatsmittelwert. Aus der aufsteigend angeordneten Einzelwerten wird der Wert bei der halben Anzahl ausgewählt und als Median bezeichnet.
Genau dieser Fall tritt für die Oktober-Temperaturen 2011 ein.
In Abb. 7 sind die Verteilungen der Einzelwerte als schwarze Punkte als sogenannte Jitterplots dargestellt. -Die Februarwerte streuen symmetrisch um das blau eingezeichnete arithmetische Mittel herum, während die Oktoberwerte unsymmetrisch mit einer Tendenz zu höheren Temperaturen um das das arithmetische Mittel verteilt sind. 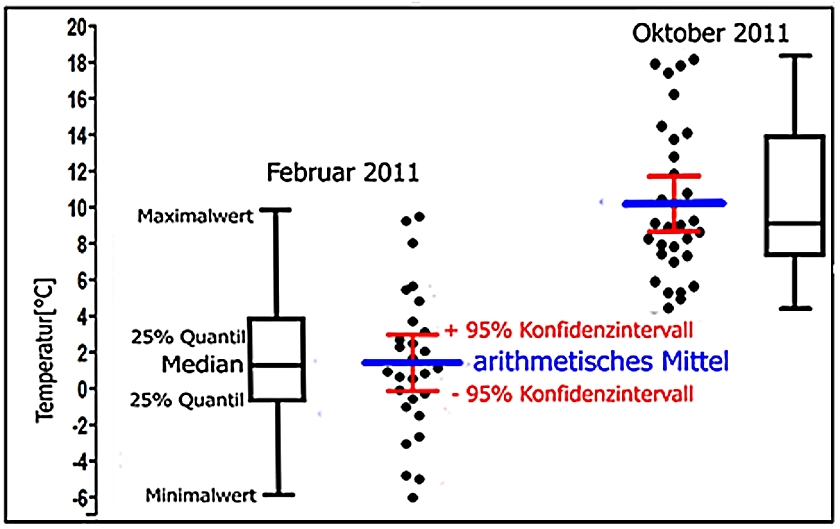
Abb. 7
Von diesem weicht der Median deutlich ab, da er sich an der Lage der meisten Einzelwerte orientiert. Die Kästchen über und unter dem Median repräsentieren die Lage von jeweils 25% der Einzelwerte (25% Quantile) und sind für den Oktober 2011 sehr unterschiedlich, während sie für den Februar fast gleich groß ausfallen. Auch sind die Werte für Median und arithmetisches Mittel fast identisch. Dies ergibt sich bei normalverteilten Grundgesamtheiten, bei denen zusätzlich Kenngrößen für die Streuung berechnet werden können.
Die rot eingezeichneten Vertrauensbereiche (Konfidenzintervalle) weisen aus, dass der zutreffende Mittelwert unter Berücksichtigung der Verteilung der Einzelwerte mit einer Wahrscheinlichkeit von 95% (95% Konfidenzniveau) in diesem Bereich liegt.
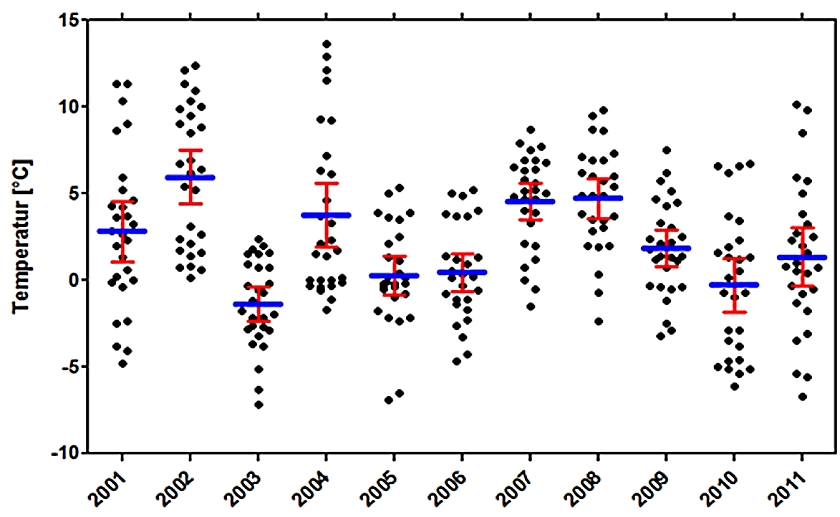
Abb. 8
Da jede Mittelwertbildung eine Schätzung darstellt, ist ihr eine von der Anzahl der Einzelwerte und deren Verteilung (eben der Grundgesamtheit) abhängiges Streuungsmaß sozusagen aufgeprägt.
Dies erlaubt die Anwendung von Signifikanztests, mittels derer zum Beispiel für ein vorgegebenes Konfidenzniveau entschieden werden kann, ob sich Mittelwerte signifikant voneinander unterscheiden. Für normalverteilte Grundgesamtheiten werden dabei andere Tests (Varianzanalyse) als für beliebige (nicht parametrische) Verteilungen angewandt, z. B. der Kruskal-Wallis Test.
Für den Vergleich der Februar-Mitteltemperaturen von 2001 bis 2011 der DWD Station Braunschweig (Abb. 8) können die arithmetischen Mittel der Tagesmittelwerte verglichen werden, da für jedes Jahr eine Normalverteilung vorliegt. Die darauf angewandte Varianzanalyse kommt zu dem Ergebnis, dass sich die Mittelwerte insgesamt auf einem Konfidenzniveau von 95% unterscheiden.
Um Jahresmittelwerte zu bilden, kann man die Tagesmittelwerte direkt verrechnen oder nach Bildung von Monats-mitteln, diese zur Mittelwertbildung verwenden.
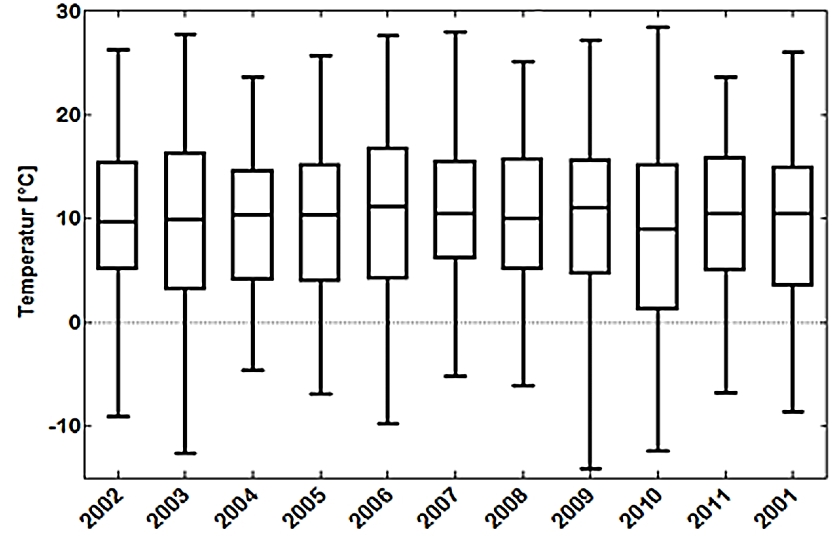
Abb. 9
Da für die DWD Station Braunschweig die Jahresverteilungen der Tagesmittel die Normalitätskriterien nicht erfüllen, müssen die Mediane benutzt werden (Abb. 9).
Zur Entscheidung, ob sich die Jahres-Mediane signifikant voneinander unterscheiden, wird der Kruskal-Wallis Test angewandt, der zu dem Ergebnis gelangt, dass insgesamt kein signifikanter Unterschied zwischen ihnen vorliegt.
In der Praxis weren jedoch die Jahresmittelwerte aus den Monatsmittelwerten gebildet, wobei einfach vorausgesetzt wird, dass die Tageswerte der Monate jeweils normalverteilt sind. Das trifft auch meistens zu, da Mittelwerte, auch wenn sie aus nicht normalverteilten Grundgesamtheiten gebildet werden, tendenziell dazu neigen, eine Normalverteilung anzunehmen.
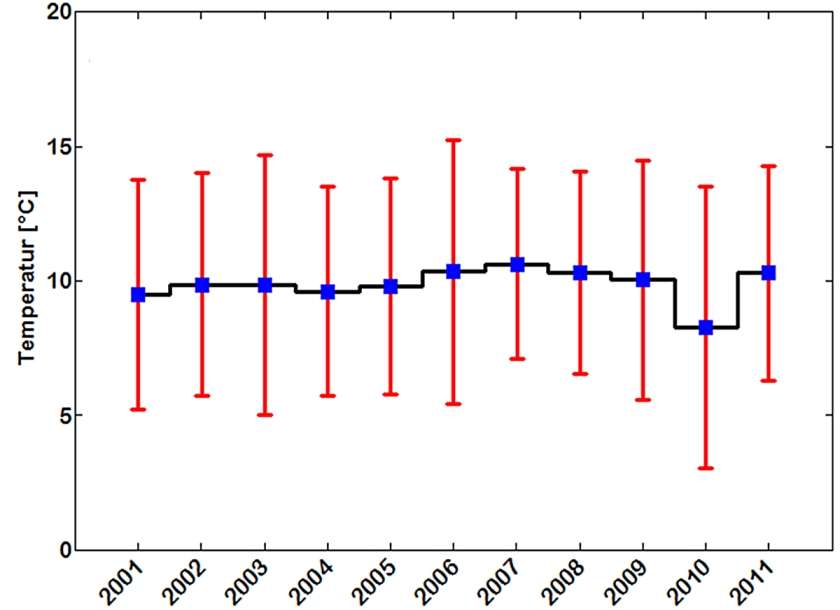
Abb. 10
Die Streungsmaße der Monatsmittel werden in den öffentlich zugänglichen Datensätzen nicht weiter berücksichtigt, was jedoch aufgrund der Fehlerfortpflanzungsregeln nach Gauss geboten ist.
Somit stehen nur solch Streuungsparameter, die sich bei der Bildung von Jahresmittelwerten aus den veröffentlichten Monatswerten ergeben, für Signifikanztests zur Verfügung.
In die Berechnung von Konfidenzintervallen geht die Anzahl der Einzelwerte als Divisor ein. Daher fallen sie für Jahresmittelwerte relativ groß aus, da diese jeweils nur aus 12 Werten (Monaten) gebildet werden (Abb. 10). Die Varianzanalyse sagt aus, dass sich die Jahresmittelwerte nicht signifikant voneinander unterscheiden und gelangt damit zum gleichen Ergebnis wie der vorige Vergleich der Mediane aus Tagesmittelwerten geführt. 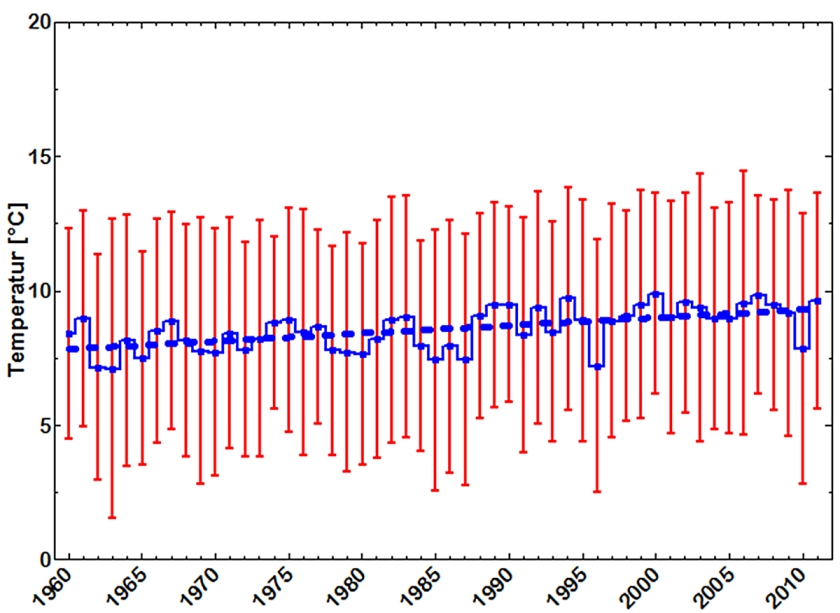
Abb. 11
Im nächsten Schritt, werden aus den Monatsmitteln einzelner Stationen Gebietsmittel gebildet. Der Deutsche Wetterdienst berücksichtigt z. Zt. 264 Stationen, die zur Berechnung einer für Deutschland relevanten Mitteltemperatur herangezogen werden. Die Monatswerte sind normalverteilt, so dass die Jahresmittelwerte durch arithmetische Mittel und ihre Konfidenzintervalle repräsentiert werden können. Eine Varianzanalyse weist keine signifikanten Unterschiede zwischen den Jahresmittelwerten seit 1960 aus (Abb. 11).
Dennoch läßt sich ein Trend berechnen, der durch eine Steigung von 0,03 ± 0,006 °C/Jahr der Regressionsgeraden charakterisiert wird, für die mit einem Bestimmtheitsmaß von R2 = 0,33 eine beträchtliche Unsicherheit besteht.
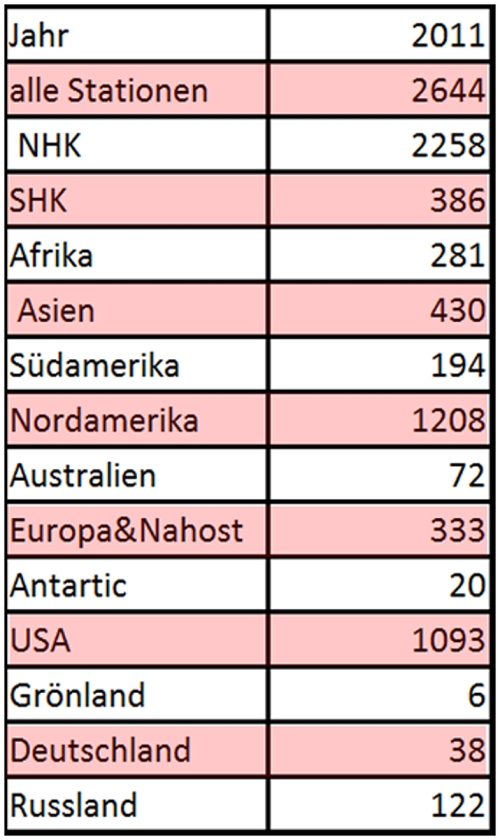
Tab. 1
Nach Angaben des Global Historical Climatology Network (GHCN), bei dem die Temperaturen der weltweit verteilten Stationen gesammelt werden, wurden 2011 zur Ermittlung der globalen mittleren Landtemperatur die Daten von 2644 Stationen berücksichtigt. Anzahl und Verteilung ist der Tabelle 1 zu entnehmen. Wie schon aus der oben gezeigten Karte hervorging, sind die Stationen nicht homogen über die Landfläche verteilt.
Temperatur – Zeit – Reihen werden im Wesentlichen von 3 von Institutionen mit unterschiedlichen Gewichtungen der Werte erstellt und publiziert.


Laure M. Montandon et al. haben die unterschiedliche Berücksichtigung der vom GHCN nach Oberflächentypen differenzierten Landstationen tabelliert (Tab. 2). Auffällig sind die hohen Anteile der urbanen Stationen.
In jüngster Zeit haben Überarbeitungen der Zeitreihen dazu geführt, dass sich die Ergebnisse weitestgehend angenähert haben. Dies gilt auch für die beiden Reihen, in denen die Messungen des TIROS-N Satelliten auswertet werden.
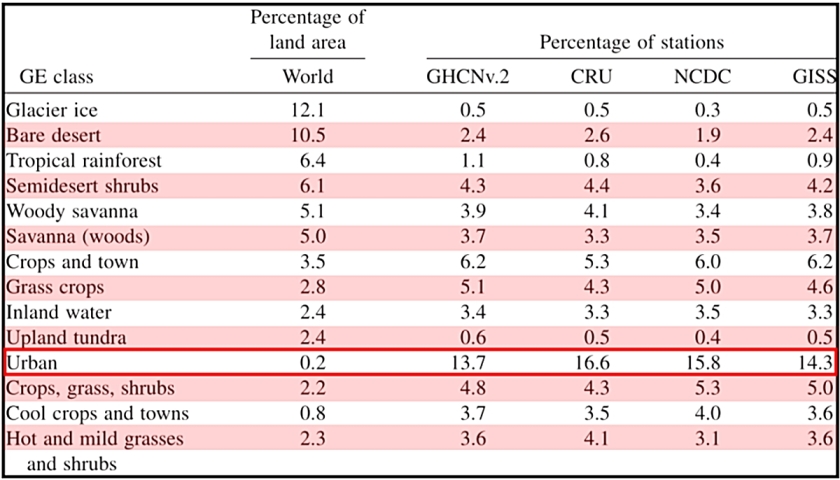
Tab. 2
Diese Daten basieren auf der Reflexion von ausgesandten Mikrowellensignalen und liefern relative Werte, die mithilfe der landgestützten Auswertungen kalibriert werden müssen, um sie in Temperaturwerte umrechnen zu können.
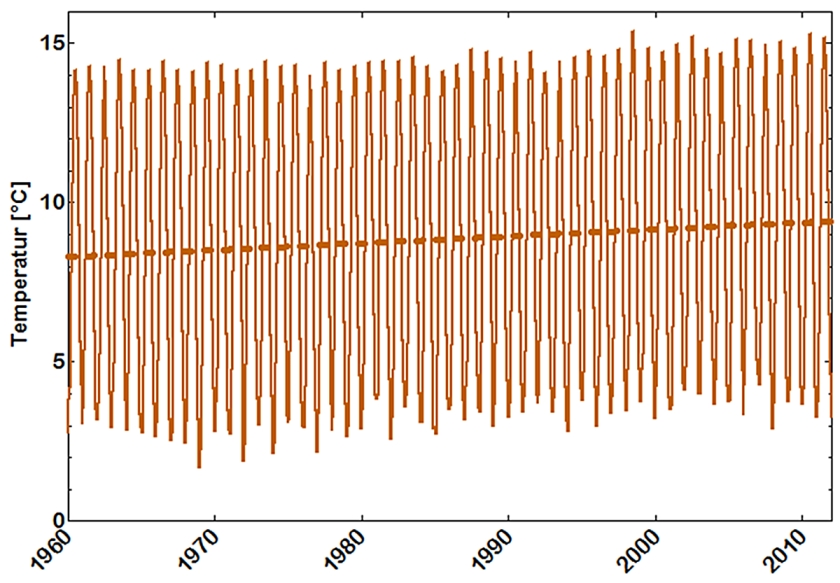
Abb. 12 stellt die Zeitreihe der globalen monatlichen Mitteltemperaturen dar, wie sie vom NCDC (National Climate Data Center) bereitgestellt wird. Es sei darauf hingewiesen, dass keine Streuungsmaße mitgeteilt werden und daher auch nicht eingezeichnet sind.
Die die Regressionsgerade weist eine Steigung von 0,022 mit einem Konfidenzintervall von ± 0,01 °C/Jahr auf und hat ein äusserst geringes Bestimmtheitsmaß von R2 = 0,006 so dass der Trend als sehr unsicher angesehen werden muss.
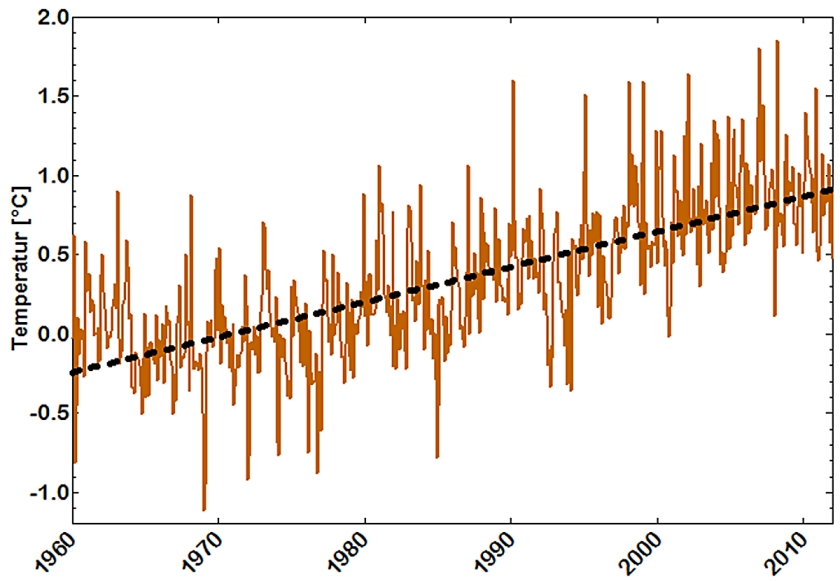
In Abb. 13 sind die Temperaturanomalien, bezogen auf die Referenzperiode von 1960 bis 1990, zu sehen.
Auch hier fehlen Streuungsmaße, die aufgrund der Subtraktion der Mittelwerte der Referenz-Monatsmittemittel von den jeweiligen monatlichen Mittelwerten nach dem Fehlerfortpflanzungsgesetz sehr beträchtlich ausfallen.
Da diese nicht berücksichtigt werden, d. h. weniger Information über die Ausgangsdaten für weitere Berechnungen vorliegt, erhält man mit R2 = 0,5 nur ein scheinbar größeres Bestimmtheitsmass für die Regressionsgerade.
Ihre Steigung unterscheidet sich mit 0,022 ± 0,001 ebenfalls nur durch ein augenscheinlich um den Faktor 10 verringertes Konfidenzintervall von der obigen.
Da die Erdoberfläche nur zu angenähert einem knappen Drittel (29 %) aus Land, zu gut zwei Ditteln (71%) aber aus Ozeanen besteht, erscheint es sinnvoll, deren Temperaturen zur Berechnung einer Global-Mitteltemperatur einzubeziehen. Früher wurde dazu eine Wasserprobe mit einem Schöpfeimer (Pütz oder Bucket) genommen und die Temperatur des Wassers darin gemessen. Deren Schöpftiefe sollte 1 m betragen. Das wurde aber aus praktischen Gründen selten eingehalten. Man kann unterstellen, dass sie je nach Geschwindigkeit des Schiffes und Sorgfalt der beauftragten Person, diese irgendwo zwischen wenigen Zentimetern und max 1 bis 1,5 m lag. Heute wird die Wassertemperatur im Kühlwassereintritt der Schiffe in 3m bis 15 m Tiefe bestimmt. Stationäre Bojen messen die Wassertemperatur in 2m Tiefe (nach Mitteilungen von M. Limburg).
Die solchermaßen gewonnenen Wassertemperaturen werden als SST (Sea Surface Temperatures) bezeichnet.
In Abb. 14 sind die NCDC Zeitreihen für die SST Monatsmittel-Temperaturen und Anomalien abgebildet:
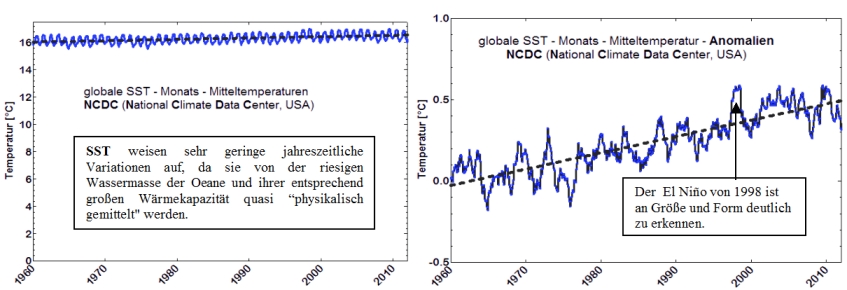
Abb. 14
Die Steigungen der Regressionsgeraden sind mit 0,009 ± 0,001 und 0,01 ± 0,0002 nahezu identisch. Für die Anomalien ergibt sich ein R2 = 0,7, das aber auf dem Hintergrund fehlender Fehlerfortpflanzung kritisch zu betrachten ist.
Die Kombination von Land- und Ozeanberflächentemperaturen wird in Abb. 15 gezeigt:
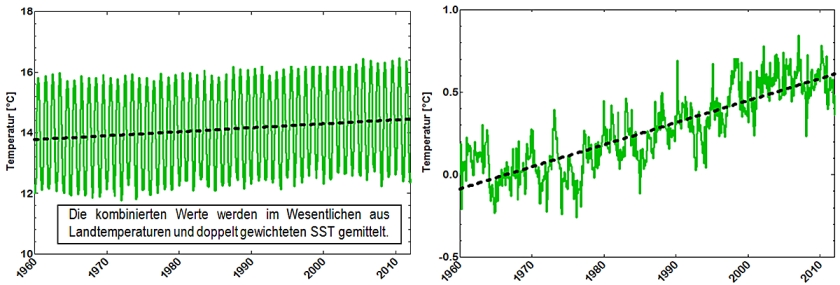
Abb. 15
Die Steigungen der Regressionsgeraden fallen mit 0,013 ± 0,004 bzw. 0,013 ± 0,0004 auch hier praktisch gleich aus. Das Bestimmtheitsmaß ist mit R2 = 0,7 für die Mittelwert-Anomalien größer als für die Mitteltemperaturen mit R2 = 0,02.
Zwar ist es bemerkenswert, dass die Steigung für die Landwerte rund doppelt so hoch wie für SST und Land + SST Werte, jedoch sollte immer bedacht werden, dass die Bestimmtheitsmaße recht gering sind, bzw. für die Anomalien wegen der nicht berücksichtigten Fehlerfortpflanzung nur gesteigert erscheinen.
Werden aus den Monatsmittelwerten Jahresmittel gebildet und die Signifikanzintervalle berechnet und dargestellt, ergibt sich die Abb. 16 für Landtemperaturen der NCDC Reihe. 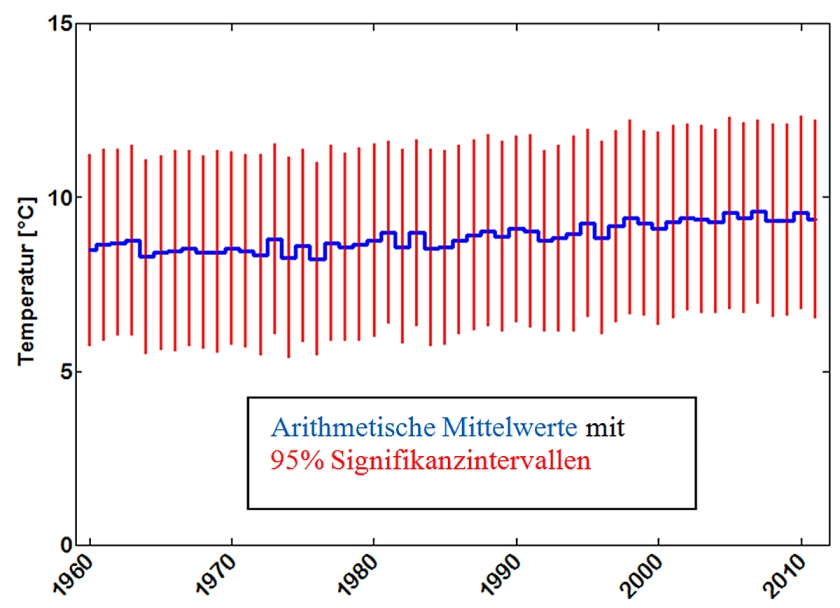
Abb. 16
Für die normalverteilten Werte der globalen Monatsmittel ergibt eine Varianzanalyse, dass sich zwischen den arithmetischen Jahresmitteln keine signifikanten Unterschiede nachweisen lassen.
Hierbei wird deutlich, dass bei der üblichen Darstellung von Temperaturreihen als Anomalien ohne Angabe von Streuungsparametern wichtige Informationen unterdrückt werden und dadurch ungesicherten Spekulationen über Temperaturunterschiede und -trends Vorschub geleistet wird.
Die Angabe einer globalen Mitteltemperatur bzw. der Veränderung einer globalen Mittelwertanomalie (z. B. um 2°C gegenüber einem definierten Zeitpunkt) ist daher unter Beachtung statistischer Gesetzmäßigkeiten, ohne Angabe von Konfindenzintervallen als sinnlos zu betrachten.
Autor: PD Dr. habil Dr. Eckhard Schulze < eckhard.schulze@gmx.org >
Quellen:
zu Tab. 1 http://fzuber.bplaced.net/NOAA-GHCN-Stations-E.pdf
zu Tab. 2 Laure M. Montandon et al. Earth Interactions Volume 15 (2011) Paper No. 6
zu Abb.1 http://cdiac.ornl.gov/trends/temp/hansen/graphics/gl_land.gif
zu Abb.2 http://data.giss.nasa.gov/gistemp/station_data/
zu Abb.3 http://www.osdpd.noaa.gov/ml/mspps/surftprd.html
zu Abb.4 http://imk-msa.fzk.de/Wettervorhersage/images/Huette.jpg
zu Abb. 5 bis 10 avacon.com/cms/ContentFiles/Internet/Downloads/Netze_SN_unterbrVerbrauchseinr_Tagesmitteltemp_2012.xls
zu Abb.11 http://www.dwd.de/bvbw/generator/DWDWWW/Content/Oeffentlichkeit/KU/KU2/KU21/klimadaten/german/download__gebietsmittel__temp,templateId=raw,property=publicationFile.xls/download_gebietsmittel_temp.xls
zu Abb.12 u. 13 http://junksciencearchive.com/MSU_Temps/NCDCabsLand.csv bzw. http://junksciencearchive.com/MSU_Temps/NCDCanomLand.csv
zu Abb.14 a u.b http://junksciencearchive.com/MSU_Temps/NCDCabsOcean.csv bzw. http://junksciencearchive.com/MSU_Temps/NCDCanomOcean.csv
zu Abb.15 a u. b http://junksciencearchive.com/MSU_Temps/NCDCabs.csv bzw. http://junksciencearchive.com/MSU Temps/NCDCanom.csv
Der gesamte Text kann als pdf im Anhang herunter geladen werden