Angeregt von den Kommentaren und zu U.Webers Berichten über die Tagestemperaturen, die von einer direkten Sonneneinstrahlung erzeugt werden, versuchen manche Leser dies anhand von imaginierten Versuchen, anhand der Wirksamkeit des S-B Gesetzes, zu ergründen. Dies ist der einzige Möglichkeit der Wahrheit näher zu kommen. Hier ein Versuch, der einiges davon – allein mittels Strahlungstemperaturen – untersucht.
von Michael Mechtel
Zielsetzung und Motivation
Die Lebensbedingungen auf unserem Planeten Erde lassen sich letztlich auf die Einstrahlung von Energie durch die Sonne zurückführen. Diese Energie unterliegt vielfachen Umwandlungs- und Transportprozessen, an denen neben physikalischen auch chemische und biologische Vorgänge beteiligt sind. Nicht zuletzt die klimatischen Bedingungen, die wir vorfinden, gehen auf solche Prozesse zurück, und ein wichtiger, heutzutage häufig bemühter Parameter zur Charakterisierung des Klimas ist die Temperatur, sei es als regionale Temperatur mit ihren charakteristischen Schwankungen, sei es als zeitlicher und/oder räumlicher Mittelwert.
Zielsetzung dieses Artikels ist es, ein örtliches Temperaturniveau für die Regionen der Erde herauszuarbeiten, wenn allein der primäre Strahlungseinfluss der Sonne berücksichtigt wird und alle sekundären Nachfolgeeffekte (Transport und Umwandlung von Energie) beiseite gelassen werden. Die Anregung hierzu erfolgte durch die Artikel des Autors Uli Weber, der hier sein ‘hemisphärisches Stefan-Boltzmann-Modell‘ mehrfach vorgestellt hat. Die Schlussfolgerungen seines Modells werden aber nicht geteilt!
Beschreibung des Modells
Die genannte Zielsetzung und die Begrenzung des Rechenaufwandes erfordert ein sehr vereinfachtes Modell der Erde, das selbstverständlich nicht mehr die Realität abbildet, aber sehr wohl eine Basis für das Verständnis unserer Realität abgeben kann.
Zunächst erfordert es die Begrenzung des Rechenaufwandes, dass wir einen ideal kugelförmigen, homogenen Erdkörper voraussetzen, der auf einer exakten Kreisbahn in genau 365 Tagen die Sonne umkreist.
Um die genannten Sekundärprozesse von Energieumwandlung und –transport auszuschließen, sind auch einige physikalische Voraussetzungen erforderlich:
– Keine Atmosphäre vorhanden, damit also keine Luftströmungen
– Kein Wasser, damit also keine ozeanischen Strömungen und keine Phasenumwandlungen (Verdunsten, Kondensieren, Gefrieren, Schmelzen)
– Wärmeleitung vernachlässigbar klein
– Andere Energiequellen wie Restwärme aus dem Erdinneren oder die kosmische 3-K-Hintergrundstrahlung werden ebenfalls vernachlässigt.
Schließlich fordern wir noch eine schnelle Rotation dieser Modellerde, so dass sich keine nennenswerten Tag-Nacht-Unterschiede der Temperatur herausbilden können. Das bedeutet, dass jeder Punkt der Erdoberfläche zu jedem Zeitpunkt einzeln für sich im Strahlungsgleichgewicht mit der pro Erdumdrehung zugestrahlten Sonnen-Energie steht.
Weil die Erde um die Sonne umläuft, werden sich die Strahlungsbedingungen von Tag zu Tag ändern („Tag“ meint hier den bekannten Erdentag, also ein 365-stel Jahr). Da aber Wärmeleitung keine Rolle spielen soll, müssen wir keine Speichereffekte berücksichtigen, denn es wird nur eine dünne Oberflächenschicht an diesem Strahlungshaushalt beteiligt sein. Diese dünne Schicht kann sich schnell genug der sich ändernden Strahlungssituation anpassen, so dass das Strahlungsgleichgewicht von Tag zu Tag erhalten bleibt.
Auf dieser Voraussetzung beruhend, lässt sich die lokale Temperatur eines Oberflächenpunktes aus der momentanen Einstrahlung unter Anwendung des Stefan-Boltzmann-Gesetzes bestimmen. Es zeigt sich, dass diese Temperatur allein vom Breitenkreis und der Position der Erde auf ihrer Umlaufbahn abhängt. Jeder Breitenkreis weist damit einen eigenen Jahresgang der Temperatur auf.
Weitere Annahmen unseres Modells, angelehnt an unsere Realität:
– Albedo a = 0.3, selbstverständlich homogen auf der ganzen Oberfläche,
– Emissivität im Infraroten = 0.95 (die Erde also nicht als schwarzer, sondern als dunkelgrauer Körper)
– Die Schrägstellung der Erdachse wird berücksichtigt.
Die breitenkreisspezifischen Temperaturverläufe wurden für diese Modellerde berechnet und sollen im folgenden dargestellt werden. Der Rechengang selber ist für Interessierte im Anhang skizziert.
Ergebnisse
Mit der extraterrestrischen Solarkonstante I0 = 1361 W/m² und der genannten Albedo ergibt sich die maximal absorbierbare Intensität an der Oberfläche zu Imax = 953 W/m², was einer maximal möglichen Gleichgewichtstemperatur von 365 K = 92 oC entspricht (gerundete Werte).
1. Jahresgänge der Temperatur bei 23,45 Grad Achsneigung
Die Schrägstellung der Erdachse gegenüber der Erdbahnebene beträgt 23.45 Grad. Der damit sich ergebende Jahresgang der Temperatur unserer Modellerde auf verschiedenen Breitenkreisen der Nordhalbkugel ist in Abb. 1 dargestellt (für die Südhalbkugel gelten entsprechende Kurven, nur unter Vertauschung von Sommer- und Winterhalbjahr).
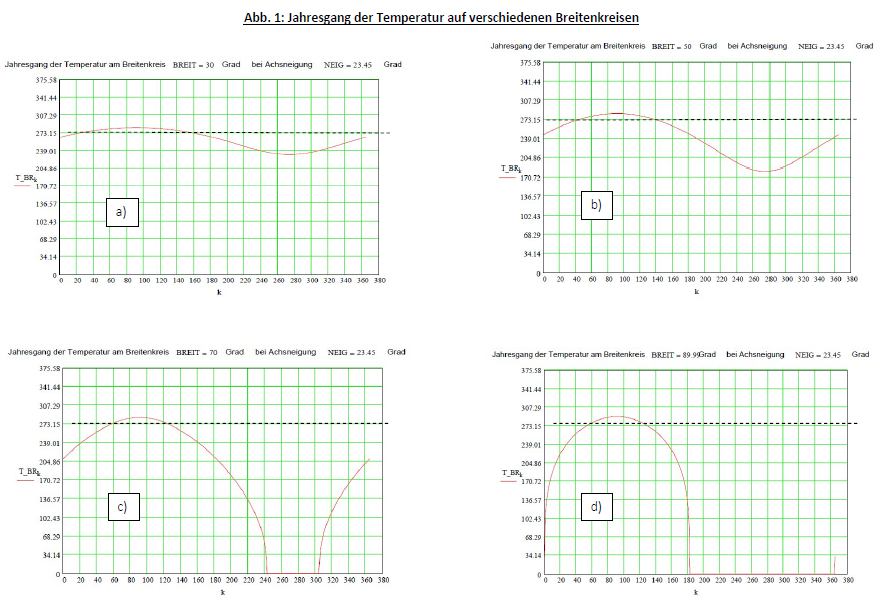
Auf der x-Achse ist die Tagesnummer aufgetragen, d.i. die Nummer des konventionellen Erdentages, beginnend mit Frühlingsanfang (21. März). Die Skala reicht bis 380, ein Jahr ist mit Nr. 365 beendet.
Auf der y-Achse ist die Absolut-Temperatur in der Kelvin-Skala aufgetragen, beginnend bei 0 K. Die gestrichelte Linie in den Diagrammen markiert den Nullpunkt der Celsius-Skala (273,15 K).
Bild a) gilt für den Breitenkreis 30 Grad.
Bild b) gilt für den Breitenkreis 50 Grad, das entspricht der Lage der Stadt Mainz. Man erkennt, dass der Unterschied zwischen Sommer- und Winterhalbjahr deutlich ausgeprägter ist als am 30. Breitengrad.
Bild c) gilt für den Breitenkreis 70 Grad. Diese Breite liegt nördlich des Polarkreises, deshalb tritt hier im Sommer Mitternachtssonne und im Winter Polarnacht auf. In der Polarnacht haben wir keine Sonneneinstrahlung, so dass die Temperatur rasch auf den absoluten Nullpunkt sinkt (würden wir die kosmische Hintergrundstrahlung in Betracht ziehen, lägen wir bei 3 K.)
Bild d) gilt für den „Breitenkreis“ 90 Grad, also den Nordpol. Hier haben wir ein halbes Jahr Mitternachtssonne (wechselnder Höhe) und ein halbes Jahr Polarnacht.
Insgesamt ist festzustellen, dass durchwegs, selbst in äquatornahen Gebieten, die Null-Grad-Celsius-Grenze kaum je überschritten wird, allenfalls um wenige Grad in den Sommermonaten. Zum Zweiten fällt in Regionen, die nicht von der Sonne beschienen sind, die Temperatur schnell sehr tief ab. Das macht sich in der zunehmenden Ausbeulung der Kurven nach unten im Winterhalbjahr bemerkbar, je weiter man sich vom Äquator weg in polnahe Regionen bewegt. Extrem wird es dort, wo Polarnächte auftreten.
2. Abhängigkeit des Temperaturganges von der Neigung der Erdachse
Man kann sich die Frage stellen, wie die Neigung der Erdachse sich auf den Verlauf der Temperaturwerte auswirkt. Dies wurde für den bereits in Abb. 1 aufgeführten 50. Breitengrad Nord untersucht, der exemplarisch für Deutschland stehen kann. Ergebnisse siehe Abb. 2.
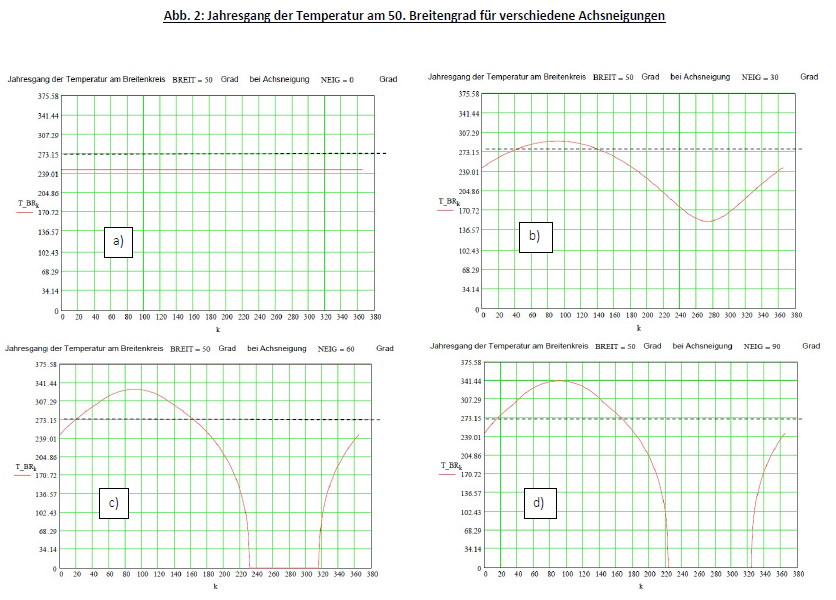
Die x- und y-Achsen sind die gleichen wie in Abb. 1.
Fall a) gilt für den Neigungswinkel 0 Grad. Hier steht die Erdachse senkrecht auf der Erdumlaufbahn. Damit ändert sich im Jahresverlauf nichts, es gibt keine Jahreszeiten (Annahme: die Sonne strahlt gleichmäßig in alle Richtungen).
Fall b) gilt für den Neigungswinkel 30 Grad. Der ist etwas größer, als es der Realität entspricht, die Jahreszeiten sind also etwas stärker ausgeprägt. Die Graphik ist mit der in Abb. 1 b) zu vergleichen, wobei sich zeigt, dass die Maximaltemperatur im Sommer leicht erhöht, die Winterdelle jetzt aber deutlich tiefer ausgeprägt ist.
Fall c) gilt für den Neigungswinkel 60 Grad. Der Polarkreis liegt dann bei 30 Grad, und das bedeutet, dass wir in Deutschland bereits Mitternachtssonne und Polarnacht erleben.
Fall d) gilt für den Neigungswinkel 90 Grad. Zur Sommersonnenwende zeigt die Erdachse also genau in Richtung Sonne, die Sonne steht über dem Nordpol, die höchsten Temperaturen treten auf. Beachte: auf der weiteren Umlaufbahn der Erde bleibt die Erdachse raumfest liegen! Das bedeutet: bei Herbstanfang liegt sie (ebenso wie bei Frühlingsanfang) tangential zur Erdbahn, und die Sonne steht nicht über dem Pol, sondern wandert über den Äquator. Beide Pole liegen auf der Grenze der beschienenen Erdhälfte. Im weiteren Verlauf wandert der Nordpol in die Polarnacht und der Südpol in die Mitternachtssonne. Auch die polnahen Gebiete der Nordhalbkugel erfahren eine Polarnacht.
Insgesamt fällt auf, dass die Stellung der Erdachse Einfluss auf die Höchsttemperatur im Sommer hat. Diese steigt, je größer der Neigungswinkel ist, weil dann die Sonne immer steiler über dem Horizont steht.
Dies kann jedoch nicht darüber hinwegtäuschen, dass die Minimaltemperatur im Winter immer tiefer fällt und damit die Jahresmitteltemperatur nach unten zieht, je schräger die Erdachse liegt.
Das Temperaturniveau liegt in allen Fällen sehr tief und selbst bei Neigungswinkel 0 Grad unterhalb der Null-Grad-Celsius-Marke. Dies soll zum Anlass genommen werden, Mitteltemperaturen näher zu untersuchen.
3. Extremal- und Mitteltemperaturen
Wir werfen einen Blick auf die mit dem Jahresgang verbundenen Maximal-, Minimal- und Mitteltemperaturen und beginnen wieder mit der Achsneigung 23.45 Grad aus Abb. 1. Ergebnisse siehe Tabelle 1 (gerundete Werte).
| Extremale und mittlere Breitengrad-Temperaturen [K] | ||||
| bei Neigung der Erdachse um 23,45 Grad | ||||
| Breitengrad: | 30 | 50 | 70 | 90 |
| Maximum | 283 | 284 | 286 | 290 |
| Minimum | 231 | 181 | 0 | 0 |
| Jahresmittel | 261 | 239 | 177 | 124 |
Tabelle 1
Die sommerlichen Maximalwerte nehmen mit dem Breitengrad etwas zu (von 10 auf 17 oC). Dies liegt daran, dass die Dauer der Nachtzeit abnimmt.
Die Jahresmittelwerte werden jedoch durch die winterlichen Minima umso mehr in die Tiefe gezogen, je weiter man nach Norden kommt. Sie liegen in der Tabelle zwischen -12 und -149 oC, auf dem 50. Breitengrad bereits bei ungemütlichen -36 oC. Es ist offensichtlich, dass wir hiermit weit entfernt sind von den realen Gegebenheiten, die wir kennen.
Angelehnt an Abb. 2 betrachten wir nun die Temperaturen in Abhängigkeit von der Neigung der Erdachse:
| Extremale und mittlere Breitengrad-Temperaturen [K] | ||||
| am 50. Breitengrad | ||||
| Achsneigung: | 0 | 30 | 60 | 90 |
| Maximum | 246 | 293 | 330 | 352 |
| Minimum | 246 | 151 | 0 | 0 |
| Jahresmittel | 246 | 235 | 198 | 194 |
Tabelle 2
Man erkennt einen Anstieg der sommerlichen Höchsttemperatur mit wachsender Achsneigung, was auf den immer steileren Sonnenstand und die zunehmende Sonnenscheindauer zurückzuführen ist. Der Bereich erstreckt sich von -27 bis +79 oC.
Aber auch hier zieht die zunehmende Nachtperiode die Jahres-Mitteltemperatur nach unten, der Bereich geht von -27 bis auf -79 oC.
Haben wir bisher breitenkreisspezifische Temperaturen und zusätzlich deren zeitliche Mittelung übers Jahr betrachtet, so wollen wir uns nun an eine räumliche Mittelung über die gesamte Oberfläche wagen. Diese lässt sich hier am Modell, im Gegensatz zur realen Erde, rechnerisch exakt durchführen. Exemplarisch zeigen wir den Jahresverlauf der globalen Mitteltemperatur am 50. Breitengrad für verschiedene Achsneigungen:
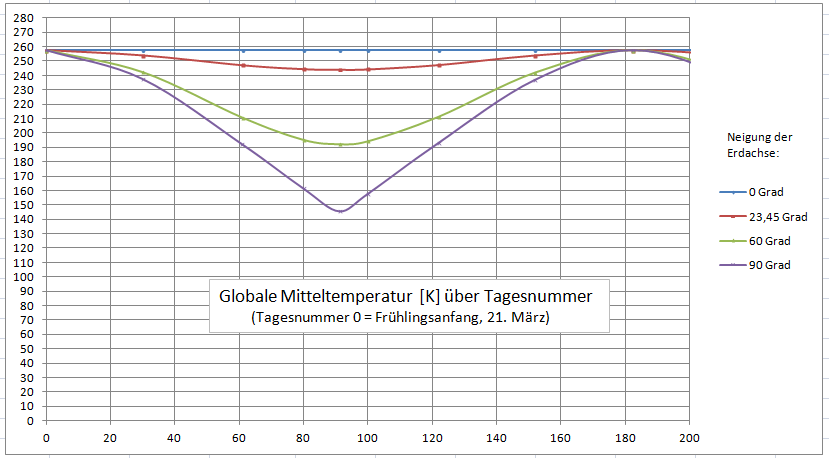
Abb.3: Halbjahresverlauf der globalen Mitteltemperatur am 50. Breitengrad
Bei Abb. 3 ist zu beachten, dass sie nur den Verlauf über ein halbes Jahr zeigt! Das nächste Halbjahr verläuft aus Symmetriegründen exakt genauso, wobei nur die Rolle von Nord- und Südhalbkugel vertauscht sind. Die x-Achse zeigt wieder die Tagesnummer, beginnend bei 0 (Frühlingsanfang) bis zur Tagesnummer 200, wobei das Halbjahr bei Nummer 182,5 (Herbstanfang) abgeschlossen ist.
Zunächst ist bemerkenswert, daß die Globaltemperatur überhaupt einen Jahresverlauf zeigt. Dieser ist besonders ausgeprägt bei 90 Grad Achsneigung und soll nun diskutiert werden. An den Äquinoktien (Frühlings- und Herbstanfang) ist die Globaltemperatur am höchsten und unabhängig von der Achsneigung. Die Sonne hat dann ihren Höchstand zur Mittagszeit senkrecht über dem Äquator, und kein Teil der Erde bleibt im Laufe einer Umdrehung unbesonnt, mit Ausnahme der beiden Pole, die aber nur punktförmig sind.
Das andere Extrem sind die Sommer- und die Wintersonnenwende: hier liegt ein Teil der Erde in der Polarnacht, am ausgeprägtesten bei 90 Grad Achsneigung, dann nämlich eine volle Erdhälfte. Da sich in der Polarnacht die Temperatur auf dem absoluten Nullpunkt einstellt, wird der globale Mittelwert stark nach unten gezogen, wie wir das auch schon in den Abschnitten 1 und 2 festgestellt haben.
Die Extremal- und Mittelwerte zu Abb. 3 sind in Tabelle 3 zusammengestellt. Wir erkennen wieder das Fehlen von Jahreszeiten bei Senkrechtstellung der Erdachse (0 Grad Neigung). Das globale Jahresmittel liegt hier – oh Wunder – bei den altbekannten (fast) 255 K. Dass es etwas mehr als 255 K sind, liegt daran, dass wir die Erde nicht als schwarzen, sondern als dunkelgrauen Körper behandeln (s.o.).
Sobald sich die Erdachse neigt, verschlimmert sich die Situation sogar noch: bei 23,45 Grad Neigung haben wir nur noch 250 K oder -23 oC Mitteltemperatur, und das senkt sich bei 90 Grad Achsneigung bis auf -70 oC ab.
| Globale Mitteltemperatur [K] | ||||
| in Abhängigkeit von der Achsneigung | ||||
| Achsneigung: | 0 Grad | 23,45 Grad | 60 Grad | 90 Grad |
| Maximum | 257 | 257 | 257 | 257 |
| Minimum | 257 | 244 | 192 | 145 |
| Jahresmittel | 257 | 250 | 221 | 203 |
Tabelle 3
Eine andere Erkenntnis lässt sich ebenfalls aus Tabelle 3 ziehen: in all den dort aufgeführten Fällen erhält die Erde als Ganze über eine Umdrehung hinweg zweifellos die gleiche Energie von der Sonne geliefert, nämlich genau den Energiebetrag, den sie während der Umdrehungszeit auf die Tagseite einstrahlt. Trotzdem unterscheiden sich die Globaltemperaturen! Berechnet man die Mitteltemperatur einfach aus der mittleren globalen Einstrahlung, wie es oft getan wird, kommt man in all diesen Fällen auf den gleichen Wert von 257 K.
Dass der aus der Globaleinstrahlung berechnete Wert i.d.R. nicht zutreffend ist – außer im Spezialfall senkrecht stehender Erdachse – liegt an der T-hoch-4-Abhängigkeit des Stefan-Boltzmann-Gesetzes. Dieser nichtlineare Zusammenhang hat zur Folge, dass es einen Unterschied macht, ob man wie hier Einzeltemperaturen berechnet und direkt über diese mittelt, oder ob man über die Einstrahlung mittelt und daraus eine Temperatur berechnet.
Der Fehler, den man mit letzterem Vorgehen macht, lässt sich anhand der Tabelle 3 quantifizieren: bei unserer Achsneigung von 23,45 Grad beträgt er +7 K oder, relativ ausgedrückt: 7/273 = 2,5 %.
Bei 90 Grad Achsneigung beträgt der Fehler (257 – 203) K = 54 K oder 54/273 = 19,9 %. Er ist deswegen größer, weil auch die Temperaturspanne, über die gemittelt wird, größer ist (vgl. Abb 1 b mit Abb. 3 c).
Zusammenfassung und Diskussion
Wir haben die Temperaturen untersucht, die sich auf der Erdoberfläche einstellen, wenn wir alle sekundären Einflußfaktoren ausschalten und uns allein auf die Sonne als primäre Energiequelle und das Strahlungsgleichgewicht der Erde mit ihr bzw. dem Weltall konzentrieren.
Zusammenfassend fällt dabei ins Auge, dass die Oberflächentemperaturen, die uns die Sonne unter diesen Umständen spendieren kann, weit unter dem Temperaturniveau liegen, welches wir real auf unserer Erde vorfinden! In Deutschland würden selbst im Hochsommer maximal nur rund 10 oC erreicht. Das liegt daran, dass wir in unserem Modell eine ungehinderte Abstrahlung ins Weltall haben und keinerlei Puffer- und Ausgleichseffekte für die Wärme.
Daraus wird ersichtlich, welch große Rolle all die Sekundäreffekte spielen, die wir im Modell ausgeschlossen haben: an vorderer Stelle zweifellos die riesige Wärmespeicherung in den Ozeanen und die Ausgleichsprozesse durch Wärmetransport in den Meeres- und Luftströmungen. Und nicht zuletzt müssen wir der Atmosphäre eine erhebliche Schutzfunktion gegenüber der Auskühlung zugestehen. Die kann nur in einer Behinderung der Abstrahlung bestehen, die landläufig unter dem Stichwort Treibhauseffekt bekannt ist.
Oft wird dagegen eingewandt, dass der Erdboden direkt von der Sonne erwärmt wird und die kühle Atmosphäre nicht den warmen Erdboden noch weiter erwärmen könnte. Doch, sie kann! Indem sie nämlich als Hindernis für die Abstrahlung fungiert. Das lässt sich vergleichen mit dem Anziehen einer Wollmütze im Winter. Kann die kühle Wollmütze die warme Kopfhaut erwärmen? Ja, sie kann es indirekt. Die eigentliche Heizquelle für die Kopfhaut ist natürlich der warme Blutkreislauf. Aber die Wollmütze stellt ein Hindernis für die Wärmeabgabe nach draußen dar, und das beschert der Kopfhaut eine höhere Temperatur und dem Träger ein wohliges Gefühl. Anderes Beispiel: Jeder Bauphysiker weiß, dass die Außendämmung einer Hauswand bei gegebener Heizleistung im Inneren die Wandtemperatur anhebt.
Auf die einzelnen Mechanismen des Treibhauseffektes und die beteiligten atmosphärischen Komponenten einzugehen, lag nicht in der Zielsetzung dieser Arbeit. Insbesondere die Rolle des CO2 wird nicht behandelt. Als gute Quelle hierfür lässt sich der Vortrag von Prof. Ganteför heranziehen, der kürzlich von EIKE präsentiert wurde: https://eike-klima-energie.eu/2024/02/24/treibhauseffekt-und-waermestau-auf-der-erde/
Bei der Untersuchung hat sich gezeigt, dass die Neigung der Erdachse ebenfalls die Oberflächen-Temperaturen beeinflusst, und zwar sowohl den Jahresverlauf als auch den Mittelwert.
Nachbemerkung
Schließlich noch eine allgemeine Bemerkung zur Temperaturmittelung: es wurde hoffentlich klar, dass dieses Verfahren seine Berechtigung hat. In Deutschland leben wir auf mittleren Breiten in einer gemäßigten Klimazone. Wir haben ein allgemeines Temperaturniveau von geschätzt etwa 10 oC, um das sich die tatsächlichen Temperaturen übers Jahr gruppieren. Man bemerke, dass insoweit noch nicht von Mittelung die Rede ist (auch wenn Meteorologen einen auf Messreihen beruhenden Mittelwert nennen, der nicht weit von diesen 10 oC entfernt ist). Vergleicht man nun dieses Temperaturniveau mit dem breitengradtypischen Mittelwert von 239 K oder -34 oC aus unserem Modell (Tabelle 1), so sollte auch dem hartgesottensten Mittelungsskeptiker einleuchten, dass diesem Parameter eine Aussagekraft zukommt. Im vorliegenden Fall die, dass das Modell nicht die Realität beschreibt.
Im Prinzip ist der Parameter auch zur Beurteilung von IPCC-Modellen brauchbar, wenn sich eine Möglichkeit findet, deren Ergebnisse mit der Empirie abzugleichen.
Anhang: Berechnungsmethode
Grundlage für die Berechnung der Temperatur im Strahlungsgleichgewicht ist die an der Oberfläche absorbierte Energie-Flussdichte , auch Intensität genannt und meist in W/m² angegeben. Deren Wert für senkrechte Einstrahlung haben wir mit max = 953 W/m² angesetzt. Bei Schrägeinstrahlung unter dem Winkel h erhält man
= max * sin(h). h ist eine Koordinate im Horizontsystem und wird auch als Elevation der Sonne bezeichnet.
Zur Erklärung astronomischer Koordinaten sei auf die Fachliteratur verwiesen, s. z.B. die Quellenangaben.
Die Bestimmung von h im Jahres- und Tagesverlauf gelingt durch Rückgriff auf das ruhend-äquatoriale Koordinatensystem (, t). Dafür gibt es die grundlegende Gleichung [1], [2]
sin(h) = sin() * sin() + cos() * cos() * cos(t). ()
ist der betrachtete Breitengrad, die ruhend-äquatorialen Koordinaten sind und t, also Deklination und Stundenwinkel der Sonne. Alle Winkel sind im Bogenmaß zu verstehen.
sin wiederum hängt von der Position der Erde auf ihrer Umlaufbahn (hier: Kreisbahn) ab. Numeriert man die Tage ab Frühlingsanfang mit der Tagesnummer TNR, dann ist der zugehörige Ekliptikwinkel der Erde auf ihrer Kreisbahn, von der Sonne aus betrachtet, = TNR/365 * 2. Damit und mit dem Neigungswinkel der Erdachse gegen die Erdbahnebene (Schiefe der Ekliptik) erhält man sin() = sin() *sin() [3].
Um die mittlere Intensität auf Breitengrad am Tag TNR zu bestimmen, muss man (h) unter Einsetzen von Gleichung () über eine Erdumdrehung integrieren und das Ergebnis auf die zu gehörige Ringfläche verteilen. Für die Integrationsgrenzen wird der Stundenwinkel t0 der Sonne bei Sonnenaufgang benötigt.
Bei der Bestimmung von t0 ist eine Fallunterscheidung erforderlich: man erhält t0 durch Nullsetzen von Gleichung () für Breitengrade unterhalb der Polarregion, wo weder Mitternachtssonne noch Polarnacht herrschen. Der Grenzbreitengrad, der die Polarregion vom Rest abtrennt, hängt natürlich vom Datum ab und bestimmt sich zu grenz = /2 – ||. Oberhalb grenz ist t0 = zu setzen.
Die zu gehörige Gleichgewichtstemperatur berechnet man schließlich nach Stefan-Boltzmann zu
T = ( / ( * ))^0.25. Für einen schwarzen Körper wäre die Emissivität = 1, wir haben uns aber für den Wert 0,95 entschieden. = 5,67E-8 W / (m² * K4) ist die Stefan-Boltzmann-Konstante.
Für die Jahresgänge der Abb. 1 und 2 wurden nach diesem Schema die täglichen Temperaturen über ein Jahr berechnet. Hierfür wurde die Mathematik-Software Mathcad 2000 Professional verwendet.
Die Globaltemperatur-Kurven der Abb. 3 wurden mit Hilfe von Microsoft EXCEL gewonnen, indem für eine Anzahl von Stütztagen die Gleichgewichts-Temperatur aller Breitenkreise mit Schrittweite 1 Breitengrad berechnet und daraus der Mittelwert gebildet wurde. Die dargestellten Kurven sind zwischen den Stütztagen interpoliert. Die globalen Mittelwerte aus Tabelle 3 wurden näherungsweise ebenfalls mittels Stütztagen abgeschätzt.
Quellen
[1] Keller, H.-U.: Astrowissen, Stuttgart 1994
[2] https://de.wikipedia.org/wiki/Astronomische_Koordinatensysteme
[3] E. Boeker, R. v. Grondelle: Physik und Umwelt, Braunschweig 1997

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"@Manfred Bergmann am 16. März 2024 um 1:14
Sehr geehrter Herr MechtelFür die Erde funktioniert Ihr Modell tatsächlich sehr gut, (egal was H. Kramm behauptet,) aber der Mond dreht sich in der Tat so langsam, dass die Temperaturunterschiede von Tag und Nachtseite über die T^4 Beziehung den Temperaturmittelwert am Ende deutlich verfälschen würden.
Herr Bergmann gehen Sie zurueck zur Schule, denn was Sie behaupten, ist vollkommen falsch.
Für Neuleser der Hinweis: eine lesbare Version von
findet sich weiter unten im Kommentarbereich (Datum 3. März um 17:56).
Zweitens ist in der Bildunterschrift zu
der Zusatz „am 50. Breitengrad“ zu streichen. Bitte um Nachsicht für die Versehen!
@ Mechtel
Sie schrieben:
„Grundlage für die Berechnung der Temperatur im Strahlungsgleichgewicht ist die an der Oberfläche absorbierte Energie-Flussdichte Φ, auch Intensität genannt und meist in W/m² angegeben.“
Das ist barer Unsinn. Die Energieflussdichte der Strahlung unterscheidet sich von der Intensitaet folgendermassen (z.B. Chandrasekhar, 1960, Liou, 2002):
Φ = π I
Sie schrieben weiterhin:
„Um die mittlere Intensität Phimittel auf Breitengrad BREIT am Tag TNR zu bestimmen, muss man Phi(h) unter Einsetzen von Gleichung (*) über eine Erdumdrehung integrieren und das Ergebnis auf die zu BREIT gehörige Ringfläche verteilen. Für die Integrationsgrenzen wird der Stundenwinkel t0 der Sonne bei Sonnenaufgang benötigt.“
Die Integration der lokalen solaren Einstrahlung,
Φ = (r0/r)² S (sin φ sin δ + cos φ cos δ cos h) ,
erfolgt ueber die Zeitspanne zwischen lokalem Sonnenaufgang und lokalem SonnenUuntergang, was dem Tagesbogen 2 H entspricht, wobei H der halbe Tagesbogen ist. Hierin sind r und r0 die heliozentrische und dei mittlere heliozentrische Entfernung, S = 1361 W/m² die Solarkonstante, φ der Breitengrad, δ die Deklination der Sonne und h der Stundenwinkel, der ab dem lokalen solaren Mittag berechnet wird.
Zur Integration ist der Stundenwinkel durch die Zeit oder die Zeit durch den Stundenwinkel zu ersetzen, was ueblicherweise vorgenommen wird. Die Loesung lautet:
W = (r0/r)² (d/π) S (H sin φ sin δ + cos φ cos δ sin H) ,
wobei d der Tag ist. Dieses Ergebnis ist seit Wiener (1877, 1879) im deutschsprachigen Bereich bekannt. Das Ergebnis wurde in der Fachliteratur vielfach ueberprueft.
Sie schrieben weiterhin:
„Bei der Bestimmung von t0 ist eine Fallunterscheidung erforderlich: man erhält t0 durch Nullsetzen von Gleichung (*) für Breitengrade unterhalb der Polarregion, wo weder Mitternachtssonne noch Polarnacht herrschen. Der Grenzbreitengrad, der die Polarregion vom Rest abtrennt, hängt natürlich vom Datum ab und bestimmt sich zu BRgrenz = Pi/2 – |delta|. Oberhalb BRgrenz ist t0 = Pi zu setzen.“
Das geht auf Wiener (1877, 1879) zurueck und ist korrekt Aber fuer die Aequinoktien (δ = 0) spielt das keine Rolle. Man erhaelt naemlich:
W = (r0/re)² (d/π) S cos φ ,
wobei re der heliozentrische Abstand zum jeweiligen Aequinoktium ist. Das waere also kein Problem.
Sie schrieben weiterhin:
„Die zu Phimittel gehörige Gleichgewichtstemperatur berechnet man schließlich nach Stefan-Boltzmann zu T = (Phimittel / (epsilon * sigma))^0.25. Für einen schwarzen Körper wäre die Emissivität epsilon = 1, wir haben uns aber für den Wert 0,95 entschieden. sigma = 5,67E-8 W / (m² * K4) ist die Stefan-Boltzmann-Konstante.“
Und genau das ist vollkommen falsch. Sie haben die Arbeit von Gerlich & Tscheuschner (2009), auf die sie sich berufen, ueberhaupt nicht verstanden. Was Sie treiben, ist genauso falsch wie das Vorgehen, aus dem globalen Mittel eine Temperatur mit dem Stefan-Boltzmann-Gesetz zu berechnen.
Im Falle des Ansatzes des lokalen Strahlungsgleichgewichtes,
(1 – α) Φ = ε σ Teq^4
muss zuerst die Temperatur des lokalen Strahlungsgleichgewichtes bestimmt werden, d.h.:
Teq = ((1 – α) Φ/(ε σ))¼
Hierin sind α die Albedo im solaren Bereich.
Damit ergibt sich die Verteilung der Temperatur des lokalen Strahlungsgleichgewichtes. Und ueber diese Verteilung wird dann global gemittelt. Das koennen bei Gerlich & Tscheuschner (2009), Unterkapitel ‚3.7.4. The average temperature of a radiation-exposed globe‘ nachlesen. Im Gegensatz zu Gerlich & Tscheuschner haben Kramm et al. (2017) nicht nur die Rotation der Erde, sondern auch die Schiefe der Rotation beruecksichtigt und so das Ergebnis von Gerlich & Tscheuschner fuer das lokale Strahlungsgleichgewicht naeherunsweise bestaetigt.
Selbstverstaendlich muss die Wirkung des Regolith beruecksichtigt werden, worauf Gerlich & Tscheuschner bereits hinwiesen.
@Gerhard Kramm am 17. März 2024 um 4:30 und am 15. März 2024 um 19:12
Leider ist Ihre Kritik sehr harsch und in weiten Teilen nicht sachgerecht. Wenn Sie z.B. die Gleichsetzung von Energieflussdichte und Intensität als ‚baren Unsinn‘ bezeichnen, ist das ziemlich dick aufgetragen! Fakt ist: die Nomenklatur ist in diesem Punkt keineswegs einheitlich. Wenigstens scheinen wir uns beim Begriff Flussdichte einig zu sein.
Des weiteren kritisieren Sie die von mir verwendete Stefan-Boltzmann-Formel als ‚vollkommen falsch‘. Das ist absurd, zumal Sie selber die gleiche Formel in der Schreibweise Teq = ((1 – α) Φ/(ε σ))¼ anbieten! Vermutlich haben Sie übersehen, dass mein Phimittel die absorbierte, nicht die eingestrahlte Flussdichte ist und somit den Faktor (1-α) bereits enthält:
es gilt Phimittel = (1 – α) Φ. Evtl. stören Sie sich an der Bezeichnung Phimittel, weil Sie eine lokale statt einer gemittelten Flussdichte möchten. Sie übersehen dabei offenbar, dass bei der schnellen Rotation meiner Kugel die Energie sich sehr gleichmäßig über den Breitenkreis ausschmiert. Die ermittelte Flussdichte gilt also in guter Näherung lokal auf dem gesamten Breitenkreis, und daraus ergibt sich dann automatisch eine lokale Temperatur.
Übrigens habe ich mich entgegen Ihrer Aussage nirgends auf Gerlich & Tscheuschner berufen. Meine Quellen und Hilfsmittel habe ich alle angegeben.
In diesem Zusammenhang greife ich gern noch Ihre abgespeckte Bilanzgleichung (2) vom 15.03.2024 auf, um mein Rotationsmodell zu präzisieren:
R dT/dt = (1 – α) FS↓ – ε σ T^4
Während einer Eigenrotation seien sowohl FS↓ als auch T^4 näherungsweise konstant. Das Zeitintervall hängt mit der Rotationsfrequenz f zusammen über Δt = 1 / f. Die Gleichung geht dann nach Umstellung über in die Form
ΔT = {(1 – α) FS↓ – ε σ T^4} /(f R).
Nach dem Gesagten ist die Bedingung ΔT ≈ 0 zu erfüllen. Dies wird erreicht mit
f >> {(1 – α) FS↓} / R UND f >> ε σ T^4 / R (logisches UND).
Gleichung (2) zeigt auch, warum es sinnvoll war, mein Modell so wählen, wie ich es getan habe. Bei lokalem Strahlungsgleichgewicht ist nämlich die rechte Seite Null. Damit wird auch dT/dt = 0, und auf R kommt es dann nicht an. Genau das war meine Überlegung. Die Beschäftigung mit komplizierteren Szenarien (z.B. auch Gleichung (3)) überlasse ich gern den Experten, die dafür bezahlt werden.
Wie ich Ihrem Text entnehme, haben Sie auch schon selber solche Szenarien durchgerechnet. Warum verlangen Sie dann von mir, dass ich nochmals das gleiche mache?
Zum Thema Integration der solaren Einstrahlung kann ich keine grundsätzliche Diskrepanz zu meiner Rechnung feststellen. Zu bemerken wäre lediglich, dass ich (r0/r) = 1 gesetzt habe.
„Es ist geradezu laecherlich, mir erzaehlen zu wollen, dass waehrend der Nacht kein Strahlungsgleichgewicht existiert. Dieser Sachverhalt ist im Falle des Mondes seit Wesseling (1948) bekannt ...“
Unter Strahlungsgleichgewicht verstehe ich Einstrahlung = Ausstrahlung. Wie das in der Erdnacht funktionieren soll, müssten Sie oder Herr Wesseling mir erklären. Selbst beim Mond erscheint mir das nicht glaubhaft. Der ist allerdings das denkbar ungeeignetste Vergleichsobjekt für mein Modell.
„Haetten Sie eine solche Antwort auf eine Pruefungsfrage abgeliefert, haetten Sie ein ‚fail‘ erhalten“
Herr Kramm, ich bleibe dabei: eine Antwort sollte sich nach der gestellten Frage richten. Daran habe ich mich in meinen Prüfungen immer erfolgreich gehalten.
Hallo Herr Bergmann,
wir beobachten die Speicherung von Wärme vom Tag in die Nacht. Das versuchen einige Modell hier abzubilden. Mit der spezifischen Wärmekapazität cp [J/(Kelvin kg)] mal Dichte ρ [kg/m³] mal Volumen V [m³] ergibt sich die Wärmekapazität C [J/Kelvin] bei aus den von Ihnen angegebenen Werten (siehe Bergmann am 05. März 2024 um 12:54 Uhr hier im Kommentarbereich) dann ein C = 1.6 x 1000 J/(Kelvin kg) x 3300 kg/m³ x 1m x 1m x 0.2 m = 1.056.000 J/Kelvin. Folgt die Speicherung vom Tag in die Nacht über 12 Stunden folgt für die Wärmeleitfähigkeit λ:
λ [W/(Kelvin m)] = C [J/Kelvin] x Eindringtiefe [m] / ( Kontaktfläche [m²] x t [sec] = 1.056.000 J/Kelvin x 0.2 m / ( 1m x 1m x 12 x 60 x 60 sec ) = 4.89 W / (Kelvin m)
(Ich halte Ihren Wert von 4.89 in Ihrem Modell für plausibel. Rechnet man ein cp aus 70% Wasser und 30% Sedimentgestein mit ρ = 2600 kg/m³ für gemittelte Ersatzverhältnisse einer Modellerde erhalte ich ein λ von 4.36 W/(K m) .) Ihre Modellerde hätte Erdeigenschaften.
Setzt man als Unterschied ∆ T zwischen Tag und Nachttemperatur 14 Grad Celsius lokal für den Transport vom Tag auf die Nachtseite, stellt sich die Frage:
Welcher Wärmestrom qz [W/m²] wirkt hierfür lokal aus der Eindringtiefe z (m) für globale mittlere Modell Materialeigenschaften und wie ist dieser zu interpretieren?
qz [W/m²] = λ [W/(Kelvin m)] x ∆ T (Kelvin) / z (m) = 4.89 W/(Kelvin m) x 14 K / 0.2 m = 342 W/m²
Messungen begrenzen den Wärmestrom aus reiner Leitung im globalen Mittel auf rund 91,6 Milliwatt/m². Würde eine Wärmeleitung 4.89 W/(Kelvin m) das Eindringen der Strahlung in Materie als auch die Strahlungsabgabe aus Materie in irgendeiner Weise behindern, wäre eine Wärmespeicherung vom Tag in die Nacht bei obigen Materialeigenschaften grundsätzlich nicht möglich.
qz Gesamt = qz Wärmeleitung [W/m²] + qz Strahlungsabgabe durch das Material [W/m²] = 0.1 W/m² + 341.9 W/m²
Wärmeleitung bei den oben angesetzten Materialeigenschaft begrenzt die Strahlungsdurchdringung dieses Materials damit nicht. Wärmeleitung und Strahlungsdurchdringung sind bei diesen Materialeigenschaften voneinander unabhängige Wege der Abgabe des Energietransportes durch Materie.
Prof. Gerlich und Dr. Tscheuschner, 2015, in Kap 3.8 „In vielen klimatologischen Texten wird impliziert, dass die Wärmestrahlung nicht berücksichtigt werden muss, wenn man die Wärmeleitung betrachtet, was nicht richtig ist.“
Deshalb kann auch eine Strahlung zwischen 250 W/m² und 300 W/m², die kleiner ist als 342 W/m² das gesamte Material mit diesen physikalischen Parametern durchdringen. Vielfältige Argumente sprechen gegen die Treibhaushypothese. Gibt es keinen THE, dann erklärt ein Hemisphären-Modell mit radiogener Tiefenwärme zwischen 250 bis 272 W/m² vollständig die durch Thermometermessung beobachteten, Tag – und Nachttemperaturen auf den Breitenkreisen der Erde, siehe (hier).
Herr „Agerius“, radiogene Tiefenwärme zwischen 250 bis 272 W/m² würde natürlich den THE erstzen und wäre phantastisch für Wärmepumpen. Aber leider irren Sie gewaltig, denn der Erdwärmestrom beträgt nur etwa 50 mW/m² (!!), was nach S-B vernachlässigbare 0,009 Grad bringt. Wenn man ½ Jahr lang aus Tiefbohrungen z.B. 5 kW zum Heizen entnehmen will, benötigt man ein Grundstück von 50.000 m².
Hallo Herr Dietze,
50 milliWatt/m² sind meiner Meinung nach nicht zutreffend:
zu den theoretischen Grundlagen:
Der Wärmestrom aus dem Durchschnitt von 38.347 Messungen weltweit, vgl. Prof. Christoph Clauser, 2. Auflage 2015, Geophysik – Globale physikalische Felder und Prozesse in der Erde, Springer Verlag, S. 268, beträgt 91,6 milliWatt/m² und nicht 50milliWatt/m².
Aus obiger Quelle, S. 270 Kap. 6.3 Zitat: „Erzeugung, Speicherung und Transport von Wärme in der festen Erde werden durch eine Diffusions-Advektionsgleichung mit Quellterm beschrieben.“ Dies ist Tensorgleichung (6.46) mit mehreren Komponenten. Hierin addieren sich zum Diffusionsanteil, der die Wärmeleitungskomponente λ beinhaltet, ein zweiter Advektionsanteil und addiert sich ein dritter Wärmeproduktionssanteil, der den radiogenen Anteil beschreibt. Aus diesem Tensor folgt für die z– Richtung dann qz = qz Wärmeleitung [W/m²] + qz Strahlungsabgabe durch das Material [W/m²]
Zum meinem Modell, das dies dann umsetzt, Quelle hatte ich angegeben, S. 240:
Einstrahlung 1368 W/m², Albedoabzug mit 5-jährigen ERBS-Satellitenwert a = 0,269 und kleiner Abzug für Satm (Aerosole, Staubpartikel) folgt bei Ansatz von 250 W/m² radiogener Abstrahlung und bei Ansatz von Speicherung von Tag in die Nacht und mit Werten in W/m²:
Taghemisphäre 564/2 + 250 (radiogen) – 100 (LH) -17 (SH) = 415 oder ~ +19.3 °C
Nachthemisphäre 400/2 + 250 (radiogen) – 69 (LH) -17 (SH) = 364 0der ~ + 9.9 °C
SH und LH im Mittel 84.5 17 zusammen ~ 102
(zum Vergleich KT97 78 24 zusammen = 102)
Bleibt im Modell (in einer rein theoretischen Variante) die Albedo unverändert und fallen zudem SH und LH weg, was ergäbe im Mittel für diese Modellkugel dann für einen Vergleich mit anderen Modellen?
½ ( 564/2 + 400/2) = 241 W/m² oder ~ – 18 °C
Kontinuierliche Wärmeabgabe von 250 W/m² ~ aus dem Erdinneren schafft – 16 °C. Über Jahrmillionen hat die Wärme der Sonne die Tiefenwärme an der Oberfläche der Kruste sehr langsam überlagert. Dieses Modell erklärt die beobachtete Temperaturen an der Erde ohne THE. (415 + 364) / 2 = 389.5 W/m² ~ 14.7 °C als rein theoretische Modelltemperatur im rechnerischen Mittel beider Modellhemisphären.
50.000 m² sind Ihre Polemik, haben aber nichts mit der Realität bzw. der Praxis zu tun.
Zu Praxis der Bemessung von Erdwärme-Flächenkollektoren:
Eine Wärmepumpe habe eine Heizleistung von 9 KW. Die elektrische Leistungsaufnahme P sei 2 KW. Kälteentzugsleistung (KW) über Erdkollektoren = Q – P = 9 KW – 2KW = 7 KW. Der Boden ist bindig. Es dürfen dann 40 W/m² dem Boden entzogen werden, gemäß den anerkannten Regeln der Technik bzw. dem Verein deutscher Ingenieure .
Kollektorfläche = Kälteentzugsleistung in W / Entzugsleistung in W/m² = 7000 W / 40 W/m² = 175 m²
Für den Abstand der Kollektorrohre werden 85 cm veranschlagt. Rohrlänge = Kollektorfläche in m² / Abstand in m = 175 m² / 0.85 m = 206 m.
Herr „Agerius“, das Bayerische Landesamt für Umwelt (https://www.lfu.bayern.de) sagt zu Erdwärme, der Energiequelle aus der Tiefe: Dieser geothermische Wärmefluss beträgt in Bayern rund 60 bis 80 Milliwatt pro Quadratmeter.
Bei dem Waermestrom aus Ozeanen und Oberflaeche muss man zusaetzlich noch die tagsueber eingelagerte Waerme hinzufuegen. Da die Erde im Durchschnitt 480 W/m2 auf der Tagseite erhaelt aber nur 240 W/m2 abstrahlt, kommen zum Erdwaermestrom noch 240 W/m2 hinzu, die als Waerme in der Nacht abgestrahlt oder abgefuehrt werden kann.
Herr Schultz, nun schlägt’s aber Dreizehn! Auch Sie wenden S-B falsch an. Bei Uli Weber erhält doch die ruhende (!) Tagseite auf 2PiR² dauernd 480 W/m, was im Gleichgewicht nach S-B korrekt +15 Grad Mittelwert erzeugt (siehe auch Prof. Gerlich). Dabei werden aber die 480 W/m² auch wieder abgestrahlt. Der Erdwärmestrom aus der Tiefe ist vernachlässigbar und die Nachtseite nimmt 0 K an. Falls die Tagseite (zugunsten der Nachtseite) nur die Hälfte abstrahlen würde, so wäre deren Mittelwert nur 288/2^0,25=242,2 K (-30,8 Grad). Und diesen Temperaturmittelwert würde auch die Nachtseite annnehmen wenn die Tagseite (wie bei Ihnen und Uli Weber) dorthin rotiert wird.
Herr Dietze, ich wende SB gar nicht an. Aber wenn sie 480 W/m2 einer Temperatur von 15 Grad C zuordnen, welche Emmissionszahl nehmen sie dann und warum?
Wenn ich das nachrechne, was sie auch tun sollten, dann it bei einer Emmissinszahl von 1 die Temperatur um die 30 Grad C und nicht 15 Grad C. Das ist witzigerweise das doppelte von 15 Grad C auf der Tagseite.
Vielleicht wissen sie ja warum es nicht im Durchschnitt so warm auf der Tagseite ist, wie es SB angeben wuerde.
Vielleicht hat ja die Spezifische Waermekapazitaet von Wasser was damit zu tun und der Umstand, das 70 % der Erde von Wasser beddeckt ist.
Werner Schulz am 15. März 2024 um 3:26
Sie können bei Herrn Weber doch nachlesen, wie er auf der Tagseite auf 15°C kommt. Das ist die einzige Stelle, die man in seinen Artikeln nachvollziehen kann. Und Herr Dietze bezieht sich genau auf diesen Wert.
Sie berechnen das mit einer gleichmäßig verteilten Temperatur und nicht wie Herr Weber mit einem lokalen Strahlungsgleichgewicht.
Das wissen alle, die sich auch nur ein wenig für das Thema interessieren. Die Ursache ist die T^4-Abhängigkeit der Abstrahlung von der Temperatur, die bei einer nicht gleichmäßigen Temperatur zu einer niedrigeren mittleren Temperatur führt. Könnten Sie auch bei Gerlich und Tscheuschner nachlesen …
Hallo Herr Schulz,
ausgehend vom Äquinoktium, rechnet man (nach Albedoabzug und kleinem Satmabzug für Aerosole bzw. Staubpartikel) 964 W/m²/ 2 erhält man 482 W/m2 ~ 480 W/m².
Ich habe festgestellt, wenn man über jeden einzelnen Breitengrad rechnet, die Albedo gemäß Satellitenmessung ausdifferenziert und SH und LH ebenso ausdifferenziert und hierbei gleichzeitig den jeweiligen Einfallswinkel der Sonne mitberücksichtig, dass auf der Taghemisphäre sofort 58.5 % abgestrahlt werden. Gespeichert werden 41.5 % vom Tag in die Nachthemisphäre. Wenn man dies so macht und hierbei eine radiogene Abstrahlung ansetzt, erhält man alle auf den Breitenkreisen beobachteten Temperaturen.
Dies zu den weiter oben angeführten Werten:
Tagseite: 964 W/m² x 0585 = 564 W/m² , sofort abgestrahlt und bezogen auf eine Hemisphäre = 282 W/m² , zu zuzüglich
In die Nachtseite gespeichert 964 W/m² x 41.5 % = 400 W/m² und bezogen auf eine Hemisphäre = 200 W/m²
Der THE ist unnötig. Wir benötigen weitere Beweise, die den THE seiner Unmöglichkeit überführen.
Hallo Herr Agerius,
ihre Berechnung sollte ungeffaehr der Differenz der gemittelten Tag und Nachttemperaur entsprechen.
Tags ist es eben waermer und nachts kaelter!
Meine Rechnung ist da eher grob angelegt.
Danke fuer die Verfeinerung.
@Agerius
Was nicht zutreffend ist, sind Ihre Behauptungen. Der Waermefluss aus dem Innern der Erde ist in einer Tiefe von 10 m oder so vernachlaessigbar.
Hallo Herr Prof. Kramm,
sind Sie der Ansicht, dass an der Grenzfläche zwischen Erdoberfläche und Atmosphäre (surface) eine aus der Atmosphäre nach unten gerichtete Gegenstrahlung, oft auch als back radiation bezeichnet, die lokale, örtliche Temperatur dieser Grenzfläche (surface) mitverursacht?
@Agerius
Offensichtlich existiert fuer Sie die Fachliteratur nicht, denn sonst wuerde sich die Frage eruebrigen. Selbstversaendlich ist die atmosphaerische Gegenstrahlung bei der lokalen Bilanzierung der Gesamtenergie zu beruecksichtigen, wie sie fuer eine duenne Schicht des Wassers bzw. des Bodens vorzunehmen ist, die nach aussen hin durch die Oberflaeche begrenzt wird. Wenn man von einem unbewachsenen ebenen Erdboden ausgeht, dann lautet diese lokale Bilanzgleichung
R dTs/dt = (1 – α) G↓ + ε F↓ – ε σ Ts^4 – Ha – Ea – Hsl
Hierin sind R = ρ c D der thermische Inertialkoeffizient (wobei ρ die Dichte, c die spezifische Waerme und D die Dicke der Bodenschicht Schicht sind), Ts die die Temperatur der Schicht, t die Zeit, G die Globalstrahlung, die die direkte und die diffuse Komponenten der solaren Strahlung umfasst, α die Albedo im solaren Bereich, ε das relative Emissionsvermoegen, σ die Stefansche Konstante, Ha und Ea die Flussdichten von sensibler und latenter Waerme in der oberflachennahen Luftschicht und Hsl die Waermeflussdichte, die den Austausch von Waerme zwischen der duennen Deckschicht und den tieferen Bodenschichten bewirkt. Im Falle von Wasser ist Hsl durch das Analogon im Wasser zu ersetzen, wobei hinzukommt, dass die Stroemung des Wassers zu beruecksichtigen ist. Selbstverstaendlich laesst sich auch die Rolle der Vegetation beruecksichtigen, einschliesslich des Wurzelwerks im Boden.
Waehrend der lokalen Nacht (G↓ = 0), aendern sich oft die Vorzeichen von Ha, Ea und Hsl, was einer Richtungsaenderung entspricht. Sind Ha und Ea aufwaertsgerichtet (meistens tagsueber), so herrscht thermische Instabilitaet vor. Waehrend der lokalen Nacht ist Ha meistens abwaertsgerichtig, was mit thermisch stabiler Schichtung einhergeht; die Wasserdampf-Flussdichte, womit Ea verknuepft ist, kann sowohl aufwaerts als auch abwaerts (Tau- oder Reifbildung) gerichtet sein.
Die Differenz ΔF = ε σ Ts^4 – ε F↓ wird auch als Netto-Strahlung im Infrarotbereich bezeichnet.
Im Falle von Stationaritaet (dTs/dt ≈ 0) ergibt sich:
(1 – α) G↓ = ΔF + Ha + Ea + Hsl
Diese Vereinfachung, in der Fachliteratur sehr bekannt und meistens verwendet (siehe Deardorff, 1978), verschleiert aber, dass es sich immer noch um eine Schicht handelt, und nicht um eine Oberflaeche. Fuer eine Oberflaeche laesst sich grundsaetzlich keine Energiebilanzgleichung formulieren, denn Energie ist eine extensive Groesse (siehe Planck, 1897, Ehrenfest, 1911, Tolman, 1917).
Eine globale Mittellung, 〈…〉, ueber diese Gleichung liefert dann
〈(1 – α) G↓〉 = 〈ΔF〉 + 〈Ha〉 + 〈Ea〉
wobei 〈Hsl〉 ≈ 0. Nach Peixoto & Oort (1992), Physics of Climate“, gelten folgende Werte
〈(1 – α) G↓〉 = 170 W/m²
〈ΔF〉 = 68 W/m²
〈Ha〉 = 20,4 W/m²
〈Ea〉 = 81,6 W/m²
Das sog. Bowen-Verhaeltnis W = 〈Ha〉/〈Ea〉 betraegt danach W = 1/4; das Erdmann-Qu-Verhaeltnis KQ = 〈ΔF〉/(〈ΔF〉 + 〈Ha〉) = 2/3 (benannt nach Kasimir E. Erdmann und Celestina T. Qu)
Wenn jemand behauptet, dass an der Grenzflaeche Erde – Atmosphaere ein Strahlungsgleichgwicht existiert, dann dokumentiert er nur, dass er die Fachliteratur nicht kennt. Ich zitiere Kiehl & Trenberth (1997):
„1.Introduction
There is a long history of attempts to construct a global annual mean surface–atmosphere energy budget for the earth. The first such budget was provided by Dines (1917).“
Unabhaengig davon, dass das nicht ganz richtig ist, denn bereits Arrhenius (1896) hatte schon einen solchen Versuch vorgenommn, sollten Sie doch eigentlich die Arbeit
Dines, W. H., 1917: The heat balance of the atmosphere. Quart. J. Roy. Meteor. Soc., 43, 151–158.
kennen (siehe https://rmets.onlinelibrary.wiley.com/doi/10.1002/qj.49704318203). Aus dieser Arbeit stammt die folgende Abbildung:
Was Sie also zu Kiehl & Trenberth (1997) formuliert haben, belegt nur, dass es vorteilhaft ist, unter einem Pseudonym zu agieren.
@Agerius
Ihr Zitat
„Prof. Gerlich und Dr. Tscheuschner, 2015, in Kap 3.8 „In vielen klimatologischen Texten wird impliziert, dass die Wärmestrahlung nicht berücksichtigt werden muss, wenn man die Wärmeleitung betrachtet, was nicht richtig ist.“
belegt, dass Sie noch nicht einmal richtig zitieren koennen. Und Ihre Kritik an Kiehl & Trenberth (1997) beruht auf einfaeltige Besserwisserei. Sie haben das physikalische Prinzip, auf der das Diagramm von Kiehl & Trenberth (1997) beruht, ueberhaupt nicht verstanden.
Ihre wissenschaftliche Darbietung ist rein nach Ihren VORSTELLUNGEN ausgerichtet. Es ist eine zielgerichtete, stark vereinfachte Modellierung, mathematisch hoch komplex unterlegt. Die Fragestellung in Ihrem Denken wird längst nicht mehr von der Möglichkeit bestimmt, ob ein Ereignis eintritt, sondern 👉DAß ‼️
Solch determiniertes Denken ist menschlich verständlich, aber wissenschaftlich betrachtet suboptimal. Im ungünstigsten Fall sogar kontraproduktiv. Vor allem ist es bereits teilweise Gepflogenheit im Wissenschaftsbetrieb. Der Promovierende formuliert die Vorstellungswelt seines Doktor-Vaters und Herr Lesch forscht im Namen des IPCCs für Klimahysterie und CO2-Ablaßwesen.
Hätte EINSTEIN nicht geistig völlig unabhängig über das Michelson-Morley- Experiment hinweg- gedacht, das Unmögliche wahrscheinlich angenommen, existierte keine Relativitätstheorie.
Sie agieren vice versa. Sie wollen ein Resultat geistiger Begrenzung, den THE, u n b e d i n g t verifizieren ; mit hochkomplexer Mathematik in einem stark vereinfachten Modell. Sie verpacken ausgesuchte Parameter, teilweise aus Durchschnittswerten zweifelhafter Provenienz, in unantastbare mathematische Gleichungen. Zum Nachrechnen. Melden Sie sich bei der Absorptionsbande. Die freuen sich über jedes Mitglied.😁👍
Sie haben jetzt Ihr Unverständnis gegenüber Modellbildungen mehrfach und, wie ich denke, ausreichend dokumentiert. Auch der Letzte wird inzwischen begriffen haben, dass Sie damit nichts anfangen können. So lange Leitungen haben die Leute nicht, dass Sie das noch unbedingt weiter dokumentieren müssten.
Wenn Sie mit dem ganzen Artikel ein Problem haben, dann lassen Sie es doch einfach auf sich beruhen und lesen etwas anderes.
M. Mechtel.
Sachlich und souverän, Herr Mechtel. Schätze, daß gibt Ihrem Beitrag den „letzten Schliff“.
Würde nicht behaupten, daß ich mit dem Artikel ein „Problem“ habe.
Sie allerdings mit Kritik.
MfG 😁✌️
Herr Mechtel,
zu welchem Schluss sind sie denn gekommen? Das ihr Model die reele Atmosphaere nicht nachbildet?
Das die alleinge Betrachtung von Strahlung die Temperaturen der Erde nicht erklaeren kann?
Ihrer Zusammenfassung kann ich nicht zustimmen.
Sie sagen:
Dazu sollten sie sich fragen wie warm es sein muss wenn 560 W/m2 von der Sonne eintreffen aber keine Wasserverdunstung oder Konvektion die Waerme abfuehrt!
Nach ihrem dafuerhalten und in ihrem Konstrukt muessten auch 560 W/m2 angestrahlt werden. Wie warm soll es im Hochsommer maximal werden?
In ihren Strahlenmodel sollten sie beruecksichtigen, das die Temperaturunterschiede noch extremer als in einem Wuestengebiet sein wuerden.
Alle diese Rechnungen sind so oder so schon da gewesen. Was fehlt ist, das jemand nicht -2.6 Grad C am Aquator ausrechnen kann oder 10 Grad im Hochsommer in Deutschland.
Was fehlt ist eine eindeutige Angabe wie denn die Wohlfuehltemperatur der Erde sein soll. Was soll die Politik mit ihrer Rechnerei anfangen? Wie soll sie ein Ziel erstellen, wenn es keine Anfangsgroesse gibt?
Ihre Rechenarbeit in Ehren, sie haben sicher viel gelernt. Aber was den Atmosphaereneffekt angeht, gibt es keine Zusatzerkenntnisse.
mfg Werner
@ Mechtel
Sie irren sich gewaltig. Eine Modellbildung, die auf der Vernachlaessigung relevanter physikalischer und astronomischer Gegebenheiten beruht, ist so ueberfluessig wie ein Buckel.
Sie schrieben:
Beschreibung des Modells
Die genannte Zielsetzung und die Begrenzung des Rechenaufwandes erfordert ein sehr vereinfachtes Modell der Erde, das selbstverständlich nicht mehr die Realität abbildet, aber sehr wohl eine Basis für das Verständnis unserer Realität abgeben kann.
Zunächst erfordert es die Begrenzung des Rechenaufwandes, dass wir einen ideal kugelförmigen, homogenen Erdkörper voraussetzen, der auf einer exakten Kreisbahn in genau 365 Tagen die Sonne umkreist.
Um die genannten Sekundärprozesse von Energieumwandlung und –transport auszuschließen, sind auch einige physikalische Voraussetzungen erforderlich:
– Keine Atmosphäre vorhanden, damit also keine Luftströmungen
– Kein Wasser, damit also keine ozeanischen Strömungen und keine Phasenumwandlungen (Verdunsten, Kondensieren, Gefrieren, Schmelzen)
– Wärmeleitung vernachlässigbar klein
– Andere Energiequellen wie Restwärme aus dem Erdinneren oder die kosmische 3-K-Hintergrundstrahlung werden ebenfalls vernachlässigt.
Schließlich fordern wir noch eine schnelle Rotation dieser Modellerde, so dass sich keine nennenswerten Tag-Nacht-Unterschiede der Temperatur herausbilden können. Das bedeutet, dass jeder Punkt der Erdoberfläche zu jedem Zeitpunkt einzeln für sich im Strahlungsgleichgewicht mit der pro Erdumdrehung zugestrahlten Sonnen-Energie steht.
Welchen Erkenntnisgewinn wollen Sie mit so einem Modell gewinnen? Mit einem numerischen Modell zu spekulieren ist wohl die teuerste und duemmste Form der Spekulation.
Dass unser Mond eine Atmosphaere hat, ist bekannt. Aber die Dichte dieser Atmosphaere ist so gering, dass die Absorption von solarer und infraroter Strahlung in der Mondatmosphaere sowie Zirkulationseffekte vernachlaessigbar sind. Dass keine Ozeane auf dem Mond existieren, wissen wir ebenfalls.
Aber Waermeleitung im Regolith existiert, und die ist nicht vernachlaessigbar. Folglich ist der Ansatz eines lokalen Strahlungsgleichgewichtes aus physikalischer Sicht zu verwerfen, was seit Wesselink (1948) bekannt ist.
Der Mond befindet sich nicht nur zusammmen mit der Erde auf einem gemeinsamen Orbit (Erde-Mond-Baryzentrum), sondern auch um eine Umlaufbahn um die Erde. Diese astronomischen Gegebenheiten muessen auf jeden Fall beruecksichtigt werden.
Was besonders wichtig ist, dass Beobachtungen zum Mond existieren, waehrend die von Ihnen beschriebene Erde ohne Atmosphaere sich jeder Beobachtung entzieht. Es ist also die Bewertung der Modellphysik an einem realistischen Beispiel des Gedankenmodells einer Erde ohne Atmosphaere wie unserem Mond zu bewerten, wobei die unterschiedlichen astronomischen Gegebenheiten zu beruecksichtigen sind. Die Annahme
„einer schnellen Rotation dieser Modellerde, so dass sich keine nennenswerten Tag-Nacht-Unterschiede der Temperatur herausbilden können“
gehoert nicht dazu, denn das ist barer Unsinn.
Bei der Evaluation der Ergebnisse von Modellsimulationen z.B. zur Oberflaechentemperatur der realen Erde oder des Mondes sind nicht nur der Vergleich der berechneten Oberflaechentemperaturen mit den beobachteten Oberflaechentemperaturen erforderlich, was der notwendigen Bedingung entspricht, sondern auch der Vergleich der berechneten Energieflussdichten mit den Beobachteten Energieflussdichten, was der hinreichenden Bedingung entspricht.
„Sie irren sich gewaltig. Eine Modellbildung, die auf der Vernachlaessigung relevanter physikalischer und astronomischer Gegebenheiten beruht, ist so ueberfluessig wie ein Buckel“.
😂🤣…..gefällt mir. 🪷
@Gerhard Kramm
Worin denn soll mein Irrtum bestehen? Ich bitte zu bedenken: alle Abweichungen von der Realität sind gewollt.
Wenn Sie ein realistischeres Modell des Klimasystems bevorzugen, muss ich Sie auf das IPCC verweisen. Aber auch diese Modelle irren bekanntlich, sowohl hinsichtlich der Voraussetzungen als auch der Ergebnisse. Sie werden ihrem Anspruch, das reale Klima zu beschreiben, nicht gerecht. Mein Anspruch ist weit tiefer gesteckt, ich meine aber immerhin, ihn erfüllt zu haben. Denn was „richtig“ ist, hat ja auch mit der Zielsetzung zu tun.
Und bitte haben Sie Nachsicht in folgendem Punkt: ich bin Privatmann und habe weder einen universitären Apparat im Rücken noch einen Großrechner im Wohnzimmer stehen.
Es war insbesondere nicht mein Ziel, den Mond zu beschreiben. Und was die schnelle Rotation meines Modells betrifft: der Begriff ist ja relativ. Es meint in diesem Fall: schnell gegen die Zeitkonstante der strahlungsbedingten Abkühlung (ins Weltall) bzw. Aufheizung durch die Sonne. Diese Annahme war notwendig, um der Zielsetzung „Strahlungsgleichgewicht“ aus der Überschrift gerecht zu werden. Bei realistischer Rotation stellt sich nämlich kein Strahlungs-gleichgewicht ein, sondern eine Tag-Nacht-Schwankung der Temperatur. Über die hätte ich dann mitteln müssen, was einigen Lesern auch nicht behagt. Die Ergebnisse wären letztlich ähnlich ausgefallen. Aber gerade das Strahlungsgleichgewicht stellt sicher, dass die aus- und eingehenden Energieflussdichten vergleichbar (sogar gleich!) sind, was Sie doch fordern.
Letztendlich: wenn Sie mein Modell uninteressant finden, bin ich nicht böse, das ist jedermanns Recht. Andere fanden es nicht so uninteressant, und es hat doch eine rege Diskussion angestoßen und somit einen sinnvollen Zweck erfüllt.
@ Mechtel
Sie schrieben:
„Es war insbesondere nicht mein Ziel, den Mond zu beschreiben. Und was die schnelle Rotation meines Modells betrifft: der Begriff ist ja relativ. Es meint in diesem Fall: schnell gegen die Zeitkonstante der strahlungsbedingten Abkühlung (ins Weltall) bzw. Aufheizung durch die Sonne. Diese Annahme war notwendig, um der Zielsetzung „Strahlungsgleichgewicht“ aus der Überschrift gerecht zu werden. Bei realistischer Rotation stellt sich nämlich kein Strahlungs-gleichgewicht ein, sondern eine Tag-Nacht-Schwankung der Temperatur. Über die hätte ich dann mitteln müssen, was einigen Lesern auch nicht behagt. Die Ergebnisse wären letztlich ähnlich ausgefallen. Aber gerade das Strahlungsgleichgewicht stellt sicher, dass die aus- und eingehenden Energieflussdichten vergleichbar (sogar gleich!) sind, was Sie doch fordern.“
Offensichtlich haben Sie nicht begriffen, was Sie treiben. Sie muessen grundsaetzlich die Physik eines numerischen Modells anhand eines realistischen Beispiels ueberpruefen. In unserem Sonnensystem bieten sich dazu der Planet Merkur und unser Mond an, wobei der Mond wegen der bereits vorhandenen Beobachtungsdaten zu bevorzugen ist. Diese Ueberpruefung haben Sie unterlassen. Ihre Ergebnisse sind also vollkommen wertlos. Sie haben noch nicht einmal eine Literaturrecherche vorgenommen, denn sonst haetten Sie sofort aufhoeren koennen. Sie hinken naemlich um Jahrzehnte hinterher.
Sie gehen von voellig falschen Annahmen fuer das Gedankenmodell einer Erde ohne Atmosphaere aus. Wie Weber unterstellen Sie ein lokales Strahlungsgleichgewicht, denn Sie ignorieren die Waermeleitung. Im Gegensatz zu Weber, der davon ausgeht, dass die Erde nicht taeglich rotiert bzw. zur Sonne ‚tidally locked‘ ist wie der Mond zur Erde, wollen Sie die Erde so schnell rotieren lassen, „dass sich keine nennenswerten Tag-Nacht-Unterschiede der Temperatur herausbilden können“.
Man koennte auch sagen, bis die Erde auseinanderfliegt.
Was ist denn fuer Sie die Zeitkonstante, wenn Sie z.B. den thermischen Inertialkoeffizenten nicht beruecksichtigen? Lokales Strahlungsgleichgewicht bedeutet:
(1 – α) FS↓ = FIR↑ (1).
Hierin sind FS↓ die Flussdichte und α die Albedo im solaren Bereich und FIR↑ = ε σ Teq^4 die emittierte infrarote Strahlung gemaess des Stefan-Boltzmann-Gesetzes fuer graue Strahler, wobei Teq die Temperatur des lokalen Strahlungsgleichgewichtes, ε das relative Emissionsvermoegen und σ die Stefansche Konstante sind.
Das ist eine diagnostische Beziehung, die ueberhaupt keine Zeitkonstante kennt. Selbst wenn man die Waermeleitung ignoriert, lautet die abgespeckte Form der lokalen Bilanzgleichung fuer die Gesamtenergie, angewandt auf eine duenne Schicht des Regolith, die nach aussen hin von der Oberflaeche begrenzt wird, immer noch:
R dT/dt = (1 – α) FS↓ – ε σ T^4 (2),
wobei R = ρ c D der thermische Inertialkoeffizient und t die Zeit sind. Hierin sind ρ, c, D und T die Dichte, die spezifische Waerme, die Dicke und die Temperatur dieser Deckschicht. Diese Form wird in der Fachliteratur als ‚forcing method‘ bezeichnet (Deardorff, 1978). Diese Methode geht auf
University of California, Los Angeles, 103.
Long Period Integrations. Quarterly Journal of the Royal Meteorological Society , 98, 809-832.
Model. Technical Note. Meteorological Office, Bracknell, Berkshire.
Layer of Vegetation. Journal of Geophysical Research, 83, 1889-1903.
zurueck. Und die Integration dieser Gleichung laesst sich mit Hilfe der numerischen Mathematik bequem vornehmen. Dazu ist kein Grossrechner erforderlich. Die heutigen PCs haben ein Vielfaches an RAM, im Vergleich zu den Vektorrechnern aus den 1980er und 1990er Jahren. Diese Gleichung wurde von Kramm et al. (2017) ausfuehrlich diskutiert.
Wird die Waermeleitung nicht ignoriert, so erhaelt man als lokale Bilanzgleichung fuer die Gesammtenergie (siehe ausfuehrliche Herleitung bei Kramm et al., 2017):
R dT/dt = (1 – α) FS↓ – ε σ T^4 – Hsoil (3).
Nach Deardorff (1978) wird diese Gleichung, die auf Bhumralkar (1975) und Blackadar (1976) zurueckgeht, als ‚force-restore method‘ bezeichnet. Auch diese Gleichung laesst sich mit Hilfe der numerischen Mathematik bequem integrieren. Und da Kramm et al. (2017) den Waermefluss und die Verteilung der Temperatur im Regolith bis in eine Tiefe von 3,2 m mit Hilfe eines Vielschichtmoduls numerisch simuliert haben, haben wir das als ‚multilayer-force restore method‘ bezeichnet.
Ihre Behauptung:
„Bei realistischer Rotation stellt sich nämlich kein Strahlungsgleichgewicht ein, sondern eine Tag-Nacht-Schwankung der Temperatur. Über die hätte ich dann mitteln müssen, was einigen Lesern auch nicht behagt. „
ist absurd. Offensichtlich unterstellen Sie den Lesern, dass sie genauso von Unkenntnis gepraegt sind wie Sie. Ihre Behauptung.
„Die Ergebnisse wären letztlich ähnlich ausgefallen.“
ist zudem vollkommen falsch.
Es ist geradezu laecherlich, mir erzaehlen zu wollen, dass waehrend der Nacht kein Strahlungsgleichgewicht existiert. Dieser Sachverhalt ist im Falle des Mondes seit Wesseling (1948) bekannt, wobei Wesselink wegen der relativ geringen Rotationsgeschwindigkeit des Mondes von folgender Gleichung (stationaere Form) ausging:
0 = (1 – α) FS↓ – ε σ T^4 – Hsoil (4).
Diese Gleichung wurde fuer den Mond und den Planeten Merkur, der noch langsamer rotiert als der Mond, fast ausschliesslich verwendet (siehe z.B. Wesselink, 1948, Jaeger, 1953, Cremers et al., 1971, Mitchell & de Pater, 1994, Vasavada et al., 1999, 2012,
Temperatures and Thermophysical Properties: Test of a Thermal Model in Preparation of the MERTIS Experiment Onboard BepiColombo. Planetary and Space Science , 101, 27-36.
Mercury in Preparation of the MERTIS Experiment Onboard BepiColombo. Icarus , 354, Article ID: 114083.
und Hu et al. , 2015). Ich habe die beiden Artikel von Bauch et al. ausfuehrlich zitiert, weil diese Arbeiten an der Universitaet Muenster angefertigt wurden. Was treiben Sie eigentlich?
Selbstverstaendlich haben Kramm et al. (2017) mit der Gleichung (3) gearbeitet. Das numerische Modell, programmiert in FORTRAN, wurde fuer den Mond entwickelt, um die Modellphysik an einem realistischen Beispiel testen zu koennen, fuer die eine Reihe von Beobachtungen existieren, sogar aus der Zeit der Apollo-Missionen. Dann wurde es auf das Gedankenmodell einer Erde ohne Atmosphaere angewendet. Das globale Mittel ueber die Verteilung der berechneten Oberflaechentemperaturen lieferte:
〈T〉 = 220,7 K .
Fuer FS↓, Q = (1 – α) FS↓, FIR↑ und Hsoil ergaben sich also globale Mittel:
〈FS↓〉 = 340,2 W/m²,
〈Q〉 = 279,7 W/m²,
〈FIR↑〉 = 279,6 W/m²,
〈Hsoil〉 = 〈Q〉 – 〈FIR↑〉 = 0,1 W/m².
Nun noch zu einigen Ihrer Behauptungen. Sie behaupten:
„Denn was „richtig“ ist, hat ja auch mit der Zielsetzung zu tun.“
Haetten Sie eine solche Antwort auf eine Pruefungsfrage abgeliefert, haetten Sie ein ‚fail‘ erhalten, denn diese Behauptungen ist haarstraeubender Unsinn und belegt, dass Sie heillos ueberfordert sind.
Sie behaupten:
„Aber gerade das Strahlungsgleichgewicht stellt sicher, dass die aus- und eingehenden Energieflussdichten vergleichbar (sogar gleich!) sind, was Sie doch fordern.“
Offensichtlich haben Sie nicht begriffen, was ich schrieb. Im Falle der realen Erde existiert an der Grenzflaeche Erde-Atmosphaere auf der lokalen Skala im Allgemeinen kein Strahlungsgleichgewicht, auf der globalen Skala existiert es grundsaetzlich nicht. Dafuer sind vor allem die Flussdichten von sensibler und latender Waerme in der oberflaechnnahen Luftschicht verantwortlich.
An der Obergrenze der Atmosphaere existiert auf der lokalen Skala im Allgemeinen ebenfalls kein Strahlungsgleichgewicht, jedoch auf der globalen Skala (zumindest im Rahmen der Beobachtungsgenauigkeit, falls die Bedingung der Stationaritaet erfuellt ist).
Im Falle des Gedankenmodells einer Erde ohne Atmosphaere existiert weiterhin auf der lokalen Skala kein Strahlungsgleichgewicht. Dass waehrend der lokalen Nacht die Oberflaechentemperatur auf 0 K absinken soll, gehoert in den Bereich der Maerchen und Sagen. Auf der globalen Skala existiert wiederum ein Strahlungsgleichgewicht, und zwar im Rahmen der Messgenauigkeit.
Sie schrieben weiterhin:
„Letztendlich: wenn Sie mein Modell uninteressant finden, bin ich nicht böse, das ist jedermanns Recht. Andere fanden es nicht so uninteressant, und es hat doch eine rege Diskussion angestoßen und somit einen sinnvollen Zweck erfüllt.“
Bei Ihrem Modell handelt es sich um esoterischem Muell, der nur dazu dient, Verwirrung zu stiften. Fuer Sie existiert nicht die Fachliteratur, sondern nur das, was sich Klein Fritzchen als Wissenschaft vorstellt.
Fazit: Sie wollten das Rad neu erfinden, landeten beim Vierkant und freuen sich nun, dass es besser rollt als ein Dreikant.
Sehr geehrter Herr Mechtel
Für die Erde funktioniert Ihr Modell tatsächlich sehr gut, (egal was H. Kramm behauptet,) aber der Mond dreht sich in der Tat so langsam, dass die Temperaturunterschiede von Tag und Nachtseite über die T^4 Beziehung den Temperaturmittelwert am Ende deutlich verfälschen würden.
Für das instationäre FE-Modell ist dies jedoch möglich. Das Modell liefert in diesem Fall im eingeschwungenen Zustand (nach 150 Erdtagen) folgendes Ergebnis:
Die gemittelte Temperatur beträgt im Modell -50°C was recht gut zu den in der Literatur angegebenen -55°C passt.
Zusätzlich lässt sich das Modell noch am Beispiel des Kraters Tycho überprüfen. Hierzu gibt es Auswertungen aus Messungen an verschiedenen Stellen des Kraters (farbige Linien).
Die Auswertung des FE-Modells auf Höhe des Kraters Tycho bei 42° Süd liefert im Vergleich folgenden Temperaturverlauf (schwarze Linie):
[Das Bild oben ist eigentlich ein animated Gif. Da die Animation vermutlich hier nicht läuft, kann das ganze leider nur hier richtig dargestellt werden: https://ibb.co/MRQY1MR ]
Nach eigenen Aussagen kannte Einstein das MM-Experiment gar nicht vorher. Und in Einsteins grundlegender Arbeit zur SRT kommt es auch nicht vor
Deshalb steht da sicher auch: völlig unabhängig
Korrektur:
Die Bildunterschrift zu Abb. 3 muss einfach heißen
„Abb.3: Halbjahresverlauf der globalen Mitteltemperatur“
Der Zusatz „am 50. Breitengrad“ macht natürlich keinen Sinn, sonst wäre es nicht global.
Man muss das Modell gar nicht so weit vereinfachen wie es oben beschrieben wird.
Die korrekte Rotation der Erde kann durchaus mit einem Finite Element Programm abgebildet werden. Indem man der Erdoberfläche eine gewisse Wärmekapazität zuweist, kann dadurch der Wärmetransport von der Tag auf die Nachseite abgebildet werden.
Zunächst starte ich mit dem Modell von Herrn Weber – also einer nicht rotierenden Erde. Da meine Oberfläche eine Wärmekapazität aufweist, muss ich das Modell mehrere Tage bestrahlen bis sich nach rund 16 Tagen der folgende Zustand eingestellt hat:
Bildet man aus diesem Ergebnis auf der Tagseite einen Mittelwert erreicht das Modell zu diesem Zeitpunkt eine mittlere Temperatur von +12°C (im Vergleich zu +14.1°C bei H. Weber). Da ich die Rechnung mit einer Temperatur von gleichmäßig verteilten 0 °C gestartet habe, hat sich die Nachtseite nach 16 Tagen immerhin auf bereits -140°C abgekühlt – mit weiter abnehmender Tendenz.
Ein Vergleich einiger ausgewählter Punkte aus meinem FE-Modell (Rote Punkte) mit dem Ergebnis von Herrn Weber (blaue Kurve) für die Tagseite zeigt die Vergleichbarkeit beider Ergebnisse.
Die interessante Frage ist nun, was passiert wenn man die Rotation der Erde mit berücksichtigt? Mit einem FE-Modell ist das problemlos möglich. Wir lassen die Erde mit einer Umdrehung pro Tag rotieren und warten wieder einige Tage bis sich ein (dynamisches) Gleichgewicht eingestellt hat, das nach 16 Tagen wie folgt aussieht:
Dieser Zustand ist nun keineswegs konstant, da die heiße und kalte Seite nun kontinuierlich bei jeder Umdrehung der Erde mit der Rotation umläuft. Da es sich aber um einen zwar dynamischen aber eingeschwungenen Zustand handelt, kann durchaus die mittlere Temperatur des gesamten Modells angegeben werden.
Diese beträgt nach 16 Tagen -16°C und ändert sich ab diesem Zeitpunkt auch praktisch nicht mehr.
In meinem Modell ist übrigens die Erdachse nicht geneigt. Ansonsten sind die Parameter praktisch identisch.
Vielleicht klappt es wenigstens so ????
Bild1 https://ibb.co/cTRGdgP
Bild2 https://ibb.co/1GbC51g
Bild3 https://ibb.co/ggyHPPh
Darf Herrn Grun zitieren:
Thomas Grun am 3. März 2024 um 14:54
Egal was damit „bewiesen“ ist, Temperatur ist und bleibt eine Intensive Variable und somit ist sie nicht mittelbar. Ob dies für manche Annahmen hilfreich scheint oder nicht, das ist ein Fakt.
und Prof. Puschner:
Was also bleibt, ist ein Modell, bei dem man bestenfalls erkennen kann, ob die unter falschen Annahmen durchgeführten Rechnungen richtig oder falsch sind, also eine Bewertung der angewandten Mathematik.
Schade, dass die Bilder nicht zu sehen sind.
Aber interessant, dass die eingeschwungene Mitteltemperatur mit meinem Modell bei senkrecht stehender Erdachse übereinstimmt, nämlich -16 Grad Celsius (vgl. Tab. 3).
Noch ein Test:
Bild1:
Bild2:
Bild3:
@ Manfred Bergmann am 5. März 2024 um 10:35
Den Test für wissenschaftliche Redlichkeit haben Sie jedenfalls nicht bestanden:
Sie zeigen hier ohne Quellenangabe eine Grafik von mir mit eigenen (?) Einfügungen! Meine Originaldarstellung ist hier zu finden.
Schöne Darstellung. Ich denke, Sie mussten dafür Annahmen über die Wärmeleitfähigkeit und die Wärmekapazität machen, und die haben sicher Einfluss auf das Ergebnis, zumindest in Bild 1 und 2.
Wenn man lange genug wartet, wäre Bild 1 unabhängig von der Wärmekapazität, da sich dann Wärmeabstrahlung und Wärmeeinstrahlung überall im Gleichgewicht befinden und sich so ein statischer thermischer Zustand eingestellt hätte. Auf der Nachtseite in Bild 1 ist dies aber tatsächlich noch nicht der Fall, da die Abkühlung dort noch längst nicht abgeschlossen war. Und der Zustand dort hängt dann natürlich von der Zeit und von der Wärmekapazität ab. Auf der Tagseite herrscht hingegen bereits sehr bald ein Strahlungsgleichgewicht, weswegen dort ja auch meine Ergebnisse mit den Ergebnissen von H. Weber korrelieren, der ein Strahlungsgleichgewicht in seinen Formeln ja bereits vorausgesetzt hat. (s. Bild 2)
Die Wärmeleitung, obwohl im Modell vorhanden, spielt hingegen keine Rolle, weil die Elemente so groß sind (~430km Seitenlänge), dass der Effekt in dem betrachteten Zeitraum von jeweils ca. 16Tagen vernachlässigbar ist.
Wesentlich größer ist der Einfluss hingegen bei rotierender Erde ( Bild 3), da es sich jetzt um einen dynamischen thermischen Zustand handelt. Für jedes Element ist nun kein Gleichgewichtszustand mehr vorhanden. D.h. entweder wird mehr Energie eingestrahlt als abgestrahlt oder umgekehrt. Die Temperatur ändert sich also fortlaufend und damit wird die Wärmekapazität die entscheidende Größe. Sie definiert den Tagesgang der lokalen Temperatur und damit die Tagesamplitude. Allerdings ist im eingeschwungenen Zustand der lokale Mittelwert, als auch der Mittelwert über die ganze Erde hinweg, wieder (fast) unabhängig von der Wärmekapazität.
#Manfred Bergmann am 4. März 2024 um 21:59
Mathematik ist geduldig, sie kommt mit jedem beliebig falschem Ansatz zurecht und liefert dennoch ein Ergebnis.
Aber es ist nur ein Ergebnis aufgrund korrekt angewandter Mathematik, falsche Annahmen werden dadurch grundsätzlich nicht verbessert im Sinne des richtigen Systemverständnisses.
Es handelt sich hier um bekannte physikalische Gesetze, angewandt auf jedes einzelne finite Element.
Die einzigen (!) verwendeten Parameter bzw. Annahmen sind:
Einstrahlung 1367 W/m²
spezifische Wärmekapazität 1.60 KJ/(kg•K)
Dichte 3300 kg/m³
Elemente: Länge ~ 430 km; Dicke 20 cm (siehe Bild)
Erddurchmesser (modelliert) ~ 12000km
ABSORPTIONSGRAD 0.70
EMISSIONSGRAD 0.93
Starttemperatur Erde 0.0 °C
Temperatur Umgebung (Weltraum): -270 °C
Drehgeschwindigkeit: 1 Umdrehung je Tag
Der Rest ist nur noch Geometrie, Mathematik und Mechanik. Mehr steckt nicht dahinter. Im Gegensatz zu den Klimamodellen wird sich dieses Ergebnis auch immer gleich einstellen, egal mit welcher Software man das berechnet – weil jeder einzelne Schritt eindeutige definiert ist.
#Manfred Bergmann am 5. März 2024 um 12:54
Sehr geehrter Herr Bergmann,
bis auf Erddurchmesser, Drehgeschwindigkeit (=> Drehzahl) und vielleicht Temperatur Weltraum finde ich keine Parameter die nicht einzig Annahmen sind und daher wie Naturkonstanten benutzt werden dürfen. Sie nennen das „bekannte physikalische Gesetze“.
Mit welcher Software Sie mit den gleichen Annahmen rechnen, wird sich natürlich unabhängig davon das Ergebnis gleich einstellen. Damit ist aber nur die Richtigkeit des Rechengangs erwiesen, nicht, dass sich die Welt entsprechend Ihrer Annahmen auch tatsächlich so verhält.
Mit freundlichen Grüßen
Peter Puschner
@ Bergmann
Was Sie treiben, belegt, dass Sie besser zurueck zur Schule gehen sollten.
Die lokale solare Einstrahlung, FS↓, ist gegeben durch (z.B. Wiener. 1877, 1879, Milankovitch, 1941, Liou, 2002)
FS↓ = (r0/r)² S (sin Φ sin δ + cos Φ cos δ cos h)
Hierin sind r der heliozentrische Abstand der Erde, r0 der mittlere heliozentrische Abstand (ungefaehr 1 AU), fuer den die Solarkonstante von etwa 1361 W/m² gilt, Φ der Breitenkreis, δ die Deklination der Sonne und h der Stundenwinkel. Die Deklination der Sonne ist fuer die astronomischen Jahreszeiten verantwortlich; mit dem lokalen Stundenwinkel, der sich auf den lokalen solaren Mittag (h = 0) bezieht, wird die Rotation der Erde beruecksichtig, deren mittlere Winkelgeschwindigkeit Ω = 2 π/86164 s = 7.292 E-05 pro Sekunde betraegt. Nur im Falle von δ = 0, dem Kriterium der Aequinoktien, ist der Tagesbogen fuer alle Breitenkreise gleich, sonst unterscheiden sich die Werte von Breitenkreis zu Breitenkreis. wobei ueber der polaren Kalotte der Sommerhemisphaere die Sonne nicht untergeht.
Wenn man das Zwielicht beruecksichtig, dann haben wir bereits jetzt schon eine etwas laengere Periode des Tageslichtes als Berlin. Und vom 19. Maerz bis zum 22. September 2024 haben wir erheblich mehr Tageslicht als Berlin. Fuer etwa 2 Monate geht hier (nahe des Arctic Circle) die Sonne praktisch nicht unter. Ich empfehle Ihnen und einigen der Foristen ein Lehrbuch der Sekundarstufe 2 zu den Grundlagen der Astronomie zu studieren.
Der Ansatz eines lokalen Strahlungsgleichgewichtes
(1 – α) FS↓ = ε σ Teq^4
auf dem Webers hemisphaerischer S-B-Ansatz beruht, ist aus physkalischen Gruenden zu verwerfen, egal ob es sich um eine Erde mit oder ohne Atmosphaere handelt, denn es handelt sich um eine unzulaessige Approximation der lokalen Bilanzgleichung fuer die Gesamtenergie. In dieser Gleichung sind α die lokale Albedo im solaren Bereich, ε das integrale Emissionsvermoegen, σ die Stefansche Konstante und Teq die Temperatur des lokalen Strahlungsgleichgewichtes.
Offensichtlich betrachtet Sie eine Erde ohne Atmosphaere, was die Existenz von Ozeanen ausschliesst. Die Horizontalkomponente der Waermeleitung im Erdboden ist selbst bei geringen horizontalen Abstaenden vernachlaessigbar, nicht jedoch die Vertikalkomponente. Und die vernachlassigen Sie.
Was koennen wir also Ihren Ergebnissen entnehmen? Nichts!
Hat ihr Model eine Atmosphaere? Ansonsten kann man auch – 18 Grad C akzpeptieren und 2 K als Modeldifferenz.
Was aber fehlt ist, wie sieht es mit der Oberflaechentemperatur mit Atmosphaere aus.
Ist 14 Grad C normal oder 15 Grad C oder 17 Grad C?
Welche Varation existiert, Wolken, Albedo, Eisbedeckung, Wasser/Landverteilung?
Man kann die Atmosphaere nicht erklaeren indem man sie weglaesst. Und wenn man sie weglaesst kann man hoechstens einen Atmosphaereneffekt erklaeren, aber nur wenn man Model mit Wirklichkeit abgleicht.
Was dann fehlt ist die physikalische Erklaerung.
Warum ist es mit einer Atmosphaere mit doppelter Masse waermer als mit einfacher Masse?
Da es sich hier um eine Beobachtung handelt und nicht um eine blosse Behauptung, wie sieht das physikalische Model aus?
Nein, das Modell hat keine Atmosphäre.
Modelle werden erstellt um bestimmte Fragen zu beantworten, wobei die Komplexität eines Modells so gewählt wird, dass die Frage mit minimalem Aufwand beantwortet werden kann. Die Modelle, die wir hier diskutieren, sollen die Frage beantworten, welche mittlere Temperatur bei gegebenen Randbedingungen die Erde hätte, WENN sie keine Atmosphäre hätte. Denn die Temperaturdifferenz zur realen Erde muss dann wohl durch die Atmosphäre, und somit auch u.a. durch den sogenannten Treibhauseffekt verursacht sein.
Nun hat Herr Weber mit seinem Modell eine mittlere Temperatur von +15°C ermittelt und daraus geschlossen, dass der Treibhauseffekt vernachlässigbar sei. Seit dem wird in den Foren hier heiß diskutiert und dabei können weitere Modelle, auch wenn sie sehr einfach sind, bei dieser Diskussion durchaus hilfreich sein.
Es geht also letztlich um die Frage: Ist das Webersche Modell korrekt oder nicht? Und wenn nicht – wo liegt der Fehler?
@Bergmann
Offensichtlich haben Sie nicht begriffen, dass Webers hemisphaerischer Stefan-Boltzmann-Ansatz vollkommen falsch ist und keiner Bewertung aus physikalischer Sicht standhaelt. Nicht ein einziges von Webers Ergebnisse ist mit den Beobachtungen vereinbar, wobei fuer das Gedankenmodell einer Erde ohne Atmosphaere sowieso keine Beobachtungen existieren.
Aus diesem Grunde versuchte Weber seinen hemisphaerischer Stefan-Boltzmann-Ansatz anhand von Beobachtungen zum Mond zu bewerten, u.a. mit den „Beobachtungen“ zur Landestelle der Apollo 15-Mission. Ein Flaechenmittel mit einer Punktmessung bewerten zu wollen, ist vollkommen unsinnig, denn die Verteilung der Oberflaechentemperatur des Mondes ist nicht gleichfoermig. Dass Webers Ergebnisse bis zu 150 K von den „Beobachtungen“ abweichen, sei nur am Rande erwaehnt. Uebrigens handeltes sich nicht um Beobachtungen, sondern aus einer Kombination von Modellrechnungen und Messungen (siehe Keihm et al., 1973). Die Messungen gelten nur fuer die lokale Nacht.
Es ist zudem ein Unding, eine Temperatur, hergeleitet fuer eine Hemisphaere, mit dem globalen Mittel der beobachteten Temperaturen der oberflaechennahen Luftschicht vergleichen zu wollen.
@Manfred Bergmann
Das sieht doch schon recht gut aus. Aber die Temperatur von +12°C (285 K) im ersten Bild ist doch nicht korrekt? Das ist auf keinem Fall die flächengewichtete Temperatur der Hemisphäre, wenn man vom solaren Pol der Hemisphäre (Winkel zwischen Flächennormalen und Sonne ist 0°) ausgeht. Das sieht mir nach einem arithmetischen Mittel aus, und das wäre falsch.
Werner Holtz schrieb am 05/03/2024, 18:24:55 in 363324
Wenn man die Zuordnung zwischen Einstrahlung/Temperatur und Fläche nicht vergurkt, kommt das raus. Sie haben bei Ihrer flächengewichteten Mittelung allerdings die größte Einstrahlung/Temperatur mit der größten Fläche gewichtet und sind daher auf einen falschen Wert gekommen. (Bei Ihnen hatte der 10° Kreis um den solaren Pol, auf den die höchste Einstrahlung wirkt, die Fläche zwischen dem Äquator und dem 10. Breitengrad und anders rum) …
Zitat: Sie haben bei Ihrer flächengewichteten Mittelung allerdings die größte Einstrahlung/Temperatur mit der größten Fläche gewichtet und sind daher auf einen falschen Wert gekommen.
Nein, Sie müssen die wirksame Fläche der Temperaturen betrachten.
Überschlagmäßig aus Ihrem Bild 1:
+ Temperatur beim solaren bzw. energetischen oder thermischen Pol β = 0° der Hemisphäre beträgt 88°C (361 K)
+ Temperatur beim energetischen oder thermischen Breitengrad β = 30° der Hemisphäre: 53°C (326 K)
+ Temperatur beim energetischen oder thermischen Breitengrad β = 90° der Hemisphäre: -110°C (163 K)
Die Fläche zwischen dem Pol (β = 0°) und einem Breitengrad β ergibt sich aus: A = 2π·r²·sin(β). Die Fläche zwischen zwei Breitengraden ermittelt sich nach: ΔA = 2π·r²·[sin(β2) – sin(β1)] für β2 > β1.
Die „mittlere Temperatur“ für die hemispärische Teilfläche zwischen den energetischen oder thermischen Breitengrad 0° und 30° ist unter Beachtung, dass das Stefan-Boltzmann-Gesetz für die energetische Berechnung herangezogen wurde:
{[T(β1)^4 + T(β2)^4]/2}^(1/4) = {[361^4 + 326^4]/2}^(1/4) = 344 K. Das heißt, die hemispärische Teilfläche (50%) hat eine „mittlere Temperatur“ von 344 K (71°C).
Die „mittlere Temperatur“ für die hemispärische Teilfläche zwischen den energetischen oder thermischen Breitengrad 30° und 90° ist unter Beachtung, dass das Stefan-Boltzmann-Gesetz für die energetische Berechnung herangezogen wurde:
{[T(β1)^4 + T(β2)^4]/2}^(1/4) = {[326^4 + 163^4]/2}^(1/4) = 278 K. Das heißt, die hemispärische Teilfläche (50%) hat eine „mittlere Temperatur“ von 278 K (5°C).
Die „mittlere Temperatur“ der Hemisphäre mittels der Überschlagsrechnung ergibt sich zu: (1/2·344^4 + 1/2·278^4)^(1/4) = 316 K (43°C).
Ihre Rechnung klingt zwar plausibel, aber sie ist vermutlich zu grob.
Nachfolgend mache ich mal eine Auswertung mit 4 Teilbereichen, die das ganze vielleicht eher nachvollziehbar machen. Ich teile das Modell der rechten Hemisphäre wie folgt auf:
Für die einzelnen Streifen ergeben sich die Teilflächen und die zugehörigen mittleren Temperaturen wie folgt:
Wie in der Tabelle dargestellt ergibt sich aus diesen 4 Teilflächen bereits ein Temperaturmittelwert von 15,7°C.
Was rechnen Sie da zusammen? Das versteht doch keiner! Und nehmen Sie Kelvin statt Grad Celsius, weil ihre T*A plötzlich negativ wird. Geben Sie mal genau an wie Sie die Fläche der Teilflächen berechnen und wie Sie die „mittlere Temperatur“ für diese Teilfläche bestimmen haben. Alles andere bringt nur Verwirrung.
Werner Holtz schrieb am 7. März 2024 um 19:32
Nein, die Fläche ergibt sich aus A = 2π·r²·(1-cos(β)). Kann man im Zweifelsfall bei Wikipedia/Kugelsegment nachlesen.
Diese Formel gilt für unsere normalen Breitengrade, bei denen der Grad 0 am Äquator ist[1]. Hier ist aber 0° am solaren Pol und damit die Fläche zwischen zwei Breitengraden ΔA = 2π·r²·[(1-cos(β1)) – (1-cos(β2))] = 2π·r²·[cos(β2) – cos(β1)] …
[1] Das kann man prüfen, indem man β durch (pi/2 – β) ersetzt und das ganze vereinfacht
@ Marvin Müller am 8. März 2024 um 18:49
Ach Herr M. Müller, mit dem Lesen und Verstehen scheint es bei Ihnen etwas zu hapern.
M = 2π·r²·(1-cos(θ)) ist die Mantelfläche vom Kugelsegment (Kugelkalotte + Grundkreis) und nicht die Oberfläche der Kugel bzw. Hemisphäre bei einem Breitengrad β!
Werner Holtz schrieb am 11/03/2024, 15:33:03 in 364032
Das ist einfach nur Mathematik und damit eigentlich leicht prüfbar. Und ich hatte das auch getan, als ich verifiziert habe, dass sich mit der Formel für die Fläche zwischen 80° und 90° (Pol) das gleiche ergibt wie bei Ihrer Formel zwischen 0° (Äquator) und 10°. Sogar mit einem Link auf Wolfram mathematica, das die entsprechende Äquivalenz zeigt : (1-cos(pi/2 – x)) – (1-cos(pi/2-y)) = sin(y) – sin(x)
Die Mantelfläche ist die Fläche ohne Grund und Deckfläche, die Oberfläche ist Mantelfläche + Grund und Deckfläche. Kann man auch einfach prüfen für einen Winkel von 90°. Da müßte bei dem einen die Hälfte der Kugeloberfläche 4π·r²/2 und beim anderen die Hälfte der Kugeloberfläche 4π·r²/2 + die Fläche eines Kreises π·r² herauskommen (sin(90°) = 1, cos(90°) = 0):
Mantelfläche M = 2π·r²·(1-cos(θ)) , 2π·r²·(1-cos(90°)) = 2π·r²
Oberfläche O = 2π·r²·(1-cos(θ) + 1/2 * sin²θ), 2π·r²·(1-cos(90) + 1/2 * sin²90) = 2π·r²(1 + 1/2) = 2π·r² + π·r²
Sieht für mich danach aus, dass Sie sich an der Stelle irren. Könnten Sie das vielleicht einfach nochmal prüfen?
vielen dank, Herr Müller, für diesen interessanten Ausflug! Diese Rechenfolge werde ich bei mir abspeichern.
MfG
Marvin Müller schrieb am 11/03/2024, 18:24:51 in 364052
In dem Kommentar, den ich gestern geschrieben habe[1], steht “ zwischen 80° und 90° (Äquator)“ und nicht Pol. Ist der Kommentar bearbeitet worden?
Herr Holtz definiert den „solaren bzw. energetischen oder thermischen Pol β = 0° „, während bei unseren Breitengraden die 0° am Äquator sind. Er berechnet die Einstrahlung/Temperatur basierend auf 0° am Pol, die Fläche mit einer Formel, die auf 0° am Äquator basiert. Daraus resultieren dann die falschen/zu hohen Werte.
Christian Freuer schrieb am 11/03/2024, 21:23:28 in 364067
Ich glaube, ich muss meinen Ironiedetektor zum Justieren in die Werkstatt schaffen. Der schlägt hier zu beissendem Sarkasmus aus, was aber eigentlich nicht die Art von Herrn Freuer ist 🙂
[1]Ich hebe mir meine Kommentare immer auf für den Fall, dass sie durch ein technisches Problem verloren gehen.
Das war ernst gemeint, Herr Müller! Ich kann diese Rechung in einem anderen Zusammenhang gut gebrauchen. Allerdings kämpfe ich noch ein wenig, sie noch besser zu verstehen.
Nochmals: es war nicht ironisch gemeint!
MfG
Christian Freuer schrieb am 12/03/2024, 13:00:42 in 364146
Danke für die Bestätigung. Ich bin schon davon ausgegangen 🙂
Wenn Sie genauer sagen, an welchem Schritt es klemmt, kann ich das ergänzen, detaillierter erklären. Gerne auch per email.
Mann oh Mann, Herr Müller, nun reicht es! Für Sie ganz einfach und zum „Mitmeißeln“.
Für die Oberfläche der Kugelkalotte gilt: A = 2π·r·h (h – Abstandslot vom Pol)
Ein Viertel der hemisphärischen Oberfläche (h = r/4) ist A = 2π·r·(r/4) = 2π·r²·sin(14,48°), wobei die 14,48° der Breitengrad vom Pol ausgehend ist.
Ein Drittel der hemisphärischen Oberfläche (h = r/3) ist A = 2π·r·(r/3) = 2π·r²·sin(19,47°), wobei die 19,47° der Breitengrad vom Pol ausgehend ist.
Die Hälfte der hemisphärischen Oberfläche (h = r/2) ist A = 2π·r·(r/2) = 2π·r²·sin(30°), wobei die 30° der Breitengrad vom Pol ausgehend ist.
Zwei-Drittel der hemisphärische Oberfläche (h = 2·r/3) ist A = 2π·r·(2·r/3) = 2π·r²·sin(41,81°), wobei die 41,81° der Breitengrad vom Pol ausgehend ist.
Drei-Viertel der hemisphärische Oberfläche (h = 3·r/4) ist A = 2π·r·(3·r/4) = 2π·r²·sin(48,59°), wobei die 48,59° der Breitengrad vom Pol ausgehend ist.
Oder schauen Sie sich den Aufriss einer Kugel an – Siehe: https://iam.tugraz.at/ergkurs/beispiele/kugelFrontalkreise.php
Werner Holtz schrieb am 14/03/2024, 16:14:18 in 364506
Sie wollen also nicht klären, ob ich nun Mantelfläche und Oberfläche verwechselt habe oder nicht. OK.
Statt dessen greifen Sie zu einer anderen Formel für die Mantelfläche, um dann dort die Höhe oder den zur Berechnung der Höhe herangezogenen Winkel zu verwechseln. Die Höhe h vom Pol bis zur Schnittebene ist h = r – r * cos(θ) = r * (1 – cos(θ)), wenn für den Pol θ = 0° gilt. Und dann kommt man auch zu der von mir verwendeten, ebenfalls von Wikipedia aufgeführten Formel A = 2π·r·h = 2π·r·r·(1 – cos(θ)) = 2π·r²·(1 – cos(θ)). Sie rechnen dann auch nicht mit der Höhe weiter, oder erklären, wie sie die Höhe mit Hilfe es Winkels bestimmen sondern wechseln natlos auf die IMHO falsche Formel …
Das kann man sich ja einfach mal optisch veranschaulichen:
30° vom Pol aus wäre der 60° Breitengrad. Denken Sie wirklich, die Hälfte der Fläche der nördlichen Hemnisphäre würde vom Pol bis zum 60. Breitengrad gehen? Sieht es nicht eher so aus, als wäre dies die Fläche zwischen Äquator und 30. Breitengrad? Und die Fläche vom Pol bis zum 60. Breitengrad nur 13%?.
Und ein viertel der Fläche zwischen Pol und 75. Breitengrad … spätestens da sollte man doch ins stutzen geraten …
Bildquelle
Werner Holtz schrieb am 14.3.2024, 16:14:18 in 364506
Vielleicht ergänzend zum vorher geschriebenen verbunden mit einem Bild, in dem die Größen der Formeln stehen, so dass es keine Missverständnisse gibt. Bild aus Wikipedia
Bezugnehmend auf die im Bild gezeigten Größen erhält man h als Differenz zwischen dem Radius und dem Teil vom Mittelpunkt bis zu Schnittstelle. cos(θ) = Ankathete / Hypotenuse = (r-h)/r, dann ist die Höhe h = r – r * cos(θ) = r * (1 – cos(θ)). Damit kommt man dann auf 2π·r^2· (1 – cos(θ))
Nimmt sin(θ) = Gegenkathete/Hypothenuse = a / r, dann erhält man nicht h, sondern a = r·sin(θ). Herr Holtz rechnet also die Fläche mit A = 2π·r·r·sin(θ) = 2π·r·a und kommt damit auf falsche Ergebnisse.
(Falls ich da einen Fehler gemacht haben sollte, wäre ich für eine Korrektur dankbar.)
@ Marvin Müller
Sie haben wie immer nichts verstanden auch nicht das FE-Modell vom Herrn Bergmann, worauf sich mein Kommentar bezog! Der Pol einer Kugel ist eine Definitions- und Betrachtungsfrage. Für die rotierende Erde hat man die Enden der Drehachse oder Dipolachse als Drehachsen-Pole oder Dipolachsen-Pole definiert. Für die Bestrahlung der Erde (Hemisphäre) von der Sonne liegt der „solare“ Pol dort, wo der Winkel zwischen Flächennormalen und Sonne ist 0° und damit die Bestrahlung ein Maximum erreicht.
Um diesen Zentral-Solarpunkt oder „solaren“ Pol (β=0°) bilden sich isoenergetische bzw. isotherme konzentrische Kreise (= Breitengrad β) – Das stellt die Abbildung vom Herrn Bergmann dar.
Werner Holtz schrieb am 17.3.2024, 11:18:12 in 364872
Ich bin Ihrer Definition gefolgt, der solare Pol ist die Stelle, „wo der Winkel zwischen Flächennormalen und Sonne ist 0° und damit die Bestrahlung ein Maximum erreicht.“ Im referenzierten Bild zur Mantelfläche ist das die Stelle, an der h den Kreis berührt. Und dann erklärt, dass die Fläche bezugnehmend auf diesen Pol mit A = 2π·r^2· (1 – cos(θ)) berechnet wird.
Sie berechnen die Fläche statt dessen A = 2π·r·a = 2π·r·r·sin(θ) und erhalten dadurch falsche Bezugsflächen. Statt einer Erklärung, warum das doch korrekt ist, kommen nur Vorwürfe, was ich alles nicht verstehen würde. Räumt man einen Vorwuirf aus, kommt nur ein neuer Vorwurf, einer absurder als der andere.
Doch, die mittlere Temperatur von +12°C ist tatsächlich der Mittelwert meines Modells für die TAGSEITE. Auf Bild 1 ist das die rechte Hälfte des Modells ab der Mittellinie.
Da alle Elemente nahezu gleich groß sind, ist der Wert auch unabhängig davon, ob ich das arithmetische Mittel der Elementtemperaturen verwende oder die Elementtemperaturen mit den jeweiligen exakten Elementflächen wichte. Tatsächlich habe ich über das Elementvolumen gewichtet. Da aber alle Elemente die gleiche Dicke von 20cm haben spielt das letztlich keine Rolle.
Ich gebe Ihnen aber insofern recht, als man optisch den Mittelwert eher bei der gelben Farbe vermuten würde. Ich vermute, dass der Großkreis am Übergang von der Tag- zur Nachtseite, den Mittelwert so deutlich nach unten zieht.
@ Bergmann
Warum spielen Sie nicht mit Foermchen im Sandkasten?
Hallo Herr Mechtel,
Ein Epsilon von 0.8 halte ich nicht für passend. Sie hatten ja auch geschrieben, dass es offen ist, ob 0.8 zutreffend wären.
Für die Erde wird meist bereits ein Epsilon von 0.95 gesetzt. Ein rauhes Granitgestein hat eine Emissivität Epsilon von 0.97, eine graue Betongehwegplatte hat ein Epsilon von 0.974. 0.97 kommt vielleicht vom Matrial als Gestein und von der Farbe dem Mondregohlit am nächsten. 4 Wurzel ( 1367 x 0.88 / 0.97 / 5.67 E-8) – 273 = 111.4 Grad Celsius oder 1240 Watt/m2.
Gemessen wurden auf dem Mond maximale 130 Grad Celsius, die 1500 Watt/m2 entsprechen. Es würden damit 1500 – 1240 = 260 W/m2 aus der Tiefe des Mondes langwellig kontinuierlich entweichen. Es wären mittlere Verhältnisse. (Die Chinesen Wissenschaftler hatten mitgeteilt, die festgestellte Wärme ist Ihnen unerklärlich. Sie sprachen sogar von Hotspots auf dem Mond.)
Für die Erde bewegt sich bei mir im Modell der Wert der radiogenen Tiefenabstrahlung zwischen 250 und 272 W/m2. Der Wert des Mondes wäre demnach in der Mitte.
Was die Wärmetransportmechanismen angeht so sind diese sehr gut in der Arbeit von Prof. D. Hebert dargestellt:
https://drive.google.com/file/d/1mq-lIaA2s0SbnJBql7w06ZlrlX86SWR4/view
Kapitel 3. Energiespeicherung und -transport in der Troposphäre
…
Eine weitere interessante Größe ist der meridionale Wärmetransport, den die Mittelbreiten-
Zyklone vollbringen. Der Antrieb dieses Transportphänomens ergibt sich aus der Breitenabhängigkeit der Wärmebilanz an der Erdoberfläche (Abb. 10).
Sie ist zwischen 35°N und 35°S positiv und beträgt 35…40 W⋅m-2. Für die Polarregionen ist diese Bilanz stark negativ (–60 … –100 Wm-2). Der Wärmeaustausch findet hauptsächlich durch Advektion fühlbarer Wärme über die Luft statt.
….
Dazu sind etwa 10 große Mittelbreitenzyklone (Leistung nach KRAUS jeweils etwa 500 TW) notwendig, deren Kernabstand bei φ = 50° im Mittel 2300 km beträgt (lange Wellen). Dieser gewaltige, solar angetriebene Wärmetransport übersteigt in jeder Hemisphäre das 500-fache des zivilisatorischen Energieumsatzes.
Das mit der Berechnung für Erde und Mond hat hier übrigens Markus Rex 2007 vom AWI schön erklärt.
https://www.wer-weiss-was.de/t/durchschnittstemperatur-ausrechnen/3980445
Ich zitiere kommentarlos aus Wikipedia „Lithosphäre“ zum Temperaturgradient: „In den obersten 10–15 Metern wird die Bodentemperatur durch atmosphärische Faktoren, wie Sonneneinstrahlung, Luftkontakt und versickerndes Regenwasser bestimmt. Darunter bis in ca. 50 Meter Tiefe herrschen über das Jahr konstant etwa 10 °C. Unterhalb von 50 Metern beginnt der Bereich, der hauptsächlich durch den Wärmestrom aus dem Erdinneren bestimmt wird; eine Erwärmung um einen Kelvin erfolgt in dem Teil der Kruste durchschnittlich alle 33 Meter bzw. alle 100 Meter steigt die Temperatur um etwa 3 Kelvin an.“
Wirkt unter den genannten Randbedingungen und Voraussetzungen solide und nachvollziehbar, auch wenn man nicht jeden Rechenschritt wird nachrechnen können, dafür sind die geometrischen Überlegungen bereits recht komplex. Leider immer noch notwendig, den wärmenden Effekt einer Wollmütze zu erklären – ohne Verletzung des 2. Hauptsatzes…
Der Wärmespeichereffekt der Ozeane dürfte sich auf die Temperaturschwankungen in diesem Modell eher ausgleichend und bremsend auswirken, in beide Richtungen. Allerdings haben wir ohne Atmosphäre, also bei 255 Kelvin, die Eiskugel-Erde. Was dann den Modellannahmen wieder näher kommt. Eine globale Mitteltemperatur, ohne isolierende Atmosphäre, von etwa 255 Kelvin wird wieder einmal bestätigt.
In dem zitierten Ganteför-Video ist der Strahlungsanteil sicherlich zutreffend erklärt. Weniger der vom IPCC unkritisch übernommene ECS-Wert von 3 Grad sowie ein angeblicher CO2-Treibhauseffekt von 500 Grad auf der Venus.
Was genau haben eigentlich die Corona Lockdowns und der Golfkrieg mit seinen 500 brennenden Ölquellen Meßtechnisch zum Klimatheorienachweis beigetragen ? Man sieht nirgends Daten !
Da der Berechnungteil verunglückt ist, weil offenbar keine griechischen Buchstaben akzeptiert werden, möchte ihn hier nachtragen:
Grundlage für die Berechnung der Temperatur im Strahlungsgleichgewicht ist die an der Oberfläche absorbierte Energie-Flussdichte Phi, auch Intensität genannt und meist in W/m² angegeben. Deren Wert für senkrechte Einstrahlung haben wir mit Phimax = 953 W/m² angesetzt. Bei Schrägeinstrahlung unter dem Winkel h erhält man Phi = Phimax * sin(h). h ist eine Koordinate im Horizontsystem und wird auch als Elevation der Sonne bezeichnet.
Zur Erklärung astronomischer Koordinaten sei auf die Fachliteratur verwiesen, s. z.B. die Quellenangaben.
Die Bestimmung von h im Jahres- und Tagesverlauf gelingt durch Rückgriff auf das ruhend-äquatoriale Koordinatensystem (delta, t). Dafür gibt es die grundlegende Gleichung [1], [2]
sin(h) = sin(BREIT) * sin(delta) + cos(BREIT) * cos(delta) * cos(t). (*)
BREIT ist der betrachtete Breitengrad, die ruhend-äquatorialen Koordinaten sind delta und t, also Deklination und Stundenwinkel der Sonne. Alle Winkel sind im Bogenmaß zu verstehen.
Sin(delta) wiederum hängt von der Position der Erde auf ihrer Umlaufbahn (hier: Kreisbahn) ab. Numeriert man die Tage ab Frühlingsanfang mit der Tagesnummer TNR, dann ist der zugehörige Ekliptikwinkel der Erde auf ihrer Kreisbahn, von der Sonne aus betrachtet, tau = TNR/365 * 2 Pi. Damit und mit dem Neigungswinkel NEIG der Erdachse gegen die Erdbahnebene (Schiefe der Ekliptik) erhält man sin(delta) = sin(NEIG) *sin(tau) [3].
Um die mittlere Intensität Phimittel auf Breitengrad BREIT am Tag TNR zu bestimmen, muss man Phi(h) unter Einsetzen von Gleichung (*) über eine Erdumdrehung integrieren und das Ergebnis auf die zu BREIT gehörige Ringfläche verteilen. Für die Integrationsgrenzen wird der Stundenwinkel t0 der Sonne bei Sonnenaufgang benötigt.
Bei der Bestimmung von t0 ist eine Fallunterscheidung erforderlich: man erhält t0 durch Nullsetzen von Gleichung (*) für Breitengrade unterhalb der Polarregion, wo weder Mitternachtssonne noch Polarnacht herrschen. Der Grenzbreitengrad, der die Polarregion vom Rest abtrennt, hängt natürlich vom Datum ab und bestimmt sich zu BRgrenz = Pi/2 – |delta|. Oberhalb BRgrenz ist t0 = Pi zu setzen.
Die zu Phimittel gehörige Gleichgewichtstemperatur berechnet man schließlich nach Stefan-Boltzmann zu T = (Phimittel / (epsilon * sigma))^0.25. Für einen schwarzen Körper wäre die Emissivität epsilon = 1, wir haben uns aber für den Wert 0,95 entschieden. sigma = 5,67E-8 W / (m² * K4) ist die Stefan-Boltzmann-Konstante.
„Die genannte Zielsetzung und die Begrenzung des Rechenaufwandes erfordert ein sehr vereinfachtes Modell der Erde, das selbstverständlich nicht mehr die Realität abbildet, aber sehr wohl eine Basis für das Verständnis unserer Realität abgeben kann.“
Allein dieser Satz ist die reine Kapitulation.
Danach rechnen Sie sich tüchtig und ergiebig quer durch die Parameter, um schließlich lapidar zu konstatieren : „Das lässt sich vergleichen mit dem Anziehen einer Wollmütze im Winter.“
Das ist Ihr Problem. Sie möchten anhand Ihrer Vorstellung eine Analogie herstellen. Sie kreieren ein Treibhaus, eine Wollmütze für die Welt. Dafür wird gemittelt und „vereinfacht“, 👉 Rechenakrobatik bis der Arzt kommt. Aber so simpel ist das Klima nicht gestrickt, Herr Mechtel, weder in tatsächlicher, vorherrschender Komplexität, noch in Ihrem fatal abgespeckten Modell.
Einstein: Man soll die Dinge so einfach wie möglich machen, aber nicht einfacher.
Sie können keine Dinge einfach machen, die Ihnen in ihrer Vollständigkeit nicht einmal bekannt sind.
Ansonsten schließe ich mich vollumfänglich der Meinung von Prof. Puschner an. 🥰👍
…und der von besso keks 😁.
<<Aber so simpel ist das Klima nicht gestrickt>>
Ganz meine Meinung, Frau Schönfelder. Steht auch im Artikel drin.
„Das ist der Vorteil in der Physik: man kann störende Komponenten einfach mal beiseite räumen, indem man ein überschaubares Modell bastelt.“
Kann man, aber das entspricht eben nicht der Realität.
Wenn ich in meinem Leben alle störenden Komponenten „einfach mal beiseite räume“, wird es auch völlig übersichtlich, entspricht aber nicht der Realität. Keine Steuern, brave Kinder, weniger Arbeit, freie Autobahnen, vernünftige Politik, keine Inflation……
Gutes Modell !
Ist dies nun die Art von Disput, die Sie führen wollen, auf der Basis von Unverständnis des Disputgegenstandes?
Sie haben gar nicht mitgekommen, dass Herr Mechtel hier erneut bewiesen hat, dass Webers Modell falsch ist: die beobachtbare Temperatur ist nicht erklärbar über Webers Annahme, dass die beobachteten Temperaturen an der Erdoberfläche daraus resultieren, dass sich die Tagseite gemäß SB mit der am lichten Tag zugeführten Sonneneinstrahlung erwärmt.
Die „Wollmütze“ (Treibhauseffekt) ist nur das missing link, welches zwischen Weber und der Realität fehlt und welches aus der Diskrepanz zwischen Weber und der Realität zwingend folgt. Ich sehe daran nichts zum Disputieren, Sie etwa? Wenn ja, dann liefern Sie Argumente, die nicht belegen, dass Sie nichts verstanden haben. Wenn Sie das können, wäre es „disputabel“. Alles andere rangiert je nach Fall unter Unwissenheit in der Sache oder Trollen.
Heinemann, denke habe meinen Standpunkt bereits deutlich formuliert und sehe keine Veranlassung für „Argumente, die nicht belegen, dass ….“..😂
Argumente, die nichts belegen, belegen nichts. 😁😎
….aber da kennen Sie sich ja aus….
Hallo Herr Michael Mechtel,
vielen Dank für Ihren interessanten Einblick in Ihren Modellansatz und daß Sie Ihre Ergebnisse in die EIKE Diskussion einbringen. Die Randbedingung haben Sie für mich nachvollziehbar begründet.
Meine Frage: Haben Sie Ihr Modell für auch schon mal für einen Albedowert von 0.12 durchlaufen lassen unter sonst gleichen Bedingungen? Oder könnten Sie das machen? Wie groß wäre dann bei 0 Grad Achsneigung die minimale, die mittlere und die maximale Temperatur? Sie ahnen worauf meine Frage hinzielt- auf den Mond.
Mit dem Albedowert 0.12 bei unverändertem epsilon = 0.95 würde man in der Achsstellung 0 Grad die maximale Ein- und Abstrahlung am Äquator mit 383 W/m² und T = 290 K erhalten und ein globales Mittel von 273 K. Das sagt aber nichts über den Mond aus, weil der im Gegensatz zu meinem Modell sehr langsam um die eigene Achse rotiert.
Dem Mond würde man näher kommen mit Achsstellung 90 Grad zur Zeit der Sommer-Sonnenwende: die Maximalintensität wäre dann 1203 W/m² und dazu die Temperatur 387 Kelvin. Allerdings dürfte dieser Wert zu hoch liegen, weil das Mondgestein ja eine Wärmeleitfähigkeit hat und Wärme zwischenspeichert.
Aus dem gleichen Grund liefert mein Modell keinen realistischen Wert für die Minimaltemperatur auf der Nachtseite, und somit ist auch die globale Mittel-Temperatur von 155.5 K bzw. der semiglobale Mittelwert von 311 K für die Tagseite mit Vorsicht zu genießen!
Hallo Herr Mechtel,
vielen Dank für die Werte Ihres Monddurchlaufes. In meiner Berechnung für einen ruhenden Mond bin ich als maximale mögliche Temperatur nur aus solarer Einstrahlung von 1368 W/m2 auf 109 Grad Celsius oder effektiv 1204 W/m2 gekommen. Im Ergebnis stimmen wir in dieser Modellstufe überein.
Gemessen werden gemäß neuster Chinesischer Infrarotkarte, die jetzt den gesamten abdeckt, Achtung: Rund 130 Grad Celsius. Dies entspricht einer äquivalenten effektiven Abstrahlung von 1500 Watt/m2. Die gemessene Leistung ist meiner Meinung nach nur möglich, zusätzlich rund 300 W/m2 aus dem Mondkern radiogene abstrahlen.Genaus diese Phänomen nimmt die NASA für den Pluto an. (Hierzu hatte ich mich ja schon auf dem EIKE Blog und auch Quellen angegeben.) Dies ist ein Grund, weshalb ich mit meinem Modell für die Erde mit Tiefenwärme rechne. Ferner rechne ich Wärmespeicherung vom Tag in die Nacht, über Breitengrade ausdifferenzierte Albedo gemäß Satellitenmessung, ausdifferenziertes SH und LH, Berücksichtigung von Satm( Staubpartikel, Aerosole), einer Rotation in 24 h und einen vom Breitengrad abhängigen Lichteinfall. Zum Schluss bildet die energetische Bilanzierung Satellitmesswerte ab. Das war mein Modellansatz. Es ist auch ein Hemisphärenmodell. Ach ja, was ist rausgekommen bei mir, eine mittlere Temperatur von 14.7 Grad Celsius.
Wir unterscheiden uns in der Beurteilung eines THE. Das ist ja klar. Nochmals danke für Ihre Modellwerte.
Hallo Herr Agerius,
die besagten 1500 W Abstrahlung erzielen Sie tatsächlich mit einer absolut schwarzen Mondoberfläche. Ohne mich jetzt festlegen zu wollen: aber man könnte in Erwägung ziehen, dass die Emissivität epsilon der Mondoberfläche < 1 ist, dann wären die 130 oC auch mit dem solaren Strahlungswert erreichbar.
Konkret: die STB-Gleichung nach epsilon aufgelöst ergibt epsilon = Intensität / (epsilon * T^4). Zahlenwerte eingesetzt: epsilon = 1203 / (5.67E-8 * (273 + 130)^4 = 0.80.
Dieser Wert klingt nicht unvernünftig, aber ich kann nicht beurteilen, ob er stimmt.
Hallo Herr Ketterer,
Sie haben nicht genau genug gelesen, was ich geschrieben hatte. Erst hatte ich vom Mond geschrieben . Danach steht, Zitat: „Dies ist ein Grund, weshalb ich mit meinem Modell für die Erde mit Tiefenwärme rechne. “ Und dann kommen die 14.7 Grad Celsius für das Erdemodell, in dem ich beschreibe, wie ich die Erdatmosphäre modelliere. Latent Heat und Sensibke Heat, bzw. LH und SH gibt es auf dem Mond nicht. Spätestens hier hätte Ihnen auffallen müssen, dass ich nicht mehr vom Mond spreche, denn der hat keine Wasserdampf Atmosphäre.
Sehr geehrteR Pseudonymus Agerius,
sie schreiben über dei mittlere Temerpatur des Mondes:
„Ach ja, was ist rausgekommen bei mir, eine mittlere Temperatur von 14.7 Grad Celsius.“
Dies steht im deutlichen Widerspruch zu diesem wissenschaftlichen Artikel
https://www.hou.usra.edu/meetings/lpsc2023/pdf/2198.pdf
‚Die täglichen Temperaturschwankungen im Mondboden der Äquatorregion sind in einer Tiefe von etwa 80 cm ausgeglichen, und es herrscht eine eine Temperatur von etwa -21°C.‘
Und auch im Widerspruch zu den gemessenen an den Apollo-Landestellen.
MfG Ketterer
Sehr geehrter Pseudonymus Agerius,
Sie haben recht, ich habe Ihren Beitrag nicht gründlich genug zu Ende gelesen. Denn nachdem sie das hier geschrieben haben:
„[…] zusätzlich rund 300 W/m2 aus dem Mondkern radiogene abstrahlen.[…] Dies ist ein Grund, weshalb ich mit meinem Modell für die Erde mit Tiefenwärme rechne.“
war für mich das gründliche Weiterlesen gescheitert. Wenn ich Sie richtig verstehe, nehmen Sie eine radiogene Abstrahlung aus dem Mondkern an der Mondoberflächen von ca. 300W/m² an. Das ist cum grano salis im Bereich der mittleren solaren Einstrahlung. Warum also soll ich da ernst- und gewissenhaft weiterlesen?
Es stimmt, Ihre 14°C waren für die Erde ermittelt. Welcher radiogenen Wäremfluss an der Erdoberfläche liegt dem zu Grunde?
MfG
Ketterer
Leider sind die Formeln im Artikel bei der Veröffentlichung unter die Räder geraten. Man kann daher leider nicht sehen, was konkret gerechnet wird. Besteht die Möglichkeit, das zu korrigieren oder vielleicht den Original-Artikel als PDF anzuhängen?
Das Modell von Herrn Weber ist im Laufe der Zeit mehrfach verändert worden. Ich habe das Gefühl, das momentan niemand genau sagen kann, wie es wirklich aussieht. Dafür springen die Artikel dazu zu sehr zwischen den verschiedenen Versionen hin und her. Das rein auf Strahlung bezogene gehört eher zu einer der ersten Versionen, als er noch postulierte, die Temperatur/Abstrahlung auf der Rückseite wäre 0., da es keine Einstrahlung gibt (bzw. die Temperatur auf der Rückseite des Mondes wäre Resultat der Einstrahlung von der Erde, wenn ich mich recht entsinne)
Sie diskutieren hier also einen Fall, den Herr Weber schon lange ad acta gelegt hat und erlauben ein leichtes vom Tisch wischen Ihrer Rechnung, wie man an den ersten Kommentaren schon sieht. Könnten Sie sich vorstellen, das zu modifizieren, indem Sie eine Oberflächenschicht modellieren, deren Temperatur sich entsprechend der zu- und abfließenden Energieflüsse ändert? So wie es andere vor ihnen schon gemacht haben (Spender, Kramm, (ich)). Ich würde das sehr begrüßen.
Eine Berücksichtigung von Energieflüssen müsste Energie-Speichereigenschaften einbeziehen. Das würde den Rahmen sprengen. Es würde auch nur das Modell verkomplizieren, ohne eine realistische Annäherung an die wirkliche Erde zu erreichen.
Es ging mir übrigens nicht um eine Bestätigung von Uli Webers Modell, in welcher Version auch immer. Ob Abstrahlung an unbeschienenen Stellen auftritt, hängt davon ab, wie lange diese unbeschienen sind. In meinem Modell rotiert die Erde schnell genug, um Oberflächenwärme ’nach hinten‘ mitzunehmen und auch dort abzustrahlen. Bleibt aber eine Region einen konventionellen Tag (ein 365-stel Jahr) oder länger unbesonnt, soll sie sich schnell gegen Null Kelvin bewegen, weil keine nennenswerte Energiespeicher vorhanden sind.
Michael Mechtel am 3. März 2024 um 17:28
Sie sehen allerdings, wie schnell Ihre Arbeit aufgrund dieses fehlenden Teils abgelehnt wird. Herr Dietze versucht seit Jahren das, was Sie hier für die ganze Erde und den Jahresgang der Einstrahlung gemacht haben, am einfachen Beispiel des Äquators zu erklären. Der Erfolg ist gleich null. Man kann das der eigenen Vorstellung widersprechende mit der einfach Begründung leicht vom Tisch wischen. Das finde ich sehr schade, daher meine Anmerkung.
Das wollte ich auch nicht unterstellen.
Egal was damit „bewiesen“ ist, Temperatur ist und bleibt eine Intensive Variable und somit ist sie nicht mittelbar. Ob dies für manche Annahmen hilfreich scheint oder nicht, das ist ein Fakt.
Der nächste „Pippi Langstrumpf“ Physiker – Ich mach‘ mir die Welt Widdewidde wie sie mir gefällt.
Mit ihrem Erdmodell können Sie zwar rechnen, aber dieses Modell hat absolut nichts mit der realen Erde zu tun, und ist damit physikalisch völlig wertlos.
Was wollen Sie damit verifizieren? Ihre Fähigkeit mit sinn- und realitätsferner Physik zu hantieren – Die Verifizierung ist Ihnen gelungen!
<<Was wollen Sie damit verifizieren?>> Das steht ja im Artikel drin.
Übrigens ist Modellbildung ein sehr gebräuchliches und legitimes Mittel in der Physik, und jede experimentelle Überprüfung einer Theorie lebt davon, Störfaktoren weitestgehend auszuschalten, um sich auf den untersuchten Einfluss konzentrieren zu können.
„Übrigens ist Modellbildung ein sehr gebräuchliches und legitimes Mittel in der Physik, und jede experimentelle Überprüfung einer Theorie lebt davon, Störfaktoren weitestgehend auszuschalten, um sich auf den untersuchten Einfluss konzentrieren zu können.“
Herr Mechtel, es kommt immer darauf an, WAS MAN UNTERSUCHEN möchte. Wenn Sie beweisen wollen, ob sich die Erde dreht, können Sie die Atmosphäre eventuell 😁 vernachlässigen. Wenn Sie ergründen wollen, ob Ihre Frau Sie betrügt, reicht es nicht, Ihr Schlafzimmer leerzuräumen, der Gattin Handy zu beschlagnahmen und das Auto zu zertrümmern. Das schafft zwar Übersicht, aber völlig nutzlose.
Vielleicht sollten Sie Ihre Wollmütze einfach ablegen. Eventuell hat die Erde gar keine auf !,
sondern verfügt über Filtersysteme in dynamischen Prozessen, die automatisch Ausgleich schaffen ?
Ihre Annahmen sind doch schon vollkommen falsch!
Zum Beispiel die Annahme, dass die Erde ein schnell rotierender sphärischer Körper ist, stimmt nicht. An welchen energetisch-bestimmten Parameter machen Sie fest, ob man von einem sehr schnell, schnell, moderat, langsam oder sehr langsam rotierenden sphärischen Körper sprechen kann?
Wenn Sie das erkannt haben (Siehe: Gaußsche Theorie der periodischen Dämpfung), dann werden Sie feststellen, dass alle Ihre Berechnungen für die Tonne sind.
So ist es. Auch direkt zu sehen am Ausstrahlungsspektrum der Erde, oder Venus. Durch die Atmosphäre wird weniger Wärme abgestrahlt, als ohne Atmosphäre. Dadurch stellt sich eine höhere Bodentemperatur ein.
Aber weil ich das sage, bin ich ja ein Gaukler des IPCC.
„Durch die Atmosphäre wird weniger Wärme abgestrahlt, als ohne Atmosphäre. Dadurch stellt sich eine höhere Bodentemperatur ein.“, konsequent zu Ende gedacht, hätten wir uns alle längst den S.ck verbrannt. Durch die Atmosphäre wird nicht weniger abgestrahlt, sondern zweifelsfrei erfolgt die Abstrahlung nur zeitversetzt und das ist ansich gut so, weil dadurch das Auskühlen langsamer vonstatten geht und uns des Nächtens ohne Energiezufuhr nicht ganz erfrieren lässt.
Ach so, Strahlung! Sonst nichts.
So wie bei einer Hauswand. Die Strahlung ist die „erhebliche Schutzfunktion gegenüber der Auskühlung“, oder nicht?
Ach so, nur wenn man die Hauswand weglaesst und das Zimmer direkt ins Weltall abstrahlt!
Schluessiger Vergleich! Es ist immer Strahlung und Ohne Atmosphaere, wenn man nicht mit Strahlung und mit Atmosphaere plus Konvektion und Latente Waerme alles erklaeren kann.
Das ist aber notwendig fuer unsere Atmosphaere!
Weniger als was? Hoeher als was?
Wie der Autor selbst schreibt, sollen die vereinfachenden Annahmen dazu dienen, den Rechenaufwand überschaubar zu machen. Unter anderem wird eine schnell rotierende Erde angenommen, damit die Unterschiede zwischen Tag und Nacht verschwinden. Eine Vorstellung, ob dann eine Rotation in 1 Stunde oder 5 Minuten erfolgen soll, wird nicht vermittelt.
Den Ausführungen kann ich mich nicht anschließen, wobei einer Temperaturmittelung das Wort geredet wird. Dabei handelt es sich nicht um Mittelungen der Signale eines einzelnen Temperatursensors, um Störeinflüsse zu minimieren, sondern um Mittelungen aus Temperaturen an verschiedenen Messpunkten und damit im Bereich unterschiedlicher Zonen mit unterschiedlichen Eigenschaften. Grundsätzlich lassen sich Leistungs- und Energiegrößen nicht aus Mittelwerten berechnen, sondern einzig aus Augenblicksgrößen. Und Wärme, wenn man also eine Erderwärmung erkennen will, ist eben eine Energiegröße. Ohne tieferes Physikverständnis kann man das schon an den unterschiedlichen Einheiten °C und Ws erkennen.
Auch gibt es nur ein Stefan-Boltzmann Gesetz, aber kein „Hemisphärisches Stefan-Boltzmann Gesetz“. Bestenfalls kann man versuchen, das Gesetz einschränkend auf eine Erdhalbkugel mit fragwürdigen Ergebnissen anwenden. Die gesamten Annahmen (keine Atmosphäre, kein Wasser, vernachlässigbare Wärmeleitung, Ausschluss anderer Energiequellen) beschreiben alles Mögliche, nicht aber unseren Globus, was der Verfasser ja auch einräumt.
Was also bleibt, ist ein Modell, bei dem man bestenfalls erkennen kann, ob die unter falschen Annahmen durchgeführten Rechnungen richtig oder falsch sind, also eine Bewertung der angewandten Mathematik. Das entscheidende ist jedoch, ob ein gemachter Ansatz auf das zu berechnende Objekt passt und richtig ist. Das ist hier jedoch per Definition bereits ausgeschlossen worden.
Eines kann man den Ausführungen jedoch entnehmen: Das System Erde ist derart kompliziert, dass die Menschen weit weg von einem theoretisch denkbaren Verständnis sind. Daraus folgt der Zwang, an seine Annahmen zu glauben – und schon landen wir bei einem sektenhaften Verständnis von Greta, Luisa oder von mir aus auch Rahmstorf, Schellnhuber oder Edenhofer. Wer dennoch daraus abgeleitet glaubt, notwendige und zerstörerische Einflüsse auf die Lebensbereiche der auf dem Globus lebenden Menschen nehmen zu müssen, muss die Voraussetzung derzeitiger Politiker mit sich bringen, die die für die Menschen notwendige Energieversorgung zerstören und das Lebensgas CO2 in gutes und schlechtes CO2 aufteilen können. Zu allem Überfluss wollen sie das schlechte CO2 vergraben, vielleicht vermuten sie, dass man das schlechte CO2 an der Farbe derer Pantoffeln erkennen kann.
<<Auch gibt es nur ein Stefan-Boltzmann Gesetz, aber kein „Hemisphärisches Stefan-Boltzmann Gesetz“. >>
Das sehe ich ganz genau so, und ich hoffe, dass nicht der Eindruck entstanden ist, ich würde das letztere verteidigen. Im Gegenteil, ich entwerfe ja gerade ein Gegenmodell dazu.
Auch haben Sie völlig recht, dass das System Erde / Atmosphäre viel zu kompliziert ist, um es leicht verstehen zu können. Das ist der Vorteil in der Physik: man kann störende Komponenten einfach mal beiseite räumen, indem man ein überschaubares Modell bastelt, und kann schauen, was dann übrig bleibt. Im Idealfall kann man das Modell im Labor nachbilden und experimentell überpüfen. Oder vielleicht einzelne Einflussfaktoren gezielt dazuschalten, um ihre Auswirkung zu studieren. Beim Klimasystem hat man aber leider keine Laborsituation, sondern die komplexe Wirklichkeit.
@Mechtel
Nach der Definition der World Meteorological Organization (WMO), eine Definition, die 1992 nochmals bekräftigt wurde, ist Klima als
„Synthesis of weather conditions in a given area, characterized by long-term statistics (mean values, variances, probabilities of extreme values, etc.) of the meteorological elements in that area“
aufzufassen.
Der Begriff „long-term statistsics“ beinhaltet, dass eine Klimaperiode mindestens 30 Jahre umfasst, weil sonst die statistische Forderung der stochastischen Verteilung von Daten gar nicht zu erfüllen ist. Wenn also ein Klimawandel zu diagnostizieren ist, dann sind mindestens zwei sich nicht überlappende Klimaperioden erforderlich, wovon eine als Referenzzustand dient. Folglich sind Zeitreihen der meteorologischen Größen, die sich über mindestens 60 Jahre erstrecken, erforderlich, um zwei voneinander unabhängige Klimaperioden bestimmen zu können.
Von Prof. Dr. habil. Gerlich stammt die Aussage (Gerlich, 1995):
„Die Abstrahlung eines Körpers richtet sich aber nach der tatsächlichen Temperatur und nicht nach irgendwelchen Temperaturmittelwerten! Temperaturmittelwerte müssen immer aus gegebenen Temperaturverteilungen bestimmt werden und für diese Mittelwerte gibt es keine lösbaren theoretischen Modelle. Damit ist wohl deutlich gezeigt, daß alle Berechnungen mit einem „mittleren Strahlungsbudget“ oder einer „Strahlungsbilanz“ nichts mit mittleren Erdtemperaturen zu tun haben.“
#Gerhard Kramm am 3. März 2024 um 19:59
Dem Kollegen Gerhard Kramm ein großes Dankeschön für das Zitat vom Kollegen Gerlich, womit doch jeder den Unsinn mit sog. Global-Temperaturen endlich einmal ad acta lagen sollte. Und das ohne überhaupt noch schlimmer, mit der 4. Potenz zu agieren.
Wer es wissenschaftlich genau nimmt, kann nur zu dem einzig richtigen Schluss kommen, dass die ganzen stolzen Berechner zur Erderwärmung, insbesondere in Potsdam, einfach nur völlig daneben liegen, auch wenn sich die Politiker ausbeutend über CO2-Steuern wie die Schmeißfliegen auf deren Ergebnisse stürzen. Anstatt einer Zunahme des Verständnisses hochkomplexer Vorgänge und stiller Anerkennung, dass es uns Menschen nicht gegeben ist, die gesamte Welt in ihren Zusammenhängen zu verstehen, nimmt leider nur eines zu: Die Verblödung – oder um im gängigen Sprachgebrauch zu bleiben, die Global-Verblödung (ob gemittelt oder nicht spielt dabei keine Rolle mehr)!
„Dem Kollegen Gerhard Kramm ein großes Dankeschön für das Zitat vom Kollegen Gerlich, womit doch jeder den Unsinn mit sog. Global-Temperaturen endlich einmal ad acta lagen sollte. Und das ohne überhaupt noch schlimmer, mit der 4. Potenz zu agieren.“ 👍😎
Me too. Angenehm, daß es doch noch kluge Menschen gibt.
👉 „Wer sich mit Raten, Vermutungen und unbewiesenen Schlussfolgerungen zufrieden gibt, der wird nie gescheit.“
Mark Twain
Peter Puschner, Prof. Dr.-Ing. schrieb am 04/03/2024, 14:59:00 in 363116
Die Kritik von Herrn Kramm richtet sich gegen die Art und Weise der Berechnung der Temperatur, nicht gegen die Temperatur an sich. Er hat ja seine eigene Veröffentlichung zu dem Thema, in der er die wohl auf eine Art und Weise ermittelt, die seiner Meinung nach richtig ist. Auch Gerlich und Tscheuschner haben Varianten der Berechnung gezeigt, die ihrer Meinung nach richtig sind.
@Kramm
„Die Abstrahlung eines Körpers richtet sich aber nach der tatsächlichen Temperatur und nicht nach irgendwelchen Temperaturmittelwerten!“
Volle Zustimmung von meiner Seite. Es ist bezeichnend, dass einige Kommentatoren, die sich enthusiastisch zu diesem Zitat von Herrn Gerlich bekennen – und möglicherweise auch Sie? – gar nicht mitbekommen haben, dass ich im Artikel genau nach diesem Grundsatz vorgegangen bin. Die Namen brauche ich nicht zu nennen, die haben sich ja selbst geoutet.
Und es ist denen offenbar auch entgangen, dass ich die Rolle, die ein globaler Temperaturwert spielen kann diskutiert und den Fehler, der damit verbunden sein kann, sogar an 2 Beispielen quantifiziert habe. Das zeigt deutlich die „Qualität“ mancher Kommentare.
#Michael Mechtel am 3. März 2024 um 17:06
Leider sind die, die ausgeräumt werden, nicht die störenden Komponenten, sondern solche, die mit ihren damit verbundenen Ausgleichsprozessen gerade das momentane Klima schaffen. Wenn dann für die Tagestemperatur z. B. -80°C herauskommen, hat man mindestens die Falschen als störende Komponenten bezeichnet und ausgeräumt.
Was man studieren kann, ist einzig, wie ein falsches „überschaubares“ Modell antwortet, wenn man einzelne angenommene Einflussfaktoren ausschaltet. Das auf das reale Klima zu übertragen, kann man zwar machen, rückt die falschen Annahmen aber nicht näher an die realen Verhältnisse.
Dass man auch empirisch erzeugte Formeln einerseits anwenden kann, zeigt das Bernoulli-Gesetz bei der Betrachtung, warum ein Flugzeug fliegt. Sieht alles richtig aus, versagt aber, wenn ein Flugzeug auf dem Rücken fliegt, was zwar real funktioniert, aber theoretisch gar nicht sein kann.
An welcher Stelle habe ich den Anspruch erhoben, die Ergebnisse auf das das reale Klima zu übertragen? Und wie größenwahnsinnig müsste man sein, mit einem EXCEL-Arbeitsblatt das reale Klima modellieren zu wollen? Sie haben den Sinn des Beitrages offenbar nicht verstanden.
Wenn ich Sie richtig verstanden habe, Herr Mechtel, so wollen Sie der Erde eine Außendämmung verordnen, und damit den THE in „Realität“ begründen.
„Jeder Bauphysiker weiß, dass die Außendämmung einer Hauswand bei gegebener Heizleistung im Inneren die Wandtemperatur anhebt.“
Mal davon abgesehen, daß diese starke Vereinfachung an der Absurdität scheitert, daß Sie einen erschaffenen „Status Quo“, die Außendämmung, mit emergenten, dynamischen Prozessen des Klimas vergleichen, frage ich mich, was Sie mit Ihrem Vortrag bezwecken, wenn nicht angenommene Phänomene eines r e a l e n KLIMAS zu beschreiben ?
„An welcher Stelle habe ich den Anspruch erhoben, die Ergebnisse auf das das reale Klima zu übertragen? Und wie größenwahnsinnig müsste man sein, mit einem EXCEL-Arbeitsblatt das reale Klima modellieren zu wollen? Sie haben den Sinn des Beitrages offenbar nicht verstanden.“
Sie modellieren also eine Fiktion ? Da kommen wir der Sache schon näher…😁✌️
Oh Gott, was man alles berechnen will und kann. Wenn wir als Maschinenbauer (habe u.a. Statik und Stahlbau gemacht) mit derartigen Annahmen eine tragegende Konstruktion errichtet hätten, wäre es lustig geworden. Aber solche Berechnungen über irgendwas richten ja keinen Schaden an, wenn sie nicht politisch Mißbraucht werden.
Herr Dr. Voge,
Sie haben mit Ihrer Anmerkung einen zentralen Punkt getroffen, und das meine ich ganz ohne Polemik. Ich habe seit längerem den Eindruck, dass es einen grundlegenden Unterschied gibt zwischen ingenieurmäßigem Denken und physikalischem Denken.
Der Ingenieur denkt grundsätzlich erstmal in Kategorien, die realisierbar sind, und das ist für seine Tätigkeit auch sehr vernünftig. Ich fahre auch lieber über Brücken, von denen ich weiß, dass sie fachkundig und realistisch geplant und gebaut sind.
Das verstellt aber anscheinend oft den Blick für physikalische Denkweisen. Der Physiker konstruiert nichts. Er untersucht Zusammenhänge, und dafür ist es mitunter auch nützlich, Extremsituationen zu betrachten oder Gedankenexperimente durchzuführen. Der von allen Besserwissern gern zitierte Einstein war ein Meister im Erfinden von Gedankenexperimenten. Den Physiker bringt so etwas weiter, auch wenn der Ingenieur erstmal damit nichts anfangen kann.
Schade, dass es einigen Leuten nicht möglich ist, über den eigenen Tellerrand zu schauen, wie man hier im Kommentarteil hinreichend studieren kann.
„Oft wird dagegen eingewandt, dass der Erdboden direkt von der Sonne erwärmt wird und die kühle Atmosphäre nicht den warmen Erdboden noch weiter erwärmen könnte. Doch, sie kann! Indem sie nämlich als Hindernis für die Abstrahlung fungiert.“
Mamma mia!
Gut, daß ich beim Überfliegen diesen Satz gelesen habe.
Kann mir also sparen diesen „Beitrag“ zur Volksverblödung im Detail zu lesen
@besso keks
Ja kann ich nur zustimmen!
ich kann nur noch wiederholen, was ein Mensch (Araber) in Dubai auf die Behauptung, dass es dort so warm ist , liegt nicht ander Sonne sondern an einer Strahlung, die angeblich aus der Luft kommt, lachend antwortete.
“ Warum ist es den bei euch so kalt, ihr habt doch auch Luft, oder?“
Es gibt auf der Erde einiges, was ganz einfach ist, aber gerne sehr kompliziert gemacht wird.
Ist ja menschlich, denn die meisten Menschen bewundern andere, wenn diese angeblich komplizierte Sachverhalte verstehen!
Aber um die These vom THE,(denn mehr ist sie nicht), ad absurdum zu führen, muß man nicht sehr kompliziert denken, oder Handeln.
Es reichen zwei Glasplatten und etwas schönes Wetter!
Oder ein dunkler Stein, Thermometer und einmal bei Sonnenschein den Stein auf dei Terrasse legen und ein andermal den Stein bei bedeckten Himmel auf die Terrasse legen, und jeseils nach ca einer halben Stunde die Temperatur des Steines messen!
Und welch Überraschung, der Stein müßte nach dem THE Aberglauben viel wärmer werden!
Die Atmosphäre wirkt wie eine Isolierung?
Kann man so sehen, aber dann in beide Richtungen, die starke Sonnenstrahlung kommt nicht bis zum Boden!
Siehe Mond, ohnew Atmosphäre, max. Temperaturen bis ca 130 Grad C – auf der Erde nur bis ca 80 Grad C!
Und auf der Venus kann es auch verdammt kalt werden!
„Rund 125 Kilometer über der Planetenoberfläche wird es nach ihren Erkenntnissen dort mehr als eisig. Mit einer durchschnittlichen Temperatur von rund minus 175 Grad Celsius existiert dort eine Atmosphärenschicht, die kälter als jede Luftschicht der Erde ist“
https://www.spektrum.de/news/hoellisch-kalt-auf-der-venus/1166478
Warum es so heiß ist auf der Venus, kann man auf der Erde in jedem Deiselmotor beobachten!
Und wenn man an einer Gasflasche das Gas ausströmen läßt, wird das Ventil eiskalt!
Ganz einfache Experimente, ohne die,die ganze Physik nur ein Kapitel in der Pholosophie wäre!
Gut zu beobachten bei den Diskussionen über die Gravitation oder Evolution!
Viele Fragen offen, weil keine Beweise durch Experimente!
ich bleibe dabei:
THE wurde erfunden niemals entdeckt und bewiesen!
CO2 erwärmt nicht die Erde, eher das Gegenteil!
Herr Ordowski, lesen Sie mal den Kommentar von Herrn Bergmann am 4. März 2024 um 21:59.
Sein solarer globaler Temperaturmittelwert erreicht nach 16 Tagen realer Rotation -16 Grad. Dabei ist die Erdachse nicht geneigt. Mein globaler Mittelwert bei idealer Speicherung über Tag/Nacht auf allen Breitenkreisen ist -21 Grad und NICHT +15 Grad. Trotzdem bleiben Sie bei Ihrem dunklen Stein und dabei dass der THE erfunden, niemals entdeckt und experimentell bewiesen wurde – toll! CO2 und Gegenstrahlung erwärmen also nicht die Erde, eher das Gegenteil…
Herr Ordowski, damit meine Berechnung zu der global-mittleren solaren Temperatur von -21 Grad (im Gegensatz zu den +15 Grad von Uli Weber) Ihnen nicht skurril vorkommt, ein Hinweis: Wenn man meine 252 K mit (1/0,93)^0,25 multipliziert (ich habe mit dem Emissionsgrad 1 gerechnet) und meine Solarkonstante von 1364 W/m² auf 1367 erhöht, kommen 257 K, also die -16 Grad von Herrn Bergmann heraus. Auch er hat übrigens ein flächengewichtetes Mittel berechnet.
Da muss ich Ihnen vollkommen zustimmen, insbesondere das Beispiel Mütze zeigt das Problem auf. Wenn es so wäre wie behauptet, dann müssten allenthalben Leute mit Brandwunden an der Rübe rumrennen, tun sie aber nicht, weil die Mütze einzig die Geschwindigkeit der Wärmeabgabe dämmt aber nicht verhindert.
Sie sind sich doch dessen bewusst, dass in einem nicht-abgeschlossenen System eine Umhüllung einen innenliegenden Körper auf höhere Temperaturen erwärmen kann als ohne diese Umhüllung. Das hatten Sie so zum Gedankenexperiment mit Eisschicht um beheizten Kaffee im Weltall geschrieben.
Warum sollte das bei der Atmosphäre und Erdoberfläche anders sein?
Wenn sie die Atmosphaere als Isolierschicht ansehen wollen, dann muss diese auch so gerechnet werden.
Welche Dicke der Isolierung nehmen sie an? Wie ergibt sich diese?
Mit Hilfe des Gradienten kann man dann ganz einfach die Temperatur innerhalb der Isolierung bestimmen.
Kein Mensch hat je bezweifelt (denke ich zumindest), daß Speicherfähigleit für Energie (=Wärme) einen wichtigen Einfluß auf die Energiebilanz ausübt. Dieser Einfluß ist offenbar die Differenz zwischen einer theoretischen Rechnung „ohne alles“ und der Wirklichkeit.
Daß es so eine Differenz gibt, ist aber kein Beleg für das, was allgemein Treibhauseffekt genannt wird.
So gesehen kann man zur Probe an jedem beliebigen Punkt der Erde Messungen machen und wird an keinem Ort einen Effekt feststellen können, daß die lokale Temperatur um ca. 33°C höher liegt, als es die lokalen vollkommen plausiblen Meßwerte ergeben (also ohne jeden Hinweis auf einen THE-Anteil). Natürlich erschweren Strömungen (Wasser, Wind) häufig eine direkte Interpretation der Meßwerte. Weil z. B. die Hitze einer Hitzewelle nicht lokal dort entsteht, wo sie gemessen wird.
Wer einen THE nachweisen will, muß ganz konkret und auf Basis der tatsächlichen Moleküleigenschaften (Wasserdampf, CO2, Methan, usw.) eine plausible Herleitung durchführen. Und zwar eine, die auch dem Energieerhaltungssatz genügt (Energie ist Leistung mal Zeit).
Daß es einen Riesenunterschied ohne und mit Speicherung gibt, erkennt man am Tag/Nacht-Wechsel. Ohne Speicherung wechselt sich ein positiver Halbsinus mit einer Phase Null Kelvin ab, in der Wirklichkeit gibt es nur minimale Unterschiede zwischen Tag und Nacht. Die Wassertemperatur eines Binnensees etwa hat keinen nennenswerten Tagesgang sonder nur einen Jahresgang.
stefan strasser schrieb am 3.3.2024, 10:11:58 in 362852
Auch mit Berücksichtigung der Speicherfähigkeit stellt sich ohne Atmosphäre eine deutlich geringere mittlere Temperatur ein, siehe Kramms „Moon as testbed“-Artikel… (sorry für das unvollständige Zitat). Die Speicherung von Wärme sorgt nur für eine Verringerung der Amplituden, wie Sie selbst korrekt schreiben, aber nicht für ein Anheben der mittleren Temperaturen auf das Niveau, das wir erleben. Wollen Sie nicht doch vielleicht Ihre eigene Rechnung aufgreifen und das in die Richtung weiter verfolgen? Sie waren auf einem guten Weg …
Herr Müller, „Die Speicherung von Wärme sorgt nur für eine Verringerung der Amplituden“ berücksichtigt nicht dass bei grossen Amplituden wegen Abstrahlung mit T^4 der Temperaturmittelwert deutlich geringer wird. Ich erwähne deshalb für meine Rechnung mit dem solaren Strahlungsmittelwert z.B. bei den -2,6 Grad über Tag/Nacht am Äquator (mit Albedo und Zenith-Sonne am Mittag) die ideale Speicherung, so dass man weiss das der reale Mittelwert niedriger ist. Herr Mechtel erreicht das bei geringer Speicherung durch sehr schnelle Erdrotation, was m.E. eher zu Kritik an den Ergebnissen Anlass gibt.