Vorbemerkung
Die Zeitreihen der Meßgrößen Temperatur und Anzahl der Sonnenstunden weisen ab den 1990er Jahren einen Anstieg auf, der über dem Mittel des Anstiegs dieser Größen von Aufzeichnungsbeginn bis Aufzeichnungsende liegt. Die Autoren Kowatsch,J. und Baritz,M. [1] haben den Beginn des Anstiegs der Temperatur auf das Jahr 1988 gelegt. Es sind jedoch keine Kriterien für diese Festlegung angegeben. In Diskussionen wurde das Fehlen der Angabe von Kriterien kritisiert. Im Folgenden werden Kriterien vorgestellt, die die Frage beantworten, wann ein Anstieg einer Zeitreihe beginnt. Dazu werden Funktionen der Kriterien über den Zeitreihen ermittelt.
Zerlegung von Zeitreihen
Bild 1 zeigt die Zeitreihe der an der Station Frankfurt/Main gemessenen jährlichen Sonnenstunden. Es ist ersichtlich, dass gegen Ende der Zeitreihe ein größerer Anstieg der Regressionsgeraden zu erwarten ist als über weite Teile des Verlaufs. Es ist nun die Frage zu beantworten, wo dieser Anstieg beginnt. Zu diesem Zweck wird die Zeitreihe in zwei Regressionsgeraden zerlegt, die miteinander verglichen werden. Nach den folgenden Kriterien wurden alle geeigneten Zeitreihen der Meßstationen für die Anzahl der Sonnenstunden und der Temperatur mit der Methode der fortschreitenden Regression untersucht.

Bild 1 Zeitreihe jährliche Sonnenstunden gemessen an der Station Frankfurt/Main
Methode der fortschreitenden Regression
Eine Zeitreihe enthalte n Meßwerte. Wird die Zeitreihe wird an einer Stelle t geteilt, ergeben sich zwei Teile mit nl Werten links von t und nr Werten rechts von t . Es gilt
n = nl + nr + 1.
Die Teilstelle t wandert schrittweise von links nach rechts. Da die Regressionsgeraden am Beginn und Ende der Zeitreihen aus mindesten drei Werten bestehen müssen, werden Start- und Endgeraden mit der Anzahl von nl0 und nr0 Werten für den Beginn und Ende der Regression festgelegt. Für die erste linke Regressionsgerade gilt somit nl = nl0. Die erste rechte Gerade beginnt mit dem Wert der Stelle nl0 – 1. Das rührt daher, dass der Endwert der linken Geraden und Anfangswert der rechten Geraden derselbe Wert sein sollen. Daraus ergibt sich die Anzahl der zu berechneten Regressionsgeraden zu
Z = 2 (n – nl0 – nr0 + 2)
Beispiel:
Bild 2 zeigt den Startpunkt der fortschreitenden Regression am Beispiel der Meßreihe Frankfurt/Main für die Anzahl der Sonnenstunden. Es liegen 73 Meßwerte vor. Die Anzahl der Start- und Endwerte werden mit nl0 = 5 und nr0 = 5 festgelegt. Es müssen somit Z = 2 (73 – 5 – 5 + 2), Z = 130 Regressionsgeraden berechnet werden.

Bild 2 Startpunkt der fortschreitenden Regression für die Sonnenstunden Frankfurt/Main
Beurteilungskriterien
Kriterium Maximaler Sprung
Wie an der Teilungsstelle in Bild 2 zu erkennen ist, stoßen die beiden Regressionsgeraden nicht in einem Punkt zusammen, es liegt ein Sprung vor. Dieser Sprung wird in [1] als Kriterium für den beginnenden Anstieg angenommen. In Bild 3 ist der Sprung zwischen den beiden Regressionsgeraden an der Stelle 1988 dargestellt. Da für die gesamte Zeitreihe die Sprünge berechnet sind, können diese über den Jahren aufgetragen werden und der maximale Sprung in positiver als auch in negativer Richtung ermittelt werden.

Bild 3 Sprung an der Teilungsstelle 1988 der Zeitreihe der Sonnenstunden
Kriterium Minimale Summe der Fehlerquadrate
Eine Regressionsfunktion wird üblicherweise dadurch ermittelt, dass die Summe der Quadrate der Abweichungen (SQA) zu den Meßpunkten minimal sein soll. Im Fall der geteilten Regressionsfunktion (hier in die beiden Geraden links und rechts der Teilungsstelle) soll eine gemeinsame Summe SQA gesamt nach
SQA gesamt = (SQA links + SQA rechts) / n
gebildet werden, wobei die Summe noch durch die Anzahl der Meßpunkte der Zeitreihe geteilt wird. Bei Anwendung dieses Kriteriums liegen die beiden am besten an die Meßpunkte angepassten Geraden vor. Wie sich jedoch bei der Auswertung der in Tabelle 1 zusammengefassten Zeitreihen gezeigt hat, muss die minimale Fehlerquadratsumme nicht mit dem Anstiegsbeginn übereinstimmen.
Kriterium Anstiegsbeginn
Gemäß der Fragestellung „Wann beginnt der maßgebliche Anstieg einer Zeitreihe“ erscheint es logisch, ein Kriterium zu verwenden, mit dessen Hilfe auch der Anstieg ermittelt werden kann. Um das Jahr des Anstiegsbeginns feststellen zu können, wird der Anstieg der rechten Regressionsgeraden
yr = a0r + a1r x
mit y als Meßgröße (Sonnenstunden, Temperatur) und x als Jahr der Messung, berechnet. Der Faktor a1r stellt den Anstieg der rechten Regressionsgeraden dar. Dieses Kriterium ist von den drei Möglichkeiten jenes, dass die Fragestellung beantwortet.
Beispiel: Zeitreihe Frankfurt /Main
Die in Bild 1 abgebildete Zeitreihe wird nach den drei o.g. Kriterien untersucht. Die Messung erstreckt sich über den Zeitraum 1950 bis 2022. Die Zeitreihe umfasst 73 Meßwerte.

Bild 4 Sprung der Anzahl der jährlichen Sonnenstunden
Als Startpunkt der fortschreitenden Regression wird der Meßwert des Jahres 1954 gewählt. Die linke Regressionsgerade wird aus den Werten 1950 bis 1954 berechnet. Die rechte Regressionsgerade beginnt 1954 und endet 2022. Im zweiten Schritt enthält die linke Gerade die Werte von 1950 bis 1955, die rechte Gerade die Werte 1955 bis 2022 usw. In den folgenden Bildern sind die Ergebnisse der Berechnungen nach den drei o.g. Kriterien dargestellt.
Bild 4 zeigt den Sprungverlauf an der Trenn- bzw. Berührungsstelle der beiden Regressionsgeraden. Es gibt Sprünge in Richtung Vergrößerung der Anzahl der Sonnenstunden oder der Verminderung von deren Anzahl. Der maximale Sprung bezüglich der Erhöhung der Anzahl fällt auf das Jahr 1988. An den Rändern des Verlaufs treten Einschwingerscheinungen auf, da die Regressionsfunktionen an Anfang und Ende der Zeitreihe sehr kurz sind. Das gilt auch für die Darstellung in Bild 5 und Bild 6.

Bild 5 Verlauf der Summe der Fehlerquadrate SQA ges
Etwas ungewöhnlich ist für die Station Frankfurt/Main der Verlauf der Summe der Fehlerquadrate SQA gesamt nach Bild 5. Das Minimum liegt hier bei 2012. In der Regel liegt dieses bei den größten Sprüngen – entweder in der positiven oder auch in der negativen Richtung.
In Bild 6 sind die beiden Anstiegsfunktionen, also die Werte des Anstiegs der linken und rechten Regressionsgeraden dargestellt. Von Interesse ist der Anstieg a1r der rechten Regressionsgeraden. Dieser sagt aus, wann der Anstieg der betrachteten Größe, hier der Anzahl der Sonnenstunden, beginnt. Wie in Bild 6 ersichtlich ist, steigt die Anzahl der jährlichen Sonnenstunden ab dem Jahr 2002 steil an. Ab 1988 beginnt eine Abweichung der bis dahin fast parallel zur Zeitachse verlaufenden Anstiegsfunktion. Der Anstiegsbeginn wird nach diesem Bild mit dem Jahr 2002 festgelegt.
Vergleicht man die Anstiegsfunktion mit der Sprungfunktion ist ersichtlich, dass auch für 2002 ein größerer Sprung vorliegt, der jedoch nicht das Maximum darstellt.

Bild 6 Verläufe des Anstiegs der linken und rechten Regressionsgeraden
In Bild 7 sind die Regressionsgeraden mit den Teilungspunkten 1988 und 2002 zusammen mit dem Konfidenzintervall der 2002 beginnenden Geraden dargestellt.

Bild 7 Vergleich der Regressionsgeraden mit den Teilungspunkten 1988 und 2002
Naturgemäß ist der Anstieg der 2002 beginnenden Geraden steiler. Allerdings liegt auch die 1988 beginnende Gerade im Konfidenzintervall, so daß kein signifikanter Unterschied besteht.
Zusammenfassung
Ausgehend von Artikeln zur Temperaturentwicklung in Deutschland, die das Jahr 1988 als Beginn des Temperaturanstiegs festlegen, aber keine belastbaren Kriterien dafür angeben, wird hier der Versuch unternommen, Kriterien für den Startpunkt zu formulieren. Es erscheint logisch, für die Beurteilung des Anstiegs diesen auch zu berechnen und nicht über den Behelf der Abweichung zweier Geraden in einem Punkt (Sprung) den Beginn des Anstiegs festzulegen. Das Beispiel Frankfurt/Main belegt das deutlich.
In Teil II wird die Auswertung der verfügbaren Zeitreihen der DWD-Stationen bezüglich Sonnenstunden und Temperatur vorgestellt.
Teil II Auswertung Bundesländer
Nachdem in Teil I die Methoden beschrieben wurden, beinhaltet Teil II die Auswertung der verfügbaren Zeitreihen für das Verhalten der Sonnenstunden und der Temperatur. Es wurden bezüglich der Temperatur nur die Stationen berücksichtigt, für die auch Zeitreihen der gemessenen Sonnenstunden vorliegen, um einen Vergleich zu ermöglichen (einige Temperaturzeitreihen wurden allerdings zusätzlich aufgenommen). In Tabelle 1 ist die Anzahl der Zeitreihen zusammengestellt, die von den Meßstationen der Bundesländer für den hier genannten Zweck auswertbar sind. Als auswertbar sind solche Zeitreihen zu werten, die eine genügend große Anzahl von Meßwerten (ca. größer. 40) und deutlich über das Jahr 2000 reichen. Meist also bis 2022.
| Bundesland | Sonnen- | Temperatur |
| stunden | ||
| Baden-Württemberg | 24 | 31 |
| Bayern | 33 | 19 |
| Brandenburg | 9 | 14 |
| Bremen/Hamburg | 3 | 4 |
| Hessen | 16 | 12 |
| Mecklenburg-Vorpommern | 5 | 13 |
| Niedersachsen | 15 | 14 |
| Nordrhein-Westfalen | 11 | 11 |
| Rheinland-Pfalz | 8 | 14 |
| Saarland | 2 | 2 |
| Sachsen | 5 | 14 |
| Sachsen-Anhalt | 7 | 7 |
| Schleswig-Holstein | 8 | 7 |
| Thüringen | 8 | 9 |
| Summe | 154 | 171 |
Tabelle 1 Anzahl der untersuchten Zeitreihen in den Bundesländern
Die älteste Zeitreihe für Temperaturmessung liegt von der Station Hohenpeißenberg (Bayern) vor und beginnt 1781. Die Aufzeichnung der Sonnenstunden begann 1921 an der Station des Fichtelbergs (Sachsen). In Bild 8 und Bild 9 sind die Häufigkeiten für Sprung, Anstiegsbeginn und Summe der Fehlerquadrate dargestellt. Die Zeitachse ist in diesen Bildern abgeschnitten, da vor 1980 sehr wenige Werte ermittelt wurden Eine Ausnahme bildet die minimale Fehlerquadratsumme. Hier wurden von 1946 bis 1980 60 Werte für die Zeitreihen der Sonnenstunden gezählt. Die Fehlerquadratsumme soll jedoch hier nicht weiter betrachtet werden.
Sonnenstunden
Bei den Sonnenstunden ist das Jahr 2002 dasjenige, bei dem der Anstieg am häufigsten begann (114 Werte), das sind 74 % der untersuchten Zeitreihen. Auch der maximale positive Sprung trat hier mit 42 % am häufigsten auf. Nach 2002 folgt das Jahr 1988, bei dem ebenfalls eine Anhäufung der Werte vorliegt.

Bild 8 Häufigkeiten von Sprung, Anstiegsbeginn und Summe der Fehlerquadrate für die Anzahl der Sonnenstunden
Temperatur
Bei den Temperaturmessungen ragt das Jahr 1987 heraus. In diesem Jahr wurden der maximale positive Sprung 104-mal (61 %) und die minimale Fehlerquadratsumme 91-mal (52 %) ermittelt. Der Beginn des Anstiegs mit acht Werten spielt in diesem Jahr keine Rolle. Um auf der Zeitachse eine sinnvolle Darstellung zu ermöglichen, wurde diese wie bei der Darstellung der Sonnenstunden vor 1980 abgeschnitten. In den Jahren davor liegen nur sehr wenige Werte für Sprung und Anstiegsbeginn vor (max. 6 Werte). Eine Ausnahme bildet die minimale Fehlerquadratsumme. Hier wurden von 1946 bis 1980 60 Werte für die Messung der Sonnenstunden gezählt.

Bild 9 Häufigkeiten von Sprung, Anstiegsbeginn und Summe der Fehlerquadrate für die Temperaturentwicklung
In Bild 10 sind die Häufigkeiten des Anstiegsbeginns von Sonnenstunden und Temperatur gemeinsam dargestellt. Das Jahr 2022 ragt beim Verhalten der Sonnenstunden mit 114 Werten deutlich aus der Verteilung heraus. Nun wäre eigentlich zu erwarten gewesen, dass dies auch für das Verhalten der Temperatur zutrifft. Bei dieser Größe verteilt sich jedoch der Anstiegsbeginn auf die Jahre zwischen 1985 und 2003. 1997 ist das Jahr, wo 55 Werte für den beginnenden Anstieg vorliegen.

Bild 10 Häufigkeiten des Anstiegsbeginns von Sonnenstunden und Temperatur
Zusammenfassung
Angeregt durch Diskussionen zu Artikeln über den Verlauf von Wetterdaten wurden hier drei Kriterien für die Festlegung des Anstiegsbeginns einer Zeitreihe untersucht. Wenn die Frage nach dem Beginn des Anstiegs gestellt ist, ist es logisch, diesen auch, sofern möglich, zu untersuchen. Als Methode ist eine fortschreitende Regressionsanalyse verwendet worden. Dabei wird die Zeitreihe an jedem Meßpunkt (abgesehen von der Start- und Endgeraden) in zwei Regressionsgeraden unterteilt und Anstieg, Sprung und Fehlerquadratsumme beider Geraden ermittelt. Somit erhält man eine Funktion dieser Größen über der gesamten Zeitachse. Die Beurteilung der Größen ist somit für die gesamte Zeitreihe möglich.
Wird das Kriterium des beginnenden Anstiegs angewendet (was aus der Logik folgt), zeigt sich, dass der Anstieg der gemessenen Sonnenstunden deutlich 2002 beginnt. Für den Anstieg der Zeitreihen der Temperatur bildet sich möglicherweise eine glockenförmige Verteilung (eventuell sogar Normalverteilung) um 1997 heraus. Um dieses zu bestätigen, sind jedoch mehr Zeitreihen zu untersuchen.
Verweise
[1] Der Sommer wird in Deutschland erst seit 1988 wärmer!
https://eike-klima-energie.eu/2024/09/11/der-sommer-wird-in-deutschland-erst-seit-1988-waermer/
DWD Wetterstationen Tageswerte
https://opendata.dwd.de/climate_environment/CDC/observations_germany/climate/daily/kl/historical/
Voge, K.
Entwicklung der Anzahl der Sonnenstunden
https://eike-klima-energie.eu/2024/10/15/entwicklung-der-anzahl-der-sonnenstunden/

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Kommentar von Hr. Kowatsch:
Die Originaltemperaturreihen des DWD seit 1881 sehen so aus: leichter Temperaturanstieg bis 1943, der eigentlich vom Anstieg der Wärmeinseleffekte verursacht ist. Dann ab 1943 bis 1987 Beginn einer Abkühlung, und zwar 45 Jahre lang, dann 1987/88 die plötzliche Änderung auf Erwärmung. Die neun Ursachen der plötzlichen Erwärmung haben wir in unserem letzten Artikel aufgeführt:
https://eike-klima-energie.eu/2025/01/13/das-neue-dwd-temperatur-rekordjahr-2024-teil-2/
„…zur vermeintlichen „Abkühlung“, die eher ein statistisches Artefakt ist,..“
Danke für Ihre Schreibtischmeinung anhand statistischer Berechnungen, Herr Schwerdt. Sie befassen sich erst kurz mit der Klimahistorie. Lesen Sie sich in die Historie der Wetterbeobachtungen ein. Sie werden dann mitbekommen, dass die Meteorologen ab Mitte der 70-er Jahre besorgt waren über den leichten Abkühlungstrend und eine neue kleine Eiszeit vorhersagten, der dann Ende der 1980-er abrupt beendet wurde.
Ich erinnere mich auch noch persönlich als damaliger Kirchgänger an diese Zeit. Bei uns fanden Bittgebete und Prozessionen statt, damit die Sonne wieder mehr scheint und es wärmer wird, damit die Ernte im Sept/Okt. nicht ausfällt und die Äpfel/Birnen im Herbst reif werden.
Laut ihren Berechnungen hat es das alles nicht gegeben.
Herr Schwerdt, und nun zurück zum Thema.
Das Thema des Artikels stamt von Herrn Dr.Voge. es geht um das Jahr des Erwärmungsbeginnes, also das Startjahr des Klimawandels in zur jetzigen Erwärmungsphase. Ihnen wurden drei Argumentationsverfahren angeboten. Bitte äußern Sie sich dazu. Wie Sie aus den Kommentaren ersehen, haben sowohl Kosch, M.Müller, und Heinemann gekniffen, trotz meiner direkten Aufforderung.
Herr Kowatsch, Sie haben gar nicht verstanden, dass die verschiedenen Analysemethoden zeigen, dass es gar keinen Erwärmungsbeginn gab, den man auf ein Jahr genau festmachen kann.
Das haben wir sehr gut verstanden, und haben das so ähnlich wie Sie jetzt auch immer wieder geschrieben. Eine interne Diskussion über mail mit Herrn Dr. Voge wird sich anschließen. Aber Sie wollen eben meiner ständigen Aufforderung nicht nachkommen, für was Sie sich entscheiden. Natürlich können Sie auch als Beginn auch Mitte der 80-er oder auch 90-er Jahre schreiben, uns interessieren die Begründungen der sachkundigen Leser. Und da kneifen Sie ständig.
Warum bloß?
Tut mir leid, offensichtlich haben Sie nichts verstanden, wenn Sie mich immer noch nach meiner „Entscheidung“ fragen.
Die Untersuchungen beweisen doch, dass es nichts zu entscheiden gibt, denn jede Auswahlmöglichkeit ist bewiesenermaßen ja falsch. Kapieren Sie das nicht?
Wenn ich Sie recht verstehe, berechnen Sie einen Korrelationskoeffizienten R im Modell I der Statistik. D.h. es gibt eine feste Variable, das Jahr und eine zufällige Variable, die Temperatur. Das geht aber nicht. Um R zu berechnen sind zwei Zufallsvariable erforderlich. Modell II der Statistik.
Neun Ursachen für etwas, was es nicht gibt. Wer bietet mehr?
Kosch, noch nicht in der realen Welt angekommen? Mit einem Fuß immer noch im Mutterleib, oder? Passen Sie auf, dass Ihr ökologischer Fußabdruck nicht zu groß wird, das könnte zu Schäden führen.
Die Schäden sind offensichtlich schon sowas von vorhanden ….
Vielen Dank an das Forum für die interessante Diskussion. Hier einige Bemerkungen.
„..Vielleicht sollten wir das chaotische System Wetter einfach Wettersein lassen und uns dem Biertrinken mehr widmen…“
Hallo Herr Dr. Voge. Das denken wir auch immer wieder. Aber unabhängig davon, nochmals vielen Dank für die Darstellung Ihrer Vorgehensweise und die Begründung ihres Ergebnisses. (Klimaerwärmung begann rasant 1996). Das führt nun keinesfalls zu einer Verwirrung oder Zerfleischung wie dies M.Müller und Heinemann irgendwie darstellen wollten. So jedenfalls hab ich deren Kommentare eingeordnet. Jeder der 3 vorgestellten wissenschaftlich begründeten Ansätze hat Realitäten als Grundlage. Vielleicht findet sich noch ein weiterer Ansatz, evt. aus Österreich, der Schweiz oder den Benelux-Ländern.
Die Tausenden von EIKE-Leser sind somit nun auf dem neuesten Stand der Wissenschaft. Eine spannende Wissenschaft, wenn ergebnisoffen diskutiert wird. Niemand sonst beschäftigt sich mit der Frage, wann begann der plötzliche Erwärmungsschub in Mitteleuropa auf ein höheres Temperaurniveau, das bis jetzt anhält?
Im Gegensatz zu EIKE wird beim PIK noch auf Klima-Steinzeitniveau mit Hexenglauben dumm rumgeschwätzt und ein Geschäftsmodell am Laufen gehalten, das weiträumig Deutschland für Dumm verkaufen will.
Herr Dr. Voge, bitte machen Sie weiter und finden Sie neue Begründungen für ihren Erwärmungsbeginn. Greifen Sie evt. einzelne Jahreszeiten raus, z.B. ist der Sommer interessant. Es ist durchaus möglich, dass einzelne Jahreszeiten, andere Startjahre haben. Wir machen das ja auch.
Vielen Dank, Herr Kowatsch. Es ist ja so, dass ich noch Einiges vorhabe. Das mit separaten Betrachtungen der Jahreszeiten hatte ich auch schon überlegt. Derzeit bin ich aber mit der Korrelation von Sonne und Temperatur befasst. Es ist da noch allerhand vor mir. Wir machen natürlich weiter. Schätze, so in drei Monaten könnte ich damit fertig sein. Übrigens ist das Untersuchen von Zyklen auch interessant. Etliche Zeitreihen weißen ja Muster auf.
Ein sehr spannendes Thema, viel Erfolg.
Schließe mich an!
Danke Herr Dr Voge für Ihre Antwort……..wenn der Anstiegsbeginn festgelegt werden soll, warum wird er dann nicht auf direktem Wege, sondern über eine Hilfsgröße gesucht? …… Man geht dann der Maulerei aus dem Weg….. Man kann es diesen Leuten nicht recht machen. Geht man auf deren Forderungen ein, finden die etwas anderes zum Maulen. Sehr oft wurden Korrelationsberechnungen und deren Signifikanz gefordert. Haben wir alles geliefert, zwischen Tmax und der SSH. Siehe unseren Herbstartikel. Reicht denen nicht!
Jetzt fordern einige dieser Leute, dass wir Ihre Berechnungen auf unsere Daten übertragen sollen. Ihnen brauche ich nicht zu sagen, wie zeitaufwändig dies wäre. Unmöglich für mich, zumal ich noch voll im Berufsleben stehe.
Nochmals die Frage bzgl des äußerst kalten Jahres 1996: Wie stark wirkt sich dies, statistisch gesehen, auf Ihren Anstiegsbeginn aus? Es ist ja nur ein Jahr und wenn dies normal temperiert gewesen wäre, hätte man überhaupt keinen Anstiegsbeginn 1996 nachweisen können. Davor und danach nur Jahre, die zu warm waren.
Treibhausgase sind als Ursache der aktuellen Erwärmung zweifelsfrei bekannt. Wenn Sie das nicht wahrhaben wollen, stochern Sie in der Tat bis an Ihr Lebensende im Trüben. Sie suchen etwas, wovon alle wissen, dass es das nicht gibt. Zur Beruhigung kann ich Ihnen sagen: Sie sind nicht der Einzige.
Weder hier noch von sonst irgendeiner vergleichbaren Gruppe auf der Welt ist eine einzige wissenschaftlich valide Begründung geliefert worden, warum Treibhausgase als wesentliche Ursache der globalen Erwärmung auszuschließen sind. Wäre man hier ehrlich zu sich selbst, würde man klipp und klar sagen: „Ich bin dafür, unabhängig von den negativen Folgen weiter ohne Einschränkung CO2 zu produzieren, weil das finanziell zu meinen Lebzeiten Vorteile bringt.“
…..Weder hier noch von sonst irgendeiner vergleichbaren Gruppe auf der Welt ist eine einzige wissenschaftlich valide Begründung geliefert worden, warum Treibhausgase als wesentliche Ursache der globalen Erwärmung nicht relevant sind….. Hier schon, lesen Sie die vielen Artikel von uns. LESEN !!!
LESEN!!
Wer lesen kann hat Vorteile! Das Sprichwort ist nicht ganz richtig, es kommt auf das Gehirn an und damit, womit man sein Geld verdient.
Wer sein Gehalt damit bestreitet, dass er die Glaubensgrundsätze der CO2-Treibhauskirche verbreitet, bei dem nützt Lesen gar nichts.
Nein Herr Baritz, es gibt hier auch keine wissenschaftlich valide Begründung, warum Treibhausgase nicht relevant sind.
Herr Dietze nennt zwar immer einen sehr niedrigen Einfluss von CO2 auf die Temperaturentwicklung von 0,X °C bei Verdopplung der CO2-Konzentration, kommt aber in Erklärungsnot bei der Tatsache, dass wir heute bereits einen Anstieg von fast 1,5°c gegenüber dem vorletzten Jahrhundert messen, der nach Stand der Wissenschaft ausschließlich auf die Wirkung der Treibhausgase zurück zu führen ist und sich die CO2-Konzentration nur um 50% erhöht hat.
Und dass es, gemessen von Satelliten, zu 80% die Sonneneinstrahlung ist, Wärmeinseln kommen hinzu, das dringt bei Ihnen nicht durch. Weil es in der grünen Klima-Kirche nicht vorkommen darf und die korrumpierte Alarm-„Forschung“ weiter lügen muss: Dann steuert das „Schadgas“ eben die Wolken, dem vorgegebenen Schuld-Dogma folgend. Doch auch das ist widerlegt. Es fehlt, wann und wo immer gemessen wurde, die Korrelation mit dem CO2, die bei einem ursächlichen Zusammenhang (Kausalität) zwingend ist.
Lassen Sie sich nicht jeden Unsinn erzählen und glauben den auch noch, Herr Ullrich.
Die Sonneneinstrahlung macht überhaupt nichts, wie extra für Leichtgläubige wie Sie von Fachleuten wunderschön aufbereitet wurde.
Behauptung: „Die Sonne verursacht den Klimawandel“ | Helmholtz-Klima-Initiative
Zitat: „Die Wissenschaft kennt keinen physikalischen Prozess, der erklären könnte, wie die Sonne trotz gleichbleibender oder leicht abnehmender Aktivität den in den vergangenen Jahrzehnten beobachtete Temperaturanstieg der Erde bewirkt haben soll.“
Es sind die Wolken, die die Sonneneinstrahlung steuern, und offenbar nicht das CO2! Es ist der alte Trick, nur die Sonnenintensität oberhalb der Atmosphäre anzugeben und nicht das was unten ankommt. Sorry, aber das ist der alte Verdummungs-Schnee von gestern.
Entweder partizipieren Leute wie Silke direkt oder indirekt an den Verbrechen der Klimaastrolgen / Klimakirche oder sie haben sich so verängstigen lassen von PIK ff., dass sie eher viele Termine bei einem Klapsdoktor wahrnehmen sollten, als hier ihre „Wahrheiten“ zu verbreiten. Falls bei denen Intelligenz vorhandensein sollte, dann wird die mißbräuchlich benutzt (siehe oben erster Halbsatz..), denn ein bißchen Logik würde reichen, dieses verbrecherische Ablassmodell zu durchschauen.
Sehr geehrter Herr Dr. Voge,
mit großem Interesse habe ich Ihren Beitrag gelesen und hatte, weiter unten, schon einige kritische Bemerkungen angeführt.
Hiermit wende ich mich nochmal persönlich an Sie.
Wie Sie sehen, hängen die Ergebnisse von der statistischen Herangehensweise ab. So kommt Herr Schau zu einem Zeitpunkt 1980, ab dem ein Anstiegsbeginn der Temperaturen bestimmt wurde. Er nennt es Verlaufsänderung. Wir hingegen haben in der Gruppe Kowatsch et.al. den Zeitpunkt auf 1988 bestimmt. Die Gründe dafür sind vielfältig und in unseren Artikeln immer wieder verifiziert.
Eine kritische Frage an Sie: Das Jahr 1996 war ein extrem kaltes Jahr und spielt bei Ihrer statistischen Betrachtung wahrscheinlich eine entscheidende Rolle. Könnte es sein, dass ein einziges, etwas nicht so kaltes Jahr 1996 ein ganz anderes Ergebnis geliefert hätte? 1996 ist eingebettet in mehrere warme Jahre davor und danach!
Wir hingegen haben das Jahr 1988 genommen, weil die Jahre davor aus einer kälteren Phase kamen und die Temperaturen dann sprunghaft auf ein höheres Niveau kamen.Dies können Sie beim DWD (link unten) sehr schön erkennen. In unseren vielen Grafiken aus den unterschiedlichsten Regionen z.B. West- und Nord-Europa haben wir das immer wieder dargestellt.
Wir gehen daher davon aus, dass die Erwärmung 1988 begann und außerdem, ganz am Rande, dies mit CO₂ nichts zu tun hat.
Mit freundlichen Grüßen
Matthias Baritz
Ich meine, man sollte eine möglichst weit in die Vergangenheit reichende Meßwertreihe verwenden und diese dann zusätzlich sanft glätten. Technisch ähnlich wie z. B. die UAH-Satellitenmessung von Roy Spencer. An solchen Darstellungen sieht man dann sehr schön, ob oder wann sich Trends ergeben, ändern, umkehen usw.
Das Problem ist meistens, daß man nicht für ale Kriterien, die man vergleichen möchte, gleich lange Zeitreihen hat. Also Temperaturen gibt es rel. lange, Sonnenscheindauer vermutlich viel weniger lang.
Trotzdem geben gleichlaufende Korrelationen einen Anknüpfungshinweis, zu untersuchen, ob es sich um einen Zufall oder eine Ursache/Auswirkungskorrelation handelt.
Fast wichtiger als Korrelation ist aber Nichtkorellation. Weil Nichtkorrelation ist ein starker Hinweis, daß es sich eben nicht um eine Ursache/Wirkungs Situation handelt.
Beachtet werden müssen allerdings auch Schwingungscharakteristik und Phasenverschiebung. Weil in der Natur vollziehen sich viele Vorgänge in Form von Schwingungen mit verschiedenen Wellenlängen und Reaktionen darauf erfolgen selten direkt, sondern mit einer gewissen zeitlichen Verzögerung.
Interessant was Sie schreiben, die sich ergebenden Korrelationen sind noch keine Beweise, aber die Nichtkorrelationen sehr wohl!
Das ist gute Falsifizierung!
Suchen Sie Fälle von Nichtkorrelationen von CO2- und Temperaturänderungen, so wie bei Ihren Nachttemperaturen (Tagestieftemperaturen).
Oder allgemeiner, suchen Sie Fälle wo gleicher CO2-Trend, örtlich und/oder zeitlich das Wetter/Klima gegensätzlich/unterschiedlich treibt, oder?
Herr Lange, schauen Sie sich die Grafiken in unseren Artikeln an. Immer der Zeitraum zwischen 1945 und 1987.
Koennen die Autoren bitte die Groesse „Sonnenstunden“ genau erklaeren?
5 Sonnenstunden im Jahr finde auch ich recht wenig.
Einschlaegige Klimatabellen operieren scheinbar mit aehnlichen Zahlen:
https://de.climate-data.org/europa/deutschland/hessen/frankfurt-am-main-447/
Aber dann machen Angaben von 24 Sonnestunden fuer Baden Wurtemberg oder gar 33 fuer Bayern keinen Sinn.
Sinn kommt erst dann rein wenn man die Definition sieht:
Beim DWD wird die Einheit in Minuten angegeben, Statistische Verarbeitung Stundensumme, Zeitreihe
Das gilt dann aber nur wenn die Sonne scheint?
Sehr verwirrend.
Danke fuer die Arbeit.
Zum Auffinden von Punkten, bei denen sich ein Verlauf ändert (Change Point Detection) gibt es eine Reihe von Funktionen in kommerziellen bzw. Open Source Programmen. Für MATLAB, Octave und R z. B. BEAST. In MATLAB gibt es zudem die Funktion ischange. In Verbund mit einer abschnittsweisen linearen Regression ergibt sich z. B. folgender Verlauf (siehe Kurve) für die DWD-Temperaturen (Deutschland).
Ich würde aber nicht von Sprüngen sprechen, sondern besser von Verlaufsänderungen. Die Sprünge sind zumindest teilweise das Ergebnis eines linearen Fits und treten bei anderen Funktionen so nicht auf.
Herr Schau,
auch Sie haben einen anderen Zeitpunkt (1980) für den Anstiegsbeginn der Temperatur, nennen es aber Verlaufsänderung. Je nachdem welche statistischen Funktionen und Verfahren zu Grunde gelegt werden, scheint man andere Zeitpunkte zu erhalten.
Herr Dr Voge hat 1997 als Anstiegsbeginn besimmt. 1996 war ein extrem kaltes Jahr, eingebettet in eine deutlich wärmere Phase davor und danach. Könnte es sein, Herr Dr Voge, dass dies Ihre Berechnungen in die falsche Richtung beeinflußt?
Bei unserer Bestimmung kommen wir aus einer kälteren Phase vor 1988 sprunghaft auf ein höheres Niveau einer deutlich wärmeren Phase.https://www.dwd.de/DE/leistungen/zeitreihen/zeitreihen.html#buehneTop. Hier die Grafik mit den Jahrestemperaturen einstellen.
MfG Matthias Baritz
Ein grundsätzlicher Unterschied scheint aus meiner Sicht darin zu bestehen, dass bei mir die Geraden zusammenhängen (quasi wie Stäbe mit einem Gelenk verbunden). Dadurch entstehen natürlich immer stetige Verläufe.
Ich verwende neben den genannten Methoden zusätzlich eine systematische Suche um die gefundenen Änderungspunkte (CP) im Bereich +-10 a. Kriterium ist die minimale Abstandsquadratsumme. Als Letztes erfolgt eine nichtlineare Regression, wobei alle Parameter frei gegeben sind und die vorherigen Ergebnisse nur als Startwerte dienen. Bei einem CP ergibt sich übrigens 1985 als Zeitpunkt. Da die Berechnungen bei der nichtlinearen Regression durch den gesamten Verlauf gestützt werden, dürften einzelne Punkte das Ergebnis nur wenig beeinflussen.
Meiner Meinung nach ist die Betrachtung einzelner Stationen oder Länder nicht sinnvoll. Besonders interessant ist die Tatsache, dass der globale Anstieg zwischen 1910 und 1940 mit dem ab 1980/90 vergleichbar ist. Insbesondere bei den Ozeantemperaturen. Warum? Leider habe ich derzeit keine Diskussionspartner, was die Sache erschwert. Die DWD-Temperaturen habe ich eigentlich nur zum Test der Methoden gerechnet, da sie im Vergleich zu den globalen stark streuen.
Danke Herr Schau, auch Ihnen für Ihre Argumente zu Auffinden der plötzlichen Temperaturerwärmung in Deutschland. Meine Anregung an Sie ist nun diesselbe wie ich vor einem halben Jahr an Dr. Voge geschrieben habe.
Machen Sie aus Ihrem Kommentar doch einen Artikel und stellen ihn bei EIKE zur Diskussion. Begründen Sie einfach Ihre obigen Hinweise näher. Die Leser bei EIKE können dann selbst die Argumente abwägen und sich für einen Erwärmungsbeginn entscheiden.
Wir sind etwas im Vorteil, da wir die Daten für alle Mittel- und Westeuropäische Staaten haben, und die sollten bei einer Gegenprobe natürlich deckungsgleich sein. Und bei 87/88 ist das der Fall.
Danke Herr Dr. Voge für die statistische Behandlung der Temperaturzeitreihen. Für uns, und insbesondere Herrn Baritz ein sehr interssanter Artikel. Sie kommen aufgrund ihrer Betrachtungskritierien zum vorläufigen Schluß: „…Für den Anstieg der Zeitreihen der Temperatur bildet sich möglicherweise eine glockenförmige Verteilung (eventuell sogar Normalverteilung) um 1997 heraus..“
Mein erster Gedanke war: Damit haben zu erst recht bewiesen, dass CO2 nicht der Haupttemperaturtreiber sein kann. Denn CO2 kann nicht seit 1997 mit seiner Erwärmungswirkung beginnen und zuvor gar nicht.
Nun zu ihrem ermittelten Zeitpunkt des Erwärmungsbeginns: Mein Gegenargument als Naturbeobachter und Naturschützer, der sich an der Realität draußen orientiert:
Bereits 1990, und zwar im Februar war unserer Naturschutzgruppe klar, dass es plötzlich wärmer ist und wir diskutierten intern über die Gründe, natürlich gab es auch eine CO2-Glaubensgruppe. Mit irgendwelchen Temperatur-Reihen hatten wir uns noch gar nicht beschäftigt, das kam erst gute 10 bis 15 Jahre später, weil der Leiter der Ostalbwetterwarte, ebenfalls Naturschützer, sogar in einem Zeitungsartikel schrieb, dass die Klimaerwärmung erst Ende der 1980-er begann. Und mit Ende der 1980-er stimmte ich mit Herrn Kämpfe überein, der berufsmäßig die Fauna der Weimarer Umgebung kartiert hatte. So hatte ich Herrn Kämpfe auch kennengelernt, da ich seine umfangreiche Kartierungs-Arbeit gelesen habe.
Zu dritt – Kämpfe, Kowatsch, Baritz- haben wir den Erwärmungsbeginn dann auf 1988 festgelegt, Kämpfe/Kowatsch mehr aufgrund der Naturbeobachtungen, Herr Baritz aufgrund seiner beruflichen Erfahrung im Umgang mit der Statistik. Kurze Zeit später fanden wir in der Literatur Forschergruppen aus anderen Ländern, die gleichfalls aufgrund anderer Überlegungen dieses Sprungjahr 1987/88 erwähnten.
Wie auch immer, vielen Dank für Ihre Behandlung des Themas aus mathematischer, statistischer Sicht. So funktioniert Wissenschaft, nämlich die Betrachtung eines Themas aus verschiedener Sicht. Vielleicht noch ein Tipp, wenn Sie mit den Sonnenstunden irgendwelche Korrelationen finden wollen, dann nehmen Sie doch auch die T-max Temperaturen vom Tage.
Josef Kowatsch schrieb am 28. Januar 2025 10:13
Können wir dann vielleicht hoffen, dass Ihre subjektiven „Sprunganalysen“ durch objetive ersetzt werden, die auch statistischen Kriterien standhalten?
Eigentlich hätte Ihr erster Gedanke sein sollen: „Oh Mist, dann machen wir es also wirklich die ganze Zeit falsch, wie uns das schon oft von den verschiedensten Seiten erklärt wurde …“
„Oh Mist, dann machen wir…“ Dieser Müller-Gedanke ist lustig.
Oh, Herr M. Müller, an Ihren Äußerungen sehen wir, dass Sie die Klimawissenschaft überhaupt nicht verstehen. Sie sind ein Schreibtischwissenschaftler mit physikalischem Ursache-Wirkungsdenken. Sie haben wie viele hier noch immer nicht verstanden, dass beim Klima und auch bei den Zeitreihen viele Betrachtugsweisen einfließen müssen, um die Wirklichkeit draußen vor der Tür zu erfassen.
Und falls Sie die Arbeit von Herrn Dr. Voge nachvollziehen möchten, dann ist CO2 erst recht kein Temperaturtreiber.
Josef Kowatsch schrieb am 28. Januar 2025 14:13
Genau das Gegenteil ist der Fall. Ich weise seit einer gefühlten Ewigkeit darauf hin, dass
Aber das ignorieren Sie geflissentlich …
Irgendwie entgeht mir hier der Zusammenhang. Was hat das Nachvollziehen des Textes von Herrn Voge mit der Frage zu tun, ob CO2 zu höheren Temperaturen führt?
*) Auch die mittlere Temperatur Deutschlands ist noch eine lokale Größe. Sie betonen doch sogar in Ihren eigenen Artikeln, dass eine einfache Änderung der Großwetterlage einen starken Einfluß auf die Temperaturen hat.
Herr Müller, wie kommen Sie denn darauf? Wirkt jetzt das anthropogene CO2 nur global? Geheimnisvolle Fernwirkung der CO2-Moleküle, die erst wärmen, wenn sie sich von ihrer globalen Wirkung vergewissert haben? Ist die angebliche stärkere Erwärmung der Pole, mit der wir alarmiert werden, jetzt nicht-anthropogen, weil sie nicht global ist? Machen wir es kurz: Die Klimakirche bestimmt, was das anthropogene CO2 alles machen muss. Die Temperaturen global, Hitze, Kälte, Trockenheit, Stürme, Starkregen lokal. Und Kälte kommt von Wärme. Halt so, wie es die Klimakirche zur Verdummung der Menschheit braucht.
Dr. Roland Ullrich schrieb am 28. Januar 2025 19:39
Einfach den vorangegangenen Punkt mit berücksichtigen. Lokal wirken viele Einflüsse zusammen, die lokal für eine große Variablilität sorgen. In diesem starken Rauschen ein Signal zu finden ist schwierig. Kucken Sie sich dagegen die globalen Temperaturreihen an, dann finden Sie da zwar Dinge wie Vulkanausbrüche, Enso, …, die für Variablität in der Temperaturkurve sorgen, aber die kann man da berücksichtigen. Dinge wie Umstellungen der Großwetterlage, wie sie von Herrn Kowatsch angeführt wird, mitteln sich da raus. Die wärme Luft, die jetzt bei uns ist, war vorher woanders und dort dürfte es dann kühler sein.
Irgendwie signalisierte Ihr Kommentar aber auch eher mehr Emotionen als tiefes Nachdenken.
Völlig falsch. Damit wäre den Unsinn Tor und Tür geöffnet.
Die Zeitreihe der Temperatur enthält nur genau die Informationen über das Klima, die sie enthält: eine Menge von zeitlich geordneten Zahlen. Wenn sie die Hahresmittel eines Ortes über 30 Jahre enthält so besteht die vorliegende Information aus 30 zeitlich geordneten Zahlen. Mehr nicht! Die Zahlenreihe enthält nichts darüber, was dafür verantwortlich war, dass das Temperaturmittel in einem Jahr anders als im anderen war. Ob ein zu warmer Winter und Frühling oder ein extrem zu warmer Herbst oder ein stets etwas zu mildes Wetter das ganze Jahr über die Ursache war. Sie gibt auch jeine Info, ob es zu trocken war.
Alles, was Sie also hineininterpretieren, was über die rein mathematische Analyse der Zahlenreihe hinausgeht und keine weiteren Informationen hinzunimmt, ist Humbug.
Eine Zeitreihenanalyse muss stets unabhängig davon sein, was die Zahlen messen. Wenn ein Aktienindex dieselben Zahlen (ohne Einheiten) wie die Temperaturreihe hat (oder proportional dazu ist), so ist das Analyseergebnis der beiden exakt dasselbe.
Oh Herr Heinemann, Sie leben auch noch, nur war ihr Kommentar völlig umsonst, sie wollten wohl ein Späßle machen mit Ihrer Allgemeinbetrachtung. Um was geht es? Es geht hier um den Beginn der Erwärmung in den DWD-Temperaturreihen. Sie haben 3 Begründungen zukünftig zu Auswahl
1) Die Erwärmung begann etwa 1997
2) Die Erwärmung begann 1987/88
3) Die Erwärmung begann etwa 1980, siehe oben Herr Schau.
Sie dürfen sich die Argumente durch den Kopf gehen lassen und dann selbst nach den Kriterien entscheiden, die Sie für die besten halten. Ich bin Ihnen nicht böse, wenn sie den mathematisch statistischen Ansatz von Herrn Dr. Voge wählen. Aber dann fangen Sie im nächsten Kommentar endlich damit an und begründen Sie ihre Ansicht und schreiben nicht wieder irgendwas rum, das vom Thema ablenkt. Dasselbe gilt für M.Müller. Auch Herr Dr. Voge wäre dankbar, wenn Sie endlich kritische Anmerkungen, Fragen oder Zustimmungen zu seinem Artikel bringen würden und dann auch kundttun, für welches Jahr Sie sich entscheiden.
Herr Kowatsch,
Sie haben nichts verstanden. Es geht um Objektivität und Informationstheorie. Nochmals:
Ja darum geht es. Aber die Analyse beruht auf Zahlenreihen und mehr nicht. Jede Interpretation, die mehr Information benötigt/vorausetzt als die in der Zeitreihe vorhandenen Informationen (also, die die Zahlenreihe enthält und per Datenanalyse (z.B. Regressionsgeraden) extrahiert werden können) ist unzulässig!
Also, lesen Sie nochmal.
Lieber Herr Heinemann. Dann fangen Sie doch endlich mal selbst an mit ihrer Objektivität und legen Sie dar, welchen Zeitpunkt der Erwärmung in den DWD-Reihen Sie als richtig ansehen. Begründen Sie Ihren Standpunkt, dann werden Sie sehen, dass mein Ton Ihnen gegenüber sofort freundlicher wird, weil Sie sich mit dem Thema befassen.
Ihre allgemeinen Ausführungen und Bekenntnisse können Sie sich an die Wand hängen, darum geht es überhaupt nicht. Sie wollen bis jetzt nur Nebengleisdiskussionen erzeugen und vom Thema ablenken.
Wie Sie sich vielleicht erinnern, habe ich bereits vor Monaten eine ähnliche Analyse wie Herr Voge gemacht und die Zeitreihe in zwei Teilreihen mit variablem „Sprungpunkt“ untersucht. Läßt man den Sprungpunkt durch die Jahre laufen und nimmt die Reduktion der Standardabweichung auf, so kann man ein paar Jahre finden, an dem die Reduktion maximal wird, darunter ist etwa 1988.
Der Punkt ist – und das hat Herr Voge erst ansatzweise bedacht, dass man die selbe Übung mit entsprechenden Zufallsreihen machen muss, um zu testen, ob sich das Verhalten der Temperaturreihe vom Verhalten jeder Zufallsreihe signifikant unterscheidet, also der Sprung sich von einem „glücklichen Zufallstreffer“ unterscheidet.
Nur mal ein Tip: Sie scheinen gar nicht mehr zu merken, wo Sie Annahmen machen. Die Analyse von Herrn Voge und mir untersucht, ob Ihre Annahme von einem Sprung auszugehen, überhaupt vom Zeitreihenverlauf objektiv gegeben ist.
Was meinen sie? Sie sagen doch selber das man die Analyse an den Zahlen machen muss. Und sie wollen ja nicht sagen, das sie den Aktienindex in Grad C bewerten oder?
DAS ist eben typisch Heinemann, und ich behaupte, dass er diesen Schwurbelsatz selbst versteht, wenn „gewisse Einflüsse“ nachgelassen haben.
Dass „Zahlen messen“ hatte ich“ vor Heinemann“ auch noch nicht mitbekommen ….., und ich messe schon Jahrzehnte …. (hauptsächlich Temperaturen und „damit verbundene physik. Größen“.
(Eine wirkliche „Physikalische Größe“ kann H. also nicht sein ….)
Korrektur:
DAS ist eben typisch Heinemann, und ich behaupte, dass er diesen Schwurbelsatz selbst NICHT MEHR versteht, wenn „gewisse Einflüsse“ nachgelassen haben.
Sorry …
Ja der Heinemann, der will einfach dagegen sein. In diesem Fall gegen uns Kämpfe/Kowatsch/Baritz. Deshalb unterstützt er hier den Betrachtungsansatz von Herrn Dr. Voge, der als abruptes Temperaturänderungsjahr 1996 mit seiner Methode ermittelt hat. Dabei begreift Heinemann, genausowenig wie M.Müller nicht, dass mit diesem späteren Jahr das Treibhausgas CO2 als Haupttemperaturtreiber für diese abrupte Temperatur-Änderung erst recht widerlegt wurde.
Die beiden Anhänger der Treibhauskriche sollen endlich ihre Argumente bringen, weshalb Sie eher für 1996 sind und nicht für 1980 oder für 1987/88
Ich bin gegen Unfähigkeit und Unwissenheit, finden Sie das verwerflich?
Was haben Sie dagegen, wenn Sie Kritik bekommen, wenn Sie nicht den Erfordernissen entsprechendes abliefern?
Jammern Sie nicht rum, sondern nehmen Sie die Tipps, die Sie von vielen hier bekommen (nicht nur von mir) ernst.
Schrieb ich doch oben: „Alles, was Sie also hineininterpretieren, was über die rein mathematische Analyse der Zahlenreihe hinausgeht und keine weiteren Informationen hinzunimmt, ist Humbug.“
Herr Kowatsch beruft sich bei der Analyse der Temperaturreihe auf seine Beobachtungen der Natur. Das ist unzulässig, denn seine Beobachtungen sind nicht Teil des Datensatzes, der analysiert wird.
Das Ergebnis der Zeitreihenanalyse darf nicht davon abhängen, was man sich wünscht, wie es sein soll oder plausibel wäre, damit es zu einer subjektiven Beobachtung passt.
Auch auf die Gefahr, das sie wieder davon reden, das ich sie nicht verstehe oder das ich ihre Aussage falsch representiere oder was anderes
Diese Aussage:
Gilt die auch fuer den Zusammenhang CO2 und Temperaturentwicklung?
Aus welchen Zusammenhang beziehen Sie sich dabei?
Der Einfluß von CO2 auf den Strahlungstransport ist physikalisch quantifizierbar. Dazu braucht man nicht nach Auswirkungen in Temperaturreihen zu suchen.
In diesem Fall ist Ihre Frage zu sinnlos gestellt. Das isg eine weitere Ihre Spezialitäten, dass Sie nie konkret fragen.
Na ja, Wenn man ihre Frage so sieht
Ich frage
Sie fragen
Dann kann ich nur antworten:
fuer den Zusammenhang CO2 und Temperaturentwicklung
Danke uebrigens fuer die Antwort:
Braucht man ihn nicht suchen oder kann man ihn nicht finden?
Herr Schulz,
Wie groß ist denn der gemäß Wissenschaft erwartete Temperatureffekt durch CO2 in der Kowatschen Zeitreihe?
Herr Heinemann, Sie argumentieren: „Eine Zeitreihenanalyse muss stets unabhängig davon sein, was die Zahlen messen. Wenn ein Aktienindex dieselben Zahlen (ohne Einheiten) wie die Temperaturreihe hat (oder proportional dazu ist), so ist das Analyseergebnis der beiden exakt dasselbe.“
Nur damit ich Sie richtig verstanden habe. Wären die Zahlen (Aktienindex und Temperatur) und damit ohne Einheiten zufällig identisch, sind die drei einzigen zulässigen Aussage es steigt oder fällt oder ist konstant, sonst nichts. Eine zusätzliche Interpretation darüber wäre per se unzulässig. Oder somit könnte gerade nicht aus der Zahlenveränderung auf eine Klimaveränderung geschlossen werden, für den Zufall, es waren die Zahlen doch z.B. steigende Temperaturwerte.
Aber genau so wird doch von Klimaalarmisten argumentiert für den Temperaturanstieg in Mitteleuropa. Der „Zahlenanstieg“ ,jetzt seinen es wieder Temperaturzahlen in einem betrachteten Zeitraum, sei hauptsächlich durch den C02-Anstieg getrieben.
Sind Argumente nur noch zulässig, wenn diese das herrschende Klimanarrativ – CO2 sei gefährlich- stützen? Oder habe ich Sie hoffentlich falsch verstanden?
Herr Stock, genau meine Frage. Aber erst gesehen, nachdem ich meine abgschickt habe.
Nun, Herr Kowatsch behauptet, daraus auch noch Sprünge rauslesen zu können.
Das habe ich nicht geschrieben. Aus Zeitreihen kann man auch mehr herauslesen. Nur darf man nichts implizit hinzunehmen, was nicht im Datensatz ist. So wird die Signifikanz eines Trends nicht dadurch größer, dass der Trend im Einklang mit subjektiven Beobachtungen, die nicht im Datensatz quantifiziert sind, stünde.
Ich weiß nicht, ob ich Sie richtig verstanden habe. Wenn die Zahlen einen signifikanten Trend oder eine signifikante Änderung zeigen, so zeigen sie unbestritten eine Änderung in diesen Parameter an (hier der Temperatur). Und da die Temperatur ein wichtiger Klimaparameter ist, kann man auch von Klimaänderung sprechen. Die Signifikanzprüfung findet natürlich immer gegenüber einem Zufallsresultat statt.
Die Aussage, dass der Temperaturanstieg hauptsächlich durch den CO2 Anstieg bedingt ist, beruht klimawissenschaftlich selbstverständlich nicht alleine auf empirischen Trendanalysen. Es ist nur so, dass der beobachtbare Trend im Rahmen dessen ist, was klimaphysikalisch zu erwarten ist.
Das habe ich offensichtlich an keiner Stelle behauptet.
Sie haben offensichtlich meinen Text nicht korrekt gelesen und damit nichts verstanden.
Herr Schwerdt,
wir haben gezeigt, dass die Korrelation Tmax/CO2 erst ab 1988 signifikant ist, p=5E-07. Von 1959 (Beginn der CO2-Aufzeichnung) bis 1987 gab es keine Korrelation, p=0,75 !!!
Sie vergleichen wieder Äpfel mi Birnen und nehmen statt Tmax die Tagestemperaturen und eine anderen Zeitraum. https://eike-klima-energie.eu/2024/12/07/herbst-wie-kann-es-sein-dass-der-deutsche-wetterdienst-dwd-sich-so-irrt-und-gegen-seine-eigenen-daten-argumentiert/
Matthias Baritz schrieb am 30. Januar 2025 9:40
Wie soll er denn Ihr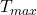 nehmen, wenn Sie die Daten nicht zur Verfügung stellen und auch nicht ausreichend Informationen zum Generieren der Daten zur Verfügung stellen (Stationsliste, Bestimmung
nehmen, wenn Sie die Daten nicht zur Verfügung stellen und auch nicht ausreichend Informationen zum Generieren der Daten zur Verfügung stellen (Stationsliste, Bestimmung  – einfaches Mittel, flächengewichtetes Mittel, …)?
– einfaches Mittel, flächengewichtetes Mittel, …)?
Welche Temperatur mit welchen CO2-Werten?
Alles gegriffene, hochgerechnete, manipulierbare, gemittelte, gewichtete, … Rechenwerte eines nicht repräsentativen Zeitraumes, natürlich gute Fleißarbeit, oder?
Herr/Frau Schwerdt betet erneut sein Treibhaus-Glaubensbekenntnis runter: „Seien Sie gewiss dass CO2 nicht erst seit 1997 mit seiner Erwärmungswirkung beginnt…“
Wenn das tatsächlich Ihre Überzeugung ist, dann müssten Sie ein furchtbar schlechtes Gewissen haben über Ihren eigenen ökologischen Fußabdruck.
Frage: Haben Sie sich bei der Kirche schon freikauft und auf das Kirchen-Konto gespendet. Dort können Sie Ihren ökologischen Fußabdruck für 2024 berechnen lassen, automatisch wird Ihnen angegeben,wieviel der Freikauf kostet. Bitte schreiben Sie jetzt, was Sie bezahlen mußten. Nur dann würden wir sehen, dass Sie es auch ernst meinen mit ihrem Geschreibsel.
Frankfurt hat nach Grafik 1 also um die 5,0 Sonnenstunden pro Jahr. Das ist ein düsterer Ort.
Warum fehlen die Jahre 2023 und 2024? Das waren deutschlandweit gesehen beides von der Temperatur her Rekordjahre,, hatten aber deutlich weniger Sonnenstunden als 2022.
Davon abgesehen zeigt Bild 1 auf den ersten Blick: Da springst nichts.
Frau Kosch, die Sonnenstunden haben am Frankfurter Flughafen ab 1988 bis 2024 um durchschnittlich 6 pro Jahr zugenommen, die Tagestemperaturen Tmax um 0,6 Grad/Jahrzehnt. Dazu kam noch der Temperatursprung von 87/88
Sehr geehrter Kowatsch,
hier sind die fehlenden Jahre 2023 und 2024 und der Ausblick für 2026.
Auch der Temperatursprung von 87/88 ist dabei.
März/April 2024 ist nicht weit weg von Trendwende September-2023.
Siehe Seite 11 von ECC_doc.pdf
(https://magentacloud.de/s/6jP9e97DTTyEWBq)
Danke Herr Wähner, nur nebenbei, wir -Baritz/Kowatsch – sind nicht die Autoren dieses Artikels. Ich weiß auch nicht, weshalb Dr. Voge die Jahre 2023 und 2024 weggelassen hat.
Mit etwas Recherche und Nachdenken haetten sie das gefunden zu der Beschreibung des duesteren Ortes:
https://opendata.dwd.de/climate_environment/CDC/observations_germany/climate/hourly/sun/BESCHREIBUNG_obsgermany_climate_hourly_sun_de.pdf
Vielleicht nicht die beste Benennung der Groesse, aber immerhin macht es dann Sinn.
Fuer sie auch?
5 x 365.25 = 1,826.25 Minuten (siehe Definition DWD)
= 30.4 Stunden
= 1.27 Tage Sonne?
Eher nicht.
Sollen das Stunden pro Tag sein?
Wie gesagt, dann sind Angaben von 24 oder 33 unsinnig.
Es wurden also 33 Zeitreihen zu Sonnenstunden untersucht?
Danke, hatte schon den Koffer gepackt, um in Bayern mehr Sonnenstunden abzugreifen.
Trotzdem sind laut DWD die Angaben in Minuten! Siehe Link oben.
Brille hin oder her, das ist schlecht zu verstehen.
Heist das jetzt also 5 Minuten Sonne pro Stunde?
Frau/Herr Schwerdt. Bitte setzen Sie Ihren Verstand endlich sinnvoll ein, und überlegen Sie sich, weshalb die Temperaturen in Mittel- und Westeuropa von einem ganz bestimmten Zeitpunkt an rasant gestiegen sind und zuvor nicht.
Es gilt die gleiche Aufforderung an die vielen möglichen Gewschlechter der Person Schwerdt wie an M.Müller oder Herrn Heinemann:
1) Wählen Sie von den drei im Artikel wissenschaftlich erarbeiteten Zeitpunkten einen aus und begründen Sie, damit endlich eine Diskussion entstehen kann. Lassen Sie endlich ab von ihrem zerstörerischem Rumgeeiere.