[Alle Hervorhebungen und Formatierungen im Original]
„In der Mathematik wird das ±-Zeichen [oder einfacher: +/-] verwendet, wenn es darum geht, die zwei Möglichkeiten des gewünschten Wertes zu zeigen, von denen eine durch Addition und die andere durch Subtraktion erhalten werden kann. [Es bedeutet, dass es zwei mögliche Antworten für den Ausgangswert gibt. In der Wissenschaft wird es in erheblichem Maße verwendet, um die Standardabweichung, experimentelle Fehler und Messfehler darzustellen.“ (Quelle) Dies ist zwar eine gute Erklärung, aber nicht ganz korrekt. Es geht nicht darum, dass es zwei mögliche Antworten gibt, sondern darum, dass die Antwort so viel oder so wenig wie die „zwei möglichen Werte des Anfangswertes“ sein könnte – zwischen dem mit der Absoluten Unsicherheit addierten und dem mit der absoluten Unsicherheit subtrahierten Wert.
Die Angabe „2,5 +/- 0,5 cm“ wird verwendet, um darauf hinzuweisen, dass der zentrale Wert „2,5“ nicht unbedingt der tatsächliche Wert ist, sondern dass der Wert (der wahre oder richtige Wert) zwischen den Werten „2,5 + 0,5“ und „2,5 – 0,5“ liegt, oder vollständig berechnet „Der Wert liegt zwischen 3 cm und 2 cm“. Oft wird angegeben, dass dies mit einem bestimmten Prozentsatz der Wahrscheinlichkeit, z. B. 90 % oder 95 % (90 %- oder 95 %-Konfidenzintervall), zutrifft. Der Haken an der Sache ist, dass der tatsächliche genaue Wert nicht bekannt ist, er ist unsicher; wir können nur korrekt angeben, dass der Wert irgendwo in diesem Bereich liegt – und das auch nur „meistens“. Bei einer Wahrscheinlichkeit von 95 % liegt der Wert in einem von 20 Fällen nicht innerhalb des Bereichs der oberen und unteren Grenze des Bereichs, und bei einer Sicherheit von 90 % kann der wahre Wert in einem von zehn Fällen außerhalb des Bereichs liegen.
Dies ist wichtig. Wenn es um Messungen in der physikalischen Welt geht, wird in dem Moment, in dem das Wort „Ungewissheit“ verwendet wird, insbesondere in der Wissenschaft, ein riesiges Thema in einem einzigen Wort zusammengefasst. Und damit eine Menge Verwirrung.
Viele der Messwerte, die in vielen wissenschaftlichen Bereichen präsentiert werden, werden als Durchschnittswerte, als arithmetische oder probabilistische Mittelwerte (in der Regel „Mittelwerte“) angeboten. Wenn also eine Unsicherheit oder ein Fehler angegeben wird, handelt es sich in vielen Fällen nicht um die Unsicherheit des Mittelwerts der Messgröße, sondern um die Unsicherheit des Mittelwerts der Werte. Allein diese Merkwürdigkeit ist für einen Großteil der Verwirrung in der Wissenschaft verantwortlich.
Das klingt komisch, nicht wahr? Aber es gibt einen Unterschied, der wichtig wird. Der Mittelwert einer Menge von Messungen wird in der Formel angegeben:
Der Durchschnitt – das arithmetische Mittel – ist also durch diese Formel selbst mit der Unsicherheit der ursprünglichen Messungen (Beobachtungen) verbunden. Wenn die ursprünglichen Beobachtungen wie folgt aussehen: 2 cm +/- 0,5 cm, dann hat der Wert des Mittelwerts die gleiche Form: 1,7 cm +/- die Unsicherheit. Wir werden weiter unten sehen, wie dies richtig berechnet wird.
In der modernen Wissenschaft hat sich die Tendenz herausgebildet, stattdessen die „Unsicherheit des Mittelwerts“ zu verwenden – mit einer abweichenden Definition, die etwa so lautet: „Wie sicher sind wir, dass dieser Wert der Mittelwert ist?“. Auch dazu später mehr.
Beispiel: Messungen von High-School-Football-Feldern, die grob auf 0,3 bis 0,6 Meter genau vorgenommen werden, indem beispielsweise die Abstands-Markierungen* am Spielfeldrand gezählt werden, ergeben eine reale Messunsicherheit von +/- 24 Inches [~61 cm]. Mit einem ähnlichen Verfahren könnte ein Mittelwert aus den Messungen vieler Highschool-Footballfelder gebildet werden, wobei die Unsicherheit des Mittelwertes angeblich auf einige Inches reduziert würde. Dies mag trivial erscheinen, ist es aber nicht. Und es ist nicht selten, sondern eher der Standard. Die Behauptung, dass die Messunsicherheit (manchmal auch als ursprünglicher Messfehler bezeichnet) um eine ganze Größenordnung reduziert werden kann, indem man sie als „Unsicherheit des Mittelwertes“ angibt, ist eine schlechte Ausrede für die Wissenschaft. Wenn man wissen will, wie sicher wir uns über die Größe dieser Footballfelder sind, dann muss man die tatsächliche ursprüngliche Messunsicherheit kennen.
[*Im American Football {von welchem der Übersetzer ein großer Fan ist} wird das Spielfeld mit Linien markiert, die jeweils 5 Yards voneinander entfernt sind. Am Spielfeldrand sind die Markierungen von 1 zu 1 Yard gezeichnet. – Die Sportart darf nicht mit unserem europäischen Fußball verwechselt werden, der in den USA als „European Soccer“ bekannt ist. A. d. Übers.]
Der Trick besteht darin, den Mittelwert nicht mehr mit seiner tatsächlichen ursprünglichen Messunsicherheit (ursprünglicher Messfehler) anzugeben, sondern ihn durch die Unsicherheit des Mittelwerts zu ersetzen. Die neue, viel kleinere Unsicherheit des Mittelwertes ist das Ergebnis von zwei Dingen: 1) es ist das Produkt der Division oder 2) Wahrscheinlichkeit (zentraler Grenzwertsatz).
Fall 1, das Beispiel mit dem Footballfeld, ist ein Beispiel für ein Divisionsprodukt. In diesem Falle besteht die Ungewissheit nicht mehr in der Länge des Fußballfeldes oder irgendeines Fußballfeldes. Es geht nur noch darum, wie sicher wir uns des arithmetischen Mittels sind, das normalerweise nur davon abhängt, wie viele Fußballfelder in die Berechnung einbezogen wurden. Die ursprüngliche Messunsicherheit wurde durch die Anzahl der gemessenen Felder geteilt, um die zentrale Grenzwerttheorie zu untergraben.
Fall Nr. 2: Wahrscheinlichkeit und zentraler Grenzwertsatz. Ich werde dieses Thema für einen anderen Teil dieser Serie aufheben.
Weiter. Falls es nur um das arithmetische Mittel geht, kann man also den Mittelwert der Spielfeldgrößen nehmen, der bei etwa 5351 Quadratmetern liegt, ohne Rücksicht auf die ursprüngliche Messunsicherheit. Und dann auf den Mittelwert der Kosten für die Anlage eines Kunstrasenplatzes. Da die „Installation eines Kunstrasen-Fußballfeldes zwischen 750.000 und 1.350.000 Dollar kostet“ [Quelle], ist es offensichtlich, dass man sich besser mit Messwerkzeugen in Vermessungsqualität auf den Weg macht und die genauen Abmessungen des gewünschten Feldes misst, einschließlich der gesamten Fläche um das Spielfeld herum, die man abdecken muss. Es zeigt sich, dass die Kostenschätzungen in einer Spanne von über einer halben Million Dollar liegen.
Wir würden diese Kostenschätzung als Mittelwert mit einer absoluten Unsicherheit schreiben – 1.050.000 $ (+/- 300.000 $). Wie hoch die tatsächlichen Kosten sein werden, hängt von einer Vielzahl von Faktoren ab. Im Moment, ohne weitere Informationen und Details, ist das, was wir haben … die beste Schätzung der Kosten ist irgendwo da drin -> zwischen 750.000 und 1.350.000 $ – aber wir wissen nicht wo. Der Mittelwert von 1.050.000 $ ist nicht „genauer“ oder „weniger unsicher“. Die richtige Antwort mit den verfügbaren Daten ist die SPANNE.
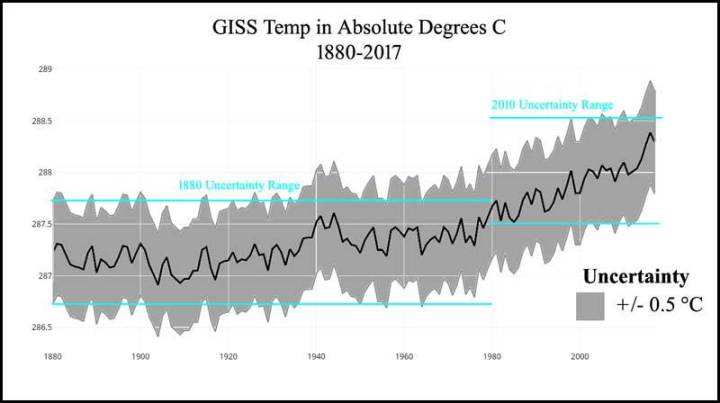
Dieser Gedanke lässt sich am Beispiel [der Temperaturkurve] von GISTEMPv4 leicht veranschaulichen:
Die Absolute Unsicherheit in GISTEMPv4 wurde von Gavin Schmidt angegeben. Die schwarze Kurve, die einen Mittelwert darstellt, ist nicht der tatsächliche Wert. Der tatsächliche Wert für das Jahr 1880 liegt in einem Bereich von etwa 287,25° +/- 0,5°. Richtig geschrieben, lag der GISTEMP im Jahr 1880 irgendwo zwischen 286,75°C und 287,75°C. Das ist alles, was wir sagen können. Der GISTEMPv4-Mittelwert für 1980, hundert Jahre später, liegt immer noch innerhalb dieses Bereichs, wobei sich die Unsicherheitsbereiche beider Jahre um etwa 0,3 °C überschneiden; das heißt, es ist möglich, dass die Mitteltemperatur überhaupt nicht gestiegen ist. In der Tat überschneiden sich die Unsicherheitsbereiche für die globale Temperatur bis etwa 2014/2015.
Gavin Schmidt sagt zu genau diesem Punkt:
„Denken Sie aber daran, was passiert, wenn wir versuchen, die absolute globale Mitteltemperatur für, sagen wir, 2016 zu schätzen. Die Klimatologie für 1981-2010 beträgt 287,4±0,5K, und die Anomalie für 2016 beträgt (aus GISTEMP im Vergleich zu dieser Basislinie) 0,56±0,05ºC. Unsere Schätzung für den absoluten Wert beträgt also (unter Anwendung der ersten oben dargestellten Regel) 287,96±0,502K, und unter Anwendung der zweiten Regel reduziert sich dieser Wert auf 288,0±0,5K. Der gleiche Ansatz für 2015 ergibt 287,8±0,5K, und für 2014 287,7±0,5K. Alle diese Werte scheinen innerhalb der Unsicherheit gleich zu sein. Wir verlieren also die Fähigkeit zu beurteilen, welches Jahr das wärmste war, wenn wir nur die absoluten Zahlen betrachten.“ [Quelle]
Um genau zu sein: es ist absolut richtig, dass die globalen Jahresmitteltemperaturen mit weitaus mehr Unsicherheiten behaftet sind, als von Gavin Schmidt gezeigt oder zugegeben wird, aber zumindest hat er den bekannten ursprünglichen Messfehler (Unsicherheit) der Thermometer gestützten Temperaturaufzeichnungen einbezogen. Warum ist das so? Warum ist er größer als das? …. weil die Unsicherheit eines Wertes die kumulativen Unsicherheiten der Faktoren sind, die in die Berechnung des Wertes eingeflossen sind, wie wir weiter unten sehen werden (und +/- 0,5°C ist nur einer davon).
Mittelwertbildung von Werten mit Absoluten Unsicherheiten
Absolute Unsicherheit: Die Unsicherheit einer gemessenen Größe ist auf inhärente Schwankungen im Messprozess selbst zurückzuführen. Die Unsicherheit eines Ergebnisses ist auf die kombinierten und kumulierten Auswirkungen dieser Messunsicherheiten zurückzuführen, die bei der Berechnung dieses Ergebnisses verwendet wurden. Wenn diese Unsicherheiten in den gleichen Einheiten wie die Größe selbst ausgedrückt werden, nennt man sie Absolute Unsicherheiten. Unsicherheitswerte werden normalerweise an den angegebenen Wert einer experimentellen Messung oder eines Ergebnisses angehängt, wobei ein gängiges Format ist: (Größe) ± (absolute Unsicherheit in dieser Größe). [Quelle]
Gemäß der obigen Formel zur Berechnung des arithmetischen Mittels werden zunächst alle Beobachtungen (Messungen) addiert und dann die Gesamtsumme durch die Anzahl der Beobachtungen geteilt.
Wie kann man dann zwei oder mehr unsichere Werte mit jeweils eigener absoluter Unsicherheit addieren?
Die Regel lautet:
Wenn man zwei (oder mehr) Werte addiert oder subtrahiert, um einen Endwert zu erhalten, ist die absolute Unsicherheit (angegeben als „+/- ein numerischer Wert“), die dem Endwert zugeordnet ist, die Summe der Unsicherheiten. [viele Quellen: hier oder hier]
Zum Beispiel:
5,0 ± 0,1 mm + 2,0 ± 0,1 mm = 7,0 ± 0,2 mm
5,0 ± 0,1 mm – 2,0 ± 0,1 mm = 3,0 ± 0,2 mm
Es spielt also keine Rolle, ob addiert oder subtrahiert wird – die absoluten Unsicherheiten werden addiert. Dies gilt unabhängig davon, wie viele Elemente addiert oder subtrahiert werden. Wenn im obigen Beispiel 100 Elemente (z. B. der Anstieg des Meeresspiegels an verschiedenen Orten) jeweils eine eigene absolute Messunsicherheit von 0,1 mm aufweisen, dann hätte der Endwert eine Unsicherheit von +/- 10 mm (oder 1 cm).
Dies lässt sich im Prinzip leicht in einer Grafik veranschaulichen:
In Worten: zehn plus oder minus eins PLUS zwölf plus oder minus eins IST zweiundzwanzig plus oder minus zwei. Zehn plus oder minus 1 steht für den Bereich von elf bis neun und zwölf plus oder minus eins für den Bereich von dreizehn bis elf. Die Addition der beiden höheren Werte der Bereiche, elf und dreizehn, ergibt vierundzwanzig, was zweiundzwanzig (die Summe von zehn und zwölf auf der linken Seite) plus zwei ist, und die Addition der beiden niedrigeren Werte der Bereiche, neun und elf, ergibt die Summe von zwanzig, was zweiundzwanzig minus zwei ist. Unsere korrekte Summe ist also zweiundzwanzig plus oder minus zwei, wie oben rechts dargestellt.
Etwas kontraintuitiv gilt das Gleiche, wenn man eine unsichere Zahl von einer anderen subtrahiert. Die Unsicherheiten (die +/-) werden addiert, nicht subtrahiert, was zu einem Ergebnis (der Differenz) führt, das unsicherer ist als entweder der Minuend (die obere Zahl) oder der Subtrahend (die Zahl, die von der oberen Zahl subtrahiert wird). Wen das nicht überzeugt sind, derskizziere sein eigenes Diagramm wie oben für ein Subtraktionsbeispiel.
Welche Auswirkungen hat diese einfache mathematische Tatsache?
Wenn man zwei Werte mit Unsicherheit addiert (oder subtrahiert), addiert (oder subtrahiert) man die Hauptwerte und addiert die beiden Unsicherheiten (die +/-) in beiden Fällen (Addition oder Subtraktion) – die Unsicherheit der Gesamtsumme (oder der Differenz) ist immer höher als die Unsicherheit der beiden ursprünglichen Werte.
Was ist, wenn wir multiplizieren? Und was ist, wenn wir dividieren?
Wenn man einen Wert mit absoluter Unsicherheit mit einer Konstanten multipliziert (eine Zahl ohne Unsicherheit), wird die absolute Unsicherheit ebenfalls mit der gleichen Konstante multipliziert.
z.B. 2 x (5,0 ± 0,1 mm ) = 10,0 ± 0,2 mm
Wenn man einen Wert mit absoluter Unsicherheit durch eine Konstante (eine Zahl ohne Unsicherheit) teilt, wird die absolute Unsicherheit ebenfalls durch den gleichen Betrag geteilt. [Quelle]
Also, 10,0 mm +/- 0,2 mm geteilt durch 2 = 5,0 +/- 0,1 mm.
Wir sehen also, dass das arithmetische Mittel der beiden addierten Messungen (hier haben wir multipliziert, aber es ist dasselbe wie die Addition von zwei oder zweihundert Messungen von 5,0 +/- 0,1 mm) gleich der Unsicherheit der ursprünglichen Werte ist, weil in diesem Fall die Unsicherheit aller (beider) Messungen gleich ist (+/- 0,1). Wir brauchen dies, um die Mittelwertbildung – die Ermittlung eines arithmetischen Mittels – zu bewerten.
Schauen wir uns nun an, was passiert, wenn wir einen Mittelwert einer bestimmten Messgröße finden. Ich werde einen Gezeitenpegel verwenden, da Messungen des Gezeitenpegels in Metern angegeben werden – es handelt sich um addierbare Größen (extensive Eigenschaft). Im Oktober 2022 betrug der mittlere Meeresspiegel am Battery Park [New York City] 0,182 Meter (182 mm, bezogen auf den letzten von NOAA CO-OPS festgelegten mittleren Meeresspiegel). Beachten Sie, dass mit diesem Wert keine Unsicherheit verbunden ist. Doch selbst der mittlere Meeresspiegel relativ zum Meeresspiegel-Datum ist bis zu einem gewissen Grad unsicher. Die Einzelmessungen der Gezeitenpegel haben eine spezifizierte Unsicherheit von +/- 2 cm (20 mm). (Ja, wirklich. Sie können die Spezifikationen unter dem Link nachlesen).
Und doch wird in denselben Spezifikationen eine Unsicherheit von nur +/- 0,005 m (5 mm) für Monatsmittelwerte angegeben. Wie kann das sein? Wir haben soeben gezeigt, dass die Addition aller Einzelmessungen für den Monat alle Unsicherheiten (alle 2 cm) ergeben würde, und dann würden die Gesamtsumme UND die kombinierte Unsicherheit durch die Anzahl der Messungen geteilt – und es blieben wieder die gleichen 2 cm als Unsicherheit für den Mittelwert übrig.
Die Unsicherheit des Mittelwertes kann und darf mathematisch nicht geringer sein als die Unsicherheit der Messungen, aus denen er sich zusammensetzt.
Wie haben sie es geschafft, die Unsicherheit auf 25 % ihres tatsächlichen Wertes zu reduzieren? Der Hinweis liegt in der Definition: Sie bezeichnen sie richtigerweise als „Unsicherheit des Mittelwerts“ – im Sinne von „wie sicher sind wir uns über den Wert des arithmetischen Mittels?“ Sie berechnen es so: [gleiche Quelle]
„181 eine-Sekunde-Wasserstandsproben, die auf jede Zehntelstunde zentriert sind, werden gemittelt, ein Ausreißertest mit drei Standardabweichungen wird durchgeführt, der Mittelwert und die Standardabweichung werden neu berechnet und zusammen mit der Anzahl der Ausreißer angegeben. (3-Minuten-Mittelwert des Wasserstandes)“
Wie man sieht, haben sie „die Zielpfosten verschoben“ und geben nun nicht mehr die Unsicherheit des Mittelwerts an, sondern die „Standardabweichung des Mittelwertes“ an, wobei „die Standardabweichung ein Maß für die Streuung der Zahlen in einer Datenmenge von ihrem Mittelwert ist.“ [Quelle oder hier]. Es handelt sich nicht um die Unsicherheit des Mittelwerts. In der Formel für das arithmetische Mittel (Bild etwas weiter oben) wird der Mittelwert durch ein einfaches Additions- und Divisionsverfahren bestimmt. Das numerische Ergebnis der Formel für den absoluten Wert (der numerische Teil ohne das +/-) ist sicher – Addition und Division ergeben absolute Zahlenwerte – es gibt keine Unsicherheit über diesen Wert. Ebenso wenig gibt es eine Ungewissheit über den numerischen Wert der summierten Unsicherheiten geteilt durch die Anzahl der Beobachtungen.
Lassen Sie mich hier etwas klarstellen: Wenn man den Mittelwert von Messungen mit bekannten absoluten Unsicherheiten ermittelt, gibt es keine Unsicherheit über den Mittelwert oder seine absolute Unsicherheit. Es ist ein einfacher arithmetischer Prozess.
Der Mittelwert ist sicher. Der Wert der Absoluten Unsicherheit ist sicher. Wir erhalten ein Ergebnis wie zum Beispiel:
3 mm +/- 0,5 mm
Das bedeutet, dass der numerische Wert des Mittelwerts in einem Bereich von 3 mm plus 0,5 mm bis 3 mm minus 0,5 mm oder im Bereich von 1 mm liegt: 3,5 mm bis 2,5 mm.
Der Bereich kann nicht weiter auf einen einzigen Wert mit geringerer Unsicherheit reduziert werden.
Und komplexer als das ist es wirklich nicht.
# # # # #
Kommentar des Autors dazu:
Ich hörte einige stottern und protestieren… Aber… aber… aber… was ist mit dem (absolut universell anwendbaren) Zentralen Grenzwertsatz? Ja, was ist damit? Hat man Ihnen beigebracht, dass es immer dann angewandt werden kann, wenn man einen Mittelwert und dessen Unsicherheit sucht? Glauben Sie, dass das wahr ist?
In einfachen pragmatischen Worten habe ich oben die Regeln für die Bestimmung des Mittelwerts eines Werts mit absoluter Unsicherheit aufgezeigt – und gezeigt, dass die korrekte Methode bestimmte (nicht unsichere) Werte sowohl für den Gesamtwert als auch für seine absolute Unsicherheit liefert. Und dass diese Ergebnisse einen Bereich darstellen.
Im weiteren Verlauf dieser Serie werde ich erörtern, warum und unter welchen Umständen der Zentrale Grenzwertsatz überhaupt nicht verwendet werden sollte.
Als Nächstes, in Teil 2, werden wir uns mit den kaskadierenden Unsicherheiten von Unsicherheiten befassen, die als Wahrscheinlichkeiten ausgedrückt werden, wie z. B. „40 % Chance auf“.
Vergessen Sie nicht zu sagen, „mit wem Sie sprechen“, und beginnen Sie Ihren Kommentar mit dem Namen des Kommentators, wenn Sie sich an einen anderen Kommentator (oder an mich selbst) wenden. Verwenden Sie etwas wie „OldDude – ich glaube, Sie haben recht….“.
Link: https://wattsupwiththat.com/2022/12/09/plus-or-minus-isnt-a-question/
Übersetzt von Christian Freuer für das EIKE


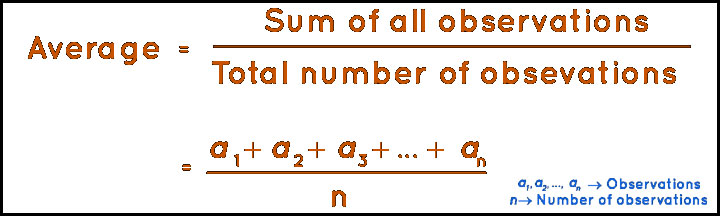
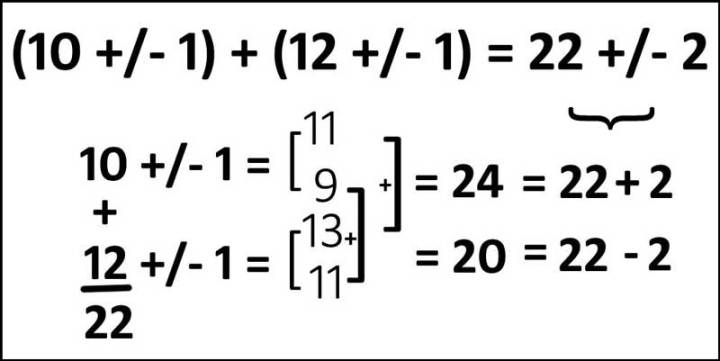













Beispiel: Tagesmitteltemperatur. Man misst zu jeder vollen Stunde (1), summiert die Werte (2) und teilt durch die 24 Stunden eines Tages (3). Die Schritte (1) und (2) sind völlig analog zur Gesamtlängenbestimmung. Dem Lineal entspricht das Thermometer. Man muss aber noch bedenken, dass das Ablesen einer Temperatur am Thermometer nicht bedeuten muss, dass dies auch die Temperatur der Umgebungsluft ist. Die Messung hat noch systematische Fehler. Dies ist jedoch ein anderes – wenn auch sehr wichtiges – Thema. Bei Kip und hier geht es aber nur um die statistischen Fehler. Wenn man also jede Stunde die Lufttemperatur mit einer Genauigkeit von sagen wir 0,5°C ablesen kann, wie genau ist dann das Tagesmittel (= Summe der 24 Stundenwerte/24) angebbar?
a) 0,5°C / wurzel (24) = 0,1 °C
b) (0,5°C x 24)/24 = 0,5 °C
Addieren sie Temperaturen zusammen, um eine sinnvolle Zahl wie, alle TemperaturenZusammen zu bekommen? Aka Gesamtlänge?
Oder wie soll man ihren Kommentar deuten?
…. bissel wichtig machen, … mehr is da nich ….., etwas trollig eben ….
ich haben den Artikel gelesen und auf die meteorologische Definition des Tagesmittels angewandt.
Haben Sie eine sachbezogene Meinung zu meiner Frage?
Vielleicht haben sie meine Frage nicht verstanden aber sie sagten:
Eine Gesamtlaenge setzt sich meines Erachtens nach, aus mit Fehlern behaftenen gemessenen Einzellaengen zusammen. Die werden dann addiert aber es wird kein Mittel gebildet.
Wie sie da einen Vergleich zu einem Mittel der Temperaturen sehen, war meine Frage.
Aber vielleicht haben sie sich ja nur falsch ausgedrueckt.
Wie ist denn Ihre Antwort zu ihrem Multiple Choice und warum?
Da ist der Herr H. wohl sinnbildlich über die eigenen Beine gestolpert 😉
Sie fragen was. Fragen sind keine Meinung.
Die Analogie ist, dass in beiden Fällen streuende Einzelwerte addiert werden. Dass die Summe durch die Zahl der Werte N zum Schluß geteilt wird, ist statistisch gesehen ja nur eine Umskalierung (Teilen durch N) der statistischen Kenngrößen Summe S und Quadratsumme der Abweichungen Q in die Größen Mittelwert m=S/N und Quadrat der Standardabweichung (=Varianz) s^2=Q/N.
Sind Sie jetzt fit, um sich zwischen Antwort a) oder b) zu entscheiden? – ich glaube nicht, Sie sind noch nicht soweit…
wollen sie damit sagen, das sie mit dem Durchschnitt von verschiedenen gemessenen Laengen eine sinnvolle Aussage machen koennen?
Ich glaube sie haben nicht verstanden, was sie da als Analogie angeben, und warum wieder mal ihr Analogon nicht in der Lage ist die Realitaet darzustellen.
Nehmen wir die Einzellaengen die sie zu einer Gesamtlaenge zusammensetzen wollen. Als Anwednungsbeispiel nehme ich die Vermessung einer Strasse!
Der Wert den sie suchen ist die Gesamtlaenge der Strasse.
Welchen Durchschnitt der Einzelmessungen brauchen sie hier?
Jede Einzelmessung ist mit einem Fehler behafted, der sich wie im Hauptartikel angegeben nicht verringern laesst.
Im Vergleich mit Temperaturen koennen sie Temperaturen addieren und einen sinnvollen Wert erhalten?
Nehmen sie die Fehlerbetrachtung von einer anderen Anwendung.
Sie vermessen Bauteile. Sie messen die Bauteillaenge. Sie messen immer die gleiche Laenge. Je oefter sie Messen desto besser koennen sie den Fehler einschaetzen den sie haben. Hier macht die Durchschnittsbildung Sinn, da sie die gleiche Laenge messen.
Bei der Temperatur muessen sie sich ueberlegen wie sie den Wert Temperatur methodisch deklarieren.
Messen sie immer die gleiche Temperatur oder messen sie immer eine neue Temperatur?
Obwohl sie immer am gleiche Ort messen, sind die Temperaturmessungen ueber die wir hier reden nicht immer neue Temperaturen, da zeitlich versetzt?
Ist das nicht vergleichbar mit den Einzellaengen?
Koennen sie mir jetzt sagen, welches Ergebnis sie denken, das es das richtige ist und warum?
Wenn Ihnen das Mitteln der Temperatur zu emotionsgeladen ist, übertrage ich meine Frage einfach auf die Gesamtlängenmessung:
Bei Kip und hier geht es aber nur um die statistischen Fehler! Wenn man also 24 Längenstücke mit einer Genauigkeit von sagen wir 0,5 mm ablesen kann, wie genau ist dann die Gesamtlänge (= Summe der 24 Teilstücke) angebbar?
a) 0,5 mm × wurzel (24) = 2,4 mm
b) 0,5 mm x 24 = 12 mm
Ich dachte den haben sie gelesen.
In der Annahme, das sie jetzt emotionsgeladen sind, werde ich die Antwort zurueckhalten, bis sie den Hauptbeitrag verstanden haben.
Ja, meinen Sie? Warum sind Sie zu feige, a) oder b) zu sagen? Vor mir aus machen Sie auch ein c). Wer keine Meinung äußert, der hat auch nichts zu sagen.
Sicher, daraus resultiert ja auch meine Frage, damit lernt man was über den Artikel. Grundsätzlich falsch wäre es, jedem Artikel blind zu glauben. Eigenes Denken ist besser.
Na also, klappt doch mit dem Denken. In der Tat ist das der Punkt, an dem manche scheitern, die mathematisch korrekte Methode zu finden.
Das Messgerät ist immer dasselbe und damit ist der statistische Fehler unabhängig von Wert bei jeder Einzelmessung immer gleich groß. Zudem ist jede Einzelmessung statistisch unabhängig.
Nun die Bonusfrage für Sie (ob Ihre Antwort richtig ist, erfahren Sie natürlich nach Beantwortung): Wie sind die Fehler verschiedener Messwerte (Längen/Temperaturen) mit demselben Gerät zum Gesamtfehler der Gesamtlänge/Temperatursumme zu verechnen im Vergleich dazu, wenn immer derselben Messwert mehrmals einzeln gemessen wird?
a) gleiche Formel oder b) andere Formel?
Kamen Sie gerade vom Weihnachtmarkt, wo Sie etwas „gedopten“ Glühwein zuviel genossen haben???
Ihre Hybris hat heute wieder einmal ein absolutes Maximum …..
Auf den messtechnischen Unsinn, den Sie im „Beitrag“ „abgelassen“ haben, möchte ich lieber nicht eingehen. Die messtechnische Praxis scheint Ihnen so fremd zu sein, wie ein gewisser Anstand anderen fachlichen Auffassungen gegenüber.
ich kann mir gar nicht vorstellen, dass nicht jeder mit Kompetenz in der messtechnische Praxis meine Frage kennt und spontan richtig beantworten kann. Wäre nicht vertrauenserweckend wenn er sich schwer damit täte.
was wollen sie mit der
anfangen bitte? Wie ich ausgefuehrt habe, macht die Gesamtlaenge bei einer Strassenvermessung Sinn, aber das Aufsummieren von Temperaturen?
Und die Mittelbildung von Temperaturen von verschiedenen Tageszeiten macht warum Sinn?
Wenn, wie sie sagen,
ist, dann kann das Ergebnis doch nur eines sein oder nicht? So wie im Hauptartikel angegeben.
Also doch zu emotionsgeladen für Sie, Sie kommen ja gar nicht mehr davon weg. Mathematisch ist wurscht, ob Temperatursumme oder Längensumme. Nehmen Sie die Längensumme und kommen Sie endlich zum Thema und der Frage zurück. Also welche Formel für den Fehler der Gesamtlänge a) oder b)?
ist, dann kann das Ergebnis doch nur eines sein oder nicht? So wie im Hauptartikel angegeben.
Das Temperaturmessungen von Zeitreihen statistisch unabhängig sind stimmt auch nicht, denn sie sind sowohl mit ihren Vorgängerdaten autokorreliert, als auch mit denen in der näheren und weiteren Nachbarschaft. Details dazu bspw. hier und hier
Das stimmt, Temperaturreihen sind autokorreliert, aber hier geht es um die statistischen Fehler E_i (E_i=M_i-W) der Messwerte M_i und nicht um die Statistik der wahren Messgröße W (zB. über die Zeit) selbst (W(t) = aus den n (i=1…n) Messwerten M_i zu ermittelnder wahrer Wert zur Zeit t bzw. des Teilstücks Nr. t). Bei statistischen Fehlern ist der nachfolgende Fehler E_i (t+1) unabhängig vom vorhergehenden E_i(t). Diesen Fehlertyp betrachten wir hier. Der Schlüssel zur Beantwortung der Frage, ob a) oder b) für den stat. Fehler der Messwertsumme gilt, liegt darin, sich klarzumachen, dass es bei egal für den statistischen Fehler ist (sofern wie es vorausgesetzt wird, dass die Fehlertoleranz von 0,5 mm über den gesamten Messbereich gleich ist), ob dasselbe Teilstück mehrmals (n mal) gemessen wird oder für die n Messungen verschiedene Teilstücke genommen werden (in unserem Fall von 24 ggf. verschieden langen Teilstücken, sollte n also idealerweise ein Vielfaches von 24 sein).
a) Gauß: 0,5 mm × wurzel (24) = 2,4 mm
b) Kip: 0,5 mm x 24 = 12 mm
Was ist also richtig, a) oder b)?
Mit einem Satz Messdaten bekommen Sie nur ein Ergebnis, ja, nicht zwei oder drei…, wie lautet nun Ihre Antwort a), b),… ? Ich höre.
Wie gesagt, hat man einmal aus Tausenden per Satellit gemessenen Temperaturen den Mittelwert gebildet, ist damit für eine physikalische Weiterverwendung Schluss und Ende. Kein noch so großes Genie kann den jeweils zu Mittelwerten verarbeiteten Temperaturen die zugehörigen Massen und deren Masseneigenschaften zuordnen, da sie nicht gleichzeitig gemessen wurden. Und wenn man besonders unphysikalisch arbeiten will, kann man die Massen und Masseneigenschaften ja auch noch erfassen und auch noch mitteln und so gebildete Mittelwerte in mathematische Beziehungen setzen. Dann kann man nur noch sein Beileid aussprechen, vielleicht reicht es bis nach Potsdam.
Die Untauglichkeit, mit Temperaturmittelwerten der Atmosphäre über Temperaturmessgeräte in 2 m Höhe über dem Boden oder über Gewässern eine Erwärmung feststellen oder ableiten zu können, folgt aus der anerkannten Tatsache, dass die einfallende Strahlung gerade nicht die Atmosphäre erwärmt. Die Atmosphäre ist für die Strahlung praktisch durchlässig. Eine Erwärmung durch Strahlung mit deren Umwandlung in Energie findet allein durch die auf unter den Messpunkten befindlichen Massen statt, auf die die Strahlung auftrifft. Und diese sind über den Globus verteilt sehr unterschiedlich und auch alles andere als unveränderlich und statisch.
Insofern ist die Luftschicht zwischen diesen unzähligen unbekannten Massen vereinfacht ausgedrückt einzig der Überbringer der dort erzeugten Temperaturen, die dort erfolgten Temperaturmessungen geben also in erster Näherung die Temperatur der darunter liegenden Massen an, wie man am Beispiel der Sahara oder der Antarktis auch ohne Physikkenntnisse sehr gut als Laie beobachten kann.
Wer also bei seiner angeblich festgestellten Erderwärmung (Energiezunahme der gesamten Erde) die unterschiedlichen Massen in seine Rechnung nicht mit einbezieht, kann zwar ggf. von einer etwas erhöhten Mittelwert-Temperatur sprechen, nicht jedoch von einer Erderwärmung unter dem physikalischen Verständnis der Energiezunahme. Denn Energien, die man im Gegensatz zu Temperaturen physikalisch aufsummieren darf, wurden über die Temperatur-Messstellen zu keiner Zeit ermittelt.
Das Aufsummieren von 1000 einzelnen Temperaturen ergibt den gleichen (Un-)Sinn, wie das Aufsummieren von den einzelnen Geschwindigkeiten von 1000 Autos, auch wenn man die jeweilige Summe anschließend durch 1000 dividiert. Kann man zwar machen, man kann aber nichts mehr damit anfangen, außer die Zahlen in einer Statistik darstellen.
Diesen Artikel müssten sich die vielen „Heinemänner“ und „Koschs“ ff. hier hinter den Spiegel stecken oder unters Kopfkissen legen. Leider werden die beschriebenen Zusammenhänge viel zu oft (bewußt?) ignoriert / ausgeblendet.