Wenn die Reihe also z. B. (1, 3, 7, 10) lautet, ist die neue Reihe, die die kumulative Summe der alten Reihe ist, (1, 4, 11, 21). Sie wird berechnet als
- 1
- 1 + 3 = 4
- 4 + 7 = 11
- 11 + 10 = 21
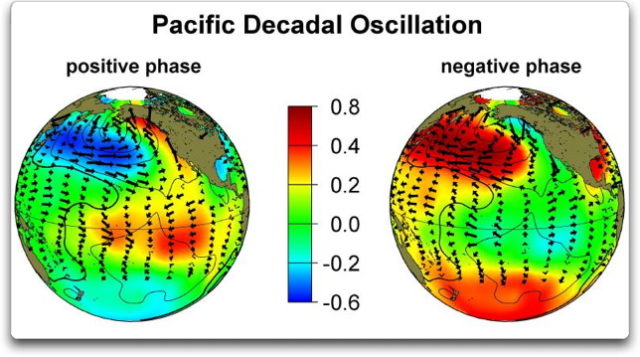
Warum ist eine kumulierte Summe von Interesse? Sie kann zugrunde liegende Trends und Veränderungen in Datensätzen aufzeigen. Man nehme zum Beispiel die „Pazifische Dekadische Oszillation“ PDO. Dies ist eine langsame Veränderung im Pazifik, bei der der nördlichste Teil alternierend kühler und wärmer wird.
Abbildung 1: Die beiden Extreme der Wassertemperatur des Pazifiks bzgl. der PDO.
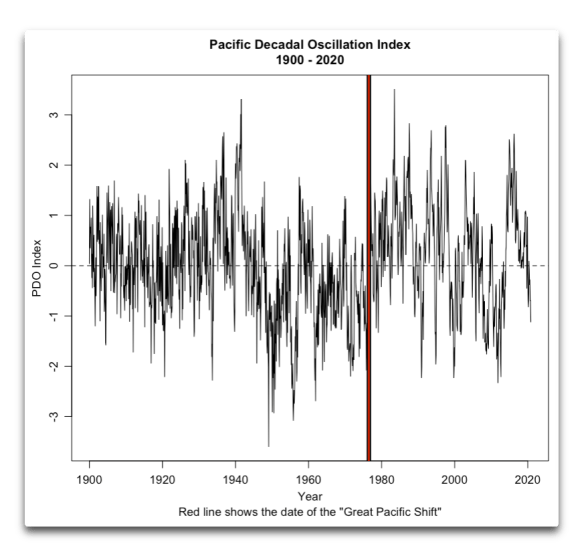
Und hier eine Graphik des PDO-Index‚, einer Maßzahl für die Phase der PDO:
Abbildung 2. PDO-Index, und das Datum der „Großen Pazifischen Klimaverschiebung“ von 1976-1977.
Und was ist die „Große Pazifische Klimaverschiebung“, wenn sie stattfindet? Es war das Datum der ersten Verschiebung der Pazifischen Dekadischen Oszillation, die von Wissenschaftlern identifiziert wurde. (Als langjähriger kommerzieller Lachsfischer weiß ich die Tatsache sehr zu schätzen, dass die PDO zuerst in Aufzeichnungen von Lachsfängen im pazifischen Nordwesten bemerkt wurde … aber ich schweife ab). Aus dem Journal of Climate Artikel „The Significance of the 1976 Pacific Climate Shift in the Climatology of Alaska“:
Im Jahr 1976 erfuhr die nordpazifische Region, einschließlich Alaska, eine dramatische Verschiebung zu einem Klimaregime, das einen großen Anstieg der Winter- und Frühlingstemperaturen und einen geringeren Anstieg der Sommer- und Herbsttemperaturen im Vergleich zu den vorangegangenen 25 Jahren sah“.
Und was hat die pazifische Klimaverschiebung von 1976 mit den kumulierten Summen zu tun? Es wird deutlich, wenn wir die kumulative Summe des PDO-Index‘ wie unten gezeigt graphisch darstellen:
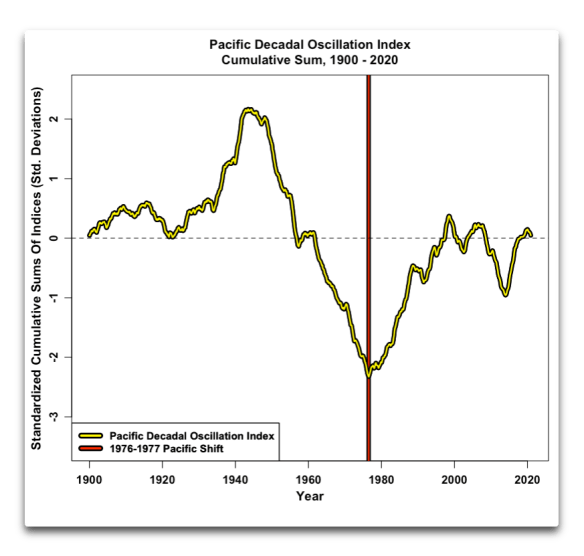
Abbildung 3. Kumulative Summe des PDO-Index‘, und das Datum der pazifischen Klimaverschiebung von 1977
Wie man sieht, zeigt die kumulative Summe des PDO-Index‘ eindeutig das Datum der Verschiebung des pazifischen Klimas in die warme Phase der PDO.
Was können kumulative Summen noch tun? Sie können uns zeigen, ob zwei Datensätze in Beziehung zueinander stehen. Hier sind die kumulativen Summen von:
-
The NINO34 Index
zusammen mit der PDO:
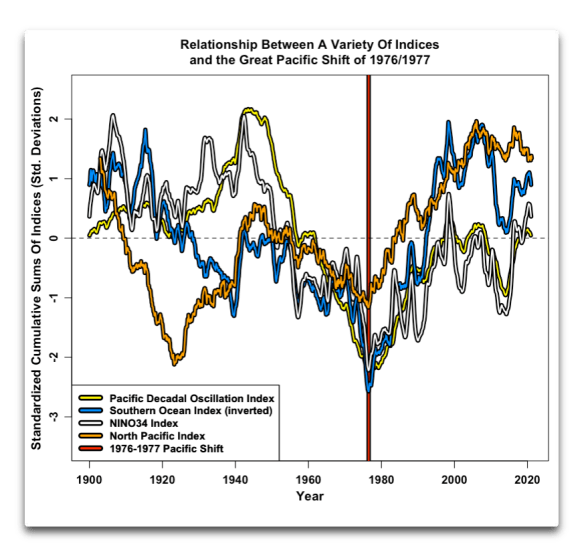
Abbildung 4. Kumulative Summe des PDO-Index und das Datum der pazifischen Klimaverschiebung von 1977
Diese vier Indizes des Klimas beruhen auf sehr unterschiedlichen Dingen. Der PDO-Index ist die erste Hauptkomponente der Meeresoberflächentemperaturen nördlich von 20°N. Der Southern Ocean Index basiert auf der Differenz des Luftdrucks zwischen Tahiti und Australien. Der NINO34-Index basiert auf den Meeresoberflächentemperaturen in der Region 5°N-5°S und 170°W-120°W. Und der Nordpazifik-Index basiert auf dem flächengewichteten Meeresspiegeldruck über der Region 30°N-65°N, 160°E-140°W.
Und trotzdem zeigen sie alle deutlich die pazifische Klimaverschiebung von 1976 …
Was können wir noch mit kumulativen Summen machen? Nun, wir können sie auch verwenden, um zu zeigen, welche Datensätze nicht zusammenhängen … hier sind ein paar Beispiele:
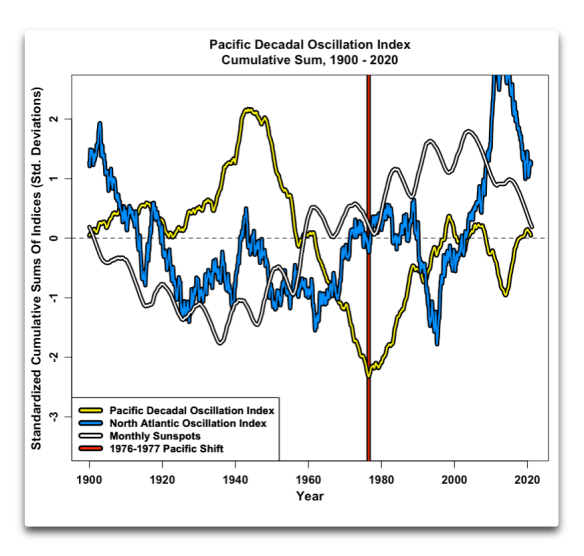
Abbildung 5 Kumulative Summen, Pazifischer Dekadischer Oszillationsindex, Nordatlantischer Oszillationsindex und monatliche Sonnenflecken
Es gibt nicht viele Gemeinsamkeiten bei diesen drei. Und das zeigt, dass die Sonnenflecken und die Nordatlantische Oszillation auch nicht eng mit den in Abbildung 4 gezeigten El-Nino-Indizes zusammenhängen … und das war’s mit den kumulativen Summen für den Moment.
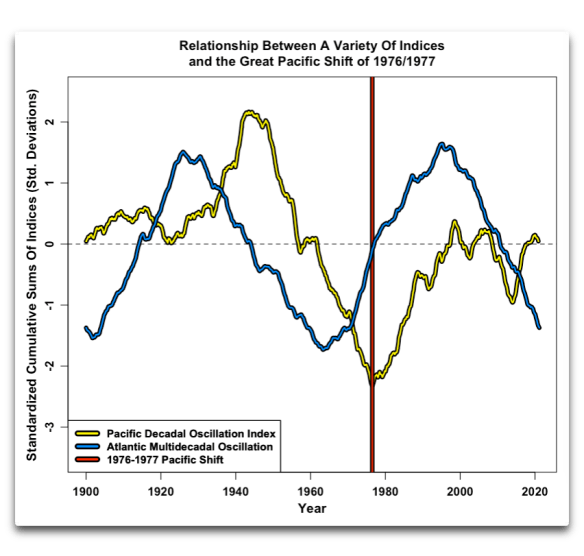
Aktualisierung: Ein Kommentator wies mich darauf hin, dass ich die Atlantische Multidekadische Oszillation (AMO) nicht in die Analyse einbezogen hatte. Hier ist die Grafik:
Anmerkung: Kumulative Summen sind sehr empfindlich gegenüber Anfangsbedingungen und Anomalien. Wenn es einen Aufwärtstrend in den Daten gibt, oder wenn der Nullpunkt niedriger ist als die Werte, wird eine kumulative Summe in den Himmel steigen und umgekehrt. Die Anomalie der gleichen Daten wird sich jedoch ganz anders verhalten. Alle obigen kumulativen Summen wurden zunächst als Anomalie um den Mittelwert des jeweiligen Datensatzes ausgedrückt. Für trendlose Indizes macht dies kaum einen Unterschied. Es stellt jedoch sicher, dass sie zu dem Wert zurückkehren, bei dem sie begonnen haben. Nimmt man sie als Anomalien um einen beliebigen anderen Nullpunkt, so ergibt sich je nach gewähltem Punkt ein Gesamttrend. Infolgedessen ist der Trend einer kumulativen Summe im Allgemeinen bedeutungslos, aber wie oben gezeigt, können die Variationen in der kumulativen Summe recht aussagekräftig sein.
Link: https://wattsupwiththat.com/2021/04/09/adding-it-up/
Übersetzt von Chris Frey EIKE
Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Sehr geehrter Herr Wachsmann,Klima ist die Statistik des Wetters – also reine Mathematik. Erst wenn die Mathematik festgestellt hat, welche Effekte zu beobachten sind, kann man sich in der Physik (und Chemie und Geologie und …) Gedanken machen, warum es diesen Effekt gibt. Genau diese übliche Vorgehensweise macht Herr Eschenbach hier.MfG
Naja, das ist mir eine zu starke Vereinfachung. Mein Gebiet ist die Temperaturmessung. Da wurde und wird eine Menge Schindluder getrieben mittels Mathematik. Die allein nützt nämlich auch nix, wenn die Messwertgewinnung schon Schwächen hat. Bsp. Temperaturdaten gewinnung bis 2001 und heute: Früher wurde 3 x am Tag abgelesen, ein vierter Wert wurde nach Mannheimer Formel zur Mittelwertgewinnung „dazuerfunden“. Seit 2001 wird der Tagesmittelwert aus 24 zur vollen Stunde gemessenen Werten ermittelt. So darf man eigentlich alte Zeitreihen mit denen noch 2001 überhaupt nicht zusammenwürfeln für irgendwelche „Klimadaten“, wird aber aus ideologischen Gründen gemacht. Genauso ist es mit den Messunsicherheiten. In internen Papieren ist dem DWD durchaus bekannt, dass die Messfehler mehrere K betragen können, aber Mittelwerte werden mit zwei Stellen nach dem Komma verbreitet, also vergewaltigte / mißbrauchte Mathematik.
Mathematik ohne Physik ist und bleibt Spielerei. Dieser Artikel ist wie ein „i“ auf dem der Punkt fehlt. Er kommt mir vor wie eine mathematische Spielerei. Wo ist die Physik dazu?
Das sollte aber schon Allgemeinwissen sein, daß sich mehrere Systeme in ihrer Wechselwirkung sowohl verstärken als auch aufheben können. Beim Klima sind es sogar eine unbekannte Anzahl wiederkehrender Oszilationen die mit oder gegeneinander wirken. Genau das zu untersuchen wäre Aufgabe der Klimawissenschaft. Aber dazu müßte man auch eingestehen daß man bisher nur sehr wenig weiß.