Wie Monckton von Brenchley et al. (2015) in einer Studie für die Chinesische Akademie der Wissenschaften im Jahr 2015 betonten, braucht man kein komplexes, milliardenschweres Computermodell, das bei jedem Einschalten den Stromverbrauch einer Kleinstadt verschlingt und ein Dutzend Eisbären umfallen lässt, falls man nur die ECS berechnen will. ECS ist ein nützlicher Standardmaßstab, weil der verdoppelte CO2-Antrieb ungefähr dem gesamten anthropogenen Antrieb entspricht, den wir in diesem Jahrhundert bei einem Business-as-usual-Szenario erwarten könnten. Diese Studie wurde übrigens von der Website der Zeitschrift der Chinesischen Akademie häufiger heruntergeladen als jedes andere in ihrer 60-jährigen Geschichte, und zwar um eine ganze Größenordnung.
Hier ist ein praktischer ECS-Rechner zum Selbermachen, der auf den neuesten Daten basiert:
Das IPCC (1990) hatte eine mittelfristige anthropogene Erwärmung von 0,34 K pro Dekade simuliert. In der Realität jedoch beträgt der Least-Squares-Trend über die 30 Jahre 1991-2020 der mittleren Anomalien in zwei monatlichen Temperaturdatensätzen für die Oberfläche (GISS und HadCRUT) und zwei für die untere Troposphäre (RSS und UAH) 0,2 K pro Dekade, wovon 70 % (Wu et al. 2019), also 0,14 K, auf uns zurückzuführen sind.
Daher hat sich die ursprüngliche mittelfristige Erwärmung der unteren Atmosphäre des IPCC als 2,4-fach überbewertet erwiesen. John Christy (2021) hat kürzlich in einem faszinierenden Online-Vortrag gezeigt (Abb. 1), dass die CMIP6-Modelle die mittelfristige Erwärmung der mittleren Troposphäre ebenfalls um das 2,4-fache überbewertet haben:

Abb. 1: Die 2,4-fache Übertreibung der mittleren Erwärmung der mittleren Troposphäre in den CMIP6-Modellen.
Man kann eine erste grobe Schätzung der mittleren ECS erhalten, indem man die mittlere CMIP6 ECS-Vorhersage von 3,7 K (Meehl et al. 2020) nimmt und durch 2,4 dividiert. Antwort: 1,5 K: nicht genug, um sich Sorgen zu machen.
Um ECS ΔE2 genauer abzuleiten, indem man die Ideen der Studie von der Chinese Academy weiter entwickelt, braucht man nur sieben leicht zugängliche und vernünftig eingeschränkte mittlere Parameter aus dem Mainstream:
1: Der Planck-Sensitivitätsparameter P ist die erste Ableitung der Stefan-Boltzmann-Gleichung: d.h. das Verhältnis der Oberflächentemperatur zum 4-fachen der Albedo-angepassten einfallenden Strahlungsflussdichte über der Atmosphäre (Schlesinger 1988). Somit ist P= 288 / (4 x 241), oder 0,3 K/Wm². Dieser unumstrittene Wert variiert mit der Oberflächentemperatur: aber von 1850 bis zur Verdoppelung des CO2 im Vergleich zur heutigen Temperatur ist er nahe genug an 0,3 und macht damit keinen wesentlichen Unterschied.
2: Der Verdopplungs-CO2-Strahlungsantrieb ΔQ2 wurde in Andrews (2012) mit 3,45 W/m² angegeben, dem Mittelwert von 15 CMIP5-Modellen. Für CMIP6 geben Zelinka et al. (2020) 3,52 W/m² an. Da wir die neuesten Mainstream-Daten verwenden, ziehen wir Letzteren heran.
3: Der exponentielle Wachstumsfaktor H pro Rückkopplungs-Einheit mit der Referenzsensitivität wird hier vorsichtshalber mit dem Wert von 1,07 pro K gleichgesetzt, der in Wentz (2007) als Clausius-Clapeyron-Zunahme der spezifischen Feuchtigkeit bei Erwärmung angegeben wird. Auch diese Größe variiert mit der Temperatur, kann aber über das hier relevante enge Temperaturintervall sicher als konstant angenommen werden. In der Realität wird das exponentielle Wachstum der spezifischen Luftfeuchtigkeit durch die logarithmische Temperaturreaktion auf dieses Wachstum ausgeglichen, und das IPCC (2013) schätzt, dass im mittleren Bereich alle anderen Rückkopplungen sich selbst aufheben. In der Realität gibt es wahrscheinlich nur ein geringes oder gar kein Wachstum der Einheitsrückkopplung unter den heutigen Bedingungen. Doch selbst falls man H = 1,2 annehmen würde, was deutlich über der Realität liegt, würde sich ECS kaum ändern.
4: Der anthropogene Antrieb ΔQ1 von 1850-2020 betrug 2,9 W/m², die Summe des 3,2 W/m² akkumulierten Treibhausgasantriebs und der 0,4 W/m² Ozon-, -0,8 W/m² Aerosol- und 0,1 W/m² Black-Carbon-Antriebe (NOAA AGGI; Gaudel+ 2020; Dittus+ 2020; IPCC 2001, S. 351).
5: Der anthropogene Anteil M der Erwärmung und des Strahlungsungleichgewichts von 1850-2020 betrug 0,7 (Wu et al., 2019; Scafetta 2021). Die Arbeit von Wu hat Gerald Meehl als Co-Autor.
6: Die vorübergehende Erwärmung T1 von 1850-2020 betrug 1,07 K (HadCRUT5: Morice et al. 2020). Basierend auf Wu et al. waren nur 70% davon, also 0,75 K, anthropogen bedingt.
7: Das Energieungleichgewicht ΔN1 der Erde von 1850-2020 berücksichtigt die Verzögerung des Einsetzens der Erwärmung nach einem Forcing. Schuckmann et al. (2020) geben die aktuelle Mainstream-Mittelwertschätzung 0,87 W/m².
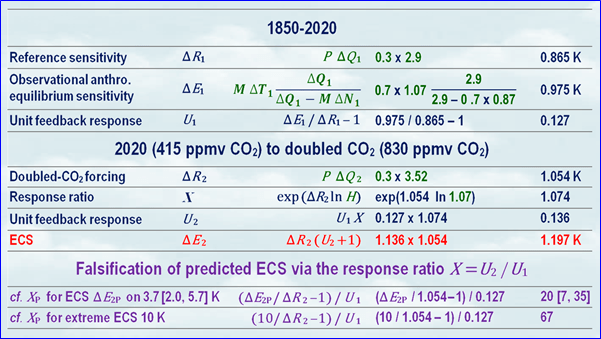
Mit diesen sieben Größen (Abb. 2), alle im mittleren Bereich, alle aktuell, alle aus klimatologischen Mainstream-Quellen, kann man nicht nur eine verlässliche mittlere Schätzung des beobachteten ECS direkt ableiten, ohne auf überkomplexe, unzureichend falsifizierbare und fehleranfällige Computermodelle zurückgreifen zu müssen, sondern auch die Vertretbarkeit des derzeit projizierten ECS-Intervalls 3,7 [2,0, 5,7] K (mittlerer Bereich Meehl et al., 2020; Grenzen Sherwood et al., 2020) falsifizieren. Die Berechnungen sind in Abb. 3 dargestellt. Diese einfache Tabelle bedeutet den Untergang für die Profiteure des Untergangs.
Wie es funktioniert: Seit 1850 haben wir nun angeblich 170 Jahre lang das Klima beeinflusst. Davor war unser Einfluss vernachlässigbar. Aus den sieben Größen in Abb. 2 lässt sich eine entscheidende Größe ableiten – die Einheitsrückkopplungs-Reaktion, die zusätzliche Erwärmung durch Rückkopplung pro Grad Referenzsensitivität. Damit lässt sich diese Reaktion für den Zeitraum von jetzt bis zur CO2-Verdoppelung mit Hilfe des Exponentialwachstumsfaktors H finden, woraus sich ECS ΔR1 ableiten lässt.
1850-2020: Die Periodeneinheit der Rückkopplungsreaktion U1 ist 1 kleiner als das Verhältnis der Gleichgewichtssensitivität ΔE1 zur Referenzsensitivität ΔR1: d. h. 1 kleiner als das Verhältnis der Periodenerwärmung einschließlich Rückkopplungsreaktion zur Periodenerwärmung ohne Rückkopplungsreaktion).
Die Perioden-Referenzsensitivität ΔR1, die direkte Erwärmung vor Hinzurechnung der Rückkopplung, beträgt 0,865 K, das Produkt aus dem Planck-Parameter 0,3 K W-1 m2 und dem anthropogenen Perioden-Antrieb ΔQ1 von 2,9 W/m².
Die Perioden-Gleichgewichts-Sensitivität ΔE1, die eventuelle Erwärmung, nachdem alle kurzzeitigen Rückkopplungen gewirkt haben und sich das Klima wieder im Gleichgewicht befindet, ist etwas komplizierter. Sie ist das Produkt aus zwei Ausdrücken: dem anthropogenen Anteil M ΔT1 der beobachteten vorübergehenden Erwärmung ΔT1 und dem Energie-Gleichgewichts-Verhältnis.
Das Energie-Ungleichgewichts-Verhältnis ist der periodische anthropogene Antrieb ΔQ1 geteilt durch die Differenz zwischen ΔQ1 und dem anthropogenen Anteil M ΔN1 des periodischen Energie-Ungleichgewichts der Erde ΔN1. Im Gleichgewicht gäbe es kein Energieungleichgewicht: der Divisor und der Dividend wären beide gleich ΔQ1. In diesem Fall wäre ΔE1 gleich M ΔT1. Besteht jedoch (wie derzeit) ein Energieungleichgewicht, wird es auch ohne weiteren Strahlungsantrieb nach 2020 zu einer weiteren Erwärmung kommen, so dass ΔE1 das Produkt aus M ΔT1 und dem Energieungleichgewichtsverhältnis ist: also 0,975 K.
Die Einheits-Rückkopplungs-Reaktion U1, die Rückkopplungs-Reaktion pro Grad der Perioden-Referenzempfindlichkeit, ist 1 kleiner als der Systemverstärkungsfaktor ΔE1 / ΔR1. Er beträgt nur 0,127. Vergleichen Sie diesen einfachen, aus Beobachtungen abgeleiteten Mittelwert mit dem Wert von 3,0, der in der folgenden Passage aus Lacis et al. (2010) impliziert ist, die die fehlerhafte offizielle Position zusammenfasst:
„Nicht-kondensierende Treibhausgase, die 25 % des gesamten terrestrischen Treibhauseffekts ausmachen, … sorgen für die stabile Temperaturstruktur, die die gegenwärtigen Niveaus des atmosphärischen Wasserdampfs und der Wolken über Rückkopplungsprozesse aufrechterhält, die die restlichen 75 % des Treibhauseffekts ausmachen“ (Lacis et al., 2010).
2020 auf verdoppeltes CO2: Wie bei 1850-2020, so bei verdoppelter CO2-Konzentration im Vergleich zu den 415 ppmv im Jahr 2020, beginnen Sie mit der Periode die Referenzsensitivität ΔR2, die direkte Erwärmung vor der Addition jeglicher Rückkopplung. ΔR2 ist 1,054 K. Es ist das Produkt aus dem 0,3 K/Wm² (Planck-Parameter) und den 3,52 W/m² anthropogenen Periodenantrieb ΔQ2.
Als nächstes wird die Rückkopplung berücksichtigt, um ECS ΔE2 zu erhalten. Die Methode besteht darin, die Rückkopplungsreaktion U1 der Einheit 1850-2020 entsprechend dem Exponential-Wachstumsfaktor H zu erhöhen.
Das Einheits-Rückkopplungsverhältnis X ist gleich exp(P ΔQ2 ln H), d. h. exp(ΔR2 ln H), oder, einfacher, aber für Mathematik-Puristen anstößig, HΔR2, was 1,074 ist.
Die Einheitsrückkopplung U2 ist das Produkt aus U1 und X, d. h. 1,136.
ECS ΔE2 ist das Produkt aus der Referenzsensitivität ΔE2 auf verdoppeltes CO2 und dem Systemverstärkungsfaktor U2 + 1, d. h. 1,2 K. Nicht 3,7 K (CMIP6: Meehl et al. 2020). Nicht 3,9 K (CMIP6: Zelinka et al. 2020). Nur 1,2 K mittlere anthropogene globale Erwärmung als Reaktion auf verdoppeltes CO2, oder auf alle anthropogenen Antriebe über das gesamte 21. Jahrhundert. Kein großer „Klimanotstand“ also, oder?
Falsifizierung von ECS-Vorhersagen über das Rückkopplungsverhältnis X: Mit dem Wissen, dass die aus Beobachtungen abgeleitete Einheits-Rückkopplungs-Reaktion U1 für 1850-2020 0,127 betrug, ist es möglich, den Wert von XP abzuleiten, der in jeder ECS-Vorhersage ΔE2P impliziert ist: XP = (XP / ΔR2 – 1). Zum Beispiel impliziert der von Meehl et al. (2020) und Sherwood et al. (2020) vorhergesagte ECS von 3,7 [2,0, 5,7] K impliziert XP auf 20 [7, 35]. Selbst die untere Grenze X = 7 würde unhaltbar suggerieren, dass die Rückkopplungsreaktion pro Grad direkter Erwärmung nach 2020 das absurde Siebenfache der Rückkopplungsreaktion pro Grad vor 2020 beträgt. Der in mehreren extremen Arbeiten vorhergesagte High-End-ECS von 10 K ist noch unmöglicher und impliziert X = 67.
Die Unsicherheiten sind gering, da sich die Klimatologie inzwischen auf die Werte der sieben Schlüsselparameter geeinigt hat, die für die Ermittlung des ECS ausreichen. Würde man die 40 Jahre der etwas schnelleren Erwärmung von 1980-2020 als Berechnungsgrundlage nehmen, statt 1850-2020, würde der mittlere ECS auf nur 1,4 K steigen. Selbst falls die gesamte Erwärmung der Industriezeit anthropogen wäre, würde der ECS nur 2 K betragen, aber es wäre nicht mehr der mittlere ECS auf der Basis der aktuellen Mainstream-Daten.
Was sie falsch verstanden haben: Wie haben sich die Klimawissenschaftler dann jemals vorstellen können, dass die globale Erwärmung etwa dreimal so hoch sein würde, wie es die realen Beobachtungen, die sich in ihren neuesten Midrange-Daten widerspiegeln, einen unvoreingenommenen Untersucher erwarten lassen würden?
Klimamodelle verkörpern den Feedback-Formalismus nicht direkt. Ihre ECS-Vorhersagen spiegeln jedoch den Fehler wider, indem sie eine 2,4-mal höhere mittelfristige, anthropogene Erwärmung zeigen als während der letzten 30 Jahre beobachtet, und sie prophezeien das Dreifache der realistischen mittelfristigen ECS.
Im Jahr 2006, in Vorbereitung auf meinen ersten Artikel über die globale Erwärmung, schrieb ich an den verstorbenen Sir John Houghton, damals Vorsitzender der wissenschaftlichen Arbeitsgruppe des IPCC, um zu fragen, warum man dachte, dass die eventuelle globale Erwärmung etwa das Dreifache der direkten Erwärmung betragen würde. Er antwortete, dass der natürliche Treibhauseffekt – die Differenz zwischen der 255 K Emissions-Temperatur ohne Treibhausgase und der 287 K gemessenen Temperatur im Jahr 1850 – 8 K Referenzsensitivität auf Treibhausgase und 24 K Rückkopplungsreaktion darauf umfasste.
Es war diese Erwartung von 3 K Rückkopplung auf jeweils 1 K direkte Erwärmung, also insgesamt 4 K Erwärmung, die die Modellierer dazu brachte, 3 oder 4 K ECS im mittleren Bereich zu erwarten.
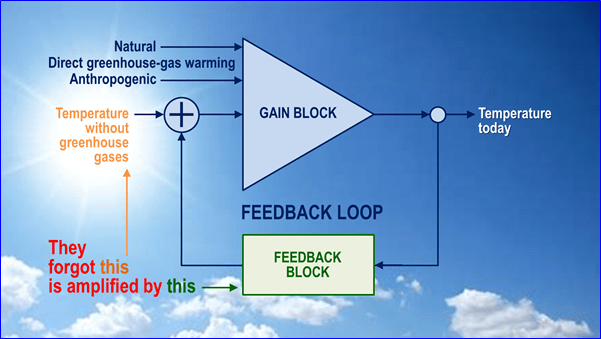
Die Klimatologen hatten vergessen, dass die Sonne scheint (Abb. 4). Was sie übersehen hatten, als sie Mitte der 1980er Jahre die Rückkopplungsformel aus der Regelungstheorie entlehnten war, dass die 24 K vorindustrielle Rückkopplungs-Reaktion nicht nur eine Antwort auf die 8 K direkte Erwärmung durch Treibhausgase war. Ein großer Teil dieser 24 K war eine Reaktion auf die 255 K Emissionstemperatur, die sich auf der Erde auch ohne Treibhausgase eingestellt hätte.
In Wirklichkeit war die vorindustrielle Referenztemperatur die Summe der 255-K-Emissionstemperatur und der 8-K-Referenzsensitivität für vorindustrielle Treibhausgase: also irgendwo in der Gegend von 263 K. Da die 255-K-Emissionstemperatur das 32-fache der 8-K-Referenzsensitivität für Treibhausgase ist, war ein erheblicher Teil der gesamten vorindustriellen Rückkopplungsreaktion von 24 K auf die erstere zurückzuführen, was den Anteil der letzteren entsprechend reduzierte.
Rückkopplung ist eine allgemein gültige Eigenschaft dynamischer Systeme (Systeme, die ihren Zustand mit der Zeit ändern), von elektronischen Schaltkreisen bis zum Klima. Falls und nur falls die gesamte vorindustrielle Referenztemperatur 8 K betrug und es überhaupt keine Rückkopplungsreaktion auf die Emissionstemperatur gab, wäre es zulässig, sich vorzustellen, dass die Rückkopplungsreaktion der Einheit so groß wie 3 war. Selbst dann würde nicht automatisch folgen, dass die Rückkopplungsreaktion der Einheit heute auch nur annähernd so groß wie 3 sein könnte.
Das IPCC wiederholte den Fehler in seinem Fünften Sachstandsbericht von 2013 (AR 5) und wird ihn in seinem bevorstehenden Sechsten Sachstandsbericht (AR 6) erneut begehen. Man definiert „Klima-Rückkopplung“ als Reaktion nur auf Störungen (fünfmal in der Definition erwähnt), schweigt aber über die weitaus größere Rückkopplungsreaktion auf die Emissionstemperatur selbst. Sie sollte ihre mehrtausendseitigen Berichte durch die einzige Monstergleichung (Abb. 5) ersetzen, die die schrittweisen Berechnungen in Abb. 3 zusammenfasst:
Wären Sie bereit, Ihren Namen unter einen Bericht an das IPCC zu setzen, unter dessen Fehlerprotokoll, und es darüber zu informieren, dass ECS grob überbewertet wurde und um Korrektur bitten? Falls ja, kontaktieren Sie mich über das erste Wort meines Nachnamens [at] mail [dot] com und lassen Sie es mich wissen. Denn die neuesten Mainstream-Mitteldaten, auf die sich das IPCC zwangsläufig stützen muss, schließen die schnelle, gefährliche Erwärmung aus, die es so lange, so zuversichtlich, so gewinnbringend, aber so fehlgeleitet vorhergesagt hat.
Link: https://wattsupwiththat.com/2021/02/01/how-much-global-warming-should-ipccs-next-report-predict/
Übersetzt von Chris Frey EIKE
Anmerkungen des Übersetzers hierzu: Auch mit diesem Beitrag zeigt sich, dass Lord Monckton von einer Erwärmungswirkung durch CO2 aujsgeht – wenn gleich auch viel geringer als vom IPCC prophezeit. Nun mehren sich die Zweifel an einer solchen Wirkung immer mehr, was heißt, dass auch Lord Monckton irgendwo einem Trugschluss unterliegen muss. Vielleicht kann ein versierter Kommentator dazu etwas sagen?



















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Für jeden, der hier mit gemittelten Temperaturen und Stefan Boltzmann argumentiert und dabei missbräuchlich eben Mittelwerte und nicht Einzeltemperaturen mit diesen zugeordneten schwarzen bis weißen Körpern glaubt verwenden zu dürfen, empfehle ich eine einfach per EXCEL-Blatt ausführbare Rechnung: ———-Man nehme einmal die Zahlen 1, 2, 3 und 4, bilde deren Mittelwert 2,5 und behandle diesen entsprechend dem T^4 Gesetz mit der 4. Potenz, das ergibt 39,1. ——— Nun nehme er die Einzelwerte in die 4. Potenz: 1^4=1, 2^4=16, 3^4=81 und 4^4=256. Er summiere dann die Ergebnisse zu 354 und bilde daraus den Mittelwert. Ergebnis 88,5. ———-Wer dann immer noch mit SB und gemittelten Temperaturen weiter arbeitet, sollte sich besser mit anderen Themen beschäftigen. Z. B. mit der Messung (Messung!) von Temperatur-Anomalien, frei nach Rahmstorfs Hütte auf dem Berg.
=> Für jeden, der hier mit gemittelten Temperaturen und Stefan Boltzmann argumentiert und dabei missbräuchlich eben Mittelwerte und nicht Einzeltemperaturen…
Herr Prof. Puschner, Ihr Rechenbeispiel das die vereinfachte gobale Klimamodellierung mit Mittelwerten und S-B niedermachen soll, gründet auf einem Missverständnis. Wenn man Mittelwerte aus Temperaturen in Kelvin nimmt, die für den grössten Teil der Erdoberfläche allenfalls um ein paar Prozent voneinander abweichen, so ergeben sich für die 4.Wurzel aus dem Mittelwert nur Fehler von wenigen Promille.
Die Kurve S=Sigma•T^4 weist im Nahbereich um 288 K eine nur geringe Krümmung auf. Daher gilt annähernd deltaS ~deltaT. Im linearen Fall liefert die Mittelwertbildung sogar ein exaktes Ergebnis, und da die Modellierung des TE – also die Berechnung der globalen Klimasensitivität deltaT bei CO2-Verdoppelung mit S-B – ohnehin nicht ganz exakt ist, spielt der Mittelwertfehler keine grosse Rolle.
Sehr geehrter Herr Dietze,
bei Temperaturen am Südpol um 200°K und am Äquator um 325°K müssen Sie mir den von Ihnen behaupteten Promille-Fehler bei der 4. Potenz erst einmal vorrechnen. Danach gehen wir das Problem an, an welchen Stellen, wo Temperaturen, die für die globale Mittelung herangezogen werden, die jeweils zuzuordnende Fläche ein schwarzer Körper im Sinne von Stefan Boltzmann ist und an wie viel tausend Stellen sich die Oberfläche davon und wie viel unterscheidet.
Peter Puschner, Prof. Dr.-Ing. schrieb am 11. Februar 2021 um 12:34
„Earth’s global energy budget„, Trenberth et. al., 2009 hat eine Diskussion zur räumlichen und zeitlichen Temperaturverteilung (Spatial and temporal sampling, Seite 5) und kommt auf eine Korrektur von 6W/m².
Das interessante an Ihrem Rechenbeispiel ist aber das Spiel mit der Temperaturverteilung. Da kann man sehr schnell sehen, dass eine gleichmäßige Temperaturverteilung zur gleichen Abstrahlung bei höherer mittlerer Temperatur führt (3,067^4 * 4 = 353,9 mit 3,067 > 2.5). Wenn es also um eine Abschätzung einer maximal möglichen Temperatur geht, kann man schonmal mit Mittelwerten rechnen.
Herr Prof. Puschner, hier ein Beispiel der Mittelwertbildung sowie für die 4.Wurzel aus T^4 wenn der weitaus grösste Teil der Erdoberfläche für die beiden Hemisphären z.B. mit je drei Zonen mit max. ±12 K Abweichung angenommen wird (die kleinen Polarregionen, wo ohnehin der TE unter -50 Grad gegen Null strebt, können wir vernachlässigen):
(276 K+288 K+300 K)/3=288 K
und
((276^4+288^4+300^4)/3)^0,25=288,5 K
Der Fehler ist 1,7 Promille. Sie sollten auch nicht bestreiten dass die Erdoberfläche (sogar Schnee, Eis, Wasser, Wolken) im IR-Bereich nahezu ein Schwarzstrahler ist.
Stefan-Boltzmann berechnet die Abstrahlungsleistung, die ein „Schwarzer Strahler“ abstrahlt, wenn er eine gewisse Temperatur hat. Echte schwarze Strahler gibt es aber nicht, es handelt sich also um eine Näherungsrechnung, da in der Wirklichkeit noch andere Eigenschaften wirken, z. B. der Emissionsgrad.
Klimatologen wenden Stefan-Boltzmann nun „umgekehrt“ an, also um eine Oberflächentemperatur aufgrund einer Strahlungsleistung zu berechnen.
Da wird es ganz diffus, weil die tatsächliche Erwärmung bzw. deren zeitlicher Verlauf von einer Vielzahl weiterer Eigenschaften abhängt, z. B. Masse, Material, Bestrahlungsdauer, thermodynamische Einflüsse, usw. Trotzdem ist der „Schwarze Strahler“ zunächst die Basis, von der ausgegangen wird. Durch Messungen kann man die Unterschiede zwischen Theorie und Realität feststellen. 1368 W/m² ergeben rechnerisch auf eine tiefschwarze Oberfläche ca. 120°C, real gemessene Oberflächentemperaturen an Land gehen meines Wissens bis zu ca. 80°C bei Sonne im Zenit. Ozeanoberflächen erwärmen sich bis ca. 32°C.
In der Klimadebatte geht es aber nicht um die Materialtemperatur der Oberfläche, sondern um die Lufttemperatur in 2 m Höhe, theoretisch noch reduziert auf Normalnull. Zur Bestimmung der Lufttemperatur 2 m über der Oberfläche ist aber Stefan-Boltzmann vollkommen ungeeignet. Stefan-Boltzmann ist eine reine Strahlungsrechnung, die Lufttemperatur in 2 m Höhe ist aber zu fast 100% thermodynamisch bestimmt.
Diese Diskrepanz stört die Klimatologie aber offenbar nicht. Wie seriös ist das?
Jede Berechnung eines zusätzlichen Wärmeeintrags in die bodennahe Atmosphäre aufgrund von mehr CO2 müßte zwei Bedingungen erfüllen: erstens müßte sie nicht nur einen Wert für Verdoppelung ab z. B. 300 ppm liefern, sondern die gesamte Kennlinie von 0 ppm bis z. B. 1000 ppm CO2 und zweitens müßte sie das physikalische Prinzip beschreiben, aufgrund dessen diese Wärme entsteht. Als Bestätigung sollte dann auch die behauptete 33°C Erwärmung durch den THE harmonisch in die Rechnung passen. Bei einer „exponentiellen Annäherung“ bewirken minimalste Änderungen der Eingangsgröße bereits große Änderungen der Resultatsgröße, die mit größer werdenden Eingangsgrößen immer geringer werden. Mit welcher Eigenschaft von CO2 das erklärbar ist, wäre nachzuweisen. Zur Abb. 4 wäre zu sagen, so eine Schaltung übersteuert auf jeden Fall bis in die Sättigung, wenn der Gain Block eine Verstärkung von größer 1 hat. Eine Gegenkopplung, die diese Bezeichnung verdient, ist auf den invertierenden Eingang zurückgeführt, während das Nutzsignal auf den nicht invertierenden Eingang eines realen Op-Amps geführt wird. Für mich entsteht durch so eine Darstellung mehr Skepsis als Aufklärung.
Wer ist eigentlich dieser „Christopher Monckton of Brenchley“ ? Von dem würde ich gerne mal etwas zum Thema „Globale Erwärmung“ und „Klimawandel“ lesen. Für einen link zu einem seiner Berichte, welches in einem anerkannten Journal veröffentlicht wurde, wäre ich dankbar. Hier bin ich nur bis „Die Mainstream-Klimawissenschaftler ……………………………………………..“ gekommen.Silke Kosch
Warum sollen sich immer die anderen die Arbeit machen? Suchen Sie, dann werden Sie fündig.
@Chris FreyZitat: Auch mit diesem Beitrag zeigt sich, dass Lord Monckton von einer Erwärmungswirkung durch CO2 aujsgeht … Kommentator dazu etwas sagen?Der Planck-Sensitivitätsparameter P von M. Schlesinger mit P = 288K/(4 x 241) = 0,3 K/(W/m^2) und auch die Variante P = 1/[4*σ*ε(eff)*Teff^3] = 1/[4*σ*1*255^3] = 0,27 K/(W/m^2) ist falsch, weil die falsche Energiebilanz vom Erdsystem zur Umgebung für die Bestimmung der Sensitivität(en) benutzt wird.Deshalb sind alle „Klimasensitivitäten“ wissenschaftlicher Unrat, die auf Basis von diesem „Planck-Sensitivitätsparameter“ P = 0,3 K/(W/m^2) oder P = 0,27 K/(W/m^2) ermittelt werden.MfgWerner Holtz
Ich habe mir die Mühe gemacht das Blatt von Dipl. Ing. Peter Dietze durchzulesen:
„Wollen wir die Temperaturerhöhung (im Gleichgewicht) abhängig von einer Erhöhung der CO2 -Konzentration logarithmisch berechnen … können wir die Verdoppelungssensitivität wie folgt verwenden: ΔT = 0,6∙ln(C/Co)/ln(2) “
Das bedeutet, wenn es nicht wollen, da es in den Grundlagen der Thermodynamik so nicht gelehrt wird, dann gilt die Formel eben nicht. Richtig!
Die Auswirkung dieser „wissenschaftlichen“ Festlegung:
Der Mond wird mit der gleichen Intensität bestrahlt und es gelten dort die gleichen SB Gesetze, also wenn man es dort gemütlich warm haben will, setzt man 1 Molekül CO2 aus, dann verdoppelt man auf 2, noch mal auf 4 u.s.w. bis man die, eventuell nach der Verdopplungssensitivität berechnete, Wunschtemperatur erreicht hat.
Man muss nur aufpassen, dass nicht aus Versehen ein ganzer Liter CO2 in der Mondatmosphäre entweicht, dann brennt uns der Mond weg, das wäre schlecht für die Gezeiten.
Der Papstberater Schellhuber läßt seinen Adlatus sprechen, in der BILD:Das mit der Eiseskälte kommt von der Klimaerwärmung. Nicht selten kaltes Wetter ist es, sondern KLIMAWANDEL!https://www.bild.de/ratgeber/wissenschaft/ratgeber/schnee-chaos-globale-erwaermung-schuld-ist-schuld-erklaert-wissenschaftler-75260762.bild.htmlDas habe ich nun immer schon befürchtet: Egal wie das Klima wird, oder meinetwegen auch das Wetter: Es ist immer das CO2 schuld!Und es muss ja stimmen, denn das behaupten ja die „Wissenschaftler!“
=> Nun mehren sich die Zweifel an einer solchen Wirkung immer mehr, was heißt, dass auch Lord Monckton irgendwo einem Trugschluss unterliegen muss. Herr Frey, Ihr Hinweis ist berechtigt. Grundsätzlich verwendet IPCC garkeinen (falsch beschalteten) Bode-Verstärker als Multiplikator. Es gilt der aus Transmissionsspektren berechnete „Strahlungsantrieb“ von 3,7 W/m² an TOA für jede CO2-Verdoppelung – allerdings ohne Wolken, Wasserdampf und Feedback. Für das deltaT am Boden wird das Gesetz von Stefan-Boltzmann angewendet nachdem die 3,7 W/m² wegen der Hin- und Herstrahlung noch mit 1/Eps=390/240 erhöht wurden. Grundsätzlich wird von IPCC nicht die Sonne vergessen (!) und der Bode-Schaltkreis kennt nicht die Strahlungsphysik des Modells. Er weiss nicht dass CO2 unter Wolken nahezu wirkungslos (!) ist und wie gross der Einfluss der Wasserdampfüberlappung sowie Feuchtkonvektion ist. Lord Monckton berücksichtigt auch nicht dass der CO2-Effekt nur etwa 25% der seit vorindustrieller Zeit gemessenen Temperaturerhöhung beträgt und geht so fälschlich von 100% aus. Auch der wahre Wert des Feedbacks ist ihm nicht bekannt. Die +170% des IPCC (welche 1,11*2,7=3 Grad liefern) sind ein durch Ausgasungswerte von Eisbohrkernen bedingter etwa 4fach zu hoher FAKE-Wert. Daher geht der Ansatz, nur mit Hilfe eines Bode-Multiplikators einen verbesserten ECS-Wert von 1,2 Grad zu ermitteln, völlig an der Realität vorbei.
Die Leute, die hier immerzu vertreten, dass das Klima der Zukunft unter allen Umständen nicht bestimmbar ist, da das Klimasystem ja so arg chaotisch ist, müssten jetzt Sturm auf diesen Adeligen laufen. Wie steht EIKE denn zu der angeblich so einfachen „Klimaphysik“ dieses Lord?
Versuchen Sie es selber!
Wo sind ihre Sachargumente?
Herr Wörst,
sie Unterliegen einem Irrtum. Hier wird nach meiner Erfahrung nicht „Sturm gelaufen“, sondern versucht, Fakten auf rationaler Ebene zu bewerten.
@ Herrn Frey: Offenbar ist bei dem Autor der anthropogene Anteil 70%. Weil er dabei Scafetta zitiert, vermute ich, dass er die restlichen 30% hauptsächlich den Wärmeinseleffekten zuschreibt. Der große Rest ist bei ihm offenbar dem anthropogenen CO2 geschuldet. Aber wie immer, wenn ich die Ausführungen von Lord Monckton nachzuvollziehen versuche, komme ich spätestens nach dem ersten Drittel ins Schleudern… Völlig d’accord aber mit dem Autor, dass die IPCC-Modelle wie schon immer übertreiben. Das Klima-Geschehen in der Atmosphäre ist einfach zu kompliziert und weitgehend unverstanden ist, was hier durch viele „übereinstimmend“ geschätzte Parameter kaschiert wird. Da halte ich ein Oberflächen-Bilanzmodell für ungleich transparenter, das, ähnlich der Kirchhoff’schen Knotenregel, trotzdem sehr nützliche und nachvollziehbare Ergebnisse liefert. Aber, wenn etwas kompliziert und weitgehend unverstanden ist und dementsprechend eine riesige Fehlerspanne aufweist, dann bewahrt sich m.E. die Alarmforschung den gewünschten Spielraum, um das überforderte Publikum auch weiterhin in Klimapanik zu versetzen. Man stelle sich vor, der IPCC käme jetzt nach 30 Jahren Computerspielen zu dem Ergebnis, dass kein Grund zu Panik bestünde – dann lieber doch noch ein paar neue Kipppunkte…
=> Offenbar ist bei dem Autor der anthropogene Anteil 70%. Weil er dabei Scafetta zitiert, vermute ich, dass er die restlichen 30% hauptsächlich den Wärmeinseleffekten zuschreibt.
Herr Dr. Ullrich, wie kommen Sie denn darauf? Lord Monckton berechnet doch nirgends den WI-Effekt (siehe Abb.3). Aber den kann man leicht überschlägig global mit dem fossilen Energieverbrauch der Menschheit von etwa 12 TW (11 GtC in 8760 h) und deltaT=0,3 Grad pro W/m² (ohne Feedback) sowie der Erdoberfläche 4PiR² (510 Mio km²) berechnen. Es kommt der vernachlässigbare Wert von nur etwa 0,007 Grad heraus – übrigens ein Schock für alle diejenigen welche eine Dekarbonisierung fordern.
Abb. 4 erschließt sich mir nicht. Es ist wohl der Versuch, Klimawirkungen mit Regelungstechnik irgendwie darzustellen. Wenn der Gain Block ein operativer Teil mit Verstärkung (Gain) ist, dann hat er wundersame Eingänge:Direct greenhouse-gas warming => Energie ———- darunterTemperature ….. ——— und über das Feedback noch einmalTemperature. ———-Wenn man in der Schule unbedarft Rechnungen ohne Betrachtung der Einheiten macht, können da als Ergebnis Zahlen herauskommen. Wie man allerdings Temperatur zu Energie summiert, ist mir bislang nicht bekannt. Vielleicht kann man ja auch Drehmoment und Drehzahl addieren und ich muss da einfach dazu lernen.
Abgesehen von https://www.fachinfo.eu/dietze2018.pdf kann man ECS auch ohne Verwendung von HITRAN ganz einfach rechnen – gestützt auf die beobachtete transiente Temperaturerhöhung von 70% von ca. 1 Grad seit vorindustrieller Zeit – wenn CO2 daran etwa nur 25% Anteil hat deltaT*0,25=ECS*0,7*ln(410/280)/ln(2) und erhält ECS=0,65 Grad pro CO2-Verdoppelung (all inclusive, also mit Wolken, Wasserdampf und Feedback). Solch ein geringes ECS (~1/5 von IPCC) wurde auch von Prof. Harde sowie von MODTRAN berechnet – und das ist nur etwa die Hälfte der 1,2 Grad von Lord Monckton.
Zu der Anmerkung des Übersetzers Herr Frey:Auf Youtube gibt es den Vortrag von Prof. William Happer (Princeton) „Why has global warming paused?“. Genau bei 17:27 min gibt es einen slide mit dem Titel „The Villain“, gemeint ist das CO2-Molekül. Aus der Religion, genauer in der Offenbarung des Johannes ist die „Zahl des Satans“ mit 666 angegeben. Dies ist auch die Wellenzahl pro cm wo das CO2-Molekül durch Biegeschwingungen IR-aktiv ist. Wahrscheinlich hat der Teufel oder Satan seine Hand im Spiel. So jedenfalls William Happer mit seinem speziellen Humor zu „Satans Number“. Fragen wir doch einmal den Berater des Papstes Franziskus (Prof. Schellenhuber) ob diese Hypothese zutreffend sein könnte.
Wir lachen darüber aber glauben Sie mir, mit „Satans number“ lässt sich Politik machen, mit den HS der Thermodynamik hingegen nicht. Die grünen Schlümpfe glauben ehe an den Klima-Satan als dass sie die Thermodynamik verstehen….