Ich werde darauf aufmerksam, dass Zeke Hausfather neben vielen Anderen behauptet, dass das Jahr 2018 das wärmste Jahr jemals hinsichtlich der Ozeane gewesen sei, und zwar bis zu einer Tiefe von 2000 m. Er drückte es so aus:
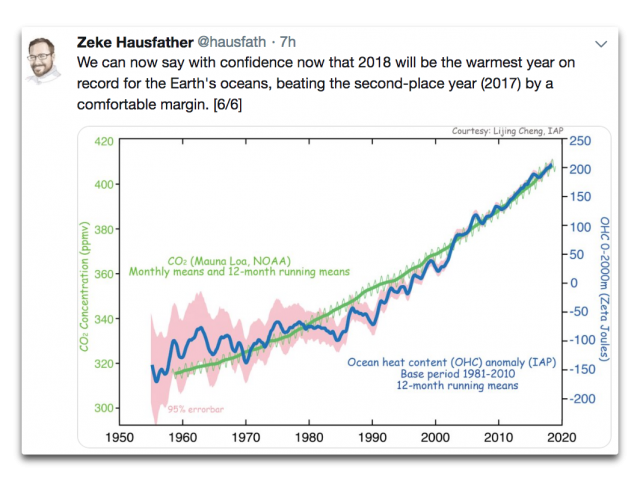
Abbildung 1: Änderung des ozeanischen Wärmegehaltes von 1955 bis 2018. Daten vom Institute for Applied Physics (IAP).
Als ich die Graphik in Zekes Tweet sah, leuchtete mein innerer Detektor für schlechte Zahlen sofort grell rot auf. Was mir verdächtig erschien war, dass die Vertrauens-Intervalle viel zu klein aussahen. Nicht nur das, sondern auch, dass die Graphik Einheiten verwendet, die für die Meisten bedeutungslos sind. Nun ja …
Die Einheiten in dieser Graphik sind „Zettajoules“, abgekürzt ZJ. Ein Zettajoule sind 110 Joule. Das wollte ich in eine allgemein bekanntere Einheit umrechnen, nämlich Grad Celsius (°C). Dazu musste ich berechnen, wie viele Zettajoules man braucht, um die Temperatur in den obersten 2000 Meter der Ozeane um 1°C zu erhöhen.
Man betrachte die zugehörige Mathematik im Anhang [wird hier nicht übernommen. Wer nachrechnen möchte, klicke auf den Link zum Original. Anm. d. Übers.] Es genügt an dieser Stelle zu sagen, dass man etwa 2600 Zettajoule braucht, um die Temperatur in dieser Ozeanschicht um 1°C zu erhöhen. Noch einmal: 2600 ZJ pro Grad.
Jetzt betrachte man noch einmal Abbildung 1. Sie behaupten, dass ihre Fehlerbandbreite der Werte von 1955 plus/minus 95 Zettajoules ausmacht … und das rechnet sich um zu ± 0.04°C. Vier Hundertstel eines Grades Celsius … tatsächlich …
Man mag mich für dumm halten, aber ich glaube einfach NICHT, dass wir die Wassertemperatur der oberen 2000 Meter der Ozeane bis auf plus/minus vier Hundertstel Grad genau kennen.
Es kommt aber noch schlimmer. Im Jahre 2018 behaupten sie, dass die Fehlerbandbreite eine Größenordnung von plus/minus neun Zettajoules aufweist … was umgerechnet drei Tausendstel Grad Celsius sind – 0,003°C. Also wirklich! Man frage irgendeinen Verfahrenstechniker – die Bestimmung der mittleren Wassertemperatur in einem normalen Swimmingpool auf drei Tausendstel Grad genau würde mindestens ein Dutzend Thermometer erfordern …
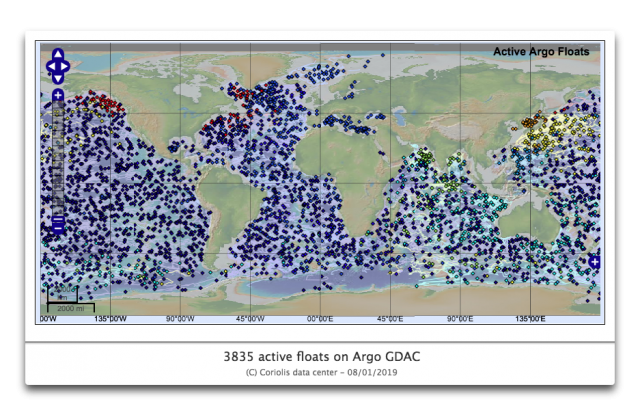
Sie begründen ihre Behauptung, diesen Grad an Genauigkeit zu erreichen, mit den ARGO-Bojen. Diese Bojen treiben in verschiedenen Tiefen im Ozean. Alle zehn Tage steigen sie langsam an die Oberfläche und messen auf dem Weg dorthin die Temperatur. Gegenwärtig, das heißt vor drei Tagen, waren 3835 Bojen in Betrieb.
Abbildung 2: Verteilung aller aktiven ARGO-Bojen am 8. Januar 2019
Das sieht nach einer ziemlich großen Abdeckung aus in dieser Graphik, nicht wahr? Vielleicht nicht ein paar Dutzend Thermometer pro Swimmingpool, aber dicht … Tatsächlich ist es aber so, dass auf jeweils 93.500 km² Ozean nur eine ARGO-Boje kommt. Das ist ein Kasten mit jeweils 300 km Seitenlänge und einer Tiefe von 2 km … die genau ein Thermometer enthält.
Das ihrer Schätzung der Fehlerbandbreite zugrunde liegende Problem ist Folgendes: Wenn die Anzahl der Messungen steigt, nimmt die Fehlerbandbreite um 1 geteilt durch die Quadratwurzel der Anzahl der Beobachtungen ab. Und das heißt, falls wir mehr Dezimalstellen in unserer Fehlerbandbreite haben wollen, müssen wir einhundert mal die Anzahl der Messpunkte haben.
Beispiel, falls wir einen Fehler von – sagen wir – einem Zehntelgrad Celsius aus zehn Messungen haben wollen, dann brauchen wir eintausend Messungen, um den Fehler um ein Hundertstel Grad zu reduzieren …
Umgekehrt ist es genauso. Nehmen wir also einmal an, dass ihre Schätzung der Fehlerbandbreite von ± 0.003°C der Daten aus dem Jahr 2018 korrekt ist und das dies der ausgezeichneten Abdeckung mit 3835 ARGO-Bojen geschuldet ist.
Das würde bedeuten, dass wir eine zehn mal so große Fehlerbandbreite bekommen, also ± 0.03°C, falls es nur 38 ARGO-Bojen gäbe …
Tut mir leid, das glaube ich nicht. 38 Thermometer, von denen jedes drei Vertikalprofile der Temperatur pro Monat aufzeichnet, um die Temperatur der oberen 2000 Meter der gesamten globalen Ozeane zu messen – auf plus/minus drei Hundertstel Grad genau?
Mein Detektor für schlechte Zahlen leuchtete immer noch rot. Also führte ich eine Art „Monte Carlo“-Analyse durch. Benannt nach dem berühmten Casino impliziert eine Monte Carlo-Analyse, dass man Zufallsdaten einer Analyse unterzieht, um zu sehen, ob die Antwort vernünftig ist.
In diesem Falle nahm ich mir ein Gitternetz von 1° Breite mal 1° Länge vor und betrachtete die Ozeantemperaturen in verschiedenen Tiefen bis zu 2000 m aus dem Levitus World Ocean Atlas. Dieser enthält die monatlichen langzeitlichen Mittelwerte in jeder Tiefe für jedes Gitterquadrat für jeden Monat. Dann berechnete ich das globale Mittel für jeden Monat von der Oberfläche bis zu einer Tiefe von 2000 m.
Nun gibt es 33.713 Gitterquadrate von 1° x 1° mit Ozeandaten. (Die Gebiete jenseits der beiden Polarkreise habe ich mal außen vor gelassen, weil es dort fast keine Bojen gibt). Und es gibt 3825 ARGO-Bojen. Im Mittel befinden sich etwa 5% davon in einem normalen Gitterquadrat. Die ARGO-Bojen vermessen also größenordnungsmäßig zehn Prozent der Gitterquadrate … was bedeutet, dass trotz der vielen ARGO-Bojen zu jeder gegebenen Zeit 90% der 1°x1°-Gitterquadrate in den Ozeanen nicht vermessen werden! Ich meine ja nur …
Um zu sehen, welchen Unterschied das ausmacht, unterzog ich 3825 zufällig ausgewählte Ozean-Gitterquadrate wiederholten Analysen. Dabei machte ich genau das Gleiche wie zuvor – errechnete die Mittelwerte in jeder Tiefe und berechnete dann die globale mittlere Temperatur Monat für Monat für jene Gitterquadrate. Hier folgt eine Graphik typischer Zufallsorte für simulierte ARGO-Punkte für einen Lauf:
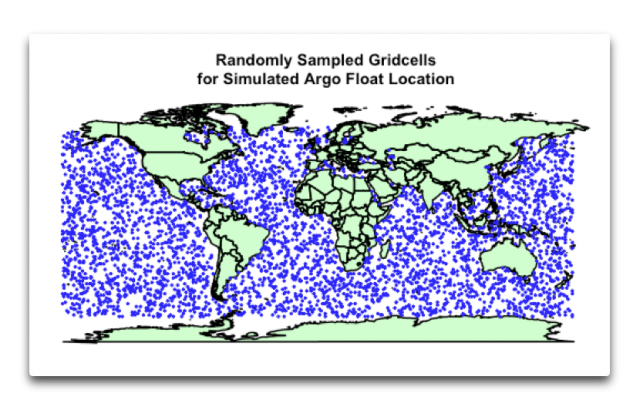
Abbildung 3: Typische simulierte Verteilung von ARGO-Bojen für einen Lauf einer Monte Carlo-Analyse.
Und dabei fand ich das, was zu finden ich mir gedacht hatte. Ihre behauptete Genauigkeit stammt nicht aus Experimenten. Abbildung 4 zeigt die Ergebnisse eines typischen Laufs. Das 95%-Vertrauensintervall der Ergebnisse variierte zwischen 0,05°C und 0,1°C:
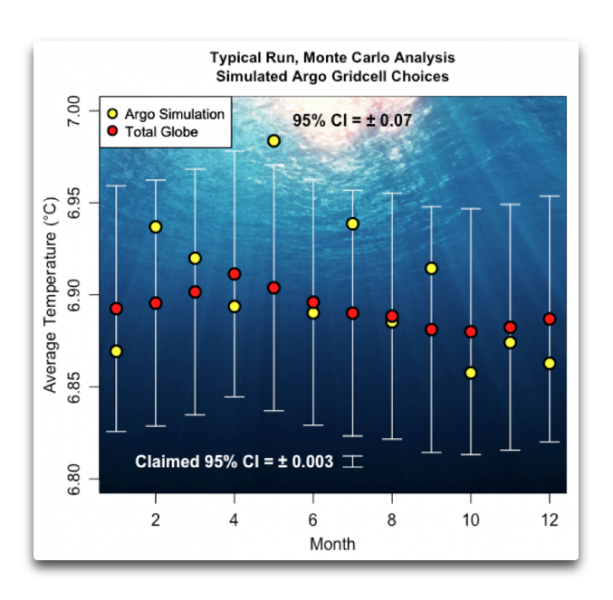
Abbildung 4: Typischer Lauf, mittlere globale Ozean-Temperatur von der Oberfläche bis 2000 m tief, aus dem Levitus World Ocean Atlas (rote Punkte) und den 3825 simulierten ARGO-Punkten. Weiße Federstriche zeigen das 95%-Vertrauensintervall (95% CI). Für diesen Lauf betrug das 95% CI 0,07°C. Der kleine Federstrich unten Mitte zeigt das behauptete 95% CI aus dem Jahr 2018 von 0,03°C.
Wie man sieht, erhält man mittels der simulierten ARGO-Messpunkte eine Antwort, die dem tatsächlichen Temperaturmittel ziemlich nahe kommt. Monatliche Mittelwerte liegen innerhalb eines Zehntelgrades des tatsächlichen Mittelwertes … aber weil die ARGO-Bojen nur etwa 10% der 1° x 1°-Ozean-Gitterquadrate vermessen, ist das immer noch eine Größenordnung mehr als das für das Jahr 2018 behauptete 95% CI der Daten in Abbildung 1.
Also denke ich, dass mein Detektor für schlechte Zahlen weiter angeschaltet bleiben sollte …
Und schließlich sagt Zeke, dass die Ozeantemperatur im Jahre 2018 die Temperatur des Jahres 2017 um eine „komfortable Spanne“ übertrifft. Aber in Wirklichkeit ist es nur 8 Zettajoule wärmer … was geringer ist als die für 2018 behauptete Fehlerbandbreite. Oh nein, das ist keine „komfortable Spanne“. Es liegt noch deutlich innerhalb ihres behaupteten unglaublich geringen Fehlers, den sie mit ± 9 ZJ für das Jahr 2018 angeben.
Letzte Bemerkung: Man mache bitte nicht Zeke hierüber Vorwürfe. Er ist einer der Guten, und wir alle liegen mitunter falsch. Wie ich immer wieder nachgewiesen habe, hatte der amerikanische Wissenschaftler Lewis Thomas völlig recht mit seiner Bemerkung „Wir sind erschaffen, um Fehler zu machen, programmiert auf Irrtümer…“
Link: https://wattsupwiththat.com/2019/01/11/a-small-margin-of-error/
Übersetzt von Chris Frey EIKE
Vor 4 Wochen durften wir hier bei Eike über Frau Baerbock lachen, die si h mal eben um den Faktor 1 Milliarde bei der CO2 vertan hatte. Vor einiger Zeit lächelten wir über Herrn Özdemir, der die Last im Stromnetz in GB messen wollte. Im diesem Artikel wird nun ein Zetta-Joule mit 1 hoch 10 Joule angesetzt. Aha, ein Zetta-Joule ist also ein Joule und nicht 10 hoch 21 Joule. Sehr interessant.
Ich finde es schön, dass Herr Eschenbach die Aufregung über den Wärmegehalt der Ozeane auf das gelenkt hat, was gemessen wird: das Tiefenprofil der Ozean-Temperaturen. Zur Messung des Wärmegehalts der Ozeane benötigt man ein Kalorimeter. Man kann dies im Labor ausführen. Man kühlt 1 kg Ozeanwasser auf den absoluten Nullpunkt (-273 °C) ab und misst bei konstantem Druck die benötigte Wärmemenge um das Eis/Wasser auf z.B. 7 °C zu erwärmen. (Schätzwert: 600 kJ/kg) Der Wärmeinhalt ist dann das Produkt aus diesem Wert und der Masse des Ozeanwassers (1,4*10^21 kg), also etwa 8*10^26 J. Die Erde absorbiert während eines Jahres 4*10^24 J Sonnen-Energie. Aber dies ist ebenso wie die Anomalie des Wärmegehalts meiner Meinung nach von weniger Interesse.
Die Messung des Tiefenprofils der Ozean-Temperaturen könnte vielleicht nützlich sein zum Verständnis und der Vorhersage von El Nino- und La Nina-Ereignissen. Die Temperaturen werden bisher nur bis 2 km Tiefe gemessen. (mittlere Ozean-Tiefe 4 km). Das sollte für El Nino- und La Nina-Ereignisse aber ausreichen.
Guten Abend,
Eigentlich entbehrt es jeder Grundlage sich mit diesem Hokus- Pokus zu beschäftigen. Wie ich schon schrieb, bezieht sich die Übersicht zu dem betrachteten Medium, auf Kenntnisse im Promille Bereich und es wird behauptet hier alles so genau zu kennen wie eine Zwiebelmembran unterm Mikroskop.
Ich würde hier noch einen anderen Einwand bringen, in Bezug auf die Möglichkeit des Energieeintrages. Die Propheten wollen uns ja weiß machen das es ja hier auch das verteufelte CO² Molekül, vornehmlich das vom Menschen ist, welches dafür zu Verantwortung zu ziehen wäre.
Also, eine Argo Boje, welche ein Temperaturprofil in der Nähe von Zonen, wie den Phlegräischen Feldern oder entlang des Mittelatlantischen Rückens erstellt, was wird sie wohl messen wenn sie Tolleranzen feststellt?
Aber wie gesagt: eigentlich gibt es keinen Grund sich damit überhaupt zu beschäftigen….
Ich glaube zum Beispiel auch nicht das irgendjemand von den Ozeanforschen überhaupt ansatzweise versteht, warum der Nordostatlantische Strom solch gravierenden Schwankungen unterliegt. Erst schlägt der eine Alarm, dann relativiert der nächste, beide behaupten alles genau wissenschaftlich zu ergründen und zu messen, aber eigentlich tappen beide im Dunkel der Tiefe mit der Hoffnung die Erkenntnis ans Licht zu bringen. Ist dann allerdings eher so, als ob man im Mikroskop alle Spektrenfilter gleichzeitig vor die Linse schiebt.
Mit freundlichen Grüßen!
Christian Möser
Zimmerer
Abstand der einzelnen Bojen etwa 100 Km. Das heißt für die 100 Km dazwischen gibt es keine Messungen. Ich schätze mal, dadurch gibt es mindestens +- 2° Ungenauigkeit, egal wie genau die Thermometer sind. Abstände auf der Y-Achse in der Abbildung 50ZJ entspricht 0,02°. — Wenn ich mir einen Kuchen backe, ist es egal, ob ich 200 g, oder 200,02 g Mehl nehme.