- Die Erde hat zwar ein heißes Inneres, aber der Wärmestrom an ihrer Oberfläche ist äußerst gering. Auch die Gezeitenreibung liefert keine klimawirksame Energie. Die alleinige „natürliche“ Eigentemperatur der Erde würde vielmehr bei etwa minus 240 Grad Celsius liegen. Die Erde selbst ist also primär an der Temperaturgenese auf ihrer Oberfläche nicht beteiligt.
- Die Sonne ist der bestimmende Energielieferant für die Temperatur- und Klimagenese auf unserer Erde; die Sonne ist also ihr eigentlicher Klimamotor.
- Und das Stefan-Boltzmann-Gesetz beschreibt den physikalischen Zusammenhang von Strahlung und Temperatur.
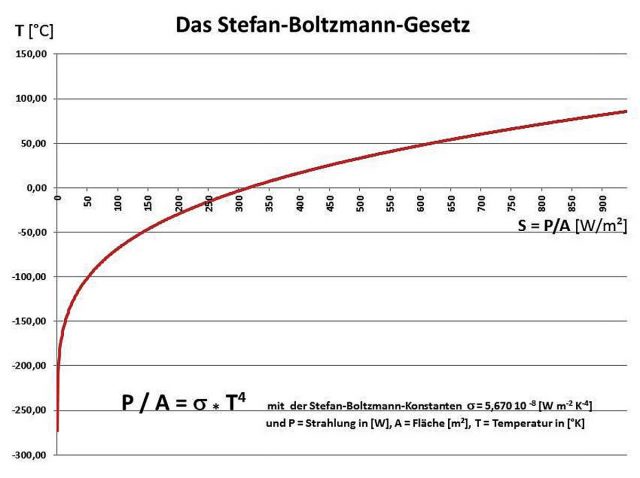
Das Stefan-Boltzmann-Gesetz kann also, bei richtiger Anwendung, zur Beschreibung der Temperatur- und Klimagenese unserer Erde dienen. Es beschreibt für einen Schwarzen Körper den in Abbildung 1 dargestellten physikalischen Zusammenhang von Strahlung und Temperatur im thermischen Gleichgewicht:
Das Gleichheitszeichen im Stefan-Boltzmann-Gesetz bedeutet aber leider nicht, dass man einfach irgendwelche Durchschnittswerte in dieses physikalische Gesetz einsetzen darf, um die Situation auf der Erde zu beschreiben, denn dieses S-B Gesetz ist eben ein Gesetz und keine Gleichung. Es stellt vielmehr einen direkten physikalischen Bezug von singulären Strahlungs- und Temperaturwerten im gemeinsamen thermischen Gleichgewicht her. Und nur in diesem Gleichgewichtszustand entspricht ein konkreter Strahlungswert einer durch dieses Gesetz eindeutig definierten Temperatur nach der in Abbildung 1 dargestellten Funktion. Die jeweilige Temperatur muss also physikalisch konkret vorliegen, um den spezifischen Strahlungswert nach dem Stefan-Boltzmann-Gesetz zu erzeugen.
1. ERKENNTNIS: Berechnungen von und aus Durchschnittswerten sind mit dem Stefan-Boltzmann-Gesetz physikalisch nicht zulässig. Eine Berechnung von Mittelwerten kann vielmehr erst dann durchgeführt werden, wenn bereits für alle beteiligten Wertepaare von Temperatur und Strahlung eine individuelle Umrechnung nach dem Stefan-Boltzmann-Gesetz erfolgt ist. Grundvoraussetzung ist, dass diese Wertepaare in einer direkten physikalischen Beziehung miteinander stehen müssen.
Machen wir an dieser Stelle zunächst einmal ein Gedankenexperiment: Es gibt gar keine Erde!
Dazu verbringen wir zu einem Zeitpunkt “0” ein Duplikat unserer Erde aus einem Dunkelkammer-Weltraumlabor an den aktuellen Standort unserer Erde. Dieses Duplikat soll eine voll funktionsfähige Erde in einem „tiefgefrorenen“ Zustand mit einer Eigentemperatur von minus 240 Grad Celsius darstellen:
- Nun setzen wir dieses Duplikat unserer Erde zum Zeitpunkt „0“ der Sonnenstrahlung aus und messen die Zeit „A“, bis die aktuelle Temperaturverteilung auf unserer Erde erreicht ist und alle atmosphärischen und ozeanischen Zirkulationen mit Wärmeenergie „aufgeladen“ sind. Dieser Zeitpunkt „A“ ist gekennzeichnet durch ein erstmaliges Gleichgewicht von eingestrahlter und abgestrahlter Energiemenge.
- Nachdem dieser Gleichgewichtszustand erreicht wurde, verbringen wir das Duplikat unserer Erde zum Zeitpunkt „B“ wieder ins Labor und messen den Zeitraum „b”, bis wieder die ursprüngliche Ausgangstemperatur von etwa 240 Grad Celsius herrscht.
Wir werden dann herausfinden, dass beide Zeiten “A” und “b” größer als “Null” sind. Die Zeit “A” repräsentiert ein Maß für die Wärmekapazität unserer Erde, während die Zeit “b” ein Maß für die Qualität der thermischen Isolierung unserer Erde gegen das Weltall darstellt. „A“ und „b” repräsentieren in erster Näherung einen Zeitraum von Jahrhunderten bis Jahrtausenden. Das Stefan-Boltzmann-Gesetz gilt aber nur in einem thermischen Gleichgewichtszustand zwischen Strahlung und Temperatur, also im Zeitraum „t“ mit (A < t < B). In einem solchen Gleichgewichtszustand spielt aber die Wärmekapazität zunächst keine Rolle. Die einzige temperaturbestimmende Einflussgröße im thermischen Gleichgewichtszustand auf unserer Erde ist damit die eingestrahlte Energie von der Sonne in [W/m²] auf der Tagseite. Wie groß der Energieinhalt des Systems Erde dabei wirklich ist und wie lange die Aufladung gedauert hat, ist dafür zunächst unerheblich, wenn wir diesen Zeitraum „t“ mit (A < t < B) betrachten.
Dieser statische Fall zeichnet sich offensichtlich durch eine relativ stabile globale Durchschnittstemperatur (NST=Near Surface Temperature) von 14,8 Grad Celsius aus. Die globalen Zirkulationen sind mit Energie „gesättigt“ und alle atmosphärischen und ozeanischen Prozesse sind in eine Art mittleren klimatischen Gleichgewichtszustand „eingeschwungen“ – das Wettergeschehen spiele in dieser Abstraktion keine Rolle. Bei einer solchen statischen Betrachtung ergeben sich dann folgende Rechengrößen:
Solarkonstante: 1.367 W/m²
Temperaturwirksame Sonneneinstrahlung: 940 W/m²
Durchschnittliche Abstrahlung nach Energiebilanz: 235 W/m²
Anmerkung: Um den Beweisweg nicht zu komplizieren, werden hier vereinfachte Werte zugrunde gelegt. Der hemisphärische Zweischichtfall für Atmosphäre und Oberfläche mit einer temperaturwirksamen Nettostrahlung von 780 W/m² wird hier nicht betrachtet.
Für eine hemisphärische Sonneneinstrahlung von 940 W/m² bei lotrechter Position der Sonne ergibt sich nach dem Stefan-Boltzmann-Gesetz dann eine maximale Gleichgewichtstemperatur von 85,7 Grad Celsius. Und eine beliebige örtliche SB-Maximaltemperatur lässt sich in Abhängigkeit von der geographischen Breite mit dem hemisphärischen S-B Ansatz folgendermaßen beschreiben:
S,Z = 940 [W/m²] * cos mit S,,Z = breitenabhängiger hemisphärischer Netto-Strahlungsantrieb im solaren Zenit und =auf den jahreszeitlichen Sonnenstand korrigierte Breite der Ortslage
Die aus dieser S-B Beziehung ableitbaren hemisphärischen S-B Gleichgewichtstemperaturen werden auf der Erde weder im Maximum noch im Minimum erreicht. Wenden wir uns daher zunächst einmal dem Mond als vergleichbarem Himmelskörper ohne Ozeane und Atmosphäre zu. Nachfolgend ist eine Abbildung dargestellt, die bereits auf EIKE veröffentlicht worden war:
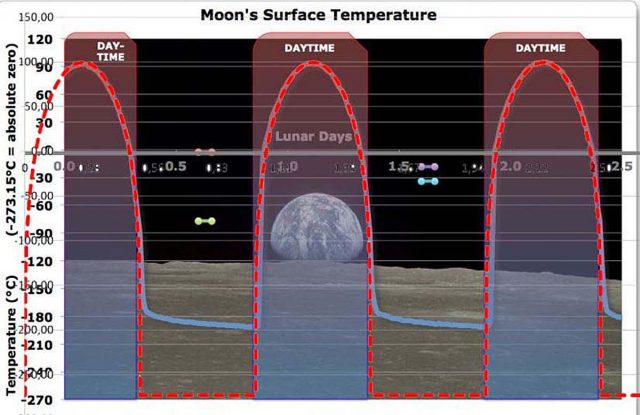
Abbildung 2: Vergleich der gemessenen Oberflächentemperatur auf dem Mond (blau) mit der hemisphärischen S-B Gleichgewichtstemperatur (rot)
Blau: Gemessene Oberflächentemperatur auf dem Mond am Landeplatz von Apollo 15
Zugrunde liegt die Originalabbildung aus einem EIKE-Artikel (Primärquelle Eschenbach auf WUWT)
Rot: Verlauf der hemisphärischen S-B Gleichgewichtstemperatur für die geographischen Position des Apollo 15 Landeplatzes ohne Berücksichtigung der lunaren Achsenneigung mit den nachfolgenden Eckwerten:
Landepunkt von Apollo 15: Mond @ 26° 7′ 55.99″ N 3° 38′ 1.9″ E
Solarkonstante: 1.367 [W/m²]
Albedo des Mondes: 0,11
Temperaturwirksame Solarstrahlung: 1.217 [W/m²]
dito bei 26,125° geogr. Breite: 1.092 [W/m²]
Effektive Solarstrahlung Seff für α = [0° – 360°]: IF SIN α >0 THEN Seff = SIN α* 1.092 [W/m²]
IF SIN α <0 THEN Seff = 0 [W/m²]
Abbildung 2 zeigt, dass die gemessene und die hemisphärisch berechnete S-B Gleichgewichtstemperatur am Landepunkt von Apollo 15 bei Tage hervorragend überein stimmen, während die Nacht-Temperaturen um etwa 70 Grad differieren. Diese Differenz ist aber eher ein Problem zwischen Theorie und Praxis, denn in der S-B Berechnung wird für die Nachtseite des Mondes streng mit 0 [W/m²] gerechnet, während der Mond in der Realität reflektierte Sonnenstrahlung von der Erde erhält, deren Albedo immerhin etwa 30% betragt. Eine Temperatur von -196 °C entspricht nach Stefan-Boltzmann einer Strahlung von 2 {W/m²], wie Abbildung 1 erkennen lässt, und dafür dürfte die Rückstrahlung der Erde von etwa 400 [W/m²] allemal ausreichen.
2. ERKENNTNIS: Auf dem Mond funktioniert der hemisphärische S-B Ansatz ganz hervorragend, warum sollte er also für die Erde nicht anwendbar sein?
Im konventionellen S-B Ansatz wird eine globale Durchschnittstemperatur aus der durchschnittlichen Energiebilanz der Erde mit einem Viertel der wirksamen Solarkonstanten ermittelt. Wie wir bereits gesehen haben, „verkraftet“ das Stefan-Boltzmann-Gesetz solche Durchschnittswerte aber gar nicht.
Schauen wir aber trotzdem einmal näher hin und beschränken wir uns auf die Abstrahlung:
Die durchschnittliche globale Abstrahlung unserer Erde kann in erster Näherung unter Berücksichtigung der Albedo tatsächlich mit einem Viertel der temperaturwirksamen netto-Sonneneinstrahlung von 235 W/m² beschrieben werden, auch wenn sie in Wahrheit sicherlich tages- und jahreszeitlichen sowie breitenabhängigen Schwankungen unterworfen ist.
Nur zur Erinnerung: Diese Betrachtung der Erde findet im Zeitraum „t“ mit (A < t < B) statt.
Die Wärmespeicher des Systems Erde sind also „voll aufgeladen“ und die globale Abstrahlung geschieht kontinuierlich parallel zur hemisphärisch getakteten solaren Einstrahlung. Beim Mond war das ja noch ganz einfach, denn der verfügt neben seiner Oberfläche über keine zusätzlichen Wärmespeicher. Damit stellt sich die Frage, wo bei einer Betrachtung nach der globalen Strahlungsbilanz eigentlich der Wärmeinhalt der globalen Zirkulationen berücksichtigt wird.
3. ERKENNTNIS: Im Gegensatz zum Mond kühlt unsere Erde über Nacht nicht schnell genug aus.
Das Stefan-Boltzmann-Gesetz für einen schwarzen Körper in einer erwärmten Umgebung lautet nun:
S = S – S0 = * (T4 – T04) mit S = P/A [W/m²] Quelle: Gerthsen-Kneser “Physik” (1971)
Nach Abbildung 3 ist es also nach dem Stefan-Boltzmann-Gesetz überhaupt nicht egal, bei welcher Umgebungstemperatur „T0“ wir eine globale Emission von S=235 W/m² ansetzen:
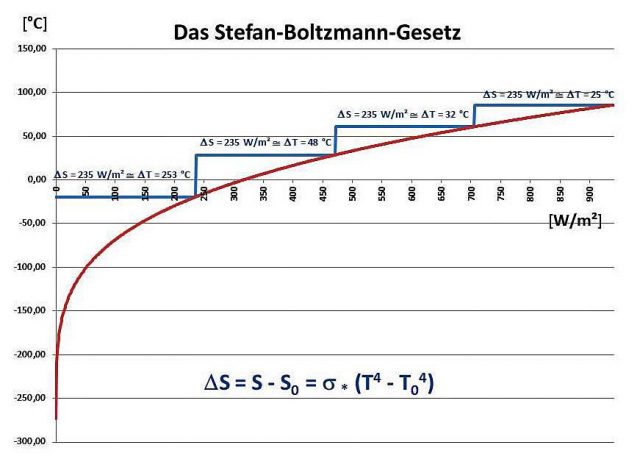
Abbildung 3: Der Temperaturbereich für eine pauschale Abstrahlung von S = 235 W/m² ist abhängig von der Basistemperatur T0 und ergibt nach dem S-B Gesetz keine eindeutige Lösung
Rot: Der Zusammenhang von Strahlung und Temperatur nach dem Stefan-Boltzmann-Gesetz aus Abbildung 1
Blau: Das S-B Temperaturäquivalent für S = 235 W/m² abhängig von der jeweiligen Umgebungstemperatur T0
Abbildung 3 macht also deutlich, dass es beim Stefan-Boltzmann-Gesetz von ganz entscheidender Bedeutung ist, bei welcher Umgebungstemperatur eine Abstrahlung nach der globalen Energiebilanz erfolgt. Jedenfalls kann die Temperatur eines Schwarzen Körpers nicht unter seine Umgebungstemperatur fallen.
4. ERKENNTNIS: Mit der Umgebungsgleichung des S-B Gesetzes ist jetzt das einzige Manko der hemisphärischen S-B Ableitung geheilt, nämlich das Fehlen einer Erklärung für das Verhalten der örtlichen Nachttemperatur.
Der konventionelle S-B Ansatz aus der globalen Energiebilanz geht nun davon aus, dass das Umgebungsniveau „T0“ unserer Erde null Grad Kelvin beträgt. Von dort aus werden nämlich nach S-B die ominösen 18 Grad Celsius mit S = 235 W/m² „hochgerechnet“, wie das in Abbildung 3 durch die erste „Treppenstufe“ von 0 bis 235 W/m² dargestellt wird. Die konventionelle S-B Ableitung für die „natürliche“ globale Durchschnittstemperatur von 18 °C ignoriert also den Wärmeinhalt der globalen Zirkulationen als unmittelbar wirksame Wärmespeicher unserer Erde.
5. ERKENNTNIS: Allein der Wärmeinhalt der globalen Zirkulationen sorgt dafür, dass das Temperaturniveau der Erde nachts nicht in die Nähe von null Grad Kelvin zurückfällt, wie wir das auf dem Mond beobachten können.
Abschätzung für die S-B Größe „T0“ in dieser Betrachtung: Das „T0“ in der S-B Umgebungsgleichung dürfte in etwa durch die global gemittelte Morgentemperatur der Ozeane kurz vor Sonnenaufgang repräsentiert werden. In dem auf EIKE veröffentlichten Artikel „Über die schwer fassbare globale mittlere Temperatur – ein Vergleich Modell ? Daten “ (von Bob Tisdale, übersetzt von Chris Frey, EIKE) heißt es über die durchschnittlichen Meerestemperaturen, Zitat:
„Die mittlere absolute globale Wassertemperatur ICOADS beträgt während der letzten 30 Jahre (1984 bis 2013) 19,5°C, während deren absolute globale Wassertemperatur 19,3°C beträgt.“
Zunächst einmal ist hier festzustellen, dass die globalen Durchschnittswerte der oberflächennahen Bodentemperatur (NST) und der Wassertemperatur stark differieren. Diese Differenz dürfte aber eher der natürlichen Begrenzung der Wassertemperatur durch den Gefrierpunkt des Wassers geschuldet sein. An diesem begrenzten Minusbereich für die Wassertemperatur scheitert also eine direkte Vergleichbarkeit beider Durchschnittswerte. Setzen wir hier also einfach einmal voraus, dass sich beide Durchschnittstemperaturen (Land und Meer) in etwa entsprechen würden. Da aber die globale Wassertemperatur zu tiefen Temperaturen hin eingeschränkt ist liegt es nahe, als gemeinsame Basis auf die durchschnittliche oberflächennahe Lufttemperatur zurückzugreifen. Und wenn wir in der S-B Umgebungsgleichung als Ausgangswert „T0“ diese global gemittelte gemessene Durchschnittstemperatur (NST) von 14,8 Grad Celsius ansetzen, dann ist der imaginäre atmosphärische Treibhauseffekt plötzlich verschwunden.
6. ERKENNTNIS: Wenn die bodennahe örtliche Nachttemperatur nach der Umgebungsgleichung des S-B Gesetzes durch einen Wärmezufluss aus den atmosphärischen und ozeanischen Zirkulationen gestützt wird, dann sind alle weiteren Spekulationen über einen „natürlichen“ atmosphärischen Treibhauseffekt hinfällig.
Sinkt also nachts die örtliche bodennahe Temperatur unter die Temperatur des ortsnahen Ozeans, dann erfolgt sofort ein Wärmefluss aus diesem Wärmespeicher. Anstelle einer weiteren Abkühlung der betrachteten Senke erfolgt dann also ein zusätzlicher Wärmefluss in diese Senke hinein. Im Umkehrschluss wird diese Senke also umso tiefer werden, je weiter entfernt vom Ozean sie sich befindet. Für eine anschauliche Darstellung des tageszyklischen Wärmeaustausches von Land und Meer wird hier auf Wikipedia verwiesen.
Anmerkung: Der direkte Einfluss der Atmosphäre wird hier nicht weiter diskutiert, weil sie sehr viel komplizierter zu beschreiben ist. Der Wärmeinhalt der Atmosphäre selbst weist nämlich wegen stark schwankender Wassergehalte eine wesentlich größere Variabilität auf und eine Wolkenbedeckung kann außerdem die nächtliche Abstrahlung deutlich vermindern.
Wenn wir jetzt einmal realistisch das S-B Temperaturäquivalent für eine globale Abstrahlung von S = 235 W/m² betrachten, dann dürften wir irgendwo im Bereich der zweiten „Treppenstufe“ in Abbildung 3 fündig werden, also im Bereich von T = 48 Grad Celsius. Dieser Wert ist als tägliche Schwankungsbreite selbst für extreme Wüstengebiete sehr ambitioniert, also dort, wo die globalen Zirkulationen nur einen geringen Beitrag gegen die Nachtabkühlung liefern können. Für die meisten individuellen Ortslagen kommt also im Umkehrschluss tatsächlich ein unterstützender Wärmestrom aus den globalen Zirkulationen zum Tragen. Das in Abbildung 4 dargestellte Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite nach HÄCKEL (1990) weist diesen Zusammenhang eindeutig nach.
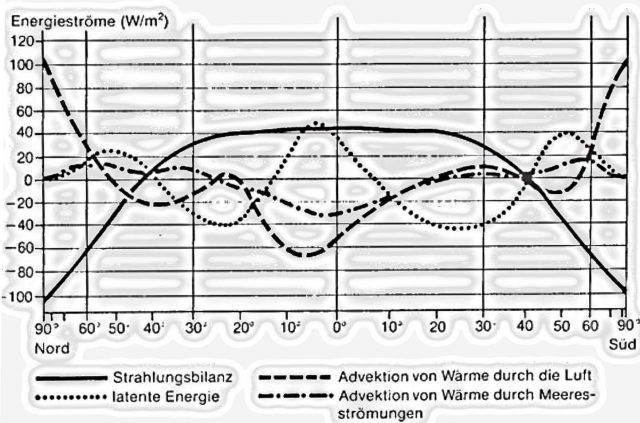
Abbildung 4: Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite. QUELLE: HÄCKEL, Meteorologie, Verlag Eugen Ulmer, Stuttgart 1990, zu finden auch hier
Diese Abbildung 4 zeigt zum Beweis der oben gemachten Ausführungen den durchschnittlichen horizontal verfrachteten jährlichen Wärmestrom durch die globalen Zirkulationen in mittlere und höhere geographische Breiten hinein. Da die abschließende Argumentation über die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes auf der globalen Energiebilanz von 235 W/m² aufsetzt, reiht sich diese Abbildung 4 von Häckel (1990), die ebenfalls auf einer Energiebilanz von 235 W/m² beruht, widerspruchslos in die vorliegende Argumentation ein und weist deren Richtigkeit nach.
7. ERKENNTNIS: Die theoretische Schwankungsbreite für das Temperaturäquivalent einer durchschnittlichen globalen Abstrahlung von 235 W/m² kann, außer vielleicht in extremen Wüstengebieten, auf der Erde kaum erreicht werden. Vielmehr wirkt der Wärmezufluss aus Atmosphäre und Ozeanen einer örtlichen Nachtabsenkung der Temperaturen entgegen.
Fassen wir die Temperaturgenese auf unserer Erde also noch einmal abschließend zusammen:
- Die Sonne heizt auf der Tagseite der Erde Landflächen, Atmosphäre und Ozeane auf.
- Die hemisphärisch berechnete Maximaltemperatur nach dem Stefan-Boltzmann-Gesetz wird dabei nirgendwo auf der Erde erreicht. Vielmehr werden insbesondere in niederen und mittleren Breiten die globalen Zirkulationen tagsüber mit Wärmeenergie „aufgeladen“.
- Der Wärmeinhalt in den globalen Zirkulationen wird also auf der Tagseite aus der hemisphärischen Sonneneinstrahlung gespeist, was dort zu einer Reduzierung der gemessenen Temperaturen gegenüber den berechneten hemisphärischen S-B Gleichgewichtstemperaturen führt.
- Für eine individuell betrachtete Ortslage auf der Nachtseite der Erde bestimmen der Wassergehalt der Atmosphäre und die Entfernung zum Ozean, wie stark sich die Erdoberfläche dort abkühlen kann.
- Damit ist die Nachtabkühlung in meeresnahen äquatorialen Gebieten am geringsten und in kontinentalen Wüstengebieten niederer Breiten am größten.
- Der Wärmezufluss aus den globalen Zirkulationen trägt also zur örtlich gemessenen Nachttemperatur bei. Diese Wärmeflüsse sorgen während des jeweiligen Winterhalbjahres in mittleren und höheren geographischen Breiten auch für einen generellen Temperaturanstieg gegenüber den hemisphärisch berechneten S-B Gleichgewichtstemperaturen.
Am Ende führen also eine physikalisch falsche Anwendung des Stefan-Boltzmann-Gesetzes und die Nichtbeachtung des Wärmeinhalts der globalen Zirkulationen bei der konventionellen S-B Herleitung einer globalen Durchschnittstemperatur über die Energiebilanz unserer Erde zu einem imaginären „natürlichen atmosphärischen Treibhauseffekt“ von 33 Grad. Tatsächlich aber folgt die globale Temperaturgenese auf der Erde einem hemisphärischen Strahlungsansatz über das Stefan-Boltzmann-Gesetz, während die Nachtabkühlung auf der Erde mit der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes unter Einbeziehung des Wärmeinhaltes der globalen Zirkulationen beschrieben werden kann.
ERGEBNIS: Es sind in Wirklichkeit also die wärmebeladenen globalen Zirkulationen, die unter dem Pseudonym „natürlicher atmosphärischer Treibhauseffekt“ für lebensfreundliche Temperaturen auf unserer Erde sorgen, indem sie hier auf der Erde eine dem Mond vergleichbare extreme Schwankung von tageszyklischer Aufheizung und Nachtabsenkung verhindern.
Schlussbemerkung: Wegen des imaginären Konstruktes eines „natürlichen atmosphärischen Treibhauseffektes“ aus einer fehlerhaften Anwendung des Stefan-Boltzmann-Gesetzes sollen wir uns jetzt also alle einer „globalen Dekarbonisierung bis zum Jahre 2100“ unterziehen. Und damit wird dann unsere fossil betriebene Industrie, unser damit erwirtschafteter Lebensstandard sowie auch noch die Überlebensperspektive zukünftiger Generationen zerstört – ja geht’s denn eigentlich noch?

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Wie kann es sein dass das S-B-Gesetz nach Abb.1 eindeutig ist, aber nach Abb.3 eine mehrdeutige Lösung liefert? M.E. sinkt bei jeder exponentiellen Funktion y=x^n der Zuwachs von y wenn x in gleichen Schritten vergrößert wird. Hier liegt offenbar ein Missverständnis vor.
Spannende Diskussion. Aber ich denke, das System ist zu kompliziert (vielleicht auch nur für meinereiner) um hier sicher sagen zu können „das ist es jetzt“! Was mich insbesondere stört, ist die Annahme/Voraussetzung einer Erd-„Umgebungstemperatur“. Einerseits lustig, denn genau das ist einer der Punkte der mich persönlich seit Monaten nervt (abgesehen davon, dass ich vom SBG wenig Ahnung habe). Denn im Prinzip ist die treibende Kraft bei praktisch jeder Energieübertragung immer der Temperaturgradient, der in diesem Fall relevant geringer ist / wäre. Andererseits ist m.M.n. eher das Weltall als Umgebung anzusehen und die Atmosphäre mehr als dünne Grenzschicht, wobei wie gesagt hier leider das Verständnis fehlt! Vom Bauchgefühl schätze ich, es reduziert den Betrag der Strahlung. tatsächlich müsste man einen Temperatur-Mittelwert o.ä, nehmen. Zumindest begreife ich nicht, weshalb man über diese ganz gravierenden Gegebenheiten nur bei EIKE u.a. spricht!? Das sind doch ganz entscheidende naturwissenschaftliche Grundlagen, die man doch ignorieren kan?!?
Merke: Schon wer eine Religion diskutiert, wird zum Ketzer! Er muss verbrannt, gesprengt, erstochen zumindest aber ignoriert werden!
Herr Uli Weber,
Ihre Ausarbeitung ist soweit ganz gut, besser als diejenigen, die man sonst so liest.
Dass ein physikalisches Gesetz keine Gleichung ist, ist mit Verlaub gesagt, Unsinn. Worin soll der Unterschied bestehen? Alle physikalischen Gesetze bzw. deren Gleichungen (Zusammenhang der Prozeßvariablen/-werte) beziehen sich immer auf den Prozeßzeitraum und die Prozeßumgebung. Auch das Stefan-Boltzmann-Gesetz bzw. die Gleichung lässt sich aus der Thermodynamik herleiten.
++ Ihre „erste Erkenntnis“ ist richtig. Die Energien, also die Prozeßwerte dürfen nicht über den Prozeßzeitraum und die Prozeßumgebung hinaus gemittelt werden, sonst würde man das Ursache-Wirkungs-Prinzip verletzen.
Das sieht man an den sinnfreien Werten, die die „ERBE Messungen“ angeben. Die sind nämlich nicht gemessen, sondern berechnet oder besser umgerechnet.
+ Globale mittlere solare Einstrahlung (All-Sky) auf Oberfläche (22 Jahre 1983-2005): 4,526 kWh/m^2/day (188,6 W/m^2) -> hemisphärischer Wert: 755 W/m^2
+ Globale mittlere solare Einstrahlung (Clear-Sky) auf Oberfläche (22 Jahre 1983-2005): 5,932 kWh/m^2/day (247,2 W/m^2) -> hemisphärischer Wert: 989 W/m^2
+ Globale mittlere solare Einstrahlung am TOA (22 Jahre 1983-2005): 8,195 kWh/m^2/day (341,4 W/m^2) -> hemisphärischer Wert: 1365 W/m^2
Die berechnete globale mittlere solare Einstrahlung auf die Oberfläche der Erde ist 4,53 kWh/m^2/day (day = 24h), laut den hemisphärischen Messungen (Prozeßzeitraum und -Umgebung ist die sonnen-zugewandte Hemisphäre). Auf die sonnen-zugewandte Hemisphäre wieder zurückgerechnet (12h) bedeutet das 4,53*2 = 9,06 kWh/m^2/12h oder 32,6 MJ/m^2/12h bzw. 32,6*10^6/(12*60*60) = 755 W/m^2. Da diese hemisphärischen Satelliten-Messungen nicht die latente und konvektive Umsetzung der eingestrahlten Sonnen-Energie berücksichtigen, liegt der „wahre Wert“ bei ca. 858 W/m^2 mittlerer solarer Input auf der sonnen-zugewandten Oberflächen-Hemisphäre.
Alles ist eine Frage der Energiebilanz-Erhaltung. Das Erd-System oder der Erd-Mond ist kein statisch-konservatives System, wo der Energie-Input und Energie-Output in jedem Zeitintervall gleich ist. Nur in einem statisch-konservatives System gilt: Energie-Input(t) = Energie-Output(t). Bei dynamischen und dissipativen Systemen mit externen/internen Einflüssen treten immer Divergenzen (bzw. dynamische Divergenzen) zwischen Input und Output auf, das ist die Realität. Für ein dynamisch dissipativen System gilt: Energie-Input(t) + div(t,in) = Energie-Output(t) + div(t,out).
Was meinen Sie, warum man in der Wissenschaft eigentlich verpflichtet ist, gemessene oder berechnete Werte immer in der Form:
„Wahrer Wert = scheinbar wahrer Wert +/- Wert-Variationsbereich“ angegeben sollte. Der Grund dafür liegt in diesen Divergenz-Termen.
++ Ihre „dritte Erkenntnis“ ist aber nicht korrekt. Hier verweise ich mal auf die Veröffentlichung:
Jamie Molaro and Shane Byrne – Rates of temperature change of airless landscapes and implications for thermal stress weathering
Die Erd-Oberfläche kühlt rund 6 mal schneller aus, als die Erdmond-Oberfläche. Grund: Die Erde hat zusätzlich noch effiziente Energie-Umwandlungs-/Transportprozesse an der Oberfläche, als der Erdmond. Die ihrerseits eine effizente groß-räumige Umverteilung der Energie innerhalb der Atmosphäre und den fluiden Oberflächen-Bereich in Gang setzen, wodurch die energetischen Divergenzen zwischen Oberfläche/Atmosphäre/Weltraum geringer ausfallen (ihre „vierte, fünfte und sechste Erkenntnis“).
++ Ihr „Ergebnis“ ist die richtige Schlussfolgerung.
So etwas wie einen „atmosphärischen Treibhauseffekt“ kann es aus energetischen Gründen nicht geben.
@ALL: Natürlich kann man mit dem Stefan-Boltzmann-Gesetz die breitengrad-abhängige Temperatur der sonnen-zugewandten Erdmond-Hemisphäre berechnen. Was wäre das sonst für ein physikalisches Gesetz, wenn es nur in eine Richtung funktioniert würde.
Versucht es doch einfach mal, die maximal gemessene Temperatur beträgt 410K (Kraterränder am Äquator – Siehe: http://staff.diviner.ucla.edu/science.shtml). Die Werte der Kraterrand-Messungen ergeben für den Emissionsgrad e = 0,92 und für die Albedo a = 0,0516.
Mfg
Werner Holtz
1.) Vielleicht könnten es alle mal endlich mal begreifen: Es geht nicht um die Begriffe, sondern dass eine „Gleichung“ oder ein „physikalisches Gesetz“ ZWINGEND einen Gleichgewichtszustand voraussetzt! Ansonsten heißt es „Ungleichung“ oder das physikalische Gesetz wird zu einer höheren Differentialgleichung o.ä.!
Wer hierfür unbedingt ein Beispiel braucht: Richtet man einen Strahler für nur eine Millisekunde auf einen Körper, hat er noch nicht die Endtemperatur und das Gesetz gilt noch nicht!
2. ) Zum Rest: Meine Güte, ich will nicht beleidigend werden, aber das tut ja weh beim Lesen! Gewöhnen Sie ich bitte dringend ab, irgendwelches Zeug zusammenzureimen!
Der Bolzen ist eingesetzt
Bei den vielen Artikeln die Sie zum Thema „Stefan-Boltzmann Gesetz“ geschrieben haben, stand immer eine Botschaft im Vordergrund: Die traditionelle, auch vom ICCP, anerkannte Berechnung des Treibhauseffektes ist schlicht falsch. Ich habe das schon mal als eine echte Entdeckung bezeichnet, weil absolut alle Schlussfolgerunen, die diese Berechnung als Grundlage verwenden, ebenso falsch sein müssen und das sind eine ganze Menge, bevorzugt im Segment der CO2-Klimalehre.
Sowas kann in der Wissenschaft schon mal vorkommen und passiert auch entsprechend häufig. Es war dies ursprünglich nicht weiter schlimm, denn letztlich blieb es ja egal ob sich da in der theoretischen Lehre zu Klima und Atmosphäre ein Fehler eingeschlichen hatte. Es tat ja keinem weh.
Tragisch wird es aber wenn ein solcher Irrtum als Grundlage für eine vollkommen verfehlte Umwelt- und Gesellschaftspolitik bis hin zu dem vom WBGU verbreiteten „Gesellschaftsvertrag für eine Große Transformation“ führt.
Auch davor hatte Weber schon in seinem Artikel zur Pariser Klimakonferrenz 2015 gewarnt (hier).
Ich denke dass Herr Weber uns in einer bewundernswerten Hartnäckigkeit vorgeführt hat wie man durch immer wieder gebotene neue Ansätze und Blickwinkel gezeigt bekommt, dass einfach viel mehr hinter der Geschichte steckt als vermutet. Soviel sogar dass man auf bestechende Art und Weise den ganzen ICCP zur Fabel machen könnte. Was ich mir wünsche ist nunmehr eine echte Grundlagendebatte zum Treibhausefek. Vor allem aber wünsche ich mir ein Ende der öden Ermahnungen zum Klimaglauben, den nun wirklich keiner braucht.
„Was ich mir wünsche ist nunmehr eine echte Grundlagendebatte zum Treibhausefek.“
Gerne.
Es gibt ihn nicht!
Zum Verständnis des Lemmas ist dieser Chart m.E. unerlässlich.
http://i736.photobucket.com/albums/xx10/Oliver25/parkersburg1.png
Das ist eine statistische Auswertung des nächtlichen Temperaturverlaufs einer US Kleinstadt in Abhängigkeit der Bewölkungslage. Die X Achse gibt die Zeit ab Sonnenuntergang in 10 Minuten Schritten an, die Y-Achse den Temperaturverlauf an (mit 1 = Ausgangstemperatur).
Für den Bewölkungsgrad gibt es Werte von 0 – 8, wobei 0 für klaren Himmel steht und 8 für eine druchgehende Bewölkung. Es sind Daten aus zwei Jahren ausgewertet, in Klammern ist die Größe des Samples genannt (also die Zahl der Nächte).
Was diese Auswertung sehr schön zeigt, ist wie stark die Wolkenlage über den Emissionsgrad bestimmt, und wie präzise dieser Differenzierung funktioniert. Nicht nur sinkt der Emissionsgrad durch Wolken um bis zu 85%, im Durchschnitt senken die verschiedenen Wolkenlagen den Emissionsgrad um ca. 35%. Das ist extrem viel, zumal dieser Wert eine gute Annäherung für den globalen Effekt des „cloud forcing“ ist, QED.
Das bedeutet nun, dass das verbliebene „Fenster“ von 65% eben jenen 236 (235?) Watt/m2 an Emissionen entspricht, die ja als solche außer Streit stehen. Dann beträgt aber das cloud forcing selbst 236/65 * 35 = 127W/m2. Und wir können für die Strahlungsausgangsleistung 236 + 127 = 363W/m2 bestimmen.
363W/m2 sind nun immer noch weniger, als jene 390W/m2 die sich theoretisch für die Erdoberfläche bei gegebener Temperatur bestimmen lassen, womit allfälligen Treibhausgasen immerhin noch 27W/m2 übrig blieben, was allerdings nur mehr eine marginale Größe wäre. Nun basieren die 390W/m2 aber wiederum auf der falschen Annahme, die Oberfläche hätte einen Emissionsgrad von 1, den sie nicht hat. Rechnet hingegen 363/390 = 0,93, dann ergibt sich ein Wert der dem realistischen Emissionsgrad weitgehend entspricht. Immerhin beträgt der Emissionsgrad von Wasser 0,94, der von festen Oberflächen aber z.T. noch weit niedriger (Sand ~0,7).
Anders formuliert, der Emissionsgrad der Erdoberfläche beträgt, wenn das cloud forcing hinzurechnet, ca. 0,6. Und damit geht sich die Rechnung wunderbar auf. Denn es gilt 279 * (0,69 / 0,6)^0,25 = 289K
PS. keine Ahnung ob das mit dem Attachment funktioniert hat..
„Was diese Auswertung sehr schön zeigt, ist wie stark die Wolkenlage über den Emissionsgrad bestimmt..“ .. Leider führt Sie „die amerikanische Kleinstadt“ in die Irre, denn an 71% der Erdoberfläche sind die Oberflächentemperaturen unabhängig von der Wolkenlage im Tagesverlauf nahezu konstant. Im Jahresverlauf variieren die Temperaturen zwischen -2Grad C in den Polarzonen und etwa 30Grad C am Äquator um einige Grad C.
Das ist ein logisches Missverständnis. Schon richtig, dass die Temperaturen über dem Meer bzw. in Meeresnähe deutlich geringer sind. Ich habe die Auswertung übrigens sehr wohl an einigen Küstenorten betrieben. Das heißt aber nicht, dass das beschriebene Delta zwischen klaren und bewölkten Nächten dann geringer ausfiele.
Auch ist der Gedanke eher abwegig, wonach das cloud forcing abhängig von der Emissionsquelle darunter wäre. Wolken fragen nicht danach, woher die Wärmestrahlung kommt, bevor sie sie zurück reflektieren. Die sind da quasi vorurteilsfrei.
Wegen Regelverletzung gelöscht.
Einstein: „Es sind zwei Dinge, die menschliche Dummheit und das Universum sind unendlich. Beim Universum bin ich mir noch nicht ganz sicher.“
Die Temperaturverteilung in der Troposphäre und das SB Gesetz zeigen, dass die Emission von Wärmestrahlung in den Weltraum aus diesem Volumen bei einer mittleren Temperatur deutlich unter minus 18 Grad C (!!!) erfolgt. Emitter sind zweifelsfrei Eis- und Wasserpartikel. Sie senken z. B. die Temperatur der Tropopause den Erdball umspannend bei einer Emission von etwa 130 W/m^2 unter -50 Grad C ab. Da die Partikel Temperaturen in Richtung Erdoberfläche ansteigen, ist der Rückfluss von Energie zur Materie an der Erdoberfläche stets größer, als die Emission in den Weltraum. Ohne diesen „TE“ wäre es auf der Erde tatsächlich bitter kalt.
CO2 ist an diesem Effekt energetisch nicht beteiligt!
https://de.scribd.com/doc/248025848/Atmospharischer-Treibhauseffekt-und-Wasserkreislauf
Eigentlich hätte Uli Weber nach seiner richtigen 1. Erkenntnis über das S-B-G gar nicht mehr weiterschreiben brauchen. Das S-B-G ist „durch“ !! Die Treibhauseffekt-Gläubigen haben bereits im Ursprung das S-B-G definitiv falsch angewendet, als sie vom Watt/m²-Wert (= 240 Watt/m²) auf die Temperatur (= -18°C“) als angeblich eine Erde OHNE Treibhauseffekt geschlossen haben. Das war der definitiv FALSCHE Ausgangspunkt/ANSATZ für das Konstrukt einer Treibhauseffekt-Hypothese, weil diese Richtung, nämlich von einer Wattzahl auf eine Temperatur zu schliessen, gibt das S-B-G gar nicht her, weil – wie Uli Weber richtig schreibt -, sich bei dem S-B-G um ein GESETZ (!) und eben um KEINE GLEICHUNG handelt. Bei diesem S-B-Gesetz ist die Temperatur der wichtige Ausgangspunkt, um auf eine Watt-Zahl zu schliessen. Und die THE-Gläubigen drehen einfach die Richtung um, und schliessen – eben falsch – von einer Wattzahl (= 240W/m²) auf die Temperatur (= -18°C). Unglaublich, dieser Irrsinn.
Damit ist das ganze Thema „Treibhauseffekt“ DURCH. Diese falsche Anwendung und Herleitung des S-B-G zum Zwecke eines THE-Konstruktes hat sich damit bereits eindeutig als Junk-Science enlarvt. WIR HABEN FERTIG !! Man kann sich das Weiter-Lesen des Textes von Uli Weber daraufhin sparen.
Ob SB Gesetz oder Gleichung ist doch einerlei. Das funktioniert im Prinzip sehr wohl, weil laut SB die Erde 279K hätte, was lediglich eine Abweichung von 9K gegenüber der Durchschnittsoberflächentemperatur wäre.
Verhunzt wird die Sache erst dadurch, dass wir erstens im Unklaren verbleiben was „Oberfläche“ ist (zur Abstraktion: was ist die Oberfläche der Erde? Was die Oberfläche der Venus?? Was die Oberfläche des Jupiter????), und zweitens in dem wir einen Absorptionsgrad von ~0,69 unterstellen, bei einem Emissionsgrad von 1!?
Regelmäßig sind aber Absorptions- und Emissionsgrad in der Praxis (wie auch in der Theorie, siehe Kirchhoffs Gesetz) korreliert. Beispielsweise liegen Absorptions- und Emissionsgrad von Wasser bei jeweils 0,94 (trotz unterschiedlicher Wellenlängen), und diese Oberflächentyp ist für die Erde nicht ganz unwichtig.
Ob SB Gesetz oder Gleichung ist doch einerlei.
Versuchen Sie mal mit der Energie einer beliebigen Strahlung einen Körper zu erwärmen. Und messen Sie dann dessen die Temperatur, die sich einstellt. Sie werden sich wundern,wie stark sie von der SB-Temperatur abweicht.
Nochmal: das hängt dann wohl davon ab, ob man korrekte Absorptions- UND Emissionsgrade unterstellt, oder aber man den Fehler macht nur den Absorptionsgrad, nicht aber den Emissionsgrad zu berücksichtigen. Für den Fehler kann S.B. nämlich genau gar nichts.
@Erich Schaffer
Sie haben offensichtlich NICHT VERSTANDEN, warum das S-B-G nicht anwendbar ist. Sie raffen nicht, dass die „Treibhauseffektler“ das S-B-G einfach aus der falschen Richtung angewendet haben, nämlich aus Richtung der Strahlung, statt aus der korrekten Herleitungsrichtung, nämlich aus der Vorgabe der Temperatur, von der aus ein Strahlungswert ermittelt wird. Denn man kann das S-B-G nicht anwenden, um von einer Strahlungswattzahl auf eine Temperatur zu schliessen.
Ich kann die Ausführungen hier absolut nicht nachvollziehen. Und ich sage das obwohl ich zugleich feststellen muss, dass die Theorie des Treibhausffekts Unsinn ist.
Also ich würde die Argumentation gerne nachvollziehen, ich schaffe es aber nicht. Das mag man meiner beschränkten Intelligenz liegen, allein mir ist ein IQ von über 145 höchst offiziell ausgewiesen. Somit bleibt der Eindruck, dass das Unsinnige gesagt, das Wesentliche aber ignoriert wurde.
Um das grob verkürzt darzustellen: Emissions- und Absorptionsgrad tendieren dazu gleich zu sein. Atmosphären und damit strahlungstechnische Barrieren tendieren dazu, „Oberflächen“ nach oben, also über eine feste Oberfläche zu verschieben. Darunter gilt das Prinzip der adiabatischen Konpression.
Auf der Erde spielen hier Wolken die entscheidende Rolle. Sie verschieben thermodynamisch die Oberfläche nach oben, und bewirken somit eine Erwärmung.
Auf Basis von Wetterdaten lässt sich bestimmen, dass „cloud forcing“ ca. 127W/m2 zum vermeintlichen „Treibhauseffekt“ beiträgt, und besagter Treibhauseffekt eben deshalb ein Irrtum ist.
Zitat: „Auf der Erde spielen hier Wolken die entscheidende Rolle. Sie verschieben thermodynamisch die Oberfläche nach oben, und bewirken somit eine Erwärmung.“ -( im Treibhaus Erde!)
Im Treibhaus des Gärtners wird thermodynamisch die Oberfläche nach oben verschoben und und bewirkt so eine Erwärmung.
Irrtum ist 1. die Quantifizierung der Wirkung und 2. die angebliche energetische Mitwirkung der mehr als zweiatomigen Gase!
Nein, es geht einzig um das Verständnis des Begriffs „Oberfläche“. Es ist sinnlos zu versuchen Oberflächentemperaturen zu bestimmen, wenn wir uns darüber im klaren sind, was überhaupt die „Oberfläche“ ist.
Die Oberfläche trennt feste und flüssige Materie von Gasen!
Demzufolge ist die Oberfläche des Jupiter wo…?
Gasplaneten haben keine Oberfläche!!!
Der verführerische Traum von einer angeblich möglichen mathematischen Darstellung des Zustandes im menschlichen Lebensraumes („die Modellitis“) lebt auch hier fort. – Die energetische Rückkopplung des von Eis und Wasser der Atmosphäre erzeugten atmosphärischer Treibhauseffektes wäre eine Illusion, behauptet der Autor. – Die Fakten zeigen dagegen etwas anderes:
Das Produkt aus einem mittleren solaren Energiezufluss von etwa 235 W/m^2 und der Speicherzeit hebt bekanntlich an 72% der Erdoberfläche die Wassertemperaturen an der Oberfläche der Ozeane von -240 Grad C auf Werte zwischen -2 Grad C und 30 Grad C an. Der von dort emittierte Energiefluss umfasst: Wärmestrahlung zwischen etwa 305 bis 480 W/m^2 + die Wärme zur Verdampfung der Niederschläge, zur Konvektion und zur Wärmeleitung bis in die mit – 50 Grad C kältere Tropoause, also auch die zum Betrieb der horizontalen „Wärme/Kraft Machine Atmosphäre“ erforderliche Energie. – Das funktioniert, weil der von dem Wasser/Eis Wärmespeicher in der Troposphäre ausgehende Rückfluss von Energie die Energiebilanz der Ozeane ausgleicht. Als Wärmestrahlung an vielen Orten kontinuierlich gemessen ist dieser Nachweis für jedermann zugänglich!
Warum bringt EIKE einen derartigen Unsinn?
Kann ja sein, dass ich hier gerade einen Blackout habe, aber wieso sollen auf dem Mond von den 400 W Aldeborückstrahlung der Erde auf der Mondoberfläche 2W/m² ankommen?!?!
Es geht doch nicht nur um die tageszyklischen Schwankungen, sondern vor allem um die Tagesmittelwerte. Mit diesen Argumenten können Sie den natürlichen atmosphärischen Treibhaus-Effekt nicht wegdiskutieren. Es wurde bereits z.B. von Link et al 2011 „A new Basic 1-Dimension 1-Layer Model obtains excellent agreement with the observed Earth Temperature“ dass der konventionelle Ansatz prinzipiell richtig ist. Vergleicht man all diese Modelle jedoch lokal mit den gemessenen Oberflächen-Temperaturen der Erde, sieht man dass die Übereinstimmung nur mäßig ist. Das System ist einfach zu komplex für einfache Modelle.
Herr Weber, Sie schreiben am Anfang “ Die alleinige „natürliche“ Eigentemperatur der Erde würde vielmehr bei etwa 240 Grad Celsius liegen.“ Das wäre aber sehr heiß! Sie meinen wohl 240 K = -33 °C. Der gleiche Fehler erscheint weiter unten noch mal. Davon abgesehen ist Ihr Aufsatz eine gute Widerlegung des Märchens vom Treibhauseffekt.
danke für den Hinweis. Es muss minus 240 °C heißen. Ist korrigiert.
Um ganz ehrlich zu sein, halte ich diese Betrachtungsweise für sehr kritikanfällig.
1) Das S-B Gesetz gilt nur für ideale, schwarze Körper, die auch in ihrer Masse die gleiche Temperatur haben, wie an der Oberfläche, und die Energie wird nur über Strahlung abgegeben.
Davon ist die Erde weit entfernt. Die Erdoberfläche besteht aus sehr unterschiedlichen Materialien, mit unterschiedlichen spezifischen Wärmen.
2) Die Erde ist ein sich zyklisch abkühlender und wieder erwärmender Körper (Sonne). Somit kann man niemals aus der zugeführten Energiemenge auf seine tatsächliche Temperatur schließen.
3) Auf der Erde herrscht zu keinem Zeitpunkt ein thermisches Gleichgewicht.
4) Laut den Berechnungen mit den S-B Gesetzen dürfte es auf dem Mond nur zur einer Maximaltemperatur von ca 120 Grad C kommen. Gemessen werde aber dort ca 130 Grad C.
5) Somit ist der Ansatz, die Temperaturen und Strahlungsleistungen mit den S-B Gesetzen zu bestimmen, absolut falsch.
Das würde ich so nicht sagen. Bei einer Albedo von 0,12 sollte der Mond maximal 279 * (4 * (1 – 0,12))^0,25 =382K erreichen, bzw. 109°C. Wobei 279K halt SB die Temperatur eine perfekten Schwarzkörpers wäre.
Darin läge aber der grundlegende Fehler die Albedo zu berücksichtigen, also den Absorptionsgrad um diese zu reduzieren, die Abweichung des Emissionsgrades 1 aber unberücksichtigt zu lassen. Das führt zuverlässig zu völlig falschen Ergebnissen.
Richtiger ist es da schon so zu rechnen: 279 * 4^0,25 = 394,6K = 121,6°C. Dann kommt man auch annähernd auf die schon genannten 120°C, andernfalls nicht. Jetzt muss aber noch bedenken, dass es am Mond auch Täler und Krater gibt, die wie eine Parabolschüssel wirken. Natürlich lassen sich dort Temperaturen erreichen, die noch ein paar Grad höher liegen. Das SB Gesetz funktioniert also durchwegs sehr gut, und führt bei richtiger Anwendung auch zur Erkenntnis, dass es keinen THE gibt.
Natürlich haben Sie recht, der Mond ist kein idealer, schwarzer Körper!
Und seine Albedo von 0.12 ist ja korrekt – nur dann wird die Diskrepanz zwischen berechneter und gemessener Temperatur noch viel größer – trotz Täler und Krater!
Was ich meine ist, dass der Emissionsgrad wahrscheinlich ähnlich groß wie der Absorptionsgrad ist. Das heißt man müsste so rechnen: 279 * (4 * (1 – 0,12) / 0,88)^0,25 = 394.6K. Da die 0,88/0,88 = 1 ist, stellt das eine ziemlich sinnlose Übung dar. Reale Körper erreichen tendenziell immer die gleiche Temperatur wie ein perfekter Schwarzkörper.
Sie schreiben:
„Reale Körper erreichen tendenziell immer die gleiche Temperatur wie ein perfekter Schwarzkörper.“
Wie kommen Sie denn darauf?
Nur ein idealer, schwarzer Körper hat den Absorptions- wie Emissionsgrad = 1.0!
Reale Körper nicht! Somit erreichen reale Körper, auch „tendenziell“ nicht die Temperatur des schwarzen Körpers.
Was die Emission betrifft, kann man nur sagen, im thermischen Gleichgewicht ist sie gleich der Absorption! (Im Weltraum).
@Eugen
Wie kommen Sie denn darauf?
Weil tendenziell gilt: Absorptionsgrad = Emissionsgrad. Ich könnte dafür viele Beispiele nennen, etwa Wasser wo E = A = 0,94 gilt. Ich könnte ausführen, dass das Weglassen der Albedo bei der Bestimmung von Oberflächentemperaturen auf Basis SB quer durchs Sonnensystem zu weit besseren Annährungen führt, als wenn man einseitig den Absorptionsgrad um die Albedo reduziert. Ein sehr gutes Beispiel hierfür wäre auch Enceladus, der trotz einer Albedo von 0,99 halt nicht bloß 28K hat, sondern ca. 75K.
Und ich könnte auf das Kirchhoffsche Gesetz verweisen, wonach eben E = A sein muss. Auch wenn das bei unterschiedlichen Wellenlängen so nicht mehr stimmt, gibt es doch keine einseitige Tendenz die vorgeben würde, dass A < 1 und E = 1 sei.