Häufig sieht man den Hinweis auf die nominelle 30%-Albedo der Erde hinsichtlich des Energiehaushaltes und der vermeintlichen anthropogenen Erwärmung. Allerdings listet das CRC Handbook of Chemistry and Physics in den jüngsten Ausgaben einen Wert von 36,7%. Die Albedo ist eine Maßzahl der scheinbaren Reflektivität des sichtbaren Lichtes von Himmelskörpern wie Mond, Mars und Asteroiden. Dies funktioniert gut bei der Abschätzung des Typs der Oberflächen-Beschaffenheit und der Partikelgröße von Objekten, die nichts als blanken Fels und Schutt aufweisen. Um die Albedo über einer beobachteten Atmosphäre, der Sonne, einem vermessenen Körper angemessen zu messen, sollten sich das Objekt und der Beobachter (Erdlinge!) angemessen abgleichen. Die Albedo der Erde wird geschätzt mittels Messung der Albedo des Mondes (12%) bei Vollmond und der nachfolgenden Messung des Erdscheins (Earthshine) bei Neumond. Diese Messungen erfassen zumeist die diffuse Reflektion von Vegetation, Erdboden, Schutt und vor allem Wolken. Allerdings sind darunter auch einige sekundäre spiegelähnliche Reflektionen von glatten Objekten (wie Felsen, vor allem aber Wasserwellen), deren Oberflächen so orientiert sind, dass die einfallende Strahlung in Richtung Mond reflektiert wird.

Allerdings wird der beschienene Teil der Erde immer etwas unterschiedlich sein sowie variierend mit der Zeit und der Messstellen. Dies trägt wahrscheinlich zur beobachteten Variation der gesessenen Albedo mit der Zeit bei. Weil sich der Mond nicht in der Ebene der Ekliptik befindet, erfolgen jedwede Messungen des Erdscheins mit der Zeit über verschiedene Blickwinkel und unterschiedliche Regionen der Erdoberfläche zusammen mit Änderungen aufgrund von Wetter und Jahreszeit. Das heißt, es ist zu erwarten, dass die Albedo, wie sie aus Messungen des Erdscheins geschätzt wird, aus geometrischen Gründen deutlich variiert. Diese Messungen bieten eine scheinbare Reflektivität an, integriert über eine gesamte Hemisphäre der Erde.

Ich sage „scheinbare“ Reflektivität, weil nicht alles die Erde erreichende Licht zurück zur Sonne reflektiert wird. Die Albedo ist im besten Falle eine untere Grenze des von der Erde reflektierten Lichtes. Sie zu verwenden wäre nur dann angemessen, falls die Erde vollständig von Wolken bedeckt wäre wie die Venus (Albedo = 65%) oder vollständig bedeckt mit Schutt wie der Mars (Albedo = 15%) ohne Wasser oder Vegetation.

Außerdem ist die Albedo eine Augenblicksmessung. Weil sich Vegetation und Wolken mit den Jahreszeiten ändern, muss eine weitere, kompliziertere Korrektur angebracht werden, damit man trotz dieser Effekte ein Jahresmittel ableiten kann.

Zur Illustration (oder vielleicht sollte ich sagen Erhellung) betrachte man, wie die Lage wäre, falls die Erde eine Hollywood-Wasserwelt wäre (à la Kevin Kostner). Man nehme mal an, dass es nur einen Ozean frei von Sedimenten gebe, keine Wolken und leichte Winde, was Schaumkronen minimiert. Das Wasser reflektiert stark spiegelähnlich (wie jeder Fischer oder Seemann nur zu gut weiß) im Gegensatz zu der starken diffusen Reflektion der meisten anderen Dinge auf der Erde.

Spiegelnde Reflektion wird quantitativ berechnet mit der Fresnel’schen Reflektions-Gleichung, in die der Index der Refraktion und der Auslöschungs-Koeffizient eingeht (manchmal auch Absorptions-Koeffizient genannt), was den Complex Refractive Index CRI konstituiert. Der Index der Refraktion, der den meisten Lesern vermutlich bekannt ist, wird einfach definiert als das Verhältnis zwischen der Lichtgeschwindigkeit in einem Vakuum und der Lichtgeschwindigkeit in der vermessenen Materie. Der Auslöschungs-Koeffizient für Wasser variiert mit der Wellenlänge – er ist größer für rot und Infrarot als am anderen Ende des Spektrums – aber wir können dies als vernachlässigbar ansehen für die folgende Illustration. Folglich hat der CRI für Wasser eine imaginäre Komponente, die man mit Null ansetzen kann. Dies vereinfacht die Berechnungen. Der CRI variiert mit Temperatur, Salzgehalt und der Wellenlänge des einfallenden Lichtes. Ich habe eine Approximation verwendet (n = 1,34) für typisches Meerwasser bei einer Wellenlänge von 550 nm. Dies ist der Spitzenwert der Emission von Sonnenlicht.

Zur Erinnerung, der Winkel der Reflektion ist gleich dem Einfallswinkel, wobei der Einfallswinkel gemessen wird von der Normalen der Oberfläche [surface normal]. Nehmen wir an, dass wir auf unsere Wasserwelt schauen aus einem geostationären Orbit und dass diese Wasserwelt eine perfekte Sphäre ist anstatt des an den Polen abgeflachten Sphäroids (Geoid), was die reale Erde ist. Das Sonnenlicht kommt in Strahlen, die auf diese Distanz parallel zueinander sind. Ein Strahl, der normal zur Wasseroberfläche auftrifft, hat den Einfallswinkel 0°. Alle anderen Strahlen, die auf die Oberfläche der beleuchteten Hemisphäre treffen, haben größere Einfallswinkel, bis hin zu 90° an den Rändern. Neunzig Grad sind grazing the surface; es herrscht eine Reflektivität von 100%, und der Charakter des Lichtes ist spektroskopisch der gleiche wie von der Quelle (der Sonne).

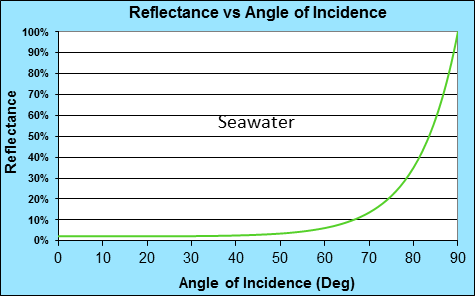
Die folgende Graphik zeigt den Reflexionsgrad für alle Einfallswinkel auf Meerwasser. Man beachte, dass jenseits von etwa 40° der Reflexionsgrad merklich zu steigen beginnt. Bei 60° steigt der Reflexionsgrad scharf, und über 79° liegt er über der nominellen Albedo (30%), die gemeiniglich in Diskussionen über den Energiehaushalt der globalen Erwärmung Eingang findet.

Abbildung 1: Gesamt-Reflektivität von Meerwasser

Würde man von der Position des geostationären Satelliten herunter schauen, würde man einen Lichtfleck sehen, der vom etwa in der Normalen einfallenden Bündel von Strahlen von der Wasseroberfläche reflektiert wird. Das wäre ein Reflexionsgrad von 2%. Alles andere würde schwarz aussehen mit Ausnahme einiger zufälliger weißer Schaumkronen, die blitzartig etwas Licht reflektieren. Dies bedeutet jedoch nicht, dass das gesamte Licht absorbiert wird! Die orbitale Position wäre einfach falsch für die Messung des in den Weltraum reflektierten Lichtes weg von der Sonne. Die in größerer Entfernung vom Normal-Strahl einfallenden Strahlen werden einen größeren Einfallswinkel haben infolge der Krümmung der Wasserwelt. Folglich werden sie eine größere Prozentzahl des Reflexionsgrades aufweisen. Die Bedeutung hiervon ist, dass der Reflexionsgrad mit zunehmendem Einfallswinkel ebenfalls zunimmt. Die Absorption und damit die Erwärmung nimmt proportional dazu ab.

Die Fresnel’sche Gleichung lässt sich in ihrer Urform nicht leicht integrieren. Ein Polynom 6. Ordnung ergibt eine ziemlich gute Annäherung, was es mir erlauben würde, sie irgendwie mechanistisch zu integrieren und die Fläche unter der Kurve zu erhalten. Allerdings haben einige Leser Bedenken hinsichtlich von Polynomen höherer Ordnung zur Anpassung von Kurven. Ich glaube, dass dies etwas zu tun hat mit einer Phobie über hin und her schwingende Elefantenrüssel. Darum habe ich den einfachen Weg gewählt und die Gesamtfläche der Graphik auf Papier gewichtet. Danach habe ich die Fläche unter der Kurve ausgeschnitten und gewichtet. Das Verhältnis der beiden Wichtungen ergibt die Proportion der beiden Flächen.

Die Fläche unter Reflexionsgrad-Kurve für Meerwasser (Abbildung 1 oben) macht etwa 9% aus. Weil sich die Sonne mit konstanter Winkelgeschwindigkeit bewegt, ist der Wert des über die Zeit gemittelte Reflexionsgrades eines Punktes auf der Oberfläche der Wasserwelt derjenige für einen Zeitraum von 6 Stunden. Das bedeutet, dass jede einzelne Stelle auf der Oberfläche des Ozeans mit Beginn zu Sonnenaufgang am Äquator einen initialen Sofort-Reflexionsgrad von 100% aufweisen würde. Mit der Rotation des Planeten unter der Sonne wird die Prozentzahl des von der Stelle reflektierten Sonnenlichtes bis zu einem Minimum von rund 2% beim lokalen Sonnenhöchststand an dieser Stelle abnehmen. Danach kehrt sich der Prozess um bis Sonnenuntergang, bis an der Stelle erneut der Maximum-Reflexionsgrad erreicht wird. Die Gesamtmenge des reflektierten Lichtes an diesem Punkt über einen nominellen 12-stündigen Sonnenschein wird etwa 18% des einfallenden Lichtes ausmachen. Dies ist mehr als der zweifache Wert, der für den diffusen Reflexionsgrad für Wasser gelistet ist, und er liegt innerhalb der Bandbreite der Werte für Vegetation.

Außerdem sollte man nicht vergessen, dass an einem Punkt der Schattengrenze bei 60° Breite (N & S) eine Abnahme der Reflektivität bis zum lokalen Sonnenhöchststand erfolgen würde, genau wie am Äquator, aber sie wird niemals unter sechs Prozent sinken! Die Minimum-Reflektivität nimmt mit zunehmender Breite zu, was zu einem größeren mittleren Reflexionsgrad führt.

Dies beschreibt jedoch die Lage nicht angemessen, weil die Oberflächengebiete mit der größten Reflektivität ausgedehnter sind als die Gebiete mit niedrigster Reflektivität. Weil die Erde rotiert, ist es von Bedeutung, wo sich Wasser befindet relativ zu Festland und Wolken. Während ein mittlerer Reflektivitäts-Wert nützlich sein könnte für eine initiale Approximation erster Ordnung, muss die Variation mit der Zeit/dem Ort für eine akkurate Modellierung einbezogen werden.

Ich habe auch eine diskrete Aufsummierung der Kegelstümpfe [frustrums, ?] einer Hemisphäre durchgeführt (Af = 2πR DX). Multipliziert man die (auf ein Einheitsgebiet für die Hemisphäre) normalisierten Kegelstumpf-Gebiete mit der mittleren Reflektivität für den Einfallswinkel für jeden Kegelstumpf, ergibt sich die nach Gebiet gewichtete Reflektivität für jeden Kegelstumpf. Die Aufsummierung derselben ergibt eine gebietsgewichtete mittlere Reflektivität von etwa 18%. Dies ist der momentane gebietsgemittelte Reflexionsgrad über eine Hemisphäre. Dies ist fast eine Größenordnung größer als das von einer kleinen Stelle der Ozeanoberfläche reflektierte Sonnenlicht direkt unter der Mittagssonne während eines Äquinoktiums. Es ist weit größer als die offensichtliche Albedo (≪2%) unserer hypothetischen Wasserwelt!

Selbst auch der realen Erde sind diese Spiegel-Reflektions-Effekte bedeutsam, weil etwa 71% der Oberfläche mit Wasser bedeckt ist, von der die NASA behauptet, dass sie einen Reflexionsgrad von etwa sechs Prozent aufweist. Das bedeutet, dass die tatsächliche Gesamt-Reflektivität der Erde größer sein muss als die Schätzung der diffusen Reflektivität, die sich aus Erdschein-Albedo-Messungen ergibt (siehe „Terrestrische Albedo”).

Jetzt werden die Dinge komplizierter, fügen wir doch jetzt Festland und Wolken hinzu, und die verhalten sich anders als Wasser. Nackter Boden und Vegetation erzeugen eine Kombination von Spiegel- und diffuser Reflektion, die am besten beschrieben wird durch die Bidirectional Reflectance Distribution Function (BRDF). Dies ist eine mathematische Beschreibung, wie das Licht gestreut wird mit den beiden Effekten von diffuser und Spiegel-Reflektion bei variierenden Einfallswinkeln. Es gibt immer einen starken Vorwärts-Flügel [a strong forward lobe, ?] des Reflexionsgrades (anisotropy) für schräge Beleuchtung, sogar für Schnee. Ursache hierfür sind Schneeflocken (und Blätter von Pflanzen), die flach und plan sind und dazu tendieren, parallel [sub-parallel] zur Erdoberfläche angeordnet zu sein. Folglich werden Messungen der Albedo direkt darüber zu Werten führen, die niedriger sind als der wahre Gesamt-Reflexionsgrad, den man durch Integration der BRDF über eine ganze Hemisphäre erhalten würde.

Es wurde mit der Modellierung von CERES-Satelliten-Messungen gearbeitet; allerdings zeigen die folgenden Illustrationen, dass sie es nicht hinbekommen haben [they don’t have it right]. Die Illustration rechts in Abbildung 2 zeigt eine Hemisphäre mit einem großen Festlands-Anteil. Die Ozeane erscheinen dunkler als mit Vegetation bedecktes Festland (Albedo 8% bis 18%). Tatsächlich scheint ein Wert von 6% für den offenen Ozean total unangemessen. Daher scheint diese Illustration primär der diffuse Reflexionsgrad der Wasser-Albedo zu sein und nicht der Gesamt-Reflektivität. Weil der Wert so niedrig ist, wurde offensichtlich nicht berücksichtigt, wie sich der Spiegel-Reflexionsgrad mit der Zeit und der Position ändert. Das heißt, dies ist ein Mittel des Spiegel-Reflexionsgrades des kleinen Einfallswinkels (≈2%) des direkten Sonnenlichtes, wie es von Satelliten erfasst wird; Schaumkronen, Reflexionsgrad vom Grund flacher Gewässer, diffuser Reflexionsgrad schwebender Partikel nahe der Wasseroberfläche sowie Streulicht vom Himmel, das aus allen Winkeln einfällt.

Abbildung 2: Terra/CERES-Ansicht der Welt bei der ausgestrahlten langwelligen Strahlung (links) und des reflektierten Sonnenlichtes (rechts). Bild: NASA.

Vegetation verhält sich anders als nichtorganische Reflektoren. Erstens, Blätter tendieren dazu, flach zu sein, mit einem wachsartigen Überzug, der Spiegelreflexion begünstigt. Weiter, während Pflanzen infolge der Absorption blauen und roten Lichtes grün aussehen (sie sind auch hoch reflektiv im Nahen Infrarot), trägt nicht das gesamte einfallende absorbierte Licht zu Erwärmung bei. Das Chlorophyll in den Pflanzen konvertiert einfallendes Licht in Kohlenhydrate und resultiert nicht in Erwärmung. Die Schätzungen der Effizienz, mit der diese Konversion vor sich geht, variieren mit den Pflanzen und den Wachstumsbedingungen. Allerdings wird allgemein angenommen, dass sich dies im kleinen einstelligen Prozentbereich abspielt. Folglich sollte der effektive Reflexionsgrad des sichtbaren Lichtes nach oben adjustiert werden, um der fehlenden Erwärmung Rechnung zu tragen. Phytoplankton und Algen im Ozean fangen genauso Sonnenlicht ein und konvertieren es in Biomasse, anstatt das Wasser zu erwärmen bis zu einem Grad, wie eine Schätzung erster Ordnung der Reflektivität allein nahelegen würde.

Normaler trockener Sand kann einen diffusen Reflexionsgrad bis zu 45% besitzen! Schotter, Sand und Erde haben typischerweise einen diffusen Reflexionsgrad. Durch Landwirtschaft freigelegte Erde kann von sehr hellem Gelb, kalziumreichen Wüstenboden bis zu dunklen, organisch angereicherten Böden variieren. Wenn die Böden nass sind, werden sie dunkler und haben eine stärkere spiegelnde Komponente [a stronger specular component]. Und natürlich liegt kaum Erde bloß während der Wachstums-Saison, wenn überhaupt welche. Jedweder ,mittlere‘ Wert freiliegender Böden wird wahrscheinlich öfter falsch als richtig sein. Schätzungen der Reflektivität von Erde sollte aus Erdboden-Karten abgeleitet werden, um besser nach Gebiet gewichtete Werte für verschiedene Regionen der Welt zu erhalten und der Wachstums-Saison stärker Rechnung zu tragen.

Das andere Extrem ist der diffuse Reflexionsgrad von Wolken, welcher nahe des wahren Lambert’schen Reflexionsgrades liegt. Die Lambert’sche Reflexion ist eine Bedingung, bei der Licht gleichmäßig in alle Richtungen reflektiert wird, und die Wolken sehen aus allen Richtungen einheitlich weiß aus, außer unter den Wolken und in Schattengebieten dazwischen. Wolken können stark hinsichtlich ihrer Albedo variieren, aber ein allgemein akzeptierter mittlerer Wert liegt um 50%.

Was die Wolken zum Energie-Gleichgewicht beitragen, ist die Differenz zwischen ihrem Reflexionsgrad und dem Reflexionsgrad der Materialien an der Erdoberfläche, die sie überdecken. Wolken leiten Licht auch um, was die Berechnungen zu einer noch größeren Herausforderung macht. Allerdings haben Wolken ihre größte Auswirkung auf Reflektivität und Albedo, wenn sie innerhalb etwa 50 Grad der zur Sonne zeigenden Oberflächen-Normale haben [when they are within about 50 degrees of the surface-normal pointing towards the sun].

In den Polargebieten ist es immer wolkig. Das ist ein Grund dafür, dass die Wikinger den Gebrauch des Sonnensteins [Näheres zu ,Sonnenstein‘ hier bei Wikipedia; Anm. d. Übers.] einführten. Der sollte ihnen navigieren helfen, wenn ein Kompass unbrauchbar und Sterne nicht erkennbar waren. Die meisten Zeit des Jahres spielt es nicht wirklich eine Rolle, ob offenes Wasser oder Eis vorhanden ist, weil die Wolken sich mit Sonnenlicht überlagern [interfere], welches den Erdboden während es Arktischen Sommers erreicht, und im Arktischen Winter gibt es kein Sonnenlicht! Wenn Sonnenlicht wirklich die Oberfläche erreicht, hilft die Reflektivität von 100% an den Rändern der Erde zumindest teilweise zu erklären, warum es an den Polen so kalt ist. (Dies ist auch um den Umfang [perimeter] der Ozeane an den Schattengrenzen des Planeten der Fall, nicht nur an den Polen). Schnee auf Eis streut Licht tatsächlich in alle Richtungen, einschließlich nach unten [downward]. Folglich gibt es tatsächlich mehr Absorption bei einem Blickwinkel [glancing angle] mit dem Vorhandensein von Schnee als es über ruhigem, offenen Wasser der Fall wäre!. Es gibt Austausch [tradeoffs], welcher die Lage kompliziert, und ich glaube nicht , dass dies von den meisten Klima-Modellierern berücksichtigt worden ist. Die vereinfachende Erklärung abnehmenden arktischen Eises, dass dies für die Verstärkung der Erwärmung ursächlich ist, ist möglicherweise nur ein Gedanke all jener, denen die Fresnel’schen Gleichungen nicht bekannt sind.

Wolken sind das beste Beispiel dafür, dass die naive Behauptung „die Wissenschaft ist settled“ falsch ist. Wolken sind hinsichtlich ihrer Lage, Ausdehnung und Albedo hoch variabel und ziehen oftmals rasch unter dem Einfluss von Wind. Es gibt Gründe für die Annahme, dass eine Abnahme der Bewölkung einen größeren Einfluss auf den Rückzug von Gletschern hatte als die vermeintliche Zunahme der Lufttemperatur (≪1°C pro Jahrhundert in Mittleren Breiten). Schmelzendes Eis ist nicht direkt proportional zu einer Temperaturzunahme, falls die Temperatur niemals über den Gefrierpunkt steigt. Im besten Falle würde man erwarten, dass der Gletscherrückzug dem adiabatischen Temperaturgradienten [lapse rate] folgt, falls die Temperatur der kontrollierende Faktor wäre. Was man sieht ist, dass der Gletscherrückzug an Südhängen von Bergen ausgeprägter ist. Dies zeigt, dass es eine Abnahme der Bewölkung gegeben haben muss, die zuvor Eis und Schnee vor dem direkten Sonnenlicht abgeschirmt hatten.

Noch frustrierender ist, dass die Energie zur Phasenänderung, die in den Wolken stattfindet, nicht in einer Größenordnung modelliert werden kann, die zur Erfassung von Details erforderlich ist, die in die Globalen Zirkulationsmodelle eingehen. Es gibt einfach nicht ausreichend Computerleistung, um die Berechnungen durchzuführen, und Vereinfachungen sind erforderlich. Es gibt das alte Sprichwort „Der Teufel steckt im Detail“. Das gilt so ziemlich auch für das Problem des Energieaustausches in Wolken. Weil sich Wolken so rasch ändern und einen bedeutenden Einfluss auf Albedo und Gesamt-Reflektivität haben, ist es möglicherweise unangebracht davon auszugehen, dass die Albedo der Erde irgendwie konstant ist. Wolken ändern sich fortwährend!

Zusammengefasst: Albedo wird allgemein definiert als die „Weiße einer Oberfläche“. Wasser wird allgemein so charakterisiert, dass es eine geringe Reflektivität aufweist, weil Albedo herangezogen wird. Wasser kann schräg [obliquely] beschienen werden und eine höhere Reflektivität als Schnee aufweisen, aber es wird einem Beobachter, der sich nicht in der Reflexionsebene befindet, schwarz vorkommen. Die von Klimatologen allgemein verwendete Albedo liegt am unteren Ende einer Bandbreite gemessener Werte. Selbst hohe Albedowerte sind zu niedrig, um für eine Schätzung der gesamt-terrestrischen Reflektivität herangezogen zu werden, weil Albedo fast alle Spiegel-Reflexionen ausschließt. Albedo ist eine Unterschätzung der Reflektivität der Oberflächen-Materialien der Erde; sie ist nur angebracht für Wolken und in geringerem Maße für bloßen Sand. Die genaueste Repräsentation würde man durch gemessene BRDF für alle Winkel der einfallenden Sonnenstrahlung auf die wesentlichen Oberflächenmaterialien erhalten.

Link: https://wattsupwiththat.com/2016/09/12/why-albedo-is-the-wrong-measure-of-reflectivity-for-modeling-climate/

Übersetzt von Chris Frey EIKE

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken