Sie schreibt:
Wie sich herausstellt, haben die Klimamodelle eine Sicherheit von 95%, basieren jedoch auf der Ableitung von abhängigen Variablen mit einer Sicherheit von 0%, und das ist ein ,No No‘. Das möchte ich erklären: Effektive Klimamodelle modellieren eine hypothetische Welt, in der alles in einem konstanten Zustand eingefroren wird, während sich ein Faktor verdoppelt. Aber in der realen Welt ändern sich viele Variable gleichzeitig mit anderen Regeln.
Partielle Ableitungen abhängiger Variablen sind eine ,Wild Card‘ – manchmal könnte dabei eine ordentliche Schätzung herauskommen, aber in anderen Fällen wird nur Unsinn erzeugt, und bedrohlicherweise gibt es keinen effektiven Weg, dies herauszufinden. Falls die Klimamodelle das Klima prophezeien, würden wir wissen, dass sie damit durchgekommen wären. Sie sind es nicht, aber wir können nicht sagen, ob sie an partiellen Ableitungen gescheitert sind. Es könnte auch etwas anderes sein. Wir wissen nur, dass es ein schlechtes Verfahren ist.
Die partiellen Ableitungen abhängiger Variablen sind strikt hypothetisch und nicht empirisch verifizierbar. Bzgl. Klima kann man nicht nur eine Variable variieren und alles andere konstant halten und die Änderung an einer anderen interessierenden Variablen messen. Verwendet man partielle Derivative im Bereich Klima, kommt es zu unbekannten Approximationen – und darum ist das unzuverlässig.
Nun könnte man argumentieren, dass die partiellen Ableitungen gute Approximationen sind und vielleicht alles, was wir haben und besser als gar nichts. Aber es ist eine unbekannte Angabe, weil die partiellen Ableitungen auf abhängige Variable Bezug nehmen. Man könnte argumentieren, dass bestimmte Klima-Variable fast unabhängig sind, in welchen Fällen partielle Ableitungen hinsichtlich jener Variablen nur leicht unzuverlässig sind – und man stünde auf einem festeren Fundament. Aber man wüsste nicht, wie fest, weshalb jedes Modell, das sich auf diese partiellen Ableitungen verlässt, gegen die Wirklichkeit getestet werden müsste. Falls sich dabei herausstellt, dass das Modell nicht allzu gut abschneidet, dann könnte der Grund dafür sein, dass die partiellen Ableitungen die falschen Werte haben, oder auch, weil sie konzeptuell ungeeignet sind, oder das Ganze aus anderen Gründen auch komplett versagen könnte; und man würde es nicht erfahren, weil vorgegebene partielle Ableitungen nicht empirisch verifizierbar sind.
Dies klingt für mich so, als ob jene Schätzung so ziemlich eine ,Wild Card‘ in diesem Falle ist, und vielleicht ist es dieser Faktor, der so unterschiedliche Ergebnisse der Klimamodelle zeitigt, wie das folgende Bild veranschaulicht:
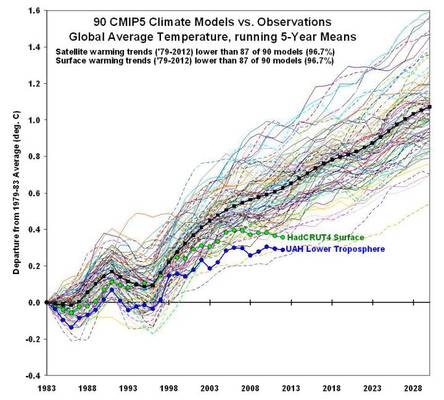
Evans hat schon zuvor auf diesem Gebiet gearbeitet, dass teils vielversprechend aussah. Aber er hat meiner Ansicht nach diese Arbeit zu früh veröffentlicht, und sie wurde heftig kritisiert.
Dies sieht aus wie ein viel konkreteres Thema, dass kaum zu rechtfertigen und/oder hinweg zu erklären ist.
Link: http://wattsupwiththat.com/2015/09/28/wild-card-in-climate-models-found-and-thats-a-no-no/
Übersetzt von Chris Frey EIKE
‘Joker’ in der Klimamodellierung gefunden – in der normalen Wissenschaft ein absolutes NoGo!
Sehr geehrter Herr Ohle, wie ich schon in #71 schrieb, habe ich meine Kontaktdaten weitergeleitet. Ist noch nichts angekommen? Da können wir das Ganze fortsetzen.
@86: Sehr geehrter Herr Hader
Ich freue mich, dass Sie so meine Argumentation abschließend bestätigen.
Wie ich das in #46 bereits hergeleitet habe: „… brauchen sie mehr Speicher als Atome im Universum“
Ihr Einwand war insofern überflüssig weil ich mich selbstverständlich auf die theoretischen Möglichkeiten einer Turingmaschine bezogen habe.
Leider scheint eine weitere Diskussion des Themas von EIKE nicht mehr erwünscht.
Ich schließe damit hier und kann mein Angebot nur wiederholen, lassen Sie sich bei Interesse meinen Kontakt von EIKE geben.
MfG
Christian Ohle
Sehr geehrter Herr Ohle, da muss ich Ihnen leider widersprechen. Nicht jede rationale Zahl ist mit einem Computer exakt darstellbar. Es gibt bekanntermaßen unendlich viele rationale Zahlen. Ein Computer hat immer einen begrenzten Speicherplatz, mit dem man entsprechend nur endlich viele verschiedene Zahlen darstellen können. Daraus folgt, dass es unendlich viele rationale Zahlen gibt, die sich mit einem Computer nicht darstellen lassen. Dasselbe gilt auch für die natürlichen Zahlen.
#75: Herr Sören Hader, leiden Sie an Fieber? Haben Sie welchen?
Zitat: „[…] Herr Heinzow ist kein diplomierter Meteorologe. […]“
Warum ist dieser Punkt absolut unwichtig, irrelevant?
Eines scheint sicher. Sie kennen das unbekannte (!) Universum, so absolut sicher, wie Ihre Westentasche. Das zertifiziert Sie wiederum, als Geisterfahrer. Die Tatsache, dass Sie vom Osten in den Westen gegangen sind, hat sich bei Ihnen nicht niedergeschlagen.
Worauf kommt es allein in der Wissenschaft an?
Apropos, können Sie überhaupt programmieren? Nur aus Neugier.
Lieber Herr Ohle,
ich bin zwar neugierig, Sie können mir aber wohl nicht viel bieten. Finden Sie es nicht aberwitzig bei Ihren Benehmen von anderen noch Entschuldigungen (für was?) zu erwarten?
Tatsache ist, daß die Frage nach der „Tauglichkeit“ eines physikalischen Computermodells die angestrebte Genauigkeit maßgeblich ist. Ein mathematisch auch exaktes physikalisches Modell gibt es für gar nichts. Bedenken Sie das.
Wenn die Basis der Zahlendarstellung beliebig wechseln kann, so läßt sich jede rationale Zahl exakt darstellen, aber nicht bei nur einer festen Basis. Beispiel: 1/7 dezimal
= 0,142857142857143… periodisch, bricht nicht ab.
im 7-er System ist es einfach 0,1 = 1 x 7 hoch -1. Oder? (ich bin kein Informatiker).
Wenn Sie glauben, in #77 Fehler gefunden zu haben (außer die im Zitat, natürlich), so lassen Sie hören und zeigen mir mal, wie eine irrationale Zahl als Gleitkomma exakt darstellt (also nicht nur implizit)
@ #73 Chr. Ohle
„Ich bin heute zu Müde, er bekommt morgen sein Fett weg.“
Da wird er Ihnen aber für die Abmagerungskur dankbar sein.
Jedenfalls haben die Nullsatzschreiber S. Hader und das Pseudonym NicoBaecker dass mit shr und shl nicht bemerkt.
Und S. Hader macht aus Ihrem „Ich bin auch kein Meteorologe, mische mich da auch nicht ein,“
Sie würden annehmen ich sei diplomierter Meteorologe.
Und das mit dem Tieffliegern ist lustig, denn unsereins kann im Gegensatz zu denen tatsächlich Tiefflieger sein. Jedenfalls da, wo es erlaubt ist: z.B. über dem FKK-Strand in Wyk/Föhr. 😉
#80: Fabian Paul
Sie haben Recht, meine Shift Taste klemmt 🙂
@78: NicoBaecker
Auch wieder falsch.
Der Computer kann jede rationale Zahl exakt darstellen.
Lernen Sie doch einfach erst mal und dann kommen Sie wieder.
MfG
Zitat #79:
„In Ihren Drei Sätzen stecken Drei Fehler!
Ich sage die Ihnen aber nicht, nur Wenn Sie sich Entschuldigen.“
In diesen 2 Sätzen stecken 4 Fehler. Das wollte ich nur gesagt haben.
Fabian Paul
@77: NicoBaecker
In Ihren Drei Sätzen stecken Drei Fehler!
Ich sage die Ihnen aber nicht, nur Wenn Sie sich Entschuldigen.
MfG
Lieber Herr Ohle,
Sie haben recht, der Computer kann nicht mal jede rationale Zahl exakt darstellen.
Nur hat dies Problem wenig mit der Möglichkeit physikalischer Modellierung mit Gleitkomma -Approximation zu tun, denn da erhält man explizit sowieso nur Approximationen. Das ist jedem Physiker klar. Der Punkt ist alleine, daß man ermitteln muß, wie weit die Approximation von der exakten Lösung entfernt ist und ob diese Ungeauigkeit akzeptabel ist. So läuft das eigentlich durchgehend in der Physik.
Lieber Herr Heinzow, #72
“ „Jede Computerberechnung ist eine Approximation auf Basis rationaler Zahlen.“
Wohl kaum, kennt ein Prozessor doch nur Dualzahlen. Division durch 2 ist Schieben der Bits nach links. “
Die Basis für die Darstellung von Zahlen – ob Dezimal oder Dual – ist für die Eigenschaft einer Zahl, reell, rational, komplex oder ganz zu sein, egal!
Ein Computer kann selbstverständlich nie irrationale Zahlen wie z.B. die exakte Wurzel aus 2 oder pi produzieren, sondern nur rationale Approximationen dafür. Dass diese binär dargestellt werden, ist offenkundig belanglos, auch Wurzel 2 in seiner Binärdarstellung ist irrational.
@70: NicoBaecker
„Ihnen ist hoffentlich klar, daß dies jeder ohnehin so Computer macht. Jede Computerberechnung ist eine Approximation auf Basis rationaler Zahlen.“
Das kann man so natürlich nicht sagen aber ich will das nicht, in der Ihnen üblichen Weise, zerpflücken um vom Problem abzulenken.
Sie meinen wahrscheinlich Gleitkommazahlen wenn Sie von Approximation sprechen und
weil die, je nach Format, Teilmengen rationaler Zahlen darstellen.
Ist denn der gedankliche Schritt für Sie so schwierig gleich mit echten rationalen Zahlen zu arbeiten?
Muss man mit Ihnen Grundschulwissen wiederholen was rationale Zahlen sind und wie man damit rechnet?
Ist Ihnen klar, dass sie damit ohne Fehler, ohne schätzen, ohne approximieren, ohne Stabilitätsprobleme präzise rechnen können?
Das googeln Sie sich mal bitte selber.
Solange Sie das nicht verstanden haben, können Sie aber mein #59 auch nicht verstehen.
Wenn Sie es verstanden haben, dann können Sie es sich aber auch selber herleiten.
Mehr noch, dann wären Sie in der Lage präzise Aussagen für f(t) zu treffen.
Sicher ahnen Sie was dabei rauskommt und dazu brauchen Sie nicht mal einen Computer.
Damit würden Sie sich dann eben selber widerlegen und davor haben Sie Angst.
Wenn Sie das auch wieder nicht verstanden haben dann ist es mir auch egal.
Ihnen fehlen einfach zu viele Grundlagen als dass man das hier alles erklären könnte.
MfG
#72: „Wohl kaum, kennt ein Prozessor doch nur Dualzahlen.“
Lieber Herr Heinzow, jede Maschinenzahl ist auch eine rationale Zahl (bis auf solche Geschichten wie NaN, Inf usw.).
An der Stelle muss ich noch Herrn Ohle korrigieren. Herr Heinzow ist kein diplomierter Meteorologe. Nur mal zur Klarstellung.
@ # 73 Chr. Ohle
Spielverderber!
Die Frage war, ob das Pseudonym Nicobaecker den Fehler bemerkt.
Wenn man damals mit den Supercomputern (TR 440) schnell sein wollte (Rechenzeit war knapp), mußte man seine Programme intelligent schreiben: Addition statt Multiplikation. Und natürlich möglichst Integer verwenden.
Inzwischen machen das die Compiler. Aber früher nicht.
@72: T.Heinzow
Division durch 2 -> schieben Sie bitte eins nach Rechts, nach Links ist * 2
Aber das ist kein Kritik, Sie verstehen worum es geht, darauf kommt es an.
Bevor Sie von irgendwelchen Tieffliegern angegriffen werden.
Ich bin auch kein Meteorologe, mische mich da auch nicht ein, wenn aber jemand Müll erzählt merkt man es aber eben doch.
Bäcker labert schon wieder Müll und er weiß nicht mal was eine Rationale Zahl ist.
Ich bin heute zu Müde, er bekommt morgen sein Fett weg.
Gruß Christian
@ #70 Pseudonym NicoBaecker
„Jede Computerberechnung ist eine Approximation auf Basis rationaler Zahlen.“
Wohl kaum, kennt ein Prozessor doch nur Dualzahlen. Division durch 2 ist Schieben der Bits nach links.
@Christian Ohle, ich habe meine Kontaktdaten an EIKE weitergeleitet.
Lieber Herr Ohle, #46
ich beziehe meine Frage an Sie auf diese Aussage von Ihnen in #46:
„Ich arbeite unter anderem seit 20 Jahren an sowas.
Dabei geht es um Simulationen in technischen Systemen.
Dabei sind die Systeme leider nicht mehr ganz so einfach.“
Sind Sie in der Lage, Ihr System zu beschreiben und Ihr Problem damit? Oder muß ich davon ausgehen, daß es dieses nicht gibt und Sie bluffen?
„Wir haben aber eine Methode gefunden und das sollte für Sie nachvollziehbar sein:
Man kommt nur weiter wenn man konsequent mit rationalen Zahlen rechnet.“
Ihnen ist hoffentlich klar, daß dies jeder ohnehin so Computer macht. Jede Computerberechnung ist eine Approximation auf Basis rationaler Zahlen.
#64: Doktor Professor Nico Baecker Herr!
Zitat:
„Im Gegensatz dazu ist die Kommunikation zwischen Programmierer und programmierter Maschine so scharf, wie sie schärfer nicht sein kann! Die größte Hürde beim Einstieg in das Programmieren ist es, ein Verständnis dafür zu entwickeln, dass Maschinen nicht [!!] intelligent sind.
Die An- oder Abwesenheit eines einzigen Zeichens in einem Programmtext kann über Erfolg oder Misserfolg eines Programmierprojektes entscheiden.
Eine Maschine ist nicht fähig, über ihr eigenes Programm nachzudenken und darin enthaltene Fehler, wie klein und unbedeutend sie auch erscheinen mögen, selbstständig zu erkennen und zu beheben.
Die Sprache, in der ein Programmierer mit seiner Maschine redet, die Programmiersprache also, besitzt eine viel strengere Grammatik als jede natürliche Sprache.
Der Programmierer muss sich peinlich genau an die Regeln dieser Grammatik halten oder er wird unweigerlich fehlerhafte Programme erzeugen.
Während des Programmierens darf er nichts voraussetzen, was nicht definitiv in der Sprachbeschreibung dokumentiert oder daraus herleitbar ist, will er der Maschine seinen Willen erfolgreich aufzwingen.“
[Quelle: Ziegler2002, S. 3.]
a.) Programmieren ist die eine Aufgabe.
b.) Den dazu passenden Algorithmus zu entwerfen, ist eine Kunst, die eigentliche Aufgabe, die kein Mensch, und auch keine Gruppe derselben, auf dieser Welt beherrschen kann. Zumindest nicht in absehbarer Zeit. Ich bin der festen Überzeugung, es wird nie möglich sein. Aber, wer bin ich schon?
Mit humorvollen Grüßen
Wäre Ihre Art der Kommunikation doch so scharf wie Maschinencode, Doktor Nico Baecker Professor Herr! Und eines ist absolut sicher. Ihnen wird kein Erfolg auf dem Gebiet zu bescheinigen sein.
@49: NicoBaecker Noch mal Sachlich
Ich habe mir überlegt: kann es sein, dass Sie mich gar nicht beleidigen wollten?
Und dass sie nicht betrunken waren sondern sich einfach nur verschrieben haben?
„nun, ich nehme an, Sie scheitern nicht an einem…“
Meinten Sie hingegen:
„nun, ich nehme an, Sie arbeiten nicht an einem…“
Ihr Statement würde so einen ganz anderen Sinn bekommen, das müssen Sie zugeben.
In dem Fall haben Sie natürlich auch eine korrekte Antwort verdient:
Nun, ich arbeite an Berechnungskernen für statische und dynamische Systeme bis hin zur Visualisierung.
Auf Basis dieser sogenannten Enginen entwickeln wiederrum andere Firmen Speziallösungen
für den ingenieurtechnischen Bereich. Dabei geht es meist um Hightech Bauteile in Systemen
die heutzutage bis an die Grenzen des Machbaren optimiert und trotzdem entsprechend belastbar sein müssen.
Befinden Sie sich das nächste Mal in einer größeren Halle dann schauen Sie einfach mal zur Decke.
Sollte Ihnen diese plötzlich in Folge einer Windböe auf den Kopf fallen –
dann könnte das daran liegen das ich geschlampt habe.
Ich hoffe das reicht Ihnen als Erklärung und dass Sie meine Kompetenz nicht weiter in Frage stellen.
MfG
@#65: Christian Ohle, zu „… einen Artikel zu schreiben wo ich das alles mal zusammenfassen …“
Ich schreib‘ Ihnen das gern zusammen, in Deutsch und/oder Englisch; wird ja wohl nicht schwierig sein die Referenzen aufzufinden in
– http://citeseerx.ist.psu.edu/
– https://scholar.google.de/
Lassen Sie sich von Admin meine Email geben.
MfG
#64: NicoBaecker
Ich kann Ihnen nur empfehlen dringen ein Arzt aufzusuchen
Damit Sie nicht mehr so schlimm leiden müssen.
Selber merkt man das nicht, aber andere, Ihre Familie, Ihre Freunde und wir hier auch
MfG Christian
@62: S.Hader „meine geistige Beschränktheit “
Nein, Sie sind nicht beschränkt, Sie sind wesentlich intelligenter als dieser NicoBaecker.
Weil dieser NicoBaecker mit seinen Klima Modellen gescheitert ist, mir zu unterstellen ich würde sowas können wollen?
Für mich ist das eine Beleidigung!
Es ist ein Unterschied physikalische Gesetze zu kennen oder sie auch zu verstehen.
NicoBaecker weiß aber versteht nichts – er ist ein wissenschaftlicher Zombie.
Die größte Frechheit ist wohl mir zu unterstellen „ich würde die Mathematik wiederlegen wollen“
Wobei dieser Dilettant nur schätzen kann während ich präzise rechne.
Aber egal
Für den Fall das Ihre Frage ernst gemeint war:
Ich überlege Herrn Limburg anzubieten einen Artikel zu schreiben wo ich das alles mal zusammenfasse.
Es wäre alles mal aus dem Gesichtspunkt einer ganz anderen Fachrichtung zu betrachten.
Das ist vom Arbeitsaufwand vergleichbar mit einer Doktorarbeit und sie verstehen –
Alle die Referenzen zusammen suchen, all dies populär verständlich zu formulieren,…
Jede Menge Arbeit, ich habe eine Firma, vier Kinder und wenn meine Berechnungen nicht stimmen:
trage ich indirekt Verantwortung für das Leben vieler Menschen.
Also, ich muss abwägen…
Das Problem hat NicoBaecker nicht. Er kann labern, schwätzen, trägt keine Verantwortung und bekommt sogar noch Geld dafür.
Egal, andere Option: lassen Sie sich meinen Kontakt von Eike geben.
Der Block hier ist doch abgelaufen, da liest doch keiner mehr mit.
Wenn Ihre Frage ernst gemeint war, ich kann erklären, kann mich auf Ihren intellektuellen Hintergrund einstellen.
Wir sind alle nur Experten in einen Fachbereich.
Außer dem Intelektuellen Tiefflieger NicoBaecker natürlich.
MfG
Christian Ohle
Lieber Herr Hader, 62
habe ich auch nicht verstanden, aber Herr Ohle kann ja selbst sein Problem, an der er seit 20 Jahren herumrechnet, nicht beschreiben.
@ #61 H. Burowski
„“Sie können ja bei Wiki nachschauen.“
Seit wann greift T.Heinzow auf Wiki zurück?“
Unsereins nicht, aber Sie sollten es tun. Englisch ist doch zu schwer für Sie.
@Christian Ohle, #59: „… und es ist ein Indiz dafür das es sich NICHT um ein physikalisch basiertes Klimamodell handelt.“
Sorry, diesen Satz verstehe ich nicht. Sie können es gerne auf meine geistige Beschränktheit schieben, aber vielleicht würde auch eine Begründung mit anderen Worten Ihrerseits weiterhelfen.
MfG
S.Hader
#60:T.Heinzow
„Ach Gottchen, ich vergaß, daß Sie aus der „DDR“ stammen. Da gab es Compiler, die überstzten Todesstreifen mit Metallgitterzaun und Selbstschußanlagen in Antifaschistischer Schutzwall. Aber die hießen anders, Schnitzler glaub ich oder so. Und Englisch hatten Sie ja auch nicht als Fremdsprache, sondern Russisch. Da können Sie natürlich nicht wissen was Compiler sind.“
Ist das bei Ihnen genetisch bedingt?
„Sie können ja bei Wiki nachschauen.“
Seit wann greift T.Heinzow auf Wiki zurück?
####################################
„Aber ich erkläre es Ihnen nicht.“
Das kann ich verstehen – weil Sie es nicht wissen. So, und nun passen Sie mal schön auf Herr T. Heinzow, aus der Gegend Deutschlands, aus der ich komme, würde man Sie als Rumbranzer bezeichnen.
Compiler sind Programme, die aus eine Programmiersprache (z.B. FORTRAN) in den Maschinencode des Zielsystemes übersetzen. Abhängig davon, welchen Grammatiktyp in der Chomsky-Hierachie die Sprache zu zuordnen ist, sind mehrer Compilerläufe notwendig. Da FORTRAN eine Typ-1-Grammatik ist, sind hier mindestesn 2 Pässe notwendig, um die Kontextsensitivität im Maschinencode vollständig auflösen zu können.
Im Pass 1 (lexikalische, syntaktische und semantische Analyse) wird der Programmcode in Morpheme (auch als Tokens bezeichnet) geparst und ein Objektcode in Objektmodulen erzeugt. Im Pass 2 wird aus dem Objektcode abarbeitungsfähiger Maschinencode erzeugt, bei dem externe Adressbezüge aber noch nicht aufgelöst sind. Dass macht der Linker, der letztendlich referenzierte Bibliotheken und Objektmodule zusammenfügt und ein Executable erzeugt.
Auf Spezialcompiler, wie Cross-Compiler oder Embedded Compiler gehe ich Ihnen zuliebe mal nicht ein.
Wenn Sie wünschen, dürfen Sie gerne den Quelltext meiner Diplomarbeit, die lexikalische, syntaktische und semantische Analyse von FORTRAN-IV validieren und verifizieren – aber vorallem erstmal verstehen, daran wird’s schon scheitern!
@ #57 H. Burowski
Ach Gottchen, ich vergaß, daß Sie aus der „DDR“ stammen. Da gab es Compiler, die überstzten Todesstreifen mit Metallgitterzaun und Selbstschußanlagen in Antifaschistischer Schutzwall. Aber die hießen anders, Schnitzler glaub ich oder so. Und Englisch hatten Sie ja auch nicht als Fremdsprache, sondern Russisch. Da können Sie natürlich nicht wissen was Compiler sind.
Aber ich erkläre es Ihnen nicht. Sie können ja bei Wiki nachschauen. Da werden Sie geholfen.
@55: S.Hader
„Wenn trotz kleiner Änderungen der Startwerte die Ergebnisse sich nur in einem gewissen Rahmen bewegen, dann ist das ein Indiz für die Stabilität.“
… und es ist ein Indiz dafür das es sich NICHT um ein physikalisch basiertes Klimamodell handelt.
… und wenn das trotzdem geht ist es ein Indiz dafür, dass in betrügerischer Absicht manipuliert wurde.
So Einfach ist das
MfG
Christian
@49: NicoBaecker
Sie reden wirre, haben Sie was getrunken?
„nun, ich nehme an, Sie scheitern nicht an einem Klimamodell, Ihre praktisch Erfahrung läßt sich nicht verallgemeinern. Und schon gar nicht können Sie damit die Mathematik widerlegen.“
Schade, ich hätte gerne mit Ihnen diskutiert aber auf dem Niveau hat das wohl keinen Sinn.
MfG
#51: T. Heinzow
„Haben Sie schon mal was von Compilern gehört?“
Seit wann machen Sie Ihre Selbstgespräche öffentlich?
Zur Ihrer Beruhigung, ich habe von Compilern mehr als nur was gehört. Ich weiß nicht, was BWLer/Soziologen für Vorstellungen von Compilern haben, aber vielleicht können Sie das in der Öffentlichkeit mal mitteilen.
#54: T.Heinzow sagt:
„Wenn ihr uns Geld gebt, werden die Modelle beweisen, daß die These richtig ist“
Sehr schön, muß ich mir einrahmen!
Hallo Christian Ohle, eine kurze Antwort von mir auf:
„und wir wissen definitiv, dass bei der Zahl der rekursiven Schritte der Fehler sich soweit potenziert…
dass das Ergebnis vom Fehler soweit verfälscht ist das wir uns nicht mal auf das Vorzeichen verlassen können…
dann macht auch die Spielerei mit Startwerten keinen Sinn mehr.“
Mit dem Variieren der Startwerte kann man erkennen, wie stabil das numerische Verfahren ist. Wenn trotz kleiner Änderungen der Startwerte die Ergebnisse sich nur in einem gewissen Rahmen bewegen, dann ist das ein Indiz für die Stabilität.
„Ich kriege Angst um Sie wenn Sie so was schreiben“
Das ist freundlich von Ihnen, aber um mich müssen Sie sich wirklich keine Sorgen machen. 🙂
MfG
S.Hader
@Y #47 Chr. Ohle
„Um Beweise für ihre Thesen haben sich die Brüder ja nun offensichtlich gar nicht erst bemüht.“
Das ging anders: Wenn ihr uns Geld gebt, werden die Modelle beweisen, daß die These richtig ist:
Münchhausen zieht sich am eigenen Schopf hoch.
Was wird denn mit einem Rechenmodell für die Atmosphäre gemacht?
Nun, ist doch ganz einfach: Ob nun die Auflösung T42 beträgt oder T106: Es wird so lange an den Stellschrauben gedreht, bis das Rechenprogramm einen quasistabilen Output liefert mit minimalem statistischen Fehlern. Man ist natürlich auch so clever ein künstliches Konstrukt herzunehmen: Die globale arithmetrisch gemittelte Temperatur der Gitterpunkte (flächengewichtet) in 2m-Höhe.
Vielleicht findet ja mal einer der Gläubigen an die unheimlichen Fähigkeiten der Dualsystemrechner eine vernünftige Validation eines der Modelle zu präsentieren.
Das ECHAM5 jedenfalls ist nicht korrekt validiert worden. Es weist immense statistische (systematische) Fehler auf.
#44: Lieber Student NicoBaecker,
Ihr knapper Kommentar zeigt deutlich, dass chaotisches Verhalten und „Ljapunov“ wohl etwas zu schwer für Sie ist.
Lernen Sie erst mal die Definition eines dynamischen Systems:
das ist:
Eine mathematische Beschreibung der zeitlichen Entwicklung real existierender Systeme aus Physik, Biologie oder anderen Wissenschaften.
Die entscheidende Arbeit von Ljapunov 1892 heist (übersetzt):
„Ein allgemeines Problem der Stabilität einer Bewegung“
Und damit mussten die Physiker einsehen, dass sie nie in der Lage sein werden, die reale Zukunft zu berechnen.
In den populären Formulierungen wird leider immer zu sehr auf den „Anfangsbedingungen“ herumgeritten, die allerdings nicht den Kern des Indeterminismus treffen, sondern es ist der positive(>0) Ljapunov-Exponent der diese Instabilität brillant definiert,
und die Ljapunov-Zeit ist ein gutes Maß
für den Informationsverlust eines dissipativen chaotischen Systems, bzw. wann die Trajektorie sozusagen das Gedächtnis an ihren Startpunkt komplett verloren hat.
Ich weis, ein harter Schlag für den kausalitätsliebenden menschlichen Geist aber die Kurzfristigkeit der Wettervorhersage ist doch nun jedem bekannt.
mfG
#47: Christian Ohle sagt:
„Was haben die Brüder mit dem ganzen Geld eigentlich gemacht?
Jahrzehnte lange Forschung für einen Open Source Zickzack-Linien-Generator.“
Hallo Herr Ohle,
ich meine die Klima“wissenschaft“, die wir kritisieren, hat weder mit Klima noch mit Wissenschaft zu tun.
Es handelt sich dabei lediglich um die Marketingabteilung einer Organisation, deren Ziel in Abzocke und Umverteilung besteht.
Und das funktioniert mit Hilfe der gleichgeschalteten Medien ja auch ganz passabel.
„Wissenschaftliches“ zum Thema Klima kann man aus dieser Ecke nicht erwarten.
Und natürlich auch keine Anleitung zum „wissenschaftskonformen“ Handeln.
MfG
@ #48 H. Burowski
„Aber sicher, weil eine NEC SX-6 eine ganz andere Prozessorarchitektur als eine IBM-Maschine der i-Serie hat und demnach auch einen völlig anderen Befehlssatz in der Maschinencodeebene.“
Oha!
Herzlichen Glückwunsch:
Der Satz ist Vorschlag Nr. 2 für die Jahresnullsatzhitparade.
Haben Sie schon mal was von Compilern gehört?
Es ist löblich zu sehen wie sich sachkundige Forumsteilnehmer bemühen den Schwindel mit den Klimamodellen aufzudecken. Leider eine unmögliche Aufgabe. Die Wetterkapriolen machen dem Menschen seit Jahrzehntausenden Angst, man versuchte mit Opfergaben und sonstigem Schabernack die „Götter“ zu besänftigen. Das hat einen Wiederhall in den Genen gefunden, die Menschen beschäftigen sich instinktiv mit Wetterphänomenen. Und da setzt die Klimakirche den Hebel an. Erderwärmung durch vom Menschen freigesetztes CO2, allein diese Behauptung ist stärker als alle Argumente. Finden sich jetzt noch verblendete oder korrupte „Wissenschaftler“ (PIK) die das Ganze in eine pseudowissenschaftliche Tüte packen, dann ist die Sache gegessen. Der Glaube an die „Klimakatastrophe ist rational nicht mehr zu entkräften, zu stark wirken die Archetypen in den Köpfen der grünen Schlümpfe; der Wettergott wird uns alle töten…
Trotzdem sollten die wenigen Realisten nicht aufhören zu widersprechen, denn nur das gibt uns die Würde zurück die die Klimakirche den Menschen raubt. Deswegen, weiter so EIKE!
Lieber Herr Ohle, #46
nun, ich nehme an, Sie scheitern nicht an einem Klimamodell, Ihre praktisch Erfahrung läßt sich nicht verallgemeinern. Und schon gar nicht können Sie damit die Mathematik widerlegen.
Um was für ein System handelt es sich bei Ihnen?
#36: T.Heinzow
„Sie werden sicher erklären können, warum der Code für die SX-6 nicht auf der nachfolgende IBM lief. Mit Ihrem Wissen aus der „DDR“-Informatik.“
Aber sicher, weil eine NEC SX-6 eine ganz andere Prozessorarchitektur als eine IBM-Maschine der i-Serie hat und demnach auch einen völlig anderen Befehlssatz in der Maschinencodeebene. Weiter in die Tiefe des Unterschiedes zwischen CISC- und RISC-Befehlssätzen und der Architektur von Maschinen mit Skalar- oder Vektorprozessoren dringe ich aus Zeitgründen nicht ein.
Wesentlich scheint Ihre Unkenntnis zu sein, dass Maschinencodekompatibiltät zwischen Maschinen unterschiedlicher Architektur (eigentlich) nicht möglich ist. Ich gehe davon aus, dass BWL- respektive Soziologiestudenten in den 1970ern/1980ern Informatik nur als Nebenfach hatten und solche Werkzeuge, wie virtuelle Maschinen nicht kennen; deshalb „eigentlich“ in Klammern.
Die Kompatibilität wird in der Sourcecodeebene hergestellt; gleicher Sourcecode auf unterschiedlichen Maschinen muss gleiche Ergebnisse liefern, wenn das nicht der Fall ist, haben entweder die Hardwarehersteller oder Compilerbauer geschlampt.
Bevor Sie der Meinung sind, hier dazu anderslautende Statements abzugeben, empfehle ich Ihnen, diverse Fachliteratur über Compilerbau und Grammatik der Programmiersprachen zu lesen (und zu verstehen!).
@43: besso keks
Es drängt sich natürlich auch die Frage auf:
Was haben die Brüder mit dem ganzen Geld eigentlich gemacht?
Jahrzehnte lange Forschung für einen Open Source Zickzack-Linien-Generator.
Für das Geld hätte man wenigstens eine Fourier-Glättung erwarten können.
Wahrscheinlich weiß bei den Brüdern aber gar keiner wie sowas geht.
Um Beweise für ihre Thesen haben sich die Brüder ja nun offensichtlich gar nicht erst bemüht.
Also gar nichts. Nur warme Luft – voller CO2 und Methan.
Der Begriff „Klimakiller“ bekommt dieser Tagen eine ganz neue Bedeutung.
MfG
@38: NicoBaecker
Sie sind doch ein hoffnungsloser Fall eines Theoretikers
„Für beliebige Anfangswerte ist es jedoch selbstverständlich numerisch lösbar“
„…analytisch nicht lösbare … und wird numerisch gelöst.“
Sie wollen dem Leser hier vermitteln Sie können das… numerisch.
Das können Sie aber nicht!
Das funktioniert nur beschränkt für einige der einfachsten Systeme.
Ich arbeite unter anderem seit 20 Jahren an sowas.
Dabei geht es um Simulationen in technischen Systemen.
Dabei sind die Systeme leider nicht mehr ganz so einfach.
Mit Ihren Methoden lassen sich keine brauchbaren Ergebnisse mehr erzielen.
Wir haben aber eine Methode gefunden und das sollte für Sie nachvollziehbar sein:
Man kommt nur weiter wenn man konsequent mit rationalen Zahlen rechnet.
Der Aufwand dafür ist immens und man muss die Systeme geometrisch gesehen linearisieren.
Um irrationale Terme zu vermeiden ist es notwendig in höheren Dimensionen zu rechnen etc.
Aber es funktioniert und technische Systeme haben den Vorteil, dass man es auch überprüfen kann.
Nun können Sie sagen: Na also, dann geht ja doch, was will der Kerl eigentlich von mir?
Nun, machen Sie sich das Rechnen mit rationalen Zahlen klar,
Grundschulmathematik, einfach das Rechnen mit Brüchen aus ganzen Zahlen.
Dabei entstehen erst gar keine Fehler.
Das Problem ist aber, dass dabei sukzessive riesige Zahlen entstehen.
Bei jeder Multiplikation oder Division zum Beispiel kann sich die Zahl der Digits verdoppeln.
Kennen Sie die Geschichte mit dem Schachbrett und den Reiskörnern? http://tinyurl.com/mcnjclt
So ist es mit der Methode auch und ab einer bestimmten Zahl an iterativen Schritten ist der Speicher voll.
Wird die Aufgabenstellung noch etwas komplexer würde aller Speicher der Welt nicht mehr reichen.
Wollen Sie Klima simulieren brauchen sie mehr Speicher als Atome im Universum.
Aber das wäre wohl sogar schon der Fall bei Ihrem simplen 3-K Beispiel.
Also theoretisch können Sie das – praktisch aber nicht.
MfG
Christian
@ #44 Pseudonym NicoBaecker
„bitte nicht wieder nur irgendwas behaupten und dann auch noch falsch.“
Das Jahr nähert sich dem Ende und es entbrennt ein Wettkampf um Platz 1 in der Nullsatzhitparade des Jahres.
Aber erst mal ist das ein orschlag für die Hitparade des Monats Oktober.
Lieber herr Paul,
bitte nicht wieder nur irgendwas behaupten und dann auch noch falsch. Wie schon mehrmals erklärt: Lyapunov war Mathematiker und hat sich mit der Dynamik von deterministischen Systemen beschäftigt und nicht mit indeterministischen Zufallsprozessen.
#39: Christian Ohle sagt:
„Können Sie sich die (politischen) Konsequenzen überhaupt vorstellen?
Die sogenannte Energiewende hätte keine Grundlage mehr.“
Lieber Herr Ohle,
die Grundlagen der sog. Energiewende sind Mangel an Führungsfähigkeit, Rückgratlosigkeit und Machtgeilheit.
An diesen Faktoren besteht auch für die nähere
Zukunft kein Mangel.
Leider!
MfG
Vielen Dank an alle Beitragschreiber für diesen großartigen Blog.
Wo außer bei EIKE ist sowas im deutschsprachigen Raum zu finden?!
Nochmals besten Dank
#38: NicoBaecker FALSCH,
was mathematisch-logisch dahinter steckt, ist der seit 1892 (Lyapunov) mögliche Nachweis der Indeterminiertheit bestimmter real existierender dynamischer (zeitabhängiger) Systeme.
Das hat nichts mit der Kenntnis der „Ausgangssituation“ zu tun.
Das Wetter gehört auch dazu.
mfG
Hallo,
Dazu fällt mir das Zitat von Norbert Wiener – Mathematiker ein: „Das beste Modell für eine Katze ist eine Katze. Möglichst dieselbe Katze.“
Mfg
Werner Holtz
Herr Hader
Der zweite Teil Ihrer Post. Ist Ihnen eigentlich klar was Sie da raus hauen?
„Der Open Source Code wird genau dazu verwendet, um die Kurven zu erzeugen.“
Um Gottes willen, fragen Sie erst mal Ihren Chef!
Wenn das stimmt und diese gequirlte Scheiße wirklich die wissenschaftliche Grundlage sein soll…
Können Sie sich die (politischen) Konsequenzen überhaupt vorstellen?
Die sogenannte Energiewende hätte keine Grundlage mehr.
Oder wollen Sie sich auf diesem Weg einfach nur Outen?
Ich kriege Angst um Sie wenn Sie so was schreiben
Gruß Christian
Lieber Herr Schoenfeld, #2
„Leonard Euler hat 40 Jahre vergeblich versucht, die Mondbahn im Schwerefeld von Erde und Sonne, anhand von Newtons Gleichungen zu berechnen und ist gescheitert. Ein simples Problem, im Vergleich zum Klima. Poincaré hat dann mathematisch bewiesen, dass selbst das eingeschränkte Dreikörperproblem nicht exakt lösbar ist.“
Richtig. Analytisch ist es allgemein nicht lösbar. Das wurde von Poincare bewiesen.
„Es müssen erst die passenden Anfangsbedingen gefunden werden.“
Nicht „passene Anfangsbedingungen“, sondern das 3-K-Problem ist für spezielle Anfangswerte analytisch lösbar.
Für beliebige Anfangswerte ist es jedoch selbstverständlich numerisch lösbar. Dabei muß man auf die Stabilität der numerischen Lösung achten, was praktisch darauf hinausläuft, daß man die Lösung nicht für beliebig großes t in endlicher Rechnenzeit beliebig genau bekommt.
Im Prinzip basiert jedes interessante physiklaische Problem auf analytisch nicht lösbare partielle DGLs und wird numerisch gelöst. Die obigen Bemerkungen gelten also allgemein.
„Ergo: Mit dem Klimamodellen kann man alles ausrechnen, auch das Alter von Franz Beckenbauer.“
Haha, für Klimamodellen gilt auch dasselbe wie oben. Schließlich gehören sie auch zu den physikalischen Modellen.
@34 Hallo S.Hader
Na dann kommen wir ja weiter.
Der Terminus “Iterationsverfahren”, in der Praxis verwendet für elementare iterative Algorithmen
oder nur “iterativ”, was alles Mögliche sein kann im Sinn von “wiederholend”
was in unserem Fall, den Simulationen (wie in #5), meint wieder und wieder Ergebnisse als Eingabe zu verwenden.
Können wir stehen lassen auch wenn zum Thema Konvergenz und Heron in dem Zusammenhang, noch einiges zu präzisieren wäre.
“Werkzeug”, im Sinne von Englisch “Tool” verwenden wir in der Praxis für eigenständige Programme…
was in dem Zusammenhang eigenständige (Test)Software bedeutet hätte… aber das haben Sie ja schon relativiert.
Thema “Startvariablen minimal zu ändern… Äh? Es ist eine gängige Methode”
Klar, aber an dem Punkt haben Sie gar nicht verstanden worum es bei all dem eigentlich geht.
Da tue ich mich jetzt auch schwer dies einfacher auszudrücken ohne das die Formulierungen wieder angreifbar wären.
Daher mal kurz und ganz doof:
Vergessen Sie erst mal Ihren Test und stellen Sie sich vor wir rechnen, rekursiv, wie bei den Klimamodellen notwendig…
und wir wissen definitiv, dass bei der Zahl der rekursiven Schritte der Fehler sich soweit potenziert…
dass das Ergebnis vom Fehler soweit verfälscht ist das wir uns nicht mal auf das Vorzeichen verlassen können…
dann macht auch die Spielerei mit Startwerten keinen Sinn mehr.
Oder?
MfG
Christian
#31: Holger Burowski
Sie haben Recht, ich habe die 0 vergessen, sorry.
Also Korrektur: 18446744073709551615 + 1
Es ging mir darum die Größenordnungen zu zeigen.
Klar auch dass es für 64 bit floating point je nach Standard auch noch weniger ist…
ohne dass ich das jetzt hier Seitenlang darlegen muss.
Für den Fall das Ihre Frage nach der Verteilung ernst gemeint war:
http://tinyurl.com/no7md97, gleich die erste Grafik
MfG
@ #32 H. Burowsky
Sie werden sicher erklären können, warum der Code für die SX-6 nicht auf der nachfolgende IBM lief. Mit Ihrem Wissen aus der „DDR“-Informatik.
Was waren der „DDR“-Meteorologe stolz darauf die Meßwerte seiner elektrischen Instrumente von einer Digitalanzeige auf der Professor Vise ablesen zu können.
Nun ja, auf der Meteor brauchte man sowas nicht mehr. Da konnte alles direkt gedruckt, geplottet und auf Band abgespeichert werden. Und selbstverständlich wurde es auf Monitoren angezeigt. Nicht so ein paar stromfressende Glühlampendigitalanzeigen. Ach ja, die Radiosonden wurden noch mit Röhren betrieben … . Aber das wußte der aus der „DDR“ nicht. Der durfte nämlich nicht von Bord wegen Fluchtgefahr.
@Christian Ohle
Sie haben mit Ihrem Einwand natürlich Recht. Es gibt Iterationsverfahren, da nimmt die Genauigkeit zu, weil unabhängig vom Startwert das Ergebnis konvergiert. Das Heron-Verfahren mit x_neu= 0,5*(x+Zahl/x) für die Quadratwurzel funktioniert ja deshalb, weil bei x=Wurzel(Zahl) keine Änderung von x_neu mehr eintritt. Mit anderen Worten, Wurzel(Zahl) ist der Attraktor für dieses Iterationsverfahren. Bei den Iterationsverfahren bezog ich mich auf Fälle, die Sie in #5 beschrieben haben und wo das Ergebnis nicht konvergiert.
„Unsinn, Sie brauchen gar kein Werkzeug weil gerade diese Algorithmen eine bestimmte Genauigkeit implizieren.“
Das steht doch überhaupt nicht im Widerspruch zu der Aussage, dass diese Werkzeuge existieren.
„Nun, und das wird Ihnen nicht gefallen, jedwede Klimasimulation basiert praktisch nur auf iterativen Funktionen deren Ergebnisse mit Grundrechenarten zusammen gerechnet werden. Dafür sind die Genauigkeiten exakt bekannt.“
Genau DAS meine ich mit einem „Werkzeug“! Ein Verfahren, mit dem Sie die numerische Genauigkeiten bestimmen können. Ich hätte auch Methode oder Formel sagen können. Sorry, vielleicht hatte ich mich zu undeutlich ausgedrückt und Sie hatten bei „Werkzeug“ andere Assoziationen.
„Die von Ihnen erwähnte Spielerei, Startvariablen minimal zu ändern, ist unter dem Gesichtspunkt der blanke Hohn.“
Äh? Es ist EINE gängige Methode, um die Stabilität von Ergebnissen von numerischen Iterationen. Sie würde auch bei der Heron-Formel funktionieren. Welches Problem haben Sie damit?
„Sicher werden solche Tests durchgeführt. Sie beweisen nur die Ungeheuerlichkeit mit denen in den Programmen manipuliert wurde.
Diese Programme, die die lustigen bunten Linien erzeugen, rein numerisch gar nicht möglich zu erzeugen ohne gezielte Manipulationen.“
Okay, haben Sie neben der Behauptung auch konkrete Belege, dass die Programme auf Manipulationen beruhen.
„Ich möchte darauf hinweisen, dass ich hier nur ein einfaches numerisches Problem von vielen betrachtet habe.“
Wo ich Ihnen auch vollkommen zugestimmt habe, dass dieses numerische Problem bekannt ist.
„Was wir aber brauchen sind die Quellen mit denen die lustigen Kurven erzeugt wurden.“
Der Open Source Code wird genau dazu verwendet, um die Kurven zu erzeugen. Es gibt auch Forschergruppen, die Ihren Programm Code komplett freigegeben haben, wie beispielsweise das National Center for Atmospheric Research (NCAR) in den USA.
@Thomas Heinzow, also ich habe gestern die 25 Jahre deutsche Einheit gefeiert. Sie auch?
#18: Christian Ohle
„Eine 64 Bit Zahl kann 2^64, also 18446744073709551615 verschieden exakte Werte repräsentieren.“
Falsch.
„Das sieht zunächst viel aus aber die exakten Werte verteilen sich hier in einem Bereich von +/- 10 ^ 308.
….
Es sollte aber vorstellbar sein wie dünn exakte Zahlen über den Bereich verteilt sind.“
Wie sind die Zahlen denn verteilt? Gleichmäßig oder nicht gleichmäßig? Könnte von Vorteil sein, dass zu wissen.
PS: Erste Antwort hatte leider eine falsch geschrieben Mailadresse.
#29: T.Heinzow
„Als ob es überhaupt Leute gibt, die in der Lage wären den vollständigen Programmcode – der übrigens maschinenspezifisch ist – zu verstehen und ihn daraufhin zu überprüfen, was denn der Code tatsächlich simuliert.“
Das entspricht dem Wissenstand diplomierter Soziologen mit Wissenstand Informatik Anfang bis Mitte der 1980er.
#18: Christian Ohle
„Eine 64 Bit Zahl kann 2^64, also 18446744073709551615 verschieden exakte Werte repräsentieren.“
Falsch.
„Das sieht zunächst viel aus aber die exakten Werte verteilen sich hier in einem Bereich von +/- 10 ^ 308.“
..
Es sollte aber vorstellbar sein wie dünn exakte Zahlen über den Bereich verteilt sind.“
Wie sind sie denn nun verteilt? Gleichmäßig oder gibt es Stellen, wo Genauigkeit größer wird?
@#28: Christian Ohle, zu „…mal ganz unabhängig von den Modellen und der prinzipiell mathematischen und physikalischen Unmöglichkeit.“
Und weiter? Dass apokalytisch tödliche CO2-Strahlung in den Modellen, bei Zunahme von CO2, bilanziert wird wie zusätzliche Solarstrahlung wird doch hier auf EIKE (und sonstwo) schon lange moniert.
Und was hat das bisher gebracht, ausser nix? Beide Seiten haben (wollen?!) sich m.E. nicht auf gegenseitig akzeptable Fakten (mögliche Schiedsrichter) verständigen, denn sie ziehen beide weiter ihr Ding durch. Na sowas.
MfG
S. Hader kriegt den Nullsatzpreis des Jahres:
„Wie gesagt, es gibt Klimamodelle, die als Open Source zur Verfügung stehen.“
Als ob es überhaupt Leute gibt, die in der Lage wären den vollständigen Programmcode – der übrigens maschinenspezifisch ist – zu verstehen und ihn daraufhin zu überprüfen, was denn der Code tatsächlich simuliert.
Nun ja, unser bester Nullsatzschreiber kann auch problemlos mit seiner Wonderdoofs-Maschine oder was immer er auch hat, die nc- und GRIB-Output-Dateien entschlüsseln und beliebige Datenreihen herausfiltern.
Sehr erheiternd der Tag nach dem 25. Volkstrauertag, an dem die „DDR“ 1.0, das Original, aufhörte zu existieren. Es lebe die „DDR“ 2.xxx!
Sehr geehrter Herr oder Frau Hader
Sie verstehen da wohl so einiges nicht:
“Durch Iterationsverfahren wachsen diese Ungenauigkeiten“
Im Gegenteil. Mit Iterationsverfahren können Sie sogar beliebige Genauigkeiten erzielen.
Denken Sie an elementare Iterationsverfahren wie die in Funktionen zur Berechnung von Wurzel, Sinus, usw.
Wir nutzen eine Vielzahl, auch sehr komplexer Verfahren, um im allgemeinen iterativ die Präzision zu verbessern.
Die Verfahren haben gemeinsam, dass es immer ein- oder mehrere klare Vergleichskriterien bzw.
Abbruchkriterien gibt.
“Das Gute ist, man hat Werkzeuge die numerischen Ungenauigkeiten… einzuschätzen”
Unsinn, Sie brauchen gar kein Werkzeug weil gerade diese Algorithmen eine bestimmte Genauigkeit implizieren.
Die gewünschten Genauigkeiten stellen quasi die Abbruchkriterien dar.
Nun basieren beim rechnen mit (ir)rationalen Zahlen aber praktisch alle Funktionen auf Iterationsverfahren bis auf Grundrechenarten.
Für die Grundrechenarten sind die Genauigkeiten aber sowieso exakt bekannt, vom verwendeten Zahlenformat und dem Prozessor definiert.
Es existieren diverse nicht rekursive Algorithmen um zBsp. über Integrale die Präzision zu verbessern – aber auch die haben eine klare Charakteristik.
Nun, und das wird Ihnen nicht gefallen, jedwede Klimasimulation basiert praktisch nur auf iterativen Funktionen
deren Ergebnisse mit Grundrechenarten zusammen gerechnet werden. Dafür sind die Genauigkeiten exakt bekannt.
Sie brauchen kein Werkzeug um abzuschätzen zu können welchen Wert ein Ergebnis nach Milliarden von Additionen noch hat.
Die von Ihnen erwähnte Spielerei, Startvariablen minimal zu ändern, ist unter dem Gesichtspunkt der blanke Hohn.
Die Ergebnisse sind dann sowieso Unsinn und den Grad der Unsinnigkeit zu bestimmen – ist Quatsch.
Sicher werden solche Tests durchgeführt. Sie beweisen nur die Ungeheuerlichkeit mit denen in den Programmen manipuliert wurde.
Diese Programme, die die lustigen bunten Linien erzeugen, rein numerisch gar nicht möglich zu erzeugen ohne gezielte Manipulationen.
Es ist ein Skandal ohne Ende, zu vergleich mit der Hockey stick Affäre.
Diesmal eben auf Software ebene, mal ganz unabhängig von den Modellen und der prinzipiell mathematischen und physikalischen Unmöglichkeit.
Ich möchte darauf hinweisen, dass ich hier nur ein einfaches numerisches Problem von vielen betrachtet habe.
Wir haben da noch zum Bsp. das Problem mit iterativen Verfahren deren Abbruchkriterien von anderen iterativen Zwischenergebnissen abhängen.
Das sollte bei derartigen Simulationsversuchen sogar der Normalfall sein.
Dort gibt es keine klaren Abbruchkriterien mehr. Dabei entstehen katastrophale Fehler die bewiesener Maßen auch nicht kalkulierbar sind.
Ein Beweis ist einfach: da es sich im allgemeinen um den Versuch handelt Lösungen für nichtlineare Gleichungssysteme zu finden
die mathematische gar keine haben usw. usw.
Das aber wie gesagt nur mal als ein Beispiel.
”es gibt Klimamodelle, die als Open Source zur Verfügung stehen.”
So was habe ich mir sogar schon mal zur Belustigung angesehen.
Was wir aber brauchen sind die Quellen mit denen die lustigen Kurven erzeugt wurden.
Nur so können wir den wissenschaftsgeschichtlich ungeheuren Betrug aufklären und beweisen.
Wir haben die Forschung bezahlt und bekommen nur die Ergebnisse zu sehen.
Die Ergebnisse, auf deren Basis politische Entscheidungen getroffen werden.
Die Ergebnisse einer Forschung sind aber WERTLOS ohne nachvollziehbare Quellen.
Die Quellen sind in unserem Fall die Source Codes der Programme.
MfG
Christian
Sehr geehrter Christian Ohle,
ich will Sie nicht veralbern. Ich versuche es mal vereinfacht auszudrücken; bei der Simulation physikalischer Systeme gilt es neben anderen Dingen auf zwei wesentliche Aspekte zu achten. Auf das Erste haben Sie schon mehrfach hingewiesen, die Ungenauigkeiten der numerischen Mathematik. Durch Iterationsverfahren wachsen diese Ungenauigkeiten der Variablen. Alles soweit richtig, was Sie sagen. Das Gute ist, man hat Werkzeuge die numerischen Ungenauigkeiten in ihrer Größenordnung einzuschätzen. Ein einfaches Mittel ist die Startvariablen minimal zu ändern und die Auswirkung der Ergebnisse nach x Iterationsschritten zu vergleichen.
Der zweite wichtige Aspekt ist, die Simulation physikalischer Systeme wie auch des Klimas benötigen als Startparameter reale gemessene Werte. Die sind wesentlich ungenauer als die Maschinengenauigkeit von Floatingzahlen. Da ist man schon froh, einige wenige sichere Dezimalstellen zu haben. Das trifft auch auf die Klimadaten zu.
Was ich damit sagen will, die Probleme und Werkzeuge sind schon lange bekannt. Eigentlich ist das Basiswissen, was beispielsweise Informatik-Studenten in Numerik vermittelt bekommen. Nun würde ich nicht für alle Experten die Hand ins Feuer legen, dass sie mit der Numerik immer angemessen umgehen und die Werkzeuge richtig anwenden. Genauso falsch ist es aber auch zu behaupten, alle Experten seien quasi korrupt oder nicht fähig, die Werkzeuge zu benutzen.
„Ist ja auch Egal, solange das Geld fließt und keiner es nachprüfen kann oder?“
Wie gesagt, es gibt Klimamodelle, die als Open Source zur Verfügung stehen.
„PS. Ein Schmetterling kann auch einen Sonnensturm auslösen, eine Eiszeit und eine Supernova!!!“
Das halte ich jetzt doch für stark übertrieben. Die Chaostheorie besagt nicht, dass alles möglich ist.
MfG
S.Hader
@24: Katrin Meinhardt
Hallo Frau Meinhardt
„Die heiligen Hallen der Wissenschaft sind unterwandert … durch die Lügen“
So ist es.
Gruß Cristian
Und bitte nicht böse sein auf Programmierer
Es gibt überall gute und schlechte Menschen
@16 S.Hader
”wozu braucht man bei der Beschreibung und Simulation von physikalischen Systemen eine exakte Arithmetik?…
Einige Dutzend Nachkommastellen von Pi reichen aus, um sämtliche Größendynamiken im Weltraum abzubilden.”
Sie wollen mich veralbern oder?
Im technischen Bereich haben wir schon bei einfachen statischen Systemen riesen Probleme mit der Präzision.
Das ist dann wohl sehr bezeichnend für die Art Wissenschaft die Sie offensichtlich vertreten.
Ist ja auch Egal, solange das Geld fließt und keiner es nachprüfen kann oder?
Einfach Mittelalterlich, Sie und Ihre Experten die alles Prüfen und doch Quatsch berechnen.
MfG
Christian
PS. Ein Schmetterling kann auch einen Sonnensturm auslösen, eine Eiszeit und eine Supernova!!!
Wenn Sie schon die Chaostheorie als solche akzeptieren dann sollten Sie sich auch über die Konsequenzen klar werden.
Wir haben keine isolierten Systeme in diesem Universum.
#18: Verehrter Herr Christian Ohle, geschrieben haben Sie, Zitat:
„Damit nun will man Klimaentwicklung über die nächsten Jahrhunderte simulieren?
[…]“
a.
Für mich, sehr viel wichtiger zu wissen ist, wie kommen diese Typen, diese Heinis, dazu, dies wäre überhaupt (!!) möglich? Bevor man solch ein Vorhaben unternimmt, setzt man sich vorher hin und sinniert, denkt, kritisiert, und philosophiert, fragt also die Weisheit.
b.
Was für ein Weltbild setzt das voraus? Damit so etwas möglich sein sollte?
c.
Java ist eine streng typisierte Sprache. Eine Programmiersprache selbst, ist hochkomplex.
d.
Die (h)eiligen „Hallen der Wissenschaft“ sind unterwandert, infiltriert worden, durch die Lügen.
e.
Irrational ist es, das Wetter für ein Datum zu simulieren, wenn derjenige dann überhaupt nicht mehr da sein kann, zwecks Verhaftung und Verurteilung.
Mit sehr freundlichen Grüßen
Es ist (wohl wieder) die Macht, das Geld, die Gier, der Neid. Nichts Neues. Hochschule für Intrigen.
@ #18 Chr. Ohle
„Selbst wenn es ein Modell gäbe, dass die physikalische Realität hinreichend genau beschreiben würde.“
Jeder weiß, daß das bei Systemen mit letztndlich unendlichen Freiheitsgraden nicht geben kann.
Die Hypothese der GCM (Global Circulation Models) beruht auf der Annahme, daß dann, wenn ein Modell eine korrekte stabile Statistik (bei konstanten externen und internen Inputs) über einen Zeitraum von X Jahren Modellaufzeit liefert, die Ergebnisse bei Änderung der externen Inputs (Solarstrahlung) oder der internen Inputs (Aerosole, Spurengase) korrekt sind.
Leider läßt sich die Hypothese mangels zuverlässiger Messdaten aus der Vergangenheit nicht an der Realität überprüfen.
Nach Angaben der Weltorganisation für Meteorologie (WMO) besteht das heutige globale hauptamtliche Beobachtungsnetz aus über 10.000 automatischen und bemannten Bodenstationen, etwa 1000 Radiosondenstationen, circa 7000 Bordstationen und ca. 1100 Bojen (um die 100 davon sind ortsfest). Hinzu kommen mehrere Hundert Wetterradare, 15 operationelle geostationäre sowie 9 polarumlaufende Satelliten (Stand: Februar 2014)
Neben den hauptamtlichen Bodenwetterstationen gibt es aber noch zahlreiche nebenamtliche Messsysteme. So liegt die Anzahl aller offiziell betriebenen Wetterstationen schätzungsweise zwischen 20.000 und 25.000.
Quelle: http://tinyurl.com/of2dtj3
Deshalb gilt für diese Modelle das gigo-Prinzip. Kann man auch nachweisen, wenn man diese Dateien auslesen kann:
http://tinyurl.com/q7df87t
Der Normalbürger kann das nicht. Und deshalb findet auch keine Kontrolle statt. So wie bei VW jetzt, wo das kleine Programm irgendwo in einer Subroutine versteckt war.
Nochmal als Ergänzung an Christian Ohle, ich würde Ihnen nicht prinzipiell widersprechen. All das was Sie da ansprechen ist den Experten, die sich berufsmäßig mit dem Thema befassen, bekannt. Genau aus dem Grund wurden Werkzeuge entwickelt, um die numerische Stabilität von Simulationen zu testen. Eine ganz einfache Methode ist es beispielsweise, Eingangsgrößen minimal zu ändern (in der Größenordnung der Maschinengenauigkeit von Floating-Zahlen) und zu beobachten, inwieweit das Einfluss auf das Endergebnis bzw. Rechenverlauf hat.
Die Leute, die sowas täglich machen und damit ihr Geld verdienen, drücken nicht nur einfach ein Knöpfchen und vertrauen den Ergebnissen blindlinks, die da rauskommen, davon können Sie ruhig ausgehen.
@#17: Albert Kass, zu „Im Sinne eines SW-Tests für ein physikalisches Modell: ein klares Nein, da man nicht wissen kann, ob das Modell selbst unzutreffend ist oder die Software Fehler aufweist.“: d’accord,
trifft ja auf Modellrechnungen i.A. zu die Prophezeiungen der nicht-triviale Art machen wollen. Daher die Frage nach Software Verification and Validation, mit der m.E. bisher noch jedes (Mammut-)Projekt entweder abgeschossen wurde oder (irgendwie, €doch$ €noch$) erledigt werden konnte.
Zu „agressiv“ Nö, wer so einen Schuh erfindet und dann ggfs. auch noch anzieht ist selber Schuld. Fragen in Foren mit kurzlebigen Fäden dürfen die Frage als Motiv haben.
MfG
@Christian Ohle, #14: „Aber wie Sie richtig schreiben: wir kommen ja an die Programmcodes nicht ran.“
Es gibt eine Reihe von Open Source Klimamodellen und Simulationen. Einfach mal danach googeln.
#10 Alwin Bruno
„handelt es sich bei Quadratwurzeln um einen Kettenbruch der sich mit rationalen Zahlen abbilden lässt.“
Also bitte, als Kettenbruch: [1;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2…unendlich]
Jeder periodische Kettenbruch ist eine quadratische irrationale Zahl und umgekehrt
Super, also dann rechnen wir mal fleißig 🙂
MfG
(Spaß, bringt zwar nichts aber danke für Ihre Reaktion)
Vielleicht für Interessierte noch ein paar Fakten:
Die Zahlen mit denen in den Klimamodellen gerechnet wird sind mit Sicherheit 32- und/oder 64 Bit floating point Zahlen.
Dies aus praktischen Gründen und weil höhere Präzision das grundsätzliche Problem auch nicht lösen würde.
Eine 64 Bit Zahl kann 2^64, also 18446744073709551615 verschieden exakte Werte repräsentieren.
Das sieht zunächst viel aus aber die exakten Werte verteilen sich hier in einem Bereich von +/- 10 ^ 308.
Also 1000000000000000000000000000000000000000000000000000000000000000000000000000000000………..
ich erspare uns hier die exakte Zahl mit den 308 Stellen aufzuschreiben.
Es sollte aber vorstellbar sein wie dünn exakte Zahlen über den Bereich verteilt sind.
Die überaus meisten Werte und Zwischenergebnisse mit denen gerechnet wird sind also Näherungen,
nur nahe am nächsten exakten Wert.
Damit nun will man Klimaentwicklung über die nächsten Jahrhunderte simulieren?
Die Klimamodelle bei denen nun Milliarden solcher Zahlen milliardenfach immer und immer wieder
mit einander addiert, multipliziert, subtrahiert, dividiert (und schlimmeres) werden müssen?
Bei jeder einzelnen Operation vergrößern sich nun aber fast immer die Abweichungen…
die Fehler addieren und potenzieren sich, die Fehler werden immer größer…
schon in kürzester Zeit haben die Zwischenergebnisse nichts mehr mit der Modell-Realität zu tun…
absurdes Vorhaben
Ich will ja nur Zeigen:
Selbst wenn es ein Modell gäbe, dass die physikalische Realität hinreichend genau beschreiben würde.
(Es ist mir schon klar, das dies nach Stand der (echten) Wissenschaft ausgeschlossen ist)
Wir könnten trotzdem nichts damit anfangen, jedenfalls nicht die zukünftige Entwicklung berechnen.
Das kann nur Mojib Latif. (Bei dem Preisgeld könnte ich es allerdings sicher auch.)
#13 Alwin Bruno
Herr Bruno, wenn Sie substantielle Anmerkungen zu meinem Beitrag haben, bin ich gerne bereit, diese mit Ihnen zu diskutieren. Einen aggressiven Tonfall vermag ich zu tolerieren, persönliche Angriffe hingegen nicht.
Zu Ihren Anmerkungen:
###
1. Sie keinen sich mit Software Verification and Validation nicht aus, oder? es sieht aus wie abgetippt, dürfen wir die Quelle erfahren. Danke.
###
Ich denke, nach mehr als 30 Jahren bezahlter Tätigkeit im Bereich SW-Entwicklung bei internationalen Beratungsunternehmen kann ich schon ein wenig beurteilen, was machbar ist und was nicht. Im Übrigen ist es nicht meine Art, irgendwo etwas abzuschreiben.
###
2. Buchhaltungsprogramme: haben physikalische Modelle kein Balance zu berechnen? dann gelten dieselben Vorschriften, auf Punkt und Komma.
###
Ich verstehe nicht, was Sie hier meinen. Aber soweit mir bekannt ist, werden mit physikalischen Modellen kein Kontostände berechnet. Oder meinen Sie mit „balance“ etwas Anderes?
###
3. ausser den erwähnten Grenzfällen, ist die Realität kein Testfall?
###
Im Sinne eines SW-Tests für ein physikalisches Modell: ein klares Nein, da man nicht wissen kann, ob das Modell selbst unzutreffend ist oder die Software Fehler aufweist. Wenn Sie z.B. ein Modell hätten, das die Temperaturentwicklung der letzten 100 Jahre berechnen soll und das Ergebnis stimmt mit den tatsächlichen Messwerten in diesem Zeitraum überein, so ist keineswegs sicher, dass das Modell stimmt. Eine fehlerhafte SW-Implementierung könnte trotz eines unzutreffenden Modells ein scheinbar korrektes Ergebnis liefern.
Einfacher scheint mir der Fall der aktuell verfügbaren Klimamodelle zu sein. Deren Ergebnisse haben zumindest für die vergangenen 18 Jahre nichts mit der Realität zu tun.
@Christian Ohle: „Exakte Arithmetik ist nur begrenzt möglich.“
Umgedereht könnte man die Frage stellen, wozu braucht man bei der Beschreibung und Simulation von physikalischen Systemen eine exakte Arithmetik? Einige Dutzend Nachkommastellen von Pi reichen aus, um sämtliche Größendynamiken im Weltraum abzubilden. Ich weiß, in der Schule und im Studium gab es immer ein paar „Experten“, die physikalische Größen besonders genau ausrechnen wollten, aber die von der Eingangsgröße gerade mal zwei Zehnerstellen bekannt waren. Spätestens in der beruflichen Praxis lernt man recht schnell sich einen sinnvollen Pragmatismus anzueignen.
„Es wird also geschätzt was das Zeug hält. Das ist schon deswegen Katastrophal weil bei den nichtlinearen Systemen kleinste Abweichungen in den Eingangsdaten zu völlig verschiedenen Endergebnissen führen.“
Im Englischen wird der Ausdruck „estimation“ für alle Prozesse verwendet, um nicht den exakten Wert sondern was dem sehr nahe kommt zu bestimmen. Schätzen hat in der deutschen Umgangssprache eine recht abfällige Bedeutung, wird aber in der Wissenschaft als wichtiges Werkzeug angesehen, weil man da sehr genau weiß, dass die exakte Bestimmung von physikalischen Größen nicht möglich ist. Diese Exaktheit hätte auch keine praktische Bedeutung.
Sie haben vollkommen Recht, kleinste Abweichungen in den Eingangsdaten bei nichtlinearen Systemen können zu den unterschiedlichsten Ergebnissen führen. Deshalb gehört es zum täglichen Brot derjenigen, die sich berufsmäßig mit solchen Fragen beschäftigen, die Stabilität solcher Endergebnisse zu bestimmen.
„Also, mal ganz abgesehen von der Unsinnigkeit beim Klima irgendetwas simulieren zu wollen. Es ist ja schon mathematisch soweit unsinnig wenn die Chaostheorie stimmt (wovon ich natürlich ausgehe).“
Die Chaostheorie lässt sich nun mal nicht undifferenziert auf alle wissenschaftlichen Fragestellungen gleichermaßen übertragen. Um nur ein Beispiel zu nennen, es ist ein himmelweiter Unterschied, ob ich eine Zustandsgröße zu einem bestimmten Zeitpunkt vorhersagen will oder die mittlere Zustandsgröße über ein größeres Zeitintervall. Nehmen Sie ein Doppelpendel. Man hat keine Chance kurz nach dem Anschubsen die genaue Position zu einem Zeitpunkt t zu bestimmen. Der Vorhersagefehler ist aber deutlich geringer, wenn es darum geht, die mittlere Position innerhalb eines Zeitintervalls zu bestimmen. Das chaotische Verhalten in den Wetterdaten streitet niemand ab, ein 30-Jahres-Mittel reduziert hingegen dieses chaotisches verhalten erheblich. Oder mit anderen, einfacheren Worten ausgedrückt, ein Schmetterling kann zwar einen Orkan auslösen, aber keine neue Eiszeit.
Klima- und auch Wirtschafts- Rechenmodelle kranken grundsätzlich dran, dass die eingegebenen Berechnungsparamater unvollständig sind und dass diese Eingabe- Parameter, soweit sie überhaupt quantifizierbar sind, sich außerdem auch noch sehr oft im Verlaufe der Zeit gegenseitig beeinflussen.
Partielle Ableitungen und die Ceteris-paribus-Klausel müssen deshalb hier wie dort wohl immer ein ungenügender Versuch bleiben, dem abzuhelfen.
Hinweis auf die zufällig ergoogelte :
Physikerin und Philosophin Rafaela Hillerbrand:
http://tinyurl.com/ofj5fj8
(@ EIKE- Team : „Warum in die Ferne schweifen? Sieh, das Gute liegt so nah“ 🙂 )
Sie unterscheidet zwei verschiedene Arten von Unsicherheiten, die in Klimamodellen enthalten sind:
“Auf der einen Seite gibt es eine Unsicherheit in Bezug auf die Werte darin eingehender Parameter.
Auf der anderen Seite treten konzeptuelle Unsicherheiten auf, die ihren Ursprung in der nicht angemessenen Modellierung
kausal relevanter Mechanismen haben.
Während man erstere Unsicherheiten durch den Einsatz von Monte-Carlo-Simulationen relativ problemlos quantifizieren kann,
ist eine genaue Abschätzung im Fall der konzeptuellen Unsicherheiten laut Hillerbrand nicht möglich. Dies liegt daran, dass eine Abschätzung von Unsicherheiten hier zentral auf der jeweils gängigen Forschungspraxis beruht, das heißt auf dem, was innerhalb der Forschergemeinschaft implizit geteilt und
vorausgesetzt wird.“
Quelle :
http://tinyurl.com/okcupm4
#12: Albert Kass
Nun, zunächst einmal unterstützen heutige Prozessoren noch keine 128-bit float Arithmetik.
Das sind alles Softwarelösungen, langsam und ehr ungeeignet für physikalische Probleme.
Sie meine übrigens 128-bit dezimal Zahlen wenn Sie von 33 Stellen Genauigkeit sprechen.
Das ist etwas ganz anderes.
Es geht dabei darum um wenigstens im Dezimalbereich fehlerfrei rechnen zu können, also Finanzen usw.
Binäre floating point Zahlen können nämlich schon einfache Dezimalzahlen nicht mehr exakt darstellen:
1.1 wird 1.10000002384185791015625 bei 32 bit floating point
1.1 wird 1.100000000000000088817841970012523233890533447265625 bei 64 bit floating point
Aber selbstverständlich können sie mit binären floating point Zahlen beliebiger Genauigkeit rechnen.
Und selbstverständlich reichen die Genauigkeiten für die meisten physikalisch technischen Probleme aus.
Es bleiben freilich Schätzungen aber beliebig nahe an der Realität.
Es gibt aber Probleme, insbesondere wenn es um Simulationen dynamischer Systeme geht,
wo keine begrenzte Genauigkeit ausreicht um Ergebnisse nahe an der Realität zu berechnen.
Eingangswerte sind nicht mehr proportional zu den Ergebnissen.
Kleinste Toleranzen führen zu jeweils total verschiedenen Ergebnissen.
Dazu braucht es noch nicht einmal ein chaotisches System.
Das passiert schon wenn im Modell, in den Algorithmen Entscheidungen getroffen werden müssen,
die auf Vergleich solcher ungenauen Zahlen beruhen.
Wir können bspw. noch nicht einmal exakt berechnen ob ein Punkt auf, in oder außerhalb eines Kreis liegt.
Das geht nicht einmal mal mit rationalen Zahlen weil die Wurzeln schon meist irrational sind.
Eine Fehlschätzung führt aber zu katastrophal anderen Ergebnissen wenn es um Simulationen geht.
Höhere Genauigkeiten verbessern die Situation nicht wirklich denn es werden einfach nur
genauere Zahlen verglichen und es besteht trotzdem keine Sicherheit ob der Vergleich stimmt.
Man nennt das übrigens Epsilon Problem und in dem Zusammenhang von der Robustness eines Algorythmus.
Das wird jetzt hier aber zu komplex.
Würde man die Algorithmen in den Klimamodellen einmal unter diesem Gesichtspunkt untersuchen.
Es gäbe mit Sicherheit ein erschreckendes Ergebnis.
Dieses Ergebnis würde mit Sicherheit zeigen das alle Ergebnisse,
die lustigen bunten aufsteigenden Kurven, immer schon nur mit Manipulation zustande kamen.
Aber wie Sie richtig schreiben: wir kommen ja an die Programmcodes nicht ran.
MfG
@#12: Albert Kass, zu „Ich sehe die wesentliche größere Herausforderung im Test … […] … dummerweise, außer für einige Grenzfälle, gar nicht weiß, was am Ende herauskommt.“
1] Sie keinen sich mit Software Verification and Validation nicht aus, oder? es sieht aus wie abgetippt, dürfen wir die Quelle erfahren. Danke.
2] Buchhaltungsprogramme: haben physikalische Modelle kein Balance zu berechnen? dann gelten dieselben Vorschriften, auf Punkt und Komma.
3] ausser den erwähnten Grenzfällen, ist die Realität kein Testfall?
Fragen, Fragen, Fragen, ich vermute ‚mal Ihre Quellen sind zu weit weg vom Schuss. Hätten Sie vielleicht einen Computer Sciences / Complexity of Computation Lehrstuhlinhaber anzubieten der darüber veröffentlich hat?
MfG
P.S. NASA/JPL hat Planetary and Lunar Ephemerides herausgebracht welche über etliche Jahrtausende getestet wurden anhand von Beobachtungen und Rückmeldung. Ist halt nicht so esoterisch an Unwissenheit ausgerichtet wie talentfreie Amateur-Programmierer welche über sich behaupten: „ich“ kann es nicht also kann es keiner /sarc
#5 Christian Ohle
Ihren Ausführungen zur Genauigkeit von Computerberechnungen kann ich nicht zustimmen. Heutige Prozessoren und Programmiersprachen bieten, wenn man davon Gebrauch machen will, 128-bit floating point Arithmetik. Damit erreicht man, dezimal gesprochen, bis zu 33 Stellen Genauigkeit. Dies ist in der Regel für die Abbildung physikalischer Prozesse völlig ausreichend.
In der Vergangenheit kam es häufig zu Problemen bei Verwendung von 32-bit floating point Arithmetik, hier insbesondere bei Berechnungen mit dünn besetzten Matrizen, was häufig aufgrund von Rundungen zu teilweise beliebigen Ergebnissen führte.
Ich sehe die wesentliche größere Herausforderung im Test der Programme, die häufig sehr umfangreich und komplex sind. Hier Testfälle zu definieren, mit denen die korrekte Funktion des Programms in allen Bereichen überprüft werden kann, ist wegen Datenmengen und Programmlaufzeiten de facto nicht möglich. Das sind eben keine Buchhaltungsprogramme, bei denen man leicht prüfen kann, ob eine Buchung von Konto A nach Konto B funktioniert hat. Bei Modellen hat man es da schon etwas schwieriger, da man ja dummerweise, außer für einige Grenzfälle, gar nicht weiß, was am Ende herauskommt.
Ein wirkliches Problem sehe ich eher in der völligen Intransparenz solcher Programme, um z.B. Klimamodelle zu rechnen. Auch wenn die Physik und Mathematik dieser Modelle in Veröffentlichungen dargelegt werden, so sagt das doch nichts darüber aus, ob das als Programm korrekt umgesetzt wurde. Mir ist nicht bekannt, dass z.B. das PIK den Programmcode seiner Modelle offenlegt. Mithin ist eine unabhängige Prüfung gar nicht möglich.
Sehr geehrter Herr Ohle #5
Schön und treffend, Ihre Analyse. Aber, Es wird eine 4(Vier schaffen das) zum radizieren vorgelegt.
Also die Probleme(die keine waren, aber politisch herbeigeredet wurden)werden als lösbar definiert.(Luftnummern-Stromspeicherung) z.B. )
@Christian Ohle, zu „Beispiel Wurzel 2 = 1.414…. unendlich“:
Ohne Ihren guten Kommentar schmälern zu wollen handelt es sich bei Quadrawurzeln um einen Kettenbruch der sich mit rationalen Zahlen abbilden lässt. Die Unendlichkeit ist sowieso nur eine akademische Schamanen Erfindung die bei physikalischer Beobachtung in Naturwissenschaften scheitert (ja auch auch beim Auslösungsvermögen von Hubble Photoshop Bildern).
B.t.w. alle Dezimalstellen-Eingaben sind fehleranfällig, lassen sich aber in der Praxis in den Griff bekommen wenn Länge der Ausgabe-Form = Länge der Eingabe-Form umgewandelt wird.
Rundungsfehler betreffen auch Unternehmens-bilanzen, speziell bei Tochtergesellschaften in Hochinflationswährung. Aber auch da gibt es Methoden um Null-Komma-Nix Rundungsfehler korrekt in den Griff zu bekommen.
Nur die Klimamodellierung (so wie alle Öko*-Modelle) nimmt das überhaupt nicht ernst, ganz im Gegenteil, denn die Prophezeiungen werden als nächstes ja immer wieder kassiert /nicht-sarc
Wird Operations Research überhaupt noch gelehrt?
MfG
#5: Verehrter Herr Christian Ohle, sofern ich Sie nicht falsch verstanden haben sollte,
doch wurde es, in der Vergangenheit, entweder dieses Jahr, oder dasjenige davor, von mindestens zwei Menschen. Einer davon unser Hausheiliger (T. Heinzow), der andere wohl der verehrte und geehrte Herr Alwin Bruno. Bzgl, der Präzision von albernen Maschinen, die nur zwei Buchstaben kennen (1,0). Wirklich albern, was für Amöben, diese Maschinen. Schlimmer. Viel schlimmer. Programmierer wissen das.
Mit sehr freundlichen Grüßen
P.S.: Das ist und soll keine (!) Kritik an Ihrem interessanten Beitrag (sein).
#7: Chris Frey sagte am Donnerstag, 01.10.2015, 19:47:
„Ich möchte vor allem den konstruktiven … Tenor … hervorheben.“
Es gab auch bereits beim Original-Artikel auf WUWT jede Menge konstruktive Kommentare, z.B. von Eschenbach, Svalgaard, Stokes. Der Tenor war allerdings, dass Evans sich da irrt …
Hallo Herr Kass #3,
auch von mir vielen Dank! Ohne das Adjektiv ,partielle‘ hätte ich auch Ableitungen geschrieben, nur leider kann ich mit darunter wenig vorstellen.
Ich möchte vor allem den konstruktiven und fast wohlwollenden Tenor Ihrer zutreffenden Anmerkung hervorheben.
Chris Frey, Übersetzer
Ach ja, da war ja noch der dumme Spruch:
‚Wir machen die Modelle und Simulationen ja nur um die Probleme besser verstehe zu könne.‘
Kam glaub ich von Bäcker und Fischer.
Gut, verstanden haben Sie es immer noch nicht aber kosten tut es und Milliarden.
Bei aller Diskussion über die Unsinnigkeit der Klima Simulationen wurde eines noch nie angesprochen:
Die Computer rechnen nur mit begrenzter Genauigkeit.
Jeder kennt es vom Taschenrechner, die Anzahl der Dezimalstellen ist begrenzt.
In der Tat rechnen die Computer intern mit einer begrenzten Zahl von Stellen wenn auch binär und nicht dezimal.
Der Computer kann daher auch nur schätzen. Exakte Arithmetik ist nur begrenzt möglich.
Man kann mit Rationalen Zahlen rechnen was zwar extrem langsam ist, jedoch absolut präzise Ergebnisse liefern kann. Das funktioniert aber nur für einfache Operationen wie +, -, *, /
Funktionen wie Wurzel, trigonometrische Funktion etc. liefern im allgemeinen nicht rationale Zahlen.
Beispiel Wurzel 2 = 1.414…. unendlich, und das lässt sich nicht exakt durch einen Bruch darstellen.
Nun sollte es schwierig sein ein physikalisch basiertes Klimamodell aufzustellen das mit Grundrechenarten auskommt. Es wird also geschätzt was das Zeug hält.
Das ist schon deswegen Katastrophal weil bei den nichtlinearen Systemen kleinste Abweichungen in den Eingangsdaten zu völlig verschiedenen Endergebnissen führen.
Aber egal, selbst wenn alle Eingangs- oder Messdaten fehlerfrei wären:
Um in die Zukunft zu rechnen muss man iterativ immer wieder die ohnehin fehlerbehafteten Ergebnisse als Eingabe verwenden. Fehler summieren sich dabei auf und egal mit wie vielen Stellen nach dem Komma gerechnet wird, der Fehler wird dramatisch.
Also, mal ganz abgesehen von der Unsinnigkeit beim Klima irgendetwas simulieren zu wollen.
Es ist ja schon mathematisch soweit unsinnig wenn die Chaostheorie stimmt (wovon ich natürlich ausgehe).
Mit der heutigen Rechentechnik, und das ist keine Theorie, ist es einfach nicht machbar.
Das ist allerdings lange bekannt, mindestens seit, Lorenz, Mandelbrot, Feigenbaum etc.
Alle die so etwas postulieren wie etwa Mojib Latif – alles Spinner, Dummköpfe oder einfach nur Betrüger.
In der Differential- und Integralrechnung der Mittelstufe des (ehemaligen klassischen) Gymnasiums wurde gelehrt, differenzieren bzw. integrieren kann man nur stetige Funktionen.
Bereits die Zustandsgleichungen von chemischen Stoffen wie Wasser sind unstetige Funktionen beim Phasenübergang. Energieflüsse, auf die es bei der CO2 Frage ankommt, können daher grundsätzlich nicht mittel Differential- und Integralrechnung a priori berechnet werden, sondern hier sind stoffspezifische Messreihen erforderlich, die man dann in engen Grenzen in empirische Gleichungssysteme übertragen kann.
Davon völlig losgelöst, rechnet die Meteorologie und die Klimatologie mit dem zum Beispiel für alle chemischen Stoffe der Erdoberfläche mit dem für Fixsterne gültigen Modell des „Schwarzen Strahlers“.
Es ist nicht nur die Mathematik, die falsch ist, sondern es sind die elementaren Grundlagen, die falsch sind“
Dr. Gerhard Stehlik, Hanau (Google findet mich!)
Hallo Herr Frey,
ich meine, die korrekte Übersetzung für „derivatives“ in diesem Zusammenhang wäre wohl „Ableitungen“.
Leonard Euler hat 40 Jahre vergeblich versucht, die Mondbahn im Schwerefeld von Erde und Sonne, anhand von Newtons Gleichungen zu berechnen und ist gescheitert. Ein simples Problem, im Vergleich zum Klima. Poincaré hat dann mathematisch bewiesen, dass selbst das eingeschränkte Dreikörperproblem nicht exakt lösbar ist. Es müssen erst die passenden Anfangsbedingen gefunden werden. Ergo: Mit dem Klimamodellen kann man alles ausrechnen, auch das Alter von Franz Beckenbauer.
„Partielle Differentiale* abhängiger Variablen sind eine ,Wild Card‘ – manchmal könnte dabei eine ordentliche Schätzung herauskommen, aber in anderen Fällen wird nur Unsinn erzeugt, und bedrohlicherweise gibt es keinen effektiven Weg, dies herauszufinden.“
Genau dies ist das Problem aller Klimamodelle. Es gibt nicht nur keinen effektiven Weg, es gibt übehaupt keinen Weg, dies heraus zu finden. Alle Klimamodelle berechnen nur die Annahmen eines Klimawissentschaftlers. Ein Computermodel kann niemals mit nicht linearen Faktoren ein „richtiges“ Ergebnis produzieren.