Also was gefällt uns nicht an diesen jüngsten Erkenntnissen von Kemp and Michael Mann?
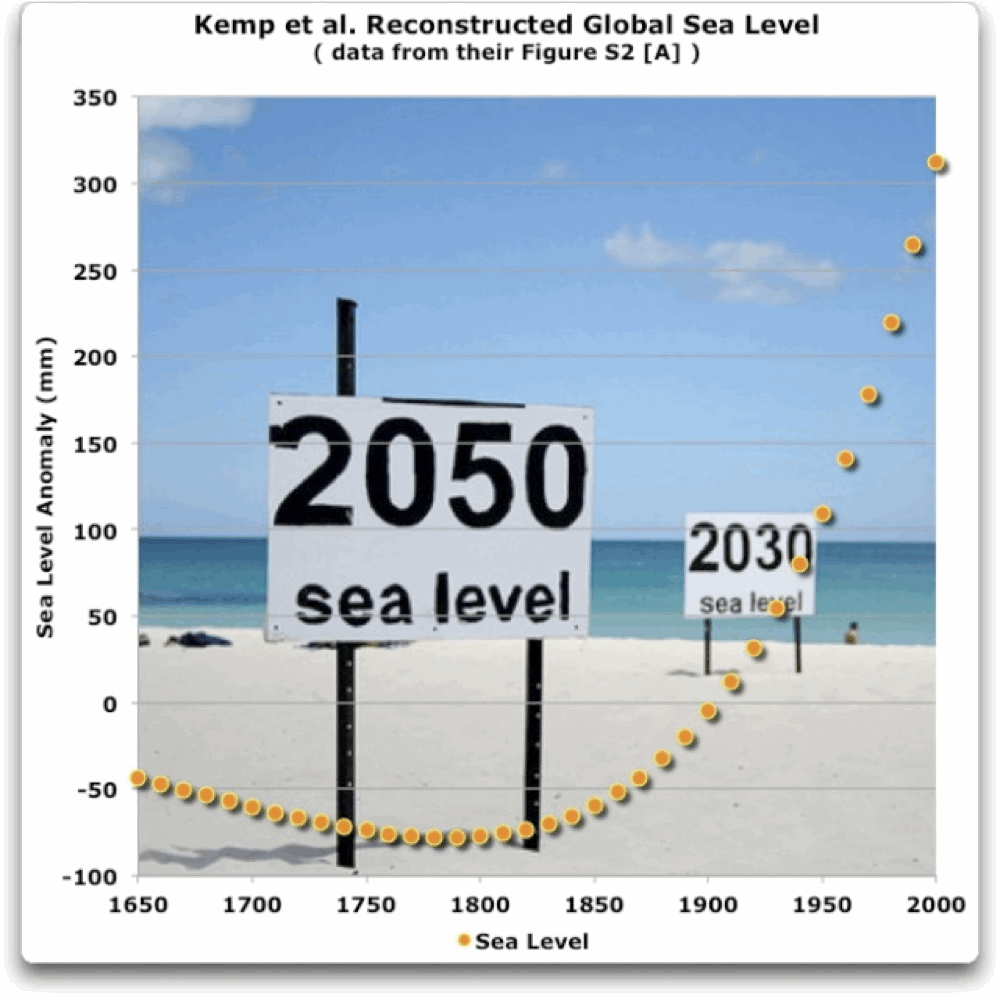
Figure 1. Kemp Fig. S2 (A) (Zur Quelle)
Ich habe den Teil der Grafik von 1650 weiter digitalisiert, um ihn mit jüngeren Beobachtungen zu vergleichen. Abb. 2 zeigt die Ergebnisse:
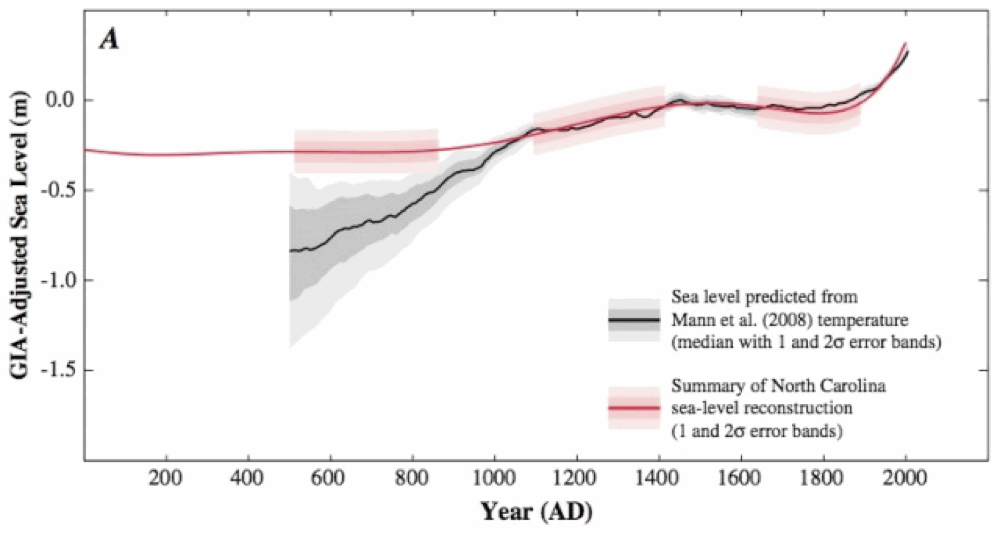
Abb. 2. Der von Kemp 2011 rekonstruierte Anstieg des Meeresspiegels, 1650-2000
Zunächst erscheint merkwürdig, dass sie behaupten, es hätte global ein Meeresspiegelanstieg von 200 mm in den vergangenen fünfzig Jahren (1950-1999) gegeben. Ich kenne niemanden sonst, der das behauptet. Church and White schätzen den Anstieg von 1950-2000 auf 84 mm, und Jevrejeva sagt 95 mm. Also, ihre Rekonstruktion beträgt mehr als das Doppelte der allgemein akzeptierten Schätzungen.
Das nächste Problem zeigt sich, wenn man die Rate des Anstiegs betrachtet. Abb. 3 zeigt die Ergebnisse aus der Kemp (2011) Studie, zusammen mit dem durchschnittlichen Meeresspiegelanstieg wie von Jevrejeva und Church & White aufgrund weltweiter Pegelanzeigen geschätzt.
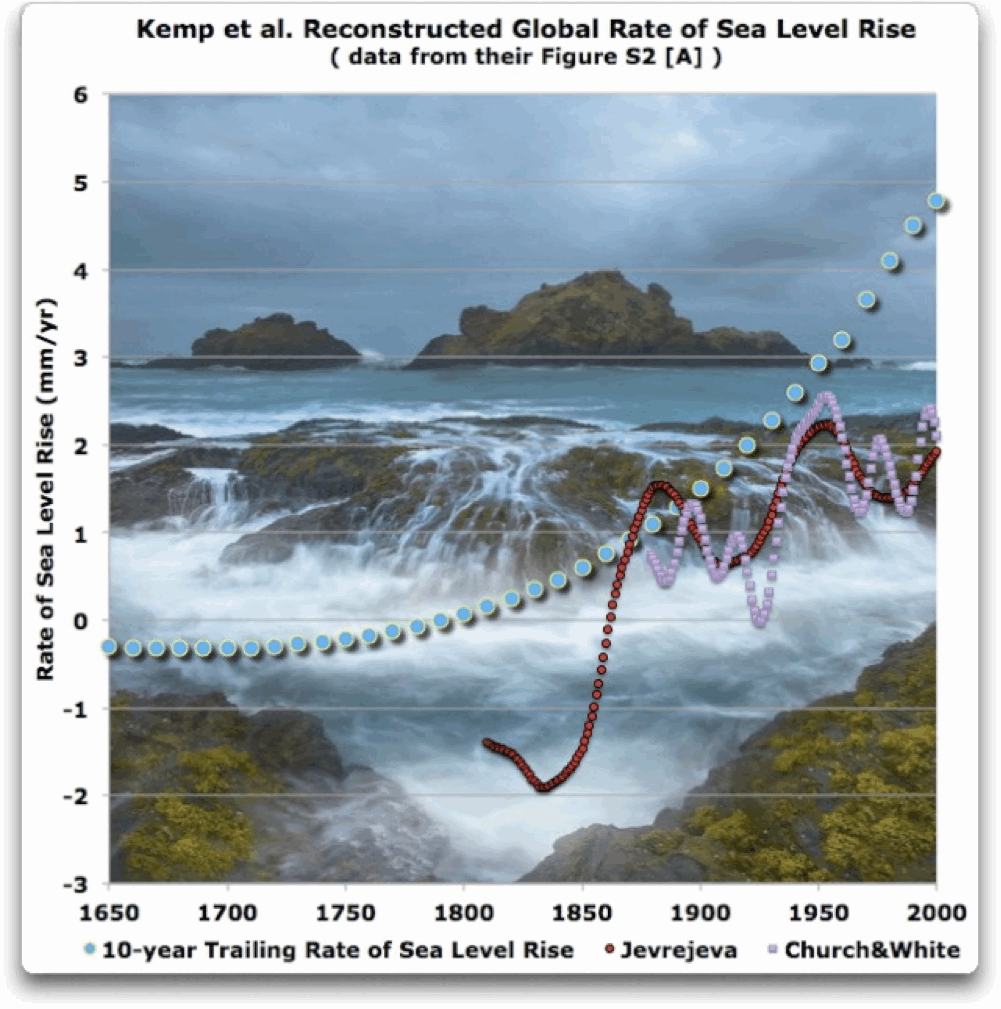
Abb. 3. Die von Kemp 2011 rekonstruierte Rate des globalen Meeresspiegelanstiegs von 1650-2000. Dazu die Beobachtungen von Jevrejeva (rote Kreise) und Church and White (violette Quadrate).
Kemp et al. sagen, dass die globale Rate des Meeresspiegelanstiegs seit 1870 ständig höher geworden sei, dass sie 1950 mehr als 3 mm pro Jahr betragen und seitdem ständig zugenommen hätte. Im Jahre 2000 wären es fast 5 mm/Jahr gewesen.
Jevrejeva und Church & White dagegen sagen, dass sie niemals über 3 mm/Jahr gelegen hätte und dass sie im zeitlichen Verlauf rauf und runter ginge. Im Jahre 2000 hätte sie ~ 2 mm/Jahr betragen. Mit anderen Worten, die Behauptungen stimmen überhaupt nicht mit den Beobachtungen überein.
Darüber hinaus zeigen die Ergebnisse von Kemp 2011 eine Zunahme der Rate des Meeresspiegelanstiegs, beginnend etwa 1700 … Wieso denn das? Und die Anstiegsrate hätte sich seitdem ohne Pause erhöht.
Daher können wir mit diesen beiden Hauptpunkten anfangen — die Schätzungen von Kemp et al. für die Höhe und den Anstieg des Meeresspiegels sind sehr verschieden von den Schätzungen der auf diesem Forschungsfeld anerkannten Experten. So etwas haben wir schon einmal erlebt, als Michael Mann behauptete, dass die Temperatur-Geschichte der vergangenen tausend Jahre ganz anders als die damalige anerkannte Meinung gewesen wäre. In keinem der Fälle gab es irgendwelche Hinweise auf außergewöhnlicher Belege, um die merkwürdigen Behauptungen zu stützen.
Mit dem Papier gibt es noch weitere Probleme, nachfolgend nicht in besonderer Reihenfolge aufgeführt:
1. Ungewissheiten. Wie sind sie berechnet? Sie [die Autoren] behaupten eine Gesamtgenauigkeit bei der Abschätzung des Meeresspiegels bei Tump Point von ± 40 mm. Sie sagen, dass ihre “Transferfunktion” eine Fehlerbreite von ± 100 mm hat. Weil die Transferfunktion nur ein Teil ihrer gesamten Transformation ist, wie kann das Endprodukt so genau sein?
2. Ungewissheiten. Die Ungewissheiten in ihrer Abb. S2 (A) (schattiert dunkel und hellrosa in obiger Abb. 1) sind über der Zeit konstant. Mit anderen Worten, sie sagen, dass ihre Methode zur Vorhersage des Meeresspiegels von vor 2000 Jahren so gut ist, wie für heute … das scheint zweifelhaft zu sein.
3. Ungewissheiten. In Abb. 4(B) des Hauptpapiers zeigen sie die Zusammenfassung ihrer Rekonstruktion nach GIA-Anpassung [Glacial-Isostatic Adjustment] mit den gleichen Fehlerbändern (dunkelschattiert und hellrosa) wie in der oben gezeigten Abb. S2 (A). Aber getrennt davon zeigen sie in Abb. 4(B) eine viel größere Weite von Unsicherheiten wegen der GIA-Anpassung. Sicher, diese beiden Fehler addieren sich mit der Quadrierung und ergeben schließlich ein weitere Gesamtbandbreite für die Fehler.
4. Tidenhub. Wenn der Tidenhub sich mit der Zeit verändert hat, müsste er sich in ihre Berechnungen als ein Nebenanstieg oder Fall in den Ergebnissen zeigen. Sie sehen das mögliche Problem, aber sie meinen, es könnte nicht eintreten aufgrund der Computer-Modellierung. Sie wären dennoch besser beraten gewesen, auf die Daten zu achten, anstatt närrischerweise den auf Sand gebauten Modellen zu vertrauen. Der Tidenhub bei der Oregon Inlet Marina, in kaum 16 Km Abstand von ihrer Sand Point Hauptörtlichkeit, ist mit einer Rate von 3 mm pro Jahr angestiegen. Das ist schneller als der von Kemp rekonstruierte Meeresspiegel-Anstieg in Sand Point. Weil wir mit Sicherheit wissen, dass Änderungen im Tidenhub stattfinden, klingt ihre computerisierte Zusicherung von der Unmöglichkeit mehr als nur ein wenig hohl. Das gilt ganz besonders angesichts der großen Veränderungen in der örtlichen Unterwasser-Geographie bei Sand Point. Abb. 4 zeigt einige dieser Veränderungen:
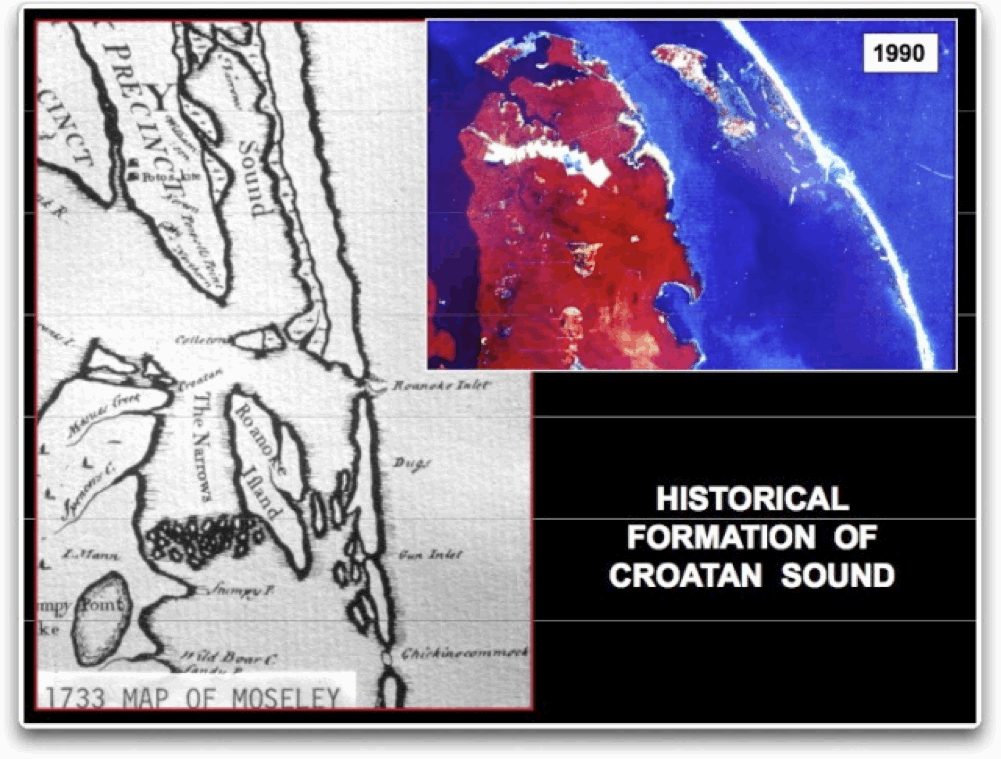
Bild 4. Die Veränderungen im Kanal zwischen Roanoke Island und dem Festland, von 1733 bis 1990.
Man beachte die Untiefen zwischen dem Festland und der Südspitze von Roanoke Island 1733, die bis 1870 auf Karten verzeichnet sind. Sie sind seitdem langsam verschwunden. Man sieht auch zwei Zuflüsse durch die meerseitig vorgelagerten Barriere-Inseln (Roanoke Inlet und Gun Inlet), die sich seit 1733 völlig aufgefüllt haben. Die Veränderungen an diesen Zuflüssen könnten für die Veränderungen der Tiefen südlich Roanoke Island ursächlich sein, weil das bedeutet, dass die Fläche zwischen Roanoke und dem Festland sich nicht mehr wir früher durch den Roanoke Inlet an der Nordspitze der Insel entleeren kann. Ihre [der Autoren] Behauptung, dass Veränderungen in dieser Größenordnung den Tidenhub nicht verändern würden, erscheint höchst unwahrscheinlich.
5. Unterschiedliche Auffassungen in Bezug auf lokale Trends beim Meeresspiegelanstieg. Die nächstgelegene Pegelmessstation in Wilmington zeigt keine statistisch signifikante Änderung beim Trend der mittleren Meereshöhe (Mean Sea Level – MSL) seit 1937. Kemp et al. behaupten, der Anstieg sei in diesem Zeitraum von 2 mm/Jahr auf 4,8 mm pro Jahr hochgegangen. Wenn dem so wäre, warum hat sich das nicht in Wilmington (oder in anderen benachbarten Orten) gezeigt?
6. Und wieder Ungewissheiten, wenn man genau auf die Rechnungen schaut. Sie sagen, der Fehler der mittleren Quadratwurzel RMS (root mean square) ihrer Transferfunktion betrüge 26% des gesamten Tidenhubs. Sie haben aber nicht den gesamten Tidenhub angegeben. Darauf komme ich gleich zurück. Wenn 26% der durchschnittlichen Quadratwurzelfehler ist, dann ist der 2-Sigma-Fehler doppelt so groß, oder 50% des Tidenhubs. Das halte man sich kurz vor Augen. Die Transferfunktion ist auf die Ansammlung von Foraminfera auf mittlere Meereshöhe bezogen, aber der Fehler beträgt die Hälfte des Tidenhubs. Daher kann ihre Methode im besten Falle noch nicht einmal sagen, ob die Ansammlung von oberhalb oder unterhalb der mittleren Meereshöhe stammt…
Weil die Gezeiten innerhalb der Barriere-Inseln so komplex und so schlecht dokumentiert sind benutzen sie das VDatum-Werkzeug von der NOAA, um den mittleren Tidenhub an ihren Örtlichkeiten abzuschätzen. Das Werkzeug wird aber in der Dokumentation für das Gebiet innerhalb des Pamlico SOund als ungenau bezeichnet. Laut Dokumentation beruhen die Schätzungen für Pamlico SOund auf einem „hydrodynamischen Modell“, anders als bei allen anderen Stationen, wo der Tidenhub anhand von Pegelstandsmessungen abgeschätzt wird.
Sie behaupten auch, dass ihre Transferfunktion für jede Abschätzung „unter 100 mm“ die “speziellen vertikalen Fehler” angäbe. Das bedeutet, dass ihr 2-Sigma-Fehler 100 mm betrug. Verbindet man das mit der Vorstellung, dass ihr VLSI Fehler bei 50% des Tidenhubs liegt, so impliziert das einen Tidenhub von nur etwa 200 mm an der SAND POINT Örtlichkeit. Das stimmt mit der Abschätzung des VDatum überein. Er beträgt fast genau 200 mm.
Die Gezeiten im Gebiet sind extrem ortsabhängig. Der Tidenhub kann innerhalb weniger Meilen um 100% schwanken. Und das bedeutet, dass sich die Spannweite der örtlichen Tidenhube (er ist stark ortsbezogen und extrem abhängig von der lokalen Geographie) sehr wahrscheinlich im Laufe der Zeit verändert hat. Unglücklicherweise werden derartige lokale Variationen nicht vom VDatum-Werkzeug erfasst. Dieses kann man von hier zusammen mit den Daten herunterladen. Beim Vergleich mehrerer Örtlichkeiten wird man feststellen, dass VDatum im PAMLICA SOUND ein sehr grobes Instrument ist.
Für die gleiche VDatum-Örtlichkeit im Pamlico Sound ergeben sich 2-Sigma-Fehler (mit 95% Zuverlässigkeitsintervall) beim Umrechnen von mittlerer Meereshöhe auf mittlere obere Fluthöhe mit 84 mm, und für mittlere untere Ebbe mit 69 mm. Die Schwierigkeit ergibt sich weil die Spanne des Tidenhubs so klein ist. Alle ihre Daten sind auf einen Standardisierten Wasserhöhen-Index (Standardized Water Level Index – SWLI) umgerechnet. Dieser drückt die Meereshöhe als einen Prozentsatz vom Tidenhub aus, von 0 bis 100. Null bedeutet, dass die Höhe auf der Höhe von mittlerer unterer Ebbe liegt, 100 bedeutet, dass sie auf der Höhe der mittleren oberen Flut liegt. Der Tidenhub wird mit 200 mm angegeben… weil er klein ist und die Fehler groß sind, beträgt das Zuverlässigkeitsintervall bei diesem Tidenhub 90 mm bis 310 mm, eine Spannweite der Veränderung von mehr als drei zu eins.
Sie berechnen den Standardisierten Wasserhöhen-Index (SWLI) wie folgt:
SWLI = (Sample Elevation – MLLW) / (MHHW – MLLW) x 100 (Gleichung 1)
[Standardized Water Level Index -> standardisierter Wasserhöhen-Index
Mean Lower Low Water (MLLW) -> mittlere Höhe der Ebbe
Mean Higher High Water (MHHW) -> mittlere Höhe der Flut]
Beim Addieren und Subtrahieren von Werten addieren sich die Fehler quadratisch. Der Höhenfehler beim Beispiel (aus der Transferfunktion) ist ± 100 mm. Die MLLW und MHHW 2-Sigma-Fehler sind jeweils 69 mm and 84 mm.
Nun denn … wir können ein paar Zahlen in die Gleichung 1 einsetzen. Zur Vereinfachung des Berechnens nehmen wir einmal an, für ein Beispiel sei die Höhe 140 mm, MLLW sei 0 mm, und MHHW sei 200 mm. Die mittlere Meereshöhe sei halbwegs zwischen Hoch und Niedrig, also etwa 100 mm. Die Fehler berücksichtigen wir (als “±” Werte dargestellt). Beim Einsetzen der Werte (in mm) in Gleichung 1 erhalten wir den Zähler:
(Sample Elevation – MLLW) = (140 ± 100 – 0 ± 69)
Die Fehler addieren sich quadratisch (der zusammengefasste Fehler ist die Quadratwurzel der Summe der Quadrate der einzelnen Fehler). Wir erhalten als Nenner 140 ± 122 mm
Der Nenner ist beim Einsetzen der quadrierten Fehler von Gleichung 1:
(MHHW – MLLW) = (200 ± 84 – 0 ± 69) = 200 ± 109 mm
Beim Dividieren oder Multiplizieren von mit Fehlern behafteten Zahlen muss man zuerst die Fehler in Prozent des Betrags des Bezugswerts angeben, und diese dann im Quadrat addieren. So erhalten wir:
(140 ± 87%) / (200 ± 55%) *100
Das ist gleich (.7 ± 103 %) x 100, oder 70 ± 72, wobei beide Zahlen Prozentwerte des Tidenhubs mal 100 sind. Da der Tidenhub 200 mm beträgt, bedeutet das für unser Beispiel eine Gesamt-Ungewissheit von etwa 72 Prozent, oder ± 144 mm. Am Schluss all ihrer Transformationen ist die Ungewissheit bei der Höhe des Beispiels (± 144 mm) größer als die Höhe des Beispiels selbst (140 mm).
Bei all dem ist natürlich die Annahme, dass ich ihre sehr unklaren Aussagen über die Ungewissheiten in ihrer Studie richtig interpretiere. Auf alle Fälle ist ein großes Geheimnis, wie sie für Tump Point einen 2-Sigma-Fehler von etwa 40 mm aus all dem erhalten.
Das sind die Probleme, die ich mit der Studie habe. Sowohl der Umfang wie auch die Rate ihres rekonstruierten Meereshöhen-Anstiegs während der vergangenen Jahre sind viel größer als die Beobachtungen; die Gezeitenhöhen schwanken in dem betroffenen Gebiet ständig, sie haben auch sehr wahrscheinlich in der Vergangenheit geschwankt, trotz der Behauptung der Autoren, dass dem nicht so gewesen wäre. Schließlich unterschätzen ihre Methoden zur Abschätzung der Fehler die Gesamt-Ungewissheit grob.
Weitere Punkte. In Bezug auf die C14 Datierung sagen sie:
C14-Altersdaten mit hoher Genauigkeit (8) wurden erhalten durch Bildung von doppelten oder dreifachen Proben aus dem gleichen Tiefenintervall und durch Benutzung eines „gepoolten Mittelwerts“ („pooled mean“ (Calib 5.0.1 software program)) für die Kalibrierung.
Das klang wie ein völlig logisches Verfahren … bis ich auf die Daten schaute. Abb. 5 ist ein Plot der einzelnen Daten, er zeigt Alter versus Tiefe, aus Supplementary Tables DR3 und hier. Sie haben das “pooled mean” von drei Proben aus 60 cm Tiefe benutzt und drei Proben aus 80 cm Tiefe.
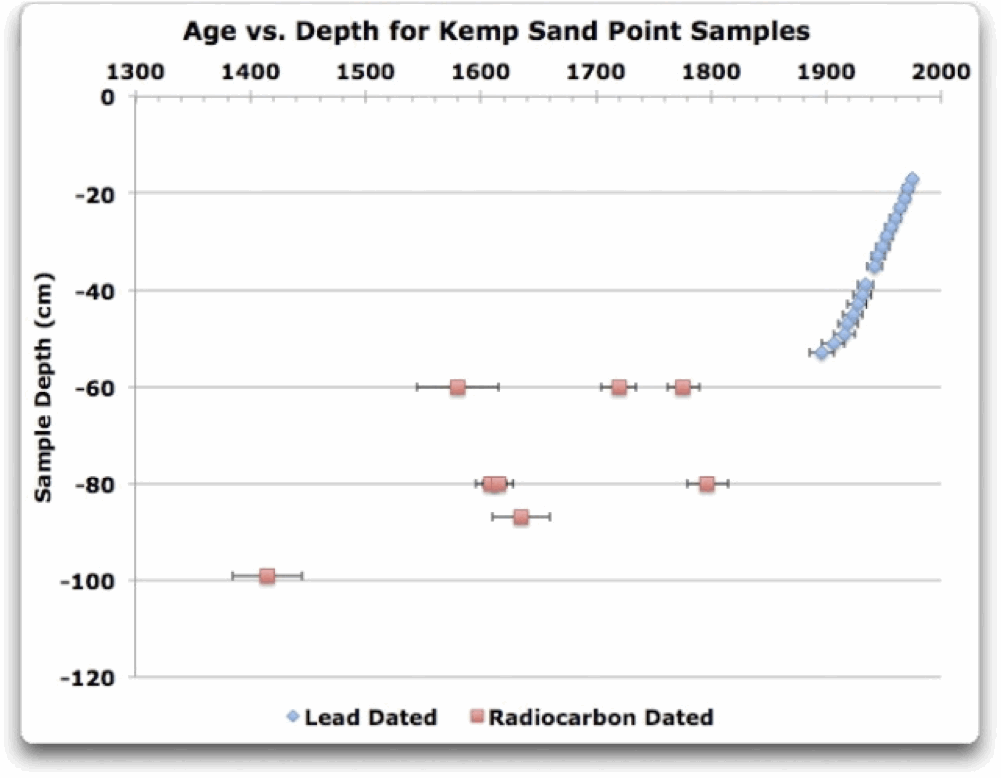
Abb. 5. Alter und Tiefe für die Sand Point Proben im oberen Meter des Bohrkerns. Rote Quadrate zeigen C14 Daten. Horizontale schwarze Balken zeigen die 2-Sigma Ungewissheit (95% Zuverlässigkeits-Intervall).
Sehen Sie sich die 60-cm-Tiefe an. Die drei getesteten Proben beziehen sich auf 1580, 1720, und 1776. Keiner der Fehlerbalken überlappt, also haben wir es klar mit drei Proben zu tun, die nachprüfbar unterschiedliche Alter haben.
Also, bevor wir deren Mittelwerte bilden und sie zur Kalibrierung der Alters/Tiefen-Kurve benutzen würde es da nicht Sinn machen, kurz nachzudenken, warum zwei Proben aus der genau gleichen 1-cm-dicken Scheibe des Bohrkerns nahezu zweihundert Jahre im Alter auseinander sind?
Das gleiche gilt für die 80-cm-Tiefe, wo das Alter von 1609 bis 1797 geht. Das sind wieder beinahe zweihundert Jahre Zeitunterschied.
Was übersehe ich hier? Macht es Sinn, diese ungleichartigen Daten zu mitteln, ohne zuvor darüber nachgedacht zu haben, was damit los ist?
Beitrag von Willis Eschenbach vom 26. Juni 2011
Die Übersetzung besorgte Hellmut Jäger EIKE
(1) Reduce your CO2 footprint by recycling past errors!
(2) “Climate related sea-level variations over the past two millennia”
Schneller Anstieg des Meeresspiegels: Paper von Rahmstorf, Kemp & Mann erneut zweifelhaft

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"#1
Sehr geehrter Herr Baecker,
mit etwas Verspätung: danke für den Hinweis auf die richtige Dekodierung von GIA.
Ist ja inzwischen vom Admin korrigiert.
Ihr Hinweis auf Google ist wohl etwas forsch.
Ich hatte bei der Übersetzung „gegoogelt“ und dabei 1Mrd350Mio Treffer erhalten. Nach Durchsicht der ersten 5 Trefferseiten habe ich es aufgegeben und stattdessen den Hinweis auf u.U. falsche Dekodierung der Abkürzung gegeben.
Was ist daran vorwerfbar oder was veranlasst Sie zu Ihrer Häme?
Gruss
Helmut Jäger
Herr Bäcker,
„Ich finde das kritisierte Rahmstorf-paper nun unabhaengig von Willis Argumenten (die ich nicht nachvollzogen habe) ziemlich dünn und angesichts dessen vollkommen überbewertet.“
Na das ist dochmal ’ne Meinung. Da hätten Sie auch was zu Willis sagen können. Hat er das nicht schön gemacht und ohne Fehler?
@Fischer #10
Also dann mal ran an ihren Artikel über das menschengemachte C02 in Verbindung mit unserem Klima. Erläutern Sie uns mal die ständig steigende Klimaerwärmung in Verbindung mit dem menschengemachten C02. Warum wird es global nicht immer wärmer und wärmer? Warum haben wir die letzten Winter so lange und hart frieren müssen? Warum haben wir noch solche Sommer wie diesen – kühl und nass? Die Sommer müssten trocken und heiß sein, die Winter mild und nass. Welchen Einfluss hat nun das menschengemachte CO2 auf die globale Klimaerwärmung? Erklaren Sie uns die 2 Grad Marke. Oder ist Deutschland zum Schluss nicht als „Global“ anzusehen und lebt in seiner eigenen Taumwelt…?!
#10: Norbert Fischer
Die Themenauswahl liegt in der Tat fest:
„Was spricht gegen ein AGW“
Das ist doch nun wirklich fast unerschöpflich!
Muss wohl an der AGW-Theorie selbst liegen.
Ein gewisses Niveau wird dabei natürlich gewünscht
und die Einhaltung der Forenregeln.
Wenn Sie das stört, suchen Sie doch ein anderes Forum.
Gruss
@ Hofmann
Gute Idee! So könnte man sicherstellen, dass der Autor den Text verstanden hat und peinliche Fehler vermieden werden.
Vielleicht würde es auch helfen, den sehr verengten Blickwinkel aufzuweiten. Alleine die Themenauswahl folgt ja schon ganz eigen(artig)en Gesetzen.
@Fischer Norbert #4
Nachdem Sie eh schon alles besser wissen als der Rest der Welt, was in Zunkunft auf die Menschheit zukommen wird, wie wäre es dann, wenn Sie und Hr. Bäcker den nächsten Fachbeitrag schreiben würden….?!
Hier ist noch eine Sache, die Herr Eschenbach uebersehen hat: Es gibt eine globale Temperatur fuer das globale Eismasseaequilibrium, bei dem global genausoviel Eis abschmilzt, wie neu gebildet wird. Nun liegen die globalen Temperaturen von 1600-1700 tiefer („Kleine Eiszeit“), globales Eis wurde zusaetzlich gebildet und der Meeresspiegel muss daraufhin um einige Zentimeter sinken (in reziproker Umkehrung: bei hoeheren Temp. – hoeherer Meeresspiegel). Was sehen wir bei Kemp (bitte auf Originalseite 300% vergroessern): Der Spiegel sinkt nicht, sogar ein Meeresspiegel“Berg“ (Anstieg)(nach Simulationen von PIK Rahmstorf)ist zu erkennen!
Ab 1700 steigen die globalen Temp, aber bei Kemp faellt der Ozeanspiegel bis 1850!
Die Temperaturabhaengigkeit zu Ozeanspiegel 1600 – 1850 ist bei Kemp und Rahmstorf nichts weiter als ein Saftladen, stimmt hinten und vorne nicht… schlechte Messungen, weiter nichts… liebe Blogger, besser ISBN 978-3-86805-604-4 konsultieren,
da ist der globale Zusammenhang genau vorgerechnet….. Ihr „weltklima@googlemail“
Herr Frey,
ich finde den Fehler an sich nicht schlimm. Nur etwas peinlich, denn auch wenn es Jäger nicht weiß, dauert es ja nur 5 Sekunden bis man per google weiß, was GIA heisst. Die Arbeit könnte sich Jäger doch machen egal, ob er mit dem Begriff letztlich was anfangen kann.
Wer sich mal nicht nur mit Texten, sondern auch mit den fachlichen Aspekten des MSL beschäftigt, weiß dass GIA ein grosser Unsicherheitsfaktor bei der Meerespiegelrekonstruktion ist.
Ich finde das kritisierte Rahmstorf-paper nun unabhaengig von Willis Argumenten (die ich nicht nachvollzogen habe) ziemlich dünn und angesichts dessen vollkommen überbewertet.
#4: Hochgeschätzter Fischer,
Sie schreiben „wir“ ???
wen meinen Sie damit, ha, ha
nur kurz, um nicht Regel 3 zu verletzen, zu #1 und #4,
beide Herren geben hier ein Triumphgeheul von sich, das seinesgleichen sucht! Ein Glück für sie, dass meinem Übersetzerkollegen Herrn Jäger ein solcher Fehler (?) unterlaufen ist! Warum sind sie ihm dafür nicht dankbar?
Was ein solches Triumphgeheul über diejenigen aussagt, die es ausstoßen, stelle ich jedem anheim. Ich freue mich jedenalls schon, wenn ich in meiner nächsten Übersetzung für EIKE den beiden Herren ebenfalls Anlass dazu gebe; es sei ihnen gegönnt!
Vielen Dank, Herr Jäger, für die Übersetzung! Ich glaube immer noch, dass Sie es fast noch besser können als ich!
Chris Frey
Wofür brauchen wir einen EIKE-Fachbeirat? Wir haben Bäcker!
Ladies and Gentlemen, „German-Wissenschaft“ proudly presents a new funny „Klimaschutz-Story“ !
Leider sind unserer „überragenden PIK-Comedy“ unbegreifliche Rechenfehler unterlaufen; wie konnte bei der Berechnung von Temperatur und Anstieg des Meeresspiegels, die „Rahmstorf-Konstante“ und dann auch noch der „Transformationshubersche-Faktor“ unberücksichtigt bleiben ?
Meiner Berechnung nach wird die „Globale Durchschnitts-Temperatur “ am 17.05.2027, genau um 8,7 Grad Celsius gestiegen sein, der Meeresspiegel klettert um 9,81m (wenn zwischenzeitlich ein Komet entsprechender Größe, in einen der Ozeane einschlägt, kann der Wert noch beträchtlich steigen !). Sie haben sich also absichtlich verrechnet, um uns weiter zu belügen, denn wie wir sehen, wird alles noch viel schlimmer kommen (:-)) !
Wenn ich jetzt gefragt werden sollte, ob ich dies beweisen kann, muss ich euch leider enttäuschen, da halte ich es genauso wie die AGW-Fraktion; denn laut deren „wissenschaftlichen“ Methoden reicht die jahrelange Behauptung, basta ! In diesem Sinne, bis zum nächsten „Klimaschutz-Joke!“
Your greatest fan
Carl Johnson
Herr Bäcker,
es wundert mich, Willis konnten Sie noch nie leiden aber mehr haben Sie nicht auszusetzen?
Herr Jäger,
„GIA-Anpassung [Anm. d. Ü.: Abkürzung GIA? Global Increase Anomaly ?] “
Wie wäre es, erstmal die Fachbegriffe zu klären:
GIA = Glacial-Isostatic Adjustment
und nicht „Global increase anomaly“, wie einfallsreich…