Weist der globale Meeresspiegelanstieg eine sinusförmige Schwankung auf? – Teil 1

Eine Untersuchung anhand von Gezeitenpegel-Daten – Teil 1: Vorläufige Analyse

Dr. Alan Welch FBIS FRAS

Einführung

Die Frage „Warum weist der globale Meeresspiegelanstieg eine sinusförmige Schwankung mit einer Periode von etwa 26 Jahren auf?“ wurde 2023 in den Kommentaren zu einer meiner Veröffentlichungen gestellt. In meiner Antwort wies ich darauf hin, dass die Satellitenabdeckung nur 95 % betrug und daher möglicherweise die Ereignisse in den übrigen 5 % relevant sein könnten. In meinem Folgeartikel „Measuring and Analysing Sea Levels using Satellites during 2023 – Part 2“ [etwa: Messung und Analyse des Meeresspiegels mit Satelliten im Jahr 2023 – Teil 2] analysierte ich die Ergebnisse von Gezeitenmessern in 9 Häfen in den nördlichen Regionen des Atlantischen Ozeans und bis hinauf zum Arktischen Ozean. Die Analyse war sehr vereinfacht, aber vielversprechend, sodass nun eine detailliertere Analyse unter Verwendung neuerer Verfahren durchgeführt wird.

Bevor wir fortfahren, könnte eine weitere Frage lauten: „Na und?“ Die Kurve ist im Grunde genommen fast linear (R² = 0,99), wobei quadratische oder sinusförmige Anpassungen nur sehr wenig dazu beitragen. Im Jahr 2018 veröffentlichten Nerem et al. jedoch ihre Arbeit, in der sie sich auf eine quadratische Kurve konzentrierten und den kleinen quadratischen Koeffizienten als repräsentativ für eine Beschleunigung verwendeten. Hätten sie sich auf die Daten beschränkt, wäre alles akzeptabel gewesen, aber sie extrapolierten über 80 Jahre und veröffentlichten ihre Arbeit. Die Arbeit wird immer noch jeden Monat in vielen Arbeiten als Referenz verwendet. In den letzten 8 Jahren wurde sie verwendet, um dramatische Szenarien von überfluteten Städten zu entwerfen und alle Kinder zu erschrecken. Die Untersuchung einer Sinuskurve hat versucht, ein ausgewogenes Bild zu zeichnen. Ein Punkt, der bei der Verwendung der quadratischen Kurve übersehen wurde ist, dass die Berechnungen, wenn sie 2008 begonnen hätten, jetzt eine Verlangsamung zeigen würden. Welche Arbeit würden Nerem et al. dann schreiben?

Der Beitrag besteht aus zwei Teilen.

Teil 1 enthält vorläufige Analysen, in denen jeder Gezeitenmesser bis zur Stufe der Spektralanalyse verarbeitet wird.

Teil 2 führt eine Kurvenanpassung durch, bei der die Residualwerte (Ist-Werte minus Werte auf einer Best-Fit-Kurve) anhand einer Kurve beurteilt werden, die aus zwei oder drei Sinuskurven unter Verwendung der aus den Spektralanalysen abgeleiteten Spitzenperioden besteht.

Vorläufige Analyse

Diese Studie nutzt eher Daten von Gezeitenmessern als Daten der NOAA, verwendet jedoch Spektralanalysen.

Die 9 Standorte sind Reykjavik – Island, Torshavn – Färöer-Inseln, Aberdeen – Schottland, Lerwick – Schottland, Bergen – Norwegen, Barentsberg – Spitzbergen, Narvik – Norwegen, Murmansk – Russland und Tiksi – Russland.

Nur Aberdeen und Bergen verfügen über Datensätze, die mehr als 100 Jahre umfassen, während Torshavn nur etwa 50 Jahre abdeckt.

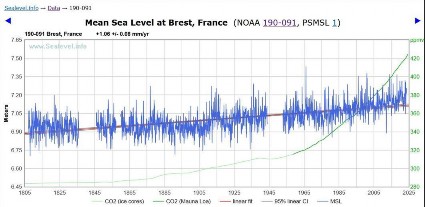
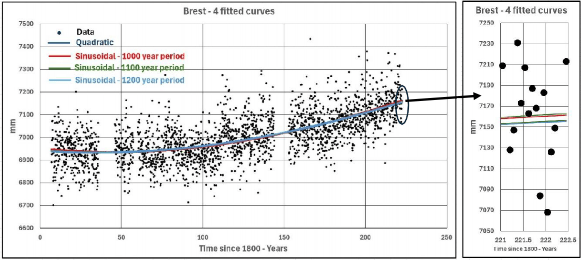
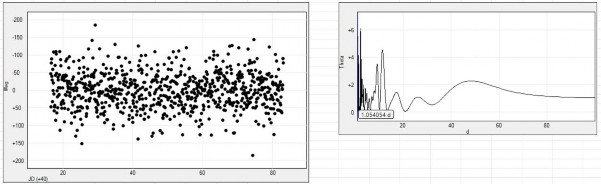
Vor der Analyse dieser 9 Häfen werden die Ergebnisse für Brest untersucht, da diese über 210 Jahre umfassen, obwohl es einige größere Lücken in den Daten gibt. Diese Arbeit wurde bereits früher durchgeführt, aber einige Aspekte sind von Interesse. Die Daten sind in Abbildung 1 dargestellt:

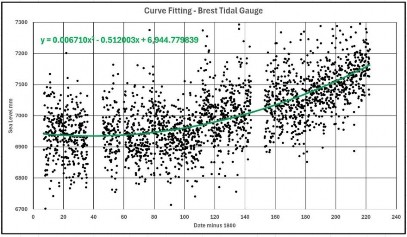
Die übliche Kurvenanpassung wird wie in Abbildung 2 dargestellt durchgeführt. Auch hier wurde möglicherweise eine übermäßige Genauigkeit verwendet, um auf der sicheren Seite zu sein. Dies dient nicht dazu, eine genaue Anpassung anzuzeigen, sondern aufgrund möglicher hoher Werte auf der „x“-Achse könnten die Leistungsterme diese zusätzliche Genauigkeit erfordern.

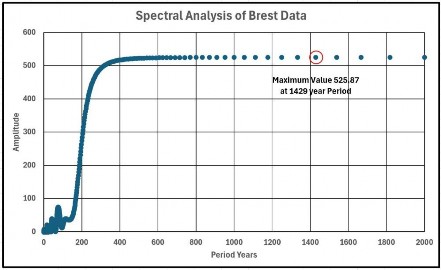
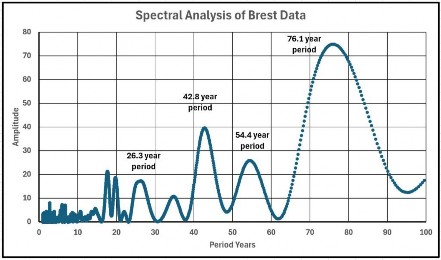
Eine Spektralanalyse wurde an den Daten durchgeführt, und die Abbildungen 3 und 4 zeigen die Ergebnisse für lange und kurze Zeiträume:

Abbildung 3 zeigt einen Spitzenwert (kaum erkennbar) bei einer Periode von 1429 Jahren. Die meisten anderen Gezeitenmessgeräte zeigen viel höhere Perioden, aber es wäre interessant zu sehen, wie Sinuskurven mit Perioden im Bereich von 1000 Jahren mit der quadratischen Anpassung verglichen werden könnten.

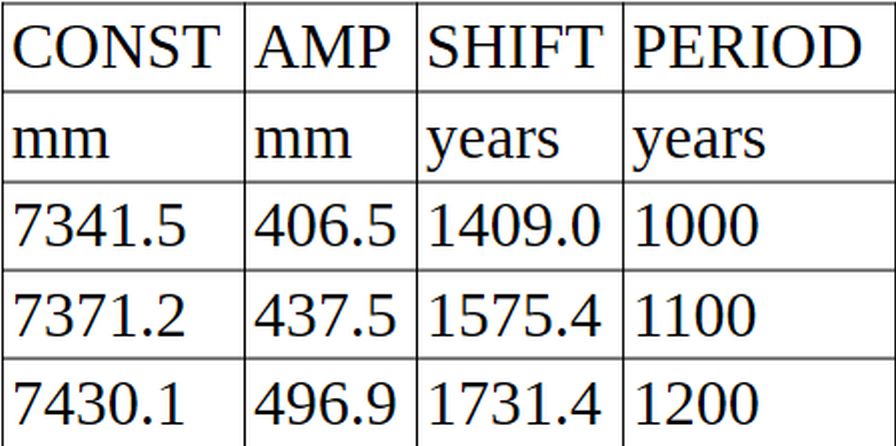
Die Kurvenanpassung wurde für Kurven mit Perioden von 1000, 1100 und 1200 Jahren durchgeführt. Die Gleichungen werden im Excel-Format angezeigt.

= CONST + AMP * SIN(((SHIFT + 2 * A1)/PERIOD) * PI()) (Gleichung 1)

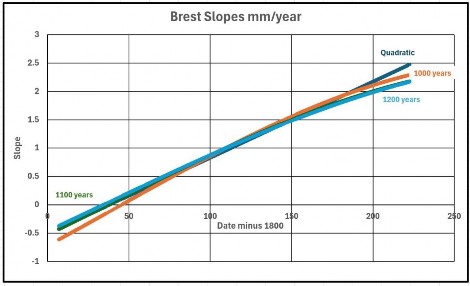
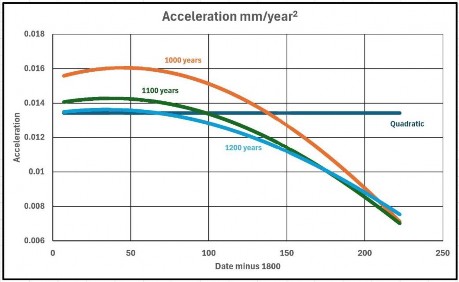
Die Abbildungen 5, 6 und 7 vergleichen die quadratische Kurve mit den drei Sinuskurven und stellen dabei Steigung und Beschleunigung gegenüber:

Der nächste Teil könnte gutes Querdenken sein oder ein bisschen mehr La La Land!

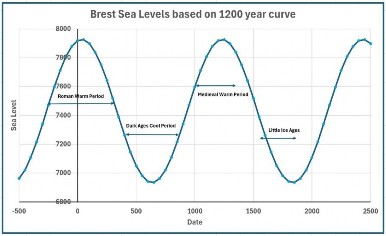
Wenn man die 1200-Jahres-Kurve verwendet und von 500 v. Chr. bis 2500 n. Chr. extrapoliert, erhält man folgendes Ergebnis:

Die angegebenen Zeiträume sind möglicherweise umstritten. Ich war überrascht, dass die letzte Thames Ice Fair erst 1814 stattfand. Eine beunruhigendere Interpretation dieser Grafik, sofern sie überhaupt aussagekräftig ist wäre, dass der Meeresspiegel (und die damit verbundenen Temperaturen) erst um 2450 ihren Höchststand erreichen. Könnten die Ereignisse wirklich so schlimm werden? Wie warm war es während der römischen und der mittelalterlichen Warmzeit?

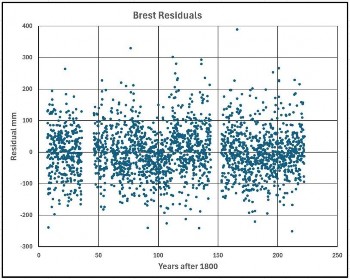
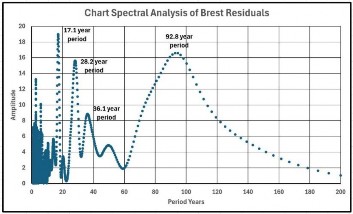
Schließlich zeigt Abbildung 9 die Residuen, d. h. die tatsächlichen Werte abzüglich der Werte auf der quadratischen Kurve, und Abbildung 10 die Spektralanalyse dieser Residuen:

Die Perioden der Spitzenwerte weichen von denen der vollständigen Spektralanalyse ab, und auf Abbildung 9 ist nicht ohne Weiteres zu erkennen, dass es möglicherweise eine dekadische Schwankung von etwa 93 Jahren gibt. Dies wurde

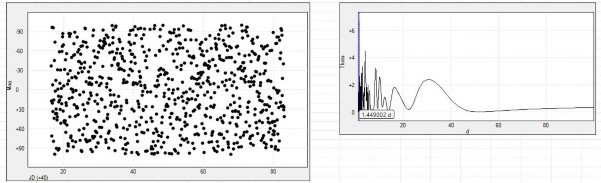
untersucht, indem Datendateien mit Zufallswerten erstellt wurden, wobei ein Satz als einfache Zufallswerte und ein Satz als Zufallszahlen mit einer Standardabweichung festgelegt wurde. Es wurden viele Fälle durchgespielt, und die Abbildungen 11 und 12 zeigen jeweils einen Fall aus jeder Reihe:

Der erste Eindruck ist etwas beunruhigend, da er Kurven mit Perioden im Bereich von 10 bis 100 Jahren anzeigt, aber bei genauerer Betrachtung zeigt sich, dass diese alle eine geringe Amplitude (in diesen Diagrammen mit „Theta” bezeichnet) von etwa 2 haben, während sie in den tatsächlichen Gezeitenmessdiagrammen zwischen 10 und 30 für die Residuen liegen. Diese Theta-Werte sind relative Werte und geben keine tatsächlichen physikalischen Werte an.

(Möglicherweise habe ich den Prozess nicht klar und korrekt beschrieben, daher wäre ich für jede Hilfe sehr dankbar.

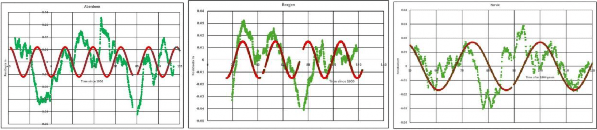
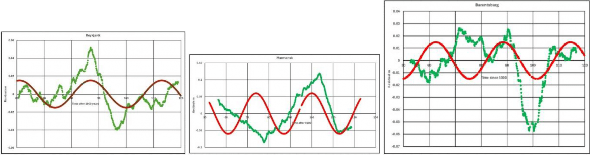
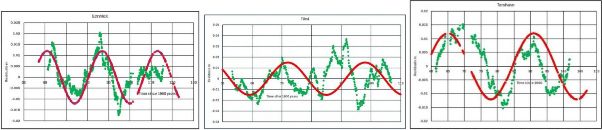
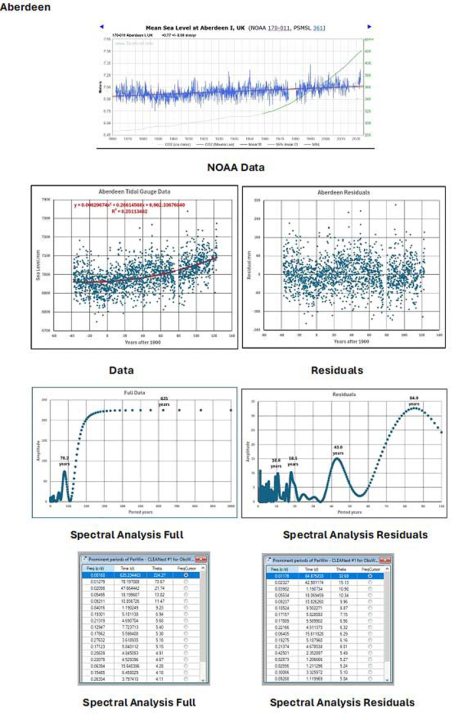
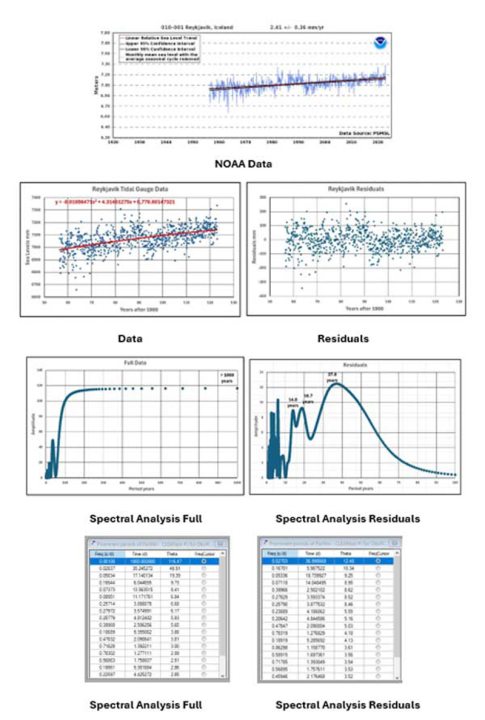
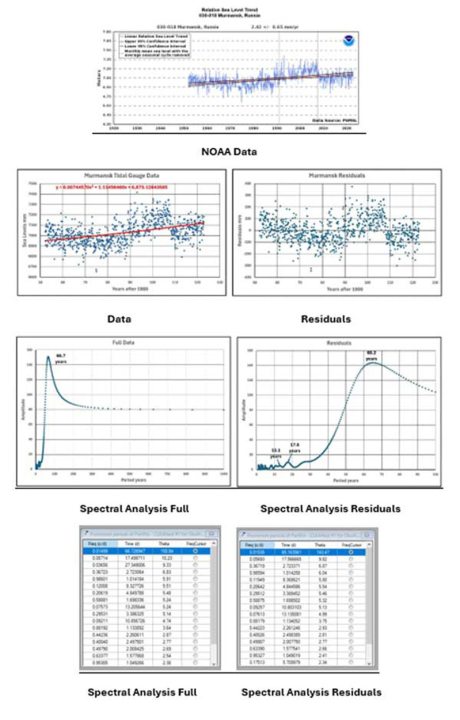
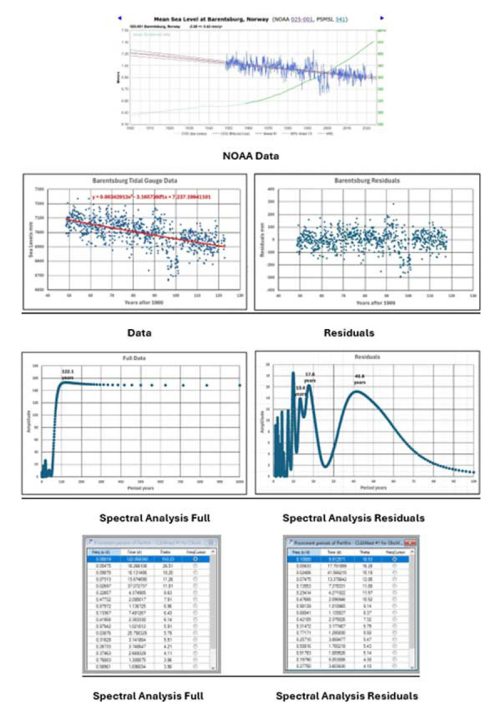
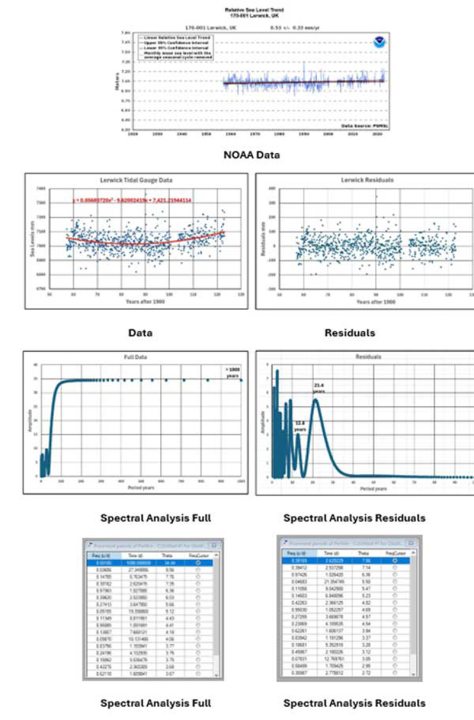
Wenden wir uns nun den 9 Datensätzen der Gezeitenpegel zu, die wir beginnend mit dem längsten Messzeitraum und dann in etwa in der Reihenfolge abnehmender Zeiträume betrachten werden. Bevor wir jedoch fortfahren, zeigen die folgenden 9 kleinen Abbildungen das Ergebnis der früheren Kurvenanpassung einer 26-Jahres-Kurve an die Diagramme der Residualwerte, d. h. der tatsächlichen Werte abzüglich des Wertes der quadratischen Anpassung. Während eine Kurve mit einer Periode von etwa 26 Jahren an vielen Stellen passt, gibt es Hinweise auf andere, in der Regel längere Periodenkomponenten, wie aus dem Diagramm für Aberdeen ersichtlich ist, wo eine größere Schwankung von etwa 85 Jahren offensichtlich ist. Die größeren Spektralanalyse-Peaks beziehen sich auf Primärmodi, während die kürzeren andere Primärmodi oder Sekundärmodi sein können. Ein Problem bei diesen 9 Analysen war, dass die dargestellten Daten ein gleitender Durchschnitt basierend auf 101 Datenpunkten sind. Ohne Unterbrechungen in den Daten entspricht dies etwas mehr als 8 Jahren, aber da es mehrere Lücken in den Daten gibt, kann dies zu Verzerrungen führen. Durch die Mittelwertbildung werden die meisten kurzfristigen Frequenzen entfernt, wodurch die allgemeine Form leichter zu erkennen ist.

Jeder der 9 Gezeitenmesser wird nun unter Berücksichtigung der Ausgangsdaten von der NOAA-Website, der verarbeiteten Daten mit der am besten passenden quadratischen Kurve, der Residuen (tatsächlicher Wert minus Wert auf der am besten passenden Kurve), der Spektralanalyse-Diagramme und der Ergebnistabellen betrachtet. Die Tabellen enthalten im Wesentlichen Werte aus der ursprünglichen Verwendung der Software, nämlich der Analyse variabler Sterne. Die erste Spalte enthält die Frequenz

(1/Periode) in Zyklen pro Jahr. Die Zeit ist die Periode, in der diese Frequenz in Jahren auftritt. Theta wird in diesem Artikel als Amplitude bezeichnet.

In dieser Phase wurde keine Kurvenanpassung durchgeführt, da in den meisten Fällen zwei oder mehr Peaks vorhanden sind. Die bei der Spektralanalyse verwendeten Amplituden (amp) und die Amplituden der Sinuskurven (AMP) wurden für bekannte Mehrfach-Sinuskurven untersucht, und es wurde festgestellt, dass die Amplituden für ein Kurvenpaar, 1 und 2, durch die folgende Gleichung miteinander in Beziehung stehen:

AMP2 = AMP1 * SQRT(amp2/ amp1) (Gleichung 2)

Damit lässt sich die relative Dominanz jeder in den Spektralanalyse-Diagrammen dargestellten Kurve abschätzen.

Aberdeen:

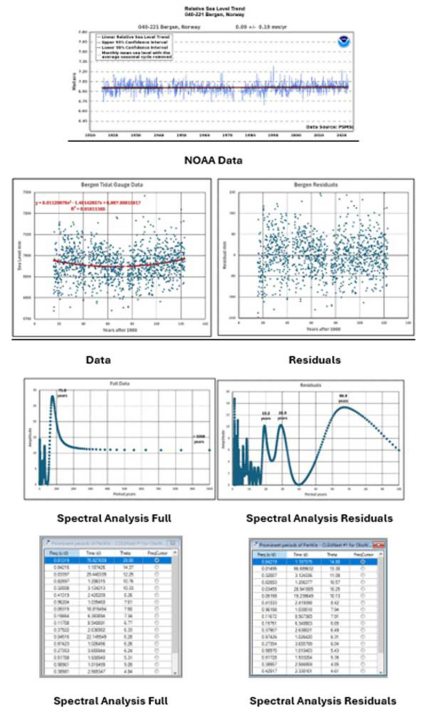
Bergen:

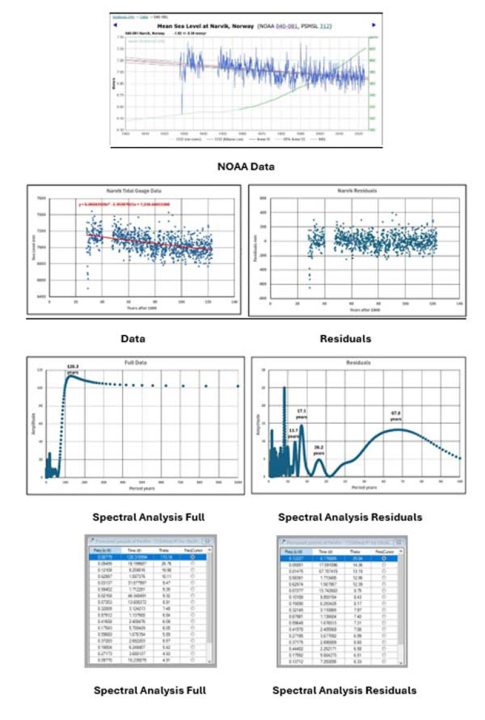
Narvik:

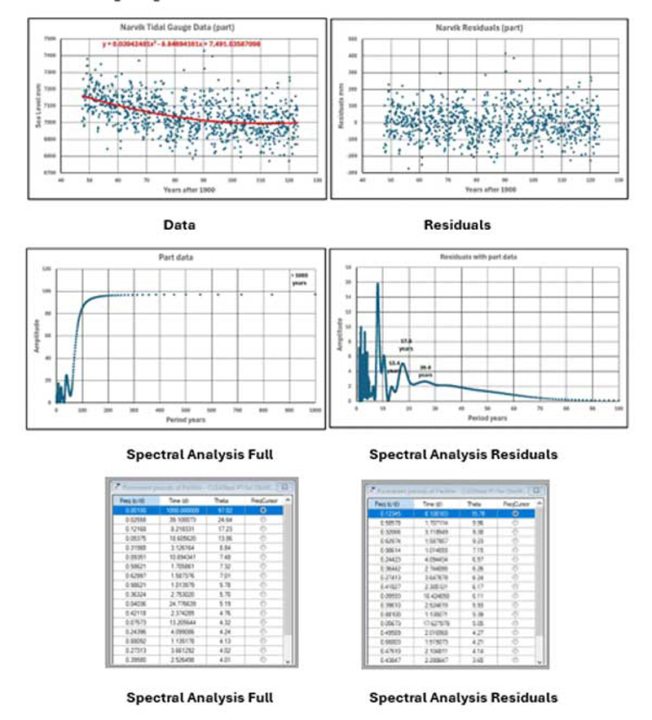
Narvik (reduzierter Datensatz):

Die Daten vor 1947 wurden aufgrund der großen Lücke in den Messwerten und der verdächtigen Anfangswerte nahe dem Beginn der Datenreihe verworfen.

Reykjavik:

Murmansk:

Barentsburg:

Lerwick:

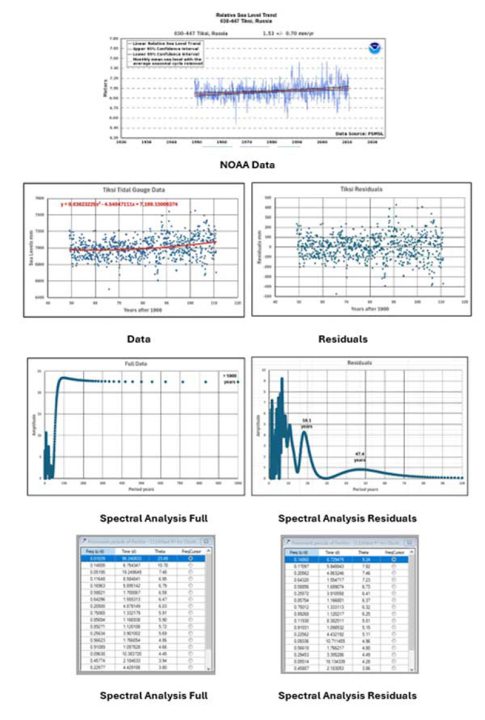
Tiksi:

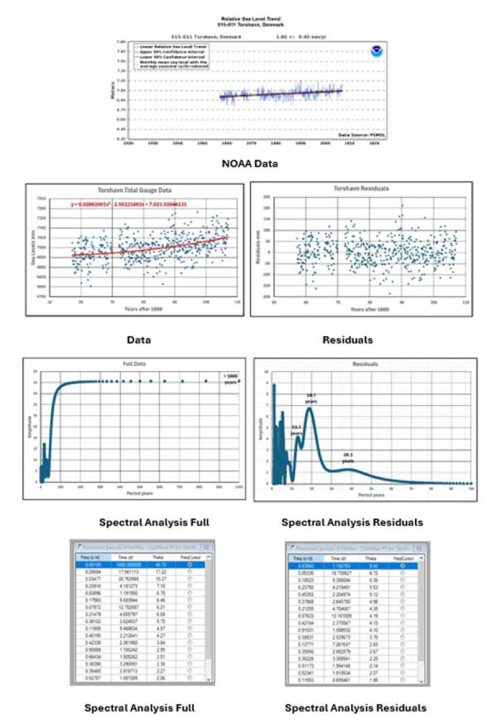
Torshavn:

Demnächst:

Nachdem die Spektralanalyse auf eine Reihe von Gezeitenmessgeräten angewendet wurde, werden in Teil 2 die Ergebnisse zur Ableitung von Sinuskurven verwendet.

Link: https://wattsupwiththat.com/2025/12/02/does-the-global-sea-level-rise-have-a-sinusoidal-variation/

Übersetzt von Christian Freuer für das EIKE