Ich habe kürzlich einen Dokumentarfilm von National Geographic gesehen, in dem es um den Einsatz von Lidar-Geräten aus der Luft ging, mit denen man durch die Bäume des guatemaltekischen Dschungels hindurchsehen kann, um Maya-Ruinen freizulegen. Der Kommentator sagte: „Wenn wir gerade Linien auf dem Boden sehen, ist das nicht natürlich. Es ist etwas, das der Mensch gemacht hat.“
Und das ist wahr – die Natur macht im Allgemeinen keine geraden Linien.
Daran erinnert mich die in meinen Augen lächerliche Behauptung, dass die etablierten Klimawissenschaftler in Bezug auf das Klima, eines der komplexesten Systeme, die wir je zu analysieren und zu verstehen versucht haben, eine lineare Beziehung zwischen den Veränderungen der abwärts gerichteten langwelligen Strahlung am oberen Rand der Atmosphäre und der Oberflächentemperatur herstellen. Dies ist eine zentrale Überzeugung in ihrem Verständnis des Klimas:
∆T = λ * ∆F (Gleichung 1 – und die Einzige)
Demnach ist die Änderung (Delta, „∆“) der globalen durchschnittlichen Temperatur („T“) gleich der Änderung (∆) des „Forcings“ („F“) mal einer Konstante namens Lambda (‚λ‘), die als „Gleichgewichts-Klimaempfindlichkeit“ (ECS) bekannt ist.
Und was ist Forcing [Antrieb] genau? Forcing ist ein Kunstbegriff in der Klimawissenschaft. Der Strahlungsantrieb wird vom Intergovernmental Panel on Climate Change (IPCC) wie folgt definiert:
„Die Änderung des Nettostrahlungsflusses (nach unten minus nach oben) (ausgedrückt in W/m²) aufgrund einer Änderung eines externen Treibers des Klimawandels, wie z. B. einer Änderung der Kohlendioxidkonzentration (CO₂), der Konzentration vulkanischer Aerosole oder der Sonneneinstrahlung.“
Die „abwärts gerichtete“ Strahlung an der Oberseite der Atmosphäre (TOA) ist die einfallende Sonnenstrahlung. Das ist die gesamte Strahlung, die in das System eintritt.
Die „Aufwärtsstrahlung“ ist die langwellige Wärmestrahlung, die in den Weltraum geht. Sie ist die Summe aller Energie, die das System verlässt.
Diese Behauptung der Linearität ergibt für mich absolut keinen Sinn. Lassen Sie mich erklären, warum.
Erstens kann sich die Temperatur ändern, ohne die TOA-Strahlungsbilanz zu beeinflussen. Das Klimasystem ist eine riesige Wärmekraftmaschine. Die Wärme kommt am heißen Ende jeder Wärmekraftmaschine herein: in diesem Fall sind es die Tropen. Dann wird ein Teil der Wärme verarbeitet, und der Rest der Wärme wird am kalten Ende der Wärmekraftmaschine abgeführt: in diesem Fall an den Polen.
Beachten Sie, dass nur ein Teil dieser Wärme in Arbeit umgewandelt wird. Der Rest ist nur ein Durchlauf, der durch den Ozean und die Atmosphäre von den Tropen zu den Polen und zurück ins All getragen wird. Jede Veränderung des prozentualen Anteils des Gesamtstroms, der in Arbeit umgewandelt wird, verändert die Temperatur, ohne dass sich die TOA-Strahlungsbilanz ändert.
Außerdem ist das Klimasystem nicht frei, irgendeine Konfiguration anzunehmen. Es unterliegt dem Konstruktionsgesetz, und wie ein Fluss, der sich zum Meer schlängelt, bewegt es sich nicht in geraden Linien. Wie alle Strömungssysteme, die nicht im Gleichgewicht sind, maximiert der Fluss seine Strömung und wählt daher den längsten möglichen Weg zum Meer.
In ähnlicher Weise versucht das Klima als konstruktives System immer, die Strömung von den Tropen zu den Polen zu maximieren. Und wenn sich diese Strömungsgeschwindigkeit ändert, ändert sich die Temperatur … ohne eine entsprechende lineare Änderung der TOA-Strahlungsbilanz.
Schließlich setzt ihre Gleichung 1 eine Größe, die erhalten bleibt (Watt pro Quadratmeter), mit einer Größe gleich, die NICHT erhalten bleibt (Temperatur). Mir ist nicht klar, wie das überhaupt möglich ist.
Für die Zwecke dieser Diskussion nehmen wir jedoch an, dass sie mit dieser speziellen Beziehung zwischen TOA-Antrieb und Temperatur richtig liegen. Wir werden diesen Weg weiterverfolgen und sehen, wohin er führt.
Als ersten Schritt auf diesem Weg möchte ich auf die Idee zurückkommen, dass sich das Klima nicht in geraden Linien bewegt. Unten sehen Sie zum Beispiel ein Diagramm der gesamten Wolkenabkühlung/-erwärmung für jede einzelne Gitterzelle, die eine Kombination aus den Auswirkungen der Wolken auf die lang- und kurzwellige Strahlung und der Verdunstungskühlung im Zusammenhang mit den Niederschlägen ist. Ich habe sie mit den Temperaturen der Gitterzellen in einem Streudiagramm mit Konturlinien verglichen.
Aus einem einfachen Grund habe ich begonnen, diese Streudiagramme wie in Abbildung 1 unten zu erstellen, in denen zwei Variablen für jede Gitterzelle von 1° Breitengrad und 1° Längengrad des Planeten verglichen werden. Sie zeigen die langfristige Beziehung zwischen den beiden Variablen. Jede Gitterzelle auf dem Planeten befindet sich in einem langfristigen, allgemeinen Gleichgewichtszustand in Bezug auf die verschiedenen messbaren Faktoren, wie z. B. die Häufigkeit von Gewittern. Die Jahresdurchschnitts-Werte dieser Beziehungen variieren nur wenig, und ein 24-Jahres-Durchschnitt offenbart die zugrunde liegende langfristige Beziehung zwischen den Variablen.
Und dies ermöglicht uns, Dinge wie den langfristigen Wert der Gleichgewichts-Klimasensitivität zu untersuchen … aber ich greife mir selbst vor …
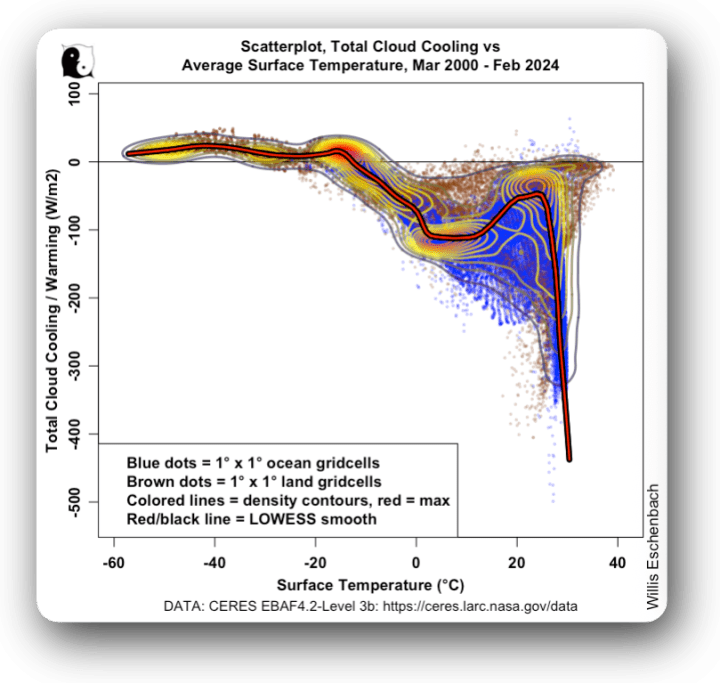
Abbildung 1. Streudiagramm plus Dichtekonturlinien und LOWESS-Glättung. Gesamte Wolkenabkühlung im Vergleich zur Temperatur, gesamter Planet.
In Abbildung 1 gibt es viel Interessantes zu sehen. Erstens erwärmen die Wolken in den Gitterzellen mit Durchschnittstemperaturen unter etwa -20 °C die Oberfläche, also in Grönland und der Antarktis. Wenn dann der gefrorene Ozean ins Spiel kommt, d. h. von -20 °C bis zu dem Punkt, an dem die Gitterzellen im Durchschnitt etwa den Gefrierpunkt erreichen, kommt es zu einer mit der Temperatur zunehmenden Abkühlung.
Dann kehrt sich der Trend um, und die Abkühlung nimmt mit der Temperatur bis zu den Gitterzellen mit einer Durchschnittstemperatur von etwa 25 °C ab. Und darüber nimmt die Abkühlung radikal und fast vertikal zu, bis zu dem Punkt, an dem sie diese Gitterzellen um -400 W/m² oder so abkühlt.
Beachten Sie nebenbei den Spitzenwert um 25 °C. Steigt die Temperatur darüber, kühlen die Wolken immer stärker ab, bis hin zu einer radikalen Abkühlung. Und wenn die Temperatur unter ~ 25°C sinkt, verringern die Wolken die Abkühlung. Dies ist ein klarer Beweis für die thermoregulierende Wirkung der Wolken, die mehr kühlen, wenn es wärmer ist, und weniger, wenn es kälter ist.
Schließlich ist die vorherrschende Rolle des Ozeans sowohl an der engeren Gruppierung als auch an der größeren Anzahl der blauen ozeanischen Punkte im Vergleich zu den braunen Punkten der Land-Gitterzellen erkennbar.
Und um den Kreis zu schließen, ist die rot/schwarze Linie, die die Veränderung der Abkühlung mit der Temperatur zeigt, sozusagen die Definition von nichtlinear …
Diese Art von Diagrammen ist aus einem einfachen Grund sehr nützlich. Die Steigung der rot/schwarzen Linie an einem beliebigen Punkt gibt die durchschnittliche Änderung der Variablen auf der y-Achse für eine Änderung der Temperatur um 1 °C an. So können wir zum Beispiel sehen, dass bei einer Temperatur über 25 °C die Gesamtabkühlung der Wolken mit jeder Temperaturerhöhung um 1 °C extrem schnell zunimmt.
Was können uns solche Diagramme über die langfristige Beziehung zwischen Temperatur und Antrieb zeigen?
Die gängige Theorie lautet wie folgt:
– Eine Verdoppelung der CO₂-Menge fängt mehr von der aufsteigenden langwelligen Strahlung ab, die in den Weltraum gelangt.
– Dies führt zu einem Strahlungsungleichgewicht an der Oberseite der Atmosphäre (TOA).
– Die Erde erwärmt sich dann, bis das Gleichgewicht wiederhergestellt ist.
Es stellt sich also die Frage, wie stark sich die Erde erwärmen muss, um das Ungleichgewicht der TOA-Strahlung von 3,7 Watt pro Quadratmeter (W/m²) wiederherzustellen, das sich aus einer Verdoppelung des CO₂ (2xCO₂) ergeben soll.
[Hervorhebung im Original]
Diese erforderliche Erwärmung, um das Ungleichgewicht der TOA-Strahlung auszugleichen, wird als „Gleichgewichts-Klimasensitivität“ (ECS) für eine Verdoppelung des CO₂ bezeichnet. Sie ist das „lambda“ in der linearen Gleichung 1 (und nur dieser) oben.
Um den Wert der ECS zu untersuchen, hier das Streudiagramm des TOA-Ungleichgewichts gegenüber der Temperatur:
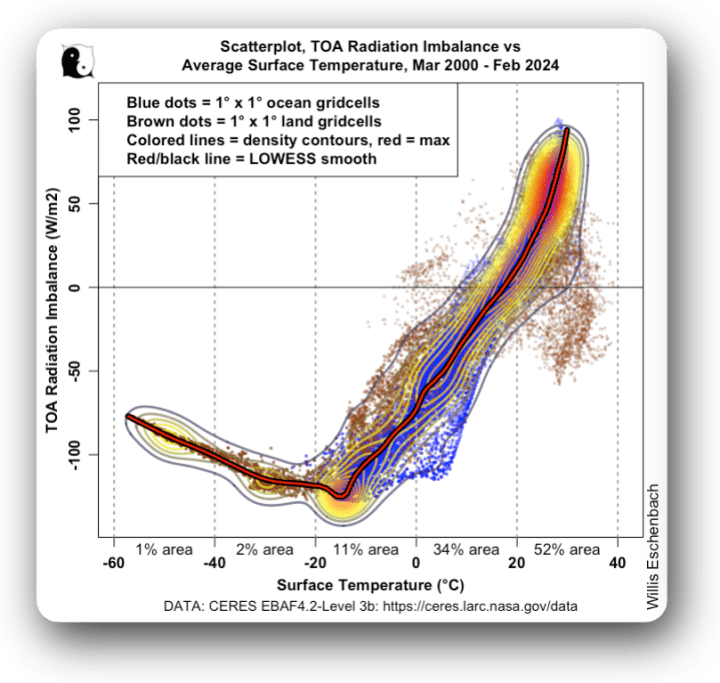
Abbildung 2. Streudiagramm plus Dichtekonturlinien und LOWESS-Glättung. Strahlungsungleichgewicht am oberen Rand der Atmosphäre gegenüber der Temperatur, gesamter Planet. Die Prozentzahlen (% Fläche) zeigen den prozentualen Anteil der Oberfläche in jedem Temperaturintervall.
Ich liebe es, von meinen Untersuchungen überrascht zu werden. Das ist der beste Teil meiner wissenschaftlichen Ausbildung. Ich habe definitiv nicht erwartet, dass das Diagramm so aussehen würde. Aber Fakten sind Fakten.
Bei Temperaturen unter -20 °C zeigen die braunen Punkte, dass es sich nur um Land handelt – Grönland und die Antarktis. Und dort wird das TOA-Ungleichgewicht merkwürdigerweise für jedes 1°C Erwärmung negativer. Dann, bei etwa -15°C, kehrt sich die Neigung um, da der gefrorene Ozean ins Spiel kommt. Bis etwa 20°C steigt sie einigermaßen linear an, danach beginnt das Ungleichgewicht schneller zuzunehmen.
[Hervorhebung im Original]
Wir können diese Veränderungen im Detail veranschaulichen, indem wir die Steigung an jedem Punkt der rot-schwarzen Linie berechnen. Erinnern Sie sich, dass die Steigung die Veränderung des TOA-Strahlungsungleichgewichts pro Grad Erwärmung ist. Hier ist das Ergebnis:
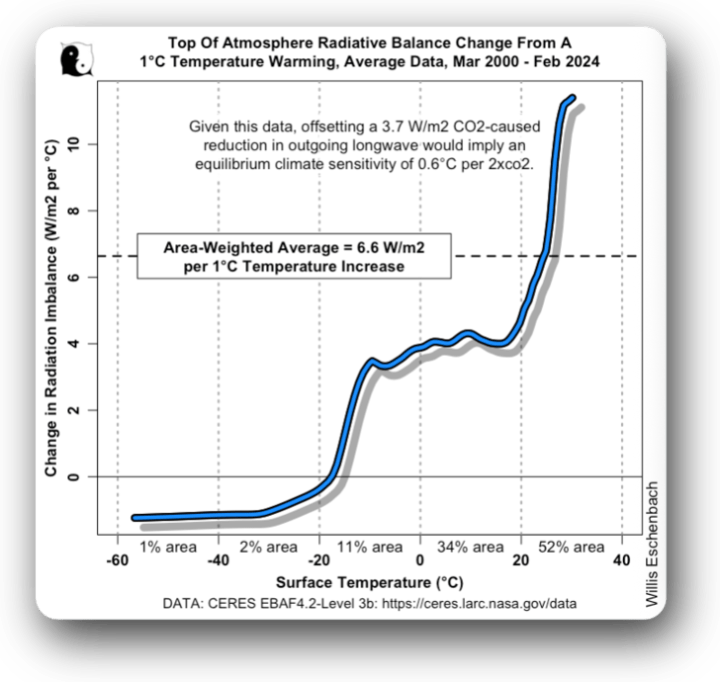
Abbildung 3. Steigung der rot/schwarzen Trendlinie in Abbildung 2 oben. Wenn Sie sich fragen, warum die flächengemittelte Veränderung so hoch ist, sehen Sie sich die prozentualen Anteile der globalen Fläche mit jährlichen Durchschnittstemperaturen in jedem Temperaturintervall an.
Ich habe den flächengewichteten Durchschnitt der Veränderung der TOA-Bilanz bei einem Anstieg der Oberflächentemperatur um 1° eingefügt. Sie beträgt 6,6 W/m² pro °C. Daraus ergibt sich eine Gleichgewichtsempfindlichkeit (ECS) von 0,6 °C pro CO₂-Verdoppelung
Ich behaupte, dass dies eine vernünftige Schätzung für die ECS ist, und zwar aus mehreren Gründen.
Erstens liegt diese ECS-Schätzung von 0,6 °C nicht außerhalb des Bereichs anderer Beobachtungsschätzungen der CO₂-Empfindlichkeit. Der Knutti-Datensatz enthält die Ergebnisse von 172 Berechnungen des ECS, die mit unterschiedlichen Verfahren durchgeführt wurden. Meine Schätzung liegt am unteren Ende, aber sie ist nicht die niedrigste.
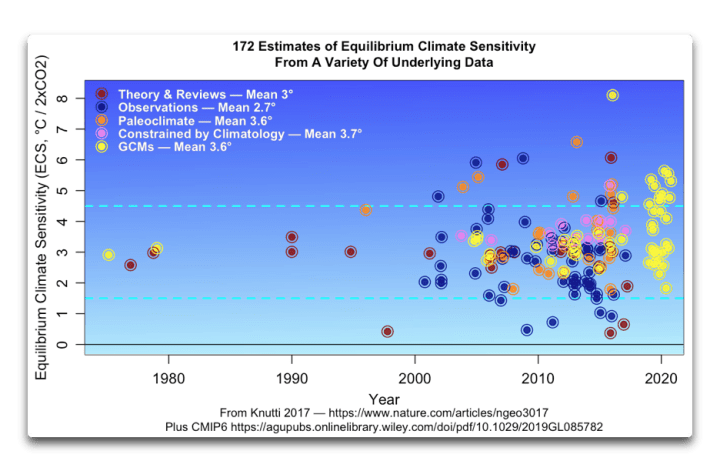
Abbildung 4. Schätzungen des ECS aus Theorie und Übersichten, Beobachtungen, Paläoklimastudien, Klimatologie und Klimamodellen. Man beachte, dass diese Schätzungen im letzten halben Jahrhundert nicht weniger, sondern mehr gestreut haben. Und das gilt besonders für die Klimamodelle (gelbe Punkte).
Der zweite Grund, warum ich meine ECS-Schätzung von 0,6°C pro 2xCO₂ für gültig halte ist, dass sie mit dem übereinstimmt, was ich über meine frühere Schätzung der ECS gesagt habe, die auf meiner Implementierung von Bejans Constructal-Klimamodell basierte. Das Modell ist hier beschrieben.
Ich fürchte, die meisten Leute verstehen nicht, wie wichtig das von Bejan entwickelte Modell des globalen Klimasystems ist. Wie ich gezeigt habe, leistet es sehr genaue Arbeit bei der Berechnung mehrerer kritischer Klimaparameter unter Verwendung eines einzigen, abgestimmten Parameters, der Leitfähigkeit. Leitwert bedeutet in diesem Zusammenhang, wie schnell das Klimasystem die Wärme aus der heißen Zone in die kalte Zone transportieren kann. Die Übereinstimmung des Modells mit der Realität ist unheimlich gut. Lesen Sie den Beitrag.
Anhand dieses Modells konnte ich experimentell meine beste Schätzung der Klimasensitivität ermitteln. Aus dieser früheren Analyse:
Dieses Konstruktionsmodell zeigt einige interessante Dinge über die Klimaempfindlichkeit auf.
Erstens ist die Empfindlichkeit eine Funktion der Veränderungen von rho (Albedo) und gamma (Treibhausanteil). Aber sie ist keine direkte Funktion. Sie ist das Ergebnis physikalischer Prozesse, die „q“ [den Fluss von der heißen in die kalte Zone] unter Berücksichtigung der Einschränkungen von rho und gamma maximieren.
Außerdem ist die Empfindlichkeit leicht unterschiedlich, je nachdem, ob die Änderungen der Albedo und des Treibhausanteils in der heißen Zone, in der kalten Zone oder in beiden auftreten.
Unter der Annahme, dass die abwärts gerichtete Strahlung aufgrund von Änderungen der Albedo oder des Treibhausanteils gleichmäßig von Pol zu Pol um 3,7 W/m² zunimmt, zeigt das konstruktive Modell einen Temperaturanstieg von ~1,1°C. (3,7 W/m² ist die Strahlungszunahme, die bei einer Verdopplung des CO₂-Anteils vorhergesagt wird).
Schließlich handelt es sich bei dieser Gleichgewichts-Klimaempfindlichkeit von 1,1 °C um eine maximale Empfindlichkeit, die die verschiedenen entstehenden thermoregulatorischen Prozesse nicht berücksichtigt, die sich tendenziell jeder Erwärmung oder Abkühlung widersetzen. Das bedeutet, dass die tatsächliche Empfindlichkeit niedriger ist als ~1,1°C pro 2xCO₂.
Und meine letzte Schätzung, 0,6°C pro 2xCO₂, ist tatsächlich niedriger als die obere Grenze von 1,1°C pro 2xCO₂, die in Bejans Modell gefunden wurde, genau wie ich vorhergesagt hatte.
Und damit endet meine Abhandlung über Nichtlinearität und wie sie mich zu meiner neuesten ECS-Schätzung geführt hat.
Link: https://wattsupwiththat.com/2025/07/12/moving-but-not-in-a-straight-line/
Übersetzt von Christian Freuer für das EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Sieht so aus als wenn Willis ueber den negativen Treibhauseffekt an den Polen gestolpert ist.
Aber ein zweites unabhaengiges Model das 0.6 Grad C fuer eine CO2 Verdopplung stipuliert?
Herr Dietze hat hoffentlich mitgelesen!
Im Studium habe ich noch gelernt, wie man die Bahnkurve eines
Satelliten beim Durchfliegen eines Doppelsternsystems berechnet.
Von daher habe ich eine ganz andere Sichtweise.
Was ist die eigentliche Ursache für die zeitweise Erwärmung/Abkühlung?
Im Klimasystem der Erde wird man die Antwort nicht finden,
sondern nur im Sonnensystem:
ECC_doc.pdf (https://magentacloud.de/s/WtrcBaxsqrdbiP2)
Da wir nicht in einem Doppelsternsystem leben,
kommt die GESAMT-ENERGIE für das Klimasystem
der Erde von einer einzigen Sonne.
Und diese GESAMT-ENERGIE schwankt eben im Zyklus von 165 Jahren.
Aus
https://eike-klima-energie.eu/2024/07/07/die-klima-zyklen-sind-planeten-gemacht-vorbestimmt-und-konstant/
„Zur Y- Achse, dort steht als Beschriftung „[sE.dNS]“, das für „Summe Energie delta (Nord -Süd)“
steht, wobei mit delta() NICHT das Minuszeichen im Term (Nord -Süd) gemeint ist.
„delta“ bedeutet „Variation der Leistung“, so wie es von Valentina Zharkova [06] definiert wurde.
Delta ist identisch mit 0.0, wenn es KEINE Planeten geben würde.
Analog zur X-Achse ist mit „[sE.dNS]“ die Änderung der Energie gemeint, die auf der Erde
ankommt, Integral mit einer zeitlichen Auflösung von 14.4 Minuten, unter Berücksichtigung der
Position der Erde, Neigung der Erdachse, Jahreszeit, Breitengrad und Tageszeit.“
GESAMT-ENERGIE zurzeit:
ECC_2023_45_sE_dNS.jpg
Physikalisch wird die Strahlung durch eine Intensität in W/qm beschrieben. Das ist kein „Fluß“ und also auch kein Vektor. Die Strahlung geht immer von einer Fläche aus. In Richtung der Flächennormalen ist die Strahlungsintensität maximal. Daher werden gerne Pfeile eingezeichnet, wodurch der Eindruck eines Vektors entsteht. Zu den Rändern der strahlenden Fläche fällt die Intensität mit dem Sinus des Strahlungswinkels gegen null ab. Fourier (1768- 1830) schloß daraus, dass die Strahlung aus einer gewissen Tiefe der Materie kommt. Strahlung in Richtung der Flächennormalen hat dann einen kürzeren Weg zur Oberfläche (auf dem Weg erfolgt Absorption) als wenn sie unter einem Winkel abgestrahlt wird. Er stellte auch fest, dass polierte Oberflächen mehr reflektieren als unpolierte und ene geringere Strahlungsleistung haben (Kichhoff´ sches Gesetz). Das wird auch daran liegen, dass die polierten Oberflächen auch den Austritt von innen nach außen durch Reflektion nach innen erschweren. Fourier´s Erklärung des atmosphärischen Wärmeeffektes hat auch sehr wenig mit dem sog. Treibhauseffekt zu tun. Für ihn ist das ein Wärmeleitungsphänomen, was durchaus auch mit heutigem Kenntnisstand noch sinnvoll ist. Die Beschreibung der Strahlung durch eine Intensität ergibt sich einfach daraus, dass man die Strahlung nur dann erfassen kann, wenn man sie absorbiert und damit umwandelt. Einen „Strahlungsfluß“ kann man nicht messen ohne ihn zu unterbrechen. Nun haben Gerlich und Tscheuschner bereits darauf hingewiesen, dass es für Intensitäten keinen Erhaltungssatz gibt. Anders als für die Energieerhaltung. Ein Strahlungsgleichgewicht zwischen zwei Körpern gibt es nur dann, wenn sich beide auf der gleichen Temperatur befinden. Natürlich kann man sagen, dass im Verlauf eines Jahres die mittlere Intensität der Einstrahlung gleich der mittleren Intensität der Ausstrahlung ist. Allerdings gibt es auf der Erde zu keinem konkretem Zeitpunkt und an keinem Ort ein „Strahlungsgleichgewicht“. Die Natur berechnet keine Mittelwerte und stört sich auch nicht an solchen. Eine konkret an einem Ort und zu einer festen Zeit zu messende „Strahlungsbilanz“ (Intensität der Einstrahlung minus Intensität der Ausstrahlung) ist nie ausgeglichen. Das wird ja auch genau so gemessen. Da es für Intensitäten „keinen Erhaltungssatz gibt“ ist es nicht sinnvoll, anzunehmen, dass die Natur bestrebt ist, Intensitäten in einer Strahlungsbilanz durch eine Temperaturerhöhung auszugleichen. Die Strahlung ist alleine eine Funktion der Temperatur und der Eigenschaften der Materie und nicht eine Funktion der Einstrahlung (Gerlich und Tscheuschner, sehr empfehlenswert).
„Die Natur berechnet keine Mittelwerte und stört sich auch nicht an solchen.“
Das ist einer der schönsten Sätze, die Sie geschrieben haben und ergeben den Sinn meines Andromedanebel-Vergleichs, wo es vermutlich nicht einmal Thermometer gibt, aus denen man physikalisch unzulässige Mittelwerte bilden kann. (Vermutlich weil weder ich noch evt. andere jemals dort waren!)
Nur, wer von den Klimaaktivisten wird das überhaupt verstehen oder gar in sein „Geschäftsmodell“ einbauen wollen?
Ggf. unterschätzen Sie die Jungs, die gerade im Andromedanebel leben, ggf. haben die „das Klima“ schon gebändigt, die Klimatisten der Erde sollten Kontakt aufnehmen, oder?
Sie haben recht, ggf. sind sie schon außerhalb des Universums, ohne zu wissen, ob es ein „außerhalb“ überhaupt gibt!