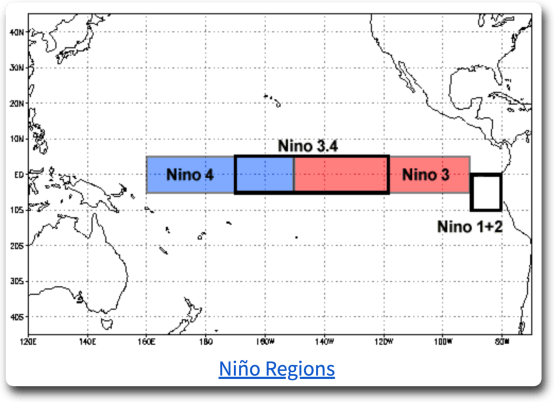
Bei einem meiner nächtlichen Streifzüge durch die Klimaliteratur stieß ich auf eine Studie aus dem Jahr 2021 mit dem Titel „Evidence of solar 11-year cycle from Sea Surface Temperature (SST)“ von Daniele Mazza und Enrico Canuto, im Folgenden MC21 genannt. Sie behaupten, mit Hilfe der Fourier-Analyse nachweisen zu können, dass die Meerestemperatur im tropischen Pazifik im Bereich des Nino 4 (5°N bis 5°S, 160°E – 150°W) im Zeitraum 1948-2021 ein Signal des Sonnenzyklus‘ enthält. Die gleiche Behauptung machen sie auch für ein breiteres Band im gleichen Nino-4-Gebiet der Tropen (10°N bis 10°S, 160°E – 150°W).
In dieser Analyse werde ich zwei sehr unterschiedliche Gründe aufzeigen, warum ihre Schlussfolgerungen nicht gerechtfertigt sind.
Lassen Sie mich mit der Frage beginnen: Was ist die Fourier-Analyse, eigentlich? Nun, im Jahr 1807 veröffentlichte ein französisches Genie namens Joseph Fourier seine brillante Erkenntnis. Er hatte erkannt, dass jedes Signal, z. B. eine Zeitreihe von Temperaturbeobachtungen, in eine Reihe von perfekten Sinuswellen zerlegt werden kann. Diese Sinuswellen, jede mit ihrer eigenen Amplitude, Periode und Phase, lassen sich addieren, um das ursprüngliche Signal exakt zu rekonstruieren.
Die Fourier-Analyse ist ein sehr leistungsfähiges Verfahren zur Zerlegung eines Signals. Sie hat sich bei der Analyse, Synthese und dem Verständnis von Signalen aller Art als äußerst erfolgreich erwiesen und wird für eine Vielzahl von Analysen verwendet. Sie ist jedoch nicht das einzige relevante Verfahren.
CEEMD steht für „Complete Ensemble Empirical Mode Decomposition“. Wie die Fourier-Analyse zerlegt sie ein Signal in eine Reihe von einfacheren Signalen. Die Fourier-Zerlegung zerlegt ein Signal jedoch nur in reine, gleichbleibend regelmäßige Sinuswellen. CEEMD hingegen zerlegt das Signal in „empirisch bestimmte“ zugrundeliegende Signale. Das bedeutet, dass der Bereich der Zykluslängen der Signale in jeder Gruppe durch die Daten selbst bestimmt wird. Ich erörtere CEEMD ausführlich in meinem Beitrag mit dem Titel Noise Assisted Data Analysis.
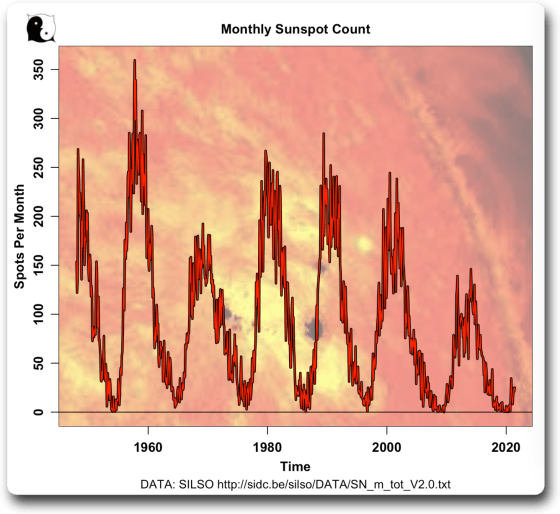
Was bedeutet das in der Praxis? Nun, lassen Sie mich CEEMD auf die Daten anwenden, die sie in ihrer Analyse verwendet haben. Zunächst sehen Sie hier die monatlichen Sonnenfleckendaten von 1948 bis Mitte 2021:
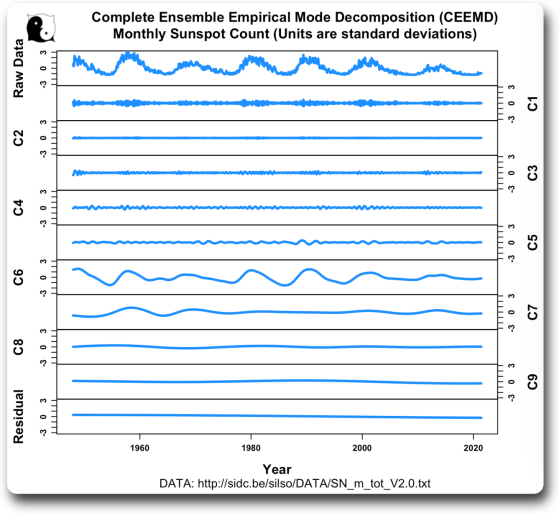
Und hier ist die vollständige empirische Zustands-Dekomposition (CEEMD) desselben Sonnenfleckensignals:
Was sehen wir uns hier also an? Das obere Feld zeigt die Rohdaten. Die Felder C1 bis C9 zeigen das Signal in jedem der neun empirischen Modi. Zusammen mit dem Resttrend im unteren Feld ergibt sich daraus eine perfekte Rekonstruktion des ursprünglichen Signals. Der größte Teil des Sonnenfleckensignals liegt eindeutig im empirischen Modus C6.
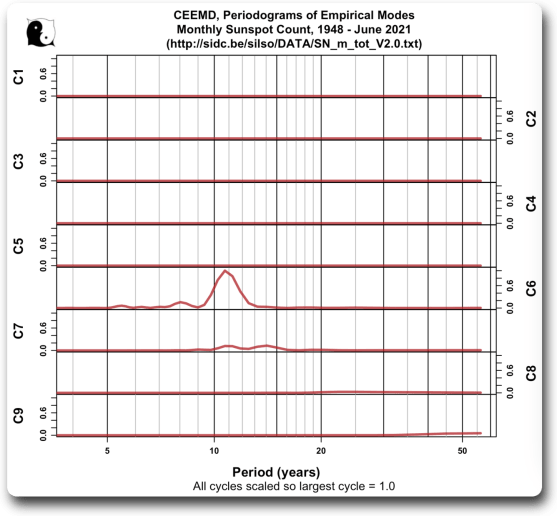
Im Folgenden wird die CEEMD-Sonnenfleckenzerlegung auf eine andere Weise betrachtet. Dazu werden die Periodogramme der einzelnen empirischen Modi betrachtet. Periodogramme zeigen die Perioden (Zykluslängen) der Signale, die den jeweiligen empirischen Modus bilden. Abbildung 3 zeigt dieses Ergebnis:
Hier sehen wir, dass der empirische Modus C6 einen starken Sonnenfleckenzyklus enthält, der mit knapp 11 Jahren seinen Höhepunkt erreicht, mit etwas mehr sonnenfleckenbezogener Stärke im empirischen Modus C7. Ansonsten gibt es wenig zu sehen.
Nun können wir die langperiodischen Schwankungen im Sonnenfleckensignal nachbilden, indem wir einfach die in Abbildung 2 gezeigten empirischen Modi von ~ 11 Jahren und länger addieren. Dabei handelt es sich um die Modi C6 bis C9 plus den Resttrend. Abbildung 4 zeigt dieses Ergebnis, überlagert mit den zugrunde liegenden Sonnenfleckendaten:
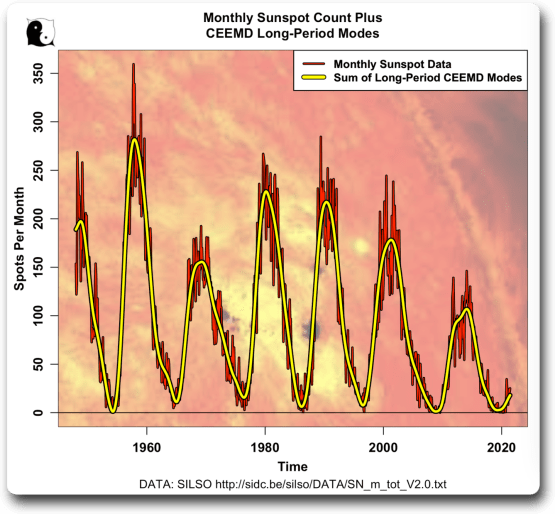
Abbildung 4. Sonnenfleckenzahlen wie in Abbildung 1, überlagert mit der Summe der empirischen Modi von 11 Jahren und länger.
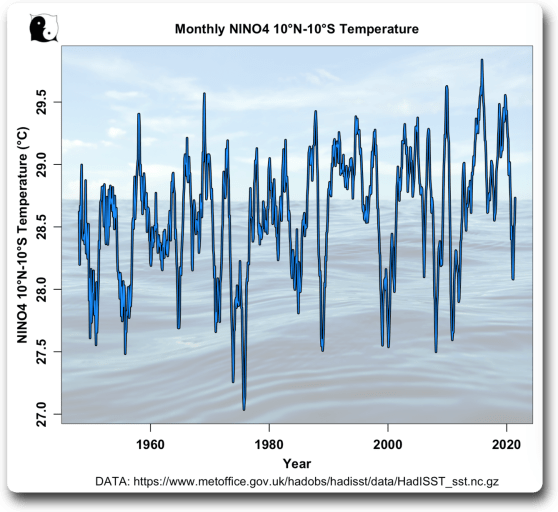
So weit, so gut. Sie können sehen, wie gut der CEEMD die Schwankungen in den Sonnenfleckendaten wiedergibt. Als Nächstes zeige ich die gleiche Art von Analyse für den großen NINO4-Bereich, der in der MC21-Analyse verwendet wurde. Hier sind zunächst die Rohdaten von 1948-2021:
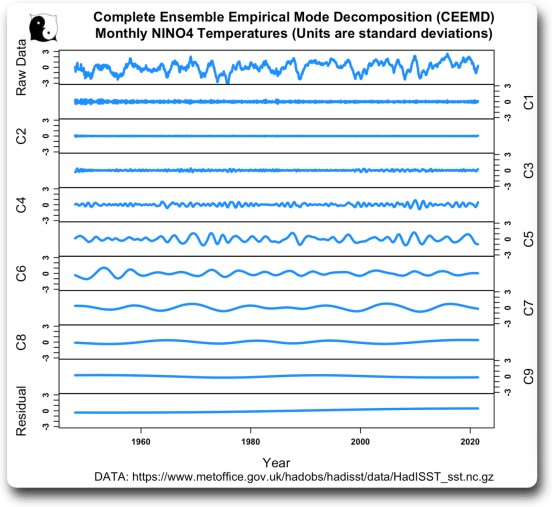
Als Nächstes wird die vollständige empirische Zustands-Zerlegung (CEEMD) desselben Temperatursignals dargestellt:
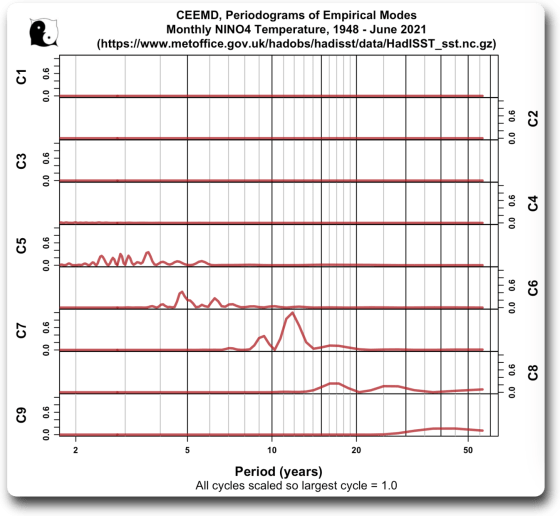
Dann haben wir die Periodogramme jedes der empirischen Modus-Signale:
Hier können wir sehen, dass es einen starken Zyklus gibt, der bei 12 Jahren seinen Höhepunkt erreicht … und das ist der Grund, warum die Autoren von MC 21 ein „Sonnensignal“ in den Ozeantemperaturen geltend machen. In den Sonnenfleckendaten gibt es jedoch keinen 12-Jahres-Zyklus. Sehen Sie sich Abbildung 3 an. Er ist ein paar Monate kürzer als ein 11-Jahres-Zyklus.
Schließlich können wir, wie in Abbildung 4, den zugrundeliegenden Temperaturzyklus in den NINO4-Daten von 10°N-10°S rekonstruieren, indem wir die 11-jährigen und längeren empirischen Modi plus den Rest addieren. Abbildung 8 zeigt dieses Ergebnis:
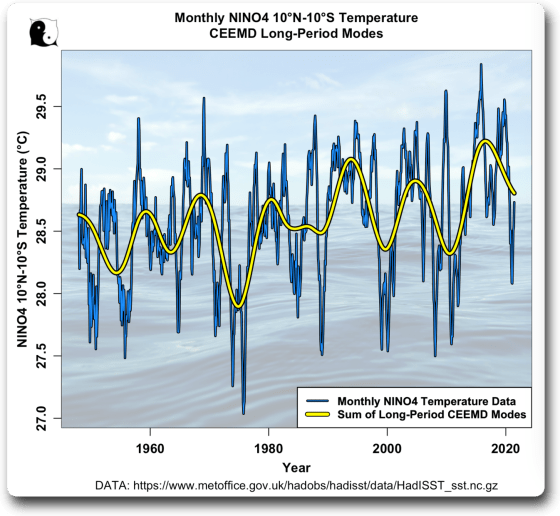
Abbildung 8. Temperaturen wie in Abbildung 1, überlagert mit der Summe der empirischen Modi von 11 Jahren und länger.
Wie man sieht gibt es ein Signal, und die CEEMD-Analyse ergibt eine sehr gute Übereinstimmung … aber es ist ganz anders als das Signal der Sonnenflecken. Um die Unterschiede zu verdeutlichen, möchte ich die Summen der CEEMD-Modi über elf Jahre für die Sonnenflecken und die Temperaturen zeigen:
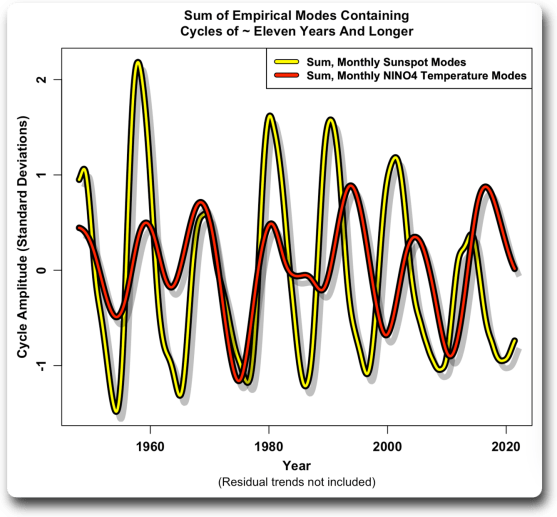
Abbildung 9. Vergleich der zugrundeliegenden Zyklen der Sonnenflecken und der NINO4 10°N-10°S Temperaturen. Um einen direkten Vergleich zu ermöglichen, wurden die CEEMD-Resttrends in beiden Ergebnissen nicht berücksichtigt.
Hier werden die Fehler in ihrer Analyse ganz offensichtlich. Sie haben behauptet, dass ein 12-Jahres-Zyklus in den Temperaturdaten auf Sonnenschwankungen zurückzuführen ist. Aber wie Sie sehen können, gibt es zwar eine passable Übereinstimmung bis 1980, aber selbst in diesem Abschnitt sind die Spitzen und Tiefpunkte des Temperatursignals dem Sonnensignal manchmal um bis zu anderthalb Jahre voraus. Das würde bedeuten, dass es unmöglich ist, dass die NINO4-Temperatur den Sonnenfleckenzyklus verursacht … und zu anderen Zeiten liegen die Flecken bis zu dreieinhalb Jahre vor den Temperaturen.
Schlimmer noch, nach 1980 verschieben sich die NINO4-Temperaturen mehr und mehr nach rechts. Dies spiegelt den Unterschied zwischen dem 10,75-Jahres-Zyklus der Sonnenfleckendaten im Zeitraum von Januar 1948 bis Juni 2021 und dem 12-Jahres-Zyklus der NINO4-Temperaturen im gleichen Zeitraum wider.
Kurz gesagt, die Zyklen liegen zwar nahe beieinander, aber sie zeigen keinen Zusammenhang zwischen dem 11-jährigen Sonnenfleckenzyklus und dem 12-jährigen Temperaturzyklus in diesem Zeitraum.
Warum also gibt es eine Ähnlichkeit? In ihrer Studie zeigen sie den Grund auf, nämlich:
Nachdem wir Hunderte von Temperaturaufzeichnungen der Erdoberfläche heruntergeladen und analysiert hatten, fanden wir schließlich in einigen wenigen Fällen eindeutige Beweise für die 11-Jahres-Zyklus-Signatur der Sonne, während diese in der überwiegenden Mehrheit der anderen Fälle nicht nachweisbar war, da sie unter anderen (saisonalen oder El-Nino-bedingten) Schwingungen oder Rauschen begraben war.
(Nebenbei bemerkt gefällt mir ihre völlig unbelegte Behauptung, dass der Sonneneffekt überall vorhanden ist, aber nur nicht „nachweisbar“ ist, weil er unter Gründen „begraben“ ist … aber ich schweife ab).
Das Problem ist, dass man, wenn man an genügend Stellen sucht, schließlich ein ähnliches Signal findet … aber das ist wahrscheinlich statistisch nicht signifikant. Hier ist ein Beispiel:
Nehmen wir an, Sie haben einen Zufallszahlengenerator, der bei jeder Benutzung eine neue Zufallszahl zwischen eins und hundert erzeugt. Ein Mann sagt: „Ich kann den Bereich der nächsten Zahl erraten. Sie wird zwischen eins und fünf liegen“. Und tatsächlich, die nächste Zahl ist drei.
Da die Wahrscheinlichkeit, dass er sie zufällig richtig errät, nur eins zu zwanzig (0,05) beträgt, gilt dieses Ergebnis bei einem „p-Wert“ von 0,05 als statistisch signifikant, und vielleicht hat der Mann Recht, dass er die Zahl erraten kann. Natürlich besteht bei einem p-Wert von 0,05 immer noch eine 5 %ige Chance, dass es sich um reines Glück handelt.
Nehmen wir aber andererseits an, die nächste zufällige Zahl ist zweiunddreißig. Der Mann liegt falsch. Also sagt er: „Lass es mich noch einmal versuchen“ … und wieder scheitert er. Also versucht er es noch einmal und noch einmal, und natürlich hat er irgendwann schließlich Recht.
Ist dieses Ergebnis statistisch signifikant? Darf er sich als erfolgreich bezeichnen?
Nun … nein. Wie mein Vater zu sagen pflegte, als ich ein Kind war: „Selbst ein blindes Huhn findet ab und zu ein Korn“.
Nein, es ist nicht signifikant, und er kann keinen Erfolg für sich beanspruchen, denn wenn man genügend Versuche unternimmt, oder im Falle der aktuellen Sonnenflecken, wenn man an genügend Stellen nachsieht, wird man schließlich ein positives Ergebnis erhalten.
Um dies auszugleichen, verwenden wir die so genannte „Bonferroni-Korrektur“. Dabei handelt es sich um eine Erweiterung der Arbeit des italienischen Mathematikers Carlo Emilio Bonferroni (1892-1960). Die Korrektur selbst wurde von einer Frau namens Olive Jean Dunn entwickelt und 1961 veröffentlicht. Sie erwähnte Bonferroni nur einmal in ihrer Analyse, aber sie war in den 1960er Jahren eine Frau, so dass Bonferroni den Ruhm erntete … man stelle sich das vor.
Auf jeden Fall besagt die Bonferroni/Dunn-Korrektur, dass man, wenn man nach statistischer Signifikanz bei einem bestimmten p-Wert von „α“ suchen (sagen wir 0,05 wie im obigen Beispiel, ein Wert, der in der Klimawissenschaft häufig verwendet wird) und man an „n“ Stellen danach sucht, man den p-Wert wie folgt nach unten anpassen muss:
Nach ihrer eigenen Beschreibung suchten die Autoren nach dem Sonnensignal in „Hunderten von Temperaturaufzeichnungen“ … um also etwas statistisch Signifikantes zu finden, muss es eine sehr, sehr gute Übereinstimmung sein, mit einem Bonferroni-korrigierten p-Wert von
α von 0,05 / n von 100 = korrigierter p-Wert von 0,0005
Dies ist eine Übereinstimmung, wie sie in der Klimawissenschaft nur selten vorkommt … und in ihrer Analyse erwähnen sie nicht einmal die statistische Signifikanz.
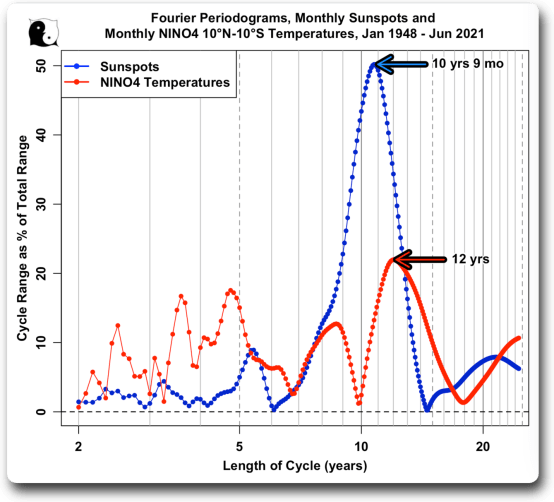
Das ist also meine Analyse der MC21-Studie. Und, hoppla, wenn sie einfach eine einfache alte Fourier-Analyse verwendet hätten und sie mit der Fourier-Analyse der Sonnenflecken für den gleichen Zeitraum verglichen hätten, anstatt sie nur mit den NINO4-Temperaturen durchzuführen, hätten sie das Problem sofort erkannt:
Wie man sieht sind die Perioden bei weitem nicht gleich, was bedeutet, dass sie in und aus der Phase zueinander gehen. Das wiederum bedeutet, dass, wie oben in Abb. 9 gezeigt, die Veränderungen der NINO4-Temperaturen zeitweise die Veränderungen der Sonnenflecken anführen … und das bedeutet, dass die Sonnenflecken unmöglich die Ursache für die NINO4-Temperaturen sein können.
Und eine weitere Sonnenstudie beißt ins Gras.
Zur Erinnerung: Ich habe vor einigen Jahrzehnten begonnen, mich mit der Frage eines Zusammenhangs zwischen Sonnenflecken und Wetter zu beschäftigen, und ich war ein wahrer Gläubiger des Zusammenhangs zwischen Sonnenflecken und Wetter. Ich dachte, es wäre einfach, Beweise dafür zu finden, dass Sonnenflecken in irgendeiner Form das Wetter beeinflussen.
Aber obwohl ich mir eine Reihe von Temperaturen, Niederschlägen, Fluss-, See- und Meeresspiegeln und anderen Phänomenen angesehen habe, von denen behauptet wurde, sie enthielten ein Sonnenfleckensignal, habe ich nie eine Behauptung gefunden, die einer genauen Prüfung standhielt. Hier finden Sie Links zu 24 meiner Sonnenfleckenanalysen, die alle … nichts zeigten. Das bedeutet nicht, dass es keinen Zusammenhang zwischen Sonnenflecken und Oberflächen-Phänomenen gibt – es bedeutet nur, dass ich, falls es ihn gibt, ihn nicht finden konnte.
Link: https://wattsupwiththat.com/2023/02/20/ceemd-vs-joe-fourier/
Übersetzt von Christian Freuer für das EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Wenn ein Signalmaximum später als ein anderes erscheint, heißt das nMn nicht, daß es nicht die Ursache des früheren Signals sein kann. Es kann eine Verzögerung vorliegen, aber auch könnte das Minimum die Ursache des Maximums des 2. Signals sein.
Was ergibt eine Betrachtung über mehrere Sonnenzyklen? Da müsste die Abweichung der Signale doch größer werden? Vielleicht jeden Zyklus 1 Jahr mehr Abweichung?