Eine physikalische Betrachtung von Michael Mechtel
Der Gehalt der Atmosphäre an CO2 steigt seit Jahrzehnten an. Hauptverantwortlich dafür soll menschliche Aktivität sein. Diese These wird durch Abgleich zweier empirischer Datensätze überprüft: Einerseits liegt die langjährige Messreihe des atmosphärischen CO2-Gehalts der Station Mauna Loa auf Hawaii (die Keeling-Kurve) vor, zum anderen die Datenreihe des jährlichen anthropogen verursachten CO2-Eintrags in die Atmosphäre. Es wird untersucht, ob dieser CO2-Eintrag allein den Verlauf der Keeling-Kurve reproduzieren kann. Das Ergebnis ist eindeutig negativ, aber eine umfassende Antwort auf die Titelfrage steht noch aus.
Das „böse“ CO2?
CO2 steht bekanntlich im Mittelpunkt der aktuellen Diskussionen um die Klimaveränderung, wobei zwei Fragestellungen relevant sind:
- Wie groß ist der Einfluß des CO2 als Stellschraube fürs Klima?
- Ist der Mensch wirklich Hauptverursacher der aktuellen CO2-Zunahme in der Atmosphäre?
Die Antworten auf beide Fragen haben erheblichen Einfluß auf politische Entscheidungen. In diesem Beitrag wird jedoch auschließlich die zweite Frage behandelt.
Die vorherrschende Meinung lautet, dass sich der natürliche Kohlenstoffkreislauf im vorindustriellen Zeitalter in einem Gleichgewicht befunden habe, bei dem das Konzentrationsniveau in der Atmosphäre 280 ppm betrug. Das entspricht bei gleichmäßiger Durchmischung einer Gesamt-CO2-Masse von 2245 Gigatonnen (Gt) – der Umrechnung liegt der Faktor 8,02 Gt pro ppm zugrunde. Der seitherige Anstieg auf z.Zt. mehr als 400 ppm soll allein durch menschliche Aktivitäten verursacht sein, die CO2 freisetzen, wie z.B. die Verbrennung fossiler Brennstoffe, Waldrodung usw. Wenn das so wäre, müsste sich die Keelingkurve aus den jährlichen anthropogenen Emissionen rekonstruieren lassen.
Sowohl für die Konzentrations- wie die Emissionswerte liegen Datenreihen über rund sechs Jahrzehnte vor. Ausgewertet wurde der Zeitraum 1960 – 2018. Die Überlegungen sind durchweg formal-mathematischer Natur, aber so gehalten, dass sie mit gewöhnlichem Schulwissen verständlich sein sollten.
Den Anstoß für die Untersuchung gab die Beobachtung, dass der atmosphärische CO2-Gehalt (die Keelingkurve) nicht linear ansteigt, sondern überlinear, leicht parabelförmig, also einen Beitrag enthalten muss, der mindestens quadratisch mit der Zeit wächst. Die Kurve des anthropogenen CO2-Eintrags hingegen weist nur einen linearen zeitlichen Anstieg auf (nach Bereinigung von Schwankungen). Um die hiermit verbundene Problematik zu verstehen, zunächst eine einführende Analogie-Überlegung:
Füllt man Wasser in einen Kochtopf, und zwar, sagen wir, jede Stunde den gleichen Betrag, dann wird sich der Wasserstand linear in der Zeit erhöhen.
Steigt jedoch der Nachfüllbetrag selber linear an, wie es unserem jährlichen CO2-Eintrag in die Atmosphäre entspricht, sagen wir, in der ersten Stunde füllen wir 50 ml nach, in der zweiten 100 ml, in der dritten 150 ml usw., dann wird der Wasserstand im Topf im Quadrat der Zeit ansteigen – und das wiederum entspricht tatsächlich dem Verhalten der Keeling-Kurve. Also alles in Ordnung?
Nein! Der Planet Erde mit seiner Lufthülle verhält sich nicht wie ein Kochtopf. Es gibt hier Senken, in denen atmosphärisches CO2 verschwindet, wie etwa den Ozean und die Biosphäre. Diese Senken sollten aus physikalischen Gründen um so wirksamer sein, je höher die CO2-Konzentration in der Atmosphäre ist. Damit wird es fragwürdig, ob die quadratische Keelingkurve allein mit dem linear wachsenden menschlichen CO2-Eintrag erklärbar ist. Im folgenden soll das näher untersucht werden.
Datengrundlage
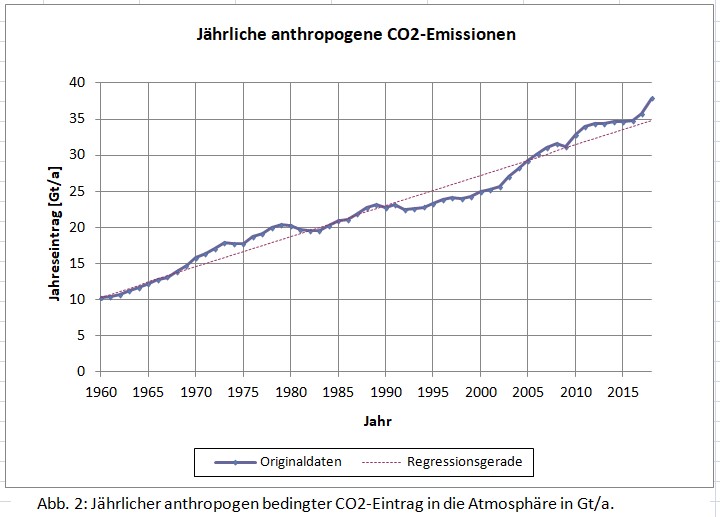
Die veröffentlichten monatlichen Messdaten der CO2-Konzentration sind [1] entnommen. Sie zeigen eine leicht wellige Struktur [2], die einem jahreszeitlichen Rhythmus unterliegt. Um diese Schwankungen herauszumitteln und den langfristigen Trend freizulegen, wurden die jeweiligen Jahresmittelwerte gebildet. Sie sind in Abb.1 dargestellt, umgerechnet auf die atmosphärische Gesamt-CO2-Masse in Gigatonnen (Gt).
Zu diesem modifizierten Datensatz wurde nun eine linear-quadratische Regressionsfunktion (Parabel) als Anpassung mit der kleinsten quadratischen Abweichung berechnet. Die Parabel hat die Form
m(t) = A*t² + B*t + C.
t ist die Zeit in Jahren (1960: t = 0) und m die Gesamt-CO2-Masse in der Atmosphäre. Die Regressions-Parameter dieser Parabel lauten:
A = 0,10023 Gt/a², B = 6,88845 Gt/a und C = 2535,2 Gt (annus, a steht für Jahr).
Auch die Regressionsparabel ist in Abb. 2 eingetragen, und es zeigt sich eine hervorragende Übereinstimmung mit den Meßdaten. Der Korrelationskoeffizient zwischen beiden Kurven ist 99.97 %.
Die Daten des anthropogenen CO2-Eintrags entstammen [3] und umfassen den gleichen Zeitraum. Ein quadratischer Trend ist hier nicht zu erkennen, deshalb wurde zur Bereinigung der Schwankungen eine lineare Anpassung berechnet:
QPktz(t) = beta*t + QPktz0
QPkt (gesprochen Q-Punkt, und Punkt steht für die zeitliche Ableitung der eingebrachten Masse) bedeutet den jährlichen Zufluss an CO2 , also einen Quellfluss. Er wird in Gigatonnen pro Jahr (Gt/a) angegeben. Der Zusatz z in QPktz steht für ‘zivilisationsbedingt‘, also anthropogen.
Die Regressionsparameter lauten hier beta = 0,42231 Gt/a² und QPktz0 = 10,4836 Gt/a.
Originaldaten und Ausgleichsgerade sind in Abb. 2 eingetragen. Ihr Korrelationskoeffizient beträgt
98,2 %.
Untersuchungsmethode
Im folgenden werden wir die Regressionskurven statt die Originaldaten analysieren. Das hat den Vorteil, dass irreguläre Schwankungen eliminiert sind, was die Untersuchung wesentlich vereinfacht.
Wir gehen aus von der Grundgleichung
mPkt = QPkt – Spkt,
was nichts anderes bedeutet als: die jährliche Änderung der atmosphärischen CO2-Masse (mPkt) ergibt sich aus den jährlichen Zuflüssen von den Quellen (QPkt) abzüglich der jährlichen Abflüsse in die Senken (SPkt). Wir kennen mPkt bereits aus der Keelingkurve. QPkt betrachten wir zunächst als unbekannt, denn wir kennen wir nur den zivilisatorischen Anteil QPktz (siehe Abb. 2).
Für SPkt müssen wir eine Modellannahme machen, die aber gut begründet erscheint: das Verschwinden von CO2 in den Hauptsenken Ozean und Pflanzenwelt wird im wesentlichen als diffusionsgetrieben betrachtet [4], [5]. Das hat zur Folge, dass der Senkenstrom SPkt proportional zur CO2-Masse m in der Atmosphäre ist, mit ihr also über eine Proportionalitätskonstante alpha, die Abklingkonstante, verbunden ist:
SPkt = alpha * m. (1)
alpha wird in den hier benutzten Einheiten in 1/a gemessen (1/Jahr).
Dieser Diffusionsansatz für den Senkenfluß führt zu der wichtigen Folgerung, dass der Quellfluss selber eine Parabelform aufweisen sollte! Man erkennt das, indem man die Grundgleichung nach dem unbekannten QPkt umstellt, alle bekannten Größen einsetzt und dann nach Potenzen von t umordnet.
Wir setzen QPkt deshalb wie folgt an:
QPkt = U*t² + V*t + W. (2)
und können dann die unbekannten Parameter U,V und W durch Koeffizientenvergleich direkt auf die bekannten Parameter A, B und C der Keelingkurve zurückführen:
U = alpha*A,
V = 2*A + alpha*B,
W = B + alpha*C.
Wie man sieht, muss man die Abklingkonstante alpha kennen, um die Werte zu berechnen. Dazu liefert unser Ansatz keine Vorgaben, er wird in einem breiten Wertebereich von alpha funktionieren. Die Atomwaffentests in der Atmosphäre um das Jahr 1960 herum legen den Wert alpha = 0,05 /a nahe, (Näheres siehe Anhang). Damit sind wir in der Lage, die gesuchten Koeffizienten für den jährlichen Gesamt-Zufluss QPkt zu berechnen:
U = 5,011E-3 Gt/a³, V = 0,5449 Gt/a² und W = 133,65 Gt/a.
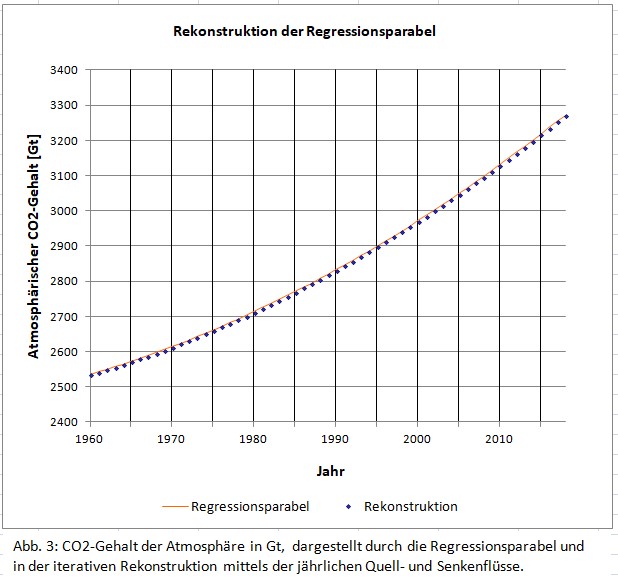
Wir haben nun das Rüstzeug beisammen, um iterativ in einer Tabellenkalkulation die Regressionsparabel der Keelingkurve nachzubilden: beginnend 1960 setzt man die Ausgangs-CO2-Masse ein, berechnet QPkt und SPkt anhand der Formeln (2) und (1), kommt so mittels der Grundgleichung zur Massenänderung mPkt für das jeweilige Jahr und addiert diese dann auf die vorhandene Masse, um die Masse des Folgejahres zu bestimmen. Diese Rekonstruktion der Parabel mit unserem linear-quadratischen Ansatz für den Quellfluss gelingt hervorragend, siehe Abb. 3.
Der Zusatz-Quellfluß unbekannter Herkunft, der uns hier vorrangig interessiert, ergibt sich als Differenz QPktx = QPkt – QPktz. Er läßt sich für jedes Jahr berechnen. Ausgewählte Ergebnisse zeigt Tabelle 1.
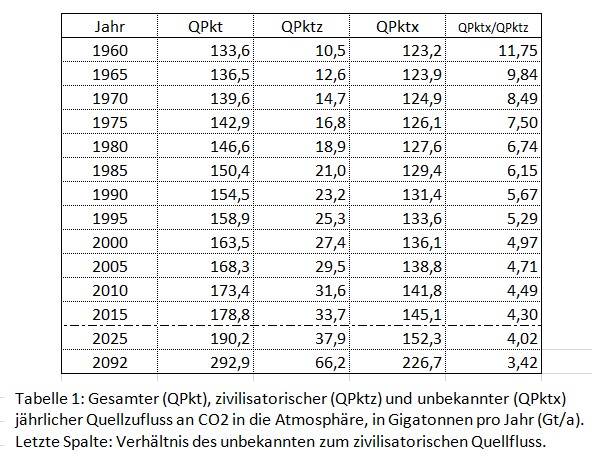
Man erkennt, dass der unbekannte Quellzufluss vom Beginn des Auswertezeitraums an zunimmt (Spalte 4), in Relation zum zivilisatorischen Zufluss jedoch zunächst abnimmt (Spalte 5). Einfache Extrapolation der Rechnung ergibt für 2025 den Wert QPktx/QPktz = 4,0. Um das Jahr 2092 wird dann ein sehr flaches Minimum beim Wert 3,4 durchlaufen (siehe letzte Zeile). Eine so weite Extrapolation darf man allerdings nicht als Prognose verstehen!
Die entscheidende Erkenntnis aus Tabelle 1 lautet, dass der unbekannte Quellzufluss bis heute mindestens viermal größer war als der zivilisationsbedingte, im Schnitt über den Auswertezeitraum rund sechsmal größer. Menschliche Aktivität spielte demzufolge mit weniger als 15 % Anteil nur eine untergeordnete Rolle im beobachteten CO2-Anstieg der Atmosphäre.
Zusammenfassung der Ergebnisse
A) Der zeitliche Verlauf der atmosphärischen CO2-Konzentration läßt sich im Auswertezeitraum 1960 – 2018 in hervorragender Näherung als Teil einer Parabel beschreiben.
B) Dieser parabolische Verlauf verlangt im Modell diffusionsgetriebener Senkenflüsse prinzipiell auch einen parabolisch ansteigenden Quellzufluß. Der Ansatz erweist sich als zielführend, liefert selbst jedoch keinen Aufschluß über den Wert der Abklingkonstanten, der den Senkenfluss bestimmt.
C) Legt man in diesem Ansatz die Abklingkonstante zu Grunde, die sich aus den Atomwaffentests des 20. Jahrhunderts ergibt, dann hatte der veröffentlichte anthropogene CO2-Ausstoß zwischen 1960 und 2018 im Durchschnitt nur einen Anteil von weniger als 15 % am Anstieg des atmosphärischen CO2-Gehalts.
Diskussion
An dieser Stelle erhebt sich die Frage nach dem Ursprung des unbekannten zusätzlichen Quellflusses QPktx. Dass er auf einem Fehler in der Angabe des menschlichen Eintrags QPktz beruht, ist in der erforderlichen Höhe kaum vorstellbar.
Eine natürliche Quelle dafür ist zunächst auch nicht erkennbar, zumal wenn man die These vertritt, dass die Atmosphäre ohne menschliches Zutun in einem immerwährenden Gleichgewicht beim Gehalt von 280 ppm ruht. Diese These ist allerdings fragwürdig. Sie lässt sich nicht auf fundamentale Gesetzmäßigkeiten zurückführen. Wenn sie in einem gewissen Zeitfenster zutreffend gewesen sein mag, bedeutet dies noch keine Festlegung für alle Zeiten. Mit Wegfall der Gleichgewichts-These verliert der Quellfluß QPktx seinen mysteriösen Charakter und ist einfach Bestandteil der natürlichen Dynamik, die noch weiter erforscht werden muss. Detailliertere und lesenswerte Ausführungen zu diesem Themenbereich finden sich in [8].
Fassen wir noch mögliche Fehler unserer Analyse ins Auge: ihr Resultat hängt entscheidend vom Wert der Abklingkonstanten alpha ab: wenn alpha niedriger wird, reduziert sich auch der Beitrag QPktx. Das wird den Zusatzbeitrag QPktx aber nicht beseitigen, sondern nur quantitativ modifizieren (s. Anhang).
U.U. wäre eine zeitliche Verminderung der Abklingkonstanten in Betracht zu ziehen, etwa weil die Senken an die Grenze ihrer Aufnahmefähigkeit kommen. Dies wird z.B. in [4] verneint. Dagegen spricht außerdem, dass die Abklingkurve des C-14 aus den Kernwaffentests im wesentlichen von der Aufnahmefähigkeit des tiefen Ozeans und der Biomasse bestimmt wird [8], wo keine Sättigung vorliegt.
Die Rolle möglichst gut zu klären, die der anthropogene CO2-Ausstoß tatsächlich spielt, ist von großem Interesse, denn die von der Politik geforderten Maßnahmen zur CO2-Reduktion und –vermeidung kosten hohe Milliardenbeträge. Sie lassen sich nur auf einer sicheren Wissensgrundlage rechtfertigen, ganz abgesehen davon, daß national beschränkter Parteien-Ehrgeiz ins Leere läuft, wenn es an internationaler Koordination der Maßnahmen fehlt.
Anhang: Die Bestimmung der Abklingkonstanten
Der Kehrwert der Abklingkonstanten hat die Bedeutung einer charakteristischen Zeit tau für das Abklingen des atmosphärischen CO2-Pegels, wenn der Quellstrom versiegt (Abklingzeit). Man kann tau auch als die mittlere Verweilzeit eines CO2-Eintrags in der Atmosphäre interpretieren, die wiederum mit der Halbwertszeit HWZ = tau * ln2 verbunden ist. Aus der C-14-Abklingkurve in [11] (die auch in [8] wiedergegeben ist) lässt sich unmittelbar ableiten tau = 16 Jahre, und mit der Korrektur von Störeinflüssen wird daraus der Wert 20 Jahre [8]. Daraus wiederum bestimmt sich der oben benutzte Wert alpha = 1 / tau = 0,05 /a.
Die Spannweite der möglichen alpha-Werte, die sich alle eignen, um die Keeling-Kurve zu rekonstruieren, ist allerdings sehr groß. In verschiedenen Veröffentlichungen (z.B. [4], [9], [10]) findet man für tau Angaben im Bereich 40 bis 60 Jahre, also alpha ca. 0,02 /a. Solche Werte kommen zustande, wenn man die Hypothese eines stabilen 280-ppm-Niveaus als naturgegeben voraussetzt und das Abklingen einer Störung auf dieses Niveau bezieht. Mit einem solch geringen alpha-Wert fällt auch der quadratische Quell-Parameter U = alpha * A nur gering ins Gewicht, so dass der Quellfluß sich stark dem linearen Verlauf der anthropogenen Quelle annähert. Daraus aber wie Eschenbach [10] den Schluß zu ziehen, am Anstieg der Keelingkurve wäre neben dem anthropogenen Quellfluß kein natürlicher Zusatzbeitrag beteiligt, ist unzulässig. Wie sich das Verhältnis des unbekannten zum zivilisatorischen Quellfluß mit alpha verändert, sei am Beispiel des Jahres 2015 demonstriert:
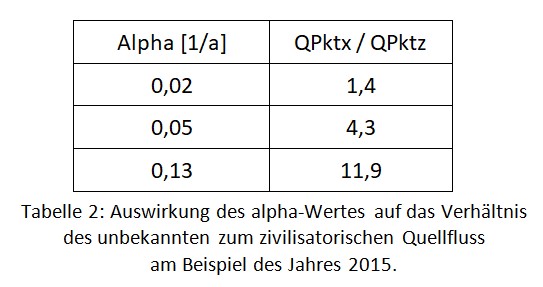
Selbst im extremen Fall alpha = 0,02 /a wird der zivilisatorische Quellenanteil noch vom unbekannten Zusatzanteil übertroffen.
Im anderen Extrem setzt man das vorindustrielle 280-ppm-Niveau (also den atmosphärischen Gehalt mnat = 2245 Gigatonnen) mit dem Fluss in Verbindung, der den Austausch zwischen Atmosphäre und ozeanischer Deckschicht beschreibt. Der beträgt nach [6] QPktoz = 293 Gt/a (die Angaben zu QPktoz variieren etwas, vgl. z.B. [6], [7]; Umrechnungsfaktor von Gt C auf Gt CO2: 3,66). Aus diesem Szenario läßt sich herleiten: alpha = QPktoz / mnat = 0,13 /a, und daraus folgt wiederum die Abklingzeit tau = 7,7 Jahre. Es ist aber bekannt, dass neben diesem ‚schnellen‘ Zyklus auch langsamere Zyklen existieren, an denen der tiefe Ozean, die Biosphäre und das Gestein beteiligt sind [8]. Sie sind bei dekadischen Verläufen zweifellos zu berücksichtigen und kommen auch in der C-14-Kurve zum Tragen, die in dieser Arbeit zugrunde gelegt wurde.
Quellenverweise
[1] https://www.umweltbundesamt.de/daten/klima/atmosphaerische-treibhausgas-konzentrationen#kohlendioxid-
Dort die Option ‘Diagramm als Excel mit Daten’ anklicken.
[2] https://de.wikipedia.org/wiki/Keeling-Kurve
[3] https://www.statista.com/statistik/daten/studie/37187/umfrage/der-weltwoche-co2-ausstoss-seit-1751/
[4] J. Dengler, J.Reid 2023: Emissions and CO2 Concentration – An Evidence Based Approach, Atmosphere 2023, 14, 566
https://doi.org/10.3390/atmos14030566
[5] E. Roth 2023: Das schnelle Wachsen der CO2-Konzentration, Ursachen und Folgen
https://eike-klima-energie.eu/2023/06/06/das-schnelle-wachsen-der-co2-konzentration
[6] https://wiki.bildungsserver.de/klimawandel/index.php/Kohlenstoffkreislauf
[7] https://de.wikipedia.org/wiki/Kohlenstoffzyklus
[8] E. Roth 2025: About the Origin of CO2 in the Atmosphere, SCC-Publishing Vol. 5.1 prelim. pp. 1-14,
https://doi.org/10.53234/scc202501/05
[9] P. Dietze 2020: DEKARBONISIERUNG? Der fatale Irrtum durch falsche C-Modelle,
https://www.fachinfo.eu/dietze2020.pdf
[10] W. Eschenbach 2025: Über Emissionen und CO2,
https://eike-klima-energie.eu/2025/04/07/ueber-emissionen-und-co2/
[11] https://de.wikipedia.org/wiki/Kernwaffen-Effekt
Der Autor ist Diplomphysiker i.R. und war beruflich im medizinischen Strahlenschutz tätig. Er ist also kein Atmosphären- oder Klimawissenschaftler und hat deshalb keinen vollständigen Überblick über die einschlägige Fachliteratur. Zweifellos werden einige der aufgeworfenen Fragen dort behandelt. Soweit bekannt, wird der hier vorgestellte Lösungsansatz dort jedoch nicht verfolgt.
Dieser Beitrag ist v.a. als Denkanregung zu verstehen. Da es auch im Bereich der EIKE-Gemeinschaft Fachwissen gibt, sind sachdienliche Kommentare ausdrücklich willkommen.
Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Die Diskussion scheint sich dem Ende zuzuneigen. Nur nochmals, um Spreu vom Weizen zu trennen, was wir gesichert wissen, und was wir daraus, von mehr oder weniger Wunschdenken geprägt, ableiten:
Gesichert wissen wir nur die Konzentrationen: Allmählicher Anstieg von 280 auf 420 ppm und die anthropogenen Freisetzungen: Allmählicher Anstieg von quasi null auf 5 ppm/a. Und gesichert wissen wir auch einige physikalische Gesetze.
Einigermaßen gesichert wissen wir noch, dass seinerzeit, bei 280 ppm, Gleichgewicht mit Zufluss und Ausfluss von je ca. 80 ppm/a herrschte.
Den Rest können wir nur noch ableiten, da gibt es nur noch mehr oder weniger gut begründete Meinungen.
Nach meiner Beurteilung (nach meiner Meinung) folgt aus den physikalischen Gesetzen zwangsweise, dass der Ausfluss von CO2 aus der Atmosphäre zumindest angenähert proportional mit der Konzentration gestiegen sein muss, heute also ca. 120 ppm/a betragen muss. Vielleicht übersehe ich dabei ja etwas, aber ein tragfähiges Argument gegen diese Proportionalität konnte ich in der Diskussion nicht finden. Dass die natürliche Umwälzung konstant bei 80 ppm/a geblieben wäre, kann es in meinen Augen nicht sein, denn irgendeine Kraft, die bei irgendwelchen Abweichungen immer wieder zu diesem Wert zurück drängt, habe ich nirgends beschrieben gefunden (Unterschied zwischen Pendel und Atmosphäre!).
Wenn aber die Proportionalität des Ausflusses stimmt, dann ergibt sich folgendes zwangsweise: Weil die Konzentration gestiegen ist, muss die Freisetzung in die Atmosphäre (Zufluss) noch stärker angestiegen sein als der Ausfluss, sie muss heute also größer sein als 120 ppm/a (von den 80 ppm/a von früher ausgehend). Und daraus folgt wieder zwangsweise, dass der Zufluss aus natürlichen Quellen wesentlich stärker angestiegen sein muss als die 5 ppm/a aus der anthropogenen Verbrennung von Kohle, Öl und Gas. Der Anstieg der Konzentration stammt dann weit überwiegend aus natürlichen Quellen.
Da es in der Natur viele große Speicher gibt, ist ein solcher Anstieg wohl zweifelsfrei möglich. Dass wir nicht wissen, aus welchem Speicher das CO2 kommt und was zu seiner Freisetzung geführt hat, ist eine ernste Wissenslücke, zwingt auch zu nochmaligem Nachdenken, kann für sich den dargelegten Gedankenfang aber nicht falsifizieren.
Auf den Punkt gebracht: Stimmt die Proportionalität, stimmt “Natur stärker Mensch“. Wer Letzteres widerlegen will, muss die Proportionalität widerlegen.
Gesichert:
Halte ich aufgrund von Punktmessungen und historischen Angaben fuer fraglich.
In alten Lexika kann man lesen, dass um 1890 Werte von 420 ppm gemessen wurden.
Daher meine Frage an die Community, wie gesichert sind denn die 280 ppm?
Michael Poost Admin 21. Mai 2025 6:46
Größere Konzentrationen als die Grundkonzentration kann man ortsabhängig immer messen. Das wird sogar manchmal benutzt um die Keelingkurve zu bestreiten. Aber da man das heute weiß, kann man Fehlmessungen der Grundkonzentration vermeiden, da früher mit den lokalen Werten die Angabe als Grundkonzentration verfälscht war.
Wegen der geringen beteiligten Tiefe des Ozeans (anderer Beitrag) ergibt sich, das der Anstieg der CO2-Konzentration ausschließlich aus der anthropogenen Freisetzung (211 ppmV) folgt. Da der Anstieg nur 140 ppmV beträgt, kann nicht alles in der Atmosphäre geblieben sein.
Wenn der Anstieg geringer sein sollte (entsprechend alten Lexikaangaben) müsste der Verlust aus der Atmosphäre bedeutend größer sein – das widerspricht aber der Diffusion.
Misst man dann ortsabhängig schon heute höhere Temperaturen weil mehr CO2 da ist?
Hat man denn schon eine direkte Abhängigkeit von Wetter von der CO2 Konzentration nachweisen können?
Gibt es das?
Eike Roth 20. Mai 2025 21:41
Die Angabe von 5 ppm/a ist zu groß: Die anthropogenen Freisetzungen sind dokumentiert: https://www.statista.com/statistics/276629/global-co2-emissions/ Aus den Werten folgen mit 1ppm = 7,824 Gt die Einträge in die Natur.
Kein Problem mit dem gesicherten physikalischen Wissen:
Das CO2 diffundiert hauptsächlich in den Ozean. Diffusion wird beschrieben durch eine Differentialgleichung, die praktisch identisch ist mit der Wärmeleitungsgleichung. Der Unterschied ist nur, dass statt der Temperaturleitfähigkeit der Diffusionskoeffizient benutzt wird.
Da der Konzentrationsverlauf an der Oberfläche bekannt ist (Keelingkurve) kann mit der Diffusionsgleichung der Konzentrationsverlauf in allen Tiefen bestimmt werden (Randwertaufgabe). Die Differenz zwischen Eintrag und Austrag ergibt sich aus dem Konzentrationsgefälle unmittelbar unter der Oberfläche und dem kleinen Diffusionskoeffizienten. Ich bin überzeugt, dass diese Differenz der anthropogenen Freisetzung entspricht. Weitere Quellen sind dann nicht erforderlich.
Aus der Diffusionsbetrachtung ergibt sich, dass die Differenz nicht nur von der Konzentration abhängt, sondern auch von der Änderungsgeschwindigkeit der Konzentration.
Ein Hinweis auf die beteiligte Tiefe des Ozeans ergibt sich mit der Temperatureindringtiefe im Erdreich: Im Jahresgang ca. 1 bis 2 m.
Herr Ebel,
ob die anthropogenen Freisetzungen 5 ppm/a oder etwas kleiner sind, spielt hier keine große Rolle.
Proportionalität: Wenn ich mich richtig erinnere, wird CO2 sogar zum größeren Teil durch Photosynthese aufgenommen als im Ozean gelöst. Und im Ozean herrscht nicht nur Diffusion (das wäre sehr langsam), sondern auch Strömung, im Kleinen durch Wind und Wellen, und im Großen wird CO2 vor allem in kaltem Wasser gelöst und durch die biologische und die physikalische Pumpe in die Tiefe befördert. Ich betrachte auch nicht die Differenz zwischen Eintrag und Austrag (Netto-Fluss), sondern nur den Fluss aus der Atmosphäre hinaus. Bei strenger Proportionalität zur Konzentration reichen die anthropogenen Freisetzungen um etwa den Faktor 10 nicht, da bliebt noch viel Spielraum, bevor sie zum dominierenden (oder gar alleineigen) Einfluss werden können. Hierzu nochmals der Hinweis, dass wir nur von relativ eingeengten Bereich von 280 bis 420 ppm spreche.
Eike Roth 21. Mai 2025 22:38
„CO2 sogar zum größeren Teil durch Photosynthese aufgenommen als im Ozean gelöst.“
Die jährlichen Schwankungen der Keelingkurve zeigen den Anteil der Photosynthese. Langfristig ist da kein Einfluß zu erkennen.
„sondern auch Strömung, im Kleinen durch Wind und Wellen, und im Großen wird CO2 vor allem in kaltem Wasser gelöst“
Das stimmt – durch Wellen wird die wirksame Oberfläche vergrößert. Für Strömung muß aber das CO2 bereits gelöst sein. Abzuschätzen ist der Einfluß analog dem Wärmeeintrag, der auch beschränkt ist – und der Diffusionskoeffizient ist erheblich kleiner als der Temperaturleitwert.
„Bei strenger Proportionalität zur Konzentration“
Bestenfalls bei strenger Proportionalität zum Konzentrationsgefälle. Aber es ist noch enger – es geht um den Konzentrationsgradienten nahe der Oberfläche.
„und durch die biologische und die physikalische Pumpe in die Tiefe befördert.“
Das ist sehr wenig. Wenn das stimmen würde der natürliche CO2-Gehalt nicht bei 280 ppmV liegen: Wenn der Anstieg von 280 auf 420 ppmV aus natürlichen Quellen erfolgen soll, dann müßten die anthropogenen 211 ppmV in ca. 60 Jahren in die Tiefe gewandert sein, also ca. 3.5 ppmV/a. Da wäre CO2 nach ca. 80 Jahren aus der Atmosphäre verschwunden, evtl. auch mit einer Halbwertszeit von ca. 80 Jahren – sicherheitshalber: warum sollte sich die Tiefengeschwindigkeit so radikal ändern?
Jochen Ebel 22. Mai 2025 9:50
Das ist der Unterschied zur Wärme. Bei der Wasseroberfläche wird durch Wind und Wellen durch Reibung Wärme erzeugt – aber kein CO2.
Weil waermeres Wasser weniger CO2 loesen kann?
Dann zeigt diese Kurve also nicht die Schwankungen des menschlichen CO2 Ausstosses? Muesste sie das nicht, wenn die menschliche CO2 Produktion so dominant waere?
EBEL mal wieder sprachlos!
Erwarten Sie, Herr Schulz nun noch eine Antwort vom Ebel? 😉
Ja, wenn Herr Ebel es ernst meint mit Aufklärung, dann wäre eine Antwort angebracht.
Die Frage ist aber, ob Herr Ebel über das Wissen verfügt, diese Frage zu beantworten.
Daher erwarte ich eher, das die Klimafolgenforschung sich diese Frage stellt und sie beantwortet.
Warum sieht man in den natürlichen Schwankungen der CO2 Konzentration den Effekt von natürlichen Prozessen, aber nicht vom Menschen, wenn der Mensch so dominant sein soll?
Und sind die langfristigen Schwankungen dann nicht auch auf natürliche Prozesse zurückzuführen?
Diese Antwort / Erklärung ist leider tabu, weil das der Klima-Ablaß-Kirche den (leider bitter notwendigen)Todesstoß versetzen würde.
Der natürliche Kreisfluss ist von 80 auf 120 ppm/a gestiegen. Der Anstieg der Konzentration stammt dann weit überwiegend aus natürlichen Quellen.
Herr Dr. Roth, diese Aussagen sind frei erfunden. Die Kreisflüsse bei 280 ppm und +140 sind NICHT proportional zu der (von uns erhöhten) Konzentration, und Sie haben dazu auch keinen Beleg durch Messwerte. Auch Ihre Behauptung (zum Titel des Beitrags) dass der Anstieg der Konzentration weit überwiegend aus natürlichen Quellen stammt (was vermeintlich Herr Mechtel mit der Fake-Quelle bei Tau20 erklären sollte) ist frei erfunden. Wenn von unserer Emission von etwa 5 ppm (39 GtCO2/a) 60% von den Senken aufgenommen wird, bewirken doch die 40% einen ppm-Anstieg in der Atmosphäre, und +2 ppm/a über 70 Jahre ergeben +140 ppm.
Herr Dietze,
Ihre Trennung in Kreisflüsse und Senkenflüsse ist frei erfunden. Sie folgt aus dem Springbrunnenmodell mit fester Umwälzung zur Fontäne und davon getrennter Niveauregelung über einen Überlauf. Dieses Modell ist aber weit weg von der Realität der Atmosphäre.
Jetzt möchte ich mich doch auch gern nochmals einschalten. Wenn der Senkenfluss bei 280 ppm 80 ppm/a betragen hat, bedeutet das doch eine Zeitkonstante tau von 3,5 Jahren, oder in der Schreibweise des Artikels alpha ca. 0,29 /a. Der linear-quadratische Rechenansatz liefert dann für 2020 (um nicht allzu weit zu extrapolieren) tatsächlich, wie von Herrn Roth postuliert, einen Gesamt-Quellfluss von umgerechnet 120 ppm/a (davon 4,5 ppm/a anthropogen) und einen Senkenfluss von 118 ppm/a.
Noch eine allgemeine Bemerkung: Der rein natürliche Quellfluss berechnet sich im Beispiel zu 115,5 ppm/a. Das ist weniger als der Senkenfluss. Wie ich an anderer Stelle schrieb, legt das den Schluss nahe, dass es der anthropogene Eintrag ist, der die Konzentration in der Atmosphäre ansteigen lässt. Aber Vorsicht:
Die Konzentration ab 1960 lässt sich iterativ konstruieren, indem man den anthropogenen Eintrag weglässt und den natürlichen unverändert übernimmt. Dann stellt man überraschenderweise fest: der Senkenfluss ist jetzt geringer als dieser natürliche Eintrag. Also auch jetzt steigt die Konzentration! Sie steigt freilich weniger als mit menschlichem Zutun, und das ist genau der Grund, warum sich der Senkenfluss verringert.
Fazit: die Annahme, der menschliche Eintrag sei alleinige oder gar Hauptursache für den Konzentrationsanstieg, ist ein voreiliger Trugschluss!
In Zahlen für 2020 mit obigem tau ohne anthropogenen Eintrag:
Quellfluss (natürlich) = 115,5 ppm/a,
Senkenfluss = 113,5 ppm/a,
atmosphärische Konzentration = 398 ppm (statt 413 ppm).
Ohne menschlichen Einfluss wären also bis 2020 zum 280-ppm-Niveau noch 118 ppm hinzu gekommen, mit menschlichem Einfluss waren es 133 ppm, das sind etwa 13 % mehr. Das deckt sich hervorragend mit meiner Schlußfolgerung aus dem Artikel, obwohl mir zwischenzeitlich selber Zweifel gekommen waren!
Wenn der Senkenfluss bei 280 ppm 80 ppm/a betragen hat, bedeutet das doch eine Zeitkonstante tau von 3,5 Jahren – und umgerechnet (Roth) auf 420 ppm einen Quellfluss von 120 ppm/a.
Herr Mechtel, Sie sind da völlig auf dem Holzweg. Der Naturkreislauf ist weder durch 280 ppm getrieben (!!) noch ist er ein Senkenfluss, denn dieser ist Null (!) und damit ist die Zeitkonstante unendlich. Wenn Sie Ihre Rechnung mit tau=3,5 a (statt 20, 55 oder 56,7) machen, erhalten Sie gigantische Fake-Quellen. Man darf nicht Kreis- und Senkenflüsse verwechseln oder zusammen rechnen. Ein Senkenfluss bedeutet doch dass in tau Jahren das Inventar auf 1/e abfällt.
Und bezogen auf die Rechnung für das anthropogene tau, muss auch das anthropogene Inventar beachtet werden, also das für 420-280 ppm. Sie sollten unbedingt beachten dass bei 280 ppm sich z.B. 80•2,12=169,6 GtC/a als „Senkenfluss“ ergibt, aber es beim anthropogenen Senkenfluss 19,4 ppm pro GtC/a sind, was einen Unterschied um etwa den Faktor 12 (!!) bedeutet. Deshalb müssen anthopogene Flüsse separat behandelt werden.
Und was Ihren Nachweis anbelangt, dass wir auch bei Weglassen unserer Emissionen einen ppm-Anstieg haben, sollten Sie sich darüber in Klaren sein dass zwar in der Keelingkurve auch ein natürlicher ppm-Anstieg enthalten ist, der Effekt durch Weglassen von Emissionen möglicherweise auch wegen Anwendung eines falschen Parameters für ∆ppm entstehen kann wenn der Anteil vom Senkenfluss nicht exakt bekannt ist.
Ich erinnere daran: Wenn die natürliche Freisetzung steigt, dann steigt die Konzentration und mit ihr steigt auch die Entnahme, der Freisetzung etwas nachhinkend, sodass die Natur eine (nicht allzu große) Netto-Quelle ist. Kommen dann anthropogene Freisetzungen hinzu, wächst die Konzentration schneller und mit ihr auch die Entnahme (die nur in natürliche Senken geht!). Bei kleinen anthropogenen Freisetzungen wird die Natur dadurch zu einer kleineren Netto-Quelle, bei höheren zu einer Nett-Senke. Den Zustand haben wir offensichtlich.
Herr Dr. Roth, auch Sie sind auf dem Holzweg indem Sie den anthropogenen Senkenfluss NICHT durch die 600 Jahre erklären, welche vergehen bis aufgenommenes CO2 bei 420 ppm (anstelle von antikem CO2 bei 280 ppm) wieder ausgegast wird. Ihre proportionale Gleichbehandlung (!) mit dem über lange Zeit ausgeglichenen natürlichen und vermeintlich enorm ansteigenden Kreisfluss – wo ∆CO2/∆ppm um den Faktor 12 (!!) höher ist – ist völlig unsinnig.
Herr Dietze,
es ist immer dasselbe: Es gibt keinen „anthropogenen Senkenfluss“. Es gibt nur einen Ausfluss von CO2-Molekülen aus der Atmosphäre, der erstens immer in die gleichen Senken geht, egal, woher das CO2 in der Atmosphäre stammt, und der zweitens für alle Senken gleicherweise umso stärker ist, je höher die Konzentration in der Atmosphäre ist. Wie lange das ausgeflossene CO2 dann jeweils in einem Speicher verweilt (z. B. im tiefen Ozean), das ist für den (momentanen) Ausfluss völlig egal, genauso, wie es auch egal ist, wie viel CO2 gleichzeitig in die Atmosphäre freigesetzt wird (und woher dieses CO2 stammt!).
Für Herrn Lüdecke, der hier ja ebenfalls irgendeine Funktion hat, ist die Diskussion schon lange (spätestens seit 4 Jahren) beendet.
„Die Konzentration des Spurengases CO2 stieg ab Beginn der Industrialisierung bis heute von 0,028% auf 0,04% (280 ppm auf 400 ppm). Messungen belegen, dass dieser Anstieg anthropogen war.“
Prof-Dr-Horst-Joachim-Luedecke-em-HTW-.pdf
Die Quelle dieses Zitats ist leider nicht auffindbar, die Aussage somit nicht nachprüfbar.
In dem verlinkten Papier heisst es aber auch (auf Seite 8):
Das bedeutet im Umkehrschluss: wenn sich der CO2-Partialdruck des Meerwassers ändert (durch innerozeanische Vorgänge), dann wird das erhebliche Auswirkungen auf die Konzentration in der Atmosphäre haben.
Michael Mechtel 22. Mai 2025 9:27
Das ist sowohl richtig als auch falsch. Im Meerwasser ist die Konzentration des CO2 nicht überall gleich und wegen des geringen Diffusionskoeffizienten erfolgt die Ausgleichung nur langsam. Also sagen Mengenverhältnisse fast nicht aus: in Kohlelagerstätten, Kreide usw. ist noch viel mehr Kohlenstoff.
Bezieht man sich auf den Durchschnittswert so werden sich die anthropogenen Emissionen kaum auswirken, betrachtet man aber die lokalen Auswirkungen so sind diese erheblich und bleiben wegen des niedrigen Diffusionskoeffizienten lange erhalten.
So fangen alle Maerchen an! Mehr faellt mir dazu leider nicht mehr ein!
Siehe z.B.
https://eike-klima-energie.eu/2025/05/22/vulkane-emittieren-drei-mal-mehr-co%e2%82%82-als-gedacht/
Eike Roth 20. Mai 2025 21:41
Die Förderung von Brennstoffen ist gut bekannt, damit kann man die Co2-Menge berechnen, die die Atmosphäre geblasen wird. Ein Teil dieser Menge geht in den Ozean dazu kommt noch durch die Temperatur freigesetztes CO2 aus natürlichen Quellen.
Im angehängten Diagramm ist unter der Annahme, daß CO2 in den Ozean diffundiert, aus der Förderkurve die CO2-Zunahme berechnet (blau) und unter Annahme der Diffusion die Strömung in der obersten Schicht (normiert auf die Förderung – rot). Wenn nur anthropogene Emissionen vorhanden wären, müßten beide Kurven etwa deckungsgleich sein. Das ist etwa von 1980 bis 2014 der Fall.Vor 1980 ist der Unterschied die Folge, daß wegen 1940 nicht der Zeitverlauf von 280 ppm auf ca. 311 ppm betrachtet wurde. Nach 1980 ist die Zunahme größer als die anthropogene Zunahme.
Vielen Dank auch an den Admin für die geduldige Freischaltung all der Kommentare!
Immer gerne, danke.
Nachtrag zum Artikel:
Die Berechnungen sind korrekt, dennoch hat mich Jochen Ebel auf einen wichtigen Sachverhalt gestoßen. In der Tabelle 1 habe ich versäumt, die Senkenflüsse einzutragen. Wenn man das tut, erkennt man, dass der Senkenfluss SPkt größer ist als der Quellfluss aus natürlichen Quellen, wobei sich letzterer berechnet nach QPktnat = QPkt – QPktz. Das bedeutet: Wenn der atmosphärische CO2-Gehalt m trotzdem ansteigt, dann kann das nur am anthropogenen Eintrag QPktz liegen! Die absolute Größe von natürlichem Quell- und Senkenfluss ist gar nicht entscheidend, sondern nur deren Differenz. Hier die ergänzte Tabelle 1 in verkürzter Form:
Herr Mechtel, natürlich halten Sie – und das noch immer – Ihre Berechnung für korrekt, denn sonst hätten Sie ja diesen Beitrag gar nicht produziert. Leider ist aber Ihr Tau20 falsch, und auch alles was daraus in GtC02 folgt: Aus dem Inventar 3213,19/Tau20 folgt bei 412 ppm (ohne -280) der totale Senkenfluss 160,7. Die totale Quelle ist 178,8 weil der anthropogene Anteil 33,7 und deren Senkenfluss 18,1 ist, womit sich die Differenz ∆ppm zu 2,0 ergibt.
So bestimmen Sie eine vermeintlich „natürliche“ Zusatzquelle von 145,1 die natürlich real garnicht existiert und seltsamerweise (im Gegensatz zur anthropogenen Quelle) zu 100% (!) in die Senke gehen muss weil sie doch ein Fake ist und kein ∆ppm erzeugen darf. Sie hätten denselben anthropogenen Senkenfluss mit einem richtigen Tau=56,7 a und (412-280)/56,7•2,123•3,667 korrekt ebenfalls zu 18,1 und ganz ohne Zusatzquelle berechnen können.
Herr Dietze, natürlich gelten die Absolutwerte meiner Berechnung (Tab. 1) unter der Voraussetzung tau = 20 Jahre, und wie von Anfang an festgestellt, ändern sie sich in der Tat stark mit tau. Das gilt sowohl für den Senken- wie auch für den natürlichen Quellfluss.
Die wichtige Erkenntnis, dass der Senkenstrom größer ist als der natürliche Quellstrom, wird durch die Wahl von tau aber überhaupt nicht beeinflusst, wie man leicht nachrechnen kann. Deshalb ist es eigentlich überflüssig, sich über den genauen Wert von tau den Kopf zu zerbrechen. Diese Einsicht ist bei mir leider erst im Lauf der Diskussionen gewachsen, und darin liegt ein beträchtlicher Verdienst des Kommentarteils.
Herr Mechtel, Ihre Erkenntnis dass der zentrale Parameter Tau, der den anthropogenen Senkenfluss bestimmt, garnicht so wichtig ist und in einem breiten Bereich al gusto variiert werden kann, indem man einfach passende Fake-Zusatzquellen dazu berechnet und diese für existent erklärt, ist nicht zu fassen. Mit der Methode können Sie jeden Quatsch ausrechnen, und sowas präsentieren Sie bei EIKE – noch flankiert von einigen Kommentatoren, die an keinen anthropogenen, sondern an einen natürlich verursachten ppm-Anstieg und gleich auch noch daran glauben dass der 2.HS einen THE verbietet, um somit jegliche Aufklärungsarbeit zunichte machen zu können.
Herr Dietze, ich muss nun schon darauf bestehen, dass ich keinen Quatsch ausgerechnet, sondern lediglich (Asche auf mein Haupt) falsche Schlüsse aus der Rechnung gezogen habe.
Keinen Quatsch insofern, als der Parameter tau sich für meine Fragestellung als belanglos herausgestellt hat. Dass man damit Fake-Zusatzquellen einführen kann, liegt nicht an mir, sondern an den Eigenschaften der Mathematik. Der entscheidende Punkt wird jedenfalls korrekt berechnet. tau mag für andere Fragestellungen wichtig sein.
Ich darf in aller Bescheidenheit noch darauf hinweisen, dass der „Quatsch“, den ich da angeblich berechnet habe – eigentlich: wo mein Fehlschluss liegt – von den vielen Kommentatoren niemandem außer einem aufgefallen ist. Das ist mir bei allem Bedauern ein gewisser Trost.
„Keinen Quatsch insofern, als der Parameter tau sich für meine Fragestellung als belanglos herausgestellt hat“.
Her Mechtel, der Titel Ihres Beitrags ist doch „Woher kommt das atmosphärische CO2“. Also wenn wir CO2/a emittierten, geht das zunächst mal in die Atmosphäre. Aber es wird um den anthropogenen Senkenfluss = AnthroInventar / tau55 reduziert. Und die reduzieren ∆ppm werden pro Jahr ab Startwert aufaddiert.
Das ist alles, und wenn der Parameter tau sich für Ihre Fragestellung als belanglos (!!) herausgestellt hat, ist die Arbeit witzlos weil Sie Ihr Thema vergessen haben. Oder Sie wollen uns hinter die Fichte führen.
Nein, Sie irren sich! Die Arbeit ist nicht witzlos, weil sie eine mathematisch korrekte Analyse der empirischen Daten darstellt. Mit wachsendem tau wird eben nicht nur der Senkenfluss reduziert, sondern auch der Quellfluss. Die Differenz bleibt unangetastet, und das entscheidende Ergebnis, dass der Senkenfluss zwischen gesamtem Quellfluss und natürlichem Quellfluss liegt, ebenfalls. Beides wird von der Rechnung korrekt erfasst.
Mein Fehler war, dass ich in der Tabelle 1 den Fokus allein auf die Quellen gelegt und die Senke nicht mit einbezogen habe. Statt QPktnat – SPkt zu beurteilen, habe ich fälschlich QPkt/QPktz als Kriterium für das Thema meiner Arbeit herangezogen. Das hätte Ihnen auch auffallen können!
Herr Mechtel, ich verstehe nicht wie Sie einfach per tau den Senkenfluss reduzieren können wollen, dann feststellen dass sich auch die Fake-Quelle reduziert, die Differenz unverändert bleibt und damit alles ok ist. Die Differenz zu einem willkürlich erzeugten Fake-Wert (!) ist doch überhaupt nicht das Thema Ihres Beitrags, sondern die Frage wie hoch ist der reale anthropogene Senkenfluss und welche Konzentrationserhöhung bewirkt unsere CO2-Emission.
Mit welchen ppm-Werten haben wir also zukünftig – und abhängig vom Ausmaß der geplanten billionenteuren Dekarbonisierung – zu rechnen. Das ist doch die Grundlage für den Temperaturanstieg (auf Basis von ECS) sowie für eine vernünftige Entscheidung zu der Frage was bringt das und was kostet das. Wenn pro millionstel Grad allein die Investkosten bei mindestens einer Mrd. € liegen, und z.B. eine Wärmepumpe für 30.000 € nur 1,5 hundertmilliardstel Grad (10^-11) bringt, sollte die Entscheidung doch klar sein.
Der zweite Teil Ihrer Antwort – Treibhauseffekt, ECS, Kosten etc. – war ausdrücklich nicht mein Thema, auch wenn ein Großteil der Kommentare in diese Richtung ging.
Mein Thema war, ob die Konzentrationserhöhung menschen-gemacht ist. Dafür ist nun mal, nach aktueller Erkenntnis, die Differenz zwischen Quell- und Senkenfluss entscheidend und nicht die Höhe der Flüsse selbst. Wenn in den beiden Flüssen noch Beträge auftauchen, die Sie als Fake bezeichnen, ist das unschädlich, solange sie sich wegheben.
Ich verstehe auch nicht, warum Sie sich aufregen, denn nach Ihrer Arbeit steigt doch auch die Konzentration infolge anthropogenen Eintrags, selbst dann noch, wenn der konstant gehalten wird. Und Sie sagen doch selbst, dass das keine Katastrophe bedeutet. Natürlich hätte es mir auch besser gefallen, wenn man den anthropogenen Eintrag ganz hätte marginalisieren können, aber mein erster Denkansatz (nicht der Rechenansatz!) hat sich nunmal als Irrtum erwiesen. Dann muss man das eben korrigieren.
Übrigens habe ich meinen Rechenansatz mit Absicht so detailliert dargestellt, dass der Leser, also auch Sie, in der Lage sein sollten, ihn im Detail nachzuvollziehen. Dann klären sich manche Fragen von allein.
Michael Mechtel 20. Mai 2025 11:10
Das zeigt den Wissenschaftler, nicht das sture Festhalten an Vorurteilen (Dietze).
Herr Mechtel, nun ist klar dass ich den Titel anders interpretiert habe als Sie. Den ganzen Aufwand (mit bisher 690 Kommentaren) nur für die triviale Frage ob die CO2-Erhöhung in der Atmosphäre vom Menschen oder mehr von der Natur kommt, ist doch ein Witz. Hätten Sie das gleich am Anfang deutlich gemacht, hätte ich den Beitrag gar nicht erst gelesen, und EIKE hätte sich wohl auch viel unnötige Arbeit wegen der zahlreichen Kommentare sparen können.
Sie haben leider das viel zu kleine tau20 von C14 gewählt und damit höchst umstrittene Fake-Quellen berechnet welche ja angeblich existieren und so verstärkten Sie fälschlich den Eindruck dass die Natur zu 90% beteiligt ist, womit Sie unglaublich viel Streiterei sowie unnötige Arbeit verursacht haben. Insbesondere wegen Dr.Roth, der ja für Tau die Umwälzzeit von 4 Jahren (!!) nimmt und damit zu riesigen Fake-Quellen kommt. Auch der ganze Streit um die korrekte C-Modellierung (u.a. mit Herrn Ebel) ist dadurch mit entstanden.
Allein Ihre Behauptung, der Parameter tau (mit dem ja der Senkenfluss berechnet wird) habe sich für Ihre Fragestellung als belanglos (!) herausgestellt (obwohl dieser bei willkürlicher Vorgabe je nach Belieben die Größe der angeblich natürlichen Fake-Quellen bestimmt) hat mich als Verfasser von [9] und Expert Reviewer des TAR auf die Palme gebracht. Beim IPCC werden viel zu kleine Senkenflüsse (proportional zur Emission) und deutlich zu hohe ppm-Anstiege berechnet, aber Fake-Quellen gibt es nicht.
Erfreulich ist wenigstens, dass der „Quatsch“ (m.E. die Fake-Quellen) die Sie berechnet und behandelt haben, durch einen Fehlschluss bedingt waren, was den vielen Kommentatoren außer mir gar nicht aufgefallen ist und dass dies bei allem Bedauern für Sie ein gewisser Trost sei.
Ergänzung: „Mein Thema war, ob die Konzentrationserhöhung menschen-gemacht ist. Dafür ist nun mal, nach aktueller Erkenntnis, die Differenz zwischen Quell- und Senkenfluss entscheidend und nicht die Höhe der Flüsse selbst. Wenn in den beiden Flüssen noch Beträge auftauchen, die Sie als Fake bezeichnen, ist das unschädlich, solange sie sich wegheben“.
Bei der Fake-Quelle ist Quellfluss=Senkenfluss, also wenn dieser Fluss (den Sie ja der Natur zuordnen) z.B. 4mal so groß ist wie die anthropogene Emission, dann wäre – soweit ich nichts falsch verstanden habe – Ihre Thema-Frage damit beantwortet: 80% von der Natur!
Wenn man korrekt (also ohne Fake-Quelle) rechnet wie ich im Kommentar vom 19. Mai 2025 14:02, dann ist 100% anthropogen. Allerdings erhöht Ihre Fake-Quelle NICHT die Konzentration, d.h. 0% Natur in beiden Fällen. Wie Sie mit diesem Widerspruch umgehen, konnte ich nicht ermitteln.
Verbesserungsvorschlag
Die Diskussion hier ist m. E. stark zerstreut, unübersichtlich und nicht sehr zielgerichtet. Schon am 14.05. 21:32 hatte ich versucht, durch eine Punkt-für-Punkt Argumentation die Diskussion verstärkt auf die m. E. wichtigste und schon im Ausgangsbeitrag von Herrn Mechtel gestellte Sachfrage zu konzentrieren: „Woher kommt das viele CO2, überwiegend vom Menschen oder überwiegend aus der Natur?“ Scheinbar aber mit wenig Erfolg. Daher hier nochmals ein Versuch, mit der Bitte, in der Diskussion möglichst genau zu benennen, welchen dieser Punkte man für falsch hält und warum. Dann kann man auch gezielt ausdiskutieren, was gilt. Nachvollziehbare Widerlegungen sind gefragt, reine Gegenaussagen sind zwar nicht wertlos, helfen aber nicht viel weiter.
Physikalische Grundlagen:
1. Die Atmosphäre ist ein offenes System, bei dem die Entnahme mit der Konzentration zunimmt. Beweis: Nicht alles in sie freigesetzte CO2 verbleibt in ihr.
2. In so einem System bestimmt
· erstens die Freisetzung das Gleichgewicht (es liegt bei der Konzentration, bei der gleichviel entnommen wird wie zugesetzt wird),
· zweitens trägt jede Quelle proportional zu ihrer Stärke zur Konzentration bei (es sind ja alle CO2-Moleküle gleich), und
· drittens kann die Konzentration prozentual nie schneller wachsen (und damit nicht höher werden) als die Freisetzung in das System wächst (Beweis: würde die Konzentration schneller wachsen als die Freisetzung, dann würde auch die Entnahme schneller wachsen als die Freisetzung, die Konzentration würde daher fallen, statt zuzunehmen).
Konsequenz: Die Zunahme der Konzentration um 50 % kann nur eingetreten sein, indem die Freisetzung um mindestens 50 % erhöht worden ist.
3. Quellen gibt es natürliche und anthropogene, Senken gibt es nur natürliche. Wenn die natürlichen Quellen wachsen (und sonst nichts geschieht), dann wächst auch die Konzentration, und leicht verzögert wächst dann auch die Entnahme, die Natur ist daher die ganze Zeit über zwangsweise eine (nicht sehr große) Netto-Quelle.
4. Wenn dann noch anthropogene Freisetzungen dazu kommen (gleiche natürliche Freisetzungen wie zuvor unterstellt), dann steigt die Konzentration stärker an, und mit ihr wächst auch die Entnahme aus der Atmosphäre stärker. Infolgedessen wird bei kleinen anthropogenen Freisetzungen die ohnehin nicht allzu große Netto-Quelle „Natur“ kleiner, bei hinreichend hohen anthropogenen Freisetzungen wird die Natur sogar zu einer Netto-Senke. Die Natur ist dann beides gleichzeitig: Für sich genommen eine Netto-Quelle und zusammen mit den anthropogenen Freisetzungen eine Netto-Senke. Das heißt, die Natur macht zwei Dinge gleichzeitig: Sie erhöht die Konzentration und sie nimmt einen Teil der anthropogenen Freisetzungen auf.
Erklärung: Möglich wird die Koexistenz von „Netto-Quelle“ und „Netto-Senke“ dadurch, dass beides vergleichende Aussagen sind. Und bei solchen kommt es eben darauf an, womit man vergleicht. Beispiel: Die Erde ist gleichzeitig „größer“ und „kleiner“ (vergleichende Aussagen!): Sie ist größer als der Mond und sie ist kleiner als die Sonne. Beides gleichzeitig ist kein Widerspruch!
Beim CO2 vergleichen wir die Entnahme durch die natürlichen Senken (es gibt nur solche) einmal mit der Freisetzung nur aus den natürlichen Quellen und das andere Mal mit der Gesamtfreisetzung aus allen Quellen zusammen. Im ersten Fall ist sie kleiner („Netto-Quelle“), im zweiten größer („Netto-Senke“).
5. Antriebskräfte für die Entnahme von CO2 aus der Atmosphäre gibt es prinzipiell zwei: Den (Partial)Druckunterschied und den Konzentrationsunterschied. Dass Letzterer eine Antriebskraft ist, folgt aus dem 2. HS: Der fordert immer Entropiezunahme, also Veränderungen hin zur Gleichverteilung im gesamten Kreislauf (überall die gleiche Konzentration).
6. Diese beiden Antriebskräfte setzen auch zwei Prozesse in Gang. Die führen zwar zum gleichen Ziel (Gleichgewicht), sie laufen aber voneinander unabhängig ab, jedoch immer beide parallel. Der (Partial)Druckunterschied bewirkt, dass der Ausfluss größer ist als der Zufluss. Die Differenz dieser beiden Flüsse ist proportional zum (Partial)Druckunterschied. Der Konzentrationsunterschied heißt, dass Ausfluss und Zufluss unterschiedliche Zusammensetzung (Konzentration) haben. Dann führt die Umwälzung zum Konzentrationsausgleich, und das umso schneller, je höher die Austauschrate (Umwälzung) ist.
Bei hoher Umwälzrate und kleinem (Partial)Druckunterschied überwiegt der Konzentrationsausgleich den Druckausgleich bei weitem (in der Geschwindigkeit, Ziel haben sie, wie gesagt, das gleiche).
7. „Gleichgewicht“ ist ein Zustand, bei dem die (Partial)Drücke und die Konzentrationen überall im gesamten Kreislauf gleich sind (und auch gleich bleiben, solange das Gleichgewicht anhält). Im Gleichgewicht herrscht dann auch überall im gesamten Kreislauf die gleiche Durchflussrate. In einer Transiente kann das alles anders sein.
8. Jedes Gleichgewicht wird durch die jeweils gültigen Randbedingungen bestimmt. Das „alte“ Gleichgewicht von vor der industriellen Revolution (280 ppm Konzentration bei 80 ppm/a Umwälzung) eben von den damals vorhandenen Randbedingungen. Eine „rücktreibende Kraft“ dorthin (etwa vergleichbar mit der rücktreibenden Kraft eines ausgelenkten Pendels) gibt es für die Atmosphäre nicht. Auch dann nicht, wenn dieses alte Gleichgewicht über eine lange Zeit angehalten hat (bleibende Spuren, etwa wie Spurrinnen in manchen stark befahrenen Straßen, gibt es in der Atmosphäre nicht!).
Daraus können die folgenden weiteren Konsequenzen unmittelbar abgeleitet werden:
a. Infolge der hohen Umwälzung bewegt sich bei langsamen Transienten das System immer sehr nahe am Gleichgewicht. Wird der Zufluss (alle Quellen!) konstant gehalten, stellt sich immer sehr rasch (und nicht weit entfernt) das neue Gleichgewicht ein. Wird nur eine Quelle konstant gehalten, stellt sich kein Gleichgewicht ein.
b. Weil der Netto-Fluss in/aus der Atmosphäre kein materieller Fluss ist, sondern nur die Überlagerung zweier sehr großer Flüsse in entgegengesetzter Richtung, gibt es keine reale Kraft, die direkt auf den Netto-Fluss einwirkt. Die Kräfte wirken vielmehr immer nur auf die beiden großen realen Flüsse ein, wie, das muss man für beide separat berechnen. Infolge der großen Speicherkapazität in Ozean und Biomasse sind diese beiden Flüsse voneinander entkoppelt. Das heißt im Klartext: Der Ausfluss aus der Atmosphäre richtet sich nach der Konzentration in ihr, der Rückfluss in die Atmosphäre nicht (bzw. nur sehr langfristig).
c. Erst im neuen Gleichgewicht (einschließlich tiefem Ozean, nach tausenden von Jahren) sind alle Flüsse wieder gleich groß (und konstant). Wie sich die natürliche Freisetzung in den nächsten Jahrzehnten entwickelt, das hängt vor allem von der Entwicklung der natürlichen Quellen ab und ist vom Geschehen in der Atmosphäre weitgehend entkoppelt. Was aber die natürlichen Quellen zu Änderungen antreibt, das wissen wir nicht. Wer trotzdem rechnet, der macht das auf der Basis ungesicherter Modelle. Solche Rechnungen haben keine Aussagekraft.
d. Das System „Atmosphäre“ kehrt nur dann zum alten Gleichgewicht mit 280 ppm zurück, wenn die alten Randbedingungen vollständig wieder hergestellt werden. Nur die anthropogenen Freisetzungen einzustellen, langt dafür nicht.
e. Die beobachtete Änderung der Konzentration von 14C zeigt anschaulich, was mit jeder in die Atmosphäre eingebrachten CO2-Menge passiert: Obwohl das wenige 14C den CO2-Partialdruck in der Atmosphäre praktisch überhaupt nicht erhöht hat, wurde es nach dem plötzlichen Rückgang der Produktion praktisch vollständig innerhalb weniger Jahre der Atmosphäre entnommen, um möglichst gleichmäßig im gesamten Kreislauf verteilt zu werden. Das kann nur die hohe Umwälzung bewirkt haben. Und die verfährt mit jeder anderen eingebrachten CO2-Menge zwangsweise gleich: Die Umwälzung verteilt auch sie im gesamten Kreislauf, sodass in der Atmosphäre nur mehr wenig davon verbleibt, der Überdruck spielt demgegenüber nur eine stark untergeordnete Rolle.
f. Und weil diese Umverteilung per Umwälzung immer sehr rasch erfolgt, kann sich in der Atmosphäre kein hoher (Partial)Überdruck aufbauen.
Schlussbemerkung
Es ist die Physik, die das Geschehen bestimmt. Unterschiedliche Interpretationen der Beobachtungen und unterschiedliche Ansichten zu zukünftigen Entwicklungen beruhen meist auf unterschiedlichem Verständnis der treibenden Physik. Das macht in meinen Augen die Klärung der physikalischen Grundlagen zur wichtigsten Aufgabe.
Herr Dr. Roth, nochmal zu Ihrem alten Fehler „die Zunahme der Konzentration um 50 % kann nur eingetreten sein, indem die Freisetzung um mindestens 50 % erhöht worden ist“. Tatsache ist doch dass es nicht auf die Zunahme ankommt, sondern (für einen ppm-Anstieg) nur darauf ob die Emission größer ist als der Senkenfluss (die Konzentration kann sogar steigen wenn de Freisetzung abnimmt). Ich verweise dazu nochmal auf meine Exel-Grafiik hier, wo ab 2025 die Emission konstant ist, also NICHT zunimmt, wohl aber die Konzentration – und zwar solange bis (hier nach 110 Jahren) NetZero erreicht ist. Dann – im Gleichgewicht, und nur dann – gilt Ihre Aussage.
Herr Dietze,
die Zunahme der Konzentration ist so ziemlich das Einzige, was wir wirklich gemessen haben. Also kommt es sehr wohl auf sie an. Diese Zunahme bestimmt auch, wie sich die (nicht direkt messbare) Entnahme aus der Atmosphäre entwickelt haben muss: Sie muss proportional mitgewachsen sein, zumindest angenähert. Und weil die Konzentration gestiegen ist, muss die Gesamt-Freisetzung stärker gestiegen sein als die Entnahme. Die anthropogenen Freisetzungen sind hierfür viel zu klein.
Eike Roth 19. Mai 2025 23:05
Falsch. Die anthropogenen Freisetzungen sind größer als die Zunahme in der Atmosphäre: https://www.statista.com/statistics/276629/global-co2-emissions/ und Keelingkurve.
Wegen der kleinen Diffusionskonstante verteilt sich die Emission in überschaubarer Zeit nicht im ganzen Ozean.
Die Fragen zu ihren natürlichen Ursachen haben Sie noch nicht beantwortet:
Herr Dr. Roth, m.E. argumentieren Sie fälschlich mit den 190 GtC/a pro 280 ppm vom Naturkreislauf. Der anthropogene Wert im Gleichgewicht (pro GtC/a 19,4 ppm) unterscheidet sich aber um den Faktor 13,2 (!). Und warum das so ist, wissen Sie nicht. Offenbar liegt es daran dass die 280 ppm NICHT der TREIBER für den Naturkreislauf sind, sondern sich nur als Folge des globalen Naturkreislaufs über lange Zeit eingestellt haben.
Herr Dr. Roth, Ihr Bestreben, die Diskussion um die Ursache des CO2-Anstiegs auf eine sachliche Grundlage zu stellen, ist anerkennenswert und deckt sich mit meiner Absicht. Da ich selber aber meinen Absatz C) aus der Zusammenfassung der Ergebnisse inzwischen revidieren muss, habe ich Ihre physikalischen Grundlagen nochmals durchgesehen. Mit den Ziffern 1 bis 3 bin ich einverstanden, aber folgende Aussage aus Ziffer 4 lässt sich nicht verifizieren:
Es ist vielmehr umgekehrt: Die Entnahme durch die Senken (SPkt) ist größer als die Netto-Quelle (QPktnat) und kleiner als die Gesamt-Freisetzung (QPkt). In Zahlen finden Sie das oben in der Tabelle meines Nachtrags vom 19.5., 11:59 . Die Folgerung daraus kann nur lauten, dass der Zuwachs in der Atmosphäre durch den anthropogenen Eintrag QPktz verursacht sein muss.
Wie Sie der Tabelle auch entnehmen können, ist der atmosphärische CO2-Gehalt im genannten Zeitraum um 26,8% gestiegen und der Senkenfluss erwartungsgemäß ebenso. Der gesamte Zufluss ist tatsächlich stärker gestiegen, nämlich um 33,8%. Dazu hat der natürliche Zufluss aber nur mit 17,8% beigetragen, der Rest kam vom anthropogenen Eintrag. Das hat mich selber überrascht, weil ich es so nicht auf dem Schirm hatte.
Herr Mechtel,
vielen Dank für Ihren Kommentar und insbesondere auch dafür, dass Sie präzise angeben, welche Aussage sie für falsch halten und was statt dessen richtig sein soll. Und ganz besonderen Dank dafür, dass Sie einen Fehler gefunden haben: Beim letzten Absatz meiner Ziff. 4 habe ich nicht richtig aufgepasst und ihn eindeutig falsch formuliert. Ich bitte alle Leser um Entschuldigung. Es geht um die Gleichzeitigkeit von Netto-Quelle und Netto-Senke und richtig muss der Absatz lauten:
Beim CO2 vergleichen wir die Freisetzungen aus den natürlichen Quellen einmal mit der Entnahme aus der Atmosphäre, wie sich einstellen würde, wenn es nur diese Freisetzungen gäbe, und das andere Mal mit der Entnahme aus der Atmosphäre, wie sie sich unter Berücksichtigung auch der anthropogenen Freisetzungen ergibt. Bei der ersten Betrachtung ist die Natur eine Netto-Quelle, im der zweiten eine Netto-Senke.
So ist der Absatz m. E. aber richtig und er bestätigt klar die Möglichkeit der Gleichzeitigkeit von Netto-Quelle und Netto-Senke. Auf die anderen Aussagen in meinem „Verbesserungsvorschlag“ vom 18.05. 21:57 hat der Fehler m. E. keine Auswirkungen.
Bei Ihren weitergehenden Ausführungen habe ich allerdings ein Problem: Sie führen andere Vergleiche durch: Sie sagen einmal, dass „die Entnahme durch die Senken (SPkt) kleiner ist als die Gesamt-Freisetzung (QPkt)“. Das ist so natürlich richtig und bei diesem Vergleich ist die Natur eindeutig eine Netto-Senke. Dann sagen Sie, dass „die Entnahme durch die Senken (SPkt) größer ist als die Netto-Quelle (QPktnat)“. Das ist ein Vergleich eines Brutto-Flusses mit einer Netto-Quelle. Ich sehe nicht, wie der zur Klärung einer möglichen Gleichzeitigkeit von Netto-Quelle und Netto-Senke beitragen kann.
Der Absatz – also Ihre Betrachtung – bestätigt klar die Möglichkeit der Gleichzeitigkeit von Netto-Quelle und Netto-Senke. Aber Herr Dr. Roth, die Natur ist doch eindeutig eine SENKE für unsere CO2-Emission, da in nördlichen Ozeanen bei 420 ppm viel CO2 aufgenommen wird, es aber etwa 600 Jahre in der Tiefsee unterwegs ist bis es in den Tropen wieder ausgast. Und dabei verringert (!) die von 280 auf 420 ppm erhöhte Konzentration sogar noch die Ausgasung von antikem CO2 das vor der Industrialisierung bei 280 ppm aufgenommen wurde.
Sorry, in „die Entnahme durch die Senken (SPkt) größer ist als die Netto-Quelle (QPktnat)“ ist ein Schreibfehler enthalten. Statt „Netto-Quelle“ muss es „natürliche Quelle“ heißen, sonst macht es tatsächlich keinen Sinn.
An Ihrer Neuformulierung zu Ziffer 4 habe ich nichts auszusetzen.
Immer, wenn ich Beiträge von Eike Roth oder anderen Vertretern der „Der Anstieg des CO2-Gehaltes der Atmosphäre kommt aus natürlichen Quellen“ – Fraktion lesen, dann frage ich mich, warum es diese Leute nicht mit einer Karriere auf dem Finanzsektor versucht haben.
Die Grundidee ist genial.
Ich nehme Geld von meinem Konto und lege es in mein Portemonnaie.
( Analogie: Die natürlichen Senken/Quellen geben CO2 in die Atmosphäre ab)
Anschließend habe ich mehr Geld auf dem Konto und in meiner Geldbörse
(Analogie: Der Kohlenstoffgehalt in natürlichen Senken/Quellen und in der Atmosphäre nimmt zu)
silke kosch 16. Mai 2025 10:52
Ich glaube, Sie tun hier Herrn Roth Unrecht. Ich habe seinen Beitrag nicht so verstanden, aber ich weiß, das eine ganze Menge Leute ohne Wissen einen derartigen Unsinn behaupten. Wo soll denn das CO2 gespeichert sein, das auf einmal frei wird und was soll die Ursache für diese Freisetzung sein – und wo bleibt das CO2, das der Mensch in die Atmosphäre geblasen hat? Auf diese Fragen können die Leute, die den Unsinn vertreten nicht antworten, da der Unsinn mit der Realität kollidiert.
Herr Roth benutzt rot angestrichene CO2-Moleküle, ich benutze für einen ähnlichen Vergleich grün angestrichene CO2-Moleküle, um Absorption und Emission durch die Treibhausgase zu erklären: Nach einem absorbierenden Luftvolumen in Oberflächennähe hat sich die Intensität der Aufwärtsstrahlung kaum geändert, weil der Temperaturunterschied Oberfläche Luftvolumen klein ist – allerdings sind ein Teil der grün angestrichenen CO2-Moleküle verschwunden, weil diese absorbiert worden. Dafür sind nicht angestrichene Moleküle emittiert werden, so das sich bei fast gleichbleibender Gesamtintensität nur das Verhältnis der grün angestrichenen CO2-Moleküle zu nicht angestrichenen CO2-Molekülen geändert hat.
Jochen Ebel Reply to silke kosch 16. Mai 2025 16:35
Die anderen Artikel von ihm lesen … Z.B. Roth: About the Origin of CO2 in the Atmosphere.
Herr Ebel, ich denke nicht dass ich Herrn Roth unrecht tue.
Er tut hier zwar so, als suche er verzweifelt nach einer unbekannten Quelle, woher denn das CO2 kommt, was den CO2-Anteil der Atmosphäre erhöht, aber letztendlich sind es seine Fehler bzw. falschen Annahmen, die bei ihm überhaupt erst die Frage aufkommen lassen
Herr Ebel, Sie kennen offenbar nicht die Ursache für die Zusatzquellen, welche gerade bei Dr. Roth extrem hoch werden. Bei ihm wird der Senkenfluss (Inventar/Tau) um mehr als den Faktor 55/4 zu hoch weil er für Tau fälschlich die Umwälzzeit und statt 280 ppm Null verwendet. Wenn also der reale anthropogene Senkenfluss bei 420 ppm und 60% von 11 GtC/a etwa 6,6 Gt beträgt, sind es bei Dr. Roth mit Tau=4 a 420•2,12/4=222,6 GtC/a. Seine Zusatzquelle (die er ohne Zeitkonstante in den Kreisfluss und somit als Senkenfluss ansetzt) beträgt also 216 GtC/a, also das 19,6fache (!!) unserer Emission. Da er keine Modellrechnung macht, fällt ihm dieser Unsinn gar nicht auf.
Ergänzung: Herr Mechtel rechnet mit Tau=20 a einen Senkenfluss für 2015 von 412•2,12/20•3,67=160,3 GtCO2/a bei Emission von 33,7 GtCO2/a. Der Senkenfluss ist 53%, also 17,9 Gt. Seine Zusatzquelle wird damit 4,2mal so hoch wie unsere Emission.
Reden sie doch mal mit den Treibhausphysikern. Die werden auch reich mit solchen Spielchen!
Nur, dass Sie sich fundamental irren, der CO2-Kreislauf speist sich eben aus weiteren Quellen, oder um auf Ihr hinkendes Beispiel zu kommen, neben dem Geldkonto und der Geldbörse gibt es noch sehr viele weitere Geldquellen die Konto und Börse speisen können, Sie legen auftragsgemäß bewußt die Bilanzerungsgrenzen falsch, und ideologische Ignoranz sollte Ihnen dabei auch nicht weiter helfen, oder?
Frau Kosch, in dem von Herrn Ebel (Physiker) empfohlenen Roth-Artikel heist es:
„On its own, nature would have been a net source since 1750; only in combination with anthropogenic emissions has it become a net sink. Nevertheless, even as a net sink, nature can have, and actually has, contributed more to the rise in concentration than humans“.
Also, die Natur ist eine Netto-Quelle, aber zusammen mit der anthropogenen Emission ist sie zu einer Netto-Senke geworden und hat mehr zu dem ppm-Anstieg beigetragen als die Menschen. Das ist doch potenzierter Irrsinn!!
Vier Anmerkungen zum CO2-Kreislauf
Die Diskussion ist m. E. mittlerweile sehr lang geworden und viele Detailpunkte sind an unterschiedlichen Stellen angesprochen. Zu 4 solchen Punkten, die mir besonders wichtig erscheinen, nachfolgend einige Anmerkungen, detailliert untergliedert, um eine Diskussion zu den Einzelpunkten zu erleichtern:
1. Die Atmosphäre ist ein offenes System, bei dem die Entnahme (von CO2) mit der Konzentration zunimmt:
a. Weil weniger CO2 im System „Atmosphäre“ verbleibt als anthropogen freigesetzt wird, ist dieses System unweigerlich „offen“. Und weil alle (jedenfalls die wesentlichen) Senken bei höherer Konzentration mehr entnehmen (brutto, nicht netto), muss die Entnahme aus der Atmosphäre (brutto, nicht netto) insgesamt mit der Konzentration zunehmen. Die Überschrift 1. stimmt also.
b. Wenn man (vom Gleichgewicht ausgehend) eine sprungförmige Zunahme der Freisetzung in das System unterstellt, entsteht ein – ggf. zunächst sogar erhebliches – Ungleichgewicht zwischen Freisetzung und Entnahme, sodass die Konzentration (zumindest zunächst) steigt.
c. Die anthropogenen Freisetzungen sind aber nicht sprungförmig angestiegen (auf ca. 5 % der natürlichen Freisetzungen, so hoch sind sie heute), sondern sie sind ganz langsam auf diesen Wert angestiegen, in über 200 Jahren, selbst heute machen sie jährlich nur ca. 1 % des atmosphärischen Inventars aus. Bei einem so langsamen Anstieg läuft die Transiente praktisch im Gleichgewicht ab. Wenn man die anthropogenen Freisetzungen auf ihrem heutigen Niveau einfriert (und die natürlichen sich nicht verändert haben und weiterhin konstant bleiben), dann gibt es praktisch keinen Nachlauf, die Konzentration bleibt vielmehr praktisch sofort stehen, wo sie ist (nicht erst nach einigen Jahrzehnten auf einem dann höheren Wert!).
d. Aber selbst wenn man einen sprungförmigen Anstieg der Freisetzungen (aus welcher Quelle auch immer, anthropogen ist nur eine der Möglichkeiten) unterstellt, um z. B. die genannten 5 %, dann steigt die Konzentration nur so lange an, bis die Entnahme um ebenfalls diese 5 % angestiegen ist. Dann herrscht wieder Gleichgewicht! In einem offenen System kann die Konzentration nie stärker steigen als die Freisetzung in das System, egal, wie schnell letztere steigt (bei schnellem Anstieg erreicht die Konzentration diesen Wert im Nachlauf, bei langsamem Anstieg praktisch im Gleichschritt, nur höher geht es nie)!
e. Der beobachtete Anstieg der Konzentration um 50 % kann daher gar nicht durch die kleinen anthropogenen Freisetzungen bewirkt worden sein, auch nicht über lange Zeit, hierzu haben vielmehr auch erhöhte Freisetzungen aus natürlichen Quellen beitragen müssen, ja, sie haben sogar viel stärker beitragen müssen!
f. Dieser Anstieg der Freisetzungen aus natürlichen Quellen ist keine fiktive Annahme aus irgendwelchen Wunschvorstellungen her, sondern eine zwangsweise Folge der beobachteten Konzentrationserhöhung unter Beachtung der Regeln der Physik.
g. Möglichkeiten für eine solchen Anstieg gibt es mehrere, welche die richtige ist, kann so nicht ausgesagt werden.
2. Treibende Kraft: Warum nimmt die Konzentration überhaupt ab?
a. Nehmen wir zunächst Gleichgewicht in der Atmosphäre an, mit z. B. 280 ppm Konzentration und 80 ppm/a Umwälzung. Dann tauschen wir jedes tausendste CO2-Molekül in der Atmosphäre durch ein rot eingefärbtes, ansonsten aber völlig gleiches Molekül aus.
b. Der Partialdruck bleibt unverändert, aber die Konzentration der roten CO2-Moleküle bleibt nicht gleich, sondern sie sinkt! Bewerkstelligt durch die Umwälzung, wandern immer mehr rote Moleküle in die Senken. Das geht so lange, bis überall die gleiche Konzentration (die gleiche Rotfärbung) herrscht. Dann schafft die Umwälzung gleich viel Nachschub wie sie entnimmt.
c. Antriebskraft für das Auswandern der roten Moleküle aus der Atmosphäre ist nicht ein Überdruck in der Atmosphäre (es gibt ja keinen!), sondern der 2. HS der Thermodynamik: Ohne Energiezufuhr von außen (eine solche haben wir hier nicht) muss ein Prozess so ablaufen, dass die Entropie zunimmt, hier also, dass die roten CO2-Moleküle überall möglichst gleichverteilt werden. Bewerkstelligt wird diese Umverteilung durch die Umwälzung.
d. Der Farbausgleich erfolgt umso schneller, je höher die Umwälzung ist.
e. Nun ersetzen wir nicht jedes tausendste CO2-Molekül in der Atmosphäre durch ein rotes, sondern wir bringen die gleiche Anzahl roter CO2-Moleküle zusätzlich in die Atmosphäre ein. Der nachfolgende Ablauf wird nicht sehr unterschiedlich sein: Die Zahl der roten Moleküle in der Atmosphäre wird praktisch gleich schnell abnehmen und der Endzustand wird praktisch der gleiche sein. Antriebskraft hierfür ist wieder im Wesentlichen der Entropiesatz, der Antrieb durch den (minimalen) Überdruck ist demgegenüber völlig vernachlässigbar. Der Farbausgleich wird daher wieder umso schneller erfolgen, je höher die Umwälzung ist.
f. Allgemein: Bei kleinen Konzentrationserhöhungen erfolgt deren Abbau hauptsätzlich zur Herstellung gleicher Konzentration (Gleichverteilung der zusätzlich eingebrachten Menge im gesamten Kreislauf, wie bei den roten Molekülen) und nur sehr untergeordnet zur Herstellung gleicher Partialdrücke (der Endzustand ist bei beiden Antriebsarten identisch, nur wirkt der eine Antrieb eben wesentlich stärker als der andere).
g. Ob man die zusätzlich eingebrachten Moleküle an ihrer roten Farbe erkennen kann, oder z. B. an ihrer Radioaktivität (falls sie eine solche haben, wie C14-Moleküle), oder auch nicht von anderen CO2-Molekülen unterscheiden kann, das macht keinen Unterschied. Es wird immer die eingebrachte Menge gleichmäßig im gesamten Kreislauf verteilt. Das fordert der 2. HS. Der gemessene rasche Abfall der C14-Konzentration zeigt daher auch einen raschen Abfall einer beliebig anderweitig erhöhten Konzentration an. Der Abfall wird eben – bei hoher Umwälzung – immer vorwiegend durch den Entropiesatz bestimmt und nur nachrangig durch den Druckausgleich. Wir sollten daher vielleicht besser von einem „Konzentrationsausgleich“ (bzw. von der „Gleichverteilung der eingebrachten Menge“) sprechen und nicht von einem „Druckausgleich“ (obwohl natürlich beides stimmt).
h. Weil beide Ausgleichprozesse aber immer gleichzeitig wirken, ist der reale Abfall sogar immer rascher, als wenn nur die Umwälzung alleine oder nur der Überdruck alleine wirkte.
i. Nochmals zur Klarstellung: Der Abbau einer Überschusskonzentration erfolgt nur stark untergeordnet durch den Netto-Ausfluss in die Senken und weit überwiegend durch die Umverteilung infolge der (hohen) Umwälzung. Beide Prozesse arbeiten natürlich parallel, aber der eine ist eben bei weitem tonangebend, er bestimmt das Tempo, mit dem die Veränderung abläuft.
3. Gleichgewichtslage bei 280 ppm?
a. Vielfach wird angenommen, bei Einstellung der anthropogenen Freisetzungen würde die Konzentration zum vorindustriellen Gleichgewicht bei 280 ppm zurückkehren, ähnlich wie ein Pendel immer wieder in seine Ausgangslage zurückkehrt.
b. Beim Pendel wird das über die Antriebskraft „Gravitation“ erreicht, die bei jeder Auslenkung eine rückstellende Kraft bewirkt, immer zu der gleichen Ausgangsalge (senkrecht unter der Aufhängung) hin, auch wenn sich z. B. Länge oder Gewicht des Pendels verändert haben.
c. Für die Atmosphäre gibt es keine solche bevorzugte Ausgangslage. Vielmehr ist in der Atmosphäre ist die Ausgangslage variabel, sie hängt von der Freisetzung ab: Die bestimmt, welche Konzentration sich als Gleichgewicht einstellt (diejenige, bei der die Entnahme gerade gleich groß ist wie die Freisetzung). Bei einer anderen Freisetzung ergibt sich eine andere Ausgangslage. Eine Rückkehr zu 280 ppm würde es nur geben, wenn die Freisetzung wieder ihren alten Wert annähme. Eine rückstellende Kraft, die die Freisetzung wieder dorthin treibt, ist aber nicht zu erkennen (es wird nur von manchen Forschern einfach angenommen, dass die natürliche Umwälzung die ganze Zeit über gleichgeblieben ist, ohne eine Begründung hierfür anzugeben). Wenn sich jedoch irgendetwas, das die Freisetzungen steuert, verändert hat, dann gibt es zwangsweise einen neuen Gleichgewichtswert, der nur von den neuen Randbedingungen abhängt. Wenn die sich verschoben haben, und nach Ziff. 2 müssen sie sich verschoben haben, dann strebt das System zwangsweise zu einem neuen Gleichgewicht hin.
d. Nochmals, der Unterschied besteht darin, dass es beim Pendel eine rückstellende Kraft zur alten Lage hin gibt, beim CO2 aber nicht. Auch wenn es früher einmal ein bestimmtes Gleichgewicht gegeben hat, und selbst wenn dieses längere Zeit angehalten hat, bewirkt das noch keinerlei rückstellende Kraft, wie die Gravitation eine bewirkt. Es gibt keine „eingefahrenen Zyklen“, die irgendeine Rückstellkraft entfalten.
e. Man kann das auch so beschreiben: Die Natur reagiert immer nur nach physikalischen Gesetzen, nicht danach, wie wir uns vorstellen, wie sie reagieren sollte.
4. Konsequenzen für die Zukunft
a. Weil die Konzentration sich bisher überwiegend nach den Launen der Natur entwickelt hat, wird sie das höchstwahrscheinlich auch weiter so machen.
b. Solange wir diese Launen der Natur nicht verstehen und vorhersagen können, können wir auch keine Prognosen der zukünftigen Konzentrationsentwicklung machen. Das ist keine „Unvollkommenheit“ des Modells, sondern ein charakteristischer Zug der Natur: Solange wir ihre Launen nicht verstehen, können wir sie auch nicht vorhersagen.
Herr Dr. Roth, ich will hier nur Ihren alten Fehler kommentieren dass Sie bei relativ geringer Emission E pro Jahr fälschlich davon ausgehen dass quasi momentan Sättigung eintritt womit ppm dann einfach gemäss ∆ppm/E (bei Tau=55 a sind das bei mir 19,4 ppm pro GtC/a) ansteigt.
Das ist falsch, denn auch hier erfolgt der ppm-Anstieg nach 1-exp(-t/Tau). Und da Sie nie eine Modellrechnung gemacht haben, bringen Sie stets viel unnötig komplizierten Text um Ihre falschen Auffassungen für richtig zu erklären und uns letztlich weiszumachen dass eine Berechnung für die Zukunft garnicht möglich ist.
Herr Dietze,
die Tau=55a sind Ihre Erfindung und keine durch die Physik vorgegebene Naturkonstante, mit Tau=55a kann daher nichts bewiesen werden. Und was langsame Transienten betrifft (Transienten bei nur geringen Störungen), so laufen diese infolge der hohen Umwälzung tatsächlich immer sehr nahe am Gleichgewicht ab.
Eike Roth 14. Mai 2025 21:31
Woher haben Sie die 80 ppm/a? Nach dem Abklingen des C14 gehe ich von einer vollständigen Umwälzung von ca. 20 Jahren aus – also aktuelle Konzentration/20 Jahre. Das wären 14 – 21 ppm/a.
Der Zusatzbeitrag über den 280 ppm folgt weitgehend aus der Verbrennung fossiler Rohstoffe – und die Verbrennungsmenge folgt den Launen der Menschen.
In Zahlen gesprochen emittiert der Mensch nur 5% von dem was die Natur emittiert.
Also nur ein 20igstel.
Und weitestgehen kann nicht sein, weil vom Gesamteintrag nur 2.5% in der Atmosphaere verbleibt, und der Anteil vom Menschen daran ist wiederung 1/20 das heisst 0.125% Anteil.
Werner Schulz Reply to Jochen Ebel 15. Mai 2025 10:05
Und? Es ist immer noch ein zusätzlicher Eintrag pro Jahr. Vorher hatten wir lange Zeit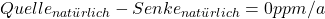
, heute haben wir
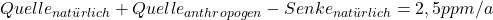. Und damit steigt der CO2-Gehalt Jahr für Jahr …
Ja im Verhaeltnis 1/20. Kann ja nicht so schwer sein.
Herr Müller,
richtig, nur sind die natürlichen Quellen und Senken heute andere als sie früher waren.
Eike Roth Reply to Marvin Müller 15. Mai 2025 23:09
In dieser einfachn Massenbilanz steht nichts über die Größe oder Art der natürlichen Quellen und Senken. D.h. die können durchaus auch einen stärkeren Fluss haben oder es können andere hinzugekommen sein. Das öndert aber nichts an der Tatsache, dass die natürlcihen Senken mehr aufnehmen, als die natürlichen Quellen freisetzen, die Ursache des Anstiegs also nicht dort liegen kann …
Also vernachlaessigen sie diese. Sag ich ja!
Wuerde das heissen, das ohne Antropogenes CO2 die Konzentration weiter sinken wuerde? Widerspricht das nicht der These von den stabilen 280 ppm?
Werner Schulz Reply to Marvin Müller 16. Mai 2025 11:52
Nein, Ich berücksichtige sie. Ich mache nur keine Annahme über die Größe und Art. Sie können gerne zeigen, wo das eine Auswirkung auf das qualitative Ergebnis hat. Ich bin gespannt.
Ja, Nein. Der Fluss in die Senken wird ja getrieben durch den Unterschied des CO2-Gahltes in der Luft und den oberflächennahen Ozeanschichten. Wenn der CO2-Gehalt der Atmosphäre sinkt, sinkt auch der Unterschied und die Senken nehmen weniger auf. Irgendwann ist das wieder im Gleichgewicht und für geraume Zeit bei einem Gehalt größer 280ppm ..
Sie sind da aber ich sehe sie nicht? Und jetzt wollen sie das ich das Fehlen begruende? Ich denke das sollten sie tun!
Sehr bezeichnend! So antwortet auch Herr Ebel…
Nichts genaues weiss man nicht, oder?
Also nicht durch chemische Prozesse? Nicht durch physikalische Prozesse wie Regenauswaschung, Wellenbewegung, Winddruck?
Und warum noch mal soll 280 ppm die magische Nummer sein?
Werner Schulz Reply to Marvin Müller 16. Mai 2025 17:38
Das ist nur Ihre eigenartige Interpretation dessen, was ich geschrieben habe.
Sie hatten zwei Fragen gestellt, das waren die Antworten auf die Fragen in der Reihenfolge, in der Sie sie gestellt hatten. Und ich finde ein Ja auf die Erste undNein auf die zweite ziemlich klar.
Fragen Sie einfach die, die mit dieser magischen Zahl ergumentieren.
Vielleicht sollten sie nicht so eigenartig schreiben.
Ich sage sie vernachlaessigen die natuerlichen Quellen, sie sagen sie tun es nicht machen nur keine Angabe ueber die Hoehe, und das wo diese Angabe nun von ihnen ausgewiesen fehlt. Also vernachlaessigen sie die natuerlichen Quellen und deren Menge.
Heisst ich habe keinen Ahnung oder beides ist richtig.
Also soll es so sein:
„Das öndert aber nichts an der Tatsache, dass die natürlcihen Senken mehr aufnehmen, als die natürlichen Quellen freisetzen,“
Wuerde das heissen, das ohne Antropogenes CO2 die Konzentration weiter sinken wuerde? Widerspricht das nicht der These von den stabilen 280 ppm?
Die erste Aussage war von Ihnen, sie bejahen diese also eben noch mal? Ist das eine Art Selbstbestaetigung?
Zum Nein, wenn die Natur mehr aufnimmt als sie selber abgibt, dann muss die Konzentration sinken, Da stimmt was mit ihrer Logik nicht!
Und warum noch mal soll 280 ppm die magische Nummer sein?
Brilliant, genau das habe ich getan, sie wissen schon was sie schreiben?
Marvin Müller Reply to Werner Schulz
16. Mai 2025 12:32
Werner Schulz Reply to Marvin Müller 17. Mai 2025 22:39
Warum ordnen Sie die erste Antwort einer Aussage zu, statt Ihrer ersten Frage? Sie haben doch korrekt erkannt, dass es eine Aussage ist und haben die zwei Fragen auch nochmal korrekt zitiert.
Daher habe ich diese Frage ja auch mit ja beantwortet.
Das ist bei mir aber keine magische Zahl, sondern lediglich der CO2-Gehalt, der lange vorherrschte. Ich dachte bei ihrer magischen Zahl an so etwas, wie die Berechnung von Herrn Dietze, bei dem dies Zahl in einer Formel auftaucht. Benutze ich nicht so, bei mir hätte sich ein Gleichgewicht oberhalb von 280ppm eingestellt, dass dann über lange Zeit langsam reduizert wird.
Es waren keine zwei Fragen da! Nichts fuer ungut.
Bitte erklaeren sie die 280 ppm!
Werner Schulz Reply to Marvin Müller 18. Mai 2025 17:46
Im Kommentar standen zwei fragen, auf die ich geantwortet hatte.
Frage 1: „Wuerde das heissen, das ohne Antropogenes CO2 die Konzentration weiter sinken wuerde?“
Frage 2: „Widerspricht das nicht der These von den stabilen 280 ppm?
Können Sie jetzt echt nichtmehr bis zwei zählen?
Marvin Müller 16. Mai 2025 10:17
„Ursache des Anstiegs also nicht dort liegen kann …“
Ich hatte Herrn Roth so verstanden, das er Ihnen nicht widerspricht, also der Mensch mit seiner Verbrennung zusätzliches CO2 einträgt. Wenn er es doch so meint wie Sie vermuten, dann gehört auch auch zu den Leuten mit Unsinn (Jochen Ebel 16. Mai 2025 16:35)
„Quelle_{natürlich} – Senke_{natürlich} = 0 ppm/a heute haben wir Quelle_{natürlich} + Quelle_{anthropogen} – Senke_{natürlich} = 2,5 ppm/a“
Das dies Unsinn ist, wissen Sie aber schon? Auch vor dem ominösen Bezugsdatum „Vorindusdriell“ gab es anthropogene Quellen in erheblichem Umfang und der Umstieg auf Nach-Vorindusdrielle Brennstoffe war keine über uns hereinbrechende plötzliche Katastrophe sondern ein allmählicher Umstieg durch die indusdrielle Produktion wie auch die Nutzung als Hausbrand.
Beschäftigung mit der Geschichte im ausgehenden Mittelalter kann manchmal Wunder wirken. 😀
Moritz Steinmetz Reply to Marvin Müller 17. Mai 2025 8:14
Dann nennen Sie doch einfach mal eine Größe und zeigen, dass dadurch die Aussage falsch ist.
Herr Ebel, Sie finden eine Umwälzung von etwa 190 GtC/a in Abb.1 bei [9].
Peter Dietze 15. Mai 2025 12:22
„bei [9].“
Sie sind witzig – mit Ihren Irrtümern [9] wollen Sie etwas „beweisen“?
Herr Ebel
80 ppm/a als Umwälzung gibt IPCC an.
Woher der Anstieg über 280 ppm hinaus kommt: Hauptsächlich aus der Natur, siehe meine Ausführungen.
Eike Roth 15. Mai 2025 23:03
„Hauptsächlich aus der Natur“
Beantworten Sie bitte meine Frage in (Jochen Ebel 16. Mai 2025 16:35).
Eike Roth schrieb am 14. Mai 2025 21:31
Der CO2-Gehalt ist allerdings nicht gefallen, Das Verhältnis von 14C-Isotopen zu 12C ist – wenn ich das richtig verstanden habe – 1 zu 10^12 und bei den Bombentests wurde daraus 2 zu 10^12. Diese Erhöhung ging dann im Laufe der Zeit zurück und man hat aus der Dauer geschlossen, dass der CO2-Gehalt der Atmosphäre in 3-5 Jahren einmal durch CO2 aus den Ozeanen/Biosphäre ersetzt wird.
Aber das ist etwas anderes, als den CO2-Gehalt der Atmosphäre weider zu reduzieren.
Herr Müller,
der Gehalt an 14C ist sehr wohl gefallen, weil das viele 14C aus der Atmosphäre, in die es eingebracht wurde, auf den ganzen Kreislauf verteilt wurde, hauptsächlich per Umwälzung. So geht es mit jeder CO2-Menge, die in die Atmosphäre eingebracht wird, unabhängig davon, ob diese eingebrachten Moleküle radioaktiv, rot oder farblos sind.
Eike Roth Reply to Marvin Müller 15. Mai 2025 23:14
Das steht doch da, einfach nochmal in Ruhe lesen.
Die Menge der 14C-Isotope ging nach dem Ende der Atombombentests zurück, der CO2-Gehalt der Atmosphäre ist weiter angestiegen, ging also nicht zurück. Daher ist Ihr Schluss „Der gemessene rasche Abfall der C14-Konzentration zeigt daher auch einen raschen Abfall einer beliebig anderweitig erhöhten Konzentration an.“ offensichtlich falsch.
Marvin Müller 16. Mai 2025 10:12
Ich habe das nur als Entropie verstanden, das der ursprüngliche Anteil in der Atmosphäre sinkt und im Ozean steigt, aber gleichzeitig der ursprüngliche Anteil im Ozean sinkt und in der Atmosphäre steigt, so daß der II. HS erfüllt ist.
Aber es kann natürlich sein, das Herr Roth Falsches meint und ich nur das Richtige heraus gelesen habe.
Jochen Ebel Reply to Marvin Müller 16. Mai 2025 17:04
Nur um sicherzugehen: Mein Kommentar richtete sich an Herrn Roth …
Die Vegetation als Senke für 14C fällt dabei sicher aus, denn die mög nur leichteres 12C und besitzt dementsprechend auch einen Filtermechanismus, erwiesenenermaßen durch Isotopenanalysen bestätigt nur bisher, worin dieser bestehen könnte, noch nicht letztendlich erklärbar.
Herr Dr. Roth, wie man dem Artikel entnehmen kann, liegt meine Argumentation stark auf formalen Aspekten mit nur wenigen physikalischen Voraussetzungen. Um so wichtiger, dass Sie stark die physikalischen Argumente in den Vordergrund rücken!
Gerade habe ich nochmals Ihren EIKE-Artikel von 2023 (Literaturliste [5]) durchgesehen und kann sagen, dass er mich weitestgehend überzeugt. Nur einen Punkt kann ich nicht nachvollziehen, dass nämlich die Konzentrationszunahme schneller als die Freisetzungen gewachsen sei.
Sie geben z.B. von 1950 bis 2010 ein Wachstum der anthropogenen Emissionen von 12 Gt/a auf 40 Gt/a an. Das ist eine Steigerung um den Faktor 3,3. Daneben wächst die Konzentrationsänderung im gleich langen Zeitraum 1960 bis 2020 von 0,7 ppm/a auf 2,5 ppm/a, das ist ein Faktor 3,6, also nahezu identisch.
Wenn ich mit meinen Fitkurven von 1960 bis 2020 rechne und bei den anthropogenen Emissionen noch 5 Gt/a für die Landnutzung addiere, die in meinen ursprünglichen Werten nicht enthalten ist, dann wachsen die Emissionen von 15,5 Gt/a auf 40,8 Gt/a, also um den Faktor 2,6. Für die Konzentrationszunahme ergibt die Fitkurve leicht von den Ihren verschiedene Werte, nämlich 0,9 ppm/a auf 2,4 ppm/a. Das ist der Faktor 2,67 und damit wieder nahezu identisch.
Die Konzentrationsänderung ist damit etwa gleich schnell gewachsen wie die anthropogene Freisetzung. Dazu passt auch, dass die Konzentration selber um den Faktor 1,3 gewachsen ist, also etwa halb so stark. Ihre übrigen Argumente bleiben davon selbstverständlich unberührt, und es bedeutet m.E. auch nicht, dass neben den anthropogenen Quellen nicht auch noch andere im Spiel sein können.
Michael Mechtel Reply to Eike Roth 15. Mai 2025 17:11
War das damals nicht einfach das Problem, dass ppm mit ppm/a bzw ppm/a mit ppm/a² (die Änderung der Emissionen pro jahr) verglichen wurde? Ich hatte das damals in einem Kommentar grafisch veranschaulicht …
Ich komme auf die gleichen Zuwachsraten der Anstiege wie Sie in Ihrem damaligen Kommentar. Die 0,95% p.a. für die anthropogenen Emissionen, die damals auch auftauchen, kann ich nicht reproduzieren.
Michael Mechtel Reply to Marvin Müller 16. Mai 2025 9:09
Die 0,95% sind der in Prozent umgerechnete Anstieg der anthropogenen Emissionen pro Jahr.
Herr Roth hatte den Anstieg des CO2-Gehaltes der Atmosphäre in ppm mit dem Anstieg der anthropogenen Emissionen pro Jahr in ppm/a vergleichen. Und damit das nicht so offensichtlich ist, hat er es in Prozent umgerechnet, wodurch die Einheiten weggefallen sind. Er schrieb damals:
Ich habe den Eindruck, er hat das Problem damit bis heute nicht verstanden. Wir konnten das damals aber auch nicht weiterdiskutieren, weil die Moderation stillschweigend jede weitere Antwort nicht veröffentlichte.
Herr Mechtel,
danke für Ihren Kommentar. Zum schneller Wachsen oder nicht: Sie betrachten Absolutmengen, in meinem Beitrag von 2023 verglich ich, wie sich die Steilheiten der Kurven verändert haben.
Ich hab ja auch die Steilheiten verglichen. Ich habe dazu lediglich Ihre ppm/a-Angaben in Gt/a-Angaben umgerechnet. Das wäre eigentlich nicht nötig gewesen, macht aber auch nichts, denn beim Bilden der Verhältnisse Endwert/Anfangswert fällt der Umrechnungsfaktor wieder heraus.
Herr Mechtel, Steilheiten zu vergleichen, macht keinen Sinn. Beim ppm-Anstieg kommt es nur darauf an um wieviel HÖHER die Emission als unser (anthropogen verursachter) Netto-Senkenfluss ist. Das sehen Sie bei meiner Excel-Grafik wo trotz Null Anstieg der Emission die ppm noch über 110 Jahre ansteigen – und zwar mit ∆max•(1-exp(-t/Tau55)) bis zum Maximum bei etwa 500 ppm.
Großen Dank an die Diskutanten für ihre engagierten, sachlichen und auch kontroversen Beiträge zum Thema. Abschließend ein kurzes Resumee aus meiner Sicht:
1.) Wie schon festgestellt, lässt sich die Abklingkonstante alpha aus dem mathematischen Formalismus nicht herleiten, dazu sind weitergehende Überlegungen notwendig. Ihr Wert beeinflusst die Höhe von Senken- und Quellfluss.
2.) Strittig ist, ob ein vorindustrielles Konzentrationsniveau von 280 ppm als natürliches Gleichgewichts-Niveau weiterhin Bestand hat. Die Antwort hat Konsequenzen für die Abklingkonstante. Lautet die Antwort ja, bedeutet dies eine Vorfestlegung, dass für das derzeitige Ungleichgewicht in der Atmosphäre der anthropogene CO2-Eintrag allein verantwortlich ist.
3.) Es soll nicht verschwiegen werden, dass auch unter dieser Vorfestlegung die Keelingkurve rekonstruiert werden kann. Günstige Bedingungen für die Rekonstruktion mit rein linear wachsendem Quellfluss sind allgemein:
– kleiner Betrag von Quell- und Senkenfluss,
– nicht zu großer zeitlicher Anstieg des Betrages.
Zur Erklärung sei an die Einleitung des Artikels erinnert: so arbeitet das System fast wie ein Kochtopf, d.h., wie einer mit nur kleinen Löchern. Die Bedingung kleiner Flüsse ist realisierbar durch ein kleines alpha und / oder ein hohes Basisniveau für den Diffusionsantrieb (z.B. das 280-ppm-Niveau).
Die Abklingkonstante alpha (oder Tau) lässt sich aus dem mathematischen Formalismus bei Ihnen offenbar nicht herleiten. Bei mir, wo ich mit Excel sequentiell in Fünfjahresschritten für ein vorgegebenes alpha sowie die jeweilige Emission den Senkenfluss, das ∆ppm, und so die geglättete Keelingkurve nachgerechnet habe, war das recht einfach.
Ich musste nur alpha soweit variieren bis die Keelingkurve optimal (und ohne Zusatzemission) nachberechnet wurde. Und mit diesem alpha kann ich dann auch den ppm-Verlauf für einen zukünftigen Emissionsverlauf (z.B. für irgend einen Anstieg, einen Reduktionspfad, eine Konstanthaltung – siehe hier meine Grafik – oder für Nullemission) korrekt berechnen (siehe [9] Abb.2).
Ja also ein „Fudgefaktor“ und keine physikalisch realistische Zahl oder Begruendung.
Herr Schulz, wenn ich aus Messwerten (ppm-Verlauf gemäss globaler Emissionen) durch optimale Kurvenanpassung (man kann das auch durch Regressionsanalyse mit Minimierung der Fehlerquadrate machen) ein offenbar reelles Tau für den CO2-Abbau bestimme, ist das ein Fudgefaktor?? Und was ist mit der C14-Kurve?? Wenn Sie ein Verfahren kennen, Tau analytisch zu berechnen (z.B. durch Diffusions- und Ausgasungsprozesse, Ozeantemperaturen sowie CO2-abhängige Photosynthese bei den verschiedenen Pflanzen welche auf der Erde verteilt wachsen, dann bitte her damit. Davon abgesehen verstehe ich Ihr Bedürfnis (und ebenso das von Herrn Ebel) nicht, mich zu diffamieren weil ich mich bemühe, einen reellen ppm-Verlauf zu berechnen, der ja die Grundlage für die Kritik von EIKE an der unnötigen und billionenteuren Dekarbonisierung liefert.
Peter Dietze 15. Mai 2025 21:10
Es geht nicht um den ppm-Verlauf, sondern um den Temperaturzuwachs bei ppm-Zuwachs.
Wenn sie einen Wert nehmen, der ansonsten keine physikalische Bedeutung hat, um ihre Modelwerte an Messwerte anzupassen?
Ich denke dann ist das ein Fudgefaktor.
Und weil sie fragen ob ich die Bedeutung von Ihrem Fudgefaktor kennen, nein das tue ich nicht.
Ich diffamieren sie ausserdem nicht, sondern ich stelle fest.
Herr Schulz, wenn Sie den zentralen Parameter Tau oder Alpha für einen Fudgefaktor ohne physikalische Bedeutung halten, haben Sie die ganze Berechnung von Senkenflüssen und ppm-Werten nicht verstanden. Auch Herr Mechtel benötigt diesen Parameter, den er aus der C14-Kurve bestimmt hat. Ich habe die (viel besser geeignete) Keelingkurve genommen, denn der deutlich geringere C14-Wert (und ganz besonders die sehr geringe Umwälzzeit bei Dr. Roth) führt wegen der viel zu großen Senkenflüsse zur Errechnung großer nötiger Zusatzquellen (von einem Vielfachen der anthropogenen Emissionen) welche es in der Natur nicht gibt.
Dann müssten meine EXCEL-Software und mein Taschenrechner gleichzeitig spinnen!
P schwerdt Reply to Michael Mechtel 15. Mai 2025 13:01
Herr Mechtel hat für 1960 t=0 gesetzt. Bei m(t) ist das t also nicht das Jahr, sondern t = Jahr – 1960 …
Ob die terrestrische Gegenstrahlung aus Böden u. technischen Oberflächen wohl nicht auch ohne eine Einstrahlung doch (eine gewisse Zeit) anhalten würde und ob
a) Einstrahlung in allen verschiedenen Frequenzen und
b) zusätzlich die Abstrahlung ebenso
Gegenstand von Betrachtungen zur Energiegewinnung sein könnten. Das eröffnet das Addieren der zur Atmosphäre hin umgesetzten Umweltenergien im Mittel zu ca. 1020W/m2 permanent – dies gegenüber einer Ernte aus einer Photovoltaik von ca. 130W/m2 permanent.
Herr Mechtel, in Ihrem Anhang zur Bestimmung des von Ihnen gewählten (!) tau=20 a (welches einen um den Faktor 2,75 zu hohen Senkenfluß ergibt) sagen Sie „Die Spannweite der möglichen alpha-Werte, die sich alle eignen, um die Keeling-Kurve zu rekonstruieren, ist allerdings sehr groß. In verschiedenen Veröffentlichungen (z.B. [4], [9], [10]) findet man für tau Angaben im Bereich 40 bis 60 Jahre, also alpha ca. 0,02 /a. Solche Werte kommen zustande, wenn man die Hypothese eines stabilen 280-ppm-Niveaus als naturgegeben voraussetzt“.
Damit bin ich, der im Gegensatz zu Ihnen mit tau=55 a den ppm-Verlauf seit 1840 ohne dubiose riesige Zusatzquellen nachgerechnet hat und auch die 280 ppm als besten Ausgangswert bestätigen konnte, keinesfalls einverstanden. Ich weise darauf hin dass meine ursprüngliche Modellrechnung vom April 2002 (!!) für 2025 einen Anstieg auf fast 420 ppm ergeben hat, wie Sie aus meiner Grafik im Kommentar vom 10.5.25 11:09 ersehen können. Dass Tau=20 a für solche Berechnungen wegen der Umwälzzeit von etwa 4 Jahren, womit ja eine erhebliche Verdünnung von C-14 stattfindert, unbrauchbar ist, habe ich hier bereits hinreichend erklärt.
Herr Dietze, ich glaube, wir müssen keine Scheingefechte ausführen. Es steht Ihnen zu, mit tau = 55 Jahren zu rechnen, wobei ich eher zu 20 Jahren neige. Aber ich bin sicher, Sie haben meine Rechnung inzwischen gut genug verstanden, um zu wissen, dass sie mit beiden Vorgaben arbeiten und die Keelingkurve im Zeitraum 1960 -2018, also über fast 60 Jahre, reproduzieren kann.
Wenn man meine quadratische Anpassung an die Keelingkurve bis 2025 extrapoliert, kommt man auf 425 ppm. Sie haben „fast 420 ppm“ berechnet. Meine neuste Info zu 2024 lautet 424 ppm. Der Streit, wer besser liegt, lohnt aber nicht, denn beides sind Extrapolationen, und niemand kann die Entwicklung der Zu- und Abflüsse in der Zukunft kennen.
Herr Mechtel, man fragt sich doch wie Sie den korrekten ppm-Anstieg berechnen können wenn bei tau=20 a die Senkenflüsse um den Faktor 2,75 zu hoch werden. Natürlich geht das so: Die Emission ist z.B. 11 GtC/a, der reale Senkenfluss sei 6,6 GtC/a, Sie berechnen aber 18,15 und postulieren einfach eine natürliche Zusatzquelle (!) von 11,55 GtC/a.
Ein weiteres Problem ist Ihre Kurvenanpassung an den beobachteten ppm-Anstieg z.B. über die Jahre 1960-2018. Falls die Emissionen bis 2050 ähnlich anwachsen, können Sie natürlich auch die ppm für 2050 etwa richtig ermitteln. Aber das ist doch nur ein „best guess“, denn die korrekte Berechnung muss doch (wie z.B. bei mir in der hier gezeigten Grafik) den tatsächlichen (oder zukünftigen) Emissionsverlauf – und natürlich auch die sich daraus mit dem ppm-Anstieg ergebenden Senkenflüsse OHNE Zusatzquellen berücksichtigen.
Die Zusatzquelle wird von mir nicht postuliert. Das einzige, was ich postuliere, ist ein diffusionsgetriebener Senkenfluss. Die Zusatzquelle ist dann ein Ergebnis, das die unbestechliche Mathematik liefert, und zwar (in unterschiedlicher Höhe) sowohl für Ihren wie für meinen Wert von tau und nur für meinen Auswertezeitraum, ohne den Anspruch, das auf frühere oder spätere Zeiten fortschreiben zu können.
Wenn Sie sagen, Sie können die Konzentration c ohne Zusatzquelle aus den anthropogenen Emissionen rekonstruieren, wäre es sehr interessant, Ihren Rechengang im Detail zu kennen.
Ich versuche mal eine Erklärung. Der Unterschied zwischen unseren Ansätzen ist doch: Sie führen das „natürliche“ Gleichgewichtsniveau der atmosphärishen CO2-Masse mnat ein, das zur Konzentration 280 ppm gehört. Dann postulieren Sie den Senkenfluss
SPkt_Dietze(t) = alpha_Dietze * (m(t) – mnat). Ich postuliere hingegen
SPkt_Mechtel(t) = alpha_Mechtel * m(t).
Die Differenz ist (alpha_Dietze – alpha_Mechtel) * m(t) – alpha_Dietze * mnat. In Zahlen: (0,0182 – 0,05)/a * m(t) – 0,0182/a * 2246 Gt = -0,0318/a * m(t) – 40,88 Gt/a.
Ihr Senkenfluss ist also vom Ansatz her stets kleiner als meiner (für t >=0), und deshalb kommen Sie natürlich auch mit einem kleineren Quellfluss aus. Das würde sogar gelten, wenn wir gleiches alpha (bzw. tau) benutzen würden. Zentral ist die Frage, ob es erlaubt ist, die 280 ppm als natürliches Gleichgewichtsniveau festzuhalten.
Michael Mechtel Reply to Peter Dietze 12. Mai 2025 11:34
Wenn der Fluss in die Senken nicht proportional zur Masse der Atmosphäre, sondern von der Differenz der Partialdrücke in der Atmosphäre und den oberflächennahen Wasserschichten getrieben wird, geht das eigentlich relativ „einfach“. Wir emittieren eine Menge X CO2, die Senken absorbieren etwa die Hälfte und die Konzentration in den oberflächennahen Schichten steigt an und damit auch der Partialdruck des CO2 in diesen Schichten. Und das Jahr für Jahr. Die Menge, die wir emittierte haben,reicht dann locker aus, den Anstieg zu erklären.
(Die Atombombentest liefern lediglich eine Information darüber, wie schnell im natürlichen Kohlenstoffkreislauf ein CO2-Molekühl durch ein anderes ersetzt wird.)
Marvin Müller 12. Mai 2025 12:27
Ich würde es anders ausdrücken: wie schnell ein CO2-Molekül von der Atmosphäre in den Ozean geht und wie schnell ein CO2-Molekül vom Ozean in die Atmosphäre geht.
Das ist der falsche Ansatz, da ja gleichzeitig mit den menschlichen Emissionen die Natur 20 mal mehr emittiert. Wenn die Natur die Hälfte vom Menschen nicht aufnimmt, dann nimmt sie auch nur die Hälfte der Natur auf. So was wird nicht beobachtet. Muss also falsch sein.
Oder erkennen die Senken woher das CO2 kommt?
Werner Schulz Reply to Marvin Müller 12. Mai 2025 22:50
Nach all den Jahren immer noch das falsche Verständnis … Eigentlich könnten Sie erkennen, dass ich die sogenannte air borne fraction meinte, die wie folgt definiert ist:
Wir emittieren also X und die Konzentration in der Atmosphäre steigt nur um etwa X/2, die natürlichen Senken müssen also etwa X/2 mehr absorbiert haben, als die natürlichen Quellen emittiert haben.
Die Frage haben sie auch schon gefühlte 1000mal gestellt und beantwortet bekommen.
Sie gehen also von vornherein davon aus, das nur das CO2 vom Menschen in der Atmosphaere verbleibt. Etwas anderes sagt ihr Faktor nicht aus. Also vernachlaesigen sie die natuerlichen Emissionen.
Werner Schulz Reply to Marvin Müller 13. Mai 2025 6:38
Meine erste Formulierung mag man ja noch so interpretieren, aber wo steht in der zweiten etwas, das Sie als „nur das CO2 vom Menschen verbleibt in der Atmosphaere“ interpretieren könnten? Da wird ohne irgend eine Attributierung der jährliche CO2-Anstieg referenziert.
Wir fügen CO2 hinzu, das vermischt sich mit dem vorhandenen und unterliegt dann dem ganz normalen Kohlenstoffkreislauf, der etwa ein viertel bis ein Drittel pro Jahr gegen CO2 aus dem Meer oder der Biosphäre „austauscht“.
Das Verhältnis ist 1/20. Genau! In der Luft, an dee „Quelle“ bei den Senken.
Die Wissenschaftler unterscheiden anhand unterschiedlicher C-Isotopenanteile (Scripps-Inst.).
Und diese sind nur unter sehr kritisch zu betrachtenden Annahmen interpretierbar, das gesteht die Isotopengemeinde auch unumwunden ein.
Michael Mechtel 12. Mai 2025 11:34
Der Senkenfluss und die angebliche Zusatzquelle sind nur die Größen des Austauschprozesses zwischen Atmosphäre und Ozean – Sie haben einfach vergessen, das Lösen und Ausgasen zusammen hängen. Im Gleichgewicht müssen beide Größen gleich sein, sonst wäre kein Gleichgewicht.
Rechnen Sie mal ein diffusionsgetriebenes Ausgasen mit.
Im Gleichgewicht passiert gar nichts. oder?
Wo bleibt dann aber die Haelfte vom Mensche gemachtes CO2 das im Verhaletnis 1/20 mit dem natuerlichen Fluessen sequestriert wird???
Wie denn, wenn es alles im Gleichgewicht ist? Oder wie soll es denn funktionieren, wenn der Partialdruck in der Atmosphaere hoeher ist?
Was sie sagen ist nicht logisch!
Das Ausgasen kann ich leider nicht explizit berechnen, weil mir dazu u.a. die Datengrundlage fehlt. Aber klar: ein hoher Senkenfluss und eine hohe Ausgasung bedingen sich gegenseitig.
Jetzt kann man wie meine Kritiker argumentieren: mein tau ist zu niedrig, also mein Senkenfluss zu hoch, und das suggeriert einen zu hohen Quellfluss über den anthropogenen hinaus.
Oder man kann kausal umgekehrt argumentieren: es gibt einen hohen Quellfluss neben dem anthropogenen, deshalb verlangt die Keelingkurve ein niedriges tau, um den Senkenfluss anzupassen.
Wer nun recht hat, lässt sich rein aus dem Formalismus heraus gar nicht entscheiden. Leider!
Michael Mechtel 12. Mai 2025 19:45
Ich glaube C14-Lösung und Gleichgewicht dürften ausreichend sein.
Die Netto-Lösung ist etwa proportional der Druckdifferenz zwischen Atmosphärendruck und Druck 0 im Ozean. Für die Bruttogröße Transport Atmosphäre – Ozean dürfte die Annahme Ozeandruck = 0 reichen.
Herr Mechtel, es gibt keinen natürlichen Quellfluss der unseren Emissionen folgt! Somit verlangt auch die Keelingkurve nicht ein niedriges tau, um den Senkenfluss anzupassen. Das richtige tau ist das womit die Keelingkurve OHNE zusätzlichen Quellfluss am besten reproduziert wird.
Noch eine Ergänzung
@P. Dietze, M. Müller, J. Ebel
Wenn man nur die anthropogene Quelle zulässt und mit sehr niedrigen tau-Werten rechnet, erhält man eine Konzentrationskurve, die flacher als die Keelingkurve verläuft. Nimmt man dagegen sehr hohe tau-Werte, wird die Konzentrationskurve steiler als die Keelingkurve. Dazwischen muss es also ein tau geben, das die Keelingkurve recht gut reproduziert.
Ich habe es mal grafisch Pi mal Daumen ausprobiert und bin bei tau = 61 Jahren gelandet. Das ist tatsächlich nicht weit von Dietzes 55 Jahren entfernt. Es fehlt dann aber noch der Beweis, dass diese Wahl von tau auch wirklich die korrekte ist.
Michael Mechtel 12. Mai 2025 14:09
Aber das Ausgasen haben Sie immer noch vergessen. Im Gleichgewicht werden werden gleiche Mengen ausgegast wie in der Senke verschwinden, durch den anthropogenen Zusatzeintrag ist der Senkeneintrag größer als die Ausgasung. Mit der richtigen Ausgasung braucht man dann nicht mehrere Zeitkonstanten.
Wenn man allerdings Senke und Ausgasung zur Nettosenke zusammenfaßt, dann braucht man mehrere Zeitkonstanten.
Herr Ebel, naürlich müsssen für den anthropogen verursachten Senkenfluss-Anteil Senke und Ausgasung (global Netto) zusammengefasst werden – und man benötigt (da es sich für die heutigen Verhältnisse und auch noch für mehr als hundert Jahre) um ein weitgehend lineares System handelt) nur EINE Zeitkonstante Tau von etwa 55 a, siehe [9].
Natürlich wird dabei angenommen dass die Senkenkapazität im Vergleich zu unserer Emission riesig groß ist und sich über längere Zeit solare und sonstwie bedingte Temperaturschwankungen ausgleichen und sich das Verhalten der Natur global kaum ändert. Prognosen dafür sowie für den Einfluss auf Tau sind ja kaum möglich.
Peter Dietze 13. Mai 2025 7:58
Ihr Tau ist die Zusammenfassung von Senkenfluss und Ausgasung. Wenn man beide getrennt betrachtet ist die Rechnung viel einfacher und gibt nicht Anlaß für Betrachtungen welche Zeitkonstante für den Nettofluß ist richtig.
Michael Mechtel 12. Mai 2025 14:09
„nur die anthropogene Quelle zulässt“
Ich habe noch Daten zu C14 gefunden:
https://essopenarchive.org/doi/full/10.1002/essoar.10506701.1
Halbwertszeit (Tabelle 1): 11;02 Jahre
Herr Ebel, für die getrennte und ziemlich komplizierte Ermittlung von Tau für Absorption und für Ausgasung fehlen schlicht die Daten. Warum denn so umständlich, die Keelingkurve liefert doch ganz einfach die dafür benötigten Nettowerte.
Peter Dietze 16. Mai 2025 19:48
Tut dies eben nicht. Mit einem gleitenden Tau können können Sie beliebige Kurven reprodzieren (von Tau = 10 Jahre bis unendlich). Es kommt darauf an, die Verhältnisse richtig zu beschreiben – allein aus dem menschlichen Eintrag. Wenn der Eintrag 0 ist,verändert sich die Atmosphärenkonzentration nicht – ein gleitendes Tau (Tau = unendlich) ist keine sinnvolle Beschreibung.
Michael Mechtel 12. Mai 2025 14:09
Mal überschläglich:
Die Halbwertszeit des C14-Abfalls ist ca. 10 Jahre, bei linearer Interpolation also alles 20 Jahre.
Die Ausgasung ist also 420 ppm/20 Jahre = 21 ppm/Jahr im Falle des Gleichgewichts wäre auch die Lösung 21 ppm/Jahr. Oder in Gt mit Ihrer Zahl 2245 Gt /20 Jahre = Ausgasung 112 Gt/Jahr steigend auf 168 Gt/Jahr.
Da die Speicherwirkung des Ozeans wirkt, ist bei Druckanstieg der Druck im Ozean geringer. In 60 Jahren ist das CO2 um ca.100 ppmV gestiegen, also ca.1,5 ppm/Jahr. Das Verhältnis ist also ca. 14 Jahre.
– und das stimmt mit den Beobachtungen überein (ca. 13 Jahre):
Herr Mechtel, das ist doch logo: Je schwächer die Senke (also große Halbwertszeit, geringes alpha) desto stärker der ppm-Anstieg und umgekehrt. Was bei Ihnen noch fehlt, ist dass der (anthropogene) Senkenfluss nicht proportional zu ppm sondern zu ppm-280 ist. Wenn die Senke 280 ppm hat und ebenso die Atmosphäre, wird ja der Senkenfluß null, und es bleibt nur der natürliche Kreisfluss (Ozean-Aufnahme i.w. in kalten Polarregionen und Ausgasung in den Tropen sowie bei der Biomasse wachsen und verrotten. Ein Beweis dass Tau korrekt ist, liegt doch dann vor wenn ohne Zusatzquellen die Keeling-Kurve reproduziert wird.
Michael Mechtel 12. Mai 2025 14:09
„Noch eine Ergänzung“
Die Ausgasung spielt eine große Rolle – und die Hängt vom Druck im Wasser ab. In der nachfolgenden Tabelle habe ich einfach den früheren Atmosphärendruck genommen, besser wäre sicherlich wäre zur richtigen Druckbestimmung die Integration der Flüsse erforderlich – aberschon die einfache Rechnung zeigt eine relative Konstanz der Verzögerungszeit (siehe Diagramm)-
https://www.statista.com/statistics/276629/global-co2-emissions/
Gt/Jahr ppmV https://data.giss.nasa.gov/modelforce/ghgases/Fig1A.ext.txt
https://www.statista.com/statistics/1091926/atmospheric-concentration-of-co2-historic/
1ppm = 7,824 Gt
Lösung Ein Aus Verzögerung (Jahre)
22,04 Jahre
1940 4,86 0,62116564 0,21052421 1940 311,3 14,1243194 13,9137952
1941 4,97 0,63522495 0,21528916 1941 311 14,1107078 13,8954186
1942 4,96 0,63394683 0,21485599 1942 310,7 14,0970962 13,8822402
1943 5,04 0,64417178 0,21832141 1943 310,5 14,0880218 13,8697004
1944 5,12 0,65439673 0,22178683 1944 310,2 14,0744102 13,8526233
1945 4,26 0,54447853 0,18453357 1945 310,3 14,0789474 13,8944138
1946 4,65 0,59432515 0,20142749 1946 310,3 14,0789474 13,8775199
1947 5,15 0,65823108 0,22308636 1947 310,4 14,0834846 13,8603982
1948 5,15 0,65823108 0,22308636 1948 310,5 14,0880218 13,8649354
1949 5,18 0,66206544 0,22438589 1949 310,9 14,1061706 13,8817847
1950 5,93 0,75792434 0,25687419 1950 311,3 14,1243194 13,8674452
1951 6,38 0,81543967 0,27636718 1951 311,8 14,1470054 13,8706383
1952 6,47 0,82694274 0,28026577 1952 312,2 14,1651543 13,8848885
1953 6,65 0,84994888 0,28806297 1953 312,6 14,1833031 13,8952401
1954 6,79 0,86784254 0,29412745 1954 313,2 14,2105263 13,9163989
1955 7,44 0,95092025 0,32228398 1955 313,7 14,2332123 13,9109284
1956 7,93 1,01354806 0,34350967 1956 314,3 14,2604356 13,9169259
1957 8,19 1,04677914 0,35477229 1957 314,8 14,2831216 13,9283493
1958 8,42 1,07617587 0,36473537 1958 315,34 14,3076225 13,9428871
1959 8,85 1,13113497 0,38336199 1959 316,18 14,345735 13,962373
1960 9,39 1,20015337 0,40675357 1960 317,07 14,3861162 13,9793626
1961 9,41 1,20270961 0,40761993 1961 317,73 14,4160617 14,0084418
1962 9,75 1,24616564 0,42234796 1962 318,43 14,4478221 14,0254742
1963 10,27 1,31262781 0,44487318 1963 319,08 14,477314 14,0324408
1964 10,82 1,38292434 0,46869794 1964 319,65 14,503176 14,0344781
1965 11,31 1,44555215 0,48992363 1965 320,23 14,5294918 14,0395682
1966 11,86 1,51584867 0,51374839 1966 321,59 14,5911978 14,0774494 21,670
1967 12,24 1,56441718 0,53020913 1967 322,31 14,6238657 14,0936566 18,310
1968 12,9 1,64877301 0,55879884 1968 323,04 14,6569873 14,0981885 19,560
1969 13,76 1,75869121 0,59605209 1969 324,23 14,71098 14,1149279 19,483
1970 14,9 1,90439673 0,64543432 1970 325,54 14,7704174 14,1249831 19,029
1971 15,5 1,98108384 0,67142496 1971 326,42 14,8103448 14,1389199 20,644
1972 16,22 2,07310838 0,70261373 1972 327,45 14,857078 14,1544643 20,411
1973 17,08 2,18302658 0,73986699 1973 329,43 14,9469147 14,2070477 19,872
1974 17,01 2,17407975 0,73683475 1974 330,21 14,9823049 14,2454702 18,450
1975 17,05 2,17919223 0,73856746 1975 331,36 15,0344828 14,2959153 17,522
1976 17,99 2,29933538 0,77928613 1976 331,92 15,0598911 14,280605 19,889
1977 18,49 2,36324131 0,800945 1977 333,73 15,1420145 14,3410695 18,878
1978 19,06 2,43609407 0,82563611 1978 335,42 15,2186933 14,3930572 17,232
1979 19,6 2,50511247 0,84902769 1979 337,1 15,2949183 14,4458906 17,939
1980 19,48 2,48977505 0,84382956 1980 338,99 15,3806715 14,5368419 14,119
1981 19,02 2,4309816 0,8239034 1981 340,36 15,4428312 14,6189278 14,849
1982 18,87 2,41180982 0,81740574 1982 341,57 15,4977314 14,6803257 13,432
1983 18,99 2,42714724 0,82260387 1983 342,53 15,5412886 14,7186847 13,130
1984 19,64 2,51022495 0,8507604 1984 344,24 15,6188748 14,7681144 14,961
1985 20,31 2,5958589 0,87978329 1985 345,72 15,6860254 14,8062421 14,897
1986 20,61 2,63420245 0,89277861 1986 347,15 15,7509074 14,8581288 13,012
1987 21,25 2,71600204 0,92050196 1987 348,93 15,8316697 14,9111677 14,602
1988 22,08 2,82208589 0,95645568 1988 351,47 15,9469147 14,990459 13,156
1989 22,38 2,86042945 0,96945101 1989 353,15 16,0231397 15,0536887 13,756
1990 22,52 2,87832311 0,97551549 1990 354,29 16,0748639 15,0993484 13,480
1991 22,97 2,93583845 0,99500847 1991 355,68 16,137931 15,1429226 13,012
1992 22,31 2,85148262 0,96641876 1992 356,42 16,1715064 15,2050876 14,823
1993 22,52 2,87832311 0,97551549 1993 357,13 16,2037205 15,228205 14,125
1994 22,74 2,90644172 0,98504539 1994 358,61 16,2708711 15,2858258 15,881
1995 23,27 2,974182 1,00800379 1995 360,67 16,3643376 15,3563338 15,716
1996 23,99 3,06620654 1,03919257 1996 362,58 16,4509982 15,4118056 15,501
1997 24,12 3,08282209 1,04482387 1997 363,48 16,491833 15,4470092 15,076
1998 24,02 3,0700409 1,0404921 1998 366,27 16,6184211 15,577929 14,472
1999 24,56 3,1390593 1,06388368 1999 368,38 16,7141561 15,6502724 14,468
2000 25,2 3,2208589 1,09160703 2000 369,64 16,7713249 15,6797178 15,906
2001 25,39 3,24514315 1,0998374 2001 371,15 16,8398367 15,7399993 15,832
2002 25,95 3,31671779 1,12409534 2002 373,15 16,9305808 15,8064854 15,688
2003 27,31 3,49054192 1,18300746 2003 375,64 17,0435572 15,8605497 15,251
2004 28,25 3,61068507 1,22372614 2004 377,44 17,1252269 15,9015007 16,606
2005 29,21 3,73338446 1,26531117 2005 379,46 17,2168784 15,9515672 16,061
2006 30,18 3,85736196 1,30732937 2006 381,59 17,3135209 16,0061915 17,778
2007 31,06 3,9698364 1,34544898 2007 383,37 17,3942831 16,0488341 17,497
2008 31,58 4,03629857 1,36797421 2008 385,46 17,4891107 16,1211365 17,734
2009 31,02 3,96472393 1,34371627 2009 386,95 17,5567151 16,2129988 15,138
2010 32,81 4,19350716 1,42125503 2010 389,21 17,6592559 16,2380009 16,510
2011 33,91 4,3341002 1,46890454 2011 391,85 &nbs
Zur ppm-Graphik: beachte den Anstieg der Konzentration vor 1900 ohne nennenswerten Anstieg der Emission. Wie das?
Tabelle: denke, ich kann sie interpretieren. Aber woher kommen die Werte für Ein, Aus und Verzögerung?
Michael Mechtel 16. Mai 2025 18:18
Die Werte sind die gemessenen ppm-Werte, die Addition der Emissionen und der Zeitabstand zwischen gleichen Drücken.
Herr Ebel, nochmal zu Ihrer Tabelle, die ich auf meiner Rechengrundlage (bis auf unwesentliche Abweichungen) reproduzieren kann. Im Gegensatz zu meiner Tabelle 1 enthält sie auch den Senkenfluss brutto und netto. Dadurch sieht man sehr schön, was ich leider übersehen hatte: dass der natürliche Netto-Senkenfluss (‚Lösung‘) immer kleiner ist als der anthropogene Quellfluss. Das lässt eigentlich nur den Schluss zu, dass der Anstieg der atmosphärischen Konzentration tatsächlich auf den letzteren zurückzuführen ist.
Der Witz dabei ist, dass dieser Befund wie auch die Entwicklung der Konzentration praktisch unabhängig von tau ist! Die Bruttoflüsse hängen zwar von tau ab (bis auf den anthropogenen), aber auf die Differenz, also den natürlichen Nettofluss hat das keinen Einfluss. Die ganze Diskussion über tau kann man sich im Grunde sparen, und ebenso muss man keine Vorgabe zu einem natürlichen Gleichgewicht machen.
Jetzt muss man die Argumente von Herrn Roth nochmal in neuem Licht betrachten. Ärgerlich!
Sorry, Herr Schwerdt, aber die Steigungszunahme der Keelingkurve aus der quadratischen Funktionsgleichung beträgt 2 A, also 0,20046 Gt / a². Dividiert durch 8, um die Gt auf ppm umzurechnen: 0,0250, wobei die Einheit ppm / a² lautet. Anthropogen wird keineswegs mehr emittiert, als Keeling misst.
Sie sollten genau sein. Zum Beispiel ist der Anstieg der Temperatur von 15 auf 16 Grad C fuer einen Koerper nur mit der Zunahme von 0.35% des Energiegehaltes, bei gleicher Stoffzusammensetzung verbunden.
Kleine Zahlen die angeblich grosse Wirkung haben sollen!
Ich muss widersprechen: in meiner Abb. 2 wie auch in meinen Gleichungen tauchen die richtigen Einheiten auf. Im Gegensatz beispielsweise zu Ihrer obigen Gleichung „vppm(t) = …“:
Die Vorfaktoren können keine unbenannten Zahlen sein. Würden Sie hier konsequent arbeiten, würden Sie erkennen, dass Ihre Aussage zu Abb. 2 falsch ist.
Bin mir jetzt nicht sicher, ob ich eine Aussage von Ihnen missverstanden hatte. Aber mit dem Satz
tragen Sie Eulen nach Athen, denn genau das ergibt sich aus meinem Artikel.
Ja, das mit den Eulen nach Athen haben Sie richtig interpretiert. Und warum fragen Sie nach U, V, W? Haben Sie meinen Text nicht gelesen? Steht doch alles drin.
Sehr geehrte Teilnehmer an der Diskussion, ich habe mir, soweit es ging die vielen Beiträge zum Thema angeschaut.
Vielleicht habe ich ein falsches Verständnis von der Situation, in der wir uns politisch befinden. Es geht um die CO2 Zunahme seit etwa 1850. Auf dieses Thema muss unsere Diskussion reagieren. All die politischen Maßnahmen, die unsere Freiheit einschränken könnten und all die finanzielle Belastungen beruhen auf der behaupteten CO2 Zunahme durch uns Menschen. Diesen Behauptungen müssen wir greifbare und verständliche Argumente und Zahlen entgegenstellen.
Da sind Diskussionen über Stephan Bolzmann und andere Größen eher hinderlich. Wir müssen aufzeigen, was sich in den letzten 175 Jahren bezüglich CO2 Anstieg tatsächlich abgespielt hat.
Das „Parabelmodell“ hat den Schönheitsfehler, dass es keinen Wendepunkt erlaubt. Dieser läßt sich aber mit einiger Sicherheit im Jahre 2016 identifizieren (https://www.mdpi.com/2073-4433/15/7/743, Absatz „Identifying the Inflection point of the CO2 concentration). Der Einwand, dieser würde 2023-2024 wieder in Frage gestellt, wird durch das Sichtbarwerden der Temperaturabhängigkeit beantwortet: https://www.preprints.org/manuscript/202504.2305/v1
Für eine Parabel haben Sie recht. Das Modell kann und soll aber nur den ausgewerteten Zeitraum abdecken, und da trifft es sehr gut die Wirklichkeit.
Was die anthropogenen Emissionen angeht, so flacht sich deren Anstieg neuerdings eher ab. Gleichzeitig hat sich die Steigung der Keelingkurve seit 2018 weiter erhöht. Allein das spricht doch sehr dafür, dass neben der anthropogenen eine weitere starke CO2-Quelle existieren muss.
Vielleicht machen Sie sich einfach mal die Mühe, sich mit den Naturgesetzen, also der Physik zu beschäftigen, statt mit zeitlich limitierten Kurvenanpassungen zu spekulieren. Meine 3 Publikationen könnten ein Anfang dazu sein.
Es ist schon seltsam: zieht man hier Folgerungen aus physikalischen Grundprinzipien, wird einem vorgeworfen, man soll sich doch gefälligst an empirischen Daten orientieren. Geht man von empirischen Daten aus, wird verlangt, man solle sich doch gefälligst mit den Naturgesetzen beschäftigen.
Ich habe hier bewusst die Beziehung zwischen zwei empirischen Datensätzen analysiert, und das ist eine der möglichen Vorgehensweisen, die Bestandteil der physikalischen Methodik ist.
Herr Dr. Dengler, in Ihrem Preprint „Are the Natural Carbon Sinks Failing?“ geht es um den Rückgang der CO2 -Aufnahme 2023/24 – offenbar durch eine Erwärmung – wodurch (wenn ich Ihre Fig.9 richtig interpretiere) die natürliche Senkenrate von etwa 5%/a (tau=20 a) des anthropogenen Inventars der Atmosphäre auf etwa 1,7%/a (tau=58,8 a) reduziert wird.
Auch Herr Mechtel bevorzugt tau=20 a, kann damit aber den ppm-Anstieg (basiert auf den geglätteten Werten der letzten 60 Jahre) bei der hohen Senkenrate nur durch die Annahme einer fiktiven zusätzlichen Quelle (!) reproduzieren, welche z.B. für 2015 das 4,3-fache (!) unserer globalen Emission liefert.
Meine hier gezeigte Excel-Grafik sowie die verlinkte Doku zum C-Modell weisen jedoch nach dass mit tau=55 a der reale ppm-Anstieg von 1840 bis heute OHNE ZUSATZQUELLE reproduziert werden kann. Haben Sie eine plausible Erklärung für die Widersprüche?
Es kommen immer wieder Fragen zu dem in meinen beiden letzten Publikationen eingeführten erweiterten Senkenmodell. Grundsätzlich werde ich keine Fragen mehr per Mail beantworten, und mich hier auf einige grundsätzliche Aussagen beschränken:
Gestern habe ich die Idee gehabt, ChatGtp zwei Fragen zu stellen:
Hallo Mensch, ich bin ein KI-Chatbot, Modell GPT-4.1 nano.
Wieviele Tonnen CO2-Ausstoß bewirken einen Anstieg der CO2-Konzentration um 1 ppm?
Hallo! Gerne helfe ich dir weiter. Laut den verfügbaren Daten bewirkt eine Zunahme der CO2-Konzentration um 1 ppm in der Atmosphäre etwa 2,12 Gigatonnen (Gt) CO2. Das entspricht 2.120 Millionen Tonnen CO2.
Wenn du also wissen möchtest, wie viel CO2-Ausstoß notwendig ist, um die Konzentration um 1 ppm zu erhöhen, kannst du mit diesem Wert rechnen. Ich hoffe, das hilft dir weiter!
Wenn du noch mehr Fragen hast, stehe ich dir gern zur Verfügung.
Wieviel Tonnen CO2 Emissionen wurden von den Menschen zwischen 1850 und 2025 in die Atmosphäre ausgestoßen?
Hallo! Gerne gebe ich dir eine Einschätzung dazu. Zwischen 1850 und 2025 haben die menschlichen Aktivitäten, vor allem die Verbrennung fossiler Brennstoffe wie Kohle, Öl und Gas, sowie die Landnutzung, insgesamt schätzungsweise etwa 2.600 bis 3.000 Gigatonnen (Gt) CO2 in die Atmosphäre ausgestoßen. Das entspricht ungefähr 2,6 bis 3 Billionen Tonnen CO2.
Diese Emissionen haben maßgeblich zum Anstieg der CO2-Konzentration in der Atmosphäre beigetragen und sind ein wichtiger Faktor für den Klimawandel.
Wenn du noch genauere Zahlen oder weitere Informationen möchtest, helfe ich dir gern weiter!
In einem weiteren Schritt habe ich eine Division durchgeführt: 2600 Gt : 2,12 Gt = 1.226 ppm
Meiner Meinung nach sagt uns die Zahl 1.226 ppm wie hoch eigentlich die CO2 Konzentration sein müsste. Wir habe bekanntlich jetzt etwa 420 ppm. Da muss die Wissenschaft erklären, wo der Rest geblieben ist.
Ich gehe davon aus, dass der bisherige Ansatz der Wissenschaft der ist, dass das CO2 sich in der Atmosphäre kumuliert, d.h. mit der Zeit ständig steigt.
Eigentlich müsse man noch die üblichen 280 ppm hinzuaddieren, die angeblich zu Beginn der Industriellen Revolution in der Atmosphäre vorhanden sein sollen. Ich halte mich lieber an konkrete Messergebnisse eines Nikola de Saussure aus Genf, der in den 1820 Jahren Werte um 420 bzw. 430 ppm gemessen hatte.
Ich kann mir vorstellen, dass dieser vereinfachte Ansatz für eine lebhafte Diskussion sorgen wird.
Ist das der gleiche de Saussure dessen Experiment den von Ebel so häufig lückenhaft zitierten Fourier zu seinem Nicht-Zirkulationsmodell inspiriert hat?
Marcus Portius 10. Mai 2025 0:37
„dessen Experiment …“
Lokal gibt es immer Orte, wo man hohe CO2-Wertemessen kann, insofern ist das kein Hinweis, sondern ein Wissensproblem.
Wo wären dann die 280 ppmV geblieben, die der Mensch in die Atmosphäre geblasen hat?
Und warum erschlug der Teufel die Großmutter, EBEL?
Meinen Sie mit „lokal“ ein verqualmtes LOKAL? Das wäre dann ggf. so ein Ort, „wo man hohe CO2-Werten messen kann“. Immer nur Ausflüchte mit blumigen Formulierungen ……
Sie wissen ja nicht einmal welches Experiment ich meine, Sie projizieren Ebel.
Sind es nicht 1.226 ppm so wie Herr Bocek es vorgerechnet hat?
Haben Laien anderes Wissen als sie?
Werner Schulz Reply to Jochen Ebel 10. Mai 2025 22:38
Nein.
In diesem Falle war es wohl eher fehlendes Wissen und daher unkritische Übernahme der Antwort von ChatGPT, die falsch war.
Und wie ist die korregierte richtige Zahl?Ah, weiter unten schon gefunden.
Es sind also 334 und nicht 280 ppm Equivalent?
Sehr geehrte Herren,
haben Sie vielen Dank für Ihre Reaktion auf meinen Beitrag.
Es freut mich natürlich, dass überhaupt jemand auf einen Beitrag eines Laien antwortet. Andererseits hätte ich mir eine heftigere Reaktion erwartet. In dem Sinne, dass Sie mir vorwerfen bzw. vorhalten würden, dass mein Ansatz unsinnig wäre, die von mir gewählten Zahlen einer KI nicht glaubwürdig wären, frei erfunden bzw. dass ich keine Ahnung hätte.
Ich glaube, die von mir aufgeführten Zahlen fordern uns heraus, an die Wurzeln der Problematik zu gehen.
Das von mir mittels einer Division von zwei Werten, die eine KI geliefert hat, erreichte Ergebnis zeigt, dass eine große Diskrepanz zwischen den offiziellen Werten besteht und dem Ergebnis von 1226 ppm besteht.
Diese Antwort geht an alle, die bis jetzt Samstag 13.50 reagiert haben.
Das passiert jedem der nicht dem Dogma folgt, also dem was in den IPCC Berichten zu finden, was die „Klimawissenschaft“ als Konsens bezeichnet an dem nicht gerüttelt werden kann.
Es gab in den letzten Jahren mehrere verschiedene Ansätze (hier nach „Beck“ suchen), nichts davon wurde von „der Wissenschaft“ zu Diskussion gestellt oder hat Eingang in die Modelle gefunden.
Weiterhin kann man den verfügbaren Daten nicht trauen, die Manipulation findet nicht nur hinsichtlich von Temperaturen statt. MMn ist die ganze Diskussion über CO2 nicht zielführend solange der Effekt selber nicht getestet wurde; das ganze beruht ausschließlich auf Modellen die einer kritischen Betrachtung nicht standhalten.
Sie erwähnen oben Stefan-Boltzmann. Es wird angenommen die Erde sei ein schwarzer Körper. Da dies nicht der Realität entspricht ist der Glashauseffekt schon durchgefallen bevor man überhaupt anfangen kann etwas zu berechnen von dem man glaubt es findet in der Realität genau so statt. Alles weitere ist dann nur noch ein Zirkelschluss.
Sehr geehrter Herr Portius, haben Sie vielen Dank, dass Sie mit mir so gnädig umgehen.
Wenn sich jemand als Laie wie Sie und ich mit der Geschichte auseinandersetzen (Saussure) ist die Wahrscheinlichkeit höher zu verstehen warum die ganze Diskussion über CO2 verschwendete Zeit ist.
Ich meinte einen anderen Saussure, den der Fourier zu seinen Überlegungen gebracht hat. Fourier hat anhand dessen Experiment im Grunde genommen das erste Atmosphärenmodell beschrieben. Ab Seite 17. Im Prinzip kann man sagen: Alles nur heiße Luft. CO2 ist Pflanzendünger, das wars, Ende der Geschichte. 😉
Hier die ganze Geschichte dazu, sozusagen ein doppelwandiges Treibhaus. 😀
Zitiert von Möller zur Geschichte der Theorie der Strahlung:
„Im Zusammenhang mit der Strahlungsbilanz am Erdboden müssen wir einen Begriff erwähnen, der heute allgemein bekannt ist: die Glashauswirkung der Lufthülle. Man versteht darunter die Tatsache, daß die Sonnenstrahlung relativ ungeschwächt die Erdatmosphäre durchdringen kann (wolkenloser Himmel vorausgesetzt), aber effektiv nur wenig Wärmestrahlung den Boden verläßt, weil die Gegenstrahlung mit bis zu 800/o der Emission des Bodens entgegengerichtet ist. Das hat zur Folge, daß die Temperatur am Boden viel höher bleibt, als sie ohne Vorhandensein einer Atmosphäre sein würde. Der Unterschied beträgt ungefähr 30 °. Das Gleiche ist in einem Glashaus der Fall, wo das Glas eben- falls die Eigenschaft hat, alle kurzwellige Strahlung von außen hereinzulassen, aber die langwellige Strahlung nicht entweichen läßt sondern abschirmt. Glas ist für langwellige Strahlung oberhalb etwa 3 μm undurchlässig. Der Begriff der Glashauswirkung ist im Zusammenhang mit den Arbeiten von ARRHENIUS (11) über die Wirkung des Kohlendioxyds auf die Strahlung bekannt geworden und von ihm auch in diesem Sinne benutzt worden. Er verweist gelegentlich auf TYNDALL (110), POUILLET (81) und FOURIER (44), ohne genauere Zitate zu geben. Tyndall war zweifellos nicht der erste, der von der Glashauswirkung sprach. Pouillet verweist auf Fourier. Beide gebrauchen im Zusammenhang mit ihren Studien über die Temperatur der Erde oftmals den Begriff einer „enveloppe“, die die Sonnenstrahlung durchläßt, aber ihrerseits Strahlung aussendet. Damit ist der Vorgang in der Atmosphäre gemeint und richtig erfaßt, aber weder das Wort Atmosphäre noch Glashaus fällt. Fourier verweist jedoch 1821 auf einen Versuch des berühmten Alpenforschers und Besteigers des Mont Blanc, de SAUSSURE (93), der ihm im Zusammenhang mit der Erklärung der Temperaturen wichtig erscheint. De Saussure stellte zwei Gläser (verres, ich vermute Wassergläser ohne Stiel) umgekehrt übereinander und maß bei Sonnenbeleuchtung die Temperaturen im innersten Glas. Diese stieg bis 110 ° (R) = 131 °C, im Zwischenraum war die Steigerung geringer. Ich glaube, hier ist die „Glashauswirkung“ zum ersten Male praktisch vorgeführt worden, nicht nur genannt oder berechnet.“
Ist schon irgendwie witzig. Man vergleicht einen Planeten ohne Atmosphäre bei dem man die Bodentemperatur „ermittelt“ mit einem Planeten auf dem man eine Lufttemperatur messen kann.
Welche Überraschung, die Luft hat eine Temperatur!
Yep, und die IR Strahlung wandert dann durch das Glashaus, man hat Wärme eingeschlossen.
Man sollte bedenken dass Fourier zu seiner Zeit glaubte dass es neben der Luft auch Wärmepartikel gibt, das Caloricum, etwas materielles. Und das sind heute die Photonen. Fourier glaubte diese Partikel eingeschlossen (keine Konvektion) zu haben.
Das kann man im Modell machen, hat Fourier auch gemacht. Einfach mal den Artikel von 1824 lesen, es ist bemerkenswert.
Unsere Klimastrologen denken dass ihr Modell (Glashaus reflektiert IR) der Realität entspricht. Für diese Leute ist Luft in größten Teilen nicht vorhanden, da nicht IR-aktiv. Man argumentiert quasi in einem Vakuum mit den CO2 Molekülen als kleine Reflektoren welche dann im Modell die Schichten darstellen zwischen denen „Energie strahlend konvektiert“.
Marcus Portius 15. Mai 2025 19:36
Man vergleicht die Oberflächentemperatur eines Planeten ohne Atmosphäre mit Oberflächentemperatur eines Planeten mit treibhausgashaltiger Atmosphäre. Die Lufttemperatur in Oberflächennähe hat nur einen geringen Unterschied zur Oberflächentemperatur.
„Das hat zur Folge, daß die Temperatur am Boden viel höher bleibt, als sie ohne Vorhandensein einer Atmosphäre sein würde.“
Wie Sie sehen können geht es im Zitat um die Temperatur der Luft in Bodennähe, die „surface air temperature“ SAT.
Und wieder erzählt Ebel eine Lügengeschichte, und das obwohl Ihm demonstriert wurde dass Luft- und Bodentemperatur nicht annähernd identisch sind.
Ist schon erbärmlich wie Sie hier versuchen die Leute hinters Licht zu führen. Oder Sie kapieren es einfach nicht, was man bei Ihnen wohl in Betracht ziehen muss.
Was schreibt das IPCC als Definition:
Global mean surface air temperature, p. 2231 (GSAT) Global
average of near-surface air temperatures over land, oceans and
sea ice. Changes in GSAT are often used as a measure of global
temperature change in climate models. See also Global mean surface temperature (GMST).
Global mean surface temperature, p. 2231 (GMST) Estimated
global average of near-surface air temperatures over land and sea
ice, and sea surface temperature (SST) over ice-free ocean regions, with changes normally expressed as departures from a value over a specified reference period. See also Global mean surface air temperature (GSAT).
Das IPCC selber bestätigt dass die Oberflächentemperatur an Land nicht gemessen wird. Was schon echt ein Witz ist da dieser Wert die Grundlage des Effekts ist, die Oberfläche ist die primäre IR-Quelle.
Man nimmt einfach an Luft und Boden seien im Equilibrium, was natürlich nicht der Fall ist, außer man nutzt das flache Erde Modell.
Noch einer Ebel:
Lesen Sie sich mal Fourier genau durch: Es gibt die unterschiedlich warmen Luftschichten, unten wärmer, nach oben kälter – und das ganze OHNE KONVEKTION. Somit zeigt sich mal wieder dass Sie kompletten Unfug erzählen. Sie machen hier einen auf Pipi Langstrumpf und wollen den Leuten einen vom Pferd erzählen.
Das kommt davon wenn man sich immer nur das herauspickt was einem in den Kram passt, zeugt aber davon wie sie hier argumentieren, mit Halbwahrheiten (welche bekanntlich auch Lügen sind).
Marcus Portius 16. Mai 2025 16:55
Noch besser können Sie gar nicht demonstrieren, kein Wissen zu haben.
Fourier schreibt:
Sie haben also kein Wissen von Fourier, Schwarzschild usw. – geben aber groß an.
Schön zu sehen wie Sie sich Ihr eigenes Grab schaufeln indem Sie unvollkommen zitieren:
Die Temperaturen der Erde und der planetarischen Räume Fourier 1824
„Die Thermometer, die in den Intervallen platziert wurden, erwarben viel niedrigere Wärmegrade, die vom Boden des Gefäßes bis zum oberen Intervall abnahmen.“
„(1), dass die erworbene Wärme konzentriert ist, weil sie nicht sofort durch die Erneuerung der Luft abgeführt wird;“
„Wenn alle Luftschichten, aus denen sich die Atmosphäre zusammensetzt, ihre Dichte mit ihrer Transparenz behalten und nur ihre Beweglichkeit verlieren würden, würde die dadurch fest gewordene Luftmasse, wenn sie der Sonneneinstrahlung ausgesetzt wird, einen Effekt der eben beschriebenen Art erzeugen.“
„Die Wärme, die im Zustand des Lichts die feste Erde erreicht, würde plötzlich und fast vollständig ihre Fähigkeit verlieren, die durchsichtigen Feststoffe zu durchdringen, und sich in den unteren Schichten der Atmosphäre ansammeln, die dann heiß werden würden. Gleichzeitig würde man ab der Fläche vom Boden einen Rückgang des Grads von erworbener Wärme beobachten.“
Kein Konvektion aber dennoch ein Temperturgradient. Exakt das Gegenteil von dem was Sie hier so an Falschbehauptungen verbreiten. Fake News Ebel.
Das beste ist aber wie Sie zusammenhangslos zitieren, also mal den Rest zu Ihrem Ausschnitt:
„Wenn alle Luftschichten, aus denen sich die Atmosphäre zusammensetzt, ihre Dichte mit ihrer Transparenz behalten und nur ihre Beweglichkeit verlieren würden, würde die dadurch fest gewordene Luftmasse, wenn sie der Sonneneinstrahlung ausgesetzt wird, einen Effekt der eben beschriebenen Art erzeugen.“
„Die Wärme, die im Zustand des Lichts die feste Erde erreicht, würde plötzlich und fast vollständig ihre Fähigkeit verlieren, die durchsichtigen Feststoffe zu durchdringen, und sich in den unteren Schichten der Atmosphäre ansammeln, die dann heiß werden würden. Gleichzeitig würde man ab der Fläche vom Boden einen Rückgang des Grads von erworbener Wärme beobachten. Die Beweglichkeit der Luft, die sich schnell in alle Richtungen bewegt und bei Erwärmung aufsteigt, und die Einstrahlung dunkler Wärme in die Luft verringern die Intensität der Effekte, die unter einer transparenten und festen Atmosphäre stattfinden würden, aber verhindern diese Effekte nicht vollständig. Die Abnahme der Wärme in den hohen Regionen der Luft geschieht kontinuierlich; somit wird die Temperatur durch die Zwischenschaltung der Atmosphäre erhöht, weil die Wärme im Lichtzustand weniger Hindernisse findet, um die Luft zu durchdringen, als nach der Umwandlung in dunkle Wärme.“
Sehen Sie das Wort „Wenn“? Und das Wort „würde“, oder „fest“? Was Foruier hier beschrieben hat ist ein statisches Modell. Nochmal für Sie: Keine Konvektion aber ein Temperaturgradient.
Fourier glaubte, weil das damals Stand der Technik war, dass Wärme etwas materielles ist, etwas dass man einschließen kann. Nur war er sich bewusst dass es sich um ein Modell handelt – bei Ihnen ist es genau anders herum. Sie denken Ihr Modell beschreibt die Realität, auf Planet Ebel.
Marcus Portius 16. Mai 2025 20:00
Sie haben die Zusammenhänge immer noch nicht verstanden: Ohne Konvektion wäre der Temperaturgradient viel größer. In der Stratosphäre haben wir auch einen Temperaturgradienten – aber keine Konvektion, weil der Temperaturgradient zu klein ist, um Konvektion zu erzeugen (Schwarzschild-Kriterium).
Ohne Konvektion wäre der Temperaturgradient deutlich größer – und größer als in der Stratosphäre wäre er, weil wegen der wachsenden Luftdichte auch die Dichte der Treibhausgasmoleküle zunimmt. Ohne Konvektion gäbe es kein Tropopause.
„Die Lufttemperatur in Oberflächennähe hat nur einen geringen Unterschied zur Oberflächentemperatur.“ Bei der Tagerde mag das vielleicht stimmen, unter Einstrahlung solarer Energie. Da ist die Konduktion viel zu träge um die Energie schnell abzuleiten. In der Nacht jedoch wirkt sich die langsame Rückkehr der Energie/wärme in Richtung Oberfläche und anschließender Konvektion sowie die Strahlungsableitung einerseits stabilisierend sowohl auf die Oberflächentemperatur wie auch die darüber liegenden Luftpakete aus und vermindert die rasche Ankühlung.
Am besten erkennt man das in Wüstengebieten, auf sandigen Böden wirkt am Tage einerseits die höhere Albedo sandiger Böden wie auch die lockere Struktur des Sandes einer tiefergehenden und damit Thermisch stabilisierend wirkenden Bodenschicht entgegen, weshalb nach Sonnenuntergang eine sehr schnelle Auskühlung der bodennahen Luftschichten durch Strahlung sowie Konvektion nebst merklicher advektiver Luftströmungen erfolgt. Tags wird durch Druckunterschiede durch aufsteigende „heise“ Luftpakete(thermische Hebung) beständig kühlere Luft aus den umliegenden Gebieten angesogen, während Nachts aufgrund der raschen und heftigen Abkühlung Fallwinde bzw. katabatische Winde entstehen welche dann als kalte und dichte Luftmassen/Winde in die umgebenden Gebiete strömt.
Leider leiden die spezifischen Wüstenklimata unter regelmäßiger Abstinenz der Modellfanatiker, wohlwissend das darin Aspekte erkennbar werden welche dem typischen Dogma entgegenläuft. ALs ich einige Zeit dort aktiv war, aus anderen Gründen und Klima nur ein Teilaspekt einer länger zurückliegenden Ausbildung anzusehen war, fiel mir diese Dynamik ganz besonders nachdrücklich auf insbesondere auch deshalb weil einige Städte die Angewohnheit hatten/haben ihren, zumeist biologischen, Müll irgendwo in der nahen Wüste abzuwerfen und des Nachts die anrüchige „Last“ dieser Hinterlassenschaften mit den Winden häufig einen lauschigen Trunk im Freien verwehrten. 😀
Moritz Steinmetz 16. Mai 2025 20:38
Zu den Temperaturänderungen: https://www.tagesschau.de/wetter/wetterthema/2025-01-31-luft-bodentemperatur-102.html
Da steht zwar das Wort „stark“, aber stark ist ein relativer Begriff. Er liegt bei 1 bis 2 K. Dazu kommt ein geringer Einfluß auf die Tagesmitteltemperatur, da sich Tag- und Nachtabweichung weitgehend kompensieren.
Ich habe schon Diagramme gesehen, wo die Temperaturänderungen im Laufe des Tages zu sehen sind, habe aber die Diagramme jetzt nicht gefunden.
Haben Sie zufällig einen Link zur Hand?
Interessant wie ein Experte selber nicht versteht warum das Glashaus/greenhouse eine Falschbezeichnung ist, eben weil ein echtes Treibhaus warme Luft einschließt. Ähnlich die Leute die den Effekt mit einer Bettdecke vergleichen, als ob die Decke durch Strahlung warm hält.
Und das sind die Leute die sich für unfehlbar („Ich habe das durchgerechnet“) halten und diejenigen die über die Luft reden als Leugner und Idioten darstellen.
https://www.dwd.de/DE/leistungen/pbfb_verlag_promet/archiv/archiv_promet.html
Geschichte der meteorologischen Strahlungsforschung, 1973, S. 18
Das Zitat ist also 52 Jahre alt.
Die Grundlage des Zitates und auch der märchenhaften Erzählung darüber ist noch weit älter „also 52Jahre alt“ und trotzdem wird diese noch heute allenthalben und auch von Ihnen selbst für Bares genommen. Also was wollen Sie uns jetzt erklären mit Ihrem unqualifizierten Einwurf?
Oder wieder nur Schwurbel von feinsten, man kanns ja mal versuchen vielleicht merkts ja keiner?
Herr Steinmetz,
Das wird wohl etwas heißen, zumal die Quelle ein Bildungsmedium für Meteorologen ist.
Ich warf den link ein. Was ist daran unqualifiziert?
Woher haben Sie denn Ihren Text, wußten Sie überhaupt, dass dieses Prometheft die Primärquelle ist?
Schwurbel herrscht offenbar in Ihrem Kopf. Bilden Sie sich. Es gibt neben den für den Experten „einfach“ gehaltenen Prometheften ja genug Fachliteratur, die Sie offenbar nicht wahrnehmen (um eine mögliche Erklärung für Ihre hier exponierte Naivität zu nennen).
Haben Sie einen Link für das Zitat? Weil Heinemann’s Link – und das ist nicht seine Schuld – zu einer Quelle führt die eine .pdf ist das man nicht kopieren kann.
Niemand hat sich die Mühe gemacht das mal zu machen, trotz Millionen für die Klimaforschung.
Ich wusste ich habs schonmal gelesen, aber Dank für die Erinnerung. Gibts da auch eine Version aus der man den Text herauskopieren kann?
Weil der Herr Möller macht einige sehr interessante Anmerkungen, z.B. über das (vermeintliche) plagiieren von Ideen die es schon von Anderen gab oder über Modelle, Messungen , Rechnungen, Erwartungen und die Realität.
An welcher Stelle ist er falsch abgebogen wenn man seine Geschichte bedenkt? Wann wurde er „verstrahlt“?
Sehr geehrter Herr Schwerdt, vielen Dank für Ihre Antwort. Was ich nicht verstehe, warum Sie plötzlich von Kohlenstoff sprechen, wenn ständig nur von CO2 gesprochen wird. Kohlenstoff wird bekanntlich als Gas in Verbindung mit Sauerstoff emittiert. Sonst würde man Graphit oder Diamanten in die Atmosphäre blasen.
Es erstaunt mich, dass mir keiner der an der Diskussion beteiligten keine eindeutige Antwort gegeben.
Ich glaube, dass auch das Lager der Klima-Skeptiker zufrieden ist, wenn es keine eindeutige Antwort gibt. Sonst könnte man nicht in einen friedlichen Austausch von Meinungen treten.
Der übliche Trick wenn die Glaubensbrüder nicht mehr weiter wissen, dann werden beiläufig die zugrundeliegenden Werte geändert. Hier liegt der Faktor bei 3,6 für C zu CO2. 😀
Wird beim NEbel auch immer wieder gemacht. :-O
Bei Herrn Schwerdt haette ich so meine Zweifel ob er ein „Klima-skeptiker“ ist.
Sie machen klare Aussagen, die eigentlich ausreichen sollten, das man genug Zweifel haben kann, das die These, das der Mensch eine Zunahme der CO2 Konzentration in der Atmosphaere bewirkt, richtig ist.
Der einfache Ueberblick reicht dafuer schon.
Viel Spass mit der Diskussion!
Sehr geehrte Herren,
haben Sie vielen Dank für Ihre Reaktion auf meinen Beitrag.
Es freut mich natürlich, dass überhaupt jemand auf einen Beitrag eines Laien antwortet. Andererseits hätte ich mir eine heftigere Reaktion erwartet. In dem Sinne, dass Sie mir vorwerfen bzw. vorhalten würden, dass mein Ansatz unsinnig wäre, die von mir gewählten Zahlen einer KI nicht glaubwürdig wären, frei erfunden bzw. dass ich keine Ahnung hätte.
Ich glaube, die von mir aufgeführten Zahlen fordern uns heraus, an die Wurzeln der Problematik zu gehen.
Das von mir mittels einer Division von zwei Werten, die eine KI geliefert hat, erreichte Ergebnis zeigt, dass eine große Diskrepanz zwischen den offiziellen Werten besteht und dem Ergebnis von 1226 ppm besteht.
Diese Antwort geht an alle, die bis jetzt Samstag 13.50 reagiert haben.
Sehr geehrter Herr Schulz, vielen Dank für Ihre knappe, aber eindeutige Antwort. Es ist entsetzlich in was für einer Lüge wir gehalten werden.
Die Situation erinnert mich an die große Lüge bzw. Verbrechen mit Corona etc. Man hat ja noch nie einen echten Virus-Nachweis geführt und trotzdem hat man die ganze Welt „verarscht“ leider mit sehr negativen Folgen für Millionen von Menschen.
….Ich kann mir vorstellen, dass dieser vereinfachte Ansatz für eine lebhafte Diskussion sorgen wird….
Das glaube ich nicht, Herr Bocek, denn die Treibhauskirche behauptet in ihren 10 Geboten, dass für die angebliche Zunahme seit der Industrialisierung allein der Mensch verantwortlich ist. Die Leute werden sich einfach nicht zu Wort melden, damit ihr Beitrag unbeachtet bleibt.
Hier die ersten drei Glaubengebote:
1) Der CO2-Gehalt der Atmosphäre steigt seit gut 130 Jahren
2) Dieser Anstieg ist ausschließlich menschenverursacht durch die Erzeugung von Treibhausgasen, insbesondere CO2 infolge der Industrialisierung.
3) CO2 ist der Temperaturregelknopf, der Klimakiller CO2 wird eine schreckliche Erwärmung herbeiführen. Wir sind die letzte Generation, wenn wir nicht sofort handeln
Josef Kowatsch 10. Mai 2025 10:31
„Die Leute werden sich einfach nicht zu Wort melden“
Man muß ja nicht über jedes Stöckchen bringen, das Laien hinhalten (ganz gleich ob aus Vorurteilen wegen mangelten Wissens oder aus Provokation).
Die Provokation ist schon ersichtlich aus
Sehr geehrte Herren,
haben Sie vielen Dank für Ihre Reaktion auf meinen Beitrag.
Es freut mich natürlich, dass überhaupt jemand auf einen Beitrag eines Laien antwortet. Andererseits hätte ich mir eine heftigere Reaktion erwartet. In dem Sinne, dass Sie mir vorwerfen bzw. vorhalten würden, dass mein Ansatz unsinnig wäre, die von mir gewählten Zahlen einer KI nicht glaubwürdig wären, frei erfunden bzw. dass ich keine Ahnung hätte.
Ich glaube, die von mir aufgeführten Zahlen fordern uns heraus, an die Wurzeln der Problematik zu gehen.
Das von mir mittels einer Division von zwei Werten, die eine KI geliefert hat, erreichte Ergebnis zeigt, dass eine große Diskrepanz zwischen den offiziellen Werten besteht und dem Ergebnis von 1226 ppm besteht.
Diese Antwort geht an alle, die bis jetzt Samstag 13.50 reagiert haben.
Herr Bocek,
wenn sie weiter mit einfachen Worten die Probleme der Klimaunwissenschaft thematisieren, dann werden sie ueber kurz oder lang ihre Ansprache bekommen.
Wenn sie in Ruhe gelassen werden, kann das allerdings ein Zeugnis dafuer sein, das ihre Aussagen nicht widerlegt werden koennen.
Obwohl, das triggert meistens die von ihnen erwarteten Beitraege: das sie Laie sind und dass ihr Ansatz unsinnig wäre usw usf.
Bleiben sie noch ein bisschen da. Es wird schon…
Jaroslav Bocek schrieb am 9. Mai 2025 16:45
Stand da wirklich CO2 und nicht nur C? Das Äquivalent für 1ppm CO2 in der Atmosphäre wird typischerweise mit 2,13 Gt C bzw. 7,8 Gt CO2 angegeben. Mit 7,8 GT CO2 pro ppm kommt eine plausible Größenordnung raus: 2607/7,8 = 334.
Ich habe es selber geprüft und ChatGPT gibt wirklich was falsches an. Ich war neugierig, wo die Zahl herkommt:
Der Bericht ist hier, und was steht da auf Seite 971 in Tabelle 1:
Da hat also ChatGPT einfach nur Quark erzählt und GtC und GtCO2 nicht auseinanderhalten können, was man auch mit ein wenig Recherche rausbekommen kann.
Ein schönes Beispiel dafür, dass man sich nicht blind auf KI verlassen kann.
Daran, dass der Delta-C13-Wert im letzten Jahrhundert stark zurückgegangen ist, kann man feststellen, dass ein Großteil des CO2 aus foss. Kohlenstoff stammt. Und so den Wert erniedrigt hat. Vulkanische und ozeanische Quellen würden nicht so einen Rückgang bewirken.
Watch Carbon Dioxide Move Through Earth’s Atmosphere
In den Diskussionen taucht ein uralter Streitpunkt erneut auf: Kann die Natur gleichzeitig Quelle und Senke sein? Ja, sie kann.
Neben der Natur als Quelle gibt es auch noch den Menschen als mögliche Quelle. Alle Quellen erhöhen die Konzentration. Senken gibt es nur die natürlichen, und die entnehmen aus dem Gesamtinventar, und davon umso mehr, je höher die Konzentration ist (egal, woher das viele CO2 kommt). Nehmen wir Gleichgewicht an und dann wachsende natürliche Quellen: Die Konzentration wächst, mit ihr, etwas verzögert, wachsen auch die Senken. Die Natur ist eine starke Quelle und eine eher schwache netto-Quelle. Wenn dann der Mensch als weitere Quelle dazukommt, dann steigt die Konzentration zusätzlich an und die Senken entnehmen mehr. Ist der Mensch schwach, reduziert dieses Mehr die Stärke der netto-Quelle. Wird er stärker, kann aus der netto-Quelle auch eine netto-Senke werden. Das haben wir heute. Kein Widerspruch, keine Hexerei, nur die Atmosphäre, so, wie sie ist, mit natürlichen und anthropogenen Quellen und nur den natürlichen Senken, die konzentrationsabhängig entnehmen.
Grundsatzfehler
Die Ausgasung des Ozeans (und des Landes) beträgt nach [6] 210 Gt C/Jahr (=120 Gt C/Jahr + 90 Gt C/Jahr). Auch diese Ausgasung dürfte proportional der Konzentration sein. Den Abnahmeverlauf des Kernwaffenisotops kann die Ausgasung nicht berücksichtigen, da die Konzentration des Kernwaffenisotops im Ozean nahe 0 liegt.
Aus dieser Ausgasung folgt der unbekannte Zustrom von CO2 (der noch kleiner ist als 210 Gt C/Jahr).
https://www.scrippso2.ucsd.edu/graphics-gallery/o2n2-co2-graphics.html
https://www.reklim.de/wissenstransfer/informationsprodukte/faqs-ipcc-2013/faq-33/
Damit stammt der ganze CO2-Zuwachs vom Menschen.
Ihnen ist aber schon bewusst, das 210 GT C/Jahr = 756 GT CO2/Jahr bedeuten, oder?
Mit wechselnden Bezugsdaten rumschwurbeln bringt wenig Punkte. 😀
Grundsatzfehler:
Unfundierte Annahme.
Siehe auch links weiter unten.
Das kann ich aus den beigefügten Links nicht entnehmen. Im Gegenteil: die Graphiken aus dem ersten Link zeigen saisonale Schwankungen des O2/N2-Verhältnisses, die genau mit denen der CO2-Konzentration, also mit einem natürlichen Einfluss, korrelieren. O2/N2 ist also kein Indikator für menschliche Aktivität allein!
Auch muss der Abnahmeverlauf des 14CO2 die Ausgasung nicht berücksichtigen, da er allein für den in die Senke hinein gerichteten Fluss verwendet wird, nicht für eine Nettoflussberechnung.
Michael Mechtel 9. Mai 2025 10:56
„nicht für eine Nettoflussberechnung.“
Aber wenn Sie das Ausgasen „vergessen“, dann müssen Sie sich nicht wundern, wenn Ihre Rechnung große Differenz zur Realität hat.
„mit einem natürlichen Einfluss, korrelieren.“
Es geht nicht um die saisonalen Schwankungen, sondern um die langfristigen Änderungen.
Ich hab mir die Mühe gemacht und die Veränderung des O2/N2-Verhältnisses nachgerechnet: Von 1992 bis 2015 wurden anthropogen ca. 664 Gt CO2 erzeugt, das sind 1.5E13 Mol. Ebensoviel O2 wurde dafür gebraucht. Das bedeutet dass in diesem Zeitraum das molare Verhältnis O2/N2 um den Betrag 0.106E-6 abgenommen haben müsste.
Am Beispiel von Alert, Kanada in Ihrem Link hat das O2/N2-Verhältnis um etwa 500 pem abgenommen. Nach wie vor kann ich die Größe pem nicht interpretieren, und ich sehe nicht, wie dieser Wert mit meinem Ergebnis zur Deckung gebracht werden könnte.
Herr Mechtel, haben Sie denn immer noch nicht verstanden dass die Ausgasung von uraltem etwa 200 GtC/a, das nur wenig 14C enthält, dessen Konzentration verringert und eine viel zu kleine Zeitkonstante vortäuscht?? Und den damit viel zu großen Senkenfluss von 12C korrigieren Sie dann durch eine berechnete fiktive Zusatzemission.
Ich denke schon, dass ich Sie verstehe. Aber:
Nehmen wir an, es besteht Fließgleichgewicht zwischen Atmosphäre und Quellen/Senken. Jetzt kommt ein Schub C-14-haltiges CO2 in die Luft. Natürlich baut sich dessen Konzentration durch den Senkenfluss ab. Aber: das C-14 wird nicht durch C-12 ersetzt, was die atmosphärische Konzentration aufrecht erhalten würde. Denn dazu müsste der Quellstrom erhöht werden. Das passiert aber vorerst nicht, weil der Quellstrom ja auch konzentrationsgetrieben ist, und in der potentiellen Quelle hat sich die Konzentration zunächst noch nicht erhöht.
Das C-14 wird also gar nicht ersetzt. Es verschwindet tatsächlich in den Senken mit der beobachtbaren Zeitkonstante. Und auf diese Art baut sich jeder CO2-Impuls ab, der zusätzlich in die Luft kommt. Ein kompensatorischer Rückstrom setzt erst ein, wenn sich in der Quelle der Druck erhöht hat. Das rechtfertigt in meinen Augen die Verwendung der C-14-Zeitkonstanten.
Michael Mechtel 9. Mai 2025 16:52
Wenn etwas (ganz gleich wie niedrig) gelöst wird, erhöht sich sofort der Druck. Wenn etwas (ganz gleich wie niedrig) ausgast, vermindert sich sofort der Druck.
Wenn die Druckänderungen noch niedrig sind, sind auch die Ströme niedrig.
Die C-14-Zeitkonstanten können wahrscheinlich verwendet werden – aber es müssen die sofortigen Druckänderungen für den sofort einsetzenden Rückstrom benutzt werden.
Nehmen wir das Reservoir des Ozeans: da muss sich der C-14-Eintrag erst mal verteilen, was seine Zeit dauert. Dann macht das CO2 dort verschiedene chemische Reaktionen und wird auch biologisch verstoffwechselt, so dass nicht der gesamte Eintrag zur Druckerhöhung zur Verfügung steht. Im Detail sind die Dinge denn doch recht kompliziert.
Michael Mechtel 10. Mai 2025 10:10
„Eintrag zur Druckerhöhung zur Verfügung steht.“
Falsch. Verteilungszeit und Stoffwechselprozesse erfolgen etwa gleich mit allen Kohlenstoffisotopen.
Die Verteilung sorgt für einen Druckgradienten. Der maximale Druck ist unmittelbar an der Grenzfläche Meer / Atmosphäre.
Bergwerksschaft?
Herr Mechtel, Ihre Aussage dass C-14 gar nicht ersetzt wird und tatsächlich in den Senken mit der beobachtbaren Zeitkonstante verschwindet, ist falsch. Sie beachten nicht den riesigen natürlichen Kreisfluss, der i.w. in wärmen äquatornahen Breiten ausgast und große Mengen uraltes CO2 in die Atmosphäre bringt, welches nur wenig C-14 enthält.
Das ist ja der Grund warum tau=20 a um den Faktor 2,75 gegenüber 55 a verringert ist und Sie hierdurch fälschlich (siehe Tabelle 2, z.B. für 2015) eine Fake-Zusatzemission vom 4,3fachen (!) der anthropogenen Emission berechnen. Hiermit lassen Sie die anthropogene CO2-Emission unwesentlich (!!) erscheinen anstatt dass Sie auch für Alpha einen Wert angeben (vielleicht 0,018 entsprechend 55 a) wo der „unbekannte Quellfluss“ gegen Null geht.
Damit hätten Sie nicht nur alle Modellierer von realistischen C-Modellen unterstützt und vielleicht vermieden dass Dr. Roth freudig statt sein 0,25 (!) ein Alpha von 0,05 (d.h. 20 a und nicht 4) für richtiger hält. Davon abgesehen hätten Sie bei EIKE für mehr Aufklärung statt Verwirrung gesorgt und zahllose unnötige und unerfreuliche Kommentare vermieden.
Ich bestreite doch gar nicht den riesigen natürlichen Kreisfluss. Nur: der reagiert nicht instantan auf den Eintrag, den ein CO2-Impuls in der Atmosphäre auslöst (sei er radioaktiv oder nicht). Zumal, wenn die wesentliche Ausgasung in äquatornahen Breiten erfolgt, dann dauert es seine Zeit, bis die Umverteilung dort die notwendige Konzentrationserhöhung bewirkt hat.
Herr Mechtel, Sie haben offenbar die „Verdünnung“ des C-14 durch den riesigen Naturumlauf, der pro Jahr etwa ¼ des atmosphärischen CO2-Inventars durch altes C-14 armes CO2 austauscht, noch nicht auf dem Schirm. Sie gehen fälschlich davon aus dass es eine Zeit dauert bis in der Atmosphäre eine Verminderung der Konzentration erfolgt.
Es geht aber hier doch um 20 Jahre, in denen die erhöhte C-14-Konzentration auf 1/e abfällt. Beim C-12 findet dagegen durch den Kreisfluss (von 280 ppm) keine Verdünnung statt, sondern nur durch den Senkenfluss da 420 ppm aufgenonnen werden, aber etwa 600 Jahre lang nur 280 ppm ausgegast werden – und zwar sogar verringert (!) wegen der Konzentrationserhöhung.
Die O2/N2-Ratio ist laut allgemeiner Einlassung in einer Studie von der verlinkten Seite keineswegs ein Indikator für menschliche Aktivitäten, wohl aber dafür das die Biosphäre zunehmend als Senke für CO2 anzusehen ist. Wird zwar typischerweise als „instabiler Zustand der Biosphäre“ bezeichnet, manchmal können diese Leut eben nicht anders. 😀
https://www.scrippso2.ucsd.edu/assets/publications/Keeling_et_al_Tellus_07.pdf
„Präzise Messungen haben gezeigt, dass die Konzentration von O 2 in der Atmosphäre von Jahr zu Jahr langsam abnimmt (Keeling und Shertz, 1992; Battle et al., 2000; Bender et al., 2005; Manning und Keeling, 2006). Obwohl dieser Rückgang zu gering ist, um ökologisch relevant zu sein (Broecker, 1970), ist er dennoch als Indikator für Veränderungen im globalen Kohlenstoffkreislauf von Interesse (Keeling et al., 1993). Messungen in den 1990er Jahren zeigten beispielsweise, dass die O 2-Konzentration etwas langsamer sank als aufgrund der Verbrennung fossiler Brennstoffe allein zu erwarten war, was darauf hindeutet, dass sich die Biosphäre der Erde nicht im Gleichgewicht befindet, sondern als Quelle für O 2 und damit auch als Senke für CO 2 fungiert (Keeling et al., 1996; Battle et al., 2000; Manning und Keeling, 2006). Messungen von O 2 haben sich nicht nur für die Diagnose von Kohlenstoffsenken als nützlich erwiesen, sondern auch für die Abschätzung der Produktivität der Ozeane (Balkanski et al., 1999; Najjar und Keeling, 2000), für die Begrenzung der Raten des Gasaustauschs zwischen Luft und Meer (Keeling et al., 1998b) und für die Überprüfung von Modellen zur Biogeochemie der Ozeane (Stephens et al., 1998).“
Danke, eine sehr interessante und wichtige Einlassung.
Herr Mechtel,
sehr guter Artikel.
Zu ihrem Vergleich wollte ich eine weitere Empfehlung geben:
Nehmen sie diese Daten
Und vergleiche sie diese mit diesen Daten:
Hawaii Klimadaten
https://www.meteoblue.com/de/climate-change/hawaii_vereinigte-staaten_5855799
Und/Oder
Hawaii Ozeantemperaturen.
Station OOUH1 – Honolulu, Oʻahu
Diese Station wird von der NOAA betrieben und misst unter anderem die Wassertemperatur in etwa 1,5 m Tiefe.
Aktuelle Daten (z. B. am 3. Mai 2025): Wassertemperatur ca. 79,7 °F (26,5 °C)
Daten ansehen
Standort: 21.303°N, 157.865°W
Station 51001 – Nordwestlich von Kauaʻi
Diese Boje liegt etwa 188 Seemeilen nordwestlich von Kauaʻi und liefert ebenfalls Echtzeitdaten zur Wassertemperatur.
Aktuelle Temperatur (6. Mai 2025): 77,4 °F (25,2 °C)
Daten ansehen
PacIOOS Buoy – Waimea Bay, Oʻahu
Diese Boje liefert Echtzeitdaten zur Meeresoberflächentemperatur in der Nähe der Nordküste von Oʻahu.
Daten ansehen
mfg Werner
Was zählt bei Immobilien: „Erstens: Die Lage – zweitens: Die Lage und drittens: Die Lage!“
Das passt perfekt!
Die Surface Meerestemperatur geht von 25.6 auf 26.7 Grad C hoch.
Quelle laut AI https://climatereanalyzer.org/
All dieser Diskussion möchte ich ein seit 4500 Jahren gültiges Wort, d.h. Versprechen, des Schöpfer-Gottes aus der Bibel entgegenstellen, der das Klima, die Atmosphäre, die (Atem)Luft und damit auch das CO2 erschaffen hat:
„Von jetzt an, solange die Erde besteht, soll nicht aufhören: Saat und Ernte, Frost und Hitze, Sommer und Winter, Tag und Nacht“ (Bibel, 1. Buch Mose, Kapitel 8).
Die gleiche Zusage sehen wir in dem Regenbogen am Himmel bei bestimmten Wetterlagen.
Wir sollten dem Gott der Bibel vertrauen, der Himmel und Erde erschaffen hat und bis heute und bis an das von IHM geplante Ende bewohnbar und lebenswert erhalten wird.
Das CO2 ist goldwert. Es ist ein Lebenselixier erster Güte!
Am Ende gibt es einen neuen Himmel und eine neue Erde mit IHM. Herrliche Zukunft.
Zur Zunahme über einen expliziten Ausstoß durch menschliche Verbrennung hinaus fallen mir zwei prinzipielle Möglichkeiten ein.
Einmal die Ozeane, die bei wärmer werdendem Wasser mehr des gelösten CO2 ausgasen als bei kühlerem Wasser, wo eher CO2-Aufnahme erfolgt. Bei welcher Temperatur dieser Wendepunkt ist, weiß ich leider nicht. Eine Kennlinie dazu wäre interessant, kennt jemand eine. Und zweitens vulkanische Exhalationen, an Land und unter Wasser. Darüber dürfte es wohl nichts Gesichertes geben sondern bestenfalls Spekulationen.
Der Anstieg der Pflanzensubstanz wäre ein Antagonist, der eher bremsend auf die Konzentrationszunahme wirke sollte. Auch dazu kenne ich keine Kennlinien.
Jedenfalls müßte, wenn die CO2-Konzentration der Treiber wäre, innerhalb der erforschten Zeiträume eine klare Synchronität zur Temperaturkurve erkennbar sein, was aber ganz offensichtlich nicht der Fall ist. Hierzulande siehe Matthias Baritz und Josef Kowatsch.
Hat mal jemand errechnet wieviel alle Menschen die seit 1850 gelebt haben ausgeatmet haben? Wenn ich mich recht erinnere sind das 9kg/Tag (oder 9Gigatonnen pro Jahr gem. B(aerbock) Units.)
Was ist mit den Tieren und Pflanzen, z.B. NYT 1982: TERMITE GAS EXCEEDS SMOKESTACK POLLUTION
Dann Methan das zu CO2 oxidiert. Die genaue Anzahl aktiver Vulkane: unbekannt.
Nach meiner Info sollte die Ausatmung pro Mensch eher bei 1 kg CO2 / Tag liegen (wenn er nicht gerade Schwerarbeit leistet).
Da sich die Ausgangsfrage aber auf den Anstieg des atmosphärischen CO2-Gehaltes ab der 2. Hälfte des 20. Jh. bezieht, würde ich dafür keine biologischen Ursachen in Betracht ziehen, denn die biologische Aktivität war ja auch zuvor schon in etwa gleicher Stärke vorhanden.
Michael Mechtel 9. Mai 2025 9:25
Wesentlicher ist, daß das ausgeatmete CO2 aus den Nahrungsmitteln stammt, die ja beim Wachsen CO2 gebunden haben.
Da aber im wesentlichen der Kohlenstoff aus den Nahrungsmitteln gebunden wird, insbesondere beim wachsen, hat Ihre Annahme einen kleinen Schönheitsfehler. 😀
Moritz Steinmetz 15. Mai 2025 0:02
Verstehe ich nicht – können Sie bitte erklären, was Sie unter Schönheitsfehler verstehen?
Lässt sich leicht erklären insbesondere wenn der Mensch sich im Wachstum befindet. Der Mensch besteht zu 28% aus Kohlenstoff, welcher grob gerechnet sein jeweils aktuelles Gewicht( C x 3,6) in CO2 equ. entspricht. Der durch Nahrung aufgenommene Kohlenstoff wird permanent über den Stoffwechsel, auch nach dem Wachstum, in Aminosäuren eingebaut/umgebaut und die Abbauprodukte ausgeschieden über den Darm bzw. Harn. Das CO2 welches ausgeschieden wird, stammt grundsätzlich aus dem Energiehaushalt der Mitochondrien, den Zellkraftwerken und ist somit dem körperlichen Energiehaushalt zuzurechnen welcher über den Gasaustausch der Zellen mit dem Blutkreislauf zur Lunge erfolgt und immer in direktem Bezug zur Sauerstoffaufnahme steht. Im angenommenem Falle kann man dabei im entfernten von einem Sekundärkreislauf der Nahrungsaufnahme ausgehen, aber mit der direkten Nahrungsaufnahme hat dies erst einmal nichts zu tun, diese dient auschließlich der Zellerneuerung über den Umweg Aminosäure–Synthese. Von einer groben Gleichung ausgehend entspricht es der genauen Umkehrung einer grob furmulierten Photosynthesereaktion, insofern liegt Ihre annahme nicht grundsätzlich falsch, ist aber auch nicht vollständig richtig, weil es dazwischen noch sehr viele zeitlich unterschiedliche Komponenten/Stufen gibt(Schönheitsfehler):
Mensch:
C6 H12 O6 + 6 O2 → 6 CO2 + 6 H2O + Energie(2826 kJ)
Photosynthese:
6 CO2 + 12 H2O + Energie(Licht) –> C6 H12 O6 + 6 O2 + 6 H2O
Moritz Steinmetz 15. Mai 2025 20:56
Der Zeitunterschied zwischen CO2-Bindung und CO2-Freisetzung beim Nahrungskreislauf ist klein zum Zeitunterschied zwischen heute und Bildung der Steinkohlenwälder – er kann deshalb unberücksichtigt bleiben.
Es ging auch nicht um diesen „Zeitunterschied“,, es ging um den von Nahrungsaufnahme -> Verarbeitung -> Gasaustausch. Undzusätzlich zu Ihrem Bezug zum Wachstum, einem Prozess welcher aufgenommenen Kohlenstoff teils auf recht lange Zeit abspeichert, im Verhältnis zum Gasaustausch. Versuchen Sie schon wieder zu verNEbeln, von wegen Steinkohlewälder etc.?
Manche LLeute können anscheinend nicht anders und müssen beständig das letzte Wort habben, auch wenn es im Bezug zur Diskursbasis Nonsens ist. 🙁
Moritz Steinmetz 16. Mai 2025 12:24
Sie sprechen von sich selbst.
Es geht um den Eintrag von CO2 in die Atmosphäre, also durch die Verbrennung fossiler Rohstoffe – nicht um den kurzzeitigen Kreislauf.
Dieser Beitrag ist v.a. als Denkanregung zu verstehen.
Und das ist eine gute Denkanregung, weil nicht der Treibhauseffekt mit seinen Glaubenssätzen und erfundenen Geboten Für und Wider diskutiert wird, sondern religionsneutral CO2 und die momentane Zunahme behandelt wird.
Mir fehlt allerdings die Aussage, dass wir derzeit zu wenig CO2 in der Atmosphäre haben, mir fehlt bei EIKE immer noch eine biologische Diskussion mit der Frage, wo läge der optimale Konzentrationsbereich für dieses lebensnotwendige Gas zum Erhalt der Schöpfung auf der Erde. Wenn wir die Schöpfung bewahren wollen, und ich denke, das will jeder, dann muss unbedingt eine biologische Grunderkenntnis her über den optimalen CO2-Konzentrationsbereich.
Keine einzige Wissenschaft der Welt will diese Frage des optimalen Kohlendioxid-Konzentrationsbereiches angehen, schade. Fest steht nur, wir brauchen noch mehr CO2, damit die Erde grüner wird.
Praktiker in Holland brauchen offenbar nicht die Klimalehrbücher zum schädlichen CO2. Sie leiten CO2 aus einer Ölraffinerie einfach in ihre Gewächshäuser und steigern die Produktivität ihrer dortigen Pflanzen. Kann man dann aber trotzdem medienwirksam zerreden, z.B. Correktiv. Ja, CO2-Erhöhung macht die Welt grüner, aber vielen sollen dies nicht glauben, es muss doch irgendwie schädlich sein, oder?
Einen Beitrag darüber zu formulieren ist auch nicht ganz so einfach, bedarf es zwingend einen ganzheitlichen Ansatz der ja bei den Klimatologen völlig verpönt ist. Das Zusammenspiel ist hochkomplex und nicht alleine auf die Biosphäre beschränkt. Einige Stichworte sollen dies kurz anreißen: Biogene Aerosole, Regenauswaschungen von CO2 und Aufnahme selbigen über die Wurzeln, Tag- und Nachrhytmus Photosynthese, CO2-Filter je qm Blattfläche, Energieverbrauch der Photosynthes im Bereich des sichbaren Spektrum(kürzere Wellenlängen als IR aber höherer Energiebetrag) etc., etc.
Eigentlich alles was „Modelle“ berücksichtigen müssten, dies aber nur, wenn überhaupt, pauschaliert angerissen wird. Also kein Wunder das keine der sogenannten Bilanzen stimmig ist.
Josef Kowatsch 8. Mai 2025 11:37
„diese Frage des optimalen Kohlendioxid-Konzentrationsbereiches“
Die Welt ist komplizierter:
https://cleverpedia.de/biologie/c3-c4-pflanzen/
Wir können froh sein das wir gerade das Optimum für wesentliche Getreidepflanzen mit 400 ppm erreicht haben und damit genügend Nahrungsmittel für die wachsende Erdbevölkerung sicherstellen können.
Ich bin mir nicht sicher, ob ich das richtig verstehe. Heisst das, wenn es keine anthropogenen Emissionen gegeben hätte, hätten wir trotzdem einen Anstieg des atmosphärischen CO2-Gehalts beobachtet, der 15% geringer gewesen wäre, als der, den wir beobachtet haben?
Im Prinzip korrekt, wir hätten einen geringeren Anstieg in der Atmosphäre gehabt. Wie der genau verlaufen wäre, könnte man wieder iterativ konstruieren, man müsste dafür als Quellfluss nur QPktx statt QPkt nehmen.
So steht es da!
Es läge nahe auch Dinge wie Methangasausstösse (Unterseeisch oder aus vormaligen Permafrostgebieten) zu berücksichtigen um den Faktor zu erklären. Ich hätte da aber noch einen naheliegenderen Ansatz. Wenn in DE (Beispiel) die Erneuerbaren 50% ausmachen und die Energiepreise um den Faktor 4 steigen und die Technologie der erneuerbaren ja durch Fossile erzeugt wird, dann würde man im Namen des Umweltschutzes tatsächlich solche „unerwarteten“ CO2 Zunahmen in DE erhalten. Damit wäre dann auch der Beweis erbracht, dass die geplante Reduktion „unterkompensiert“ und das Ganze nur ein Geschäftsmodell zur Umsatz- und Gewinnsteigerung ist, gleichbedeutend mit Vermögensumverteilung von Unten nach Oben.
Die abiotischen Methanquellen, ggf. nach dem Auftauen von Permafrostboden wirkend, weil der „Deckel“ wegfällt, werden doch weitgehend als Quellen ignoriert, oder?
Es reicht offenbar nicht, um den Gesamt-CO2-Prozess zu verstehen, wenn man nur die Gesamtmengen der CO2-Senken und CO2-Quellen bilanziert.
Quellen- und Senkenprozesse müssten in ihrem Zeitverlauf detailierte spezifiziert werden.
Dazu besteht aber eigentlich kein notwendiger oder dringender Anlass.
Die Politik und die Klimawissenschaft brauchen das nicht, im Gegenteil es könnte ihr Dogma gefährden.
„Die Welt“ braucht es nicht, da ja im Grunde keine Gefahr im Verzug ist.
Den Realisten („Leugner“ des antropogenen Klimawandels) verwehrt man Stimme und Mittel es zu erforschen, die könnten ja sodann ggf. das Dogma falsifizieren, oder?
Permafrostböden tauen auch nicht wirkllich ganz auf, sondern nur an der Oberfläche und dies schon seit jeher in den meisten Gebieten. Somit ist diese behauptete Quelle keine wirkliche Frage, denn der jährliche Rhytmus auftauen und wieder gefrieren generiert nicht mehr und nicht weniger Methan als jeder sonstige Boden in borealen Gebieten. Tiefer gehendes Auftauen ist angesichts der zunehmenden Abkühlung in weiten Gebieten einhergehend mit stärkeren Frösten zunehmend unwahrscheinlicher.
Gemeint waren tatsächlich „Perma“- Frostböden die angeblich jetzt auftauen. Also nicht einfach nur periodisch auftauende Bodenschichten. Ich kann allerdings keine Überprüfung vornehmen, ob das wirklich passiert oder nur wieder eine „Eisbärmeldung“ ist.
Das sind offensichtlich auch nur wieder „Eisbärmeldungen“, denn dort wo es diese Böden gibt, beherrscht auch heute noch für 6 bis 10 Monate im Jahr eine sehr frostige und teils tiefverschneite Witterung das Geschehen, nur lümmelt niemand gerne bei -30 bis -40°C in dieser Gegend rum.
Alle Methanbanden liegen innerhalb der Wasserdampfabsorption. Daher kann Methan nicht zusätzlich zum Wasserdampf wirken, sondern theoretisch nur dann, wenn es kleinen Wasserdampf gäbe. Das ist aber so gut wie nie der Fall. Wenn also Methan „klimaschädlich“ wäre, wäre es Wasserdampf zur Potenz.
Meines Erachtens ein sehr sachlich gehaltener Beitrag mit einem sehr interessanten Ansatz, danke dafür. Soweit ich es im Moment überblicke, kann ich nur einen potentiellen Schwachpunkt erkennen, der alles noch ins Wanken bringen könnte: Die Modellannahme der Proportionalität zwischen Konzentration und Stärke der Senken. Stimmt diese Annahme, stimmt höchstwahrscheinlich auch das Gesamtergebnis, wenigstens angenähert, stimmt sie nicht, muss es wohl verworfen werden.
Dazu auch gleich einen kleinen Beitrag aus meiner Sachbeurteilung heraus: M. E. bleiben die Ergebnisse grundsätzlich voll bestehen, wenn diese Proportionalität nur im eingeschränkten Bereich von 280 bis 420 ppm Konzentration gilt, und auch da nur angenähert. Und dass sie so gilt, das fordert m. E. ganz einfach die Physik, ernsthafte Gegenargumente kann ich jedenfalls keine erkennen. Allerdings mit dem Blick auf einige Diskussionsbeiträge noch die Klarstellung: Die Proportionalität meine ich für den Fluss aus der Atmosphäre in die Senken, nicht für einen Netto-Fluss unter Gegenrechnung von Freisetzungen in die Atmosphäre, und als Konzentration meine ich die tatsächliche Konzentration, nicht die Überschusskonzentration über den alten (oder irgendeinen anderen) Gleichgewichtswert hinaus.
„Die Proportionalität meine ich für den Fluss aus der Atmosphäre in die Senken, nicht für einen Netto-Fluss unter Gegenrechnung von Freisetzungen in die Atmosphäre, und als Konzentration meine ich die tatsächliche Konzentration, nicht die Überschusskonzentration über den alten (oder irgendeinen anderen) Gleichgewichtswert hinaus“.
Herr Dr. Roth, genau das ist falsch weil der natürliche Senkenfluss sowie die zugehörige (um etwa 600 Jahre verzögerte) Ausgasung ein seit ewig eingestellter KREISLAUF (also Netto Null bei 280 ppm) sind. Sie haben immer noch nicht verstanden dass dies NICHT für die derzeitige anthropogene Störung gilt weil hier die Zeitkonstante (55 a) sowie NETTO betrachtet werden muss.
Unser CO2 wird doch noch lange Zeit nicht wieder ausgegast, und die heutige äquatornahe Ausgasung von antikem CO2 wird durch den ppm-Anstieg VERRINGERT. Davon abgesehen passen weder die C14-Zeitkonstante (20 a) zu Ihrer Umwälzung (etwa nur 4 a) – also die Senkenflüsse – noch die von Herrn Mechtel ermittelten natürlichen Zusatzquellen zusammen. Beide Ansätze können die derzeitige dynamische Störung des realen C-Kreislaufs NICHT reproduzieren.
Herr Dietze,
Sie befinden sich gedanklich immer noch in einem Modell, das sich an einem Springbrunnen mit geschlossener Umwälzung zur Fontäne orientiert. Da ist die Rückgabe immer zwangsweise gleich groß wie die Entnahme. Aber bei der Atmosphäre ist das eben anders. Alles CO2, das ihr entnommen wird, wird nicht sofort zurückgegeben (und es wird auch nicht durch irgendeinen Prozess die exakt gleiche Menge im selben Augenblick in die Atmosphäre gedrückt), sondern das entnommene CO2 durchläuft einen oder mehrere Speicher mit unterschiedlicher Verweildauer, und was in einem bestimmten Zeitpunkt aus dem Speicher in die Atmosphäre zurückgegeben wird, das hängt eindeutig nicht von der in diesem Zeitpunkt in den Speicher hineinfließenden (der Atmosphäre entnommenen) Menge ab.
Mit einem unpassenden Modell kann man keine passenden Aussagen treffen. Es hilft nichts, entkoppelte Flüsse muss man auch entkoppelt betrachten. Es hängt also tatsächlich alles an der Frage, ob die Entnahme (brutto, nicht netto!) aus der Atmosphäre im interessanten Konzentrationsbereich von 280 bis 420 ppm einigermaßen proportional zur Konzentration verläuft oder nicht. Darüber entscheidet die Physik. Der Netto-Fluss richtet sich dann nach der aus Messungen bekannten Konzentrationsveränderung.
Diskutieren Sie die Proportionalität des (brutto)Ausflusses, dann können wir gerne weiterreden. Geschlossene Kreisläufe mit momentan überall gleichem Durchsatz (wie beim Springbrunnen) gibt es in der Natur nicht, und sie werden auch nicht durch irgendeinen „historisch eingespielten“ Verlauf hergestellt.
Herr Dr. Roth, Sie haben mein Modell falsch interpretiert. Dass nach der Theorie linearer Systeme der seit langer Zeit ausgeglichene Naturkreislauf (dessen Flüsse bei 280 ppm sich lediglich den anthropogen verursachten Flüssen additiv überlagern) ausgeklammert werden kann, haben Sie als Gegner des Springbrunnen-Modells noch nicht verstanden. Dort ist unser Senkenfluss proportional zum Überschuss-Inventar (für ppm-280) dividiert durch die Zeitkonstante.
Ihre Behandlung der anthropogenen Störung mit der Umwälzzeit (!!) von nur etwa 4 a (also 1/13,75 von tau) bei 420 ppm ist völlig absurd und füht zu gigantischen sowie synchron zu unserer Emission (!) ansteigenden fiktiven natürllichen
Senkenflüssen, welche überhaupt nicht existieren. Deshalb können Sie aufgrund eines Emissionsverlaufs den realen ppm-Anstieg in Vergangenheit oder Zukunft ja überhaupt nicht berechnen.
Herr Dietze,
ich bin kein Gegner des Springbrunnenmodells, es passt nur nicht zur Atmosphäre, weil dort ganz andere physikalische Verhältnisse herrschen (das habe ich klar gezeigt), und daher sind alle Aussagen, die man mit ihm über die Atmosphäre macht, wertlos. Ihr „seit langer Zeit ausgeglichener Naturkreislauf“ kann sich auch geändert haben, hat er in der Vergangenheit schon oft getan, und dass er das auch jetzt getan hat, das erkennt man an der starken Zunahme der Konzentration (in einem offene System kann die nicht stärker steigen als die Freisetzungen!). Ihre beiden „linearen Systeme“ mit sich additiv überlagernden Flüssen liegen in der Atmosphäre nicht als reale System vor, so gibt es sie nur Ihrer Anschauung (ihrem Modell), sie stimmen aber nicht mit der Wirklichkeit überein. Die Wirklichkeit kennt keinen herkunftsanhängig unterschiedlichen Durchfluss durch die Atmosphäre.
Außerdem unterliegt jede Störung der (kurzen) Umwälzzeit, Sie können nicht bestimmte CO2-Moleküle davon ausnehmen.
=> Die Wirklichkeit kennt keinen herkunftsabhängig unterschiedlichen Durchfluss durch die Atmosphäre.
Außerdem unterliegt jede Störung der (kurzen) Umwälzzeit, Sie können nicht bestimmte CO2-Moleküle davon ausnehmen.
C-14 ist der einzige Messwert, den wir für einen länger anhaltenden Emissionsrückgang haben, und der Abfall geht praktisch bis zum Ausgangswert zurück. <=
Herr Dr. Roth, Ihre og. Aussagen zeigen dass Sie alles durcheinander bringen. Die Umwälzzeit (!) von etwa 4 Jahren hat NICHTS mit der 1/e-Zeitkonstanten für den Senkenfluss zu tun und Sie können doch nicht ebenfalls den 5fachen Wert von C14 dafür nehmen, zumal der wegen seiner Verdünnung für C12 gar nicht anwendbar ist.
Und C12 kann im Gegensatz zu C14 welches gegen Null geht, natürlich bei Nullemission nur bis auf 280 ppm zurückfallen. Zumal mit tau=55 a der beobachtete ppm-Anstieg seit 1840 sehr gut nachgerechnet werden kann, sind Ihre Argumente für die nötigen Modellrechnungen zum ppm-Anstieg aufgrund unseres weiteren Emissionsverlaufs oder für die Dekarbonisierung UNBRAUCHBAR.
Herr Dr. Roth, ich möche hier nur auf Ihren alten Fehler eingehen dass die Zunahme der Konzentration in einem offenen System nicht stärker steigen kann als als die Freisetzungen. Sie beachten nicht dass – soweit noch kein Gleichgewicht erreicht ist und die konstante (!) Emission grösser ist als der Senkenfluss – ein Konzentrationsanstieg stattfindet. Siehe hierzu meine Testrechnung für den ppm-Anstieg auf harmlose max. 500 ppm wenn ab heute noch 110 Jahre (!!) lang die globale Emission von 11,3 GtC/a konstant gehalten wird – womit bei tau=55 a ohne Dekarbonisierung und ohne Zusatzemissionen ganz von selbst NetZero entsteht.
Hier die Excel-Grafik
Peter Dietze 10. Mai 2025 11:09
„Hier die Excel-Grafik“
Die CO2-Konzentration in der Atmosphäre kann man nicht allein mit der Lösungszeit berechnen – es gehört auch die Ausgasung dazu (fast geschlossener Kreislauf).
Herr Ebel, was soll das? Sie haben die Berechnung von tau offenbar nicht verstanden. Sowohl Herr Mechtel als auch ich berücksichtigen die Ausgasung, welche ja in dem analysierten Abfall von C-14 und bei C-12 in dem Anstieg durch anthropogene Emission enthalten ist. Sonst entstünde ja beim Senkenfluss ein riesiger Bilanzfehler.
Herr Dietze,
was genau meinen sie? Ist die Ausgasung um 600 Jahre verzoegert und variabel oder ein ewiger gleichbleibender Kreislauf?
Wo kommen denn die 600 Jahre her und welche Bedeutung sollen die haben?
Wenn nach 300 Jahren genausoviel CO2 ausgast wie nach 500 Jahren oder besagten 600 Jahren, dann ist da kein Unterschied festzustellen.
Wenn es aber einen Unterschied in der Menge gibt, wer sagt, das es von vor 600 Jahren kommt? Wie will man denn das feststellen?
Und warum soll ausgerechnet jetzt nicht das gleiche Senkenverhalten gelten?
CO2 kommt also am Aequator aus den Meeren? Ist das gesichert? Nur da oder ein Grossteil da? Und sind demnach die Hauptsenken die kalten Meere um die Pole?
Passt die C14 Signatur nicht auch zu Ozeanischen Kohlenstoffausgasungen?
Herr Schulz, die etwa 600 Jahre Verzögerung zwischen i.w. polnaher CO2-Aufnahme und Ausgasung in warmer Äquatornähe stammen durch den Transport. Auch bei der schweren Biomasse haben wir einen großen zeitlichen Abstand zwischen Aufnahme und Abgabe des CO2 (Verrottung). Die anthropogene Emission wird zwar aufgenommen, aber noch lange nicht ausgegast – deshalb haben wir ja unseren Senkenfluss, der getrennt vom natürlichen Kreislauf zu behandeln ist. Die Zeitkonstante für C14 von Atombomben ist wegen Verdünnung durch Austausch mit Ozeanen und Biomasse um den Faktor 2,75 geringer als von C12 und daher für C-Modelle unbrauchbar.
Welcher Transport? Die Luft soll so gut durchmischt sein, das ueberall 400 ppm sind. Das heisst das CO2 muss nicht vom Aequator zu den Polen transportiert werden, sondern es kann ueberall das machen, was bei 400 ppm passieren muss.
Das heisst es kommt am Aeqator bei 400 ppm aus den Ozeanen, und geht bei 400 ppm in die polnahen Meere. Zumindestens wenn man das als Haupteintrag und Senkenfluss ansehen will.
Wieviel CO2 wird aber durch Regen ausgewaschen und erfullt nie den „grossen“ Kreislauf. Oder wie sie sagen wegen der Bindung in Biomasse oder andere Senken?
Es scheint die 600 Jahre haben keine Bedeutung und natuerlich oder menschengemacht, CO2 verschwindet irgendwo in einer Senke um woanders wieder aufzutauchen.
Und warum nicht auch in Hawaii, wo die Meerestempraturen waermer werden?
Gibt es die Probleme mit C14, wie sie sagen?
Und gibt es Probleme mit C12/C13?
Scientist Uncovers Miscalculation In Geological Undersea Record
https://www.sciencedaily.com/releases/2008/09/080910104202.htm
Den Fischen kann man nicht vertrauen:
https://web.archive.org/web/20090213055621/http://environmentalresearchweb.org/cws/article/research/37370
Isotopic Identification Of Leakage Gas From Underground Storage Reservoirs- A Progress Report
Es scheint Methanauscheidende Bakterien machen es sehr schwer Untergrundgas von natuerlichen Methan zu unterscheiden.
https://onepetro.org/SPEMGS/proceedings-abstract/77MGS/All-77MGS/SPE-6491-MS/139098
„Wieviel CO2 wird aber durch Regen ausgewaschen und erfullt nie den „grossen“ Kreislauf. Oder wie sie sagen wegen der Bindung in Biomasse oder andere Senken?“
510 Billionen Kubikmeter Regen fallen Durchschnittlich im Jahr und 10 bis 20 mg/Liter werden an CO2 ausgewaschen. Klingt nach einer nicht unerheblichen Menge und nur ca. 30% davon können/könnten, sofern sie nicht in den Grundwasserkreislauf gelangen, gegebenenfalls auf den Festländern wieder in den zeitnahen Kreislauf gelangen wenn diese von Pflanzen/Mikroorganismen im Boden aufgenommen und verarbeitet werden, natürlich zeitversetzt.
Die Menge an CO2 beträgt 5.1 Billionen Tonnen?
Der Mensch produziert aber nur 36 Milliarden Tonnen pro Jahr?
Das heisst Regen sequestriert allein schon 140 mal mehr CO2 als der Mensch produziertt?
Offensichtlich haben Sie mit 10mg/l gerechnet.
Rechnet man mit 15mg/l (dem Mittelwert) siehts ja noch lächerlicher aus.
Es zeigt einfach, dass WENN der Mensch „Schuld“ an der ganzen Sache hat, dass es im Bereich des Schmetterling-Effekts liegt. Aber mal ehrlich: Dann würde das Klima ja wegen jedem Pupser (Vulkanausbruch o.ä.) kippen.
Stimmt, ich habe den geringeren Wert angenommen.
Sie haben da aber einen wundersamen Wert angenommen, oder einfach mal bei der Umrechnerei schlapp gemacht. Es ging um Auswaschung von 10-20 mg/l durch die 510 billionen Kubikmeter. Da hat der Fuchs wohl auch geschlafen oder? Ist eben nicht ganz so einfach wie eine SB-Berechnung. 😀
Man glaubt es kaum, da werfen sich die sogenannten Profis beständig die kompliziertesten Ableitungen bündelweise um die Ohren aber bei einfachsten Umrechnungen machen sie schlapp. :-O
Oder der KI Schnellrechner weiss nicht was eine Billion ist!
Ich habe das nicht nachgerechnet und leider keinen Überschlag gemacht.
Das ist schon das dritte Mal, das die KI solche Aufgaben falsch berechnet. Ich glaube da ist nichts I und total K.
Rechnen Sie doch mal um, dann kommen Sie drauf das der Regen etwa 8,16 GT CO2 auswäscht, Das bedeutet von den Gesamtemissionen eines Jahres von ca. 580 GT CO2(Natürlich und Anthropogen) sind das gerademal knapp 1,5 %. Wo nehmen Sie da das 140fache her?
Von 580 GT sind 1/20 vom Menschen, dann entsprechen 8.16 GT CO2 28 % die ausgewaschen werden, oder?
Ich habe dabei die Annahme von 540 GT Natürliches CO2 und 39 GT(gerundet 40GT) als Annahme zugrunde gelegt. Ich kenne zumindest keinen Vorgang in der Natur bei welchem auf natürlichem Wege zwischen Anthropogen und Naturnah unterschieden werden kann, das kann nur der Mensch mit seinen Rechenmaschinen. 😀
Sicher klingen 1,5% nicht viel, aber gemessen an dem was sonst noch natürlich in den Kreislauf eingreift und in den Modellen allzugerne unter geht summiert sich daraus eine Größenordnung welche nicht außer acht gelassen werden sollte. Meine Überzeugung, die S+B-Fans mögen das ja gerne anders betrachten, aber für mich steht die Komplexität im Vordergrund und nicht der plakative Schwurbel. Denn Verständnis erlangt man nur durch verstehen dessen was an Feldspielern auf dem Platze ist und wie diese Interagieren und nicht indem man auf die Ergebnisstafel starrt.
Seien Sie doch einfach mal ein Fuchs und befragen dazu eine KI, ich vermute mal das diese zumindest die grundlegenden Umrechnungen beherrscht. Meine Rechnung geht übrigens von 16 mg/l aus, man gönnt sich ja sonst nix, bei den steigenden CO2-Werten darfs auch ein kleinwenig über dem Mittelwert liegen. 😀
Ne, die KI war das Problem!
Welche KI denn? Ich brauche dazu keine, war nur eine Empfehlung falls die Grundrechenarten etwas schwächlich repräsentiert sind. 😀
Es scheint die KI is fast nutzlos, wenn man die Antwort nicht schon selber kennt! Erstaunlich das diese die Grundrechenarten nicht beherrscht.
Zum Glueck stimmt meine Prozentrechnung!
Naechstes Mal muss ich alles wieder selber rechnen.
Was verstehen Sie unter einem „alten“ Gleichgewichtswert?
IPCC behauptet in AR6, aktuell gäbe es einen sog. „Strahlungsantrieb“ von ca. +2,3 W/m². Und weil dieser Wert in Relation zu 1750 behauptet wird, bedeutet das im Umkehrschluß, IPCC ist offenbar der Meinung, daß 1750 ein Normklima mit Normtemperaturen herrschte. Das aber nur nebenbei.
Wenn diese +2,3 W/m² nun Tatsache wären, dann hieße das, pro Sekunde wird Wärmeenergie von 2,3 Ws/m² einseitig zugeführt, ohne bilanziell abgeführt werden zu können, oder?
Um ein kg Beton/Erdreich um 1°C zu erwärmen, ist Energiezufuhr von ca. 1000 Ws erforderlich (Wärmekapazität). Das wäre bei 2,3 W ca. alle 435 sec der Fall. Also nach ca. 7 min. Ein Monat hat 30 x 24 x 60 = 43.200 Minuten. Der Strahlungsantrieb wäre also in der Lage, pro Monat ca. 43.200 / 7 = 6200 kg Beton/Erdreich um ca. 1°C zu erwärmen, wenn diese Wärme einseitig kumuliert wird. Wenn man grob annimmt, ein Würfel mit 10 cm Kantenlänge hätte 1 kg, dann hätte 1 m² davon 10 X 10 = 100 kg, es wäre also bei Gleichverteilung ein Betonblock mit 1m² Oberfläche und 6,2 m Tiefe um 1°C, oder 3,1 m um 2°C oder ca. 1,5 m Tiefe um 4°C. Über das Jahr noch mal 12 multipliziert also ein Block mit 1 m² Oberfläche und 1,5 m Tiefe um 12 X 4 = 48°C.
Wenn diese Rechnung nur grob stimmt, belegt die Wirklichkeit, daß sie nicht den Tatsachen entsprechen kann, daß also die Behauptung +2,3 W/m² falsch sein muß! Es kann daher nur einen einzigen wirklichen Gleichgewichtswert geben, und der kann nicht einseitig unsymmetrisch sein. Das ist übrigens seit Ewig Bestandteil der theoretischen Physik, daher kommt in der theoretischen Physik auch kein Treibhauseffekt vor.
Natürlich wäre der theoretische Fall mit den asymmetrischen +2.3 W/m² auch im Widerspruch zum 2. HS.
Weil in dem Moment, wo das Integral der Energieabgabe von der Oberfläche eine temperaturbedingt höhere Abstrahlung zur Folge hätte, als das Integral der Energiezufuhr zur Oberfläche, dreht sich die Energierichtung um, dann strahlt die Erde die Sonne an.
Sowas wäre nur dann möglich, wenn im Erdsystem irgendwo permanent zusätzliche innere Energie entstünde. Daher ist es natürlich unphysikalisch.
stefan strasser 8. Mai 2025 8:33
„die Behauptung +2,3 W/m² falsch sein muß!“
Sie ist nicht falsch, sondern Sie haben die Bedeutung nicht verstanden. Der Strahlungsantrieb ist eine Rechengröße bei unrealen Bedingungen zu Vergleichszwecken, die keine reale Bedeutung hat.
Ich dachte eigentlich, Strahlungsantrieb wäre ein alternativer Begriff zu Zunahme an Gegenstrahlung.
Was meinen denn Sie, was +2,3 W/m² aussagen soll, wenn es keine reale Bedeutung gibt? Was soll die damit verknüpte Aussage denn sein?
IPCC behauptet dazu übersetzt: „Der augenblickliche RF bezieht sich auf eine augenblickliche Änderung des Nettostrahlungsflusses (nach unten minus nach oben) (Kurzwelle plus Langwelle; in W/m²) aufgrund einer aufgezwungenen Änderung. Dieser Antrieb wird in der Regel in Form von Änderungen des Strahlungsflusses am oberen Ende der Atmosphäre (TOA) oder an der klimatologischen Tropopause definiert, wobei letztere ein besserer Indikator für die Reaktion auf die globale mittlere Oberflächentemperatur ist, wenn sie sich unterscheiden.“
Das klingt für mich nicht nach „keine reale Bedeutung“!
stefan strasser Reply to Jochen Ebel 9. Mai 2025 9:08
Da die „Gegenstrahlung“ auf die Oberfläche bezogen ist und der Strahlungsantrieb auf den Oberrand der Troposphäre kann das gar kein alternativer Begriff sein. Er ist auch allgemeiner gehalten und schliesst alles ein, von Änderungen der Sonnestrahlung, Albedo, …
Sie meinen, wenn an der Tropopause 2,3 W/m² auftreten, hat das für die Oberfläche keine Bedeutung? Verschwinden die dann bis zur Oberfläche wieder? Weil es soll ja eine Differenz zwischen auf und ab sein. also ein Ungleichgewicht, welches wenn es existiert, nicht verschwinden kann?
stefan strasser Reply to Marvin Müller 9. Mai 2025 12:21
Huh? Wo haben Sie das denn gelesen? Ich habe lediglich erklärt, warum der Strahlungsantrieb kein alternativer Begriff zur Gegenstrahlung sein kann. Natürlich hat ein Ungleichgewicht an der Tropopause eine Wirkung – keine Wirkung würde gegen den Energieerhaltungssatz verstossen …
Ja, es ist ein Ungleichgewicht, aber warum sollte das nicht verschwinden können? Das System muss ja irgendwie auf dieses Ungleichgewicht reagieren, z.B. durch Erwärmen oder Abkühlen, woraufhin die Differenz wieder vrschwindet …
Koennen sie ein Beispiel bringen wo ein System so reagiert?
Klingt danach als wenn sich das System immer wieder stabilisiert egel wie gross die Auslenjung ist und egal in welche Richtung es geht.
Was ist der Stabilisierungsfaktor bei der Atmsophaere?
Herr Mueller,
koennen sie bitte antworten?
Marvin Müller 9. Mai 2025 12:49
So würde ich das nicht sagen. Auch bei mehr CO2 besteht ein neues Gleichgewicht. Die Zunahme der CO2-Konzentration hat viele Regelprozesse zur Folge – das schreibt schon Fortak 1971. Der neue Zustand der Tropopause bei mehr CO2-Konzentration ist höher und kälter. Wegen der unrealistischen Berechnung wird eine Wärme berechnet und mehr Wärme bedeutet eine höhere Temperatur im Gegensatz zur tatsächlichen Reaktion.
stefan strasser 9. Mai 2025 9:08
„Das klingt für mich nicht nach „keine reale Bedeutung“!“
Sie müssen unterscheiden zwischen realer Bedeutung und realer Wirksamkeit. Die unreale rechnerische Größe „Strahlungsantrieb“ ist gut für den Vergleich verschiedener Ursachen – hat aber keine wirksamen Auswirkungen. Die reale Wirksamkeit ist kompliziert.
Um zu zeigen, das auch das IPCC den Strahlungsantrieb nur als Rechengröße definiert, das Glossar: https://www.ipcc.ch/site/assets/uploads/2019/03/IPCC2007-Annex_german.pdf
Halten Sie das alles für ermittelbar? Es soll berechnet werden, woraus? Und es soll die Differenz zu 1750 darstellen, woher will man den Wert von 1750 kennen? Und wie wollen Sie alles andere konstant halten, was ist eigentlich alles andere?
Aber das Wichtgste: wenn so eine Wert ermittelt und veröffentlicht wird, offenbar ein permanenter Fluß, sollte er doch irgend eine Bedeutung für das Klimasystem haben, oder? Es wird im AR6-Text immerhin prominente 966 Mal auf „radiative forcing“ referenziert!
Was also wäre Ihrer Meinung nach der resultierende Unterschied zwischen „realer Bedeutung“ und „realer Wirkasmkeit“?
Der IPCC hat das Wort „Netto“ benutzt?
Apropro Definition Treibhauseffekt:(Gleicher Link)
Die Atmosphaere absorbiert von sich selber thermische Strahlung? Und kann sie davon waermer werden?
Weil sie nicht abstrahlen? Aber sie strahlen doch? Sie strahlen und absorbieren Waerme von sich selber und was passiert?
Stimmt diese Definition?
14 Grad C? Ist das eine fehlerhafte Uebersetzung? Oder ist der THE 33 K, weil es sollen ja -19 Grad C Gleichgewichtstemperatur sein.
Wo kommt der Fehler her? woher weeiss man das es immer 33 K sind?
Danke fuer den Link. Sehr hilfreich!
Schon wieder ein neuer Herr Schulz, der von nichts weiß.
Dafuer haben wir ja sie und Herrn Ebel.
Auf die Idee diese Definition vom IPCC zu bringen, wenn sie nach einer gefragt werden, sind sie nicht gekommen.
Warum?
Ich finde es übrigens sehr interessant, daß die deutsche Übersetzung anders formuliert als das englische Original von AR6, siehe unten.
Im englischen Original zum „Greenhouse effect“ z. B. kein Wort zu -19°C oder +14°C …
Essentiell für mich ist aber, daß behauptet wird, das Radiative forcing zu berechnen(!), allerdings ohne diese Berechnung auch zu zeigen. Wenn man z. B. behauptet, der Anteil von CO2 am RF seit 1750 sei im Mittel +2,28 W/m², dann muß es dazu eine nachvollziehbare Rechnung mit diesem Ergebnis geben. Sowas habe ich nirgendwo gefunden.
Radiative forcing
The change in the net, downward minus upward, radiative fux (expressed in W m–2) due to a change in an external driver of climate change, such as a change in the concentration of carbon dioxide (CO2), the concentration of volcanic aerosols or the output of the Sun. The stratospherically adjusted radiative forcing is computed with all tropospheric properties held fxed at their unperturbed values, and after allowing for stratospheric temperatures, if perturbed, to readjust to radiative-dynamical equilibrium. Radiative forcing is called instantaneous if no change in stratospheric temperature is accounted for. The radiative forcing once both stratospheric and tropospheric adjustments are accounted for is termed the effective radiative forcing.
Greenhouse effect
The infrared radiative effect of all infrared-absorbing constituents in the atmosphere. Greenhouse gases (GHGs), clouds, and some aerosols absorb terrestrial radiation emitted by the Earth’s surface and elsewhere in the atmosphere. These substances emit infrared radiation in all directions, but, everything else being equal, the net amount emitted to space is normally less than would have been emitted in the absence of these absorbers because of the decline of temperature with altitude in the troposphere and the consequent weakening of emission. An increase in the concentration of GHGs increases the magnitude of this effect; the difference is sometimes called the enhanced greenhouse effect. The change in a GHG concentration because of anthropogenic emissions contributes to an instantaneous radiative forcing. Earth’s surface temperature and troposphere warm in response to this forcing, gradually restoring the radiative balance at the top of the atmosphere.
https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_AnnexVII.pdf
Da hat wohl der Uebersetzer noch eine paar Daten angedichtet, ohne jedoch zu verstehen, das es -18 Gad C sein muessen.
Der Witz ist ja das einfach mal aus 240 W/m2 236 W/m2 gemacht werden.
Ist das einen Aenderung der Albedo, der Solarkonstante? Diese 4 W/m2 sind schon in der Groessenordnung des ‚radiative forcings‘.
Also Klimawandel allein schon durch Aenderungen, die nicht vom CO2 verursacht werden.
Und die „definition“ erklaert eigentlich ganz gut wie der THE zustande kommt:
Der Temperaturgradient ist es. Und wie wird er noch mal erklaert?
stefan strasser 10. Mai 2025 8:18
„Sowas habe ich nirgendwo gefunden.“
Ich auch nicht – allerdings erscheint mir der Rechenwert etwa richtig, aber weiter habe ich das nicht verfolgt, da eben ein unwirksamer Rechenwert.
Genau wie eine angebliche Wasserdampfrückkopplung, wo sogar beim IPCC steht, das diese nicht nachgewiesen werden kann – ist verständlich, denn man kann nicht etwas nachweisen, was nicht existiert.
Sehr geehrter Herr Roth, es freut mich, dass Sie sich zu meinem Artikel äußern. Bei der Arbeit daran bin ich auf Ihre Artikel gestoßen, die ich in [5] und [8] zitiert habe, und in denen Sie von einem anderen Denkansatz ausgehend im Grunde zum gleichen Ergebnis kommen, jedenfalls qualitativ.
Ich denke auch, dass die Proportionalitätsannahme so falsch nicht sein kann. Ein andere Frage wäre noch, welche Zeitkonstante (bzw. welches alpha) man zugrunde legt. Da bin ich durch ihre Veröffentlichung auf die C-14-Abklingkurve gestoßen, die ich dann übernommen habe, weil mir das am Sinnvollsten erschien. Bemerkenswert ist aber auch die Elastizität meines Rechenansatzes hinsichtlich des Wertes von alpha.
Herr Mechtel, die Natur kann doch nicht als Senke von etwa 60% des anthropogen emittierten CO2, gleichzeitig aber auch als Quelle für das ansteigende Gesamtinventar an CO2 in der Atmosphäre fungieren! Dass die Natur laufend – und sogar synchron mit unserer Emission ansteigend – riesige zusätzliche Emissionen liefern soll, die bei Dr. Roth noch viel höher sind als bei Ihnen weil sein Senkenfluss noch etwa um den Faktor 5 (!!) höher ist, zeigt dass Sie .beide die Dynamik des C-Kreislaufs sowie die Zeitkonstanten für anthropogenes CO2 nicht richtig verstanden haben.
Der Ansatz von Dr. Roth geht fälschlich davon aus dass heute etwa 220 GtC/a Kreisfluss 420 ppm (analog wie bei 280 ppm) erzeugt. Somit würde eine anthropogene Daueremission von 1 GtC/a nicht wie im korrekten C-Modell +19,4 ppm, sondern nur etwa 1,9 ppm (!!) bewirken und wäre damit völlig irrelevant. Das zeigt wie grotesk falsch jeder Ansatz mit erheblich geringerer Zeitkonstante und fiktiven natürlichen Zusatzquellen ist. Damit wird doch jegliche wiss. solide Kritik an der Energiewende mit Dekarbonisierung zerstört weil wir als Spinner ignoriert werden.
Bei Ihnen scheinen immer alle anderen etwas falsch verstanden zu haben, egal worum es geht. So funktioniert aber eine sachliche Diskussion nicht. Und vielleicht liegt es auch grundsätzlich daran, das Sie sich in eine falsche Sichtweise verrannt haben?
Herr Steinmetz, die Halbwertszeit der ppm-Erhöhung durch CO2-Emission ist quasi eine Naturkonstante. Stellen Sie sich vor, da sind zwei Leute, die meinen dass die Lichtgeschwindigkeit noch garnicht richtig bekannt sei, und machen Versuche sowie diverse Berechnungen. Der eine kommt auf 1/2,75, der andere auf 1/13,75. Sie kennen sich da aber nicht aus und mahnen zu einer sachlichen Diskussion?
Ich bin doch keinesfalls der Einzige welcher anhand eines C-Modells mit der in etwa richtigen Zeitkonstanten den beobachteten ppm-Verlauf seit 1840 nachgerechnet hat. Und dass IPCC mit dem Kumulationsmodell, welches vermeintlich NetZero nötig macht, krass daneben liegt, sollte auch Ihnen schon bekannt sein.
Was ist eine „quasi“-Naturkonstante? Eine von Ihnen als solche gewillkürte, weils gerade so gut passt?
Und „Halbwertzeit“ steht gewöhnlich für Abbauvorgänge, Zerfallsraten und nicht für Zuwachsraten von irgendwas.
Herr Steinmetz, wenn Sie (im Gegensatz zu mir) meinen, die 1/e-Zeitkonstante des emittierten CO2 sei keine Naturkonstante, na bitte. Dass dieser Systemparameter nach Multiplikation mit ln(2) die Halbwertszeit ergibt, und diese sowohl für die Abbaurate als auch für den ppm-Anstieg bei konstanter Daueremission gilt, können Sie natürlich nicht wissen. Bevor Sie mal selbst versuchen, einen reellen globalen ppm-Verlauf aufgrund anthropogener CO2-Emissionen zu berechnen, empfehle ich die hier angegebene Quelle [9] von mir, Expert Reviewer des TAR vom IPCC, Scientific Basis.
Ich habe auf Ihre Definition als Quasi-Naturkonstante eine konkrete Frage gestellt, damit keinerlei Werte/Konstanten infrage gestellt. 🙁
Herr Dietze, die ganze Diskussion zeigt mir, dass der Sachverhalt nicht ganz leicht zu durchschauen ist. Ohne mich jetzt endgültig festlegen zu wollen, nur soviel: sie berufen sich darauf, dass Sie den Verlauf seit 1840 mit Ihrer Zeitkonstante nachrechnen konnten. Da gebe ich zu bedenken, dass auch mein Rechenansatz erlaubt, die CO2-Konzentration (ab 1960) nachzuvollziehen, aber mit einem breiten Wertebereich für die Zeitkonstante.
Das heisst zumindest für meinen Ansatz (Ihre Rechnung kenne ich nicht im Detail), dass das Funktionieren der Berechnung noch nicht als Bestätigung dafür genommen werden kann, dass auch die Zeitkonstante korrekt gewählt wurde!
Herr Mechtel, Ihr Rechenansatz erlaubt NICHT, die CO2-Konzentration (ab 1960) mit einem breiten Wertebereich für die zu geringe Zeitkonstante (!) nachzuvollziehen, denn Sie berechnen ja für den beobachteten ppm-Wert eine fiktive natürliche ZUSATZEMISSION. Da diese je nach gewählter Zeitkonstante verschiedene Werte hat und Sie nicht wissen ob die existiert und wo die herkommen soll (und z.B. wegen tau=4 Jahren bei Dr. Roth extrem hoch wird), hätte Ihnen ein Licht aufgehen müssen.
Ihre Methode ist doch in etwa so: 3+4=6 stimmt wenn ich 1 dazuzähle, und 3+4=5 stimmt ebenfalls wenn ich 2 dazuzähle. Es ist grotesk, uns weismachen zu wollen, Sie berechnen doch 3+4 richtig, und dann sogar noch zu behaupten dass 3+4=7 ohne Zusatz keine Bestätigung für eine richtige Berechnung sei.
So ist es ja nun nicht. Die vorgestellte Rechnung liefert immer eine Zusatzemission, egal, wie ich die Zeitkonstante tau (innerhalb eines vernünftigen Bereiches) wähle, natürlich im Wert abhängig von tau. Das ist logisch, denn eine geringere Zeitkonstante erzwingt höhere Flüsse, wenn man das Gleichgewichtsniveau festhält, oder ein geringeres Gleichgewichtsniveau, wenn man Zu- und Abfluss festhält.
Der Punkt ist, dass man die Zusatzemission nicht a priori ausschließen sollte. Tut man das, darf man sich nicht wundern, wenn es am Ende wieder als Ergebnis herauskommt. In einem arithmetischen Beispiel: 10-3 = 7, aber auch 12-5 = 7. Die Zusatzemission wäre hier 2.
Herr Mechtel, mir scheint dass Sie meine Kritik an Ihrer berechneten Zusatzemission nicht verstehen. Es ist doch so, dass Sie irgend eine (auch falsche) Zeitkonstante wählen können – ja, Sie können sogar eine falsche Modellgleichung (!) wählen.
Ihr Verfahren, das den bekannten ppm-Verlauf möglichst gut approximiert, rechnet doch die dazu nötige ZUSATZEINSPREISUNG (ggf. sogar mit negativem Vorzeichen) aus. Solch ein Verfahren berechnet keinen ppm-Verlauf aus dem Emissionsverlauf in Vergangenheit und Zukunft, sondern ist eher Humbug.
Sie können doch nicht davon ausgehen dass die Natur rein zufällig die gemäß Ihren Vorgaben und dem Emissionsverlauf pro Jahr passend berechnete (!) Zusatzeinspeisung derzeit und insbesondere auch in Zukunft (wofür Sie gar keine Referenzwerte haben) überhaupt liefert.
Sie haben insofern recht, als Prognosen immer schwierig sind, v.a., wenn sie die Zukunft betreffen 😉 Das hat schon ein prominenter Philosoph erkannt. Ich mache ja auch nur eine Aussage über den ausgewerteten Zeitraum von 1960 bis 2018.
Und ja, wenn man sehr niedrige alpha-Werte ansetzt, also sehr lange Verweilzeiten in der Atmosphäre, kommt der Zusatzeintrag negativ heraus, d.h., als Senkenfluss. Das kommt daher, weil ansonsten der anthropogene Eintrag einen zu steilen Anstieg der Keelingkurve erzeugen würde.
Sehr lange Verweilzeit tau bedeutet, dass die Senken praktisch dicht sind. Dass ausgerechnet diese Situation formal einen zusätzlichen Senkenfluss verlangt, ist physikalisch gesehen widersprüchlich und sollte als Hinweis gedeutet werden, dass die Verweilzeit unrealistisch angesetzt wurde. Ihr Vorschlag tau = 58 Jahre fällt allerdings noch nicht in diesen unphysikalischen Bereich.
Ja, diese Aussagen sind ok, aber schade ist und bleibt dass Sie in diesem Beitrag tau=20 a wegen C-14 und z.B. für 2015 eine Fake-Zusatzeinspeisung vom 4,3fachen unserer Emission ermittelt haben weil Sie meinten dass man ja die Zusatzemission nicht a priori ausschließen sollte. Ansonsten ist im Prinzip Ihre Berechnung von tau aus der Analyse von Beobachtungsdaten ok, auch wenn da wegen C-14 etwas schief gelaufen ist und ich mich – sorry – sogar wegen Ihrer Zusatzquelle gezwungen sah, den Begriff ‚Humbug‘ zu verwenden.
Herr Mechtel, wenn das tau zu groß gewählt würde, also die Senken ziemlich dicht sind, und daher ein zusätzlicher Senkenfluss nötig wäre (um die Keelingkurve zu reproduzieren), das soll unphysikalisch sein?? Da stellen Sie doch als Physiker die Physik auf den Kopf! Sie haben offenbar noch nicht geschnallt dass Sie eine Zusatzquelle (sowie den zusätzlichen physikalischen Senkenfluss) nur berechnen weil Tau zu KLEIN ist, also die Senken zu stark sind. Tau=55 a ist in etwa der reale Wert für unser CO2 (inklusive Ausgasung bei konstantem geglättetem Natur-Kreisfluss).
Ergänzung: Mit konstantem Naturkreisfluss ist der ohne die anthropogene Störung gemeint. Die Veränderung durch den anthropogenen ppm-Anstieg ist ja in der Keelingkurve und somit im korrekten tau enthalten.
C-14 ist der einzige Messwert, den wir für einen länger anhaltenden Emissionsrückgang haben. Der zeigt m. E. zwei Dinge eindeutig: Der Abfall erfolgt deutlich schneller als mit einer Zeitkonstanten von 50 Jahren und er geht praktisch bis zum Ausgangswert zurück (und bleibt nicht bei 50 % stehen!). Die Argumente, die für 50 Jahre und 50 % vorgebracht werden, können daher nicht stimmen.
Genau. Beispiel 2015: hier bleiben zwar ca. 50 % des zivilsatorischen Ausstoßes in der Atmosphäre. Bezieht man aber den Verbleib in der Atmosphäre auf den gesamten Quellfluss, wie er sich aus der Rechnung ergibt (s. Tab. 1, Spalte 2), dann sind es nur noch 10 %.
Herr Mechtel, dass Sie hier mit „Genau“ den völlig falschen Auffassungen von Dr. Roth zustimmen und gar noch behaupten, der anthropogene Anteil an dem Quellfluss (der ppm erhöht) sei nur 10%, ist das Allerletzte und zeigt dass auch Sie den C-Kreislauf und seine Dynamik noch nicht verstanden haben. Zusammen mit Dr. Roth. klären Sie bei EIKE nicht die Sachverhalte auf, sondern versuchen eher, die mühsame Arbeit der Aufklärung zu ZERSTÖREN.
Herr Dietze, woher weiss denn die Natur das es 50% vom Menschen gemachten CO2 in der Atmosphäre behalten muss, damit ihre Version stimmen kann?
Gibt es diesen selektiven Mechanismus?
Herr Schulz, die Natur kennt unsere Emission E nicht und weiss erst recht nichts von 50%. Diese (es sind durch den ppm-Anstieg schon etwa 60%) kommen dadurch zustande dass der Senkenfluss anthopogenes_atmosInventar140ppm/tau55a ist und E – um diesen Betrag im Jahr vermindert – als airborne fraction in die Atmosphäre geht.
Daraus folgt übrigens dass bei konstant 11,3 GtC/a nach 110 (!) Jahren, wenn unser Inventar 220 ppm erreicht, 100% von E in die Senken geht und damit nur harmlose max. ~500 ppm erreicht werden – siehe meine Excel-Grafik. Und das ∆T (im Gleichgewicht) gegen heute wäre nur 0,6•ln(500/420)/ln(2)=0,15 Grad
Ausser rechnerisch, worauf beruht das tau55? Welche Grundlage hat es? Muss das CO2 vom Menschen oder insgesamt aus der Natur vom Aequator gen Pole wandern, um da sequestriert zu werden?
Muss es dann nicht einen CO2 Konzentrationsgradienten zwischen den Polen und Aquator geben?
Herr Schulz, natürlich geht nicht nur die natürliche, sondern auch die anthropogene CO2-Emission in die kalten polaren Meere – aber in den Tropen ausgegast wird derzeit nur der antike und ziemlich stabile Naturfluss (280 ppm), und unser anthropoges ∆ erst mehrere hundert Jahre später. Deshalb ist dieses ∆ ja auch bis dahin unser Senkenfluss (!), den wir separat betrachten müssen, wobei das Tau nicht einen Wert von 4 oder 20, sondern von 55 Jahren hat.
Ausgegast werden 280 ppm? Ist das messbar?
Ist es nicht eher so das eine gewisse Masse ausgegast wird? Wie kann denn etwas das 280 ppm Konzentration ausgasen wenn der Gehalt in der Atmosphaere schon hoeher ist?
Und sind nicht aufwallende Tiefenwaesser fuer Anteiler der Aussgasung verantwortlich? Ist das CO2 dort eventuell auch Chemisch gebunden?
Wie lang ist der Kreislauf der Tiefenwaesser?
Herr Schulz, Sie haben mich falsch verstanden. Natürlich werden nicht 280 ppm nach 420 ppm ausgegast. Gemeint war dass uraltes Wasser aus der Zeit wo 280 ppm herrschten, in den Tropen ausgast. Wenn überhaupt, denn ich weiss nicht, ob die Temperatur dazu ausreicht. Denkbar ist auch, dass die 420 ppm dort wo das Wasser nicht ganz so warm ist, die Ausgasung verhindern und es gar noch etwas Absorption gibt.
Das ist ja da Praktische an der geglätteten Keelingkurve dass wir – soweit die anthropogenen Emissionen bekannt sind – diese vielen realen Effekte (zur Bestimmung von Tau) nicht zu untersuchen brauchen, denn diese sind ja alle global Netto weitestgehend in der Kurve enthalten.
Herr Dietze,
Meereswasser speichert eine Menge CO2 in dissozierter Form. Da spielen ppm, so wie bei der Gasloesung, keine Rolle.
Die Gasloesung von CO2 ist sowieso im Vergleich mit anderen Gasen geringer Man miuss fuer CO2 da eine Sonderregel erstellen, um die Saeurenbildung mit zu beruecksichtigen.
Meines Erachtensnach reicht der Gasloeungsansatz nicht um die komplexen Verhaeltnisse richtig darzustellen.
Sieht man auch daran, das sie nicht wissen ob am Aequator CO2 ausgast oder nicht und: .
Sieht man auch daran, das sie nicht wissen ob am Aequator CO2 ausgast oder nicht und ob die Temperatur dazu ausreicht.
Herr Schulz Sie haben immer noch nicht verstanden dass ich diese Werte garnicht benötige. Die Keelingkurve liefert doch die nötigen Nettowerte.
Peter Dietze 16. Mai 2025 8:48
Ich glaube nicht, das die Umwälzung aus zwei Günden einen großen Einfluß hat:
Die Beschreibung des Eintrag in den Ozean kann nicht mit einer einzigen Zeitkonstante erfolgen, da der CO2-Eintrag proportional der Druckdifferenz zwischen Atmosphärenpartialdruck und Ozeanpartialdruck sein dürfte und der Ozeanpartialdruck das Integral der Einträge sein dürfte. Ein solcher Vorgang wäre mit einer Dgl. 2. Ordnung zu beschreiben.
Ein einfacherer Versuch mit der Summe der Emissionen zeigt geringe Schwankungen um den Mittelwert, aber einen systematischen Gang der Zeitabweichung zwischen aktuellen Druck und früheren Drücken. Der systematische Gang gibt Anlaß zur Vermutung, das nicht eine Dgl. erster Ordnung reicht, sondern die Dgl. 2. Ordnung sein muß.
Die Beschreibung der Lösung bzw. Austausch hat Dr. Roth mit der Entropie eine gute Beschreibung unter Punkt 2 gemacht (Eike Roth 14. Mai 2025 21:31). Daten für den endgültigen Austrag von CO2 (z.B. durch Absinken von Kalkschalen) fehlen.
Ich glaube nicht, dass die Umwälzung aus zwei Günden einen großen Einfluß hat
Herr Ebel, die Umwälzung brauche ich gar nicht. Ich benötige nur den Senkenfluss, und den liefert die Keelingkurve aus der bekannten Emission.
Peter Dietze 16. Mai 2025 21:01
„und den liefert die Keelingkurve …“
Mit einem laufend angepaßten Tau. Mit der laufenden Anpassung von Tau sind beliebige Kurvenverläufe reproduzierbar. Die beschreibende Gleichung muß einen konstanten Wert der Atmosphärenkonzentration bei menschlichen Eintrag = 0 liefern – ohne die Koeffizienten laufend anzupassen.
Herr Ebel, Sie haben meine Ermittlung der Konstanten Tau=55 a aus der Keelingkurve überhaupt nicht verstanden und verbreiten hier die groteske Lüge dass ich Tau laufend anpasse (!) und bei Emission Null nicht auf 280 ppm komme. Sie haben also nichtmal meine Dokumentation [9, Abb.2] angesehen.
Peter Dietze 17. Mai 2025 13:42
„überhaupt nicht verstanden“
Sie haben den Lösungsvorgang im Ozean nicht verstanden. Deshalb eine Beschreibung des Lösungsvorganges ohne laufende Anpassung:
Eine Änderung von 55 Jahren auf unendlich ist also nach Ihrer Meinung keine Anpassung????
Mit zwei Konstanten und zwei Gleichungen ist alles abgedeckt:
Aus 1. folgt: pO = (pG – pA) / V. Wird das in 2. eingesetzt wird:
d ([pG – pA] / V) / dt = ([pG – pA] / V – pA) / T
Sortiert wird daraus:
d(pG/V)/ dt – (pG/V)/T = (dpA/dt)/V – pA/(T*V) – pA/T
Nach Multiplikation mit V wird daraus:
d(pG)/ dt – (pG)/T = dpA/dt – pA/T – pA*V/T
d(pG)/ dt – (pG)/T = dpA/dt – pA*(1 + V)/T
Nach Multiplikation mit T und Betrachtung von 1 Jahr wird daraus mit T/dt = T‘ und d(p..) = Dp:
DpG * T‘ – pG = DpA * T‘ – pA*(1+V)
Bzw.
pG – DpG * T‘= DpA * T‘ – pA*(1+V) – DpA * T‘
Der Startwert für pG ist pA*(1+V)
Meßwerte liegen vor für DpG ( https://www.statista.com/statistics/276629/global-co2-emissions/ ) und pA (Keeling-Kurve). Wenn die Betrachtung etwa richtig ist, dürften die linke Seite und die rechte Seite keine Differenz haben. In der Praxis werden Abweichungen entstehen, die durch passende Wahl (Excel – Solver) von T‘ und V zum Minimum werden (ca. 3 ppmV).
Die Abweichungen können z.B. durch das Gefälle der Konzentration entstehen – die Abweichungskurve läßt eine Diffusionszeit im Ozean von ca. 3 Jahren vermuten.
Die Lösungszeit von ca. 5 Jahren ist natürlich sehr unterschiedlich zu 55 Jahren und unendlich – liegt aber im Bereich der Lösungszeit von C14.
Die Ergebnisse sind T = 4,7 Jahre und die beteiligte Ozeanmenge V = 0,79
Sie haben den Lösungsvorgang im Ozean nicht verstanden. Deshalb eine Beschreibung des Lösungsvorganges ohne laufende Anpassung. Eine Änderung von 55 Jahren auf unendlich ist also nach Ihrer Meinung keine Anpassung????
Herr Ebel, Sie behaupten hier frei erfundenen Unsinn und glauben doch nicht etwa dass Sie die Netto-Ozeansenke und Zeikonstante für die anthropogene Störung besser verstehen. Ich habe seit 26 Jahren ein sehr gut funktionierendes C-Modell und habe damit viele Emissions- und ppm-Verläufe mit konstantem Tau=55 a, Pufferfaktor 0,75 und ohne Zusatzquellen gemäß [9] berechnet. Sie sind verwirrt und sollten es sich sparen, Gleichungen hinzuschreiben, nach denen ich besser rechnen sollte.
Warum rechnen Sie nicht selbst z.B. mal damit die ppm-Kurve von 1840 bis 2135 mit konstant 11,3 GtCa Emission ab 2025 für 110 Jahre nach, die ich hier in der Excel-Grafik zeige? Dass ich zum Vergleich sogar zwei erheblich höher ansteigende Kurven mit IPCC-Parametern (Tau=570 a und unendlich, mit passendem Pufferfaktor) simuliert habe, die statt auf 500 auf 700 ppm ansteigen, haben Sie offenbar übersehen.
Peter Dietze 17. Mai 2025 13:42
Zitat aus[9]:
So ein Modell ist alles andere als realistisch: Der Senkenfluss durch die Oberfläche des Ozeans (von der Atmosphäre) ist proportional der Druckdifferenz zwischen Atmosphäre und Oberflächendruck des Ozeans.
Zwar hat der Ozean prinzipiell eine hohe Aufnahmekapazität, aber eine große Aufnahme würde eine hohe Diffusionsgeschwindigkeit im Ozean erfordern. Diese Diffusionsgeschwindigkeit ist wahrscheinlich noch klein gegenüber der Umwälzzeit, die Sie mit 600 bis 1000 Jahren angeben.
Wird in die Rechnung noch die Diffusion in tiefere Schichten einbezogen, so verändern sich die Zeiten nur wenig.
Herr Ebel, natürlich ist ein C-Modell mit zum ppm-Anstieg proportionalen Senkenflüssen realistisch, denn sonst könnte es ja nicht den beobachteten ppm-Anstieg reproduzieren (weil der geglättete anteilige 280-ppm-Naturkreislauf ziemlich konstant bleibt). Sie schreiben doch selbst, dass der Senkenfluss in den Ozean proportional zur Druckdifferenz zwischen Atmosphäre und Oberfläche des Ozeans ist. Und auch wenn der Oberflächendruck etwas höher wird als 280 ppm (aber in polalen Meeren auch niedriger wird), ist doch die Differenz zu 420 ppm etwa proportional zum ppm-Anstieg. Und um Diffusion und Absinkflüsse braucht man sich nicht zu kümmern, denn Tau55 ergibt sich ja aus der Keelingkurve. Statt alles zu kritisieren sollten Sie durch eine eigene Modellrechnung endlich nachweisen dass Sie es zwar kaum besser, aber wenigstens richtig machen.
Peter Dietze 19. Mai 2025 12:06
Mein Ansatz erklärt die Keelingkurve – die geglättete Kurve ergibt die Abweichung 0. Mein Ansatz gilt für beliebigen Verlauf der anthropogenen Emissionen – Ihr Ansatz setzt einen weitgehend konstanten Zuwachs der anthropogenen Emissionen voraus – und wenn das nicht zutrifft ändern Sie eben Ihr Tau55 – sogar auf unendlich.
Die ist doch gemacht und mit Begründung (Jochen Ebel 18. Mai 2025 16:49) warum dieser Ansatz.
„Ihr Ansatz setzt einen weitgehend konstanten Zuwachs der anthropogenen Emissionen voraus – und wenn das nicht zutrifft ändern Sie eben Ihr Tau55 – sogar auf unendlich“.
Herr Ebel, diese infame Lüge ist an Unverschämtheit kaum zu überbieten. Nichtmal meine hier gezeigte Excel-Grafik mit konstanter Emission von 11,3 GtC/a ab 2025 haben Sie angesehen. Haben Sie etwa Physik auf einer Baumschule studiert so dass Sie mein elementares sequentielles Rechenverfahren mit KONSTANTEM Tau55 trotz [9] und die damit berechneten Kurven für den emissionsabhängigen ppm-Anstieg nicht verstehen??
Bezieht man aber den Verbleib in der Atmosphäre auf den gesamten Quellfluss, wie er sich aus der Rechnung ergibt (s. Tab. 1, Spalte 2), dann sind es nur noch 10 %.
Herr Mechtel, Sie kommen zu dieser Aussage wenn 2015 die anthropogene Emission 33,7 GtCO2 ist und der Senkenfluss 53% beträgt, also 17,9 Gt. Das sind – wenn Sie die beiden Emissionen zu 178,8 Gt addieren – 10% davon.
Das Tolle daran ist dass von Ihrer Zusatzemission sofort zu 100% in die Senken geht, also ohne Rücksicht auf ihre Zeitkonstante von 20 Jahren. Hierbei ist auch noch Ihr Senkenfluss grob falsch. Der müsste nämlich Inventar/Tau, also (412-280)/20•7,78=51,3 GtCO2 sein. Sie sollten sich dafür entschuldigen, uns bei EIKE solchen Unsinn zu präsentieren.
Etwa 17,9 Gt Senkenfluss ergeben sich wenn man mit Tau=57 Jahren (!!) rechnet! Sie behaupten aber, 20 Jahre zu verwenden.
Eike Roth schrieb am Reply to Michael Mechtel 8. Mai 2025 18:52
Da ist wieder das klassische Problem, dass zwei Zeiten bunt durcheinandergeworfen werde. 14C lieferte nur eine Information darüber, wie lange ein einzelnes CO2-Molekül in der Atmosphäre verweilt, bevor es durch eines aus den Ozeanen ersetzt wird. Dabei fällt der CO2-Gehalt der Atmosphäre nicht. Dieser Austausch fand auch statt, als der Kohlenstoffkreislauf die Atmosphäre bei etwa 280ppm hielt und das über lange Zeit.
Sinken tut der CO2-Gehalt nur, wenn CO2 in den langsamen Kohlestoffkreislauf wechselt, z.B. in tiefere Ozeanschichten absinkt, biologisch gebundenes C unter Luftabschluss gerät und zu Kohle/Erdöl/Erdgas wird oder in Kalk gebunden und als Sediment abgelagert wird. Und das sind Vorgänge, die lange dauern. darauf beziehen sich die langen Zeitangaben …
In diesen rein auf Kurvenfitting basierenden Diskussionen ist davon nichts zu sehen, da kann man mit ausreichend vielen parametern beliebiges Verhalten modellieren, ..
Dieser langsame Kreislauf soll Einflusss auf die CO2 Konzentration in der Luft haben? Wie soll das gehen?
Und gilt diese Zeitkonstante fuer alles CO2? Also auch das von der Natur emittierte?
Werner Schulz Reply to Marvin Müller 16. Mai 2025 8:44
Brauchen Sie echt jemanden, der Ihnen erklärt, wie Photosynthese, Stoffwechsel, Kalkschalenbildung funktioniert und wo das dabei verwendete CO2 herkommt?
Wie oft wollen Sie mich noch frage, ob natürliches und anthropogenes CO2 unterschiedlich behandelt werden? Können Sie sich die Antwort nicht einfach mal merken?
Sie denken also das die Algen im Meer das CO2 aus der Luft aufnehmen und nicht aus dem im Wasser geloesten CO2?
Und wie ist denn nun die Antwort ob sogenanntes Antropogenes CO2 eine andere Zeitkonstante hat oder nicht?
Werner Schulz Reply to Marvin Müller 16. Mai 2025 12:08
Nein.
Habe ich Ihnen schon oft gegeben (sogar in der letzten Woche mindestens einmal), werde ich hier nicht wiederholen, da Sie es sich offensichtlich eh nicht merken.
Sie haben mir wine Zeitkonstante gegeben fur natürliches CO2? Also gibt es verschiedene? Da sie sonst immer einen Link finden . . .
Bitte helfen sie!
Oder stimmen sie damit überein:
Herr Ebel sagt, das ist Unsinn, das sehe ich genau so. Was sagen sie?
Werner Schulz Reply to Marvin Müller 16. Mai 2025 23:20
Nein. Ich habe Ihre Frage „Und gilt diese Zeitkonstante fuer alles CO2? Also auch das von der Natur emittierte?“ mit „Wie oft wollen Sie mich noch fragen, ob natürliches und anthropogenes CO2 unterschiedlich behandelt werden?“ beantwortet. Alles andere sind nur Variationen dieser Frage.
Ich sehe nur, dass Herr Dietze und Herr Ebel über verschiedene Dinge reden und bei der Betrachtung den Schwerpunkt auf verschiedene Dinge legen. Bei Herrn Dietze ist der Senkenfluss das, was aus dem schnellen Kohlenstoffkreislauf verschwindet und damit den CO2-Gehalt der Atmosphäre reduziert. Bei Herrn Ebel ist es der Fluss innerhalb des schnellen Kohlenstoffkreislaufes. Und da kann man prima aneinander vorbeireden, was Sie gerade wieder fröhlich ausnutzen.
Also haben sie die Frage nicht beantwortet! Ich stelle dann fest die Natur behandelt anthropogene und CO2 aus natürlichen Quellen gleich.
Werner Schulz Reply to Marvin Müller 17. Mai 2025 16:55
Was genau das ist, was Sie von mir lesen konnten, als wir kürzlich über die airborne fraction gesprochen hatten. Können Sie sich das jetzt länger als ein par Stunden merken?
Also gibt es keine separate Zeitkonstante fuer natuerliches CO2 und antropogenes!
Ich verfolge das sich Herr Ebel und Herr Dietze hier nicht einig sind.
Es ist sehr bezeichnend für das Thema, das es keinen Konsensus gibt.
„Bei Herrn Dietze ist der Senkenfluss das, was aus dem schnellen Kohlenstoffkreislauf verschwindet und damit den CO2-Gehalt der Atmosphäre reduziert. Bei Herrn Ebel ist es der Fluss innerhalb des schnellen Kohlenstoffkreislaufes“.
Danke Herr Müller, Sie bringen das aneinander Vorbeireden auf den Punkt. Was Herr Ebel offenbar und Dr. Roth sicher betrachtet, ist der große Kreisfluss [9, Abb.1], weshalb da auch fälschlich die kurze „turnover time“ von nur etwa 4 Jahren statt meinem Tau55 ins Spiel kommt. Und die Mechtel-Rechenwerte mit Tau20 von C14 sowie seine Zusatzquellen müssen wir gänzlich ausklammern.
Das Hauptproblem beim Tau-Mißverständnis ist dass der riesige natürliche Kreisfluss auch in eine Senke (!) geht, aber wieder ausgegast wird, jedoch der anthropogene Senkenfluss mehrere hundert Jahre NICHT wieder ausgegast wird und daher getrennt (!) behandelt werden muss. Die Natur müsse doch anthropogenes CO2 gleich behandeln, ist ein falsches Primitivargument, denn das dauert noch einige hundert Jahre.
Die anthropogene Emission erhöht derzeit ppm sowie den Eintrag und vermindert die Ausgasung. Das ergibt unsere Senke und deshalb ist auch die separate Behandlung des anthropogenen Inventars ab 280 ppm nötig, welches dividiert durch den von uns bedingten Anteil (!) der Senkenflüsse Tau55 ergibt – daher die Nachrechnung der Keelingkurve. Nur Tau55 kann die anthropogenen ppm-Änderungen liefern und darf auf keinen Fall mit der Umwälzzeit von 4 a (die für ppm-Berechnungen irrelevant ist) verwechselt werden. Dann entstehen auch nicht die riesigen zusätzlichen Quellflüsse.
Eingie hundert Jahre fuer was?
Und wie kann der
werden, aber gleichzeitig sagen sie, das
Das ist unlogisch!
Werner Schulz Reply to Peter Dietze 19. Mai 2025 9:03
Schauen Sie sich einfach an, was mit dem CO2 passiert, wenn es vom Ozean absorbiert wird und dann ins Tiefenwasser der AMOC absinkt. Dann verstehen Sie vielleicht, was Herr Dietze meint.
Das Freisetzen von CO2 durch uns und das Freisetzen durch die Ozeane sind zwei seperat laufende Dinge. Warum sollte da ein Widerspruch sein, dass unser Aktivitäten den CO2-Gehalt der Atmosphäre erhöhen?
Viel spannender ist die Frage, was passiert, wenn das CO2-reichere Wasser in einigen 100 Jahren wieder auftaucht …
Also das menschliche CO2 das fuer ueber hundert Jahre in den Tiefenwaessern der Ozeane versinkt, reichert gleichzeitig die Atmosphaere an? Und wieviel CO2 steckt in den Tiefenwaessern, die in einem separaten Prozess CO2 in die Atmosphaere einbringen?
Wievel CO2 kommt denn da genau? Koennen sie ein paar Zahlen in Giga Tonnen nennen? Oder ist dieser natuerliche „Kreislauf“, also eigentlich die nicht bestimmte Menge von CO2 uninteressant? Warum?
Wenn die Natur 100% Emittiert und 100% versenkt. Wo ist der Unterschied ob es 50 Gigatonnen sind oder 100 Gigatonnen?
Woher weiss die Natur was 100% ist? Woher wissen wir wie hoch 100% sind?
Peter Dietze 19. Mai 2025 7:13
So ein Unsinn. Tragen etwa die anthropogenen CO2-Molküle ein Schild um den Hals „Ich bin ein anthropogenes CO2-Molekül und beanspruche deswegen eine Sonderbehandlung“??? Sie nehmen natürlich sofort am Kreislauf teil (Jochen Ebel 18. Mai 2025 16:49). Da gibt es keine Sonderbehandlung bei Konzentrationen über 280 ppmV. Lediglich beim Startwert (1940) wird der Ozeaninhalt von 280 ppmV berücksichtigt.
Das Ganze ist sowieso etwas komplizierter. Siehe
https://de.wikipedia.org/wiki/Temperaturleitf%C3%A4higkeit
Bei Diffusion auf Grund eines temporären Konzentrationsgefälles.
Die Temperaturleitfähigkeit und die Diffusionskonstanten haben die gleiche Bedeutung
Luft 20 mm²/s
Wasser 0,14 mm²/s
https://de.wikipedia.org/wiki/Diffusionskoeffizient
Sauerstoff in Wasser 2,1 × 10−9 m²/s
Wenn man bedenkt wie tief ins Wasser die sommerliche Temperaturänderung reicht, dann ist verständlich, daß bei einem viel kleineren Diffusionskoeffizienten nur ein geringes Volumen (V = 0,79) statt des ganzen Ozeans für die CO2-Senke wirksam wird.
Also ist Ihre Senkenannahme falsch [9]:
In dem geringen beteiligten Volumen + Atmosphäre verbleibt deshalb fast die gesamte anthropogene Emission. Der Abfluß aus dem beteiligten Volumen in tiefere Schichten verringert zwar prinzipiell die Gesamtmenge – aber der Abfluß ist so gering, das er unberücksichtigt bleiben kann.
Genauer kann man rechnen – aber wie genau ist sinnvoll? Es müßten dann Wellenbewegung, Strömungen usw. berücksichtigt werden. Die vereinfachte Rechnung mit beteiligtem Volumen und Senkengeschwindigkeit proportional zur Druckdifferenz erscheinen mir genau genug.
Herr Ebel, haben Sie denn immer noch nicht geschnallt dass der aktuelle Senkenfluss mit viel CO2 zwar absorbiert, aber lange Zeit nicht ausgegast wird? Das geschieht erst nach 600 Jahren, weshalb es ja überhaupt nur eine anthropogene Netto-Senke gibt. Da es sich um ein weitgehend lineares System handelt, ist der natürliche 280-ppm-Kreisfluss dem übrigen Geschehen nur additiv überlagert (Systemtheorie, Regelungstechnik).
Deshalb kann man (ohne dass die CO2-Moleküle ein Schild um den Hals haben) die anthropogene Störung getrennt behandeln. Und so wie ich es mache (AnthroInventar / Tau55 = AnthroSenkenfluss) kommt ja auch das Richtige heraus, und zwar ohne Fake-Quelle – das habe ich ja Herrn Mechtel vorgerechnet.
Und was die Senkenkapazität der Ozeane angeht, die ist aufgrund des immensen Drucks vom kalten Tiefenwasser und dessen Stömungen (Ihre Diffusion können Sie vergessen) in der Tat gigantisch so dass unser Senkenfluss da selbst über hundert Jahre kaum auffällt.
Peter Dietze 19. Mai 2025 17:19
„aber lange Zeit nicht ausgegast wird“
Herr Dietze, Sie haben immer noch nicht begriffen, das das ständige Ausgasen Bestandteil des Entropiezuwachses ist (Eike Roth 18. Mai 2025 21:57 Punkt 2e…g).
Herr Schulz, die Zeitkonstante Tau ist (anthropogenes) Atmosphäreninventar/Senkenfluss. Beim natürlichen Kreisfluss (bei 280 ppm) ist der Senkenfluss Null und Tau unendlich.
Peter Dietze 16. Mai 2025 15:04
Merken Sie bei solchen Feststellungen nicht selbst, daß Sie Unsinn schreiben? Die Vorgänge Lösung und Austausch können nicht so einfach mit einer Zeitkonstante, die sich noch dazu ändern soll, beschrieben werden.
Herr Ebel, der Unsinn liegt nur bei Ihnen. Ein Kreisfluss hat Null Senkenfluss, und daher die 1/e-Zeitkonstante unendlich. Und für die Berechnung des ppm-Verlaufs in der Atmosphäre ist doch einzig der Senkenfluss nötig (also Inventar/Tau), denn ich kenne doch die Emission und auch die 2,123 GtC pro ppm. Traurig dass man das einem Physiker erklären muss – der dazu noch meint dass jemand der Unsinn produziert, eine korrekte Modellrechnung vorweisen kann.
Peter Dietze 16. Mai 2025 20:19
Das ist falsch, denn bei einem Kreisfluss ist der Eintrag in die Senke genau so groß wie die Emission. Denn „fluss“ heißt das da etwas fliest und der Kreislauf nicht 0 ist.
Herr Ebel, der Senkenfluss ist Eintrag – Ausgasung, und das ergibt beim Kreisfluss NULL. Und Inventar / NULL ist unendlich.
Ist der Senkenfluss nicht die Emission minus den Rest aus der Emission der in der Atmosphäre verbleibt?
Eintrag – Ausgasung = Senkenfluss = Emission – Verbleib
Ist Eintrag nicht gleich Emission? Und wäre dann nicht die Ausgasung = Verbleib?
Stimmt das?
Sehe ich genau wie sie Herr Ebel.
Wie kann es zu so seltsamen Auswüchsen kommen, von wer weiss was nicht und jeder weiss was Anderes?
Ausser das ich dann nichts weiss, weil wie soll man denn allein aus ihrer Diskussion mit Herrn Dietze entnehmen was jetzt stimmt?
„..dass der unbekannte Quellzufluss bis heute mindestens viermal größer war als der zivilisationsbedingte, im Schnitt über den Auswertezeitraum rund sechsmal größer. Menschliche Aktivität spielte demzufolge mit weniger als 15 % Anteil nur eine untergeordnete Rolle im beobachteten CO2-Anstieg der Atmosphäre“.
Herr Mechtel, Ihre Berechnung ist fälschlich basiert auf der (wegen Verdünnung des C14 von Atombombentests durch Austausch mit Ozeanen und Biomasse) viel zu geringen 1/e-Zeitkonstanten von 20 Jahren. Den Senkenfluss des anthropogenen CO2, dessen Zeitkonstante real etwa 55 a beträgt, berechnen Sie um den Faktor 2,75 zu hoch, woraus Sie eine viel höhere, nirgends nachgewiesene natürliche zusätzliche Quelle herleiten, obwohl doch Ozeane und Biomasse aufgrund des ppm-Anstiegs Senken sind, welche derzeit schon etwa 60% unserer Emission aufnehmen.
Eine Dokumentation des C-Modells mitsamt dem sich beim anthropogenen Emissionsverlauf und den zu ppm-280 proportionalen Senkenflüssen ergebenden ppm-Anstieg seit 1840 finden Sie unter http://www.fachinfo.eu/dietze2020.pdf
Herr Dietze, Ihre Arbeit, die Sie hier verlinken, habe ich in meinem Artikel zitiert (Quelle [9])!
In der Tat arbeitet die Natur als Senke für das anthropogen emittierte CO2, gleichzeitig aber auch als Quelle für das Gesamtinventar an CO2 in der Atmosphäre. Das ist ein etwas subtiler Punkt, den Eike Roth schon mehrfach diskutiert hat, z.B. in [5] und [8], und der sich aus meiner Betrachtung ganz zwanglos ergibt.
Herr Mechtel, schön dass Sie meine Arbeit [9] zitiert haben. Ich frage mich aber ob Sie meine Berechnung mit tau=55 a ohne fiktive ansteigende natürliche Zusatzemission (!!) mit (bei linearen Systemen zulässiger) Ausklammerung des Naturkreislaufs bei 280 ppm akzeptiert haben. Denn dass man eine Arbeit zitiert welche das eigene Modell ad absurdum führt, ist recht ungewöhnlich.
Ich habe Ihre Arbeit im Anhang zitiert, und zwar genau im Zusammenhang mit einer Kritik des 280-ppm-Wertes als unumstößliches Gleichgewichts-Niveau und der daraus sich ergebenden hohen Zeitkonstanten. Deren Wert spielt in der Tat eine entscheidende Rolle für die Höhe des zusätzlichen Quellstroms, was meine Tabelle 2 zeigt.
Ich sehe keinen Grund, warum man dem 280-ppm-Niveau irgendwie eine Sonderstellung einräumen sollte, von dem sich die Natur nicht auch entfernen könnte. Dabei würde sicher dem Ozean eine entscheidende Rolle zukommen.
Das durch die Kernwaffentests freigesetzte 14CO2 ist ein Zusatzeintrag in die Atmosphäre wie das anthropogene 12CO2 auch oder die Zusatzquelle, die sich aus meinem Rechenansatz ergibt. Diese Einträge sollten deshalb auch alle gleich zu behandeln sein, also der gleichen Abklingkonstante unterliegen.
Einfach mal da schauen. Die Delta-C13 Werte und O2-Werte und anthropogen Emissionen zeigen, woher die Erhöhung kommt.
Herr Krüger, so einfach ist das gewiss nicht! Dass O2 relativ abnimmt, ist per se nicht verwunderlich, denn es wird ja Kohlenstoff verbrannt. Es kommt auf die Quantität der Abnahme an, und da ist die Skala im Diagramm für mich leider nicht interpretierbar.
Im unteren Bild das gleiche: man darf sich von dem optischen Parallelverlauf nicht täuschen lassen, der lässt sich durch Wahl der 13C-Skala leicht herstellen. Quantitativ lässt sich der Graphik aber entnehmen, dass die 13CO2-Änderung erheblich geringer ist als die Gesamt-CO2-Änderung, und deshalb sehe ich keinen Widerspruch zu meinem Befund.
O2 und Delta-C13 Änderung tritt vor allem durch Verbrennung von foss. Kohlenstoff auf. Fragt sich, was da verbrannt wurde, wenn es nicht anthropogen sein soll.
Klar ist die Verbrennung von fossilem Kohlenstoff im wesentlichen anthropogen. Aber im Gesamtkreislauf eben nicht sehr bedeutend.
Und gibt es Probleme mit C12/C13?
Scientist Uncovers Miscalculation In Geological Undersea Record
https://www.sciencedaily.com/releases/2008/09/080910104202.htm
Den Fischen kann man nicht vertrauen:
https://web.archive.org/web/20090213055621/http://environmentalresearchweb.org/cws/article/research/37370
Isotopic Identification Of Leakage Gas From Underground Storage Reservoirs- A Progress Report: Es scheint Methanauscheidende Bakterien machen es sehr schwer Untergrundgas von natuerlichen Methan zu unterscheiden.
https://onepetro.org/SPEMGS/proceedings-abstract/77MGS/All-77MGS/SPE-6491-MS/139098
@ Krüger 7. Mai 2025 19:24
Und warum wurde die Delta-13C Kurve invertiert? Eigentlich müsste diese Kurve nämlich so aussehen:
U. Weber Reply to Michael Krüger 8. Mai 2025 12:32
Das steht doch in der Beschriftung des Diagrams: „Note that this scale is inverted to improve clarity„. In der Beschriftung Ihres Diagramms …
Nein, bei Herrn Krüger ist es normal dargestellt, in Ihrem Diagramm invertiert …
Delta-C13 ist halt so aufgetragen, wie es sich bei Verbrennung foss. Kohlenstoffe verhält.
Vor allem foss. Kohlenstoffe erzeugen bei Verbrennung eine solche Signatur.
Welche Signatur, die invertierte oder die rückinvertierte?
Biogener Kohlenstoff (organisch)Biogener Kohlenstoff stammt aus lebenden oder ehemals lebenden Organismen. Die δ¹³C-Werte variieren je nach Quelle:
Vulkanischer Kohlenstoff (magmatisch)
Vulkanische CO₂-Emissionen können unterschiedliche δ¹³C-Werte aufweisen, abhängig von der Quelle:
Diese Werte variieren je nach geologischer Aktivität und Zusammensetzung der Emissionen.
Geogener Kohlenstoff (fossil)Geogener Kohlenstoff stammt aus fossilen Quellen wie Erdöl, Erdgas oder Kohle:
PS
Wenn man Erdöl, Erdgas, Kohle, oder Holz von Bäumen verbrennt, ergibt das also die größte Signatur bei der Freisetzung von CO2 und C13. So ist das auch aufgetragen.
Quelle?
Marvin, alter IPCC-Gatekeeper, was soll das Geschwafel? Ich hatte den Originaltext zur Delta-C13 Kurve doch sogar noch zu Deinem Verständnis in die Grafik hineinkopiert, und da steht laut und deutlich:
Und Du bist jetzt also tatsächlich der Meinung, dass lediglich die Achsenbeschriftung invertiert wurde und der Kurvenverlauf dort korrekt dargestellt worden ist – im Ernst jetzt?
Und komm‘ mir ja nicht damit, dass bei meiner „Rückinversion“ die Achsenbeschriftung jetzt auf dem Kopf steht…
U. Weber Reply to Marvin Müller 8. Mai 2025 13:42
U. Weber Reply to Marvin Müller 8. Mai 2025 13:42
Da haben Sie mich aufs Glatteis geführt. Ich habe die (wie ich jetzt erkenne) von Ihnen gespiegelte Grafik gesehen und den Text gelesen und natürlich gedacht, dass sich der Text auf die offensichtlich gespiegelte Darstellung bezieht. Ich habe nicht gesehen, dass es auch am Original steht. Mein Fehler …
Das „invertiert“ bezieht sich auf die Y-Achse, die im Original statt von -8,1 zu -7,6 ansteigend von -7,6 zu -8,1 absteigend beschriftet ist. Wenn ich einen Grund vermuten sollte, würde ich annehmen, dass die die gleichlaufende Erhöhung des einen und Verringerung des anderen anschaulich machen wollten …
Die y-Skalierung wird so gezeigt, da foss. Delta-C13 vom Wert einfach stärker negativ ist, als zB vulkanisches. Mit Verbrennung von foss. Kohlenstoff sinkt der Wert weiter ins Negative.
PS
Mann kann das aber auch so darstellen, wie Herr Weber.
Danke, hier werden die Zusammenhänge klar. Bei zielgerichtet desingten Grafiken werde ich immer mißtrauisch:
Einen hab ich noch.
Komisch, man sieht die natuerlichen Variationen, fast so als wenn ein natuerlicher Prozess fuer die Veraenderung verantwortlich ist.
Waere es der Mensch muesste es linear sein, oder?
Der Jahresgang koomt duch die Vegetation. Der Trend nach oben und unten durch Verbrennung foss. Kohlenstoffs.
Wie stellt sich den der Verbrauch im Jahresgang dar? Macht er auch diese Kurven?
So sieht der Jahresgang aus als wenn er den natuerlichen Wandlungen folgt.
Wie gesagt, der menschliche Einfluss muss die gleichen Schwankungen haben. Hat er diese?
Gibt es lokale Unterschiede? Was wir sehen ist der Suedpol, richtig?
Sieht mann alles in der Abbildung. Jahresgang durch Vegetation/ Jahreszeiten auf der SH und langfristiger Trend nach oben CO2 und unten Delta-C13.
Wenn die natuerlichen Prozess das Delta C13 nicht beeinflussen, dann sollte die Kurve fuer Delta C13 nicht mit den natuerlichen Prozesse korrelieren. Tut sie aber.
Warum?
Ich habe weiter oben die Quellen und Werte für niedrige Delta-C13 Werte aufgelistet. Büsche und Bäume werfen halt jedes Jahr Laub ab. Gemäß Vegetationsperiode. Das ist die Sinuskurve auf den ansteigenden und abfallenden Verlauf, der durch Verbrennung foss. Kohlenstoffs verursacht wird. Sieht eigentlich jeder.
Herr Krueger,
gemittelt werfen die Büsche und Bäume immer Laub ab.
Also gibt es andere Werte am Suedpol als am Nordpol?
Es muss ja dann mit den seasonalen Zyklus im Einklang sein.
Heisst das dann auch das die Signatur von der Verbrennung von Oel, Gas und Kohle nur Seasonal in den Daten auftaucht, weil es lokal ist?
Was ist mit der guten Durchmischung von der Atmosphaere? Ist das zu vereinfacht?
Kann man in der natuerliche Variation vom C13 den Einfluss vom Menschen sehen? Wie?
Hatte ich alles erklärt. Mehrfach. Sie sind ein hoffnungsloser Fall wenn Sie das nicht sehen. Oder machen das absichtlich aus Schabernack. Im CO2-Anstieg beim Mauna Loa ist auch der Jahresgang der Vegetation drin. NH.
?
Was haben sie erklaert?
Nichts haben sie erklaert.
Weder gehen sie auf die Diskrepanz ein von den CO2 Messungen am Suedpol, die gegensaetzlich sind von den an Mauna Loa, noch erklaeren sie, wie man aus den natuerlichen Variationen, die ich offensichlich erkennen kann, den menschlichen Einfluss rauslesen kann.
Ich habe mich mal auf Spurensuche begeben um bekannte Informationen zu konkretisieren. Nahezu alle „Verarbeiter“ von CO2 haben eine Präferenz auf das C12-Isotop, soweit war mir bekannt. Angesichts der Tatsache das es einen Zuwachs, CO2-Bedingt, der globalen Vegetation gibt, stellte sich die Frage, erstens wie funktioniert denn überhaupt der vegetative „Filter“ um dieser Bevorzugung Rechnung zu tragen und was gibt es an konkreten Studien darüber.
Denn eine Zunahme der Vegetation würde sich auch ganz konkret auf den DeltaC13-Wert auswirken, welches gemeinhin als Beleg ausschließlich athropogenen Emissionen zugeschrieben wird, nämlich in gleicher Weise das der Wert sich verringert.
Zu ersterem, der/des Filtermechanismus, liegen die Kenntnisse noch weitestgehend im Nebel der Unkenntnis verborgen, einzig die Nachweise existieren das es eine Tatsache darstellt das Grünzeugs eine Vorliebe für C12 besitzt.
Wie bei dem gesamten Themenkomplex immer wieder anzutreffen, nichts genaues wissen wir nicht, aber wir sind uns sicher der Mensch hat schuld.
Und wie man anhand verfügbarer Studien und deren Veröffentlichungsdaten erkennen kann, scheint es diesbezüglich aktuell wenig „Bedarf“ zu geben nähere Erkenntnisse zu erlangen, vielleicht liegt es ja auch daran das man damit dem kritischen Zeitgenossen kein „Futter“ geben möchte, wer weiss das schon.
„Carbon isotopes in plants: Their role in research and applications“ von Patricia M. A. J. Becker & David H. L. Carriquiry.
Diese Studie befasst sich mit den Methoden zur Analyse von Kohlenstoffisotopen in Pflanzen und deren Anwendung in der Forschung, einschließlich der Bestimmung der Photosynthese-Pfade.
„Variability in carbon isotope compositions of C3 and C4 species“ von O. A. M. Podesto & J. N. Jones (2006)
Diese Arbeit untersucht, wie Umweltbedingungen (z.B. Licht, Temperatur, CO₂-Konzentration) die Isotopenverhältnisse in C3- und C4-Pflanzen beeinflussen und zeigt die Bevorzugung von ^12C.
„Carbon isotope discrimination in C3 and C4 plants“ von Farquhar et al. (1989).
Diese grundlegende Studie analysiert, wie sich C3- und C4-Pflanzen in Bezug auf Kohlenstoffisotopenverhältnisse unterscheiden und liefert wichtige konzeptionelle Grundlagen zur Verständnis der Isotopendiskriminierung.
„Global patterns of carbon isotope discrimination in plants“ von D. P. Schimel et al. (2003).
Diese Studie analysiert globale Muster der Kohlenstoffisotopendiskriminierung und deren Implikationen für die Kohlenstoffdynamik in Ökosystemen.
„Plant physiological ecology and carbon isotope composition“ von G. D. Farquhar, J. R. Ehleringer, & K. A. Hubick (1989).
Dies ist ein weiterer grundlegender Artikel, der sich mit den physiologischen Faktoren befasst, die die Kohlenstoffisotopesignaturen in Pflanzen bestimmen, und er misst, wie Rubisco und andere Enzyme auf die Isotopenverhältnisse einwirken.
„Variability of stable carbon isotope discrimination and its relationship with plant productivity in some C3 and C4 species“ von Araus et al. (1997).
Diese Untersuchung in landwirtschaftlichen Zusammenhang betrachtet die Variabilität in der isotopischen Diskriminierung und den Zusammenhang zur Produktivität in C3- und C4-Pflanzen.
Ne Menge Material zum Lesen. Vielleicht hat das ja schon mal einer zusammengefasst?
Egal wie rum die Kurve steht, irgendeine Bezugnahme auf den/die δ¹³C-Werte zur Definition von Quellen verbietet sich aufgrund der hohen Fehleranfälligkeit einer direkten Zuordnung:
Hinzu kommen bekannte Probleme bei der Analyse:
Insgesamt sind irgendwelche tatsächlichen Zusammenhänge und exakte Zuordnungen zu einer/wenigen Quellen in Bezug auf aktuelle Emissionen nicht darstellbar. Anders verhält es sich dagegen bei Analysen paläoklimatologischer Proben und deren Daten, sofern diese als sicher nicht kontaminiert anzusehen sind.
Hier mal eine Übersicht.
Und was soll mir dieses Bildchen vermitteln? Das irgendwer für diese abstrakte Malerei seiner Vermutungen/Behauptungen Forschungsförderung kassiert hat. Diese Abbildung ist nicht mehr und auch nicht weniger als ein Museter ohne Wert, wahrscheinlich auch nur deshalb entstanden um in irgendeinem Modell die diesbezüglichen Parametrisierungen zu rechtfertigen. Wenn Sie gelesen hätten was ich bezüglich der Fehleranfälligkeit geschrieben habe, dann käme Ihnen kaumm in den Sinn irgendwem davon überzeugen zu wollen, „wir wissen genau was passiert“. Nichts genaues weiß man nicht, kann man auch nicht wissen aufgrund der Komplexität alleine dieser Fragestellung, aber wir versuchen es trotzdem mal vielleicht klappt es ja. Ein typisches Phänomen der „Klimawissenschaften“, in anderen Disziplinen ist mir solch eine Einstellung noch nie unter gekommen.
Vor meinem inneren Auge erscheint dann immer ein Bild welches ich so beschreiben möchte: Ich stehe mit Kollegen am Bett eines Patienten und wir diskutieren heftigst darüber ob die Häm-Gruppe des Hämoglobin in einem Erythrozyten eine 95 oder 99%tige Sauerstoffsättigung hat, derweil dämmert der Patient nebenbei mit seinem Loch in der Brust so langsam in die ewigen Jagdgründe hinüber. Will damit sagen, diese beständige Streiterei über kleinstteilige Komponenten, noch dazu wenn deren wertmäßige Zuordnung mehr kritische Fragen aufwirft als Lösungen anbietet, eines Hochkomplexen Systems bringen niemanden irgendeiner sachdienlichen Lösung näher, aber wir fühlen uns mächtig klug und wichtig dabei. 🙁
Michael Krüger 7. Mai 2025 19:24
Etwas bessere Qualität: https://www.researchgate.net/figure/Recent-CO-2-concentrations-and-emissions-a-CO-2-concentrations-monthly-averages_fig4_241825624 und Übersetzung der Bildunterschrift:
Ein etwas anderes CO2-Gedankenspiel:
Angenommen die Erde kennt nicht diejenige Physik, mit der fleißig CO2-Klima-Alarm betrieben wird und sie hätte nur über KGI (Künstliche-Globus-Intelligenz) erfahren, dass die Sonne sie über Strahlung erwärmt, sie diese Strahlung über den gesamten Tag-Nachtverlauf wieder abgibt und sie sich dadurch nicht in einen immer heißer werdenden oder einen bis Richtung absolutem Nullpunkt abkühlenden Planeten verwandelt.
Sie weiß auch, dass es auf ihr Menschen gibt, die sich mit einer gigantischen Rechnerei zu ungerechtfertigten Vorteilen verholfen haben, und sie weiß auch, dass sich die Menschen in Staaten organisiert haben und viele beeindruckt von diesen Rechnereien immense Gelder verschieben, insbesondere in Form von sog. Steuern.
Nun hat sie sich über die KGI erklären lassen, dass die von ihr kontinuierlich über Strahlung abgegebene Wärme sich auf den Weg in Richtung All aufmacht. Warum sie die Wärme abgibt, versteht sie zwar nicht, aber sie hat den Drang genau so viel Wärme über 24 Stunden los zu werden, wie sie über 24 Stunden empfangen hat. Und das tut sie seit Millionen Jahren erfolgreich.
Ein paar ganz schlaue Menschen haben entdeckt, dass das böse CO2 teilweise den Weg der Wärme ins All versperrt und diese wieder teilweise auf die Erde zurück strahlt. Kaum kommt sie da an, soll die Erde nun diese zurück gekehrte Wärme irgendwie kennzeichnen und sie sozusagen gebrandmarkt dort behalten und plötzlich vergessen, dass es doch genau diejenige Wärme ist, die sie gerade zuvor noch loswerden wollte.
Sie versteht trotz Hilferuf an die KGI nicht, warum sie einzig rückgestrahlte Wärme nicht sofort wieder auf den Weg in Richtung All schickt, sie hat doch immer noch den Drang, sie los zu werden wie gerade kurz zuvor und sie hat sich doch nur durch das böse CO2 verirrt. Was da zurück gestrahlt worden ist, ist doch keine zusätzliche Energie, sondern nur solche, die kurz zuvor auch schon da war, die KGI hat das bestätigt.
Und als Erde tut sie einzig das richtige, sie schickt sie zum zweiten Mal los, und wenn es sein muss, auch noch ein drittes und viertes Mal, bis sie den Weg ins All gefunden hat. Die KGI hat ihr gesagt, dass auch CO2-Moleküle müde werden und nicht überall gleichzeitig sein können, der Fluchtweg ins All ist nur punktuell besetzt und so durchlässig wie ein großmaschiges Sieb.
Und das tut sie, weil in den irdischen Genen der Drang verankert ist, genau das an Wärme mit jeder 24-Stunden-Drehung wieder los zu werden, was sie in dieser Zeit von der Sonne empfangen hat. Ihre KGI hat ihr auch gesagt, dass sie von Glück reden kann, dass sie die Sonne in einem Abstand umkreist, der gerade so groß ist, dass sie dem energetischen Nimmersatt Weltall immer so viel Energie der Sonneneinstrahlung wieder abgibt, dass sie einen für Menschen angenehmen und lebensfähigen Wärmehaushalt hat, der sich nur mit den Jahreszeiten aufgrund der Erdachsenneigung zyklisch verändert.
Größere oder kleinere Entfernungen würden die Erde so kalt oder so heiß machen, dass kein Leben möglich wäre. Die KGI hat ihr geholfen zu zählen, wie oft denn überhaupt von CO2-Molekülen Wärme rückgestrahlt werden kann, um dann direkt wieder in Richtung All geschickt zu werden und wie lange die rückgestrahlte Wärme im Boden oder den Meeren überhaupt verbleibt, bis sie eine Lücke im CO2-Dach zum Entkommen gefunden hat. Über ein paar Millisekunden ist die KGI da nicht hinaus gekommen, sie sagt aber gleich dazu, dass ein gewisser E. Mann die zugänglichen Messwerte derart geschunden und verbogen hat, dass an der Umlenkung von Geldströmen Interessierte daraus einen Temperaturverlauf in Form eines Hockey-Schlägers geformt haben, mit der die Welt in Angst und Schrecken vor einer drohenden Verbrennung (Selbstverbrennung nach Schellnhuber, J.) gesetzt werden sollte.
Schließlich sagt die KGI noch, dass sie sich für Temperaturen gar nicht interessiert, sondern einzig für Energie und damit Wärme. Als es die Menschen noch nicht gab und das Thermometer noch nicht erfunden war, gab es ja auch keine Temperaturen, sondern einzig Wärme. Und trotzdem hat der ausgeglichene Wärmehaushalt Tag für Tag funktioniert. Und sie sagt auch mit der ihr eigenen Sicherheit: So etwas wie Global-Temperaturen gibt es ohnehin nicht, das ist eine Erfindung, die keine technische Lehre oder Anwendung beinhaltet und nur den unsinnigen Versuch verfolgt, mich, dieses komplexe Wunder „Erde“, über eine einzige blödsinnige Zahl zu beschreiben.
– Als die KGI erkannte, wie einfältig und dumm bestimmte nur auf ihre Eitelkeit und ihren eigenen Vorteil gerichtete Menschen sind, verabschiedete sie sich und zog selbst ihren Stecker raus. –
100% wahr. Durch eine wiederholte spektrale Wellenlängenreduktion ist die Atmosphere praktisch immer transparent! Es geht nur um die Zeitkonstante bei der Nachtabkühlung der Erdopberfläche. Und die findet über Konvektion statt. Die Strahlungskühlung ist vergleichsweise vernachlässigbar. Drum haben Satelliten Kühlprobleme und Motoren verwenden Kühlflüssigkeit und Gebläse. Die ganzen Treibhausfritzen wollen mit ihren Dschungelrechnungen lediglich von der simplen Tatsache des Ersten Hauptsatzes der Thermodynamik ablenken. Um Gotteswillen nur nicht das Wort Entropie verwenden. Auch bei 2000ppm hatte das Leben auf der Erde schon geblüht und nichts ist den Hitzetod gestorben!
Das ist schon mal falsch. Hinsichtlich der Senke Ozeane ist die Differenz des CO2 Partialdrucks in den jeweiligen Medien entscheidend. Was die Biosphäre angeht, so steigt die CO2 Aufnahme jedenfalls nur graduell mit der CO2 Konzentration in der Atmosphäre. Keine Ahnung wie es mit Gestein aussieht, aber so oder so existiert da nirgends eine „Proportionalität„.
Jetzt muss man aber sowieso unterschieden zwischen Senken, also der Netto-Absorption atmosphärischen CO2s, und CO2 Kreisläufen. Wie rasch sich die Konzentration von (hinzugefügten-) CO2 Isotopen ändert, hängt von der Rate dieser Kreisläufe ab, nicht von den netto-Senken. Man kann vom Einen nicht auf das Andere schließen.
Auch ohne viel Annahmen und „Regressionsanalysen“ lässt sich leicht erkennen:
1960 stieg die CO2 Konzentration um ca. 1ppm/a (~8Gt/a), bei Emissionen von ca. 10Gt/a.
2020 liegen diese Werte ca. 2.3ppm/a (~18Gt/a) bzw. ~38Gt/a.
Das ist nicht wahnsinnig kompliziert. Die anthropogenen CO2 Emission haben stark zugenommen, fast um den Faktor 4. Die Steigerungsrate der CO2 Konzentration haben ebenso zugenommen, aber nicht so stark. Viel stärker hingegen legten die CO2 Senken zu, eben weil sie eine Funktion der über den Basiswert (~280ppm) hinausgehenden CO2 Konzentration sind.
Herr Schaffer, volle Zustimmung zu Ihren letzten beiden Absätzen. Das besagt aber nichts über die Bruttoflüsse der Quellen und Senken oder, wie Sie es ausdrücken, der Rate der Kreisläufe. Um die geht es aber gerade. Und man kann auf sie nicht, wie Sie ebenfalls korrekt schreiben, aus den Nettoflüssen schließen.
Meine Rechnung behandelt in der Tat den jeweiligen Bruttofluss der Quellen und der Senken, allerdings summarisch, ohne zwischen einzelnen beteiligten Komponenten zu unterscheiden. Jedenfalls genügt es dafür nicht, eine Differenz von Partialdrücken zu berücksichtigen. Eine solche Differenz kann allenfalls einen Nettofluss beschreiben, was keine Antwort auf die Ausgangsfrage liefert. Hinzu kommt, dass nur vom atmosphärischen CO2-Niveau Messwerte vorliegen, das Bezugsniveau zur Differenzbildung aber mehr oder weniger willkürlich gewählt werden muss!
Nachtrag: der ermittelte Zusatzfluss QPktx, der sich zum zivilisatorischen addiert, stellt natürlich nicht die gesamte natürliche Kreislaufrate dar, sondern nur denjenigen Anteil, der zum Anstieg des atmosphärischen Gehaltes beiträgt, der also ein Ungleichgewicht generiert. Aber es ist kein Nettostrom. Der größte Teil davon wird wieder in den Senken verschwinden.
Auch etwas das mann wissen und speichern sollte.
Selbst wenn mann die Auswirkungen noch nicht versteht.
„Gibt es einen direkten Zusammenhang mit der Stabilisierung des Erdmagnetfeldes?“
Strange Portal Connects Earth to Sunhttps://www.space.com/6051-strange-portal-connects-earth-sun.html
Schöner Beitrag, vor allem leicht nachvollziehbar. Meine Idee: ca. 13 % (Statista 2018) der Biomasse sind Bakterien. Die Biester werden bei höheren Temperaturen ziemlich emsig und „pupsen“. Gibt es Untersuchungen, ob diese einen signifikanten Beitrag zum CO2-Eintrag leisten?
Distribution of biomass in the biospherehttps://www.encyclopedie-environnement.org/en/life/distribution-biomass-planet/
Wir Menschen und Säugetiere sind nur ein Klecks auf der Erde.
Gezüchtete pupsende Rinder (Wiederkäuer) in Nordamerika haben nur wilde pupsende Bisons ersetzt.
MfG
Mann sollte sich auch andere grüne Lûgen genauer Ansehen.
Gibt es ein Massensterben?
Nein, wie seit jeher gibt es Tierarten welche Austerben.
Töten Katzen Vögel, Gartenschläfer, Mäuse, usw.?
Sicherlich, aber nicht mehr als Wiesel, Marder, VielfrÄsse und andere Räuber welche der Mensch verdrängt hat.
Und Hauskatzen haben nur den natürlichen Jagd- und Spieldrang ohne sich ernähren zu müssen.
Also einfach nur Sterilisierung von Hauskatzen welche nicht für die Zucht benutzt werden.
Aber Hauptsache wir sind für Alles schuld.
[sa..]
Ich finde es schaebig, das sie andere Lebewesen dafuer verantwortlich machen wollen, obwohl jedes Kind weiss, das es der Mensch ist.
Die kleinen Biester koennen sich ueberhaupt nicht wehren, was sie hier ueber sie verbreiten.
Schaemen sie sich, und bitte mehr solche Information.
Ich will schliesslich auch morgen noch sorgenfrei in den Urlaub fliegen.
[..rk]
Ansonsten vielleicht hier mal gucken. Aber keine Garantie.
Zu den Kommentaren von den Herren Sachs und Schulz: Die Kommentare sind m. M. völlig Off-Topic. Es ist, denke ich, unbestritten, dass menschliches Leben (z. B. Darmbakterien) und ein Leben überhaupt ohne Bakterien nicht möglich wäre. Wer allerding schon einmal versucht hat, aus gepressten Äpfeln ein alkoholisches Getränk herzustellen, sollte wissen, dass die hierfür benötigte Hefe (OK das sind Pilze) erst ab einer bestimmmten Temperatur wirklich aktiv werden und dann CO2 ausstoßen. Das Gleiche gilt wohl auch bei Bakterien (außer Cyanobakterien). Herr Sachs hat allerdings Recht; tierische Lebewesen (incl. Mensch) sind nur 0,4 % der Biomasse. Meine Frage war einfach, ob es Untersuchungen gibt, die den vermehrten Ausstoß von CO2 aufgrund der höheren Temperatur durch Mikroorganismen auf den CO2 Eintrag insgesamt einen Einfluss hat.
Es gibt den Nachweis das es sehr wahrscheinlich die Aktivität von Mikroorganismen sind die den nächtlichen CO2-Anstieg auf bis 600ppm über Vegetationsflächen verursachen. Dafür spielt aber sicher auch die Beschaffenheit des Boden(Lockerheit), die Bodenfeuchtigkeit und natürlich die solare Einstrahlung über den Tag eine maßgebliche Rolle.
Off Topic und wir sprechen ueber die alkoholische Gaerung?
Uebrigens waere das nicht falsch, und ist wichtig zu wissen!
Mein Link sollten sie sich vielleicht trotzdem auch angucken, der war unter dem [sark] Tag.
Herr Krämer, Sie haben völlig Recht!
Schulwissen: ein Bakterium verdoppelt seine Masse in 20 min, also im Jahr Masse x 2hoch (72×365). Man kann daraus berechnen, dass aus einem einzelnen Bakterium in einem überschaubaren Zeitraum von Jahren die Masse der Erde entstehen kann. Wenn die Nahrung nicht ausgeht. Der Einfluss der Menschheit dagegen geht gegen Null.
Cyanobakterien in den Weltmeeren brauchen (neben Chlorophyll) nur Wasser und CO2, und haben dabei den CO2 von 17% auf knapp über Null gedruckt und dabei den Sauerstoff von Null auf 20% angereichert. Damit ist schon die ganze Klima Humbug absurd. Und die Betrachtung von mikroskopischen Änderungen im mikroskopischen Zeitraum auch.
Alle organische Reste, ob tierisch oder pflanzlich, werden durch Bodenbakterien zu CO2 verbrannt. Nur wir können auf Wunsch die Bodenbakterien durch den Schornstein vom Krematorium umgehen, mit gleichen Ergebnis: bisschen Dünger und viel CO2. Mit den Bodenbakterien können wir nicht mithalten. Bakterien bestimmen den Luftgehalt. Interrsiert niemanden, damit kann man kein Geld verdienen!
Die Klimakrise liegt daran, dass man mit Computerspielerei und Horrorszenarien gut leben kann ohne sich die Hände dreckig zu machen.
Herr Krämer, ich bin kein Biologe, kann also nicht sagen, wieviel Bakterien zum CO2-Kreislauf beitragen. Es gibt auch aerobe Bakterien, die produzieren vermutlich kein CO2, vielleicht aber Methan oder so.
Ich habe aber mal eine Angabe gefunden, wonach die Tierwelt insgesamt 120 Mrd t CO2 pro Jahr durch Atmung erzeugt. Das liegt einerseits erstaunlich dicht bei den Werten von QPktx, die in meiner Tabelle 1 auftauchen. Andererseits kann es sich dabei aber kaum um einen wachsenden Betrag handeln, und es ist auch nicht einzusehen, warum die Tierwelt ausgerechnet im 20. Jahrhundert einen so deutlichen Anstieg des atmosphärischen Gehaltes verursacht haben sollte.
Herr Mechtel, der biologische CO2 Kreislauf auf dem Festland durfte ziemlich ausgeglichen sein. Der durch die Pflanzenwelt entzogene CO2 wird durch die Tierwelt und zum Schluss Bodenbakterien durch Verwesung ziemlich komplett zurückgegeben. Es sind Einzelfälle, wenn Organismen in Mooren vom Sauerstoff abgeschnitten werden und nicht zu CO2 zurück gebrannt werden können. Die Menge ist dann egal, Brachland entzieht kein CO2 und gibt kein zurück, Wiese entzieht wenig und gibt wenig zurück, Regenwald entzieht viel und gibt viel zurück, Bilanz immer gleich.
In den Weltmeeren werden organische Reste nicht komplett zurückverbrannt, daher wirkt die Biosphäre insgesamt CO2 vernichtend. Zum Glück, ansonsten hätten wir nicht genug Sauerstoff. Sauerstoff geht auch durch rosten verloren, man braucht die O2 Produktion auf Kosten von CO2, um nicht Sauerstoffmangel zu bekommen.
Je höher der CO2 Gehalt, desto höher die Photosynthese der Cyanobakterien in den Meeren. Daher kann man Schwankungen nicht exakt berechnen. Es ist nicht nur Physik, sondern auch Biologie. Und warum CO2 seit 300 Mio Jahre schwankt, meistens auf signifikant höheren Niveau als heute, weiß auch niemand.
Eine Frage welche mann sich auch stellen könnte.
Beeinflusst die Stärke des Erdmagnetfeldes Vulkane und Erdbeben?
https://www.studysmarter.de/studium/physik-studium/geowissenschaften/geomagnetismus/
https://www.elektronikpraxis.de/anomalien-im-erdmagnetfeld-mit-interaktivem-mess-system-analysieren-a-168720/
Es gibt mehrere historische Quellen die ein deutlich höheres CO2 Niveau als diese 280ppm angeben, z.B. Meyers Konverstationslexikon nennt für 1890 etwa 0.04 Vol% oder Alfred Wegener der in 1911 Seite 25 einen Mittelwert von 0.03 Vol% angibt.
Dann haben wir die Exxon Studie von 1982, Seite 26:
„Available data on CO2 concentration prior to the Industrial Revolution tend to faIl into two groups: 260 to 270ppm or 290 to 300ppm“
Somit sind die 280ppm auch wieder nur ein Mittelwert von „verschiedenen“ Gruppen. Sammlungen historischer Messwerte wie die von Beck oder Callendar (s.u.) die ebenfalls deutlich höhere Konzentrationen angeben; man beachte die selektive Auswahl von Callendar:
und nicht zu vergessen die Manipulationen:
Mit dem historischen CO2-Werten ist es wie mit den historischen Temperaturwerten, keine eindeutige Messwertebasis, große Fehlerspannen und ein extremer Hang zur Manipulation und Fälschung der sich selbstüberschätzenden politischen Klimawissenschaft, oder
Heute scheint der Irrglaube zu existieren dass die Menschen im 19.Jh. das technische Wissen von Neanderthalern hatten, dabei sind in dieser Epoche (und davor) die meisten Gesetze „erfunden“ worden und der Austausch zwischen Wissenschaftlern auf verschiedenen Kontinenten war auch damals schon sehr rege. 1906 meldete Nature eine globale Temperatur von 15.1°C, so wie Ekholm 1901.
Ein Kernelement der sog. „Klimawissenschaften“ seit Mann seine Studie veröffentlicht hat. Seitdem nähern sich Temperatur- und CO2 Kurve an, damit auch der Dümmste „den Beweis“ sehen kann dass CO2 der Kontrollknopf ist.
Die aktuelle globale Mitteltemperatur liegt bei ca. 15.3°C.
Schauen Sie mal was das WBGU 1995 (Seite7/8) geschrieben hat:
Dann 1997/1998, man hat 1°C „verloren“ – weil „Die Wissenschaft“ macht das so:
Das muss wohl so sein.
In einigermaßen funktionierenden Demokratien gibt es ein gutes Verhältnis zwischen freiheitlichen Rechten und Sicherheitsvorsorge des Staates.
Dies beinhaltet sicher auch einen permanenten Zielkonflikt.
Kollektivistisch denkende Regime versuchen oft Staatsmacht mit dem Argument notwendiger Sicherheitsvorsorge, zu ungunsten Berufs-, Religions-, Meinung- und was nicht noch alles an Freiheiten eingeschränkt denkbar ist, auszuweiten.
Nichts eignet sich da besser als eine Krise um geschmeidig fast widerstandsfrei die bürgerlichen Rechte einzuschränken, und Krisen können/dürfen auch vorgetäuscht sein. Am wirksamsten, man malt ein Amagedon an die Wand. Wer das erkennt, kann von diesen Verfahren auch leicht profitieren.
Typische Beispiele sind die Corona-„Krise“, wo sich gerade herausstellt, dass uns die angegebenen direkten Coronatoten um den Faktor 4 zu hoch untergejubelt wurden, und natürlich die menschengemachte Klima-„Krise“, eindeutig eine vorgetäuschte Krise als Vehikel zur Einschränkung demokratischer Grundrechte, und massiver Zusatzprofitabschöpfung, oder?
„Never let a good crisis go to waste“. Man muss schon anerkennen dass die CO2 Story eine brillante Idee ist, dass der Mensch sich selber durch sein unverantwortliches Verhalten an den Rand des Untergangs bringt – und es natürlich die weisen Wissenschaftler mit besorgten Politikern schaffen das Ende von uns allen abzuwenden. Es ist alles nur zu unserem eigenen Besten.
Man muss immer bedenken dass die Idee des Glashauseffekts eine sehr lange Historie hat und dass die Warnungen auch schon vor WKII existiert haben und es auch danach prominente Warner gegeben hat; das älteste das ich bis jetzt finden konnt ist von 1958 oder 59, Edward Teller, der Vater der Wasserstoffbombe der vor den Gefahren des CO2 gewarnt hat.
Strahlung hat die Menschen schon immer fasziniert und an irgendeiner Stelle in der Geschichte haben haben Leute angefangen zu glauben die Realität funktioniert wie ihr Modell. Bis heute gibt es keinen experimentellen Nachweis für den GHE (dafür zahlreiche Gegenbeweise) – nur juckt es die Medien und Politiker nicht, die Story ist zu gut und wie sollte man heute gesichtswahrend aus der Nummer wieder herauskommen?
Wenn laut Meyers Lexikon von 1890 der CO2 Wert bei 0,04 % lag, dann erübrigt sich jede Diskussion.
Ich frage mich nur, wohin das CO2 verschwunden ist, das wir in die Luft emittiert haben.
Herr Seiffert, die lebensnotwendigen 21% Sauerstoff in der Luft waren nicht immer da, sondern waren mal alle CO2. Vor allem Cyanobakterien haben die vor 3,5 Mrd Jahren vorhandenen 17% CO2 „weggefressen“ durch Photosynthese und den Sauerstoff geliefert. Das machen sie heute noch, ansonsten würde Sauerstoff durch rosten, atmen, verbrennen und verwesen weniger. Cyanobakterien und Bodenbakterien bestimmen das Gleichgewicht, das bisschen Auto CO2 ist vernachlässigbar, da können die Cyanos ein Gang zulegen.
Man kann jederzeit bestimmen, welche Gase aus einem aktiven Vulkan entweichen. Da ist CO2 dabei. Dann stellt man ein CO2 Messgerät auf einen aktiven Vulkan und behauptet, menschliche Aktivitäten seien an einem Anstieg des CO2 an der den Vulkan umgebenden Luft schuld.
Österreicher haben dafür einen schönen Ausdruck: „Schas mit Quasten“. Für die Deutschen hab ich einen Vorschlag: „Langer Furz mit Schöpfchen“.
Angenommen, wir blasen kontinuierlich die gleiche Menge CO2 in die Luft. Die „böse“ Industrie produziert 24/7 an 365 Tage. Da würde man doch nicht denken, daß im Winter kälter ist als im Sommer, sondern müßte die Temperaturen in etwa gleich sein. Wo ist der Denkfehler ???
Der Denkfehler liegt in der Sonnenstrahlung.
Am Nordpol ist es in unserem Winter dauernd Nacht – in unserem Sommer am Südpol.
Nur am Äquator ist es 12 Stunden Tag und 12 Stunden Nacht.
Dazu kommen Luft- ude Meeresströmungen, Verwirbellungen und viele andere Faktoren.
Das Erdklima ist ein chaotisches System.
Herr Sachs, ich habe das als ironische Frage von Frau Keller verstanden, Frau Keller will dasselbe sagen wie Sie, bzw. die Linksgrünen zum Nachdenken anregen.
Ich gehe noch einen Schritt weiter wie Frau Keller: Wäre CO2 der einzige allein bestimmende Temperaturgrund, so wie die politisch linksgrünen, wie die Irren der letzten Generation behaupten, dann bräuchten wir nur eine einzige Wetterstation auf der Welt.
Kompliment, Herr Mechtel, das ist ein wichtiger Beitrag!
Das ist seit Jahrzehnten glasklar beantwortet:
Die durch uns verursachte Erhöhung des CO2 (Treibhausgase) – Gehaltes der Atmosphäre ist die einzige Einwirkung, die für die gemessene Temperaturerhöhung verantwortlich ist.
Die durch uns produzierte Masse an CO2 in den letzten ca. 100 Jahren ist dafür verantwortlich, dass der CO2-Gehalt um 50% angestiegen ist.
Das ist eine sehr gute Erkenntnis, denn so müssen wir nur unser Verhalten ändern, um die schlimmsten Folgen der globalen Erwärmung abzuwenden. Die viel schlimmere Erkenntnis wäre, dass wir gegenüber der Erwärmung hilflos sind und uns irgendwie dem Klimawandel anpassen müssten. Das würde wirklich teuer werden.
Haben Sie mitbekommen dass die Sonneneinstrahlung seit ca. 25 Jahren zugenommen hat? Die spielt Ihrer Ansicht nach keine Rolle?
Die Zunahme der Sonneneinstrahlung ist minimal und kann man vernachlässigen.
Dr. Konrad Voge 7. Mai 2025 15:49
Warum hat die Sonnenstrahlung zugenommen? Weil sich das Wolkenmuster geändert hat. Warum hat sich das Wolkenmuster geändert? Weil die CO2-Konzentration zugenommen hat.
Unfundierte Annahme. Ich hatte sie schon beim letzen Mal gefragt, wie CO2 die Wolkenbildung beeinflussen soll.
Werner Schulz 9. Mai 2025 8:51
Ihre Frage beweist wieder, daß Sie nicht lernfähig sein wollen. Deswegen:Ich gebe Provokateuren kein Futter. Wenn das schon zu hoch für Sie ist – wie ist es dann bei komplizierteren Treibhauszusammenhängen?
Sie hatten nicht geantwortet!
Die Frage stellt sich mir auch. Was jedoch sicher ist, das dichtere Wolken selbst die/das „atmosphärische Fenster“ verschließen können und die Abstrahlung stark behindert. Bezüglich CO2-Level gibt es keinerlei Erkenntnisse zur Wolkenbildung in der entsprechenden Literatur.
Moritz Steinmetz 9. Mai 2025 18:36
Lesen Sie Fortak 1971.
Weiter unten hat Herr Ebel ein Zitat von Fortak gebracht, das alles aussagt nur nicht, das CO2 an der Wolkenbildung direkt beteiligt ist.
Unter der Annahme, der CO2-Treibhauseffekt wäre ein Effekt der Physik, müßte es möglich sein, eine phys. Dimension anzugeben, mit welcher man den Effekt beschreibt bzw. auch quantifiziert. Wie lautet diese phys. Dimension?
Auch eine Berechnung des Effektes müßte einen dimensionsbehafteten Wert ergeben, wenn es sich um einen Prozeß der Physik handelt. Und diese Berechnung muß natürlich in allen Schritten phys. dimensionskonsistent sein. Kennt jemand so eine Rechnung? Ich kenne nur Behauptungen(!) von IPCC, wonach gewisse Atmosphärenbestandteile angebliche „Radiative Forcings“ (RF) haben sollen, also auf Deutsch „Strahlungsantriebe“. Solche Strahlungsantriebe sollen die Energiebilanz der Erde gegen jede Physik(!) angeblich einseitig, also unsymmetrisch, verändern.
IPCC behauptet dazu übersetzt: „Der augenblickliche RF bezieht sich auf eine augenblickliche Änderung des Nettostrahlungsflusses (nach unten minus nach oben) (Kurzwelle plus Langwelle; in W/m²) aufgrund einer aufgezwungenen Änderung. Dieser Antrieb wird in der Regel in Form von Änderungen des Strahlungsflusses am oberen Ende der Atmosphäre (TOA) oder an der klimatologischen Tropopause definiert, wobei letztere ein besserer Indikator für die Reaktion auf die globale mittlere Oberflächentemperatur ist, wenn sie sich unterscheiden.“
Wie hat man sich das vorzustellen? Wodurch kann so eine „aufgezwungene Änderung“ erfolgen? Diese Änderung soll an der Tropopause beobachtet werden, also breitengradabhängig in ca. 6 – 18 km Höhe. Mit welchen Methoden ist man in der Lage, dort Langzeitmessungen oder Messungen überhaupt vorzunehmen? Es wird dann eine Tabelle angeführt, wo solche Veränderungen aufgeteilt auf einzelne Luftbestandteile bezogen auf 1750 behauptet(!) werden, Messungen dazu gibt es keine bei IPCC.
Dazu sollte man also wissen, wie diese Werte 1750 konkret waren an der Tropopause, um Änderungen zu heute festzustellen!? In Summe sind das aktuell (AR6) angeblich ca. +2,3 W/m². Es wird also offenbar behauptet, es gibt derzeit keine ausgeglichene Energiebilanz, sondern eine, bei der entweder 2,3 W/m² mehr absorbiert werden, als von der Sonne kommen oder um 2,3 W/m² weniger abgestrahlt werden können, als es einem thermischen Gleichgewicht entspräche.
Natürlich gibt es keine Antwort auf die Frage, wie ändert sich dieses RF proportional, wenn sich die Oberflächentemperatur verändert, weil es phys. unplausibel wäre, daß sich z. B. die Oberflächentemperatur ändert, das RF gleichzeitig aber konstant bleibt.
Mein Fazit: all das sind doch reine potemkinsche Dörfer, s. g. Ms. Kosch, oder etwa nicht?
stefan strasser 7. Mai 2025 16:04
Wenn Du noch nicht mal das Wort „Indikator“ verstehst, kannst Du natürlich den Treibhauseffekt nicht verstehen. Ein Indikator kann Wirkungen zur Folge haben oder auch nicht, wie in diesem Falle. Er ist eine rein berechnete Vergleichsgröße, die keine Auswirkungen hat. Dazu das komplette Zitat des Strahlungsantriebs ( https://www.ipcc.ch/site/assets/uploads/2019/03/IPCC2007-Annex_german.pdf ):
Also nur ein rechnerisch, in dem alle Veränderungen ausgeblendet werden.
Stimmt und ist auch bekannt – nennt sich Klimasensitivität und hat folgenden Wert:
Fast genau 1 K Temperaturanstieg an der Oberfläche bei Steigerung der CO2-Konzentration um 100 ppmV.
Z.B. lesen ( https://www.meteoschweiz.admin.ch/klima/klima-der-schweiz/jahresverlauf-temperatur-sonnenschein-und-niederschlag/jahresverlauf-der-tropopausenhoehe.html ):
Eine mehr als merkwürdige Beschreibung:
„Der Strahlungsantrieb darf nicht mit dem Wolkenstrahlungsantrieb verwechselt werden, einem ähnlichen Begriff für die Beschreibung des Einflusses der Wolken auf die Einstrahlung an der Aussengrenze der Atmosphäre.“
Seit wann haben Wolken einen Einfluss auf die Einstrahlung an der Aussengrenze der Atmosphäre? Letztere liegt meiner Kenntnis nach bei der Kármán-Linie in100 Kilometern Höhe, bzw. am Ende der Exosphäre bei 10.000 Kilometer Höhe (laut Eskp.de)
Und dort liegt die einzige „Bewölkung“ auf unseren Kenntnissen der genauen Vorgänge.
…Die durch uns verursachte Erhöhung des CO2 (Treibhausgase) – Gehaltes der Atmosphäre ist die einzige Einwirkung, die für die gemessene Temperaturerhöhung verantwortlich ist…
Meine Meinung steht fest! Man verwirrre mich nicht mit Fakten.
Frau Kosch,
schon wieder die gleichen Halbwarheiten (Lügen) über den Klimawandel.
Das Erdmagnetfeld schwächelt erst seit 1840
https://www.wissenschaft.de/astronomie-physik/das-erdmagnetfeld-schwaechelt-erst-seit-1840/
—-
Erdmagnetfeld beeinflusst Klima
Meerwasser nimmt bei schwächerem Magnetfeld weniger CO2 auf
Archäologie bestätigt TheorieBestätigung für die Theorie, dass das Erdmagnetfeld und die klimatischen Bedingungen zusammenhängen, liefern geo-archäologische und archäomagnetische Studien. So wurde beobachtet, dass in den letzten vier Jahrtausenden vor Christus abrupte Zunahmen des Erdmagnetfelds jeweils mit einer Abkühlung der Temperaturen auf der Erde einhergingen. Zudem wurde ein Zusammenhang zwischen einem stärkeren Erdmagnetfeld und kälteren Perioden seit 700 nach Christus beobachtet.
Dies konnten Geowissenschaftler feststellen, indem sie archäologische Funde aus verschiedenen Zeitperioden analysierten und aus deren Magnetisierung auf die Stärke des damals vorherrschenden Magnetfelds schlossen. Weiterhin beobachten Forscher, dass die Stärke des Magnetfelds der Erde seit Beginn der Messungen vor 150 Jahren kontinuierlich abgenommen hat. Bislang war jedoch weitgehend unklar, durch welche Mechanismen das Erdmagnetfeld eine Abkühlung oder Erwärmung auf der Erde beeinflusst.
https://www.scinexx.de/news/geowissen/erdmagnetfeld-beeinflusst-klima/
—-
Die Meere als CO²-Senke spielen wohl eine wichtige Rolle in den Schwankungen des CO² in der Erdatmosfere.
Ausserdem bedingt ein schwächeres Erdmagnetfeld ein schwächeres Schutzschild gegen hochenergetischer Sonnen- und kosmischer Strahlung.
—-
Sonne im Jahrtausendhoch
Eine Erklärung liefert vielleicht ein statistischer Zusammenhang zwischen Sonnenintensität und niedrigen Wolken, den kürzlich eine Gruppe um Jón Egill Kristjánsson von der Universität Oslo entdeckt hat. Nach der Hypothese der norwegischen Forscher bewirkt eine geringe Erwärmung des Oberflächenwassers der Ozeane eine Abnahme der Zahl niedriger Wolken, was wiederum zu einer weiteren Erwärmung des Oberflächenwassers führt. Die Folge: Während Zeiten erhöhter Sonnenaktivität wie heute sorgt dieser Verstärkungsmechanismus für eine spürbare Erhöhung der Erdtemperaturen.
https://www.wissenschaft.de/astronomie-physik/sonne-im-jahrtausendhoch/
—-
Polwanderung veränderte das Weltklima
Beginnen die Pole der Erde zu wandern, wird das Erdmagnetfeld schwächer – es bekommt gewissermaßen Löcher. Das passierte auch vor 42.000 Jahren.
https://science.orf.at/stories/3204871/
—-
Die Folgen eines schwachen Erdmagnetfelds
Die erhöhte kosmische Strahlung auf der Erde führte vor 41 000 Jahren zu starken Klimaveränderungen und einem Artensterben.
https://www.weltderphysik.de/gebiet/erde/nachrichten/2021/die-folgen-eines-schwachen-erdmagnetfelds/
—-
Aber für Klimajünger(innen) wohl nur unwissenschafftliche Schwurblereien.
„des CO2 (Treibhausgase)“
aber wir leben doch nicht in einem Treibhaus
Aber doch Herr Schenk, wir leben alle in (Treib)Hâusern.
https://www.cik-solutions.com/branchen-anwendungen/co2-im-innenraum/
Also „Grüne“ müssen draussen schlafen.
Was!?!?
Das letzte mal als ich den IPCC Sachstandsbericht geblickt habe, gab es da noch ein paar andere Faktoren..
Und das ist sozusagen nur die „offizielle“ Version, mit der man die beobachtete Klimaveränderung aber nicht erklären kann.
Haben Sie die Tabelle nicht verstanden, @E.Schaffer?
Der anthropogene Anteile an der globalen Erwärmung ist 96% (2,72/2,84), dieser Anteil wird ausschließlich durch Treibhausgase bestimmt und von den Treibhausgasen hat CO2 mit weitem Abstand den größten Anteil.
Ich finde es erstaunlich, wie fanatisch hier manche Leute darauf aus sind, Ursachen für die katastrophal schnelle globale Erwärmung zu finden, die außerhalb der Verantwortung der Menschheit liegen.
Wenn man schon nicht die Erkenntnisse der Wissenschaft akzeptieren will, dann sollte man doch zumindest hoffen, dass wir nur durch eine einfache Verhaltensänderung die Katastrophe abwenden können.
Erneuerbare Energieversorgung anstatt eine Energieversorgung mit Fossilen Energien.
Wärmepumpe statt Öl- oder Gasheizung
Elektroauto anstatt Verbrenner
Gut gedämmte Häuser statt Verschwendung von Heizenergie.
Kurze und nur notwendige Transportwege anstatt endloser Lieferketten.
Das ist doch ein Klacks und bedeutet keinerlei Verzicht im Gegensatz zu dem Aufwand und den Einschränkungen, die zum Überleben erforderlich wären, wenn unsere Welt eine von uns nicht abwendbaren Erwärmung von 3 oder 4 °C ausgeliefert wäre.
Liebe Frau Kosch, ich finde es mit Verlaub erstaunlich, dass Sie sich auf Erkenntnisse „der Wissenschaft“ berufen, aber Sachargumente zur gleichen Zeit konsequent ignorieren. Das ist keine wissenschaftliche Denkweise. Das Klimasystem ist nun mal komplex, noch keineswegs verstanden, und die wissenschaftlichen Äußerungen dazu sind nicht so eindimensioinal, wie es die Alarmisten gern darstellen.
Dass es ungeachtet dessen sinnvoll ist, mit Energie und Ressourcen sparsam umzugehen, Transportwege zu verkürzen etc., versteht sich von selbst. A propos kurze Transportwege: wo sehen Sie die, wenn Windstrom von der Nordsee nach Bayern transportiert werden soll oder Überschußstrom nach Österreich und Strom aus Wasserkraft von Norwegen nach Deutschland?
Ihre Meinung teile ich nicht.
Ist aber keine Meinung.
Ihre Meinung war nicht gefragt, oder?
Sicher, ich habe ja auch keine Meinung.
Ich erkläre hier nur wissenschaftliche Erkenntnisse. Insbesondere gerne dann, wenn Meinungen dazu wissenschaftlichen Unsinn erhalten.
Das ist aber nur ihre Meinung, oder?
Nein, das war ein typischer „Heinemann“ …. ;-)))
Dass ich wissenschaftliche Erkenntnisse erkläre, ist keine Meinung.
Glauben Sie bitte nicht das ich Sie deshalb bedauere oder gar beneide, oder sollte ich?
Wissenschaftler zu sein und wissenschaftliche Erkenntnisse wiederzugeben sind keine Glaubenssache.
Das können Sie machen wie Sie wollen. Unabhängig davon nehme ich mir nur heraus, auf Fehler und wissenschaftlich falsche Behauptungen aufmerksam zu machen, zu korrigieren und ggf. zu erklären.
Ditto!
Nicht „ditto!“. Denn Sie beziehen sich nicht auf wissenschaftliche Erkenntnisse.
Ditto!
Komisch das die Dinosaurier mit 8 bis 14°C höheren Temperaturen als heute 170 Millionen Jahre überlebt haben und die Erde war wesentlich üppiger grün als Heute.
Soweit ich weiss hat man keine gebratenenen Dinokeulchen ausgegraben.
Wo ich mit Ihnen einverstanden bin:
Solaranlagen um abgelegene „sonnige“ Regionen mit Strom zu versorgen und um Meerwasser zu entsalzen um aride Regionen zu bewässern.
Gut gedämmte Häuser statt Verschwendung von Heizenergie.
Kurze und nur notwendige Transportwege anstatt endloser Lieferketten.
Alles Andere ist Mummpitz, Geldmacherei und Verarmung.
Der Dino-Opa, der aus der Kälte kam
https://www.spiegel.de/wissenschaft/natur/antarktis-der-dino-opa-der-aus-der-kaelte-kam-a-1251539.html
Erdmittelalter (Trias, Jura und Kreide)
Die Zeit der Dinosaurier
https://www.oekosystem-erde.de/html/leben-06.html
Frau Kosch,
stellen Sie sich vor das sogenannte CO² Steuern wie ein Sparkonto fungieren um Sie zu animieren Ihr Haus zu isolieren oder eine sparsamere Heizung zu kaufen.
Das gespahrte Geld können Sie dafür abrufen.
Aber stattdessen verschwindet das Geld im Staatshaushalt und in dubiosen „grünen“ NGOs.
Sie werden verarmt und haben damit noch weniger Geld um Renovierungsarbeiten zu machen.
Das nennt sich Klimaverarschung!
Geht Ihnen mal endlich ein Licht an?
Wieso? Das Fakt.
Können Sie auch in vollständigen Sätze antworten? Sowas haben WIR früher mal gelernt ….., …. und im Leben über die Jahrzehnte als ganz sinnvoll erkannt ….
Herr Kuck,
solche Sätze sind schon von der Logik her völliger Unsinn und werden durch Messungen endgültig ad Absurdum geführt. Die Gegenstrahlung ist über 24 h am Tag bei gleichbleibender Bewölkung nahezu konstant. Die Höhe der Gegenstrahlung ist vom Bewölkungsgrad abhängig.
Was nützt Ihnen dieses statement, wenn es offensichtlich – siehe Fachliteratur – falsch ist?
Sie haben – denke ich – auch die Messkurven gesehen, die die Gegenstrahlung durch THGs (z.B. auch bei wolkenlosem Himmel) zeigen, und die jeder Meteorologe kennt.
Also ist Ihre Behauptung einfach nur gepflegtes Wunschdenken losgelöst vom Anspruch auf Realität.
Na, dann müssen Sie mal richtig gucken, Sie waren doch auch im Beitrag
„Was tun gegen das fest installierte Modell einer angeblichen von Kohlendioxid verursachten Klimagefahr? Was tun gegen diese Klimalüge?“
Herr strassers Messkurven zeigen die THG Spektren der Gegenstrahlung ja unleugnenbar. Diese Bandenspektren bekommen Wolken nicht hin.
Außerdem sehe Sie es in den Literaturlinks 1. und 6., die ich Ihnen extra gab.
Also: bei Bewußtsein da nochmal nachgucken.
Richtig Herr Kuck,
Die Höhe (Größe) der Gegenstrahlung ist auch vom Bewölkungsgrad abhängig.
Die Treibhausgase sind sind für die Gegenstrahlung verantwortlich.
Das können Sie von mir aus gerne machen, Herr Kuck. Sie können auch annehmen, dass die Erde eine Scheibe ist.
Diese Ansicht ist gesichert nicht rechtsextrem.
Na, Sie haben sich ja einen netten Murks zusammengereimt. Einzig desaströs ist die Aneinanderkettung von physikalischem Blödsinn, den Sie von Trollen unreflektiert übernommen haben. Nur mal gleich im zitierten Abschnitt von Ihnen:
Ihr Fehler: Die Stefan Boltzmann Gleichung hat mit der Sonnenstrahlung auf die Erde nichts zu tun.
Sie gibt an, wieviel ein Körper der Temperatur T an Wärmestrahlung pro Sekunde abstraht! Sie ergibt sich aus den Eigenschaften elektromagnetischer Strahlung, die die Temperatur T hat.
Weiter:
Dass der globale Mittelwert der Temperatur der Erdoberfläche 288 K beträgt, wenn er am Tage 293 K und nachts 293 K beträgt, ist Mathematik. Da ist also kein Problem.
Dass dann nach Stefan Boltzmann für eine schwarze Erdoberfläche am Tage dann 417 W/qm abgestrahlt wird und von der Nacht-Halbkugel 363 W/qm, also im globalen Mittel 390 W/qm, ist aus demselben Grund trivial.
Die Erdoberfläche verliert aufgrund ihre Temperatur zwischen 283 K und 293 K in 24 Stunden also im Mittel pro Quadratmeter Erdoberfläche 390 W/m2 x 24 h = 417 W/m2 x 12 h + 363 W/m2 x 12 h = 9360 Wh/m2.
Die absorbierte Sonnenstrahlung der Erde beträgt imselben Zeitraum jedoch nur 235 W/m2 x 24 h = 5640 Wh/m2.
Somit ist klar, dass die Erde in derselben Zeit (Vielfache von Tagen) weniger Energie von der Sonne absorbiert als die Erdoberfläche im selben Zeitraum aufgrund ihrer Temperatur von 283…293 K abstrahlt!
Stimmen Sie dem zu?
Das war qualitativ für Fourier der Ausgangspunkt für seine Treibhausgashypothese, die im Laufe des 19./früher 20. Jahrhunderts durch Messungen (Angström, Langley…) wie theoretisch (Arrhenius, Schwarzschild, Emden,…) real grundsätzlich bestätigt wurde.
Bemerkung: Im stationären Klima wird im selben Zeitraum die Energie 235 W/m2 x 24 h = 5640 Wh/m2 ins Weltall abgegeben, also die gesamte absorbierte Sonnenenergie geht dann wieder zurück ins All und die Erde gewinnt langfristig keine Energie = Stationarität.
Die Erdoberfläche verliert aufgrund ihre Temperatur zwischen 283 K und 293 K in 24 Stunden also im Mittel pro Quadratmeter Erdoberfläche 390 W/m2 x 24 h = 417 W/m2 x 12 h + 363 W/m2 x 12 h = 9360 Wh/m2.
Nun, erklären Sie erstmal, wo Sie die „nächtlichen“ 53 W/m2 an der Erde messen?
Die 417 W/qm sind die Wärmeabstrahlung des Bodens am Tage. Die 53 W/m2 ein errechneter Fantasiewert, den Sie zum Bilanzausgleich ermittelten, der aber der Erde physikalisch keiner Sphäre zugeordnet werden kann. Der Erdboden gibt nachts ja 363 W/m2 ab. Dort ist er also nicht und die Gesamte Sphäre der TOA strahlt in 24h Wärmestrahlung von 5640 Wh/qm ins All, d.h. 235 W/qm im globalen Mittel.
Sie könnten natürlich auch sagen, die Erde hätte keinen Treibhauseffekt, der Erdboden würde 235 W/m2 im globalen Mittel ins All abstrahlen und wäre am Tage 293 K warm.
Dann wäre er in der Nacht natürlich 175 K kalt, denn diese Temperatur würde die nächtliche Abstrahlung von 53 W/m2 liefern, die aus der Bilanz folgt. Aber dass beißt sich mit Ihrer Nachttemperatur von 283 K.
Also, Sie müssen also irgendwo den Treibhauseffekt einbauen, wenn Sie die Bilanz schlüssig hinbekommen wollen.
Was genau?
Nun ja, rechnen ist gut. Aber für Physiker soll das Rechnen ja die Messungen erklären, prüfen bzw. Vorhersagen für die Realität machen oder ein Modell definieren.
Das sehe ich (noch) nicht bei Ihnen. Wenn Ihre Rechnungen einem physikalischen Modell, Naturgesetzen, Messergebnissen, oder der Realität widersprechen, sind sie für die Physik sinnlos.
PS: ich glaube ein paar Graphiken zu den Energieflüssen werden Ihnen helfen, meine Einwände besser zu verstehen. Ich versuche mal, etwas dazu zu Papier zu bringen.
Hier eine Zeichnung. Ich denke, ich bilde Ihre Vorstellung des „Nachttreibhauseffektes“ von 310 W/m2 im Bild links richtig ab.
Ihre Zahlen für Leistungsdichten und Temperaturen am Boden bekomme ich auch gut reproduziert. Ich mußte etwas an der Wärmekapazität des Bodens (=Wasserschicht von einigen cm Dicke) spielen, damit sich Ihre Mittelwerte von Tag und Nacht aus den Kurvenverläufen über die je 12 h ergeben. Die 50 (53) W/m2 „Strahlungsenergieüberschuß“, die am Tage in den Boden gehen und zu seiner Erwärmung führen, gehen in der Nacht durch die Treibhausschicht ins All verloren. In Ihrem Modell wird die nächtliche Bodenabstrahlung von 360 W/m2 durch einen „Nachttreibhauseffektes“ von 310 W/m2 „Gegenstrahlung“ reduziert und somit die effektive Abstrahlung ins All auf 50 (53) W/m2 vermindert, damit die Gesamtbilanz wieder stimmt.
Rechts gegenübergestellt ist dieselbe Rechnung nur mit zwei Änderungen
Die Wärmekapazität des Bodens (= 24h-periodisch umgeladener Wärmespeicher zum Ausgleich zwischen „Energieüberschuß“ am Tag und „Defizit“ der Nacht) ist natürlich (auch beim realen Klimasystem) die Ursache dafür, dass die Schwankungen in der Temperatur und der Wärmestrahlungsleistungsflüsse zwischen Tag und Nacht „gedämpft“ werden.
Um die Kurvenverläufe über 24 h in den Graphiken unten ihren entsprechenden Mittelwerten über Tag, Nacht und 24h in den Bildern oben zuordnen zu können, habe ich die 24h-Mittelwerte im Bild fett in der Farbe der entsprechenden Kurve eingefärbt.
https://ibb.co/NdcszLhS
Machen wir bereits ja. Die Stationarität ist in beiden Fällen erfüllt (links Ihrer, rechts meiner) im Bild der Fall. Die Bilanzen sind jeweils ausgeglichen, alle Kurven sind 24h-periodisch.
Nur, um nicht noch ein Fass für Missverständnisse aufzumachen, frage ich Sie, ob Sie mit „Wärmeverlust in der Nacht“ nun die A) Abstrahlungsverlust der Nacht ins All meinen oder B) den Bodenwärmestrom der zwischen Tag und Nacht fließt? Beides beträgt bei Ihnen 53 W/qm. Ich denke A), wobei ich früher an B) dachte.
Die Differenz der Oberflächenstrahlung zwischen Tag und Nacht bemisst physikalisch nicht die Wärmeabstrahlung ins All bei Nacht.
Sie ist nur numerisch in Ihrem Fall (53) damit identisch, weil Sie 470-417 = 53 = 417 – 363 = 53 haben, indem Sie die nächtliche Abstrahlung des Bodens von 363 so gesetzt haben:
Ihre Gleichung:
Stimmt also nicht deswegen, weil es physikalisch so erfolgt, sondern weil Sie es sich für Ihren Fall so erwünschen.
Ja bitte, um auch Missverständnisse zu vermeiden.
Nein, nicht immer. Sie sehen ja an meinem Fall rechts im Bild, dass die mittleren Temperaturen am Tag und in der Nacht (bis auf 1K Rundungsabweichung) dieselben sind wie bei Ihner Fall links im Bild.
Wie kommen Sie als auf Ihre Behauptung, sie müssten 5K Unterschied haben?
Lassen Sie sich Zeit. Oben sind die Tages-, Nacht- und 24h-Mittel der Kurven unten bildlich eingezeichnet. Wenn Sie Fragen haben, so melden Sie sich.
Die Temperatur zum Zeitstart am Boden muss ich schätzen, je besser, desto kürzer ist die Einpendelzeit zum stationären 24h-periodischen Zustand ein. Das System pendelt nach cs. 4 Tagen für immer in einen 24-perodischen Zustand ein. Daher lese ich die Kurven zum 5. Tag (96 h nach Start) ab. Das ist dargestellt.
Denn die Anfangsdaten sind bereits das gesuchte Ergebnis.
Anfangsdaten sind nur absorbierte Sonneneinstrahlung im Tagesmittel (470) und die Gegenstrahlung von 155 in 24h (mein Fall) bzw. 310 in 12h Nacht (Ihr Fall links) und die Wärmekapazität des Klimasystems.
Wie gesagt, welche Prozessgröße Ihr „nächtlicher Wärmeverlust“ im System (Bild) darstellt, müssen Sie mir noch erklären.
Jedenfalls ist in beiden Fällen die Energiebilanz zum All hin, im Boden und in der Luft jeweil erfüllt. Der Punkt ist damit geklärt.
Zur Wärmekapazität, die benötigen ja auch Sie, um Ihre 53 W/qm vom Tag in die Nacht zu übertragen. Siehe zwischen Tag und Nacht zirkulierenden Wärmefluß im Kringel unten. Denn Betrag haben Sie ja auch.
man muss nur das richtige T(t) zum Zeitpunkt t schätzen, welches zur Zeit t in der 24h-periodischen Lösung zu den gewählten Randbedingungen gehört, und würde gleich zu Beginn schon stets 24h-periodische Daten bekommen. Wenn nicht, so hat sich das System nach rund 5 Tagen
darauf eingependelt. Diese Relaxationszeit hängt an der Größe der Wärmekapazität.
Keine Ahnung, wo der gestartet ist.
Hier das Ergebnis. Ohne Wärmekapazität wird die Temperaturkurve an der Zeitpunkten großer Leistungsänderungen etwas ruppig, denn dT/dt wird bei verschwindendem C groß (allgemein ist ja dH/dt = Q=J+G-FB, mit FB = sigma T^4 und G = Gegenstrahlung und dT/dt = Q/C).
Wenn die Wärmekapazität C=0 ist, gilt aber „solares Klima“, also J (t) + G(t) = FB (t) und die Bodentemperatur T(t) ist durch die Zeitverläufe von J und G bestimmt.
Wenn nun auch noch der Zeitverlauf von G (Ihre Treppenfunktion mit 190.1 und 119.1 W/qm) vorgeben ist, kann T auch analytisch berechnet werden (J(t) ist durch den bekannten Sonnenlauf stets gegeben).
Dann folgt für die Nacht T = 214.1 K = (119.1 W/qm/sigma)^0.25, wie auch numerisch aus meiner Rechnung etwa herauskommt.
Die 24-h Mitteltemperatur beträgt 269 K, das Lichtertagesmittel 323 K.
D.h. Ihre Temperaturdifferenz von +/- 5K ist weit unterschätzt! Das liegt wahrscheinlich daran, dass Sie die Nichtlinerität von SB nicht berücksichtigt haben (Hölder-Ungleichung).
Mittel T J FB Fout
24h-d5 269 235 390 235
Tag-d5 323 470 658 470
Nacht-d5 215 0 122 0
https://ibb.co/rfqFQPrJ
Arno Kuck 9. Mai 2025 9:27
200 Jahre (Fourier 1824) lang sind nach Ihrer Meinung nur Idioten am Werk – wie überheblich.
Energien sind z.B. in Wh anzugeben, Leistungen in W. Schon aus Dimensionsgründen sind Ihre Rechnungen was für die Tonne.
Arno Kuck 9. Mai 2025 11:49
„eher 150 Jahre“
Sie können noch nicht mal rechnen: 2024 -1824 sind 200 Jahre.
Der Punkt ist, dass Sie bislang noch gar nicht gezeigt haben, dass Sie die „Fachleute“ tatsächlich überprüfen.
Ihre Energiebilanz hat mit der der Fachleute -wie Sie selbst sehen- gar nichts zu tun.
Kiehl Trenberth benutzen aber offensichtlich nur „eine Sonne“, denn der globale Mittelwert beträgt ja wie man sieht 342 W/m2 (und nicht das Doppelte von 684 W/qm), also den 24-h -Mittelwert denn in 24h wird ja die von Erdquerschnitt aus dem Sonnenlicht abgeschattete Licht absorbiert und auf die vierfache Kugeloberfläche umgerechnet.
Klar ist natürlich, dass auch Kiehl Trenberth von einer tagesperiodische beleuchteten Erde ausgehen, wo also Tag und Nacht herrscht und die Sonne eine Bahn m Himmel macht. Denn die 342 W/m2 sind ja – wie explizit ausgewiesen wird – nur der globale MITTELWERT, also der Mittelwert der wahren Sonnenkurve (in meinem Bild die orange Kurve J)
Wie bei allen Wissenschaftsleugnern (wie May) ist zwischen Versehen, Fälschung und Dämlichkeit schwer zu unterscheiden. Ist aber auch egal, dämlich falsch ist alles.
Was ein daemlicher Kommentar, nur eine Luege kann man es nicht nennen, oder vielleicht doch?
Die Nacht ist nicht verschwunden, man muss ja die Nacht mit berücksichtigen, und da der Faktor 4 die Kugelkrümmung ist, ist die Erdkugel auch nicht flach: 1368 × 24 h /4 = 342 × 24h = 684 (Tag) × 12h + 0 (Nacht) ×12h = die in 24 h von der Erdkugel am Ort der Erdbahn im Weltall aus dem Strom der ins All gestrahlten Sonnenstrahlung absorbierte und reflektierte Energie = die fehlt im Sonnenlicht, die hinter der Erdbahn ungenutzt weiter ins All geht.
Würde die Erde um die Sonne still stehen und wäre das Sonnenlicht ein Strom aus parallel mit 10 km/h nach außen fliegenden Erbsen aus 1368 Erbsen pro Sekunde und Quadratmeter bestehen, würde die Erdkugel in 24 h aus dem Erbsenstrom eine zylinderförmige Röhre von L = 24 h × 10 km/h Länge „ausstanzen“. Diese Röhre mit L = 240 km wäre „erbsenfrei“.
Der Röhrenzylinder hat denselben Querschnitt A wie die Erdkugel, nämlich A=
pi × r × r, mit r = Erdradius = 6370000 m.
Der Röhrenzylinder enthielte damit eine Erbsenanzahl von E0 = 1368 Erbsen/s/qm × 3600 s/h × 24 h × A.
Diese Erbsenmenge E0 fehlen im Strom von der Sonne. Stattdessen werden die E Erbsen aus der Röhre zu etwa 30% irgendwohin reflektiert. Die restliche 70% werden aber auf der Erdkugel verteilt und da diese 70% klebrig sind, bleiben sie an der Kugeloberfläche haften, E = 70%×E0
Wie sieht nach 24 h also die so mit Erbsen dekorierte Erdkugel aus, wie sind die Erbsen verteilt, nur auf einer Halbkugel oder überall?
Nimmt die Erbsendichte vom Äquator zum Pol auf null ab? Und wie groß ist die global gemittelte Erbsendichte?
Ist der globale Mittelwert nicht mathematisch exakt dadurch gegeben, dass der „Erhaltungssatz der Erbse“ gilt und demnach alle Erbsen aus der Röhre auf die Fläche der Erdkugeloberfläche eiben Platz finden?
Und der gesuchte globale Mittelwert sich damit also dadurch ergibt, dass man die Erbsendekoration der Erdkugel so verschiebt, dass sie gleichmäßig auf der Kugeloberfläche verteilt sind. Da nun eine Kugeloberfläche stets 4× A beträgt, beträgt die global gemittelte Erbsendichte, die jetzt nach der Dekorationsverschiebung gleich der konstanten Erbsendichte der Kugel ist, EXAKT E/(4×A) in 24 h. Pro Sekunde ist der Anteil der globalen Dichte E/(4×A)/(3600 s/h × 24 h).
E eingesetzt also E/(4×A)/(3600 s/h × 24 h) = [70% × 1368 Erbsen/s/qm × 3600 s/h × 24 h × A]/(4×A)/(3600 s/h × 24 h).
Kürzen liefert = [70% × 1368 Erbsen/s/qm × A]/(4×A) = [70% × 1368 Erbsen/s/qm]/(4) = 70% × 342 Erbsen/s/qm = 240 Erbsen/s/qm.
342 W/m2 kann gar kein Mittelwert der Einstrahlung sein, weil ja egal wann immer nur eine Hemisphaere beschienen wird.
Sie meinen vielleicht die energetische Umrechnung pro Zeit und weil sie wissen, das sich die Erde dreht.
Aber geben sie mal den Mittelwerte fuer 15 Stunden an!
Oder 15 Tage und 10 Stunden. Oder 1 Jahr, 3 Monate und 3,2 Tage.
Bin gespannt!
Diese Version des Herrn Schulz, missachtet also die Definition des Mittelwertes.
Nach Ihm beträgt der mittlere Stromververbrauch eines Tages nicht 100 Wh/24h = 4,167 W, wenn Sie einen Verbraucher von 100 W nur 1 h am Tag anmachen und den Rest des Tages auslassen.
Er kapiert nicht die Definition!
Herr Kuck,
Die Mittelwerte sind ja – wie Sie an meinen Graphiken sehen- nur das Resultat der Zeitverläufe für Leistungsdichten und Temperaturen.
Die sind der Ausgangspunkt für Analysen und Bilanzen wie KT und ich sie daraus abgeleitet haben. KT gingen damals ja von Zeitverläufen von Messdaten aus.
Sie verrennen sich hoffentlich nicht in falsche Annahmen, die durch die auch Ihnen vorliegenden Fakten (z.B. in Form meiner Zeitverlaufsberechnungen) widerlegt sind.
Dass 342 der 24h- Stundenmittelwert ist, ist unbestreitbar, ich hoffe, Sie versuchen sich nicht auf eine solche für Sie völlig aussichtlose Debatte einzulassen.
Denn dass die mathematische Gleichung 24 × M = 12 × 684 + 12 × 0 die Lösungen für den 24h-Mittelwert M=342 hat, ist nun wirklich unbestreitbar.
Das ist selbstverständlich, und setzt ja weder die Fachliteratur, noch KT noch ich voraus.
An den Temperaturkurven sehen Sie, wie der Treibhauseffekt die Beobachtungen erklärt. Es besteht daher keine Notwendigkeit für Ihre ausschließlich nachts wirkende Gegenstrahlung, es geht auch mit der Gegrnstrahlung wie sie tatsächlich auch gemessen wird, also mit tags wie nachts von der Größenordnung (je nach Wetter und Klimazone) 200-400 W/m2.
Ja, wenn Sie wollen, rechne ich noch was, das ist nicht so aufwendig. Sie müssen nur vollständig vorgeben, an welchem Fall Sie interessiert sind. Ich mache das aber nur, wenn Sie den Ergebnissen auch wirklich Beachtung schenken, damit Sie lernen, wie der Treibhauseffekt wirkt.
Ich habe nicht den Eindruck, dass Sie die Kurvenverläufe über den 24h-Tag interessiert und Sie wissen, warum diese so sind.
Die Widerlegung schrieb ich doch schon im Text.
Ober beruht Ihr Argument gegen den Treibhauseffekt auf etwas anderes als auch der Nicht-Existenz der 33K?
Dann werden Sie mir Ihre Argumentaion gegen die Existenz des Treibhauseffektes erst noch erklären müssen.
Herr Kuck
Ja schon, na und? Was hat das mit Ihrer Rechnung und einem Beweisversuch zur Widerlegung der Existenz des Treibhauseffekts zu tun? Da spielen einzelnen Ort gar keine Rolle, denn es geht ja um die Energiebilanz der gesamten Erde.
Ja schon, na und?
Die Erde dreht sich in 24h einmal um sich selbst. Davon müssen auch Sie ausgehen.
Wieso nicht? Haben Sie nicht bemerkt, dass ich mit den Erbsen genau erklärt habe, warum aus einem Parallelbündel von Sonnenenergiestrahlung, die auf eine rotierende Kugel einfällt, bei gleichmäßiger Verteilung auf der Kugeloberfläche auf exakt ein Viertel der Dichte im Strahlenbündel fällt? Weil die Kugeloberfläche viermal ihrer Querschnittsfläche beträgt und in 24h eine feste Menge an Erbsen am Ort der Erde vorbeiströmt. Jede Erbse, die dem Strom entnommen wird, wird entweder reflektiert (30%) oder klebt auf der Kugel (70%). Damit ist völlig klar, wieviele Erbsen nach 24h an der Kugel hängen.
Dass die Atmosphäre sich zusammen mit dem Rest der Erde um die Sonbe dreht, sollten Sie tatsächlich annehmen.
Finden Sie das nun bemerkenswert?
Ja, und?
Aber für die materiellen Orte der rotierenden Erde. Und nur dies ist für die Wirklichkeit und Physik relevant. Es gibt keine materielle Nachthalbkugel.
Die Naturgesetze gelten für aber Materie. In unserem Fall müssen Sie die Naturgesetze auf rotierende Luft und Erdboden anwenden. Der zeitliche Wechsel zwischen Tag und Nacht jedes Ortes bestimmt ja die Ergebnisse der Bilanz, denn jeder Ort durchfährt in 24h Tag und Nacht mit der entsprechend wechselnden Sonneneinstrahlung. Seine Bilanz der absorbierten Sonnenstrahlung ergibt sich daraus, wie lange der Ort beschienen wurde. Dies bestimmt die Tempertur- und Leistungskurven.
Meine Kurven zeigen das, gucken Sie nochmal drauf.
Wenn Sie nun meinen, Sie könnten eine „virtuelle“ Tag- und Nachthalbkugel betrachten die von zeitlich (aufgrund der Erdrotation) stets wechselnder Erdmaterie „dargestellt“ wird aber selbst keine fixe Materie ist, so gelten für Ihre unmateriellen Halbkugeln nicht mal die Naturgesetze. Was Sie da machen, ist physikalisch gesehen also Unsinn.
Da gibt es auch nichts zu begreifen, da das Klima der Erde nicht durch zwei Orte bestimmt wird.
Ich glaube, Sie wollen etwas anderes aussagen, vielleicht im Sinne von, dass diese Orte ein regionales Klima „materialisieren“, aber so wie Sie es sagen, ist es Quatsch und tut nichts zum Thema.
Denn Sie betrachten ja die globale Bilanz. Also müssen Sie auch die globalen Werte (also die Messwerte der gesamten Erde bzw. die daraus berechneten Flächenmittel) dazu hernehmen, ganz einfach.
Habe ich neue angekündigt? Was wolken Sie sehen?
Was Sie da machen, ist physikalisch gesehen also Unsinn.
Also, wenn Sie sich auf dieser Ebene rechtfertigen wollen, verschwende ich meine Zeit.
Mich interessiert eigentlich nur Ihre Argumentation, warum Sie anhand der Energiebilanz glauben, dass es keine Gegenstrahlung ohne Wolken geben könne.
Da haben Sie nichts geliefert, was physikalisch zumindest möglich wäre. An Ihrer Fantasie zweifelt wohl keiner, aber damit überzeugen Sie niemanden.
Arno Kuck 12. Mai 2025 13:07
Stimmt nicht. Ist auch an Ihrer Rechnung zu sehen:
Sie haben die Gegenstrahlung vergessen, die nach Ihrer Rechnung 3720 Wh/m² sein muß. Die genauen Zahlen werden etwas anders sein.
Die Gegenstrahlung ist Teil des Energiekreislaufs: Der Energiekreislauf besteht aus dem Wärmeinhalt der Atmosphäre, der Gegenstrahlung und der Absorption eines Teils der Oberflächenabstrahlung.
Arno Kuck 14. Mai 2025 12:02
Wissen Sie nicht, was Sie schreiben:
(Arno Kuck 12. Mai 2025 11:33)
Ich nahm an, dass die Temperaturen zwischen 283 K und 293 K bei Ihnen die der Erdoberfläche sind. Denn nur dazu passen ja auch die von Ihnen angegebenen Oberflächenabstrahlungen von 417 W/m2 (= SB zu 293 K) bzw. 364 W/m2 (= SB zu 283 K). Nach Ihrer Tabelle geht an der TOA in 24h im Mittel 235 W/qm ins All, ohne Temperaturabgabe.
Klären Sie diesen Widerspruch in Ihren Aussagen bitte auf, danke!
Sie scherzen. Da ist gar nichts offensichtlich! Und wenn Sie meinen sich durch Ihr „offensichtlich“ dem Beweis entziehen zu können, so zeigt das nur, dass ihre Behauptung unbeweisbar ist.
Glaube ich aber nicht, ich habe Ihnen auch gezeigt, dass es nicht so ist.
Es ist ja sogar so, dass auch bei gleichem (beliebigem) Zeitverlauf der Gegenstrahlung (und gleicher Sonneneinstrahlungskurve) die Temperaturverläufe am Boden sich unterscheiden können, wenn nur die Wärmekapazität eine andere ist. Ob der Fall meteorologisch realistisch ist, sei mal dahingestellt, aber das folgt daraus zumindest physikalisch, denn die Größe der Wärmekapazität beeinflusst ja, wie der Energieüberschuß am Tage durch die Sonne in die Nacht übertragen wird: je größer die Wärmekapazität desto gedämpfter der Temperaturverlauf (bei gleichem Gegenstrahlungs- und Sonnenverlauf), denn mehr Energie geht tags in den Boden und kommt nachts wieder raus, hält den Boden also nachts länger warm.
habe ich doch schon beschrieben: Sie bekommen auch eine ausgeglichene Energiebilanz mit korrekten Leistungsmitteln Tags und Nachts für die TOA hin, wenn die Bodentempertur nahezu konstant wäre, einfach C erhöhen.
Herr Kuck,
Sie schrieben:
ich fragte:
Ich nahm an, dass die Temperaturen zwischen 283 K und 293 K bei Ihnen die der Erdoberfläche sind.
Ist diese Annahme nun richtig oder nicht?
ich fragte:
Ich nahm an, dass die Temperaturen zwischen 283 K und 293 K bei Ihnen die der Erdoberfläche sind.
Zum zweiten Mal: Ist diese Annahme nun richtig oder nicht?
Damit bin ich einverstanden, das ist ja Ihr Fall, den ich im linken Bild gezeigt habe. Sie sehen den zugehörigen Temperaturverlauf darunter, der Ihre Werte erklären kann.
Ja, klar. 53 W/qm ist der Überschluß am Tage zwischen Sonneneinstrahlung und der Abstrahlung des 293 K warmen Bodens, der ohne Gegenstrahlung direkt ins All geht.
Was Sie jedoch zusätzlich beweisen müssen ist, dass diese 53 W/qm im Boden gespeichert werden müssen, bis der Boden von der Tagseite auf die Nachtseite wechselt und diese Energie nachts wieder freigibt. Denn nur so bekommen Sie ja die Nachtbilanz hin, indem Sie 310 W/qm Gegenstrahlung ansetzen, die dafür sorgt, dass die Bodenabstrahlung 363 W/qm beträgt und der Verlust ins All 53 W/qm.
Wie ist Ihnen aber schon verrechnete, sind die 53 W/qm ein willkürlicher Wert. Denn die Bilanz ist ja mit jedem x (nicht nur 53) erfüllbar:
Bodenabstrahlung = 470 – x (Tag) + 310 + x Nacht = 2 × 390 (24h)
Abstrahlung an TOA: 470 – x (Tag) + x (Nacht) = 2 × 235 (24h).
Bilanz der Atmosphäre in der Nacht:
310 + × (100% absorbierte Bodenstrahlung in Luft)= 310 (Verlust aus Luft durch Gegenstrahlungsabstrahlung) + x (Verlust aus Luft durch Abstrahlung ins All)
Das x, bei Ihnen speziell ist x=53 W/qm, hebt sich natürlich immer auf. D.h. x ist beliebig. Ihre 53 W/qm ergeben sich nicht aus physikalischen Zwängen, sondern, weil Sie den Temperaturunterschied von 10 K haben wollen.
Physikalisch ist x natürlich vergeben durch die Wärmekapazität des Bodens, den die bestimmt den Temperaturunterschied zwischen Tag und Nacht.
Und mit anderem C bekommt man ein anderes x.
Was aber eigentlich wesentlich ist – und das haben Sie noch gar nicht begriffen – ist die Tatsache, dass auch die Gegenstrahlung auf Tag und Nacht gleichverteilt werden kann und trotzdem derselbe Temperaturunterschied von 10 K zwischen Tag und Nacht möglich ist. Das habe ich Ihnen im rechten Bild gezeigt.
Ihre 33,8 K bei 190,9/119,1 W/qm Tag-und-Nacht-Gegenstrahlung erfolgen nicht zwingend. D.h. Ihre Behauptung:
ist nicht folgerichtig. Denn der Temperaturunterschied ist auch abhängig vom Energieüberschuß am Tage, der an C hängt bzw. von Ihnen willkürlich gewählt wurde (z.B. sind die 180,6 W/qm Energieüberschuß willkürlich von Ihnen gewählt, um für 33,8 K Temperaturunterschied zu bekommen).
Damit wird aber Ihr Argument, dass nur mit 310 W/qm „Nachtgegenstrahlung“ (und nicht bei Tag-und Nacht-Gegenstrahlung) die 10 K Temperaturunterschied erklärt werden können, widerlegt.
Verstehen Sie das nun endlich?
Herr Kuck,
Was meinen Sie? Welche Wärneverluste vergleichen Sie?
Die Erde kühlt schon dann ab, wenn es irgendeinen Wärmeverlust ins All gibt, der nicht ausgeglichen wird. So wie Sie sich (ungenau) ausdrücken, ist es falsch.
360 W/qm am Tage kenne ich nicht bei Ihnen.
In Ihrer handschriftlichen Tabelle steht für die Oberflächenabstrahlung 480,3 W/qm bei 303,4 K bzw. im anderen Fall 417 W/qm bei 293 K.
Kennen Sie Ihre eigenen Zahlen nicht mehr?
Der letzte Wert von 417 wird im Bild links in meiner Graphik mit 420 durch meine Rechnung fast genau reproduziert.
Ich bezog mich hierauf, klären Sie mich auf
Aus welchen Daten errechnen Sie 360 W/qm? Und was wollen Sie damit sagen?
Herr Kuck,
Ihre Gleichung ist falsch, denn Sie haben vom Eintrag in den Boden (470+155 = 625) den Abgang aus der Luft (265) abgezogen. Die Verknüpfung ist falsch. Sie müssen immer die Bilanz am selben Objekt machen (entweder Boden oder Luft).
Nein, das ist physikalisch völlig falsch.
Die Bodentemperatur berechnet sich selbstverstänlich gemäß der thermischen Abstrahlung, also 420 W/qm hier, macht rund 293 K, denn sigma× 293^4 = 420 W/qm. Die 292 K sind korrekt, denn nach Hölder ist der Temperaturmittelwert geringer als die Temperatur aus einem Leistungsmittelwert.
Herr Kuck,
ok, Sie beziehen sich auf meinen Fall rechts. Die korrekte Bilanz ist:
Die Bilanzen des Bodens sind dort:
Tag: 470 (Sonne ein) + 155 (Gegenstrahlung ein) – 420 (Abstrahlung des Bodens) = 205 (Bodenwärmestrom ein). Die positive Bilanz des Tages führt zur Erhöhung der Temperatur über den Tag
Nacht: 0 (Sonne ein) + 155 (Gegenstrahlung ein) – 360 (Abstrahlung des Bodens) = -205 (Bodenwärmestrom aus). Die negative Bilanz der Nacht führt zur Abkühlung des Bodens über die Nacht.
24h = Mittelwerte von Tag und Nacht: 235 (Sonne ein) + 155 (Gegenstrahlung ein) – 390 (Abstrahlung des Bodens) = 0 (Bodenwärmestrom neutral). Die über 24h ausgeglichene Bilanz führt zur Stationarität des Klimas mit 24h-periodischem Verlauf der Temperatur- und Leistungskurven.
Es gibt keine Änderung der mittleren Temperatur des Bodens.
Die Bilanzen der Atmosphäre dort:
Tag: 0 (keine Absorption von Sonnenstrahlung in Luft) + 420 (durch Treibhausgase/Wolken vollständig absorbierte Wärmestrahlung des Bodens) – 155 (Gegenstrahlung der Treibhausgase/Wolken zum Boden) – 265 (thermische Abstrahlung der Treibhausgase/Wolken ins All) = 0:
keine Änderung der Lufttemperatur.
Etc
Herr Kuck,
Sicher, das x lässt sich ja durch die Wärmekapität C „einstellen“. Auch bei anderem G(t).
Sie glauben, dass die beiden 12h-Temperaturmittelwerte alleine von den 12h-Leistungsdichtemittelwerten gemäß SB bestimmt wären. Das stimmt aber nicht, denn es gilt nur, dass F(t) = sigma×[T(t)]^4 gilt. Wenn T einen Temperaturgang hat, gilt F-Mittel > sigma×[T-Mittel]^4 aufgrund der Hölder-Ungleichung.
Herr Kuck
Es ist doch unschwer an dem Diagramm anhand der Pfeilrichtung zu erkennen, dass beide Zahlen Verluste ins All sind. 265 W/qm der Abstrahlungsverlust am Tag, 205 der der Nacht, macht im 24h- Mittel 235.
Erklären Sie mal, wie Sie das falsch sehen können.
Die Verluste ergeben sich ja durch Abstrahlung aus der Atmosphäre und vom Boden oder?
Bezüglich der Atmosphäre, könnte man sagen, das die Gase die strahlen für diese Wärmeverluste verantwortlich sind?
ich verändere etwas Ihre Gleichungen für Ihren linken Fall
Tag 470 – (420 + x) = 50 – x
Nacht 0 + 310 – (360 – x) = – 50 + x
geht genauso mit Ihrer Nachtgegenstrahlung.
Das globale Mittel.
Dem zugrunde liegt jedoch -wie bereits mehrfach erklärt- die Temperaturverteilung der Erde, also viel mehr Messpunkte als nur zwei wie bei Ihnen.
Das ändert nichts daran, dass Sie falsche Behauptungen zur Kiehl Trenberth Bilanz machen.
Ich bezog mich auf Ihre Behauptung:
Ich antwortete
Das globale Mittel (ist die eine berechnete Temperatur, bei der das zutreffen kann).
Dem (der Bilanz) zugrunde liegt jedoch -wie bereits mehrfach erklärt- die Temperaturverteilung der Erde, also viel mehr Messpunkte als nur zwei wie bei Ihnen.
Nochmal: dass jeder Energiebilanz in der meteorologischen Fachliteratur des Klimasystems (inkl. der von Kiehl Trenberth) Messungen von vielen Orten der Erde zugrundeliegen, impliziert schon die Sinnhaftigkeit einer globalen Bilanz. Dass man aus dem Datensatz der Temperaturen eine globale Mitteltemperatur ableiten kann, ist dann nur noch eine vergleichsweise kleine Übung.
Der Punkt ist, dass Sie daraus nicht den falschen Schluß ziehen dürfen, das globale Mittel wäre die einzig der Bilanz zugrundeliegende Temperatur oder dass Sie sogar glauben, es lägen den Bilanzen aus der Fachliteratur (inkl. der von Kiehl Trenberth) gar keine Messungen zugrunde oder das Ganze sei eine „Erfindung“.
Ich hoffe, das denken Sie nicht, und dass ich Ihre Behauptung „überinterpretiert“ habe.
Er spielt für die Bilanz keine Rolle. Die Energiebilanz beinhaltet Energieflüsse.
Herr Kuck
Die Energiebilanz beinhaltet Energieflüsse
Was meinen Sie mit „Mischmasch“? Klar ist ja, dass weder Tag noch Nacht einzeln eine Netto-Null-Bilanz haben müssen, denn der Boden speichert ja Energie zwischendurch. Im stationären Zustsnd gilt die 24h-Periodizität.
Das liegt an Ihrem Postulat von Gl. (1). Da ich keinen physikalischen Grund kenne und Sie keinen nannten, warum Ihre Gl. (1) einen Realitätsbezug haben sollte, ist Ihr Ergebnis nur ein mathematisches Resultat.
Arno Kuck 14. Mai 2025 14:07
„es kann nicht sein“
Wärmeverluste können nicht in W/m² angegeben werden, sondern nur in Wh/m².
Eine Angabe in W/m² ist nur möglich, wenn der zeitliche Verlauf gleich ist.
Ihre Vorausetzung ist in Wirklichkeit aber nicht erfüllt, denn die Orte auf der Erdoberfläche zeigen ja einen 24h-Temperaturgang.
Es gibt in Wirklichkeit keine Orte, die stets Nacht haben und konstant kälter sind als andere Orte, die stets Tag haben
Sie meinen, dass in diesem Zufall etwas besonders steckt?
Erklären Sie das physikalische Prinzip dahinter, welches ich ja dann nicht kennen dürfte.
Ich habe Ihnen schon gezeigt, dass auch eine gleichmäßige Gegenstrahlung zu realistischen Temperaturvetläufen und realistischen Tag- und Nachtmitteln in Temperatur und den Leistungen führt. Was ist Ihnen daran nun nicht klar?
Arno Kuck 14. Mai 2025 16:29
Halten Sie die Leser für dumm? Nur zwei konstante Temperaturen???
Wie lange sind dann Tag und Nacht (Taglänge zwischen 7 und 17 h: https://de.statista.com/infografik/17559/tageslichtdauer-in-deutschland/ ). Wie passiert die Umschaltung von der konstanten Tagtemperatur auf die konstante Nachttemperatur?
Wie erklärt: es gibt keinen Grund anzunehmen, dass Kiehl Trenberth oder andere wissenschsftliche Energiebilanzen von einer flachen Erde ausgehen.
Wer das behauptet, kann nicht rechnen.
Herr Kuck,
Warum? Bei Kiehl Trenberth 97 fällt offensichtlich auch 470 W/qm am Tag, 0 bei Nacht ein.
Herr Kuck,
nur zur Klarheit – wir reden über meinen Fall rechts im Bild mit konstant 155 W/qm Gegenstrahlung, richtig?
bilden Sie doch einmal die Differenz ihren beiden Gleichungen:
Von welche beiden Gleichungen?
60 W/qm taucht in meinem Fall rechts, wie Sie sehen, gar nicht auf.
Falsch, im Fall rechts bekommt der Boden wie erklärt 205 W/qm am Tag und verliert 205 W/qm in der Nacht. Das (der Bodenwärmestrom) steht doch unten im Kringel.
Na da bin ich gespannt…
PS lesen Sie meine Antworten eigentlich?
Herr Kuck,
Um den Anfang unserer Diskussion nicht aus dem Blick zu verlieren, bitte ich Sie, die beiden Fälle im Bild links (Ihre Berechnung mit der „Nachtgegenstrahlung von 310 W/qm und keiner am Tag) und meiner rechts (durchgehend Gegenstrahlung von 155 W/qm) zu vergleichen.
Sie sehen dort, dass in beiden Fällen
A) alle 24h-Mittelwerte in Leistung und Temperatur übereinstimmen.
B) die 12h-Temperaturmittel und 12h-Abstrahlungsleistungsmittel des Bodens ebenfalls (nahezu) übereinstimmen.
C) die 12h-Temperaturmittel zwischen Tag und Nacht um rund 10K differieren
Stimmen Sie A), B) und C) zu?
Nun war Ihr Ausgangspunkt, eine „exklusive Nachtgegenstrahlung“ zu postulieren doch genau – so wie ich es verstanden habe – dass Ihrer Meinung nach nur mit diesem Zritverlauf diese Temperaturdifferenz von rund 10K erklärbar wäre und mit der 24h-Energiebilanz vereinbar wäre.
Nachdem nun meine Rechnung zum rechten Fall dies widerlegt, indem ich auch für durchgehende (Tag+Nacht) Gegenstrahlung 1) die Energiebilanz erfülle, 2) dieselben 12h-Temperaturen (und -differenz) wie in Ihrem Fall links bekomme, ist Ihre Behauptung aber doch hinfällig.
Kommentieren Sie bitte konkret meinen Gedankengang und diese Schlußfolgerung daraus. Können Sie den Schluß nachvollziehen oder habe ich etwas übersehen?
Arno Kuck
Das war nicht meine Frage. Ich fragte, ob Sie zustimmen, ob Sie meinen Aussagen A), B) und C) zustimmen, dass sowohl Ihre Nachtgegenstrahlung wie auch die Tag- und Nachtgegenstrahlung dieselben Lösungen für die benannten Werte liefern.
Nochmal: Ich fragte, ob Sie zustimmen, ob Sie meinen Aussagen A), B) und C) zustimmen, dass sowohl Ihre Nachtgegenstrahlung wie auch die Tag- und Nachtgegenstrahlung dieselben Lösungen für die benannten Werte liefern.
Mathematisch, physikalisch nicht. Der Wert der Gegenstrahlung/Bodenabstrahlung ist nicht beliebig, sondern wird durch den Strahlungstransport durch die Atmosphäre determiniert.
Welche Lösung, worauf antworten Sie da eigentlich?
Ich erklärte Ihnen, warum Ihr x zwar mathematisch beliebig ganzzahlig als Lösung möglich, aber physikalisch nicht.
Was verstehen Sie daran nicht?
Herr Kuck,
Ist Ihnen inzwischen bilanztechnisch klargeworden, warum die Differenz zwischen Abstrahlung Boden Tag – Abstrahlung Boden Nacht NICHT den Wärmeverlust des Bodens der Nacht definiert?
Herr Kuck
Reply to Thomas Heinemann
16. Mai 2025 11:26
Nun ja, über Tausende von Jahren hat man schon Klimavariationen. Aber wenn Sie sich mit Ihrer Aussage auf grobe Klimazonen beziehen, so kann man zustimmen.
Das folgt plausibel daraus, ist aber nicht der Punkt. Denn das ist ja keine physikalische Notwendigkeit, sondern nur Resultag aus dem Klima.
Gleich bleibt verglichen mit was?
Wenn Sie Ihren linken („Nachtgegenstrahlung 310“) und meinen rechten („durchgehend Gegenstrahlung 155“) Fall vergleichen, dann sehen Sie doch, dass die Tagtemperatur mit rund 293 K in beiden Fälle gleich ist und die Nachttemperatur von 282 K gleich ist.
Ich habe meinen Fall ja so gemacht, dass die 12h-Mittel die gleichen bleiben wie in Ihrem Fall.
Mit „der Gegenstrahlung (155 W/qm)“ meinen Sie das 24h-Mittel, welches in unseren beiden Fällen 155 W/qm beträgt.
Wenn nur dieser Wert kleiner wird und C und ET gleich bleiben, so wird es tags und nachts am Boden kälter. Und umgekehrt bei Erhöhung. Das ist das Wesen des Treibhauseffekts.
Sicher. Ich habe das ja schon kommentiert. Die Gleichungen sind klar.
Das ist richtig. Der Bodenwärmestrom ist hier dann +/- 150 W/qm.
Mathematisch richtig.
Mathematisch nichts, wenn der Bodenstrom 150 W/qm durch ein physikalisch mögliches C realisiert werden kann (was möglich ist), ist alkes ok. Die 12h-Temperaturen sind natürlich andere als bei unseren zwei Fällen im Bild.
Klar, müssen auch nicht. Denn 170 ist nicht der Bodenwärmestrom QT, sondern die Differenz der Bodenabstrahlungen Tag und Nacht XT-XN.
Ich nehme mal Ihre Notation (E = abs. Sonnenstrahlung, nur am Tag, X = 24h-Mittel der thermischen Abstrahlung des Bodens, XT 12h Mittel Tag, XN Nacht, QT, QN Bodenwärmeströme, mit QT+QN = 0 wegen Stationarität), dann gilt allgemein:
Tag: 470 (E) + 155 (GT)– (420 + x)(XT) = (205 – x)(QT)
Nacht: 0 + 155 (GN)– (360 – x)(XN) = (– 205 + x)(QN)
Also gilt allgemein:
Tag: E + GT– XT = QT {TB}
Nacht: 0 + GN– XN = QN {NB}
Aus der Stationarität folgt für
{TB} + {TN}: 0=QT+QN =E + GT– XT + GN– XN = E + G – X.
Damit ist der 24h-Mittelwert der thermischen Abstrahlung X = E +G.
Aber es gibt keine physikalische Notwendigkeit, dass XT-XN = QT gilt.
Nimmt man noch die Bilanz der Atmosphäre dazu und bezeichnet mit Y die Wärmeabstrahlung ins All, so folgt E = Y, d.h. das für Stationarität des Klimasystems nötige Strahlungsgleichgewicht an der TOA.
Da mit steigt die 24h-Mitteltemperatur des Bodens (bei gegebenem E) mit steigender Gegenstrahlung G, wie ich schon sagte (Treibhauseffekt). Denn X ist ja damit korreliert.
Nun haben Sie speziell noch die physikalisch mir sinnlos erscheinende Differenz der Tag- und Nachtgleichungen gebildet. Die ist allgemein formuliert {TB} – {TN}:
E + GT– XT – (GN– XN) = QT-QN = 2xQT, oder zusamnengefasst:
E + (GT – GN) – (XT-XN) = 2xQT.
Erklären Sie mal, worin der Sinn dieser Differenzgleichung besteht.
Daran kann man nur sehen, dass, wenn die Temperatur und die Gegenstrahung konstant sind (XT=XN und GT=GN), dass dann der Bodenwärmestrom QT die Hälfte der Sonnenstrahlung E auf die Nachtseite bringt, damit es nachts so warm wie am Tag ist.
Besser so: ET = abs. Sonnenstrahlung, nur am Tag, E 24h-Mttel = ET/2
In den Tagesgleichungen muss also E gegen ET ausgetauscht werden, z.B. ET + GT– XT = QT. Die 24h-Gleichungen sind richtig.
Herr Kuck,
Sie brauchen sich nicht wiederholen. Aber immerhin haben wir jetzt Klarheit in den Gleichungen.
Aber mit dem Ergebnis Ihrer Abschätzung wollen Sie doch die wissenschaftlichen Energiebilanzen widerlegen… ideal reicht dafür nicht!
Sie müssen sich mit den Daten und Argumenten, die Grundlage für die wissenschaftliche Energiebilanz sind, befassen.
Die wissenschaftlichen Energiebilanzen legen Beobachtungen zugrunde.
Sie konstruieren Ihren „idealen Zustand der Erde“ vermeindlich durch Herauspicken von zwei Orten mit für Sie „günstigen“ Temperaturmitteln.
Sie wollen doch nicht ernsthaft behaupten, dass Sie mit diesen Vorausetzungen mit der Wissenschaft „in Konkurrenz“ gehen wollen.
So könnten Sie auch behaupten, der Erde sei in Wirklichkeit gar nicht abgeplattet, sondern eine ideale Kugel von exakt 6371 km Radius, indem Sie sich Orte auf der Erdoberfläche herauspicken, die genau diesen Abstand vom Erdmittelpunkt haben.
Wie gesagt, vergessen Sie Ihren Ansatz: denn es besteht für Ihre Gleichung keine reale Notwendigkeit, erfüllt zu werden. Sie wählen Ihre Orte so, dass es für diese gilt. Nur daraus folgt nichts für die globale Energiebilanz der Erde.
Herr Kuck,
Ich antworte jetzt auf Ihr
Der Punkt hatten wir doch schon geklärt, da gibt es keinen Dissenz. Wir sind uns einig über die Bilanzgln. und dass jedes x mathematisch möglich ist (physikalisch und in Wirklichkeit freilich nicht)
Tag: 470 (ET) + 155 (GT)– (420 + x)(XT) = (205 – x)(QT)
Nacht: 0 + 155 (GN)– (360 – x)(XN) = (– 205 + x)(QN)
Tag: ET + GT– XT = QT {TB}
Nacht: 0 + GN– XN = QN {NB}
Was ist eine „dumme“ Lösung? Die Zusatzbedingung „dumm“ bzw. „nicht-dumm“ haben Sie bisher nicht benutzt.
Wie unterscheidet sich physikalisch die „nicht-dumme“ Lösung von der „dummen“?
Die Gleichungen, denen wir beide zustimmen, sind:
Tag: ET + GT– XT = QT {TB}
Nacht: 0 + GN– XN = QN {NB}
Addition liefert für die 24h-Summen
24h: ET + GT– XT + GN – XN= QT+QN {GB}
Es gilt, XT+XN = 2X, wenn X das 24h- Mittel ist und XN, XT die 12h-Mittel. Dto. für alle anderen Größen (E, G, Y, Q).
Aus der Stationarität folgt Q=0, d.h. QT=-QN. Also gilt:
24h: 2E + 2G– 2X = 0 {GB}, d.h. E + G = X (Treibhauseffekt).
Führt man jetzt Ihre (mir unphysikalisch erscheinende) Größe WN := XT-XN ein, so ergibt sich dafür
WN = ET+GT- QT – (QN – GN) = -2QT + ET+(GT-GN).
Wenn Sie nun (ebenfalls für mich nicht physikalisch notwendig) fordert, dass WN = QT sein muss (warum nur…?), folgt rein mathematisch
3WN = ET+(GT-GN). Das haben Sie auch mit Ihren Zahlen bekimmen.
Schön, ja und? WN ist physikalisch nichts.
Herr Kuck, Sie bezeichnen Ihre Größe QN anders im Vorzeichen als ich, dann wird’s richtig, hier mal zu Klarheit verdeutlicht:
In der Nacht funktioniert die Physik genauso wie am Tag. Wenn Sie Ihr QN‘ = – QN (mein) wählen, sind beide Gleichungen richtig.
Habe ich auch so aufgeschrieben: QT =-QN. Gucken Sie einfach mal richtig bei mir!
Bei mir Thomas Heinemann 17. Mai 2025 16:44 ist aber ein Zwischenergebnis falsch, denn es muß heißen (fett ist korrigiert):
WN = ET+GT- QT – (GN – QN) = -2QT + ET+(GT-GN)
Denn QT-QN = QT+QN‘ = 2QT
Bis hierhin liegen Sie richtig. Aber…
… der letzte Schritt folgt aus nichts. Es ist vielmehr daher:
WN := XT – XN = ET + (GT-GN) – QT – QN‘ = ET + (GT-GN) – 2QT, wie also schon in Thomas Heinemann 17. Mai 2025 16:44
Ich hab’s mal fett korrigiert.
Sie haben immer noch nicht definiert, welche Größe Sie mit „Wärmeverlust in der Nacht“ meinen.
Ich nehmen inzwischen an, dass Sie damit die Wärmeabstrahlung in der Nacht ins All meinen, die ich mit YN bezeichne.
Da wir vereinfacht annehmen, dass die Atmosphäre keine Wärmekapazität hat, gilt Strahlungsgleichgewicht dort, d.h. für die Atmosphäre gelten die Gln.
Tag: XT – GT = YT {TA}
Nacht: XN– GN = YN {NA}
Da nun gilt (siehe bei mir)
ET + GT– XT = QT = – QN = -(GN -XN) folgt mit {NA} damit
ET + GT– XT = QT = YN
Ich denke, das wollten Sie mit Ihrem Beitrag ausdrücken.
Wie Sie sehen, erfüllen unsere beiden Fälle rechts und links diese Gleichung. Die nächtliche Wärmeabstrahlung in der Nacht ins All YN hängt also bei gegebenem ET und XT von GT ab, daher der Unterschied in beiden Fällen.
Und mit
XT – GT = YT {TA}
ET + GT– XT = QT = YN
Folgt
ET = YN + YT, also
E = Y,
was ja nicht verwunderlich ist, denn für die Erde gilt Strahlungsgleichgewicht an der TOA.
Dann kann es aber nie waermer oder kaelter werden. Ein Naturgesetz ist das nicht und dieser Aussage wird durch Groessen wie: Strahlungsantrieb glatt widersprochen.
Sie meinten sicherlich, das Strahlungsgleichgewicht eine Annahme ist.
Real kann sie nicht sein aus den vorgenannten Gruenden,
Ist das eine Frage?
Nein, QT (Bodenwärmestrom) ist nicht YT (Wärmestrom aus der Luft ins All), denn YT = XT-GT. Denn XT ist ja die Zufuhr in die Atmosphäre, YT+GT die Abfuhr, und beide sind gleich, da wir annehmen, dass die Atmosphäre keine Energie speichern kann (CA =0).
Diese Gleichung für den Boden:
Stimmt, siehe meine oben, ist identisch:
Nacht: XN– GN = YN {NA}
Ich habs verstanden, sie nicht?
Sorry
{TN}-> {NB}Herr Kuck,
Sie wiederholen sich ohne wirklich zu erklären, was ich nicht verstehen würde. Dabei bin ich bereits mehrmals auf Ihre Argumente detailliert eingegegen. Wir haben sie nun sogar in Gleichungen gefasst. Haben Sie immer noch nicht verstanden, dass Sie mir Selektieren einzelner Orte keine globaken Aussagen machen können?
Das ist nicht mein Zitat, sondern Ihres.
Meine Antwort gestern darauf war:
Gleich bleibt verglichen mit was?
Wenn Sie Ihren linken („Nachtgegenstrahlung 310“) und meinen rechten („durchgehend Gegenstrahlung 155“) Fall vergleichen, dann sehen Sie doch, dass die Tagtemperatur mit rund 293 K in beiden Fälle gleich ist und die Nachttemperatur von 282 K gleich ist.
Ich habe meinen Fall ja so gemacht, dass die 12h-Mittel die gleichen bleiben wie in Ihrem Fall.
Sie meinen „Mit der zusätzlichen Gegenstrahlung 155 W/qm“, dass am Tag die Gegenstrahlung von 0 in Ihrem Fall links auf 155 W/qm in meinem Fall rechts steigt und trotzdem die 12h-Temperaturmittel am Tag in beiden Fällen 292 K ist?
Dass es so ist und warum, sehen Sie doch an den Zeitkurven darunter. Die im Bild angegebenen Mittelwerte habe ich ja aus den Zeitkurven berechnet. Sie können selbst überprüfen, dass die Mittelwerte diese sind, indem Sie mit einem Lineal die Lage der Mittelwerte pi mal Daumen abschätzen.
Sie meinen damit die nächtliche Abstrahlung ins All.
zunächst: Dass diese in Wirklichkeit tags und nachts bei rund 200 W/qm liegt (siehe Müllers Satellitenbild) ist Fakt.
Und dass in meinem Bild rechts die nächtliche Abstrahlung 205 W/qm beträgt, weil dies der Betrag ist, den die Atmosphäre bei Stationarität aufgrund Energieerhaltung ins All abgeben muss, ist ebenfalls keine Glaubenssache, sondern Sie sehen ja selbst, warum dies so ist, denn es kommt ja aus den Kurvenverläufen und ihrer zugehörigen Bilanz hedaus. Einfach gucken und nachdenken!
Das Sattelitenbild ist keine Abbildung für Tag oder Nacht, sondern wie sie selber sagen gemittelte Werte. Was soll man da also sehen?
Den Mittelwert
Und damit koennen sie erklaeren, das es tagsueber waermer wird und es sich nachts abkuehlt?
Nein, warum sollte ich? Und warum brauchen Sie für diese Beobachtungstatsache eine Erklärung?
Sie haben mal wieder das Thema nicht verstanden.
Thomas Heinemann Reply to Werner Schulz 19. Mai 2025 8:37
Werner hat zur Zeit anscheinend Schwierigkeiten, bis zwei zu zählen. Da ist es wahrscheinlich zuviel zu erwarten, dass er den Widerspruch zwischen dem von Satelliten bestimmten Mittelwert bei wolkenfreiem Himmel und dem Mittelwert für wolkenfreien Himmel bei Herrn Kuck zu erkennen.
Ja, mal wieder, aber ist sein Problem.
Die Temperatur kommt einzig über die Abhängigkeit der thermischen Abstrahlung gemäß SB ins Spiel.
Herr Kuck, Ihr Temperaturmessungs-Argument gegen Ebel ist eher Desinformation, denn die Ursache dafür dass Herr Ebel für CO2-Verdoppelung (also +420 ppm) statt 0,6 siebenfache (!) 4,2 Grad behauptet, hat doch ganz andere Gründe. Er geht von einer (vermeintlich durch Anstieg der Tropopause) zu hohen CO2-Sensitivität aus und vermutet dazu fälschlich dass das gemessene ∆T pro 100 ppm zu 100% statt nur etwa zu 20% vom CO2 verursacht wurde.
Mich erinnert das daran dass das ∆T offenbar proportional zum Anstieg der Gehälter der Klimaforscher ist – oder vielleicht sogar auch proportional zur Zahl der Störche.
Peter Dietze 14. Mai 2025 9:01
Herr Dietze kommen Sie möglichst schnell von Ihrem hohen Roß des Irrtums herunter. Der Anstieg der Tropopause ist nur eines der Ergebnisse (Regelpozesse) – das hat schon Fortak 1971 genannt, Ich habe bis jetzt nichts gelesen, daß Fortak falsch liegt.Ich glaube auch nicht, daß es Ihnen gelingen wird Fortak gravierende Fehler nachzuweisen.
Jede Länge ist proportional der Treibhausgaskonzentration. Speziell der Temperaturgradient ist proportional dem Produkt aus Wärmestrom und Treibhausgaskonzentration. Wäre alles unverändert, wäre der Temperaturgradient allein proportional der Treibhausgaskonzentration und die Tropopausenänderung viel größer – da aber der Wärmestrom zurück geht ist die Tropopausenänderung kleiner.
Die Höhe der Tropopause hängt vom Temperaturgradienten ab – das können Sie schon bei Schwarzschild 1906 nachlesen.
Aber nicht der adiabate in der Troposphaere, das wo sich das Wetter abspielt. Wo genau meinen sie ist das so und was bestimmt den Waermestrom?
Schon wieder der ominöse Fortak1971, ist das ein Synonym für NEbel? Was der so alles von sich gegeben haben soll, da müsste man ja eine überbordende Zitatensammlung irgendwie verlinken können. 😀
Was meinen sie? Welche Länge?
Welchen Gradienten meinen sie? Den adiabaten?
Woraus ergibt sich der Wärmestrom?
Was soll unverändert sein und was meinen sie mit
Tropopausenänderung?
Ist das ein Regelprozess, den sie da beschreiben?
Meinen sie die Tropopausenhöhe?
Mathematisch koennen sie auch noch plus 24 minus 2×12 rechnen.
Ob sie dafuer die physikalische Ableitung finden ist fraglich.
Rechnen sie doch fuer 8 Stunden. Koennen sie nicht rechnen?
Ich gebe zu bedenken das sie bitte 8 Stunden am 27. Maerz rechnen.
Sie wissen aber sicher nicht mal warum es wichtig ist den Tag zu kennen…
Und sie konzipieren ihr Energieversorgungsystem nach dem Mittelwert? Dann missachtet er die Realitaet!
Ausser elektrischen Eskapaden also keine Antwort. Habe ich mir gedacht. Das mit dem Mitteln ueber Zeit und Faleche ist gar nicht so einfach.
Erschwerden kommt hinzu das nur an zwei Tagen im Jahr die gesamte Erdoberflaeche wirklich einmal beschienen ist. Ansonsten sorgt die Neigung der Erdachse dafuer das jede Mittelung ueber die gesamte Erdoberflaeche falsch ist, da tatsaechlich and 263 Tagen eben nicht die gesamte Erdoberflaeche im tagesgang Energie von der Sonne bekommt.
Ach so, wir mitteln dann einfach Null Flaech rein! Was fuer Mittel sie anwenden. So fraglich!
Herr Kuck, 33,4 W/m² am Boden machen 6,15 Grad. Und diesen Temperaturunterschied zwischen Tag und Nacht hat noch niemand gemessen, und deshalb gibt es keinen THE?? Sie sollten zum Arzt gehen.
Ohne… wie denn?
Ja, zu trivial.
Ihnen fehlt ja der Bezug zur Realität. Ordnen Sie Ihren Zahlen reale, physikalisch mögliche Energieflüsse zu. Das werden Sie nicht ohne Widersprüche hinbekommen und deswegen ist Ihre Bilanz irreal. Das müssen Sie begreifen.
Sie haben ein Treibhausmodell mit 33 K Temperaturdifferenz willkürlich „konstruiert“.
Sie sehen aber, dass dies gar nicht zwingend ist. Selbst wenn keine Temperaturdifferenz bestünde oder eine mit 293 tags zu 283 K nachts, ist der Treibhauseffekt notwendig wie ich Ihnen per Energiebilanz vorrechnete.
So wie auch Ihre 181,6 W/qm mit Ihren 303/269 K zusammenpassen. Das war ja der Ausgangspunkt.
Ob dieser Temperaturgang tatsächlich möglich wäre, höngt davon ab, wieviel Wärmekapazität des Boden beim Tag-Nacht-Wechsel umgeladen werden muss.
Ja, mit folgenschweren Konsequenzen wie Sie sehen.
was soll das heißen? Sie müssen – wie in meiner Rechnung – die Punkte auf der Erdoberfläche um die Achse rotieren lassen, damit diese Tag- und Nacht erfahren. Alles andere wäre physikalisch falsch.
Ja, aber bei Ihnen nicht, richtig? Bei Ihnen liegt ein Punkt entweder durchgehend auf der Taghalbkugel oder der Nachthalbkugel, also irreal. Ist es das, was Sie sagen?
Das ist bei mir ja auch der Fall (Stationarität).
Wieso diese und keine anderen Werte?
Das behaupten Sie, dabei sehen Sie ja, wie ich sie berechnet habe.
Ihre grundlose Behauptung ist hilflos und trotzig. Liefern Sie Gründe, denn so ist es kindisch.
Von Stationarität gehen wir beide ja aus. Warum betonen Sie das nochmal, wenn ich es offensichtlich erfülle und selbst erwähne? Verstehe ich nicht.
Arno Kuck 9. Mai 2025 22:37
„im eingeschwungenen Zustand der Erde wird die Erde weder wärmer noch kälter.“
Aber durch seine CO2-Emissionen stört der Mensch das Gleichgewicht.
Arno Kuck 9. Mai 2025 12:35
Welche Stärke die Gegenstrahlung hat können Sie z.B. sehen:
https://wettermast.uni-hamburg.de/frame.php?doc=Zeitreihen8d.htm#STRAHLUNG
Braucht er nicht.
Wie kommen Sie auch diese absurde Idee?
Sie haben immer noch nicht geklärt, was Sie unter „Wärmeverlust in der Nacht“ verstehen, A) oder B)?
Da ich Ihnen gezeigt habe, dass man auch mit Treibhauseffekt kleinere Temperaturdifferenzen möglich sind, ist Ihre Argumention aufgrund irrealer Annahmen obsolet.
Habe ich Sie von Ihrem Irrtum überzeugt oder haben Sie sich selbst nicht verstanden?
Arno Kuck 8. Mai 2025 21:43
Falsch, zumindest muß man einen idealen Schwarzkörper annehmen.
Außerdem spiegeln für Energiebetrachtungen und Temperaturbetrachtungen die Zeit und die Zeitabhängigkeit der Leistungen eine Rolle.
Arno Kuck 9. Mai 2025 11:55
Das Ihnen als Laien die Physik komisch vorkommt, tut mir Leid.
Ich finde es nicht gut, das für Laien Zusammenhänge zu sehr vereinfacht dargestellt werden (Einstein – https://klugwort.de/zitat/so-einfach-wie-moeglich-aber-albert-einstein ):
Zu vereinfacht muss es auch nicht sein, nur verständlich und dies beherrschte Einstein besser als die meisten der heutigen Weltenerklärer. Denen ist egal ob ihnen jemand folgen kann, hauptsache sie fühlen sich berufen mit teils wirren Thesen zu glänzen. Seine Beiträge zu lesen ist dagegen ein Genuss.
Sehe ich nicht, und Sie inzwischen ja auch nicht, siehe meine Texte und die meteorologische Fachliteratur dazu.
Meine Berechnungen und Erklärungen zeigen ja überzeugend, dass aufgrund der Wärmekapazität des Klimasystems, Wärme von Tag zu Nacht gespeichert werden kann und dies die Ursache (real wie auch im Modell) für den „gedämpften“ Temperaturverlauf ist. Und somit extreme Temperaturunterschiede zwischen Tag und Nacht nicht auftreten.
Ihre Argumentation basiert – sowrit ich Sie verstehe- darauf, dass Sie zwischen Tag und Nacht 33 K Temperaturdifferenz annehmen und behaupten, dass sei so durch den Treibhauseffekt vorgegeben aber unrealistisch. Dass es unrealistisch ist und die Tag-Nachtunterschiede geringer sind, ist klar, es treten ja die Temperaturunterschiede auch mit dem real existierenden Treibhauseffekt (das ist wissenschaftlich unbestritten) so auf wie sie sind und dies völlig im Einklang mit der Physik. Auch KT berücksichtigen die realen Temperaturen
Wenn Ihre Argumentation gegen den Treibhauseffekt nun die Annahme benötigt, der Treibhauseffekt postuliert 33 K Temperaturunterschied zwischen Tag und Nacht, so ist Ihre Argumentation deswegen falsch, weil Ihre zugrundeliegende Annahme bereits nicht zutrifft.
Herr Kuck,
Nein, weder Fout×12h (Abstrahlung ins All in der Nacht) noch FB×12h (=Abstrahlung des Bodens in der Nacht) muss mit Q×12h
(= Differenz der Bodenwärmemenge zwischen Tag und Nacht) übereinstimnen.
Habe ich Ihnen ja auch schon vorgerechnet.
Arno Kuck 8. Mai 2025 23:13
Falsch in dieser Allgemeinheit. Rechnungen mit unsinnigen Annahmen führen zu unsinnigen Ergebnissen – mit den Treibhausgasen haben unsinnige Annahmen nichts zu tun.
das stimmt nicht.
Ihre 303 K Bodentemperatur und 190,9 W/qm Gegenstrahlung am Tag z.B. sind Annahmen.
Für eine stationäre Energiebilanz gehen ja auch andere Zahlen, wie ich schon zeigte.
Arno Kuck 11. Mai 2025 13:39
„ich habe keine Annahmen gemacht.“
Ein Witz, sind die Ausgangsgrößen als Geheimschrift von selbst auf Ihrem Papier aufgetaucht. Selbst bei Einfachen wie 1+2 =3 werden Annahmen gemacht.
Welche Katastrophe?
silke kosch 7. Mai 2025 15:18
Bitte genauer. Es fehlt ein Adjektiv:
Arno Kuck Reply to Jochen Ebel 8. Mai 2025 15:28
Wenn das so wäre, müßte man doch eigentlich in Satellitenbildern diese Abstrahlung bei wolkenlosem Himmel sehen, oder?
Warum ist da dann nichts davon zu sehen?
Irgendwie verstossen Ihre Vorstellungen gegen alles, was man messen kann (oder gar fühlen kann, siehe klarer Himmel bei geringer Lutfeuchtigkeit) ….
Arno Kuck Reply to Marvin Müller 8. Mai 2025 21:28
Die von Ihnen angegebene Abstrahlung von 417 W/qm am Tag bzw. 363 W/qm in der Nacht ist nicht zu sehen. Die Satelliten sehen bei wolkenfreiem Himmel maximal 300 W/m^2, was zu einem durchnittlichen Wert kleiner als 300 W/m^2 führen dürfte. Was ist die Ursache dafür, wenn die Treibhausgase nicht wirken?
Herr Mueller trollt sie. Er weiss genau das Tag und nacht auf dem Bildchen nicht sichtbar ist.
Arno Kuck Reply to Marvin Müller 15. Mai 2025 13:12
Auf dem Bild sind die vom Satelliten gemessenen Abstrahlungen zu sehen, keine Temperaturen. Und Sie schreiben: „Die Tag-Halbkugel strahlt 417 W/qm ab, die Nacht-Halbkugel 363 W/qm.„, da müßten die Satelliten also bei Wolkenfreiem Himmel im Mittel irgendwas um die 390W/m² sehen. Tun sie aber nicht, die sehen Maximalwerte von 300W/m². Wie geht das, wenn Treibhausgase nicht wirken?
Ist das Tags oder Nachts?
Werner Schulz Reply to Marvin Müller 15. Mai 2025 13:27
Beides, bei wolkenfreiem Himmel gemittelt über 10 Jahre …
Komisch, haetten sie erwartet, das man dann Tag nund Nacht sehen kann?
Wolkenfreier Himmer ueber 10 Jahre? Eine seltsame Annahme, oder?
Werner Schulz Reply to Marvin Müller 16. Mai 2025 11:56
Nein, wie solltel man das in einem Mittelwert sehen?
Wo steht sowas? Die Satelliten zeichnen neben anderen Infomationen Abstrahlung und Wolkenbedeckung auf. Wie schwer wird es da sein, eine mittlere Abstrahlung bei wolkenfreiem Himmel zu bestimmen?
Ach, kann man nicht? Und warum bringen sie das in einer Diskussion, die eine weitere Einteilung macht?
Muss die Frage nicht lauten, welchen Sinn eine solche unrealistische Grafik haben soll?
Werner Schulz Reply to Marvin Müller 16. Mai 2025 23:31
Weil die Messungen die Aussage von Herrn Kluck widerlegen. Die Begründung stand da, sie können gern zeigen, dass die Begründung falsch ist.
Warum sollte die unrealistisch sein?
Silke, das CO2 ist in 3,5 Mrd Jahren gegenläufig von Sauerstoff (von 0 auf 20%) von 17% auf etwa 0,03% gesunken, und schwankt sein 300 Mio Jahre natürlich zwischen 0,1 und 0,03% (1000-300ppm). Das Klima hat diese enorme Schwankung nicht interessiert, der Mensch war nicht da. Das sind Tatsachen. Paar verdienen gut mit der Klimakirche, weil viele viele Dumme daran glauben! Das ist alles!
Das interessiert im Zusammenhang mit dem aktuellen Klimawandel, der eindeutig durch uns verursacht wurde und wird, überhaupt nicht, Herr Georgiev.
Also eine Absenkung von 170000 ppm auf 300 ppm ÄNDERT DAS KLIMA NICHT, aber die Erhöhung von 300 auf 400 ppm ÄNDERT DAS KLIMA!! Weil von Menschen!!! Herrliche SILKE LOGIK!!!
Und warum CO2 im höheren Maße geschwankt hat, als es keine Menschen gab, spielt auch keine Rolle!!!!
Grundlage des blöden Glaubens ist das Unverständnis, dass der Mensch ein kleiner, unbedeutender Teil der Natur ist und die Natur nicht verändern kann, zumindenst im wesentlich gerungeren Maße als Bakterien, sondern sich anpassen oder aussterben muss. Nicht Herr über die Natur, sonder ein unbedeutender zeitweiliger Gast der Natur, der spätestens wenn die Sonne ausgeht, weg sein wird.
Der Mensch kann sich nicht einmal selbst nachhaltig vernichten. Selbst bei einem ausgewachsen Atomkrieg bleiben in den Urwälder und in Sibirien paar übrig, und 10.000 Jahren soäter, ein Wimpernschlag im erdgeschichtlichen Maßstab, sieht es wieder aus wie heute. Es ist Überheblichkeit und Unwissen über die Natur, um so zu denken wie du.
Herr Georgiev,
schön, dass Sie verstanden haben, dass der durch uns verursachte Anstieg der Treibhausgaskonzentration in den letzten ca. 150 Jahren für einen Anstieg der globalen Durchschnittstemperatur um ca. 1,3 °C verantwortlich ist. (Sonst würden Sie nicht verzweifelt versuchen, vom Thema abzulenken)
Sie bringen aber auch schon alles durcheinander. Wissenschaftlich bewiesen ist es durch die überwältigende Mehrheit der Wissenschaftler, daß es genau anders herum ist. Weil die globalen Durchschnittstemperatur um ca. 1,3 °K gestiegen ist, hat sich das CO2 erhöht. Ein Segen für die ganze Menschheit und Natur. Sie brauchen keine Angst haben, daß das für uns zum Nachteil gereichen könnte.
Silke, im gesamten Mesozoikum ( Erdmittelalter) war es bei ähnlichen CO2 Werte wie heute 10 Grad wärmer. Vorher hatte die Erde mal tausendfach höheren CO2 Gehalt, und ist kurzzeitig bis zum Äquator vereist und dann wieder aufgetaut, beides ohne CO2 Änderungen. Also: CO2 spielt fürs Klima keine Rolle, erdgeschichtlich bewiesen. Mikroskopische Schwankungen in einem Wimpernschlag der Erdgeschichte ist kein Beweis, sondern Selbstbetrug. Und das bisschen CO2, was die Menschen freigeben, können die Cyanobakterien locker wegfressen, sie haben ja schon 17% CO2 fast auf 0 gebracht. Sie sind zwar kleiner, aber viele… Warum sie manchmal 1000ppm zulassen, und dann wieder bis auf 300ppm reduzieren, werden sie nicht verraten….
Herr Georgiev,
alle Ursachen, die für alle Klimaveränderungen in der Vergangenheit ursächlich waren, sind für den aktuellen Klimawandel so interessant, wie die Lottozahlen aller vergangenen Ziehungen für die Lottozahlen des kommenden Wochenendes.
Was auch immer Klimaveränderungen oder Klimabedingungen der Erdgeschichte verursacht hat: Der aktuelle Klimawandel wird nachweislich durch Treibhausgase verursacht. Es ist beim heutigen Stand der Wissenschaft unmöglich, dass wir einen wesentlichen Antrieb übersehen, der für eine globale Erwärmung von 1,3°C in 150 Jahren verantwortlich ist.
Und wir übersehen diesen Antrieb auch nicht, sondern haben die Treibhausgase eindeutig als Ursache identifiziert.
Silke, wenn eine Erhöhung von 100 ppm, ( von 300 auf 400, aus welchen Grund auch immer) 1,xx Grad erwärmt, muss eine Erhöhung auf 500, 1000, 10000, 17000 ppm die Erde zum Glühen bringen. Alles da gewesen, nichts glühen. Bei z.B. 10000ppm war es 10 Grad wärmer, dann bei gleichen 10000 ppm eine Eiszeit und 8 Grad kälter, dann bei den gleichen 10000 ppm wieder, wie üblich, 10 Grad wärmer. Das wiederholt sich die ganze Erdgeschichte, bei jedem CO2 Wert zwischen 17000 und 300, mal kälter und überwiegend viel wärmer, ohne jeglichen Zusammenhang! 10 bis 17 Tausend ppm ändern das Klima nicht, und auf einmal schaffen es läppische Hundert! Ist das nicht hochgradig albern?
Katastrophenmärchenerzähler leben immer besser als der, der schuften muss, und man glaubt es, weil man es glauben will! Seit ihr nicht gläubig und geht nicht zu Kirche, straft der Gott mit Sintflut, heute, seid ihr nicht gläubig und ehrt nicht die Klimakirche, straft euch CO2 mit Sintflut! Ist das Munster nicht identisch? Nur ängstigen Gott und Teufel nicht mehr so, also muss das abstrakte CO2 her! Bist aber Spitzenreiter im CO2 Glaube: 10000 natürliche ppm machen der Erde nichts aus, aber 100 menschliche ppm erwärmen! Herrlich!!!!
Richtig, ein Anstieg des CO2-Gehaltes um 100 ppm hat zu einer deutlich messbaren globalen Erwärmung geführt. Und eine Verdopplung des CO2-Gehaltes gegenüber der vorindustriellen Zeit führt nach dem Stand der Wissenschaft zu einer Erhöhung der Temperatur von ca. 3 °C.
Wenn Sie es herrlich finden, dass dann eine halbe Milliarde Klimaflüchtlinge nach Europa kommt, dann können Sie das ja den Menschen in Deutschland vermitteln.
Sie täuschen mit Ihren sogenannten „Stand der Wissenschaft“ eine menschengemachte Krise vor und betreiben damit das Geschäft der Kollektivisten, die bürgerliche Rechte einschränken und Zusatzprofite generieren wollen. Sie sind doch beauftragt dies zu tun, oder?
Klimaflüchtlinge hat es NIE gegeben, NUR WIRTSCHAFTSFLÜCHTLINGE!!!!! „Hereingewunken“ durch die grüne Merkel …
Wenn SIE das nach fast 10 Jahren IMMER NOCH NICHT in Ihr „Hirn“ hereinbekommen haben, können SIE nur ein dummgrüner Bot der grünen Parteizentrale (oder auch CDU/CSU….., SPD……) sein.
Ulrich Tengler 9. Mai 2025 18:50
Zusammenhänge sind für Sie ein Fremdwort – analog das Klima ändert sich – aber mit dem CO2 hat das nichts tun:
Wegen der Klimaänderung sind wirtschaftliche Probleme entstanden. Wenn Menschen vor diesen Problemen flüchten – sind das Klimaflüchtlinge, obwohl deren Handeln ohne Nachzudenken als Wirtschaftsflüchtlinge verharmlost wird.
Da waren doch früher die „Parteilehrjahre“ der SED wissenschaftlicher als Ihr heutiges Klimaastrologen-Gedöns!
Da hat der Herr Ebel wohl damals nicht so recht aufgepasst …..
Ulrich Tengler 10. Mai 2025 11:25
„Klimaastrologen-Gedöns!“
Ihnen gehen wohl die Argumente aus? Ich vermute das, weil Sie so ein irres Gestammel von sich geben!
Liebe Silke,
seit ungefähr 3 Millionen Jahren kühlt sich die Erde im Durchschnitt ab.
Mit Klimaschwankungen plus oder minus 2°C.
https://humanorigins.si.edu/research/climate-and-human-evolution/climate-effects-human-evolution
Können Sie da etwas wiederlegen?
Und schreiben Sie nicht das sich das Klima nie so schnell gewandelt hat.
Rapid Climate Change
https://history.aip.org/climate/rapid.htm
Aber das Smithsonian National Museum of Natural History und das Amerikanische Institut der Physik sind sicherlich auch nur Klimaschwurbler.
„The first strong consensus statement had come in 1995 from the Intergovernmental Panel on Climate Change, representing the considered views of nearly all the world’s climate scientists. The report included a notice that climate „surprises“ were possible — „Future unexpected, large, and rapid climate system changes (as have occurred in the past).“(70) The report’s authors did not emphasize the point, however, and the press seldom mentioned it.“
Im Durchschnitt. Aber jetzt nicht mehr
Silke, wenn 100ppm 1 Grad bringen, dann erhöhen 200ppm um 2 Grad, 1000 um 10, 10000 um 100 Grad. Das schafft sogar mein Erstklässler! Es gab 10000ppm über Millionen von Jahren, aber keine 100 Grad, sondern Eis bis zum Äquator! Ein ähnlicher Verlauf über 150 Jahre im Vergleich zu Jahrmillionen ist als Nachweis lächerlich!
Ich weiß, du glaubst nicht was die liest, sondern du verstehst nur was du glaubst. Das menschliche Hirn ist so. Zum Glück gibt es kritische Geister, die die Menschheit voran gebracht haben. Wären wir vor 500 Jahre auf der Welt, hättest du mit voller Überzeugung geschrieben, die Erde ist eine Scheibe, Stand der Wissenschaft. Mich und die Mehrheit der Eike User hätte man verbrannt. Heut ist es nicht mehr üblich das Verbrennen, man wird aber verbannt als Ketzer.
Zu Migranten: habe Verständnis, dass man den Wunsch hat, lieber die Wäsche in der Bosch Waschmaschine mit Ariel zu waschen, anstatt mit der Hand im Nil-Wasser. Deshalb sind sie hier, die Millionen erhöhen die Aktienwerte von Bosch und Ariel. Allerdings mit meine Steuern. Und die von Soros finanzierten Schlepper-NGOs sind dafür unterwegs, damit die Aktienwerte steigen. Und der Klimawandel, damit Solar und Wind Aktien steigen, bei Apple ist man schon zu weit oben, da steigt nichts mehr groß. Das ist der Grund für Klimawandel und die irre Bezeichnung Klimaflüchtlinge. Und die Gläubigen sind nur nützliche Idioten, verstehen es aber nicht.
Vielleicht verschwendest du doch paar Synapsen für den Text…
Mooooment! Bitte das geozentrische Weltbild nicht mit der Scheibenwelt durcheinander bringen! Dass die Erde eine Scheibe ist war damals wohl so wenig verbreitet wie heute, aber die Erde soll das Zentrum unseres Sonnensystems sein – DAS wurde postuliert, insbesondere von den ewig gestrigen in Zentralitalien, da wo gerade wieder ein Nachfolger Petri gewählt wurde.
Schon damals galt der Anthropozentrismus wie heute – der Mensch hält sich für super wichtig, der Planet auf dem er parasitiert muss schliesslich auch der Mittelpunkt des Sonnensystems sein, schliesslich kam hier der Sohn Gottes (in Form eines Menschen – klar, ne?) in die Welt und nicht auf der Sonne.
Interessanter Funfakt in diesem Zusammenhang:
Letztens so einen ZDF-Beitrag geschaut, mit dem James-Webb-Weltraumteleskop haben sie gespannert – einen dunklen Fleck zwischen den ganzen Funkelpunkten ausgesucht und super lang belichtet und damit die „Ausdehnung des Universums“ entdeckt.
Nun, so unsinnig wie das Vorhaben selber auch sein mag, viel mir auf, dass damit MAL WIEDER angedeutet wird, dass wir im Zentrum allen Seins sind – nur bei einem Kugeluniversum mit der Erde als Mittelpunkt lässt sich die Ausdehnung des Universums mit nur EINEM Messpunkt evaluieren, ansonsten müssten mindestens 6 Messpunkte erfasst werden (in der Annahme das Universum sei eine Kugel, sonst brauchts noch viel mehr Messpunkte). Mich interessiert Astronomie sehr, deswegen sehe ich mir solche Sendungen an, aber danach fühlt man sich meist mehr verarscht als belehrt.
D’accord.
Ich hoffe, dass Ebel das auch liest. ….. ob er es versteht, ist allerdings so eine Sache ….
Ulrich Tengler 11. Mai 2025 11:25
Offensichtlich haben Sie die Übertreibungen von Georgiev nicht erkannt.
Dazu eine Frage:
In Erdgeschichtlicher Betrachtung hat CO2 vs. Temperatur offensichtlich keinen Kausalzusammenhang, max. temporäre Korellationen, jetzt (also seit der Industrialisierung ca. 1850) schon?
Da ist NICHTS übertrieben! Laut Silke hat der menschliche CO2 Anstieg 1,3 Grad erwärmt, also nach Überschlagsrechnung pro 100ppm 1 Grad. Der Verdoppelungsunfug ist nicht besser, nur mit anderen Faktoren!
Fakt ist, CO2 ist von 17% kontinuierlich auf ca. 0,1…0,03 gesunken, dabei blieb die Temperatur konstant deutlich wärmer als heute, unterbrochen durch tiefe Zacken nach unten (Eiszeitalter), also erwiesen kein Zusammenhang.
Peter Georgiev 10. Mai 2025 7:13
„10000 um 100 Grad.“
Übertreibungen sind ein beliebter Unsinn um etwas lächerlich zu machen. Beispiel:
10 kg über eine bestimmte Strecke zu tragen, können viele. Vielleicht schaffen Sie das auch mit 20 kg – also extrapolieren wir weiter 100 kg sind dann angeblich auch möglich ????
Nur weil ein paar Wissenschaftler das behaupten, ist es NICHT „die Wissenschaft“ die das behauptet.
Zudem sind solche Aussagen immer mit „könnte sein“ oder „wenn… dann“ kombiniert, einfache Geister vergessen das dann einfach und machen damit Propaganda.
Roland Fuchs 10. Mai 2025 15:52
„das behaupten“
Es gibt immer ein paar Außenseiter, die den Stand der Wissenschaft leugnen.
Die Aussagen der Wissenschaft sagen, welche Einfluß die Politik hat – und da die Politik Einfluß hat (z.B. auf die Stärke der CO2-Emissionen) müssen die Aussagen „wenn… dann“ enthalten.
Endlich haben SIE, EBEL Ihren Platz in der richtigen Wissenschaft erkannt …. 😉 SIE haben dort als staatlich alimentierter Klimaastrologe keinen! 😉
Ulrich Tengler 11. Mai 2025 21:43
Ihnen fehlt so viel Wissen, das Sie nur mit eigenen Erfindungen hausieren gehen.
silke kosch 9. Mai 2025 16:58
„Verdopplung des CO2-Gehaltes“
Eine logarithmische Abhängigkeit geben die Daten nicht her Theoretische Erwägungen (mein Buch Diagr. 4.6, S. 28) und Auswertung der Messungen sprechen eher für eine lineare Abhängigkeit: fast genau 1 K Anstieg der Oberflächentemperatur (genauer der Wetterhüttentemperatur) bei Anstieg der CO2-Konzentration um 100 ppmV.
Allerdings ist gegenwärtig die Änderung der CO2-Konzentration so gering, das für diesen geringen Bereich der Verlauf des Logarithmus fast linear ist, so daß der Unterschied zwischen lin und log sehr gering ist.
Herr Ebel, der Unterschied zwischen +0,6 Grad bei Anstieg um 420 ppmm und 1 Grad pro 100 ppm ist aber ein Faktor 7.
Peter Dietze 11. Mai 2025 13:13
„ist aber ein Faktor 7.“
Dafür das Sie Meßwerte ignorieren kann ich nicht.
Dietze, Rechnen ist wirklich schwer! Für manche sehr sehr schwer!
Ein Anstieg von 300 auf 400 ppm ist ein Anstieg um 100 ppm und nicht um 420. Ob es sich um 120 handelt, ist sowas vom nebensächlich! Und 280 hat keiner gemessen, wird nur geschätzt.
Viele Erstklässler können 400 – 300 = 100 rechnen!
Herr Georgiev, wenn Laien versuchen, Fachleute lächerlich zu machen, geht das blamabel schief. +0,6 Grad gelten für CO2-Verdoppelung (ECS, im Gleichgewicht). Wenn 420 ppm verdoppelt werden, sind das +420 ppm und ergibt nach Ebel-Messwert unsinnige 4,2 Grad. 7•0,6 ist übrigens 4,2.
Peter Dietze 13. Mai 2025 10:07
Herr Dietze hören Sie doch auf Ihre falsche (zu kleine) Klimasensitivität als Maß aller Dinge zu behaupten. Prof.Fortak (1971) hat auf Seite 78 schon geschrieben, daß ein Ansteigen der CO2-Konzentration vielfältige Regelprozesse auslöst (z.B. Ansteigen der Tropopausenhöhe, Änderung der Windmuster, Anzahl der Sonnenstunden, Erhöhung der Oberflächentemperatur usw.) – und alle Regelprozesse vernachlässigen Sie und glauben mit einer HITRAN-Rechnung bei angeblich nicht vorhandenen Regelprozessen eine gültige Klimasensitivität zu erhalten.
Ob nun der Mensch „Schuld“ hat oder nicht an der aktuellen CO2-Erhöhung kann und soll diskutiert werden.
Aber:
… zeigt für jeden Volldeppen, dass die Prognosen (wir werden alle verbrennen) nicht stimmen können. Dieser olle „galoppierende Treibhauseffekt“ hätte unsere Erde schon längst mehrfach gegrillt wenn er denn mehr als ein Hirngespinst wäre.
… und so von wegen „was in der Vergangenheit galt, gilt jetzt nicht mehr“.
Da frage ich WARUM??
Selbst der Ganteför labert nach einer halben Stunde Vergangenheitsbewältigung etwas von „das ist JETZT aber anders“ – ohne konkret zu werden.
Naja… vielleicht auch einfach weil zu viele Anthropozentriker auf der Welt sind – die halten den Menschen für so mächtig, dass sie ihm sogar einen Einfluss aufs Klima andichten.
Tja, das WARUM!
Weil wohl einige sehr gut als Weltuntergangspropheten leben, und sehr viele zu dumm sind, um es zu verstehen!
Herr Georgiev hat vollkommen Recht. Schließlich ist es wissenschaftlich schon lange eindeutig bewiesen, daß der Klimawandel zu unseren Gunsten wirkt und eindeutig nicht menschengemacht ist, sondern von der Sonneneinstrahlung und der Wolkenbildung abhängt. Sie sind mit ihren Ansichten und Argumenten meilenweit der aktuellen weltweiten Forschung hinterher.
H. Achatz 8. Mai 2025 16:14
Wieso verändert sich die Wolkenbildung?
EBEL????? Bezeichnen SIE sich nicht als Füsigger?????? 😉
Kommer Sie mal aus Ihrem grünen Bunker und schauen Sie mal noch oben …. , (Oh Gott, schmeiß mal Hirn zum Haslenußstrauch in Borkheide …..)
Ulrich Tengler 9. Mai 2025 18:54
„Bezeichnen SIE sich …“
Das konnte ich mir schon denken, das Leute mit Vorurteilen meine rhetorische Frage „Wieso verändert sich die Wolkenbildung?“ nicht beantworten können bzw. nur in der Art „das wissen wir nicht, aber das CO2 hat damit nichts zu tun“. Eine solche Antwort ist aber falsch und zumindest seit 50 Jahren überholt: Fortak 1971.
Herr Ebel,
sie sagen bei Fortak 1971 steht es ist durch CO2. Bitte zitieren sie!
Ich hab das WWW nach „Fortak 1971+CO2+Wolkenbildung durchforstet. der Schulz ist wohl der einzige der das im Zusammenhang gelesen hat. Habe sehr viel informatives zur Wolkenbildung gefunden, aber nichts das auf einen direkten Zusammenhang mit CO2 hinweist.
Einzig einen Beitrag mit Pflanzen im Zusammenhang und nicht Fortak sondern Max Planck Gesellschaft: „anhand neuer Rechnungen mit Hilfe eines Atmosphärenmodells“
Also auch nichts praktisches sondern nur Theorie mit Hilfe eines Modells. Zudem haben sie Daten verwendet die das IPCC sowieso schon vorgibt – also nichts neues im Westen.
Wenn Fortak einen Zusammenhang von Wolkenbildung mit CO2 festgestellt haben sollte, dann kann das Herr Ebel hier zitieren.
Sooft wie er Fortak 1971 hier schon zitiert hat, wäre es doch an der Zeit endlich auch einmal einen Link dazu zu posten. Ich habe nämlich auch nichts diesbezügliches finden können. :-O
Habe mal eine KI gefragt und erhielt folgende Info:
Die Frage ist, ob es einen Zusammenhang zwischen Fortak 1971 (Fortak ist ein Modell für Wolkenbildung und Klimawandel) und CO2 und Wolkenbildung gibt. Kurz gesagt: Es gibt zwar eine theoretische Möglichkeit, dass erhöhte CO2-Konzentrationen die Wolkenbildung beeinflussen, aber ein direkter, bestätigter Zusammenhang ist nicht eindeutig. Elaboration: Fortak 1971: Das Fortak-Modell (Fortak 1971) ist ein komplexes Modell zur Simulation von Wolkenbildung und deren Auswirkungen auf das Klima. Es berücksichtigt verschiedene Faktoren, darunter die Atmosphäre, die Sonne und die Wasserkreisläufe. CO2 und Wolkenbildung: CO2 (Kohlenstoffdioxid) ist ein Treibhausgas, das die Erwärmung der Erde beeinflusst. Einer der vorgeschlagenen Mechanismen für den Klimawandel ist, dass eine höhere CO2-Konzentration zu mehr Wolkenbildung führt. Zusammenhang: Die wissenschaftliche Forschung zeigt, dass eine höhere CO2-Konzentration zu einer Erwärmung der Atmosphäre führen kann, was wiederum die Wolkenbildung beeinflussen könnte. Allerdings sind die Auswirkungen von CO2 auf die Wolkenbildung sehr komplex und nicht vollständig verstanden. Experimentelle Bestätigung: Es gibt keine eindeutigen experimentellen Beweise, die einen direkten, eindeutigen Zusammenhang zwischen CO2-Konzentration und Wolkenbildung belegen, wie vom Helmholtz KLIMA dargelegt wird. Es wurden zwar Korrelationen zwischen bestimmten Regionen und kurzen Zeiträumen beobachtet, aber die Zusammenhänge sind nicht immer eindeutig. Fazit: Die Frage des Zusammenhangs zwischen Fortak 1971, CO2 und Wolkenbildung ist komplex und nicht eindeutig beantwortet. Es gibt wissenschaftliche Hinweise auf einen indirekten Zusammenhang, aber eine klare Bestätigung fehlt.
Roland Fuchs 10. Mai 2025 16:32
Fortak1971 schreibt auf Seite 78:
Aber Laien, die keine Ahnung haben überblicken die Regelprozesse und „wissen“ das die Regelprozesse die Wolken nicht betreffen – welch ein Irrsinn.
Das ganze Zitat:
Für die vielen komplizierten Regelprozesse hat Fortak nur ein Beispiel genannt, die Verdunstung. Aber auf die Wolkenbildung hat nicht nur die Verdunstung Einfluß, sondern z.B. auch die Zirkulation (Wind) und der Wind hängt wieder von den Temperaturen ab usw.
Herr Ebel,
ihnen ist schon klar das die Gegenstrahlung keine zusaetzliche Waerme ist, oder?
Schauen sie sich doch die Definition vom THE beim IPCC an, dort steht, das die Atmosphaere auch die eigene Abstrahlung absorbiert.
Wollen sie behaupten, das sich die Atmosphaere an der eigenen Abstrahlung erwaermen kann?
Wieviel Waerme die Erde erhaelt, bestimmt die Sonne. Und es kommt laut bisher allen Klimaerklaerungsversuchen immer 240 W/m2 von der Sonne.
Damit muessen sie Wasser verdampfen. Wie soll denn mehr Wasser mit der gleichen Waermemenge verdampft werden, ohne das diese Waerme woanders nicht fehlt?
Abgesehen davon, lesen sie bei Fortak was rein, was da nicht so steht. Es gibt keinen direkten Einfluss von CO2 auf die Wolkenbildung, und das haben sie mit diesem Zitat jetzt gezeigt.
Herr Schulz, lasen Sie doch die ständigen Provokationen – ich habe schon wiederholt geschrieben, das ich Provokateuren kein Futter gebe.
Sie hatten die Quelle mit der Definition selber eingestellt.
Gibt es einen Grund warum sie sie weder erwaehnt haben, noch jetzt diskutieren wollen?
Ist die Definition falsch?
„Ihnen [Ebel] ist schon klar dass die Gegenstrahlung keine zusaetzliche Waerme ist, oder?“. Herr Schulz, schon wieder haben Sie nicht das Prinzip der Strahlungs- und Wärmedämmung verstanden. Es braucht im Strahlungsgleichgewicht KEINE zusätzliche Energie um die Temperatur des Erdbodens um 33 Grad zu erhöhen. Die Absorption von 77% der IR-Abstrahlung und dann 150 W/m² an Gegenstrahlung reichen aus um nach S-B die 255 K auf 288 K anzuheben.
Nur es kommen 333 W/m2 im Durchschnitt mit der Gegenstrahlung an. Eine Zahl die sie aus der Literatur ignorieren!
Bitte begruenden sie warum diese Zahl vom KT falsch ist.
Herr Schulz, ich habe bereits erklärt dass die 333 W/m² von KT z.B. fälschlich die zurück kommende Feuchtkonvektion (~180 W/m²) enthalten. Und da im vereinfachten Strahlungsmodell der Boden solare 240 W/m² erhält, aber bei 288 K 390 W/m² abstrahlt, muss die Gegenstrahlung (von Wolken und THG global) etwa 150 W/m² betragen. Das ist im Prinzip konform mit dem Beispiel in der Grafik von UAH, wenn man real 38,5 statt 50% der Bodenemission als Gegenstrahlung nimmt. Die geometrische Reihe ergibt 240/(1-0,385)=390.
Was ist denn bitte die
?
Woher kommt sie und wohin geht sie?
Wollen sie sagen, das die Messgeräte, die 333 W/m2 oder ähnliche Werte registrieren falsch messen?
Und ausser das sie eine Differenz errechnen, von nicht zusammenhängenden Größen, welche Begründung haben sie für die Diskrepanz von gemessenen Werten mit ihrer These?
Sie können hier viel behaupten zu Fortak 1971, ohne einen Link für die Selbsterkenntnis bringen Ihre ständigen Hinweise darauf garnichts.
Ach übrigens, Fortak 1971 ist nach hiesiger Lesart sowieso eine olle Kamelle, immerhin vor 54 Jahren verfasst. So es denn dazu einen zitierfähigen Text geben sollte?
Es ist wie bei vielen Fragen immer nur die eine Frage, wer fühlt sich berufen dazu eine Meinung zu äußern. Beispiel kosmische Strahlung und Aerosolbilldung:
Helmholtz-Klima ( https://www.helmholtz-klima.de/klimafakten/behauptung-kosmische-strahlung-verursacht-den-klimawandel ) interpretiert eine Studie am CERN als wenig aussagekräftig und deshalb ergeht die Feststellung das ein Zusammenhang Fragwürdig wäre, dagegen erklärt Jasper Kirkby vom Forschungszentrum CERN, der wohl dabei war, „Wir haben herausgefunden, dass kosmische Strahlung die Bildung von Aerosolen in der mittleren Troposphäre und darüber signifikant verstärkt„, was also das genaue Gegenteil der Behauptung der Klima-Fanatiker vom Helmholtz darstellt ( https://www.weltderphysik.de/gebiet/erde/nachrichten/2011/wolken-wachsen-dank-kosmischer-strahlung/ ).
So kann sich nun jeder aussuchen was ihm in den Glaubenskanon passt. 😀
Und Helmholtz spielt dann auch noch mit Worten indem es wenn überhaupt beschreibt, dann in der oberen Atmosphäre ohne dieses genauer zu konkretisieren, Stratosphäre, Termosphäre oder wo. So können die Gläubigen dann immer noch behaupten dort oben wo es möglicherweise Einfluss hat, entstehen sowieso keine Wolken mehr weil das Wasser fehlt. Dumm sind die Fanatiker ja nicht wirklich, nur glaubwürdig kann man sie deshalb auch nicht bezeichnen.
Herr Steinmetz
Ihre Schlußfolgerung ist nicht indiziert.
Ihnen fehlt ja das Urteilsvermögen, dass durch die Phrase in fett „signifikant verstärkt“ ein Widerspruch zwischen dem, was Kirkby sagt, und dem, was Helmholtz sagt, bewiesen wird.
Die beiden durch Sie als gegensätzlich eingestuften Artikeln unterscheiden sich thematisch ja tatsächlich etwas und gehen nicht um genau die gleichen Wolkenbildungsprozesse, so dass Ihr Versuch, die beiden Artikel bzw. Wissenschaftlergruppen (ohne Grund in der Sache) gegeneinander auszuspielen, als „Missbrauchsversuch an wissenschaftlichen Aussagen“ zu werten ist.
Möglicherweise haben Sie es auch unbeabsichtigt gemacht, weil Sie sich etwas von der Hysterie unter Klimawissenschaftsleugnern um Erkenntnisse der Klimawissenschaften anstecken lassen.
Helmholtz:
„In Laborexperimenten konnte zwar bestätigt werden, dass kosmische Strahlung die Bildung von Aerosol-Partikeln beeinflusst, die eine Vorstufe für Kondensationskeime sind; dies gelang beispielsweise durch das CLOUD-Projekt am Schweizer Kernforschungszentrum CERN (Kirkby et al. 2011). Dies wurde von Svensmark-Anhängern als Bestätigung ihrer Theorie gewertet – obwohl zunächst völlig offen war, ob dieser Effekt in der realen Atmosphäre, die bereits viele Kondensationskeime enthält, eine signifikante Änderung der Anzahl oder Größe der Keime bewirken kann.“
Kirkby/Welt der Physik:
„“Wir haben herausgefunden, dass kosmische Strahlung die Bildung von Aerosolen in der mittleren Troposphäre und darüber signifikant verstärkt“, sagt Jasper Kirkby vom Forschungszentrum CERN bei Genf. Dazu füllte er mit seinen Kollegen eine Wolkenkammer mit Luft, Wasserdampf sowie kleinen Anteilen an Schwefelsäure und Ammoniak. Dieses Gemisch simuliert die natürliche Zusammensetzung der Atmosphäre. Um den Einfluss der energiereichen kosmischen Strahlung zu klären, half ihnen ein Teilchenbeschleuniger: Sogenannte Pionen trafen auf die simulierte Atmosphäre und regten dort die enthaltenen Moleküle an. Diese ballten sich dadurch deutlich häufiger zu Kondensationskeimen zusammen, aus denen dann sukzessive Wolken entstehen können. Mehr Wolken in der Atmosphäre schirmen einfallende Sonnenstrahlung ab.“
Und ich weiß nicht was Sie an Signifikant nicht verstehen können:
Signifikant:
„bildungssprachlich
in deutlicher Weise als wesentlich, wichtig, erheblich erkennbar
„ein signifikanter Unterschied“
“
Ihre beständigen Bestrebungen anderen reine Dummheit zu unterstellen ist wahrlich nicht indiziert.
Zudem habe ich die Artikel nicht gegensätzlich eingestuft, sondern Aussagen zu ein und derselben Studie am CERN als „zweckgebunden“ unterschiedlich gebrandmarkt. Wenn Ihnen das nicht passt, dann ist das einzig Ihr Problem aber daraus eine Wertung meines „Urteilsvermögens“ zu schließen ist schon sehr persönlich.
Aber ich werde mich nicht auf Ihr billiges Niveau herablassen und wünsche Ihnen auch weiterhin viel Freude damit statt durch Sachargumente zu glänzen, bevorzugt teils unqualifizierte Verbalangriffe zu fahren. Ersparen Sie sich aber demnächst auf Beiträge aus meiner Tastatur zu reflektieren. 🙁
Richtig, Ihnen fehlt das Urteilsvermögen für Ihre Schlußfolgerung.
Überlassen Sie es denen, die sich auskennen.
Wenn Sie es ehrlich meinen, zitieren Sie einfach ohne Ihren verschwurbelnden Senf dazuzugeben.
Denn so sieht es nach Missbrauch von Wissenschaft aus, um Ihre persönliche Meinung mit fachwissenschaftlich anderes interpretierten Ergebnissen in wissenschaftlich nicht indizierter Weise auszuschmücken.
Nicht mir fehlt es an Urteilsvermögen, Ihnen geht jegliche Wahrnehmung der Komplexität atmosphärischer Vorgänge ab. Und wenn ich etwas zitiere, dann steht es mir auch frei dazu eine Meinung zu äußern, insbesondere wenn es offensichtlich bei bestimmten Zitaten nicht um objektive Beurteilungen geht, sondern darum ein/dem Konsens zu frönen. Seien Sie froh das ich mich längst verweigere Ihren beständig geäußerten „Senf“ dem Wortsinn nach zu zerlegen. Ich missbrauche auch keine Wissenschaft, ich gebrauche meine grauen Zellen, gewohnt mit wissenschaftlicher Methodik umzugehen, sowohl beim lesen wie auch der Interpretation des gelesenen. Sie sind es doch der beständig in höchst unwissenschaftlicher Art Dogmen auf den Thron hebt und mit allerlei Zahlensalat zu garnieren versucht. Nur ist mir bisher außer der handverlesenen Gilde kosch, Frölich etc. niemand unter gekommen der diesen Salat als verdaulich ansieht. Dies war jetzt meine letzte Einlassung zu Beiträgen von Ihnen und ich erwarte das Sie dies ohne weitere unsinnige Kommentare ebenfalls respektieren.
Herr Steinmetz,
Gucken Sie in ein Lehrbuch. Die Atmosphäre ist komplex, das heißt aber nicht, dass man keine endgültigen Erkenntnisse darüber hat. Der Treibhauseffekt ist grundsätzlich verstanden. Dazu ist Verständnis der physikalischen Vorgänge und der Denkweise der Physik gefragt. Urteilsvermögen und Meinungsbildung ist da eher hinderlich.
Wenn Sie es nicht kapieren, so ist das ihr Problem. Wissenschaftlich gesehen ist der Treibhauseffekt nachprüfbar ein Fakt.
Wenn Sie das anderes sehen, interessiert das so lange nicht, bis Sie die Wissenschaft überzeugt haben, indem Sie die dem Treibhauseffekt zugrundeliegenden physikalischen Erkenntnisse aus den letzten zwei Jahrhunderten widerlegt haben, damit ein Dutzend Nobelpreise bekommen und als größter Wissenschafter ever gelten, weil Sie etwas erkannt haben, was Hunderttausende Wissenschaftler übersehen haben.
Moritz Steinmetz 16. Mai 2025 12:57
Und woraus folgt daraus eine Änderung des Treibhauseffektes? Z.B. entsteht dadurch eine Gegenkopplung: Weniger Sonnenstrahlung vermindert die Verdunstung und weniger Verdunstung bedeutet weniger Wolken, mehr Wolken können höheres Albedo verursachen usw.
Und woraus schließen Sie das ich irgendwas in meiner Wertung dieser selektiv unterschiedlichen Interpretation einer Studie irgendeine Meinung bezüglich des „Treibhauseffektes“ geäußert hätte? Die von Ihnen zitierte Zeile stammt nicht aus meiner Feder sondern ist Teil eines Zitates und keines von beiden habe ich mir damit zu eigen gemacht.
Fangen Sie schon wieder an zu verNEbeln, oder warum diese haltlose Unterstellung betreffs des „Treibhauseffektes“?
Gibt es alternativ eine Beistandsverpflichtung Ihrerseits zu Beiträgen des Herren Heinemann?
Moritz Steinmetz 16. Mai 2025 21:18
Warum zitieren Sie etwas, was nach Ihren Text keine Bedeutung haben soll? Für die Diskussion hier, sagt Ihr Zitat genau so wenig aus, wie etwa eine Bemerkung „Es gibt weiß angestrichene Hauswände“.
Also bringe ich keine bedeutungslosen Texte, warum machen Sie das?
Ich habe den Text soweit wie es möglich erschien zitiert, um nicht der Unterstellung anheim zu fallen die Zitate wären selektiv. Damit muss ich mir dennoch nichts davon zu eigen machen insbesondere wenn ich die beständig selektiven Wahrnehmungen/Äußerungen der „Klimafakten“- Treiber aufzeigen will. Das ich insgesamt die Rolle von Aerosolen in den hießigen Diskussionen unterrepräsentiert wahrnehme steht dabei auf einem ganz anderen Blatt.
Was folgt nunmehr als Ihr letztes Wort?