von Uli Weber
Mein hemisphärisches Stefan-Boltzmann-Modell ist kein Strahlungsmodell, sondern war von Anfang an ein Strahlungsantriebsmodell; denn es wird von der Leistungsdifferenz zwischen der solaren Einstrahlung und der tatsächlichen individuellen Ortstemperatur angetrieben. Es wird also höchste Zeit, dieses Modell einmal am Stand seiner Weiterentwicklung über mehr als 50 EIKE-Artikel hinweg (mit Dank an Herrn Dipl.-Ing. Michael Limburg) zu betrachten. Der Anstoß für diese Betrachtung lieferte ein Artikel von Dr. Markus Ott, der zufällig passend zum 8. Jahrestag der EIKE-Erstveröffentlichung meines S-B-Ansatzes erschienen war. Nein, einen Link auf diesen Artikel gibt es hier nicht, denn ich werde Herrn Dr. Ott nicht sehenden Auges die üblichen pawlowschen Haßprediger auf den Hals hetzen – nicht nur mein Modell hat sich umfänglich weiterentwickelt, sondern auch die Zahl meiner ad-hominem-Kritiker. Mein erster Artikel über dieses Modell war am 23. Januar 2017 hier auf EIKE erschienen, und ein Herr Frank Endres hatte am selben Tag seherisch kommentiert, Zitat:
„Jetzt fallen die Ökofanatiker über ihn her. Das – selbstverständlich selbstgebraute – Bier ist kalt gestellt, nur Chips bzw. Popcorn habe ich leider noch nicht besorgt. Zum ‚Klimaschutz‘ verzichte ich darauf, einkaufen zu gehen und warte hier auf die ersten Beschimpfungen und Zurechtweisungen der anerkannten ‚Elite-Wissenschaftler‘.“
Aber sei‘shaltwieshaltist – jedenfalls ist es eine völlig neue Sichtweise, wenn man einen fremden Artikel über ein Modell liest, das man über fast ein Jahrzehnt kontinuierlich weiterentwickelt hatte. Dieser hemisphärische S-B-Ansatz hatte zunächst einfach nur die terrestrische Temperaturgenese auf eine physikalisch korrekte S-B-Inversion für die Tagseite unserer Erde reduziert. Eine rechnerische Approximation mit einer flächengetreuen Durchschnittsbildung für das Stefan-Boltzmann-Temperaturäquivalent konnte später die sogenannte „gemessene globale Durchschnittstemperatur“ unserer Erde ohne den sogenannten „natürlichen atmosphärischen Treibhauseffekt“ erklären. In der weiteren Folge wurde dieser Ansatz schließlich zum S-B-Modell, das neben seiner fortlaufenden Weiterentwicklung auch an unterschiedlichen atmosphärischen und geografisch-jahreszeitlichen Phänomenen validiert worden war. In dem o.g. Ott-Artikel wird die ausdrückliche Unterscheidung zwischen dem rechnerischen Temperaturäquivalent aus der S-B-Inversion und der tatsächlichen gemessenen Ortstemperatur noch einmal ganz besonders hervorgehoben. Es wird dort ebenfalls nochmals verdeutlicht, dass innerhalb dieses Modells bei der Erwärmung der Erdoberfläche durch den gleichzeitigen Abfluss von Energie in die globalen Zirkulationen bereits eine Art Mittelung stattfindet. Da sich mein Modell also sehr weit von der ursprünglich namensgebenden S-B-Inversion entfernt hat, ist die bisherige Benennung für einen interessierten Betrachter inzwischen eher fehlleitend geworden, weil sich das weiterentwickelte Modell eben nicht mehr allein auf diese Inversion reduzieren lässt – und schon gar nicht auf ein reines Strahlungsmodell.
Von daher werde ich künftig die Bezeichnung „hemisphärisches Konvektionsmodell“ verwenden.
Als hemisphärisches Konvektionsmodell stellt dieses Modell das Klimasystem unserer Erde vom makroskopischen Standpunkt der Klimadefinition als Durchschnitt von 30 Jahren Wetter dar. Daraus lassen sich dann wiederum die primären Wirkmechanismen der terrestrischen Temperaturgenese auf unserer realen Erde qualitativ ableiten. Am Ende ist dieses einfache hemisphärische Konvektionsmodell Modell dann in der Lage, den Unterschied von Tag und Nacht zu berücksichtigen, ein durchschnittliches jahreszeitliches Wetter zu erklären und analog zu den Beleuchtungsklimazonen sogar ganz grob die geografischen Klimazonen nachzuempfinden. Im Prinzip handelt es sich also um ein hybrides Modell, das auf eine Kombination von Berechnungen (Tagseite) und der Existenz von terrestrischen Wärmespeichern (Nachtseite) aufbaut. Und weil nicht jeder monothematische Artikel sämtliche Aspekte dieses hemisphärischen Konvektionsmodells abdecken kann, seien nachfolgend noch einmal dessen wesentliche Eckpunkte zusammengefasst:
1. AUSSAGE: Die hemisphärische S-B-Inversion kann die sogenannte globale Durchschnittstemperatur ohne den vorgeblichen „natürlichen atmosphärischen Treibhauseffekt“ erklären [Berechnungen, Grafiken und weitere Erklärungen].
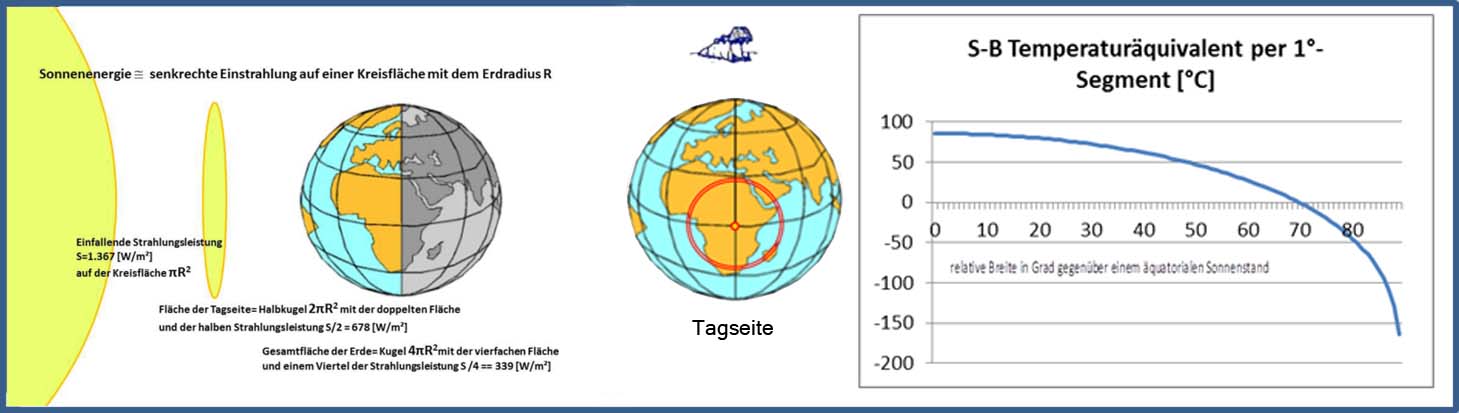BEWEIS: Die Berechnungen für die Tagseite unserer Erde beruhen auf dem S-B-Temperaturäquivalent aus einer ortsgetreuen S-B-Inversion der hemisphärisch eingestrahlten spezifischen Strahlungsleistung der Sonne für die jeweiligen individuellen Ortslagen.
Abbildung 1 Links: Geometrie der solaren Einstrahlung im Äquinoktium
Mitte: Berechnungsschema für das S-B-Temperaturäquivalent in 1° Segmenten
Rechts: S-B-Temperaturäquivalent in Abhängigkeit vom Zenitwinkel der Sonne
Das flächennormierte Temperaturmittel aus dieser Approximation beträgt 14,03°C und wird durch eine Verdoppelung der G&T-Integrallösung bestätigt. Das berechnete S-B-Temperaturäquivalent wird jedoch nirgendwo auf der Erde erreicht. Vielmehr finden mit der morgendlichen Erwärmung der Oberfläche sofort auch Verdunstung und Konvektion statt, durch die wesentliche Mengen der örtlich eingestrahlten Energie in die globalen Zirkulationen übergehen und abgeführt werden. Nach dem 1. HS der Thermodynamit geht diese Energie aber nicht verloren, sondern wird lediglich von den Strömungen in Atmosphäre und Ozeanen aufgenommen und von diesen großflächig verteilt.
BEISPIEL: Jahreszeitlicher Abfluss und Zufluss von Energie auf einer konkreten Ortslage am Beispiel Potsdam [aus Anmerkungen zur Bestimmung der hemisphärischen solaren Einstrahlung auf „Mittelerde“]:
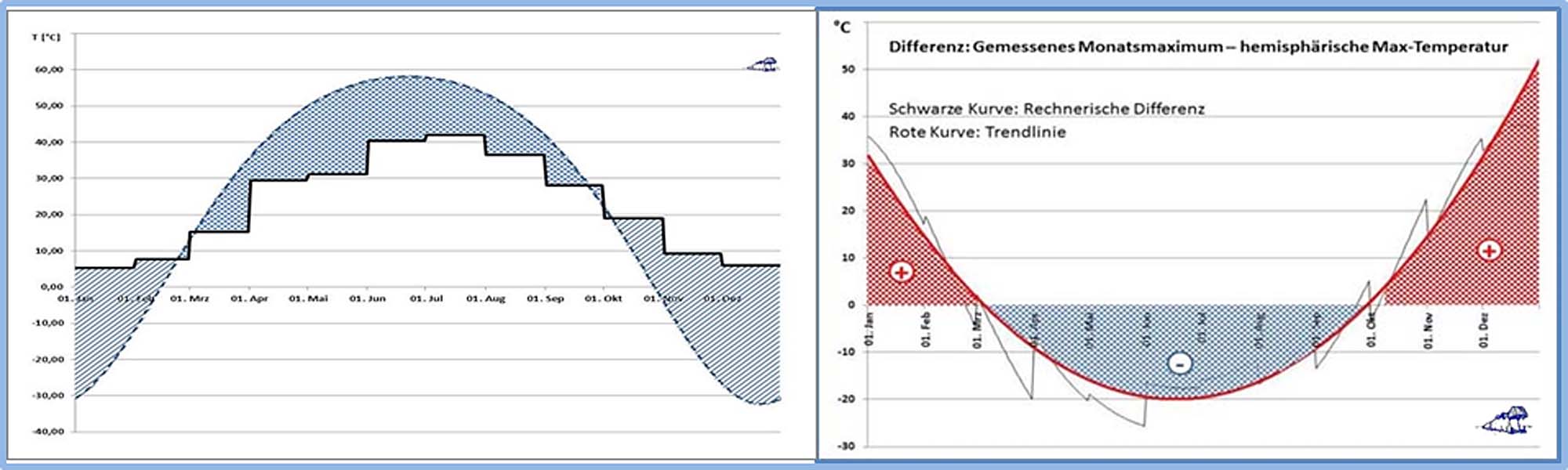Wie weiter oben bereits ausgeführt wurde, wird das maximale S-B-Temperaturäquivalent auf unserer Erde aufgrund von Konvektion und Verdunstung in der Realität niemals erreicht; umgekehrt wird aber der nächtliche Temperaturabfall durch Kondensation und Advektion abgemildert. Letzteres gilt übrigens auch für das Strahlungsdefizit in mittleren und höheren Breiten der jeweiligen Winterhemisphäre, dazu nachfolgend das Beispiel für Potsdam:
Abbildung 2: Konvektion und Advektion über das Jahr an einer konkreten Ortslage (Potsdam)
Links: Treppenkurve: Maximale monatliche Bodentemperatur in Potsdam
Blau gestrichelt: Maximales jahreszeitliches S-B-Temperaturäquivalent
Rechts: Differenz zwischen der maximalen monatliche Bodentemperatur in Potsdam und dem maximalen örtlichen S-B-Temperaturäquivalent
Rote Kurve: Trendlinie für die Differenz (schwarze Zackenkurve) zwischen maximaler monatlicher Bodentemperatur und dem maximalen örtlichen S-B-Temperaturäquivalent in Potsdam
Rot schraffiert: Zufluss von Wärme im Winterhalbjahr
Blau schraffiert: Abfluss von Wärme im Sommerhalbjahr
Im Sommerhalbjahr fließt also Energie in die globalen Wärmespeicher und im Winterhalbjahr wird die Ortstemperatur durch einen Wärmezufluss aus diesen Wärmespeichern gestützt. Und deshalb müssen Atmosphäre und Ozeane als „globale Wärmespeicher“ zwingend in die Bestimmung einer „natürlichen Temperatur“ unserer Erde einbezogen werden.
2. AUSSAGE: Dieses Modell kann die Umkehrung der vektoriellen Strahlungsrichtung zwischen solarer HF-Einstrahlung und terrestrischer IR-Abstrahlung erklären [ausführlich dargestellt in Zeigt der Poynting-Vektor auf „Mittelerde“ oder auf die sogenannte „Abstrahlungshöhe“?].
BEWEIS: Die konventionelle Faktor4-Ableitung einer „natürlichen“ terrestrischen Temperatur aus der globalen IR-Abstrahlung unserer Erde kann die Umkehrung der vektoriellen Strahlungsrichtung zwischen solarer HF-Einstrahlung und terrestrischer IR-Abstrahlung nicht erklären und arbeitet mit einem unphysikalischen skalaren 24h-Durchschnittswert der solaren Einstrahlung. Beim hemisphärischen Modell beschränkt sich die Temperaturgenese jedoch auf die Tagseite der Erde, wo die Sonneneinstrahlung planparallel einfällt und mit dem Cosinus der geografischen Breite temperaturwirksam wird. Denn eine Veränderung der vektoriellen Strahlungsrichtung von HF auf IR kann nur über die zwischenzeitliche Erwärmung von Materie erfolgen:
Einstrahlung HF-solar => Erwärmung von Materie an der Oberfläche => Abstrahlung IR-terrestrisch
Die auf der Tagseite erwärmte Materie gelangt durch die kontinuierliche Erddrehung schließlich auf die Nachtseite, wo sie weiterhin die terrestrische IR-Strahlung senkrecht zur Erdoberfläche abstrahlt.
3. AUSSAGE: Das hemisphärische Konvektionsmodell kann die jahreszeitlichen Schwankungen der örtlichen solaren Einstrahlung abbilden [hier eine ausführliche Darstellung].
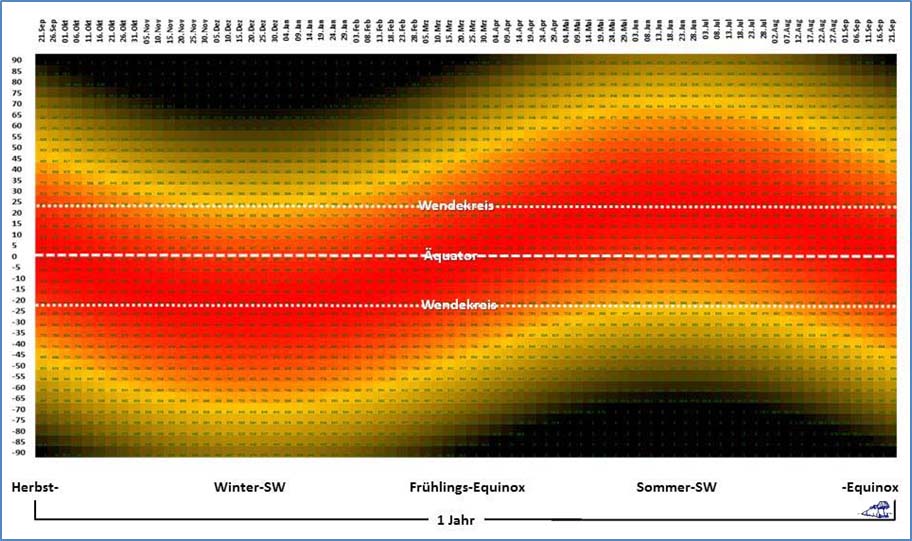BEWEIS: Hier bei uns in Deutschland schwankt die solare LEISTUNG zwischen etwa 90% der Solarkonstanten am Sommerpunkt (21.06.) und etwa 30% am Winterpunkt (21.12.). An den Polen unserer Erde geht es noch extremer zu, dort schwankt die Sonnenscheindauer als Indikator für die solare ARBEIT (=Leistung x Zeit) zwischen 0 Stunden (Wintersonnenwende am Pol der Winterhemisphäre) und 24 Stunden (Sommersonnenwende am Pol der Sommerhemisphäre), was das hemisphärische Konvektionsmodell tatsächlich abzubilden vermag:
Abbildung 3: Das örtliche Maximum der breitenabhängigen temperaturwirksamen spezifischen Strahlungsleistung der Sonne für die gesamte Erde über ein volles Jahr von Herbstäquinoktium zu Herbstäquinoktium (Abszissenbeschriftung aus Sicht der Nordhalbkugel)
Spez. Strahlungsleistung: MAX (Si) @24h-Tag mit (Si = 1.367W/m² * (1-ALBEDO) * cos PHIi)
und (PHIi = örtlicher Zenitwinkel) – Farbdarstellung: 0 [W/m²] (schwarz) – 940 [W/m²] (rot)
Linke Skala: Grad geografische Breite (Süd = „-“)
Skala oben: Datum ab Herbstäquinoktium
Anmerkung: Ein vergleichbarer geografischer Verlauf ergibt sich für das daraus abgeleitete S-B-Temperaturäquivalent (SBT) zwischen (-273°C=schwarz) und (86°C=rot)
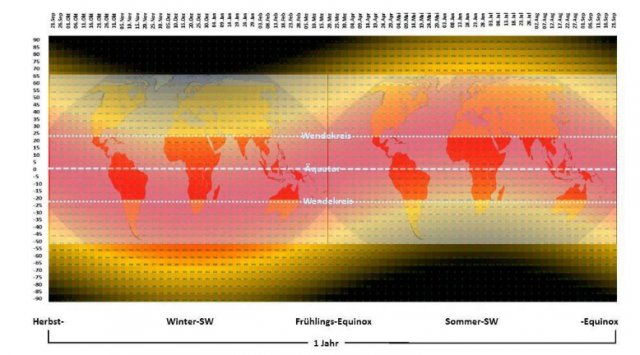Das konventionelle Faktor4-THE-Modell vermag diese Schwankungen nicht abzubilden, im Gegenteil, es wirft grundsätzlich dieselbe „natürliche theoretische Globaltemperatur“ für alle Ortslagen auf unserer Erde aus, selbst für die Polkappen und die Wüstengebiete in niederen geografischen Breiten. Da aber das hemisphärische Konvektionsmodell den jahreszeitlichen solaren Zenitwinkel berücksichtigt, kann es sogar die Beleuchtungsklimazonen unserer Erde abbilden:
Abbildung 4: Tentative Gegenüberstellung der Beleuchtungsklimazonen mit dem Jahresverlauf der maximalen solaren Strahlungsleistung im Sommerhalbjahr (Südsommer linke Hälfte und Nordsommer rechte Hälfte)
Overlays rechts und links: Die Beleuchtungsklimazonen der Erde: von oben/unten zur Mitte: Polarzonen, Mittelbreiten, Tropenzone (Quelle: Wikipedia, Autor: Fährtenleser, Lizenz: GNU Free Documentation License)
Darunter farbgebend rot-gelb-schwarz: Das örtliche Maximum der breitenabhängigen temperaturwirksamen spezifischen Strahlungsleistung der Sonne für die gesamte Erde über ein volles Jahr von Herbstäquinoktium zu Herbstäquinoktium
4. AUSSAGE: Das hemisphärische Konvektionsmodell berücksichtigt den physikalischen Unterschied zwischen solarer Leistung und solarer Energie und vermag dadurch den grundsätzlichen Wechsel der Wetterlagen über den Verlauf der Jahreszeiten zu skizzieren [hier eine ausführliche Darstellung].
BEWEIS: Wenn wir uns die Nord- und Südhemisphäre unserer Erde einmal im Verlauf der Jahreszeiten vergegenwärtigen, dann besteht der wesentliche Unterschied zwischen vergleichbaren geografischen Ortslagen in jahreszeitlich erheblichen Gegensätzen der solaren LEISTUNG und der solaren ARBEIT. Die LEISTUNG ist über den solaren Zenitwinkel mit dem rechnerischen maximalen S-B-Temperaturäquivalent verknüpft, während die solare ARBEIT von der lichten Tageslänge (=Sonnenscheindauer) abhängig ist. So ist die solare LEISTUNG aufgrund des hohen Sonnenstandes in den Tropen stets am größten und generiert dort auch das höchste S-B-Temperaturäquivalent. Es ist aber weitgehend unbekannt, dass die solare ARBEIT (Energie=Leistung x Zeit) aufgrund der örtlichen Sonnenscheindauer am Pol der jeweiligen Sommerhemisphäre höher ist als in den Tropen:
Abbildung 5: Tentative räumliche und zeitliche Auswirkungen der hemisphärischen jahreszeitlichen solaren Einstrahlung (nicht flächengetreu)
Rot: Maximale solare ARBEIT auf der Polkappe der Sommerhemisphäre
Grün: Maximale solare LEISTUNG in Tropen und mittleren Breiten der Sommerhemisphäre
Blau: Minima von solarer ARBEIT und solarer LEISTUNG auf der Winterhemisphäre
Links: Sommer auf der Nordhemisphäre plus Tropen der Südhemisphäre
Rechts: Sommer auf der Südhemisphäre plus Tropen der Nordhemisphäre
Wir erkennen hier ganz deutlich, dass die Polarregion der jeweiligen Sommerhemisphäre einen solaren ENERGIE-Hotspot mit dem Maximum zur jeweiligen Sommersonnenwende darstellt. Dieser sommerliche solaren ENERGIE-Hotspot wechselt nun im halbjährlichen Rhythmus von der nördlichen zur südlichen Polarkalotte und zurück. Das bedeutet auch, dass auf den polaren Kalotten die jahreszeitlich höchsten Schwankungen des solaren Klimaantriebs auftreten. Und nicht nur das, denn gleichzeitig treten dort im jahreszeitlichen Verlauf die global stärksten Erwärmungen respektive Abkühlungen auf. Aus diesen Temperaturdifferenzen im Verhältnis zu den Tropen speist sich das Wetter, und von daher ist es kein Wunder, wenn interessierte klimareligiöse Kreise mit diesem regelmäßigen halbjährlichen Umklappen des polaren ENERGIE-Hotspots in einen Kältepol mediale Angst zu verbreiten suchen:
Abbildung 6: Vergleich zwischen der IPCC-Darstellung einer maximalen anthropogenen Klimaeinwirkung und der maximalen jahreszeitlichen Veränderung der Ortstemperatur
Links: Die IPCC-„Figure 1.SM.1 – Season of greatest warming“ aus dem Framing and Context Supplementary Material des IPCC Spezialberichts “Global Warming of 1.5°C” (SR1.5) mit der Jahreszeit der größten menschen-induzierten Erwärmung für den Zeitraum 2006-2015 gegenüber 1850-1900
Rechts: Vereinfachte Darstellung der jahreszeitlichen Veränderung der solaren Ortstemperatur
Polarkappen: violett= extrem – mittlere Breiten: grün=stark – Tropen: gelb=mäßig
Es ist in der IPCC-Grafik deutlich erkennbar, dass in der nördlichen Polarregion die größte anthropogene Veränderung im Zeitraum Dezember-Februar (ocker) sowie März-Mai (blau) stattfindet, während sich diese Veränderung in der südlichen Polarregion auf Juni-August (grün) sowie September-November (violett) beschränkt. Der maximale jahreszeitliche Anstieg der solaren Einstrahlung, und damit auch der Anstieg der Ortstemperatur, ereignet sich rein rechnerisch um die Äquinoktien, und zwar auf der Nordhalbkugel von Februar-April und auf der Südhalbkugel von August-Oktober. Es kommt hier also immerhin zu einer impliziten Übereinstimmung zwischen den beiden dargestellten Grafiken, weil in der linken IPCC-Grafik die maximale Veränderung jeweils in das Halbjahr zwischen Wintersonnenwende und Sommersonnenwende fällt. Von daher beschleicht den Autor der sicherlich nicht völlig unbegründete Verdacht, das IPCC könnte seine Zeitfenster sehr zielführend ausgewählt haben. Denn ganz zufällig fällt der natürliche jahreszeitliche Anstieg der solaren Einstrahlung auf der Polkappe der Sommerhemisphäre mit der jahreszeitlich größten menschlich-induzierten IPCC-Erwärmung zusammen. Und was die Tropen sowie insbesondere die gemäßigten nördlichen und südlichen Breiten angeht, so pausen sich dort lediglich die spezifischen Veränderungen aus der halbjährlichen Verlagerung des polaren Hotspots durch, die man als Wetter zu bezeichnen pflegt.
5. AUSSAGE: Die Wärmespeicher von Ozeanen und Atmosphäre puffern im Wechsel von Tag und Nacht den nächtliche Energieverlust durch die IR-Abstrahlung der Erde auf ihrer Nachtseite ab, während sie im Tagesverlauf regelmäßig wieder aufgefüllt werden [hier eine ausführliche Darstellung].
BEWEIS: Wir sprechen hier von der realen Erde, wir leben nämlich in einem „eingeschwungenen“ System, in dem die Energiespeicher unserer Erde (im Wesentlichen die Ozeane) bereits voll aufgeladen sind, und zwar von Anbeginn ihrer Entstehung an. Die Ozeane sind in der Frühzeit der Erde entstanden, als die Erde sich langsam abkühlte und eine feste Oberfläche gebildet hatte. Die Meere hatten sich also zunächst aus Wasserdampf kondensiert und sind dann bis zu einem Gleichgewicht zwischen Abkühlung und zugeführter Sonnenenergie abgekühlt.
Sowohl die Temperatur auf der Tagseite der Erde als auch die Temperatur auf deren Nachseite setzen nun auf der Temperatur der globalen Wärmespeicher auf, die im Wesentlichen von der Durchschnittstemperatur der Ozeane (ca. 20°C) bestimmt wird. Wasser ist der hauptsächliche Träger dieser Energie, sei es in flüssiger Form in den Ozeanen oder gasförmig in der Atmosphäre. Die örtliche Nachttemperatur der kontinentalen Landflächen wird also letztendlich über die Umgebungstemperatur ziehender Tiefdruckgebiete oder lokaler Land- Seewind Systeme bestimmt und gehorcht damit der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes. Je weiter nun eine Örtlichkeit vom Meer entfernt liegt und umso weniger Wasserdampf die örtliche Atmosphäre enthält, umso größer sind dort die Temperaturschwankungen zwischen Tag und Nacht. Die kontinentalen Wüstengebiete unserer Erde sind dafür ein ganz hervorragendes Beispiel. Seit jeher haben die Ozeane mit einem Zeitverzug von Jahrhunderten jede globale Klimaänderung „mitgemacht“ und gleichzeitig die jeweiligen individuellen Ortstemperaturen (oder meinetwegen auch eine sogenannte „globale Durchschnittstemperatur“) auf der Nachthemisphäre nach unten abgesichert:
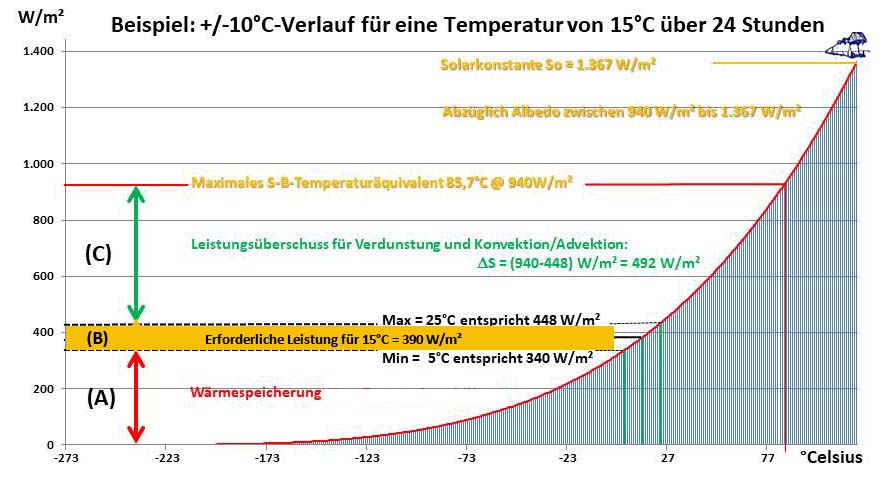
Abbildung 7: Die Beziehung zwischen Temperatur und spezifischer Strahlungsleistung im Stefan-Boltzmann-Gesetz. In diesem Beispiel entspricht die Schwankung von +/- 10°C um eine Ortstemperatur von 15°C einer Veränderung der spezifischen solaren Strahlungsleistung um 108 W/m². Die dargestellte S-B- Beziehung kann selbstverständlich auch entsprechend auf andere Ortstemperaturen und deren Schwankungsbreite in der Abfolge von Tag und Nacht angewendet werden.
Anmerkung: Das maximale S-B-Temperaturäquivalent aus der solaren Einstrahlung beträgt unter Berücksichtigung der terrestrischen Albedo 85,7°C. Der zur Aufrechterhaltung der Ortstemperatur erforderliche solare Leistungsbereich ist ockerfarben ausgehalten, darunter liegt die gespeicherte Energie und darüber die verfügbare Energie für Konvektion und Verdunstung
Unsere Erde ist ein Wasserplanet, dessen Oberfläche zu zwei Dritteln mit Ozeanen bedeckt ist. Sowohl die Temperatur auf der Tagseite der Erde als auch die Temperatur auf deren Nachseite werden von der Temperatur der globalen Wärmespeicher getragen, die deutlich größer als 0 Kelvin ist. Diese Temperatur wird im Wesentlichen wiederum von der Durchschnittstemperatur der Ozeane (ca. 20°C) bestimmt und muss nicht erst durch die tägliche solare Einstrahlung erzeugt werden, denn sie ist in diesem „eingeschwungenen“ System ja bereits vorhanden. Der Wärmeinhalt der Ozeane beträgt mehr als 4,59*10^26 Joule oder 50.000 Tage Sonneneinstrahlung, und der dagegen völlig unbeträchtliche nächtliche Wärmeverlust kann am folgenden Tag leicht ersetzt werden. Die solare Einstrahlung muss unsere Erde also gar nicht jeden Morgen von 0 Kelvin an erwärmen, sondern lediglich den nächtlichen Abstrahlungsverlust ersetzen. Von daher bleibt nach der Erwärmung der Erdoberfläche jede Menge Energie übrig, um den nächtlichen Abstrahlungsverlust der globalen Wärmespeicher allein aus der hemisphärischen solaren Tageseinstrahlung zu ersetzen.
Am Ende ist es also einfach nur korrekt angewandte Physik, mit der ein ganz simples hemisphärisches Konvektionsmodell den Ist-Zustand auf unserer Erde sowie dessen jahreszeitliche Veränderungen qualitativ richtig darzustellen vermag. Viel ist dazu gar nicht notwendig, eine Winkelfunktion für den örtlichen solaren Zenitwinkel, die Solarkonstante und das Albedo auf unserer Erde sowie eine physikalisch korrekte Stefan-Boltzmann-Inversion für das rechnerische Ergebnis – fertig. Die hier abrufbare Vergleichsliste zwischen meinem hemisphärischen Konvektionsmodell (@2PiR^2) und dem konventionellen Faktor4-THE-Paradigma (@4PiR^2) mag die Unterschiede zwischen diesen beiden Modellen nochmals verdeutlichen.
Das Stefan Boltzmann Gesetz berechnet, welche Leistung ein „schwarzer Strahler“ (der die Erde nicht ist) bei einer konkreten Temperatur abstrahlt. Die Formel je m² lautet P = Sigma x T⁴.
Die umgekehrte Rechnung, also Temperatur aufgrund von Strahlungsleistung, würde unter der Nebenbedingung gelten, daß es nur Strahlungskühlung gibt (also im Vakuum wie z. B. am Mond) und daß der Körper lange genug angestrahlt wurde, um abzüglich Albedo seine konstante Gleichgewichtstemperatur zu erreichen. Am Mond führt das zu wesentlich höheren maximalen Oberflächentemperaturen als auf der Erde. Gem. umgekehrt SB ergeben sich bei einer angenommenen Solarkonstante von erdidentischen 1368 W/m² ohne Albedo maximal ca. 394 K. Die in der englischen Wikipedia angegebenen max. gemessenen 390 K am Mondäquator bedeuten an solchen Stellen eine Albedo von nur ca. 1, also 99% Absorption.
Wenn es allerdings auch thermodynamische Kühlung (Konvektion) gibt, was mit Atmosphäre immer der Fall ist, ist diese inverse Berechnung natürlich falsch. Dann stellt sich an der Oberfläche ein Gleichgewicht zwischen Energiezufuhr durch Sonnenstrahlung, je nach Gegend ev. auch durch wärmende Thermodynamik und Energieabgabe primär durch Thermodynamik ergänzt durch Abstrahlung ein. Die obere Gleichgewichtstemperatur ist dabei niedriger als im Fall des Mondes, sie ist auch nicht langzeitstabil, weil der thermodynamische Anteil aufgrund der Beweglichkeit der Atmosphäre veränderlich ist. Es ist aber in Bezug auf Kühlung jener Vorgang, der fast zu 100% die Energieabfuhr zur = Temperierung der Atmosphäre verursacht. Und die Atmosphäre aus ca. 78% Stickstoff N₂ und ca. 21 % Sauerstoff O₂ (= 99%) kann wegen der Struktur der Moleküle de facto kaum strahlen. Sie speichert also aufgenommene Energie=Wärme so lange, bis sie irgendwo hinkommt, wo thermodynamische Energieabgabe gem. 2. HS möglich ist. Das ist überall dort der Fall, wo die Oberfläche eben kühler ist. Nur einzelne Prozente der Atmosphäre sind strahlungsfähig (CO2, Wasser, Wasserdampf, …) und tragen minimal zur Strahlungskühlung der Atmosphäre Richtung All bei. Auch Phasenübergänge spielen eine temporäre Rolle, gleichen sich im Integral aber aus.
Der Vergleich mit dem Mond belegt also, daß eine Atmosphäre einen Einfluß ausübt, der Temperaturextreme abmildert. Auf der Erde gibt es an der Oberfläche keine 390 K und auch keine 100 K wie auf dem Mond. Es ist damit aber auch klar gezeigt, daß eine umgekehrte Anwendung des SB-Gesetzes zur Temperaturberechnung auf der Erde unphysikalisch ist. Auf der Erde gibt es in Summe drei separate Energiebilanzen, erstens der Landmasse, zweitens der dynamischen Ozeane und drittens der dynamischen Atmosphäre. Diese drei Bilanzen, zwei davon hochdynamisch, müssen an den Berührungsflächen im Integral miteinander harmonieren und in der übergeordneten Bilanz im Integral Null ergeben.
Mir ist eigentlich keine Arbeit geläufig, die den genannten Sachverhalten Rechnung trägt.
Nur eine kleine Randbemerkung:
Man findet in verschiedenen Quellen diese 1368 oder 1370W/m², dies ergibt dann (inkl. Albedo) die durchschnittlichen 240W/m² mit einer Oberflächentemperatur von 255K. Emittiert von der Oberfläche werden, im Durchschnitt 390W/m², also 288K, 15°C.
Nun ist die Solarkonstante seit 2015 mit 1361W/m² definiert. Ziemlich variabel für eine Konstante. Und im letzen IPCC Bericht wird die Oberflächenemission mit 398.6W/m² angegeben – weniger Sonne gibt mehr W/m²? Im Bericht selber sind die 288K immer noch (seit dem ersten Bericht!) als durchschnittliche „optimale“ strahlende Oberflächenequilibriumtemperatur angegeben.
Die Mittelwertbildung, die inkl. 30% Albedo zu ca. 240 W/m² führt, also zu einer permanenten und überall senkrecht strahlenden Rundumsonne mit konstanten 240 W/m² Zustrahlung, ist unphysikalisch!
So eine Modellvorstellung läßt sowohl die T⁴-Beziehung als auch die Speicherfähigkeit der Erdmasse außer Acht. Ozeanwasser absorbiert zwischen 90 und 95% der Sonnenenergie und kühlt duch Konvektion, Wärmeleitung in die Tiefe und Abstrahlung. All das zusammen begrenzt die Oberflächentemperatur auf maximal knapp über 31°C, im Schnitt aber wesentlich weniger. Und die Speicherfähigkeit bewirkt so gut wie keine Nachtabkühlung trotz 12 Stunden fehlender Energiezufuhr.
Daß sich die „Solarkonstante“ im Laufe der Zeit geringfügig ändern kann, ist bekannt, ändert aber nichts an den Prinzipien.
stefan strasser 3. März 2025 1:11
„als auch die Speicherfähigkeit der Erdmasse außer Acht“
Die Speichermasse hat Einfluß auf die Zeitverzögerung zwischen Absorption, Emission und konvektiver Abgabe – hat aber keinen Einfluß auf den Durchschnitt der Bilanz.
„So eine Modellvorstellung läßt sowohl die T⁴-Beziehung … außer Acht.“
Die aktuelle lokale Emission folgt der T⁴-Beziehung, aber für die Durchschnittswerte der Bilanz gilt die Höldersche Ungleichung. wird eine Durchschnittstemperatur von 15°C vorgegeben, so ist die emittierte Leistung größer 390 W/m², ist die emittierte Leistung (= der absorbierten Leistung) vorgegeben, so ist die Durchschnittstemperatur deutlich unter -18°C.
Na die Bilanz ist Null, rein und raus das gleiche, nur nicht alles durch Strahlung an der Oberflaeche. Das wird auch der Grund sein, warum Herr Heinemann seine Aufgabe nicht ausrechnen kann.
Die Speichermasse hat aber einen Einfluss auf die Temperatur.
Versuchen sie mal 1 kg Wasser durch einen Strahler um 5 Grad C zu erwaermen und 2000 kg Wasser. wo brauchen sie mehr und schaffen sie es bevor die Sonne untergegangen ist?
Herr strasser,
Immer noch nicht verstanden.
Merke: die Werte einer zeitlich veränderlichen Größe (absorbierte Sonnenleistungsdichte P über den Tag) mit dem Mittelwert dieser Größe (240 W/m2) gleichzusetzen, ist falsch.
Warum machen Sie das?
Zur Übung:
A) (leicht): sie berechnen die zu 240 W/m2 korrespondierende Strahlungstemperatur per SB
B) (ein wenig schwieriger): sie berechnen die momentane Strahlungstemperatur unter der physikalisch unrealistischen Annahme, dass diese stets mit der momentanen Sonnenleistungsdichte P per SB korrespondiert (a la Weber)
C) (zu schwierig für Sie, aber Routine in Klimamodellen): sie berechnen die korrespondierende Temperaturverteilung im Klimasystem zum zeitlichen Verlauf von P
Eine Uebung fuer sie, bei der ich ihnen versichere, das sie scheitern werden.
Sie fuegen einem Planeten 122.4 Petawatt an Waerme zu, und der Planet gibt 122.4 Petawatt wieder ab. Wie warm ist der Planet an der Oberflaeche?
Brauchen sie noch irgendwelche Angaben?
Wie Sie selbst gemerkt haben, fehlen Angaben. Was soll das also?
Kommen Sie selbst darauf, warum Sie Ihre Frage falsch gestellt haben und welche Angaben fehlen?
Ein Beispiel: die Größe des Planeten fehlt, warum ist die neben anderen Angaben wichtig für eine eindeutige Fragestellung?
Das is didaktisch. Welche Angaben fehlen denn?
Der Planet hat ungefaehr eine Aquatorialen Durchmesser von 40000 km. Wozu ist diese Angabe wichtig? Ich brauche diese Angabe nicht.
Kleiner Tip, sie koennen die Groesse des Planete ganz einfach aus der Flaechenangabe berechnen…
Vorallem notwendig.
Das gehört mit zu Ihrer Aufgabe.
oha, pi-mal so groß wie die Erde. Wie heißt dieser Planet?
Nachdenken könnte abhelfen.
…weil Sie eh nichts kapieren, oder warum nicht?
Sicher per Kugeloberfläche, aber auch die haben Sie nicht angegeben.
Die 240 W/m² ist eine Reaktion auf Marcus Portius. Sie sollten die Beiträge lesen, bevor Sie absurde Vorwürfe machen. Am besten mitsamt dem Initialposting vom 2. März 2025 17:02
Stefan strasser schrieb am 3. März 2025 1:11
Herr Kramm, Spencer und andere haben das unter Berücksichtigung der Speicherfähigkeit berechnet und kommen auf Temperaturen unter 255K. Gerade die T⁴-Abhängigkeit der Abstrahlung sorgt dafür, dass eine gleichmäßige Oberflächentemperatur 255K das Maximum der erreichbaren Mitteltemperatur ist.
Wenn Sie das anders sehen, zeigen Sie doch einfach mal mit Zahlen, dass das doch anders geht.
Kann er doch nicht, strasser kann nur desselbe blabla.
Marvin, die Wirklichkeit zeigt es, bitte Messungen machen!
Alle Modelle, die nicht mit der Wirklichkeit übereinstimmen, sind falsch, so einfach ist das!
Alle die von -18°C daherreden, stehen schwer auf Kriegsfuß mit der Physik!
stefan strasser schrieb am 4. März 2025 2:03
Die Messungen sind doch da. Und die zeigen, dass in Ihrer Beschreibung die Abstrahlung der Atmosphäre fehlt. Wenn Sie die in die Energieflussbilanz der Erdoberfläche einbeziehen (so wie sie auch Herr Kramm in einer seiner Veröffentoichungen darstellt), sind die beobachteten Temperaturen natürlich erklärbar.
Aber Sie behaupten ja, dass es ohne die ginge. Das müßten Sie dann schonmal quanititativ belegen. Kramm, Spencer, Gerlich/Tscheuschner zeigen Ihnen mögliche Temperturverteilungen die alle zu Mitteltemperaturen unter 255K führen. Ignorieren Sie das bewusst?
stefan strasser 4. März 2025 2:03
„Alle die von -18°C daherreden, stehen schwer auf Kriegsfuß mit der Physik!“
Rumgedreht, alle, die die -18°C nicht verstehen, stehen schwer auf Kriegsfuß mit der Physik!
Die Beziehung zwischen Temperatur (T) und Emission (E) ist lokal, aber nichtlinear: E ~ T^4
Deswegen ist der Durchschnittswert von T nicht aus dem Durchschnittwert von E zu berechnen. Ohne Atmosphäre ist der Durchschnittswert von E gegeben = Durchschnittswert der absorbierten Solarstrahlung.
Aber die Mathematik hilft weiter – mit der Hölderschen Ungleichung (können Sie sogar bei G&T nachlesen). Die Hölderschen Ungleichung liefert einen Höchstwert (tritt bei Konstanz ein) von -18°C. Dieser Höchstwert wird in der Praxis nie erreicht, G&T liefern ein Beispiel dafür mit -148°C – der Treibhauseffekt ist also deutlich größer als 33 K.
Vergroesserne sie einfach in dem Excelsheet die Dicke der Bodenschicht und berichten sie ueber die Aenderung.
Abgesehen davon halte ich das Excelsheet fuer das falsche Model.
Hier gibt es eine einfache Erklaerung.
Die kennen sie vielleicht schon…
Werner Schulz schrieb am 4. März 2025 9:36
Hatten wir doch schon des öfteren diskutiert, Sie könnten also einfach das Ergebnis wiedergeben.
Dann könnten Sie doch einfach mal den Fehler konkret aufzeigen. Da sind doch nur drei Sachverhalte drin:
Wo ist da ein Fehler, benennen Sie ihn doch einfach.
Die misteriöse Autokompression der Luft… Wer verrichtet denn die notwendige Arbeit und woher stammt die Energie dafür?
Exakt. Genau wie die 15°C die niemand nachmisst und die implizieren die Erde sei ein schwarzer Körper der 390W/m² konstant emittiert, Tag wie Nacht. Es ist ein Modell das im Prinzip auf einer flachen Erde beruht – wobei die Form eigentlich egal ist, es könnte auch ein Würfel oder eine Banane sein.
Am Prinzip nicht, aber am Resulat der Modellrechnungen – es geht schließlich nur um ein paar Watt (3.7W/m² iirc). Nicht zu vergessen was in der „IPCC-Bibel“ steht, nämlich dass die Solarkonstante tatsächlich nicht variabel ist. Sonst könnte noch jemand auf die Idee kommen dass die Sonne das Erdklima bestimmt (so wie es die Ursprungsbedeutung des Wortes im Griechischen beschreibt). Die Sonne ist halt variabel, in den 1970ern war der WMO das auch noch bekannt:
THE PHYSICAL BASIS OF CLIMATE AND CLIMATE MODELLING Report of the International Study Conference in Stockholm, 29 July-10 August 1974, Organized by WMO and ICSU and supported by UNEP, Page 128
Herr Portius, was soll das? So dumm sind Sie glaube ich nicht, dass Sie nicht wissen, dass die Erdoberfläche entsprchend der lokalen Temperatur abstrahlt. Lesen Sie mal Webers Modell oben. Für die beleuchtete Hemisphäre geht er vom solaren Klima aus, dummerweise auch für die unbeleuchtete, was sein Modell unphysikalisch macht.
Klimamodelle rechnen dahingegend richtig, indem sie zeit- und ortsaufgelöst rechnen, die brauchen keine Mittelwerte. Heutige Ergebnisse basieren auf raum- und zeitaufgelösten globalen Zirkulationsmodellen.
Ihr „Flacherdepostulat“ findet in der Klimawissenschaft keine Verwendung. Selbst bei primitiven eindimensionalen Lehrmodellen ist der Ausgangspunkt immer noch die Erdkugel.
Klima ist fast schon die Definition von Mittelwert. Warum addressieren sie nicht die gezeigten Werte der „Solarkonstante“? Welcher Mittelwert gilt denn nun? Immerhin 10 W/m2 Unterschied nur vom gucken! Da ist mehr als das angenommene CO2 „Forcing“.
Und wenn Klimamodelle richtig rechnen, warum kommen die meisten nicht mal mit Wolken klar oder berechnen langfristige Trends auf wenigstens 1 Kelvin genau?
Das Flacherdepostulat finden sie allein schon bei KT.
Aber in einem stimmen wir ueberein, die Erde hat eine Kugelgestalt!
Für Sie, strasser, Portius, und die anderen THE-nichtraffer reicht eine Genauigkeit von 10 K allemal.
KT haben Sie also nicht verstanden.
Werner Schulz 4. März 2025 9:27
„meisten nicht mal mit Wolken klar“
Die Änderung der Wolken ist eine Folge der Erhöhung der CO2-Konzentration und sorgt damit auch für die Konstanz des feuchtadiabatischen Temperaturgradienten und ist damit Bestandteil der Klimasensitivität: fast genau 1 K bei Zunahme der CO2-Konzentration um 100 ppmV.
Heinemann, Sie verstehen ja nicht einmal Ihr eigenes Modell; das erklärt Ihre verworrenen Aussagen.
„Die gesamte Einstrahlung auf eine horizontale Fläche wird als Globalstrahlung (QG) bezeichnet.“ Quelle: 978-3-623-29070-6 TERRA Geographie für Sachsen, Oberstufe, Schülerbuch, S. 48/49
Es will offenbar nicht in Ihren Kopf dass Ihr Effekt nur im Durchschnitt, also im Modell funktioniert. Schon toll wie Sie das immer wieder eindrucksvoll beweisen. LOL
@ stefan strasser 2. März 2025 17:02, Ihr Zitat:
Und ein solcher Kommentar steht jetzt ausgerechnet hier unter diesem Artikel? Bitte ausdrucken, ankreuzen, fotografieren und an Ihre Antwort anhängen:
O Nicht gelesen
O Nicht nachgedacht
O Beides zu anstrengend
Worüber beschweren Sie sich? Es wäre noch zu ergänzen, daß in zwei der drei Energiebilanzen auch Umwandlung von Energie in Arbeit stattfindet (Strömungen, Winde), die man natürlich mitberücksichtigen muß.
stefan strasser 4. März 2025 9:37
„die man natürlich mitberücksichtigen muß.“
Wenn Sie das extra berücksichtigen, dann müssen Sie auch diese Veränderungen als Folge der Zunahme der CO2-Konzentration berücksichtigen.
Macht alles nur komplizierter, ändert aber am Ergebnis nichts und ist Bestandteil der Klimasensitivität: fast genau 1 K bei Zunahme der CO2-Konzentration um 100 ppmV.
@ ALL: Mein Dank geht an Herrn Dipl.-Ing. Michael Limburg für die Möglichkeit – und die damit verbundene Motivation – meine physikalisch korrekte S-B-Inversion über mehr als 50 EIKE-Veröffentlichungen hinweg auf den in diesem Artikel dargestellten Stand entwickelt haben zu können. Die Veröffentlichung des ursprünglichen S-B-Ansatzes hier auf EIKE liegt nun gut 8 Jahre zurück, aber einigen Kommentatoren ist der damalige Kenntnisstand bei ihrem üblichen Hemisphären-Bashing immer noch anzumerken. Diesmal waren immerhin auch einige konstruktive Kommentare dabei, insbesondere von den Herren Portius, Zinga und Oelschläger, was mich sehr gefreut hat! Ebenfalls erwähnenswert ist Frau Gosch, die diese Runde aus MINT-befreiter Verständnislosigkeit heraus mit einem Raumschiff-Enterprise-Kommentar zu erheitern gewusst hatte. Den moralischen Tiefpunkt setzte dann ein Heinemann mit einer beweisfreien Verleumdung von Professor Lindzen.
Oje. Und ich dachte da kommt noch was zu den physikalischen Fehlern im Modell.
Mein Fazit. In Ihren Modell scheint die Sonne 24 Stunden. Ähnlich wie bei Herrn Kwass und Kraus.
Die Sonne scheint 24 Stunden jeden Tag!
Schreiben Sie wie Kwass, Kraus auch im Dunkeln.
Ja, aber die Erde ist nicht flach!
Die Theorie zum Treibhauseffekt ohne Treibhauseffekt hat Herr Thieme auch schon 2001 veröffentlicht.
http://real-planet.eu/atmoseff.htm
Herr Weber,
wenn sie eine Korrelation pruefen wollen, vielleicht diese hier:
https://www.youtube.com/watch?v=WfuafZbpyII
Gruss Werner
@ Werner Schulz 28. Februar 2025 15:26
Danke für den Hinweis, hatte ich hier im Anhang schon mal abgewählt.
Ah ja, ich habe es gefunden.
Ihre Begruendung ist jedoch nicht ganz verstaendlich. Was meinen sie mit „Korrekturfaktor für die Kondensation“
Meinen sie fuer die feuchtadiabatische Lapsrate? Aber das ist keine Korrektur sondern genau begruendet.
Vielleicht finden sie ja noch mal die Zeit, diesen Ansatz mit ihrem zu vergleichen.
Wie vielmals hier festgetellt wurde, kann man die Temperaturen durch Strahlung allein eh nicht erklaeren.
Vielleicht ist Herr Ebels Hinweis auf isenthalp/adiabat nicht unbedingt falsch. Das kann man doch bei ihrem Ansatz mit einbauen denn es schliesst sich nicht grundsaetzlich aus. Immerhin scheint die Sonne 24 Stunden jeden Tag, bescheint aber nur eine hemisphaerische Flaeche.
@ Werner Schulz 2. März 2025 16:33
Hallo Herr Schulz, ich bedanke mich für Ihre Rückmeldung, aber: Ich hatte in den dort angegebenen Unterlagen einen Wünschel-Faktor entdeckt und das konvektiv-adiabatische Modell deswegen abgewählt. – Das war schon alles, Grüße U. Weber
Herr Weber, die ganze Diskussion und Betrachtungen über Strahlen ist überflüssig. Strahlenphysik kann nicht die Temperatur auf Erden, in einem bestimmten Punkt, in diesem Fall die willkürlich gewählte Höhe von 2 Meter über der Oberfläche mit einem gemittelten Schätzwert von 15 Grad, bestimmen. Die Temperatur ist das Ergebnis von Thermodynamischen Wechselwirkungen innerhalb des Systems Erde/Atmosphäre, wobei der massenlose Energietransport mittels Strahlung gegenüber Luftbewegungen eine verschwindend geringe Rolle spielt.
Der Energieaustausch mittels Strahlen zwischen dem System und dem Weltall ist ausgeglichen und nicht messbar. Das Problem der Messung beginnt schon damit, wo ist die grenze des Systems, da wo das letzte Luftmolekül anzutreffen ist oder hundert km tiefer? Ist die Energiebilanz nicht ausgeglichen, kommt ein Eiszeitalter oder schmelzen die Pole. Auftauchende paar Grad Differenz an bestimmten Punkten innerhalb des Systems haben mit der Strahlenbilanz nichts zu tun. Die einzige „Größe“, mit der man versucht künstlich so etwas wie eine Energiebilanz aufzustellen ist hinter dem Wort „Albedo“ versteckt. Damit versucht man das Verhältnis zwischen der Energie, die absorbiert wird und die, die zurückgestrahlt wird, festzulegen. Sinnlos, erstmal wieder wo, direkt am Boden oder 100 km höher, und zweitens, man kann jeden beliebigen Wert zwischen 0 und 1 ansetzen, stellenweise und zeitweise hat man mit jeder Zahl Recht!
Und die ständige „Berechnungen“ mittels SB Gleichung? Welche Temperatur ist denn die Referenztemperatur der Erde für den Ansatz der Strahlung nach SB? Da wo ich in den Urlaub fahre, hat der Sand am Strand die Temperatur 50 Grad, kurz vorher wurde im Flieger die Außentemperatur von minus 50 gemeldet. Also man kann einen beliebigen Wert zwischen +/- 50 ansetzen und hat immer Recht!
Die Erde wird von Sonnenstrahlen tagsüber erwärmt, nachts wird, bezogen auf der ganzen Erdoberfläche die gleiche Energiemenge zurückgestrahlt, und die Temperatur, die sich in Bodennähe einstellt, ist von thermodynamischen Prozesse abhängig. Zum Beispiel wird es bei Saharawind in Europa 20 Grad wärmer, bei arktischen Wind 20 grad kälter bei selbstverständlich konstanter Strahlenbilanz.
Gäbe es die Diskussion nicht, müsste zum Beispiel Kramm arbeiten gehen, anstatt für die Menschheit überflüssige Pamphlete zu schreiben! Daher wird diskutiert….
@ Peter Georgiev 27. Februar 2025 9:39
Herr Georgiev, eine höfliche Nachfrage: Sind Sie ganz sicher, diesen Artikel auch wirklich gelesen zu haben?
Nur sehr grob Überflogen Herr Weber. Die Bezeichnung „hemispärisches Konvektionsmodell“ bedeutet selbst schon, dass Sie es tiefgründiger betrachten als die meisten Strahlenakrobaten hier. Nicht nur eine primitive Strahlungsgleichung von -18 +33 =15, sondern die Konvektion richtigerweise mit einbeziehen.
Meine Kritik bezieht sich nicht auf Ihren Beitrag hier, sondern auf alle Beiträge über Temperaturberechnungen, in denen die Begriffe „Albedo“ und „SB-Gleichung“ vorkommen.
Hatte schon länger einen Anlass für diesen Beitrag gesucht, der Anstoß war wohl dieser Teil der Überschrift „….mein SB Modell wird ….“.
Kann nicht ausschließen dass ich den Falschen getroffen habe, ich meinte alle.
@ Peter Georgiev 27. Februar 2025 10:51
Vergessen wir mal Ihren kapitalen Bock und wenden wir uns Ihrer Motivation zu, Zitat:
Dazu meine Frage an Sie: Auf welchem Weg und mit welchen Mitteln sollten die technisch und wirtschaftlich unzureichend aufgestellten Klimarealisten der medial permanent geängstigten Öffentlichkeit denn klar machen, dass sie vom alimentierten wissenschaftlichen Arm der politischen Klimareligion zwecks Einzug von CO2-Ablasszahlungen hinter die Fichte geführt wird?
So wie es schon immer gemacht wurde: Mit einem jederzeit und überall reproduzierbaren Experiment. Faule Ausreden gelten nicht.
Es gibt zahlreiche Experimente welche den THE widerlegen – ironischerweise ist es sogar das Experiment von 1792 welches die theoretische Grundlage der Theorie bildet das die Theorie selbst widerlegt. Ein kälterer Körper wird solange keine Arbeit verrichtet wird einen wärmeren Körper kälter machen, auch durch Strahlung.
Wenn jemand das Gegenteil behauptet: Experiment an die Sonne!
Ähnliches gilt für den Temperaturgradienten: Wenn jemand behauptet dieser hat nichts mit der Gravitation zu tun, dass Loschmidt falsch gelegen hat: Beweise in Form eine Experiments auf den Tisch!
Wäre doch mal interessant zu sehen wie Alarmisten ein existierendes Experiment (und das zugehörige Atmosphärenmodell) widerlegen wollen. Da kommt nix außer Gelaber, Scheinargumenten und Zirkelschlüssen.
Wie hat es Roy Spencer so schön formuliert: „The alarmists need to put up, or shut up.“
@ Marcus Portius 27. Februar 2025 19:05
Hallo Herr Cato, auf meine Frage an Herrn Georgiev hatten Sie geantwortet, Zitat:
Sehen Sie, ich hatte vor gut acht Jahren Tag und Nacht in die Klimabetrachtung eingeführt, was überall für jedermann reproduzierbar ist und was jedes Vorschulkind begreifen kann. Denn nirgendwo in unseren gemäßigten Breiten beträgt er Unterschied zwischen der Tages- und Nachttemperatur 33°C=THE. Aber das reicht nun mal nicht aus, solange die Medien die CO2-Klimareligion befeuern und die Klimarealisten dort keinen Zugang erhalten. Und „faule Ausreden“ zählen leider sehr wohl in der medialen Öffentlichkeit, und zwar insbesondere bei den Klimarealisten selbst. Denn von den Adepten der vermeintlichen „Klima-Gurus“ ist schon mal gar nix zu erwarten; die bemerken ja noch nicht einmal, dass sich ihre Gurus gegenseitig widersprechen, wie die nachstehende Abbildung beweist.
Links eine Aussage von Kramm@Sternke und rechts eine Aussage aus der deutschen Übersetzung von G&T (2009) die beide als höchste Autoritäten des deutschen Klimarealismus‘ gelten:
Salve U. Weber. 😉
Die beiden Diagramme (ich habe eine kleine Sammlung davon, es gibt einige) zeigen doch schon wo hier das Problem liegt. Es geht um ein Modell; welches in unserem Fall auf Basis einer flachen Oberfläche mit einer konstanten Temperatur funktionieren soll, im Durchschnitt und quasi im Vakuum.
Worum geht es denn bei der ganzen Diskussion? Wer das schönere Modell hat? Verstehen Sie mich nicht falsch, es ist gut dass man verschieden Ansätze verfolgt. Joe Postma hat auch ein Modell das dem Ihren ähnlich ist, dann sind da Nikolov&Zeller, Wilde oder Cotton, nur mal so als Beispiele.
Mal darüber nachgedacht diese Leute zu kontaktieren? Um ein „besseres“ Modell zu kreieren.
Aber Herr Weber, seit wann ist der THE (33°C) denn der Unterschied zwischen der Tages- und Nachttemperatur??
@ Marcus Portius 28. Februar 2025 0:14
Modellunterschiede sind eine Inversion des Scheinriesen: Je genauer man hinschaut, umso größer werden sie…
PS: Am Ende dieses Artikels hatte ich mich mal mit Vinós & May beschäftigt und hier am Ende mit dem konvektiv-adiabatischen Modell.
Herr Portius, wenn Sie fälschlich behaupten dass ein kälterer Körper einen wärmeren Körper kälter machen wird, auch durch Strahlung, so haben Sie die Strahlungsdämmung in kälterer Umgebung schlicht vergessen. Sie erinnern sich sicher daran dass selbst Uli Weber die „Umgebungsgleichung“ S=Sigma•(T⁴-To⁴) eingeführt hatte um die 100% Strahlungskühlung seiner (ruhenden) Tagseite bei +15 Grad so zu verringern dass Wärmeenergie für die Nachtseite übrig bleibt – was ja de facto eine Gegenstrahlung bedeutet.
Wärme geht immer von warm nach kalt.
Um einen Körper zu erwärmen muss man Wärme zuführen.
Beide Bedingungen zusammen, bedeuten ein kalter Körper kann einen wärmeren nicht noch weiter erwärmen.
Werner Schulz 1. März 2025 10:27
„Wärme geht immer von warm nach kalt.“
Ihre Wortwahl ist unvollständig. Es muß heißen: „Nettowärme geht immer von warm nach kalt.“
„ein kalter Körper kann einen wärmeren nicht noch weiter erwärmen.“
Ich verstehe manche nicht. Einmal „die Sonne macht das Klima“ und andererseits wird nur die Atmosphäre betrachtet und die Sonne vergessen!
Die Oberflächentemperatur stellt sich so ein, das die Energieänderung der Oberfläche im Mittel Null ist. Der Oberfläche wird Energie zugeführt von der Sonne und der Gegenstrahlung (die Gegenstrahlung als Netto von der Gesamtstrahlung), abgeführt wird die Energie durch Abstrahlung und Konvektion. Wenn die Gegenstrahlung steigt, ergibt sich das Energiegleichgewicht bei einer höheren Temperatur. Können Sie schon bei Stefan 1879 nachlesen.
Übrigens beruhen die Meßgeräte für die Gegenstrahlung auf dieser Tatsache.
Energie geht hin und her im Strahlungsaustausch, Wärme nur in eine Richtung.
Der Definition nach ist es die Energie die am Ende des Prozesses von warm nach kalt übertragen wird.
Werner Schulz 1. März 2025 12:37
„Wärme nur in eine Richtung.“
Richtig ist „Nettowärme nur in eine Richtung.“
„geht hin und her“
Und die Gegenstrahlung sorgt für eine höhere Oberflächentemperatur.
Aha, warum gibt es dann Strahlungsfrost? Warum ist es in der Wüste Nachts saukalt?
Michael Poost 1. März 2025 13:42
„Aha, warum gibt es dann Strahlungsfrost?“
Ohne Gegenstrahlung wäre es noch kälter. Zur Stärke der Gegenstrahlung (langwellige Einstrahlung): https://wettermast.uni-hamburg.de/frame.php?doc=Zeitreihen8d.htm#STRAHLUNG
Was meinen Sie, wieviel Frost wäre, wenn 200 W/m² wegfallen (In der Wüste könnte auch ein andere Wert wegfallen, vielleicht sogar mehr).
Meine Definitionen stehen da. Diese stimmen mit der Thermodynamik ueberein.
Was sie als „Nettowärme“ gibt es so nicht. Sie koennen aber gerne die Quelle nennen.
Im uebrigen meinen wir wahrscheinlich sogar das gleiche, nur das wir in der Wirkung eine unterschiedliche Auffasung haben. Allerdings klingen viele ihrer Erklaerungen oder Aussagen sehr schief.
Ich habe diese bemaengelt. Mehr werde ich jetzt nicht tun.
mfg Werner
Werner Schulz 1. März 2025 14:12
„Sie können aber gerne die Quelle nennen.“
https://archive.org/details/sitzungsbericht543klasgoog/page/410/mode/2up Seite 411
Wenn auch das Wort „Netto“ nicht auftaucht. Das Wort Überschuss wird heute Netto genannt.
Die Messgeräte für die sogenannte „Gegenstrahlung“ beruhen wohl eher auf Aberglauben: Anmerkungen zum Gegenstrahlungs-Paradoxon aus einem hemisphärischen Blickwinkel
U. Weber 1. März 2025 13:03
„„Gegenstrahlung“ beruhen wohl eher auf Aberglauben:“
zitiert von Ihnen:
„Die Erde soll sich durch die Rückstrahlung ihrer eigenen Abstrahlung (= Gegenstrahlung)“
Falsch: die Gegenstrahlung ist keine Rückstrahlung, sondern die übliche Abstrahlung eines warmen Körpers (Einstein 1917) – mit Rückstrahlung hat das nichts zu tun. Hier ist der warme Körper die kühle Atmosphäre. Damit sich die Temperatur in der Atmosphäre trotz des Energieverlusts nicht ändert, muß dieser Energieverlust ersetzt werden. Der Ersatz erfolgt durch Strahlungen von unten und oben und in der Troposphäre auch durch konvektiven Wärmetransport (latente und sensible Wärme.
@ Jochen Ebel 1. März 2025 13:52
Schau’n Sie mal unten rechts in die anhängende Grafik, Herr Ebel. Damit die Erdoberfläche 390 W/m² abstrahlen kann, benötigt sie 155 W/m² aus der Gegenstrahlung, die wiederum nur dadurch existiert, dass die Erdoberfläche 390 W/m² abstrahlt. Das ist doch mal ein schöner physikalischer Treppenwitz, den ich unter dem nachfolgenden Link ausführlich diskutiert hatte: Schwarzschild und die Lösung der Strahlungstransfergleichung – ein physikalischer Hütchentrick?
Herr Weber,
Sie glauben also Ihren „Treppenwitz“ nicht. Demzufolge beherrschen Sie also das Kirchhoffsche Gesetz nicht.
Nehmen Sie Nachhilfe in Physik…
Mal als Tipp. Damit Sie aus Ihrem Dilemma mit dem scheinbaren Zirkelschluß rauskommen: betrachten Sie die Energiebilanz zum All.
Wer glaubt, die Gegenstrahlung würde die Bodenabstrahlung und die Bodenabstrahlung wiederum die Gegenstrahlung determinieren, hat ein Brett vorm Kopf.
@ Thomas Heinemann 1. März 2025 15:21
Nun mach’ hier mal nicht den alten Kirchhoff zum Affen, das habt Ihr THE-Fuzzies ihm doch selbst angehängt. Immerhin habt Ihr das Gegenteil der Abgasrückführung beim Verbrenner erfunden, denn die kostet Leistung. Velleicht wirst Du mit „Heinis zirkular amplifizierendem Leistungsknoten“ ja noch zum Retter der vergurkten Energiewende. Ein paar von Deinen ominösen Leistungsknoten hintereinandergeschaltet, und schon ist der 70%-Verlust bei der Herstellung von „grünem“ Wasserstoff ausgeglichen – versuch’s einfach mal…
Sie flippen aus…dann hab‘ ich wohl getroffen.
Empfehle die Arbeit von Herrn Ebel,
https://www.researchgate.net/publication/45885336_The_Greenhouse_Effect_Does_Exist
U. Weber 1. März 2025 14:37
„benötigt sie 155 W/m² aus der Gegenstrahlung,“
Ja, aber um ein „Treppenwitz“ zu sein, müssen Sie schon erklären, was nicht stimmt: Die Atmosphäre hat eine Temperatur größer 0 K oder die Abstrahlung nach Planck stimmt nicht.
Zwischen dem Energieverlust durch Abstrahlung (Temperatur Nacht) und Ersatz dieses Energieverlustes (Temperatur Tag) kann eine lange Zeit liegen. Wenn eine Reflexion vorliegen würde, dürfte keine Zeitverzögerung sein.
@ Jochen Ebel 1. März 2025 18:16
Sie schreiben, Zitat:
Sehen Sie, Sie haben es nicht verstanden, denn bei einer physikalischen Gleichung müssen auf beiden Seiten des Gleichheitszeichens nicht nur gleiche Werte stehen, sondern auch noch zur selben Zeit. Denn um mit einer Abstrahlung von 390 W/m² eine Rückstrahlung von 155 W/m² zu erzeugen, benötigt es zu den vorhandenen 235 W/m² genau zu diesem Zeitpunkt diese ominösen 155 W/m².
Um es mit anderen Worten zu sagen, Ihr THE kann übers Wasser gehen!
Und damit wären wir auch schon beim Punkt, es ist Religion, Ihre THE-Religion – machen Sie damit, was Sie wollen, hängen Sie Sich den THE um oder ins Fenster, es ist mir sowas von egal.
Aber behaupten Sie nicht, es sei Physik!
Herr Weber, Sie behaupten, die Messung der sogenannten „Gegenstrahlung“ beruhe eher auf Aberglauben und zusammen mit Herren wie z.B. Holtz, Schaffer, Portius, Georgiev bestreiten Sie dass eine zusätzliche Energiezufuhr von etwa 150 W/m² bei einem durch Solarstrahlung beheizten Erdboden eine Temperaturerhöhung bewirkt. Den THE halten Sie nur für Religion und einen physikalischen Hütchenspielertrick. Dabei hatten Sie doch die Gegenstrahlung in Ihre „Umgebungsgleichung“ für die Netto-Abstrahlung S=Sigma•(T⁴-To⁴) am Boden selbst eingefüht.
Dieser 53. EIKE-Beitrag ist wieder ein gefundenes Fressen für den Mainstream. Kakophonie der Jünger des antiken Clausius (2.HS, 1887) und Irrtümer statt solider Physik-Aufklärung gegen die unnötige und unbezahlbare Energiewende sind doch kontraproduktiv und zeigen den IPCC-Anhängern dass man solche Klimakritiker welche den THE nicht verstehen und daher bestreiten, nicht ernst nehmen kann.
Starke Worte; na dann zeigen Sie mir mal dass Gegenteil von dem was im Experiment zu beobachten ist. Die ganzen Alarmisten hier behaupten immer dass alles falsch sei ohne jemals einen handfesten Beweis zu liefern. Große Worte und Anschuldigungen, gefolgt von ein paar kümmerlichen Zahlen, Wortklauberei und einer unhaltbaren Meinung.
Also: Her mit dem Experiment anstatt zu labern! Meinen Sie Sie schaffen das?
Marcus Portius 1. März 2025 15:50
„Her mit dem Experiment anstatt zu labern!“
Das Experiment wurde schon 1879 gemacht:
https://archive.org/details/sitzungsbericht543klasgoog/page/410/mode/2up Seite 391 – 428
Die Gegenstrahlung geht von der äußeren Kugel zur inneren Kugel.
Falsches Experiment. Ist Ihnen mal aufgefallen dass Dulong&Petit mit einem Vakuum gearbeitet haben – Josef Stefan macht dazu eine Anmerkung; das habe ich Ihnen schon einmal zitiert, Sie haben es ignoriert und irgedwelchen zusammenhangslosen Text zitiert. Noch mal nur für Sie:
Da haben Sie es : Kalte Luft kühlt eine warmen Körper und beginnt zu zirkulieren. Ihre eigene Quelle widerlegt Ihre dumme Theorie.
Noch einen Versuch?
Herr Weber, die Heinemann/Dietze Fraktion reagiert mit endlosen Strahlendiskussionen, die Kosch/Kwass Fraktion mit tiefen Glaubensbekenntnis und 95% der Menschheit versteht den Inhalt nicht, oder in meinem Falle, hat keine Motivation, den Inhalt richtig zu studieren und jede Zahl zu verstehen. Man kann eher durch kurze, klare Ansagen, wie „die Sonne schickt keine Rechnung“ überzeugen bzw. manipulieren.
Ich würde lieber flächendeckend empfehlen, mit eingeschalteten Logik barfuß am Strand zu spazieren. Man stellt unweigerlich fest, dass der Strand nachts 20-30 Grad abkühlt, das Wasser praktisch gar nicht. Nicht nur wegen der höheren Wärmakapazität, sondern vor allem dort nicht nur die unmittelbare Oberfläche, sondern auch in die Tiefe erwärmt wird, das wiederum abhängig vom Wellengang. Und 70% der Oberfläche ist Wasser, und diese Eigenschaften regeln die Oberflächentemperatur. Das Ganze hat mit Strahlen und SB gar nichts zu tun, und selbst mit Konvektion nur am Rande. Und ist in keinster Weise berechenbar.
Fazit: Der Wärmespeicher Weltmeere bestimmt überwiegend die Temperatur auf der Oberfläche, Luftbewegungen auch im hohen Maße, Berechnungsmöglichkeiten dafür gibt es nicht, und Strahlengleichungen auf SB Basis ist Selbstbetrug oder Betrug!
Oder man erklaert es einfach bis es jeder versteht:
https://www.youtube.com/watch?v=WfuafZbpyII
@ Peter Georgiev 28. Februar 2025 11:15
Herr Georgiev, Sie sagen, Zitat:
„… und 95% der Menschheit versteht den Inhalt nicht, oder in meinem Falle, hat keine Motivation, den Inhalt richtig zu studieren und jede Zahl zu verstehen. Man kann eher durch kurze, klare Ansagen, wie „die Sonne schickt keine Rechnung“ überzeugen bzw. manipulieren.“
Sehen Sie, das ist doch Ihre ganz persönliche Entscheidung. Wenn man andererseits im Interesse der nachfolgenden Generationen den grassierenden Klimawahn in Frage stellen will, dann muss man irgendwie die Öffentlichkeit mit nachvollziehbaren Argumenten erreichen – und eine solche Möglichkeit besteht dankenswerter Weise hier auf der EIKE-Plattform. Und was Sie abschließend schreiben, stimmt auch nur zum Teil, Zitat:
„Und 70% der Oberfläche ist Wasser, und diese Eigenschaften regeln die Oberflächentemperatur. Das Ganze hat mit Strahlen und SB gar nichts zu tun, und selbst mit Konvektion nur am Rande. Und ist in keinster Weise berechenbar.“
Die Oberflächentemperatur der Weltmeere wird durch die Sonneneinstrahlung erzeugt, was Sie unschwer daran erkennen können, dass das Meerwasser im Süden üblicherweise wärmer ist als im Norden. Und wenn das mal nicht der Fall sein sollte, dann sind mit an Sicherheit grenzender Wahrscheinlichkeit die konvektiven Meeresströmungen im Spiel…
t
Goldrichtig. Das ist das paradoxe an den ganzen Diskussionen – man redet über die Temperatur der Luft, also von Gasen, welche klar definiert ist und nichts mit Strahlung zu schaffen hat. Das entsprechende Modell existiert seit mindestens den 1920er Jahren, bekannt als das Standardatmosphärenmodell welches im Prinzip auf der kinetischen Gastheorie und der mechanischen Wärmetheorie beruht.
Selbst das IPCC definiert nicht klar um welche Temoeratur es eigentlich geht – einmal die oberflächennahe Lufttemperatur „global surface air temperature GSAT“, dann eine Mixtur aus Luft und Oberflächentempertaur „GMST“ IPCC Seite 2231
Dann wird einfach angenommen dass im Durchschnitt, also im Modell, die SAT und die Oberflächentemperatur identisch sind. Dass dies nicht der Realität entspricht sollte eigentlich jedem (außer Angehörigen der Klimasekte) einleuchten – die tägliche Erfahrung lehrt dass kälter Luft eine wärmere Oberfläche abkühlt (und sich so die Luft erwärmt). Das hat auch Josef Stefan angemerkt.
Das ganze ist eine Geisterdebatte bei der die Alarmisten das Verschieben des Torpfostens zu einer eigenen Disziplin gemacht haben. Wenn nicht mal langsam jemand hingeht und klare Definitionen welche auf empirischen, experimentell nachvollziehbaren Prämissen beruhen schafft werden diese nutzlosen Diskussionen so lange weitergehen bis die Erde das nächste mal einfriert.
Und jede Wette, auch hier wird die Sekte das CO2 verantwortlich machen: Mit dem negativen „Treibhauseffekt“ der ja angeblich in der Antarktis zu beobachten ist. Man biegt es sich solange bis es passt. Dank inkompetenter Politiker wird auch dies von einem Großteil wieder geschluckt werden: „Follow the Science!“.
Nicht nur in der Antarktis gibt es einen negativen THE, sondern auch in der Stratosphäre und Mesosphäre. Da kühlen THG. Auch bei Inversionslagen in kalten Winternächten können THG einen negativen THE hervorrufen. Größten Einfluß auf den THE haben übrigens Wasserdampf und Wolken, wie auch meine Wärmebildkamera direkt zeigt. Das glauben Sie ja auch nicht.
Sie sollten einmal nachschlagen wie die Temperatur eines Gases definiert ist und wie man diese überlicherweise misst. Es hat nichts mit Strahlung zu tun (sondern dem 0ten HS).
Aufsteigende Luft expandiert und wird deshalb kälter (Joule-Thomsom-Effekt), nicht weil sie strahlt – diese Strahlung ist das Resultat und nicht die Ursache.
Natürlich glaube ich Ihnen, nur denke ich dass Sie sich nie die Mühe gemacht haben mal nachzusehen wie Ihr Instrument im Detail funktioniert. Das ist wie mit Roy Spencer und seinem IR-Thermometer dass er gen Himmel streckt und denkt: „Heureka, der THE ist real.“
Am Ende geht es wieder um die Frage ob Ihre irreversible IR Strahlung die Luft bzw. THGs erwärmt (Verletzung des 1ten HS) und ob die von der kalten Luft emittierte Strahlung die wärmere Oberfläche erwärmt (Verletzung des 2ten HS).
Sie sind mit Ihrer Strahlung auf dem falschen Dampfer.
Also Gase die im IR aktiv sind, strahlen dann gemäß Ihnen keine Wärme ab? Und Wolken? Wird wie gesagt alles bei Herrn Weber nicht behandelt. Steht aber alles in Lehrbüchern seit 100 Jahren.
Das habe ich nicht geschrieben. Die Strahlung ist ein Resultat und nicht die Ursache der Temperatur eines Gases. Sie zäumen das Pferd von hinten auf.
Das was Sie hier propagieren steht in der Tat in Lehrbüchern – in denen von vor ca. 1880. Ihre ganzer Effekt beruht auf einer Theorie die von Rudolf Clausius et al widerlegt wurde. Insofern haben G&T mehr als richtig gelegen, Sie reiten ein totes Pferd.
Marcus Portius 27. Februar 2025 21:27
„Die Strahlung ist ein Resultat und nicht die Ursache der Temperatur eines Gases.“
Die Temperatur eines Gases ist die Folge von Absorption der Strahlung. Die Temperatur des Gases steigt infolge der Absorption (Energie- bzw. Wärme-Zufuhr) so lange, bis Emission und Absorption im Gleichgewicht sind.
„Sie zäumen das Pferd von hinten auf.“ ????
Ob Sie vom Pferde zäumen Ahnung haben, weiß ich nicht. Aber das Sie von Ursache und Wirkung keine Ahnung haben, beweist Ihr Posting.
Weil es auch abstrahlt? Und was ist mit Latenter Waerme? Kein Einfluss auf die Temperatur?
Werner Schulz 28. Februar 2025 18:13
„Weil es auch abstrahlt? Und was ist mit Latenter Waerme? Kein Einfluss auf die Temperatur?“
Ich habe nur kurz geschrieben: „so lange, bis Emission und Absorption im Gleichgewicht sind.“
Komplett muß es heißen:
„so lange, bis Emission und (Absorption und konvektive Wärmeheranführung) im Gleichgewicht sind.“
Das das keine Ausrede ist – siehe z.B.
Jochen Ebel 28.02.2025 14:31
Jochen Ebel 28.02.2025 17:02
Jochen Ebel 28.02.2025 17:31
Also alle Aussagen vor Ihrer Frage (18:13).
Jochen Ebel 28.02.2025 14:31
Was sagt der Effekt aus?
Jochen Ebel 28.02.2025 17:02
Hier wird gesagt es reicht eine Temperaturdifferenz, also jeder Gradient.
Jochen Ebel 28.02.2025 17:31
Was sagte Fourier wirklich?
Hier eine Analyse.
Sie wissen auch das Gehrlich und Tscheuchner Fourier geprueft haben. Von Ueberadibatik keine Spur bei Fourier.
1824 gab es noch nicht mal das Konzept Adiabatic.
Das Konzept des adiabatischen Prozesses wurde erstmals von James Clerk Maxwell (Scottish physicist (1831–1879) beschrieben und später von James Prescott Joule und William Thomson (Lord Kelvin) in ihren Arbeiten zur Thermodynamik weiter ausgearbeitet. Der Begriff „adiabatisch“ wurde jedoch von William John Macquorn Rankine (5 July 1820 – 24 December 1872) im Kontext der Thermodynamik eingeführt.
Ich nehmen ihnen ihre Referenz nicht ab. Sie stimmt fachlich und geschichtlich nicht.
Prof. Joseph Fourier (1768 – 1830)
1824 | Die Temperaturen der Erde und der planetarischen Räume
Nach „Saussure“ suchen, dann die folgenden Abschnitte.
Die „Saussuresche Box“ gab Fourier aber nur den Anstoß die Erdbodentemperatur erklären zu wollen.
Wenn Sie seinen Denkansatz, der zur physikalischen „Notwendigkeit“ eines die direkte Abstrahlung der Wärmestrahlung des Bodens ins All behindernden Prozesses führte, verstehen wollen, müssen Sie Fourier GANZ lesen. Mit physikalischen Erklärungen auch hier übersetzt und erklärt durch R. Pierrehumbert (engl.):
https://www.wiley-vch.de/de/fachgebiete/naturwissenschaften/the-warming-papers-978-1-4051-9616-1
Marcus Portius 1. März 2025 23:31
„Was sagte Fourier wirklich?“
http://www.ing-buero-ebel.de/Treib/Fourier.pdf
S. 13 unten S.14 oben:
Die Mobilität der Luft, die sich schnell in alle Richtungen bewegt und die, wenn sie erhitzt wird, aufsteigt und das Strahlen der dunklen Wärme in der Luft verringern die Intensität dieser Wirkungen, die in einer durchsichtigen und festen Atmosphäre stattfinden würden, aber sie heben diese Wirkungen keineswegs vollständig auf.
Werner Schulz 1. März 2025 21:56
„eines Gases bei einer isenthalpen Druckminderung.“
In der Atmosphäre findet eine adiabatische Druckminderung statt und keine isenthalpe Druckminderung: https://www.gutefrage.net/frage/unterschied-zwischen-adiabatisch-und-isenthalp
Bei der Drosselung einer Gasströmung wird keine Arbeit gegen den äußeren Druck geleistet, weil aus der Umgebung kein Druck auf das Gas wirkt – in der Atmosphäre wirkt immer der Umgebungsdruck, die Voraussetzungen für isenthalp fehlen also.
„es reicht eine Temperaturdifferenz, also jeder Gradient.“
Mein Zitat bezog sich nur auf den letzten Teil „da die Luft leicht beweglich ist“. Bei reiner Adiabatik passiert keine Strömung, da sich die Luftdichte bei einer zufälligen Änderung genau gleich wie die Umgebung verändert – also jeder Antrieb fehlt. Das kannte Fourier noch nicht, das Schwarzschild-Kriterium ist erst von 1906.
„Sie stimmt fachlich und geschichtlich nicht.“
Das G&T Unsinn geschrieben haben, können Sie nachlesen bei https://www.academia.edu/69403919/Gerlich
Ihr Irrtum mit „Sie stimmt fachlich und geschichtlich nicht.“ entsteht dadurch, das Sie nicht zum Zitat gehörenden Text einbezogen haben.
Sie sollten sich echt mal mit ein paar Definitionen auseinandersetzen und dann für Ihre steile These einen experimentellen Nachweis liefern. Genau wie Dietze behaupten Sie etwas ohne auch nur den geringsten Beweis zu liefern.
Eine Formel ist kein Beweis; also: Put Up or Shut Up!
Marcus Portius 1. März 2025 15:55
„Eine Formel ist kein Beweis“
Was ist denn nun falsch? Es gibt keine Absorption, der Energieerhaltungssatz gilt nicht oder ein höherer Energieinhalt eines Gases erhöht nicht dessen Temperatur.
Dr. Oskar Emil Meyer – Die kinetische Gastheorie
Rudolf Clausius – Die mechanische Wärmetheorie.
Lesen. Und dann kommen Sie wieder und wissen dann hoffentlich wie die Temperatur eines Gases definiert ist und wie man die Temperatur eines Gases erhöhen kann. Ansonsten macht es keinen Sinn diese Diskussion fortzuführen.
Marcus Portius 1. März 2025 20:16
Lesen Sie Clausius richtig, z.B. den Text bei „Resultat des doppelten Wärmeaustauschs“
Marcus Portius 1. März 2025 15:55
Die Experimente sind doch schon immer gemacht und in Tabellen niedergelegt
Marcus Portius 27. Februar 2025 21:27
Bestenfalls ist das ein Huhn-Ei-Problem. Das ist schon lange bekannt – Kirchhoff 1861. Jeder warme Körper (warm heißt in diesem Zusammenhang: über 0 K) strahlt und der Emissionsfaktor ist gleich dem Absorptionsfaktor. Wenn der Körper strahlt (d.h. Energie abstrahlt), verliert er Energie und wird kühler bzw. die Umkehrung: wenn der Körper Energie absorbiert wird er wärmer. Wo soll denn die absorbierte Energie bleiben, wenn nicht in dem absorbierenden Körper? Soll der Energieerhaltungssatz nicht gelten?
Wenn etwas Wärme abstrahlt, wird es dann wärmer oder kälter?
Könnte man generalisieren, das Abstrahlen was mit Energieabfluss zu tun hat und niemals mit Erwärmung? Die Eigenschaft kann also nicht für einen wärmenden Effekt zuständig sein?
Ein gewisser Clausius hat festgestellt dass es einer Temperaturdifferenz bedarf damit ein warmer Körper kühlt. Ein kaltes Objekt macht dann offenbar, entsprechend seiner Natur ein wärmeres Objekt kälter. Total normal, sozusagen.
Kalt scheint dann der Endzustand zu sein, der Wärmetod. Und hier kommt Loschmidt ins Spiel, mit der Idee dass Entropie verlangsamt werden kann. Man braucht ein wenig Arbeit, aber es geht.
Das All hat 3K ist also deutlich kälter. Wärmeabstrahlung bedeutet ein Körper der Temperatur T straht entsprechend seines Emissionsgrades bei entsprechender Wellenlänge Energie und Wärme ab.
Marcus Portius 28. Februar 2025 0:28
„Man braucht ein wenig Arbeit, aber es geht.“
Mit der Arbeit ist die Zuführung von Entropie verbunden und zwar mindestens so viel, wie man dem Körper an Entropie reduzieren will.
„Kalt scheint dann der Endzustand zu sein, der Wärmetod.“
Falsch. Unter Wärmetod versteht man eine hohe Temperatur: https://www.spektrum.de/lexikon/physik/waermetod/15400
Ich schreibe „kalt“ und Sie kommen mit dem deutschen Wort, obwohl dann in Ihrem link der „Kältetod“ genannt wird . Sie verstehen mich absichtlich falsch um hier einen Hering vom Teller ziehen zu können. Peinlich, aber typisch.
Im Englischen heißt es „heat death“, oder Big Freeze. Auch Clausius nannte es den Wärmetod. Das es in der Physik keine Kälte gibt macht Ihr Link (hat Rahmstorf das geschrieben) also keinen Sinn.
Der Wärmetod – Was ist das?
Sie demonstrieren eindrucksvoll wie Leute wie Sie „Diskussionen“ führen: Es wird gelabert! Schwache Leistung, aber erwartbar von jemandem der keine Beweise hat und ganz offenbar in einer parallelen Realität leben wo Gase durch Absorbtion von Strahlung wärmer werden als sie ohnehin sind; natürlich ohne jeglichen experimentellen Nachweis. Wie immer.
Marcus Portius 1. März 2025 16:10
Sie können nicht lesen:
„die Erwärmung aller … Systeme auf eine höhere, gemeinsame Temperatur“
Wie hoch die hohe gemeinsame Temperatur ist, hängt vom Energieinhalt des Systems ab. Da die Sonne zum System gehört, dürfte die gemeinsame Temperatur sehr hoch sein.
Marcus Portius 27. Februar 2025 20:13
„Aufsteigende Luft expandiert und wird deshalb kälter (Joule-Thomsom-Effekt)“
„Aufsteigende Luft expandiert und wird deshalb kälter“ – das ist zwar richtig (adiabatisch), aber das hat nichts mit dem Joule-Thomsom-Effekt zu tun. Die Temperaturabsenkung ist Folge der Ausdehnungsarbeit gegenüber der umgebenden Luft und wird der inneren Energie (Temperatur) entnommen. Dagegen wird beim Joule-Thomsom-Effekt die Energie aus der Bindungsenergie der Moleküle untereinander entnommen. Die Abkühlung infolge adiabatischer Expansion erfolgt bei einem Gas bei beliebiger Temperatur, für den Joule-Thomsom-Effekt muß ein Gas genügend kalt sein, damit die Moleküle untereinander genügend Bindungsenergie haben.
Marcus Portius 27. Februar 2025 20:13
„Aufsteigende Luft expandiert und wird deshalb kälter“
Damit die Luft tatsächlich aufsteigt, muß sie etwas überadiabatisch sein – etwas weil die Luft sehr beweglich ist (Fourier 1824). Allerdings wird die am Boden zusätzlich zugeführte Wärme im Laufe des Aufstiegs in Strahlungswärme umgewandelt. An der Tropopause ist dieser Wärmeüberschuß auf Null gesunken, so daß die Aufwärtsbewegung aufhört.
Peter Georgiev 27. Februar 2025 9:39
„wobei der massenlose Energietransport mittels Strahlung gegenüber Luftbewegungen eine verschwindend geringe Rolle spielt.“
Sie sollten mal die Intensitäten vergleichen.
Ich vergleiche immer Energiemengen in der Einheit Joule, alles andere ist Quatsch. Verstehen Sie offensichtlich nicht.
Peter Georgiev 1. März 2025 9:00
„alles andere ist Quatsch.“
Sie können gerne W/m² in Ws/m²s ? J/m²s umwandeln – aber am Verhältnis der Intensitäten ändert das nichts.
Es muß heißen Ws/m²s = J/m²s
Sie können angeben so viel Sie wollen, dass Sie paar physikalische Größen kennen, von Energiebilanzen verstehen Sie NICHTS!
Peter Georgiev 1. März 2025 14:59
„von Energiebilanzen verstehen Sie NICHTS!“
Das dürfte wohl eher auf Sie zutreffen – erklären Sie mal die Energiebilanz an der Erdoberfläche.
Ebel, unabhängig von der Intensität der Srahlen marschieren diese durch das Universum, ohne Energie abzugeben. Durch Luft im Wesentlichen auch, durch Wasser zum Teil (ohne Physik feststellbar, man braucht nur beim Tauchen die Augen öffnen). Eis an den Polen spiegeln dagegen die Strahlen zurück. Grünpflanzen wandeln die Strahlen Energie in Kohlenhydrate, ohne Wärmeenergie abzugeben.
Welcher Teil der Strahlung an den Prozessen teilnimmt, die zu Tempeturänderungen führen, lässt sich nicht berechnen und ist von den Eigenschaften der Strahlen kaum abhängig, im Wesentlichen von der Materie, auf der sie trifft.
Daher ist die ganze Strahlenkasperei ohne Rücksicht auf die auf Erden gespeicherten Energie überflüssig, reine Spielerei!
Laufen Sie im Sommer barfuß, vielleicht verstehen Sie es dann.
Peter Georgiev 2. März 2025 8:39
Jein, denn sowohl von den Absorptionseigenschaften der Materie als auch von der Wellenlängenverteilung der Strahlung.
Erstens läßt sich das bei ausreichend Wissen berechnen und
zweitens woher wollen Sie dann wissen welcher Teil des Wärmetransport bedeutend ist oder nicht?
Peter Georgiev 27. Februar 2025 9:39
@Ebel
Jeder analphabete Fischerjunge versteht die Absorption besser als Strahlenkasper mit meterdicken Scheuklappen, mit M12 Bolzen festgeschraubt. Beim dunklen Sand verbrennt man sich die nackten Füßen, bei hellen nicht, und die Wärmeverteilung im Wasser, somit auch die Absorption ist bei hohen Wellengang ganz anders als bei stiller See. Da berechnen Sie nichts, können nur wichtig tun!
Beim Studium musste ich zig Wärmeprozesse berechnen, dabei wurde die selbstverständlich vorhandene Strahlung als unbedeutend gering ausgeklammert!
Tja, Herr Georgiev, die Strahlungskasperei ist der einzige Ausweg für die Strahlenkasper, den in praxi nicht vorhandenen und nicht nachweisbaren THE irgendwie am köcheln zu halten. Heini und Deuti und ff. wären sonst schlagartig flüssiger als Wasser ……
Noch viel schlimmer Herr Tengler, sie müssten arbeiten. Ein Bauer, der nur dem Erdboden die Grundstoffe für Brötchen erkämpft, schafft mehr Werte für die Menschheit, als alle Strahlenkasper zusammen. Diese wollen aber mit aller Macht ihren Status ohne Leistung verteidigen. Das ist alles!
Peter Georgiev 3. März 2025 10:51
Sie widerlegen etwas – zu dem ich mich gar nicht geäußert habe.
Was mich immer wundert ist dieses:
How to convert joules to watts
Wenn man einen durchschnittlichen Apfel 1 Meter anhebt – wird er dann zu einem schwarzen Strahler der mit der Oberfläche als angenommener schwarzer Strahler im Strahlungsgleichgewicht steht und erwärmt er dann den Boden? Was ist mit seinem Schatten? Hat er beim Fallen die Oberfläche abgekühlt? Was wenn es ein saurer Apfel war?
Und wie ist der Apfel in 1m Höhe angekommen? Ebel et al scheinen nichts von guter, alter Arbeit zu halten, dem Fakt dass Energie konvertiert wird.
Tja….
Herr Portius, alle Ihre Einwände kann ich klar nachvollziehen. Mir sind logische Schlussfolgerungen wichtiger als Formeln und Quellen.
Viele Beiträge hier sehe ich als überflüssig….
Mit den Quellen ist das auch so eine Sache. Wenn man sich den „atmosphärischen Temperaturgradienten“ in seiner aktuellen Version auf Wikipedia ansieht fragt man sich ob Wikipedia bei Ebel oder Ebel bei Wikipedia abschreibt.
Wenn man sich mal die Bearbeitungen ansieht wird klar: Ebel schreibt bei Wikipedia mit, auch zum Thema EIKE! So funktioniert die „Klimawissenschaft“.
Selbiges ist mir auch beim englishen Artikel zur „lapse rate“ aufgefallen, da schreibt ein gewisser Robert Wentworth mit. Als ich ihm diesen Artikel in einer „Diskussion“gezeigt habe (weil er klar zeigt dass die lapse rate nichts mit Strahlung „negligible“ zu tun hat) hat Bob mal eben den Text dahingehend verändert dass der THE die lapse rate verursacht. Passt doch irgendwie zur ganzen Agenda:
“We must be ready to employ trickery, deceit, law-breaking, withholding and concealing truth. We can and must write in a language which sows among the masses hate, revulsion, scorn, and the like, towards those who disagree with us.”– Vladimir Ilyich Lenin
Marcus Portius 2. März 2025 1:40
Es kommt auf die Intensitäten und die bestrahlten Massen an. Z.B.
Laserkühlung: https://de.wikipedia.org/wiki/Laserk%C3%BChlung
Sie verstehen nichts davon, sonst würden Sie den adiabatischen Prozeß verstehen, wo die innere Energie (Temperatur) in Ausdehnungsarbeit gegen den äußeren Druck umgewandelt wird bzw. umgekehrt.
AMS: adiabatic process
A process in which there is no exchange of heat or mass with the environment. In an adiabatic process, a change in internal energy is solely a consequence of work. For an ideal gas and most atmospheric conditions, compression results in warming, whereas expansion results in cooling.
Jetzt erzählen Sie mir mal wo dort Wärmestrahlungstransport oder THGs eine Rolle spielen, entgegen der Definition. Erheitern Sie mich, erzählen Sie wie THG’s Luft durch irreversible 15µm IR-Strahlung/Photonen wärmer machen! Und warum Luftdruck dies nicht vermag!
Nun, Herr Ebel und Ihre Definition haben doch schon erklärt, dass bei einem adiabatischen Prozeß keine Wärme transportiert wird – so ist ja die Definition.
Damit stellt sich Ihre Frage nicht.
Bekommen Sie es echt nicht auf die Reihe, einfach mal das zu lesen, was Sie im Netz finden und hier verbreiten? Wieso müssen immer andere Ihnen erklären, was es bedeutet, was Sie gefunden haben?
Natürlich tut sie das. Wieso wollen Sie mir vorschreiben was ich frage? Wie wäre es mal mit Antworten?
Ebel und Sie fabulieren von Strahlung die aber per Definition nicht relevant ist. Also ist Ihre Theorie, per Definition: Mist!
Sie verstehen das einfach nicht.
Damit stellt sich Ihre Frage nicht.
Nein, hatte ich doch schon erklärt: denn per Definition wird bei adiabatischen Prozessen keine Wärme transportiert. Daher wird auch keine Wärme per Strahlung bei adiabatischen Prozessen transportiert. Also brauchen Sie es auch nicht voraussetzen und Fragen dazu stellen, wenn Sie das per Voraussetzung schon ausgeschlossen haben.
Ein Beispiel: eine geschlossene leere (kein Gas drin) Box hat die Hälfte der Innenseiten schwarz, ist dort ein schwarzer Strahler mit A=1, die gegenüberliegenden grauen Seiten haben einen Absorptionsgrad von A=0,9. Die Box sei 30°C warm und nach Außen isoliert. Dann strahlen die schwarzen Seiten gemäß Stefan-Boltzmann 479 W/m2 ins Innere ab und auf die gegenüberliegende Seite. Die graue Gegenseite absorbiert davon 0,9×479 W/m2 = 431 W/m2 und reflektiert den Rest von 48 W/m2. Sie strahlt (da konstante Temperatur) genausoviel ins Innere ab (Kirchhoff), wie absorbiert wurde, was die gegenüberliegende schwarze Seite 100% absorbiert (= 431 W/m2). Zusammen mit den 48 W/m2 Reflektion gewinnt also die schwarze wieder die 479 W/m2 zurück (=thermisches Gleichgewicht). Demnach findet keine Wärmeübertragung zwischen den gegenüberliegenden Seiten (schwarz A=1 und grau A=0,9) statt. Der Prozeß ist adiabatisch.
@ Thomas Heinemann 3. März 2025 0:10
Ich hatte mich ja schon gewundert, warum in Bayern so viele Leute bei Föhn unter Kopfschmerzen leiden. Naja, was sollen die armen Leut‘ denn auch machen, wenn ihnen bei Föhn ständig leere Heini-Boxen um die Ohren fliegen…
Von Heini lernen heißt siegen: Föhn ist, wenn es Tupperware regnet!
Aha, ist es wieder soweit, man läßt die Schlägertruppen rein, wenn die Argumente nichts taugen
@ Thomas Heinemann 3. März 2025 19:43
Sieh mal, Heini, ich hatte Dir sehr empathisch und humorvoll zu verstehen gegeben, dass Deine adiabatischen Kinkerlitzchen nichts taugen.
Und daraufhin hast Du hier eine Bedrohung mit körperlicher Gewalt hochgezogen – das gehört sich nicht und hat auf einer Kommentarfunktion nichts zu suchen.
U. Weber 4. März 2025 9:36
„dass Deine adiabatischen Kinkerlitzchen nichts taugen.“
Invarianten, mit denen die Klimasensitivität leicht zu bestimmen ist, sind für Dich „Kinkerlitzchen“???
Macht alles nur komplizierter ohne einfaches, ändert aber am Ergebnis nichts und gibt die Klimasensitivität: fast genau 1 K bei Zunahme der CO2-Konzentration um 100 ppmV.
Herr Heinemann meint es vielleicht so:
Ja es stimmt Strahlung spielt keine Rolle, aber sie dürfen nichts sagen, was stimmt, also sagt er sie haben es nicht verstanden, die Frage stellt sich nicht, sie verfälschen seine oder Ebels Aussagen, sie lügen, sind ein Wissenschaftfälscher, können aber kein Wissenschaftler sein, das ist je nur er, er erklärt es aber nicht, weil sie es selber rausfinden müssen, aber sie verstehen es ja sowieso nicht…..
Usw usf.
Aber dann, dann sagt stellt er klar, wie es sein muss, das also Strahlung nichts mit der Adiabatik zu tun hat. Also genau das wo er vorher versucht hat gegen zu argumentieren.
Wenn das nicht pathologisch ist, dann ist es schlechte Satire, aber mehr eher ein unwahrscheinlich arroganter Drang allein Recht zu haben.
Wahrscheinlich hat er noch nie eine wissenschaftliche Arbeit publiziert und hat keine Form einer Bestätigung seines Wissens.
Herr Schulz, diese Aussage ist einfach idiotisch.
Unter Adiabatik versteht man, dass ein thermodynamisches System eine adiabatische Zustandsänderung macht, bzw. in einem Zustand ohne Wärmeaustausch verharrt, wie mein Beispiel mit der Temperaturstrahlung der Box hier.
Wenn Luft in der Atmosphäre adiabatisch gehoben wird, so ändert sich die Temperatur des Photonengases des gehobenen Luftvolumens natürlich genauso wie die der Luft im Luftvolumen, denn beides ist ja im LTE.
Ist es idiotisch, weil Adiabatik nichts mit Strahlung zu tun hat, oder das sie das genau so erklaeren, weil es nicht so ist?
„Wenn Luft in der Atmosphäre adiabatisch gehoben wird, so ändert sich die Temperatur des Photonengases des gehobenen Luftvolumens natürlich genauso wie die der Luft im Luftvolumen, denn beides ist ja im LTE.“
Ach du meine Güte…
Das Problem mit Heinemann et al ist dass sie nicht begreifen dass Strahlung in der Thermodynamik der Atmos- bzw. Troposphäre eine untergeordnete bis nicht existente Rolle spielt. Die Atmos- bzw. Troposphere ist eine Wärme-Kraft Maschine, es geht um Luft und verrichtete Arbeit. Strahlung resp. Wärme ist nun mal ein Resultat dieser Arbeit und nicht die Ursache.
Diese Luft ist für die Verstrahlten offenbar nicht existent, da nicht IR-aktiv (bzw. mit IR Spektroskopie nicht messbar, mit der Ramam Spektroskopie allerdings schon), daher argumentieren sie in einem Quasi-Vakuum wie man in Heinemanns Kommentar sehen kann.
Es will einfach nicht in die Köpfe der Klimakultisten und Sophisten dass der THE nur ein Modell ist und sie mit ad-hoc Theorien versuchen das Modell in der Wirklichkeit anzusiedeln. Die mentale Gymnastik ist schon beeindruckend wenn Leute sich von der Realität entkoppeln und einem das dann auch noch großspurig als physikalische Wahrheit verkaufen wollen.
Es sind genau diese Widersprüche die deutlich machen wo das eigentliche Problem liegt: Es gibt keine offizielle, detailierte, technische Beschreibung wie der Effekt überhaupt funktionieren soll und was das beste ist: Niemand misst die Temperatur der Erdoberfläche. Die beobachteten 15°C sind die Lufttemperatur nahe der Oberfläche und Arrhenius, wie auch Happer haben einfach angenommen diese Lufttempertaur sei identisch mit der Oberflächentemperatur. Und dies widerspricht natürlich dem 2ten HS, insbesondere da die Luft die Oberfläche aktiv kühlt.
Sie haben die Rolle der Wärmestrahlung in der Atmosphäre gar nicht verstanden. Die Luft wird erst durch den radiativen Strahlungstransport, der zu einer nach oben stark abfallende Temperatur führt (radiativer Temperaturverlauf, siehe Manabe/Strickler 1964), in die Lage versetzt, vertikal zu zirkulieren.
Für Sie heißt das: zurück zu den Grundlagen.
Den Quatsch glauben Sie doch selbst nicht. Hören Sie auf zu fantasieren. Ich meine mit Temperaturverlauf den Temperaturverlauf der Luft (der lokal mit dem des Photonengases übereinstimmt) , das ist Ihnen doch auch klar, also albern Sie nicht rum.
Es gibt keine Widersprüche, die Realität und damit die Physik ist einfach nur anspruchsvoller als Sie sich das wünschen.
Wenn Sie nur eine technische Ausbildung haben, kommen Sie nur mit Fragen weiter, um die Physik hier zu verstehen. Alles andere ist sachlicher Unsinn und zeigt nur geistige Überforderung („Übersprungverhalten“).
Haben Sie mal gemessen, ob da ein Temperatursprung im Mittel zwischen der Kontaktfläche von festem Bodens und Luft ist? Im Laufe des Tages durchläuft der Temperaturunterschied zwischen Boden und Luft, genauer der Temperatursprung an der Kontaktfläche einen Vorzeichenwechsel. Also kann Ihre Frage nur auf eine Abweichung im Mittel abzielen.
Unbestritten ist natürlich, dass die Luftsäule der Troposphäre vertikal im Mittel kühler ist als der Boden. Das stimmt auch bei Happer und Arrhenius. Es führt dazu, dass Wärme vom Boden in die Luft geht. Sie müssen eben ausreichend differenziert nachdenken, um Ihre Verständnisprobleme mit der Physik zu klären.
Herr Ebel hat es schon erklärt. Sie lassen sich genauso wie schon Schulz irreleiten, indem Sie die Austauschgröße
des Materials mit der Umgebung, der Wärme dQ, und die Wärmemenge = innere Energie dU des Materials vermischen. Lesen Sie msl Clausius, der hat das sicher sauber erklärt.
Es gilt der 1. HS mit dQ + dW = dU, dabei ist die zweite Prozessgröße am Material (System) die Arbeit dW.
Adiabatisch bedeutet per Definition dQ = 0. D.h. – wie Herr Ebel erklärt – ändert sich dann die Wärmemenge dU, wenn Arbeit am Material verrichtet wird, z.B. durch Expansion bei adiabatischer Hebung, dW ist dann negativ und damit auch dU, das Material kühlt ab.
Erst mal heisst das Herr Schulz.
Dann sollten sie nicht irreleiten.
Weiterhin sollten sie nicht „sicher“ sagen, ausser sie hätten den Text gar nicht selber gelesen.
Ansonsten erklären sie nichts neues.
Aber mal eine Frage.
Wenn adiabat gilt dQ = 0, heißt das das man erweitert sagen kann, die absorbierte Strahlungsenergie ist gleich der emittierten?
N A C H T R A G : Die Physikalisch-Technische Bundesanstalt, das nationale Metrologieinstitut der Bundesrepublik Deutschland, folgt meiner hemisphärischen Betrachtungsperspektive, mit der ich den sogenannten „natürlichen atmosphärischen Treibhauseffekt“ widerlegt hatte. Selbst dort glaubt man inzwischen, die Messung der atmosphärischen Gegenstrahlung mit einem „hemisphärischen Schwarzkörper“ entscheidend verbessern zu können, Zitat:
Das Zauberwort „hemisphärisch“ ist also inzwischen auch beim nationalen Metrologieinstitut der Bundesrepublik Deutschland (PTB) angekommen, und auf das Ergebnis bin ich wirklich gespannt. Ich wünsche daher den Damen und Herren sowie Allengendern der PTB einen wirklich durchschlagenden Erfolg mit ihrer hemisphärischen Referenz:
Mögen die hemisphärischen Anstrengungen des nationalen Metrologieinstituts der Bundesrepublik Deutschland am Ende mit der Erkenntnis gesegnet sein, die ich schon seit mehr als acht Jahren vertrete:
Es gibt gar keinen „natürlichen atmosphärischen Treibhauseffekt“!
Wow, da benutzt noch jemand den Begriff hemisphärisch (bzw. hemispherical) – also hat Herr Weber recht. Wie einfach die Welt doch sein kann.
Dabei ist das einfach nur die Beschreibung eines Referenzkörpers, der die Form einer Halbkugel hat und zum kalibrieren anderer Messgeräte benutzt wird[1]:
Figure 2. Sectional view of the HSBB. The HSBB consists of a black coated cone in combination with a highly specular reflecting golden hemisphere and is designed to specifically calibrate broadband infrared detectors with a hemispherical acceptance angle. Marked are the positions of the Pt100 thermometers at the cone vertex (1), cone edge (2) and the hemisphere (3). In the picture, an IRIS instrument (4) is placed below the opening of the HSBB.
Ein Bild der „Halbkugel“ kann man sich hier ansehen: https://opg.optica.org/getimagev2.cfm?img=MMNjHmFYYTkJUPvhl5pK19ms6fpSrAjokkiXhJNqfXI%3D&size=full&uri=oe-30-26-46991-g004
[1]Bilateral comparison of irradiance scales between PMOD/WRC and PTB for longwave downward radiation measurements, Moritz Feierabend et. al.
[2] Development and operation of the Hemispherical Blackbody (HSBB) for the calibration of infrared radiometers with a hemispherical acceptance angle, Moritz Feierabend et. al.
Damit landest Du jetzt ganz vorn auf der Ignorieren-Liste. Sehe ich aber genauso.
@ Marvin Müller 26. Februar 2025 19:29
1:26 Stunden ist eine sehr gute Zeit für Recherche und Framing, Zitat:
Sieh mal Marvin, das grundsätzliche Problem von Referenzkörpern ist die Geometrie der Oberfläche, weil deren Krümmung ja zu einer Verfälschung der gemessenen spezifischen Strahlungsleistung führt. Von daher hätte ich eher sowas wie „flach“ oder „zweidimensional“ erwartet – aber kommen wir mal zu Dir:
Was mir bei Deinen Kommentierungen zunehmend auffällt, sind folgende drei Punkte:
Du vertrittst kein eigenes / adaptiertes Klima-Modell.
Du greifst jeden Kritiker des sogenannten THE unmittelbar an.
Du springst in fremden Threads ungefragt für THE-Verfechter ein, die mit ihrer Argumentation stecken geblieben sind.
Kann es vielleicht sein, dass Du ein professioneller THE-Gatekeeper bist?
Das Gerät; welche Temperatur hat der Detektor? Im Text steht nur etwas von Modellen und angenommnen 0K.
Haben Sie schon ein Patent auf das Wort „hemisphärisch“ angemeldet? Wäre gut zu wissen, denn zum einen habe ich es schon öfter benutzt, zum anderen bedeutet dessen Nutzung, in welchem Kontext auch immer, natürlich die totale Unterwerfung gegenüber dem Weber’schen „Intellekt“..
@ ALL: Meine Damen und Herren, Ladies and Gentlemen,
eine solche Insider-Story aus der Dunning-Kruger-Szene haben Sie noch nie gelesen – halten Sie Sich gut fest!
Herr Schaffer, der im EIKE-Beitrag von Dr. Roth (29.11.24) anhand der Grafik mit dem Gradienten und der Verschiebung der Abstrahlhöhe nach oben – wobei er fälschlich Gegenstrahlung als Ursache für den THE ausschliesst und den Gradienten auf Adiabatik zurückführt, meint:
>>Auf wissenschaftlicher Ebene hat die „kritische Seite“ wenig bis nichts zu bieten.. Das ganze Rumgestocher hier von Leuten die nichtmal den THE verstehen (damit sind insbesondere auch Sie [Dietze] gemeint!), hinkt meilenweit der Wissenschaft hinterher. Die „kritische Seite“ ist von daher eine Illusion, es gibt sie nicht. Ein paar Kinder die Cowboy und Indianer spielen sind ja auch keine Streitmacht, außer vielleicht in ihrer Phantasie. Ich dagegen bin der Wissenschaft weit voraus. Das ist eine völlig andere Liga.<<
@Weber
Unter Ihren Link steht im Text ganz unten.
es/ptb
PS
Ich bin eindrücklich gegen Gegenmaßnahmen. Da ich den THE für normal halte und nicht an Kipppunkte glaube.
@Oelschläger, Co.
Habe gerade nochmal ein Bild mit meiner IR-Kamera am Tag bei bedeckten Himmel gemacht. Das Haus gegenüber hat ca. 11°C. Der bedeckte Himmel darüber ca. 1°C und der bedeckte Himmel weiter oben ca. -2°C. Mit einen feuchtadiabatischen Temperaturgradienten von 0,7°C je 100m kommt man da auf eine Höhe der Wolkendecke von etwa 1.400-1.800 m. Von dem Wasserdampf und Wolken dort kommt die Wärmeabstrahlung. N2 und O2 strahlen im IR nicht. Sonst könnte man nichts sehen. Und CO2 strahlt vor allem bei 15 Mikrometer. Das erfässt die Wärmebildkamera nur im Randbereich. Würde die nur bei 15 Mikrometer messen, wurde man da auch nur wenig sehen.
„Von dem Wasserdampf und Wolken dort kommt die Wärmeabstrahlung“
Schon besser!
Und nun noch den Wasserdampf nicht zu wichtig nehmen…
Ist Wasserdampf für das Leben auf diesem Planeten nicht elementar? Bedrohen die Klimaarlamisten das Leben an sich? Fragen über Fragen.
Kondensierter Wasserdampf sind halt Wolken. Kommen bei Herrn Weber gar nicht vor. Die Wolken. Wasserdampf nennt er ja als Klimafaktor.
„Kondensierter Wasserdampf sind halt Wolken“
Ja, natürlich.
Aber Wolken sind
-ein Graustrahler über die gesamte Bande und
-reflektieren dazu auch noch
Der Wasserdampf hingegen…
Abstrahlung der Wolken und die Gasstrahhlung sind ja wohl zwei sehr unterschiedliche Dinge . Wie erkennen Sie welche Strahlung von gasen und welche von Wolken ausgeht?
Die Gasstrahlung von H2O und IR Strahlung von Wolken überlappen sich im Messfenster der Wärmebildkamera. Wolken strahlen dabei ähnlich stark wie Schwarzkörper. Hatte ich bei Eike aber schon über Jahre beschrieben. Siehe Fritz Möller Lehrbuch von 1973. Einführung in die Meteorologie. Und bei Herrn Weber tauchen Wolken nicht auf.
Ein Alternativvorschlag: Das Jahr hat 365 Tage und die Woche 7 Tage, in Summe also 372. Die Antwort auf alles beträgt 42, wie wir aus „Per Anhalter durch die Galaxis“ wissen. Nun ergibt 372 – 2 x 42 = 288!!! Zufall? Ich denke nicht!
Dieser „halberter“ Zeit-Raum Ansatz erklärt die Erdtemperatur perfekt, womit er bewiesen ist, und der Treibhauseffekt gleichsam widerlegt. Gern geschehen!
„Vielmehr finden mit der morgendlichen Erwärmung der Oberfläche sofort auch Verdunstung und Konvektion statt, durch die wesentliche Mengen der örtlich eingestrahlten Energie in die globalen Zirkulationen übergehen und abgeführt werden.“
Herr Weber,
die Abkühlung erfolgt doch nicht nur durch Verdunstung und Konvektion, sondern auch durch die gleichzeitge permanente Infrarotabstrahlung, deren Intensität abhängig ist von der Temperatur des abstrahlenden Körpers. Die Temperatur baut sich vom Morgen bis zu einem Maximum am späten Nachmittag auf und fällt dann aufgrund der drei Abkühlungsmechnismen ab bis zum nächsten Sonnenaufgang.
@ T. Oelschläger 25. Februar 2025 12:27
Ihre einstmalige Analyse eines Kramm’schen Pamphlets war einfach brillant.
Diesmal bleiben Sie weit unter Ihren Möglichkeiten. Ich hatte in meiner 5. AUSSAGE umfänglich die Kompensation der IR-Nachtabstrahlung beschrieben und mir tatsächlich erlaubt, nicht ausdrücklich auf die IR-Abstrahlung auf der Tagseite hinzuweisen, da haben Sie völlig Recht. Deshalb bleibt mir am Ende nur noch mit Bob Dylan zu sagen:
When I cannot please everybody, why should I then please somebody at all?
Na ja Herr Weber,
erst mal danke für die Würdigung meiner Kritik an Herrn Kramm. Wo er nicht schlüssig argumentiert, muss er sich sachliche Kritik gefallen lassen.
Ich denke, dass Sie ja einen hohen Anspruch haben und sich auch nicht wegen kleiner Auslassungen der dann harschen Kritik Ihrer besonderen „Freunde“ aussetzen wollen. Seien Sie doch glücklich, dass ein Ihnen im Grundsatz wohlwollender Leser freundlich auf die kleine Lücke hingewiesen hat, so dass Sie das korrigieren konnten.
@ T. Oelschläger 25. Februar 2025 17:06
Sie mögen’s vielleicht gar nicht so gemeint haben, aber dann haben Sie Sich mit Ihrem Kommentar einfach falsch eingereiht, beispielhaft aus diesem Thread:
Denn meine 5 Kernaussagen werden in diesem Artikel folgendermaßen angekündigt, Zitat:
Diese Aussage gilt umgekehrt natürlich genauso. Denn was detailliert in den mehr als 50 EIKE-Beiträgen über die meisten der verlinkten Kritikpunkte ausführlich abgehandelt worden war, kann nicht bei der Darstellung wesentlicher Eckpunkte dieses Modells umfänglich wiederholt werden. Genau deshalb hatte ich sogar noch auf die ausführlichen Artikel zu den einzelnen Aussagen verlinkt.
Nicht nur die Erde stahlt im IR ab, auch die Atmosphäre. Und das am Tag und in der Nacht. Meine Wärmebildkamera zeigt es.
Luft strahlt entsprechend ihrer Temperatur. Was Sie messen ist genau diese lokale Umgebungsstrahllung der Luft und nicht eine aus einer Höhe X, y oder z auf die Erd- oder Wasserobefläche gerichtete Strahlung, die die Temperatur des Bodens erhöht. Aufgrund der hohen Dichte der Atmosphäre in Bodennähe wird die IR- Abstrahlung schon in geringer Höhe absorbiert, danach dominiert die Übertragung durch Stoss bis zu dem Höhenniveau, bei dem die Dichte wieder so abnimmt, dass Abstrahlung die Stossübertragung überwiegt , was dann zur Abstrahlung ins All führt. CO2 ist dort dad Vehikel, das die Abkühlung der Atmosphäre bewirkt. Eine Rückstrahlung auf die Oberfläche findet nur statt durch die bodennahen Moleküle, die nach erster IR-Absorbtion die aufgenommene Energie nicht durch Stossübertragung verlieren. Das dürfte im Ergebnis kein nennenswertes Rückstrahlungsvolumen sein und nicht den Erwärmungseffekt von 33Grad bewirken, der der Rückstrahlung zugesprochen wird. Wenn Sie immer noch an einen THE durch Rückstrahlung glauben, sollten Sie mal die dazu von Peter Heller vor eingen Jahren veröffentlichten Erklärungen lesen ( THE aufgrund Erhöhung der Abstrahlungshöhe iVm Temperaturgradient). Im übrigen steht der von Peter Heller beschriebene Mechnismus ungeachtet der Kontroverse Heller/Weber zum THE m. E. nicht im Widerspruch zum Weber- Modell. Die Aussagen von H. Weber und H. Heller sind vereinbar. Herr Weber erklärt ja im Wesentlichen, wie die Landfläche und das Meer erwärmt werden ( hemisphärischer Ansatz) und wie die erwärmte Landfläche und das Meerwährend des Tages und der Nacht ( Wärmespeicher) die Luft erwärmen. H. Heller erklärt, wie sich dieErhöhung der CO2- Konzentration auf die Abstrahlungshöhe ins All, den dadurch erhöhten Energiegehalt der Atmosphäre und die aufgrund des Temperaturgradienten bewirkte Erhöhung der Lufttemperatur in Bodennähe (und nicht die Erhöhung der Temperatur des Bodens!) auswirken.
Genauer, nur die IR aktiven Moleküle darin.
Das ist zu ungenau, und weil es hier auf Genauigkeit ankommt, ist es falsch.
Der Weg, den empfangene Wärmestrahlung an einem Punkt zurückgelegt hat, hängt selbstverständlich von seiner Wellenlänge (äwuivalent Frequenz, Photonenergie) ab. Denn die zurückgelegte Strecke bis zur Absorption hängt auch von der Wellenlänge ab, denn die Absorptionswahrscheinlichkeit der IR Gase ist von der Photonenergie abhängig.
Das hängt von der Wellenlänge ab und stimmt nur für die zentrale Bandenwellenlängen von CO2 etc., die schon nach größenordnungsmässig weniger als 1 Meter absorbiert sind , 40 W/m2 der Wärmestrahlung des Bodens gehen direkt ins All.
Völlig falsch. Die Übertragung nahezu des gesamten Wärmestrahlungsflusses vom Boden (~ 300 W/m2) durch Stöße würde einen enormen Temperaturgradienten von der Größenordnung 10 K pro Meter (!!, nicht km) bedeuten. Von welchem Höhenbereich für Ihren dominierenden Wärmeleitungstransport (Wärmeleitfähigkeit von Luft 0,0262 W/mK) reden Sie denn?
Ab welcher Höhe soll das denn sein, ab 1 Meter über dem Boden?
Sie haben einfach übersehen, dass die IR Gase der Luft aufgrund ihrer Temperatur Wärmestrahlung abgeben und lokal zwischen Emission und Absorption ein Gleichgewicht besteht. Der vertikale Gradient darin ist der Strahlungstransport und führt einen erheblichen Anteil der Energie vom Boden ins All ab.
Völlig falsch. Die Übertragung nahezu des gesamten Wärmestrahlungsflusses vom Boden (~ 300 W/m2) durch Stöße würde einen enormen Temperaturgradienten von der Größenordnung 10 K pro Meter (!!, nicht km) bedeuten. Von welchem Höhenbereich für Ihren dominierenden Wärmeleitungstransport (Wärmeleitfähigkeit von Luft 0,0262 W/mK) reden Sie denn?
Ich rede davon, dass die Oberfläche sich durch Abstrahlung von IR, Leitung iVm Konvektion und Verdunstung permanent abkühlt und dadurch die Luft erwärmt. In der dichten bodennahen Atmosphäre dominiert die Stoßübertragung und der Austausch durch Abstrahlung und Absorbtion spielt deshalb keine wesentliche Rolle. Der Wärmetransport nach oben erfolgt durch die aufsteigende Luft/ Konvektion bis auf ein Höhenniveau, in dem aufgrund abnehmender Dichte die Stoßübertragung ihre Dominanz verliert und der Austausch durch Abstrahlung und Absorbtion überwiegt. Von diesem Höhenniveau aus erfolgt dann auch die schließliche Abstrahlung ins All. Ihre Ansicht, dass der beschriebene Vorgang einen Gradienten von 10 K pro Meter bedeuten würde, müssten Sie mal näher erläutern. Sie konzedieren ja selbst, das die Bodenstrahlung in Bodennähe absorbiert wird. Wie verlieren denn dann die absorbierenden Moleküle ihre Energie wieder? Durch Abstrahlung oder durch Stoß? Wenn es durch Stoß erfolgt, kann der Transport nach oben nur durch Konvektion geschehen.
Ab welcher Höhe soll das denn sein, ab 1 Meter über dem Boden?
Sie haben einfach übersehen, dass die IR Gase der Luft aufgrund ihrer Temperatur Wärmestrahlung abgeben und lokal zwischen Emission und Absorption ein Gleichgewicht besteht. Der vertikale Gradient darin ist der Strahlungstransport und führt einen erheblichen Anteil der Energie vom Boden ins All ab.
Die Dichte der Atmosphäre verringert sich bei ca. 5500 m so, dass Energieübertragung weitgehend wieder durch Abstrahlung erfolgt. Unterhalb dieses Höhenniveaus gibt es auch Abstrahlung und Absorbtion, aber mit wesentlich geringerem Anteil an der Energieübertragung von Molkül zu Molekül als die Stoßübertragung. In dem Bereich der Übertragung durch Abstrahlung und Absorbtion dürfte ein Gleichgewicht herrschen.
In der unteren Atmosphäre gibt es genauso viele Stroßabregungen we Stoßanregungen, so dass immer ein angeregtes Molekül abstrahlen kann. Nennt sich lokales thermodynamisches GG.
Sie können mir sicher beantworten wie groß der jeweilige Anteil der Energieübertragung durch Stoßabregung / Stoßanregung bzw. Abstrahlung/ Absorption auf den unterschiedlichen Höhenniveaus ist.Ihrer Mitteilung sehe ich in Erwartung für mich neuer Erkenntnisse entgegen.
Wozu? Was sollten Sie für ein Interesse daran haben?
Eine Frage die ganz offensichtlich nur von realitätsfernen Zahlen-Akrobaten kommen kann.
Herr Steinmetz,
Physik ist nunmal eine quantitative Wissenschaft. Ob eine physikalische Behauptung wahr oder falsch ist, richten Zahlen.
Wollen sie jedem erklären, welches Interesse er haben darf?
Darauf bin ich auch gespannt und auch darauf wie er die Vielzahl nicht anregbarer Moleküle umgeht damit ein Molekül der „unteren Atmosphäre“ direkt abstrahlen kann. 😀
Herr Steinmetz,
Sehen Sie da etwa ein Problem?
Überlegen Sie mal richtig, es geht hier darum, die Temperaturverteilung der beobachtbaren Erdatmosphäre physikalisch quantativ zu erklären. Dass alle Moleküle, strahlend oder nicht strahlend und ihr lokales Strahlungsfeld dieselbe Temperatur haben (LTE), ist eine Tatsache und erklärbar, da die Thermalisierung innerhalb von weniger als ns erfolgt.
Thomas Heinemann 1. März 2025 10:08
Wie schnell die Thermalisierung erfolgt, siehe:
https://onlinelibrary.wiley.com/doi/abs/10.1002/andp.18882700916
Sorry, ich habe mich verrechnet. Der für Ihre Idee notwendige Temperaturgradient hat eine viel größere Größenordnung von 11000K/m.
Der Wärmefluß L durch Ihre Idee der Stoßübertragung (= Wärmeleitung) ist gegeben durch
L = – k × dT/dz, dabei ist k die Wärmeleitfähigkeit der Luft mit k=0,0262 W/mK und dT/dz der Temperaturgradient.
Der Boden gibt etwa 390 W/m2 ab, davon wird vielleicht L = 300 W/m2 in den ersten Metern der bodennahen Luft durch die Treibhausgase absorbiert.
Sie behaupten nun, diese Leistung L würde dann vertikal per Stoßübertragung (= Wärmeleitung) weiter nach oben transportiert. Der dafür notwendige Temperaturgradient ist demnach dT/dz = -L/k = 11000 K/m.
Ich habe schon nach einem Beweis dieser Behauptung von Ihnen angefordert. So wie Sie das beschreiben, kann Wärmeleitung (=Ihre Stoßübertragung) nur bei einem Temperaturgradienten von 11000K/m die von Ihnen behauptete Leistung übertragen. Diesen Temperaturgradienten müssen Sie nun nachweisen.
Nochmal bei mir die physikalischen Implikationen nachlesen und dann eine Rechtfertigung Ihrer Behauptung abliefern, warum Sie trotzdem glauben, das würde so funktionieren.
Transport nach oben durch Stoßübertragung habe ich nicht gesagt. Der Transport nach oben erfolgt durch Konvektion.
Aha, dann erklären Sie mal, was die Stoßübertragung von wo nach wo übertragen soll. Und wie die Konvektion 300 W/m2 transportieren kann.
Muss die Konvektion 300 W/m2 transportieren? Wie kommen sie auf diese Zahl?
Sie haben zwar die Formel perfekt auswendig gelernt, aber ganz offensichtlich noch nie ein Lehrbuch über Meteorologie und/oder die Physik der Atmosphäre in der Hand gehabt.
Ganz guter Treibhauseffekt, den sie da mit 11000K/m errechnet haben.
Wollen sie etwa sagen, das durch den Strahlungstransport der Treibhauseffekt viel viel kleiner ist?
Das ist ein Beweis, dass Wärmeleitung alleine nicht die Wärme transportieren kann
Sie meinen durch die Wärmeleitung wird viel Wärme an der Oberfläche zurückgehalten?
Junge, probiere es mit Logik! Ich meine gar nichts, sondern liefere Fakten.
Auf welche Vorstellungen/Daten beruhen Ihre Behauptungen?
So erklärt es Richard Linden, aber Sie haben wahrscheinlich weitergehende Erkenntnisse.
Wenn das Lindzen so erklärt hat, hätten Sie es zitieren können. Er hat es nicht, denn er ist Meteorologe.
Wenn man sich mit den entsprechenden Lehrbüchern befassen würde, dann wüsste man, das die Atmosphäre unterhalb der ca. 5500 m für die Abstrahlung undurchhlässig ist. Aber, wie die hier ständigen Diskussionen auch zeigen, haben die Zahlen-Akrobaten die Oberhand und blenden dabei die irdische Realität völlig aus. Abstrahlung von Bodennähe kann es zwangsläufig nicht geben, egal ob man dies nun atmosphärisches Fenster“ nennt oder wie auch immer. Außer man erbringt den Nachweis das Photonen bevorzugt Slalom fahren können. Alleine in Bodennähe hat jedes Gasmolekül etwa 10^10 vollelastische Stoßkontakte bei denen die Energie der Stoßpartner zwangsläufig gemittelt wird, sowohl bei IR-Aktiven wie auch -inaktiven Molekülen. Was letztendlich nichts anderes bedeutet als das in Bodennähe ausschließlicher Energietransfer durch Stoßübertragung erfolgt, selbst wenn zwischendrinnen Energietransfers an IR-Aktive Moleküle durch Absorption und Emission stattfinden. Wer die Atmosphäre beständig nur als aus Formeln und Zahlen betrachtet und nicht als real existierende, gasförmige Materie, gelangt wahrscheinlich nie zu einem Verständnis dessen, dass viele absurden Aussagen und Behauptungen rein garnichts mit der Realität zu tun haben. Und Modelle werden nie auch nur annähernd diese Realität nachbilden können, geschweige denn irgendwelche genauen Vorhersagen treffen. Das trifft schon für den Normalfall zu und erst recht für unregelmäßig auftretende interne wie externe Störungen, Vulkane Erdbeben Sonnenwinde etc. beispielsweise.
Dem kann ich nur zustimmen.
Auch wenn die Strahlung der Sonne die einzige Energiequelle ist, darf der versuch unser Wetter / Klima zu erklären, nicht zu einer ausschließlichen Srahlungstransferrechnung verkommen.Je komplexer die Formel , um so höher der Anspruch auf Richtigkeit??
Es ist ja auch so, dass alle Rechnungen so tun, als müsse die eingestrahlte Energie sofort auch wieder ins All herausgehen. Das ist ja nicht so, weil die unterschiedlichsten Oberflächenbestandteile, das Meer und auch die Atmosphäre die unterschiedlichsten Wärmespeicherungskapazitäten haben und jede Form von Wärmeerhalt eine Verzögerung der Abstrahlung der einmal absorbierten Strahlungsenergie bedeutet. Zum Teil wird sogar mehr als einmal gespeichert (erwärmtes Wasser, anschließend Verdunstung, latente Wärme) Das kann man alles sicherlich nicht gut berechnen und deshalb sind diese Berechnungen eigentlich Makulatur.
Ihre Behauptung ist physikalischer Unsinn und Sie werden auch keine Rechnung vorlegen können, die dies so voraussetzt. Sie reden sich das ein.
Was klar ist, ist, dass ein stationäres Klima per Definition verlangt, dass sich Energie nicht im Klimasystem anreichert, d.h. im Mittel ist die Energieänderung null.
Wenn Sie das meinten, so müssen Sie das auch so ausdrücken. „sofort“ zu sagen, ist also falsch.
Herr Steinmetz,
Das Lehrbuch zeigen Sie mal bitte. In meinen steht das differenzierter. Und vor allem, stehen dort nicht Ihre falschen Schlußfolerungen drin.
Lehrbücher der Physik bilden die Realität in Zahlen und Formeln ab. Wenn Sie die nicht verstehen, verstehen Sie auch keine Physik.
Das z.B. haben Sie erfunden, denn das offenkundig physikalischer Unsinn und demzufolge auch so nicht im Lehrbuch zu finden.
Ebenfalls physikalischer Unsinn.
Ja, die Stoßfrequenz ist hoch, aber Ihre Schlußfolgerung daraus ist physikalischer Unsinn:
Denn Sie ignorieren (absichtlich oder wegen naiver Unwissenheit physikalischer Grundlagen), dass die Luft (die IR-Gase darin) aufgrund ihrer Temperatur ständig IR -Strahlung emittieren und absorbieren.
Es ist also nicht so, wie Sie suggerieren wollen, dass die einzige primäre Quelle für Wärmestrahlung (=IR Strahlung) der Boden ist, sondern (gemäß Kirchhoff) jede Materie entsprechend ihrem Absorptionsspektrum, also auch die IR-aktiven Moleküle der Luft.
Somit findet kein einseitiger Energiefluß von IR-Strahlung vom Boden in die Luft per Absorption statt (was Sie suggerieren wollen), sondern die bodennahe Luft steht mit dem festen Boden im Strahlungsenergieaustausch!
Die unmittelbar am Boden liegende Luft, die mit ihm im thermischen Gleichgewicht ist und gleiche Temperatur hat, strahlt dem Boden bei gleicher Temperatur in dem Spektralband, in dem alle Bodenabstrahlung von den IR-Molekülen absorbiert wird, sogar exakt dieselbe Strahlungsmenge zum Boden zurück. Nichts anderes ist ja der Inhalt des Kirchhoffschen Gesetzes als diese Aussage, es ist eine thermodynamische Notwendigkeit.
„Lehrbücher der Physik bilden die Realität in Zahlen und Formeln ab.“
Ein gutes Lehrbuch erhebt keinen solchen unsinnigen Anspruch, weil dem Autor die, unsere, Unzulänglichkeiten im Verständnis dessen was wir annehmen das in der Atmosphäre vonstatten geht, sehr wohl bewusst ist und er dies auch eingesteht. Es sind eben auch die Praktiker die weit überwiegend dem studentischen Nachwuchs die Grundlagen vermitteln, währenddessen die Zahlenakkrobaten als Dienstleister gesehen werden um allgemeine physikalische Gesetzmäßigkeiten zu lehren. Das bedeutet jedoch nicht, das letzteres zwangsläufig eindeutig zuordenbar und zweifelsfrei ist, solange man sich in weitem Felde noch mit derzeit bestmöglichen Annahmen aushelfen muss um ein grundlegendes Verständnis zu erlangen.
„Lehrbücher der Physik bilden die Realität in Zahlen und Formeln ab.“ Erstens habe ich von Lehrbüchern zur Atmosphäre und Meteorologie geschrieben und nicht von Lehrbüchern der Physik. Aber gewohnt ist man ja solches Spiel von Ihnen, sie verdrehen ein wenig die tatsächlichen Aussagen und schwurbeln dann drauf los.
Ein gutes Lehrbuch, meiner Angabe nach, erhebt keinen solchen unsinnigen Anspruch, weil dem Autor die, unsere, Unzulänglichkeiten im Verständnis dessen was wir annehmen das in der Atmosphäre vonstatten geht, sehr wohl bewusst ist und er dies auch eingesteht. Es sind eben auch die Praktiker die weit überwiegend dem studentischen Nachwuchs die Grundlagen vermitteln, währenddessen die Zahlenakkrobaten als Dienstleister gesehen werden um allgemeine physikalische Gesetzmäßigkeiten zu lehren. Das bedeutet jedoch nicht, das letzteres zwangsläufig eindeutig zuordenbar und zweifelsfrei ist, solange man sich in weitem Felde noch mit derzeit bestmöglichen Annahmen aushelfen muss um ein grundlegendes Verständnis zu erlangen.
Bei bedeckten Himmel misst man die IR-Strahlung von Wasserdampf/ Wolken aus entsprechender Höhe mit der dort vorherrschenden Temperatur. Die IR-Kamera misst im Strahlungsfenster, also dort wo CO2 wenig aktiv ist. Kann deshalb auch unterschiedliche Höhenbereiche und deren Wärmeabstrahlung bei bedeckten Himmel sehen.
„H. Heller erklärt, wie sich die Erhöhung der CO2- Konzentration auf die Abstrahlungshöhe ins All, den dadurch erhöhten Energiegehalt der Atmosphäre und die aufgrund des Temperaturgradienten bewirkte Erhöhung der Lufttemperatur in Bodennähe (und nicht die Erhöhung der Temperatur des Bodens!) auswirken.“
Quatsch!
Warum soll eine (minimale) Erhöhung der Abstrahlhöhe die Energie der Gesamtatmosphäre vergrößern und dann auch noch die Bodentemperatur erhöhen???
IR-aktive Gase treiben ja die Konvektion an und je kürzer die bodennahe Absorptionslänge ist, desto größer wird der Konvektionsantrieb, d.h.desto mehr wird der Boden gekühlt.
Erhöhung der Abstrahlungshöhe auf kältere Höhe, deswegen weniger Abstrahlung, es verbleibt mehr Energie im System, die Temperatur steigt, bis auf der höheren Höhe auch wieder eine Temperatur herrscht, bei der die Abstrahlung wieder im Gleichgewicht mit der Einstrahlung ist, aufgrund des gleichbleibenden Temperarturgradienten ( bestimmt die Wärmeverteilung der Höhe nach) erhöht sich auch die bodennahe Lufttemperatur. Niemand hat gesagt, dass sich dadurch auch die Bodentemperatur erhöht, im Gegenteil, bitte genau nachlesen.Im Übrigen wird das so wie vorstehend von Richard Lindzen erklärt, auf dessen überragendes Wissen ich sehr vertraue.
Lieber Herr Oelschläger,
vorab, ich traue niemanden aus der Scene – Ahnungslosigkeit und Korruption ist mir da zu sehr verbreitet…
Zur Sache:
Grundlage des Ganzen ist ein Transport von Wärme von unten nach oben, hauptsächlich mittels Konvektion. Gäbe es „oben“ einen Stau, so würde sich „oben“ die Temperatur erhöhen was wieder zu einer Erhöhung der Abstrahlung führen würde.
Stellen Sie sich die Atmosphäre in Schichten vor:
Die Schichten „unten“ wissen nicht auf welcher Höhe Energie abgestrahlt wird.
Und könnte die nach Außen verlagerte Abstrahlschicht die zugeführte Energie nicht abstrahlen, würde erst mal die darunter liegende Schicht wärmer werden, die Lokalen Konvektionskräfte verstärken und damit den Wärmemengentransport in die Abstrahlschicht erhöhen.
Im Übrigen frage ich mich, wie die Behauptung der Erhöhung der Abstrahlschicht experimentell überprüft werden soll.
Es gibt oben keinen Stau , weil dort die IR- aktiven Gase die auf sie mittels Stoß oder Absorption übergegangene Energie in das All abstrahlen.Insofern sind die IR-aktiven Gase ein Gateway für Energie ins All. Das ist ein das System Erde kühlender Effekt iR-aktiver Gase. Das sollte unstreitig sein.
In Bodennähe absorbieren IR-aktive Gase die IR-Strahlung der Oberfläche. Die absorbierenden Moleküle verlieren die absorbierte Energie entweder durch Stoßübertragung oder Re- emission. Stoßübertragung dürfte dabei aufgrund der Dichte der Atmosphäre vorrangig sein. Die Re-emission erfolgt im Raumwinkel, so dass 50% nach unten strahlen und wieder auf die Oberfläche treffen. Damit wird der Oberfläche Strahlungsenergie zugeführt, die im angestrahlten Körper in Wärme umgesetzt wird. Das kann man dann Gegen- oder Rückstrahlung nennen, die die Temperatur der Oberfläche gemeinsam mit der Solarstrahlung bestimmt. Der im Ergebnis die Temperatur der Oberfläche mitbestimmende Effekt dieser Rückstrahlung dürfte nicht groß sein, weil ein überwiegender Teil der IR- absorbierenden Moleküle die aufgenommene Energie nicht re-emittiert, sondern durch Stoßabregung verliert und die re-emittierenden Moleküle im Raumwinkel abstrahlen, d.h. nur 50 % gehen nach unten.
Ich bin der Ansicht, dass sowohl der gerade beschriebene Effekt (über die Größe des Effekts mag man streiten und man kann ihn meinethalben auch Treibhauseffekt nennen) als auch die Erklärung des Treibhauseffektes durch Lindzen (Erhöhung der Abstrahlungshöhe durch Zunahme der CO2 – Konzentration, weniger Energieabstrahlung, dadurch mehr Energie in der Atmosphäre, dadurch Erhöhung der Temperatur bis zu dem Punkt, an dem auf erhöhter Abstrahlungshöhe eine Temperatur eintritt, die wieder ein Gleichgewicht von Ein- und Ausstrahlung herstellt, wegen des gleichbleibenden Temperaturgradienten Erhöhung der bodennahen Lufttemperatur, nicht der Bodentemperatur) logisch sind und vor allem ganz zwanglos nebeneinander existieren können.
Genau wie sich die zwei oben beschriebenen Vorgänge nicht ausschließen, schließen sie auch nicht die Grundüberlegung von Uli Weber aus, der ja ganz richtig davon ausgeht, dass die Erde nur jeweils zur Hälfte die volle Sonnenleistung empfängt, Oberfläche und Meere als Wärmespeicher fungieren, damit die Nachttemperatur stützen und aufgrund des so gestützten Temperaturniveaus die Sonnenenergie des neuen Tages zur Erwärmung nicht bei Null aufsetzen muss.
Alle diese Beobachtungen sind doch zutreffend und Teil der Realität, die offenkundig durch das Zusammenspiel vieler Umstände geprägt wird.
Was ich in diesem Forum nicht verstehe, ist die Unfähigkeit vieler Teilnehmer, von ihrer eigenen Meinung abzurücken.Jeder beschreibt seine Erkenntnis mit einem Ausschließlichkeitsanspruch, den man auch als verengte Wahrnehmung empfinden kann.
@ T. Oelschläger 27. Februar 2025 16:09
Ihrer Analyse über den Zustand dieses Forums ist nur wenig hinzuzufügen. Üblicherweise verschwinden überkommene Paradigmen ja nicht vollständig, sondern wesentliche ihrer Elemente werden vom neuen Paradigma aufgesogen; man denke beispielsweise an die Geosynklinaltheorie, die in ihren Mechanismen erst durch die Plattentektonik wirklich verständlich geworden ist. Aber neben der Rechthaberei, wie viele Engel denn nun wirklich Platz auf einer Nadelspitze haben, mag auch die aktive Verwirrung der fachlich nicht vorgebildeten interessierten EIKE-Leserschaft ein tragendes Element von Kommentierungen darstellen.
Diese Aussage zeigt deutlich was das generelle Problem ist: Es gibt keinen klar definierten „Treibhauseffekt“ – es fängt schon beim Namen an.
Die Ehöhung der Bodentemperatur ist der Kern der Theorie, schon alleine weil der Boden die primäre IR-Quelle ist.
Dann die Aussage die Temperatur der Atmos- bzw Troposphäre würde praktisch von oben nach unten bestimmt – das widerspricht so offensichtlich der Realität dass man sich ehrlich fragen muss wie hier der generelle Denkprozess abläuft.
Dann die Annahme ein Spurengas könnte irgendwie die Temperatur von Luft erhöhen – das schreit förmlich nach einem experimentellen Beweis. CO2 absorbiert IR und wackelt ein wenig ist keine überzeugende Theorie, das ist pure Phantasie.
Das kann nicht funktionieren, das geben alleine schon die Zahlen nicht her. Und die Gesetze der Physik, Logik und der gesunde Menschenverstand geben den THE auch nicht her. Da kann man noch so zwanglos sein, alles hat seine Grenzen.
Es steht ja außer Frage, dass die Atmosphäre von der wärmeren Oberfläche (Land, See) durch Leitung, Verdunstung und IR-Abstrahlung (die von IR-aktiven Gasen absorbiert wird, die dann per Stoß sie umgebende sonstige Luftmoleküle erwärmen). Soweit sind wir uns einig.
Es ist aber auch offenkundig, dass bei fortdauernder Sonneneinstrahlung die so ins System Erde gelangende Energie wieder ins All abgeführt werden muss. Das kann nur über IR-aktive Gase gehen und zwar die, die sich an der und oberhalb der Abstrahlungsgrenze befinden. Auf diese Moleküle müssen alle Luftmoleküle ihre Energie übertragen ( durch Strahlungs- oder St0ßübertragung) Wenn sich jetzt durch eine höhere Opazität der Atmosphäre wegen erhöhter Konzentration IR-aktiver Gase die Abstrahlungshöhe erhöht, wird effektiv weniger Energie ins All abgestrahlt. Was passiert denn mit dem Minus an Energie? Nach allen mir bekannten Theorien führt ein Mehr an Energie zur Erhöhung der Temperatur. Dieses Mehr an Temperatur der Atmosphäre verteilt sich in dieser der Höhe nach entsprechend dem immer gleich bleibenden Temperaturgradienten. Die Temperatur steigt an, bis auf dem höheren Abstrahlungsniveau wieder eine Temperatur herrscht, die eine Abstrahlung im Gleichgewicht ermöglicht.
Die wesentliche Erwärmung findet natürlich an der Schnittstelle Oberfläche /Atmosphäre statt, aber der vorstehend beschriebene Prozeß trägt zur Erwärmung bei. Er erwärmt nicht den Boden.
Zu Ihrer letzten Aussage kann man nur kommen, wenn man glaubt, die in Rechenformeln zum Ausdruck kommenden Vorstellungen bildeten die ganze Realität unseres Wettergeschens ab. Das tun sie mit großer Wahrscheinlichkeit nicht (nicht-lineares, gekoppeltes, chaotisches System). Wer glaubt, das in Formeln abbilden zu können dürfte ein großes Selbstbewusstsein haben.
T. Oelschläger 1. März 2025 16:31
„Das tun sie mit großer Wahrscheinlichkeit nicht (nicht-lineares, gekoppeltes, chaotisches System). Wer glaubt, das in Formeln abbilden zu können dürfte ein großes Selbstbewusstsein haben.“
Dann sind also die Anwender einer Ansammlung von vielen Gasmolekülen, die sich chaotisch bewegen, Idioten, denn „Wer glaubt, das in Formeln abbilden zu können“ erzählt Unsinn??? Aber es sind viele Anwender, die die Gasgesetze benutzen.
„Die Re-emission erfolgt im Raumwinkel, so dass 50% nach unten strahlen und wieder auf die Oberfläche treffen. Damit wird der Oberfläche Strahlungsenergie zugeführt, die im angestrahlten Körper in Wärme umgesetzt wird. Das kann man dann Gegen- oder Rückstrahlung nennen, die die Temperatur der Oberfläche gemeinsam mit der Solarstrahlung bestimmt.“
Die mir bekannten Versuche Herrn Ordowskis, der Hähnchengrill und der Spiegel-Test beweisen eher das Gegenteil. Eine Erwärmung durch Gegenstrahlung ist nicht meßbar.
Was auch wunderbar zum 2ten HS paßt!
„Ich bin der Ansicht, dass sowohl der gerade beschriebene Effekt (über die Größe des Effekts mag man streiten und man kann ihn meinethalben auch Treibhauseffekt nennen) als auch die Erklärung des Treibhauseffektes durch Lindzen (Erhöhung der Abstrahlungshöhe durch Zunahme der CO2 – Konzentration, weniger Energieabstrahlung, dadurch mehr Energie in der Atmosphäre, dadurch Erhöhung der Temperatur bis zu dem Punkt, an dem auf erhöhter Abstrahlungshöhe eine Temperatur eintritt, die wieder ein Gleichgewicht von Ein- und Ausstrahlung herstellt, wegen des gleichbleibenden Temperaturgradienten Erhöhung der bodennahen Lufttemperatur, nicht der Bodentemperatur) logisch sind und vor allem ganz zwanglos nebeneinander existieren können.“
Der durch die Schwerkraft implizierte Temperaturgradient ist nur das Grundgerüst des tatsächlichen Temperaturverlaufes. Lokale Störungen wie z.B. durch die Ozonschicht und die damit verbundene lokale Erwärmung verändern lokal die Temperaturen entsprechend. Es ist aber nicht so, daß sich diese Störungen bis zum Boden hin auswirken müssen.
Wenn also die Abstrahlhöhe tatsächlich nach außen verschoben würde und damit bei tieferen Temperaturen abgestrahlt werden würde, so wandert die „überzählige“ Energie deswegen nicht die Atmosphäre runter, sondern führt lokal vor Ort zu einer Temperaturzunahme; ähnlich wie die UV-Absorption durch Ozon lokal die Atmosphäre erwärmt.
„Genau wie sich die zwei oben beschriebenen Vorgänge nicht ausschließen, schließen sie auch nicht die Grundüberlegung von Uli Weber aus, der ja ganz richtig davon ausgeht, dass die Erde nur jeweils zur Hälfte die volle Sonnenleistung empfängt, Oberfläche und Meere als Wärmespeicher fungieren, damit die Nachttemperatur stützen und aufgrund des so gestützten Temperaturniveaus die Sonnenenergie des neuen Tages zur Erwärmung nicht bei Null aufsetzen muss.“
Dem kann ich mich nur anschließen, ich halte diese Durchschnittsrechnerei bei intensiven Größen (Temperatur, Leistung) für falsch. Was das anbelangt hat Herr Weber sicherlich eine Pflock gesetzt.
Einfach mal den Prof.Dr. Kramm zitieren, er weiß bescheid:
„Worauf ich hinwies, ist genau das, was Prof. Dr. Heinz Fortak schon vor 50 Jahren in seinem Lehrbuch Meteorologie formuliert hat:
„Der Strahlungsanteil in Hoehe von 3.52 kWh/(m2 d) (42 %), welcher das System Erde – Atmosphaere effektiv erwaermt, besteht aus der kurzwelligen Strahlungsabsorption in der Atmosphaere und am Erdboden (17 % + 47 % = 64 %) abzueglich des Energiebetrages, der zur Verdunstung des Wassers benoetigt wurde. Worauf ich hinwies, ist genau das, was Prof. Dr. Heinz Fortak schon vor 50 Jahren in seinem Lehrbuch Meteorologie formuliert hat:
„Der Strahlungsanteil in Hoehe von 3.52 kWh/(m2 d) (42 %), welcher das System Erde – Atmosphaere effektiv erwaermt, besteht aus der kurzwelligen Strahlungsabsorption in der Atmosphaere und am Erdboden (17 % + 47 % = 64 %) abzueglich des Energiebetrages, der zur Verdunstung des Wassers benoetigt wurde. Der „Kreislauf“ der langwelligen Strahlung zwischen Erdoberflaeche und Atmosphaere traegt nicht zur Erwaermung des Systems bei. Die effektive langwellige Ausstrahlung nach oben von 64 % dient zur Aufrechterhaltung des Strahlungsgleichgewichts an der Obergrenze der Atmosphaere.“
Und genau diese Aussage wird von der Schar der Klimatisten bekaempft. Dazu gehoeren auch Dietze, Weber, Penner etc., die ja angeblich die Klimapolitik der Bunderesregierung bekaempfen.
Die Aussage von Prof. Fortak ist auch in dem Artikel von Kramm & Dlugi (2011) zitiert (uebersetzt ind Englische), zusammen mit der schematischen Darstellung Die effektive langwellige Ausstrahlung nach oben von 64 % dient zur Aufrechterhaltung des Strahlungsgleichgewichts an der Obergrenze der Atmosphaere.“
Und genau diese Aussage wird von der Schar der Klimatisten bekaempft. Dazu gehoeren auch Dietze, Weber, Penner etc., die ja angeblich die Klimapolitik der Bunderesregierung bekaempfen.
Die Aussage von Prof. Fortak ist auch in dem Artikel von Kramm & Dlugi (2011) zitiert (uebersetzt ind Englische), zusammen mit der schematischen Darstellung
Nochamls für Schnelleser:
„ Der „Kreislauf“ der langwelligen Strahlung zwischen Erdoberflaeche und Atmosphaere traegt nicht zur Erwaermung des Systems bei. „
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski 1. März 2025 18:29
„was Prof. Dr. Heinz Fortak schon vor 50 Jahren in seinem Lehrbuch Meteorologie formuliert hat“
Sie lassen sich auch von Kramm betrügen. Ihr Zitat stammt von Seite 28 und Kramm unterschlägt immer Seite 76:
Zu diesem Kommentar hat mir Prof. Kramm eine eMail geschrieben mit einem großen Verteilerkreis. Da ich nicht weiß, ob Prof. Kramm nicht zitiert werden will, nur meine Antwort:
Dipl.-Physiker Jochen Ebel
Kramm,
das nur Seite 26 zitiert wurde, die den gegenwärtigen Zustand beschreibt und nicht Seite 76 zeigt, daß viele, die sich auf Sie berufen, den Treibhauseffekt nicht verstanden haben.
Das Prof. Fortak nicht jede Einzelheit beim Treibhauseffekt untersucht hat ist verständlich – bei den unendlich vielen Einzelheiten kann niemand jede Einzelheit beschreiben, selbst im dicksten Buch kann nicht jede Einzelheit beschrieben sein.
Das Prof. Fortak weniger Einzelheiten wichtig waren (deswegen Konjunktiv) als heute 50 Jahre später bekannt sind, ist verständlich.
Auch ich kann nicht jede Einzelheit beschreiben – bei einem Gas wird selten jemand alle Moleküle mit den vielen Geschwindigkeiten und Richtungen (die sich durch Kollisionen laufend ändern) beschreiben, d.h. es werden nicht alle Einzelheiten genannt. Aber trotzdem beschreiben die Gasgesetze das Verhalten der Gase bei Änderungen von Druck und Temperatur meistens ausreichend. Auch die Entropie wird z.B. als feste Größe verwendet – obwohl laufend Schwankungen um den Erwartungswert stattfinden.
Zum Verständnis des Treibhauseffektes muß auch nicht jede Einzelheit bekannt sein (örtliche Verteilung von Temperaturen und Niederschlagsmengen usw.), für viele Zwecke reichen Mittelwerte (durchschnittliche Temperaturen usw.).
Genau das hat Fortak vor 50 Jahren genannt – das bei Änderungen der Treibhausgaskonzentration umfangreichen Regelvorgänge einsetzen (z.B. Änderung der Bewölkung, der Windverhältnisse, Eisverteilung usw.), die schwer zu überblicken sind, genau wie die Molekülbewegungen in einem Gas. Für viele Zwecke reichen bei chaotischen Systemen zum Verständnis eben Mittelwerte aus. Beim Gas sind das meistens Druck und Temperatur, beim Klima hauptsächlich die Temperatur.
Und zum Mittelwert der Temperaturen beim Klima sind 2 Invarianten nützlich: Die lineare Abhängigkeit des stratosphärischen Temperaturgradienten von der Treibhausgaskonzentration und die Konstanz des feuchtadiabatischen Temperaturgradienten in der Troposphäre in Verbindung mit dem Schwarzschild-Kriterium.
Sie können ja diejenigen, die sich nicht ausreichend informieren und nur Ihr Zitat von Seite 26 kennen, als dumm ansehen, aber das ändert nichts an den Realitäten des Treibhauseffektes wie die Messungen von über 100 Jahren zeigen:
fast genau 1 K Temperaturanstieg bei Anstieg der CO2-Konzentration um 100 ppmV.
Jochen Ebel
PS: Übrigens stört Sie die Nennung des Schwarzschild-Kriterium gewaltig. Deswegen haben Sie zuerst versucht, seine Bedeutung herunterzuspielen, indem Sie darauf bestanden, das es nur für die Sonne gilt, weil es in einer Arbeit zu Sonnenatmosphäre erschienen ist (Schwarzschild 1906). In den gegenwärtigen Diskussionen bleibt Ihnen nichts anderes mehr übrig, als zu akzeptieren, das es für jede Atmosphäre gilt – auch für Planetenatmosphären.
Herr Ebel,
Herr Prof.Dr. Kramm hat Ihnen ja schon einiges ins Stammbuch geschreiben, so auch jetzt, das sollen alle Leser Von EIKE auch mitbekomen, deshalb zitiere ich Ihn hier:
„Wie ich ebenfalls in meiner Mitteilung vom Januar 2019 schrieb, lautet Prof. Fortaks Aussage auf der Seite 78:
«Eine Erhöhung des CO2-Gehaltes verstärkt demnach die Gegenstrahlung, mit dem Resultat, daß sich die Mitteltemperatur der Erde erhöhen müßte. Allerdings setzen damit in unserem komplizierten System Erde-Atmosphäre Regelprozesse ein, die nicht einfach zu überblicken sind und es sind deshalb auch noch keine eindeutigen Schlüsse auf Klimaänderungen möglich.»
Sie unterschlagen also in Ihrem EIKE- Kommentar den zweiten Teil der Aussage.
«Allerdings setzen damit in unserem komplizierten System Erde-Atmosphäre Regelprozesse ein, die nicht einfach zu überblicken sind und es sind deshalb auch noch keine eindeutigen Schlüsse auf Klimaänderungen möglich.»
Offensichtlich sind Sie noch dümmer als ich dachte.
Dass Prof. Fortak zudem eine Konditionalform verwendet hat, scheinen Sie nicht zu begreifen. Senil wie Sie sind, interpretieren Sie „müsste“ mit „ist„.
Fazit: Mit Ihrem EIKE-Kommentar haben Sie einmal mehr dokumentiert, warum Sie nach der Vereinigung der beiden deutschen Staaten aufs Abstellgleis gelandet sind.
Gerhard Kramm“
Somit bleibe ich dabei:
Der „Kreislauf“ der langwelligen Strahlung zwischen Erdoberflaeche und Atmosphaere traegt nicht zur Erwaermung des Systems bei. „
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski 2. März 2025 11:05
„Sie unterschlagen also in Ihrem EIKE- Kommentar den zweiten Teil der Aussage.“
Nein. Deswegen mein „deswegen Konjunktiv“.
Um Ihren Unsinn zu dokumentieren, zitieren Sie weiter S. 26 und verstehen nicht Seite 76. Ich habe eindeutig geschrieben, was vor 50 Jahren (weil für Prof. Fortak unwichtig war) als Konjunktiv stand, ist heute eine gesicherte Tatsache.
Ich zitiere noch mal:
Jochen Ebel 2. März 2025 10:11
und
Es ist also nichts unterschlagen. Wie umfangreich müssen denn nach Ihrer Meinung Postings sein, damit nichts Falsches unterstellt wird?
Sie verstehen noch nicht mal den ersten Teil von Fortaks Aussage (sonst würden Sie nicht S. 26 zitieren) – mit dem angeblich unterschlagenen zweiten Teil sind Sie erst Recht hoffnungslos überfordert.
Ach Herr Ebel,
ich halte mich da an die Position von Prof.Dr. Kramm,
der da Ihnen das geschrieben hat:
„Sie haben mir öffentlich unterstellt, ich würde betrügen und zum Beweis eine Stelle Prof. Fortaks Lehrbuch zitiert, die ich angeblich unterschlagen hätte. Dass Sie dabei auch noch den zweiten Teil der Aussage von Prof. Fortak unterschlagen haben, unterstreicht Ihr kriminelles Vorgehen. „
Damit beende ich das Gespräch mit Ihnen!!!
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski 2. März 2025 11:05
zu meinen Kommentar hat mir Kramm 2 weiter eMails geschickt. Ich veröffentliche hier nur meine Antworten – Sie können gern den ganzen Text von Kramm einstellen, wenn Sie wollen.
Kramm,
„Im Gegensatz zu Ihnen weiß ich, wovon ich rede und schreibe “
Es besteht tatsächlich ein Gegensatz: Sie wollen Leuten mit mangelnden Wissen ihren Unsinn unterjubeln und ich versuche zu erklären, das es sich um Unsinn handelt.
Jochen Ebel
#####################################################
Kramm,
Sie machen sich ja zu Gespött.
Warum reiten Sie dann damit rum, das Schwarzschild das in einem Aufsatz zur Sonnenatmosphäre genannt hat?
Obwohl ich Ihren Unsinn schon einige Male mit Hinweis auf die Professoren Dullemond und Klessen von der Universität Heidelberg widerlegt habe, wiederhole ich noch mal den Link:
Die Überschrift lautet: „Atmosphären von Sternen und Planeten“ und auf den Seiten 6 und 7 steht mehrfach „Schwarzschild-Kriterium“ also ist nichts mit „nicht auf die Erdatmosphäre übertragen werden kann.“
Außerdem „zweitens einer statistischen Beschreibung der Konvektion dient?“ Warum lügen Sie schon wieder? Das Schwarzschild-Kriterium dient nicht „einer statistischen Beschreibung der Konvektion“, sondern sagt nur, wo Konvektion einsetzt.
Sie können in fast jeden Klassenzimmer am Ende einer Unterrichtsstunde 1000 ppmV messen – also was wollen Sie mit Fehlmessungen beweisen? Selbst Gerlich und Tscheuschner haben in ihrem Machwerk den Anstieg der CO2-Konzentration erklärt.
Ansonsten hat Ordowski bewieseen, daß er auf Ihre Unterschlagung hereingefallen ist, indem er nur Seite 26 zitiert hat.
Jochen Ebel
Ordowski 2. März 2025 18:20
Prof. Kramm hat mir eine weiter eMail geschrieben mit einem großen Verteilerkreis. Da ich nicht weiß, ob Prof. Kramm zitiert werden will, nur meine Antwort (Sie können gern den ganzen Text von Kramm einstellen, wenn Sie wollen.):
Kramm,
ach es gibt genug Klimaleugner und Unwissende, die sich gerne gegenseitig zitieren.
Jochen Ebel
Herr Ebel.
machen Sie immer was Sie wollen, lernen Sie einmal mit Kritk richtig umzugehen!
Ordowski 2. März 2025 11:05
zu meinen Kommentar hat mir Kramm weitere eMails geschickt. Ich veröffentliche hier nur meine Antwort – Sie können gern den ganzen Text von Kramm einstellen, wenn Sie wollen.
Kramm,
Ihre letzten eMails machen einige Fragen zu Ihren Texten notwendig:
1.) Das Sie das Schwarzschild-Kriterium lieber Bezold-Kriterium nennen wollen ist Ihre Sache. Ich geh mal mit und frage: Bezold hat sich mit der irdischen Atmosphäre befaßt, warum sollte dann das Bezold-Kriterium nur auf der Sonne gelten?
2.) Warum nennen Sie die Professoren der Uni Heidelberg dümmlich?
3.) Wo genau steht Ihr Bezold-Kriterium? Bezold hat „Zur Thermodynamik der Atmosphäre“ mindestens 5 Mitteilungen verfaßt, ich habe die Mitteilungen 1, 2 und 5 gelesen und das Bezold-Kriterium nicht gefunden. Könnten Sie bitte das genauer spezifizieren bzw. eine Kopie schicken?
4.) Wieso hat Bezold schon 1888 von der Stratosphäre geschrieben (wie er sie damals nannte ist mir gleich), wo Bezold in seinen Arbeiten „Zur Thermodynamik der Atmosphäre“ zwar Ballonfahrten (1888) gefordert hat, aber als Entdeckung der Stratosphäre erst das Jahr 1902 gilt?
5.) Hat der Name Bezold-Kriterium ein ähnliches Schicksal wie die Entdeckung der Kernspaltung? Lise Meitner gilt als Entdecker und hatte das 1939 gefunden, Ida Noack hatte diese schon 1934 entdeckt.
6.) Warum suchen Sie in Schwarzschilds Arbeit nach dem Begriff „Konvektion“ obwohl in der Wissenschaft die Namen von gleichen Sachverhalten ändern (z.B. Röntgenstrahlen: Röntgen hatte diese Strahlen X-Strahlen genannt und in der englischen Literatur heißen Sie heute noch so – https://www.bedeutungonline.de/warum-heissen-roentgenstrahlen-auch-x-strahlen-x-rays-erklaerung-bedeutung/ )? Schwarzschild schreibt für die Konvektion instabile Luftschichtung obwohl Bezold schon von Convection (damalige Schreibweise) schrieb.
7.) Wenn ich angeblich so unbedeutend bin, warum beschäftigen Sie sich einen ganzen Tag mit mir und schreiben gleich 7 eMails?
8.) Erwarten Sie, daß ich auch etwas zu Ihrer Schmäh-eMail schreibe?
Jochen Ebel
Na ja, Sie träumen. Ihre Vorstellung, dass oberhalb einer Absorptionslänge über dem Boden die gesamte Energie nur noch durch Konvektion statt radiative-konvektiv nach oben transportiert wird, wird auch von Lindzen nicht behauptet.
Als ehemals bedeutender Meteorologe greift Lindzens Art des Wissenschaftsbetrugs nicht bei den unbestreitbaren meteorologischen Grundtatsachen wie dem radiativ-konvektiven Transport und der Existenz des Treibhauseffekts an, sondern ist viel subtiler.
„Ihre Vorstellung, dass oberhalb einer Absorptionslänge über dem Boden die gesamte Energie nur noch durch Konvektion statt radiative-konvektiv nach oben transportiert wird, wird auch von Lindzen nicht behauptet.“
Und?
„unbestreitbaren meteorologischen Grundtatsachen wie dem radiativ-konvektiven Transport“
mach endlich den Spiegel-Test !
Jetzt sind sie voellig uebergeschnappt. Ich frage mich ob und wann Herr Marvin Mueller ihnen die Meinung geigt.
Lindzen und Wisseschaftsbetrug?
na na…
Ja, er ist inzwischen der Clown der community, bekommen Sie natürlich gar nicht mit, ist zu hoch für Sie.
Kein Kommentar! Ich dachte sie koenne nicht tiefer sinken, aber das schlaegt dem Fass den Boden aus.
Was hatten Sie sich denn etwa zu Lindzen eingeredet?
Es ist schon erschreckend, wie Lindzen abgeschmiert ist, seine Erklärung der QBO war genial, aber nachdem er bei der Erforschung des global warmings nicht mehr erste Geige gespielt hat und die community wuchs, hat er sich den Wissenschaftsleugner als Clown zur Verfügung gestellt.
Unterste Stufe war mal. Jetzt negativer Trend und im Absturz…
Diese Infos über Lindzen scheiben Sie wirklich zu erleuchten. Nehmen Sie sich etwas Zeit, es zu verdauen.
OMG!
Stimmt. Habe gerade nochmal eine Aufnahme mit meiner Wärmebildkamera bei bedeckten Himmel kurz nach Sonnenuntergang gemacht. Da kann man sehr schön die Wärmeabstrahlung des bedeckten Himmels sehen.
das hört sich genauso (un-) physikalisch an, wie die Gespräche auf der Brücke von Raumschiff Enterprise.
„Beam me up, Scotty“
Star Trek?
Diese linksversiffte Serie? Mittlerweile mit lauter Homo- und Kreuzsexuellen.
Eine Zukunft und Zivilisation ohne Geld 🙂
Ist ja altmodisch 🙂
Die Sonne allein schafft am Äquator ohne Gegenstrahlung, mit Albedo, mittags senkrecht und bei guter Speicherung (350 Wh pro m² und K) über Tag&Nacht mit 1364•0,7/π=303,9 W/m² im Mittel nur etwa -3 Grad – siehe EXCEL-Grafik, Berechnung im Viertelstundenraster. Herr Weber, wie soll die Sonne denn ohne Gegenstrahlung einen globalen Mittelwert von +15 Grad erzeugen??? Luftdruck scheidet doch aus – und ebenso Ihre mit unkaputtbarer Geophysik zur Energieerzeugung eingeführte Adiabatik, da hierbei mindestens so viel Energie verbraucht wie Wärme erzeugt wird.
Nur das man am Äquator schwitzt. Lassen sie sich bloß nicht durch die Realität ihre Rechnung versauen.
Herr Schulz, das Schwitzen kommt offenbar durch die Gegenstrahlung, das scheinen Sie zu übersehen. Die -3 Grad gelten für die Sonnenstrahlung allein.
Sie würden also in der Sonne allein nicht schwitzen? Halte ich für ein Gerücht.
Die -3 Grad gelten nach ihrer eigenen Rechnung nur für eine Mittelung von 24 h. Wo allerdings die Sonne nur einen Teil der Zeit strahlt. Daher schwitzen sie in der Sonne.
Herr Schulz, ohne Gegenstrahlung schafft es die Sonne bis 16:00 nur auf etwa +2 Grad. Da schwitzt man doch nicht! Es geht Ihnen doch nur darum, strahlungsphysikalische Berechnungen (die Sie offenbar nicht verstehen und für ein Gerücht halten) zu diskreditieren.
Ne ist schon klar ich verstehe nicht das man in der Sonne schwitzt, weil sie ausrechnen das die Sonne nur -2 Grad erzeugt!
Das koennen sie nicht mal im Kindergarten verkaufen.
Basiert ihre Rechnung auf einer Mittelung von 24 Stunden oder nicht? Wenn ja wieviel Stunden davon scheint die Sonne?
Werner Schulz schrieb am 26. Februar 2025 11:46
Diese Fragen werden alle vom Diagramm beantwortet, das Herr Dietze gezeigt hat. Scheitert es wieder daran, dass Sie sowas nicht lesen können?
Was Sie hier immer wieder demonstrieren, würde einen Schüler der 8. Klasse zu einem starken Kopfschütteln veranlassen. Was Herr Dietze hier zeigt, ist die einfache Änderung der Temperatur eines Körpers in Abhängigkeit von zu- und abfliessender Energie. Müßte ein Kinderspiel für Sie sein, wenn Ihre Aussagen über Ihre „fundierte Thermodynamik-Ausbildung“ stimmen würden. Und doch sehen wir von Ihnen so gut wie nie etwas, was auch nur entfernt an eine Rechnung erinnert. Woran das nur liegt ..
Ein Koerper, vor allem einer der strahlt und bestrahlt wird, aendert nicht seine Temperatur entsprechend zu- und abfliessender Energie, sondern aufgrund von zu ODER abfliessender WAERME.
Das kann man allerdings keinen Kindergartenkindern zumuten. Ihnen und Herrn Dietze sollte man das zumuten, aber sie sind seit Jahren resistent den Unterschied zu verstehen.
Werner Schulz schrieb am 26. Februar 2025 15:34
Einer der vielen Werner Schulz schrieb immer, das Wärme die Differenz der zwischen zu- und abfliessenden Energie sei. Sie brauchen die beiden Größen also, um die Wärme zu bestimmen. Fragen Sie einfach mal Ihre Namensvetter …
Wieso? Ich sehe das doch genauso wie Ihr Namensvetter das hier immer schrieb …
Na dann helfen sie doch mal Herrn Dietze, der rechnet nur die eine Seite.
Mit cos(phi) über 12 h ist die mittlere Sonneneinstrahlung über 24 h 303,9 W/m². Das ergibt (bei 100% Absorption und idealer Speicherung) mit S-B nur -2,6 Grad. Wie Sie meiner Grafik entnehmen können, geht die Sonne um 6:00 auf und um 18:00 unter, aber senkrecht steht sie nur um 12:00 und strahlt dann mit 1364•0,7 W/m². In einer Viertelstunde sind das 238,7 Wh/m².
Und wie denken sie kann die Sonne etwas erwaermen, wenn sie nicht scheint?
Oder anders herum, erwaermt die Sonne einen Koerper nicht nur dann, wenn sie scheint?
Werner Schulz schrieb am 26. Februar 2025 16:45
Auch das ist im Diagramm zu sehen – die Temperatur steigt dort nur, während die Sonne scheint…
Das wollte ich von Herrn Dietze wissen. Vielleicht sollten sue mal genau gucken, wen sie hier antworten wollen.
Herr Schulz, ich rechne nur die eine Seite?? In meiner Äquator-Grafik (die Sie offenbar gar nicht verstehen) sehen Sie sowohl die solare Zustrahlung (und die dann ansteigende Temperatur) als auch die Abstrahlung. Diese ist wegen der Speicherung stark geglättet, im Mittel gleich der Zustrahlung und führt nachts zur Abkühlung.
Dass bei Uli Weber die Abstrahlung bei global +15 statt -18 Grad (oder bei genauerer Berechnung sogar -21 Grad) erheblich höher ist als die Zustrahlung, scheint Sie (und auch einige andere Kommentatoren welche nicht mit S-B nachrechnen und statt an Gegenstrahlung an adiabatische Wärmeerzeugung glauben) gar nicht zu interessieren.
Adiabatische Waermeerzeugung? Jetzt hinken sie auf zwei Beinen, weil sie offensichtlich nicht mal verstehen was die Adiabatik aussagt und welche Rolle diese in der Atmosphaere spielt.
Herr Schulz, offenbar hinken Sie auf zwei Beinen. Herr Weber hat m.E. die Adiabatik in sein Modell (vorerst im Namen) eingeführt weil die Solarstrahlung für die globalen +15 Grad nicht ausreicht (zweite Sonne!). Wie Sie wissen, führen Einige (z.B. Cohen und Schaffer) die Erwärmung am Boden (wohl auch wegen des 2.HS) statt auf Gegenstrahlung auf den Anstieg der Abstrahlhöhe und die Gradientenverschiebung zurück, was ja durch die konvektive Adiabatik bedingt sein soll. Herr Ebel kommt damit sogar auf die +3 Grad des IPCC pro CO2-Verdopplung, obwohl diese (strahlungsphysikalisch) z.B. nach MODTRAN nur etwa 0,6 Grad beträgt.
Koennen sie denn erklaeren wie Konvektion und Adiabatik zusammenpassen? Warum kann man den beobachtbaren Gradienten in der Atmosphaere durch Adiabatik erklaeren? Wissen sie es?
Fragen Sie Herrn Schaffer, der kann das besser erklären. Auch Herr Weber setzt ja nun auf ein hemisphärisches Konvektionsmodell, welches m.E. die zusätzliche Wärme, welche durch Gegenstrahlung von 150 W/m² am Boden fehlt, durch Konvektion erklären soll.
Wo kommen die 150 W/m2 her? Kann man die messen?
Zitat: „Koennen sie denn erklaeren wie Konvektion und Adiabatik zusammenpassen?“
Das kann keiner der hier Kommentierenden beantworten, weil man dazu Kenntnisse in der Physik spricht der Thermodynamik haben müsste, welche definitiv nicht vorhanden sind.
Herr Holtz, soweit ich die Vertreter von Adiabatik und Gradient verstanden habe, geht es darum dass bei THG-Zunahme die Abstrahlhöhe ansteigt. Weil es weiter oben (vermeintlich wegen des gravitationsbedingten Luftdrucks) kälter wird, und sich der gedachte Fußpunkt (!) des (konstanten, durch Luftdruck und Adiabatik verursachten) Temperaturgradienten nach oben verschiebt, muss es am Boden dann wärmer werden.
Das bedeutet allerdings dass der Schwanz mit dem Hund wedelt und man postuliert dass die Gegenstrahlung zwar existiert, aber nicht die Ursache, sondern die Folge dieser Erwärmung sei, und somit nichts mit dem THE zu tun hat. Leider habe ich von Uli Weber, der ja den Namen des Hemisphärenmodells geändert hat, hierzu – und insbesondere auch für die Nachtseite – nichts gesehen. Vermutlich wird er das im 54. Beitrag nachholen und uns erzählen wie die Energie für die Abstrahlung der Nachseite entsteht.
Peter Dietze 28. Februar 2025 7:57
„sondern die Folge dieser Erwärmung sei, und somit nichts mit dem THE zu tun hat.“
Der THE ist die Folge von Absorption und Emission der THG. In der Stratosphäre ist Absorption und Emission der THG fast allein für den Temperaturgradienten verantwortlich – und folglich steigt der Temperaturgradient, wenn die Treibhausgaskonzentration steigt. Wenn der Temperaturgradient über einen Grenzwert steigt, setzt Konvektion mit Adiabatik ein (Schwarzschild-Kriterium 1906). Wenn also der strahlungsbedingte Temperaturgradient genügend groß ist, wird er vom feuchtadiabatischen Temperaturgradienten überdeckt.
Bei Steigerung der Treibhausgaskonzentration steigt also nach dem Schwarzschild-Kriterium die Grenze (Tropopause) zwischen der Stratosphäre und der Troposphäre – und das wird auch gemessen. Dabei ist der Anstieg der Tropopause bedeutend größer als die Ausdehnung der Troposphäre.
In Verbindung mit dem feuchtadiabatischen Gradienten führt das zu einer Fast-Parallel-Verschiebung der Temperaturkurve in der Troposphäre, allerdings wird das obere Ende kälter, weil der Temperaturgradient konstant bleibt. Die Folge ist auch das Konstantbleiben der Emission der Erde (fast gleich der absorbierten Solarstrahlung) indem durch die atmosphärischen Fenster die Oberflächenabstrahlung ins All steigt und entsprechend die Abstrahlung aus der kühleren Stratosphäre sinkt.
Also ist die Steigerung der Gegenstrahlung in Oberflächennähe eine Folge der Steigerung der Treibhausgaskonzentration. Diese Steigerung der Gegenstrahlung bei Steigerung der Treibhausgaskonzentration wird mit einem reinen Strahlungsmodell nur unzureichend erfaßt.
Herr Dietze,
Sie sprechen von:
Sie meinen sicherlich alle die, die die Standardatmosphaere kennen und akzeptieren.
Sie sagen dann weiterhin:
Das wird so nicht von mir vertreten, weil es bisher keine genaue Definition fuer eine Abstrahlhoehe gibt. Es ist allerdings so, das wenn es unten waermer wird, dann wird es oben auch waermer, wenn der Gradient nicht von Strahlungswirkung bestimmt wird. Das heisst wenn die Abstrahlhoehe steigt, und es waermer wird, dann wird oben auch mehr abgestrahlt, weil ja die Temperatur auch hoeher wird.
Schauen sie auf die Bilder von Herrn Schaffer. Da ist das gut ersichtlich.
Sie sagen:
in der Tat muss die Gegenstrahlung abhaengig von der Temperatur sein. Das geben die Strahlungsgesetze so vor oder nicht?
Als letzted sprechen sie an, das der Schwanz mit dem Hund wackelt.
Das wuerde ich nicht so sehen, weil angeblich ist die Abstrahlhoehe so definiert, das an der Stelle 240 W/m2 ins Weltall abgegeben werden.
Damit liegt diese Hoehe an einer Stelle an der die wichtige Randbedingung Waerme rein und Waerme raus genau bestimmt ist. Damit ergibt sich hier fuer dieses Model ein wichtiger Angelpunkt, wo in der Tat der Hund sitzt und dann Richtung Erdoberflaeche mit dem schraeggestellten Schwanz wackelt.
Werner Schulz 28. Februar 2025 11:48
„weil es bisher keine genaue Definition für eine Abstrahlhöhe gibt“
Es gibt keine „Abstrahlhöhe“, sondern immer eine Höhenbereich der Emission (Emissionslänge). Wenn es ins All geht, ist die Emission der entsprechende Bereich unter dem Übergang zum All – und dementsprechend ist der Emissionsbereich wellenlängenabhängig. Sehr schön ist das am Emissionstrichter des CO2 bei 15 µm zu sehen, wo in der Mitte eine Emissionsspitze zu sehen ist, weil dort die Emissionslänge im Spitzenbereich nur bis in die warme Ozonschicht reicht.
Als „Abstrahlhöhe“ könnte man die Höhe bezeichnen, wo die Temperatur gleich einer Temperatur ist, welche ein Schwarzkörper haben würde, dessen Emission gleich der Emission der Erde ist.
Hier das Bild das ich meine:
Danke Herr Schaffer.
Wie man sieht verschiebt sich das Profile zwar nach oben, aber bleibt bei der gleichen Temperatur.
Da wird nichts kaelter und mehr CO2 strahlt mehr bei gleicher Temperatur.
Der Herr Schulz hat die Frage gestellt: „Koennen sie denn erklaeren wie Konvektion und Adiabatik zusammenpassen?“ – Nur darum geht es!
Hierzu muss es doch eine physikalisch ableitbare Erklärung geben, die man auch „formelmäßig“ untermauern kann. Die energetischen Ausgleichsprozesse wirken gleichzeitig, wobei das eine das andere bedingt und umgekehrt, das scheinen viele nicht begreifen zu wollen.
Was wollen Sie immer mit der „Gegenstrahlung“? Die terrestrische „Gegenstrahlung“ oder „Rückstrahlung“ hat keine thermodynamische Einzelwirkung, weil sich die terrestrische „Gegen-/Rückstrahlung“ nur aus der Brutto-Betrachtung der Energiebilanz vom Ausgleichsvorgang der Oberfläche ergibt. Ein „Wärmetransport“ findet mit dem Temperaturgradienten statt. Ein „Wärmetransport“ entgegen dem Temperaturgradient würde eine Verletzung der Hauptsätze der Thermodynamik darstellen, dies gilt auch für die Strahlung von thermischen Strahlern und demzufolge einen „atmosphärischen Treibhauseffekt“ ausschließen.
Werner Holtz 28. Februar 2025 11:57
„Ein „Wärmetransport“ entgegen dem Temperaturgradient würde eine Verletzung der Hauptsätze der Thermodynamik darstellen“.
Ihr Wort „Wärmetransport“ kann zu falschen Schlußfolgerungen führen, wie bei Ihnen. Sauber formuliert muß es heißen „Nettowärmetransport“, wie Sie schon bei Stefan 1879 lesen können. Zum Bruttotransport „Gegenstrahlung“ gehört auch der zweite Teil, die größere Aufwärtsstrahlung.
Herr Ebel,
wo denken sie liegt der Unterschied zwischen dem von ihnen gesagten und dem von Herrn Holtz?
Er sagte:
Und „Koennen sie denn erklaeren wie Konvektion und Adiabatik zusammenpassen?“
Zu Ihrer Frage: „Koennen sie denn erklaeren wie Konvektion und Adiabatik zusammenpassen?“
Ich habe Ihnen doch gesagt, dass das keiner der hier Kommentierenden beantworten kann (mich mal ausgenommen). Die ganzen „Diskussionen“ auf EIKE sind reine Zeitverschwendung, dafür ist mir meine Lebenszeit zu kostbar. Zu 95% tummeln sich hier Pseudo-Wissenschaftler oder Scharlatane und solche, die es werden wollen.
Herr Holtz, Sie irren wenn Sie einen „Wärmetransport“ von kalt nach warm (THE) ausschliessen. Sie verwechseln Strahlung (also Energietransport durch elektromagnetische Wellen) mit Wärmeleitung. Wenn Sie Recht hätten, würde der Empfang aller TV-Sender aus einer kälteren Region ausfallen und auch die Sonnenstrahlung würde auf dem langen Weg durch den -270 Grad kalten Weltraum abkühlen.
Sie schreiben physikalischen Unsinn, aber das ist aber nichts neues!
Zitat: Sie irren wenn Sie einen „Wärmetransport“ von kalt nach warm (THE) ausschliessen.
Das schließe nicht ich aus, sondern die Physik spricht die Thermodynamik.
Zitat: Sie verwechseln Strahlung (also Energietransport durch elektromagnetische Wellen) mit Wärmeleitung.
So ein Unsinn – Die Thermodynamik gilt für jeden Wärmetransport, egal in welcher Form er stattfindet.
Zitat: Wenn Sie Recht hätten, würde der Empfang aller TV-Sender aus einer kälteren Region ausfallen …
Der nächste Unsinn – Ein thermischer Strahler (Sonne, IR-Lampe) ist entropie-behaftet, deshalb bestimmt die Temperatur die Intensität der Strahlungsquelle. Ein nicht-thermischer Strahler (Mikrowellenherd, Radiosender, TV-Sender) ist praktisch entropie-frei, deshalb bestimmt die eingestellte Signalstärke die Intensität der Strahlungsquelle.
Zitat: … auch die Sonnenstrahlung würde auf dem langen Weg durch den -270 Grad kalten Weltraum abkühlen.
Die Krönung des Unsinn – Es gilt das Abstandsquadrat-Gesetz für den Energietransport mittels Strahlung von der Sonne (Hier könnte man auch Wärmetransport sagen, weil die Sonne ein thermischer Strahler ist.).
Werner Schulz 27. Februar 2025 18:04
„Warum kann man den beobachtbaren Gradienten in der Atmosphäre durch Adiabatik erklären?“
Die Fragestellung ist schon nicht exakt genug. Die Frage müßte heißen „Warum kann man den beobachtbaren Gradienten in der Troposphäre (und nicht Stratosphäre) durch Adiabatik erklären?“ da in der Stratosphäre kaum Konvektion herrscht.
Durch Konvektion steigt (fällt) der Druck im Innern eines Luftpaketes beim Absinken (Aufsteigen). Das Äußere eines Luftpaketes leistet gegen den äußeren Luftdruck Arbeit. Diese Arbeit ändert den Energieinhalt (Temperatur) des Luftpaketes und sorgt für den Temperaturgradienten.
Sie haben recht mit der Verbesserung der Frage, wa auch gleichzeitig eine Antwort gibt. Danke.
Was ich aber nicht verstehe ist die folgende Aussage:
Adiabatisch aendert sich der Energieinhalt nicht, was meinen sie also genau?
Adiabatisch heißt kein Wärmetransport – aber das Luftpaket leistet Arbeit nach außen, indem die äußere Luft komprimiert wird und bei der Kompression wird die komprimierte Luft wärmer. Woher soll die Energie herkommen? Natürlich aus dem Luftpaket.
Das läßt sich auch molekular erklären. Am besten ist das zu erklären, wenn man sich das Luftpaket mit eine fast masselosen festen Folie umhüllt denkt. Bei Druckabfall bewegt sich die Folie nach außen. Ein Molekül, das auf die Hülle zufliegt wird reflektiert, aber wegen der Folienbewegung nach außen hat das reflektierte Molekül eine geringere Geschwindigkeit, d.h. die mittlere Geschwindigkeit sinkt – entsprechend der Maxwellschen Geschwindigkeitsverteilung sinkt die Temperatur.
Dann muss das Luftpaket, das Arbeit nach aussen leistet kaelter werden. Betrachtet die Adiabatik nicht eigentlich nur die Vorgänge innerhalb eines Luftpaketes?
Werner Schulz 2. März 2025 10:48
Genau, das ist das Geschehen beim adiabatischen Aufstieg.
Jein. Wie schnell sich eine Temperaturänderung auswirkt ist schon lange bekannt Natanson 1888 „Ueber die Geschwindigkeit, mit welcher Gase den Maxwell’schen Zustand erreichen“ https://onlinelibrary.wiley.com/doi/abs/10.1002/andp.18882700916und dazu kommt, das ja über die Größe des Luftpaketes nichts ausgesagt ist – ein großes Luftpaket können Sie auch viele kleinere teilen und die Aussage trifft auch für jedes der kleineren Luftpakete zu.
Da geht es darum was im Luftpaket passiert. Was hat das andere Paket damit zu tun?
Adiabat, Waerme wird in Expansionsarbeit umgewandelt. Mehr ist da nicht. Die Temperatur sinkt bei der Expansion.
Peter Dietze 27. Februar 2025 16:55
„… obwohl diese (strahlungsphysikalisch) z.B. nach MODTRAN nur etwa 0,6 Grad beträgt.“
Ja, nach der reinen MODTRAN-Rechnung hat Dietze Recht – aber es passieren bei höherer CO2-Konzentration noch weitere Vorgänge, was z.B. Fortak schon 1971 (S. 76) festgestellt hatte. Und zu diesen weiteren Vorgängen gehört eben die Änderung der Konvektion einschließlich der Änderung der Tropopausenhöhe. Die reine „(strahlungsphysikalische)“ Betrachtung ist also unzureichend.
„… pro CO2-Verdopplung, …“
Auch das ist unzureichend. Bei den gegenwärtigen Verhältnissen ist die Änderung der CO2-Sensitivität noch ganz weit von der Abweichung von den linearen Verhältnissen entfernt ( https://www.isbn.de/buch/9783758372926/wie-funktioniert-der-treibhauseffekt-wirklich Diagr. 4.6., S.28), so daß eine lineare Abhängigkeit besteht, die auch seit ca. 100 Jahren beobachtet wird: fast genau um 1 K bei 100 ppmV-Zunahme der CO2-Konzentration.
Herr Ebel, „beobachtet wird: fast genau um 1 K bei 100 ppmV-Zunahme (!) der CO2-Konzentration“ ist doch Unsinn, denn beobachtet wird doch i.w. die T-Zunahme durch Solaraktivität und Abnahme der Bewölkung – und der CO2-Anstieg verläuft eher zufällig etwa linear dazu. Dass (im Gleichgewicht) ∆T=ECS•ln(C/Co)/ln(2) ist, wollen Sie als Physiker doch nicht etwa bestreiten?
Peter Dietze 28. Februar 2025 14:18
„als Physiker doch nicht etwa bestreiten?“
Doch
„die T-Zunahme durch Solaraktivität und Abnahme der Bewölkung“
Der Anteil der Solaraktivität an der T-Zunahme ist marginal, die Abnahme der Bewölkung ist eine Folge der CO2-Zunahme. (aus welchen Grund sollte sich sonst die Bewölkung ändern, was zufällig (?) dem CO2-Anstieg folgen sollte.
Die Linearität folgt hauptsächlich daraus, dass der Temperaturgradient in der Stratosphäre fast linear von der CO2-Konzentration abhängt.Mit anderen Worten. Die Anzahl der Moleküle zwischen 2Temperaturniveaus ist fast konstant. Bei höherer CO2-Konzentration ist der Abstand geringer, weil eben die gleiche Menge bei geringerer Höhendifferenz erreicht wird.
Ach Herr Dietze,
schon mit den Eiswürfeln , die den Kaffee erwärmen sollen, haben Sie sich unsterblich blamiert!
Aber jetzt kommt doch noch etwas, das da heißt: Dümmer geht immer!
So rechnen Sie uns vor:
„Die Sonne allein schafft am Äquator ohne Gegenstrahlung, mit Albedo, mittags senkrecht und bei guter Speicherung (350 Wh pro m² und K) über Tag&Nacht mit 1364•0,7/π=303,9 W/m² im Mittel nur etwa -3 Grad „
Am Äquator steht die Sonne ziemlich senkrecht über einem breiten Streifen , ca 1.000 km breit, und Sie wollen den Leuten dort, weißmachen, dass sie Pelzmäntel benötigen sobald sie einen Sonnenschirm benutrzrn????
Der Dietze war wohl noch niemals am Äquator!!!!
Was wir wissen, wenn wir denn wissen wollen?
Abb 19: Die Strahlung der Sonne und ihr Verbleib. Das Bild zeigt den Energie-
.webp?itok=0-lh5wGG
anteil der verschiedenen Wellenlängen und die jeweils ausgefilterten Anteile.
Bild: Übernommen aus http://www.biokurs.de (Ernst-G. Beck), modifiziert; Original bei Kondratyev (1969) S. 247
Zum Schluß zu den IR-aktiven Gasen. Angeblich strahlt die Sonne
„kurzwelliges“ Licht aus, das die Atmosphäre „fast ungehindert
durchdringen“ könne47). Aber wie folgende Aufschlüsselung zeigt,
ist der IR-Anteil dieses kurzwelligen Sonnenlichts sehr hoch48):
Ultraviolett (UV, < 0,38 ȝm Wellenlänge) 10%
Sichtbares Licht (0,38-0,76 ȝm) 45%
Infrarot (IR, > 0,76 ȝm) 45%
Dieser IR-Anteil aber wird in der Atmosphäre schon in großer
Höhe und bei eisigen Temperaturen zu einem großen Teil von den
IR-aktiven Gasen absorbiert.49) Die in Abb. 19 in Blau darge-
stellten Energieanteile werden so vom Boden ferngehalten und
vom „Kühlsystem“ wieder ins All zurückemittiert.
In der realen Welt wirken „Treibhausgase“ also wie ein Sonnen-
schirm (Abb. 20). Statt den Boden um 33° zu erwärmen, verhin-
dern sie schon im „Heizsystem“ eine stärkere Aufheizung!50)
Hier zu finden auf Seite 11
http://ke-research.de/downloads/klimaretter-1-3.pdf
Somit sollten wir doch das als ein Faktum akzeptieren und den Abergaluben vom CO2 als Temepratur Regler in der Atmosphäre endlich beerdigen!
In der realen Welt wirken „Treibhausgase“ also wie ein Sonnen-
schirm (Abb. 20). Statt den Boden um 33° zu erwärmen, verhin-
dern sie schon im „Heizsystem“ eine stärkere Aufheizung!50)
Nur 51 % der Sonnenstrahlung erreichen die Erde!!!
.webp?itok=0-lh5wGG
http://ke-research.de/downloads/klimaretter-1-3.pdf
Hier Seite 11
!
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski schrieb am 25. Februar 2025 13:27
Wenn Ihnen die Zahlen von Herrn Dietze nicht gefallen, zeigen Sie doch einfach den Fehler in seiner Rechnung auf aoder nehmen Sie doch einfach die Werte von Herrn Kramm. Der weist in „Using Earth’s Moon as a Testbed for Quantifying the Effect of the Terrestrial Atmosphere“ Figure 22 T < 260K für den Äquator ohne Atmosphäre aus:
Figure 22. Daily mean values of (a) slab temperature; (b) solar radiation reaching the Earth’s surface; (c) absorbed solar radiation, where the local solar albedo has been predicted by Equation (6.3); (d) emitted infrared radiation; and (e) soil heat flux as predicted for one year starting with TDB = 2,455,197.5 (January 1, 2010, 00:00 UT1).
Ach Herr M.Müller,
Der Dietze, wie auch scheinbar Sie, glauben wohl, wenn sie eine Formel umstellen, dann ändern sich auch die physikalischen Gesetze!
Nehmen Sie einfach zur Kenntniss, was richtige Physiker schreiben:
Falsifizierung der
atmosphärischen CO2 -Treibhauseffekte
im Rahmen der Physik
Deutsche ¨Ubersetzung Version 4.00-de11-A4 (11. Juni 2015)
der englischen Version 4.00 (January 6, 2009)
Gerhard Gerlich
Institut f¨ur Mathematische Physik
Technische Universit¨at Carolo-Wilhelmina zu Braunschweig
Mendelssohnstraße 3
D-38106 Braunschweig
Federal Republic of Germany
g.gerlich@tu-bs.de
Ralf D. Tscheuschner
Postfach 60 27 62
D-22237 Hamburg
Federal Republic of Germany
ralfd.tscheuschner@googlemail.com
dazu auf Seite 73
„In der Globalklimatologie werden Temperaturen aus gegebenen Strahlungsintensitäten
berechnet, und dieses Verfahren tauscht die Rollen von Ursache und Wirkung aus. Man beachte:
Die aktuellen lokalen Temperaturen bestimmen die Strahlungsintensitäten und nicht
umgekehrt.“
Und
„Cooling of Atmosphere Due to
CO2 Emission
G. V. CHILINGAR,1 L. F. KHILYUK,1, and
O. G. SOROKHTIN2
1Rudolf W. Gunnerman Energy and Environment Laboratory, University of
Southern California, Los Angeles, California, USA
2Institute of Oceanology of Russian Academy of Sciences, Moscow, Russia
Abstract The writers investigated the effect of CO2 emission on the temperature of
atmosphere. Computations based on the adiabatic theory of greenhouse effect show
that increasing CO2 concentration in the atmosphere results in cooling rather than
warming of the Earth’s atmosphere.“
In der realen Welt wirken „Treibhausgase“ also wie ein Sonnen-
.webp?itok=0-lh5wGG
schirm (Abb. 20). Statt den Boden um 33° zu erwärmen, verhin-
dern sie schon im „Heizsystem“ eine stärkere Aufheizung!50)
Nur 51 % der Sonnenstrahlung erreichen die Erde!!!
http://ke-research.de/downloads/klimaretter-1-3.pdf
Hier Seite 11
!
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski schrieb am 25. Februar 2025 16:05
Die Arbeit nehme ich doch zur Kenntnis. Sie können auch gerne den von Gehrlich/Tscheuschner berechneten Wert von 144K für die globale mittlere Temperatur nehmen, die ist niedriger als die, die Herr Dietze bestimmt hat. Und bei der Berechnung von Herrn Dietze bestimmt die lokale Temperatur auch die intensität der Abstrahlung, da geht also Ihre Kritik irgendwie daneben.
Lesen Sie das, was Sie da referenzieren bzw, kritisieren auch wirklich?
Ordowski 25. Februar 2025 16:05
„Nehmen Sie einfach zur Kenntnis, was richtige Physiker schreiben:“
Sie empfehlen also den Unsinn von G&T?
Das es Unsinn ist: https://www.academia.edu/69403919/Gerlich
Unsinn ist kein Argument.
Werner Schulz 1. März 2025 10:08
„Unsinn ist kein Argument.“
Die Argumente, warum es Unsinn ist, stehen im Link.
Warum immer wieder der Hinweis auf die Email Adresse?
Ordowski 25. Februar 2025 16:05
„Mit viel CO2 kann der Welthunger bekämpft werden!“
Bei richtiger Politik gäbe es schon jetzt keinen Welthunger. Bei mehr CO2 gäbe es viel mehr klimabedingte Tote.
„Bei mehr CO2 gäbe es viel mehr klimabedingte Tote.“
Ich glaube eher, daß der Glaube an den Treibhauseffekt die Zahl der Sterbefälle erhöht.
Todesursache: Hirntod
Moin besso, habe herzlich über Deinen Kommentar gelacht, weil er so zutreffend ist.
Das glaube ich allerdings auch!
besso keks 1. März 2025 12:04
„Ich glaube eher, …“
Das ist der Unterschied: Sie glauben, ich weiß.
Wer vorgibt zu „Wissen“ ist auf den Irrglauben schon reingefallen.
Michael Poost 1. März 2025 14:03
„Irrglauben“
Dann informieren Sie sich in Krankenhäusern zur Sterblichkeit.
Übrigens sind die meisten Sterbefälle nicht bei besonders hoher Temperatur, sondern bei hoher Temperatur und gleichzeitig hoher Luftfeuchtigkeit.
Also, nur Dumme entkommen dem Irrglauben?
Möglich, aber nicht unbedingt.
Die „Klugen“ haben sich „impfen“ lassen…
Dann wissen sie auch das Hirntote auch noch rumlaufen koennen und tun?
Schőne Bilder! Wo hangen sie vorerst? Im Modernart Museum?!
Im Mittelzeit quelt di Vorscher Frage, wie viele Teufel auf eine Nadelschpitze passt und wieviel Fligen ein Teufel tägleich verzert- und si fanden keine Antwort. Konnen Sie nicht ihne post Morten helfen, mit dem Computermodelierung?!
@ Peter Zinga 25. Februar 2025 19:06
Ich hatte diese „schönen Bilder“ übrigens schon zweimal abgehängt (hier und hier). Aber es handelt sich halt um Wiedergänger eines tief verwurzelten klimareligiösen Aberglaubens…
U. Weber schrieb am 26. Februar 2025 10:53
Die Bilder entstammen allerdings einer Rechnung, die man nachvollziehen kann, wenn man das will. Von Ihnen gibt es so etwas nicht, wenn man von der Berechnung für den Mond absieht (dessen Nachtseite dort 0K hat) und der Berechnung für die Tagseite der Erdoberfläche, bei der es keine Angebaben zur Temperatur der Nachtseite gibt, bzw nur Postulate basierend auf den Werten, die wir beobachten.
Wird es irgendwann mal eine nachvollziehbare Berechnuing der Temperaturverteiluing der Erdoberfläche geben? Wir warten seit nunmehr 8 Jahren drauf …
@ Marvin Müller 26. Februar 2025 13:29
Marvin, es tut mir ja wirklich leid, aber ich verstehe Dein verfehltes Anspruchsdenken nicht – wie meinst Du das?
U. Weber schrieb am 26. Februar 2025 15:06
Ich kann nichts dafür, dass Sie so geringe Ansprüche an sich selbst stellen. Ich erwarte halt einfach von einer alternativen Erklärung, dass sie eine in sich halbwegs geschlossen Erklärung liefert, die man auch nachvollziehen kann. Geht bei Ihrer Erklärung wie gesagt nicht.
Ich erwarte allerdings auch nicht mehr, dass es sowas geben wird und weise daher lediglich auf die Lücken in Ihrem Modell hin. Bzw. auf die Ähnlichkeiten Ihrer im Buch angedeuteten Erklärung zum Treibhauseffekt mit „Stefan-Boltzmann-Umgebungsgleicheung“, in der es einen zur Gegenstrahlung äquivalenten Term gibt (den Sie nicht diskutieren möchten) und eine Verlagerung der Abstrahlung in höhere, kältere Schichten (die es nur geben kann, wenn die Strahlung nicht ungehindert ins All gehen kann).
@ Marvin Müller 26. Februar 2025 15:49
Marvin, Du wirst in Deinen Ansprüchen immer verworrener, jetzt beanspruchst Du schon meine Ansprüche, Zitat:
Vorhin (Marvin Müller 26. Februar 2025 13:29) klang das sogar noch etwas konkreter, und schon da konnte ich den Zusammenhang nicht herstellen, Zitat:
Was willst Du denn nun eigentlich von mir, verstehen musst Du schon ganz alleine!
U. Weber schrieb am 26. Februar 2025 17:34
Sie haben meine Frage „„Wird es irgendwann mal eine nachvollziehbare Berechnuing der Temperaturverteiluing der Erdoberfläche geben? Wir warten seit nunmehr 8 Jahren drauf …“ als überzogenen Anspruch bezeichnet. Was oll ich d anderes draus schlussfolgern, als „dass Sie so geringe Ansprüche an sich selbst stellen.“ Wäre das anders, hätten Sie meine Frage nicht als überzogenen Anspruch klassifiziert.
Stand doch deutlich da: „eine nachvollziehbare Berechnuing der Temperaturverteiluing der Erdoberfläche“
Was Sie an Berechnungen geliefert haben, habe ich verstanden. Aber da gibs nur die zwei einfachen und nichts, was die beobachteten Temperaturen erklärt …
@ Marvin Müller 26. Februar 2025 18:01
Sorry Marvin, mir war nicht klar, dass Du diesen Artikel gar nicht gelesen bzw. verstanden hattest. Erst Dein wiederholter Hinweis hat mir jetzt die Augen geöffnet und mir einen Zugang zu Deiner katastrophalen Unkenntnis ermöglicht, Zitat:
Also Marvin, pass jetzt mal ganz genau auf:
Abbildung 4 zeigt eine Gegenüberstellung der Beleuchtungsklimazonen mit dem Jahresverlauf der maximalen örtlichen solaren Strahlungsleistung über den Jahresverlauf vor dem Hintergrund der Beleuchtungsklimazonen unserer Erde.
Abbildung 3 gibt sowohl das konkrete Berechnungsschema für die maximale örtliche Strahlungsleistung der Sonne an als auch eine Skala für das örtliche Maximum des daraus abgeleiteten
maximalen S-B-Temperaturäquivalentes.
Abbildung 2 stellt den Jahresverlauf von Konvektion und Advektion für eine Ortslage (Potsdam) als Differenz zwischen der gemessenen Ortstemperatur und dem örtlichen Maximum des S-B-Temperaturäquivalentes dar.
Und wenn Du Letzteres jetzt für die gesamte Erdoberfläche haben möchtest, dann musst Du Dir das schon selber machen…
U. Weber schrieb am 27. Februar 2025 10:00
Nette Schutzbehauptung, aber falsch. Ich habe Ihren Artikel gelesen und auch verstanden. Daher kann ich ja relativv genau auf die Lücken/Fehler zeigen, die es immer noch gibt.
Die Abbildungen stellen die Schwankungen der Einstrahlung und die aus der Einstrahlung unter Annahme eines lokalen Strahlungsgleichgewichtes (die lokale Temperatur ist so hoch, dass die eingestrahlte Energie so groß wie die abgestrahlte Energie ist) abgeleitete Temperatur dar. (Interessanterweise ist dort die gesamte Erdoberfläche beleuchtet, was eigentlich Ihrem eigenen Ansatz widerspricht. Eigentlich müßte die Hälfte der Fläche schwarz sein, wie die Pole.) Die Berechnung für die Tagseite ist nachvollziehbar, allerdings zeigen Sie am Beispuel des Mondes, dass dann die Temperatur der Nachtseite 0K ist.
Sie wollen dann einen Teil der Energie auf die Nachtseite transferieren und sagen, dass die aus SB abgeleiteten Temperaturen auf der Tagseite nicht erreicht werden und die Temperaturen auch Nachts nicht auf 0K fallen. Welche Temperaturen dann allerdings auf Tag- und Nachtseite Ihrer Meinugn nach erreicht werden, ist bisher unbekannt. Berechnungen dafür gibt es nicht. Berechnungen von anderen, z.B. Kramm, Spencer, …, erklären Sie einfach für falsch.
Ihr Modell kann erst dann die beaobachteten Temperaturen erklären, wenn Sie sie auch wenigstens ungefähr berechnen können. Und genau daran hapert es bisher. Mit einer einfachen Rechnung sieht man, dass bei Ihnen mehr Energie von der Oberfläche abgestrahlt wird, als von der Sonne eingestrahlt wird (dass bei Ihrem Ansatz mindestene 12h * 340W/m² + 12h * 340W/m² abgegeben werde (Minimum-Temperatur für Tag und Nacht angenommen), aber nur 12h * 480W/m² + 12h * 0W/m² zugeführt werden.)
Dieses Defizit liesse sich auflösen, wenn Sie mal erklären würden, wie denn Ihre Stefan-Boltzmann-Umgebungsgleichung mit der Temperatur zusammenängt. Aber dann müßten Sie ja zum einen erklären, wie den eigentlich der
-Term der Umgebung entsteht (wenn nicht durch Abstrahlung aus der Atmosphäre, die sie immer verneinen) und Sie müßten erklären, wie dieser Term mit der Sonnenstrahlung zusammen die Erwärmung der Tagseite bewirkt. Und dann würden Sie etwas beschreiben, was dem Treibhauseffekt sehr ähnelt – was wohl auch der Grund sein dürfte, dass Sie das seit Jahren vermeiden.
@ Marvin Müller 27. Februar 2025 12:30
Marvin, Du behauptest, den Artikel gelesen und verstanden zu haben. Das mag vielleicht sogar stimmen, aber bei Deinen Formulierungen muss man ja immer ganz genau hinschauen. Und deshalb ist auffällig, dass Du ausgerechnet die von mir erwähnten Grafiken nicht verstanden hast, Zitat:
Nimm die nachstehende Erklärung von Abbildung 3 als verständnisvolle Hilfe zur Selbsthilfe:
U. Weber schrieb am 27. Februar 2025 18:01
Dass Sie das Maximum darstellen, war mir schon bewusst. Ich hatte Sie aber nach einer nachvollziehbaren Berechnung der Temperaturverteilung der Oberfläche gefragt und als Antwort darauf eine Referenz auf diese Grafik erhalten. Und da Sie doch sicherlich nicht sagen wollen, dass Sie die mittlere Temperatur aus dem Maximum berechnen, habe ich mir erlaubt darauf hinzuweisen, dass Sie hier eine Darstellung gewählt haben, die sie sonst immer kritisieren. Z.B. vor kurzem erst bei meiner Referenz auf eine vergleichbare Darstellung von Herrn Kramm, in der statt des Maximums die am jeweiligen Tag zufliessende Energie dargestellt wurde (gemittelt über 24h).
Aber es war wieder schon zu sehen, dass Sie zwar vielleicht die Kommentare lesen, aber nur auf Dinge reagieren, bei denen Sie den Kommentatoren einen Fehler unterstellen können. Sachliche Auseinandersetzung mit rest … Null …
Ach Herr M.Müller,
.webp?itok=0-lh5wGG
Der Dietze, wie auch scheinbar Sie, glauben wohl, wenn sie eine Formel umstellen, dann ändern sich auch die physikalischen Gesetze!
Nehmen Sie einfach zur Kenntniss, was richtige Physiker schreiben:
Falsifizierung der
atmosphärischen CO2 -Treibhauseffekte
im Rahmen der Physik
Deutsche ¨Ubersetzung Version 4.00-de11-A4 (11. Juni 2015)
der englischen Version 4.00 (January 6, 2009)
Gerhard Gerlich
Institut f¨ur Mathematische Physik
Technische Universit¨at Carolo-Wilhelmina zu Braunschweig
Mendelssohnstraße 3
D-38106 Braunschweig
Federal Republic of Germany
g.gerlich@tu-bs.de
Ralf D. Tscheuschner
Postfach 60 27 62
D-22237 Hamburg
Federal Republic of Germany
ralfd.tscheuschner@googlemail.com
dazu auf Seite 73
„In der Globalklimatologie werden Temperaturen aus gegebenen Strahlungsintensitäten
berechnet, und dieses Verfahren tauscht die Rollen von Ursache und Wirkung aus. Man beachte:
Die aktuellen lokalen Temperaturen bestimmen die Strahlungsintensitäten und nicht
umgekehrt.“
Und
„Cooling of Atmosphere Due to
CO2 Emission
G. V. CHILINGAR,1 L. F. KHILYUK,1, and
O. G. SOROKHTIN2
1Rudolf W. Gunnerman Energy and Environment Laboratory, University of
Southern California, Los Angeles, California, USA
2Institute of Oceanology of Russian Academy of Sciences, Moscow, Russia
Abstract The writers investigated the effect of CO2 emission on the temperature of
atmosphere. Computations based on the adiabatic theory of greenhouse effect show
that increasing CO2 concentration in the atmosphere results in cooling rather than
warming of the Earth’s atmosphere.“
In der realen Welt wirken „Treibhausgase“ also wie ein Sonnen-
schirm (Abb. 20). Statt den Boden um 33° zu erwärmen, verhin-
dern sie schon im „Heizsystem“ eine stärkere Aufheizung!50)
Nur 51 % der Sonnenstrahlung erreichen die Erde!!!
http://ke-research.de/downloads/klimaretter-1-3.pdf
Hier Seite 11
!
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski schrieb am 25. Februar 2025 19:30
Haben Siie jetzt einfach in Ihre Textbausteinsammlung gegriffen und das gleiche nochmal geschrieben? Ich hatte darauf bereits wie folgt geantwortet:
„Die Arbeit nehme ich doch zur Kenntnis. Sie können auch gerne den von Gehrlich/Tscheuschner berechneten Wert von 144K für die globale mittlere Temperatur nehmen, die ist niedriger als die, die Herr Dietze bestimmt hat. Und bei der Berechnung von Herrn Dietze bestimmt die lokale Temperatur auch die intensität der Abstrahlung, da geht also Ihre Kritik irgendwie daneben.
Lesen Sie das, was Sie da referenzieren bzw, kritisieren auch wirklich?„
Herr M.Müller,
Zu den Ausführungen vom Herrn Weber, hat der Prof.Dr. Kramm einiges zurechtgerückt, siehe
„Kommentar zu WEBER (2o19):
„Weitere Überlegungen zur hemi-
s phärischen Herleitung einer globalen
Durchschnittstemperatur“
DGG-Mitteilungen, 1/2o19: 18-25
Gerhard Kramm, Fairbanks, Alaska, US“
https://engineeringmeteorologyconsulting.com/wp-content/uploads/2021/01/dgg_2020_2_kramm.pdf
Dort können Sie auch einges über die Gültigkeit frd S+B Gesetzes nachlesen!
Und der Herr Dietze sollte mal die Graphken 3 und 4 im Artikel ansehen und sich fragen, wie auf seine Mittelwertstrahlung und Behauptung kommt?
„Die Sonne allein schafft am Äquator ohne Gegenstrahlung, mit Albedo, mittags senkrecht und bei guter Speicherung (350 Wh pro m² und K) über Tag&Nacht mit 1364•0,7/π=303,9 W/m² im Mittel nur etwa -3 Grad “ Ha, Ha, Ha!!!!!!
Gerhard Gerlich
Institut f¨ur Mathematische Physik
Technische Universit¨at Carolo-Wilhelmina zu Braunschweig
Mendelssohnstraße 3
D-38106 Braunschweig
Federal Republic of Germany
g.gerlich@tu-bs.de
Ralf D. Tscheuschner
Postfach 60 27 62
D-22237 Hamburg
Federal Republic of Germany
ralfd.tscheuschner@googlemail.com
dazu auf Seite 73
„In der Globalklimatologie werden Temperaturen aus gegebenen Strahlungsintensitäten
berechnet, und dieses Verfahren tauscht die Rollen von Ursache und Wirkung aus. Man beachte:
Die aktuellen lokalen Temperaturen bestimmen die Strahlungsintensitäten und nicht
umgekehrt.“
https://engineeringmeteorologyconsulting.com/wp-content/uploads/2021/01/dgg_2020_2_kramm.pdf
Schreibt der Prof.Dr. Kramm auf Seite 2 seiner Publikation auch!!!!
In der realen Welt wirken „Treibhausgase“ also wie ein Sonnen-
.webp?itok=0-lh5wGG
schirm (Abb. 20). Statt den Boden um 33° zu erwärmen, verhin-
dern sie schon im „Heizsystem“ eine stärkere Aufheizung!50)
Nur 51 % der Sonnenstrahlung erreichen die Erde!!!
http://ke-research.de/downloads/klimaretter-1-3.pdf
Hier Seite 11
!
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski schrieb am 26. Februar 2025 19:20
Irgendwie haben Sie wieder nur ohne Nachzudenken Textbausteine in den KOmmentar fallen lassen. Die relevanten Bilder sind die Abbildung 13 und 14. Abbildung 13 weisst – wie ich bereits schrieb – eine mittlere Temperatur < 240K für den Äquator aus. Und 240K sind docht wohl kleiner als die von Herrn Dietze genannten -3°C …
Einfach mal lesen und nachdenken. Sie können auch gern die Methode von Gerlich/Tscheuschner nur auf den Äquator anwenden. Ich bin mir sicher, da kommt viel weniger als 240K raus …
Herr M.Müller
Schauen Sie sich diese Graphik, aus dem Artikel an!:
Was können Sie da für eine Sonnenstrahlung um den Äquator
sehen, wenn Sei den sehen wollen!
„In der Globalklimatologie werden Temperaturen aus gegebenen Strahlungsintensitäten
berechnet, und dieses Verfahren tauscht die Rollen von Ursache und Wirkung aus. Man beachte:
Die aktuellen lokalen Temperaturen bestimmen die Strahlungsintensitäten und nicht
umgekehrt.“
https://engineeringmeteorologyconsulting.com/wp-content/uploads/2021/01/dgg_2020_2_kramm.pdf
Schreibt der Prof.Dr. Kramm auf Seite 2 seiner Publikation auch!!!!
In der realen Welt wirken „Treibhausgase“ also wie ein Sonnen-
.webp?itok=0-lh5wGG
schirm (Abb. 20). Statt den Boden um 33° zu erwärmen, verhin-
dern sie schon im „Heizsystem“ eine stärkere Aufheizung!50)
Nur 51 % der Sonnenstrahlung erreichen die Erde!!!
http://ke-research.de/downloads/klimaretter-1-3.pdf
Hier Seite 11
!
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski schrieb am 27. Februar 2025 10:00
Und was folgt aus der Grafik Ihrer Meinung nach? Kann die irgendwie mehr erklären als dass die Temperaturen aufgrund der schwankenden Einstrahlung auch schwanken werden – wir also ausserhalb der Wendekreise ausgeprägte Jahresezeiten haben? Wie erklärt das die beobachteten Temperturen.
Das die Intensität der Sonnenstrahlung aufgrunde der Neigung der Erdachse im Laufe des Jahres schwankt. Eigentlich eine unstrittige Tatsache. Was trägt das jetzt zur Diskussion bei?
Irgendwie haben Sie jetzt wieder nur Textfragmente zusammengestellt, über die Sie nicht nachgedacht haben. Was ist mit den tatsächlichen Berechnungen von Kramm, Spencer (von Herrn Weber im verlinkten Artikel diskutiert), Gerlich/Tscheuischner? Die leifern alle geringere Temperaturen als die Berechnung von Herrn Dietze. Wo sehen Sie in der Rechnung bzw. den präsentierten Ergebnisen von Herrn Dietze einen konkreten Fehler?
Ach M.Müller,
Mit welcher durchschnittslicher Sonneneinstrahlung rechnet der Dietze denn?
Die Sonne allein schafft am Äquator ohne Gegenstrahlung, mit Albedo, mittags senkrecht und bei guter Speicherung (350 Wh pro m² und K) über Tag&Nacht mit 1364•0,7/π=303,9 W/m² im Mittel nur etwa -3 Grad “ Ha, Ha, Ha!!!!!!
Und was zeigen die Graphiken?
Sind Sie denn farbenblind?
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Ordowski schrieb am 27. Februar 2025 13:09
Er rechnet nicht mit einer durchschnittlichen Sonnenstrahlung, sondern mit der tatsächlichen Einstrahlung. Sie sehen das an der Kurve im Bild:
Die Einstrahlung beginnt um 6:00 Uhr anzusteigen, erreicht mittag ihr Maximum und fällt dann zum Abend hin ab. Dargestellt ist die zugeführte Energie im 15 Minuten-Raster, als z.B. Mittags 1365 * 0,7 * 15 * 60 / (60 * 60) = 239Wh.
Rechnen Sie es doch einfach selber, auch gern feingranularer für eine Platte mit einer Wärmekapaazität von 1260 kJ/K. Wenn Sie etwas anderes rausbekommen, können Sie das doch gerne kundtun und Herrn Dietze korrigieren.
Dass bei Herrn Kramm und Gerlich/Tscheuschner noch kleinere Zahlen rauskommen, haben Sie wieder einmal ignoriert.
Ich habe doch beschrieben, was die Grafiken zeigen. War meine Beschreibung falsch? Haben Sie nur auf die Farben gekuckt stattt auf die Beschriftung der Achsen?
@ Ordowski 26. Februar 2025 19:20
Wer hier gegen sich selbst kommentiert, sollte dringend externe Hilfe in Anspruch nehmen, Zitat Ordowski Reply to Ordowski 25. Februar 2025 19:24:
Gemeint sind dort sicherlich die in den Kommentaren von Ordowski mehrfach aufgeführten E-Mail Adressen von Gerlich und Tscheuschner.
Und wer vorsätzlich auf Artikel mit Zitatfälschungen verlinkt, ist selber auch nicht besser:
Ach Herr Weber,
manchmal wäre es besser zu schwiegen, so aber sollte jeder heir folgendes lesen:
Kommentar zu WEBER (2o19):
„Weitere Überlegungen zur hemi-
s phärischen Herleitung einer globalen
Durchschnittstemperatur“
DGG-Mitteilungen, 1/2o19: 18-25
Gerhard Kramm, Fairbanks, Alaska, USA
https://engineeringmeteorologyconsulting.com/wp-content/uploads/2021/01/dgg_2020_2_kramm.pdf
49 % werden von der Atmosphäre absorbiert oder reflektiert und somit in den Weltraum gelenkt!
Die Atmosphäre verhindert, dass wir alle hier auf der Erde von der Sonne gegrillt werden!
Man denke nur an die Angst vor Ozonlöchern!!!
Und
Somit bleiben wir dabei:
Steter Tropfen höhlt den Stein!!!
Ohne CO2 stirbt der Wald, dann der Mensch!
Mit viel CO2 kann der Welthunger bekämpft werden!
Also
kein THE
und mehr CO2, denn CO2 wärmt nicht , sondern düngt und kühlt die Erde!!!!!!!!!!!!!
https://www.co2-kuehlt-die-erde.com/physik-gesetze
https://www.gerhard-stehlik.de/CO2/2014/131001%20Stehlik%20Hopp%20Wagner.pdf
Hr. Dietze, messen Sie einmal am Äquator die Zustrahlung spektral. Also bei welchen Wellenlängen wird welche Leistung empfangen? Nach Ihrer Theorie, müßte das Spektrum des direkten Sonnenlichtes -3°C ergeben (ca. 0,25 – 3 µm) und das Spektrum einer Gegenstrahlung (ca. 4 µm – einige 100 µm) eine Temperatur von am Äquator ca. +27°C?
Glauben Sie sowas tatsächlich? Wie könnte sowas erklärt werden?
Herr Strasser, das Spektum verschiedener (additiver) Einstrahlungen hat nichts mit der Temperatur des Bodens zu tun. Es kommt nur auf die W/m² an und nach S-B gilt SummeS=Sigma•T⁴.
ad „additiv“: Sie glauben wohl auch, daß man mit vielen Kerzenflammen einen hellen Suchscheinwerfer konstruieren kann?
Dass man bei Almeria die Einstrahlung durch mehr als tausend Spiegel additiv erhöht sowie es durch viele Lichtquellen in Kronleuchtern, in Fußballstadien und großen Büros heller macht, haben Sie immer noch nicht verstanden.
Almeria sammelt flächig Leistung von Strahlung ein, die in einem gemeinsamen Elementarprozeß entsteht (Sonne). Nur dort geht das. Bei Strahlungen aus unterschiedlichen Quellen geht das nicht! Wo haben Sie denn Ihre „Physikunkenntnis“ her?
Und Kronleuchter oder Stadionscheinwerfer machen nicht heller, sie leuchten besser aus. Beim Stadionscheinwerfer leuchtet jeder Einzelspot einen unterschiedlichen Quadratmeterbereich der Spielfläche aus! Wenn Sie einen wegnehmen, wird es dort und nur dort dunkler.
Merken Sie eigentlich nicht, daß jede einzelne Aussage von Ihnen blamabel ist und belegt, daß Sie keine blasse Ahnung von Physik haben?
Herr Strasser, da Sie sich ja so gut in Strahlungs-Pseudophysik auskennen, verraten Sie mir doch mal warum es im Raum deutlich dunkler wird wenn Sie von einen Kronleuchter einen Teil der Birnen (deren Strahlung sich ja überlagert) herausnehmen. Und dass Strahlungsflüsse verschiedener Quellen (W/m²) sich nicht am Absorber addieren sollen, entspringt nur Ihrer Fantasie – oder haben Sie (Gärtner) das auf einer Baumschule gelernt? Almeria würde ebenso mit nur der Hälfte der Spiegel funktionieren wenn die fehlende Hälfte der W/m² durch Heizstrahler oder Scheinwerfer erzeugt würde.
Sie bleiben also dabei, man muß nur genügend viele Eiswürfel nehmen, um einen lauwarmen Kaffee zum Kochen zu bringen? Ich rate dringend zum Experiment!
Stellen Sie sich das Innere eines Hohlraumstrahlers vor, also rundherum idealschwarze Wände. Dann sehen Sie mit einer Glühbirne einen Lichtpunkt und bei drei, sehen Sie drei Lichtpunkte. Alle mit der identen Helligkeit, eine Addition von Helligkeiten findet in Ihrem Beobachterauge (Absorber) aber nicht statt.
Es gibt auch kein phys. Gesetz, welches eine Leistungsaddition von windschiefen Einzelstrahlen ermöglicht. Das ist auch der Grund, warum Sie mit einem Parabolspiegel nur paralleles Licht fokussieren können und diffuses nicht!
Parallel kommt von einer Quelle, diffus sind viele Quellen. Das ist übrigens auch der Grund, warum klassische Scheinwerfer mit Einzelbirnen nie direkt strahlen, sondern nach hinten und über Parabolspiegel nach vorne, eben um paralleles Licht zu erzeugen. Und auch jede optische Linse belegt dieses Prinzip.
Ich fürchte allerdings, bei Ihnen ist mit physikalischer Logik nichts zu erreichen, Sie beharren stur auf 100% Irrtum …
Ergänzung: Bei einer punktförmigen Strahlungsquelle (Glühlampe) wird kugelförmig abgestrahlt. Das bedeutet, die Leistung nimmt mit 1/r² mit der Entfernung ab. Daher ist bei einer Glühlampe jener Punkt der Wand am hellsten, der den kürzesten Abstand hat. Konzentrisch dazu nimmt die Helligkeit der Einzelbirne ab. Mit vielen Birnen gibt es viele konzentrische Leuchtzonen, daher wird es im Sprachgebrauch als „heller“ empfunden, aber nicht absolut, sondern eben nur mehr verteilt, eben besser ausgeleuchtet!
@Weber
Und Wasserdampf ist im Infrarot transparent? Also für Wärmeabstrahlung transparent? Und strahlt auch selbst keine Wärmestrahlung ab. Z.B. ins All?
Aber bitte nur einmal Jährlich, mehr Namensänderungen pro Jahr lässt der Gesetzgeber nicht zu . 😀
@ Moritz Steinmetz 24. Februar 2025 20:44
Na gut, aber können wir dann nicht wenigstens 😀Dietze, 😀Kruger und 😀Marvin ummelden?
Mal zur Wärmeabstrahlung der Atmosphäre. Kann man ganz einfach mit einer IR-Kamera messen. Wir haben derzeit bedeckten Himmel bei etwa 10°C Bodentemperatur. Gerade ein Bild vom Haus gegenüber und dem Nachthimmel gemacht. Das Haus gegenüber 12°C, der bedeckte Himmel darüber 7°C und der Himmel weiter oben 4°C. Das wird da auch an Wärme entsprechend der Temperatur abgestrahlt. Wäre das nicht der Fall würde die Luft oben so warm werden, wie über dem Erdboden.
Toll, die ruhende (!) Taghemisphäre strahlte bisher nach S-B bei +15 Grad Mittelwert sämliche eingestrahlte Wärme wieder ab, so dass die Nachtseite mangels Energie 0 K hatte.
JETZT im 53. BEITRAG STRAHLT NICHT DIE TAGSEITE AB. DIE SOLARENERGIE FÜLLLT DIE SPEICHER TÄGLICH WIEDER AUF. DIE NACHTSEITE STRAHLT DANN DIE ENERGIE AB.
Hier nochmal ein Kommentar von mir zu Ihrem vorigen Beitrag vom 12.1.25:
„Mit meinem hemisphärischen Stefan-Boltzmann-Modell hatte ich dagegen nachgewiesen, dass ein solcher THE gar nicht existiert“.
Weber(le), das bringen Sie hier in nicht mehr zu übertreffender Unverfrorenheit zu Ihrem 52. EIKE-Beitrag nachdem ich gerade wieder nachgewiesen habe dass Ihr Modell wegen Falschanwendung von S-B grottenfalsch ist und Ihre Modellerde ohne Gegenstrahlung für globale +15 Grad ZWEI SONNEN benötigt, wie ja die von Prof. Kramm angefertigte Grafk zeigt. Dass EIKE sowas toleriert und Sie noch nicht aus dem Verkehr gezogen hat, ist mir ein Rätsel.
Wenn ich das richtig sehe hat Herrn Weber’s Modell eine Wärmekapzität – der THE hat das nicht, die ist gleich 0.
Für die 15°C/288K braucht man eigentlich nur das Ideale Gasgesetz welches uns die SAT gibt, also das Standardatmospärenmodell. Das angewendet (255K ohne Atmosphäre) zeigt und dass auf der Erde, im Modell die Luft den Boden erwärmt, per Konduktion, auf 288K. So wie in der Realität auf der Venus.
Das ist wie wenn sie ein Kaltgetränk aus dem Kühlschrank holen, irgendwann hat es Raumtemperatur. Ziemlich simples Konzept der 0te HS.
Oder denken Sie wie Müller, Ebel, Heinzelmann et al dass diese Erwärmung durch Strahlung der Luft erfolgt?
Marcus Portius 25. Februar 2025 0:08
„… Erwärmung durch Strahlung der Luft erfolgt“
Das ist nicht genau genug, es muß heißen: „… Erwärmung durch Strahlung der Treibhausgase erfolgt.“
Wer nur von der Erwärmung durch die Gegenstrahlung spricht, blendet unzulässigerweise einfach die Sonne aus, da die Temperatur der Erdoberfläche aus der gemeinsamen Absorption von Solarstrahlung und Gegenstrahlung resultiert.
Beobachten kann man natürlich nur eine sehr geringe Nettoeinstrahlung, da ein Teil der absorbierten Solarstrahlung und Gegenstrahlung die Erdoberfläche durch Konvektion, Wärmeleitung und Verdunstung verläßt.
Die Wärme wird halt immer dahin teleportiert, wo sie benötigt wird. Das war vorher auch schon so.
Das habe ich doch tatsächlich übersehen: Die Nachtseite strahlt jetzt also doch Energie nach dem S-B Gesetz ab. Welche Temperatur hat nun die Nachtseite über die 12 h? Wie sieht jetzt der Verlauf der Temperatur über die Tagseite aus? Immer noch die reine S-B Inversion? Die Erde strahl somit auf der Tag- und Nachtseite Energie ab. Da sind wir schon einmal ein Schritt weiter. Beide aber mit der absoluten Temperatur (also K) hoch 4. Die entsprechende zeitabhängigen Gleichung wären jetzt interessant.
Herr Schau, den (nur solaren und rotationsbedingten) Temperaturverlauf am Äquator – berechnet mit S-B je Viertelstunde für eine Schwarzkörper-Speicherplatte – sehen Sie auf der Tag- und Nachtseite in meiner EXCEL-Grafik. Wenn man bei der Einstrahlung die Gegenstrahlung in W/m² addiert, ergibt sich der reale Temperaturverlauf, welchen ich z.B. auch in Sri Lanka bei senkrechter Mittagssonne und leichter Bewölkung festgestellt habe.
Herr Dietze, mir ging es darum, dass Herr Weber seine Theorie und Temperaturberechnung kurz in physikalischer Form darstellt. Er schreibt viel, aber nur weiniges ist wirklich fassbar. In der Vergangenheit konnte er die Nachttemperatur mit seiner S-B Inversion nicht berechnen. Jetzt bring er das Speichervermögen der Meere ins Spiel. Den korrekten zeitabhängigen Term für die Speicherung, der direkt aus dem ersten HS folgt, negiert er aber weiterhin.
Ich bin kein Einstein, aber eine ist mir klar: die Sonne scheint NUR auf eine Hälfte der Erde und wärmt sie ein – und das mit vollen Kraft. Die „dunkle“ Seite gibt eingespeisste Wärme (Energie, wenn Sie wollen) ab. Ganz einfach. Und wieder und wieder…
Wollen Sie darüber zweifeln?! Wollen Sie behaupten, dass die dunkle Seite der Erde auch Sonne direkt erwärmt?!
Dann würden Photowolteik- Panelle nicht als „volatile“ Energieerzeuger gelten.
Ha, jetzt ist mir eingefallen, warum sie mann „erneuerbar“ nennt: sie sind mit dem Sonnenuntergang tot und mit dem Aufgang erneuern sich…wie Phänix
Peter Zinga schrieb am 24. Februar 2025 17:45
Da sind Sie fast genau der gleichen Ansicht, wie viele Kritiker der Artikel von Herrn Weber. Der begann seine Artikelserie ja mit der Ansicht, dass die „dunkle“ Seite keine Energie abstrahlen würde. Jetzt müssen Sie nur noch Ihre Sicht mit Zahlen unterlegen – wieviel Energie wird von der Sonne auf der „hellen“ Seite zugeführt und wieviel wird gleichzeitg von der „hellen“ und „dunklen “ Seite wieder abgegeben. Dann verstehen Sie die Kritk an den Artikeln von Herrn Weber …
„Jetzt müssen Sie nur noch Ihre Sicht mit Zahlen unterlegen – „
Muss ich nicht, ich nehme es als Faktum – und mehr brauch ich nicht. So wie so kann ich nichts ändern.
@ Marvin Müller 24. Februar 2025 18:17
Oh Marvin, Du primzahliges Autodouble, Du hättest bei der Wahl zur „Miss Weisung“ sehr gute Chancen auf einen der vorderen Plätze…
U. Weber schrieb am 25. Februar 2025 10:12
Läuft also wie immer, es gibt keine inhaltlichen Kommentare von Ihnen …
Wenn Herr Zinga das Problem verstehen will, kommt er nicht drum rum, seine eigene (fast) korrekte Betrachtung mit Zahlen zu unterlegen. Dann würde er merken, dass bei Ihrem Ansatz mindestene 12h * 340W/m² + 12h * 340W/m² abgegeben werde (Minimum-Temperatur für Tag und Nacht angenommen), aber nur 12h * 480W/m² + 12h * 0W/m² zugeführt werden. Er muss das natürlich nicht machen, wenn er das Problem nicht verstehen will.
Das gilt natürlich auch für Sie. Aber wahrscheinlich sind Sie sich des Problems selbst bewusst, da es von Ihnen keine nachvollziehbaren Berechnungen für Ihr aktuelles Modell gibt. Und die, die es gibt, ergeben für den Mond eine Nachttempertur von 0K und machen für die Erde keine mit Rechnungen belegte Aussage zur Nachttemperatur. Da gibt es nur Postulate auf Basis der beobachteten Temperaturen aber keine Erklärung, wie die zustande kommen. Bei Ihrem „Nehmen wir die Erde mal aus dem Tiefkühlfach und lassen sie von der Sonne erwärmen“ hatten Sie einfach behauptet, die würde sich auf die jetzigen Temperturen erwärmen, ohne das mit Rechnungen zu belegen …
Wenn Sie meinen Hiweis auf Rechnungen mit konkreten Werten als Weisung ansehen – damit kann ich gut leben …
Herr Weber, mal paar eine paar Fragen:
Wie berechnen sie letztlich den Temperaturverlauf über den gesamten Tag für die Landfläche? Mit der Stefan-Boltzmann Inversion? Da gehen aber die thermischen Eigenschaften der Oberflächenschicht gar nicht ein. Am besten geben sie den gesamten Verlauf insbesondere auch für die Nacht mal grafisch an.
Wie berechnen sie insbesondere die Oberflächentemperatur der Ozeane (also die 20 °C)?
Über welchen Prozess verliert der Ozean über Nacht seine Energie? Wärmestrahlung?
PS: Die „großen“ Klimamodelle verwenden übrigens nicht den Faktor 4. Vielmehr werden die physikalischen Gleichungen, die die Atmosphäre und die Strahlungsübertragung/Energieflüsse beschreiben, diskretisiert (FFM, FDM, FEM usw.) und numerisch gelöst. Dabei wird der Wärmetransport und die Sonneneinstrahlung lokal aufgelöst berücksichtigt. Dies sieht man daran, dass die Modelle eine Volumenaufteilung zeigen Modell. Ähnliche Methoden verwendet man in den technischen Berechnung seit so ca. 1980 (Temperatur- und Spannungsberechnungen). Wie gut die Modelle sind und wie weit sie alle Effekte berücksichtigen, ist ein anderer Punkt. Den Faktor 4 verwenden sie jedenfalls nicht.
In den Strahlungstransfermodellen taucht auch nicht der Faktor 4 auf. Die werden auch numerisch gelöst. Herr Weber sollte sich da mal die Differentialgleichungen anschauen.
@ Michael Krüger 24. Februar 2025 13:02
Man bedient sich offenbar gerne einer selbstgerechten Heller‘schen Besserwisserei, aber warum benötigt man dann wohl einen zusätzlichen Tuningparameter, um den THE überhaupt in solche Modelle implementieren zu können? – Denn ein vorgeblich real existierender THE müsste doch bereits in korrekt berechneten Strahlungstransfermodellen enthalten sein…
Tuningparameter? Welchen? Konvektion haben Sie jetzt ihren Modell hinzugefügt, fehlt noch Wärmeabstrahlung des Bodens und der Atmosphäre und was der bewirkt. Wasserdampf haben Sie ja auch schon als klimarelevant erkannt.
@ Michael Krüger 25. Februar 2025 20:42
Zur Erinnerung: Es ging um den Tuningfaktor in Deinen Strahlungstransfermodellen, durch den der sogenannte „natürliche atmosphärische Treibhauseffekt“ erst in deren fehlerhaftes Ergebnis hineinsimuliert wird.
@ Michael Krüger 25. Februar 2025 20:42
ZUR ERINNERUNG: Krugerle, Krugerle, Du entwickelst Dich zu einem klimatheoretischen Scheinriesen. Am 24. Februar 2025 13:02 hattest Du hier noch ‘rumgetönt, Zitat:
Hat der Weber auch tatsächlich gemacht und dann bei Dir am 25. Februar 2025 10:10 ganz konkret nachgefragt – und jetzt herrscht bei Dir klimatheoretisches Schweigen.
Fällt Dir dazu jetzt wirklich nichts ein oder arbeitet Heller noch an Deiner Antwort?
U. Weber schrieb am 26. Februar 2025 14:33
Ich weiss nicht, wie es Herrn Krüger geht, aber ich warte immer noch gespannt auf die Antwort auf die Frage „Tuningparameter? Welchen?„. Sie postulieren, es gäbe da einen, benennen ihn aber nicht.
Und woran erkennen wir, dass Sie sich die Gleichungen auch mal angesehen haben?
@ ALL zu Marvin Müller 26. Februar 2025 14:53
So ist das halt mit Leuten, die keinerlei Kinderstube genossen haben: Sie ziehen einfach ein „Wir“ aus dem Ärmel und mischen sich damit unaufgefordert in fremde Gespräche ein.
U. Weber schrieb am 26. Februar 2025 15:50
Was ist da jetzt anstößig, der „wir“ oder das „Einmischen“? Was ist an dem „Einmischen“ anders, als an Ihrem „Einmischen“ in meinen Austausch mit Herrn Zinga – abgesehen davon dass meine Anmerkung inhaltlich und Ihre Anmerkungen nur ad hominem waren?
Kriegen Sie das wirklich nicht hin, Inhalte zu diskutieren? Meinen Sie nicht, dass Ihre Ablenkung von der inhaltlichen Diskussion etwas durchsichtig ist?
@ Marvin Müller 26. Februar 2025 16:51
Marvin, Du alter Schlingel, meinst Du nicht auch, dass Deine Amtshilfe für den sprachlos gewordenen Kruger durch Ablenkung vom Inhalt der ursprünglichen Diskussion etwas durchsichtig ist?
U. Weber schrieb am 26. Februar 2025 17:53
Es hindert Sie doch niemand daran zur ursprünglichen Diskussion zurückzukehren und Herrn Krügers Frage zu beantworten. Falls Sie sie vergessen haben: „Tuningparameter? Welchen?„. Sie postulieren, es gäbe da einen, benennen ihn aber nicht. So hat Herr Krüger auch nichts, worauf er antworten könnte …
@ Marvin Müller 26. Februar 2025 19:33
Oh großer Marvin, Vormund eines Krugers von Bremen, verkünde uns Deine ewigen Wahrheiten über die Gedankengänge Deines hilflosen Schutzbefohlenen, der dazu schweigend seine Zustimmung signalisiert.
@ Henry Schau 24. Februar 2025 12:36, an anderer Stelle schrieben Sie, Zitat:
Und jetzt schreiben Sie: „Herr Weber, mal paar eine paar Fragen: …“
Zwischen Ihren beiden Kommentaren hat sich inhaltlich nichts an meinem Modell geändert, sondern lediglich der Name. Ich verstehe also die Beweggründe für Ihren plötzlichen Wissensdurst nicht, denn Sie hatten ja sogar Ihre ursprüngliche Aussage zwischenzeitlich ausdrücklich bestätigt.
Also: Mit Ihren Vorurteilen müssen Sie schon ganz alleine klarkommen…
Der Wissendurst entsteht daraus, dass sie viel schreiben aber das physikalische Modell nicht in konkrete Formeln fassen, die es überprüfbar machen.
Wenn sie grundlegende physikalische Gesetze (Plancksches Strahlungsgesetz, S-B Gesetz, 1. HS usw.) nicht verstehen oder verstehen wollen, ist das ein Weber-Problem. Wenn sie diese als Vorurteile bezeichnen, damit kann ich leben.
Jetzt wird weiter mit Konvektion gebastelt. Konvektion kann es nur geben, wenn Luft Wärme abstrahlen kann.
Würde ich so nicht sagen wollen.
Bodennah wird sich wegen der Tag/Nacht-Energieflüsse schon sowas wie Zirkulation einstellen. Über die gesamt Atmosphärenhöhe haben Sie natürlich Recht
Ich würde sagen Krüger, Ebel et al verwechseln hier die Definitionen, in der Meteorologie bedeutet Konvektion nämlich:
oder auch Konvektive Umlagerungen
Die THE’ler denken wie immer in ihrem flache Erde Modell wo Wärme (oder besser Energie aka Photonen) zwischen imaginären, isothermalen Schichten („geklaut“ aus dem Standardatmophärenmodell) ausgetauscht wird, durch THGs. Ungenaue Sprache und ungenaues Denken hängen zusammen; das Resultat könne wir hier bestaunen.
Luft erwärmt sich am durch die Sonne erwärmten Boden und steigt dann auf. Oben kann sie die überschüssige Wärme nur durch Wärmeabstrahlung loswerden, die es bei Herrn Weber ja nicht gibt. Dann bleibt die wärme Luft halt oben und die Vertikalkonvektion kommt zum Erliegen.
So ist es. Ich treffe aber immer wieder Menschen, die behaupten, die Sonne erwärmt die Luft.
Das ist falsch. Wird aber geglaubt. Wenn wir Klimarealisten nur diesen Punkt den Menschen bewusst machen könnten, wäre schon viel gewonnen.
Die Sonne erwärmt nur die Ozonschicht in der Stratosphäre. Und Rußpartikel in der Atmosphäre.
Korrekt, danke.
Und 15% werden durch IR aktive Gase absorbiert.
Ebel et al haben mir die Tage noch erzählt ohne THGs gäbe es keine Konvektion, dass diese Gase für die lapse rate verantwortlich sind. Der Joule Thomson Effekt scheint unbekannt zu sein.
Wie man obiger Abbildung sehen kann stimmt das nicht. Solange die Erde sich dreht und die Sonne scheint wird es die großräumigen Luftbewegungen geben, auch ohne THGs. Die Temperatur- und Druckdifferenzen sorgen dafür dass es Wind gibt. IR-Strahlung spielt eine vernachlässigbare Rolle.
Nein, es gibt keine „überschüssige“ Wärme. Am Tag kühlt die Luft die Oberfläche durch Konduktion (Evaporation nicht zu vergessen), über Nacht verhindert die Luft dass die Erde zu stark auskühlt, die Ozeane dienen hier als gigantischer Wärmepuffer. Wolken und Luftfeuchtigkeit schließen das atmosphärische Fenster und verhindern so den direkten Wärmeverlust ins All den man z.B. in sehr trockenen Regionen (Wüsten, Antarktis) beobachten kann.
Stimmt ja auch.
Ohne Treibhausgase, Wasserdampf ist übrigens das stärkste, keine Vertikalkonvektion. Nur Treibhausgase und Wolken können Wärme aus der Atmosphäre ins All abstrahlen. Ansonsten würde die Atmosphäre immer wärmer werden bis sie vom Boden nach oben die gleiche Temperatur aufweist.
Ihnen ist Konduktion bekannt? Sie gauben ernsthaft in z.B. einer reinen N2-Atmosphäre gäbe es keine Luftzirkulation, keine Winde und keinen Temperaturgradienten? Was ist mit der Graviatation?
Thermometers in a gravity gradient:
Herr Portius, Gravitation und statischer Luftdruck erzeugen doch keine Wärme! Das wäre ein Energie erzeugendes Perpetuum Mobile, denn der wärmere Boden würde ja die Wärme nach oben abstrahlen. Somit ist auch ein vermeintlich durch den Luftdruck am Boden erzeugter „THE“ Unsinn.
Selbstverständlich machen sie das, schauen Sie sich die Venus an.
Sie finden das Standardatmosphärenmodell ist Unsinn? Dieses Modell erklärt die lapse rate und gibt die 15°C Lufttemperatur bei 1bar auf Meereshöhe vor.
Wenn kalte Luft in der Atmosphäre absinkt erwärmt sie sich, der Föhn Effekt ist ein gutes Beispiel für diese adiabatische Erwärmung durch Kompression. Strahlung ist hier nicht involviert, per Definition.
Is Loschmidt’s greatest discovery still waiting for its discovery?
Man kann diesen Effekt experimentell nachweisen, mit Wasser und mit Gasen.
Marcus Portius 24. Februar 2025 21:26
„schauen Sie sich die Venus an.“
Gerade auf der Venus ist der THE durch CO2 die Ursache der Oberflächentemperatur.
Sehe ich anders:
https://www.youtube.com/watch?v=WfuafZbpyII
Werner Schulz 28. Februar 2025 15:42
„Sehe ich anders:“
Hat bloß nichts mit richtiger Physik zu tun.
P.S.
Schon einmal was von der Beverly Clock gehört?
oder von der Brunt-Väisälä-Frequenz
Herr Portius, haben Sie immer noch nicht geschnallt dass es kein Perpetuum Mobile gibt??
Marcus Portius 24. Februar 2025 21:51
„Schon einmal was von der Beverly Clock gehört?“
„https://de.wikipedia.org/wiki/Beverly_Clock“
Also ist nichts mit dem perpetuum mobile aus der Gravitation.
P.P.S.
Schon einmal etwas von einem „Heat Dome“ gehört?
Heat dome blamed for a record-challenging heatwave baking the US desert Southwest this weekend. Death Valley hits 130F = 54.4 °C – the highest temperature ever reliably recorded on Earth
Doch. Hatte ich ja genannt, dass sich die Luft am Boden dadurch erwärmt, aber oben die überschüssige Wärme nicht mehr durch Abstrahlung los wird. Da wird dann direkt über dem Erdboden die Luft stehen und durch Erdrotation horizontal zirkulieren.
Die Luft ist oben kalt weil sie wenn sie expandiert und aufsteigt abkühlt. Auch wenn es reines N2 ist wird dieses am Boden durch Konduktion erwärmt, steigt auf und kühlt ab (nochmal: Der Joule Thomson Effekt).
Selbst wenn die Luft stehen würde hätten wir einen Temperaturgradienten auf Grund der Gravitation. Es ist äußerst ermüdend mit Leuten wie Ihnen wenn Sie einfach das was Ihnen gezeigt wird ignorieren. Wollen sie den gravitationsbedingten Temperaturgradienten den man experimentell nachweisen kann etwa leugnen?
Liefern Sie mal einen Nachweis dass ein Gas in einem Graviatationsfeld KEINEN Gradienten ausbildet. Nicht irgendetwas erzählen, Beweise her!
Hatte gerade ein Foto meiner Wärmebildkamera eingestellt und gezeigt, dass die Atmosphäre Wärme entsprechend der Temperatur abstrahlt und dadurch abkühlt. Wenn sie das nicht tun würde, wirds halt oben wärmer, bis die Vertikalkonvektion zum Erliegen kommt. Und erzählen Sie bitte nicht, Luft stahlt keine Wärme ab.
Wollen Sie mir jetzt erzählen die Luft um Sie herum wärmt Sie weil sie strahlt?
Sie kennen die Defintion der Temperatur eines Gases?
Warum ignorieren Sie eigentlich was ich Ihnen gezeigt habe?
Nö. Nur das Luft entsprechend seiner Temperatur Wärme abstrahlt. In alle Richtungen. Zeigt doch das Bild der Wärmebildkamera. Nach oben hin geht die Wärme ins All verloren. Hängen Sie da eine Decke/ Dach drüber, was die Wärmeabstrahlung verhindert, so erwärmt sich die Luft darunter. Einfacher kann mann es nicht erklären. Bei Herrn Weber gibt es das ja alles nicht.
Und was ist diese Temperatur per Defintion deren Resultat Strahlung ist? Sie zäumen hier das Pferd von hinten auf und verwechseln Ursache und Wirkung.
Lassen Sie Herrn Weber aus dem Spiel, immerhin ist er kein flach Erdler wie Sie.
Erklären Sie mal wie ein Gewächshaus oder eine Wärmedämmung funktioniert, Sie denken offenbar in einem Vakuum.
Herr Krüger, ich bin schwer enttäuscht von Ihnen. Ich hatte hier etwas mehr gesunden Menschenverstand erwarted.
Warum höre ich von Ihnen nichts zur Gravitation und den dadurch bedingten Temperataurgradienten der sogar in einem Photonengas zu beobachten ist?
Weichen Sie nicht immer aus!
Und Ihnen scheint der Begriff Konduktion überhaupt nichts zu sagen? Denn der hat mit bewegter Materie, was Atmosphäre nunmal zwangsläufig ist, garnichts gemein. Einfach Suche bei Wiki kann Ihnen sicher weiterhelfen beim Erkenntniszugewinn. Leute die mit Formeln nur so um sich werfen beherrschen noch nichtmal die einfachste Nomenklatur des Faches. 🙁
Dann sollten Sie sich mal ansehen wie ein Thermometer funktioniert, wie die Temperatur eines Gases definiert ist, der 0te HS. Sie machen sich gerade lächerlich.
Luft hat eine sehr schlechte Wärmeleitfähigkeit. Warum sollte ein Wert existieren, wenn er für Luft nicht anwendbar wäre?
Ich habe nichts zu einem Wert geschrieben, sondern einzig um die richtige Verwendung klar definierter Begriffe und diese liegt für Konduktion und Konvektion nun einmal vor. Was dann jeder daraus ableitet ist völlig seinem Gusto anheim gestellt, da will ich mich nicht noch zusätzlich auf endlose Diskussionen einlassen.
Und wie man sieht, an Ihrem Beitrag, führt diese Unsauberkeit in der Begriffsverwendung gleich zu einer fehlerhaften Annahme in Bezug auf Luft, die ich so auch nicht getätigt habe.
„Während bei Wärmeleitung(Konduktion!) die Wärme innerhalb des Materials übertragen wird, ohne dass der Körper selbst bewegt wird, während bei der Konvektion die Bewegung des Materials selbst die Wärmeübertragung übernimmt“
Insofern auch an den Beitragsverfasser Portius den Pass zurück gespielt, lächerlich macht sich derjenige welcher großspurig mit Begriffen umsich wirft, deren genaue Definition er nicht verinnerlicht hat.
Und mehr habe ich in meinen vorigen Einlassungen auch nicht verlangt, denn saubere Argumentation bedingt eine klare und für Jeden nachvollziehbare Nomenklatur und dieses lässt hier wie auch anderswo in vielen Beiträgen mehr als zu wünschen übrig. Was dann letztendlich immer wieder zu endlosen Disputen führt ohne erkennbaren Erkenntniszugewinn. Und für dieses Ansinnen, mag man mich gerne als „Krümelkacker“ bezeichnen, damit kann ich gut und gerne leben, wohingegen diese immer währenden Endlosdispute auf manche Beiträge zunehmend nerven.
Herr Steinmetz,
Luft hat einen Wert der Waermeleitfaehigkeit. In ihrer Aeusserung hoerte sich das so an, als wenn dem nicht so ist. Das wollte ich feststellen, mehr nicht.
Luft ist ein guter Isolator solange man Konvektion unterbinden kann. Die guten Isolationseigenschaften stammen von der schlechten Waermeleitfaehigkeit.
Konvektion kann unterbunden werden indem man einzelne Luftzellen schafft in der Konvektion nicht weit kommt. Eine Schaumisolierung ist vielleicht die beste Veranschaulichung, oder ein Daunenbett oder eine abgesteppte Daunenjacke.
Ansonsten ist es mir auch leid, immer wieder an die Grundlagen zu erinnern, weil hier einige denken, das sie die Thermodynamik umschreiben koennen.
Nichts sagen, hilft das?
Marcus Portius 24. Februar 2025 19:19
„Was ist mit der Graviatation?“
Die Gravitation erzeugt einen Druckgradienten – aber keinen Temperaturgradienten.
Schattenspender und Wärmedecke – die Rolle der Wolken im Klimasystemhttps://www.weltderphysik.de/gebiet/erde/atmosphaere/klimaforschung/wolken/
„Ansonsten würde die Atmosphäre immer wärmer werden bis sie vom Boden nach oben die gleiche Temperatur aufweist.“
Mann, Krüger – das ist ja wieder mal ein Klops
Oder die Atmosphäre wandelt alles in Volumenarbeit um und hat einen Gradienten und dehnt sich immer weiter aus. Gibt es da eine Limitierung?
„Am Tag kühlt die Luft die Oberfläche durch Konduktion (Evaporation nicht zu vergessen), über Nacht verhindert die Luft dass die Erde zu stark auskühlt,“
Das ist in sich schonmal ziemlich falsch, weil Konduktion Wärmeleitung in fester Materie bedeutet, also ohne das die Materia/der Körper selbst bewegt wird und Konvektion in frei beweglicher, also gasförmiger Materie stattfindet. Somit ist Wärmeleitung/-ableitung in die Luft IMMER konvektiv.
Und genau darin liegt der Schlüssel zur nächtlichen, langsamen auskühlung des Boden begraben. Durch permanente Einstrahlung am Tag wird ein großer Teil der Wärme von der erwärmten Oberfläche langsam in tiefere, kühlere, Bodenschichten transferiert und nach Sonnenuntergang und konvektiv abgekühlter Oberfläche wieder aus den wärmeren tieferen Schichten langsam an die Oberfläche konduktiv transportiert und von da entweder abgestrahlt oder konvektiv, wohl überwiegend, an die Atmosphäre/Luft abgeleitet. Worin auch der Grund zu sehen ist, das der Boden nie schlagartig abkühlen kann beim „Abschalten“ der Energiequelle.
Wenn Sie die Kommentare durchgelesen haben hätte Ihnen auffallen können dass Alarmisten sehr leicht verwirrt sind. Es ist klar dass die Luft erst durch Konduktion erwärmt wird und dann durch Konvektion die Oberfläche kühlt. Nur denken Alarmisten dass die darauf folgende meteorologische Konvektion (Definition oben) ein Wärmetransport in der Atmosphäre ist den man mit entsprechenden Gleichungen errechnen kann. Im Modell mag das Sinn machen, in der Realität findet per Definition kein Wärmetransport statt. es wird nur Arbeit verrichtet.
Luft hat nun mal die Eigenschaft eine Dämmung zu sein, sie ist in der Lage Wärme zu speichern, so wie der Erdboden oder die Ozeane Wärme speichern. Das hat nichts mit IR Strahlung zu tun.
Marcus Portius 24. Februar 2025 18:18
„Der Joule Thomson Effekt scheint unbekannt zu sein.“
Für die Existenz des Joule Thomson Effekts ( https://de.wikipedia.org/wiki/Joule-Thomson-Effekt ) fehlen in der Atmosphäre jegliche Voraussetzungen. In der Atmosphäre gibt es nur Adiabatik (a-diabatic nicht-Wärmetransport zur Umgebung), d.h. nicht ganz, der Temperaturgradient ist etwas überadiabatisch, da ein Teil der nach oben transportierten Wärme in Strahlungsenergie umgewandelt wird. An der Tropopause ist Überadiabatik und Wärmetransport zu Ende, weil der Überschuss vollständig in Strahlung umgewandelt wurde.
Was soll überschüssige Wärme sein?
Was ist denn wenn die Wärme einfach in Volumenarbeit umgewandelt wird?
Herr Krüger nennt es korrekt: „Konvektion kann es nur geben, wenn Luft Wärme abstrahlen kann.“
Sie haben mal wieder Ihre eigenen link nicht gelesen/verstanden: ohne Abstrahlung durch THGs gibt es keine Konvektion.
Nehmen wir mal an, oben gäbe es keine Abkühlung, weil nichts abstahlen kann. Dann führt nur die Erwörmung von unten zur Konvektion. Dieser erwärmt die Luft stetig, damit Konvektion weiter stattfindet, muss der Boden noch wärmer werden etc.. Wo ist die obere Grenze? Na klar, wenn der Boden genausoviel Wärme ins All abgibt wie er von der Sonne empfängt, denn dann geht nichts mehr zur Erwärmung der Luft drauf. Ins All verliert der Boden die Energie aber nur per Strahlung.
Übungsaufgaben: a) man berechne daraus die nötige Temperatur des Bodens.
B) Wie warm kann die Luft dann maximal werden? C) Erklärt dies die Beobachtungen?
Danke. Reicht ja schon ein Wärmeabstrahlungsbild vom bedeckten Nachthimmel. Mal schauen was da als Erklärung kommt.
Machen sie mal eines von oben. Was sehen sie?
Herr Portius,
da möchte ich Ihnen ausnahmsweise mal nicht uneingeschränkt zustimmen.
Aufsteigen und seitlich absinken funktioniert nur unter der Annahme lokal unterschiedlicher Bodentemperaturen. Diese sind bedingt durch wechselnde Sonneneinstrahlung (Tag/Nacht, Wolken) und lokal unterschiedliche Absorptionskoeffizienten des Bodens (Wasser/Land, Wald/Sand etc.)
Also:
Im Prinzip stimme ich Herrn Krüger zu; in der Realität meine ich, gibt es halt die genannten Störfaktoren, welche die Ausbildung von Konvektion erlauben.
Nun, es gibt ja keine ausschließlich herumzirkulierende Konvektion. Sie werden erklären müssen, wie Ihre Störfaktoren Wärme ins All abführen können.
Müssen sie nicht. Die Atmosphäre kann Wärme aufnehmen und nicht mehr abgeben. Was passiert?
Wann wäre das so?
Wenn IR aktive Gase die Atmosphäre nicht mehr kühlen?
Übungsaufgaben: a) man berechne daraus die nötige Temperatur des Bodens.
B) Wie warm kann die Luft dann maximal werden? C) Erklärt dies die Beobachtungen?
Zeigen Sie mal wer wo und wie die Temperatur des globalen Erdbodens in den letzten 120 Jahren gemessen hat. Was ist Ihre Quelle für die 15°C?
Sie berechnen etwas dass Sie nicht durch Messungen verifizieren können. Ziemlich clever…
Die Frage stellt sich hier nicht. Fangen Sie einfach damit an, ob der oben postulierte Prozeß die Beobachtungen erklärt.
Wenn Sie für die Überprüfung die globale Mitteltemperatur brauchen, Sie berechnen Sie die nach einer sinnvollen und nachvollziehbaren Methode.
Das reicht schon, um zu merken, dass der oben postulierte Prozeß nicht in der Lage ist, die Beobachtungen zu reproduzieren, nicht mal ein globales Mittel.
Erklaert die Adiabatik die Beobachtungen in der Troposphaere?
Natürlich tut sie das. Sie könne oder wollen die Frage (mal wieder) nicht beantworten.
Ist Ihre dumme Theorie, also müssen Sie ein messbares Ergebnis liefern. Kann es sein dass Sie die wissenschaftliche Mehode nicht verstanden haben? Sie labern ohne irgenwelche substantiellen Beweise zu liefern.
Ich bin nicht in der Situation, Ihre unphysikalischen Behauptungen widerlegen zu müssen. Sie müssen die Wissenschaft durch Daten und Beweise widerlegen.
Ihre obige Behauptung kann jeder aufstellen. Alleine die Beweise fehlen.
Also nochmal:
Nehmen wir mal an, oben gäbe es keine Abkühlung, weil nichts abstahlen kann. Dann führt nur die Erwörmung von unten zur Konvektion. Dieser erwärmt die Luft stetig, damit Konvektion weiter stattfindet, muss der Boden noch wärmer werden etc.. Wo ist die obere Grenze? Na klar, wenn der Boden genausoviel Wärme ins All abgibt wie er von der Sonne empfängt, denn dann geht nichts mehr zur Erwärmung der Luft drauf. Ins All verliert der Boden die Energie aber nur per Strahlung.
Übungsaufgaben: a) man berechne daraus die nötige Temperatur des Bodens.
B) Wie warm kann die Luft dann maximal werden? C) Erklärt dies die Beobachtungen?
Gehts um den Boden oder die Atmosphaere?
Oder gibt es einen Zusammenhang zwischen beiden Temperaturen, wenn ja, welchen?
Welche Beobachtungen meinen sie, wenn man einen theoretischen Fall bespricht? Meinen sie erwartbare Beobachtungen?
Diese Annahme spiegelt die Realität wieder. Nun behaupten Krüger et al eine Luftzirkulation, also Konvektion und Advektion finden nur statt wenn THGs anwesend sind, wenn die Luft strahlt. Krüger:
Das würde bedeuten eine reine N2 Atmosphäre unter ansonsten gleichen Bedingungen erwärmt sich nicht, steigt nicht auf, expandiert nicht und kühlt dabei nicht ab; es gibt keinen Temperaturgradienten. Weitergedacht bedeutet dies N2, da es nicht IR-aktiv ist strahlt nicht, hat also keine Temperatur.
Nun ist die Temperatur eines Gases klar definiert, aber nicht nach dem Kriterium ob es IR-aktiv ist, oder nicht. Ob 400ppm CO2 sich abkühlende Luft überhaupt durch selektive IR-Strahlung erwärmen kann, als verglichen zu der Temperatur die durch die Konduktion an der Oberfläche bereits erreicht wurde, ist meines Wissens nach nie nachgewiesen worden. Also ob 400ppm die lapse rate verändern. Das ist Teil des Modells, nachgewiesen ist es nicht.
Krüger et al argumentieren mit den Annhamen der Theorie, wie das Model des THE bzw. GCMs desigend sind, also in einem Zirkelschluss. Beweise für diese Annahmen können sie nicht liefern, z.B. das ein „radiation equilibrium“ wirklich existiert. Das ist die Prämisse der Theorie, wieder kein Beweis.
Googlen Sie mal Gasstrahlung. N2 und O2 sind im IR weitgehend transparent. THG nicht. Gase, die im IR nicht transparent sind, strahlen dort entsprechend ihrer Temperatur und dem Emissingsgrad ab. Gibt es Tabellen zu. Bei N2 und O2 können Sie aber die Temperatur mit einem normalen Thermometer messen. Über Wärmeleitfähigkeit. Können Sie bei CO2 auch. Zusätzlich noch die Wärmeabstrahlung.
Aha. Also strahlen auch N2 und O2. Oder wollen Sie behaupten diese Gase haben zwar eine Temperatur, strahlen aber nicht?
Was zeigt denn Ihr IR-Bild, nur CO2 und H2O? Oder doch die Strahlung der gesamten Luft, inkl. N2 und O2?
Bei bedeckten Himmel strahlt insbesondere Wasserdampf/ Wolken Wärme ab. An der Temperatur können Sie auch sehen, aus welcher Höhe. Unten wärmer oben kälter. N2 und O2 strahlen im IR nicht ab.
Sie behaupten dass N2 und O2, obwohl sie eine Temperatur haben nicht strahlen? Können Sie dafür einen Beleg liefern?
Mal in Erwägung gezogen dass sie das falsche Messintrument verwenden?
Marcus Portius 26. Februar 2025 0:12
Natürlich strahlen diese Gase auch – aber im IR ist die Strahlungsintensität dieser Gase so gering, das bei der (in diesem Zusammenhang) geringen Dicke der Atmosphäre im IR kaum etwas zu messen ist. Im Mikrowellenbereich sieht es etwas anders aus – diese Strahlung wird für die Temperaturbestimmung durch Satelliten benutzt: https://www.dwd.de/DE/wetter/thema_des_tages/2019/8/10.html
Ohne Treibhausgase, …, keine Vertikalkonvektion.
Ja, das ist evident.
Das ist offensichtlich falsch.
Was das Thermometer anzeigt. Sie wissen offenbar nicht, was Tempeeatur ist, wenn Sie meinen, N2 müsste dafür strahlen. Kirchhoff nicht verstanden.
Wo soll das denn existieren? Sie faseln nur.
Ach Heinemann…
In Ihrem Modell. Manabe et al nicht gelesen?
Manabe hat die equilbrium Temperatur berechnet, so heißt ja das paper. Und damit nicht die wahre Temperatur. Das ist doch nun evident, oder kapieren Sie die Intention von Manabe/Möllers paper nicht? Da fehlt noch die Konvektion etc.. Sie sind unlogisch.
Zurück zum Thema: Sie müssen den Unterschied zwischen Temperatur und Temperaturstrahlung kennen. Ihnen ist offenbar nicht bewußt, dass die Temperatur alleine nicht die thermische Abstrahlleistung bestimmt. Also, Sie lernen erstmal, wie es geht, demonstrieren, dass Sie es dann verstanden haben und dürfen dann wieder mit sinnvollen Beiträgen mitmachen.
Ist schon wieder Kindergarten?
Koennen sie bitte den
erklaeren und warum sie denken, er waere nicht bekannt oder hier wichtig?
Temperaturstrahlung ist die Wärmestrahlung, die ein Körper entsprechend seiner Temperatur abgibt. Dies ist ein material- und frequenzspezifisches Spektrum, deren Leistung P(f, df) in jedem Frequenzintervall df mit steigender Temperatur T steigt. Maximal ist diese für den schwarzer Strahler Pm(f, df) (Planckstrahler), es gilt das Kirchhoffsche Gesetz P(f,df) = A(f)×Pm(f,df), mit dem material- und frequenzspezifischen Absorptionsgrad A(f).
Und was ist jetzt der Unterschied? Sieht eher so aus als gaebe es eine Abhaengigkeit. Wo suchen sie also den Unterschied?
Sie sind der Erste der Temperaturstrahlung hier als Begriff (der von Wikipedia kommt) bringt.
Dieser Versuch einen Unterschied zu finden, wirkt etwas ablenkend, hatten sie auch ein Argument?
Das Wort, offensichtlich. Und damit i.a. die Bedeutung des Begriffs.
Abhängig heißt nicht gleich.
Temperaturstrahlung = thermische Wärmestrahlung,
Reden Sie sich nichts ein und kaspern Sie nicht herum, denn es ist klar:
Temperaturstrahlung gleich thermische Wärmestrahlung,
Temperaturstrahlung ungleich Temperatur
Und dann?
ist das eine wichtige Erkenntnis? Für sie?
Warum bringen sie das an?
Weil Heinemann ein Saboteur ist, ein Sophist. Anstatt auf Fragen zu antworten baut Heinemann Strohmänner, er (wie die anderen Alarmisten) wirft Nebelkerzen um vom Thema abzulenken.
Er nutzt das Wort „Wärmestrahlung“ – nun sagt der 2te HS dass Wärme per Strahlung nicht von kalt zu warm hinzugefügt werden kann. Also was kommt als nächstes? Diese Wärmestrahlng ist Energie!
Es wird immer das benutzt was gerade opportun ist und genau so schnell wird es vom Tisch gewischt wenn es nicht mehr passt. So wird die „Diskussion“ seit Jahr(zehnt)en am laufen gehalten, es geht nicht vor und nicht zurück, es werden immer wieder die gleichen Argumente angeführt. Was Sie heute widerlegen ist morgen vergessen und wird wieder bis zum bitteren Ende durchgekaut. Rinse and repeat.
Niemals bekommt man etwas handfestes geliefert (experimentelle Beweise), es sind immer wieder die gleichen, falschen Argumentationen. Heinemann et al sind Trolle bei denen man sich am Ende für steigende Preise, Verbote und den allgemeinen Zustand von Gesellschaft und Wissenschaft bedanken kann. Für solche Leute sind die heißesten Plätze in der Hölle reserviert.
Oah, bitte. Der Begriff „Wärmestrahlung“ ist in der Physik wohldefiniert. Und jeder, der kein Vollidiot ist, kann sich in 30 Sekunden darüber aufklären, dass Wärmestrahlung ein Spektralbereich des elektromagnetischen Spektrums ist und Energie (zuweilen auch als Wärme) überträgt.
Und wenn Sie ein Fleißkärtchen haben wollen, lernen Sie noch, dass der Begriff
Temperaturstrahlung genaugenommen nicht äquivalent zu Wärmestrahlung ist. Denn diese bezeichnet elektromagnetische Strahlung, die eine Temperatur hat. So hat die Temperaturstrahlung im Inneren der Sonne gemäß den Temperaturen dort ihr spektrales Maximum (Wien) im Röntgenbereich.
Die Temperaturstrahlung der Atmosphäre ist hingegen Wärmestrahlung, da ihr spektrales Maximum im Infraroten liegt.
Wie ich schrieb: Blablabla.
Jupp, leider ist das so!
Na, weil Sie glauben, es gäbe keinen Unterschied. Dies waren doch Ihre Worte:
Sie meinen sie wollten irgendwas damit erklären.
Haben sie schon wieder vergessen?
Also können sie es nicht belegen!
„Ja, das ist evident.“
Nein, ist es nicht. Der Temperaturgradient ergibt sich aus der barometrischen Höhenformel
Blödsinn, siehe Feynman
Muaahh
Wie schon erklärt: Feynman widerlegt Sie durch sein Beispiel.
Die barometrische Formel ergibt keinesfalls einen bestimmten Temperaturgradienten. Bei Feynman wird das Beispiel der barometrischen Formel bei isothermer Atmosphäre, also Temperaturgradient null behandelt.
„Bei Feynman wird das Beispiel der barometrischen Formel bei isothermer Atmosphäre, also Temperaturgradient null behandelt.“
Es gibt kein isothermisches Grundgerüst in einem Schwerefeld.
Was ist daran so schwer zu begreifen???
Es kann durchaus sein dass mir der Teil mit den IR-aktiven Gasen die strahlen und anderen Gasen, obwohl sie sich bewegen, die nicht strahlen sollen, entgangen ist. Da denkste der 3te HS ist gültig und schon kommt ein Treibhausexperte um die Ecke und belehrt einen eines besseren. It’s magic.
Könnnen Sie mir Kirchhoff hier zitieren?
https://eike-klima-energie.eu/2025/02/24/namensaenderung-mein-s-b-modell-wird-jetzt-zum-hemisphaerischen-konvektionsmodell/#comment-424707
Das würde bedeuten eine reine N2 Atmosphäre unter ansonsten gleichen Bedingungen erwärmt sich nicht, steigt nicht auf, expandiert nicht und kühlt dabei nicht ab; es gibt keinen Temperaturgradienten.“
Der Temperaturgradient folgt der barometrischen Regel.
Gemäß den Entropiegesetzen werden Energie und nicht Temperatur (intensive Größe) ausgeglichen.
Genau das, zu finden in der Internationalen Standard Atmosphäre ISA, inkl. Ideales Gas Gesetz und die hydrostatische Gleichung.
Der Punkt ist doch der: Die Treibhausmodellierer bedienen sich der Zahlenwerte aus der ISA, die 6.5°C pro 1000m, die 15°C surface air temperature SAT, die effektive Emissionshöhe bei -18°C, die isothermalen Schichten und sogar der THE selbst mit seinen 33K stammen alle aus der ISA. Man simuliert quasi die ISA in einem statischen Modell und nimmt einen Wärmetransport zwischen den imaginären Schichten an, so ist das Modell konzipiert, z.B. Pierrehumbert auf Seite 34. Das mag sogar sinnvoll sein, für ein Modell.
Hier wird über ein Modell geredet weil der experimentelle Beweis für den THE nach wie vor fehlt. Aber man kann experimentell nachweisen dass sich der Temperaturgradient wegen der Gravitation einstellt; die Venus ist das beste Beispiel. Boltzmann und Maxwell haben falsch gelegen, Loschmidt hatte recht.
Was Loschmidt correct in asserting that the entropy of a closed system can be decreased?
Abstract:
Man kann sich eigentlich jegliche Diskussion mit der Treibhaussekte sparen, sie sollen ein Experiment vorlegen welches Loschmidt widerlegt. Ganz einfache Sache. Sattdessen produzieren die Alarmisten nur eines: Heiße Luft.
Es wird gelabert, geschwurbelt, geschwafelt, Strohmänner werden in Massen gebaut und wenn man keine Argumente mehr hat wird beleidigt und abgelenkt – was nie kommt ist etwas substantielles. Und das ist der Grund warum die Skeptiker von der öffentlichen Diskussion ausgeschlossen werden; hier unterscheiden sich manche Lukewarmer wie Spencer, Watts oder Heller nicht von den Alarmisten.
„Die Treibhausmodellierer bedienen sich der Zahlenwerte aus der ISA, die 6.5°C pro 1000m, die 15°C surface air temperature SAT, die effektive Emissionshöhe bei -18°C, die isothermalen Schichten und sogar der THE selbst mit seinen 33K stammen alle aus der ISA.“
Herr Portius,
wir wissen, daß weder die 15°C noch die 18°C noch das Konzept der effektiven Emissionshöhe noch die wirklich albernen 33°C physikalisch Sinn machen.
Warum das so ist wurde hier auf EIKE durch u.a. Kramm ja hinreichend dargelegt.
„Es wird gelabert, geschwurbelt, geschwafelt, Strohmänner werden in Massen gebaut und wenn man keine Argumente mehr hat wird beleidigt und abgelenkt – was nie kommt ist etwas substantielles.“
Natürlich!
Die Propagandisten der Akpokalypse folgen ja nicht den Gesetzen der Physik sondern den Forderungen ihrer Brötchengeber.
„hier unterscheiden sich manche Lukewarmer wie Spencer, Watts oder Heller nicht von den Alarmisten.“
Aus diesem Grund glaube ich nur das, was den Grundlagen meiner Ausbildung nicht widerspricht.
Und damit landen wir bei Gerlich/Tscheuschner.
Der Rest kann (mit Ausnahmen) in den Korb
Da bin ich ganz bei Ihnen. Kennen Sie den Vortrag aus 1995?
INSTITUT FÜR MATHEMATISCHE PHYSIK
D E R T E C H N I S C H E N U N I V E R S I T Ä T C A R O L O – W I L H E L M I N A
– Prof. Dr. G. Gerlich -Vortrag auf dem Herbstkongress der Europäischen Akademie für Umweltfragen
Zusammenfassung:Die physikalischen Grundlagen des Treibhauseffektes und fiktiver Treibhauseffekte
In den guten Standardlehrbüchern der Experimentalphysik und theoretischen Physik sucht man vergeblich die Stichworte Treibhaus- oder Glashauseffekt und auch deren physikalische Behandlung. Andererseits gehört die Beschreibung des Phänomens, daß im Glashaus oder im Auto bei Sonnenschein die Luft und der Boden normalerweise heißer sind als in der Umgebung, durchaus zu den Vorgängen, bei denen die Physikstu-
denten vor dem Vordiplom zeigen können, daß sie etwas von der Beschreibung der Strahlung gelernt haben und mit den betreffenden Formeln umgehen können.
Offenbar seit der Arbeit von SVANTE ARRHENIUS aus dem Jahr 1896 hat sich in vielen meteorologischen und klimatologischen Texten ein ganz anderer Glashauseffekt eingebürgert, nämlich daß eine Schicht von Gasen, die Teile des ultraroten Lichtes absorbiert, während sie das sichtbare durchläßt, wie ein perpetuum mobile zweiter Art arbeiten soll: Der äußere kältere Bereich soll kälter werden, während die innere wärmere Bereich wärmer werden soll, ohne daß äußere Arbeit aufgewandt werden muß.
Für diese Mechanismen wird untersucht, welche physikalisch begründbar sind, welche nicht. Zu den letzteren gehört das sogenannte „Strahlungsbudget“ für Mittelwerte, für die es keine physikalisch begründeten Gleichungen gibt. Rechnungen für dieses „Strahlungsbudget“ gelten aber andererseits als wesentliche moderne Begründung für den fiktiven CO 2 -Treibhauseffekt der Atmosphäre.
Das macht durchaus eine physikalischen Sinn wenn man die richtige Theorie anwendet: Wenn in 5.1km die Temperatur -18°C beträgt dann ist es am Erdboden, also die Luft, 33°C wärmer, das sind dann 15°C – so ungefähr, das schwankt in der Realität. Alles ohne IR Strahlung oder Photonen Gas, Doppler Effekt und ein paar zappelnde Moleküle in homöopathischen Dosen.
Ich denke man muss das von der „Modellierer Seite“ sehen, wie man eine dynamischen Prozess mit einem Computer und Formeln „elegant“ simulieren will, es macht ja soweit Sinn. „Aber meine Formel ist schöner als deine!“
Nur sollte man dann nicht denken die Realität funktioniert wie das Modell (das auf geklauten Zahlen beruht).
Na ja, die flache Erde werte ich mal als einen Ausrutscher von Ihnen.
Aber zu den Photonen: Sie haben also das letzte Mal nicht verstanden, dass einem einzelnen Photonen zwar eine Energiemenge E (das einzelne hat E=h×f) zugeordnet ist und damit die spektrale Energiedichte uf (Joule pro Kubikmeter pro Hz) eines Photonengases der Temperatur T gemäß Planck beträgt uf = 8×pi×h/(c×h)^3 × E^3/[exp(E/(k×T))-1]. Die Gesamtenergiedichte U des Photonengases (in Joule pro Kubikmeter) der Temperatur T ergibt sich aus dem Integral der spektralen Energiedichte u über alle Frequenzen f von null bis unendlich: U = int u df = sigma/c × T^4. Ein Photonengas strahlt damit die Leistungsdichte P = U × c = sigma×T^4 ab. Die physikalische Größe Wärme wird bekanntlich durch den thermodynamischen Prozeß definiert. Wieviel Wärme das Photonengas überträgt, hängt davon ab, wie es mit seiner Umgebung wechselwirkt.
Sie haben noch gar nicht mitbekommen, dass der Treibhauseffekt die Existenz der Standardatmosphäre erklärt.
Ihnen ist das Wesen der Physik also unbekannt, Beobachtungen (hier die Atmosphäre bzw. ihre idealisiert-vereinfachte Annahme als Standardatmosphäre) durch die Naturgesetze (Thermodynamik von Luft und Strahlung, Hydrostatik etc.) quantitativ zu erklären, indem man die Naturvorgänge per Formeln nachvollzieht und die Ergebnisse daraus mit den Beobachtungen vergleicht.
Sie haben haben also die ganze Logik der Physik noch gar nicht verstanden. .. da müssen Sie sich helfen lassen (nicht von mir, fragen Sie einen Schullehrer, damit Sie mir in Zukunft besser folgen können. Ich mute Ihnen zu viel zu, Sie haben momentan noch nicht ausreichende Vorkenntnisse für die Atmosphärenphysik).
Herr Portius, das Bild über die Zirkulationssysteme der Erde (Hadley, Extratropen, arktische Zirkulation) gilt für die Erde wie sie de facto funktioniert, also mit Treibhausgasen.
Wenn Sie beweisen wollen, dass die Erde auch ohne Treibhausgase diese Zirkulationssysteme ausbilden kann, so müssen Sie dies anhand eines entsprechenden Atmosphärenmodells zeigen.
So ist es eine Nullnummer.
Wenn ich Sie richtig verstehen, glauben Sie, dass auch ohne Abführen von Wärmeenergie der Luft an der Oberkante des Zirkulationskreises ins All (obere Troposphäre) eine solche Zirkulation aufrechterhalten werden kann. Das werden Sie zeigen müssen ohne den 2. HS dabei zu verletzen. Ich bin gespannt.
Und ich frage mich ob sie diese Zirkulationssysteme zeigen koennen wenn die „so unbedeutenden“ Gase Stickstoff und Sauerstoff O2 fehlen.
Was soll da eigentlich zirkulieren?
Gucken Sie mal z.B. zur Venus.
Hab ich. Und nun? Wenn ich gleichzeitig zum Mars gucke, ist das ein Problem?
Was denken sie sehe ich bei der Venus?
Sie wissen ja immer was ich denke!
Werner Schulz 28. Februar 2025 11:33
„Was soll da eigentlich zirkulieren?“
Wie die Venus beweist das CO2.
Also wenn nur CO2 da ist, dann zirkuliert das CO2?
Bahnbrechend.
Und das im gleichen Masse?
Warum sagt man eigentlich Luftmassen?
Werner Schulz 28. Februar 2025 18:09
„Warum sagt man eigentlich Luftmassen?“
Die Luftmasse besteht dann eben aus CO2.
Nein muss ich nicht; Sie müssen beweisen dass sich Luft ohne THGs nicht erwärmen lässt, ist schließlich Ihre Theorie und so lange Sie nicht mal was handfestes, experimentelles liefern können sind die einzige Nullnummer hier Sie.
Haben Sie Lack gesoffen? Zeigen Sie mir mal wo das steht; garantiert nicht in der Standardatmosphäre. Wieder so eine unhaltbare Behauptung. So langsam wird das Muster von Heinemann et al erkennbar: Lügen und Falschbehauptungen!
nun, ich habe nur das erklärt, was Sie im Lehrbuch finden. Wenn Sie das nicht verstehen oder überprüfen, so ist das Ihr Problem. Sie haben ja schon öfter mitbekommen, dass Ihre Vorstellungen physikalisch falsch sind.
Wenn Sie eine von der üblichen Physik abweichende Theorie haben, so müssen Sie sich „verteidigen“.
Aber Sie dürfen davon ausgehen, dass es schwer wird, wenn Sie selbst mit alternativlosen und gesicherten Konzepten wie den Photonen nicht klarkommen.
Nun ja, Sie wissen ja nicht mal, was Sie experimentell sehen wollen.
Sie haben noch gar nicht mitbekommen, dass der Treibhauseffekt die Existenz der Standardatmosphäre erklärt.
nicht so frech, ich haben Ihnen mehrmals erklärt, dass es u.a. in Manabe steht. Wenn Sie unfähig sind, das paper zu verstehen, so geben Sie es einfach zu, statt unverschämt zu werden.
Nicht ich habe eine abweichende Theorie, das sind Sie:
Tatsächlich kann man in einem stationären Experiment eine Effekt nachweisen: Den Tempertaurgradienten in einem Graviationsfeld, so wie es Loschmidt gesagt hat und somit Maxwell widerlegt hat. Der thermodnyamische Atmosphäreneffekt ist real.
Sie haben ein nur Modell. Wenn Sie glauben die kinetische Gas- und die mechanische Wärmetheorie sind falsch: Beweisen Sie es.
Auch in einem Photonegas stellt sich in einem Graviationsfeld ein Temperaturgradient ein. Auch Tolman bestätigt somit Loschmidt.
Was Sie nicht verstehen ist dass Manabe’s Ansatz auf einer obsoleten Theorie beruht welche von Clausius widerlegt wurde.
Tja. Zeigen Sie doch mal Ihre Experimente!
Sie beklagen sich also, dass der Treibhauseffekt nicht im Labor nachgestellt werden kann. Das ist aber keine „abweichende Theorie“, sondern die Theorie selber, denn es gibt ja nur die eine in der Physik anerkannte.
Im übrigens funktioniert so die Physik: man hat im Labor bewiesene in Formeln gegossene Gesetze und wendet sie auch außerhalb des Labors an. Beim Treibhauseffekt sind das die der thermischen Strahlung, die Gasgesetze, Hydrodynamik, Spektren, Quantenmechanik, Thermodynamik etc.. Kurzum, wie das eben Physiker so machen. Sie sind offenbar kein Physiker. Na ja, ein Nachteil, aber Sie können es ja noch lernen.
Das sagt Prof. Zellner (Uni Essen) sehr richtig.
Ihr paper haben Sie gar nicht verstanden. Dabei zeigt doch die Tabelle, dass im Experiment viel geringere Temperaturgradienten gemessen werden. Im Text wird der Bezug zu dem (größeren) adiabatischen Gradienten geknüpft. Der Autor erklärt diesen Zusammenhang durch den Einfluß der Außenhülle des Experiments. Damit lassen sich die Messwerte des Temperaturgradienten nicht auf die Erdatmosphäre übertragen, denn diese hat nicht die Außenhülle des Experiments. Lesen Sie einfach mal auch Ihr paper. Verlinken ist ja nett für mich, aber dumm für Sie.
Das habe ist jedich nicht behauptet. Der Treibhauseffekt erklärt sich ja mittels der klassischen Gastheorie, nur kommt eben die Strahlung hinzu. Da man beides ab Mitte des 19. Jahrhdts verstanden hatte, war der Treibhauseffekt Anfang des 20. Jahrhdts physikalisch grob quantitativ verstanden (Emden). Siehe die Historie zum Treibhauseffekt (Fleming, Weart, Lorenz).
Die Behauptung, die Tolman aufgestellt hat, müssen Sie mir noch vorlegen.
Welche Theorie sei obsolet?
Sie habe die physikalische Herangehensweise hier immer noch nicht verstanden: der Treibhauseffekt wird berechnet und dann mit den Beobachtungen verglichen. Wie Sie feststellen, gibt es keine Berechnung der beobachtbaren Temperaturverlaufs der Atmosphäte, die ohne den Strahlungstransport auskommt. Das hat Emden zuerst nachgewiesen, Manabe hat es genauer berechnet. Und kein anderes paper aus Ihrer Sammlung kommt zu einem ähnlich genauen Temperaturverlauf wie Manabe, welches aber – im Gegrnsatz zu Manabe aber gemäß Ihrem Wunschdenken – nicht vom Strahlungstransport ausgeht.
Ihre Behauptung (und anderer Wissenschaftsleugner), der Temperaturverlauf der Erdatmosphäre könnte ohne Treibhausgase erklärt werden, hat offenkundig keine wissenschaftliche Grundlage.
Denn es gibt die letzten 100 Jahre keine einzige wissenschaftlich anerkannte quantitative Argumentation gegen die bestehende Treibhauserklärung zum Temperaturverlauf (ich schreibe mal nicht „Theorie“), die in Lehrbüchern und Universitätskursen zur Atmosphärenphysik erscheint und gelehrt wird (müßte ja auch noch „alternativ“ zum anerkannten Wissen gelehrt werden). Die Wissenschaftsleugner haben keine „alternative Wissenschaft“ anzubieten, sondern nur groben Unfug, der aggressiv, oberflächlichen und einfältig und gepaart mit Weltverschwörungsfantasien
präsentiert wird (stategisch dumm, und so ungeschickt ist selbst Lindzen, er demontierte sich selbst), und daran erkannt man sie.
Thomas Heinemann 2. März 2025 7:51
Noch ein paar Ergänzungen:
Wiegen Sie mal die Erde im Labor – geht mit einer Waage nicht, die Erde ist zu groß.
Im Labor bestimmt man mit der Cavendish-Waage
https://de.wikipedia.org/wiki/Gravitationswaage
die Gravitationskonstante und kann damit die Erdmasse bestimmen.
Das sich die Erde dreht und nicht die Umgebung kann man mit dem Foucaultsches Pendel im Labor beweisen ( https://de.wikipedia.org/wiki/Foucaultsches_Pendel ).
Die Menge an Zusammenhängen, die man im Labor kaum nachstellen kann und die ganz einfach erklärt werden können, wenn man die Gesetzmäßigkeiten erforscht hat, kann man beliebig erweitern.
Wie stellen Sie sich (Marcus Portius) ein Labor-Experiment vor, das den Treibhauseffekt beweist bzw. widerlegt. Das fängt schon bei der Meßunsicherheit an. Gemäß WMO-Definition ist die Tropopause bei einem Temperaturgradienten von 2K/km – also bei einer Laborentfernung von 1 m: 0,002K. Dann müssen auch alle Fehlerquellen minimiert werden, was das Ergebnis verfälschen könnte (siehe Foucaultsches Pendel) – aber schon, um die Fehlerquellen zu erkennen, muß der Treibhauseffekt verstanden sein.
Die wichtigsten Gesetze, die den Treibhauseffekt bestimmen, hat Herr Heinemann schon genannt, Zahlenwerte für einige Gesetze sind z.B. in HITRAN ( https://hitran.org/home/ ).
Zu Emden: Schwarzschild 1906. Eine Sammlung von Schriften zum Treibhauseffekt habe ich zusammengestellt: http://www.ing-buero-ebel.de/Treib/Schriften.htm
Ganz einfach. Solche Typen versuchen, die physikalisch bewiesenen und anerkannten Erklärungen zu sabbotieren, indem sie z.B. (wissentlich) sinnlose Zusammenhänge kreieren oder unmögliche, sinnfreie Forderungen stellen. Das Ziel von Klimawissenschaftsleugnern ist stets das Ablenken vom Thema, indem man erst mit einer Frage antäuscht, um dann durch stetes Dummstellen die Diskussion ins Absurde zu führen. Entweder man echauffiert sich an Marginalitäten, oder unterschlägt wesentliche Details in der Erklärung oder man driftet gezielt vom Thema weg.
Von daher rate ich Ihnen, nicht über jedes Stöckchen zu springen, das Ihnen hingehalten wird, sondern beim Thema zu bleiben und stattdessen das Stöckchen zum Verdreschen der Banausen zu nutzen, die versuchen, ihrer selbstgeforderten Belehrung zu entgehen.
Hier ist der Treibhauseffekt gut beschrieben:
https://www.youtube.com/watch?v=WfuafZbpyII
Werner Schulz 2. März 2025 15:01
Schon der Titel zeigt den Unsinn
Für richtig kann ich hier z.B. empfehlen
Jochen Ebel 28. Februar 2025 11:29
oder ausführlicher:
https://www.isbn.de/buch/9783758372926/wie-funktioniert-der-treibhauseffekt-wirklich
Nichts zum Inhalt? Nur den Titel gelesen?
Der gefaellt mir auch nicht gut.
Was sagt denn ihr Buch. Kriegen sie es hin das in wenigen Worten zu beschreiben?
Werner Schulz 2. März 2025 19:37
Lesen Sie den Text im Link.
Das sind Behauptungen, die sicherlich eine formulierbare Begruendung haben.
z.B.
Womit begruenden sie das?
Ich unterscheide diese. Hab ich jetzt schon ihr Model verstanden? Wie funktioniert er denn, dieser Treibhauseffkt mit diesem Verstaendnis?
Selbst der kleinste Temperaturgradient in einem Gravitationsfeld bei einem nicht-IR-aktiven Gas oder einer Flüssigkeit widerlegt Ihre Theorie.
Da er meßber ist ist Ihr Einwand bedeutungslos. Insbesondere unter der Prämisse dass der THE nicht messbar ist und nur im Modell existiert.
Der Kern der Theorie kann experimentell nachgewiesen bzw. widerlegt werden. Kennen Sie das Experiment auf welchem Ihre Theorie beruht?
Genau dieses Experiment widerlegt Ihre Theorie. Witzig, oder?
Marcus Portius 4. März 2025 0:45
„Der Kern der Theorie kann experimentell nachgewiesen“
Nach Ihrer Meinung kann man also die Masse der Erde nicht bestimmen, weil keine Waage existiert, auf die man die Erde legen kann? Da sind Sie schwer im Irrtum. Im Labor bestimmt man die Gravitationskonstante (Cavendish-Waage) und berechnet damit die Erdmasse.
Z.B. Hugs Messung. Hätte er die Physik nicht vergewaltigt und schon das Wissen von 1861 (Kirchhoff) berücksichtigt, geht aus seinen Messungen schon der Treibhauseffekt hervor.
Wie ich geschrieben habe: Es geht offensichtlich doch und dies widerlegt Ihre Theorie. Man kann im Experiment nachweisen dass das was sie nicht nachweisen können nicht nachweisbar ist, es existiert nicht.
Der Atmosphäreneffekt erklärt sich auch ganz ohne Ihre Strahlung, durch die kinetische Gas- und die Wärmetheorie. So wie es Ekholm bereits 1901 geschrieben hat. Die Standardatmopshäre (ohne Strahlung) existiert seit mind. den 1920ern, Ihre Theorie hat erst in den 1970/80ern wieder an Bedeutung gewonnen als man Computermodelle gebastelt hat. Das ist Ihr THE, ein Modell.
Falls Sie es nicht wissen: James Hansen hat den Trick, den „fudge“ mit der lapse rate schon im Jahr 2000 zugegeben. Sie können einfach weiter Behaupten der THE sei Teil der Standardatmopshäre; der versierte Leser wird wissen dass Sie Märchen erzählen.
Schon der Titel von Manabe 1961 beschreibt was die Grundlage seines Modells ist: Ein theoretisches Strahlungsgleichgewicht (das auf einer obsolten, von Clausius widerlegten Theorie beruht.)
Es will nur nicht in Ihren Kopf dass man „meine“ Theorie experimentell beweisen kann, während von Ihnen nichts kommt. Null. Niente. Nada. Zero.
Zur Erinnerung: Meine Experimente widerlegen Ihre Theorie! Jetzt hauen Sie mal rein und strengen sich an was substantielles zu liefern. Oder kommt nur wieder warme Luft?
Allein dies beweist doch schon welcher „Schule“ Sie angehören. Sie sind einer der typischen Dreckwerfer. Wenn man sonst nichts kann, gelle?
Marcus Portius 24. Februar 2025 17:02
„… und wirksam Wärme von der unteren Heizfläche in höhere Luftschichten.“
Die reine adiabatische Konvektion transportiert keine Wärme, wie schon aus Begriff „keine Wärme“ (a-diabatisch) hervor geht. Damit die Konvektion passiert, muß der tatsächliche Temperaturgradient etwas überadiabatisch sein – allerdings nur wenig, da die Luft leicht beweglich ist (Fourier 1824).
Während des Aufsteigens wird laufend ein Teil der überadiabatischen Wärme in Strahlungsenergie umgewandelt, so daß das überadiabatisch an der Tropopause zu Ende ist.