Wie kommt eigentlich die sogenannte „natürliche theoretische Globaltemperatur“ von -18°C auf „Mittelerde“ zustande?
Uli Weber
Exemplarisch wird oft wie folgt vorgegangen: Man viertelt einfach die die temperaturwirksame spezifische Strahlungsleistung der Sonne (Solarkonstante * (1-ALBEDO)/4) und setzt sie ohne Rücksicht auf Tag & Nacht und die geographische Breite in das Stefan-Boltzmann-Gesetz ein. Daraus ergibt sich dann ein „rechnerisches“ S-B-Temperaturäquivalent von -18°C.
Als Argument für diesen 24h-„Flacherde“-Ansatz wird typischerweise immer wieder angeführt, die Erde würde sich schließlich in 24 Stunden einmal um ihre eigene Achse drehen, Zitat:
„Legen wir halt den Fokus auf die „es wird nur eine Hemisphäre bestrahlt“, A ist die Fläche der Erde, P ist die eingestrahlte Leistung (unter den von Herrn Weber gemachten Annahme, dass man die einfach über die Halbkugel mitteln kann), t ist die Zeit:
(A/2) * P * t = A * (P/2) * t
Es sollte wieder offensichtlich sein, dass das beides gleich ist. Es wird einfach nicht mehr Energie, wenn man den Fokus darauf legt, dass die Einstrahlung nur auf eine Halbkugel wirkt…“
Anmerkung: Der freundliche Kommentator wird hiermit höflich aufgefordert, den Beweis für seine Behauptung von einer vorgeblich „von Herrn Weber gemachten Annahme, dass man die einfach über die Halbkugel mitteln kann“ anzutreten. Tatsächlich ist gegen einen argumentativen Gebrauch von Durchschnittswerten erst einmal nichts einzuwenden, weil dadurch die Unterschiede zwischen den jeweiligen Modellen ganz pauschal verdeutlicht werden. Aber konkrete Berechnungen mit Durchschnittswerten erlaubt ein T-hoch4-Gesetz nun mal nicht. Dazu sei vielmehr auf den EIKE-Artikel „Anmerkungen zur hemisphärischen Mittelwertbildung mit dem Stefan-Boltzmann-Gesetz“ verwiesen, der die wesentlichen Berechnungen aus einer Gesamtdarstellung meines hemisphärischen S-B-Ansatzes enthält.
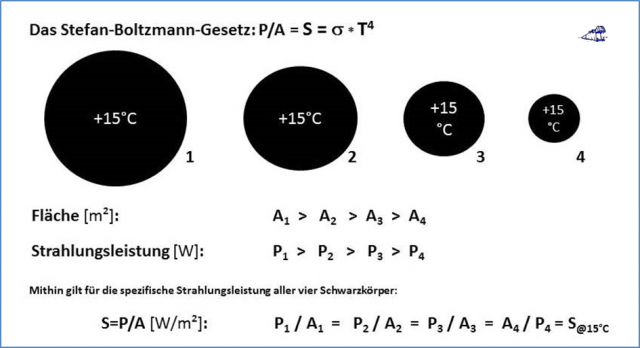
Das Stefan-Boltzmann-Gesetz ist nun mal keine mathematische Rechenanleitung, sondern eine physikalische Verknüpfung von spezifischer Strahlungsleistung und Temperatur:
Stefan-Boltzmann-Gesetz: S = * T4 mit S = P/A = Spezifische Strahlungsleistung
und = S-B-Konstante
Diese physikalische S-B-Beziehung wird sofort klar, wenn wir in der nachfolgenden Abbildung einmal vier unterschiedlich große Schwarzkörper gleicher Temperatur betrachten:
Abbildung: Zur Bedeutung der spezifischen Strahlungsleistung „S“ im Stefan-Boltzmann-Gesetz
Für einen beliebigen Schwarzen Körper mit einer Temperatur von +15°C gilt also immer:
Die SPEZIFISCHE Strahlungsleistung S@15°C dieses Körpers beträgt 390 W/m².
Aus dieser Abbildung wird unmittelbar deutlich, dass die unterschiedlichen Strahlungsleistungen „Pi“ und Flächen „Ai“ eindeutig zusammenhängen, weil sie für jeden Körper (1-4) eine augenblickliche spezifische Strahlungsleistung „S@15°C“ definieren, die wiederum über das Stefan-Boltzmann-Gesetz eindeutig mit der Momentantemperatur des jeweiligen Körpers von 15°C verknüpft ist. Allein die Temperatur (primär) bestimmt also die spezifische Strahlungsleistung (sekundär) eines Schwarzen Körpers nach dem Stefan-Boltzmann-Gesetz:
Stefan-Boltzmann-Gesetz: Temperatur (primär) => Spezifische Strahlungsleistung (sekundär)
Jede Berechnung einer Temperatur (sekundär) aus einer spezifischen Strahlungsleistung (primär) stellt aber eine Inversion des Stefan-Boltzmann-Gesetzes dar, welche nur zulässig ist, wenn alle Randbedingungen, des S-B-Gesetzes streng erfüllt sind. Da diese die aber nicht per se erfüllt werden, ist eine Inversion des S-B Gesetzes immer nur in physikalisch wohl definierten Fällen zulässig.
Stefan-Boltzmann-Inversion: Spezifische Strahlungsleistung (primär) => Temperatur (sekundär)
Also kann durch die Sonneneinstrahlung nur dort eine Temperatur erzeugt werden, wo die Sonne auch scheint. Genau deshalb fahren so viele Urlauber aus dem Norden in den sonnigen Süden, wo sie sich tagsüber – und nicht nachts – zum Anbräunen in die Sonne legen. Vielleicht vergleichen Sie einfach mal die Zeit, die Sie sich je nach Tageszeit und Ortslage ungeschützt der Sonnenstrahlung aussetzen können, ohne einen Sonnenbrand zu riskieren. Sie werden feststellen, dass es sowohl eine Abhängigkeit von der Tageszeit als auch eine Abhängigkeit von der geographischen Breite gibt. Nur nachts können Sie keinen Sonnenbrand bekommen, es sei denn, der Timer in Ihrem Sonnenstudio ist defekt.
Die Einbeziehung unbestrahlter Flächen (Nachtseite der Erde) in eine S-B-Inversion gehört damit in das Reich der MINT-fernen Sagen und Märchen.
Jetzt wird auch ganz offensichtlich, dass die Gleichung aus dem oben zitierten Kommentar in Zusammenhang mit dem S-B-Gesetz keinerlei tieferen physikalischen Sinn ergibt, weil dort schon mal die spezifische Strahlungsleistung in [W/m²] fehlt. Die Formel „(A/2) * P * t = A * (P/2) * t“ verknüpft vielmehr eine Fläche „A“ in [m²] und eine Strahlungsleistung „P“ in [W] mit der Zeit „t“ in [s]. Damit ergeben sich auf beiden Seiten des Gleichheitszeichens gleiche Beträge für eine „Wärmemenge mal Fläche“ in [Joule mal Quadratmetern]. Und was das nun physikalisch mit dem Stefan-Boltzmann-Gesetz zu tun haben soll, weiß wohl nur der freundliche Kommentator. Aus unerfindlichen Gründen muss diese postphysikalische Gleichung dann als Beweis für eine „theoretische Globaltemperatur“ von (-18°C) herhalten. Aber immerhin kann man, analog zur obigen Schwarzkörper-Abbildung, aus dieser eigenartigen Formel jeweils rechts und links des Gleichheitszeichens eine spezifische Strahlungsleistung für die Taghemisphäre und die ganze Erde ableiten:
Hemisphäre: Fläche = (A/2) Strahlungsleistung = P Spezifische Strahlungsleistung = (2P/A)
Ganze Erde: Fläche = A Strahlungsleistung = (P/2) Spezifische Strahlungsleistung = (P/2A)
Und diesen höchst unterschiedlichen Durchschnittswerten steht nun wiederum die klimareligiöse Glaubensformel gegenüber, Zitat, „Es sollte wieder offensichtlich sein, dass das beides gleich ist“…
Wie wir gesehen haben, ist also lediglich die spezifische Strahlungsleistung „S“ über das Stefan-Boltzmann-Gesetz eindeutig mit der Temperatur „T“ eines Körpers verknüpft. Das Stefan-Boltzmann-Gesetz kann also nicht als Begründung dafür herhalten, die Solarkonstante (S0=1.367 W/m²) einfach mal so eben über die gesamte Erdoberfläche und den 24h-Tag zu mitteln. Denn schließlich gibt es auf der Erde Tag und Nacht, deshalb also auf der einen – bestrahlten – Hälfte der Erde eine spezifische solare Strahlungsleistung, und auf der anderen Hälfte ist es dunkel. Man kann die eingestrahlte spezifische Strahlungsleistung auf der Tagseite auch nicht über den 24h-Tag als Wärmemenge „speichern“ und dann durch eine willkürliche Berechnung in eine spezifische „globale“ Strahlungsleistung zurückverwandeln. Das Dumme an einer solchen Durchschnittsberechnung über die Zeit ist nämlich, dass eine Wärmemenge in „Joule“ keinerlei „Erinnerung“ daran hat, auf wie vielen Sekunden mit welcher spezifischen Strahlungsleistung sie eigentlich beruht. Also könnte eine solche Wärmemenge auch sonst woher kommen:
0,1Sonnen(@136,7W/m²*(1-ALBEDO))*240h
= 1Sonne(@1.367W/m²*(1-ALBEDO))*24h
= 10Sonnen(@13.670W/m²*(1-ALBEDO))*2h24min
= 100Sonnen(@136.700W/m²*(1-ALBEDO))*14min24sec
Ein globaler Durchschnittswert für die solare Einstrahlung über 24 Stunden sagt also physikalisch gar nichts aus. Denn man kann aus einem „kochenden Suppentopf“ die ursächliche spezifische Strahlungsleistung nicht mehr physikalisch eineindeutig rekonstruieren. Aber selbstverständlich kennen die Vertreter von „Mittelerde“ die zugehörige terrestrische Ausgangssituation und berechnen daher aus dieser Wärmemenge ihre willkürlich passende „spezifische“ globale Strahlungsleistung. Eine solche Rückrechnung ist aber reine Mathematik, die gar kein physikalisch korrektes Temperaturäquivalent für das Stefan-Boltzmann-Gesetz liefern kann. Alle oben aufgeführten Beispiele für 0,1 bis 100 Sonnen liefern physikalisch gleichwertige Wärmemengen, sind aber über unterschiedliche Zeiträume durch unterschiedliche spezifische Strahlungsleistungen erzeugt worden. Und nur die originäre spezifische Strahlungsleistung der Sonne auf der Tagseite der Erde ergibt über das Stefan-Boltzmann-Gesetz ein physikalisch korrektes Temperaturäquivalent für eine individuelle Ortslage.
Wir müssen für eine solche 24-Stunden-Betrachtung also das örtliche Maximum der spezifischen solaren Strahlungsleistung auf der gesamten Erdoberfläche ermitteln, wie die nachfolgende Abbildung auf Grundlage einer Mollweide Projektion zeigt:
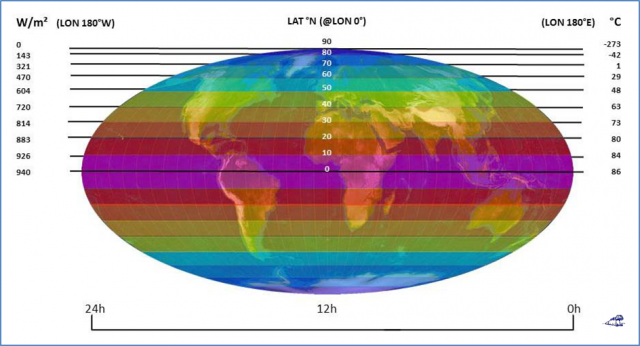
Abbildung: Die maximale breitenabhängige temperaturwirksame solare Strahlungsleistung (links) und das resultierende S-B-Temperaturäquivalent (rechts) über einen 24-Stunden-Tag im Äquinoktium für das „Mittelerde“-Modell:
Linke Skala: MAX (Si) @24h-Tag mit (Si = 1.367W/m²* (1-ALBEDO) * cos PHIi)
und (PHIi = örtlicher Zenitwinkel)
Rechte Skala: Maximales örtliches S-B-Temperazuräquivalent( SBTi) zu MAX (Si)
Mit farblich unterlegter Mollweide-Projektion (Copyright L. Rohwedder – Lizenz CC BY-SA 3.0)
Aus dieser Abbildung wird sofort deutlich, dass die maximale temperaturwirksame spezifische Strahlungsleistung der Sonne im Tagesverlauf bei gleicher geographischer Breite immer denselben Maximalwert und damit auch immer dasselbe maximale örtliche S-B-Temperauräquivalent ergibt. Im Tagesverlauf wird also zwischen 75 Grad N und S (mit jeweils 243 W/m²) und dem Äquator (mit 940 W/m²) die global gemittelte temperaturwirksame spezifische „Mittelerde“-Strahlungsleistung von 235 W/m² (≅ -18°C) weit übertroffen. Damit ist bewiesen, dass die täglich durch Sonneneinstrahlung überall auf der Erde zwischen 75°N und 75°S erzeugten Temperaturen keinerlei zusätzlichen „natürlichen atmosphärischen Treibhauseffekt“ benötigen, um die gemessenen Ortstemperatur zu erklären.
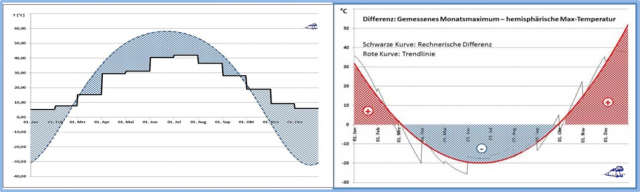
Im Gegenteil wird das maximale S-B-Temperaturäquivalent auf unserer Erde aufgrund von Konvektion und Verdunstung in der Realität niemals erreicht; umgekehrt wird aber der nächtliche Temperaturabfall durch Kondensation und Advektion abgemildert und erreicht niemals den Absoluten Nullpunkt. Letzteres gilt übrigens auch für das Strahlungsdefizit in mittleren und höheren Breiten der jeweiligen Winterhemisphäre, dazu nachfolgend ein Beispiel für Potsdam:
Abbildung: Jahresverlauf der Temperatur am Beispiel Potsdam:
Links: Treppenkurve: Maximale monatliche Bodentemperatur in Potsdam
Blau gestrichelt: Maximales jahreszeitliches S-B-Temperaturäquivalent
Rechts: Differenz zwischen der maximalen monatliche Bodentemperatur in Potsdam und dem maximalen örtlichen S-B-Temperaturäquivalent
Rote Kurve: Trendlinie für die Differenz (schwarze Zackenkurve) zwischen maximaler monatlicher Bodentemperatur und dem maximalen örtlichen S-B-Temperaturäquivalent in Potsdam
Rot schraffiert: Zufluss von Wärme im Winterhalbjahr
Blau schraffiert: Abfluss von Wärme im Sommerhalbjahr
Im Sommerhalbjahr fließt also Wärmeenergie in die globalen Wärmespeicher und im Winterhalbjahr wird die Ortstemperatur durch einen Wärmezufluss aus diesen Wärmespeichern gestützt. Und deshalb müssen Atmosphäre und Ozeane als „globale Wärmespeicher“ zwingend in die Bestimmung einer „natürlichen Temperatur“ unserer Erde einbezogen werden.
2 Scrutinizing the atmospheric greenhouse effect and its climatic impact, Natural Science 2011
Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Werner Schulz schrieb am 10. FEBRUAR 2020 UM 2:37:
Zeigen Sie doch einfach eine Temperaturverteilung für die Flächen des Würfels, bei der sich
* Ein- und Ausstrahlung gleichen und
* die Mitteltemperatur der Flächen des Würfels über der eines Würfels liegen, auf dem alle Flächen die gleiche Temperatur haben
Das wäre viel überzeugender als immer wieder nur Fragen zu stellen, Dinge einfach nur in Zweifel zu ziehen und Behauptungen aufzustellen.
Habe ich gefragt oder sie?
Also noch mal:
Herr Mueller,
beantworten sie die Frage, welche Temperatur hat dieser Wuerfel?
Suchen sie sich also von 121 bis -270 Grad C eine Temperatur aus.
Werner Schulz schrieb am 21. Februar 2020 um 17:09:
Ich habe die Frage beantwortet, die Antwort hat Ihnen nicht gefallen und Sie haben statt dessen einen anderen Temperaturbereich vorgeschlagen.
Zeigen Sie also einfach mal eine Temperaturverteilung, die Ihrem Vorschlag entspricht. Aber da wird wohl nichts kommen. Es bleibt bei einfachem Infragestellen …
Herr Mueller,
helfen sie mir noch mal, wo haben sie die Antwort gegeben?
Ich habe Ihnen einen Temperaturbereich vorgeschlagen, das ist richtig. Sie sagen ihre Antwort liege außerhalb dieses Bereiches.
Sie sollten begründen wie das gehen sollte.
Es geht nicht! Aber es scheint sie glauben sie haben eine bessere Physik.
Bisher ist ihr Glaube daran stärker.
Mein Temperaturverteilung haben sie selber hingeschrieben. Nicht gesehen? Nicht nachgedacht? Trollmodus aktiviert?
MFG Werner
Werner Schulz schrieb am 4. März 2020 um 6:12:
7. Februar 2020 um 10:52
Lesen Sie bitte nochmal nach. Falls Sie dann immer noch der Meinung sind, ich hätte das gesagt, zitieren Sie bitte die Stelle, damit ich verstehe, wie Sie darauf kommen und das klarstellen kann.
Auf WUWT war ein solches Beispiel etwas vereinfacht zur Diskussion gestellt worden: The Hot And Cold Of Space. Das Ergebnis für das WUWT Beispiel deckt sich mit meiner Aussage: Die mittlere Temperatur ist unter der, die sich bei einer Gleichverteilung einstellen würde (mittlere Temperatur im WUWT Beispiel 302K, bei gleicher Abstrahlung auf Vor und Rückseite etwa 335K).
Ja Herr Mueller,
da stand keine Antwort. Daher habe ich darunter direkt gefragt welche Temperatur sie vorschlagen.
Das von Ihnen angefuehrte Beispiel ist gut, aber nicht genau das selbe Problem wie hier angefuehrt. Aber gucken wir mal
Wie sie festellen ist das interessante an dem Besipiel, das die Loesung 383K auf der einen Seite und 221K einer Mitteltemperatur von 302 K mit einer Austrahlung von 471.6 W/m2 entspricht.
Wenn man das auf die gesamte Flaeche verteilt, gibt dieser Koerper im Durchschnitt nur 943.2 W/m2 ab. Obwohl er mit der Solarkonstante bestrahlt wird. Daher kommen sie jetzt mit 335K die als Temperatur die Notwendig waere um die richtige Abstrahlleistung zu berechnen.
Und was lernen sie daraus? Sie hatten ja bisher keine Aussage zur Temperatur gemacht oder sollen die 335K ihre Antwort sein?
@ Michael Krüger
Sie fragen nach einer Quelle für die Definition des „Treibhauseffektes“:
Die physikalische Begründung der Auswirkung infrarot-aktivierbarer Gase, die häufig Treib-hausgase genannt werden, geht auf mehrere Arbeiten von KONDRATYEV u.a. zurück (KONDRA-TYEV, 1969; KONDRATYEV und MOSKALENKO, 1977; KONDRATYEV und MOSKALENKO, 1984). Sie haben die Differenz zwischen der Temperatur der bodennahen Luft (OT= 288 K = +15 ˆoC) und der Strahlungsgleichgewichtstemperatur der Erde incl. Atmosphäre (TSt.= 255 K –18 =ˆoC) als „Treibhauseffekt“ aufgefasst und auf die wichtigsten IR-anregbaren Gase (H2O-Dampf, CO2, O3, N2O, CH4) aufgeschlüsselt.
////
Sie sehen, Ihre frei erfundene Defintion auf Basis der „Abstrahlungshöhe“ ist für die Tonne.
Herr Weber schreibt im Artikel:
Jeder, der die ursprüngliche Diskussion verfolgt hat, weiss, dass es nicht um das Stefan-Boltzman-Gesetz ging. Herr Weber stellt hier also einen Zusammenhang her, den es gar nicht gibt, um den Kommentar ins lächerliche zu ziehen. In der Diskussion, aus der Herr Weber den Kommentar selektiv entnommem hat, ging es um folgende Frage:
Es ging also nur darum, die wie von der Sonne eingestrahlte Energie verteilt wird, nicht um irgendeine Abstrahlung der Erdoberfläche, die vielleicht mit dem Stefan-Bolzman-Gesetz bestimmt wird. Man könnte das allein schon daran erkennen, dass in der Formel nichts, aber auch gar nichts aus dem Stefan-Bolzmann-Gesetz vorkommt, weder eine Temperatur noch die Stefan-Bolzman-Konstante.
Die Energiemenge, die von der Sonne auf der Erdoberfläche ankommt, ist immer die gleiche, egal, ob ich sie auf einen Kreis mit dem Radius r, eine Halbkugel mit dem Radius oder eine Kugel mit dem Radius r wirken lasse. Sie wird einfach nicht mehr, wenn sich die Geometrie ändert. Und damit die von der Erde/Atmosphäre aufgenommene und die wieder abgegebene Energie im Mittel gleich sind, führt Herr Weber dann seine Stefan-Bolzmann-Umgebungsgleichung ein, die von den Mechanismen her den Erklärungen des Treibhauseffekts sehr ähnlich sind: Die Energie der Atmosphäre verringert die vom Boden abgegebene Energie soweit, dass nur noch soviel Energie abgegeben wird, wie auch von der Sonne zugeführt wird …
Zitat: Die Energiemenge, die von der Sonne auf der Erdoberfläche ankommt, ist immer die gleiche, egal, ob ich sie auf einen Kreis mit dem Radius r, eine Halbkugel mit dem Radius oder eine Kugel mit dem Radius r wirken lasse. Sie wird einfach nicht mehr, wenn sich die Geometrie ändert.
Sie schreiben wie immer völligen Unsinn, aber das bin ich von Ihnen schon gewohnt.
Ein Zylinder oder Kreisscheibe hat ein anderes Reflexionsverhalten für Strahlung, als eine Kugel/Halbkugel.
Der Reflexionsgrad der Zylinderform ist niedriger, als bei einer Kugelform. Somit kann mehr Energie durch Strahlung aufgenommen werden, wodurch die Temperatur für die Zylinderform höher ausfallen müsste.
Man kann mit Hilfe des Phasenintegrals die Albedo von einer geometrischen Objektform in eine andere umrechnen.
Für die gegebene sphärische Albedo der Erde von 0,289 erhält man
+ für die Zylinderform einen Wert der Albedo von 0,235
+ und für die Form einer planaren Kreisscheibe einen Wert der Albedo von 0,193.
Mfg
Werner Holtz
Da sitze ich draußen, bei milden 10°C im Plusbereich. Es ist windstill und meine Hände sind warm (IR- Messung ergibt 32°C). Mein Atem erwärmt die Luft, nur ganz leicht, denn er vermischt sich schon auf den esrten Zentimetern mit der Umgebungsluft (wenn es kälter wäre könnte man ihn sehen, wenn die in ihm enthaltener Wasserdampf sichtbar kondensiert. Dafür ist es heute zu warm aber wenn dann dieser Lufstrom meine Hände trifft so wird es kühl. Ja meine Hände verlieren Energie und mein Körper heizt nach. Mein Körper, im innern immer warm, regelt durch die beim Stoffwechsel im Körper erzeugte Energie meine Temperatur. Ja er strahlt nach den Gesetzen der Physik und diese sind nicht hauptsächlich bestimmt durch die Strahlungsvorgänge, sondern von Abertrilljarden kleiner Moleküle, die mich immer wieder treffen. Eigentlich übertragen sie mit jedem Aufprall doch Energie? Warum erhizte ich mich nicht? Meinen Körper wohnt mehr Energie inne und so nehmen diese Teilchen sie mit auf die Reise in die Atmosphäre. Unwiderbringlich für mich und alle in mir lebenden Organismen verloren ist nun diese Wärme, die wir so dringend benötigen. Und so sind wir gezwungen weiter exotherme biochemische Vorgänge für unseren Weiterbestand zu nutzen.
Warum macht sich unser Gehirn nun Gedanken über einen geviertelten durchschnittlichen Strahlungsanteil wo er zur Zeit nur in 3 oder 4 Stunden ausreichend wäre meiner Körperoberfläche echte Energie zuzuführen, doch wehe es kommt ein Luftzug der wieder alles mit auf seine advektive und konvektive Reise nimmt. Latend entweichen mir die Moleküle des Wasser´s, heute ganz heimlich, ohne sich kondensierend in meiner Nähe, bei ihrer Flucht zu enttarnen…..
Mit freundlichen Grüßen!
Christian Möser
Zimmerer
Sehr geehrter Herr Uli Weber,
mit diesem Artikel haben Sie sich für uns Leser wieder viel Mühe gegeben.Der Hinweis auf die Mollweide-Projektion ist ein kleiner Schritt in die richtige Richtung.Aber prompt bei der Albedo wieder voll daneben.Was den Erdboden nicht erreicht,wird auch nicht vom Erdboden abgestrahlt.Allerdings von nennenswerten Massen in der Atmosphäre.
Die Projektion zeigt aber nur den quantitativen Verlauf der Einstrahlung am Erdboden.Wenn dann von Wärmespeicherung die Rede ist,muss dieser Speichergang auch beschrieben werden.
Solange der Energie-Impuls Tensor für ein Kästchen zum Lottospielen betrachtet wird und man Glücksspiel generell ablehnt, wird das nix mit anständiger Physik.
@ All:
Der „freundliche“ Kommentator Marvin Müller verteidigt hier in seinem Kommentar vom 5. Februar 2020 um 13:52 ganz unverfroren sein F-Wort-Zitat, „Strahlungsdurchschnitt von 470 W/m² für die tagseitige Hemisphäre“, obwohl es im Originaltext unmissverständlich heißt, „Der Strahlungsdurchschnitt von 470 W/m² (korrekt: 940W/m²*cosPHIi) umfass einen Strahlungsbereich von 0-940W/m² für die tagseitige Hemisphäre mit einem maximalen S-B-Temperaturäquivalent von 85,7°C @ 940W/m².“
Und gleichzeitig weint sich dieser kreative Zitatdesigner dann öffentlich darüber aus, dass er mit einer MINT-fernen Glaubensformel und fehlerhaften physikalischen Einheiten erwischt worden ist.
Ceterum censeo vexator fororum utgardensis SCHNEEFLOCKE est.
U. Weber schrieb am 6. Februar 2020 um 12:40:
Und? Ich habe den Kommentar korrekt verlinkt, so dass sich alle ein Bild machen können. Ich habe aus Ihrem Satz lediglich die Ungleichverteilung der Einstrahlung weggelassen, das es mir nur um den Mittelwert ging. Ein Wert, der korrekt ist (wenn man von 940W/m² nach Abzug des Albeo ausgeht) und mit dem Sie auch vorher schon argumentiert haben, wie man an dem anderen Zitat sehen konnte.
Gibt es irgend einen anderen Grund als die Ablenkung von den eigentlichen Argumenten, dass Sie jetzt darüber so einen Aufstand machen?
Öffentlich ausweinen sieht anders aus. Ich kann prima damit leben in einer Diskussion mal einen Fehler zu machen beim Versuch etwas kurz zu fassen mal daneben zu langen. Was ändert das am inhaltlichen? Wird dadurch das korrekt hingeschriebene
(mit A Erdoberfläche, S_0 Solarkonstante, a Albedo, t betrachtete Zeit) etwa falsch? Kommt auf der Erde in beiden Fällen etwa nicht die gleiche Menge an Energie an? Darum ging es in der Diskussion, aus der Sie sich ein Stück rausgepickt haben.
Aber wie nicht anders erwartet war das wieder ein Weberscher Kommentar, der sich nicht auf den Inhalt bezog sondern eher auf die Form. Wää, der hat mich falsch zitiert, kuck mal, der hat das falsche Formelzeichen benutzt. Inhaltliche Argumente zu dem, was ich geschrieben habe gabs wieder mal nicht.
Um gleich mal zu demonstrieren, dass es mir nichts ausmacht, auch mal einen Fehler zu machen, habe ich prompt einen gemacht und die Einstrahlung doppelt so hoch angesetzt, wie sie eigentlich ist. Da die Einstrahlung auf eine Halbkugel wirkt, muss man sie nochmal habieren:
Herr Mueller,
Und noch einmal, was sie da mit der Formal machen ist ein mathematisches Spielchen. So lange wie wir ueber Strahlstaerken reden, muessen sie die korrekte Flaeche nehmen von der die Strahlung kommt oder wo sie ankommt.
Im Falle der Erde ist das eine Hemisphaere.
Daher ist ihr Ansatz the Leistung zu halbieren und die Erde flach zu machen falsch und zu verwerfen.
Bei Diskussionen zum Stefan-Boltzmann Gesetz wird sehr häufig vergessen, daß es sich dabei um eine Formel handelt, die ein theoretisches Konstrukt berechnet, welches es in der Wirklichkeit aber nicht gibt, nämlich den „Schwarzen Strahler“. Das gilt besonders, wenn man die Formel für Erwärmvorgänge anwenden will, wofür sie eigentlich nicht geschaffen wurde.
Bei realen Körpern spielen bei Erwärm- und Abkühlvorgängen sowohl die Be- bzw. Abstrahldauer also die Zeit eine Rolle, als auch Materialeigenschaften wie Wärmekapazität und geometrische Abmessungen. All diese Parameter kommen bei SB aber nicht vor.
Daher kann man mit SB auch nicht ermitteln, wie sich z. B. ein Kubikmeter-Würfel einer bekannten Albedo bei Bestrahlung verhält. Einfach deshalb, weil bei SB nur eine Leistung pro Fläche vorkommt. Man kann sehr leicht durch Versuche oder Gedankenexperimente ermitteln, daß dieser Würfel nicht das macht, was bei SB-Rechnungen als Ergebnis ermittelt wird.
Bei Abstrahlvorgängen, wofür SB geschaffen wurde, fallen diese zusätzlichen Parameter weg, weil die Abstrahlleistung nur von der Momentantemperatur und der Größe der betrachteten Oberfläche abhängen, aber nicht, wie lange der Erwärmvorgang gedauert hat, ob er linear oder nichtlinear verlief und auch das Volumen des Körpers spielt keine Rolle.
stefan strasser schrieb am 6. Februar 2020 um 10:33:
Wie sich das Einbeziehen dieser Parameter auswirkt, kann man in dem neulich bereits diskutierten Modell von Spencer sehen. Vielleicht sollten Sie da doch mal einen Blick drauf werfen und tatsächlich ansehen, was da passiert? Bei der Diskussion des Modells hatten Sie anscheinend gar nicht erst hingesehen, was da gemacht wird …
In den Erklärungen des Treibhauseffektes wird „SB“ nur benutzt, um die Abstrahlung zu beschreiben. Sie sollten wirklich mal genau lesen, was da gemacht wird …
Das verstehe ich nicht: Laut GH-Teorie endet auf der Erde nur cca 160W/m2, aber auf ein solarmodul 1 00W/m2?
„Die Messung der Leistungsfähigkeit von Solaranlagen erfolgt unter Standardbedingungen bzw. Testbedingungen (STC) denen folgende Parameter zugrunde liegen:
Eine Umgebungstemperatur für die Solarzellen von 25 Grad Celsius
Eine Sonneneinstrahlung bzw. Bestrahlungsstärke von 1000 Watt/m2
Ein Sonnenlichtspektrum gemäß AM* von 1,5“
Eine weise Beobachtung!
Erst bei der Berechnung der Energieausbeute kommt es zu der geringen Scheinleistung. Diese Scheinleistung, hat aber keine Relevanz um sie als Strahlstaerke verkleidet mit dem SB Gesetz in eine Temperatur umzuwandeln.
Vorschlag: Bei einem Durchschnitt …müsste die abstrahlende Fläche auch angepasst werden, schlage eine Kürzung um 1/4 vor… Temperatur…15 Grad!
Betrachten wir die Erde dort wo nur noch gestrahlt wird, so ist die Erde rund 7 Grad warm, auch ein Durchschnitt über
24h, in welcher Höhe bleibt unbekannt…geschuldet der zunehmenden Vermischung von Strahlung, Konvektion, und Wärmeleitung… selbst wenn die Strahlung pro Fläche integriert wird, ändert die Wolkenbedeckung, Konvektion usw, usw… die Aufgabe der Berechnung der Erdtemperatur ist komplex.
Auch ich vermisse die Masse, die hier über Energiespeicherung ausgleichend wirkt und die Zeit ohne Strahlung überbrückt…ein Schwarzkörper hat ja keine Masse, er muss keine haben, weil die Tempeatur immer gleich ist. Auf der Erde ist die Temperatur aber aufgrund der Masse (Wärmekapazität von Wasser) „gleich“ und nicht „ per se“ oder aufgrund kontinuierlicher Strahlung, die Masse ist durch die Zeitversetzung entscheidend, und kann nicht mehr vernachlässigt werden. SB ist zur Berechnung der Erdtemperatur hinfällig. Uli Weber hat erkannt, dass Energie (Strahlung) und Zeit nicht übereinstimmen und hat dies in diesem Artikel erkannt, wenn auch anders ausgedrückt.
„Wie kommt eigentlich die sogenannte „natürliche theoretische Globaltemperatur“ von -18°C auf „Mittelerde“ zustande?
Uli Weber
Exemplarisch wird oft wie folgt vorgegangen: Man viertelt einfach die die temperaturwirksame spezifische Strahlungsleistung der Sonne (Solarkonstante * (1-ALBEDO)/4) und setzt sie ohne Rücksicht auf Tag & Nacht und die geographische Breite in das Stefan-Boltzmann-Gesetz ein. Daraus ergibt sich dann ein „rechnerisches“ S-B-Temperaturäquivalent von -18°C.“
1. Die -18°C sind nicht die „Globaltemperatur“ auf „Mittelwerde“.
-18°C ist die effektive Abstrahlungstemperatur der Erde ins All, die aus im Mittel 5.000 m Höhe stammt.
2. Das kann man wie von Ihnen angemerkt über SB herleiten, oder aber auch per Satellit (Aqua, Terra der NASA/ CESES) messen.
3. Da hier theoretische Herleitung über das SB und Satellitenmessungen mit -18°C übereinstimmen, zeigt doch, dass Theorie und Praxis (Messungen) gut übereinstimmen.
4. Es liegt nun an Herrn Weber aufzuzeigen, dass Herleitung der effektiven Abstrahlungstemperatur über SB von -18°C und Messungen von Aqua und Terra Satelliten (CERES) mit -18°C Abstrahlungstemperatur beides falsch ist.
Darauf warte ich immer noch.
@ Michael Krüger
Es geht bei meinem hemisphärischen S-B-Ansatz gar nicht um eine „Abstrahlungstemperatur“, sondern um die EINSTRAHLUNGSTEMPERATUR auf der TAGSEITE der Erde. Nachfolgend eine Erklärung für den Unterschied zwischen Ein- und Abstrahlung in leichter Sprache:
Entscheidend bei einer solchen Betrachtung der Tagseite ist, was da genau ‘reingeht, und nicht, was insgesamt ‘rauskommt. Und nun tanzen Sie sich beispielsweise mal ein Pferd und betrachten Sie, was vorne ‘reingeht und hinten wieder ‘rauskommt. Verstehen Sie jetzt den Unterschied zwischen ‘rein und ‘raus?
Lösungshinweis: Sie stehen gedanklich HINTER dem Pferd…
(Solarkonstante * (1-ALBEDO)/4)
Der Ansatz ist falsch und hat sich nur aufgrund irrerführender Suggestion durchgesetzt. Statt (1-ALBEDO) muss dort nämlich (Absorptionsgrad / Emissionsgrad) stehen. Natürlich gilt (1-ALBEDO) = (Absorptionsgrad), womit also lediglich der Absorptionsgrad, nicht aber der Emissionsgrad berücksichtig wird.
Würde man direkt „Absorptionsgrad“ in die Formel schreiben, dann ergäbe sich die Frage nach dem Emissionsgrad von allein. Da man aber überflüssiger Weise und verkomplizierend (1-ALBEDO) nimmt, wird dieses Problem vermieden. Meines Wissens gibt es denn auch keinen Begriff der die Abweichung des Emissionsgrades von 1 analog zur „Albedo“ beschreiben würde.
Ironischer Weise gilt nun aber näherungsweise Absorptionsgrad = Emissionsgrad, was sich etwa am Beispiel Wasser sehr schön zeigen lässt. Die Brechungsindici von Wasser im Bereich des sichtbaren Lichts (N2 = 1.33) und LWIR (N2 = 1.27) liegen sehr nahe beieinander, sodaß die Differenz der beiden Grade unter einem Prozentpunkt liegt. Selbiges gilt darüber hinaus gleichsam für Landflächen.
Somit ergibt sich näherungsweise für (Absorptionsgrad / Emissionsgrad) = 1, also die Temperatur eines perfekten Schwarzkörpers mit 278K, und eben keineswegs 255K(!?).
Darüber hinaus gibt es natürlich noch den „Trick“ mit den Wolken. Deren Reflexion von Sonnenlicht ist bereits in der Gesamtalbedo von 0.3 enthalten, ihre emissionshindernde Wirkung auf LWIR wird jedoch „vergessen“ und nur seperat, wenn unbedingt notwendig und dann auch noch viel zu gering eingestanden. Das ist schon prinzipiell falsch, denn entweder modelliert man mit Wolken, oder ohne, aber nicht sowohl als auch.
Tatsächlich zeigen nun aber alle Wetteraufzeichnungen, dass Wolken und Temperaturen positiv korreliert sind, Wolken die Erde also aufheizen. Somit muss der Erde (ganz ohne Treibhausgase) dank Wolken noch deutlich wärmer als besagte 278K sein, die die Erdoberfläche bei einer völlig transparenten Atmosphäre erreichen würde. Und somit erkennen wir schließlich, dass der „Treibhausgasen“ zurechenbare „Treibhauseffekt“ sehr klein (~5K) sein muss.
Aber Herr Weber!
Schon wieder?
Die falsche Behauptung der Klimaunwissenschaft ist, das die Strahlungsleistung der Sonne nicht ausreicht die Erde auf ueber 15 Grad C zu erwaermen.
Davon unberuehrt ist die Tatsache, das wenn man die Energie aus dieser Strahlungsleistung auf die gesamte Erdoberflaeche verteilt und dann davon ausgehen moechte, das die Energie, die die Erde erhalten hat, ueber die gesamte Flaeche verteilt als ABSTRAHLUNG die -18 Grad C Temperaturrelevanz hat. Das kann man nicht negieren. Dafuer muss sich die Energie aber auf die gesamte Oberflaeche verteilen und dort auch bleiben. Das nennt sich Waermespeicherung. Ohne diese Speicherung sind -18 Grad C auch falsch. Wie man leicht errechnen kann.
Der wichtigste Waermespeicher auf der Erde sind die Ozeane.
Die Atmosphaere hat thermodynamisch keinen Waermenden Effekt. Sondern verringert den Waermestrom durch Strahlung. Gleichermassen fuehrt die geringe Waermeleitfaehigkeit der Luft zu einer Verringerung des Waermestromes. Im Gegensatz dazu gibt es Waermetransport durch Konvektion und Latente Waerme.
Die Atmsophaere passt sich mit ihrer Temperatur an die der Oberflaeche an. Wenn die Atmoephare rueckbezueglich einen Einfluss auf die Oberflaeche haben sollte, dann haben wir ein unbestimmtes System und man kann mit jedem Wertepaar hausieren gehen und die 15 Grad oder 14 Grad C oder jede andere Temperatur begruenden, wie man auch im Kiel-Trennberth Diagramm zeigen kann.
Wie sie oben ausfuehren ist die Angabe einer Solaren Mittelleistung von 240 W/m2 falsch. Die Sonne ist die einzige wichtige Waermequelle der Erde. Ihre Leistung muss mindestens so hoch sein, das sich eine Temperatur gleich oder groesser als 15 Grad ergeben kann. Die immerwaehrende Hemisphaerische Einstrahlung entspricht dieser Bedingung und ist ueber die Hemisphaere, die fuer die Einstrahlung relevante Flaeche, gemittelt 480 W/m2.
@Werner
Erklären Sie uns doch einfach mal, warum die Erde mit -18°C ins All abstrahlt, man exakt das auch über SB theoretisch herleitet und per Messungen mit Satelliten erhält, aber am Erdboden um die 15°C misst?
Und richtig ist, die Wärme kommt von der Sonne.
Wie kommt denn Ihrer Meinung nach diese Differenz von 33°C zu Stande?
„Erklären Sie uns doch einfach mal, warum die Erde mit -18°C ins All abstrahlt,…“
Das ist Blödsinn, das tut sie nicht
„…man exakt das auch über SB theoretisch herleitet“
Jo, mit falscher Theorie.
Lesen Sie G/T, Kramm et al, Kramm/Dughli, dann wird Ihnen geholfen.
Aber anscheinend lernt man in Bremen nicht mehr lesen.
Richtig: vor Jahren waren wir schon weiter. Die 15° sind ein Zustand (Wasser- und Lufttemperatur) und und mit dem SB-Ansatz wird auf die Flussgröße eines Schwarzstrahlers geschlossen. Vernachlässigt wird der ständige Wärmeinhalt sowie die Adiabatik und dass die 15° keine Strahlungstemperatur ist sondern kinetische Energie der Moleküle mit der Dimension Joule.
Aber das wurde hier schon gefühlte 1000x erklärt, es nützt nichts. Dass man das Flussdiagramm von Trenberth als Bilanz bezeichnet ist ein schlechter Scherz. Eine Bilanz ist eine Bestandsrechnung und diese fehlt.Dann würde man erkennen, dass die tägliche Ein/Ausstrahlung nur einen Bruchteil des gesamten Energiehaushaltes beträgt. Und wie viel Pech beim Denken muss man haben um die Lufttemperatur (eine Zustandsgröße in Joule) mit einer Strahlungstemperatur (Flussgröße in W/m2) zu vergleichen. Die Erde strahlt mit mit vielleicht 240 W/m2 oder was auch immer. Das ist ein grober Durchschnitt mit erheblichen örtlichen und zeitlichen Unterschieden. Um diesen Energiefluss auf eine Strahlungstemperatur umrechnen zu können muss man zuerst sicher stellen, dass sämtliche Frequenzen aber wirklich alle die gleiche Schwarzkörpertemperatur haben. Auch daran scheitert es.
Die Antwort kennen Sie doch, thermodynamischer Atmosphäreneffekt. Erklärung hier:
https://docplayer.org/27469048-Der-atmosphaeren-effekt.html
Nicht schon wieder ein Verweis auf Thieme. Jaja, Druck erzeugt aus dem Nichts Wärme.
Ach Herr Krüger, Probleme mit der allgemeinen Zustandsgleichung der Gase? Macht ja nichts, sie gilt trotzdem…
https://www.wetter.de/cms/wetterlexikon-foehn-2398243.html
„Jaja, Druck erzeugt aus dem Nichts Wärme.“
Ich verstehe nicht, warum Sie hier ständig mit Ihrem Unverständnis protzen müssen:
Eine Atmophäre im energetischen Gleichgewicht hat „oben“ langsame Moleküle mit hoher potentieller Energie und „unten“ schnelle Moleküle mit geringer potentieller Energie. E(kin) + E(pot) = const.
Und der Druck ist proportional zur Masse der Moleküle x deren Anzahl x deren Geschwindigkeit.
Druckerhöhung im Schwerefeld IST also gleich Temperaturerhöhung.
Besuchen Sie endlich eine vernünftige Schule, ziehen Sie nötigenfalls um.
PS
Oje. Der Treibhausschwindel von Thüne wird da auch noch als Quelle aufgeführt.
Herr Krueger,
Ich weiss, das an jedem Tag die Erde an sehr vielen Stellen, wenn nicht sogar an den meisten, bei mehr als -18 Grad C in den Weltraum abstrahlt.
Bitte begruenden sie doch bitte wie sie auf die Idee kommen, das die Erde mit -18 Grad C in den Weltraum abstrahlt.
Ich denke sie verwechseln Energie pro Flaeche und Zeit mit einer Temperatur.
Karl Kowatschek bringt es fuer sie auf einen Punkt!
Das klingt ja so, als wenn die „Klimarealisten“ bei der Berechnung der Strahlungstemperatur davon ausgehen, daß die Erde eine Scheibe ist. die zugleich von der Sonne von oben und unten erwärmt wird.
Genau das ist das Problem.
Im Klimaglauben ist der Glauben and die Flache Erde eingebettet.
Die SB wurde zweckentfremdet, um eine Referenztemperatur von 15° zu bestimmen. Weil man gehofft hatte, dass die Welttemperatur diesen Betrag übersteigt. Das hat sie bisher aber noch nicht getan. — Es gibt keine Referenztemperatur. Es gibt nur einen ungefähren Temperaturbereich von etwa 12° als Minimum für Eiszeitalter und etwa 22° als Maximum für Warmklima. Das heißt, solange wir zwischen 12° und 22° liegen, ist alles paletti. Wobei auch Ausreißer normal sind. Derzeit haben wir 14,6°. Das ist mehr als 2° unterhalb der Mitte des natürlichen Temperaturbereichs. — Regt sich jemand über den Begriff „Welttemperatur“ auf? Zu Recht! Wir können erst dann eine ungefähre durchschnittliche Welttemperatur bestimmen, wenn wir 2 Systeme haben. Ein gleichmäßiges Raster zu Land und Wasser und einen Satelliten. Das gleichmäßige Raster fehlt. Wir können eine durchschnittliche Welttemperatur noch nicht bestimmen. Das heißt, wir haben noch nicht mit der Messung begonnen. — In eigener Sache: Gib meinen Namen bei YouTube ein. Ich beweise in 3 Minuten, dass es kein Klimaproblem gibt.
(In der vorangegangenen Version war ein falsches schliessendes Tag, so dass der ganze Text zum Link wird. Bitte diese Version hier veröffentlichen – ich hoffe sie ist korrekt)
Herr Weber formuliert im Artikel folgende Bitte:
Die Annahme wird im Artikel gemacht, in dem der Kommentar vorkommt. Dort findet man auch die Randbedingungen, die Herr Weber für seine Annahme setzt. Meine Anmerkung bewegte sich im Rahmen dieser Randbedingungen. Die erste Referenz ist am Beginn des Austausches, den Herr Weber hier selektiv zitiert. Im vorangegangenen wird auch klar, das die Leistung flächenbezogen gemeint war und lediglich das falsche Symbol verwendet wurde.
Man kann auch zurückschauen und in älteren Artikel diese Aussage von Herrn Weber finden, z.B. folgende: „Durchschnittliche Sonneneinstrahlung auf der Tagseite: 470 W/m² “ in „Noch einmal zum hemisphärischen Ansatz des Stefan-Boltzmann-Gesetz“. Ich füge gern hinzu, dass Herr Weber weiss, dass die tatsächliche Einstrahlung auf einen Punkt auf der Erde vom Winkel abhängig ist und er das auch anmerkt. Zur Veranschaulichung greift er aber gern auf Durchschnittswerte zurück, was IMHO auch nicht falsch ist für die Abschätzungen, die hier gemacht werden.
Ansonsten ist das wieder mal ein klassischer Artikel von Herrn Weber. Anstatt diese Anmerkung gleich in der Diskussion zu machen, pickt man sich ein anscheinend falsches Statement raus und konstruiert daraus ein sowas ähnliches wie ein Argument. Auf das viel wichtigere – das er mit dem „Stefan-Bolzmann-Umgebungsgesetz“ selbst einen von der Erklärung her dem Treibhauseffekt sehr ähnlichen Mechanismus eingeführt hat, um seinen Hemnisphärischen Ansatz zu retten – geht er lieber nicht ein.
War was?
Herr Mueller!
Einfache Frage.
Wenn sie eine Kugel ansehen, wieviel der Flaeche sehen sie?
Zusatzfrage: Wie gross ist die von der Sonne angestrahlte Flaeche!
Wenn sie Herr Mueller die Rueckseite einer Kugel sehen koennen, dann ist der Hemisphaerische Ansatz falsch. Ansonsten nicht!
Ist es nicht so das, wenn die Erde ein Schwarzkörper wäre, sie nichts von der Einstrahlung abstrahlen würde? Verfolgt man Wetterdaten, mit Angaben von Temperatur und Strahlungswerten,so lassen diese sich nie,nachgerechnet mit der S& B Formel, harmonisieren.Das müsste aber sein, wäre die Erde ein Schwarzkörper mit einem (logischen) Albedo- Multiplikationsfaktor Null.
Die Erde ist kein Schwarzkoerper.
Zusaetzlich gibt es keinen zusaetzlichen Waermeeintrag aus der Atmosphaere zur Erdoberflaeche.
Die diesbezuegliche falsche Darstellung der Klimaunwissenschaft ist absurd!
Was soll das?
Die Kugeloberfläche berechnet sich nach 4*PI()*r². Und das ist die vierfache Kreisfläche mit demselben Radius wie der Kugel.
Daß der Strahlungsauftrag von der Sonne von der Entfernung abhängig ist, ist zwar nicht irrelevant aber vernachlässigbar.
Und den Quatsch mit dem Glashauseffekt muß man sich ja nicht antun. Zwar verhindert die untere Inversion (wenn sie vorhanden ist) den Aufstieg von Thermikblasen bis zur Tropopause, ist aber bestimmt keine Glasdecke.
Ich frag mich manchmal was die Schüler nach meiner math.-nat.-Gymnasialzeit noch an Physik-Meteorologie gelernt haben. Wahrscheinlich gar nix mehr.
Daß der Strahlungsauftrag von der Sonne von der Entfernung abhängig ist, ist zwar nicht irrelevant aber vernachlässigbar.
Es gibt tatsächlich 2 TSI Werte, und zwar TSI 1 AU und TSI at Earth distance, W/m^2 – die sich arg unterscheiden.
zu finden hier
Ist spannend, die mal zu vergleichen 😀
@Uli Weber
Schauen Sie einfach bei Fritz Möller 1973 nach. Schon dort steht der richtige Ansatz mit SB für die Brechnung der effektiven Abstrahlungstemperatur der Erde. Diese wird auch von Satelliten gemessen wie Aqua und Terra der NASA mit CERES. Fritz Möller war ein Pionier der Satellitenforschung und Klimatologie mit seinem Kollegen Manabe.
https://www.youtube.com/watch?v=sBfGfombqTw
Herr Krueger,
haben sie ein ERklaerung, warum der THE auf dem Mars nur 4 Grad ausmacht, obwohl dort 99 % CO2 sind?
@Werner Schulz:
Entscheidend für Strahlungsabsorption ist nicht der prozentuale Anteil eines „Treibhausgases“ in einer Atmosphäre, sondern seine absolute Dichte. Die Atmosphäre des Mars ist viel dünner, ihr Druck auf dem Bodenniveau beträgt dort nur 0,63% des irdischen Luftdruckes (6,4 hPa). Somit ist der Partialdruck von CO2 nicht so hoch, wie sein relativer atmosphärischer Anteil von 96% (nicht 99% !) suggeriert.
Weiterhin ist der Wasserdampfanteil auf Grund der niedrigeren Temperatur (wegen größeren Abstands zur Sonne) viel niedriger, und der Aerosolgehalt (Staub) größer.
Ist das so schwer zu verstehen?
Danke Herr Schlicht.
Dieses entspricht auch meiner Sichtweise.
Demzufolge sind bei der Bestimmung des THE alle Gase in der Atmosphaere zu beruecksichtigen. Stickstoff und Sauerstoff (O2) sind die weitaus wichtigeren Treibhausgase. Diese sind ja nicht mal in der Lage Energie durch Strahlung abzugeben.
CO2 dagegen kuehlt die Atmosphaere.
„haben sie ein ERklaerung, warum der THE auf dem Mars nur 4 Grad ausmacht, obwohl dort 99 % CO2 sind?“
Es gibt keinen Treibhauseffekt,
weder auf der Erde, noch auf dem Mars oder der Venus.
Auch nicht im Treibhaus/ Glashaus?
Herr Krueger,
sie Trollen jetzt.
Es sei denn sie denken wirklich das der THE und ein Glashaus mit der gleiche Physik funktionieren.
@Werner
Herr Hoffmann hat in seinem letzten Film einen Auszug vom IPCC 1990 gezeigt. 4-Zehntel-Grad-Lüge. Da wird eine Tabelle mit Venus, Erde, Mars gezeigt. Für dem Mars sind dort -47°C Oberflächentemperatur angegeben und -57°C, als effektive Abstrahlungstemperatur des Mars ins All (ohne THE). Also 10°C THE.
Andere Quellen weisen da eine Differenz zwischen 5-10°C für den Mars aus. Auf dem Mars messen wir also in etwa 5-10°C THE.
Warum ist der dort so gering? Ganz einfach, weil auf dem Mars das wichtigste THG, nämlich der Wasserdampf fehlt. Dort hat man nur CO2 als THG. Zu sehen am Absorptionstrichter im Marsspektrum.
So oft Sie Ihre eigene Defintion des THG verbreiten, korrigiere ich Sie – nicht dass am Ende jemand Ihnen glaubt. Der THG definiert sich als Temperaturunterschied zwischen mittlerer Bodentemperatur und Strahlungsgleichgewichtstemperatur. Und dieser Unterschied ist auf dem Mars – wegen fehlendem Gasdruck, Null! Nur Ihre eigene Definition aus Abstrahlungshöhe erlaubt es Ihnen einen THG auf dem Mars zu erfinden. Das muss jedem klar sein der Ihre Beiträge liest….
Quelle dazu? Vermutlich keine?
Herr Krueger,
Oliver Schlicht hat die richtige Antwort schon gegeben.
zu: …temperatur der Erde. Diese wird auch von Satelliten gemessen…
Satelliten messen keine Temperaturen, schon garnicht die Abstrahlhöhe. Es ist zwecklos sowas immer wieder abzutippen, dadurch wird es nicht wahrer.
Was messen Sie denn mit IR-Fernthermometern?
Richten Sie die mal auf eine Wolke am Himmel. Was werden Sie da messen? Genau, die Temperatur der Wolke.
Dann richten Sie das IR-Fernthermometer auf den Boden und Sie werden die Temperatur des Erdbodens haben.
Aus der Temperaturdifferenz und dem Temperaturgradienten von 0,65°C pro 100 m erhalten Sie dann sogar die Höhe, in der sich die Wolke befindet.
Einfach mal austesten.
Hallo Herr Krüger
Wenn man die Wolken sehen kann (es also nicht regnet), dann liegt der vertikale Temperaturgradient eher bei 1K als bei durchschnittlichen 0,65K pro 100m.
MfG
Ketterer
„Wenn man die Wolken sehen kann (es also nicht regnet), dann liegt der vertikale Temperaturgradient eher bei 1K als bei durchschnittlichen 0,65K pro 100m.“
Ich habe in meinen Wetterballon-Zeitreihen für München nachgeschaut. Der Temperatur-Gradient zwischen 0,8 und 1,5 km betrug im Januar 2018 etwa 4 °C/km und im Juli 2018 etwa 7 °C/km. Im Sommer ist der Temperaturgradient stabiler als im Winter (Inversion).
Also gut. Messen Sie die thermische Anomalie des Yellowstone vom Satelliten aus.
Ich warte solange.
Rrrrrichtig! Das ist soviel wert wie eine Haus – Thermografie im Hochsommer, aber es eignet sich eben für die Alarmisten so herrlich zum Ausschlachten, zumal man glaubt, durch die mögliche Abtastung der gesamten Erdoberfläche, „globale Daten“ zu haben.
@Tengler
Ich habe doch gerade gezeigt, wie man Abstrahlhöhe und Abstrahltemperatur von Wolken mit einem einfachen IR-Fernthermometer bestimmen kann.
Geht genauso bei infrarotaktiven/ mikrowellenaktiven Gasen.
Warum sollte man mit Satelliten also keine Temperaturen messen können?
Schauen Sie mit dem IR-Fernthermometer vom Satelliten aus auf den Erdboden, so messen Sie die Bodentemperatur.
Schauen Sie mit dem IR-Fernthermometer vom Satelliten aus auf Wolken, so haben sie die Temperatur der Wolken in entsprechender Höhe.
Gehen Sie in den Spektralbereich, wo Gase stark absorbieren und emittieren, dann können Sie dort von einem Bereich mit niedriger Absorption/ Emission in einen mit starker Absorption/ Emission gehen und darüber die Temperatur in unterschiedlicher Höhe bestimmen.
Wissen Sie, ich komme aus der Thermometrie, bei uns waren auch mal „Leute“ (namhafter Hersteller von Infrarotfieberthermometern…), die Referenzen für ihre Produkte suchten. Daher, und aus Erfahrungen von befreundeten Medizinprodukteverkäufern, aus Gesprächen auf Messen mit Thermografie-Anbietern usw., weiß ich, was „geht“ und was nicht. Ich kenne die „Teile“ aus der früheren Glasindustrie und die Leute, die die Dinger früher „amtlich“ kalibriert haben. Die Bedienung ist zwar heute einfacher als früher (und damit sinkt auch leider die Bedienerqualifaktion), aber die erreichbaren Unsicherheiten stoßen auch heute an die gleichen Grenzen. Man kann ggf. sagen, dass es zwischen zwei Punkten unterschiedlich warm ist, aber absolut kennt man die Temperaturen nicht, auch wenn das Messgerät 3 Stellen nach dem Komma anzeigt. „Glauben“ Sie also gern weiter, denn für manche geht dass Messen irgendwann in Religion über …..
Ohne den Gradienten in der Atmosphaere zu kennen, wuessten sie nicht wo die Strahlung herkommt. Und die Temperatur der Strahlung kann ihnen nicht sagen aus welcher Hoehe diese kommt.
Sie koenne also nicht die Abstrahlhoehe mit einem Infrarotthermometer bestimmen. Sie machen sich da was vor!
Ein paar Gedankenexperimente zeigen schnell, wie das „Kartenhaus“ vom „Treibhauseffekt“ in sich zusammenfällt:
1) Nehmen wir einen Stahlwürfel (sehr dunkel, Absorptionsgrad rund 1.0), 1.0 m Kantenlänge, positioniert im Weltraum, (nicht sehr weit weg von der Erde),nur eine Seite zeigt dauernd senkrecht zur Sonne!
Die Solarkonstante strahlt immer nur eine Seite an!
Abgestrahlt wird aber über 6 Seiten!
Und nun?
Solarkonstante/6 = Würfeltemperatur?????
—————
2) Nehmen wir jetzt einmal an, die Erde wäre nicht eine Kugel, sondern hätte eine Eiform!
Angestrahlte Schattenfläche nicht mehr 1:4 gegenbüber der Oberläche , sondern ca 1:3.5 – !!!
Und jetzt, wie groß wird der „Treibhauseffekt“???
————-
Die These vom „Treibhauseffekt“ steht eigentlich auf 3 Beinen (alles dünne Strohhalme), bricht nur eines weg, ist die These gestorben!
Bei nur ganz oberflächlichen u. etwas logischesn Betrachtung, verschwinden auch die anderen beiden Stützen sehr schnell.
Kein „Treibhauseffekt“ – kein Thermostat namens CO2, mit dem der Mensch die Erdtemperatur regeln kann! – Was für ein mittelalterlicher Aberglaube!
Ich waere interessiert an einer Antwort.
So ein kleiner Wuerfel mit eine reellen Waermedurchgangszahl entwickelt wohl ein interessantes Temperatur profil. Schliesslich kann er ja nicht mehr abstrahlen als er erhaelt, hat aber eine Seite so ueberhitzt …
@W.Schulz
————
Im Prinzip kann sich das jeder, der etwas von Physik versteht, schnell herbeirechnen!
———————
Was will ICH zeigen?
———-
Die Anbeter der mittelalterlichen These vom sogenannten „Treibhauseffekt“ betrachten ja nur die Abstrahlung!!!
————-
Damit wird nach deren Rechnung sich folgende Temperatur (Durchschnitt) ergeben:
S (Solarkonstante) geteilt durch 6 = 228 W/m²
(der Würfel hat ja 6 Seiten)
T nach S*B Formel = -21 Grad C
===============================
(Siehe auch Erde ohne Atmosphäre)
————
Die bestrahlte Fläche ist für diese,in die Irre geleiteten Menschen völlig belanglos!
Dabei wird die bestrahlte Fläche , nach S+B Formel u. Absorptionsgrad 1.0 sicherlich gegen 121 Grad heiß (Siehe Mondoberfläche)
——————-
Und nun die entscheidende Frage?
—-
Wie heiß würde es wohl auf der bestrahlten Seite der Erde werden, wenn wir keine Atmosphäre hätten????
————-
Am Rechner sitzen, Unsinn rechnen, die Realität ablehnen, sich fiktive Planeten basteln, physikalische Gesetze neu erfinden, usw. usw. usw. – geschieht dann, wenn man den Aberglauben beweisen will!
——–
Dazu nur eine Nebenbemerkung:
Warum werden wohl die Raumanzüge der Astronauten für Temperaturen bis ca +121 Grad C ausgelegt?
———–
https://www.spiegel.de/wissenschaft/weltall/nasa-stellt-neuen-raumanzug-fuer-kommende-mondmissionen-vor-a-1291897.html
Werner Schulz schrieb am 7. Februar 2020 um 3:57:
Sie könnten eine obere Grenze abschätzen mit dem von Ihnen immer wieder abgelehnten Ansatz, dass der Würfel ein schwarzer Strahler ist und die Temperatur gleich verteilt ist. Die Temperatur, die sich mit normaler Wärmeleitung zu den anderen Flächen einstellt, wäre sicher da drunter.
Und dabei können Sie Herrn Ordowski auch gleich erklären, dass seine Verwunderung über Solarkonstante/6 -> Würfeltemperatur etwas eigenartig ist, da wie Sie so schön sagen: „Schliesslich kann er ja nicht mehr abstrahlen als er erhaelt, …“
Herr Mueller,
beantworten sie die Frage, welche Temperatur hat dieser Wuerfel?
Stimmen sie ueberein, das er auf der Sonnenbeschinenen Seite mehr als -21 Grad C hat?
Es gibt noch ein paar Bedingungen, die einen nicht unbedeutenden Einfluss auf die Loesung der Aufgabe haben.
Sie Herr Mueller reden naemlich schon wieder von einem Schwarzkoerper. Das hat Herr Ordowski ausdruecklich nicht gemacht.
Man muss also von Waermeleitung im Wuerfel ausgehen.
Daher ergibt sich ein Temperatur Profile auf den Wuerfelflaechen, das von 121 Grad C zur Hintergrundstrahlung tendiert. Die abgewandte Flaeche haette dann fast Weltraumtemperratur. Etwas was sie immer belaecheln, aber genau das ist die richtige Loesung fuer das Problem.
Suchen sie sich also von 121 bis -270 Grad C eine Temperatur aus.
Was sie jetzt realisiert haben sollten, ist, das die sonnenbeschiene Seite der Erde sich auf ueber 15 Grad C erwaermen kann. Und damit ist die Sonne allein in der Lage die Erde zu erwaermen.
Der Rest ist dann Mathematik. Physik ist, wenns die Sonne trotzdem schafft!