Einen Abgleich meines hemisphärischen S-B-Modells mit allen wesentlichen THE-Thesen hatte ich hier auf EIKE bereits als Trilogie (Darstellung, Diskussion, Ergebnis) vorgelegt. Allerdings soll dieser THE nach „neuesten Erkenntnissen“ jetzt nur noch (32°) betragen, und damit gibt es dann wiederum mehr Spielraum für den Klimaeinfluss des Menschen oberhalb von (14°C). Andererseits ist es völlig unmöglich zu beweisen, dass es irgendein Phantasieprodukt gar nicht gibt, eben weil dieses Etwas gar nicht existiert. Dazu ein Beispiel aus einer Reportage von RSH (Radio Schleswig-Holstein), gesendet am 23. Dezember 2011: Auf einem Weihnachtsmarkt wurden Besucher gefragt, ob sie denn beweisen könnten, dass es den Weihnachtsmann gar nicht gibt. Natürlich konnte keiner der Befragten einen schlüssigen Beweis erbringen. Nähern wir uns mit diesem Wissen jetzt einmal dieser sogenannten „atmosphärischen Gegenstrahlung“, die sich angeblich folgendermaßen herleitet:
1. Hochfrequente (HF) Sonneneinstrahlung (@PIR²) => Erwärmung von Materie auf der Tagseite der Erde (2PIR²)
=> 2.Erwärmte Materie strahlt über die gesamte Erdoberfläche (4PIR²) Infrarot(IR)-Strahlung ab
=> 3. Diese IR-Strahlung animiert sogenannte „Klimagase“ zu einer IR-„Gegenstrahlung“ (@4PIR²)
=> 4. Diese IR-„Gegenstrahlung“ soll wiederum vorgeblich die Erdoberfläche (@4PIR²) erwärmen beziehungsweise deren „Abkühlung verlangsamen“ =>
Jetzt wird’s schwierig, denn nun geht es gleichzeitig mit 1. (@2PIR²) und 2. (@4PIR²) weiter.
WIDERSPRUCH 1: Die Erde soll sich durch die Rückstrahlung ihrer eigenen Abstrahlung (= Gegenstrahlung) noch weiter erwärmen; eine solche „Selbstaufheizung“ widerspricht aber dem 2. HS der Thermodynamik. Denn wenn ein solcher Vorgang funktionieren würde, könnten Sie Ihren Kaminofen zum Glühen bringen, indem Sie ein paar Kästen Mineralwasser davorstellen…
Und jetzt schauen wir uns nachfolgend einmal beim Deutschen Wetterdienst (DWD) die vorgeblich gemessene atmosphärische Gegenstrahlung an:
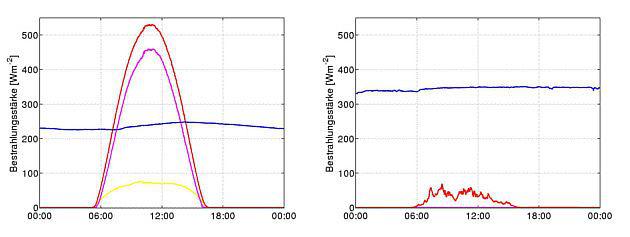
Abbildung 1: Originalbeschreibung, „Globale (rot), direkte (magenta) und diffuse (gelb) Sonnenstrahlung sowie langwellige Gegenstrahlung der Atmosphäre (blau) an einem wolkenlosen (links) und an einem bedeckten (rechts) Oktobertag in Lindenberg“ (Quelle: DWD Deutscher Wetterdienst)
Wir gehen jetzt einfach einmal davon aus, dass die beiden Beispiele einigermaßen vergleichbare Situationen darstellen. Daher halten wir an dieser Stelle fest:
- An einem wolkenlosen Oktobertag schwankt die vom DWD gemessene Gegenstrahlung zwischen 0:00 und 24:00 Uhr von ca. 220 bis 250 W/m².
- An einem bedeckten Oktobertag schwankt die vom DWD gemessene Gegenstrahlung zwischen 0:00 und 24:00 Uhr von ca. 330 bis 350 W/m².
- Es gibt nur bei wolkenlosem Himmel eine schwache optische Korrelation zwischen einem tentativen tageszeitlichen Temperaturverlauf und der sogenannten „Gegenstrahlung“, aber eine Differenz von etwa 100W/m² zugunsten einer Wolkenbedeckung.
- Die Unterschiede in der absoluten Bestrahlungsstärke der sogenannten „Gegenstrahlung“ liegen also weniger im Ablauf von Tag und Nacht, als vielmehr im Bedeckungsgrad.
WIDERSPRUCH 2: Hier treffen also eine über Nacht unverminderte „atmosphärische Gegenstrahlung“ und die Sonneneinstrahlung des neuen Tages unvermittelt aufeinander. Die sogenannte „atmosphärische Gegenstrahlung“ und die Sonneneinstrahlung des neuen Tages müssten daher zusammen eine Resonanzkatastrophe (=Selbstverbrennung der Erde) durch einen von Tag zu Tag ungebremst fortlaufenden Temperaturanstieg verursachen.
Schauen wir weiter, in Nr. 178 der „Berichte des Deutschen Wetterdienstes“ wird auf Seite 11, oben links, eine Formel zur Berechnung der Gegenstrahlung als Leistungsfluss „A“ in W/m^2 für die 1989 in der Station Hartheim am Rhein verwendete Messapparatur angegeben:
Die „gemessene“ Gegenstrahlung „A“ wird hier im Wesentlichen als Funktion der gemessenen langwelligen IR-Strahlung und der Instrumententemperatur dargestellt. Ohne die Kenntnis der ursprünglichen Messwerte „U“ und der beiden Eichkonstanten ist es schwer, eine direkt Aussage aus dieser Formel abzuleiten. Also müssen wir uns auf anderem Wege einem Verständnis nähern. Wie Abbildung 1 beweist, ist der gemessene langwellige (IR-) Anteil tagsüber wie auch nachts über 24h vorhanden, die direkte kurzwellige Sonneneinstrahlung ist dagegen nachts nicht wirksam. Wir überführen daher die Gleichung 1 in Gleichung 2 unter der Annahme, dass der Term für die Globalstrahlung bei der Messung der „Gegenstrahlung“ nachts keine Wirkung entfaltet, also:
Wenn wir nun auf die Abbildung 1 zurückgehen und den geringen Unterschied zwischen Tag und Nacht auf die Gegenstrahlung betrachten, dann ergibt sich für eine solche Messung das folgende Bild:
- Der Einfluss der direkten Sonneneinstrahlung auf die „Gegenstrahlung“ ist bei einem sehr geringen Temperaturgang am wolkenlosen Tag offenbar recht gut kompensiert worden und bei Nacht gar nicht vorhanden.
- Der Einfluss von langwelliger IR-Strahlung ist Tag und Nacht über die Thermospannung „U“ messbar.
- Der Term „SIGMA T4“, also der Einfluss der Instrumententemperatur, spiegelt sich dauerhaft Tag und Nacht im Messergebnis wider.
In der DWD-Abbildung 1 fehlt der Temperaturverlauf über die beiden dort dargestellten 24h-Tage. Da aber die Eigentemperatur „T“ des Messinstruments als ein wesentlicher Faktor in der Gleichung 1 erscheint, ergeben sich daraus erhebliche Unterschiede für die „gemessene“ Gegenstrahlung, je nachdem, ob es sich um ein beheiztes, gekühltes oder ein Instrument bei normal variabler Umgebungstemperatur handelt. In Tabelle 1 wurde der Messwert „U/el = A – T4“ für unterschiedliche Instrumententemperaturen „T“ aus der in Abbildung 1 dargestellten „gemessenen“ Gegenstrahlung „A“ hergeleitet:
Tabelle 1 gilt im Wesentlichen auch für Tagmessungen, soweit die jeweiligen DWD-Messergebnisse korrekt um den Einfluss der Globalstrahlung korrigiert wurden. Die Analyse aus dieser Tabelle ergibt nun eindeutig, dass es sich nicht um ein beheiztes Instrument handeln kann, weil dessen Messfähigkeit zu höheren Temperaturen stark eingeschränkt wäre; denn dieses Gerät kann nur eine Einstrahlung messen, deren S-B-Temperaturäquivalent höher als die eigene Temperatur ist. Selbst ein gekühltes Instrument würde nur eingeschränkt funktionieren und müsste zur Messung einer „Gegenstrahlung“ von 220W/m² unter -23,5°C gekühlt werden. Es wäre zu erwarten gewesen, dass insbesondere der wesentliche Term „U/el“, also die Geräte-Ausgangsspannung mit dem Ergebnis des langwelligen (IR-)Strahlungsanteils, einen primären und eindeutig definierten Beitrag zum Messergebnis liefern würde. Das ist offensichtlich nicht der Fall, denn das Ergebnis der Analyse aus Tabelle 1 legt nahe, dass das Messergebnis für die sogenannte „atmosphärische Gegenstrahlung“ in allen hier aufgezeigten Temperaturbereichen von der Instrumententemperatur (T=-18°C bis +15°C) majorisiert wird. So, und jetzt stellen Sie Sich als „Messinstrument“ einfach mal die Ordowski’sche Glasplatte vor, wo eine ca. 1 m über dem Boden angebrachte Glasplatte über den Tagesverlauf immer die gleiche Temperatur wie die umgebende Luft aufweist und sich nur dann noch weiter erhitzt, wenn sie nahe an den Erdboden abgesenkt wird…
WIDERSPRUCH 3: Wir stehen hier vor dem physikalischen Paradoxon, dass eine Messapparatur, die darauf ausgelegt ist, etwas WÄRMERES zu messen als ihre Eigentemperatur, tatsächlich auch etwas KÄLTERES gemessen haben will. Die Tabelle 1 beweist aber eindeutig, dass dieses Messinstrument nicht in der Lage ist, eine niedrigere Temperatur zu messen als die Instrumententemperatur „T“ selbst, denn solche Werte wären negativ.
Wie kommen wir nun aus dieser Nummer wieder heraus?
Schauen wir also einmal weiter. In Nr. 178 der „Berichte des Deutschen Wetterdienstes“ ist auf Seite 40 eine Isoplethendarstellung der über alle Wetterlagen gemittelten Bestrahlungsstärke der Gegenstrahlung abgebildet. Diese Darstellung bildet die Tageskurven der Gegenstrahlung im Verlauf des Jahres (hier in 10-Tages-Schritten) ab.
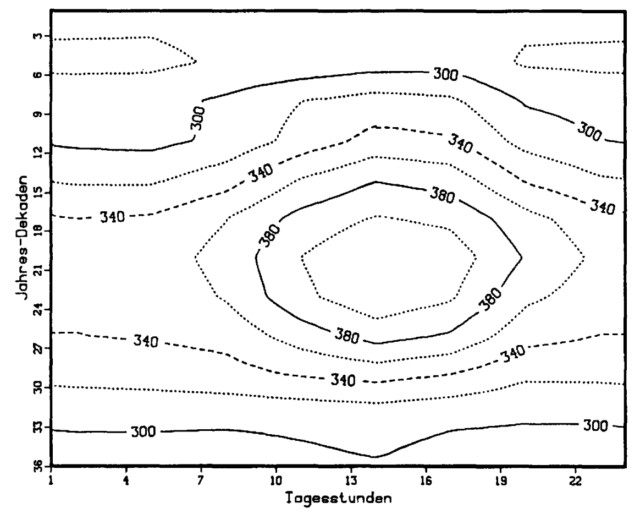
Abbildung 2: Isoplethendarstellung der über alle Wetterlagen gemittelten Gegenstrahlung (Quelle: DWD)
Dazu heißt es dort auf Seite 37 letzter Absatz rechts, Zitat: „Obgleich die Anwesenheit von Wolken verstärkend auf die Gegenstrahlung wirkt, kann daraus nicht geschlossen werden, dass bei bewölktem Wetter generell höhere Gegenstrahlungswerte auftreten. Ganz im Gegenteil liegen die absoluten (mittleren) Maxima mit 437 W /m2 Mitte Juli um 14 Uhr im Schönwettertyp und nahezu gleich beim Windtyp. Je stärker die Bewölkung eines Wettertyps wird, desto geringer wird tendenziell dieses Maximum. Lediglich bei Nebel wird diese Regel zugunsten etwas höherer Strahlung gebrochen. Zeitlich ist die Lage des jeweiligen Maximums bei allen Wetterlagen konstant am oben genannten Zeitpunkt, mit Ausnahme des Stratusschichttyps, wo der höchste Wert erst im August um 17 Uhr erreicht wird.“
Halten wir an dieser Stelle fest:
- Die über alle Wetterlagen gemittelte Bestrahlungsstärke der Gegenstrahlung an der Messstelle Hartheim liegt zwischen MIN= 280W/m² (nachts im Februar) und MAX=400W/m² (nachmittags in den Sommermonaten).
- Die absoluten (mittleren) Maxima der Gegenstrahlung liegen mit 437 W/m2 Mitte Juli um 14 Uhr im Schönwettertyp und entsprechen einem S-B-Temperatur-Äquivalent von 23,2°C.
Die Messstelle Hartheim besteht heute als forstmeteorologische Meßstelle Hartheim der Albert-Ludwigs-Universität Freiburg fort. Auf der Internetseite meteo.uni-freiburg.de wird das Jahresmittel der Lufttemperatur (1978 -2018) für diese Messstelle mit 10,6°C angegeben:
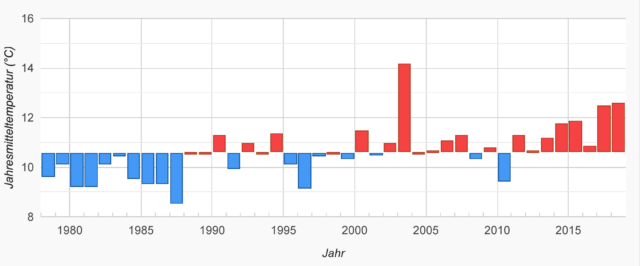
Abbildung 3: Bildunterschrift „Die Entwicklung der Jahresmitteltemperatur an der forstmeteorologischen Messstelle Hartheim von 1978 bis 2018 relativ zum 41-jährigen Mittel 1978 – 2018. Rote Jahre waren überdurchschnittlich warm, blaue Jahre kühl.“ (Quelle: Forstmeteorologische Messstelle Hartheim – meteo.uni-freiburg.de)
An dieser Stelle halten wir also fest:
- Die Jahresmitteltemperatur an der Meßstelle Hartheim von 10,6°C entspricht einem S-B-Strahlungsäquivalent von 368W/m².
ANALYSE: Da hier nur gemittelte Werte zur Verfügung stehen, kann die nachfolgende Analyse nur eine grobe Annäherung an die tatsächlichen Gegebenheiten darstellen. Das S-B-Strahlungsäquivalent von 368W/m² für die Jahresmitteltemperatur von 10,6°C an der Meßstelle Hartheim entspricht der Bestrahlungsstärke der Gegenstrahlung im Sommerhalbjahr am Vormittag und am Abend, also im Anstieg und Abfall des Nachmittagsmaximums in Abbildung 2. Gleichzeitig liegt dieses S-B-Strahlungsäquivalent von 368W/m² ziemlich nahe an dem Mittelwert von 340W/m² zwischen MIN=280W/m² und MAX=400W/m² über den Jahresverlauf der Bestrahlungsstärke der Gegenstrahlung. Damit aber spielt die „gemessene“ Gegenstrahlung vom Betrag her in derselben Liga wie die Sonneneinstrahlung, allerdings anders als diese über den gesamten 24h-Tag. Die übertragene Wärmemenge wäre damit im groben Tagesdurchschnitt pro 24h:
Gegenstrahlung: 340W/m² * 24h = 29.376.000 Joule/m²
Sonneneinstrahlung: 368W/m² * 12h* = 15.897.600 Joule/m²
*) Tentativer Durchschnittswert über das Jahr
WIDERSPRUCH 4: Wir stellen also in grober Näherung fest, dass die Wärmezufuhr durch die sogenannte Gegenstrahlung an der Meßstelle Hartheim den Einfluss der Sonne um nahezu das Doppelte übertreffen soll. Dieses Ergebnis ist insofern eigenartig, als ja nach der vorherrschenden Klimatheorie die sogenannte Gegenstrahlung selbst erst durch die Wärmewirkung der Sonneneinstrahlung erzeugt werden soll.
- Wir halten an dieser Stelle weiterhin fest, dass die wichtigsten Treibhausgase in der Reihenfolge ihrer Wirksamkeit der Wasserdampf, Kohlendioxid, Ozon, Methan und Distickstoffoxid sind.
Daraus folgt mein finaler Lösungsansatz für das Phänomen „atmosphärische Gegenstrahlung“:
Die sogenannten „Treibhausgase“ sind Gase, und auch noch durchsichtig, ihre Moleküle bewegen sich in großem Abstand voneinander und füllen den verfügbaren Raum gleichmäßig aus. Deren Klimawirkung soll auf der Aufnahme der terrestrischen IR-Abstrahlung beruhen, mit der wiederum die atmosphärische Gegenstrahlung befeuert werden soll. Der wesentliche Unterschied in der Gegenstrahlung an beiden Tagen der DWD-Abbildung 1 liegt aber zwischen einem wolkenlosen und einem bedeckten Himmel, also zwischen dem gasförmigen und dem flüssigen Aggregatzustand von Wasser. Und im flüssigen Aggregatzustand hat Wasser gegenüber gesättigtem Wasserdampf eine doppelt so hohe Wärmekapazität, also eine erhöhte Speicherfähigkeit für Wärme; gegenüber trockener Luft erhöht sich dieses Verhältnis sogar auf einen Faktor von etwa vier. Abbildung 1 beweist also, dass die sogenannten Treibhausgase bei der Bestrahlungsstärke der atmosphärischen „Gegenstrahlung“ bestenfalls eine untergeordnete Rolle spielen. Denn die Zusammensetzung der gut durchmischten gasförmigen Bestandteile der umliegenden Atmosphäre an der Meßstelle Hartheim dürfte sich zwischen den beiden DWD-Tagesgängen „wolkenlos“ und „bedeckt“ bis auf Menge und Aggregatzustand des Wassers nicht wesentlich verändert haben.
WIDERSPRUCH 5: Wenn dort beim DWD also überhaupt etwas gemessen worden sein sollte, dann war es wohl nicht die „atmosphärische Gegenstrahlung“ von IR-aktiven „Klimagasen“, sondern eher der Wärmeinhalt einer Zusammenballung von Wassertröpfchen, die man gemeinhin als „Wolken“ zu bezeichnen pflegt und die der Meßstelle Hartheim durch Advektion und Kondensation offenbar zusätzliche Wärme zugeführt hatten.
Im Ergebnis hat es den Anschein, als dass die an der Meßstelle Hartheim gemessene „Bestrahlungsstärke der Gegenstrahlung“ den jahreszeitlichen Beitrag von Advektion und Kondensation auf die Ortstemperatur spiegeln würde. Im Umkehrschluss dürften also die dort dargestellten Werte sehr viel eher die Temperatur von Messgerät und unmittelbarer Umgebung wiedergeben als einen unabhängigen Wert für die sogenannte Gegenstrahlung.
Wolken treten in meinem hemisphärischen S-B-Modell unter den Stichworten „Advektion“ als „fliegende Wärmflaschen“ auf, aber auch die „Kondensation“ erzeugt Wärme vor Ort, was ein befreundeter Segelflieger folgendermaßen beschrieben hatte, Zitat:
„… nachts ist die Luft oft sehr ruhig. Dadurch ist lokale Wolkenbildung möglich, an den Grenzschichten unterschiedlicher Luftzusammensetzung, die sich nur ungern vermischen. Die Dicke bzw. Dichte dieser Wolken nimmt in der Regel gegen Morgen hin zu, sodass die Masse an ‚Materie‘ zunehmend ist. Dass dem so ist beweisen manchmal auftretende lokale morgendliche Regenfälle, wenn diese Ruhewolken das ‚Wasser nicht mehr halten‘ können. Sobald durch Sonneneinstrahlung etwas Bewegung in die Atmosphäre kommt verschwinden diese Wolken genauso lokal wie sie entstanden sind und man hat die Chance auf einen herrlichen Tag…“
ERGO: Wir haben heute keine Angst mehr, von der „Erdscheibe“ herunterzufallen. Wir glauben heute nicht mehr, die Erde stünde im Mittelpunkt des Universums. Aber wir glauben, die spezifische Strahlungsleistung einer „atmosphärischen Gegenstrahlung“ zu messen und damit ein unzureichendes 2-dimensionales Klimamodell für unsere Erde zu bestätigen. Man könnte also sagen, dass die sogenannte „atmosphärische Gegenstrahlung“ die Rache der Mathematik für eine fehlerhafte physikalische Faktor4-Stefan-Boltzmann-Inversion ist, BEWEIS:
ERGEBNIS: Es gibt im streng „gleichzeitigen“ Stefan-Boltzmann-Gesetz keine Flächen (B), die nicht zur Strahlungsleistung (P) des Schwarzkörpers beitragen. Daher sind auch keine unbeleuchteten Flächen (B) in einer „gleichzeitigen“ S-B-Inversion erlaubt. Physikalisch „gleichzeitig“ bedeutet übrigens auch nicht, dass unterschiedliche „Gleichzeitigkeiten“ in einer einzigen S-B-Berechnung aufaddiert und gemittelt werden dürften. Damit ist eine globale Faktor4-Tag=Nacht-THE-Flacherde-Inversion der Solarkonstanten physikalisch nicht statthaft.
Versuchen Sie einfach mal den Gegenbeweis: Wenn Sie die Oberfläche eines Fußballs vollständig* mit einer Taschenlampe beleuchten können, dann wäre der Faktor4-Ansatz bewiesen.
*) Hinweis für die Sophisten unter den geschätzten Kommentatoren: Dieses Beispiel unterstellt Gleichzeitigkeit mit einer einzigen Taschenlampe ohne weitere Hilfsmittel, wie Sie das beispielsweise mit der Sonne als „Taschenlampe“ im Wechsel von Tag und Nacht auf der Erde beobachten können; aber vielleicht versuchen Sie’s einfach mal mit einer Rotationsgeschwindigkeit größer 300.000 km/s…






















Lieber Herr Limburg,ich glaube es ist an der Zeit, den Blog zu sperren! Sinnvoller Gedankenaustausch findet nicht mehr statt!
@ All Danke an alle für die offene Diskussion.Es war zuweilen etwas zäh aufgrund der unterschiedlichen Fachkenntnisse der Teilnehmer, alle in ein Boot zu bekommen. Der ein oder andere hatte auch große Probleme, eigene Fehler zu erkennen und sich eines Besseren belehren zu müssen, aber auch die sitzen jetzt mit im Boot und schweigen nun zufrieden über das zusammen erzielte Ergebnis.Die Frage entzündete sich an bloßen Begriffen. Aber dank der Analyse wurden diesen Begriffen physikalischer Inhalt verliehen, so dass nun jeder das gleiche darunter versteht.Folgende Aufgabe wurde nun einvernehmlich gelöst: Es gibt einen Körper, der bei Zufuhr von Energie mit Erwärmung reagiert. Dem Körper wird eine konstante Heizleistung zugeführt. Der Fluß der Abwärme an die stets kältere Umgebung sei ebenfalls konstant. Nun wird der Körper mit einer Isolierung umhüllt.Die Frage war: verursacht die Isolierung eine Erwärmung?Über folgende Aussagen wurden in diesem blog nun Konsens erzielt:1. Die Temperatur des Körpers nimmt nach der Isolierung zu2. Die Isolierung ist die Ursache dieser Erwärmung.
Sind Sie hier der Oberlehrer oder der Schöpfer persönlich?
Immer das Gleiche, je mehr Wissen fehlt, um so mehr wird es durch Arroganz ersetzt.
Unsinn zu schreiben ist nicht verboten, aber niemand hat das Recht, in Namen aller Unsinn als Konsenz festzustellen.
Mir fällt da spontan das Büchlein von Ralf Neitzel ein („Von der Sucht, andere zu bevormunden“), dass passt haargenau auf die rudimentären Physikkenntnisse von T.G.
Aber, Herr Georgiev, wir sind ja beide wohl schon etwas älter und haben da früher wohl eine andere Physik kennengelernt. Heute regiert die Pippi-Langsrumpf – Methode ……
Das genaue Gegenteil ist der Fall, außer bei Glauber und Kosch.
Herr Glauber,
die Temperaturen werden lokal bestimmt, deshalb gibt es die Tropen, die Wuesten, die Regenwaelder, die gemaessigten Zonen und die Kaltwuesten usw.
Die Sonnen ist in keiner Lokation bestaendig.
Wenn sie die konstante Heizleisztung postulieren, dann sind sie uns eine Erklaerung schuldig, wo diese herkommt.
Das Model das sie einem Konsens unterwerfen wollen hat ein Loch.
Stopfen sie es!
Damit koennen sie sich noch mal dem Hauptbeitrag zuwenden. Die Grundlage ist der Unterschied zwischen Leistung und Energie. Kennen sie den?
@ Thomas Glauber :
Sie schrieben : „Die Temperatur des Körpers nimmt nach der Isolierung zu2. Die Isolierung ist die Ursache dieser Erwärmung. “ Das kann aber muss nicht der Fall sein. Tatsache ist nur, dass durch die Isolierung ein Wärmeverlust verlangsamt wird. Ob durch die Isolierung eine Erwärmung auftritt oder nur eine verlangsamte Abkühlung stattfindet, hängt davon ab, wie wieviel Wärme dem Körper in welcher Zeit zugeführt wird und wie gut die Isolierung ist. Ist dies wirklich so schwer zu verstehen ??
Sehr geehrter Dr. Denzer,
Sie müssen schon alles lesen. Der Körper ist stets wärmer als die Umgebung und die Heizleistung gleicht ohne Isolierung die Wärmeabgabe in die Umgebung aus.
PS an alle, sorry, daß die Zeilenumbrüche nicht mitgenommen wurden, mein Original ist korrekt.
„Die Isolierung ist die Ursache dieser Erwärmung.“
Quatsch!
Eine Atmosphäre isoliert nicht!
Die Bodentemperatur wird über die Strahlungsstärke der Sonne und die Bewölkung moduliert
Für einen Physiker genügt es, festzuhalten, daß Wärme=Energie eine extensive Größe ist und Temperatur eine intensive.
Sehr geehrter Herr Tengler,5. MÄRZ 2021 UM 17:46schön, daß Sie ihre Darstellung zum Thema liefern und sich nicht im Heimhandwerk veräußern.
Von Regelung reden wir hier aber nicht, die ist hier irrelevant, denn die Sonne regelt sich ja auch nicht nach dem irdischen Treibhausgasmengen. Um also nicht auf nicht analog übertragbare Fälle abzuschweifen, ist eben konstante Heizleistung vorgegeben, Frau Kosch musste bei ihrer Analogie auch schon darauf hinweisen. Und um noch weiter für Klarheit zu sorgen, schränke ich weiter ein, daß in beiden Fällen in die äußere Umgebung gleiche Leistungen abgegeben werden.Beachten Sie dies, dann erscheint es Ihnen auch nicht durcheinander.Da die einzige Änderung der Wechsel von keine Isolation zu Isolation ist und die Heizleistung aus der Quelle konstant bleibt, ist die Isolation also die Ursache der Erwärmung.
Richtig, die Gleichgewichtstemperatur hängt von der Isolierung ab. Stimmen Sie also auch zu, daß diese mit zunehmender Isolierung zunimmt?
Auch der Fall eines Körpers (Schicht an der Erdoberfläche) ohne Heizquelle (Sonne) wird hier nicht betrachtet.
Sie sollten erst einmal die physikalischen und technischen üblichen Begrifflichkeiten verinnerlichen, ehe Sie hier Unsinn verbreiten.
Isolation ist niemals Ursache von Erwärmung! Erwärmung ist an Energiezufuhr gebunden, wurde hier im Faden schon mehrfach erwähnt.
In unseren Fällen ist „Leistungsabgabe“ an Temperaturunterschiede gebunden. Isolation kann den Energiefluß beeinflussen, aber niemals eine Erwärmung verursachen. Sie machen wahrscheinlich den Fehler, innere Gradienten in einem Körper hin zu seinen Begrenzungsflächen, die bei Isolation geringer werden können, als Erwärmung im physikalischen Sinne umzudeuten. Da ist aber die höchstens erreichbare Temperatur auf die Kerntemperatur begrenzt.
Herr Tengler, lesen Sie meinen Text GENAU, ihre Antworten gehen von unzutreffenden Vorausetzungen aus.
Sehr geehrter Herr Tengler,
So weit sind wir ja nicht auseinander, zumal Sie ja schon die Abhängigkeit der Gleichgewichtstemperatur von der Isolation erkannt haben.
Ihr Fehler ist nur, daß Sie die Ursache der Erwärmung (korrekt: die Isolation) mit der Quelle für die dazu nötige Energie (korrekt: konstante Heizleistung) gleichsetzen. Machen Sie sich den Unterschied klar: wenn Sie ertrinken ist die Ursache auch nicht das Wasser, sondern daß Sie nicht schwimmen können.
Das ist gar nicht der Punkt hier, da es gegeben ist.
Herr Glauber, ordnen Sie erst einmal Ihr fachliches Kauderwelsch ….., comprende?
wenn Sie ertrinken ist die Ursache auch nicht das Wasser, sondern daß Sie nicht schwimmen können
„Von Regelung reden wir hier aber nicht, die ist hier irrelevant, denn die Sonne regelt sich ja auch nicht nach dem irdischen Treibhausgasmengen. Um also nicht auf nicht analog übertragbare Fälle abzuschweifen, ist eben konstante Heizleistung vorgegeben.“
Sie machen sich die Dinge zu einfach. Wir leben auf der Nordhalbkugel und haben momentan noch Winter. Die Arktis hat sich in den vergangenen Jahren erwärmt- hauptsächlich im Winter. Was ist Ihrer Meinung nach die Ursache?
(a) Die bessere „Isolation“ durch Treibhausgase
(b) die schlechtere Isolation durch dünneres Meereis
(c) erhöhter Wärmetransport des Golfstroms
(d) erhöhte meridionaler Wärmetreansport
(e) erhöhte Absorption der solaren Einstrahlung.
(f) Es gibt keine konstante Heizleistung weder im Taeglichen noch ueber die Jahreszeiten, ergo kann auch eine Aenderung der Differenz Heizung – Abkuehlung der Grund sein.
Sehr geehrter Herr Berberich,
Warum fragen Sie mich diese Frage? Und wie sollte dies zur Klärung der konkreten Diskussion um „Erwärmung durch Isolierung“ beitragen?
Ich habe zu Ihrer Frage eine Antwort. Die ist keine Meinung, sondern eine wissenschaftlich korrekte aber wahrscheinlich für Sie unbefriedigende Antwort. Nur lassen Sie uns erstmal die „Isolationsfrage“ klären.
„Ich habe zu Ihrer Frage eine Antwort. Die ist keine Meinung, sondern eine wissenschaftlich korrekte aber wahrscheinlich für Sie unbefriedigende Antwort.“
Das ist keine Antwort auf meine Frage.
Sehr geehrter Herr Berberich,
ich bin Ihnen auch keiner verpflichtet, aber nachdem nun unter allen Beteiligten Konsens besteht, dass der beim oben spezifizierten Gedankenexperiment die Isolierung die Erwärmung verursacht, zu Ihrer Frage vom 6. MÄRZ 2021 UM 10:45, was die Ursache für die Erwärmung der Arktis in vergangenen Jahren war.
Sie haben eine Auswahl an Ursachen aufgelistet:
(a) Die bessere „Isolation“ durch Treibhausgase
(b) die schlechtere Isolation durch dünneres Meereis
(c) erhöhter Wärmetransport des Golfstroms
(d) erhöhte meridionaler Wärmetreansport
(e) erhöhte Absorption der solaren Einstrahlung
Alle haben gemein, daß es bekannte physikalische Prozesse gibt, die zwischen den aufgelisteten Effekten und der Erwärmung einen ursächlichen Zusammenhang schaffen. Die Physik liefert hier keine schwarz-weiß Antwort, was ohnehin selten ist, sondern im Bestfall in einer definierten Metrik quantitative Anteile. Wie nun die Anteile der 5 Prozesse sowie weitere denkbare Prozesse verteilt sind, kann nur eine Berechnung durch Klimamodelle liefern, alles andere wäre sinnlose Spekulation. Es ist jedoch intuitiv nachvollziehbar, daß diese Ursachenverteilung von der angewandten Metrik und dem Zeitraum abhängt.
Herr Glauber,
sie sind dicht dran die Klimaunwissenschaften zu widerlegen.
Falls sie an einer Aufklaerung interessiert sind, erklaeren sie wo die konstante Heizleistung herkommt.
mfg Werner
Herr Glauber,
sie koennten diese Frage doch beantworten, warum machen sie es nicht?
Diese Frage traegt zum Verstaendnis bei, und wenn es nur das Verstaendnis ist, was sie verstehen.
Natuerlich kann ihnen keiner vorgeben, was sie zu antworten haben, aber sie tummeln sich mit verschiedensten Beitraegen hier rum.
Herr Berberich ist eine analytische Person. Er macht sich ernsthafte Gedanken, und wenn er diese Frage stellt, dann eigentlich nur, um Licht ins Dunkle zu lassen.
Ich finde er hat eine Antwort verdient.
Im Uebrigen haben sie Klima und Wetter in die Diskussion gebracht, obwohl es um den Treibhauseffekt geht.
Ihre Antwort waere interessant!
Herr Glauber,
Vorgeben kann man alles. Ob es mit der Wirklichkeit uebereinstimmt, ist die Frage.
Die Solare Einstrahlung mag ja global konstant sein, aber fuer die lokalen Gegebenheiten sollten sie schon erklaeren wo die konstante Heisung verborgen ist. Die Sonne ist es jedenfalls nicht.
Heizung nicht Heisung.
Soviel Zeit muss sein!
@W. WSchulz.Bei den ganzen Betrachtungen geht vollkommen unter, dass die Erde ein sich zyklisch abkühlender und wieder erwärmender Körper ist(Nur Sonne)!!!! (Tag -Nacht; Sommer- Winter). Welche Energien sind zum Beispiel jetzt notwendig, um die Nordhalbkugel aus den Wintertemperaturen in die Sommertemperaturen zu bringen???Wie wir alle wissen, oder fast alle, ist hier die spezifische Wärme der Körper von absoluter Wichtigkeit!!!Gäbe es den „atmosphärischen“ Treibhauseffekt“ , in den berechneten Größenordnungen, gäbe es wohl keinen Winter bei uns oder aber meine Glasscheibe würde sich entsprechend erwärmen!!! Nichts davon, und das bischen Energie, dass die Erde im 15 Mikrometerwellenbereich abstrahlt (ca 36 W/m²), bei ca 15 Grad C verschwindet in der Atmosphäre ohne meßbare Spuren zu hinterlassen!!!
Herr Ordowski, die Wahrheit ist leider etwas komplizierter.
Der Winter ist im Vergleich zu den falschen Klimamodellen immer noch ziemlich warm.
Das erste Problem in den Klimaunwissenschaften liegt daran, das man der Sonne eine temperaturgebende Wirkung zusagt. Dem ist aber nicht so.
Wenn die Sonne im Winter auf eine Z Grad kalte Landschaft faellt, dann erwaermt sie diese um X Grad (Z +X=Y). Aber niemals von 0K auf Y Grad.
Die Rueckstrahlung ob vorhanden oder nicht erwaermt nichts.
Das naechste Problem der Klimaunwissenschaften ist, das ein Gas das nicht strahl trotzdem noch eine Temperatur hat. Temperatur hat nichts mit Strahlvermoegen zu tun. Strahlvermoegen aber mit Temperatur.
Demzufolge ignoriert die Klimaunwissenschaft 99% der Gase in der Atmosphaere. Und wie man an ihrem Glasscheibenbeispiel sieht, wendet sie die thermodynamischen Gesetze falsch an.
„Gegenstrahlung“ ist ein wissenschaftliches Unwort der Klimaunwissenschaften.
Die einzige Anwendung die ich fuer diese Unwissenschaft habe ist homeopatisch:
„Das Kalte Bier strahlt mich an und mir wird warm ums Herz.“
Gruss Werner
„Die Solare Einstrahlung mag ja global konstant sein,…“
TOA…
Am Boden nicht!
Nicht mal da!
@ All: Ich bedanke mich für die meisten Kommentare zu diesem Beitrag und die Geduld des EIKE-Admin für eine Diskussion, bei der mal wieder alles dabei war, vom unverrückbaren Kinderglauben über den Dietze-Krüger-Effekt gebetsmühlenartiger Wiederholungen bis hin zu sehr schnell berechneten Messwerten. Und wenn man die Ein- und Ausgänge auf dem Konto von Mutter Erde betrachtet, dann könnte man vielleicht auch noch die Ozeane als ihren „Geldspeicher“ einbeziehen. Herzliche Grüße – Uli Weber
Es wäre ja schon viel gewonnen, wenn den Leuten endlich klar werden würde daß die Atmosphäre nicht „isoliert“, sondern mittels Bodendruck die Bodentemperatur mit beeinflußt.
„Isolieren“ tun nur Wolken/Nebel, leider isolieren sie auch die Einstrahlung der Sonne, helfen also nur nachts.
Herr Weber, Sie haben meinen Kommentar zu den zwei nötigen Sonnen für Ihr Hemisphärenmodell bei +15 Grad globalem Mittelwert ohne Gegenstrahlung immer noch nicht beantwortet.
Wenn Sie sicher sind dass sich Prof. Gerlich mit (+15 -273)/2 = -129 (also NICHT +15) Grad für das solare Modell mit S-B um den Faktor 2 verrechnet hat, beweisen Sie das bitte. Und wenn – wie es (abgesehen von mir) auch Prof. Kramm bestätigt hat – tatsächlich zwei Sonnen erforderlich sind, so verfassen Sie bitte einen EIKE-Beitrag mit dem Titel „Korrigendum zum Hemisphärenmodell“, wo Sie die für Ihre „Umgebungsgleichung“ benutzte Gegenstrahlung und den vermeintlichen Widerspruch zum 2.HS sowie die Rotation und Wärmespeicherung und auch die Abstrahlung der Nachtseite berücksichtigen.
Ansonsten sollten Sie die Aufrichtigkeit besitzen, Ihren Titel „Geophysiker“ zurückzugeben und aufhören, das fachliche Renommé von EIKE immer wieder neu zu beschädigen und die Kommentatoren zu veranlassen, Ihre Zeit mit Hunderten unnötiger Kommentare zu verschwenden (wobei man grosse Mühe hat, jeden Tag all die neuen Antworten herauszusuchen – soweit man keine Suchfunktion für die Webseite nutzen kann).
@ All
Über die Jahre habe ich auf der Kommentarfunktion von EIKE folgende Beobachtungen gemacht:
Beobachtung 1: Manche Menschen wehren sich mit gleichförmigen Wiederholungen gegen jeden Erkenntnisgewinn und dokumentieren das auf der Kommentarfunktion.
Beobachtung 2: Solche Menschen sind üblicherweise nicht willens oder in der Lage, sich neuen Erkenntnissen zu stellen.
Beobachtung 3: Vielmehr überschätzen solche Menschen ihre eigene Kompetenz ganz erheblich.
Beobachtung 4: Von daher unterschätzen solche Menschen auch regelmäßig die überlegene Kompetenz anderer Kommentatoren.
Beobachtung 5: Die marginale Kompetenz solcher Menschen pflegt sich in einer mangelhaften Rezeption meiner Beiträge und ad-hominem-Argumenten zu erschöpfen.
Zum tieferen Verständnis sei auf die Erkenntnisse des Philosophen Dieter Bohlen verwiesen.
„Zum tieferen Verständnis sei auf die Erkenntnisse des Philosophen Dieter Bohlen verwiesen.“
Ich fange an Sie zu mögen…
Herr Weber, mir ist es ein Rätsel wie Sie darauf kommen dass die gesamte Erde eine Temperatur annimmt, welche nur durch die solare Bestrahlung einer Teilfläche (!!) erzeugt wird. Genausogut könnte man mit einem Schweissbrenner einen Bereich von 100 cm² auf 1000 Grad erhitzen. Würden Sie dann behaupten dass die gesamte Erdoberfläche 1000 Grad annimmt??
Sie verwechseln die Tatsachen dass die gesamte Energiezufuhr zwar durch den Teilbereich bestimmt ist, aber die Temperatur von der Energieverteilung auf die gesamte (!) Oberfläche und von der lokalen Abstrahlung (nach S-B) bestimmt ist.
Nicht die Modellierer (welche im Gleichgewicht und Mittel vereinfacht nahezu Isothermie annehmen und mit einer Sonne, dem Geometriefaktor 4 und Gegenstrahlung – oder genauer mit cos, Speicherung, Rotation und Nachtseite rechnen) sind die Falschanwender von S-B, sondern SIE!!! Sie sollten – anstatt die Fachleute, welche Ihre Fehler beim Hemisphärenmodell gefunden haben, überheblich als inkompetent (!!) zu diffamieren – lieber einen Beitrag „Korrigendum des Hemisphärenmodells“ verfassen.
Herr Dietze,
es ist erstaunlich, das sie eine Schweissbrenner als Beispiel bringen,
weil die Klimawissenschaften behaupten, das eine von der Sonne nichtbeieinflusste Flaeche miterwaermt wird.
Koennen sie bestaetigen, das die Sonne immer nur eine Hemisphaere anscheint oder nicht?
Sie muessen ihre Denkfehler selber finden, anstatt dessen versuchen sie diese nur bei anderen zu finden.
Das hemisphaerische Konzept stimmt wenn man es auf die Leistung bezieht.
Zusammengefasst zum Thema „Was ist Erwärmung“Eine aufgebrachte Isolierung ist bei gleichbleibender Energiezufuhr dafür verantwortlich, dass sich die Temperatur des isolierten Körpers erhöht. Diese Wirkung der Isolierung als WÄRMEN zu bezeichnen, ist verboten. Zusätzlich Treibhausgase in der Atmosphäre sind bei gleichbleibender Energiezufuhr dafür verantwortlich, dass sich die Temperatur der erdnahen Atmosphäre erhöht. Diese Wirkung der Treibhausgase als WÄRMEN, ist ebenfalls verboten. Silke Kosch
Wenn Sie sich mit Ihren Bekannten unterhalten, ist es natürlich nicht falsch zu sagen, „der Pullover wärmt“.
Wenn man den physikalischen Prozess der Temperaturerhöhung beschreibt, dann wird man im Fach Thermodynamik rausgeschmissen, wenn man behauptet, „die Isolierung wärmt“. Weil nur die Energiezufuhr wärmt.
Umgangssprachlich kann man es auch so nennen. Mir ging es darum, dass Sie verinnerlichen, dass es absolut immer, sowohl Energiezufluss gibt, der wärmt, als auch Abfluss, der kühlt, und die Temperatur vom Gleichgewicht beider Prozesse abhängig ist.
Nochmal ein Vergleich der Wirkung von Konvektion und Strahlung: Versuchen Sie beim nächsten Mal die Haare nicht mit dem Föhn (erzwungene Konvektion), sondern mit einer IR-Lampe (reine Strahlung) zu trocknen. Es dauert wahrscheinlich genau so lange, als würden die Haare von allein trocknen.
Weil Strahlungswärme meist vernachlässigbar ist.
oder den Streichholztest machen:
Handinnenfläche für 30sec 5cm UNTER das brennende Streichholz, dann 30sec 5cm ÜBER das brennende Streichholz halten.
(Rückmeldung erwünscht…)
@Peter Georgiev; Sie sind mir ja ein echter Experte in Sachen Heizung und Strahlung.
Zum Stichwort „Wandflächenheizung“ fällt Ihnen nur ein: „Aufgrund meiner Ausbildung kann ich Heizungen berechnen, Wärmebedarf, Dimensionierung, Heizflächen, Vorlauftemperaturen. Sie können mir glauben, dort kommen keine Strahlungen vor ….. “
Wenn Sie bereit wären, etwas zu lernen, dann könnten sie so etwas lesen:
„Die Wandheizung gehört zur Familie der Flächenheizungen und sorgt für die Erwärmung eines Raumes durch Wärmeabgabe der Wände mit einem relativ hohen Strahlungsanteil. Sie wird vorzugsweise im Niedertemperaturbereich betrieben.
Der Vorteil einer Wandheizung liegt in der direkten Wärmeübertragung durch die Wärmeabstrahlung der erwärmten Wandflächen, während die Raumluft nicht so stark erwärmt wird wie bei Konvektoren- oder Warmluftheizungen.“
Und jetzt erzählen Sie noch, „Strahlungswärme wäre meist vernachlässigbar“. Wollen Sie die Vorstellung des „Äthers“ hier wieder populär machen, wonach irgendein Trägermedium erforderlich ist, um Sonnenstrahlen zur Erde kommen zu lassen.
So, jetzt geht es erst einmal auf eine morgendliche Joggingrunde, wobei ich mich etwas dicker angezogen haben, als vor einer Woche. Es ist noch einmal kühl geworden. Aber kein Problem; das weiche Fleece auf der Innenseite meiner Sportsachen wärmt aber wunderbar … also bei mir zumindest.
Silke Kosch
„Diese Wandsysteme vermitteln wohlige Wärme zu einem großen Teil durch Strahlung, weil diese Heizsysteme mit sehr geringen Vorlauftemperaturen arbeiten.“
Das was Sie hier früher beschrieben haben, ist physikalischer Humbug.
Ihre oben beschrieben Heizung ist ist Elektroheizung, mehr oder weniger ein langezogen Infrarotlampe, die natürlich nur strahlt wie eine Infrarotlampe. Allerdings frisst sie Strom, mit einem mickrigen Heizlüfter haben Sie mehr Wärme für viel weniger Geld. Wer sich so etwas anschafft hat einen an der Waffel. Wenn man unsinnigerweise mit Strom heizt braucht man keine Berechnung, da man stufenlos unmittelbar die Energiezufuhr und damit die Wärmeabgabe steuern kann.
Niedlich ist natürlich der Werbetext für Dummies, richtig süß!
Strahlungswärme ist bei Wärmetauschprozesse auf der Erde meist vernachlässigbar, da hat die Thermodynamik eine andere Meinung als Sie. Und auf diese Berechnungsgrundlagen beruhen alle Verbrennungsmotoren, Turbinen und Heizungen (abgesehen von IR-Lampen , auch als „Flächen-IR-Lampen“ wie Ihre und paar andere Sonderkonstruktionen). Wenn Sie das alles berechnen würden, dann wären wir im Mittelalter. Dass der Wärmetransport in Vakuum nur durch Strahlung erfolgt ist nicht das Thema.
@Peter Georgiev; und wieder zeigen Sie, dass Sie nicht im Thema sind. Wenn von niedrigen Vorlauftemperatur gesprochen wird und von Wandflächenheizung, dann sollten Sie zumindest so schlau sein, zu erkennen, dass Wandheizungen gemeint sind, die mit einem Medium (Wasser) betrieben werden.
Ernsthaft: Wenn uns ein Handwerker (Heizungsbauer) bei einer Auftragsverhandlung oder einem Informationsgespräch so uninformiert, ahnungslos und dennoch großspurig käme, wie Sie sich hier geben, wäre der schneller wieder durch die gleiche Tür heraus durch die er herein gekommen ist, als er „Auf Wiedersehen“ sagen kann.
Silke Kosch
Frau Kosch,
es gibt mehrere Arten von Wandheizungen. Ich kenne 3 davon, welche ihre Wärme entweder mittels Luft (das kannten schon die alten Römer, auch bei Fußböden!), Wasser oder Strom an die Wand (oder den Fußboden) übertragen.
Unter der Annahme, daß die Wandoberflächentemperatur zum Beispiel 28° C (empfehle ich übrigens nur Schwimmbadbetreibern) beträgt: Können Sie herausfinden, nur mit Blick auf die Wandoberfläche, welches Medium gerade die Wandoberfläche erwärmt? Zusatzfrage: Haben unterschiedliche Medien unterschiedliche Eigenschaften, immer bezogen auf die gleiche Wandoberflächentemperatur, bezüglich ihrer Wärmeabgabequalitäten?
Hallo Frau Kosch, in aller Sachlichkeit möchte ich Sie unterstützen: ich besitze ein 300 Jahre altes Fachwerkhaus. bei der Sanierung war Wärmedämmung der Außenwände weder erlaubt noch möglich noch gewünscht. Beheizt wird das Gebäude mit einer Wandtemperierung, nichts anderes als in den Außenwänden verlegte Kupferrohre, durch die warmes Wasser fließt. Vorlauftemperatur je nach Außentemperatur zwischen 35 und 65 Grad. Bei einer Raumtemperatur von selten mehr als 20 Grad ist es in unserem Haus trotzdem gemütlich, weil die Heizung keine warme Luft umwälzt, sondern durch den höheren Strahlungsanteil alle Flächen im Raum und natürlich auch die Luft gleichmäßig erwärmt. Der optische Gewinn in der alten Stube: Es gibt keine Heizkörper. Bei 300 qm Wohn- und Nutzfläche komme ich mit 1200 bis 1400 Heizkosten jährlich aus (Holzpellets).
Herr Burger, je höher der Temperaturunterschied, um so höher die Strahlung und umgedreht. Ein klassischer Heizkörper unter dem Fenster ist relativ warm und strahlt ( vernachlässigbar) Ihre Wand und mein Fussboden sind nicht viel wärmer als die Umgebung und strahlen GAR NICHT. Die geringere Temperatur erfordert einen deutlich größeren Wärmetauscher, also den ganzen Boden oder die ganze Wand, die trotzdem durch Leitung und Konvektion wärmen. Die Luftumwältung ist nicht punktuell am Heizkörper, ist deshalb nicht spürbar und die Temperatur gleichmäßiger.
Die Werbetexte der Hersteller von wegen Strahlung sind absoluter Humbug.
Strahlen tut der heiße Draht der IR Lampe oder die Sonne bei 6000 Grad.
Bei bockigen Kinder muss ich manchmal den Klugscheißer raushängen:
Das ist ein Flach-Wandheizkörper, der letztendlich durch Leitung und Konvektion heizt und durch Warmwasser erwärmt wird:
https://www.bau99.de/kermi-flachheizkoerper-verteo-profil-155224/?number=KIVPR101640X3
Und das ist ein Wandheizkörper, der zu Ihrem Text passt und in der Tat durch Strahlung wärmt, definitiv elektrisch ist und richtigerweise Infrarot-Heizplatte heißt:
https://de.trotec.com/shop/infrarot-heizplatte-infrarotheizung-tih-1100-s.html?gclid=EAIaIQobChMIjbLrtsuZ7wIVArDtCh2uvQLlEAYYAiABEgJ8DvD_BwE
Von der zweiten Sorte gibt es zig, ist elementare Technik, und mit passenden Text wie Ihren oben an Dummies verkauft.
Dass es Warmwasserheizkörper gibt, die durch Strahlung wärmen ist Schwachsinn!
An Schwachsinn glauben ist nicht verboten!
„An Schwachsinn glauben ist nicht verboten!“
Aber modern!
„Vorlauftemperatur je nach Außentemperatur zwischen 35 und 65 Grad.“
„Und das ist ein Wandheizkörper, der zu Ihrem Text passt und in der Tat durch Strahlung wärmt, definitiv elektrisch ist und richtigerweise Infrarot-Heizplatte heißt“
Fazit: Wenn in Zukunft elektrischer Strom durch die CO2-Steuer subventioniert wird überlege ich ob es nicht am einfachsten ist im Wohnzimmer wieder zur 100 W Glühbirne zurückzukehren: Licht und Wärme am Ort wo es benötigt wird.
Klein Silke will nichts verstehen. Sie baut sich ihre Welt wie sie ihr gefällt. Wie Greta Langstrumpf. Deshalb sind Versuche, sie zu einer Antwort auf gestellte Fragen zu bewegen sinnlos. Wissen ist Macht, nix wissen macht nix.
Herr Frankel, halten Sie sich bitte an die Netiquette, sonst werde ich beim Moderator Ihre Sperrung hier beantragen. Frau Kosch hat eine respektvolle Behandlung verdient auch wenn Sie Ihr nicht zustimmen mögen. Danke.
Sind Sie hier der Blockwart?
Sehr geehrter Herr Frankel,
nein, dafür ist die Moderation zuständig. Aber zuerst ist jeder Kommentator für sich selbst fürs Einhalten der Netiquette verantwortlich. Sollte nicht so schwerfallen.
Sehr geehrte Frau Kosch
Ich darf annehmen, das meinen Sie ironisch. Der Punkt ist, daß hier einige Herren den Begriff Erwärmung mit Wärme assozieren und meinen Erwärmung ginge nur durch Wärmezufuhr. Das mag zwar vom Wort her plausibel sein, ist aber physikalischer Unsinn, einfaches Beispiel: adiabatische Kompression: Erwärmung durch Arbeit ohne Wärmezufuhr.
Natürlich kann Erwärmung auch bei konstanter Heizleitung nur durch Verstärkung der Isolation stattfinden. Wer das nicht versteht, hat in einer Klimadiskussion nichts verloren.
Sie müssen schon deutlich mehr Thermodynamik einatmen um mitreden zu können, Glauber.
Exakt richtig ist, dass die adiabate Kompression eine Erwärmung durch Zuführung von Energie erfolgt, nicht durch Arbeit, wobei Arbeit die Differenz von Energienniveaus ist und somit die gleiche Einheit Joule hat. Vor Ahnunglosen können Sie damit glänzen, verstehen aber trotzdem die Vorgänge nicht. Sie finden bei mir nirgends die Behauptung „Zuführung von Wärme“ sondern immer von „Wärmeenergie“. Damit ein Normalo, der kaum Energie von Leistung unterscheiden kann, nicht den Faden verliert, habe ich die richtigen Begriffe wie Enthalpie und Entropie vermieden. Dass jede Form von Energie vollständig in Wärme umgewandelt kann, ist hier nicht das Thema.
Von Thermodynamik haben Sie soviel Ahnung wie der Bär vom Eierlegen und betrachten damit Klimaprozesse genau so kastriert von den thermodynamischen Hauptprozesse wie alle THE Fans.
Bei Glauber und Kosch ist das alles, was Sie hier (völlig richtig!!!) schreiben leider vetane Müh. Denen das zu erklären ist so, als wenn man einem Blinden einen Stummfilm zeigt …..
Sehr geehrter Herr Tengler,
So schwer sollte das nicht sein, wenn man denn bitte auch beim Thema bleibt, Unterstellungen und Unverschämtheiten sind keine Erklärungen.
Versuchen Sie es doch mal. Aber bitte bleiben Sie beim Thema, welches Frau Kosch aufbrachte: Ein Körper (Mensch) hat eine konstante Energiezufuhr (Heizquelle) und führt Energie an eine kältere Umgebung ab. Wird um den Körper eine Isolation angebracht (Iglu), erwärmt sich der Körper ohne daß sich etwas die Energiezufuhr der Heizquelle ändert. Die Isolation ist also die Ursache für die Erwärmung.
Sehen Sie das anders?
@Thomas Glauber
5. März 2021 um 10:55
„Die Isolation ist also die Ursache für die Erwärmung.“
DAS sehe ich natürlich völlig anders und bin hier dabei in sehr guter Gesellschaft.
Das Sie mal Physik studiert haben, kann ich angesichts Ihrer Äußerungen nicht nachvollziehen.
Sie bringen da einiges SEHR durcheinander:
Bleiben wir mal beim Menschen. Dessen „Regler“ ist auf 37°C eingestellt. Nach Ihrer Theorie müssten drei Pullover zu Fieber führen, macht es aber nicht, der Körper schaltet ggf. auf Kühlung (Schwitzen), um dem gegenzusteuern, können Sie folgen? Es gibt sicherlich Temperaturgradienten in der Haut, die dem höheren Wärmeabfluß ohne und mit Pullover folgen, aber mehr passiert nicht.
Wenn Sie einen innen konstant mit einer bestimmten Leistung beaufschlagten Körper mehr oder weniger isolieren, wird seine Oberflächentemperatur (je nach Wärmeleitfähigkeit des Materials) verschiedene, von der Isolierung (und Wärmeaustauschkonstanten mit der Umgebung) abhängige Gleichgewichtstemperatur einnehmen.
Ein unbeheizter Körper mit höherer Ausgangs-Temp. als der Umgebungstemperatur wird mit „Pullover“ nur langsamer abkühlen, aber durch den „Pullover“ niemals wärmer werden. Für diese Erkenntnis reicht eigentlich die Schulphysik ……..
Sehr geehrter Herr Georgiev
4. MÄRZ 2021 UM 19:19
Danke, aber übertreiben Sie nicht, ein Physikabschluß mit Themodynamik und statistische Physik im 6. Semester sollte für diese Diskussion vollkommen ausreichen. Außerdem raten ich Ihnen, einen anderen Ton aufzulegen, Sie haben keinen Grund für dieses unverschämte Auftreten, zumal wir uns nicht kennen.
Ich weiß ja nicht, wie umfangreich Ihre Thermodynamikausbildung war, aber meine folgte wohl dem üblichen Kanon und da lernt man in den ersten Stunden schon, was adiabatisch und was der erste Hauptsatz ist. Adiabatisch heißt eine Zustandsänderung ohne Wärmezufuhr. Nach dem ersten Hauptsatz der Thermodynamik kann die innere Energie des System dann nur durch Verrichten von Arbeit am System geändert werden, z.B. wie im Beispiel Kompression von Luft.
Das Result ist Erwärmung der Luft ohne Wärmezufuhr.
Das sollte man wissen, wenn man von sich behaupten wolle, man wüßte zumindest ein bißchen von Thermodynamik.
Habe ich anders gelernt: Bei Leisten von Arbeit am System ändern sich die Lagen der Energieniveaus, bei Wärmezufuhr die Besetzungszahlen der Energieniveaus. Das ist der mikrophysikalische Unterschied.
@ Glauber und Marvin Müller
Sie sprechen über Thermodynamik auf Gymnasium-Niveau. Wenn Sie Energieumwandlung (Oberbegriff für 4 Studienrichtungen) studiert haben, dann würden Sie niemals von „Wärme“ sprechen, eher schon von Wärmeenergie. Wärme ist keine physikalische Größe, sondern ein Gefühl.
Bei der thermodynamischen Betrachtung der genannten Prozesse wird richtigerweise von Enthalpie mit der Einheit Joule gesprochen, wobei sowohl eine Druckänderung als auch eine Temperaturänderung das Niveau der Enthalpie verändern. Um das zu verstehen, braucht man mehr als 4 Semester Thermodynamik. Einfacher ausgedrückt, durch Druckerhöhung wird genau so Energie zugeführt, wie durch direkte Zufuhr von Wärmeenergie, daher steigt in beiden Fällen die Temperatur. Mit solchen aussagen fliegt man aber durch die Prüfung, es ist schon komplexer.
Die Gleichung Q plus W können Sie bei Mutti vor dem Kochtopf angeben, nicht vor ausgebildete Thermodynamiker.
Peter Georgiev schrieb am 6. MÄRZ 2021 UM 13:03
Da man bereits auf Abiturniveau weiss, dass in dem genannten Beispiel die am System verrichtete Arbeit die Ursache für die Temperaturerhöhung ist, dachte ich, das ganze sei ein Missverständnis. Nun habe ich meine Zweifel.
Herr Müller, nun mal im Ernst:
Im Gymnasium war Physik mein Lieblingsfach und dort die Wärmegleichungen. Beim Studium habe ich geschockt feststellen müssen, dass die vereinfachten Darstellung im Abiturniveau mit der eigentlichen Berechnung der Prozesse nichzs zu tun hatte. Selbst der klare Zusammenhang Masse, Energie, spez. Wärme gilt nicht. Die spez. WK ist auf einmal keine feste Größe sondern eine Funktion, und man rechnet mit Enthalpie und Entropie, Energie ist out.
Hätte ich etwas anderes studiert, hätte ich es nicht gewusst. Jeder, der etwas anderes studiert hat, kann es in dieser Tiefe nicht wissen.
Arbeit und Energiezuführung ist aus Sicht der Thermodynamik gleich, man kann vereinfacht Ihre Wortwahl nehmen. Es ändert nichts an der Tatsache, dass die Energiezuführung das Medium erwärmt. Versuchen Sie mal ohne Energie zu verdichten!
Das sagt es eigentlich alles!
Die Diskussion erinnert mich an einen klimaglaeubigen Physikprofessor, der der Meinung war das ein Luftpaket sich nicht abkuehlt wenn man es in in der Hoehe verschiebt.
Als Beispiel nannte er einen Behaelter, den er von Normal Null auf 1000 m anheben wollte.
Er sagt zwar richtig, das sich durch das anheben die Temperatur theoretisch nicht veraendert, vergisst aber vollkommen die Arbeit die notwendig ist um das Luftpaket anzuheben.
Ohne diese Arbeit muss sich die Luft abkuehlen!
Und nun kommt Herr Glauber, der diese Erkenntnis gleich mal umsetzen kann!
Was passiert mit einem Luftpaket, das sich von 1000 m auf Normal Null zubewegt?
Bitte Herr Glauber, ihre Kenntnisse sind gefragt!
Vorsicht Fallen, sie werden als Ketzer der Klimaunwissenschaft gebrandmarkt, wenn sie hier richtig antworten!
Peter Georgiev schrieb am4. März 2021 um 19:19
Irgendwie muss hier ein Missverständnis vorliegen. Die Änderung der inneren Energie U ist definiert als
mit Q als Wärme und W als Arbeit, die mit der Umgebung ausgetauscht werden (das war auch vor 40 Jahren schon Stand des Wissens im Verlag Volk und Wissen). Bei einem adiabatischen Vorgang ist Q = 0, es wird keine Wärme mit der Umgebung ausgetauscht, die Änderung der inneren Energie findet nur durch die am oder vom System verrichtete(n) Arbeit statt, wobei die Arbeit bei adiabatischer Kompression eine Volumenänderungsarbeit ist. Also das, was wir bei der Luftpumpe (bei der sich die komprimierte Luft erwärmt) oder beim Aufstieg eines „Luftpackets“ (das sich durch die Ausdehnung abkühlt) kennen …
Herr Glauber,
das Energie und Arbeit die gleiche Einheit haben ist bekannt.
Mit ihrer Spitzfindigkeit begeben sie sich allerdings auf duennes Eis.
Empfehle Adiabatische Kompression in den Diskussionen auf Eike oder wo anders zu finden.
Es gibt da eine geteilte Meinung, wo sie sich schnell ausserhalb ihres Glauben finden koennten.
Durch Beobachtung und bei Beruecksichtigung der Sonne kann man nicht von einer konstanten Heizleistung sprechen.
In Ihrer Zusammenfassung ist also ein Fehler drin.
Was sie umgangssprachlich benutzen ist eigentlich egal, aber wenn sie sich sinnvoll an der Diskussion beteiligen wollen, sollten sie sich fachlich anlesen und argumentieren.
Verboten heisst in der Fachsprache „unzulaessig“.
Da fehlt bei Ihnen an mancher Stelle die Sorgfalt.
Niemand erwartet, das sie die fachliche Kompetenz mitbringen, aber was man erwarten sollte, ist das sie sich bemuehen.
mfg
Werner
Sehr geehrter Herr Müller
Moderne Klimamodelle berücksichtigen die verschiedenen optischen Eigenschaften der Materialien des Planeten und auch seine Rotation. Die Klimamodelle sind ja vom Prinzip her Wettermodelle, d.h. sie rechnen von einem Startzeitpunkt zeitlich in die Zukunft, tages,- und jahreszeitliche Schwankungen ergeben sich damit automatisch aus dem berechneten Verlauf des Sonnenstandes, das ist einfach zu implementieren.
Die Erdwärme können Sie quantitativ für Wetter- und Klimamodelle bis 100 Jahre unter den Tisch fallen lassen, der Wärmefluß aus dem Erdinneren ist vernachlässigbar klein gegenüber den Strahlungen von oben.
Ein Klimamodell für den Mond? Leicht zu machen, der ändert sein Klima die kommenden 100 Jahre wohl kaum. Aber nehmen Sie einfach eines für die Erde und löschen die Programmteile zur Berechnung der Lufthülle, Ozeane und Vegetation, ändern die Bodeneigenschaften auf die vom Mondboden und ändern die Bahnparameter von Erde auf Mond.
Was haben Klimamodelle mit der ISS zu tun? Die Klimamodelle laufen in irdischen Rechenzentren, nicht auf der Weltraumstation!
„…Wettermodelle, d.h. sie rechnen von einem Startzeitpunkt zeitlich in die Zukunft…“
Kennen alle. Die Temperatur morgen mit einer Trefferquote von 90% und Genauigkeit von 90%, bei 10 Tagen, Quote und Genauigkeit von vielleicht 60%, 3 Wochen später kann man die Temperatur auch würfeln, ist ehrlicher.
Die ganzen thermodynamischen Wärmetauschprozesse werden weggelassen, aber die Temperatur in 100 Jahren genauer bestimmt, als die von morgen!
Hauptsache man glaubt daran!
Sehr geehrter Herr Georgiev,
Sie überschätzen Ihre Kenntnisse auf diesem Gebiet, wenn Sie nicht mal wissen, was der Unterschied zwischen einer Wettervorhersage und einer Klimavorhersage ist. Warum beteiligen Sie sich eigentlich hier, wenn Sie nichts weiter als destruktive und themenirrelevante Beiträge liefern? Wo soll darin Sinn sein?
„…Die Klimamodelle sind ja vom Prinzip her Wettermodelle…“
Bewerten Sie mal Ihren Unfug hier! Wettermodelle beruhen auf die physikalisch bekannten Grundlagen, Klimamodelle als Anzeige des statistischen Wertes „Klima“ beruhen nicht auf Physik, sondern aus (beliebig zusammengestellte) statistische Werte.
Klimamodelle sind mehr oder weniger CO2-Temperatur-Diagramme mit einem frei wählbaren Zusammenhang beider Komponenten, der Rest des Codes ist nur Tarnung, ohne den geringsten wissenschaftlichen Wert.
Ich brauche noch 1-2 Wochen, dann schicken ich an Eike eine Analyse dazu.
Sehr geehrter Herr Georgiev,
Heutige Klimamodelle basieren wie die Wettervorhersagemodelle auf Berechnung des Zeitverlaufs der Strömungen in der Atmosphäre und den Ozeanen. Die Temperatur ergibt sich an jedem Punkt aus der lokalen Energiebilanz.
Dies ist kein Geheimnis. Warum stellen Sie es also falsch dar?
Herr Glauber, Sie fragen was haben Klimamodelle mit der ISS zu tun? Nur außerhalb der Athmosphäre kann man die tatsächliche Einstrahlung messen und auch die Ausstrahlung. Ganz ohne Luft und Wasse, ohne Klima. Dabei ist das Spektrum nicht dasselbe, Mutter Erde ist blau, Mars rot, aber die Summe aller abgestrahlten Energien in allen Frequenzen muß wieder gleich sein. Nur auf Infrarot zu beziehen ist eine unzulässige Vereinfachung. Genau diese Bilanz kann man von jedem Himmelsköper aufstellen und am einfachsten von denen ohne störende Athmosphäre wie Mond. Natürlich gibt es kein Klima in unserem Sinne auf dem Mond, aber eine Strahlungsbilanz mit +-0.
Auch ich vermisse im Forum die Fairnis. Ich habe gelernt, dass selbst in in Ansichten Anderer, von denen ich meine, dass sie total falsch sind immer auch ein Zipfelchen Wahrheit steckt. Schaum vorm Mund, sofort wenn sich Frau Silke Kosch meldet, bringt keinen wirklichen Ideenaustausch. Selbst als Außenstehender unter euch Spezialisten fällt mir auf, dass immer wieder in vielen Kommentaren Wärme und Strahlung durcheinander purzeln. Es gibt den Erhaltungssatz der Energie, nicht den der Wärme. Oft wird nur der IR Teil der Strahlung gesehen. Fragen Sie mal einen Baum, der sähe das Schwergewicht bei UV.
Es scheint eine Gesetzmäßigkeit zu sein, dass Jemand, je mehr er Fachwissen auf seinem Gebiet hat, desto schmalspuriger wird er und desto verbissener kämpft er alles andere nieder. Die CO2- Apostel zweifeln deshalb nicht mehr, weil sie meinen zu wissen. Sie können aber nicht erklären, wieso ausgerechnet CO2 als einziger Stoff nur in Richtung Erde strahlt. Hat man den Wärmehalbleiter oder Strahlungshalbleiter oder gar das Perpetuum mobile erfunden und wir wissen es nur noch nicht? Auf Venus soll das CO2 für 600 Grad sorgen und auf Mars mit Athmosphäre fast nur CO2 ist es arschkalt und da macht es das CO2 nicht kuschelig warm? Gelten manche Naturgesetze nur, wenn sie passen oder nur in Potsdam?
Sehr geehrter Herr Reiner Müller,
Sie haben mit Ihrem guten Allgemeinwissen (Temperaturen und CO2 auf Mars und Venus hat nicht jeder im Hinterkopf) und den gesunden Menschenverstand die Prozesse besser verstanden als der eine oder andere Schmalspurspezialist hier. Respekt!
Ich persönlich bin überzeugt, dass das gesamte Wissen der Menschheit nicht in der Lage ist, das komplexe Klimageschehen auch nur oberflächlich zu verstehen. Und das ganze Unwissen in einem überdimensionierten Taachentechner zu stecken und damit das Klima vorauszuberechnen… dazu fehlt mir ein Wort, dass eine genügende Steigerung von Naivität ausdrückt. Abgesehen von hemmungsloses Geld machen mit der Angst.
Glückwunsch Herr Werner Schulz,die Erkenntnis formuliert im Kommentar vom 2.März 2021 17:11Mit Abstand das Beste,was ich von Ihnen gelesen habe.Die Wärmekapazität von einem Kubikmeter Erdboden ist ca. 2000 kJ/KelvinDie Wärmekapazität von 1Kubikmeter Luft ist ca. 1000 J/KelvinDie Wärmekapazität von 1Kubikmeter Wasser ist ca. 4000 kJ/KelvinIn unseren Breiten beginnt die natürliche Geothermische Tiefenstufe bei -95 MeternBis in diese Tiefe wirkt die Sonne(nicht jedes Jahr,aber immer mal wieder)Das Erdjahr hat 365 Tage.Und damit es langfristig passt, in der Zahlenwelt der Physik,alle 4 Jahre 366 Tage.Die innere Energie der Erde reicht leider nicht aus,um diese so umstrittene mittlere Temperatur in 2 Metern über dem Erdboden, ohne Sonneneinwirkung auf dem aktuellen Niveau zu halten.
Sorry, hier eingereiht wegen Strukturierungsmöglichkeit ;-))
Schon die Tatsache, daß sich Leute, die vorgeben, etwas von Physik zu verstehen, einreden lassen, mit einem Pyrgeometer könne man atmosphärische Gegenstrahlung messen, zeugt für mich davon, daß sie eben nichts von Physik verstehen.
Ein Pyrgeometer ist nichts anderes als ein Pt100-Widerstand, der seinen Wert temperaturabhängig verändert. Legt man eine konstante Spannung an, ist der sich einstellende Strom ein Maß für die Temperatur.
Gemessen soll eigentlich die Erwärmung werden, die der Meßwiderstand selektiv durch infraroten Strahlungsempfang auf einer bekannten Fläche erreicht. Infrarot von der Sonne soll aber ausgefiltert werden und auch die Wärme durch die allgemeine Außen- bzw. Gehäusetemperatur.
Innerhalb des Pyrgeometers erfolgt aber natürlich jeglicher Wärmetransport thermodynamisch über das Gehäusematerial. Man versucht nun, den gemessenen Wert mathematisch aufgrund der separat gemessenen Gehäusetemperatur zu korrigieren, was aber mangels spektraler Trennschärfe nur theoretisch funktioniert.
Es wird behauptet, ein Filterelement filtert das sichtbare Licht aus und läßt nur Infrarot von 4,5 bis 42 Mikrometer zum Meßwiderstand durch (z. B. Kipp & Zonen CGR4). Selbst wenn das stimmt, absorbiert dieser Filter aber alles, was unterhalb 4,5 Mikrometer liegt und erwärmt sich entsprechend, was sich thermodynamisch wieder auf die Gehäusetemperatur auswirkt. Das betrifft besonders das nahe Infrarot der Sonne von 780 nm bis 3 µm. Die Gehäusetemperatur selbst steht natürlich auch in thermodynamischem Austausch mit dem Boden und der Atmosphäre.
Unabhängig davon gilt bzgl. Wärmetransport aber immer auch der 2. HS! Wärme kann also von irgendwoher auf eine Meßstelle von selbst nur dann übergehen, wenn diese Quelle wärmer ist als die Meßstelle selbst. Das gilt thermodynamisch und für Strahlung und natürlich auch für den Meßwiderstand. Ist der Pt100 thermodynamisch also schon zu warm für die zu messende Strahlung, ist eine Messung unmöglich.
Fazit: der Meßwiderstand mißt natürlich etwas, wozu allerdings das Meßsignal proportional ist, hat mit der behaupteten Messung der Stärke der Gegenstrahlung im mittleren Infrarot nichts zu tun.
Und auf die Frage, welchen Einfluß Oberflächenstrahlungsphysik auf die Atmosphärenphysik in 2 m Höhe hat, die fast ausschließlich thermodynamisch wirkt, gibt ein Pyrgeometer natürlich auch keine Antwort.
Zu ergänzen wäre noch, daß selbstverständlich der Emissionsfaktor des zu messenden Materials auch nicht bekannt ist. Das Gerät verwendet einen Durchschnittswert…
MfG
Herr Peters,
mit der Temperaturzunahme von 3 Grad C pro 100 m, ist der sogenannte Treibhauseffekt in 1100 m Tiefe abgegessen. Das heisst ohne Sonne wäre es ’spätestens‘ dort wieder 15 Grad warm.
Die innere Energie der Erde ist zeitunabhängig. Der Weinkeller stört sich wenig an den Jahreszeiten. Die Temperaturen in der Sonne sind natuerlich hoeher, aber die Sonne erwärmt keinen Punkt der Erde von 0K auf eine bestimmt Temperatur, sondern erhöht diese nur um einen bestimmten Betrag.
Offensichtlich braucht es die innere Energie der Erde um das Niveau zu halten. Wie sich das auf die atmosphärische Temperatur auswirkt können sie selber erarbeiten. Der Einfluss der Atmosphäre spielt auch noch eine Rolle! Aber welche?
Was uns die krampfhafte Verteidigung der Kommentare von Silke Kosch durch Marvin Müller zu diesem Artikel demonstriert :Unter den Jugendorganisationen der im Bundestag vertretenen politischen Parteien schätze ich sehr die Julis (Junge Liberale) während ich das sektenartige Verhalten der Grünen Jugend sehr kritisiere.
Marvin Müller hat gute physikalische Kenntnisse, was viele seiner Kommentare auch bewiesen hatten aber er ist genauso naiv wie Silke Kosch, die zusätzlich noch mangelhaftes physikalisches Verständnis besitzt. Einige Kommentatoren in diesem Forum haben dies auch bereits erkannt aber nicht deutlich genug kommuniziert.
Ich möchte nun auf die erschreckende Naivität von Marvin Müller eingehen – bei Silke Kosch kann man dies als gegeben voraussetzen : Marvin Müller sollte wissen, dass unter den Kommentatoren zu diesem Artikel auch viele Personen gehören, die sowohl gutes physikalisches Wissen als auch im Speziellen klimatologisches Wissen besitzen. Solchen Experten gegenüber die Aussagen von Silke Kosch zur Erwärmung als Gleichsetzung der langsameren Abkühlung mit einer Erwärmung Klimmzugartig zu rechtfertigen zeigt, dass Marvin Müller nicht merkt, dass er sich damit lächerlich macht !
Solch eine Verteidigungsstrategie ist selbst gegenüber Laien riskant aber fatal gegenüber Expert(inn)en. Sie werden in den Antworten von Marvin Müller auf meinen Kommentar feststellen, dass er nicht begreift, dass er sich mit dieser Verteidigungsstrategie lächerlich gemacht hat und sich nur krampfhaft weiter in diese Verteidigungsstrategie verrennen wird. Ein Physiker und Klimaexperte bei den Julis hätte bei einem Parteimitglied, welches Aussagen wie Silke Kosch (man muss alle Kommentare von Silke Kosch zu diesem Artikel betrachten und nicht nur einige Sätze) getätigt hätte, sich von den Aussagen dieser Person distanziert (so etwas nennt man Souveränität) aber auf gute fachliche Kenntnisse oder Arbeiten auf anderen Gebieten hingewiesen.
Ich hatte in der Vergangenheit tatsächlich einmal eine sehr gute Email-Korrespondenz mit einem Mitglied der Grünen Jugend gehabt, der sowohl gute logische Schlussfolgerungen ziehen konnte als auch so souverän war, eigene als auch Fehler seiner Partei einzugestehen.
Von Marvin Müller hatte ich bis vor kurzem einen ähnlich guten Eindruck, der aber jetzt vollständig zerstört ist ! Marvin Müller wird aber auf Grund seiner Naivität nicht begreifen, wie sehr er seinem Anliegen geschadet hat und vielleicht sogar beleidigt sein. Er begreift nicht, dass er durch seine krampfhafte Verteidigung der Aussagen von Silke Kosch denjenigen, die er vom THE überzeugen wollte, nun einen Grund mehr gegeben hat, seine Argumente nicht ernst zu nehmen.
Dies zeigt uns wieder, dass das Gros der Mitglieder der Grünen Jugend erschreckend naiv ist und naive Menschen sind prinzipiell eine große Gefahr für eine Demokratie, weil sie von Demokratiefeinden leicht benutzt werden können !
Ich bin nicht so naiv zu glauben, dass ich hier irgend jemanden von irgend was überzeugen könnte. Wenn das nichtmal der Eike-Fachbeirat schafft, was soll da jemand bewirkken, der ein paar Kommentare schreibt.
Daher nur zwei Anmerkungen:
1. Ich hätte für eine verlangsamte Abühlung auch nicht den Begriff Erwärmung gewählt (siehe 1. März 2021 um 19:44 und 2. März 2021 um 10:27 )
2. Ich habe weniger Frau Kosch verteidigt (das kann die selbst, wenn Sie es denn möchte), sondern eher Herrn Herbert Frankel darauf hingewiesen, dass sein Beispiel falsch gewählt ist, da er – wenn er denn Bezug auf Frau Kosch Text nehmen sollte – lediglich ein langsameres Auskühlen erwarten könnte. Beispiele wie das von Herrn Frankel werden oft gebracht, um eine Erhöhung der Temperatur eines beheizten Körpers zu verneinen. Daher fand ich, dass ein Hinweis auf die fehlende Energiezufuhr in seinem Beispiel angebracht sei.
Dass sie mich dann anscheinend in die Grüne Jugend stecken wollen, erheitert mich. Jung müßte man nochmal sein (obwohl jetzt vielleicht gerade nicht …)
Frau Kosch,Sie melden sich des öfteren hier bei EIKE zu Wort.Ihnen scheint die Logik,die bis in die 70er Jahre des vergangenen Jahrhunderts an deutschen und internationalen Universitäten gelehrt wurde noch ein Begriff zu sein.Der Deutsche Wetterdienst ist eine wertvolle Einrichtung für alle Fragen rund um das Wetter und selbstverständlich auch dem Klima.Gemeinsam mit dem Bundesamt für Seeschifffahrt und Hydrologie gibt es eine Seeboje in der Nordsee ,die interessante Messergebnisse liefert.Hier ist der Begriff Erwärmung in anschaulicher Weise grafisch dargestellt.Wir wollen nur die Wassertemperaturen in verschiedenen Tiefen und Jahreszeiten für das Jahr 2020 betrachten. Nordseeboje 3(BSH)
Was bedeutet Erwärmung? Darüber gibt es offenbar geteilte Ansichten hier. Einem strahlenden Körper ohne eigene Energiequelle durch Dämmung oder Rückstrahlung Energie zuzuführen damit er langsamer auskühlt, gilt vielen hier offenbar nicht als Erwärmung. Einem strahlenden Körper mit eigener Energieversorgung durch Dämmung oder Rückstrahlung Energie zuzuführen, damit er weniger Energie aufwenden muss, um die Temperatur konstant zu halten, gilt vielen hier offenbar auch nicht als Erwärmung. Einem strahlenden Körper mit konstanter Energieversorgung durch Dämmung oder Rückstrahlung Energie zuzuführen und dadurch seine Temperatur ansteigen zu lassen, gilt vielen hier offenbar auch nicht als Erwärmung. Also logisch ist das nicht. Verlangsamte Auskühlung, konstante Temperatur bei reduziertem Energieeinsatz und höhere Temperatur bei gleichbleibendem Energieeinsatz sind natürlich nur verschiedene Seiten einer Medaille. Alle Szenarien beschreiben einen Erwärmungsvorgang. Silke Kosch
Erwärmung ist die Erhöhung der Temperatur durch Zuführung von Wärmeenergie.
Dämmung oder s.g. Rückstrahlung bedeutet keine Zuführung von Wärmeenergie, ändert an sich die Temperatur nicht und bedeutet damit keine Erwärmung. Sie können am Nordpol ein Haus bauen, dämmen wie sie wollen, ohne Heizung wird es nicht warm.
Eine Dämmung behindert nur den natürlichen, unaufhaltsamen Abfluss der Wärmeenergie, daher braucht man ohne Dämmung mehr Energie-Zufluss um die gewünschte Temperatur zu halten. Die Erwärmung erfolgt aber ausschließlich durch den Energiezuführung der Heizung.
(Erste Stunde in Thermodynamik, der Neandertaler begriff es auch ohne Thermodynamik)
@ Silke Kosch :
Erwärmung ist immer mit Temperaturerhöhung verbunden und dies sehen auch Klimawissenschaftler vom PIK so. Dies hat nichts mit bei Eike vertretenen Ansichten zu tun
Erwärmung bedeutet, daß ein Körper nachher wärmer ist, als vorher. Also wie genau soll das gehen „einem strahlenden Körper durch Dämmung Energie zuzuführen“? Bitte beschreiben Sie es im Detail. Sie sagen doch selbst, daß er nur „langsamer auskühlt“. Ist der Körper nachher, also durch die Dämmung, wärmer geworden?
Machen Sie ein einfaches Experiment. Bauen Sie in der Arktis einen Iglu oder einen Schneemann. Packen Sie ihn in beliebig dicke Dämmung ein (fast „ideal“ wäre eine freischwebende Kugel, die Sie rundherum in Dämmung einpacken). Messen Sie laufend seine Temperatur (des Schneemanns). Was werden Sie feststellen? Wird der Iglu wärmer? Nach welcher Zeitdauer?
Ich fürchte, ich werde keine Antwort bekommen?!
Herbert Frankel schrieb am1. März 2021 um 15:36
Ich weiss nicht, woran das liegt, aber liest eigentlich noch jemand die Texte wirklich? Dort stand „Einem strahlenden Körper mit eigener Energieversorgung“ und „Einem strahlenden Körper mit konstanter Energieversorgung“. Wo ist denn in Ihrem Beispiel die Quelle, die dem Körper Energie zuführt?
Wenn Sie schon beim Iglu sind[1], wäre das Beispiel eher: Sie stehen am Nordpol vor dem Iglu und frieren, nähern sich der Unterkühlung, ihre Körpertemperatur sinkt. Sie gehen ins Iglu, verlieren weniger Energie an die Umgebung und die Temperatur Ihres Körpers …
[1] Wenn wir vom Nordpol reden, reden wir auch von Energietransport über Wärmeleitung und Konvektion, das möchte ich jetzt aber mal ignorieren. Die Innenwände des Iglus haben mit Sicherheit nach einer Weile eine höhere Temperatur als die Aussenseite, wodurch man auch weniger Energie über Wärmestrahlung verliert …
Sike Kosch
1. MÄRZ 2021 UM 12:49
Einem strahlenden Körper ohne eigene Energiequelle …
Ich weiss nicht, woran das liegt, aber liest eigentlich noch jemand die Texte wirklich?
Im übrigen hoffte ich auf eine Antwort von Silke Kosch.
Herbert Frankel schrieb am 1. März 2021 um 18:14
Ich habe das Zitat von Frau Kosch mal für Sie ergänzt. Dort ging es um langsamer auskühlen. Dazu passte Ihr Beispiel offensichtlich nicht, da Sie nach „Wird der Iglu wärmer?“ fragen.
Sie mögen zwar vielleicht nicht mit Frau Kosch einer Meinung sein, dass man das als „Erwärmen“ bezeichnen könnte, aber dass das ganze zu einer langsameren Abkühlung führt, da stimmen Sie ihr doch hoffentlich zu, oder?
Warum wird zischen einer wärmenden Heizung und einer wärmenden Isolierung unterschieden?
Nehmen wir das Iglu-Beispiel.
Angenommen, die Eskimo-Familie geht zur Jagt und lässt eine kleine Öllampe brennen. Die Öllampe alleine reicht aber nicht, um die Temperatur zu halten und so sinkt die Innentemperatur im Verlauf von 12 Stunden von 20°C auf 10°C. Ohne diese Lampe würde sie auf 0°C sinken. Genauso gut könnte die Familie das Iglu zusätzlich isolieren und ohne Lampe ebenfalls erreichen, dass die Temperatur innerhalb von 12 Stunden von 20°C auf 10°C sinkt.
Und wenn sie es besonders gut dämmt, dann reicht die gleiche Öllampe aus, um die Temperatur innerhalb von 12 Stunden von 20°C auf 25°C zu erhöhen.
Die Unterscheidung, dass nur die Öllampe wärmt bzw. nur die Sonne wärmt und nicht die Isolierung bzw. Gegenstrahlung widerspricht jeder Alltagserfahrung und jeder physikalischen Betrachtung. Im Fall von warmer Kleidung im Winter ist die Kleidung viel mehr an der Erwärmung des Körpers beteiligt, als der lebende Körper selbst. Im Fall des Treibhauseffektes ist der Anteil der Gegenstrahlung mit 333 W/m² ca. doppelt so hoch wie die Sonnenstrahlung mit ihren 161 W/m².
Physikalische Gesetze werden bei dieser Betrachtung nicht verletzt.
Silke Kosch
„Warum wird zischen einer wärmenden Heizung und einer wärmenden Isolierung unterschieden?“
Weil die Isolierung nicht wärmt Silke Kosch!
Die Erwärmung ist nicht ein Einzelprozess, der mal abgeschlossen ist, sondern immer eine Bilanz zwischen zugeführte und abgeführte Wärmeenergie. Jeder Körper auf der Erde verliert unaufhaltsam Wärmeenergie, und zwar so lange, bis er exakt die Umgebungstemperatur erreicht hat. Und erwärmt wird er ausschließlich durch Zuführung von Energie, nicht durch eine Isolierung.
Der Pullover wärmt Sie nicht, sondern die Verbrennung von Kohlehydrate in Ihren Zellen. Wenn Sie lange genug nur in Pullover außerhalb vom Iglu spazieren, hören irgendwann diese Verbrennungsprozesse auf und Sie erfrieren. In sehr kurzer Zeit danach sinkt dann Ihre Körpertemperatur exakt auf die Umgebungstemperatur, weil der Pullover nun mal nicht wärmt.
Es gibt weniger grausame Beispiele:
Wenn Sie einen offenen Topf mit Wasser auf der Herdplatte bei niedrigen Stufe auf 50 Grad halten, danach mit dem Deckel zudecken, erwärmt sich das Wasser spürbar. Bei gleicher Energiezufuhr wird die Abfuhr reduziert und das Gleichgewicht stellt sich auf einem höheren Niveau, z.B. 60 Grad ein.
Ihr entscheidender Betrachtungsfehler ist, dass Sie den Grund für die Erwärmung beim Deckel suchen, es ist aber physikalisch grundfalsch. Stellen Sie die Herdplatte ab und das Wasser erwärmt sich nicht auf 60 Grad, sondern kühlt auf 21 Grad ab. Weil der Deckel nicht wärmt.
Eine Isolierung verringert den Wärmeabfluss und damit pegelt sich die Bilanz zwischen Zu- und Abfluss auf einem höheren Temperatur-Niveau ein, aber erwärmt wird das ganze ausschließlich durch die Energiezufuhr.
Marvin Müller
1. MÄRZ 2021 UM 19:44
Meister Müller verfehlt das Thema.
Es ging um die Aussage Kosch:
Wenn diese Aussage zuträfe, dann würde der strahlende Körper ohne eigene Energiequelle durch Dämmung oder Rückstrahlung erwärmt.
Also Meister Müller: Sehen Sie das auch so?
Herbert Frankel schrieb am 2. März 2021 um 5:11
Nein, es steht deutlich da, was passiert – er kühlt langsamer aus. Daraus können Sie nicht einfach machen, er erwärmt sich. Sie können gerne Anstoss darans nehmen, dass Frau Kosch das als Erwärmung bezeichnet. Ich würde das auch nicht als Erwärmung bezeichnen. Das heisst aber nicht, dass Sie aufgrund einer falschen Begriffszuordnung die klare Beschreibung ignorieren können.
Offensichtlich hat der Meister der Wortverdrehung ihnen Recht gegeben indem er Frau Kosch reindunkt, aber so wie er es sagt, haben sie kein Recht.
Im meinem naechsten Leben werde ich auch Deutschlehrer, dann gewinne ich jede Argumentation.
Fuer alle Mitleser hier, Frau Kosch und Herr Mueller machen die Aussage, das langsamer Abkuehlen eine Erwaermung ausmacht. Ohne Angabe der spezifischen Bedingungen wann das gilt, ist das als falsch zu bewerten,
Der Punkt ist, das Tee sich NICHT in einer Thermoskanne erwaermt. Ein grosser Anteil der Isolation hat aber etwas mit Strahlung zu tun.
Zur Erwaermung braucht man eine innere Heizung in welchem Falle dann die Heizung die Ursache der Erwaermung ist!
Bei der Erde ist die Grundheizung die Erdwaerme. Die Sonne muss die Erde ja nicht morgens vom Nullpunkt auf die Tagestemperatur erwaermen, sondern erwaermt die Erde nur noch zusaetzlich.
Eine Isolationswirkung der Atmosphaere ist anzunehmen, da jeder Stoff der einen anderen Ummantelt eine Isolation darstellt. Luft ist zudem ein guter Isolator.
Um den atmosphaerischen Effekt abzuschaetzen sollte man die Nachttemperaturen mitteln, da in der Nacht das Ergebnis nicht durch die Sonne verfaelscht wird. Auch gleicht sich nachts das Temperaturprofil dem der Standardatmosphaere an.
Die Annahme einer Isolation nur durch Strahlung ist in Anbetracht der geringen Waermeleitung in Luft mehr als fraglich. Den Nachweis, das die Infrarotstrahlung von Gasen die Waermedurchleitung durch Luft weiter verringert, gibt es nicht. Eher muss man davon ausgehen, das die Isolationswirkung von Luft durch Strahlungstransport geringer ausfaellt.
Siehe zum Beispiel Doppelgalsfenster mit CO2 gefuellt.
„Sie gehen ins Iglu, verlieren weniger Energie an die Umgebung und die Temperatur Ihres Körpers …“
„Energietransport über Wärmeleitung und Konvektion, das möchte ich jetzt aber mal ignorieren. Die Innenwände des Iglus haben mit Sicherheit nach einer Weile eine höhere Temperatur als die Aussenseite, wodurch man auch weniger Energie über Wärmestrahlung verliert …“
Herr Müller, wie häufig präsentieren Sie thermodynamische Ahnungslosigkeit.
1. Der unterkühlte Körper erwärmt sich im Iglu nur durch die Verbrennungsprozesse im Körper, durch nichts anderes. Er verliert im Iglu weniger Wärmeenergie als im Gelände, das ist richtig, daher pegelt sich das Gleichgewicht zwischen Wärmeerzeugung im Körper und natürlicher Wärmeverlust bei einer höheren Temperatur ein.
2. Das ganze Strahlungs-Bla-Bla können Sie in diesem Beispiel, wie in vielen anderen, getrost ins Klo runter spülen. Der Körper erwärmt die Luft durch Wärmeleitung und Ausatmung warmer Luft (auch erwärmt durch Leitung) , das Iglu behindert die Konvektion und man sitzt nicht mehr im Freien bei minus 20, sondern bei Null oder kurz drüber. Da ist der Wärmeaustausch mit der deutlich wärmeren Luft natürlich deutlich geringer, man verliert weniger Körperwärme. Ein bisschen Strahlung beeinflusst diese Wärmebilanz nicht. Die sollten Sie ausschließen.
Es hat schon sein Grund, dass ich ständig Neandertaler, und diesmal auch die Inuit, ins Spiel bringe. Die Zitierten begriffen die Wärmeprozesse mit dem gesunden Menschenverstand besser als die heutigen nur auf Strahlen-Denke beschränkte Strahlrenphysiker.
Peter Georgiev schrieb am2. März 2021 um 12:41
Sie attestieren mir Ahnungslosigkeit, beschreiben dann aber genau die gleichen Sachverhalte, wie ich. Irgendwas passt da nicht.(Vielleicht nehmen Sie ja an, ich wüßte nicht, dass der Körper durch Verbrennungprozesse Wärme erzeugt – aber nee, das wäre zu absurd …)
@Herbert Frankel
Doch, Sie werden eine Antwort bekommen, lieber Herr Frankel: Ein Mensch benutzt einen Iglu deshalb gern, weil die Temperatur darin dann ansteigt. Nimmt man ihm den Iglu weg, wird er leider erfrieren, oder? – So würde es auch den Ozeanen ohne die energetische Rückkopplung der Eis- und Wasser Aerosole ergehen. Selbst der Tee in einer isolierten Kanne bleibt wesentlich länger warm. Merke: Das Produkt aus Durchfluss Zeit und Energiefluss kennzeichnet die gespeicherte Solarenergie. Nur der direkt reflektierte Anteil liefert daher keine Beitrag zur Erwärmung. (Der zweite Hauptsatz der Thermodynamik ist an dieser Stelle flüssiger als flüssig!
Ulrich Wolff
1. MÄRZ 2021 UM 17:45
Sie haben die Fragestellung nicht verstanden.
„Ich weiss nicht, woran das liegt, aber liest eigentlich noch jemand die Texte wirklich?“
@Peter Georgiev; ich gehe davon aus, dass Sie erfrieren würden, wenn Sie im Winter die Nacht bei bei -10°C ohne Kleidung am Alexanderplatz auf einer Bank verbringen müssten. Mit Kleidung und einem halbwegs guten Schlafsack würden Sie locker überleben. Solange das so ist, werden Sie ein Problem haben den Menschen Ihre Sicht der Dinge zu vermitteln, dass es nicht die Kleidung bzw. der Schlafsack ist, der wärmt und das Überleben ermöglicht.
Vielleicht informieren Sie sich auch einmal über Wandflächenheizungen, um sich mit der Wirkung von Strahlung etwas anzufreunden. Diese Wandsysteme vermitteln wohlige Wärme zu einem großen Teil durch Strahlung, weil diese Heizsysteme mit sehr geringen Vorlauftemperaturen arbeiten.
Strahlung und Gegenstrahlung ist keine Erfindung von irgendwelchen Verschwörerinnen. Das ist ein messbarer, physikalischer Vorgang, der die Temperaturen der erdnahen Atmosphäre in einen Bereich anhebt, damit sich hier auf der Erde Leben in der heutigen Art gibt und es Menschen gibt, die sich Gedanken darüber machen können, warum wir in einer Luft mit durchschnittlich ca. 15°C leben und nicht bei den durchschnittlich -18°C, die Sonnenstrahlung allein ohne die Hilfe des Treibhauseffektes liefern würden.
Silke Kosch
Scheint, Herr Georgiev hat nur ein Problem mit dem Wort Gegenstrahlung, die Existenz der Gegenstrahlung hat er ja nicht bestritten, denn das Beispiel, dass mit einem kühleren Iglu / kühlerer Atmosphäre die Abkühlung eines wärmeren Körpers/Erdoberfläche verzögert wird, stimmt er ja zu.
Frau Kosch, in Sibirien überleben Genrationen bei Minus 50, trotzdem wärmt nicht das Fell, sondern die Verbrennung der Kohlehydrate im Körper. Legen Sie mal Ihre Kleidung und Ihr Schlafsack bei -10 auf den Balkon und messen Sie dann nach einer Weile wie „warm“ diese sind: exakt -10 Grad! Weil Ihre Körperwärme fehlt!
Das ist nicht meine Sichtweise, sondern die Sichtweise einer sehr spezifischen Fachrichtung der Physik, die Thermodynamik, die ich nun mal intensiv studiert habe. Dabei lernt man, dass die Wärmeübertragung überwiegend durch Konvektion und Wärmeleitung stattfindet, und nur in sehr geringen Maße durch Strahlung. Das Problem hier (nicht nur bei Ihnen) ist, dass man aufgrund der ganzen Klimadiskussion bei Gedankenaustausch über Wärme die entscheidende Mechanismen einfach weggelassen werden, und sich nur mit dem vernachlässigbaren Rest beschäftigt.
Aufgrund meiner Ausbildung kann ich Heizungen berechnen, Wärmebedarf, Dimensionierung, Heizflächen, Vorlauftemperaturen. Sie können mir glauben, dort kommen keine Strahlungen vor, weil der Wärmeumsatz der Strahlung gegenüber der Konvektion und Leitung nicht relevant ist. Da ist Ihnen übrigens ein Freudscher Fehler unterlaufen, mit hoher Vorlauftemperatur strahlen die Heizkörper ein wenig, großflächige Fußboden- und Wandheizungen geben praktisch keine Strahlungsleistung mehr ab (nach SB abhängig von der Temperaturdifferenz, die hier sehr gering ist). Natürlich ist es wohlig warm, aber ganz ohne Strahlung.
Die Sonne erwärmt die Oberfläche und Weltmeere durch direkte Strahlung, nicht durch Gegenstrahlung. Danach setzen Prozesse der Wärmespeicherung und Wärmeübertragung (im Wesentlichen Leitung und Konvektion) ein, die niemand berechnen oder beziffern kann. Klar ist nur, ein Großteil der Wärme bleibt gespeichert, daher wird es nachts nicht so kalt wie auf dem Mond. Strahlen spielen auch eine Rolle, aber untergeordnet.
Wenn man die Wärmeprozesse auf die pure Strahlung reduziert und die wichtigeren Mechanismen weglässt, dann kann nur Unsinn rauskommen, wie eine Gegenstrahlung von -18 auf + 15.
Dass eine ganze Menge Leute, die damit gut Geld verdienen es ständig behaupten, macht den Unsinn nicht wahrer.
Respekt Herr Georgiev, besser und vor allem auch für Laien verständlicher kann man es kaum ausdrücken. Die Anhänger der Klimakirche müßten es nur lesen, Frau Silke K ist zu wenig und will es nicht verstehen. Das gilt auch für die anderen Apostel der Klimakirche in fast allen Parteien bis ins schwarze hinein. Das Beispiel der Thermoskanne wurde hier genannt. Der warme Körper Tee + Glasbehälter innen dann unterbindet Vakuum die Konvektion. Strahlung geht trotzdem ab und an der Außenfläche erfolgt dann tatsächlich Gegenstrahlung durch die verspiegelte Außenwand. Hier gibt es richtige Gegenstrahlung, sie vermindert Wärmeverlust aber auch hier erzeugt sie keine Wärme. Unser Planet befindet sich auch in einer solchen „Thermoskanne“, rundum Hochvakuum. Nur viel komplexer. Geht es bei der Thermoskanne nur um Wärme und nur in eine Richtung, so wird Mütterchen Erde von allen Frequenzen getroffen und jeder Stoff, der getroffen wird, reagiert anders. Immer als „Frequenzwandler“ drum gibt das zurückgestrahlte Licht in verschiedenen Farben. Ein Teil wird absorbiert und erwärmt das Medium. Ich sehe schwarz, dass es in absehbarer Zeit Modelle gibt, deren Bilanz aufgeht. Solange sie nicht aufgeht, fehlt was und sind also nicht richtig. Wie ist das mit Tag und Nacht. Sind sie gleich oder der Tag doch um die Dämmerung etwas länger. Zu Beginn der Nacht ist die Abstrahlung stärker, weil wärmer als zum Ende der Nacht. Wenn man das Jahr halbiert ist die Winterhälfte länger als der Sommer. Nicht zeitlich, aber der Sommer verschleppt weniger Wärme in den Winter und der Winter mehr Kälte (Eis) in den Sommer. Als Bergmann fällt es mir schwer zu vergessen, dass die Erde eine Eigenerwärmung hat. Auch das hilft etwas die bewußte Differenz zu füllen. Wenn Modelle gültig sein sollen, dann müssen sie überall gelten, auch für den Mond. Da gibt es keine Atmosphäre, keine Konfektion auch keine Eigenwärme , natürlich auch keine „Rückstrahlung“. Leider kann ich dazu nichts finden. Fehlt das im Programm der ISS oder wird es unter der Decke gehalten, weil es den Alarmisten nicht passt? Weiß Jemand im Forum etwas dazu?
verzeihung , natürlich „Konvektion“
Es dürfte in dieser Runde nun allgemeiner Konsens darüber bestehen, daß die Sonne verwortlich dafür ist, daß die Erde nicht Weltraumkälte hat. Aber wie auch Sie schon korrekt vermerkt haben, bewirkt die Gegenstrahlung, daß die Erde nicht so stark abkühlt wie ohne Gegenstrahlung. Die Gleichgewichtstemperatur der Erde ist mit Treibhausgasen höher als ohne. Das ist nach der Diskussion hier zusammengefaßt das von allen Diskussionsteilnehmern hier vertretene Verständnis.
Thomas Glauber schrien am 3. März 2021 um 22:39
Ich denke, hier irren Sie sich. Wenn das der Fall wäre, gäbe es einen Großteil der Diskussionen hier nicht. Aber ich lass mich da auch gern positiv überraschen.
Reiner Müller schrieb am3. März 2021 um 20:29
Was soll den „Alarmisten“ denn am Mond nicht passen? Dort ist die global gemittelte beobachtete Temperatur unter der effektiven Abstrahlungstemperatur, bei der Erde ist sie darüber. Können Sie unter anderem in „Using Earth’s Moon as a Testbed for Quantifying the Effect of the Terrestrial Atmosphere“ von G. Kramm et.al. nachlesen.
„Die Gleichgewichtstemperatur der Erde ist mit Treibhausgasen höher als ohne. Das ist nach der Diskussion hier zusammengefaßt das von allen Diskussionsteilnehmern hier vertretene Verständnis.“
Lern lesen!
Es gibt keine Gegenstrahlung aus CO2 am Boden!
Eine Gegenstrahlung kann nichts erwärmen, solange die Atmophäre kälter ist als der Boden!
Hallo Herr Müller,
ich glaube nicht, dass es je Modelle geben wird, die Klimaänderungen reell beschreiben. Dazu sind die Vorgänge zu komplex und zu viele Faktoren sind unbekannt. Bei den aktuellen Modellen wird nicht die (mehr oder weniger unbekannte) Ursache eingegeben um die Wirkung zu sehen, sondern die Wirkung (Temperaturschwankungen) nachgezeichnet mit zwanghaften Zusammenhang zu CO2, der Rest wird so eingestellt das es passt. Müll vom Ansatz her. Für den Mond nicht anwendbar, da die Atmosphäre eine entscheidende Rolle spielt.
Auf dem Mond schwankt die Temperatur zwischen -150 und +140, in erster Linie aufgrund des Fehlens von Meeren und Atmosphäre. Damit beschäftigt sich keiner, es gibt ja kein Geld wenn man ein Anstieg der Mondtemperatur prophezeit.
Herr Glauber,
die Gleichgewichtstemperatur wird neben der Sonne von diesen Faktoren beeiflußt, die den Rückstrom von Energie in den All verhindert, das ist richtig.
Unabhängig davon ob und in welcher Größenordnung es Gegenstrahlung gibt, kann die Gegenstrahlung nicht als Maß von „zurückgehaltener Energie“ genommen werden. Was passiert denn mit der rückgestrahlten Energie? Nach den aktuellen Klimakirche erwärmt sie rückstandslos die Erde. Ist falsch, sie wird wieder zurückgestrahlt, zumindest teilweise. Also pendelt sie zwischen Oberfläche und CO2, bis sie a) von der Erde absorbiert wird, b) vom CO2 absorbiert wird, c) in den Weltraum zurückgestrahlt wird. Niemand kann die Gegenstrahlung beziffern und schon gar nicht, wie viel davon doch noch die Erde verlässt. Nach meiner Meinung ist der Einfluss irrelevant gering. Schon eher, wie viel Wärme das CO2 in sich speichert, da es sich aber um 0,04% der Masse handelt, auch wieder irrelevant.
Der zweite katastrophale Schwachpunkt der ganzen Theorie ist, dass man die Gleichgewichtstemperatur nur anhand der zugeführten/abgeführten Energie angeblich berechnet hat. Sie können es probieren, bei gleicher geringe Herdstufe einen Topf mit einem halben Liter Wasser stehen lassen, bis es zum Gleichgewicht kommt. Danach mit einem Liter, es erwärmt sich weniger. Noch mal das Gleiche mit einem anderen Topf. Bei jeweils exakt gleiche Energiezufuhr gleich Energieabfuhr haben sie das Gleichgewicht bei 4 verschiedene Temperaturen! Wenn Sie einen Topf entbehren können, stellen sie ihn ohne Wasser hin, er wird glühen!
Was ich damit sagen will, neben der Energiezufuhr ist die Gleichgewichts-Temperatur im sehr hohen Maße von den thermodynamischen Eigenschaften des zu erwärmenden Objekts abhängig und lässt sich nicht ohne weiteres berechnen, bei der Erde schon gar nicht. Einzig berechenbar wäre die Temperatur, wenn man beim Topfexperiment die Zeit stoppt, dann kann man anhand der Leistung und der Wassermenge die Temperatur berechnen.
Die Strahlengleichungen sind sicher nicht falsch, aber eine daraus errechenbare Temperatur (z.B. -18) ist hokus pokus.
Sehr geehrter Herr Peter Georgiev,Sie haben damals sehr gut aufgepasst und verstanden,was das Grundsätzliche in der Thermodynamik betrifft.In großem Stil sieht man diesen Effekt bei der Wärmeübertragung in den Primär-Kreislauf eines KKW(Kernkraftwerk).Hier pendelt sich die Gleichgewichtstemperatur auch automatisch ein.Das Beispiel mit dem Kochtopf ist auch gelungen.Etwas Ironie erhellt in der Regel die Gemüter.
Danke Herr Peters!
Da mein Studium schon eine Weile her ist und ich schon lange keine Heizungen mehr berechnet habe, habe ich kurz gegoogelt und brauchte nur 3 Minuten um den entscheidenden Satz für die Berechnung von Wärmetasucher (u.a. Heizkörper) zu finden:
„Es wird angenommen, dass die abzuführende- und aufzunehmende Wärmemenge gleich groß sind.Strahlungswärmeverluste werden vernachlässigt.“
in https://www.schweizer-fn.de/waerme/waermetauscher/waermetauscher.php
auf Deutsch: Strahlung wird bei der Berechnung von Heizungen vernachlässigt!
„Strahlung und Gegenstrahlung ist keine Erfindung von irgendwelchen Verschwörerinnen.“
Es gibt nur Strahlung. Es gibt auch nur Straßenverkehr. Der Gegenverkehr ist eine subjektive Erfahrung.
Werner Schulz schrieb am28. Februar 2021 um 17:59
Hiermit stimme ich teilweise überein: Wenn die Bilanz nicht ausgeglichen ist, kommt es zu einer Erwärmung oder Abkühlung. Daher ist es ja wichtig , die Bilanzen aufzustellen und dann zu prüfen, ob Sie ausgeglichen ist.
Wenn Sie wirklich ein Gleichnis zur Bilanz der Erde machen wollen, fehlt da eine Zusatzbedingung: Die Ausgänge des Kontos sind vom Kontostand abhängig (so wie die abgegebene Energie von der Temperatur abhängig ist). Und dann können Sie sehr wohl einen Kontostand bestimmen, da sich irgendwann ein Gleichgewicht zwischen Ein- und Ausgängen einstellt.Sie erinnern sich vielleicht an das Eschenbachsche Würfelbeispiel? Dort wurde genau das gezeigt, was Sie hier als unmöglich bezeichnen, die Bestimmung der Temperatur eines Objektes bei einem gegebenen Energiezufluss. Falls Sie in dem Herangehen einen Fehler sehen, wäre ich daran interessiert.
„Die Ausgänge des Kontos sind vom Kontostand abhängig (so wie die abgegebene Energie von der Temperatur abhängig ist). Und dann können Sie sehr wohl einen Kontostand bestimmen…“
Natürlich sind die Ausgänge vom Kontostand abhängig: Je mehr man aufs Konto hat, um so mehr gibt man aus! Immer!
Damit kann man aber noch lange nicht den Kontostand bestimmen, das kapieren Strahlenberechner mangels Wissen und Berücksichtigung von thermodynamischen Wärmebilanzen und die Wärmespeicherfähigkeit des „Kontos“.
Messen Sie Ihre Temperatur, sie wird um die 36,5 Grad liegen. Bestrahlen sie sich 15 Min mit einer IR Lampe, messen Sie die Bestrahlungsintensität auf der Brust und die Abstrahlungsintensität am Rücken. Die Differenz ist groß, sie bekommen viel mehr Strahlen ab (und zwar IR Wärmestrahlen) als Sie abstrahlen. Nach Ihren Formeln müssten Sie viel wärmer werden, aber o Schreck, Ihre Körpertemperatur misst nach der Wärmestrahlung immer noch 36,5 Grad!
Weil Ihr Strahlensalat nur ein winziger Bruchteil der thermodynamischen Bilanzen aufzeigt!
Ein Wort fehlt und und verfälscht damit den Inhalt: „das kapieren Strahlenberechner…“ nicht.
Bitte um Nachsicht.
Peter Georgiev schrieb am 1. März 2021 um 13:48
Man kann sicherlich alles ins lächerliche ziehen, aber dieses einfache Beispiell hat nunmal Werner ins Spiel gebracht – ich habe nur das Gleichnis etwas realistischer gestaltet. Und wenn Sie eine feste Beziehung zwischen Kontostand und Ausgaben haben (wie es bei der Temperatur eines Körpers und der von ihm abgegebenen Wärmestrahlung der Fall ist), kann man einfach berechnen, welcher Kontostand sich einstellt. Monatliches Einkommen 1000 Währungseinheiten, 90% vom Kontostand werden ausgegeben, pegelt sich das Konto bei 1111 Währunseinheiten ein. (Sie können das gerne korrigieren, falls ich mich verrechnet habe …)
Falls man sich bei diesem einfachen Sachverhalt auf eine korrekte Lösung einigen kann, könnte man schauen, ob das auf andere Sachverhalte übertragbar ist oder nicht und wenn nicht, warum nicht …
Ich habe es bitterernst gemeint Herr Krüger.
Vor vielen Jahrzehnten habe ich ein Studentenkonto verwaltet, heute eines einer Großfamilie. Habe Konten von mäßig laufende und gut laufende Firmen verwaltet. Im Vergleich zu meinem ersten Konto:
Familienkonto: Eingang, Ausgang und Stand: 100 Mal höher.
Miese Firma: Eingang, Ausgang und Stand: 1000 Mal höher.
Gute Firma: Eingang, Ausgang und Stand. 10.000 bis x00.000 Mal höher.
Der Zusammenhang ist ohne Zweifel da, aber eher philosophisch und der Stand nicht mathematisch anhand von Eingang und Ausgang ermittelbar.
Das Gleiche Zusammenhang gilt, wenn man die Wärmebilanzen eines Kochtopfs, eines Schwimmbades und der Erde vergleicht: Energie-Eingang, -Ausgang und gespeicherte Wärme sind jeweils mehrfach höher. Aber anhand von zugeführter und abgeführter Energiemenge pro Zeit kann man weder die gespeicherte Energie und schon gar nicht die Temperatur errechnen.
Das ist einer der Grundsatzfehler der Strahlenvergleiche mit Temperaturerhöhungs-Behauptung.
Peter Georgiev schrieb am 1. MÄRZ 2021 UM 20:48
So wie ich es hingeschrieben habe, ist es ein einfaches mathematisches Problem.
Das für ein beliebiges f(0) und t gegen unendlich zu lösen kann man einfach iterativ machen (konvergiert sehr schnell) und sollte zu den von mir angegebenen 1111,11 kommen. Statt also einfach mal über simple Mathematik zu reden, kommen Sie mit einem Studentenkonto und schieben es auf eine philosophische Ebene.
Sie haben mal betont, dass man zur Berechnung der Temperaturveränderung Masse, spezifische Wärmekapazität und zugeführte Energie braucht. Gilt das plötzlich nicht mehr?
Jetzt werde Sie aber richtig albern Herr Müller.
Wenn man dafür verantwortlich ist, dass rund 50 Personen am jeden 1. den Lohn bekommen und ihre Familien ernähren, dann ignoriert man solche mathematische Spielchen und und hofft nicht, dass sich der Kontostand irgendwie einpegelt. Da hat man ganz andere Sorgen. Und der Kontostand schwankt erheblich. Man kann dabei nur gut schlafen, wenn man gut schätzen kann, es sei denn die Einnahmen sind konstant über die Ausgaben, das hat man aber praktisch nie. Es ist dann doch philosophisch zu betrachten, dass ein höherer Kontostand immer mit höheren Bewegungen verbunden ist. Kann man anhand der Bewegungen den Stand zu ermitteln: Wirecard hat Milliarden bewegt und das Konto ist gesperrt! Wo ist Ihre Formal dazu?
„Aber anhand von zugeführter und abgeführter Energiemenge pro Zeit kann man weder die gespeicherte Energie und schon gar nicht die Temperatur errechnen.“
Wenn ich einen halben Liter Wasser auf dem Herd von 10 auf 30 Grad erhitze, kenne ich den Zusammenhang der Größen Leistung, Zeit und Temperatur und kann anhand von 2 die dritte Größe errechnen. Drehe ich dann die Leistung so weit herunter, dass die 30 Grad unverändert bleiben, habe ich nur noch eine Größe, zugeführte gleich abgeführte Energiemenge pro Zeit und kann nichts mehr berechnen. Wenn die Wassermenge verdopple stellt sich eine etwas niedrigere Temperatur ein, bei einer anderen Flüssigkeit oder einen anderen Topf bei gleichen Energiezufuhr stellt sich das Gleichgewicht ebenfalls bei einer anderen Temperatur ein.
Bei einer ausgeglichene Energiebilanz, kann man nicht anhand der zugeführten Energie die Temperatur errechnen, die diese von zig Einzeleigenschaften abhängig ist (im Falle Material des Topfes, Dichtheit des Deckels, Menge und Art der Flüssigkeit u.s.w.). Wenn man auf der Erde die Wassermassen halbiert, würde sich der Temperaturverlauf ändern, und das ist in der kleinen Strahlenformel nun mal nicht enthalten, die angeblich eine exakte „Normtemperatur“ ohne Gegenstrahlung von -18 Grad ermittelt. Das ist Unsinn.
Der gesunde Menschenverstand hilft da weiter als einfache Formeln. Der Erste Hauptsatz vom gesunden MV lautet „Es gibt vieles zwischen Himmel und Erden, was man nicht kennt“, daher muss man das Unbekannte schätzen und beurteilen. Bei genügend Einblick in den Bilanzen und Geschäftsmodelle von Wirecard hätte ich die Pleite kommen sehen können, nicht aber anhand einer kleinen Formel wie Ihre oben berechnen, sondern durch den gesunden MV beurteilen. Und der sagt mir, die Erdtemperatur läßt sich nicht berechnen und wird durch viel mehr Faktoren bestimmt als nur CO2.
Und sie machen den Fehler, dass Sie keinen gesunden MV nutzen, sondern alles mit Hilfe von elementaren Gleichungen berechnen wollen.
Peter Georgiev schrieb am2. März 2021 um 10:52
Gefühlt haben 80%-90% des Kommentars nichts mit dem Kontovergleich oder Energiebilanzen zu tun. Wo kommt nur dieses Bestreben her, alles mögliche in die Diskussion zu werfen? Warum nicht einfach beim Kernthema bleiben? Warum nicht einfach mal anhand eines einfachen Beispiels Dinge klarstellen und dann kucken, wie/ob man es mit der Realität vereinen kann?
1. Sie behauten, Kontostand berechnen „ist es ein einfaches mathematisches Problem“, ich beweise am Beispiel Wirecard, dass es Unsinn ist.
2. Sie behaupten, Temperatur kann man anhand der zugeführte und abgeführte Leistung berechnen, ich beweise anhand vom Wassertopf-Beispiel, dass es Unsinn ist.
3. Ich behaupte aus Lebenserfahrung, wann man einen Prozess nicht exakt in jeder noch so kleinen Einzelheit kennt, dann berechnet man mit einer vereinfachten mathematischen Formel mehr Unsinn, als würde man mit dem gesunden MV das Ergebnis grob schätzt. Da Sie keinen gMV besitzen, glauben Sie es nicht. Aber Sie haben andererseits bewiesen, dass Sie mit Ihrer ganzen wertvollen Ausbildung weniger über die Wärmewirkung des Iglus verstehen als dessen Erfinder die Inuits mit ihrem gesunden MV, ganz ohne Physik-Ausbildung.
Das sind ganz klare Botschaften. Bei Ihnen erkenne ich keine Botschaften, nur Enttäuschung, dass ich Ihre Formeln nicht beklatsche.
Peter Georgiev schrieb am 3. März 2021 um 11:26
Ich habe gesagt, dass mein Beispiel ein einfaches mathematisches Problem ist. Es sollte veranschaulichen, dass man ein Konto, bei dem es eine funktionale Abhängigkeit zwischen Kontostand und Ausgaben gibt, berechnen kann. Ich habe eine ganz konkrete Situation vorgegeben und nicht allgemein von Konten geredet. Scheint nicht angekommen zu sein.
Warum habe ich das Beispiel gebracht: Werner brachte den Vergleich Temperatur mit Konto; die per Wärmestrahlung abgegebene Energie hängt von der Temperatur des Körpers ab
, die Ausgaben betragen 90% des Kontostandes:
. (Joule pro Sekunde, da es ein kontinuierliche Prozess ist). Wenn Sie die Ähnlichkeit nicht sehen, kann ich auch nichts tun.
Sie behaupten anhand des Wassertopf-Beispiels, dass es Unsinn ist. Ich wollte eigentlich vorschlagen, das analog zu Eschenbach mal durchzuexerzieren, aber wenn es schon daran scheitert, eine einfache Analogie zu verstehen, lasse ich das.
Kurisoserweise kamen Sie zu genau den gleichen Erkenntnissen wie ich. Da verstehen wir wohl gleich wenig (oder gleich viel).
Wir wollen doch bei der Wahrheit bleiben Müller. Bei Ihnen erfolgt die Erwärmung der Luft im Iglu durch Strahlung, der Inuit hat aber ohne Physik verstanden, dass er die Konvektion unterbricht.
Wir unterhaldarüber weiter, wenn Sie mindestens das Niveau der Inuits erreicht haben. Mir ist es langsam zu blöd.
Peter Georgiev schrieb am3. März 2021 um 17:08
Es kann jeder nachlesen, was ich geschrieben habe und es sich im direkten Vergleich zu Ihrem Text ansehen. Ich habe allgemein „verlieren weniger Energie an die Umgebung “ geschrieben und extra in der Fussnote alle drei Transportmechanismen genannt. Bei der Wärmestrahlung schrieb ich extra noch ein „auch“ dazu, um klarzustellen, dass es zusätzlich zu den anderen Transportmechanismen passiert.
Ich habe kein Problem damit, wenn mal etwas von mir geschriebenes nicht so rüber kommt, wie es gedacht war, kann dann durchaus auch an mir liegen. Räume ich gerne aus und mache nache einer Klarstellung weiter. Aber hier …?
Herr Mueller,
nun muss ich ihnen etwas recht geben.
Natuerlich kann man den Kontostand kennen, wenn man davon ausgeht, das die Ausgabe gleich dem Kontostand ist.
Das ist aber nicht so. Der Fehler ist eine Leistung W/m2 als Energiemenge zu betrachten.
Die Energiemenge ist in Joule anzugeben. Auf diesen Fehler von Ihnen und der Klimaunwissenschaft mache ich sie seit Jahren aufmerksam.
Am Uebergang von Oberflaeche zur Atmosphaere kommt es ausserdem zu mehreren Abhebungen auf dem Oberflaechenkonto. Und ein Teil der Ausgaben gehen direkt ins All.
Das andere sind Einzahlungen in die Atmosphaerenschicht, die wiederum auch Auszahlungen macht. Und nun wollen sie den Kontostand des Erdkoerpers daraus bestimmen. Das kriegen sie nie hin. Das Konto auf das sie gar nicht gucken, hat ist das des Erdkoerpers.
Und dieser macht es noch besonders schwer fuer sie, weil der Erdkoerper selber Geld druckt. Das ist vielleicht nicht viel, reicht aber in der Bilanzierung aller Konten, das das Erdkonto nie leer wird.
Als Finanzexperte wuerde ich sagen, das sich die Erde ueber die Atmosphaere zwar rueckversichert, das die Ausgaben des Kernkontos nicht zu hoch sind, muss aber den Verpflichtungen der Sonne gegenueber nachkommen. Die Erde macht das mit einem geteilten Kontosystem. Besser waere es nur ein Schalenkonto zu haben, das das Hauptkonto abschirmt. Da sieht man dann genau, wie gross der Einfluss des Sonnengeldgebers ist.
Er ist wie zum Beispiel bei der Venus minimal. Das Kernkonto zahlt da fast nichts an die Sonne. Womit wir fesstellen koennen, das die Sonne vom Kontostand der Venus keine Ahnung hat. Und genau das ist der Punkt.
Werner Schulz schrieb am 2. März 2021 um 17:11
Die Beziehung stand da und sie war nicht „Ausgaben gleich Kontostand“. Stimmen Sie zu, dass man unter der Bedingung, dass die Ausgaben ene funktionale Abhängigkeit zu den Einnahmen haben, den Stand des Kontos bestimmen kann?
Ich schrieb am 2. März 2021 um 22:10
Das sollte natürlich funktionale Abhängigkeit zm Kontostand heissen, wie ich in den vorangegangenen Kommentaren schrieb …
Nein sie haben kein Recht.
Sie beziehen sich mit ihrer Äußerung auf die Temperatur, diese ist zwar funktionell ueber das SB Gesetz mit der Leistung verbunden. Aber sie koennen damit immer noch nicht den eigentlichen Energieinhalt feststellen. Den Energieinhalt können sie erst berechnen wenn sie auch die Masse kennen.
Das SB Gesetz hat nur eine Flächenabhängigkeit, aber keine zur Masse.
Die Temperatur entspricht im Beispiel nur einer Kategorisierung des Bankkontos in arm oder reich. Und natürlich nehmen sie einem reichen Konto mehr ab. Aber den Kontostand kennt man trotzdem nicht. Arm und Reich ist eigentlich dimensionslos, kann aber skaliert werden so wie die Temperatur.
Die Masse wäre eventuell der Gegenwert in Gold. Wenn sie den kennen und den Goldpreis natürlich, dann kennen sie den Kontostand. Hier hört der Vergleich spätestens auf, da es zu abstrakt wird. Das hilft auch keinem!
Werner Schulz schrieb am4. März 2021 um 15:38
Ich hatte Sie konkret nach dem Kontobeispiel gefragt. Ist das wirklich so schwer, erst mal Einigung in einfachen Dingen herzustellen und sich dann komplexeren Dingen zuzuwenden?
Sie konnten am Beispiel sehen, dass sich das Konto bei einem sehr konkreten Zahlenwert einpegelte.
Mein nächster Schritt wäre gewesen, sich den Eingang, also den Energiezufluss anzusehen (in Abhängigkeit von zufliessener Energie, Masse, spezifischer Wärmekapazität). Das hat aber kaum Sinn, wenn man sich nicht mal über so einfache Dinge einigen kann …
Herr Mueller,
machen wir es doch einfach ganz kurz.
Ich habe auf meinem Konto 100o Euro pro Monat Gehalt. Ich habe jeden Monat genau 1000 Euro Ausgaben.
Wieviel Geld ist auf meinem Konto?
Nennen sie die Bedingung, die sie noch brauchen, um eine Aussage zu machen.
Als Alternative erklaeren sie den Mitlesern wie es sein kann, das 1 Liter Wasser bei einer bestimmten Temperatur weniger Joule enthaelt, als 2 Liter Wasser bei gleicher Temperatur.
Da die Abstrahlung nur von der Temperatur abhaengig ist, aber nicht von der Masse, sehe ich nicht wie sie ueber die Temperatur und die Strahlstaerke eine Beziehung zum numerischen Energieinhalt herstellen wollen.
Wenn die Bilanz ausgeglichen ist, haben sie auch mit dem Wissen dieser zusaetzlichen Groesse (Temperatur) keine Ahnung wieviele Joule da sind, und beim Konto ist es genau so.
Werner Schulz schrieb am 5. MÄRZ 2021 UM 16:19
Kürzer und deutlicher als in 2. MÄRZ 2021 UM 0:15 kann ich es nicht formulieren. Wenn Sie dort nicht alle relevanten Informationen entnehmen können, hat eine Diskussion nicht viel Sinn. Hmm … Aber da ich dort einen Fehler beim Abschreiben gemacht habe schreib ich es einfach nochmal hin:
mit f(0) = 0. 90% des Geldes auf dem Konto werden ausgegeben, 1000 kommen hinzu …
Herr Mueller,
wieviel Geld habe ich denn nun auf meinem Konto?
Woher wollen sie denn wissen das 90% von meinem Konto 1000 Euro sind?
Fuer die Fragestellung taugt ihre Gleichung nicht.
Werner Schulz schrieb am 6. MÄRZ 2021 UM 10:44
Wenn sich ihr Konto so verhält, wie von mir spezifiziert, pegelt es sich auf dem von mir genannten Stand ein. Falls ich mich verrechnet habe, korrigieren Sie mich bitte.
Und bitte verlieren Sie nicht den Ausgangspunkt aus den Augen: 1. MÄRZ 2021 UM 10:12. Es ging um die Frage, ob man ein System, das sich in einem Gleichgewicht befindet, berechnen kann. Das Konto war nur ein Beispiel.
Ich frage mich nach der Ursache der nicht enden wollenden „Experten“-Diskussion über die Klimawirksamkeit von CO2 in der Atmosphäre. Dazu tragen sicher auch Meldungen des DWD vom 26.2.2021 bei: „Mit 1,8 Grad Celsius (°C) lag der Temperaturdurchschnitt im Winter 2020/21 um 1,6 Grad über dem Wert der international gültigen Referenzperiode 1961 bis 1990. Im Vergleich zur aktuellen und wärmeren Vergleichsperiode 1991 bis 2020 betrug die Abweichung immer noch +0,4 Grad.“ Solche Meldungen sind sowohl nach dem meteorologischen als auch nach dem astronomischen Kalender verfrüht. Die Daten sind zwar formal richtig, trotzdem meiner Meinung nach übertrieben. Wetter bedingte Temperatur-Mittelwerte sind eine stark fluktuierende Größe. Dies ist auch für 30-jährige Klimaperioden der Fall. Beispiel: Unsere Jahreszählung beginnt mit einem angenommenen Geburts-Jahr Christi. Dieses ist aber nicht genau bekannt und könnte auch 7 Jahre früher gewesen sein. Die Klimaperiode 1991-2020 könnte also auch schon 1984-2013 gewesen sein. Dann wäre die Änderung zur vorhergehenden Klima-Periode nicht 1,2°C sondern 0,8 °C. Die Klima-Periode 1961-1990 (0,2 °C) war kälter als die Periode 1901-1930 (0,4°C). Warum traut man den Menschen nicht die Fähigkeit zu Temperaturen zu beurteilen, sondern benutzt das Vehikel der Referenz-Temperaturen? Dies ist meiner Meinung nach nur Panik-Mache.
Laut Herrn Krueger hier hat CO2 eher nichts damit zu tun.
Eigentlich wusste man das schon, aber es ist gut wenn es noch mal gesagt wird.
Danke Herr Krueger!
Lieber Admin! Ich habe mal etwas überlegt, was der Fehler sein könnte, wenn auf erster Ebene bei den Kommentaren Umbrüche und Leerzeilen weg sind. Bei mir im Forum, allerdings nicht WordPress, gibt es eine Schnellansicht. Die bewirkt genau das, in dem Fall als erste Information zu einem Kommentar sinnvoll. Einfach mal bei den Einstellungen schauen, ob diese ungewollt aktiviert ist.
Liebe Leser, mal ein paar allgemeine Strahlungsgedanken!
Vorab, meine Spielwiese ist Hochfrequenztechnik, hatte nur wenige Semester Physik.
Einige Kommentare zuvor wurde der Mikrowellenofen genannt.
Üblicherweise arbeiten die Dinger mit 2,4 GHz, etwa 13 cm Wellenlänge.
Man kann einer Wellenlänge eine Temperatur zuordnen, z.B. Farbtemperatur.
Hier ein Tool online, damit man nicht per Hand rechnen muss:
https://rechneronline.de/spektrum/
Gibt man dort 2,4 GHz ein, kommt man auf knapp über 0 Kelvin, ca. -273 °C.
Damit kann man kaum eine Speise erwärmen.
Geheimnis, das Gargut (Wasser) ist üblicherweise ein verlustbehaftetes Dielektrikum.
Zudem, Wasser ist elektrisch leitend, die Speise bildet eine Art Antenne.
Es fließt Strom, das Essen (elektrischer Widerstand) wird direkt durch Strom beheizt.
In den Kommentaren ging es häufiger um Rückstrahlung durch Kohlenstoffdioxid.
Soweit mir bekannt, lässt sich CO2 hauptsächlich auf 15 µm anregen, Peak.
Gibt man die Wellenlänge beim Tool ein, kommen ca. 193 Kelvin oder -80 °C heraus.
Selbst der Südpol ist meist wärmer als -80 °C.
Mit so einem Strahler wird man wohl kaum die Erde aufheizen können.
Wenn CO2 die Erde irgendwie erwärmen sollte, muss das anders funktionieren.
Deswegen nicht ohne Grund einleitend der Mikrowellenofen als Denkanstoß.
Danke Herr Schöllhammer!
ich möchte gerne Ihre Gedanken ergänzen, zumal ich die Mikrowelle ins Spiel gebracht habe:
Bei allen Diskussionen über Strahlung und CO2 geht es immer um den thermodynamischen Prozess Wärmeübertragung durch Strahlung. Dabei kann die Wärmeübertragung nur von warm nach kalt erfolgen.
Im Mikrowellenherd passiert etwas ganz anderes, es finden zwei Energieumwandlungsprozesse statt: Strom wird in einer kalten Strahlung bestimmter Wellenlänge umgewandelt, die dann im Wasser zu Wärmeenergie umgewandelt wird, wie von Ihnen beschrieben. Es sieht so aus als könnte Wärmetransport von kalt zu warm erfolgen, was thermodynamisch ausgeschlossen ist. Es sind aber andere Prozesse als die Erwärmung durch Sonnenstrahlen.
Ich kann auch immer wieder nur plädieren, mehr den gesunden Menschenverstand als pure Strahlenformeln einzusetzen. So z.B. hat meine Mutter zu Zeiten, wo es keine Mikrowellen gab, den Suppentopf zugedeckt und mit einem Schal umwickelt damit er nicht so schnell abkühlt. Unsere Strahlenexpertin Silke Kosch dagegen wird wahrscheinlich neben dem Topf ein Glas warmes Wasser stellen, damit sich Topf und Glas mittels Strahlung gegenseitig die Abkühlung verhindern.
„Unsere Strahlenexpertin Silke Kosch dagegen wird wahrscheinlich neben dem Topf ein Glas warmes Wasser stellen, damit sich Topf und Glas mittels Strahlung gegenseitig die Abkühlung verhindern.“
Nein!
Klein-Silke wird mit dem Glas warmen Wassers den Topf zum Kochen bringen
=> Gibt man die Wellenlänge [15 mue von CO2] beim Tool ein, kommen ca. 193 Kelvin oder -80 °C heraus.
Herr Schöllhammer, Ihr Argument erinnert mich an Dr. Thüne. Man sollte beachten, dass hier lediglich nach dem Wien’schen Verschiebungsgesetz berechnet wird, bei welcher Temperatur das Maximum bei 15 mue liegt. Die gesamte Emission ist bei +15 statt -80 Grad aber wegen T^4 deutlich höher. Die Messung an der Forschungsstation Barrow/Alaska ergab bei -2 Grad eine Gegenstrahlung aus dem CO2 von etwa 42 W/m², was einen Temperatureffekt am Boden von etwa +8 Grad ergibt.
„Die Messung an der Forschungsstation Barrow/Alaska ergab bei -2 Grad eine Gegenstrahlung aus dem CO2 von etwa 42 W/m², was einen Temperatureffekt am Boden von etwa +8 Grad ergibt.“
So so, man MISST also „eine Gegenstrahlung aus dem CO2“! Also das Messgerät hat sich mit dem CO2 abgesprochen, „nur CO2-Gegenstrahlen“, wie auch immer gekennzeichnet, und gar keine andere zu messen, oder man lügt sich in die eigene Tasche! Gottchen wie simpel man im Oberstübchen gestrickt sein, um so etwas zu glauben?
Also „42 W/m2 “ ergibt +8 Grad!! Mit so einer Behauptung fliegen Sie aus jedem Thermodynamik-Seminar hochkant raus. Grad oder Kelvin können sie nur über Masse in kg, Energie in Joule und spez. Wärmekapazität in J/kg*K berechnen.
Physik muss man lernen, einfach im Lotto gewinnen oder in den Massenmedien einatmen geht nicht. Mit Ihren Behauptungen können Sie auf dem Jahrmarkt auftreten, wenn er mal wieder geöffnet ist!
Sehr geehrter Herr Dietze!
Mit o.g. Tool habe ich die Wellenlängen im Bereich -2 bis +15 °C ermittelt.
10,0 µm => 289,8 K ~ 16,7 °C
10,7 µm => 270,8 K ~ -2,3 °C
Lässt sich CO2 im Bereich 10,0 bis 10,7 µm anregen?
Der Bereich ist ja immerhin schon deutlich vom Peak bei ca. 15 µm entfernt.
Oder habe ich da irgendwo einen Denkfehler?
=> Lässt sich CO2 im Bereich 10,0 bis 10,7 µm anregen? Der Bereich ist ja immerhin schon deutlich vom Peak bei ca. 15 µm entfernt.
Herr Schöllhammer, Sie missverstehen da etwas. Ich schrieb „dass hier lediglich nach dem Wien’schen Verschiebungsgesetz berechnet wird, bei welcher Temperatur das Maximum bei 15 mue liegt. Die gesamte Emission ist bei +15 statt -80 Grad aber wegen T^4 deutlich höher. Die Messung an der Forschungsstation Barrow/Alaska ergab bei -2 Grad eine Gegenstrahlung aus dem (Spektrum des) CO2 von etwa 42 W/m²“. Das CO2 wird ja nicht nur auf der 15 mue-Linie (es gibt noch über 30.000 weitere) – sowohl durch IR-Absorption als auch durch diverse Stöße von anderen Molekülen – angeregt. Was zählt, ist doch die gesamte (!) Absorption und thermische Re-Emission zum Boden (in W/m²).
Leider gibt es diesen Modus hier nicht.
Ein paar physikalische Anmerkungen eines überzeugten Quantenmechnikers:1) Die Annahme, dass „Luft“ ein schwarzer Strahler ist (also gemäß der Planck’schen Strahlungsformel ein kontinuierliches von der Temperatur T abhängiges Spektrum an Photonen aussendet), ist sehr heikel. Gase haben im Gegensatz zu Festkörpern und Wasser ein diskretes Spektrum (nur Photonen mit gewissen Wellenlängen bzw. Frequenzen möglich, aber Doppler-Verbreiterung der einzelnen Linien möglich), so dass die Herleitung der Stefan-Boltzmann Leistungsdichte durch Integrieren über alle Photonen-Wellenlängen (bzw. Frequenzen) der Planckschen Strahlungsformel nicht funktioniert. Möller’s Taschenbücher sind unterhaltsame Literatur mit vielen mathematischen Formeln, aber bei der Behandlung der Gegenstrahlung macht er soweit ich mich entsinne auch die Schwarzkörper-Näherung für die Rückstrahlung der Luft. Und ich muss sagen, dass ich seine Herleitung sehr didaktisch finde, d.h. er umschifft alle Klippen und Untiefen durch den Brustton tiefster Überzeugung , damit ja kein Zweifel an der Richtigkeit der getätigten Hypothesen und Annahmen aufkommen möge.2) Hermann Hardes Paper von 2013 „Radiation and Heat Transfer in the Atmosphere: A Comprehensive Approach on a Molecular Basis“ geht in die richtige Richtung und zeigt, dass die mittlere freie Weglänge der von der Erde abgestrahlten Photonen der Wellenlänge 15 Miktrometer ziemlich klein ist und bei ca. 10 m über der Erde alle derartigen von der Erde ausgestrahlten Photonen bereits von den wenigen CO2-Molekülen absorbiert sind. Diese im angeregten Zustand befindlichen CO2-Moleküle regen sich nicht ab durch Emission eines 15-Mikrometer Photons sondern übertragen ihre Energie durch inelastische Kollisionen mit den umherfliegenden N2- oder O2- Molekülen. Die mittlere Kollisionsrate in der Luft bei diesen Höhen über dem Boden beträgt einige Milliarden mal pro Sekunde und damit ist diese Zeitskala wesentlich kleiner als die durchschnittliche Dauer des angeregten CO2-Zustandes: die CO2-Abregung findet durch Energieübertragung auf andere Moleküle statt. Der umgekehrte Vorgang ist jedoch weniger wahrscheinlich, wie die Analyse mit den Einstein-Koeffizienten zeigt. Damit werden die Luftmoleküle mit der Zeit immer schneller und die Luft-Temperatur nimmt damit theoretisch mit der Zeit monoton zu.3) Wie wird der Boden (=Festkörper) erwärmt? Der theoretische Festkörper-Physiker weiss, dass die Erwärmung eines idealisierten Kristallgitters durch Phononen (also quantisierte Gitterschwingungen) charakterisiert ist: die hochenergetischen Phononen heissen „optische Phononen“, weil sie durch Photonen angeregt werden. Die niederenergetischen heissen „akustische Phononen“, weil sie durch Schallwellen (hier konkret: auf den Festkörper auftreffende Luftwellen bzw. Luftmoleküle) angeregt werden. Ein einfaches Experiment im Badezimmer zeigt, dass der Heizlüfter mit warmer Luft die Kacheln wesentlich langsamer (fast überhaupt nicht) erwärmt (akustische Phononen) als im Vergleich dazu der Heizstrahler (optische Phononen). Münchner werden sich an die Vor-Chorona-Zeiten mit Föhnwetter erinnern: die Luft ist warm und man kann mitten im Winter mit T-shirt und kurzen Hosen im Cafe sitzen, aber die Flip-Flops sollte man tunlichst zu Hause lassen weil der Boden immer noch kalt ist: die warme Luft hat ohne Sonneneinstrahlung keine Chance den Boden innerhalb des Tages zu erwärmen. Das oben erwähnte Glasscheibenexperiment würde in dieses Bild hineinpassen, auch wenn die Phononen-Dispersionskurven für Glas als ungeordneter Festkörper wohl doch anders aussehen, als die üblichen Phononen-Dispersionskurven für geordnete Festkörper. 4) Wie kann die durch CO2-Kollissionen „erwärmte“ Luft mit immer weiter ansteigenden Temperaturen ihre Wärmeenergie schliesslich abgeben? Die qualitative Antwort ist leicht zu geben: eigentlich nur durch Wechselwirkung mit Wasseroberflächen. Die beschleunigten Luftmoleküle kicken H2O-Moleküle aus dem Wasserverbund heraus und verlieren damit an kinetischer Energie und die „Lufttemperatur“ sinkt ab. Quantitativ ist die Antwort weniger einfach, da man die aktuelle Mechanik der Verdunstung von Wasser noch nicht ganz verstanden hat. Alle paar Mikro- oder Millimeter haben die Luft-, Wasser- und Luft-Wasser-Schichten andere Nichtgleichgewichts-„Temperaturen“ und die Clausius-Clapeyron Gleichung für Verdunstung ist doch zu rudimentär für den komplexen Sachverhalt. Auf die anschliessenden Konvektionsvorgänge und die Kondensation des Wasserdampfs in sehr grossen Höhen vermutlich durch quantenmechanische Abstrahlungsvorgänge von 50% in den Weltraum und 50% zurück nach unten, will ich jetzt gar nicht eingehen.Fazit: die obigen Punkte stellen eigentlich ein Programm dar, wie man die Rolle von CO2 sachlich in eine Theorie der Athmosphären-Erwärmung einbauen könnte, welche auf first principles beruht. Die Verwendung der Stefan-Boltzmann Gleichung ist manchmal zulässig und manchmal halt nicht. Wichtig sind die Strahlungs-Spektren der Gase und ihre Ankopplungen an materialabhängigen Phononen-Spektren (z.B. mit Feynman Diagrammen zu rechnen) zum Verständnis der Erwärmungsvorgänge in der Umgebung. Makroskopische Transportgleichungen haben ihre Rechtferigung für Ingenieursanwendungen, sollten aber mikroskopisch vertretbar sein. Wie Meteorologen eine CO2-Rückstrahlung messen, wo die CO2-Moleküle ihre Anregungsenergie durch Kollision mit Luftmolekülen abgeben, ist mir bislang leider nicht verständlich.
Das ist glaube ich die beste Analyse die ich in dem Zusammenhang gelesen habe.
Akustische Photonen sind wohl im stofflichen Zusammenhang zu sehen, und schließt Konvektion und Molekülbewegung ein.
Ob the optischen Photonen Stofflich sind kann man sich wohl noch streiten.
Worauf man vielleicht noch Hinweisen kann, ist, das die Energielevel der Photonen eine Rolle spielen. Und die kalte atmosphärische Strahlung, so man sie abnimmt, kann einfach den Boden nicht mit niederenergetischeren Photonen erwärmen.
First Principle!
Achtung, nicht akustische / optische Photonen, sondern Phononen.
Danke fuer den Hinweis. Es sind Phononen.
Jaja. Die Realität ist mal wieder anders. In der unteren Atmosphäre herrscht das lokale, thermodynamische Gleichgewicht vor. D.h. dort halten sich abregende und anregende Stöße die Wage und Absorptionen und Emissionen sie Wage. Es befinden sich zu jeder Zeit CO2-Moleküle in angeregten Zuständen, aus denen sie auch emittieren kommen. Wer sollte es ihnen verbieten. CO2-Moleküle können bei über 0 Grad Kelvin immer emittieren. Schon da Stoßanregungen durch die umgebenden Luftmoleküle stattfinden.
„Es befinden sich zu jeder Zeit CO2-Moleküle in angeregten Zuständen, aus denen sie auch emittieren kommen. Wer sollte es ihnen verbieten.“
Die Stoßwahrscheinlichkeit im Verhältnis zur Anregungsdauer
„CO2-Moleküle können bei über 0 Grad Kelvin immer emittieren. Schon da Stoßanregungen durch die umgebenden Luftmoleküle stattfinden.“
Das du nur glauben.
Es gibt nur einen Energieerhaltungssatz – einen „Absorption = Emission-Satz“ gibt es nicht.
Geh tauchen…
Herr Krueger,
Heisst das, dass CO2 in der oberen Atmosphaere eher nicht strahlen kann?
Vorheringen Kommentar bitte löschen. Da ist etwas falsch gelaufen. Hier die Kurzversion.
Auch da strahlt es. Daher wirkt CO2 in der Stratosphäre und Mesosphäre auch abkühlend.
Die von der Erdoberfläche ausgehende Infrarotstrahlung wird von den Treibhausgasen in der Troposphäre schon (nahezu) vollständig absorbiert und kann daher die Stratosphäre und die dort vorhandenen infrarotaktiven Treibhausgase nicht mehr erreichen. Doch sie werden trotzdem noch durch Zusammenstöße mit benachbarten Molekülen anderer Atmosphärengase angeregt. Da die Luft in dieser großen Höhe schon sehr dünn ist, strahlen sie einen Großteil der so gewonnenen Energie in den Weltraum ab, bevor diese durch erneute Zusammenstöße wieder an die Stratosphäre zurückgegeben werden kann. So geht die Energie unwiderruflich verloren und die Stratosphäre kühlt ab. Dieses Abkühlungseffekt nimmt mit einer steigenden CO2-Konzentration zu und ist sowohl in der Stratosphäre, also auch Mesosphäre zu beobachten.
Herr Krüger, den Beitrag können sie dann auch löschen lassen.
Wo bleibt nur ihr logisches Denken?
Wenn das CO2 oben in Richtung All strahlt, dann tut es das CO2 in der Troposphaere auch. Somit gibt es eine beständige Strahlung aus allen Teilen der Atmosphäre.
Welches Kriterium führt denn nun dazu das die Strahlung vom CO2 zur Abkühlung beiträgt?
Es stehen ja theoretisch immer 400 Molekülen in 1 Mill. 400 anderen nach oben und unten gegenüber.
Welches Kriterium führt dazu daß Strahlung ins All geht und nicht wieder hängen bleibt?
„Auch da strahlt es.“
Joo, Krüger ist wahr.
Am stärksten strahlts in Schweden…
Geh tauchen!
@Markus Kreer
Zitat: Wie Meteorologen eine CO2-Rückstrahlung messen, wo die CO2-Moleküle ihre Anregungsenergie durch Kollision mit Luftmolekülen abgeben, ist mir bislang leider nicht verständlich.
Das Messgerät nennt sich „Atmospheric Emitted Radiance Interferometer – AERI“. In deutsch würde man das Doppel-Referenz-Fourier-Transform-Infrarot-Spektrometer nennen. Mit diesem Gerät wird nicht die Rückstrahlung gemessen, sondern die differenziell-emittierte Strahlung eines Atmosphärenbereiches.
Grundlage bildet die Veroffentlichung: Henry E. Revercomb, H. Buijs, Hugh B. Howell, D.D. LaPorte, William L. Smith, and L.A. Sromovsky, 1988, Radiometric Calibration of IR Fourier Transform Spectrometers: Solution to a Problem with the High-Resolution Interferometer Sounder, Applied Optics 27(15), 3210-3218
Siehe: Atmospheric Emitted Radiance Interferometer. Part II: Instrument Performance – Knuteson et al., 2004
Messungen finden Sie hier: Jülich ObservatorY for Cloud Evolution = JOYCE
https://obs.meteo.uni-koeln.de/doku.php?id=aeri
oder auch hier: https://www.ssec.wisc.edu/aeri/
Mfg, Werner Holtz
@Werner Holtz
Ganz herzlichen Dank für die links zum AERI. Da werden sentimentale Erinnerungen an mein F-Praktikum wach. Das Paper von Henry E. Revercomb et al. (1988) habe ich mir angesehen und soweit ich es verstanden habe, wurde dort die „upwelling radiation“ in verschiedenen Höhen mittels Flugzeugs vertikal vermessen und den einzelnen Wellenlägen durch Vergleich mit zwei blackbodies bekannter Temperatur eine Temperatur zugeordnet. So weit so gut. Interessanter ist dann das Paper von Turner and Löhnert 2014, das auf der AERI-Seite der Uni Köln verlinkt und frei herunterladbar ist. In diesem wird auf das Thema der Messung von „downwelling radiation“ ausführlich eingegangen. Inwieweit diese „downwelling radiation“ die Abstrahlung der 15 Mikrometer Photonen durch das CO2 beinhaltet, ist mir nicht ganz klar. Jedenfalls scheinen komplexe statistische Algorithmen (Maximum Likelihood Schätzungen, Bayesischer Update-Algorithmus, Neuronale Netze) zur Auswertung der Messungen notwendig zu sein, um eine physikalische Interpretation möglich zu machen. Können Sie mir sagen, ob wir tatsächlich mit AERI eine vertikal von oben kommende 15-Mikrometer Strahlung vom CO2 herrührend messen? Ich nehme an, dass die 15-Mikrometer Strahlung durch die Sonne selbst eine ziemlich geringe Intensität hat, so dass die Identifikation wirklich dem CO2 zugeschrieben werden könnte. In dem Falle wäre das theoretische Argument, dass sich mehr oder weniger alle angeregten CO2-Moleküle in Bodennähe durch inelastische Stösse abregen und nicht durch Abstrahlung der 15 Mikrometer Photonen, zu modifizieren. Der Endeffekt wäre jedoch der gleiche: die abgestrahlte Energie im 15 Mikrometer Bereich (plus minus Doppler- und Lorentz-Verbreiterung etc) bleibt (vorübergehend) am Boden.
Beste Grüsse
Markus Kreer
@Markus Kreer
Zitat: Turner and Löhnert 2014 – Die wollen aus verschiedenen AERI-Messungen in unterschiedlicher Höhe den Liquid Water Path (LWP) und Precipitable Water Vapor (PWV) ermitteln.
Zitat: Jedenfalls scheinen komplexe statistische Algorithmen (Maximum Likelihood Schätzungen, Bayesischer Update-Algorithmus, Neuronale Netze) zur Auswertung der Messungen notwendig zu sein, um eine physikalische Interpretation möglich zu machen.
Nein, man benutzt zwar bestimmte Mechanismen zur Fehlerkorrektur und -bestimmung, aber so komplex ist es auch nicht. Wo haben Sie das her?
++ Messprinzip bzw. Messverfahren der AERI
Das Problem bei der Messung ist, das man alle Intensitäten mißt (I + IE)/(I0 + IE) != I/I0. Man muss eine Möglichkeit bzw. Methode finden, diese störenden Intensitäten IE zu eliminieren.
Aus der Kalibrierung der Apparatur kann man folgendes Messprinzip und Auswertemethode ableiten:
Die Aufnahme eines Emissionsspektrums der Atmosphäre muss vom Systemrauschen befreit werden, welches vor allem durch die Eigen-Energie vom Spektrometer entsteht, um das medium-spezifische Emissionsspektrum zu erhalten. Dabei wird zusätzlich zur medium-spezifischen Aufnahme des Emissionsspektrums der Atmosphäre noch zwei simultane Referenz-Emissionsspektren von bekannten Strahlern bei zwei unterschiedlichen konstanten Temperaturen (ABB, HBB) gemessen. Die beiden Referenz-Spektrogramme sind mit demselben Systemrauschen behaftet, wie das medium-spezifische Emissionsspektrum der Atmosphäre, da für die simultanen Messungen dasselbe Spektrometer verwendet wird. Man hat jetzt drei unbekannte Größen, den messungs-abhängigen Rausch-Parameter der Apparatur, eine messungs-abhängige Geräte-Konstante und den medium-spezifischen Parameter. Somit ergibt sich ein Gleichungssystem aus drei simultanen Messungen mit drei unbekannten Größen und damit kann das Emissionsspektrum der Atmosphäre vom Systemrauschen befreit werden.
Mathematisch vereinfacht formuliert (normalerweise nutzt man die Interferogramme direkt) gilt für die simultan-aufgenommenen Spektren:
J(a) = C*{L[T(a)] + T(sys)}
J(c) = C*{L[T(c)] + T(sys)}
J(h) = C*{L[T(h)] + T(sys)}
wobei C – die messungs-abhängige Geräte-Konstante ist, die Größe T(sys) den messungs-abhängigen Rausch-Parameter und L[T(i)] bzw. J(i) den medium-spezifischen Parameter definiert. Die Indizes stehen für c = Cold-Blackbody, h = Hot-Blackbody und a = Atmosphäre.
Diese 5 Parameter/Größen kann man bestimmen bzw. können als bekannt angesehen werden J(a) – Spektrum der Atmosphäre, J(h) – Spektrum vom Hot-Blackbody und J(c) – Spektrum vom Cold-Blackbody, zudem sind die Temperaturen T(h) und T(c) der beiden Referenz-Blackbodies bekannt und somit auch L[T(h)] und L[T(c)]. Die drei unbekannten Größen sind C, T(sys) und L[T(a)]. Aus dem linearen Gleichungssystem erhält man für die (spektrale) Strahldichte L[T(a)]:
L[T(a)] = L[T(c)] + {L[T(h)] – L[T(c)]}*[J(a) – J(c)]/[J(h) – J(c)]
Hier wollte ich noch ein Bild einfügen, aber EIKE meckert dann „Kommentar zu lang“.
Zur Kalibrierung werden die beiden Blackbodies genutzt, um die Steigung und den Offset zu bestimmen, die die lineare Instrumentenreaktion bei jeder Wellenzahl definieren.
Im Dokument bei der Beschreibung der Interferogramme kann man folgende Interpretation vom Messverfahren ableiten:
Man mißt ein Spektrogramm (Complex Spectra), das sich aus zwei Spektrogrammen von bekannten Strahlern mit dem Systemrauschen und einem Spektrogramm vom Medium mit dem Systemrauschen zusammensetzt, die simultan gemessen werden. Aus den zwei Spektrogrammen der bekannten Strahler bildet man ein Differential-Spektrogramm, dass nur das Systemrauschen enthält. Aus dem gemessenen Spektrogramm (Complex Spectra) wird mit Hilfe der zwei Spektrogramme der bekannten Strahler und dem Differential-Spektrogramm vom Systemrauschen das medium-spezifische Spektrogramm der Atmosphäre extrahiert.
Der Imaginär-Teil der FFT kennzeichnet dabei den Systemfehler vom Instrument, der während der Messung auftritt.
Das ursprüngliche AERI-Instrument konnte in diesen drei Spektralbereichen messen:
Channel 1: 590 – 1070 cm^-1 (17 – 9,3 µm)
Channel 2: 1040 – 1930 cm^-1 (9,6 – 5,2 µm)
Channel 3: 2070 – 2750 cm^-1 (4,8 – 3,6 µm)
Eine Weiterentwicklung vom AERI-Instrument ist das REFIR-PAD Instrument mit einem spektralen Messbereich von 100 – 1400 cm^−1 (100 – 7,1 µm).
http://refir.fi.ino.it/refir-pad-te05_en.html
https://www.atmos-meas-tech.net/12/619/2019/amt-12-619-2019.pdf
Ich kann Ihnen die Emissionsfähigkeit vom CO2 im Oberflächen-Bereich der Atmosphäre auch aus der mikroskopischen Sichtweise (Doppler- und Druckverbreiterung) herleiten.
Siehe: ## Teil 1, 2 und 3
https://www.eike-klima-energie.eu/2020/02/08/kritisches-hinterfragen-des-ipcc-basis-modell-kt97-seines-atmosphaerischen-treibhauseffektes-seiner-ableitung-von-co2-mit-einem-strahlungsantrieb-von-32-w-m%C2%B2-und-seiner-politischen-dimension/
Mfg, Werner Holtz
@ Herrn Werner Holtz
Wie passt das von Ihnen beschriebene instrumenteninterne Rechenverfahren zu Ihrer Aussage im Kommentar vom 4. Dezember 2019 um 19:27 Uhr, Zitat:
„Welche „erheblichen Rechenprozesse“ meinen Sie? Ein völlig sinnfreies Geschwätz.“
@U. Weber
In welchen Zeiten leben Sie? Ein Rechenstab wird dafür nicht verwendet. Herrje, Herr U. Weber – Eine FFT ist unter den heutigen rechner-technischen Gegebenheiten im Bruchteil einer Sekunde erledigt. Können Sie mal mit Maple 2020 oder Mathematica oder ganz professionell mit PV Wave testen. Ich habe lange Zeit mit Cray Supercomputern gearbeitet (Die Maschinen arbeiten mit Peta-FLOPS oder neu Exa-FLOPS), die Maschinen zucken nicht mal, wenn man den Rechner tausende FFTs zur Berechnung hinwirft.
Mfg, Werner Holtz
@ Herrn Werner Holtz
Ihnen fehlen offenbar die Mittel, um zwischen RECHEN-AUFWAND und ZEIT-AUFWAND zu unterscheiden.
http://refir.fi.ino.it/refir-pad-te05_en.html
Das Gerät wird für die Messung in großer Höhe (34km) für die Messung der ausgehenden Strahlung eingesetzt. Man sieht sehr schön daß CO2 die Bodenabstrahlung absorbiert hat und mit der lokalen Temperatur abstrahlt.
Eine „Messung“ der Einstrahlung am Boden ist damit im CO2-Absorptionsspektrum nicht möglich!
@ Herrn Markus Kreer
Danke für die differenzierte Zusammenfassung. Mich würde interessieren, was Sie von einer S-B-Inversion halten, die unbeleuchtete Flächen einschließt (Faktor4-THE-Ansatz mit „-18°C“ inklusive der Nachtseite der Erde). MfG – U. Weber
=> Mich würde interessieren, was Sie von einer S-B-Inversion halten, die unbeleuchtete Flächen einschließt
Herr Weber, unbeleuchtete Flächen (und solche die krasse Temperaturunterschiede aufweisen) in die S-B Inversion einzuschliessen ist natürlich wegen T^4 Unsinn – was sich ja auch beim Mond zeigt. Bei der rotierenden, gut speichernden und Wärme umverteilenden Erde weichen aber (auf dem allergrößten Teil der Oberfläche einschliesslich der Nachtseite) die Werte von T nur um einige Prozent ± vom Mittelwert ab.
Deshalb kann man in sehr guter Näherung den CO2-Verdoppelungseffekt einfach mit globalen Mittelwerten modellieren, d.h. die solare Einstrahlung auch auf die Abstrahlfläche von 4PiR² verteilen – selbst wenn am Tag die Sonne im Zenith stark heizt, aber nachts nicht scheint. Damit erledigt sich das Hemisphären-Problem, welcher Teil der Wärme tagsüber weggespeichert wird (unter Absenkung der S-B-Temperatur, was Sie leider nicht berücksichtigen) und auf die Nachseite übertragen wird – wo dieser Anteil der Wärme mit S-B auch eine deutlich geringere Abstrahltemperatur als +15 Grad ergibt.
@ Herrn U. Weber
den guten alten Stefan-Boltzmann wende ich am liebsten nur auf eine Fläche von 1 Quadratmeter an, falls diese Fläche der Strahlung eines schwarzen Körpers ausgesetzt ist und an kein Wärmebad gekoppelt ist. Da bin ich als theoretischer Physiker auf der sicheren Seite. Ansonsten würde ich bei astronomisch grossen Objekten zuerst über die Tagesseite diese „kleinen“ Flächensegmente aufaddieren, also nur über Tagesseite integrieren a la Gerlich & Tscheuschner (2009), denn damit bekomme ich automatisch die Einstrahlwinkel berücksichtigt, welcher von der geographischen Breite abhängig ist: denn wenn die Sonne senkrecht auf das Flächenstück von 1 Quadratmeter scheint, wird die Erwärmung desselben eine andere sein, als wenn der Einstrahlwinkel im hohen Norden zur Herbstzeit sehr flach ist. Ob die Division der „Tagesseite“ durch 4 pi r^2 eine gute Näherung für die „mittlere Temperatur“ ist, bezweifle ich. Stattdessen würde ich die Nachtseite eingehender studieren und schauen, welche Wärmekapazität diese hat und welche Wärmemenge sie in den 12 Stunden vorher aufgeladen hat. Dann würde ich versuchen zu berechnen, welcher Anteil der tagsüber aufgeladenen Wärmemenge im Laufe der 12 Nachtstunden abgestrahlt werden bzw. durch Konvektion an die Atmosphäre übertragen werden. Wie die Konvektion der Wassermassen zu behandeln ist, kann ich nicht sagen, ebenso muss ich zu den Wolken schweigen. Vermutlich ist die Abstrahlung der grösste Posten im Energie-Budget bei der nächtlichen Abkühlung von Land und Wasser (beide sind übrigens in akzeptabler Näherung schwarze Strahler). Beim Erdmond ist diese Rechnung gar nicht so schwer, da es dort weder Wassermassen noch Atmosphäre gibt und die Oberfläche fast einheitlich aus Regolith besteht. Und dort sieht man auch, dass die 4 pi r^2 nicht gerade ideal zur Bestimmung der „mittleren Temperatur“ ist. Und mit dem Begriff „mittlere Temperatur“ stehe ich auf Kriegsfuss, weil das eine unphysikalische Messgröße ist. Unser thermodynamisches System ist nicht nur nicht im Gleichgewicht sondern hat neben Tag und Nacht noch unterschiedliche Jahreszeiten auf der Tag- bzw. Nacht-Seite, also eigentlich unterschiedliche Thermodynamische Phasen. In dem Sinne sollte man die Temperaturveränderungen nur lokal untersuchen, so wie das die Herren Kämpfe und Kowatsch hier auch verdientermassen tun.
Beste Grüße
Markus Kreer
@ Herrn Markus Kreer
Ich bedanke mich für die ausführliche und (bis auf den 1 qm;-) nachvollziehbare Antwort. Das Problem der Nachtseite hatte ich hier mit der S-B-Umgebungsgleichung über die Wärmespeicherung behandelt. MfG – U. Weber
PS: Gerlich&Tscheuschner (2009) hatten eine Lehrbuchformel für die solare Strahlungsleistung (beispielsweise bei Hartmann 1994, ISBN 0-12-328530-5, Gl. 2.14) über den 24h-Tag integriert. Die daraus mit dem üblichen Faktor4-Ansatz für unsere Erde berechnete Durchschnittstemperatur Tphys=(-129°C = 144K) hatte den sogenannten THE durch einen Widerspruchsbeweis (144K#33K) widerlegt, bietet allerdings kein alternatives Modell für die terrestrische Temperaturgenese. Eine auf die Tagseite korrigierte G&T-Lösung (2x144K) bestätigt wiederum mein hemisphärisches S-B-Modell.
=> Eine auf die Tagseite korrigierte G&T-Lösung (2x144K) bestätigt wiederum mein hemisphärisches S-B-Modell.
Herr Weber, mit einer Sonne ergibt sich korrekt 288 K auf der (ruhenden oder rotierenden nicht speichernden) Tagseite und 0 K auf der Nachtseite, also als Mittelwert 144 K. Wenn Sie 2*144 K (also 288 K auf jeder Hemisphäre) habe wollen, brauchen Sie ZWEI SONNEN!
Da wir aber nur eine haben, brauchen Sie die Gegenstrahlung und den Treibhauseffekt! Ihre „Umgebungsgleichung“ können Sie vergessen – die postuliert nämlich die Gegenstrahlung, welche Sie ja ausschliessen.
„Wie Meteorologen eine CO2-Rückstrahlung messen, wo die CO2-Moleküle ihre Anregungsenergie durch Kollision mit Luftmolekülen abgeben, ist mir bislang leider nicht verständlich.“
Diese Frage kann ich Ihnen beantworten:
Mit einem sog. AERI- allerdings wird dabei im CO2-Absorptionsbereich nicht „gemessen“, sondern auf der Basis von MODTRAN und HITRUN „gerechnet“.
Was nicht weiter verwundern muß, da es ja in diesem Bereich bodennah nichts zu messen gibt…
@ besso keks
Danke, das war auch meine bisherige Vermutung. Ich bin aber immer offen für experimentelle Erkenntnisse.
Beste Grüsse
Markus Kreer
@WeberAls Anmerkung zur Gegenstrahlung nochmals. Diese funktioniert nicht wie ein Hänchengrill. Es verändert sich durch THG und Wolken die Abstrahlungshöhe ins All. Es wird nicht mehr direkt vom warmen Erdboden ins All abgestrahlt, sondern aus höheren, kälteren Schichten der Atmosphäre, wo es kälter ist. Damit geht vom Erdboden weniger Wärme ins All verloren. Folglich bleibt er wärmer. Die Gegenstrahlung verhindert den direkten Wärmefluss vom Erdboden ins All.
„Damit geht vom Erdboden weniger Wärme ins All verloren.“
Der Quatsch ist auch schon 100 mal widerlegt worden.
Dem Boden ist die Temperatur in 10km Höhe völlig egal. Er führt die Wärme per Konvektion, Strahlung und Verdunstung nach lokalen Bedingungen ab.
Daran kommt auch die Bremer Hilfsschulphysik nicht vorbei.
Krüger, geh wieder tauchen…
@Keks
Wie das funktioniert wird in diesem Video erklärt. Sollten selbst Sie verstehen können.
https://www.youtube.com/watch?v=4PAbm1u1IVg
Wird die geringe Wärmeleitung der Luft erwähnt?
Wenn nicht, dann hat der Autor die schon bestehenden Fehler der Klimaunwissenschaften nur wiederholt.
Gucke ich später rein.
=> „Damit geht vom Erdboden weniger Wärme ins All verloren.“ Der Quatsch ist auch schon 100 mal widerlegt worden.
Herr Keks, Sie halten das Prinzip der Gegenstrahlung für Quatsch weil Sie es nicht verstanden haben. Wenn von der Bodenabstrahlung (im vereinfachten StrahlungsmodelI) von 390 W/m² 300 absorbiert und 150 jeweils nach oben und unten re-emittiert werden, ist die Abstrahlung ins Weltall 150+90=240 W/m², die Strahlung zum solar beheizten Boden aber 240+150=390 W/m². D.h. die dort zusätzlich absorbierte Gegenstrahlung verringert die Strahlungskühlung des Bodens um 150 W/m² – wirkt also wie eine wärmende „Strahlungsdämmung“.
„Herr Keks, Sie halten das Prinzip der Gegenstrahlung für Quatsch weil Sie es nicht verstanden haben.“
Wer hier ständig mit Perpetuum Mobiles um sich wirft und einfachste Grundprinzipien der Thermodynamik nicht kapiert hat, sollte mit solchen Behauptungen vorsichtig sein.
Zu Ihrer Aussage:
-Bodennah wird nichts remittiert
-Wenn was remittiert würde, könnte es den Boden nicht erwärmen
Sie scheitern bereits beim einfachsten aller Gegenbeweise, dem 2-ten Hauptsatz.
Den Rest erspare ich mir (und Ihnen)
Der Typ hat noch nicht mal was vom atm. Fenster gehört – ab in die Tonne!
Ich schliesse mich Herrn Keks an.
Das Video arbeitet bekannten Fehlern und es macht unhaltbare Annahmen die keiner Pruefung standhaelt.
1. Energie wird in W/m2 angegeben. Das ist keine Einheit der Energie. Das runterrechnen der Eingangsleistung der Sonne, ist falsch. Von der Kraft der Sonne, kann man sich im Fruehling selber ueberzeugen.
2. Die Annahme das die Abstrahlung von 5 km und 500 mbar kommt, beruht einzig darauf, das man dort 255K messen kann. So wird es im Video begruendet. Wie Herr Keks es sagt, wird das atmosphaerische Fenster vollstaendig ignoriert. Die Annahme das mehr CO2 die Abstrahlhoehe beinflusst ist nicht richtig begruendet, das das Entweichen von Strahlung aus der Atmopshaere nicht von der Anzahl strahlender Molekuele ausgeht sondern davon wie Wahrscheinlich es ist, dass die Strahlung wieder absorbiert wird. Da spielt der Abstand von Molekuelen eine weitaus groessere Rolle. Insofern ist die Angabe der Dichte oder des Druckes von Bedeutung.
Die 5km stellen aber auch noch ein anderes Problem fuer die Abstrahlung von CO2 dar. 5km ist noch die Hoehe in der Wolken eine wesentliche Rolle spielen.
Was auffallen sollte, ist das es im Temperaturprofile bei 5 km keine Auffaelligkeiten gibt, wenn die Strahlung dort auf einmal in den Weltraum entweicht, warum sieht man nichts am Profil? Hier wird eine Wirkung behauptet, die sichtbar keine Wirkung hat.
Als Atmopshaerenwissenschaftler sollte dieser Herr aber wissen wie man mit der Standardatmosphaere das Profil ganz ohne Einfluss von Strahlung erstellen kann.
Das Video sollte man mit Vorsicht betrachten und seine eigenen Schluesse ziehen. Meine Meinung so wie oben!
Die durchfließende Solarenergie bewirkt die beobachtete Erwärmung von Materie der Erde. Ihre jeweilige Größe steuert das Produkt aus Energiefluss und Durchfluss Zeitspanne. Die energetische Rückkopplung des Treibhauseffektes erhöht diese Zeitspanne signifikant. Ginge diese Zeitspanne gegen unendlich, so würde die Tenperatur gegen die Emissionstemperatur der Sonne ansteigen.
Quatsch!
in 100m m Tiefe in der Erde scheint keine Sonne und es ist da schoen warm.
Da fliesst auch keine Sonnenenergie hin.
in 2km Tiefe ist es uebrigens noch waermer.
Wer von nur einer Temperatur der Erde spricht hat einfachste Zusammenhaenge noch nicht verarbeitet.
Blabla … unserer Erde von (-18°C) um (33°) auf eine „gemessene“ globale Durchschnittstemperatur von (15°C) anheben soll. Finde den Fehler im Narrativ. -18 Grad weil nur ein Körper (absorbiert und) auch wieder abstrahlt. Keine Lufthülle, gelle?! 15 Grad, weil jetzt plötzlich zwei Körper netto wieder Strahlung abgeben. Jetzt haben wir aber noch eine Lufthülle, also können wir die -18 Grad auch nur in einem gewichteten Mittel beider Körper finden. Der olle Arhenius hat die Leute aber tüchtig auf’s Glatteis geführt, weil er nur von der Oberfläche der Erde gefaselt hat.
Eine geschlossene Darstellung des Zustandes der Atmosphäre und der Materie an der Erdoberfläche ist bekanntlich weder durch Messung noch mathematisch möglich. Es ist daher logisch, dass Narren das Thema übernehmen.Zur Verfügung steht lediglich mehr oder weniger genaue punktuelle Information:Erdwärme allein würde an der Oberfläche der rotierenden dann an feste Materie eine Temperatur in einem engen Bereich um 30 K einstellen. Alles weitere bestimmt der im Jahresverlauf veränderliche Energiefluss von der Sonne, von dem ein geschätzter Anteil von 30% ohne Wirkung zu hinterlassen in den Weltraum reflektiert wird.An 71% der Erdoberfläche, an der Oberfläche der Ozeane, ändern sich die lokalen Wassertemperaturen im Tagesverlauf als Folge der großen Durchfluss Zeit der aus dem oberen Halbraum zufließende Energie kaum meßbar. Am kleineren Festland Anteil erreichen tägliche Schwankungen insbesondere in den Wüsten die größten Werte.Der (solare) Energiefluss zur Materie an der Erdoberfläche umfasst folgende Quellen:1. Ein kleiner Anteil der Solarstrahlung reagiert mit Sauerstoff, die gewandelte Energie fließt in die Tropopause ab.2. Ein Anteil fließt direkt zur Materie an der Erdoberfläche.3. Der atmosphärische Wasserkreislauf lässt Wasser- und Eisaerosole entstehen, die mit an Sicherheit grenzender Wahrscheinlichkeit ein sog atmosphärisches Fenster für Wärmestrahlung schliessen und temperaturabhängig an ihrer Oberfläche Wärmestrahlung in den Raumwinkel von 360 Grad emittieren. Diese energetische Rückkopplung (der Treibhauseffekt) vergrößert die Durchfluss Zeitzeit der Solarenergie, sodass die Temperatur entsprechend ansteigen muss.4. Die den Aerosolen räumlich tiefer wirkenden Treibhausgase emittieren bekanntlich ebenfalls Wärmestrahlung in den Raumwinkel von 360 Grad. Ihre geringe Wirkung reduziert jedoch den Energiezufluss zu den dominanten Aerosolen, so dass ein Beitrag zum Treibhauseffekt nicht entstehen kann. „CO2 ist wetterneutral.
Unter den vielen Leugnern des anthropogenen Klimawandels (nach meiner Meinung sind das alle), die mit einem hilflos machendem Mangel an naturwissenschaftlichem Grundwissen glänzen, leuchten 4 Sterne besonders. Da sind einmal die, die vorgeben nicht zu verstehen, dass es für uns unmöglich ist, auf 1/100 oder 1/10 °C genau die Durchschnittstemperatur der Erde zu bestimmen, andererseits aber globale Temperaturänderungen auf unter 1/10 °C genau ermitteln können. Dann gibt es die, die vorgeben nicht zu verstehen, dass die Erde auf ihrer Projektionsfläche von der Sonne angestrahlt wird, aber auf der 4-mal so großen gesamten Oberfläche abstrahlt. Als Dritte im Bunde gibt es diejenigen die meinen, strahlende Körper erwärmen nur die Körper, die kälter sind als sie selbst. Diese Überlegung ist lustig und bei mir startet dann immer das Kopfkino von 2 Sternen nebeneinander am Himmel und der kältere schaut sich neidisch den heißeren Stern an und denkt «Näh, der ist schon heiß genug – in dessen Richtung strahle ich nicht». Meine persönlicher Favoriten sind allerdings die Schrecken aller Kleidungs- und Dämmstoffhersteller wonach ein strahlender Körper sich grundsätzlich nicht selbst erwärmen (oder abkühlen) kann, wenn die umgebende Hülle verändert wird. «Das hätten «Stefan und Boltzmann» so gesagt». Worüber will man mit jemandem noch diskutieren, wenn die wärmende Wirkung eines Pullovers als physikalisch unmöglich abgetan wird? Silke Kosch
Silke Kosch schrieb am 26. Februar 2021 um 8:41
Vielleicht nicht ganz so einfach machen. Den meisten ist klar, dass ein Eingriff in den Energieabfluss über Wärmeleitung (Pullover, „wissen schon die Neanderthaler“) oder Konvektion (gärtnerisches Treibhaus) zu höheren Temperaturen führen kann. Aus irgend einem Grund scheint es aber schwer zu sein, das auch bei einem Eingriff in den Energieabfluss über Wärmestrahlung zu sehen.
„Wärmetransport“ über Strahlung ist naturgemäß schwerer zu verstehen, weil wir es im Alltag in der Regel mit Wärmeleitung zu tun haben. Und da sagt die Erfahrung: Die heiße Herdplatte wärmt den kalten Topf, nicht umgekehrt. Aber: Eine Thermoskanne bremst die Wärmeleitung durch die doppelwandige Konstruktion, die im besten Fall ein Vakuum einschließt. Zusätzlich aber sind die Innenwände verspiegelt, um die Wärmestrahlung nicht aus dem Gefäß zu lassen. Ein Gedankenexperiment für die Thermodynamiker: Ich bringe mit einer Rakete zwei Eisenkugeln ins Weltall (Vakuum), abgeschirmt von der Sonnenstrahlung. Die eine Kugel ist 20 Grad warm, die andere 30 Grad. Kann ich mit der 20-Grad-Kugel die 30-Grad-Kugel zusätzlich erwärmen?
„Kann ich mit der 20-Grad-Kugel die 30-Grad-Kugel zusätzlich erwärmen?“
Klein-Silke kann das!
Man kann auch sachlich diskutieren, Herr „Keks“.
„Man kann auch sachlich diskutieren, Herr „Keks“.“
Was an den „Beiträgen“ von Klein-Silke ist sachlich???
@ Werner Burger :
Herr Müller hat korrekterweise von Energieabfluss über Wärmestrahlung (elektromagnetische Strahlung, die die kinetische Energie einschließlich Schwingungsenergie von Atomen oder Molekülen erhöht) und nicht von „Wärmetransport“ über Strahlung (wir beschränken uns hier ja auf elektromagnetische Strahlung) geschrieben. Energieabfluss durch Kontakt von unterschiedlich warmen Substanzen kann natürlich nur von den wärmeren Substanzen auf die kälteren Substanzen erfolgen. Zum Energieabfluss durch elektromagnetische Strahlung kann man nun Folgendes sagen. Das Missverständnis von Klein–Silke (ein großes Lob an Herrn Keks für diese zutreffende Charakterisierung von Frau Kosch !) in ihrem Beispiel mit den 2 Sonnen von unterschiedlichen Temperaturen ist, dass zwar beide Sonnen elektromagnetische Strahlung aussenden (da hat Silke Kosch Recht) aber dass die Strahlungsbilanz so ist, dass die wärmere Sonne energiereichere Strahlung emittiert als die kältere Sonne. Dies bedeutet, dass die kältere Sonne mehr Energie in Form von elektromagnetischer Strahlung von der wärmeren Sonne aufnimmt als die wärmere Sonne Energie in Form von elektromagnetischer Strahlung von der kälteren Sonne aufnimmt.
Die Frage sollten sie an Frau Kosch stellen. Sowas ist nur mit Kopfkino zu beantworten.
Aber eines ist sicher, mit so einer Frage stellen sie sicher, das auch der Letzte erkennt das sie keine Ahnung haben.
Problem ist, sie haben nicht gesagt wie weit die Kugeln voneinander entfernt sind. Aber das ist nicht das einzigste.
@ Marvin Müller
Der Grund könnte sein, dass beim Pulli ein Energiefluss behindert wird, bei Strahlungsübertragung aber ein Energiefluss von einem niedrigen Energieniveau auf ein höheres stattfinden müsste. Was aber nach dem 2. HS Thermodynamik ohne Verrichtung von Arbeit nicht gehen dürfte. Leider habe ich bis dato kein entsprechendes Experiment finden können. Ist Ihnen da etwas bekannt?
Martin Rohde schrieb am 26. Februar 2021 um 14:54
Wenn wir mal die Energieflüsse in der Atmosphäre ignorieren (damit Sie nicht über einen angeblichen Verstoss gegen den 2. HS stolpern): Wieviel Energie geht vom Boden weg und wieviel geht am Ende ins All weg?. Wenn die Energiemenge am Boden größer ist, als die, die ins All geht, dann haben sie einen ähnlichen Sachverhalt wie beim Pullover – der Energiefluss vom Boden ins All wird von der Atmosphäre behindert …
Sie haben hier auf Eike zwei Experimente von Herrn Schnell (Gibt es einen Treibhauseffekt), Schnell & Harde) und den Gebrüder Marvan und das Experiment von Roy Spencer (siehe älteren Kommentar). Oder folgendes Experiment: „Experiment Results Show a Cool Object Can Make a Warm Object Warmer Still„, was vielleicht Ihre Vorstellungen von Strahlung und zweitem Hauptsatz etwas gerade rückt.
Und Sie können sich auch mal die „Stefan-Boltzmann-Umgebungsgleichung“ von Herrn Weber ansehen. Wenn Sie genau hinsehen, werden Sie einen Term erkennen, der einen Energiefluss in Richtung Boden repräsentiert, der kleiner ist, als der vom Boden weggehende …
Beide angegebenen Experimente wurden nicht im Vakuum ausgeführt, somit ist nicht sichergestellt, dass nur Strahlungsenergie im Spiel war.
„Der Energiefluss vom Boden ins All wird durch die Atmosphäre behindert“ Richtig, je geringer der thermische Unterschied zwischen Boden und Atmosphäre, desto geringer der Energieabfluss durch Wärmeleitung und Konvektion. Was zu der Frage führt, wie eigentlich die Atmosphäre die eingeleitete Energie wieder los wird. Wärmeübertragung könnte nur auf die Erde erfolgen, ins All geht es mangels Materie nicht. Somit bleibt nur eine Energieabgabe über IR-Strahlung. Also sollte eine Zunahme der IR-aktiven Gase auch einen höheren Energieverlust der Atmosphäre zur Folge haben, was eine Erhöhung des Temperaturgefälles zw. Erde und Atmosphäre ergeben würde. Gehen wir jetzt davon aus, dass der CO2 – Gehalt der Temperatur folgt, ergibt sich ein, wenn auch stark bedämpfter, Regelkreis.
=> ..ein Energiefluss [Wärmefluss!] von einem niedrigen Energieniveau auf ein höheres stattfinden müsste. Was aber nach dem 2. HS der Thermodynamik ohne Verrichtung von Arbeit nicht gehen dürfte.
Herr Rohde, Sie gehen fälschlich davon aus dass sich ein Körper nur dann erwärmen kann wenn ihm Wärme zugeführt wird, was ja von einem kälteren Körper nicht (oder nur durch zusätzliche Arbeit) möglich ist. Den Fall dass es sich um einen (mit W oder W/m²) beheizten Körper handelt, der auch dann seine Temperatur erhöht wenn er nur gegen Wärmeverlust gedämmt oder mit Gegenstrahlung (selbst von einem kälteren Körper) beaufschlagt wird, vergessen Sie – ebenso wie Clausius 1887.
Fast richtig. Bis auf den Fakt, das man mit W nicht heizen kann sondern nur mit Waerme. Der Hinweis der Heisung des Koerpers ist wichtig. Auch der Hochofen bleibt kalt wenn diese nicht an ist.
Daemmung ist ein guter Hinweis. Luft zum Beispiel ist eine fantastische Isolierung durch eine sehr geringen Waermeleitung.
Sie werden Clausius nie wirklich verstehen, und widerlegen werden sie ihn erst gar nicht.
Gegenstrahlung ist ein Begriff der Klimaunwissenschaft. Geringere Abkuehlung ist keine Erwaermung.
Der Tee wird in der Thermoskanne nicht waermer. Bei ihnen etwa?
Herr Mueller,
Frau Kosch hat sie einen Leugner genannt!
Ich dachte sie lesen aufmerksam.
Aber hier ist ihnen glatt was entgangen.
@ Silke Kosch :
Hysterische Schuldzuweisungen an alle, die nicht Ihrer Meinung sind, sind ein Zeichen von erschreckender Infantilität bei Ihnen. Gerade bei dem Thema „Hemisphärenmodell“ gibt es so viele unterschiedliche Meinungen in diesem Forum, dass Sie sich gerade bei diesem Thema mit Ihren allgemeinen Schuldzuweisungen für alle offensichtlich lächerlich gemacht haben. Und was Sie auch nicht begriffen haben, ist, dass die globale Realisierung der „Großen Transformation“ (und nur global würde Sinn machen) eine sehr schwierige Angelegenheit ist. Dies bedeutet : selbst wenn es keine „Klimaleugner(innen)“ gäbe, würde diese „Große Transformation“ nicht schneller voran gehen. Hysterische Schreihälse wie Sie lösen kein Problem, egal welche Energie- und Klimapolitik man anstrebt. Da Sie sich aber scheinbar auf dem intellektuellen Niveau eines beleidigten kleinen Schulmädchen befinden, begreifen Sie nicht, wie und aus welchen Gründen Politiker(innen) so reagieren wie sie es tun. Ich vermute auf Grund Ihrer Äußerungen, dass Sie eine FfF sind – ist dies korrekt ?
Als Troll bezeichnet man im Netzjargon eine Person, die ihre Kommunikation im Internet auf Beiträge beschränkt, die auf emotionale Provokation anderer Gesprächsteilnehmer zielen. Dies erfolgt mit der Motivation, eine Reaktion der anderen Teilnehmer zu erreichen.
Don’t Feed The Troll , don’t feed Silke Kosch…..
Ich gestehe Silke Kosch, ich bin ein unbelehrbarer Ungläubiger, glaube nicht an den Treibhauseffekt! Auch wenn ich schon brenne wie Giordano Bruno würde ich standhaft behaupten wie Galileo „Die Sonne macht es doch (die Erde wärmen), dicht das CO2“
„…strahlende Körper erwärmen nur die Körper, die kälter sind als sie selbst. Diese Überlegung ist lustig und bei mir startet dann immer das Kopfkino von 2 Sternen nebeneinander…“
Mache Sie bitte Mikrowelle-Experiment:
Wie wir alle wissen, kann die Mikrowelle eine Suppe erhitzen, obwohl sie selbst viel kälter ist. Nun trennen Sie mal bitte die Mikrowelle vom heißen Verbrennungsprozess im Kraftwerk, also den Netzstecker ziehen. Die Suppe bleibt kalt, unweigerlich. Ohne die Hitze im Kraftwerk keine wärmende Strahlen!
Erklärung: Eine Strahlenwirkung beschreibt manchmal nur einen Teil der thermodynamischen Wärmebilanz, die man nicht überlisten kann, wobei die Energie immer von warm nach kalt fließt und niemals umgedreht. Betrachtet man den ganzen Prozess, dann findet man die Ursprungsquelle der Energie, die wärmer ist als der am Ende durch die Strahlen erwärmte Körper. Wärmer als die paar Hundert Grad am Verbrennungsprozess im Kraftwerk oder die 6.000 Grad auf der Sonne bei EE kann die Suppe unmöglich werden. Das Gleiche gilt für die Erwärmung eines jeden Körper durch Strahlen, man muss nur den wärmeren Ursprung finden…
Wenn das nicht so wäre, könnten wir uns die ganze Elekroinfrastruktur sparen und Licht und Strom mit Eimer aus dem Keller holen wie die Ostfriesen!
=> Wärmer als die paar Hundert Grad am Verbrennungsprozess im Kraftwerk oder die 6.000 Grad auf der Sonne bei EE kann die Suppe unmöglich werden.
Aber Herr Georgiev, ist Ihnen noch nicht aufgefallen dass der Glühfaden einer Lampe bis zu 3000 °C erreichen kann, obwohl die Kesseltemperatur im Kraftwerk nur 600 Grad beträgt? Und dass Strom (ebenso wieWärmer als die paar Hundert Grad am Verbrennungsprozess im Kraftwerk oder die 6.000 Grad auf der Sonne bei EE kann die Suppe unmöglich werden. Strahlung) auch von kalt nach warm fliesst und kein Gebiet der Physik mehr Spinner und Missverständnisse hervorgebracht hat als die Thermodynamik?
Sorry, da hat der Editor gesponnen. Soll heissen
„Und dass Strom (ebenso wie Strahlung) auch von kalt nach warm
fliesst..“
@Dietze
Kein Gebiet der Physik hat mehr Spinner hervorgebracht als die Strahlen-Sortierer, die häufig keine Ahnung von Thermodynamik haben, davon aber reichlich, und dazu noch Arroganz. Erwärmungsprozesse sind aber alle und ausnahmslos nur über thermodynamische Zusammenhänge berechenbar, nicht über wirre Strahlenvergleiche, in denen die Einheit Kelvin gar nicht erst vorkommt.
Besonders wirre sind Vergleiche zwischen Wärmeenergieübertragung, also immer von warm nach kalt, mittels Strahlung, einerseits, und Elektronenfluss (Strom) von plus nach minus, welcher mit der Temperatur nicht zu tun hat, andererseits. Oder Erwärmung mittel elektrischen Strom über den Widerstand des Leiters einerseits, und Erwärmung durch Strahlungsabsorbtion andererseits. Soviel physikalische Verwirrung in einem kurzen Kommentar muss man erstmal hinkriegen, Respekt!
Woran unterscheiden erkennt man ein Thermodynamiker und ein selbsternannter Strahlenexperte beim Arzt? Der erste nimmt das Fieberthermometer, der zweite rechnet dem Arzt seine Temperatur nach SB vor und erklärt arrogant dem Arzt, dass er keine Ahnung hat.
Habe herzlich gelacht, aber das bringt es wohl auf den Punkt.
Naja, dann bin ich ja nicht der Besserwisser, wenn Sie der Thermodynamikexperte sind.
Alle Spinner ausser Dietze!
Aber wer meint das der Strom von kalt nach warm fliesst, hat noch nicht mitbekommen das er von negativ nach postitiv fliesst (physikalisch), was leider nicht das gleiche ist.
„Als Dritte im Bunde gibt es diejenigen die meinen, strahlende Körper erwärmen nur die Körper, die kälter sind als sie selbst. Diese Überlegung ist lustig und bei mir startet dann immer das Kopfkino von 2 Sternen nebeneinander am Himmel und der kältere schaut sich neidisch den heißeren Stern an und denkt «Näh, der ist schon heiß genug – in dessen Richtung strahle ich nicht»“
Dokumentation von Ahnungslosigkeit und Mangel an logischem Denkvermögen.
Schlecht verstandene Mathematik mit schlecht verstandener Physik zu kontern, ist ja auch abenteuerlich. Wie wärmt der Pulli doch gleich … ?
@Lutz Herrmann; Sie verlangen zu viel. Bis zu unterschiedlichen physikalischen Prozessen kommt man ja überhaupt nicht. Manche Experten verschließen sich Grundwissen schon, bevor es überhaupt an das Verstehen von Physik geht.
Pullover anziehen = wärmer
Mehr CO2 in der Atmosphäre = wärmer
Ein kältere Sonne neben eine wärmere setzen = auch die wärmere Sonne wird wärmer
Eine kältere Kugel neben eine wärmere im Weltall setzen = auch die wärmere Kugel kühlt langsamer aus
Die Einsicht, dass diese Tatsachen nicht grundsätzlich irgendwelchen physikalischen Gesetzen widersprechen, wäre ja schon ein Riesenfortschritt. Ehrlich gesagt erwarte ich den hier nicht.
Silke Kosch
Dann vielleicht erstmal das Lehramtsstudium abschließen und an der Didaktik feilen. Nicht zu viel dumme Beispiele geben. Nicht auf andere Themengebiete ausweiten. Nicht die Sache immer von Ende her denken.
„Ein kältere Sonne neben eine wärmere setzen = auch die wärmere Sonne wird wärmer“
Was dann aber bedeutet, dass auch die kältere Sonne wärmer wird, was bedeutet, dass auch die wärme Sonne noch wärmer wird, wodurch auch die kältere Sonne noch wärmer wird usw.. Gleicher Effekt wie beim Klima. Mehr CO2 erwärmt, dadurch mehr Wasserdampf in der Atmosphäre, der zusätzlich erwärmt. Also noch mehr Verdunstung und noch mehr Waserdampf in der Atmosphäre und weitere Erwärmung. Dadurch mehr Wasserdampf in der Atmosphäre und weitere Erwärmung usw.. Klassische Mitkopplung, eine einmal eingeleitete Erwärmung wäre nicht mehr aufzuhalten. Wie ist es dann eigentlich zu Eiszeiten gekommen? Oder gab es die gar nicht?
@Marin Rohde; dass natürlich auch die kältere Sonne wärmer wird, wenn sie von einer wärmeren angestrahlt wird, stellt niemand in Frage.
H. Burger nannte oben das Beispiel von den 2 unterschiedlich warmen Kugeln im Weltraum. Beide Kugeln kühlen im Weltraum aus, fliegen sie aber nebeneinander her, so dass sie voneinander Strahlung aufnehmen können, kühlen BEIDE unabhängig von ihrer Temperatur langsamer aus. Also erwärmt auch die kältere Kugel die wärmere (umgekehrt natürlich auch) und da haben weder Stefan noch Boltzmann etwas dagegen.
Dass durch die Anreicherung der Atmosphäre mit Treibhausgasen ein Prozess in Gang kommt, der nicht mehr stoppt ist kein realistisches Szenario. Die Erde hat ja bereits viele Klimaphasen mit Abkühlung und Erwärmung durchgemacht. Wissenschaftliche Tatsache ist aber, dass wir gerade etwas anstoßen von dem wir nicht wissen (und von dem wir wahrscheinlich zu Lebzeiten nicht mehr erfahren werden), wie und wann es wieder gestoppt wird.
Zusätzlich CO2 erhöht die erdnahe Lufttemperatur, eine höhere Lufttemperatur bedeutet weniger Eisfläche (weniger Albedo), mehr Wasserdampf in der Atmosphäre (zusätzlicher Treibhauseffekt), das Auftauen des Permafrostes und damit die Freisetzung von Methan (ebenfalls ein Treibhausgas).
Auf welchem Temperaturniveau dieser Vorgang stoppt und welche heute küstennahen Städte und Landschaften es durch den ansteigenden Meeresspiegel nicht ins nächste Jahrhundert schaffen, werden vielleicht die Kinder unserer Kindes wissen.
Silke Kosch
Das
„Auf welchem Temperaturniveau dieser Vorgang stoppt und welche heute küstennahen Städte und Landschaften es durch den ansteigenden Meeresspiegel nicht ins nächste Jahrhundert schaffen, werden vielleicht die Kinder unserer Kindes wissen.“
Grüne Physik nach dem Motto „Schaun` mer mal“
Diese völlig enthemmte Zurschaustellung der eigenen Ahnungslosigkeit durch Klein-Silke ist eine schöne Dokumentation des Verhaltensmusters rot-grüner Schlümpfe
Meinen Sie das wirklich ernst ;-)?
Also: Meinereiner zieht einen Pullover an, um Wärmeverluste an die kältere Umgebung zu verringern, „wärmen“ tut z.B. nur ein mit Strom beaufschlagtes Heizkissen …..
Aber Sie haben ganz gewiss noch mehr solcher Kalauer auf Lager …. 😉
Danke an die Redaktion für die Freischaltung Ihrer Kommentare. Immer wieder lxxxxx.
Beeindruckend wie die Verdummungstaktik der linksgrünen Ideologen im Bildungssystem Früchte trägt. Klein-Silke und FfF = Top des Flop.
xxxxxxx
@ Paul Jansen :
Herr Jansen, Klein-Silke begreift nicht den Unterschied zwischen erwärmen = Temperatur erhöhen und Verzögerung eines Abkühlungsvorganges. Sie begreift auch nicht das Stefan-Boltzmann Gesetz, das ja einen Zusammenhang zwischen Temperatur und abgestrahlter Leistung (Energie pro Zeit) eines Körpers beschreibt. Ansonsten wären Klein-Silke’s Beispiele und Behauptungen nicht zu erklären. Klein-Silke begreift ja nicht einmal, was ein Perpetuum Mobile ist. Klein-Silke ist aber typisch für das Gros (nicht für alle) von linksgrünen Personen, die eine Kombination von Arroganz und Unwissenheit darstellen – aber die Tatsache, dass Wahlprognosen (vorausgesetzt die Umfragen repräsentieren die Realität) die Grünen als zweitstärkste Partei bei den nächsten Bundestagswahlen sehen, zeigt, dass das intellektuelle Niveau der deutschen Wählerschaft auch nicht viel besser ist.
„Worüber will man mit jemandem noch diskutieren, wenn die wärmende Wirkung eines Pullovers als physikalisch unmöglich abgetan wird?“
Wärme ist Energie, hat auch die selbe phys. Einheit! Ein Pullover kann aber keine Energie erzeugen, daher kann er auch nicht wärmen! Ein Pullover isoliert nur, er kann also die Geschwindigkeit der Abkühlung beeinflussen. Alles andere gehört ins Märchenbuch! Ziehen Sie einem Stein einen Pullover an und messen Sie seine Erwärmung …
Vom THE wird eine absolute Erwärmung von 33°C behauptet …
Doch, Herr Strasser, ein Pullover macht den Körper wärmer weil dieser beheizt ist und dessen Wärmeverlust behindert wird. Deshalb ist auch Wärmedämmung vorgeschrieben. Diese macht beheizte Häuser wärmer so dass weniger Brennstoff benötigt wird. Dies gilt auch für Strahlungsdämmung und wird leider, weil Clausius es 1887 vergessen hat, in der Thermodynamik nicht behandelt – weshalb viele Thermodynamiker einen TE nicht für existent halten.
Jede Wärme, die ein beheizter Körper hat, stammt aus seiner Heizung und nicht aus einer Isolationsschicht! Daß eine Isolation Einfluß auf den Wärmeverlust, also das Abkühlverhalten hat, bestreitet niemand, deswegen isoliert man ja. Eine Isolation kann aber nie Energie produzieren, die Energie kommt immer von der Heizung. Nebenbei ist Isolation (Pullover) ein thermodynamischer Effekt, während eine behauptete Gegenstrahlung ein Strahlungsprozeß ist. Es werden also Äpfel mit Birnen verglichen.
Eine Oberfläche, die an Vakuum grenzt, kann nur durch Strahlung kühlen. Eine Oberfläche, die an irdische Atmosphäre grenzt, kann durch Strahlung und Konvektion sowie Verdunstung gekühlt werden, kühlt also effizienter. Zusätzlich bewirken Luft und Wassertröpfchen aber auch Isolation. Es ergibt sich ein vielfach noch unverstandenes komplexes Gesamtverhalten der Abkühlung, in dem nur eines sicher ist, zusätzliche Energie, also zusätzliche Wärme, kann dabei nicht entstehen.
In der Klimadiskussion geht es außerdem um die Lufttemperatur in 2 m Höhe und nicht um die Temperatur der Erdoberfläche. Mit dieser Lufttemperatur beschäftigen sich z. B. Trenberth/Kiehl aber überhaupt nicht. Wer einen THE belegen will, muß alle Prozesse bis zur Luft in 2 m Höhe beschreiben. Und zwar für z. B. 300 ppm CO2 und dann für z. B. 500 ppm.
=> Jede Wärme, die ein beheizter Körper hat, stammt aus seiner Heizung und nicht aus einer Isolationsschicht! Daß eine Isolation Einfluß auf den Wärmeverlust, also das Abkühlverhalten hat, bestreitet niemand
Herr Strasser, wenn durch eine Isolation weniger Wärme verloren geht, ist die Wirkung doch dieselbe als wenn die Heizung mehr Wärme erzeugt – und damit erhöht sich die Temperatur. Logo oder was?
@ Stefan Strasser :
Ich stelle gerade fest, dass Herr Dietze auch erschreckend naiv ist ! Herr Dietze begreift nicht, dass es gerade in einem Forum. welches naturwissenschaftliche Themen behandelt darauf ankommt, dass man physikalisch korrekt ist, weil EIKE von vielen Personen gelesen wird aber nur ein ein kleiner Teil von denen innerhalb dieses Forums einen Kommentar abgibt aber dafür außerhalb dieses Forums die Möglichkeit nutzen kann, EIKE zu diskreditieren !
Nein Herr Dietze nicht Logo.
Da Ihre Temperaturquelle die Sonne angeblich so kalt ist, haben sie ein Problem, das sie behaupten, das der Tee in der Thermoskanne waermer wird, nur weil er in der Kanne isoliert ist.
Und das ist nicht so. Aber vielleicht akzpetieren sie ja die innere Heizung der Erde.
Wenn man auch nur 10 m weiter denkt, dann hat man locker eine angenehme Temperatur und muss sich wegen der Sonne keine Sorgen machen.
Frau Kosch,
ich weiss sie meinen es ernst, und mit ihrer Einfachheit bilden sie sich ein das ein Pullover eine waermende Wirkung hat.
Werfen sie diesen mal ueber ein Thermometer und messen sie die Erwaermung.
Der Pullover waermt einen Menschen nur, weil der eine innere Heizung hat.
zu ihrem Punkt ein, da habe sie scheinbar hoeheres Wissen, weil historische Messungen im hunderstelbereich sind selten, bis gar nicht da, sinnfrei, weil sich die Temperatur im Milisekundebereich aendern wuerde. Sie bestaetigen das Bild von jemanden, der immer noch nicht weiss was gemessen und was gerechned wird.
Punkt 2 kenne ich keinen der das nicht so sieht. Nur die Umrechnung von Energie in Leistung ueber eine Flaeche beherrschen manche nicht. Energie ist nun mal nicht Leistung.
Punkt 3 Empfehle das Studium der Thermodynamik. Mit Kopfkino kommen sie hier nicht weiter, aber mit Herrn Burger haben sie einen Verbuendeten und Marvin wuerde ihnen nie offen sagen das sie falsch liegen, aber er denkt es.
Rein praktisch wuede ich aber keinen Pullover in die Diskussion bringen. In Zeiten von Covid mit Temperturscannern ueberall, muss man naemlich vorsichtig sein, das man nicht ueberhitzt. Empfehle mal zu messen ob sie immer Fieber kriegen wenn sie ein Pullover anziehen.
Das Stichwort ist, langsamer abkuehlen ist nicht gleichzusetzen mit einer Erwaermung.
So Leute die mit Thermoskannen argumentieren, haben leider nicht begriffen, das der Tee in der Kanne nicht waermer wird. Ich muss den schon warm reinmachen.
Sie nicht?
CO2-Moleküle und auch Wasserdampf-Moleküle geben bei einer Temperatur über 0 Kelvin infrarote Strahlung ab – je wärmer desto mehr. Das tun sie auch in der Atmosphäre – und zwar in alle Richtungen. Deswegen geht die Hälfte dieser Strahlung auch Richtung Erdboden.In der Welt von Uli Weber wird ihnen das aber dank bestimmter Gesetze und Berechnungen verboten. Damit ist es bewiesen, dass es keine Gegenstrahlung gibt.Jetzt mal im Ernst: CO2 reflektiert nicht die Infrarote Strahlung zurück zur Erde. Es ist ein bisschen komplizierter:1. Die Erdoberfläche (Wasser und Land) strahlt Infrarot entsprechend ihrer Temperatur in Richtung Weltall.2. CO2 und Wasserdampf-Moleküle sowie die Wassertröpfchen der Wolken absorbieren diese Infrarote Strahlung. Die Strahlung wird also in Wärme umgewandelt. Und zwar komplett schon nach kurzer Strecke.3. Die durch die IR-Absorption erwärmten Moleküle geben diese Wärme durch Kontakt (Schwingungen) an die übrigen Moleküle der Luft – also Stickstoff und Sauerstoff – weiter und erwärmen damit die jeweilige Luftschicht.3. Zusätzlich wird durch Umwälzung der Luftmassen (Wind, Hurrikane, Taifune) Wärme in die Atmosphäre getragen.4. Entsprechend der Temperatur der jeweiligen Luftschicht strahlen die CO2 und Wasserdampf-Moleküle in alle Richtungen infrarot ab – und zwar in alle Richtungen. Die Hälfte der Strahlung geht also in Richtung Weltall , die andere Hälfte in Richtung Erdoberfläche.5. Schon nach kurzer Strecken trifft die IR-Strahlung wieder auf andere Moleküle. Diese absorbieren die Strahlung und geben die Wärme wieder an ihre Umgebung ab. Und das Spiel beginnt von neuem. Es ist also eine Art komplizierter Stafettenlauf in beide Richtungen.6. Da die Atmosphäre kälter ist als die Erdoberfläche, gibt es mehr Infrarotstrahlung Richtung Weltall als Richtung Erdoberfläche. Die Differenz dieser beiden Strahlungen ergibt den Wärmetransport von der Erdoberfläche Richtung Weltall. Gäbe es die Gegenstrahlung nicht, würde die Erde extrem schneller abkühlen, wie es z.B. beim Mond der Fall ist, der keine Atmosphäre besitzt.7. Oberhalb der Wolkenschicht sind kaum noch Wasserdampf-Moleküle in der Atmosphäre. Und auch die CO2 Konzentration in der Luft wird immer geringer. Deshalb haben immer mehr IR-Strahlen die Chance, zwischen den Molekülen in Richtung Weltall abzustrahlen und deshalb die Atmosphäre abzukühlen.8. Bei Berechnungen geht man deshalb vereinfacht von der Luftschicht über den Wolken aus als Oberfläche der Atmosphäre aus (Englisch: TOA = Top Of Atmosphere), wo die Abstrahlung in den Weltraum beginnt.9. Zu beachten ist auch, dass der Wasserdampf-Gehalt der Atmosphäre bis zu 4% beträgt, der CO2-Gehalt aber nur 0,04%. Deshalb hat an dem sogenannten Treibhauseffekt CO2 nur einen geringen Anteil. Die Wasser-Tröpfchen in den Wolken sind für IR-Strahlung eine Komplett-Barriere, die Strahlen werden komplett absorbiert.
@ Herbst – zu Ihrem Punkt 7 – noch in 17,5 KM Höhe, insbesondere über Äquator, sehe ICH reichlich WasserDampf auf „earth.nullschool.net“ – LuftFeuchte RH und 70 hPa gucken – bei Projection „A“ oder auch „P“ ganz übersichtlich – quasi live und mit Kalender-Funktion „rücklings“ bis 2014 – ALLES andere natürlich ebenso 😉
„CO-2-KRISE ist vorbei – liegt ALLES nur am EIS-Pulver der FLIEGEREI“ !!! – drei bis vier Tage „9/11-FLUG-Verbote“ ergaben TEMP.-DELTA von mind. EINEM Grad Kelvin an 4.000 US-Stationen (Travis et al. in Nature 08/2002) – und zur Zeit „fehlen“ immerhin über 80% „meiner“ 300 Mio. To./p.a. H2O-EIS-Aerosole „über den Wolken und vor Sonne und Mond“ in 10 KM Höhe (im JET-Stream/250 hPa auf „earth.nullschool.net“ gucken) – selbst „Rahmstorf“ ist „sprach-los“ 😉 😉 😉
EIKE veröffentlich nun zum 28. Mal (!!) den Beitrag eines Geophysikers dass es (obwohl diese gemessen ist) keine Gegenstrahlungswirkung gibt und damit auch gar kein TE durch behinderte Strahlungkühlung entsteht. Dass dann für +15 Grad solaren Mittelwert auf beiden Hemisphären jedoch ZWEI SONNEN erforderlich sind (weil für die nicht rotierende bzw. nicht speichernde Tagseite nach S-B allein eine Sonne lt. genauer Rechnung von Prof. Gerlich benötigt wird), ist immer noch nicht verstanden. Z.B. die Berechnung dass mit Speicherung über Tag/Nacht, Albedo und S-B der rein solare Mittelwert am Äquator -3 Grad (!) beträgt, was man leicht mit der mittleren solaren Einstrahlung von 1364*0.7/Pi [W/m²] überprüfen kann und was erheblich weniger als +15 Grad ist, obwohl es am Äquator am wärmsten ist, sollte zu denken geben.
„(obwohl diese gemessen ist)“
Und Dietze macht zum 100-sten Mal die Falschaussage, daß „gemessen“ wird
Schon damit ist das Narrativ einer CO2 Klimaerwärmung widerlegt. Da aber die menschengemachte Klimaerwärmung politisch gesetzt ist, und weniger als 10% der Bevölkerung einem Beitrag wie Ihrem folgen kann, wird weiter das „Klima gerettet“ was das Zeug hält. Am besten mit vielen neuen CO2 Steuern und Abgaben, alternativlos. Wir werden von Irren regiert.
Sehr geehrter Herr Uli Weber,u.a. hier:“An einem wolkenlosen Oktobertag schwankt die vom DWD gemessene Gegenstrahlung zwischen 0:00 und 24:00 Uhr von ca. 220 bis 250 W/m².“schreiben Sie über die gemessene Gegenstrahlung. Im Oktober kann man während rund 50% der vorgegebener Zeit von 0:00 bis 24:00 nur die Summe von Sonnenstrahlung plus Gegenstrahlung messtechnisch erfassen. Wer legt wie fest, wie viel der am Boden ankommende Strahlung direkte Sonnenstrahlung ist, und welcher Anteil davon Gegenstrahlung ist?Wenn es dazu keine klare, eindeutige, anerkannte Messprinzipien gibt, dann kann man die ganze Strahlendiskussion an diesem Punkt schon beenden und die ganze THE-Diskussion als sinnfreier Zeitvertreib gelangweilter Strahlenphysiker ohne jegliche Grundlage abtun.Mir ist keine wissenschaftliche Beweisführung zu diesem Thema bekannt und bin neugierig über Ihre Erklärung.MfGPeter Georgiev
@ Herrn Peter Georgiev
Sehr geehrter Herr Georgiev, Sie fragen, „Wer legt wie fest, wie viel der am Boden ankommende Strahlung direkte Sonnenstrahlung ist, und welcher Anteil davon Gegenstrahlung ist?“
Diese Frage kann ich Ihnen auch nicht beantworten, ich hatte hier ja diverse Widersprüche aus Veröffentlichungen des DWD bezüglich einer sogenannten „atmosphärischen Gegenstrahlung“ aufgezeigt. In meinem hemisphärischen S-B-Modell kommt die ominöse „Gegenstrahlung“ als Quelle eines vorgeblich „natürlichen atmosphärischen Treibhauseffektes“ jedenfalls nicht vor, Zitat:
„Mit der globalen Mittelung der hemisphärischen Sonneneinstrahlung hatte man also deren S-B-Temperaturäquivalent soweit reduziert, dass zwischen dieser fehlerhaften theoretischen Ableitung und der „gemessenen“ Realität eine Lücke von 33 Grad klafft. Diese Lücke hatte man dann mit einem frei erfundenen Perpetuum-mobile-Prozess namens THE wieder zu schließen versucht. Aber „2x falsch“ ergibt nun mal nicht „richtig“, auch wenn das Ergebnis nun scheinbar wieder stimmt.“
MfG – U. Weber
Naja, Antworten „nur“ an die Fan-Base sind nicht gerade zielführend. Herr Weber, beantworten Sie doch auch mal Fragen von Kritikern. Ich hätte z.B. immer noch gerne von Ihnen gewusst warum Sie mir u.a. geschrieben haben, das es einer Gegenstrahlung nicht bedarf und es ohne Gegenstrahlung bei Ihnen auskommt, die Wärme in Ihren Modell Tag-Erde aber von der Tagseite auf die Nachtseite u.a. transportiert wird, da die Atmosphäre der Nachtseite bei Ihnen gemäß S-B die zuvor gespeicherte Tag-Wärme an die Umgebung abstrahlt. Aber Antworten gegen Sie anscheinend nur an „Nicht-Kritiker“.
Herr Krüger, beim Weber-Modell entsteht die Temperatur auf der Tagseite durch solare Einstrahlung. Aber nur gut die Hälfte der Wärme wird abgestrahlt, der Rest gespeichert, auf die Nachtseite rotiert und dort abgestrahlt. Hierbei wird S-B leider nicht beachtet, womit sich die Temperatur der Tagseite – weil fast die Häfte der Einstrahlung nicht abgestrahlt, sondern für die Nachtseite weggespeichert wird – sich deutlich fast um den Faktor 4.Wurel(2) von 288 auf 242 K (-31 Grad !!) reduziert. Wenn beide Hemisphären +15 Gad annehmen sollen, würde die DOPPELTE solare Einstrahlung benötigt.
Ich sehe einen Widerspruch in Herrn Webers Theorie, da er meint es bedarf keiner Gegenstrahlung der Atmosphäre, diese aber auf der Nachtseite selbst verwendet um die Umgebung dort zu erwärmen.
@Dietze, @Ulli Weber
Es ist doch ganz einfach: An 71% der Erdoberfläche ist die Temperatur im Tagesverlauf de facto konstant, weil die zufließende Energie für einige hundert Jahre („im Ozeanwasser“) gespeichert wird. Nur am kleinen Anteil des Festlandes ist ein Thermometer nötig, wenn der Tagesverlauf interessiert.
@Georgiev@Uli Weber
„Wer legt wie fest, wie viel der am Boden ankommende Strahlung direkte Sonnenstrahlung ist, und welcher Anteil davon Gegenstrahlung ist?“
Die Antwort auf diese Frage kann nur qualitativ gegeben werden, denn weder die Messung, noch die Mathematik können quantifizieren. Das bleibt ein Spielfeld für Narren!
Zum gleichen Schluß komme ich auch, damit ist aber die ganze Diskussion überflüssig.
Manchmal überkommt mich der böse Verdacht, dass die ganzen Strahlenphysiker, die per Gesetzbeschluß des Atomausstiegs plus Forschungsverbot gewissermaßen arbeitslos geworden sind, über ständig neue halbgegorene atmosphärischen Strahlungstheorien nach Anerkennung in der Gesellschaft suchen.
Hmm. Ihre Meinung stellen Sie dann hier ja auch hin? Bei mir stört Sie das aber?
Sonneneinstrahlung ist kurzwellig und Wärmeabstrahlung der Erde langwellig. Wusste schon Knut Amström vor über 110 Jahren und hat zur Messung der langwelligen Gegenstrahlung das Amström-Pyrgeometer eigens konstruiert und damit schon gemessen.
Die Sonne strahlt nach dem Lehrbuch „Meteorologisches Grundwissen“ von Zmarsly/Kuttler/Pethe (Tab. 1.1 S 12) von 2007; 7,9% im Bereich von 1nm-400nm; 400nm – 760nm 44,7% und im langwelligen Bereich 760-10.000 nm immerhin 47,4% der Energie ein. Wie groß ist die Albedo im jeweiligen Bereich? Im Lehrbuch findet man (Tab 1.2 ,Seite 17) eine große Anzahl von Albedowerten, alle mit hohen Streuwerten (z.B. bei Wolken zwischen 60-90 %!) für kurzwellige Strahlung und in langwellige Strahlung (Tab 1.3, Seite 17) bezogen auf die verschiedensten Stoffe. Einen Gesamtwert gibt es nicht.
Im Lehrbuch „Witterung und Klima“ Hrsg: P.Hupfer/W. Kuttler von 1998 wird die Albedo anders als Weichet als Rückstrahlung der Gesamtstrahlung definiert. Merkwürdigerweise kommen sie wieder auf 30 bis 31% (S 60) . Sie teilen diese aber auf in 15,6 % sichtbarer Bereich, 10,8 % Infrarot und 4,2 % im UV Bereich.
Admin schrieb am 26. Februar 2021 um 9:17
Wenn man sich das graphisch veranschaulichen will, findet man im Netzt jede Menge Abbildungen, z.B. die hier: https://twitter.com/rarohde/status/1196761516051238912?lang=de
Dann ist die einfache Frage: Ist die Meßtechnik in der Lage die beiden Frequenzbereiche auseinanderzuhalten und separat zu messen. Wenn man denkt, dass das geht, dann ist die Antwort auf die Frage, wie denn Sonnenstrahlung und atmosphärische Strahlung auseinandergehalten werden, relativ einfach.
Darum ging es aber nicht. Sondern allein darum, welche spektrale Verteilung die einfallende Solarstrahlung hat. Ungefähr 50:50 Kurz/Langwellenbereich.
Admin schrieb am 26. Februar 2021 um 11:31
Meine Anmerkung sollte keine Kritik an Ihrer Aussage sein. Ich sehe (jetzt) aber, dass man es so auffassen kann. Ich wollte Ihre Aussage mit einem Bild untermauern (die von Ihnen genannte Verteilung kann man IMHO im Bild in etwa erkennen) und auf die Ursprungsaussage von Herrn Krüger ausweiten.
Hinzufügen könnte man vielleicht noch, dasss man mit rein optischen Mitteln den betrachteten Ausschnitt des Himmels auf einen Bereich beschränken kann, in dem die Sonne nicht steht …
Der Peak der Sonneneinstrahlung liegt im sichtbaren Bereich, der Peak der Erdabstrahlung und Gegenstrahlung um IR. Das kann man deutlich unterscheiden. Das Angström-Pyrgeomter ist von 1905. Mit dem hat Knut Angström schon damals Messungen der Gegenstrahlung vornehmen können.
Ich fürchte Krüger, dass seit dem Homo Erectus seit 2 Mio Jahren jeder aus der Gattung Homo weiß, dass die Sonne wärmende Strahlen zu Erde schickt. Leider lebt kein Homo Erectus und kein Neandertaler mehr, der Ihnen das erklären kann.
Sie können ja weiter behaupten, die ganze zu spürende Wärmestrahlung die umgeleitete Gegenstrahlung ist. Dann müssen sie mir aber erklären, wie die Sonne den Mond von -150 Grad (nachts) tagsüber auf 140 Gran plus erwärmt. Dort gibt es mangels CO2 keine Gegenstrahlung!
Es kommen also reichlich wärmende Infrarot Strahlen an, egal was die THE-Fans und Strahlenakrobaten für Verbiegungen erfinden!
@Georgiev
Je wärmer der Köpper, desto kurzwelliger die Abstrahlung. Bei der Sonne mit über 5.000 Grad liegt er Hauptteil der Abstrahlung um den sichtbaren Bereich herum bis 3 Mikrometer. Bei der Erde mit 15°C im IR um 10 Mikrometer rum.
Klar getrennt und zu unterscheiden. Bei 15 Mikrometer, wo CO2 absorbiert und emittiert und zurückstrahlt ist vom Sonnenspektrum nichts mehr zu finden. Und ich als Europäer habe rund 2% Neandertal-DNA. Ein Wissenschaftskollege Svante Pääbo hat nachgewiesen, dass Neandertaler sich mit dem modernen Mensch in Europa vermischt haben und Nachkommen hatten.
Sie haben das Argument wirklich nicht verstanden oder?
Die Frage war wie der Mond ohne „Gegenstrahlung“ ‚tags‘ so viel waermer als die Erde ist!
@Werner
Der Mond hat ein Rückstralungsvermögen von 12%, die Erde von 30%. Ein Mondtag dauert 29 Tage und nicht 1 Tag.
Herr Krueger,
Und was hat die Albedo hier zu suchen? Wollen sie andeuten das der Albedo-Unterschied von 18 % fast 90 Grad C ausmacht?
Sie wissen doch, dass die atmosphärische Albedo 15% ist und daher die unbewölkten Abschnitte der Erdoberfläche fast eine ähnliche Albedo wie der Mond haben. Und trotzdem gibt es diesen Unterschied.
Sollte es wirklich nur an der Tagesdauer liegen?
Noch eine Anmerkung. Was Herr Weber hier wieder macht ist, dass er eine völlig falsche Darstellung des THE präsentiert, wie sie in keinen Lehrbuch der Atmosphärenphysik oder Veröffentlichung zur Atmosphärenphysik zu finden ist. Auf diesen Strohmann drischt er dann immer wieder ein und präsentiert dann seine Tagerden-Theorie, die angeblich viel einfacher, logischer und richtiger sein soll. Dabei verbiegt er alle Grundprinzipien der Physik bis zum geht nicht mehr und erhält eine völlig falsche Theorie, wie sie nirgendwo anders zu finden ist. Ist aber davon überzeugt, ausgerechnet er hätte damit den großen Wurf gelandet und den Stein der Weisen gefunden. Leider kann man es nicht anders sagen.
Wer hier biegt was? Realität oder eine „Lehre“?!‘
Die Erde ist eine Kugel und die Sonne erwärmt direkt nur eine Seite. Im Dunkel gibt die Mutterchen Erde eingespeiste Wärme ab, bis wieder die Sonne -Gottseindank-komt.
Die Erde kann nicht mehr Wärme abgeben, als von der Sonne bekommt.
Wie viel Fliegen braucht ein Teufel täglich? Oder: wieviel Engelchen passt auf eine Nadelspitze? Gleiche bimborum, beschäftigung der „Elite“…
Co2-Moleküle und Wasserdampf-Moleküle, etc. strahlen nun mal im IR immer ab, wenn sie eine Temperatur über 0 Kelvin haben. Schon damit ist Herrn Webers Theorie, die ohne Gegenstrahlung auskommt widerlegt. Das Schöne ist dann noch, dass mir Herr Weber selbst geschrieben hat, dass auf der Nachtseite die Atmosphäre bei ihm gemäß S-B strahlt und so die Wärme von der Tagseite auf der Nachtseite ankommt.
=> Die Erde soll sich durch die Rückstrahlung ihrer eigenen Abstrahlung (= Gegenstrahlung) noch weiter erwärmen; eine solche „Selbstaufheizung“ widerspricht aber dem 2. HS der Thermodynamik. Denn wenn ein solcher Vorgang funktionieren würde, könnten Sie Ihren Kaminofen zum Glühen bringen, indem Sie ein paar Kästen Mineralwasser davorstellen…
behauptet Uli Weber. Deshalb für Sie meine volle Zustimmung, Herr Krüger. Selbstaufheizung eines beheizten Körpers widerspricht NICHT dem 2. HS der Thermodynamik, denn darauf basiert bekanntlich auch der Effekt der Wärmedämmung, wobei der Wärmeabfluss zwar behindert wird, aber stets von warm nach kalt geht. Die Gegenstrahlung transportiert sogar Energie von selbst von warm nach kalt – gemäss Planck. Auch das widerspricht nicht dem 2.HS. Man kann ja auch die Birne eines Diaprojektors zum Durchbrennen bringen wenn man einen Spiegel vor das Objektiv hält, was durch Versuche bestätigt wurde.
Ach Herr Dietze, ein Spiegel reflektiert, CO2 Moleküle haben keine Reflexionseigenschaften. Ihr Spiegel ist nichts anderes als die wärmende Decke vom Forentroll Kosch weiter oben. Wer solche Vergleich bringt um damit den 2HS ausser Kraft zu setzen und die Erde mittels CO2 Spurengase erwärmen will, hat nicht wirklich verstanden wovon er da schreibt….
Auch zum 100-sten Mal:
Dein Geschwafel vom Diaprojektor ist Quatsch, da man zwischen Reflexion und Remission zu unterscheiden hat.
Was soll der Quatsch?
xxxxx
„…er eine völlig falsche Darstellung des THE präsentiert, wie sie in keinen Lehrbuch der Atmosphärenphysik…“
Ein Lehrbuch der Atmosphärenphysik, das von einem Treibhauseffekt faselt ist kein Lehrbuch sondern ein Propagandapamphlet für Leichtgläubige und Unterbelichtete
Was mich einmal interessieren würde: In sämtlichen Betrachtungen wird immer nur die Rückstrahlung von CO2 Richtung Erde betrachtet, nie die Strahlung Richtung Weltraum. Dabei müsste doch ein erhöhter Anteil IR-aktiver Gase auch eine höhere Abstrahlung nach aussen bewirken und somit dem System Erde – Atmosphäre Energie entziehen. Auch wird nie die Höhe betrachtet, in der ein CO2 – Molekül strahlt, dabei sinkt der „Trefferwinkel“ für die Strahlung mit zunehmender Höhe enorm. Wäre es also denkbar, dass IR – aktive Gase das System nicht erwärmen, sondern abkühlen?
Martin Rohde
25. Februar 2021 um 13:13
Das wird betrachtet. Das Stichwort, nach dem Sie suchen müssen, ist „stratospheric cooling“. Ein IMHO guter Artikel dazu wäre der hier: „Stratospheric Cooling„. Dieser Aspekt ist einer der „finger prints“ der Erwärmung durch Treibhausgase.
„Das wird betrachtet. Das Stichwort, nach dem Sie suchen müssen, ist „stratospheric cooling“. Ein IMHO guter Artikel dazu wäre der hier: „Stratospheric Cooling„. Dieser Aspekt ist einer der „finger prints“ der Erwärmung durch Treibhausgase.“
Was für ein dümmliches Geschwafel!
„Oben“ kälter und „unten“ wärmer ist ein Perpetuum Mobile.
Die enthirnten AGW-Propagandisten werden das wohl nie verstehen…
Danke für die Links. Leider finde ich darin keine Gesamtenergiebilanz.
Martin Rohde schrieb am 26. Februar 2021 um 8:18
Vielleicht können Sie Ihre Frage etwas konkretisieren?
In der Ursprungsfrage ging es nur darum, ob die stärkere Abstrahlung bei mehr CO2 betrachtet wird. Und ich denke, diese Frage wird durch den Artikel auf jeden Fall beantwortet. Wenn mehr CO2 in der Straosphäre ist, strahlt es mehr ab und die Stratosphäre kühlt sich ab. Das ganze ist auch durch Messungen belegt, die im Artikel gezeigt werden.
„Wenn mehr CO2 in der Straosphäre ist, strahlt es mehr ab und die Stratosphäre kühlt sich ab. Das ganze ist auch durch Messungen belegt, die im Artikel gezeigt werden.“
Dann kann es aber „unten“ nicht wärmer werden!
Wg Perpetuum Mobile.
Ist das wirklich so schwer???
Die Strahlenakrobaten hier auf Eike können nicht in Kategorien wie Energiebilanzen denken. Dann würde ja die Konstruktion aus Antrieb und Intensität zur physikalischen Größe Temperatur in Kelvin sofort zusammenbrechen.
Daher auch die ausweichende Antworten.
Peter Georgiev schrieb am 26. Februar 2021 um 14:33
Wer von Neanderthalern. Medizinmännern und Erfahrungen im Sand am See schreibt, sollte mit solchen Vorwürfen etwas zurückhaltender sein. Die Energieflussbilanzen werden hier regelmäßig beschrieben, auch von mir. Sie können sich gerne einen der Kommentare schnappen und mir zeigen, was ich da falsch mache, statt hier einfach Behauptungen aufzustellen …
Herr Marvin Müller,
das wertvollste Geschenk der Evolution für die Gattung Homo ist der gesunde Menschenverstand, eine Mischung als Lebenserfahrung und Logik, die hilft in Situationen und Betrachtungen, die man nicht komplett überblicken oder berechnen kann, das wahre von offensichtlichen Unsinn zu trennen und die richtige Entscheidung zu treffen. Beim ständigen Kampf ums Überleben (bzw. um besseres Lebensniveau) wird er geschärft, in (West)Deutschland ist er komplett ausgerottet. Ersetzt durch Berater, google und Medien. Wenn ich im Ex-Ostblock mit Bewunderer der Deutschen Technik bezüglich „Strom aus nichts“ oder „Auto ohne Benzin“ diskutiere, verwandelt sich die Bewunderung in 5 Minuten in Lachkrämpfe. Der gesunde Menschenverstand hat sofort den Humbug erkannt. Ähnlich bei der CO2 Bedrohung.
Und hier dagegen haben paar Millionen von der Sorte Silke Kosch. Da ist Hopfen und Malz verloren. Und auch die besser gebildeten Strahlenphysiker haben gute Kenntnisse im ganz ganz engen Wissensbereich, links und recht davon sehen sie: Nichts!
Daher appelliere ich immer wieder, die Natur zu beobachten den gesunden Menschenverstand der Gattung Homo einzuschalten.
Zu Energiebilanzen: Ausgehend von den Naturbeobachtungen am Meer, frage ich mich, warum die Sonne den Mond um rund 300 Grad erwärmt (Differenz Tag/Nacht), den Sand um 40 und das Wasser praktisch nicht? Dazu die Überlegung, 70% der Erdoberfläche ist Wasser, also praktisch kaum Temperaturänderung bei 300 Grad auf dem Mond bei gleicher Intensität der Sonnenstrahlung?
Es liegt an die sehr hohe spez. Wärmekapazität des Wassers und die Bewegung, so dass nicht nur die unmittelbare Oberfläche erwärmt wird, sonder bis in gewisser Tiefe. Es wird also eine riesige Energiemenge gespeichert, die nun mal da ist. Und in der kurzen Nacht wird nur ein Bruchteil wieder abgegeben, daher kühlt sich das Meer nur 1-2 Grad ab.
Die Bilanz aus Sonnenenergie und der gespeicherte Energie auf der Erde, in den Weltmeeren und der Atmosphäre bestimmt die Temperatur auf der Erde, nicht der kleine Strahlensalat, den die THE-Fans unter Ausschluß von thermodynamischen Energiebilanzen liefern.
Das kann man dem Neandertaler und Jungs, die am Meer aufgewachsen sind und die Natur beobachtet haben, nicht einreden. Das Totschalgargument ist: „Ihr versteht den THE nicht“! Muss ich nicht, ich sehe dass die Wärme von der Sonne kommt und weiß, dass sie im Weltmeer gepeichert wird. Und das Irgendwas, was 0,04% ausmacht die Erde um 33 Grad erwärmt ist Humbug! Zumal der Anteil früher viel höher war.
Peter Georgiev schrieb am 27. FEBRUAR 2021 UM 11:05
Sie haben jetzt viel Text geschrieben, aber nur diese beiden Absätze befassen sich entfernt mit sowas ähnlichem wie einem Ansatz für einzelne Teile einer Bilanz. Wie wäre es mit einer richtigen Bilanz, wenn alle anderen es doch falsch machen? Also was kommt wie rein, was geht wie raus und was/wieviel wird wie zwischengespeichert? Und das vielleicht auch noch mit Zahlen unterlegt – anderen „Zahlen“ als „riesig“.
Wie fast immer Herr Müller, setzen Sie sich nicht mit den klaren Inhalt meiner Aussagen auseinander, sondern beschäftigen sich mit Formulierungsdetails.
Noch mal so kurz wie möglich:
1. Gleichungen mit mehr oder weniger geschätzten Strahlugsintensitäten in W/m2 beinhalten nicht im Geringsten die Wärmeenergiebilanzen und Energiemengen in Joule zwischen Erde, Atmosphäre, Weltmeere und Weltall. Daher zu Temperaturberechnung ungeeignet.
2. Das Ergebnis einer wissenschaftlichen Betrachtung unter Ausschluss wichtiger Faktoren und unter falschen Voraussetzungen kann falscher sein als die pragmatische Naturbeobachtung des Neandertalers und Feststellungen anhand seines gesunden Neadertalerverstands.
Das muss Ihnen nicht gefallen, ist aber so.
@Greorgiev
Ein Venustag dauert rund 4 Monate, die Venusnacht 2 Monate. Da müsste die Nachtseite dann eiskalt sein. Zumal es da keine Ozeane gibt. Sie ist aber kochend heiß.
Keine wissenschaftliche Theorie, und sei sie noch so sicher, bedeutet irgendeine Handlung. Nicht umsonst versuchen Geistesbeschwörer erstmal verpflichtende Protokolle zu vereinbaren [die seit spätestens der Merkelreichsgründung aus zusammengewürfelten contradictio in adiecto ohnehin nicht eingehalten werden; SCNR].
Herr Georgiev,
ich wuerde mich nicht an den Bilanzen so aufhaengen.
Zum einen ist diese doch Null, ansonsten ist die Erwaermung oder Abkuehlung doch vorprogramiert.
Zum anderen hat es noch niemand geschafft nur an taeglichen Ein -und Ausgaengen auf einem Konto den Kontostand zu bestimmen.
Hallo Herr Schulz,
Ihre Bemerkung über Bilanzen und der Vergleich mit dem Kontostand ist nicht schlecht. Der „Anfangs-Kontostand“ der Wärmebilanz der Erde ist die bereits in den Weltmeeren und Atmosphäre gespeicherte Wärme in ?Terrajoule? (reicht nicht als Einheit, daher schreibe ich von „riesigen Energiemengen“). diese Energiemengen kann niemand berechnen, bestimmen aber die Oberflächentemperatur.
Es mag sein, dass es nicht perfekt ausgedrückt ist, sofern de Gedanken nicht von THE-Scheuklappen vernagelt sind, ist der Inhalt aber einigermaßen verständlich.
@ Krüger
„Ein Venustag dauert rund 4 Monate, die Venusnacht 2 Monate. Da müsste die Nachtseite dann eiskalt sein. Zumal es da keine Ozeane gibt. Sie ist aber kochend heiß.“
Auf dem Merkur ist es viel heißer als auf der Venus, auf dem Mars viel kälter als auf der Erde. Man lernt in der Grundschule, dass es mit der Entfernung zur Sonne zusammenhängt. Offensichtlich begreift es aber nicht jeder.
P.S. Tag und Nacht sind im Mittel zeitlich immer identisch, dass der Tag auf der Venus doppelt so lang sein soll als die Nacht beurteile ich freundlich als Tippfehler, oder Sie sollten alles ab der 5. Klasse wiederholen!
@ Martin Rohde
Zitat: Auch wird nie die Höhe betrachtet, in der ein CO2 – Molekül strahlt, dabei sinkt der „Trefferwinkel“ für die Strahlung mit zunehmender Höhe enorm.
So enorm ist das nicht, wie man denkt. Der Sichtfaktor der Außenkugelsphäre (Erd-Atmosphäre) zur Innenkugel (Erd-Körper) ist nicht 1, somit fließt mehr Strahlungsenergie nach außen als nach innen. Die energetische Differenz in 10 km Höhe der Atmosphäre beträgt 170W/m^2*[1 – (6371/6381)^2] = 0,53 W/m^2 und in 30 km Höhe 170W/m^2*[1 – (6371/6401)^2] = 1,59 W/m^2, mal ganz einfach gerechnet.
Mfg
Werner Holtz
@ Martin Rohde
Zitat: In sämtlichen Betrachtungen wird immer nur die Rückstrahlung von CO2 Richtung Erde betrachtet, nie die Strahlung Richtung Weltraum.
Ja, weil man sonst zugeben müsste, dass die Gegenstrahlung die Oberfläche nicht erwärmen kann!
Der differenzieller Energietransport durch Emission über mehrere Sphären ergibt:
E(si->s1) = Ai*σ*(Ti^4 – T1^4)/[1/εi + (1-ε1)/ε1*(ri/r1)^2]
E(s1->s2) = A1*σ*(T1^4 – T2^4)/[1/ε1 + (1-ε2)/ε2*(r1/r2)^2]
E(sn->s0) = An*σ*(Tn^4 – T0^4)/[1/εn + (1-ε0)/ε0*(rn/r0)^2]
Daraus erhält man nach Umformung und Einfachung:
Ei = Ai*σ*(Ti^4 – T0^4)/{1/εi + (1-ε0)/ε0*(ri/r0)^2 + ∑[(2-εn)/εn*(ri/rn)^2]}
bzw.
Pi = Ei/Ai = σ*(Ti^4 – T0^4)/{1/ei + (1-ε0)/ε0*(ri/r0)^2 + ∑[(2-εn)/εn*(ri/rn)^2]}
++ Ein Beispiel mit drei atmosphärischen Sphären:
+ Erdoberfläche (Basis) -> Weltraum: Pi = σ*(Ti^4 – T0^4)/{1/εi + (1-ε0)/ε0*(ri/r0)^2}
Mit den Bedingungen für Erdoberfläche/Weltraum: ri = 1 und r0 = 3 und ε0=0,995, erhält man:
Pi = σ*(288^4 – 3^4)/{1/0,96 + (1-0,995)/0,995*(1/3)^2} = 374,3 W/m^2
+ Erdoberfläche (Basis) -> Atmosphäre (1 Sphäre) -> Weltraum: Pi = σ*(Ti^4 – T0^4)/{1/εi + (1-ε0)/ε0*(ri/r0)^2 + (2-εa)/εa*(ri/ra)^2}
Mit den Bedingungen für Erdoberfläche/Atmosphäre/Weltraum: ri = 1, ra = 1,003 und r0 = 3 und ε0=0,995, erhält man:
Pi = σ*(288^4 – 3^4)/{1/0,96 + (1-0,995)/0,995*(1/3)^2 + (2-0,865)/0,865*(1/1,003)^2} = 166,2 W/m^2
+ Erdoberfläche (Basis) -> Atmosphäre (2 Sphäre) -> Weltraum: Pi = σ*(Ti^4 – T0^4)/{1/εi + (1-ε0)/ε0*(ri/r0)^2 + (2-εa1)/εa1*(ri/ra1)^2 + (2-εa2)/εa2*(ri/ra2)^2}
Mit den Bedingungen für Erdoberfläche/Atmosphäre/Weltraum: ri = 1, ra1 = 1,002, ra2 = 1,003 und r0 = 3 und ε0=0,995, erhält man:
Pi = σ*(288^4 – 3^4)/{1/0,96 + (1-0,995)/0,995*(1/3)^2 + (2-0,865)/0,865*(1/1,003)^2 + (2-0,675)/0,675*(1/1,002)^2} = 90,7 W/m^2
+ Erdoberfläche (Basis) -> Atmosphäre (3 Sphäre) -> Weltraum: Pi = σ*(Ti^4 – T0^4)/{1/εi + (1-ε0)/ε0*(ri/r0)^2 + (2-εa1)/εa1*(ri/ra1)^2 + (2-εa2)/εa2*(ri/ra2)^2 + (2-εa3)/εa3*(ri/ra3)^2}
Mit den Bedingungen für Erdoberfläche/Atmosphäre/Weltraum: ri = 1, ra1 = 1,001, ra2 = 1,002, ra3 = 1,003 und r0 = 3 und ε0=0,995, erhält man:
Pi = σ*(288^4 – 3^4)/{1/0,96 + (1-0,995)/0,995*(1/3)^2 + (2-0,865)/0,865*(1/1,003)^2 + (2-0,675)/0,675*(1/1,002)^2 + (2-0,375)/0,375*(1/1,001)^2} = 45,2 W/m^2
Tabelle:
1.Spalte: Sytemelement (Info)
2.Spalte: Energiestromdichte in J/(m^2*s) bzw. W/m^2 der Sphären
3.Spalte: Differenzielle Energiestromdichte in J/(m^2*s) bzw. W/m^2 über die Sphären
4.Spalte: Summe der differenziellen Energiestromdichte in J/(m^2*s) bzw. W/m^2 über die Sphären + Oberfläche
1.Spalte 2.Spalte 3.Spalte 4.Spalte
Oberfläche (Basis) 374,3
1.Sphäre (bis 3km) 329,1 45,2
2.Sphäre (bis 12km) 238,4 90,7
3.Sphäre (bis 19km) 72,2 166,2
(Summe der Sphären) 302,1
Weltraum (Ausstrahlung am TOA) 238,4 = 166,2 + (374,3 – 302,1)
Man kann die Rechnung auch auf diese Weise interpretieren, da die Emissions- bzw. Absorptionsfähigkeit der Sphären nach außen immer weiter abnimmt, ergibt sich eine differenzielle akkumulierte Energiestromdichte der Sphären nach außen von 45,2 + (90,7 – 45,2) + (166,2 – 90,7) = 166,2 W/m^2.
Man kann zur Verifizierung die Effektivtemperatur der Atmosphäre aus der Energiestromdichte oder differenziellen akkumulierten Energiestromdichte bestimmen: Teff(atm) = [72,2/(0,375*σ)]^0,25 = 241,34K oder Teff(atm) = [166,2/(0,865*σ)]^0,25 = 241,28K.
Die Ausstrahlung am TOA vom Erdsystem setzt sich aus der differenziellen akkumulierten Energiestromdichte von 166,2 W/m^2 der Atmosphäre und der von der Oberfläche (Basis) direkt in den Weltraum gehenden Energiestromdichte von (374,3 – 302,1) = 72,2 W/m^2 zusammen. Dies ist eine zwingende Konsequenz aus der Energie-Erhaltung.
Mit dem AERI-Messinstrument (oder auch dem Pyrgeometer) wird die Energiestromdichte von 329,1 W/m^2 der 1.Sphäre bestimmt. Diese Strahlung zwischen Oberfläche (Basis) und 1.Sphäre als „Gegenstrahlung“ zu bezeichnen, ist schlich und einfach falsch, denn sie ist das Resultat der Emissionsfähigkeit der Basis (Oberfläche) zudem wirkt sie vertikal in beide Richtungen.
Mfg Werner Holtz
@ Werner Holz
Erst einmal vielen Dank für die Bemühungen. Allerdings habe ich mich der Sache nicht über Energiedichten der Atmosphäre, sondern ganz simpel über die Geometrie genähert. Demnach beträgt der „Trefferwinkel“ für die Aussendung von IR-Strahlung an der Erdoberfläche noch annähernd 180°, in 10 km Höhe nur noch knapp 46°, in 20 km noch 28°. Also je höher die Abstrahlung erfolgt, desto geringer die Wahrscheinlichkeit, dass die Strahlung die Erde überhaupt trifft. Und desto größer die Energiemenge, die in den Weltraum verschwindet.
=> Wäre es also denkbar, dass IR – aktive Gase das System nicht erwärmen, sondern abkühlen?
Herr Rohde, dass THG in der unteren Atmosphere IR-Abstrahlung von Boden absorbieren, thermalisieren und etwa hältftig nach oben und unten re-emittieren, ist doch bekannt. Daraus folgt doch dass es am Boden wärmer und oben kälter wird. Denselben Effekt durch einen erhöhten Temperaturgradienten – also innen wärmer und aussen kälter – liefert doch die Wärmedämmung.
„Daraus folgt doch dass es am Boden wärmer und oben kälter wird.“
Was bist du eigentlich?
Ein Phrasencomputer, der immer den gleichen Müll auswirft???
Herr Weber, dass Problem ist, dass Sie den sog. THE nicht verstanden haben. Ich empfehle Ihnen dazu mal die Abhandlungen von Ihren Kollegen Fritz Möller zu lesen.Möller studierte ab 1924 Geophysik und Meteorologie an der Georg-August-Universität Göttingen. 1925 ging er an die Johann Wolfgang Goethe-Universität Frankfurt am Main, die ihn 1928 mit einer Doktorarbeit bei Franz Linke zum Dr. phil. nat. promovierte. 1935 habilitierte er sich über die Dynamik der Atmosphäre. Ab 1934 arbeitete er als Meteorologe am Flugplatz Frankfurt. Zwischenzeitlich war er von 1935 bis 1938 im neuen Reichsamt für Wetterdienst tätig. Seit 1938 lehrte er an der Universität Frankfurt und der Universität Leipzig. Die Johannes Gutenberg-Universität Mainz berief ihn 1948 als Professor. Sein Institut wurde in der Strahlungsforschung international maßgeblich. 1960 folgte Möller dem Ruf der Ludwig-Maximilians-Universität München. Bis zur Emeritierung im Jahre 1972 leitete er das Meteorologische Institut und das Institut für Meteorologie und Klimatologie. Entgegen Möllers Wünschen ging der Auftrag für Meteosat im Rahmen der europäischen Zusammenarbeit an Frankreich. Möller starb im Alter von 76 Jahren. Möller, der 1959/60 mit Syukuro Manabe an der numerischen Bestimmung von Strahlungsflüssen arbeitete, weilte zweimal zu Forschungsaufenthalten in den USA, beim zweiten Mal zur Auswertung von Messdaten meteorologischer Satelliten. Im Global Atmospheric Research Program gehörte er als einziger Deutscher zum Leitungsgremium. Seine Abhandlungen zum THE finden Sie in Einführung in die Meteorologie, 1973 und Möller 1963 “On the influence of changes in the CO2 concentration in air on the radiation balance of the earth’s surface and on climate”. J. Geophys. Res 68, 3866-3877 (1963). Er berechnete auch den Einfluß von Wolken auf das Klima und wies nach, dass eine geringfügige Erhöhung der Bewölkung den CO2 Effekt kompensieren könnte. Zudem wichtig seine Abhandlungen mit S. Manabe. “Über das Strahlungsgleichgewicht der Atmosphäre” und “On the radiative equilibrum and heat balance of the atmosphere”. Z. f. Meteorologie 15, 3-8 (1961) und Monthly Weather Review 89, 503-532 (1961). https://www.youtube.com/watch?v=39uXgb5o9wI
„dass Problem ist, dass Sie …. nicht verstanden haben“
Und Ihr Problem Krüger ist, dass Sie noch nie ein Kommentar auf Eike verstanden haben, sich nicht einmal die Mühe gegeben haben, den Inhalt zu verstehen. Sondern langweilen die Leser immer wieder mit den gleichen Strophen, unterlegt mit dem Grundgedanken, dass Sie sowieso immer alles besser wissen. Wenn Sie schon anfangen hier komplette Lebensläufe unbedeutender Personen aus Langeweile zu veröffentlichen, dann sollten Sie sich lieber langsam eine Arbeit suchen!
Sollte mich das interessieren? Nö.
@Gregoriev
Wenn ich von mir schreibe stört Sie das, wenn ich von Fritz Möller schreibe und seinen Forschungsergebnissen zum THE und zu Gegenstrahlung aus den 1960ern und dazu einen Buchauszug von 1973 einstelle auch. Leute wie Sie fördern die Meinungsdiktatur. Und für eine solche Gesellschaft tue ich keinen Fingerschlag mehr. Ziehe nur noch meinen Nutzen daraus. Den Freiwillhelfern sage ich aber klipp und klar, was die falsch machen und für Schäden anrichten, damit später keiner sagen kann er hätte von nichts gewusst.
„Er berechnete auch den Einfluß von Wolken auf das Klima und wies nach, dass eine geringfügige Erhöhung der Bewölkung den CO2 Effekt kompensieren könnte.“
Er hat also nachgewiesen, daß es bei Bewölkung am Boden kälter wird.
Wahrlich ein Intelligenzbolzen…
Glückwunsch, Krüger!
Ja. Paul Crutzen hat die Idee dann ja später auch aufgegriffen.
„Ja. Paul Crutzen hat die Idee dann ja später auch aufgegriffen.“
Noch ein Genie!
Die vielen PIR² (PIR², 2PIR², 4PIR²) bereiten mir erhebliche Kopfschmerzen. Nicht, dass ich Projektionsflächen eines mit parallelen Lichtstrahlen einfallenden Lichts der Sonne auf die Erde nicht nachvollziehen kann, sondern, wie man die Projektionsflächen im Zusammenhang mit Boltzmann zu phantastischen Rechengebilden gebrauchen kann. Ich kann mich ja irren, aber nach meinem Verständnis sind die Erkenntnisse eines Stefan Boltzmann auf sog. schwarze Körper bezogen, nicht auf „schwarze“ Projektionsflächen. Und diese schwarzen Körper müssen thermisch eingeschwungen sein, also einen Ruhezustand erreicht haben. Die Forderung eines Ruhezustands ergibt sich aus der über die Strahlung zugeführten thermischen Energie zu einem massebehafteten schwarzen Körper, wozu ein zeitliches Einwirken erforderlich ist. Das ist nachvollziehbar. Frage: Wann ist eine Projektionsfläche (masselos) eingeschwungen, um dann mit Boltzmann weiter rechnen zu können?
@ Herrn Peter Puschner, Prof. Dr.-Ing.
Wie meine einfache Flächenzuschreibung, „Erwärmung von Materie auf der Tagseite der Erde (2PIR²)“, zu einer „Projektionsfläche (masselos)“ führen soll, muss Herr Prof. Dr.-Ing. Puschner hier schon selber erklären.
Und wegen der Kopfschmerzen fragen Sie besser Ihren Arzt oder Apotheker…
Sehr geehrter Herr Weber,
Ihre Antwort an Herrn Prof. Puschner zeigt nur, dass Sie die Kritik von Prof. Puschner noch nicht einmal ansatzweise begriffen haben!
Zu Ihrem letzten Satz spare ich mir mal irgendwelche Bemerkungen, sonst kriege ich Ärger mit dem admin!
MfG
Hallo Herr Weber, Sie sollten sich den Schuh gar nicht anziehen, weil ich von Ihnen lediglich die masselose Projektionsfläche für meine Fragestellung benutzt habe. Leider hat sich niemand zu einer Antwort gefunden, wie man mit einer zweidimensionalen masselosen Projektionsfläche irgendwie mit S. Boltzmann weiter rechnen kann. MfG P. Puschner
@ Herrn Dr.-Ing. Peter Puschner
Danke für die Klarstellung & viele Grüße – U. Weber
Herr Prof. Puschner, die Projektionsfläche für die Einstrahlung ist der Erdschatten PiR², die Hemisphärenfläche ist 2PiR² und die Abstrahlfläche ist 4PiR².
Faktor4 oder Exponent4?
Faktor 4, Kugel- zur Halbkugel-Oberfläche.
Nein, Faktor 4 ist 4PiR² Kugeloberfläche=Abstrahlfläche dividiert durch PiR² Projektion der Einstrahlfläche=Erdschatten
Eine Messung, die über 24 Stunden fast einen konstanten Wert zeigt, sollte uns alle doch sehr mißtraurisch machen!
Bei klarem Himmel habe ich auf meiner Terrasse mittags zwischen 12 und 14 Uhr die höchsten Bodentemperaturen (schwarzer Granitstein wird ca 57 Grad C heiß). Somit ist auch die Bodenstrahlung bei dieser Temperatur am stärksten!!! Meine Glasplatte, ca 15 cm über dem Boden befestigt wird dann auch fast 57 Grad C heiß. (Hier wird die Erwärmung nur durch die Erdstrahlung erzeugt, was man an 2 Reaktionen der Glasscheibe beobachten und messen kann.) Läßt man die Glasscheibe über einen längeren Zeitraum (ca 5 Std) so über dem Boden liegen, folgt die Glastemeperatur der Bodentemperatur, wobei die Lufttemperatur wenig schwankt!
Geht die Sonne unter oder wird durch Wolken (auch sehr diffuse Schleierwolken, die sich hier in der Nähe des kölner Flugpatzes oft bilden) die Sonnenstrahlung behindert, sinkt etwas verzögert die Bodentemperatur, sofort auch Glasscheibentemperatur!!!
Da aber nach der These des „THE“ mehr H2O in de Atmosphäre zur mehr Atmosphärenstrahlung führen muß, sollte die Temperatur der Glasscheibe nicht absinken, sondern sogar ansteigen!!! Befestigt man eine 2. Glasscheibe ca 1,2 Meter über dem Boden, so zeigt die Glasscheibe überhaupt keine Reaktion auf die Bodenstrahlung, was nur logisch so zu erklären ist, dass diese Strahlung in diesen 1.2 m Luftsäule schon komplett absorbiert wird. Für den Bereich der 15 Mikrometerwellenlänge (CO2 Absorptionslinie) kann man das über die Planckschen Strahlungsformeln auch ziemlich gut berechnen. Indem man dieese Strahlungsenergie im 15 Mikrometer Wellenlängenbereich pro Quadratmeter berechnet, dann die Anzahl der photonen in diesem Wellenbereich ausrechnet.
Die Anzahl der CO“ Moleküle im 1. Kubikmeter läßt sich auch leicht ausrechnen, dann kann man feststellen, dass die hier vorhandenen CO2 Moleküle in der Lage sind, sämtlich Photonen des 15 Mikrometer Wellenbereiches zu absorbieren! Mit der oberen 2. Glasscheibe bewiesen, da hier die Temperatur nicht ansteigt!!! Also auch hier die Folgerung, mehr CO2 Moleküle im ersten Kubikmeter Luft haben keinerlei Auswirkung, da die Energiemenge, die bei den gängigen Bodentemperaturen in den entsprechenden Absoptionsbanden schon hier komplett absorbiert wird!!! Die Glasscheibenexperimente beweisen eindeutig, die physikalischen Berechnungen!
Dann empfehle ich das mal zu veröffentlichen.
Kann es nicht sein dass die Glasscheibe bei 15 cm vom Boden konvektionsunterdrückend wirkt und sich primär deswegen aufheizt (Wood Experiment)? Bei 1,2 m Abstand ist der Luftaustausch entsprechend grösser und es tritt keine Erwärmung der Glasscheibe ein. Wie gross ist Fläche der Glasscheibe im Verhältnis zum Bodenabstand? Messen Sie die selbe Erwärmung auch bei 15 cm Abstand und starker Blauthermik genau so wie bei Windstille?
Sehrt geehrter Herr Ordowski,
ich verstehe ja ungefähr, was Sie uns mit Ihrem Glasscheibenexperiment bezwecken wollen, aber „Ihre“ Glasscheibe gibt es nicht.
Reale Klarglas-Glasscheiben haben je nach Dicke einen Transmissionsgrad von 80 – 90 % und das nur im Bereich von 0,3 µ bis 3 µ. Drunter und drüber geht sogut wie nix durch.
Was machen Ihrer Meinung nach diese Strahlungsanteile???
Und wie messen Sie die Temperatur Ihrer Scheibe ohne Beeinflussung des Experiments? Mir als Fachmann würden da nur ziemlich „wacklige“ Methoden einfallen …..
Vorschläge die die Mängel beseitigen (resp. besseres Verständnis schaffen)? Anderes Material, andere Geometrie, etc? Es sollte doch möglich sein im Experiment nachzuweisen dass die energieärmeren Komponente gegenüber energiereicheren Komponenten keine Chance haben.
Man könnte eine Scheibe aus Kieselglas (reines SiO2) benutzen, die hat ein „Strahlungsfenster“ von 0,15 µ bis 5 µ bei etwas höherer Trasmission. Es blieben trotzdem die Probleme bei der „strahlungsneutralen“ Temperaturerfassung im Glas, aber solch eine Scheibe kann Herr Ordowski auch nicht bezahlen ……..
Herr Ordowski äußert sich auch hier in diesem Faden nicht zu meinen Einwänden. Er wird sie auch nie widerlegen können ……, was Ihm ganz sicher bewußt ist.
@U. TenglerSie schreiben:“Herr Ordowski äußert sich auch hier in diesem Faden nicht zu meinen Einwänden. Er wird sie auch nie widerlegen können ……, was Ihm ganz sicher bewußt ist“Leider konnte ich bis heute nicht antworten, da ich umziehen mußte. Heute wieder on-Line und 236 Emails von EIKE mit Kommentaren gesehen, die langsam abgearbeitet werden.Aber nochmals zu Glasscheibe, wie schon öfters ausgeführt,Ich kann ja die angebliche „TH-Strahlung“ im Experiment mit IR Wärmelampen simulieren, und siehe da, die Glasscheibe wird warm entsprechende seienr spezifischen Wäreme. Das kann ich praktisch mit jeder handelsüblichen Glasscheibe zeigen.Einen weiteren Effekt kann man ebenfalls sehr gut beobachten, wenn man mehrere Glasscheiben in unterschiedlichen Höhen über dem Boden befestigt, werden diese auch unterschiedlich warm. je näher zum Boden umso wärmer, was auf eine Strahlung des warmen Bodens schließen läßt, also nicht Überraschzendes.Aber die Beobachtung, dass sich eine Glasscheibe in ca 1.2 m über dem Boden nicht mehr erwärmt, läßt nur den Schluß zu, dass hier keine Strahlung mehr absobiert wird, weil keine mehr vorhanden!Somit läßt sich mit dem Glasscheibenexperiment sehr geanu zeigen, ist Strahlung vorhanden oder nicht!Bleibt die Glasscheibe kühl, keien Strahlung – kein „Treibhauseffekt“ – ganz einfach zu beweisen!Wenn man über die Emissionsmöglichkeit von CO2 Gas spekuliert, sollte man im Labor schon längst solche Strahlung reproduzieren können. Aber was zeigen peraktisch alle Experimente, nur eines , dass das CO2 Gas IR-Strahlung absorbiert und sich erwärmt!!!Würde eien sofortige Emission stattfinden, gäbe es keine Temeperaturerhöhung, auch ganz einfach, oder?
Noch ein kleiner Nachtrag Herr Ordowski:
„…die Beobachtung, dass sich eine Glasscheibe in ca. 1.2 m über dem Boden nicht mehr erwärmt…“
Ich habe eine Glasplatte in 2 m Höhe (Dach eines kleinen Gewächshauses), wenn ich nach kühlen Sommernächte vergesse, früh die Tür zu öffnen, habe ich mittags die Temperatur einer Bratpfanne, die Glasplatte natürlich auch. Alles nur Konvektion, die erwärmte Luft kann nicht weg. Glassorte egal, gibt es auch in Plaste. Würde man als Dach schwarze Dachpappe nehmen, würde sich das Ganze noch mehr erhitzen.
Bei Ihrem Experiment kann die erwärmte Luft, die nur langsam steigt, links und rechts entweichen und erreicht die Platte in 1,2 m höhe nicht mehr.
Sicher haben vielleicht auch Strahlungen einen Einfluss, aber bei den meisten irdischen Erwärmungsprozesse irrelevant, da sie sich in der x-ten Stelle hinter dem Komma bewegen.
Es ist für mich schon etwas erstaunlich wie sehr sich alle Überlegungen auf Strahlungsprozesse aufgrund der ständigen Medienpräsenz beziehen. Das, was jeder schwach gebildete Gärtner versteht, durfte man mit gesunden Menschenverstand ohne Strahlenphysik und Wellen-Mikrometer leicht nachvollziehen können. Man muss nur das Gehirn von der Strahlungspropaganda befreien. (Die letzten Sätze sind nicht an Sie persönlich gerichtet!)
Die Erdtemperatur wird durch die thermodynamischen Wärmetausch- und Wärmespeicher-Prozesse in den Weltmeeren, Erde, Atmosphäre und All bestimmt, die niemand überblicken oder beschreiben kann. Die verschiedene Strahlungstransporte, abgesehen von der ankommenden Sonnenstrahlung, spielen dabei eine untergeordnete Rolle.
Eugen Ordowski
1. März 2021 um 12:22
Ihr „Experiment“ ist mir trotz Ihrer Ausführungen immer noch sehr „wacklig“. Infrarot-Lampen haben einen Glaskolben und damit einen Trasmissionsverlauf sehr ähnlich Ihrer Scheibe, dem Spektrum fehlen also Anteile des Sonnenlichts bzw. des langwelliger strahlenden Bodens. Die Glasplatte erwärmt sich bei der Wärmelampe also nur durch die Transmissionsverluste!
PS: Was Sie immer noch nicht verraten haben: Wie messen Sie die Temperatur der Glasplatte?
Danke.
Sehr geehrter Herr Ordowski,
bin leider erst heute auf Ihr Experiment gestoßen.
Bei der Bewertung machen Sie den gleichen Fehler wie die Strahlenakrobaten hier, den Wärmeaustausch auf Strahlung zu reduzieren. Wärmeaustausch erfolgt aber überwiegend über Konvektion und Wärmeleitung, und nur im mit Abstand geringsten Maße über die Strahlung.
Die erste Platte stoppt die Konvektion (der echte Treibhauseffekt in Gewächshäuser), durch Wärmeleitung erwärmt sich die unterste Luftschicht, durch Konvektion steigt sie nach oben und erwärmt die Glasplatte durch Wärmeleitung. Ist der abstand klein genug, misst man die gleiche Temperatur, ist „der Deckel“ höher, hat man eine Temperaturaufteilung wie im Zimmer, unten ist es kälter als oben.
Da die Konvektion mit der ersten Scheibe schon unterbrochen ist, erwärmt sich die obere Scheibe natürlich nicht. Nimmt man anstatt die Erste Scheibe eine Metallplatte, müsste sich die 2. Scheibe auch etwas erwärmen. Glas ist ein schlechter Wärmeleiter, daher kann sich die Luft über der 1. Platte kaum erwärmen. Metall leitet gut, daher wird eine zweite Konvektion zwischen Metallplatte und obere Scheiben gestartet. (Experiment zu Wärmeleitfähigkeit: Metall fühlt sich bei -10 Grad viel kälter an als Glas, da die Wärme vom Finger viel schneller abgeleitet wird!).
Man muss bei dem Experiment das Verhältnis Flächen zu Abstände berücksichtigen. Ist der Abstand zwischen Platten 2m und die Fläche relativ klein, dann hat man dazwischen durchgemischte Umgebungsluft und kann nichts messen.
Die Wärmübertragung über Strahlung ist dabei vernachlässigbar. Man erzielt sogar höhere Temperaturen bei der kompletten Unterbrechung der Strahlung.
P.S. Temperaturunterschiede werden im Fachbereich Thermodynamik untersucht, erklärt und berechnet, nicht in der Strahlenphysik. Da bei der THE Erläuterung die Thermodynamik außen vor gelassen wird, kann man die das Ganze als Temperaturberechnungsgrundlage wegwerfen.
Information zum Artikel und zur Diskussion von einem Laien für Laien und Fachleute: Wärmeaufnahme findet über Kontakt oder Strahlung statt. Dabei spielen die Wärmespeicherfähigkeit und die Wärmeleitfähigkeit des Stoffes der Wärmequelle eine Rolle. Ein Feuer ist eine Wärmeenergiequelle, die uns über die Strahlung wärmt oder über den Kontakt mit der erwärmten Luft. Luft ist wegen ihrer geringen Masse ein schlechter Wärmeleiter und ein schlechter Wärmespeicher. Außer die Luft strömt an der Kontaktstelle vorbei, dann überträgt sich mehr Kontaktwärme oder -kälte. Deshalb ist kalte Zugluft so lästig.
Für die Absorption einer Strahlung spielen die Oberflächenfarbe und die Beschaffenheit des angestrahlten Stoffes die Hauptrolle. Eine schwarze Oberfläche absorbiert die meiste Strahlung, eine weiße Oberfläche schickt viel Strahlung im sogenannten Albedo-Effekt wieder zurück. Die Meere absorbieren nicht nur wegen ihrer Größe die meiste Wärmestrahlung, sondern in erster Linie wegen der Tiefe des Eindringens der Strahlung und wegen des Wärmeaustausches durch die Strömungen. Für die globale Klimatemperatur hat deshalb die Temperatur der Troposphäre keine große Bedeutung. Die wird in erster Linie von der Temperatur der Erdoberfläche bestimmt, abhängig von der gespeicherten Sonnenstrahlung. In der Troposphäre nimmt deshalb die Temperatur pro 1000 Höhenmeter um ca. 6 ℃ ab, also insgesamt um etwa 70 ℃. Auf dem Mond wechselt die Temperatur monatlich zwischen mehr als plus 100 ℃ und weniger als minus 200 ℃. Der nur monatliche Tag- und Nachtwechsel ist dafür ausschlaggebend. Die dünne Atmosphäre spielt vermutlich gar keine Rolle.
Gegen die Theorie von den „Treibhausgasen“ spricht vor allem die Unmöglichkeit, über weniger als einem Tausendstel der Atmosphäre aus Spurengasen an die übrigen 999 Teile von einer Rückstrahlung Wärme zur Erwärmung weiterzugeben. Für ein Grad Erhöhung müsste bei einem Tausendstel die Wärmeenergie von 1000 Grad aufgenommen und weitergegeben werden. Der geringe menschengemachte Anteil bei den „Treibhausgasen“ und die Übertragungsverluste sind dabei noch gar nicht berücksichtigt. Die genaue Berechnung entsprechend der Gesetze der Entropie und Enthalpie überlasse ich den anscheinend nicht vorhandenen Experten. Dazu kommt, dass Messergebnisse aus Eisbohrkernen über hunderttausende Jahre eindeutig beweisen, dass Kohlendioxid nicht die Temperatur bestimmt, sondern die Temperatur die Menge Kohlendioxid aus der Biosphäre.
Jetzt kann sich jeder darüber Gedanken machen, wer wirklich hinter den Fake News von den „Treibhausgasen“ und vorhergehend vom „Ozonloch“ steckt.
@E.DenglerIst ja alles ganz richtig, was Sie schreiben, dann sollten Sie doch akzeptieren, dass eine Glasscheibe in erster Linie IR Strahlung absorbiert!Das Experiment zeigt eindeutig, ist Strahlung vorhanden, z.B. von IR Wärmelampen, erwärmt sich die Glasscheibe – keine Strahlung, keine Erwärmung!!!Dieses Experiment können Sie an jedem Ort und zur jeder Zeit machen, ob der Himmel bedeckt ist oder nicht, ist auch egal, da die Glasscheibe keine kurzwellige Sonnenstrahlung absorbiert, bleibt sie kühl!!!Allen, denen ich dieses Experiment vorführte, meistens im Sommer bei klaren Himmel und starker Sonneneinstrahlung, waren sehr überrascht, jeder Körper wurde warm bis heiß (schwarze Granitsteine bis 57 GradC), die Glasplatte bleibt kühl ( Da die menschliche hand sehr temperaturempfindlich ist, reicht eine Berührung schon aus,um den Effekt selber zu spüren).Da nun die spezifische Wärme von Glas bekannt ist, die angebliche Strahlung des „Treibhauseffektes“ auch, ist es nun ein Kinderspiel, auszurechnen, wie warm die Glasplatte nach ca 3600 Sekunden werden müßte!!!Ja, ich höre hier gleich wieder die alten falschen Argumente über Abstrahlung und der Konvektion, die eine Erwärmung verhindern!!!Der Granitstein wird aber sehr heiß, obwohl der noch zusätzlich Wärme an den Boden abgibt, in dem er verankert ist(Wärmeleitung)!!!Also, nochmals, keine Erwärmung der Glasplatte, keine Strahlung, jeder, der hier noch etwas logisch denken kann, sollte doch stutzen, die atmosphärische Gegenstrahlung soll in der Lage sein, die Erde, (mit ihrer riesegen Masse und den unterschiedlichen spezifischen Wärmen) um ca 33 Grad C wärmer zu machen, aber eine kleine Glasplatten wird durch diese angebliche Strahlung kein Grad C wärmer!!!