Geoff Sherrington

Teil 1 begann mit drei Feststellungen:

„Es besteht allgemeiner Konsens darüber, dass die Nützlichkeit von Messergebnissen und damit ein Großteil der Informationen, die wir als Institution bereitstellen, zu einem großen Teil von der Qualität der sie begleitenden Unsicherheitsaussagen bestimmt wird.“

„Die Unsicherheit eines Messergebnisses setzt sich im Allgemeinen aus mehreren Komponenten zusammen, die je nach der Art und Weise, wie ihr numerischer Wert geschätzt wird, in zwei Kategorien eingeteilt werden können:

A. Diejenigen, die durch statistische Methoden bewertet werden,

B. diejenigen, die durch andere Mittel bewertet werden.“

„Dissens. Die Wissenschaft profitiert von Meinungsverschiedenheiten innerhalb der wissenschaftlichen Gemeinschaft, um Ideen und Denkweisen zu schärfen. Die Fähigkeit von Wissenschaftlern, legitime Meinungsverschiedenheiten, die die Wissenschaft verbessern, frei zu äußern, sollte nicht eingeschränkt werden.

Transparenz beim Austausch von Wissenschaft. Transparenz untermauert die solide Generierung von Wissen und fördert die Rechenschaftspflicht gegenüber der amerikanischen Öffentlichkeit. Bundeswissenschaftler sollten die Möglichkeit haben, frei über ihre nicht klassifizierte Forschung zu sprechen, wenn sie dies wünschen, auch gegenüber der Presse.“

Sie führten zu einer Frage, die das australische Bureau of Meteorology BOM seit einigen Jahren schrittweise beantwortet.

„Wenn jemand den Abstand zwischen zwei Tagestemperaturen in Grad Celsius wissen möchte, der eine sichere Aussage darüber zulässt, dass die beiden Temperaturen statistisch gesehen unterschiedlich sind, um wie viel würden die beiden Werte voneinander abweichen?“

Der zweite Teil befasst sich nun mit den eher mathematischen Themen der ersten beiden Aussagen.

Kurz gesagt, wie groß ist die Unsicherheit, die mit solchen täglichen Routinemessungen der Temperatur verbunden ist? (Ab hier hat sich der Anwendungsbereich von einer einzigen Beobachtung an einer einzigen Station auf mehrere Jahre von Beobachtungen an vielen Stationen weltweit ausgeweitet).

Wir beginnen dort, wo Teil eins aufgehört hat.

Dr. David Jones schickte mir am 9. Juni 2009 eine E-Mail mit diesem Satz:

„Ihre Analogie zwischen einem Unterschied von 0,1°C und einem Trend von 0,1°C/Dekade ergibt ebenfalls keinen Sinn – das Gesetz der großen Zahlen oder der zentrale Grenzwertsatz besagt, dass zufällige Fehler einen winzigen Effekt auf die aggregierten Werte haben.“

Das Gesetz der großen Zahlen. LOLN, und der zentrale Grenzwertsatz. CLT, werden häufig verwendet, um Schätzungen kleiner Messunsicherheiten zu rechtfertigen. Eine allgemeine Zusammenfassung könnte wie folgt lauten: „Die Unsicherheit einer einzelnen Messung könnte bei +/-0,5⁰C liegen, aber wenn wir viele Messungen vornehmen und den Mittelwert bilden, kann die Unsicherheit kleiner werden.“

Diese Überlegungen müssen sich auf die Tabelle der Unsicherheits-Abschätzungen in der Stückliste beziehen, die im ersten Teil und weiter unten gezeigt wird.

Wenn die Unsicherheit eines einzelnen Messwerts tatsächlich +/-0,5⁰C beträgt, welcher Mechanismus ist dann am Werk, um die Unsicherheit mehrerer Beobachtungen auf niedrigere Zahlen wie +/-0,19⁰C zu reduzieren? Man muss sich fast vollständig auf die CLT verlassen. Wenn ja, ist dieses Vertrauen gerechtfertigt?

Die australischen BOM-Autoren haben einen 38-seitigen Bericht verfasst, in dem sie einige ihrer einschlägigen Verfahren beschreiben. Er trägt den Namen „ITR 716 Temperature Measurement Uncertainty – Version 1.4_E“ (Ausgabe vom 30. März 2022). Er dürfte in der öffentlichen Literatur noch nicht leicht zugänglich sein.

Die ausführlichen Tabellen in diesem Bericht müssen verstanden werden, bevor man fortfährt.

Auszug:

Informationsquellen bzgl. der Unsicherheit

Der Prozess der Identifizierung von Unsicherheitsquellen für oberflächennahe atmosphärische Temperaturmessungen wurde in Übereinstimmung mit dem International Vocabulary of Metrology [JCGM 200:2008] durchgeführt. Bei dieser Analyse des Messverfahrens wurden sieben Hauptursachen und zahlreiche beitragende Quellen ermittelt. Diese sind in Tabelle 3 unten beschrieben. Diese Quellen der Unsicherheit korrelieren mit den Kategorien, die im Unsicherheitsbudget in Anhang D verwendet werden.

Tabelle 3: Gewöhnliche trockene Thermometer und Lufttemperatur-PRT-Sonden, die zur Messunsicherheit beitragen. Definitionen in Übereinstimmung mit dem Internationalen Vokabular für Metrologie [JCGM 200:2008]

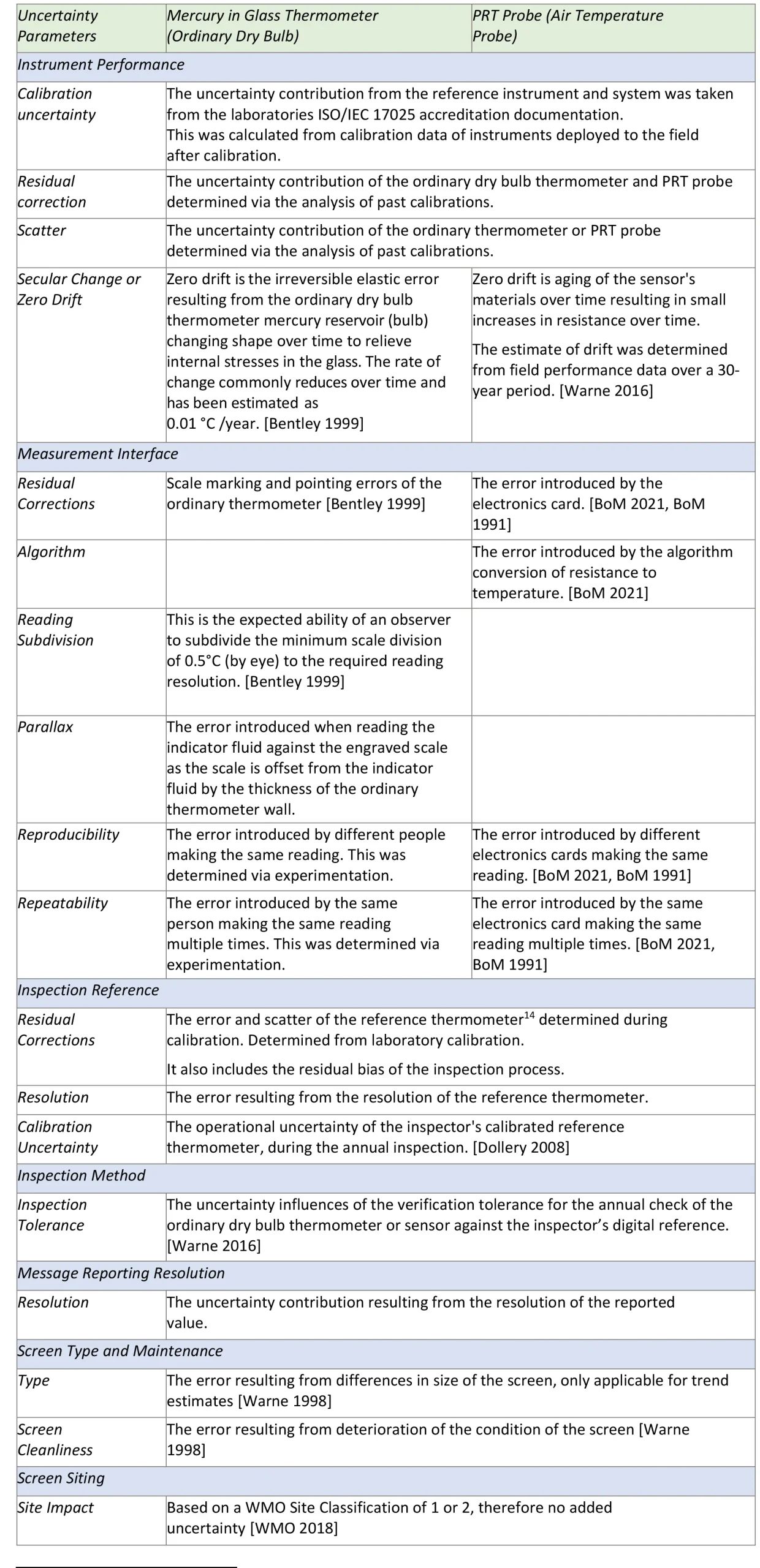
Schätzungen der Unsicherheit

Die Gesamt-Unsicherheit des gewöhnlichen Quecksilber-Glas-Trockenthermometers und der PRT-Sonde zur Messung der atmosphärischen Temperatur ist in Tabelle 4 angegeben. Diese Tabelle ist eine Zusammenfassung des vollständigen Messunsicherheitsbudgets in Anhang D.

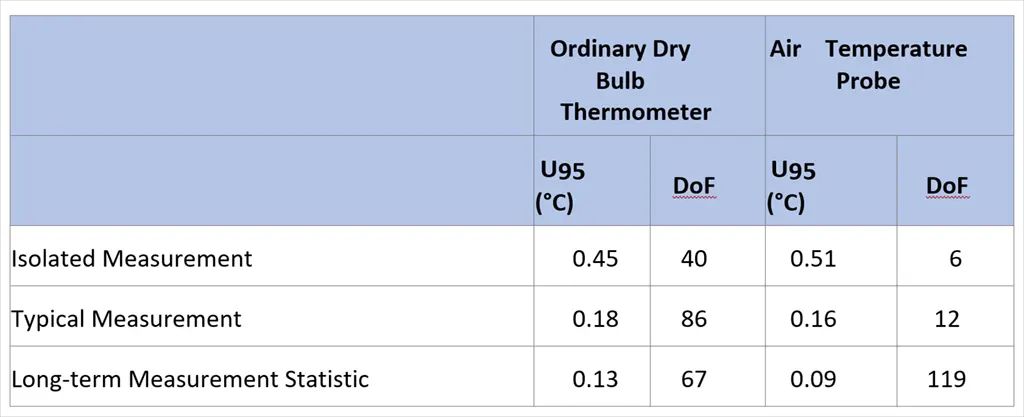
Tabelle 4: Zusammenfassende Tabelle der Unsicherheiten und Freiheitsgrade (DoF) [JCGM 100:2008] für gewöhnliche Trockenthermometer und elektronische Lufttemperatursonden, auch PRT-Sonden genannt:

Eine detaillierte Bewertung der Schätzung der geringsten Unsicherheit für das gewöhnliche Trockenthermometer und die Lufttemperatursonden ist in Anhang D enthalten. Darin werden die oben in Tabelle 3 genannten Unsicherheitsfaktoren detailliert aufgeführt.

Ende Auszug

Es gibt einige bekannte Unsicherheitsquellen, die in diesen Stücklistentabellen nicht oder nur unzureichend berücksichtigt werden. Eine der größten Quellen wird durch eine Veränderung des Standorts des Schirms ausgelöst. Es hat sich im Laufe der Zeit gezeigt, dass das Sieb empfindlich auf Störungen wie Standortwechsel reagiert. Die BOM hat, wie viele andere Betreiber von Temperaturaufzeichnungen, Homogenisierungsübungen durchgeführt, die der Öffentlichkeit nacheinander als „High Quality“-Datensatz, der eingestellt wurde, und dann als ACORN-SAT Versionen 1, 2, 2.1 und 2.2 bekannt wurden.

Die Homogenisierungsverfahren werden in mehreren Berichten beschrieben, unter Anderem hier.

Das Ausmaß der Veränderungen aufgrund von Standortverlagerungen ist groß im Vergleich zu den Veränderungen aufgrund der in der obigen Tabelle aufgeführten Effekte. Sie sind auch weit verbreitet. Nur wenige der etwa 112 offiziellen ACORN-SAT-Stationen wurden nicht um diesen Effekt bereinigt.

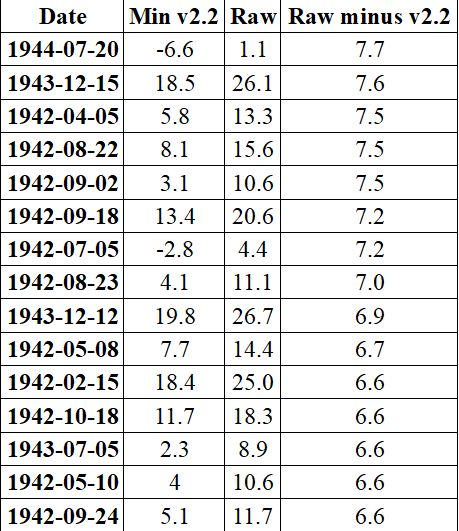
Diese Tabelle zeigt einige tägliche Anpassungen für Alice Springs Tmin, mit Unterschieden zwischen Rohdaten und ACORN-SAT Version 2.2, alle in ⁰C. Die Daten sind entnommen von hier.

Diese Unterschiede tragen zu den gesuchten Unsicherheitsschätzungen bei. Es gibt verschiedene Möglichkeiten, dies zu tun, aber BOM scheint sie nicht in die Gesamtunsicherheit einzubeziehen. Es handelt sich nicht um gemessene Unterschiede, also sind sie nicht Teil der Messunsicherheit. Es handelt sich um Schätzungen von Fachleuten, aber dennoch müssen sie einen Platz in der Gesamtunsicherheit finden.

Wir bezweifeln, dass alle oder auch nur genügend Quellen der Unsicherheit berücksichtigt wurden. Wenn die Unsicherheit so gering wäre wie angegeben, warum wäre dann eine Anpassung erforderlich, um Datensätze wie ACORN-SAT zu erstellen? Dies wurde in diesem Schreiben an die BOM angesprochen:

(Gesendet an Arla Duncan BOM Montag, 2. Mai 2022 5:42 PM)

Vielen Dank für Ihr Schreiben und die Kopie des BOM Instrument Test Report 716, „Near Surface Air Temperature Measurement Uncertainty V1.4_E.“ in Ihrer E-Mail vom 1. April 2022.

Diese Antwort ist im Sinne einer weiteren Klärung meiner vor einigen Jahren gestellten Frage:

„Wenn jemand den Abstand zwischen zwei Tagestemperaturen in Grad C wissen möchte, der eine sichere Aussage darüber zulässt, dass die beiden Temperaturen statistisch gesehen unterschiedlich sind, um wie viel würden die beiden Werte voneinander abweichen?“

Ihre Antwort hat mich in die Mitte der Tabelle in Ihrem Brief geführt, die nahelegt, dass historische Tagestemperaturen, die für viele typisch sind, Unsicherheiten in der Größenordnung von ±0,23 °C oder ±0,18 °C haben.

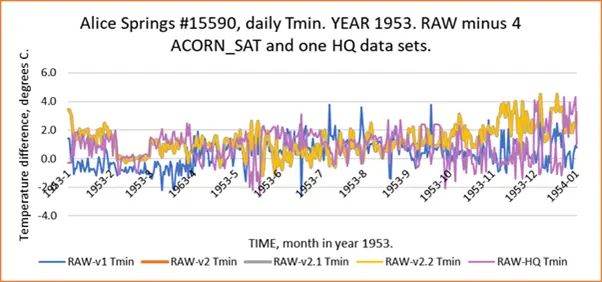
Ich habe die folgende Übung durchgeführt. Es wurde eine Station ausgewählt, hier der Flughafen Alice Springs BOM 15590 wegen seiner Bedeutung für große Regionen in Zentralaustralien. Ich wählte ein Jahr, 1953, mehr oder weniger zufällig. Für die Granularität habe ich tägliche Daten gewählt. Die Temperaturminima wurden untersucht. Es gibt frühere „Raw“-Daten von CDO sowie die bisherigen ACORN-SAT-Versionen mit den Nummern 1, 2, 2.1 und 2.2; außerdem gibt es den älteren High Quality BOM-Datensatz. Mit einer täglichen Subtraktion habe ich ihre Abweichung von RAW grafisch dargestellt. Hier sind die Ergebnisse:

Man könnte argumentieren, dass ich ein bestimmtes Beispiel ausgewählt habe, um einen bestimmten Effekt zu zeigen, aber das ist nicht der Fall. Bei vielen Stationen könnte man eine ähnliche tägliche Temperaturspanne nachweisen.

Dieser vertikale Temperaturbereich kann zu jedem beliebigen Zeitpunkt bis zu 4 Grad Celsius betragen. Grob gesagt entspricht das einer Unsicherheit von +/- 2 Grad Celsius oder mehr. Diese Zahl ist um eine Größenordnung größer als Ihre oben genannten Unsicherheitsschätzungen.

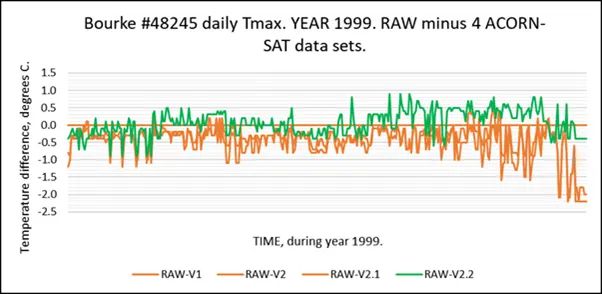
In ähnlicher Weise habe ich einen anderen Standort gewählt, diesmal Bourke NSW, #48245, ein AWS-Standort, Jahr 1999:

Dieses Beispiel zeigt auch eine große tägliche Schwankungsbreite der Temperaturen, hier etwa 2 Grad Celsius.

In der Praxis kann man fragen: „Was war der heißeste Tag, der 1993 in Bourke gemessen worden war?

Die Antworten lauten:

43,2 ± 0,13 ⁰C aus den Datensätzen High Quality und RAW

44,4 ± 0,13 ⁰C aus den ACORN-SAT Versionen 2.1 und 2.2

oder 44,7 ± 0,13 ⁰C aus ACORN-SAT Version 1

Die Ergebnisse hängen von dem gewählten Datensatz ab und verwenden die von der BOM geschätzte Genauigkeit für ein Flüssigkeits-Glasthermometer und einen Datensatz von 100 Jahren Dauer aus dem BOM Instrument Test Report 716, der in der Tabelle in Ihrer E-Mail zitiert wurde.

Dieses Beispiel stellt eine messtechnische Absurdität dar.

Die Schätzungen der Unsicherheit scheinen nicht übereinzustimmen. Ich habe mich dafür entschieden, frühere Versionen von ACORN-SAT und den alten High Quality-Datensatz zu verwenden, weil beide von Experten erstellt wurden, die versuchten, die Unsicherheit zu verringern.

Wie würde BOM diesen Unterschied in den Unsicherheitsschätzungen beheben?
(Ende des Schreibens an das BOM)

Das BOM antwortete am 12. Juli 2022 mit folgendem Auszug:

„In Beantwortung Ihrer spezifischen Fragen bezüglich der Temperaturmessunsicherheit, scheint es, dass diese aus einer falschen Anwendung des ITR 716 Near Surface Air Temperature Measurement Uncertainty V1.4_E auf Ihre Analyse resultieren. Bei den Messunsicherheiten in ITR 716 handelt es sich um einen Messfehler, der mit den Rohtemperaturdaten verbunden ist. Im Gegensatz dazu ist Ihre Analyse ein Vergleich zwischen Zeitreihen von Rohtemperaturdaten und den verschiedenen Versionen von ACORN-SAT-Daten an bestimmten Standorten in bestimmten Jahren. Unabhängig von der gewählten Station und dem Jahr resultiert Ihre Analyse aus Unterschieden in der Methodik zwischen den verschiedenen ACORN-SAT-Datensätzen und kann daher nicht mit den veröffentlichten Messfehlern in ITR 716 verglichen werden. Wir empfehlen Ihnen, die Ergebnisse einer weiteren Analyse bei einer wissenschaftlichen Zeitschrift zur Begutachtung einzureichen.“

BOM scheint nicht zu akzeptieren, dass die Auswirkungen von Standortverlagerungen als Teil der Unsicherheitsabschätzungen berücksichtigt werden sollten. Vielleicht sollten sie das aber. Zu Beginn des australischen Sommers gibt es beispielsweise häufig Nachrichten, in denen behauptet wird, dass an einem bestimmten Tag an einem bestimmten Ort eine neue Rekordtemperatur erreicht wurde. Das ist keine leichte Aufgabe. Siehe dieses Material für den „heißesten Tag aller Zeiten in Australien“:

Der Punkt ist, dass das BOM die Verwendung des ACORN-SAT-Datensatzes als offizielle Aufzeichnung fördert, während es Anfragen oft auch auf die Rohdaten auf einer seiner Websites verweist. Das bedeutet, dass eine moderne Temperatur wie die heutige, die von einer automatischen Wetterstation mit einem Platin-Widerstandsthermometer gemessen wird, mit einer frühen Temperatur nach 1910 (dem Beginn von ACORN-SAT) verglichen werden kann, die von einem Flüssigkeits-Glasthermometer auf einem Bildschirm mit anderen Abmessungen gemessen wurde, der von seinem ursprünglichen Standort verschoben und durch Homogenisierung angepasst wurde.

Auf diese Weise kann ein Vergleich zwischen der Rohtemperatur (heute) und der historischen Temperatur (früher homogenisiert und verschoben) angestellt werden.

Sicherlich ist dieses Verfahren nur gültig, wenn die Auswirkungen von Standortverlagerungen in die Unsicherheit einbezogen werden.

Wir kehren nun zum Thema des zentralen Grenzwertsatzes und des Gesetzes der großen Zahlen (LOLN) zurück.

Der zentrale Grenzwertsatz ist teilweise im BIPM GUM beschrieben, hier eine .jpg-Datei, um Gleichungen zu erhalten:

Diese Worte sind entscheidend – „selbst wenn die Verteilungen von Xi nicht normal sind, kann die Verteilung von Y aufgrund des zentralen Grenzwertsatzes oft durch eine Normalverteilung angenähert werden“. Sie könnten die wichtigste Grundlage für die statistische Rechtfertigung von Unsicherheits-Reduzierungen sein. Wie ist die tatsächliche Verteilung einer Gruppe von Temperaturen aus einer Zeitreihe?

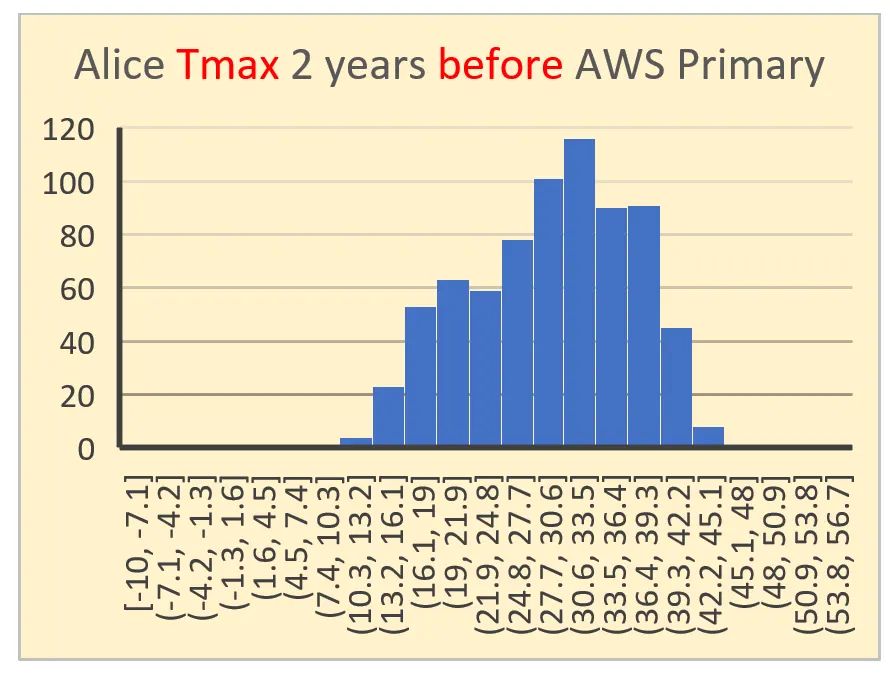
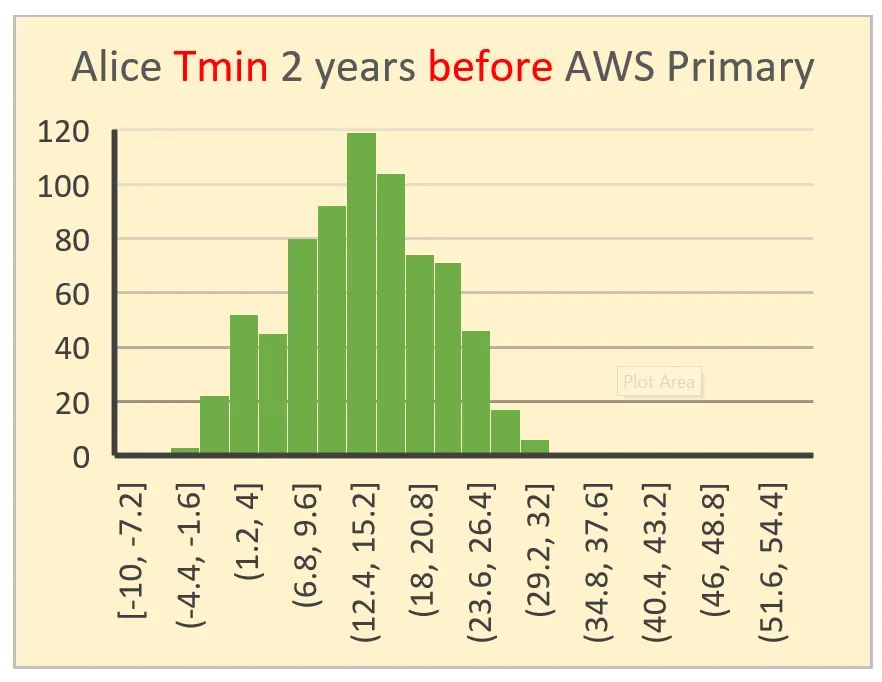
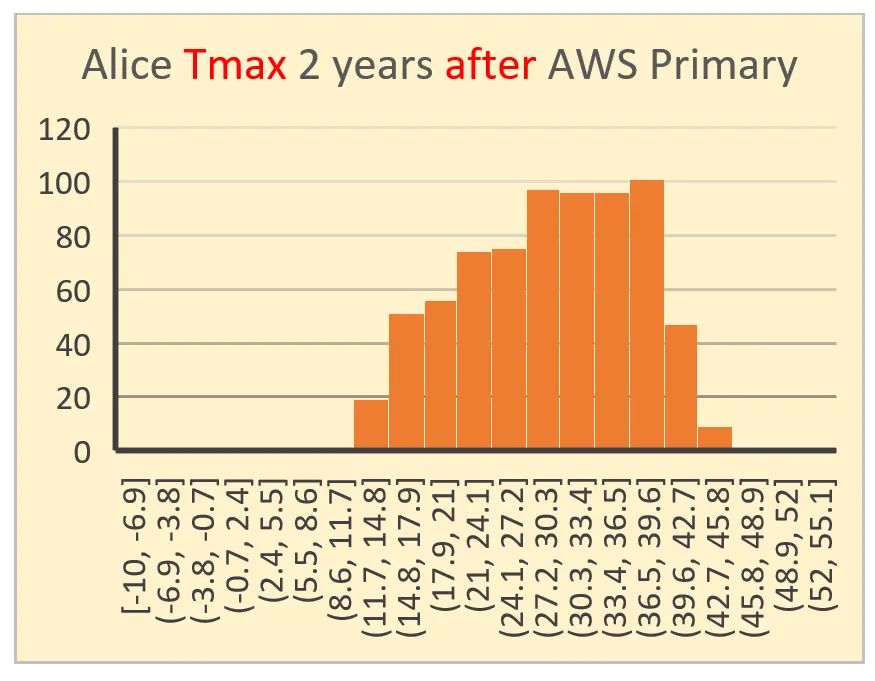
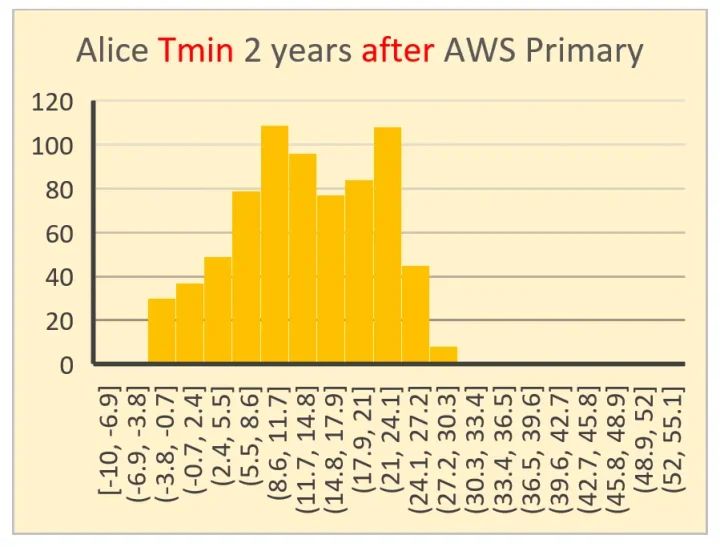
Diese 4 Histogramme wurden ausgewählt, um herauszufinden, ob sich zwei Jahre vor der Umstellung der Wetterstation von Alice Springs von Quecksilber in Glas auf Platin-Widerstands-Thermometrie im Vergleich zu zwei Jahren nach der Umstellung des Messgeräts eine Veränderung abzeichnet. Das obere Paar (Tmax und Tmin) ist vor der Umstellung am 1. November 1996, das untere Paar ist nach der Umstellung. Sowohl die X- als auch die Y-Achse sind vergleichbar skaliert.

Im groben Erscheinungsbild nähert sich nur eines dieser Histogramme visuell einer Normalverteilung an.

Die wichtigste Frage, die sich stellt, ist: „Disqualifiziert dies die Verwendung der CLT in der Art und Weise, wie BOM sie zu verwenden scheint?“

Mit Hilfe der bekannten Mathematik lassen sich diese Diagramme leicht in Teilmengen von Normalverteilungen (oder in deren Nähe) zerlegen. Aber das ist eine akademische Übung, die nur dann nützlich ist, wenn die Ursache für jede Untergruppe identifiziert und quantifiziert wird. Dieser mit einer Unterverteilung verbundene Quantifizierungsschritt ist nicht dasselbe wie die in den obigen Stücklistentabellen aufgeführten Kategorien von Quellenfehlern. Ich vermute, dass es nicht richtig ist, davon auszugehen, dass ihre Unterverteilungen mit den aus den Histogrammen abgeleiteten Unterverteilungen übereinstimmen werden.

Mit anderen Worten, es kann nicht ohne weiteres davon ausgegangen werden, dass die CLT verwendet werden kann, es sei denn, es werden Messungen der dominanten Faktoren vorgenommen, die zur Unsicherheit beitragen.

In meinem Versuch, den zweiten Teil abzuschließen und zusammenzufassen, komme ich zu den folgenden Hauptschlussfolgerungen:

1. Es bestehen Zweifel, ob die zentrale Grenzwerttheorie auf Temperaturen der beschriebenen Art anwendbar ist.

2. Der BIPM-Leitfaden zur Unsicherheit ist möglicherweise in der Praxis nicht hinreichend anwendbar. Er scheint eher für kontrollierte Umgebungen wie nationale Normungsinstitute geschrieben zu sein, wo versucht wird, Fremdvariablen zu minimieren und/oder zu messen. Sie scheint an ihre Grenzen zu stoßen, wenn die Unwägbarkeiten der natürlichen Umgebung auf sie einwirken. Es ist jedoch nützlich, um zu erkennen, ob die Autoren von Unsicherheitsschätzungen die beste Praxis anwenden. Aus dem GUM:

Der Begriff „Unsicherheit“

Das Konzept der Unsicherheit wird in Abschnitt 3 und Anhang D näher erläutert.

Das Wort „Unsicherheit“ bedeutet Zweifel, und somit bedeutet „Messunsicherheit“ im weitesten Sinne Zweifel an der Gültigkeit des Ergebnisses einer Messung. Da es keine unterschiedlichen Begriffe für dieses allgemeine Konzept der Unsicherheit und die spezifischen Größen, die quantitative Maße für dieses Konzept liefern, wie z. B. die Standardabweichung, gibt, ist es notwendig, das Wort „Unsicherheit“ in diesen beiden unterschiedlichen Bedeutungen zu verwenden.

In diesem Leitfaden bezieht sich das Wort „Unsicherheit“ ohne Adjektive sowohl auf das allgemeine Konzept der Unsicherheit als auch auf eine oder alle quantitativen Messgrößen dieses Konzepts.

Es gibt Gründe für die Annahme einer Gesamtunsicherheit von mindestens +/- 0,5 Grad C für alle historischen Temperaturmessungen, wenn sie zum Vergleich untereinander herangezogen werden. Daraus folgt nicht unmittelbar, dass diese Unsicherheit auch für andere gängige Verwendungszwecke, z. B. für Temperatur-/Zeitreihen, gelten sollte.

Dieser Artikel ist lang genug. Ich plane nun einen dritten Teil, in dem ich hauptsächlich traditionelle statistische Schätzungen der Unsicherheit mit neueren Methoden wie dem „Bootstrapping“ vergleichen werde, die für diese Aufgabe gut geeignet sein könnten.

Link: https://wattsupwiththat.com/2022/09/06/uncertainty-estimates-for-routine-temperature-data-sets-part-two/

Übersetzt von Christian Freuer für das EIKE

 

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken