Geoff Sherrington
In der modernen Klimaforschung werden in der Regel drei Leitprinzipien der Unsicherheit nicht angemessen berücksichtigt.
1. Die Abschätzung der Unsicherheit ist wesentlich für das Verständnis.
„Es besteht allgemeiner Konsens darüber, dass die Nützlichkeit von Messergebnissen und damit ein Großteil der Informationen, die wir als Institution bereitstellen, zu einem großen Teil von der Qualität der sie begleitenden Unsicherheitsaussagen bestimmt wird.“
Siehe hier: NISTTechnicalNote1297s.pdf
2. Die Unsicherheitsabschätzung hat zwei Hauptbestandteile.
„Die Unsicherheit eines Messergebnisses setzt sich im Allgemeinen aus mehreren Komponenten zusammen, die je nach der Art und Weise, wie ihr numerischer Wert geschätzt wird, in zwei Kategorien eingeteilt werden können:
A. Diejenigen, die durch statistische Methoden bewertet werden,
B. diejenigen, die durch andere Mittel bewertet werden.“
Siehe hier!
3. Bei der Unsicherheitsabschätzung müssen unterschiedliche Ansichten berücksichtigt werden.
„Im Jahr 2009 hat die Obama-Regierung sechs Grundsätze der wissenschaftlichen Integrität festgelegt.“ (einschließlich dieser beiden):
„Dissens. Die Wissenschaft profitiert von Meinungsverschiedenheiten innerhalb der wissenschaftlichen Gemeinschaft, um Ideen und Denkweisen zu schärfen. Die Fähigkeit von Wissenschaftlern, legitime Meinungsverschiedenheiten, die die Wissenschaft verbessern, frei zu äußern, sollte nicht eingeschränkt werden.
Transparenz beim Austausch von Wissenschaft. Transparenz untermauert die solide Generierung von Wissen und fördert die Rechenschaftspflicht gegenüber der amerikanischen Öffentlichkeit. Bundeswissenschaftler sollten die Möglichkeit haben, frei über ihre nicht klassifizierte Forschung zu sprechen, wenn sie dies wünschen, auch gegenüber der Presse.“
Siehe hier!
In diesem Artikel wird untersucht, inwieweit das australische Bureau of Meteorology (BOM) diese Anforderungen in Bezug auf die geschätzte Unsicherheit bei den täglichen Routinetemperaturen erfüllt.
Der erste Teil befasst sich mehr mit den sozialen Aspekten wie Transparenz. Der zweite Teil befasst sich mit Mathematik und Statistik.
In diesem Artikel werden australische Praktiken und Beispiele verwendet, die hauptsächlich die BOM betreffen. Wichtig ist, dass die Schlussfolgerungen weltweit gelten, denn es gibt viel zu reparieren.
Der bekannteste praktische Leitfaden zum Thema Unsicherheit stammt vom französischen Bureau International des Poids at Mesures (BIPM) mit seinem Leitfaden zur Angabe der Messunsicherheit (GUM; auch hier).
Vor einigen Jahren stellte ich im E-Mail-Verkehr mit dem BOM die folgende Frage:
„Wenn jemand die Differenz zwischen zwei Tagestemperaturen in Grad Celsius wissen möchte, der eine sichere Aussage darüber zulässt, dass die beiden Temperaturen statistisch gesehen unterschiedlich sind, um wie viel würden die beiden Werte voneinander abweichen?“
Das BOM hat in mehreren Anläufen versucht, diese Frage zu beantworten. Sie haben mir erlaubt, aus ihrem Schriftverkehr zu zitieren, unter der Bedingung, dass ich das vollständige Zitat anführe, was ich hier tue.
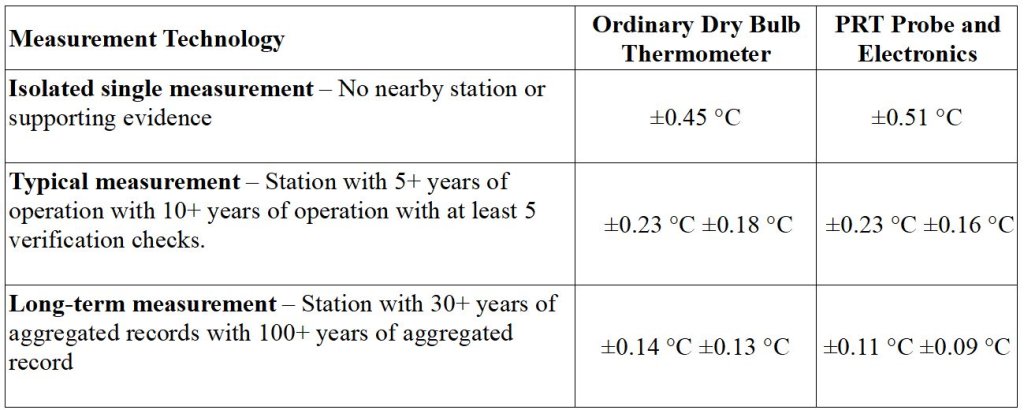
Am 31. März 2022 hat die BOM den letzten Versuch unternommen, die Frage zu beantworten. Hier ist eine Tabelle mit einem Teil des Textes:
(Zitatanfang) „Die Unsicherheiten mit einem 95%igen Konfidenzintervall für jede Messtechnik und Datennutzung sind unten aufgeführt. Zu den Quellen, die zu dieser Unsicherheit beitragen, gehören unter anderem Feld- und Kontrollinstrumente, Rückverfolgbarkeit der Kalibrierung, Messelektronik oder Beobachterfehler, Vergleichsmethoden, Bildschirmgröße und Alterung“.
Ich möchte betonen, dass zur Beantwortung Ihrer spezifischen Frage „Wenn jemand die Differenz zwischen zwei Tagestemperaturen in Grad Celsius wissen möchte, der eine sichere Aussage darüber zulässt, dass sich die beiden Temperaturen statistisch gesehen um wie viel unterscheiden, wäre die Unsicherheit der ‚typischen Messung‘ für die entsprechende Messtechnik der am besten geeignete Wert. Dieser Wert ist für eine breitere Anwendung zur Bewertung langfristiger Klimatrends nicht geeignet, da typische Messungen anfälliger für Mess-, Zufalls- und Kalibrierungsfehler sind als verifizierte Langzeitdatensätze.“ (Zitat Ende)
Diese Konfidenzintervalle beziehen sich im Wesentlichen auf einen Teil der beiden Teile, die eine vollständige Schätzung des Vertrauens ausmachen. Es handelt sich meist um Teil A, der aus statistischen Methoden abgeleitet wird. Sie sind unvollständig und für den Routinegebrauch ungeeignet, wenn Teil B, der mit anderen Mitteln bewertet wird, nicht stärker berücksichtigt wird.
Es macht einen erheblichen Unterschied bei der Interpretation von Temperaturdaten, insbesondere bei Zeitreihen, ob die Unsicherheit ±0,51 °C oder ±0,09 °C beträgt, um extreme Schätzungen aus der BOM-Tabelle zu verwenden. Es ist wichtig zu verstehen, dass die Unsicherheit einer einzelnen Beobachtung viel kleiner wird, wenn mehrere Beobachtungen auf irgendeine Weise kombiniert werden. Ist diese Kombination ein gültiger wissenschaftlicher Vorgang?
Bei routinemäßigen Temperaturmessungen (dem Testgegenstand dieses Artikels) könnte Typ B alle diese Effekte umfassen, die durch die Homogenisierung von Zeitreihen von Temperaturen bereinigt werden, ist aber nicht darauf beschränkt. In diesem Artikel verwenden wir die BOM-Anpassungsverfahren zur Erstellung des Australian Climate Observations Reference Network – Surface Air Temperature (ACORN-SAT).
ACORN-SAT beginnt mit „rohen“ Temperaturdaten als Input. Diese werden dann visuell und/oder statistisch auf Brüche in einem erwarteten (gleichmäßigen) Muster untersucht. Manchmal wird ein Muster an einer Station mit der Leistung anderer, bis zu 1.200 km entfernter Stationen verglichen. Die Temperaturen werden einzeln oder in Blöcken oder Mustern angepasst, um ein glatteres Ergebnis zu erzielen, das besser mit dem anderer Stationen übereinstimmt, vielleicht angenehmer für das Auge ist, aber oft nur unzureichend durch Metadaten unterstützt wird, die tatsächliche Änderungen in der Vergangenheit dokumentieren. Manchmal wird persönlich entschieden, wann und in welchem Umfang eine Anpassung vorgenommen wird, d. h. es handelt sich um Vermutungen.
Die BIPM-Leitlinien enthalten keine Hinweise darauf, wie Unsicherheitsgrenzen für „Vermutungen“ zu erstellen sind – aus guten wissenschaftlichen Gründen (hier und hier)
Einige andere relevante Faktoren, die sich auf die Rohdaten der Stücklisten auswirken, sind:
1. Die Daten begannen mit der Fahrenheit-Skala und wechselten dann zur Celsius-Skala.
2. Es gab Jahre, in denen eine Thermometerbeobachtung in ganzen Gradzahlen ohne Nachkommastellen angegeben wurde. („Rundungseffekte“).
3. Fast jede der etwa 112 ACORN-SAT-Stationen wurde irgendwann an einen anderen Standort verlegt.
4. In der Nähe einiger Stationen wurden neue Gebäude und Bodenbeläge wie Asphalt errichtet, was ihre Messungen beeinträchtigen kann. („Urban Heat Island“-Effekte, UHI).
5. Die Thermometer wurden von Flüssigkeits-auf-Glas auf Platinwiderstand umgestellt.
6. Das Volumen der Bildschirme hat sich im Laufe der Jahrzehnte verändert und ist im Allgemeinen kleiner geworden.
7. Es hat sich gezeigt, dass die Schirme durch die Reinigung und die Art der Außenbeschichtung beeinflusst werden.
8. Die Erfassung von Metadaten zu den Stationen, die Auswirkungen auf die Messungen haben können, war anfangs spärlich und ist immer noch unzureichend.
9. An einigen Stationen wurden an Sonntagen, dem Sabbat, keine manuellen Beobachtungen durchgeführt.
10. Und so weiter.
Mitte 2017 trafen sich Beamte des BOM und Neuseelands und erstellten per E-Mail einen Bericht, der sich mit den eben aufgeführten Variablen befasste, sich aber auf die Leistung der in letzter Zeit dominierenden automatischen Wetterstation (AWS) mit überwiegend PRT-Sensoren konzentrierte.
Ein Teil der E-Mail-Korrespondenz innerhalb des BOM und Neuseelands über diese Überprüfung wurde durch einen Antrag auf Informationsfreiheit veröffentlicht. Relevantes FOI-Material finden Sie hier.
Hier sind einige Auszüge aus diesen E-Mails. (Einige Namen wurden unkenntlich gemacht. Hervorhebungen von mir [Autor]):
„Während keine der in der Klimadatenbank gespeicherten Temperaturmessungen eine explizite Messunsicherheit aufweist, deutet die Rückverfolgbarkeitskette zurück zu den nationalen Temperaturnormalen und die Prozesse, die sowohl im Regionalen Instrumentenzentrum (der derzeitige Name des Metrologielabors im Präsidium) als auch im Feldprüfungsprozess verwendet werden, darauf hin, dass die wahrscheinliche 95%ige Unsicherheit einer einzelnen Temperaturmessung in der Größenordnung von 0,5⁰C liegt. Dies wird aus einer Kombination von Feldtoleranz und Prüfprozessunsicherheiten über einen Temperaturbereich von -10 bis +55⁰C geschätzt.
(Wir) sollten uns mit der Diskrepanz zwischen der aktuellen 0,4⁰C-Unsicherheit der BOM und dem angestrebten 0,1⁰C-Ziel der WMO befassen.
Unter Bezugnahme auf die obige Tabelle bietet die PRT-Spalte eine ähnliche Unsicherheit von +/-0,51⁰C für ‚Isolierte Einzelmessung – Keine nahe gelegene Station oder unterstützende Beweise‘; auch +/-0,37⁰C für „Typische Messung – Station mit 5+ oder 10+ Jahren Betrieb“; auch ±0,11⁰C für „Langzeitmessung – Station mit 30+ Jahren aggregierter Aufzeichnungen.“
Man weiß nicht, warum es ein weiteres Angebot für AWS von ±0,09 °C für „Aufzeichnungen mit 100+ Jahren aggregierter Aufzeichnung“ gibt. Hugh Callendar entwickelte das erste kommerziell erfolgreiche Platin-FTD [Platin-Temperatur-Messfühler] im Jahr 1885, aber seine Verwendung in automatischen Wetterstationen scheint etwa zur Zeit des Internationalen Geophysikalischen Jahres 1957-8 begonnen zu haben. Vielleicht gibt es keine Beispiele für 100+ Jahre.
Ich erinnere daran, dass ich das BOM etwa fünf Jahre vor Mitte 2022 um Schätzungen der Unsicherheit gebeten hatte, die bis Mitte 2022 nicht beantwortet wurden. Dies muss vor dem Hintergrund des Wissens betrachtet werden, das in diesem E-Mail-Austausch von 2017 offenbart wurde: „Die wahrscheinliche 95%ige Unsicherheit einer einzelnen Temperaturmessung liegt in der Größenordnung von 0,5⁰C.“ Es ist davon auszugehen, dass diese Schätzung vor mir verborgen wurde. Einer der BOM-Mitarbeiter, der meine jüngsten E-Mails beantwortet hat, war anwesend und unter den E-Mail-Schreibern des Austauschs von 2017 genannt.
Warum hat die BOM diese Schätzung nicht erwähnt? Sie wurden durch meine Hauptfrage aufgefordert, eine Antwort zu geben, aber sie taten es nicht.
Dies bringt uns zum Anfang dieses Artikels und seinen drei Grundprinzipien, von denen eines lautet: „Transparenz bei der Weitergabe von Wissen. Transparenz untermauert die solide Generierung von Wissen und fördert die Rechenschaftspflicht gegenüber der amerikanischen Öffentlichkeit. Bundeswissenschaftler sollten, wenn sie es wünschen, frei über ihre nicht klassifizierte Forschung sprechen können, auch gegenüber Vertretern der Presse“.
Was für Amerika gilt, gilt auch für Australien.
Zufällig habe ich im Laufe der Jahre einige frühere Schriften von Beamten des BOM aufbewahrt. Hier sind einige.
Erinnern Sie sich daran, dass Dr. David Jones vom BOM im Rahmen von Climategate am 7. September 2007 eine E-Mail an Kollegen schrieb:
Zum Glück sind unsere Skeptiker in Australien wissenschaftlich eher inkompetent. Für uns ist es auch einfacher, weil wir die Politik verfolgen, jedem Beschwerdeführer jede einzelne Stationsbeobachtung vorzulegen, wenn er unsere Daten in Frage stellt (das bringt ihn in der Regel zur Verzweiflung), und die australischen Daten sind ohnehin in ziemlich guter Ordnung.
David Jones war am 16. Juni 2009 noch nicht in entschuldigender Stimmung, als er mir per E-Mail seine Antwort auf eine technische Frage schickte:
Geoff, dein Name taucht häufig in Leserbriefen und Blogs auf, und du schreibst immer wieder E-Mails an Leute im BoM, die die gleichen Fragen stellen. Ich bin mit Briefen wie diesem gut vertraut. Sie haben auch eine lange Erfolgsbilanz bei der Veröffentlichung privater Korrespondenz in öffentlichen Blogs. Ich lasse mich nicht ködern.
Außerdem gibt es eine E-Mail, an der BOM Media und Big Boss Andrew Johnson und andere beteiligt sind, in der AWS Review, 24. August 2017, 9:58 Uhr:
„Ich gehe davon aus, dass wir darauf antworten werden: Das Präsidium äußert sich nicht zu Forschungsergebnissen Dritter..“
Das Thema wird mit dieser E-Mail des BOM aus dem Jahr 2017 fortgesetzt, in der ich mit Daten behaupte, dass die Hitzewellen in Australien nicht länger, heißer oder häufiger werden.
Das Präsidium ist nicht in der Lage, unveröffentlichte wissenschaftliche Hypothesen oder Studien zu kommentieren, und wir ermutigen Sie, Ihre Arbeit in einer geeigneten Zeitschrift zu veröffentlichen. Durch die von Fachleuten geprüfte Literatur können Sie Ihre Kritik an bestehenden Methoden aufgreifen und in einem Format und Forum veröffentlichen, das für andere Wissenschaftler zugänglich ist. Mit freundlichen Grüßen, Klimaüberwachung und -vorhersage.
Diese Haltung des BOM könnte von ganz oben kommen. Ein geschwärzter Name in der E-Mail-Sitzung von 2017 verriet:
„Ich bin im Wesentlichen ‚extern‘ als emeritierter Forscher, war aber Leiter des Bereichs Infrastruktur/Beschaffung/Ingenieurwesen/Wissenschaftsmessung, als ich im März 2016 im letzten Jahr aus dem Bureau ausschied.“
Bei dieser Person könnte es sich um den ehemaligen BOM-Direktor Dr. Rob Vertessy gehandelt haben oder auch nicht. Die Zeitungen berichteten 2017 über Rücktrittserklärungen von ihm. Sie senden eine Botschaft:
„Vertessys Behörde war ständigen Angriffen von Leugnern der Klimawissenschaft ausgesetzt, die – oft über die Nachrichten- und Meinungsseiten des Australian – behaupteten, dass das Wetteramt seine Klimaaufzeichnungen absichtlich manipuliere, um die jüngste Erwärmung schlimmer erscheinen zu lassen, als sie tatsächlich war.
Aus meiner Sicht sind solche Leute, die die nationale Wetterbehörde beeinflussen, unproduktiv und sogar gefährlich“, sagte Vertessy. „Jede Minute, die eine Führungskraft des BoM mit diesem Unsinn verbringt, ist eine verlorene Minute für das Risikomanagement und den Schutz der Gemeinschaft. Es ist ein echtes Problem.“
Siehe hier.
Man beachte die üblichen Medien-Spin-Methoden in diesem Presseartikel. Die BOM hat ein Problem erkannt, es auf ihre Weise formuliert und ihre Emotionen zum Ausdruck gebracht, ohne die Anschuldigungen zu bestreiten.
An dieser Stelle dieses Artikels möchte ich einige Worte von anderen Autoren anführen, um das Ausmaß der sich abzeichnenden Probleme zu verdeutlichen.
„Eine Krise der Irreproduzierbarkeit befällt ein breites Spektrum wissenschaftlicher und sozialwissenschaftlicher Disziplinen, von der öffentlichen Gesundheit bis zur Sozialpsychologie. Viel zu häufig sind Wissenschaftler nicht in der Lage, Behauptungen zu wiederholen, die in veröffentlichten Forschungsarbeiten aufgestellt wurden.1 Viele unsachgemäße wissenschaftliche Praktiken tragen zu dieser Krise bei, darunter eine schlecht angewandte statistische Methodik, Verzerrungen in der Datenberichterstattung, die Anpassung der Hypothesen an die Daten und ein endemisches Gruppendenken. Viel zu viele Wissenschaftler wenden unsachgemäße wissenschaftliche Praktiken an, bis hin zu offenem Betrug.“
National Association of Scholars NAS (USA)
Shifting Sands. Unsolide Wissenschaft und unsichere Regulierung
Bericht Nr. 1: Die Wissenschaft der Regierung auf dem Prüfstand: P-Value Plotting, P-Hacking, und PM2.5 Regulierung
In diesem Bericht wird auf Seite 36 eine Ansicht über den zentralen Grenzwertsatz gegeben:
Die Glockenkurve und der P-Wert: Der mathematische Hintergrund
Alle „klassischen“ statistischen Methoden beruhen auf dem zentralen Grenzwertsatz, der 1810 von Pierre-Simon Laplace bewiesen wurde.
„Das Theorem besagt, dass, wenn eine Reihe von Zufallsversuchen durchgeführt wird und die Ergebnisse der Versuche unabhängig und identisch verteilt sind, sich die resultierende normalisierte Verteilung der tatsächlichen Ergebnisse im Vergleich zum Durchschnitt einer idealisierten glockenförmigen Kurve annähert, wenn die Anzahl der Versuche unbegrenzt zunimmt.
Anfang des 20. Jahrhunderts, als die industrielle Landschaft von den Methoden der Massenproduktion beherrscht wurde, fand das Theorem Anwendung in den Verfahren der industriellen Qualitätskontrolle. Insbesondere entstand der p-Test natürlich im Zusammenhang mit der Frage, wie wahrscheinlich es ist, dass ein hergestelltes Teil so stark von den Spezifikationen abweicht, dass es nicht gut genug passt, um in der endgültigen Montage von Teilen verwendet zu werden.“ Der p-Test und ähnliche Statistiken wurden zu Standardkomponenten der industriellen Qualitätskontrolle.
Es ist bemerkenswert, dass sich die Anwendung des zentralen Grenzwertsatzes im ersten Jahrhundert, nachdem er von Laplace bewiesen worden war, auf tatsächliche physikalische Messungen unbelebter Objekte beschränkte. Zwar gab es philosophische Gründe, die Annahme unabhängiger und identisch verteilter Fehler in Frage zu stellen (d. h. wir können nie mit Sicherheit wissen, dass zwei Zufallsvariablen identisch verteilt sind), doch schien die Annahme plausibel genug, wenn es um Längen-, Temperatur- oder Luftdruckmessungen ging.
Später im zwanzigsten Jahrhundert begann man, den zentralen Grenzwertsatz auf menschliche Daten anzuwenden, um ihre Forschungsgebiete „wissenschaftlicher“ erscheinen zu lassen, obwohl niemand glauben kann, dass zwei Menschen – die Dinge, die jetzt gemessen werden – wirklich unabhängig und identisch sind. Die gesamte statistische Grundlage der „beobachtenden Sozialwissenschaft“ steht auf wackligen Beinen, weil sie von der Wahrheit eines Theorems ausgeht, dessen Anwendbarkeit auf die Beobachtungen, die Sozialwissenschaftler machen, nicht bewiesen werden kann.
Dr. David Jones schickte mir am 9. Juni 2009 eine E-Mail mit diesem Satz:
„Ihre Analogie zwischen einem Unterschied von 0,1 °C und einem Trend von 0,1 °C/Dekade ergibt ebenfalls keinen Sinn – das Gesetz der großen Zahlen oder der zentrale Grenzwertsatz besagt, dass zufällige Fehler einen winzigen Einfluss auf die aggregierten Werte haben.“
Geoff Sherrington, Scientist, Melbourne, Australia
Link: https://wattsupwiththat.com/2022/08/24/uncertainty-estimates-for-routine-temperature-data-sets/
Übersetzt von Christian Freuer für das EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"„Ihre Analogie zwischen einem Unterschied von 0,1 °C und einem Trend von 0,1 °C/Dekade ergibt ebenfalls keinen Sinn – das Gesetz der großen Zahlen oder der zentrale Grenzwertsatz besagt, dass zufällige Fehler einen winzigen Einfluss auf die aggregierten Werte haben.“
Was eine fragwürdige Aussage ist. Folgendes Beispiel: In der Spielbank setze man auf die einfachen Chancen schwarz und rot, die sich zufällig verteilt ergeben. Was den statistisch verteilten Fehlern plus 1 und minus 1 entsprechen soll. Wenn man sehr oft spielt, treten dann schwarz und rot gleich häufig auf? Summieren sich dann die +/- 1 Fehler zu Null? Nein, dass tun sie nicht! Die wahrscheinliche Summe nach n Spielen ist nicht Null (der Erwartungswert) sondern Wurzel(n)! Der wahrscheinliche Fehler wächst mit der Anzahl n der Messungen. Wäre es anders und Null der wahrscheinliche Grenzwert, dann gäbe es totsichere Strategien, die Spielbanken auszunehmen.
Dr. Roland Ullrich am 28. August 2022 um 15:17
Die Reihe aus der Folge der +1 und -1′ sen (= Ergebnisse aufsummiert) konvergiert mit zunehmendem n zu wurzel n. Damit konvergiert der Mittelwert (=Summe / n) zu 1/wurzel n und damit zu null. Dies besagt der Großen Grenzwertsatz!
Dazu wuerde ich die Diskussion im Original Artikel empfehlen.
Mag sein, aber entscheidend ist hier, dass durch Aufsummieren von statistisch nach +/- gleich verteilten und gleich großen Abweichungen der resultierende Fehler immer größer wird – die Statistik will es so! Sich die Fehlersumme also immer weiter von der Null entfernt. Wenn man eine Serie von n Temperaturanomalien hintereinander aufzeichnet, dann wird man die n-te Anomalie samt aufsummiertem Fehler auch nicht durch n dividieren. Auch bei der Spielbank ist es nutzlos, die reale Abweichung von der Null nach dem n-ten Spiel durch Division mit n zu verkleinern – der Geldbeutel merkt nichts davon!
Letztlich läuft es darauf hinaus, dass der wahrscheinliche Fehler, der mit Wurzel (n) wächst, im Verhältnis zu der Gesamtzahl von n Spielen/Messungen kleiner wird. Was nur dann Sinn macht, wenn man ein und dieselbe Größe n-mal misst, aufaddiert und anschließend durch n dividiert. Was weder bei Temperaturanomalien noch bei der Spielbank Sinn macht. Aber bei Mehrfachmessung z.B. eines Schraubendurchmessers die Genauigkeit verbessert.
Herr Ullrich am 31. August 2022 um 21:51
Seien x_i die Fehler in Anomaliewerten, i= 1,…n und x_i sei 1 oder -1. Die Häufigkeit beider Werte sei gleich.
Die Summe aller x_i von 1 bis n sei Xn = x_1 + x_2 + … + x_n.
Dann wächst |Xn| mit wurzel n (random walk).
Der Mittelwert der Folge x_i ist <x> = Xn/n. Somit fällt <x> mit 1/wurzel n (Kürzen). Der Mittelwert geht mit n gegen null!
Richtig, siehe oben.
Nein, das ist ja eben falsch. Wenn Sie ein Thermometer haben, welches unabhängig von Temperaturwert immer den gleichen Fehlerbereich hat und der Fehler der Einzelmessung statistisch um null schwankt, so hat z.B. das Tagesmittel aus 24 Stundenwerten einen Fehler, der 1/wurzel 24 ~ 0,2 x dem Fehler des einzelnen Stundenwertes beträgt.
Analog wird der Fehler im Monatsmittel 1/wurzel 30 x dem Fehlrer des Tagesmittels.
Siehe oben!
Herr Ullrich,
haben Sie meine Erklärung nachvollziehen können und ist Ihnen damit jetzt klar, warum Ihr Argument nicht stimmt?
Wie armselig diese Leugner-Seite ist erkennt man u.a. auch daran das solche Artikel hier veröffentlicht werden: ohne Struktur, mit episodaler und eventueller Schilderung von potentiellen Realitätselementen, ohne Einführung oder Beschreibung irgendeiner Hypothese, letztendlich ein einziger Wortsalat von einem .Scientist’ – traurig.
Natürlich kann man sich an der Frage abarbeiten, wie genau einzelne Messungen sind.
Wesentlich wichtiger ist aber eine Antwort auf die Frage, was will man eigentlich mit all diesen Messungen erreichen? Und das ist unter anderem, eine Erdmitteltemperatur oder auch nur Mitteltemperaturen einzelner Gebiete oder Länder zu ermitteln.
Soweit mir bekannt, lautet die Theorie dazu, das zu untersuchende Gebiet im möglichst kleine „Kacheln“ zu zerteilen und für jede dieser Kacheln Mittelungen über Tage, Wochen, Monate und Jahre zu erstellen, um damit dann zeitkonsistent auch die entsprechenden Mittelungen über das gesamte Gebiet oder die gesamte Erde vorzunehmen.
Dazu bräuchte man in jeder dieser Kacheln eine Meßstation, die die Werte mißt und speichert. Dann müßte man Werte von Stationen, die nicht auf Meereshöhe stehen, entsprechend auf Meeresniveau umrechnen. Weil es aber weit und breit nicht möglich ist, so viele Meßstationen zu haben, wird ausgehend von den verfügbaren Stationen der nicht gemessenen aber riesengroße Kachel-Rest aufgrund der verfügbaren Meßwerte interpoliert und gleichzeitig auf Meereshöhe umgerechnet. Dazu kommt, daß für 70% der Oberfläche (Ozeane) so gut wie keine Meßstationen vorhanden sind. Das bedeutet, 70% der Oberfläche werden aufgrund von punktuell zu zufälligen Zeitpunkten ermittelten Werten (Schiffe) abgeschätzt und extrapoliert.
Fazit: Durch Interpolationen und Extrapolationen sowie Seehöhenumrechnungen beinhaltet diese Methode Fehlermöglichkeiten, die um Klassen größer sind, als alle Fehler, die für Einzelmessungen diskutierbar sind. Das ist das eine, das andere ist aber natürlich auch die Kachelgröße, weil die Annahme, innerhalb einer Kachel herrschen konstante identische Bedingungen, natürlich auch falsch sein kann.
Und zuletzt kommt die Tatsache, daß man wie auch immer berechnete Mittelwerte zwar nennen kann, aber jede klimatologische Folgeberechnung aufgrund solcher Mittelwerte Unsinn ergibt.
Wieviel „Klassen größer“ die nun wirklich sind, findet sich ja in entsprechenden wiss. Publikationen. Die Fehler dadurch sind ja angegeben („sampling error“, u ä.).
Aber um überhaupt Ihren Stsndpunkt verorten zu klnnen, müsten Sie Ihre Vorstellung davon in Zahlen quantifizieren. Wortbeschreibungen alleine sind an dieser Stelle substanzloses Geschwurbel.
Heinemann
Um das, was Sie fordern, zu quantifizieren, wären exakte Daten zur Anzahl der verwendeten Kacheln und zur Anzahl tatsächlich vorhandener Stationen erforderlich. Außerdem Daten zur Extrapolationsmethode.
Solche Daten stehen kaum irgendwo frei zugänglich zur Verfügung. Eines kann man aber ganz leicht sagen, wenn von 100 Kacheln eine mit einer exakten punktuellen Messung ausgestattet ist und deren Messung auf die 99 anderen extrapoliert wird, dann ist das Ergebnis zu 99% zufallsbehaftet. Das heiß nicht, daß es falsch sein muß, es heißt aber, zu 99% kann kein Mensch sagen, welchen Wert das so gewonnene Mittel für diese 100 Kacheln tatsächlich hat. Von allen anderen Gesichtspunkten bzgl. Unterscheidung zwischen Wärme und Temperatur einmal ganz abgesehen. Weil Temperatur wäre nur dann eine zulässige Meßgröße für Wärme, wenn alle anderen Parameter der betrachteten Materien konstant und unveränderlich wären. Was natürlich in dynamischen Systemen nicht der Fall ist.
Alle von solchen Mittelwerten abgeleiteten weiteren Aussagen sind also alles andere als faktenbasiert, schon gar nicht auf 2 Kommastellen genau.
So viel zum substanzlosen Geschwurbel …
Der automatische Übersetzer hat ’screen‘ (= Wetterhütte) offenbar mit ‚Bildschirm‘ übersetzt.
Es wird nicht klar, und es ist dem Autoren wohl auch nicht klar, zu welchen Temperaturmessungen genau die in der Tabelle gelisteten Ungenauigkeitsintervalle gehören. Der Autor fragt nach der Genauigkeit des „Tagestemperatur“. Damit meint er wohl das 24 Stundentemperaturmittel. Aber wo steht, dass die Unsicherheitsintervalle die für diesen Messwert sind (und nicht die für z.B. Terminwerte)? Ich finde es unerklärlich, dass die Unsicherheitsintervalle abnehmen, je länger an der Station gemessen wird. Das ist doch unsinnig. Von daher meine Frage/Zweifel, ob die Unsicherheitsintervalle der 3 Zeilen überhaupt zur gleichen Messgröße gehören.