1. Messfehler
Temperaturen wurden seit etwa 250 Jahren mit Thermometern (darunter solche im englisch sprachigen Raum, die Max und Min Temperaturen anzeigen) gemessen und seit einigen Jahrzehnten mittels elektronischer Sensoren oder Satelliten. Hinsichtlich noch älterer Daten muss man sich auf „Proxys“ verlassen (Baumringe, Stomata oder andere geologische Belege, welche eine Kalibrierung bzgl. Zeit und Amplitude benötigen, historische Chroniken oder Almanache usw.). Jedes Verfahren weist einen gewissen experimentellen Fehler auf. Bei einem Thermometer sind es etwa 0,1°C, bei Proxys noch viel mehr. Springt man von einem Verfahren zu einem anderen (z. B. von Thermometer-Messungen zu elektronischen Sensoren oder von elektronischen Sensoren zu Satellitendaten), müssen die Daten kalibriert und adjustiert werden, was in den Aufzeichnungen nicht immer sauber dokumentiert wird. Wie in dieser Studie ebenfalls gezeigt wird, ist die Länge des Zeitfensters für Messungen von ultimativer Bedeutung, um Schlussfolgerungen zu ziehen hinsichtlich eines möglichen gemessenen Trends in Klimadaten. Es müssen gewisse Kompromisse eingegangen werden zwischen der Genauigkeit der Daten und deren Repräsentativität.
2. Zeitliche Mittelungs-Fehler
Falls jemand ausschließlich Thermometermessungen für „zuverlässig“ hält, muss man täglich, wöchentlich, monatlich und jährlich definieren, was die Mitteltemperatur ist. Aber vor der Einführung elektronischer Sensoren, welche eine kontinuierliche Registrierung der Daten gestatteten, wurden diese Messungen von Hand, punktuell und einige Male über den Tag verteilt durchgeführt. Der Algorithmus zur Errechnung der täglichen Mitteltemperatur war Gegenstand von Änderungen von Land zu Land und mit der Zeit, und zwar auf eine Art und Weise, die in den Datensätzen nicht perfekt dokumentiert ist und wobei einige Fehler enthalten sind (Limburg, 2014). Auch folgte die Temperatur saisonalen Zyklen, verbunden mit der Sonnenaktivität und der lokalen Exposition in dieser Hinsicht. Das bedeutet, dass wenn man monatliche Daten mittelt, man Temperaturen vergleicht (von Beginn bis zum Ende des Monats) welche mit unterschiedlichen Punkten im saisonalen Zyklus korrespondieren. Und schließlich, wie jeder Gärtner weiß, haben auch die Mondzyklen einen gewissen messbaren Einfluss auf die Temperatur (ein 14-Tage-Zyklus ist in lokalen Temperaturdaten offensichtlich, was korrespondiert mit der Harmonic 2 des Mondes Frank, 2010). Es gibt etwa 28 Mondzyklen über jeweils 28 Tage innerhalb eines solaren Jahres von 365 Tagen, aber das solare Jahr ist in 12 Monate unterteilt, was einige Verzerrungen und falsche Trends induziert (Masson, 2018).
3. Räumliche Mittelung
Zuallererst, das IPCC betrachtet global gemittelte Temperaturen über den gesamten Globus, trotz der Tatsache, dass die Temperatur eine intensive Variable ist, und zwar von einer Kategorie von Variablen, die nur eine lokale thermodynamische Bedeutung haben, und trotz der Tatsache, dass es auf der Erde mehrere gut definierte Klimazonen gibt.
Die verwendeten Daten stammen von Aufzeichnungen meteorologischer Stationen und sollen repräsentativ sein für ein Gebiet um jede der Stationen. Das Gebiet soll alle Punkte umfassen, die näher an der jeweiligen Station als an irgendeiner anderen Station liegen (Voronoi-Algorithmus). Da die Stationen nicht gleichmäßig verteilt sind und da deren Anzahl erheblich mit der Zeit geschwankt hat, sind mit diesem Verfahren der räumlichen Mittelung „Algorithmus-Fehler“ verbunden.
Voronoi Diagramm
„In der Mathematik ist ein Voronoi Diagramm die Partitionierung einer Fläche in Regionen auf der Grundlage der Distanz zu Punkten in einem spezifischen Untergebiet der Fläche. Dieser Satz von Punkten (mit den Bezeichnungen seeds, sites oder generators) ist zuvor spezifiziert, und für jedes seed gibt es eine korrespondierende Region, die alle Punkte enthält, welche näher an diesem seed liegen als an jedem anderen. Diese Regionen nennt man Voronoi-Zellen (Quelle).
Da sich die Anzahl der seed-Punkte ändert ändert sich auch Größe, Anzahl und Aussehen der korrespondierenden Zellen (Abbildungen 1 und 2):

Abbildungen 1 und 2: Beispiel eines Voronoi-Diagramms, in Abb. 2 mit einer reduzierten Anzahl von seeds (konstruiert mit http://alexbeutel.com/webgl/voronoi.html).
In der Klimatologie sind die seed-Punkte die meteorologischen Stationen, und deren Anzahl hat sich mit der Zeit signifikant reduziert. Dadurch änderten sich Anzahl und Größe der korrespondierenden Zellen (siehe die Abbildungen 3, 4 und 5).
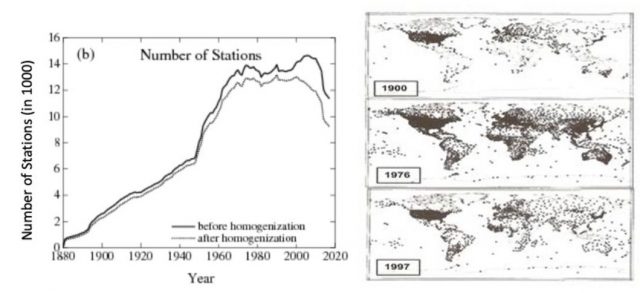
Abbildungen 3 und 4: Anzahl der Stationen nach der Zeit (links) und Ort vs. Zeit (rechts). Die Daten in Abb. 3 stammen von der GISS Surface Temperature Analysis (GISTEM v4). Quelle: https://data.giss.nasa.gov/gistemp/station_data_v4_globe/
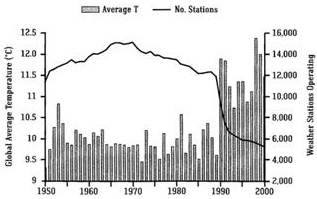
Abbildung 5: Entwicklung von Landstationen und globaler Temperatur. Ab dem Jahr 1990 sind 1000 in kühleren ländlichen Gebieten stehende meteorologische Stationen (z. B. in Sibirien und Nordkanada) ausgesondert worden (Quelle: ftp://ftp.ncdc.noaa.gov/pub/data:ghcn/v2/v2.temperature.readme). Man beachte, dass Abbildung 3 auf GHCNv4 (Juni 2019) beruht und Abbildung 5 auf GHCNv2 (vor 2011). Alle Stationen wurden re-analysiert, und das ist auch der Grund für die Unterschiede in den beiden Abbildungen.
Mitteltemperatur
Die Mitteltemperatur (genauer deren Anomalie, siehe weiter unten) wird berechnet durch Aufsummierung der individuellen Daten von unterschiedlichen Stationen, wobei jeder Datenpunkt gewichtet wird proportional zu dessen korrespondierender Zelle (gewichtetes Mittel).
Da sich die Größen der Zellen mit der Zeit geändert haben, hat sich auch die Wichtung der seed-Punkte geändert. Dies induziert einen Bias in der Berechnung des globalen Wertes der Mitteltemperatur.
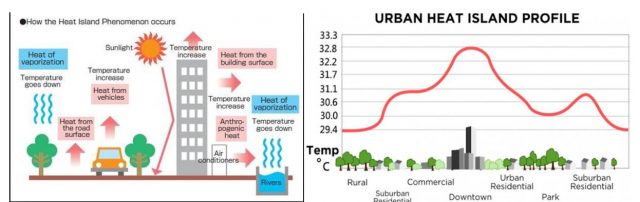
4. Der städtische Wärmeinseleffekt UHI
Außerdem sind viele ursprünglich in ländlicher Umgebung aufgestellten Messpunkte in zwischen Schauplatz einer progressiven Verstädterung gewesen, was zum „städtischen Wärmeinsel“-Effekt führte, welcher die gemessenen Temperaturwerte künstlich beeinflusste (Abbildungen 6 und 7)
Es ist also unabdingbar bei Landstationen, dass jedwede nicht-klimatischen Temperatursprünge wie der UHI eliminiert werden. Derartige Sprünge können auch induziert werden durch Änderung des Aufstellortes der Stationen oder durch eine Aktualisierung der Instrumentierung. In den adjustierten Daten von GISTEMP v4 sind die Auswirkungen solcher nicht-klimatischen Einflüsse eliminiert wo immer möglich. Ursprünglich wurden nur dokumentierte Fälle adjustiert. Das gegenwärtig von NOAA/NCEI angewendete Verfahren jedoch appliziert ein automatisiertes System auf der Grundlage eines systematischen Vergleichs mit benachbarten Stationen. Damit soll dokumentierten und nicht dokumentierten Fluktuationen Rechnung getragen werden, die nicht direkt Bezug zum Klimawandel haben. Die Verfahren nebst deren Evaluierungen sind Gegenstand vieler Veröffentlichungen.
5. Wassertemperatur
Und was ist mit der Temperatur über den Ozeanen (welche etwa 70% der Erdoberfläche bedecken)? Bis vor Kurzem wurden diese Temperaturen kaum gemessen, kamen sie doch von Schiffen, die eine begrenzte Anzahl kommerzieller Seewege befuhren.
In jüngerer Zeit wurden ARGO-Bojen in allen Ozeanen ausgebracht, was eine repräsentativere räumliche Abdeckung dieser Daten ermöglichte.
6. Temperaturanomalien
Zweitens, zu jedem gegebenen Zeitpunkt kann die Temperatur auf der Erde um bis zu 100°C variieren (zwischen Messpunkten in polaren bzw. tropischen Regionen). Um diesem Problem zu begegnen, bezieht sich das IPCC nicht auf absolute Temperaturwerte, sondern auf etwas, das man „Anomalien der Temperatur“ nennt. Dafür berechnet man zunächst die mittlere Temperatur über einen festgelegten Zeitraum von 30 Jahren: 1931 bis 1960, 1961 bis 1990. Die nächste Periode wird der Zeitraum 1991 bis 2020 sein. Dann wird jede jährliche Temperatur mit der mittleren Temperatur der nächstgelegenen zeitlichen Periode verglichen. Gegenwärtig und bis zum Jahr 2012 ist die Anomalie die Differenz zwischen der Temperatur und dem Mittelwert des Zeitraumes 1961 bis 1990.
Dieses Verfahren fußt auf der impliziten Hypothese, dass die „natürliche“ Temperatur konstant bleibt und dass jedweder erkannte Trend anthropogenen Aktivitäten geschuldet ist. Aber selbst dann würde man erwarten, dass einige Adjustierungen vorgenommen werden, wenn man von einer Referenzperiode auf eine andere übergeht. Das berührt die Kompensation eines eventuellen UHI oder die Änderung der Anzahl von Stationen – und wir haben beide als Quellen von Fehlern und Verzerrungen ausgemacht.
Aber das Schlüsselproblem ist tatsächlich der Umstand, dass die Temperaturaufzeichnungen Gegenstand lokaler natürlicher, polyzyklischer Fluktuationen sind, die nicht genau periodisch und nicht synchronisiert sind. Die Tatsache, dass der artige Fluktuationen nicht genau periodisch sind, macht es mathematisch unmöglich, dass man die Daten trendbereinigen kann mittels Subtraktion eines Sinusoids, wie es beispielsweise allgemein üblich ist bei der Eliminierung jahreszeitlicher Effekte aus den Daten.
Die Länge dieser Zyklen variiert von einem Tag bis zu jährlichen, dekadischen, hundert- oder tausendjährigen Komponenten und über zehntausende von Jahren hinaus (Milankovitch-Zyklen).
Von besonderem Interesse für unsere Diskussion sind dekadische Zyklen, weil deren Präsenz dreifach Konsequenzen hat:
Erstens, da sie wegen ihrer Aperiodizität nicht direkt trendbereinigt werden können, beeinflussen oder verstärken sie eventuelle anthropogene Effekte, welche in den Anomalien zutage treten.
Zweitens, die Zyklen induzieren Verzerrungen und falsche Anomalien bei der Berechnung der mittleren Temperatur des Referenz-Zeitraumes, wie die folgende Abbildung zeigt (nach Masson):
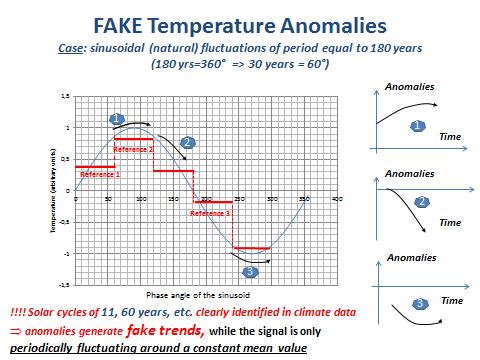
Abbildung 9: Anomalien und periodische Signale des Zeitraumes, der vergleichbar ist mit der Länge des Referenz-Zeitraumes.
Kommentar zu Abbildung 9:
Die Abbildung zeigt die Probleme zur Festlegung einer Anomalie, wenn das Signal ein periodisches Signal mit einer Länge vergleichbar mit der Länge des Referenz-Zeitraumes aufweist, der zu Berechnung dieser Anomalie herangezogen wird. Zur Vereinfachung denke man sich ein Sinusoid mit einer Periode gleich 180 Jahre (eine allgemein in Klima-bezogenen Signalen erkannte Periodizität). Folglich ist 360° = 180 Jahre und 60° = 30 Jahre (also die Länge der vom IPCC herangezogenen Referenzperioden zur Berechnung der Anomalien). Für unseren Zweck werden drei Referenzperioden mit jeweils 60° (30 Jahre) entlang des Sinusoids betrachtet (die roten horizontalen Linien markieren die Referenzen 1, 2 und 3). Auf der rechten Seite der Abbildung sind die korrespondierenden Anomalien dargestellt (Messung über die nächsten 30 Jahre minus dem Mittelwert über die Referenzperiode). Man erkennt offensichtlich, dass die Anomalien unterschiedliche Trends zeigen. Ebenfalls offensichtlich tritt hervor, dass alle diese Trends ein Fake sind, weil das reale Signal ein Sinusoid des Mittelwertes insgesamt gleich Null ist. Mit anderen Worten, es gibt gar keinen Trend, sondern nur ein periodisches Verhalten.
Der dritte fundamentale Schwachpunkt, wie das IPCC mit den Temperaturdaten umgeht, betrifft die Entscheidung, sich ausschließlich auf lineare Regressions-Trendlinien zu stützen, trotz der Tatsache, dass jeder Daten-Wissenschaftler weiß, dass man zumindest ein Zeitfenster berücksichtigen muss, das mehr als 5 mal über die Periode einer zyklischen Komponente in den Daten hinausgeht, um „border effects“ zu vermeiden. Pech für das IPCC: die meisten Klimadaten zeigen signifikante zyklische Komponenten mit (angenähert) Perioden von 11, 60 und 180 Jahren, während sie andererseits ein 30-Jahre-Fentser heranziehen, um ihre Anomalien zu berechnen.
Und so erzeugt das IPCC eine künstliche „Beschleunigung der globalen Erwärmung“, weil es kurzfristige lineare Trends aus Daten berechnet, welche eine zyklische Signatur aufweisen. Mittels Abbildung 10, entnommen FAQ 3.1 aus Kapitel 3 des IPCC-AR 4 (2007) erklärt das IPCC: „Man beachte, dass sich die Steigung über kürzere Perioden vergrößert, was auf eine beschleunigte Erwärmung hinweist“.
Die folgende Graphik (Abbildung 11) illustriert das Ganze:
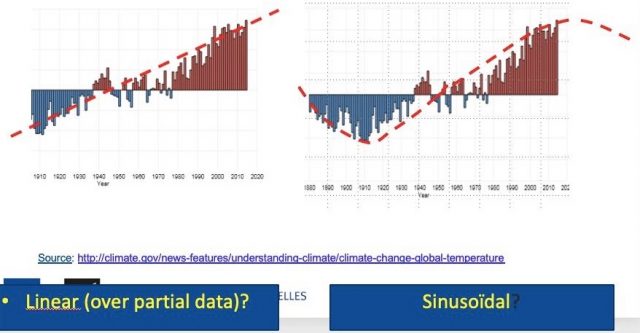
Abbildung 11: Globale Temperaturen im Vergleich zur mittleren globalen Temperatur über den Zeitraum 1901 bis 2000
Kommentar zu Abbildung 11
Die Graphik zeigt die mittlere jährliche globale Temperatur seit dem Jahr 1880, aber nicht verglichen mit einer 30-jährigen Referenzperiode (wie es bei der Berechnung von Anomalien üblich ist), sondern im Vergleich zum langfristigen Mittel im Zeitraum 1901 bis 2000. Die Null-Linie repräsentiert das langfristige Mittel für den gesamten Planeten, die Balken zeigen die globalen (aber langfristigen) „Anomalien“ über oder unter dem langfristigen Mittelwert mit der Zeit. Der behauptete lineare Trend im linken Teil der Abbildung ist (mehr als wahrscheinlich) ebenso wie der Trend im rechten Teil der Abbildung nichts weiter als der steigende Ast eines Sinusoids von 180 Jahren. Dies ist auch ein anderer Weg (der richtige und einfachste?), den „Stillstand“ zu erklären, welcher während der letzten 20 Jahre beobachtet worden ist. Der „Stillstand“ korrespondiert mit dem Maximum des Sinusoids, und als Konsequenz kann man eine globale Abkühlungsperiode während der nächsten Jahre erwarten.
7. Lineare Trendlinien und Daten, die eine zyklische Signatur aufweisen
Schließlich illustrieren die folgenden Graphiken (Abbildungen 12, 13 und 14) von Masson den „border effect“, der weiter oben schon einmal für einen schematischen Fall erwähnt worden ist. Sie zeigen die potentiellen Fehler, die man bei der Anwendung linearer Regressions-Verfahren macht, wenn Daten eine zyklische Komponente aufweisen mit einer (pseudo-)Periode von einer Länge, die vergleichbar ist mit dem betrachteten Zeitfenster. Das Sinusoid bleibt genau gleich (und zeigt keinen Trend), aber falls man die lineare Regression berechnet (mittels des Verfahrens kleinster Quadrate) über eine Periode des Sinusoids, wird eine FAKE-Trendlinie erzeugt, dessen Steigung abhängig ist von der Anfangsphase des betrachteten Zeitfensters.
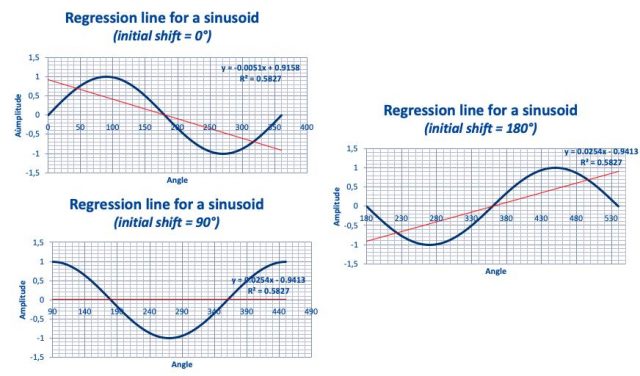
Regressions-Linie für ein Sinusoid
Um das Problem im Zusammenhang mit dem „border effect“ zu illustrieren, wenn man für ein Sinusoid eine Regressions-Linie zeigt, wollen wir ein einfaches Sinusoid heranziehen und die Regressions-Linie über ein, zwei, fünf, … X Zyklen berechnen (Abbildungen 15, 16 und 17).
Das Sinusoid ist stationär, die wahre Regressions-Linie verläuft horizontal (Steigung = Null).
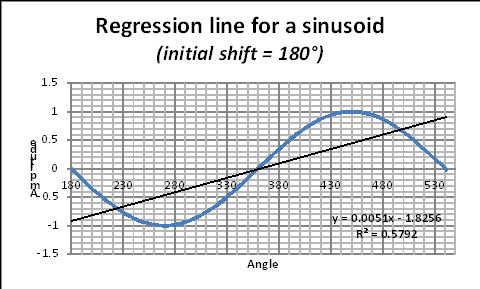
Nimmt man eine Initial-Phase von 180° (um eine Regressions-Linie mit positiver Steigung zu erzeugen), wollen wir feststellen, wie sich die Steigung der Regressions-Linie in Abhängigkeit der Anzahl von Perioden ändert:
Abbildungen 15, 16 und 17: Regressions-Linien für Sinusoids mit einem, zwei, fünf Zyklen.
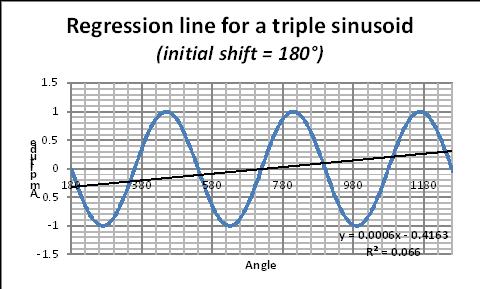
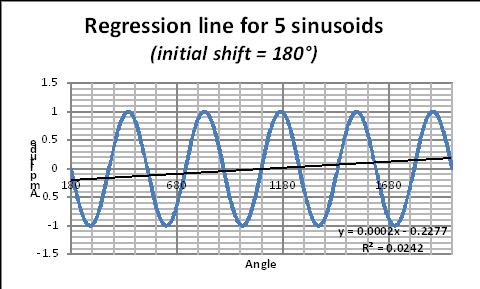
Die korrespondierende Regressions-Gleichung ist in jeder Graphik genannt. In dieser Gleichung ergibt der Koeffizient von x die Steigung der „Fake“-Regressions-Linie. Der Wert dieser Steigung ändert sich mit der Anzahl der Perioden, wie in Abbildung 18 gezeigt. Als Faustregel nennen Daten-Wissenschaftler eine Mindestzahl von 6 Perioden, die betrachtet werden müssen.
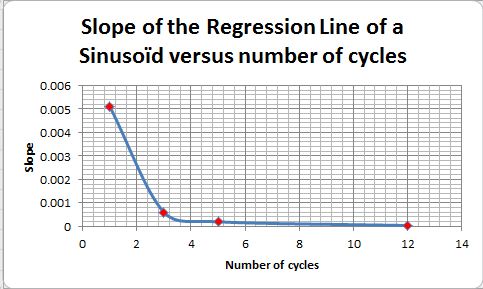
Abbildung 18: Steigung der Regressionslinie im Vergleich zur Anzahl der Zyklen. Dazu gibt es hier auch eine Excel-Illustration.
8. Ein exemplaarischer Fall
Die Überlegungen in dieser Studie mögen für erfahrene Daten-Wissenschaftler offensichtlich sein, aber es scheint, als ob die meisten Klimatologen sich der Probleme nicht bewusst sind (oder versuchen sie vielleicht, diese Probleme unter den Teppich zu kehren?), die sich aus der Länge des betrachteten Zeitfensters und dem Ausgangswert ergeben. Als finale Illustration wollen wir die „offiziellen“ Klimadaten betrachten und sehen, was passiert, wenn man die Länge des Zeitfensters sowie den Ausgangswert verändert (Abbildungen 19 bis 21). Aus diesem Beispiel geht eindeutig hervor, dass lineare Trends, die auf (poly-)zyklische Daten einer Periode ähnlich der Länge des Zeitfensters die Tür weit aufstoßen zu jeder Art von Fake-Schlussfolgerungen, falls nicht Manipulationen zugunsten einer bestimmten politischen Agenda vorgenommen werden.
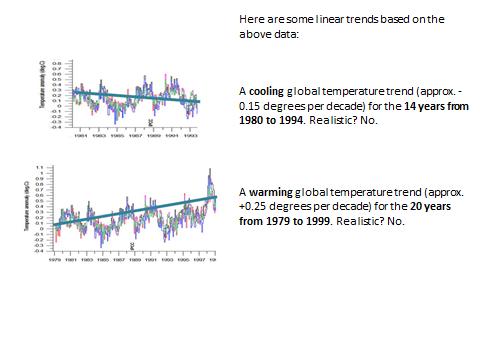
Abbildung 20: Auswirkung der Länge und des Ausgangswertes eines Zeitfensters auf lineare Trendlinien
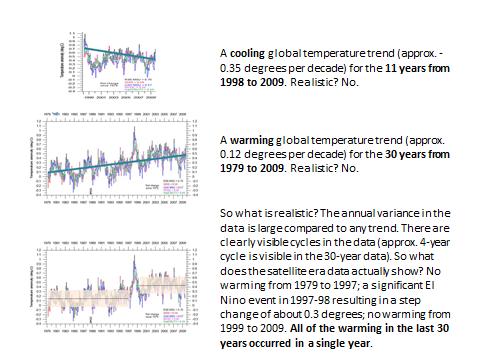
Abbildung 21: Auswirkung der Länge und des Ausgangswertes eines Zeitfensters auf lineare Trendlinien (fortgesetzt)
[Wegen der Bedeutung dieser Graphik folgt hier die Übersetzung der Bildinschrift:
obere Graphik: Ein globaler Abkühlungstrend (etwa 0,35 Grad pro Dekade) während der 11 Jahre von 1998 bis 2009. Realistisch? Nein!
Mittlere Graphik: Ein globaler Erwärmungstrend (etwa 0,12 Grad pro Dekade) während der 30 Jahre von 1979 bis 2009. Realistisch? Nein!
Untere Graphik: Was also ist realistisch? Die jährliche Varianz in den Daten ist groß im Vergleich zu jedwedem Trend. Es gibt eindeutig erkennbare Zyklen in den Daten (ein solcher von etwa 4 Jahren ist in der mittleren Graphik erkennbar). Was zeigen nun also die Daten während der Satelliten-Ära? Keine Erwärmung von 1979 bis 1997; ein signifikantes El Nino-Ereignis 1997-98 führte zu einer sprunghaften Änderung von etwa 0,3 Grad; keine Erwärmung von 1999 bis 2009. Die gesamte Erwärmung der letzten 30 Jahre ereignete sich in einem einzigen einzelnen Jahr!
Ende Übersetzung der Inschrift.]
Schlussfolgerungen:
1. IPCC-Projektionen resultieren aus mathematischen Modellen, welche der Kalibrierung bedürfen, indem man Daten aus der Vergangenheit einfließen lässt. Die Genauigkeit der Kalibrierungs-Daten ist von ultimativer Bedeutung, ist doch das Klimasystem höchst nicht-linear, und das gilt auch für die (Navier-Stokes)-Gleichungen und die (Runge-Kutta Integrations-) Algorithmen, welche in den IPCC-Computermodellen angewendet werden. Als Konsequenz daraus ist das System und auch die Art, wie das IPCC dieses präsentiert, hoch sensitiv gegenüber winzigen Änderungen des Wertes der Parameter oder der Ausgangsbedingungen (die Kalibrierungs-Daten im gegenwärtigen Fall). Sie müssen mit höchster Genauigkeit bekannt sein. Das ist aber nicht der Fall, was ernste Zweifel an jedweder Folgerung aus den Modellprojektionen aufwirft.
2. Die meisten vom IPCC herangezogenen Mainstream-Daten mit Klimabezug sind tatsächlich erzeugt aus Daten von Messpunkten auf dem Festland. Dies hat zwei Konsequenzen:
i) Die räumliche Verteilung der Daten ist höchst fragwürdig, weil die Temperatur über den Ozeanen, die 70% der Erdoberfläche bedecken, zumeist unbeachtet bleiben oder „guestimated“ werden mittels Interpolation;
ii) Die Anzahl und die Aufstellungsorte dieser Landstationen hat sich mit der Zeit deutlich verändert, was Verzerrungen und Fake-Trends induzierte.
3. Der Schlüssel-Indikator des IPCC ist die globale Temperatur-Anomalie, errechnet aus räumlicher Mittelung, ebenso wie mögliche lokale Anomalien. Lokale Anomalien sind der Vergleich der gegenwärtigen lokalen Temperatur mit der gemittelten lokalen Temperatur über einen festgesetzten Zeitraum von 30 Jahren, der sich alle 30 Jahre ändert (1930-1960, 1960-1990, etc.). Das Konzept der lokalen Anomalien ist höchst fragwürdig wegen der Präsenz poly-zyklischer Komponenten in den Temperaturdaten einschließlich deutlicher Verzerrungen und falschen Trends, wenn das Zeitfenster kürzer ist als mindestens 6 mal die längste, aus den Daten hervorgehende Periode. Unglücklicherweise ist bzgl. der Temperaturdaten genau das der Fall.
4. Lineare Trends, die auf (poly-)zyklische Daten einer Periode ähnlich der Länge des Zeitfensters stoßen die Tür weit auf zu jeder Art von Fake-Schlussfolgerungen, falls nicht Manipulationen zugunsten einer bestimmten politischen Agenda vorgenommen werden.
5. Als Folge davon ist es dringend geraten, das Konzept der globalen Temperatur-Anomalie zu verwerfen und sich auf unverzerrte lokale Daten zu stützen, um eine mögliche Änderung des lokalen Klimas aufzufinden. Das wäre ein physikalisch bedeutungsvolles Konzept, und das ist schließlich das, was für die lokalen Anwohner, für Landwirtschaft, Industrie, Dienstleistungen, Geschäftsbereiche, Gesundheit und Wohlergehen allgemein von Bedeutung ist.
Notes
[1] The GISS Surface Temperature Analysis (GISTEMP v4) is an estimate of global surface temperature change. It is computed using data files from NOAA GHCN v4 (meteorological stations), and ERSST v5 (ocean areas), combined as described in Hansen et al. (2010) and Lenssen et al. (2019) (see : https://data.giss.nasa.gov/gistemp/). In June 2019, the number of terrestrial stations was 8781 in the GHCNv4 unadjusted dataset; in June 1880, it was only 281 stations.
[2] Matthew J. Menne, Claude N. Williams Jr., Michael A. Palecki (2010) On the reliability of the U.S. surface temperature record. JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 115, D11108, doi:10.1029/2009JD013094, 2010.
[3] Venema VKC et al. (2012) Benchmarking homogenization algorithms for monthly data. Clim. Past, 8, 89-115, 2012.
[4] F.K. Ewert (FUSION 32, 2011, Nr. 3 p31)
[5] H. Masson,Complexity, Causality and Dynamics inside the Climate System (Proceedings of the 12thannual EIKE Conference, Munich November 2018.
[6] IPCC, http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-chapter3.pdf]
———————————————
Autoren: Samuel Furfari, Professeur à l’Université libre de Bruxelles et Henri Masson, Professeur (émérite) à l’Université d’Antwerpen
Übersetzt von Chris Frey EIKE



















die physikalische Grösse Temperatur bezieht sich auf einen Raum/Zeit-Punkt. Wenn man annehmen kann, eine solche lokale Temperatur sei über einen gewissen Zeit-Abschnitt konstant, kann man sie durch wiederholte Messungen schätzen. Der Schätz-Wert ist dann das arithmetische Mittel aus den einzelnen Werten. Die über eine grössere Erd-Oberfläche, bzw. über einen Raum-Bereich bestimmten Temperaturen sind dabei nicht mehr eine physikalische Grösse, sondern eine solche der mathematischen Statistik.
Durchschnitts-Werte der «Welt-Temperatur», die somit keine physikalische Grösse ist, sondern eine solche der mathematischen Statistik auf ein halbes Grad genau sind dabei grober Unfug. http://www.klima-schwindel.com
Der Artikel gefällt mir. Eigentlich ein weiterer unwiderlegbarer Beweis dafür, dass alles, was das IPCC macht, bodenloser Schwachsinn ist. Aber unsere politische „Elite“ interessiert das alles nicht. Ohne grundsätzlichen politischen Umschwung ist das das sprichwörtliche Rufen in der Wüste.
Klimaänderungen gibt es immer, das hat viele Gründe. Globale Temperaturerfassung und Mittelung über einen längeren Zeitraum gibt es nicht, da die Temperaturerfassungen früherer und heutiger Standorte nicht vergleichbar sind. Klima und Temperaturen sind immer ortsbezogen zu betrachten. Ein ständig Weltreisender wie A. Merkel kann aufgrund der persönlichen Erfahrung keine Klimaänderungen feststellen.
Zu den deutschen DWD-Werten: Wir bestreiten nicht:
1) Dass es ab 1881 bis heute wärmer wurde, 1881 lag in einer „Kältedelle“
2) Dass es ab 1985 bis heute erneut wärmer wurde, die Erwärmung erfolgt aufgrund eines Temperatursprunges zwischen 1984 und 1988.
3) Die Messmethoden haben sich geändert, die Höhe der derzeitigen Erfassung ist diskussionswürdig, aber nicht grundsätzlich die Punkte 1 und 2. Der Juli 2019 war heiß und liegt im oberen Bereich in Deutschland, es war aber bestimmt kein Rekordmonat.
4)Der Mensch bestimmt durch sein Verhalten und durch seine Eingriffe in die Natur und Umwelt die Erwärmung mit. Nicht CO2 erwärmt die Temperaturen, sondern die menschengemachte ständige Ausweitung der Wärmeinseln inzwischen zu ganzen Wärmeregionen.
5) Die CO2-Treibhauserwärmung ist eine Irrlehre, eine Verwechslung mit dem WI-Effekt. Der WI-effekt ist als UHI-Effekt überall nachweisbar, die angebliche CO2-Klimsensitivität, geschätzt auf 2 bis 4 C, jedoch nicht. Es gibt auch keine technischen Anwendungen dieses nicht nachweisbaren Effektes.
6)Ländliche, fast WI-freie Stationen zeigen auch den Temperatursprung zwischen 1984 und 1988, aber seitdem zeigen sie keine Erwärmung mehr, trotz starker CO2-Zunahme in der Atmosphäre.
7) Die DWD-Erwärmung seit 1988/89 gibt es nur in den Städten und Gemeinden und im Umland. Dort stehen auch die DWD-Messstationen.Und nur dort wurde es wärmer
Mein Vorschlag zur Erwärmungesbekämpfung der Statistik.
Die Messstationen der DWD müssen wieder an ähnlich kalte Standorte gestellt werden wie 1881: zu unbeheizten Klöstern, bei Forsthäusern am Waldrand, bei den Fischteichen vor die Tore der Stadt. Also raus aus den bewohnten Gebieten und weg von den Flughäfen. Dann ist auch der größe Teil der 140 jährigen DWD-Erwärmung aus der Statistik entfernt.
Jede Statistik hat „Auftraggeber“,die ein Auftrag (Ergebnis)stellt.Damit ist klar,das das Ergebnis immer „Auftraggeber freundlich“ sein wird.Wer nicht mitspielt ist seinen schönen Auftrag los.Jeder weiß,wie die Arbeitslosen-Statistik gefälscht wird.Alle störenden Größen werden in neuen Begriffen „versteckt“ und fallen unter den Tisch.
Beim „Klimaschutz“ist es das Gleiche.Daten werden „angepasst“.
„Als Folge davon ist es dringend geraten, das Konzept der globalen Temperatur-Anomalie zu verwerfen und sich auf unverzerrte lokale Daten zu stützen, um eine mögliche Änderung des lokalen Klimas aufzufinden.“
Richtiger geht nicht!