Der „Trick“ anomaler Temperatur-Anomalien

In den meisten Fällen ist die Anomalie sehr gering, und die Änderung wird aufgemotzt, indem die Y-Achse so gestreckt wird, bis diese geringe Änderung daherkommt wie ein steiler Anstieg (oder Fall). Die vermeintliche Aussagekraft der Graphiken wird durch die behauptete Genauigkeit der Anomalie verstärkt – bei der globalen mittleren Temperatur werden oftmals Zehntel- oder sogar Hundertstel Grad Celsius angegeben. Verschlimmert wird das Ganze, indem die Anomalien ohne oder nur mit sehr geringen „Fehler“-Bandbreiten gezeigt werden. Sollte das doch einmal der Fall sein, sind es nicht Fehler- oder Unsicherheits-Balken, sondern tatsächlich die statistische Standardabweichung (und nur selten wird das so angegeben).

Vor vielen Wochen habe ich dazu einen Beitrag geschrieben mit dem Titel [übersetzt] „Fast wie die Erde. Wir sind sicher!“ [Almost Earth-like, We’re Certain]. In dem Beitrag, der vom Weekly News Roundup des Science and Environmental Policy Project als „leicht lesbar“ charakterisiert worden ist, verlieh ich meiner Meinung Ausdruck, dass man Anomalien verwendet und so tut, als ob die Unsicherheit verringert worden wäre. Es ist nichts als Vortäuschung. Es ist ein Trick, um bekannte große Unsicherheiten zu verdecken.

Mit dem Eingeständnis, dass sich diese meine Meinung bis heute nicht geändert hat, denke ich, dass es gut ist, genauer zu erklären, wie ich zu dieser Ansicht gekommen ist – und was für einen umfangreichen Bereich in der Welt der Klimawissenschaft ziemlich kränkend sein wird. Zwei Dinge müssen wir betrachten:

1.Warum nenne ich das einen „Trick“?

2.Wer wird da ausgetrickst?

Zu Punkt 1: Warum nenne ich die Verwendung von Anomalien einen „Trick“?

Was genau ist das „Auffinden einer Anomalie“? Nun, nicht das, was man allgemein denkt. Die vereinfachte Antwort lautet, dass man die jährlich gemittelte Temperatur heranzieht und diese von jenem 30-Jahre-Klimamittel subtrahiert. Was übrig bleibt, ist „Die Anomalie“.

Das ist das, was sie sagen, aber nicht wirklich das, was sie tun. Sie fangen mit dem Auffinden von Anomalien auf einem niedrigen Niveau an und arbeiten sich empor bis zur Globalen Anomalie. Selbst wenn Gavin Schmidt den Gebrauch von Anomalien erklärt (hier), erkennen sorgfältige Leser, dass er sich rückwärts bewegen muss zu Absoluten Globalen Mittelwerten in Grad – indem die allgemein vereinbarte Anomalie dem 30-Jahre-Mittel hinzugefügt wird:

„… wenn wir versuchen, die absolute globale Mitteltemperatur für, sagen wir, das Jahr 2016 abzuschätzen. Die Klimatologie gibt im Zeitraum 1981 bis 2010 einen Wert von 287,4 ± 0,5K, und die Anomalie für 2016 (nach der GISTEMP-Grundlage) beträgt 0,56 ± 0,05°C. Folglich ist unsere Schätzung des absoluten Wertes 287,96 ±0,502 K, und bei Heranziehen des zweiten reduziert sich das zu 288,0 ± 0,5 K“.

Aber hier wollen wir einfach nur betrachten, dass die Anomalie einfach das von der berechneten GAST* subtrahierte 30-Jahre-Mittel in Grad ist.

Wie Schmidt freundlicherweise erklärt, ist die korrekte Angabe einer GAST in Grad irgendetwas auf der Linie 288,0 ± 0,5 K – das ist die Gradzahl bis auf ein Zehntel Grad genau mit einer Unsicherheits-Bandbreite von ± 0,5 K. Wenn eine Zahl auf diese Art und Weise angegeben wird, bedeutet das, dass der tatsächliche Wert nicht genau bekannt ist, aber es ist bekannt, dass er innerhalb der Bandbreite der Plus/Minus-Angabe liegt.

[*GAST = Global Averaged Surface Temperature]

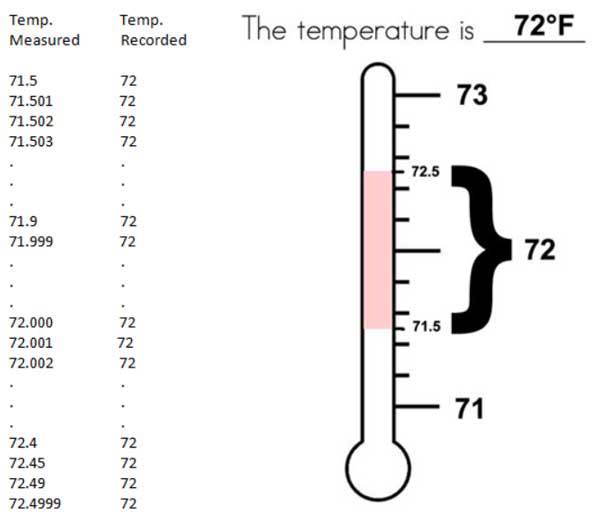
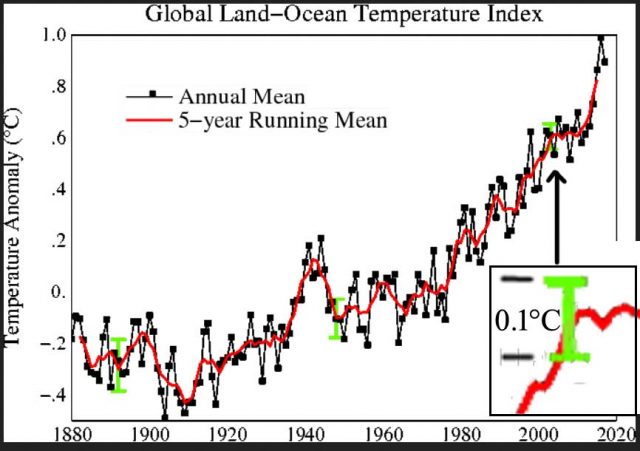
Die Abbildung zeigt dies als aktuelle Praxis mit den Temperaturaufzeichnungen … die gemessenen Temperaturen sind auf ganze Grad Fahrenheit gerundet – eine Angabe, welche IRGENDEINE der unendlichen Zahl kontinuierlicher Werte zwischen 71,5 und 72,499999… repräsentiert.

Es ist kein Messfehler, es ist die gemessene Temperatur dargestellt als eine Bandbreite von Werten 72 +/– 0,5. Es ist eine Unsicherheits-Bandbreite – hinsichtlich der tatsächlichen Temperatur sitzen wir immer noch im Dunklen – wir kennen lediglich die Bandbreite.

Nun ist die Ein-Grad-Bandbreite für normale Menschen als Information ausreichend. Knifflig wird es in manchen Fällen, wenn sich die Temperatur dem Gefrierpunkt nähert – Temperaturen über oder unter dem Gefrierpunkt sind klimatisch bedeutsam für Landwirte, bei der Straßenausbesserung und Wartung von Flugzeugen.

Egal was wir mit Temperaturaufzeichnungen machen, müssen wir uns mit der Tatsache befassen, dass die tatsächliche Temperatur nicht aufgezeichnet worden ist – wir haben lediglich Bandbreiten aufgezeichnet, innerhalb derer die tatsächliche Temperatur lag.

Dies bedeutet, dass wenn diese Temperaturen für Berechnungen herangezogen werden, müssen sie Bandbreiten bleiben und als solche behandelt werden. Was nicht ausgesondert werden kann ist die Bandbreite des Wertes. Die Mittelung eliminiert die Bandbreite nicht – der Wert hat immer die gleiche Bandbreite. (Siehe Durable Original Measurement Uncertainty).

Auf der Grundlage einfacher Logik, wenn wir schließlich zur Globalen Mittleren Temperatur kommen, ist immer noch die originale Unsicherheit vorhanden – wie Dr. Schmidt korrekt illustriert, wenn er die Absolute Temperatur für das Jahr 2016 mit 288,0 ± 0,5 K angibt.

Der Trick kommt dort ins Spiel, wo die tatsächliche berechnete Temperatur zu einer Anomalie von Mittelwerten konvertiert. Wenn man ein Mittel berechnet (ein arithmetisches Mittel – Summe aller Werte geteilt durch die Anzahl der Werte), bekommt man eine sehr genaue Antwort. Wenn man das Mittel von Werten heranzieht, welche Bandbreiten sind, wie etwa 71 +/- 0,5, dann ist das Ergebnis eine sehr präzise Zahl mit einer hohen Wahrscheinlichkeit, dass das Mittel nahe dieser präzisen Zahl liegt. Während also das Mittel ziemlich genau ist, sind die tatsächlichen Temperaturen der Vergangenheit immer noch unsicher bis +/-0,5.

Drückt man das Mittel mit der gebräuchlichen „+/-2 Standardabweichung“ aus, sagt uns das nur, welchen Mittelwert wir erwarten können – wir können ziemlich sicher sein, dass das Mittel innerhalb jener Bandbreite liegt. Die tatsächliche Temperatur, wenn wir sie ehrlicherweise in Grad darstellen wie in der folgenden Graphik, immer noch behaftet sein mit der Messungenauigkeit: +/-0,5 Grad.

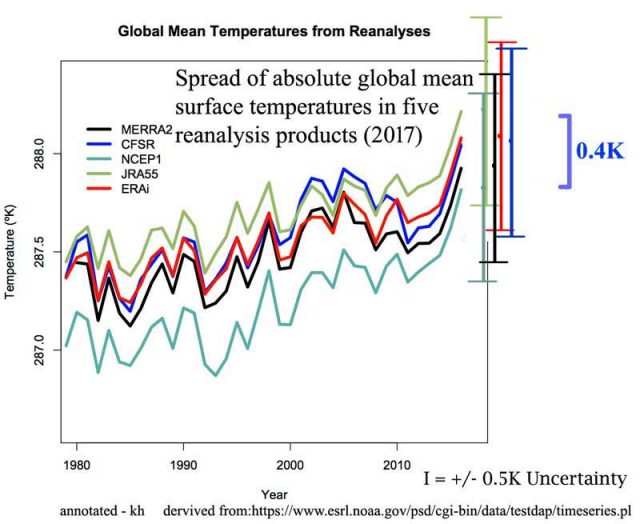
Diese Graphik wurde (ohne meine Anmerkungen) von Dr. Schmidt in seinem Beitrag über Anomalien (hier) gezeigt. Ich habe die erforderlichen I-Balken für +/-0,5 Grad hinzugefügt. Man beachte, dass die Ergebnisse der verschiedenen Re-Analysen selbst einen Spread von 0,4 Grad aufweisen – man könnte darüber sprechen, die Gesamtzahl von 0,9 Grad als die Unsicherheit der Globalen Mittleren Temperatur zu verwenden auf der Grundlage der Unsicherheiten oben (siehe die beiden grünen Unsicherheits-Balken, einer über dem anderen).

Dies illustriert die wahre Unsicherheit der Globalen Mittleren Temperatur – Schmidts eingeräumte +/-0,5 und die Unsicherheits-Bandbreite zwischen den Re-Analyse-Produkten.

Im Sinne der realen Welt sollte die oben dargestellte Unsicherheit als die Minimum-Unsicherheit betrachtet werden – die Unsicherheit der Originalmessungen plus die Unsicherheit der Re-Analyse. Es gibt noch viele andere Unsicherheiten, die man eigentlich hinzufügen müsste – wie sie etwa auftreten, wenn man Lücken in den Messungen mit berechneten Temperaturwerten füllt.

Der Trick besteht nun darin, dass der gleiche Datensatz als Anomalien präsentiert und behauptet wird, dass die Unsicherheit folglich auf 0,1 Grad reduziert ist (wenn sie überhaupt angegeben wird) – BEST halbiert diesen Wert nochmals und proklamiert 0,05 Grad!

Die Herabstufung des Datensatzes zu einem statistischen Produkt, Anomalie genannt, informiert uns nicht über die wahre Unsicherheit im tatsächlichen Parameter selbst – die Globale Mittlere Temperatur – jedenfalls nicht mehr als der Blick rückwärts auf eine Bergkette mittels eines speziellen Fernglases, das die Berge kleiner erscheinen lässt, wie stark das Auge auch immer getäuscht wird.

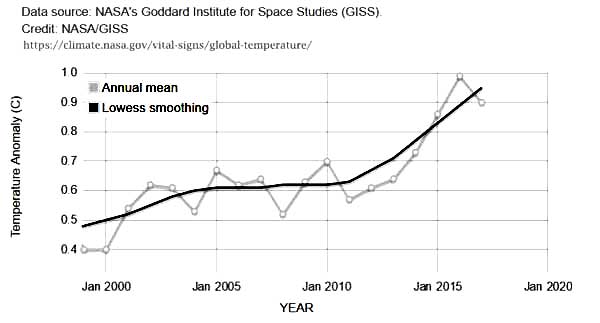
Hier folgt eine Stichprobe der Daten, welche dier Graphik ganz oben in diesem Beitrag ausmachen. Die Spalten bedeuten: Jahr – GAST-Anomalie – Glättung nach dem Lowess-Verfahren:

2010  0.7    0.62
2011  0.57  0.63
2012  0.61  0.67
2013  0.64  0.71
2014  0.73  0.77
2015  0.86  0.83
2016  0.99  0.89
2017  0.9    0.95

Die Vergrößerung der Graphik im Bereich 2000 bis 2017 sieht so aus:

7

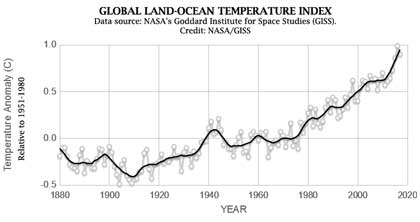
Wir sehen globale Anomalien, dargestellt bis zu einer Genauigkeit von Hundertstel Grad Celsius. Unsicherheit wird nicht gezeigt – keine einzige ist erwähnt auf der NASA-Website, auf der die Graphik zu finden ist (hier). Auf dieser NASA-Website, zu finden im Abschnitt Vital Signs – Global Climate Change, heißt es weiter, dass „diese Forschungen im Wesentlichen konsistent sind mit ähnlichen Konstruktionen durch die Climatic Research Unit und die National Oceanic and Atmospheric Administration.” Schauen wir mal:

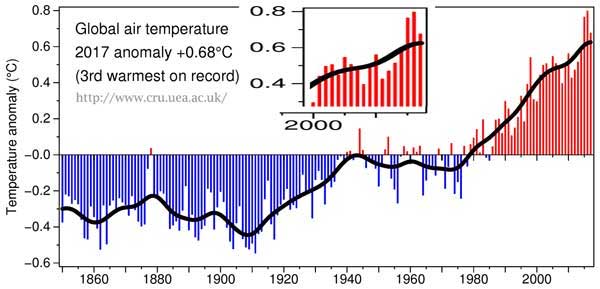
Von der CRU:

Hier sehen wir die Globale Temperatur nach CRU (Referenz-Zeitraum 1961 bis 1990) – ärgerlicherweise also mit einem anderen Referenz-Zeitraum als bei der NASA 1951 bis 1980. Die Differenz bietet ein paar Einblicke in den Umstand, welche gewaltigen Unterschiede diese verschiedenen Referenz-Zeiträume bzgl. der Ergebnisse ausmachen.

2010   0.56 0.512
2011 0.425 0.528
2012   0.47 0.547
2013 0.514 0.569
2014   0.579  0.59
2015 0.763 0.608
2016   0.797 0.62
2017 0.675 0.625

Die offizielle CRU-Anomalie für das Jahr 2017 beträgt 0,675°C – präzise bis zu einem Tausendstel Grad. Sie zeichnen das dann mit 0,68°C in die Graphik ein. CRU bringt es fertig, die gleiche Präzision in ihren geglätteten Werten zu zeigen – 2015 = 0,608.

Und der Vollständigkeit halber, die NOAA bietet folgende Werte an, präzise bis auf ein Hundertstel Grad:

2010,   0.70
2011,   0.58
2012,   0.62
2013,   0.67
2014,  0.74
2015,  0.91
2016,  0.95
2017,  0.85

Wir sehen, dass diese Anomalien anders als absolute globale Temperaturen wie jene von Gavin Schmidt bei RealClimate gezeigten (hier) mit überhaupt keiner Unsicherheit gezeigt werden. Keine SDs [Standard-Abweichungen], keine 95% CIs, keine Fehlerbalken, nichts. Und das präzise bis zu einem Hundertstel eines Grades Celsius.

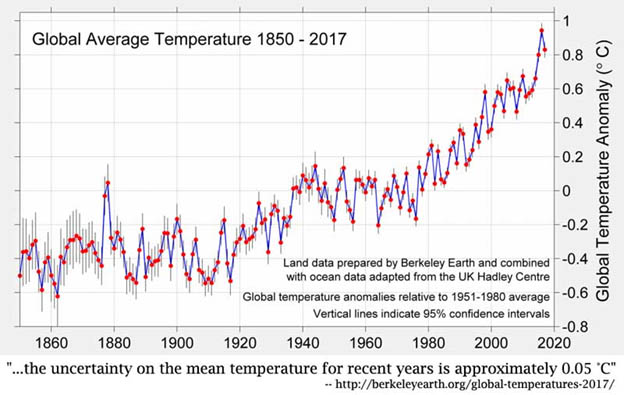
Zusammengefasst: Die großen Klima-Institutionen der Welt informieren uns über den Zustand des Klimas, indem sie uns Graphiken der Anomalien der Globalen Mittleren Temperatur [GAST] anbieten. Diese zeigen einen stetigen und alarmierenden starken Anstieg seit etwa 1980. Dieser alarmierende Anstieg besteht aus einer globalen Änderung von etwa 0,6°C. Nur das GISS liefert irgendeine Art Unsicherheits-Schätzung, und auch das nur in der Graphik mit dem grünen 0,1°C-Balken wie oben gezeigt. Betrachten wir ein einfaches Beispiel: Wir folgen Gavin Schmidt gemäß diesem seinem Beitrag vom August 2017 und verwenden GAST-Absolutwerte in Grad Celsius mit seiner angenommenen Unsicherheit von 0,5°C.

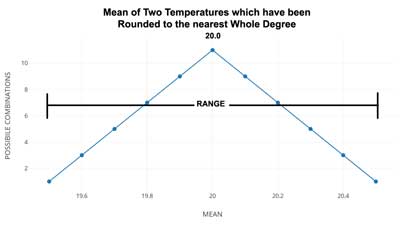
Wie sieht das Mittel der beiden GAST-Werte aus, eine für die Nord- und eine für die Südhemisphäre? Um ein wirklich einfaches Beispiel zu geben, wollen wir einmal jeder Hemisphäre den gleichen Wert zuordnen von 20 +/-0,5 Grad Celsius. Unsere Rechnung: 20 +/- 0,5 plus 20 +/- 0,5 geteilt durch 2 ergibt … Das Mittel ist genau 20. (Nun, das nennt man Präzision…).

Was ist mit der Bandbreite? Sie beträgt +/- 0,5 – ist also 1 Grad breit. Das Mittel mit der Bandbreite beträgt 20 +/- 0,5.

Aber was ist mit der Unsicherheit? Nun, die Bandbreite legt die Unsicherheit fest: wir sind sicher, dass das Mittel zwischen 20,5 und 19,5 liegt.

Schauen wir die Wahrscheinlichkeiten – hier gleiten wir in den Bereich „Statistik“.

Hier folgen einige der Werte für die Nord- und Südhemisphäre aus einer unendlichen Anzahl von Möglichkeiten, die sich aus 20 +/- 0,5 ergeben. Wenn wir gleiche Werte heranziehen, ist das Mittel natürlich das gleiche. Aber wir wollen Wahrscheinlichkeiten haben – wie viele Wege gibt es also, dass das Ergebnis 20,5 oder 19,5 beträgt? Jeweils einen Weg.

NH           SH
20.5 —— 20.5 = 20.5 einzig mögliche Kombination
20.4         20.4
20.3         20.3
20.2         20.2
20.1         20.1
20.0         20.0
19.9         19.9
19.8         19.8
19.7         19.7
19.6         19.6
19.5 —— 19.5 = 19.5 einzig mögliche Kombination

Aber wie ist das mit 20,4? Es können 20,4-20,4 oder 20,5-20,3 oder 20,3-20,5 sein – drei mögliche Kombinationen. 20,3? 5 Kombinationen. 20,2? 7 Kombinationen. 20,1? 9 Kombinationen. 20,0? 11 Kombinationen. Jetzt sind wir über den Buckel gesprungen: 19,9? 9 Kombinationen. 19,8? 7 Kombinationen. 19,7? 5 Kombinationen. 19,6? 3 Kombinationen und 19,5? 1 Kombination.

Man erkennt, wie die Verteilung aussieht:

Da wir lediglich 11 Werte für jede der gemittelten Temperaturen verwendet haben, bekommen wir eine wenig pointierte Kurve. Es gibt zwei Kleine Graphiken … die zweite (unten) zeigt, was passieren würde, falls wir das Mittel von zwei identischen Zahlen gefunden hätten, jede mit einer Unsicherheits-Bandbreite von +/-0,5, falls sie gerundet worden wären auf das nächste halbe Grad anstatt auf das normale ganze Grad. Das Ergebnis ist intuitiv – Das Mittel besitzt immer die höchst mögliche Wahrscheinlichkeit, dass es der zentrale Werte ist.

Nun, dass scheint so offensichtlich, dass es selbst Dummies einsehen. Schließlich sollte ein Mittel mathematisch immer der zentrale Wert sein. Der Punkt ist aber: mit unseren gleich verteilten Werten um das Mittel – und wir erinnern uns, wenn wir einen Temperaturrekord sehen, angegeben als XX +/- 0,5, sprechen wir über eine Bandbreite von gleichmäßig verteilten möglichen Werten – wird das Mittel immer der zentrale Wert sein, ob wir nun das Mittel einer einzelnen Temperatur oder das von tausend Temperaturwerten mit dem gleichen Wert finden. Die Unsicherheits-Bandbreite ist jedoch immer die Gleiche! Natürlich! Muss doch so sein.

Hierin liegt der Trick – wenn sie die Anomalie des Mittels heranziehen, lassen sie die Unsicherheits-Bandbreite insgesamt fallen und konzentrieren sich einzig auf die zentrale Zahl, das Mittel, welches immer präzise ist und nahe dieser zentralen Zahl liegt. Wenn überhaupt einmal eine Unsicherheit genannt wird, wird sie als die Wahrscheinlichkeit angegeben, wie nahe das Mittel der zentralen Zahl liegt – und ist getrennt von der tatsächlichen Unsicherheits-Bandbreite der Originaldaten.

William Briggs sagt dazu: „Diese Ergebnisse sind keine Statements bzgl. der tatsächlichen Temperaturen in der Vergangenheit, die wir bis auf die Messgenauigkeit bereits kennen“.

Wir kennen bereits die berechneten GAST (siehe die Re-Analysen oben). Aber wir wissen nur, dass sie irgendwo innerhalb deren bekannten Unsicherheits-Bandbreiten liegt, welche laut Dr. Schmidt +/- 0,5 Grad betragen. Berechnungen der Anomalien der verschiedenen Mittelwerte sagen uns nichts über die tatsächlichen Temperaturen der Vergangenheit – die kannten wir bereits – und wir wissen, wie unsicher das war.

Es ist ein TRICK zu behaupten, dass mittels der Überleitung jährlicher Globaler Mittlerer Temperaturwerte zu Anomalien wir die bekannte Unsicherheit UNBEKANNT machen können.

Zu Punkt 2: Wer wird ausgetrickst?

Dick Feynman würde sagen: „Sie halten sich selbst zum Narren“. Sie kennen bereits die GAST so genau wie sie dieselben mit ihren gegenwärtigen Verfahren zu berechnen in der Lage sind. Sie kennen die involvierte Unsicherheit – Dr. Schmidt räumt ein, dass sie um 0,5 K liegt. Folglich ist ihre Verwendung von Anomalien (oder die Mittelwerte von Anomalien…) einfach ein Weg, sich selbst zum Narren zu halten, indem die bekannte Unsicherheit irgendwie auf magische Weise einfach verschwindet, äquivalent zu „falls wir auf diese Weise blinzeln und unseren Kopf nach einer Seite neigen…“.

Viel Glück dabei!

——————————-

Schlussbemerkungen des Autors:

Dieser Beitrag wird einem gewissen Segment der Leserschaft hier nicht gefallen, aber das verringert nicht dessen Validität. Jene, die sich selbst zum Narren halten wollen mit dem Verschwinden lassen der bekannten Unsicherheit der Globalen Mittleren Temperatur werden den einfachen, hier dargestellten Argumenten widersprechen. Das ist deren Minus.

Ich verstehe das Argument der Statistiker, welche darauf bestehen, dass das Mittel wirklich viel genauer ist als die Originaldaten. Aber sie lassen zu, dass jene Tatsache ihnen die Erlaubnis gibt, die Unsicherheits-Bandbreite der Originaldaten aus der realen Welt zu ignorieren. Man verstehe mich nicht falsch, sie versuchen nicht, uns auszutricksen. Sie sind sicher, dass dies wissenschaftlich und statistisch korrekt ist. Sie halten sich jedoch selbst zum Narren, weil im Endeffekt alles, was sie tun, die Veränderung der Werte auf der Y-Achse ist (von ,absolute GAST in K‘ zu ,absolute GAST in K minus dem Klimamittel in K‘) und die Unsicherheit fallen lassen – mit viel Rechtfertigung aus der Statistik-/Wahrscheinlichkeits-Theorie.

Link: https://wattsupwiththat.com/2018/09/25/the-trick-of-anomalous-temperature-anomalies/

Übersetzt von Chris Frey EIKE

Beitrag als PDF speichernBeitrag drucken