Permanente Unsicherheit in Original-Messungen

In den Kommentaren zu meinen letzten Beiträgen über Tidenmessgeräte erhob sich die Frage der Beständigkeit der Unsicherheit in den Original-Messungen. Hier folgen die Fragen, die zu beantworten ich mit diesem Beitrag versuchen möchte:

Falls Originalmessungen bis auf eine Unsicherheit von +/- X (irgendein Wert in irgendeiner Einheit) durchgeführt werden, überträgt sich dann die Unsicherheit der Originalmessung auf einen oder alle Mittelwerte dieser Messungen?

Sorgt die Durchführung weiterer Messungen bis auf den gleichen Grad Unsicherheit genau die Berechnung noch genauerer Mittelwerte?

Meine Haltung in diesem Beitrag ist Folgende:

Falls jede Messung nur auf ± 2 cm genau ist, dann kann das monatliche Mittel nicht NOCH genauer sein – es muss die gleiche Bandbreite von Fehlern/Unsicherheiten enthalten wie die Originalmessungen, aus denen das Mittel gebildet worden ist. Die Mittelung bringt keine Erhöhung der Genauigkeit.

Es wäre untertrieben zu sagen, dass es sehr viel Uneinigkeit von einigen Statistikern und jenen mit einer klassischen statistischen Ausbildung gab.

Ich werde mich nicht über das Thema Präzision oder Präzision von Mittelwerten auslassen. Es gibt dazu eine gute Diskussion bei Wikipedia: Accuracy and precision.

Gegenstand meiner Bedenken hier ist diese reine Trivial-Genauigkeit [vanilla accuracy]: „Genauigkeit einer Messung ist der Grad, wie nahe Messungen von bestimmter Anzahl an dem wahren Wert jener Quantität liegt“. (,Wahrer Wert‘ bedeutet hier den tatsächlichen Wert in der realen Welt – nicht irgendein kognitives Konstrukt desselben).

Der allgemeine Standpunkt der Statistiker wird in diesem Kommentar zusammengefasst:

„Die Aussage, dass die Genauigkeit des mittleren Meeresspiegels an einer Stelle nicht verbessert wird durch die Durchführung vieler Messungen über einen verlängerten Zeitraum ist lachhaft und legt ein fundamentales Fehlen von Verständnis der physikalischen Wissenschaft an den Tag“.

Ich gebe zu, dass ich frisch von der Universität einmal diesem Standpunkt zugestimmt habe. Und zwar bis ich einem berühmten Statistiker die gleiche Frage vorlegte. Sofort und gründlich wurde ich mit einer Reihe von Hausaufgaben konfrontiert, womit ich mir selbst beweisen sollte, dass der Gedanke in vielfacher Hinsicht unrichtig ist.

Erstes Beispiel:

Beginnen wir mit einem einfachen Beispiel über Temperaturen. Temperaturen in den USA werden in ganzen Grad Fahrenheit gemessen und aufgezeichnet. (Fragen Sie mich nicht, warum wir nicht den wissenschaftlichen Standard benutzen. Ich weiß es nämlich nicht). Diese Aufzeichnungen in ganzen Grad Fahrenheit werden dann mittels eines Rechners in Grad Celsius konvertiert, und zwar bis zur ersten Dezimalstelle, also beispielsweise 15,6°C.

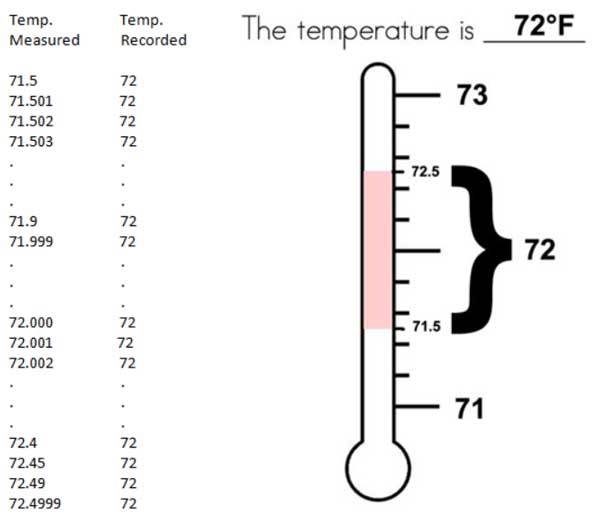
Dies bedeutet, dass jede und alle Temperaturen zwischen beispielsweise 72,5°F und 71,5°F als 72°F aufgezeichnet werden. (In der Praxis wird die eine oder andere Messung mit X,5 ausgesondert und die anderen ab- oder aufgerundet). Folglich bedeutet eine amtliche Temperaturaufzeichnung vom Battery Park um 12 Uhr mittags von „72°F“ in der realen Welt, dass die Temperatur mittels Messung in der Bandbreite zwischen 71,5°F und 72,5°F liegt – mit anderen Worten, die präsentierte Zahl repräsentiert eine Bandbreite von 1°F.

In der wissenschaftlichen Literatur könnten wir diesen Umstand in der Schreibweise 72 +/- 0.5 °F wiederfinden. Oftmals wird dies dann als eine Art „Vertrauensintervall“, „Fehlerbalken“ oder Standardabweichung missverstanden.

In diesem spezifischen Beispiel einer Temperaturmessung ist es nichts von diesen Dingen. Es ist einfach eine Form von Stenogramm für das tatsächliche Messverfahren, welches jedes Grad Bandbreite von Temperatur als eine einzelne ganze Zahl repräsentiert – wenn die Bedeutung in der realen Welt lautet „eine Temperatur mit einer Bandbreite von 0,5 Grad über oder unter der präsentierten ganzen Zahl“.

Jede Differenz zur tatsächlichen Temperatur über oder unter der präsentierten ganzen Zahl ist kein Fehler. Diese Abweichungen sind keine „Zufallsfehler“ und sind nicht „normalverteilt“.

Noch einmal zur Betonung: Die ganze Zahl einer präsentierten Temperatur an irgendeiner Stelle zu irgendeiner Zeit ist ein Kürzel für eine ein Grad große Bandbreite tatsächlicher Temperaturen, die obwohl laut Messung unterschiedlich in Gestalt der gleichen ganzen Zahl gemeldet werden. Visuell:

Obwohl in der Praxis die Temperaturen nur in ganzen Zahlen gemeldet werden, ändern sich die Temperaturen in der realen Welt nicht in Schritten von einem ganzen Grad – 72, 73, 74, 72, 71 usw. Temperatur ist eine kontinuierliche Variable. Und nicht nur das, sie ist eine sich ständig ändernde Variable. Wenn man Temperatur einmal um 11:00 und dann um 11:01 misst, misst man zwei unterschiedliche Quantitäten; die Messungen erfolgen unabhängig voneinander. Außerdem ist einer und sind alle Werte innerhalb der Bandbreite gleich wahrscheinlich – die Natur „bevorzugt“ keine Temperaturen, welche näher an der ganzen Zahl liegen.

(Anmerkung: In den USA werden ganze Grad Fahrenheit in Grad Celsius bis zur ersten Stelle nach dem Komma gerundet. 72°F werden konvertiert und ebenfalls aufgezeichnet als 22,2°C. Die Natur bevorzugt auch nicht Temperaturen, die näher an einem Zehntelgrad Celsius liegen).

Während es gegenwärtig Praxis ist, eine ganze Zahl zu melden, um die Bandbreite von ,ganzer Zahl plus ein halbes Grad und ganzer Zahl minus ein halbes Grad‘ zu repräsentieren, könnte diese Praxis auch irgendeine andere Notation sein. Es könnte auch einfach sein, dass die gemeldete ganze Zahl alle Temperaturen von der ganzen Zahl bis zur nächsten ganzen Zahl repräsentieren soll, dass also 71 bedeutet „irgendeine Temperatur von 71 bis 72“. Das gegenwärtige System der Verwendung der ganzen Zahl in der Mitte ist besser, weil die gemeldete ganze Zahl in der Mitte der sie repräsentierenden Bandbreite liegt. Allerdings ist dies einfach misszuverstehen, wenn es als 72 +/- 0.5 daherkommt.

Weil Temperatur eine kontinuierliche Variable ist, sind Abweichungen von der ganzen Zahl nicht einmal „Abweichungen“ – sie sind einfach die in Grad Fahrenheit gemessenen Temperatur, welche normalerweise durch den Dezimalanteil repräsentiert wird, welcher der Notation der ganzen Gradzahl folgen würde – der „x.4999“te Teil von 72,4999°F. Diese Dezimalanteile sind keine Fehler, sie sind nicht gemeldete und nicht aufgezeichnete Anteile der Messung, und weil Temperatur eine kontinuierliche Variable ist, muss sie als gleichmäßig verteilt über die gesamte Skala betrachtet werden – mit anderen Worten, es sind keine, keine, keine „normalverteilten Zufallsfehler“. Der einzige Grund, warum sie unsicher sind ist, dass sie selbst bei einer Messung nicht aufgezeichnet werden.

Was passiert also jetzt, nachdem wir herausgefunden haben, dass die Mittelwerte dieser Aufzeichnungen, welche – man erinnere sich – Kürzel von Temperatur-Bandbreiten sind?

Um diese Frage zu beantworten, wollen wir ein Schulexperiment durchführen…

Wir werden das Mittel von drei ganzen Grad Temperatur finden, und zwar erhalten wir diese Temperaturen in meinem Wohnzimmer:

Wie oben diskutiert, repräsentieren diese Temperaturwerte irgendwelche der unbegrenzt variablen Temperaturen, dennoch möchte ich diese kleine Graphik erstellen:

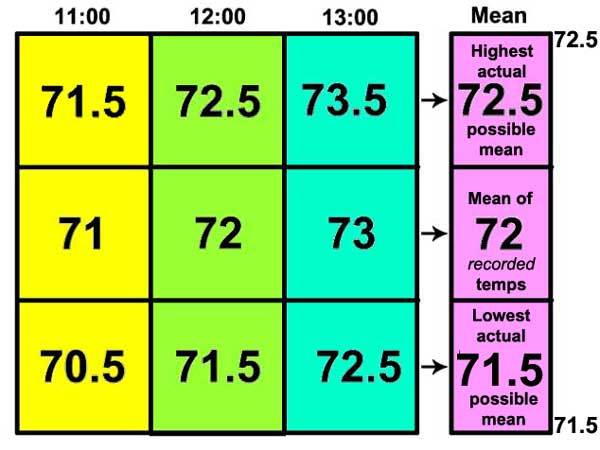
Hier erkennen wir, dass die Temperatur von jeder Stunde den höchsten Wert in der Bandbreite repräsentiert, den mittleren Wert in der Bandbreite (die gemeldete ganze Zahl) und als tiefsten Wert der Bandbreite. (Anmerkung: Wir dürfen nicht vergessen, dass es zwischen den Werten in jeder Spalte eine unendliche Anzahl von Bruchwerten gibt, die wir jetzt nur nicht zeigen). Diese Werte werden dann gemittelt – das Mittel berechnet – von links nach rechts: die höchsten Werte der drei Stunden ergeben ein Mittel von 72,5, der mittlere Wert ein Mittel von 72 und der niedrigste Wert ein Mittel von 71,5.

Das resultierende Mittel kann geschrieben werden in der Form 72 +/- 0.5, was ein Kürzel ist dafür, dass die Bandbreite von 71,5 bis 72,5 repräsentiert wird.

Die Genauigkeit des Mittels, repräsentiert in der Schreibweise +/- 0,5 ist identisch mit der Genauigkeit der Original-Messungen – sie repräsentieren beide eine Bandbreite möglicher Werte.

Anmerkung: Diese Unsicherheit stammt nicht aus der tatsächlichen instrumentellen Genauigkeit der Original-Messungen. Das ist etwas ganz anderes und muss zusätzlich zu der hier beschriebenen Genauigkeit betrachtet werden. Diese resultiert allein aus der Tatsache, dass gemessene Temperaturen als Ein-Grad-Bandbreiten dargestellt werden, wobei die Bruchteil-Informationen außen vor bleiben und für immer verloren sind, was uns mit der Unsicherheit zurücklässt – fehlendem Wissen – was die tatsächliche Messung selbst eigentlich war.

Natürlich kann die um 11:00 gemessene Temperatur 71,5; die um 12:00 gemessene 72 und die um 13:00 gemessene 72,5 betragen haben. Oder es könnte auch 70,5; 72; 73,5 gewesen sein.

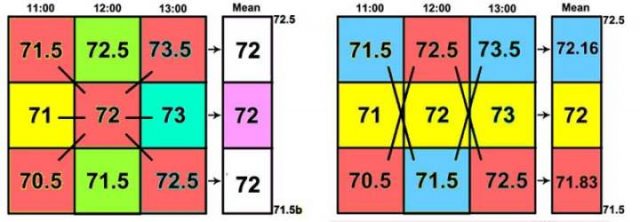
Die Berechnung des Mittels zwischen den diagonal gegenüber liegenden Ecken ergibt 72 von Ecke zu Ecke. Über die Mittelpunkte ergibt sich immer noch 72.

Jedwede Kombination von höchsten, mittigen und niedrigsten Werten von jeder Stunde ergibt ein Mittel, welches zwischen 72,5 und 71,5 liegt – innerhalb der Unsicherheits-Bandbreite des Mittels.

Selbst für diese vereinfachten Netze gibt es viele mögliche Kombinationen von einem Wert aus jeder Spalte. Das Mittel jedweder Kombination liegt zwischen den Werten 72,5 und 71,5.

Es gibt buchstäblich eine unendliche Anzahl potentieller Werte zwischen 72,5 und 71,5, da Temperatur eine kontinuierliche Variable für jede Stunde ist. Das Auftreten aller möglichen Werte für jede stündliche Temperatur ist gleich wahrscheinlich – folglich sind alle möglichen Werte und alle möglichen Kombinationen eines Wertes für jede Stunde in Betracht zu ziehen. Nimmt man irgendeinen möglichen Wert aus jeder Spalte mit stündlichen Messungen und mittelt diese drei, ergibt sich immer das gleiche Ergebnis – alle Mittel haben einen Wert zwischen 72,5 und 71,5, was eine Bandbreite der gleichen Größenordnung repräsentiert wie die der Original-Messungen, eine Bandbreite von einem Grad Fahrenheit.

Die Genauigkeit des Mittels entspricht genau der Genauigkeit aus den Original-Messungen – es ist in beiden Fällen eine Ein-Grad-Bandbreite. Sie wurde um keinen Deut reduziert durch das Mittelungs-Verfahren. Das kann es auch nicht.

Anmerkung: Eine mehr technische Diskussion zu diesem Thema gibt es hier und hier.

Und die Daten der Tiden-Messgeräte?

Es ist klar, dass sich die Unsicherheit bzgl. der Genauigkeit der Original-Messungen der Temperatur aus dem Umstand ergibt, dass nur ganze Grad Fahrenheit bzw. Grad Celsius bis zur ersten Dezimalstelle angegeben werden. Das ergibt folglich keine Messungen mit einem Einzelwert, sondern stattdessen Bandbreiten.

Aber was ist mit den Daten der Tide-Messgeräte? Unterscheidet sich ein einzelner gemessener Wert bis zur Präzision von Millimetern also von obigem Beispiel? Die kurze Antwort lautet NEIN, aber ich nehme nicht an, dass das allgemein akzeptiert wird.

Welche Daten werden denn nun von Tiden-Messgeräten in den USA (und in den meisten anderen entwickelten Ländern) gemessen?

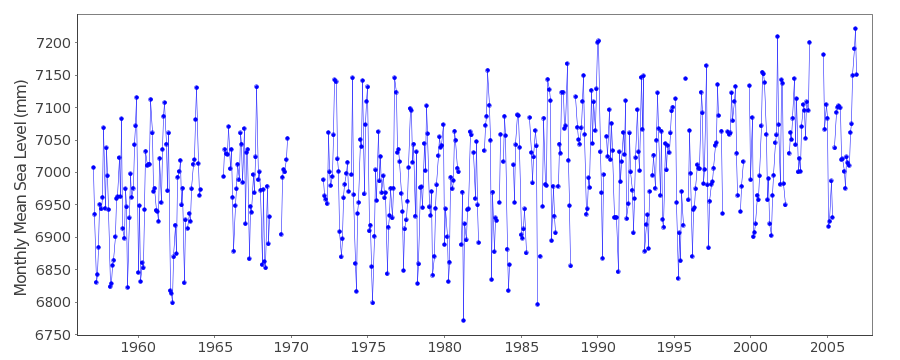
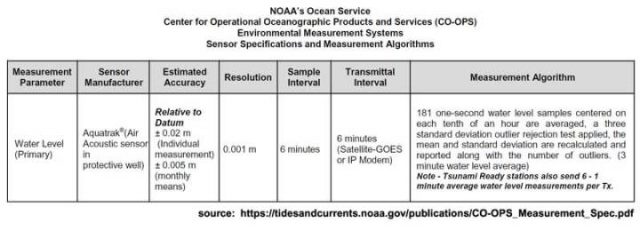
Die Geschätzte Genauigkeit wird als +/- 2 cm für individuelle Messungen angegeben, und es wird behauptet, dass diese für monatliche Mittelwerte 5 mm beträgt. Betrachten wir die Daten vom Battery-Park in New York, sehen wir etwas wie das hier:

Man beachte, dass wir laut diesem Datenblatt alle sechs Minuten (1 Zehntel-Stunde) eine Messung haben, und zwar den Wasserstand in Meter bis zum Niveau von Millimetern (4,639 m), und das „Sigma“ wird angegeben. Die Sechs-Minuten-Zahl wird folgendermaßen berechnet:

181 Eine-Sekunde-Wasserstandsmessungen zentriert um jedes Zehntel einer Stunde werden gemittelt, ein three standard deviation outlier rejection test [?] angewendet, dann werden Mittel und Standardabweichung erneut berechnet und gemeldet zusammen mit der Anzahl der Ausreißer. (3 Minuten-Wasserstandsmittel).

Um sicherzustellen, dass wir dieses Verfahren verstehen, stellte ich in einer E-Mail an @ co-ops.userservices@noaa.gov die folgende Frage:

Wenn sagen, bis zu einer Genauigkeit von +/- 2 cm meinen wir spezifisch, dass jede Messung zum tatsächlichen augenblicklichen Wasserstand außerhalb des Mess-Schachtes passt und innerhalb dieser +/- 2-cm-Bandbreite liegt.

Antwort:

Das ist korrekt! Die Genauigkeit jedes 6-minütigen Datenwertes beträgt +/- 2 cm des Wasserstandes zu jener Zeit.

(Anmerkung: In einer separaten E-Mail wurde klargestellt, dass „Sigma die Standardabweichung ist, essentiell die statistische Varianz zwischen diesen 181 1-Sekunde-Messungen“).

Frage und Antwort verifizieren, dass sowohl die 1-Sekunde-Messungen als auch der 6-Minuten-Datenwert eine Bandbreite des Wasserstandes von 4 cm, 2 cm plus oder minus vom gemeldeten Wasserstand repräsentiert.

Diese scheinbar vage Genauigkeit – jede Messung mit einer tatsächlichen Bandbreite von 4 cm – ist das Ergebnis des mechanischen Verfahrens der Mess-Apparatur, trotz der Auflösung von 1 Millimeter. Wie kommt das?

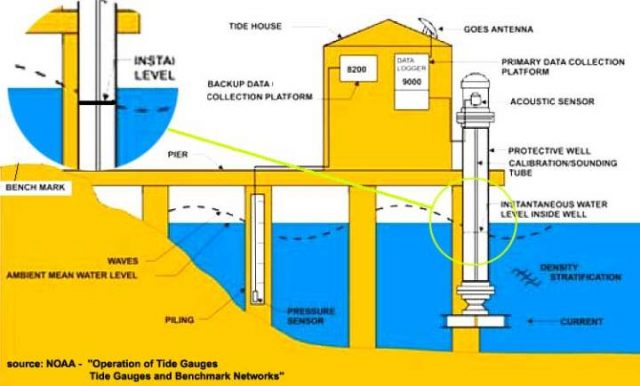
Die Illustration der NOAA des modernen Tiden-Messapparates am Battery Park zeigt den Grund. Die Blase oben links zeigt eindeutig, was während des 1-Sekunde-Intervalls der Messung passiert: Der augenblickliche Wasserstand innerhalb des Mess-Schachtes unterscheidet sich von dem außerhalb dieses Schachtes.

Diese 1-Sekunde-Ablesung wird in der „Primary data collection Platform“ gespeichert und später als Teil der 181 Messungen herangezogen, die für den gemeldeten 6-Minuten Wert gemittelt werden. Er unterscheidet sich wie illustriert von dem tatsächlichen Wasserstand außerhalb des Mess-Schachtes. Manchmal wird er niedriger, manchmal höher liegen. Der Apparat als Ganzes ist darauf ausgelegt, diese Differenz in den meisten Fällen während des 1-Sekunde-Zeitmaßstabes auf eine Bandbreite von 2 cm über oder unter dem Wasserstand im Mess-Schacht zu begrenzen – obwohl einige Ablesungen weit außerhalb dieser Bandbreite liegen und als „Ausreißer“ gelistet werden (die Regel lautet, alle 3-Sigma-Ausreißer auszusondern – aus dem Satz der 181 Ablesungen – bevor man das Mittel berechnet, welches als der 6-Minuten-Wert gemeldet wird).

Wir können nicht jede individuelle Messung als eine Messung des Wasserstandes außerhalb des Mess-Schachtes betrachten – es wird der Wasserstand innerhalb des Mess-Schachtes gemessen. Diese Im-Schacht-Messungen sind sehr genau und präzise – bis auf 1 Millimeter. Allerdings ist jede 2-Sekunde-Aufzeichnung eine mechanische Approximation des Wasserstandes außerhalb des Schachtes – also dem tatsächlichen Wasserstand im Hafen, welcher eine fortwährend sich ändernde Variable ist – spezifiziert zu der Genauigkeits-Bandbreite von +/- 2 Zentimeter. Die aufgezeichneten Messungen repräsentieren Bandbreiten von Werten. Diese Messungen enthalten keine „Fehler“ (zufällige oder andere), wenn sie sich vom tatsächlichen Wasserstand im Hafen unterscheiden. Der Wasserstand im Hafen oder im Fluss oder in der Bucht selbst ist niemals wirklich gemessen worden.

Die als „Wasserstand“ aufgezeichneten Daten sind abgeleitete Werte – und keineswegs direkte Messungen. Das Tiden-Messgerät als Messinstrument wurde so ausgerichtet, dass es Messungen innerhalb des Schachtes mit einer Genauigkeit von 2 cm, plus oder minus durchführt, welche den tatsächlichen augenblicklichen Wasserstandes außerhalb des Schachtes repräsentieren – was ja das ist, das wir messen wollen. Nach 181 Messungen innerhalb des Schachtes und dem Aussortieren jedweder Daten, die zu abwegig sind, wird der Rest der 181 Messungen gemittelt und der 6-Minuten-Wert gemeldet mit der korrekten Genauigkeits-Angabe von +/- 2 cm – der gleichen Genauigkeit also wie bei den individuellen 1-Sekunde-Messungen.

Der gemeldete Wert bezeichnet eine Werte-Bandbreite – welche immer angemessen mit jedem Wert angegeben werden muss – im Falle von Wasserständen der NOAA-Tiden-Messgeräte +/- 2 cm.

Die NOAA behauptet zu recht nicht, dass die sechs-Minuten-Aufzeichnungen, welche das Mittel von 181 1-Sekunde-Messungen sind, eine größere Genauigkeit aufweisen als die individuellen Original-Messungen.

Warum behauptet die NOAA aber dann, dass monatliche Mittelwerte bis auf +/- 5 mm genau sind? In diesen Berechnungen wird die Genauigkeit der Original-Messungen einfach komplett ignoriert, und nur die gemeldeten/aufgezeichneten Sechs-Minuten-Mittelwerte werden betrachtet (vom Autor bestätigt) – das ist der gleiche Fehler, wie er auch bei Berechnungen fast aller anderen großen Datensätze gemacht wird, indem das nicht anwendbare Gesetz Großer Zahlen [Law of Large Numbers] angewendet wird.

Genauigkeit jedoch wird, wie hier gezeigt, bestimmt durch die Genauigkeit der Original-Messungen, wenn man eine nicht statische, sich immer ändernde und kontinuierlich variable Quantität misst und dann als eine Bandbreite möglicher Werte aufzeichnet – die Bandbreite der Genauigkeit spezifiziert für das Messsystem – und die nicht durch Berechnungen von Mittelwerten verbessert werden kann.

 

Unter dem Strich:

1. Wenn numerische Werte Bandbreiten sind anstatt wahrer diskreter Werte, dann bestimmt die Größe der Bandbreite des Originalwertes (in unserem Falle die Messung) die Größe der Bandbreite jedweden nachfolgenden Mittelwertes dieser numerischen Werte.

2. Von ASOS-Stationen berechnete Temperaturen jedoch werden aufgezeichnet und als Temperaturen gemeldet mit einer Bandbreite von 1°F (0,55°C), und diese Temperaturen werden korrekt als „ganze Zahlen +/- 0,5°F“ aufgezeichnet. Die Mittelwerte dieser aufgezeichneten Temperaturen können nicht genauer sein als die Originalmessungen – weil die Aufzeichnungen der Originalmessungen selbst Bandbreiten sind. Die Mittelwerte müssen mit den gleichen +/- 0,5°F angegeben werden.

3. Gleiches gilt für die Daten von Tiden-Messapparaten, wie sie gegenwärtig gesammelt und aufgezeichnet werden. Die primäre Aufzeichnung von 6-Minuten-Werten sind trotz auf Millimeter-Genauigkeit aufgezeichneter Präzision ebenfalls Bandbreiten mit einer Original-Genauigkeit von +/- 2 Zentimetern. Dies ist die Folge des Designs und der Spezifikation des Messinstrumentes, welches das einer Art mechanisch mittelnden Systems ist. Die Mittel von Werten von Tiden-Messgeräten können nicht genauer gemacht werden als die +/- 2 cm – was weit genauer ist als notwendig zur Messung von Gezeiten und der Bestimmung eines sicheren Wasserstandes für Schiffe.

4. Wenn Original-Messungen Bandbreiten sind, sind deren Mittelwerte ebenfalls Bandbreiten von gleicher Größenordnung. Diese Tatsache darf nicht ignoriert oder missachtet werden.Tut man dies doch, erzeugt man einen falschen Eindruck von der Genauigkeit unseres numerischen Wissens. Oftmals überschattet die mathematische Präzision eines berechneten Mittels dessen reale Welt, eine weit verschwommenere Genauigkeit, was zu einer unrichtigen Signifikanz führt, welche Änderungen sehr geringer Größenordnung dieser Mittelwerte beigemessen wird.

Link: https://wattsupwiththat.com/2017/10/14/durable-original-measurement-uncertainty/
Übersetzt von Chris Frey EIKE