Temperaturen addieren sich nicht!
Technisch gesehen ist Temperatur keine extensive Quantität. Dies wird illustriert durch die Tatsache, dass wenn man einen Eimer Wasser mit einer Temperatur von 30°C hat und dem Wasser den Inhalt eines anderen Eimers von Wasser mit 30°C hinzufügt, man keine Wassertemperatur von 60°C bekommt.
Energie ist eine extensive Sache: Falls man ein Volumen Wasser mit einer thermischen Energie von 4000 Megajoule hat und ein gleich großes Volumen hinzufügt, wird man zweimal die thermische Energie haben. Die mittlere Energie pro Einheit kann verglichen werden mit dem Strahlungsenergie-Budget pro Einheit.
Das Verhältnis von Temperatur zu thermischer Energie ist nicht für alle Materialien gleich, sondern hoch variabel, abhängig von den physikalischen Eigenschaften der Substanz. Es hängt ebenso von der Menge einer Substanz ab, d. h. der Masse. In der Physik und der Materialwissenschaft ist es oft am bequemsten, die „spezifische Wärmekapazität“ zu studieren, das ist die Änderung des Energiegehalts pro Einheit der Masse pro Grad Temperaturänderung. Folglich ist es eine Eigenschaft für jede Art von Material, unabhängig von einem bestimmten Objekt.
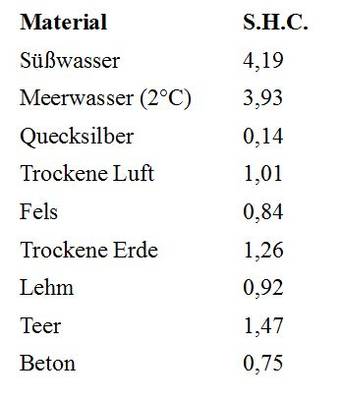
Im internationalen Standard-System (S.I.) wird dies gemessen in joule / kilogram / kelvin oder J/kg/K . Kelvin hat die gleiche Größenordnung wie Grad Celsius und ist in diesem Zusammenhang austauschbar. Einige Beispiele für allgemeine Materialien:
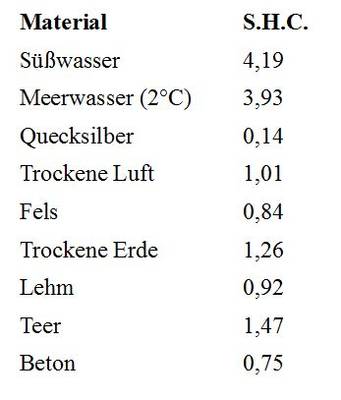
Tabelle 1: Spezifische Wärmekapazität verschiedener Materialien in J/kg/K. Datenquelle
Also könnte man Temperaturänderung als ein „Proxy“ für eine Änderung der thermischen Energie für äquivalente VOLUMINA des GLEICHEN Materials betrachten. In diesem Zusammenhang könnte man eine ,mittlere Temperaturänderung‘ berechnen für jenes Medium und auf die Änderung der thermischen Energie rückschließen, welche beispielsweise mit einfallender und ausgehender Strahlung in Bezug gesetzt wird. Falls dies eine Oberflächentemperatur ist, impliziert dies die Hypothese, dass die Erdoberfläche die Temperatur bis zu einer gewissen Wassertiefe repräsentiert und diese repräsentative Tiefe die Gleiche bleibt in den Gebieten, über die gemittelt wird, um den „Volumen“-Zustand oben zu berücksichtigen. Das ist für die ,durchmischte Schicht‘ des Ozeans einigermaßen fragwürdig, kann aber als grobe Energie-Proxy durchgehen.
Allerdings ist sofort klar, dass man nicht beginnen kann, Luft und Wassertemperatur zusammenzufügen oder zu mitteln; oder Temperaturen über Land und Wasser. Das sind keine kompatiblen Medien. Das ist wie die Frage, was das Mittel ist zwischen einem Apfel und einer Orange: Es hat keinerlei physikalische Bedeutung. Es kann mit Sicherheit nicht die Grundlage sein für eine Berechnung des Energiehaushaltes, da es nicht mehr eine Maßzahl für die Änderung der thermischen Energie ist.
Wie aus der Tabelle oben ersichtlich: Luft, Felsgestein und Erde werden eine viermal so hohe Temperaturänderung aufweisen als Wasser als Folge der gleichen einfallenden Energiemenge.
Niemand wird auf den Gedanken kommen, Temperaturaufzeichnungen in Grad Fahrenheit mit solchen in Grad Celsius zu mitteln. Trotzdem scheint es aus irgendwelchen Gründen so, als ob die Vermischung von Land- und Ozeandaten (SST Sea Surface Data) bei niemandem ein Heben der Augenbrauen auslöst.
Änderungsrate in den globalen Temperatur-Datensätzen
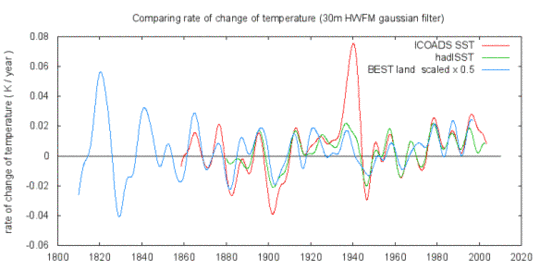
Abbildung 1: Vergleich von Änderungsraten in Temperatur-Datensätzen über dem Festland und über dem Ozean (30 Monate Gaussian low-pass filter). Quelle der Daten.
Abbildung 1 zeigt die Änderungsrate in zwei Datensätzen der Wassertemperatur und dem BEST-Datensatz vom Festland, mit einer Verkleinerung um einen Faktor zwei. Mit diesem Skalierungsfaktor sehen sie alle ziemlich eng beieinander liegend aus. Die große Spitze in den ICOADS-Daten liegt an einer erkannten Änderung der Datenmenge infolge Änderungen der Schiffsrouten und der Daten-Sammelverfahren während und nach WW II. Das UKMO bearbeitete den HadISST-Datensatz mit dem Ziel, diesen Bias zu entfernen.
Die Änderungsrate der Festlands-Lufttemperatur, wie sie vom „BEST“-Datensatz Berkeley geschätzt worden ist, ist sehr ähnlich der Änderungsrate der Wassertemperatur, außer dass die Änderungsrate doppelt so hoch ist.*
[*Original: The rate of change of near surface land air temperature as estimated in the Berkeley “BEST” dataset is very similar to the rate of change in the sea surface temperature record, except that it shows twice the rate of change. Ändert sich nicht die Landtemperatur viel stärker als die Wassertemperatur? Was verstehe ich an diesem Satz nicht? Anm. d. Übers.]
Meerwasser besitzt eine spezifische Wärmekapazität, die viermal so groß ist wie Felsgestein. Dies bedeutet, dass sich die Temperatur des Gesteins vier mal stärker ändert als Wasser bei der gleichen Änderung der thermischen Energie, beispielsweise durch einfallende Solarstrahlung.
Erde ist im Allgemeinen eine Mixtur feiner Gesteinspartikel und organischem Material mit einem signifikanten Wassergehalt. Die beiden Temperatur-Datensätze sind konsistent, wenn man Land als ,nasse Felsen‘ betrachtet. Auch erklärt dies teilweise die viel größeren Temperaturschwankungen in Wüstengebieten: Die Temperatur trockenen Sandes wird sich viermal schneller ändern als die von Meerwasser und ist zweimal so volatil wie in Nicht-Wüstengebieten.
Dies unterstreicht auch, warum es unangemessen ist, Land- und Wassertemperaturen zusammen zu mitteln, wie es in vielen anerkannten globalen Temperaturaufzeichnungen gemacht worden ist, beispielsweise bei HadCRUT4 (eine abartige Mischung von HadSST3 und CRUTem4) ebenso wie bei GISS-LOTI und bei den neuen BEST Land- und Wasser-Mittelwerten.
Es ist ein klassischer Fall von ,Äpfeln und Orangen‘. Falls man das Mittel zwischen einem Apfel und einer Orange nimmt, ist das Ergebnis ein Obstsalat. Das ist keine brauchbare Gemengelage für Berechnungen auf physikalischer Grundlage wie etwa dem Energiehaushalt der Erde und der Auswirkung von Strahlungs-„Antrieben“.
Die unterschiedliche Wärmekapazität wird die Daten zugunsten der Lufttemperaturen über Land verdrehen, welche viel schneller variieren und folglich eine irrige Grundlage liefern, um energie-basierte Berechnungen vorzunehmen. Außerdem sind die Landtemperaturen auch durch den Wärmeinseleffekt und andere Verzerrungen beeinträchtigt. Daher werden diese effektiv verdoppelt, bevor sie die globale Land- + Wasseraufzeichnung kontaminieren.
In disem Sinne bieten die Satellitendaten ein physikalisch konsistenteres globales Mittel, weil sie ein konsistenteres Medium messen. Falls man Energie-Berechnungen auf der Grundlage von Strahlung durchführen möchte, ist es wahrscheinlich bedeutsamer, SST-Daten als Kalorimeter zu nutzen.
Klimasensitivität ist definiert als das ∆rad , ∆T-Verhältnis, gewöhnlich im Zusammenhang mit einer linearen Approximation zur Planck-Rückkopplung, welche über relativ kleine Abweichungen in der etwa 300 K umfassenden Temperatur-Bandbreite gültig sind. Andere Rückkopplungen werden als Störungen gesehen, die von der dominanten Planck’schen Strahlungs-Rückkopplung addiert oder subtrahiert werden. All dies und sogar die weitaus komplexeren globalen Zirkulationsmodelle sind im Grunde Berechnungen des Energie-Gleichgewichtes. Der Energie-Erhaltungssatz ist eines der solidesten Axiome der Physik. Ein fundamentaler Test jedweder Theorie oder Gleichung ist, ob der Energie-Erhaltungssatz berücksichtigt ist.
Horizontaler Wärmetransport stellt sicher, dass die Festlandstemperatur durch die ozeanische Wärmekapazität beeinflusst wird: der thermische Anker des Klimasystems. Es ist bekannt, dass Temperaturen in Küstengebieten stabilisiert werden durch die Nachbarschaft von Land und Wasser und dass die zentralen Gebiete der Kontinente eine viel größere tägliche und jährliche Variation zeigen. Allerdings bleibt die Landtemperatur nahe der Oberfläche volatiler als die SST, und Analysen von Klimamodellen zeigen, dass sie über Land eine größere Klimasensitivität aufweisen und einen unterschiedlichen vertikalen Temperaturgradienten zeigen (1). FALLS man das als zuverlässig nehmen kann (die meisten Modelle nehmen eine konstante Relative Feuchtigkeit an).
In diesem Zusammenhang ist ein Temperaturanstieg die finale Folge aller Inputs, „Antriebe“ und Rückkopplungen, von denen viele über Land unterschiedlich sein können. Zieht man eine nicht-thermodynamisch relevante „mittlere“ Temperatur von zwei unterschiedlichen Ökologien mit unterschiedlicher Klimasensitivität heran, um ein ,Mittel‘ zu erzeugen, scheint auch die Klimasensitivität offen für Bias.
Schlussfolgerungen
Temperaturen sind keine abstrakten Statistiken; deren physikalische Bedeutung muss berücksichtigt werden bei der Auswahl, was man mit ihnen macht. Die Verwendung von Mittelwerten von Land- + Wassertemperaturen, verzerrt durch übertriebene Wichtung der volatileren landbasierten Temperaturen, wird physikalisch fehlerhafte Ergebnisse zeitigen.
Die meisten Klimadaten sind nicht einfach dimensionslose Zahlen. Jedes Processing sollte im Zusammenhang mit den physikalischen Größen betrachtet werden, die sie repräsentieren. Falls Temperaturen oder Temperaturanomalien als Energie-Proxy betrachtet werden für Berechnungen auf Energiegrundlage, sollte dies explizit erwähnt werden, und jedwede Verzerrungen, die sich hieraus ergeben, müssen angesprochen werden.
Die physikalische Signifikanz, Validität und Grenzen von „mittleren“ Land- + Wassertemperaturen sollte man berücksichtigen, wenn man sie verwendet. Dies ist jedoch nur sehr selten der Fall, wenn überhaupt.
(1) Geoffroy et al 2015 : “Land-sea warming contrast: the role of the horizontal energy transport” [ paywalled ] http://link.springer.com/article/10.1007/s00382-015-2552-y
Link: https://climategrog.wordpress.com/2016/02/09/are-land-sea-averages-meaningful-2/
Übersetzt von Chris Frey EIKE
Der (anonyme) Autor ClimateCrog hat einen Abschluss in Physik, Berufserfahrung in der Spektroskopie , Elektronik und Software-Engineering , einschließlich 3-D- Computer-Modellierung der Streuung von E- m -Strahlung in die Erdatmosphäre .
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"#27: Dr.Paul sagt:
Wieso denkt jeder beim Mittelwert immer an das arithmetische Mittel, ist mir absolut schleierhaft.
Wie ich bereits geschrieben habe:
Extensive skalare Größen bilden eine Summe und intensive skalare Größen einen Mittelwert. Mittelwerte in der Thermodynamik werden über den Molenbruch gebildet. Keiner rechnet dort mit dem arithmetischen Mittel, das wäre absolut fatal.
+ 10 g 30°C und 1000g 30°C
Masse (eine extensive skalare Größen – Summe): m = 1000g + 10g = 1010g
Temperatur (eine intensive skalare Größe – Mittelwert): T = 0,01*30°C + 0,99*30°C = 30°C
+ 10 g 50°C und 1000g 10°C
Masse (eine extensive skalare Größen – Summe): m = 1000g + 10g = 1010g
Temperatur (eine intensive skalare Größe – Mittelwert): T = 0,01*50°C + 0,99*10°C = 10,4°C
+ 10 g 10°C und 1000g 50°C
Masse (eine extensive skalare Größen – Summe): m = 1000g + 10g = 1010g
Temperatur (eine intensive skalare Größe – Mittelwert): T = 0,01*10°C + 0,99*50°C = 49,6°C
Mfg
Werner Holtz
#25: Sehr geehrter Herr Werner Holz, leider NICHT einverstanden. Sie missachten den Unterschied von intensiv und extensiv.
Versuchen wir es noch einfacher:
A)
10 Gramm 30° heißes Wasser + 1000g 30° heißes Wasser bleibt 1010g 30° (und nicht 60°, was eine „Addition“ von Temperatur wäre.
Oder wird durch Teilung von 1 Liter Wasser von 30° der halbe Liter nur noch 15° haben?
Da sind wir uns wohl einig;
jetzt kommt das Gleiche etwas schwerer zu verstehen wegen der Vermischung von beidem Temperatur und Energiegehalt, einer extensiven Größe:
B)
Ergibt die Addition von 10g 10° warmes Wasser mit 1000g 50° heißes Wasser auch 1010g 30° heißes Wasser?
Oder kommt man zum gleichen Ergebnis,
wenn die 10g 50° heiß sind und die 1000g 10°?
Genau das wollte der Autor Climategrog sagen.
Physikalische Definition:
Intensive Zustands-Größen wie die Temperatur und der Druck sind unabhängig von der Menge der Systembestandteile,
siehe A).
Extensive Größen sind dagegen abhängig von der Menge der Systembestandteile, sodass also eine Systemteilung zu einer Reduktion der Größe führt. Beispiele für extensive Größen sind Volumen, Masse oder Energie.
Ja, auch Energie ist eine extensive Größe.
Energie ist nicht gleich Temperatur.
mfG
Und das erste Mol Luft ist ja wie Sie schon bemerkt wohl haben nicht wie das zweite Mol an Luft. Sie benennen es nur wie das erste „Luft“.
Also bezogen auf das Mol, wie Sie verlangen vergleichen Sie in #18 sogar noch Aepfel mit Kartoffeln.
Kann man essen.
Aber vielleicht finden Sie ja was zur Berechnung einer sozusagen Modifikationsanederung von einem Mol an „Luft“.
Zu Wie kommt das Wasser denn hinein?
#24: Dr.Paul sagt:
Zitat: Richtig ist, dass man Temperaturen nicht einfach addieren kann, denn sie sind keine extensiven Größen.
Die Temperatur (Energiestärke) ist proportional zur Energiedichte. Schauen Sie sich mal die Zustandsgleichung der idealen Gase an, das ist eine Energiedichte-Temperatur-Beziehung. Selbst die Thermodynamik „addiert/subtrahiert“ Temperaturen bzw. bildet das Integral (eine alternative Form der Summenbildung). Die Temperatur ist eine skalare Größe, wie die Masse, die Zeit, der Druck, die Dichte oder die Energie. Grundsätzlich gilt, das nur skalare Größen mit gleicher Einheit addiert bzw. subtrahiert werden dürfen. Die Entscheidung, ob die skalare Größe eine Summe oder einen Mittelwert bilden, liegt an den Annahmen und Bedingungen des physikalischen Modells. Die Mathematik ist nur ein Hilfsmittel zur Beschreibung. Extensive skalare Größen bilden eine Summe und intensive skalare Größen einen Mittelwert.
Die Temperatur ist eine Definition der Thermodynamik, also müssen Sie mit den Annahmen leben – oder auch nicht, die dieses physikalische Modell trifft, um die Größe Temperatur zu beschreiben.
Stellt man sich die Frage, wie man die thermodynamische Temperatur richtig definiert, erhält man:
dS = dE/T -> S12 = Integral[1/T*dE|1;2] -> = E12/S12
Mit S2-S1=S12+S12(irr) würde man für ein System folgende Gleichung für die thermodynamische Temperatur (Mittel-Temperatur) erhalten:
= E12/S12 = E12/[S2 – S1 – S12(irr)]
wobei die Größe E12 alle Zustands-Energien repräsentiert. Wie man sieht, ist selbst die Temperatur, die Sie messen, nur eine Mittel-Temperatur .
Mfg
Werner Holtz
#18: Hallo Herr Holz, Sie sind wie immer ein guter Rechner. Es geht allerdings bei dem ausgezeichneten Artikel von Climategrog, den der unermüdliche Herr Frey übersetzt hat,
nicht um unterschiede in der Wärmekapazität IN der Luft, sondern um Unterschiede zwischen Wasser und Luft und auch zwischen Wasser (Ozean) und Festland, nicht nur in Bezug auf die Wärmekapazität.
Richtig ist,
dass man Temperaturen nicht einfach addieren kann,
denn sie sind keine extensiven Größen.
Gerade die Temperaturunterschiede sogar sehr kleine Temperaturunterschiede lösen Konvektion also Wärmetransport aus.
Und nach der Rayleigh-Zahl, welche die physikalische Ursache für Konvektion quantitativ beschreibt ist der Unterschied der kinematischen Viskosität zwischen Luft und Wasser noch größer als bei der Wärmekapazität,
so dass der Wärmetransport von Luft den von Wasser deutlich übertrifft, nicht nur lokal, auch global vom Äquator zu den Polen.
Wassertransport in der Luft ist ein Thema für sich, wie schon von anderen bemerkt.
Es kühlt die Erdoberfläche, kurz gesagt.
„Eben der Foehn“zin#22G.Dehren, zeigt die Realitaet, welche die Berechnung des Herrn Holtz lediglich fuer einen Stationaer Zustand, nicht wiedergibt. Also mit Aenderungetn des Partialdruck, nichtmal Temperaturaenderungen einhergehend beruecksichtigt werden duerfen. Und mit der Temperatur steigt die Faehigkeit Feuchte aufzunehmen, weshalb manche wohl Warme Luft als „trockene“ Luft bezeichnen.
Und weiter folgen manche Menschen auch der Irritation, es als warm halt zu bezeichnen, wenn nunmal eben nur hohe Luftfeuchtigkeit herrscht.
Wie bereits geschrieben erleben sie mal 30°C in den Tropen bei 80% relativen Feuchte gegenueber
30°C und 50% relativen Feuchte.
Kennen’s doch so aus der Sauna.
Nicht?
„Mit Wasser wird es erst so richtig ‚warm‘.“
#18: Werner Holtz
Sehr geehrte Herr Holtz,
vielen Dank für die umfangreiche Rechnung.
Ich vermute, sie enthält einen versteckten Fehler.
Wie kann es sonst sein, dass die trockene, abfallende Luft auf der Nordseite der Alpen um einige Grad wärmer ist als auf der Südseite die aufsteigende feuchte Luft?
Eben der Föhn.
@ #18 W. Holtz
Erzählen Sie doch mal was in der Meteorologie „latente Wärme“ ist. In der Meteorologie gibt es auch den sog. „Sättigungsdampfdruck“. Können Sie gleich miterklären.
Wikibildung genügt dazu nicht.
zu#18 und die 3% Wasserdampf sind ja nicht so einfach so – so zu dem Mol hinzu. Wissen Sie ja, dass dazu ne Menge Verdampfungsenthalpie geleistet werden muss. Also zu Aggregatzustand der Wasser aendern von flussig in Dampf und das bezieht man auf die Masse, also auch auf’s mol.
Und warme Luft alleine ist es nicht, die das Klima auf dem Erdball macht ganz schlicht.
Ohne „Wasser“ wuerde das CO2 uberhauptgarnicht so einfach an die Pflanzen transportiert werden koennen. Weil aufnehmen tun Pflanzen ja das CO2 als H2CO3 und nicht als Gas, … auch klar.
Und aus dem was Sie da so beschreiben haben Sie Thermo, aber keine Dynamik wozu Sie letztendlich Volumenangaben haben muessen.
Und 1 Liter Wasser flussig verdampft nunmal zu 1700 Liter Wasserdampf. Koennen Sie ja mal auf Mol bezogen so berechnen was da so an Energie zusaetzlich von der Luft aufgenommen wird.
Stichwort noch Verdampfungsenthalpie je Kilogramm, da findens dann ihr Mol auch wieder Werner Holtz, sie muessen ja bedenken wo die feuchte Luft denn herkommt.
Weil ohne feutche Luft gibt’s kein Regen oder Schnee und halt auch kaum Wind zu Klima aus der See.
zu#18″thermodynamisch“ arbeitet man eher mit dem Normkubikmeter, Herr Holtz, weil sich im mol keine Volumenaenderung ersehen laesst, fuer technischer Arbeit jedoch unverzichtbar.
Letztlich wird ja daraus auch m(punkt) Also der Massestrom je Zeiteinheit gefunden.
#16: G.Dehren sagt:
Zitat: Wenn Sie in Luft 30°C messen, ist es energetisch ein grosser Unterschied, ob diese Luft 0% oder 3% Wasserdampf enthält. Latente Wärme.
Die anderen Gase haben auch latente Wärmeenergie.
+ Die trockene Luft besteht hauptsächlich aus Stickstoff [78,084%], Sauerstoff [20,946%], Argon [0,930%] und Kohlendioxid [0,038%].
Für eine Temperatur von 300K ergibt sich:
cp(tLuft) = 919*0,20946+1040*0,78084+523*0,0093+849*0,00038 = 1009,754 J/(kg*K) (M=28,9647 g/mol = 0,0289647 kg/mol)
+ Die feuchte Luft besteht hauptsächlich aus Stickstoff [77,1%], Sauerstoff [20,7%], Argon [0,9%], Kohlendioxid [0,03%] und Wasserdampf [1,3%].
Für eine Temperatur von 300K ergibt sich:
cp(fLuft) = 919*0,207+1040*0,771+523*0,009+849*0,0003+1865*0,013 = 1021,279 J/(kg*K) (M=28,8290 g/mol = 0,028829 kg/mol)
M(N2)= 28,0134 g/mol, M(O2)= 31,9988 g/mol, M(Ar)= 39,948 g/mol, M(CO2)= 44,0098 g/mol, M(H2O)= 18,0152 g/mol
Da feuchte Luft eine geringere Dichte hat, ist 1 m^3 trockene Luft schwerer als 1 m^3 feuchte Luft.
Umgerechnet auf die molare Größe, ergibt sich:
Cp(tLuft) = 1009,754 J/(kg*K) * 0,0289647 kg/mol = 29,25 J/(mol*K)
Cp(fLuft) = 1021,279 J/(kg*K) * 0,028829 kg/mol = 29,44 J/(mol*K)
Damit ist die molare Wärmekapazität bei T=300K von 1 mol feuchte Luft zu 1 mol trockene Luft in etwa gleich. Wenn Sie in der Thermodynamik etwas vergleichen wollen, sollten Sie sich immer auf molaren Größen beziehen. Das hängt mit den Grund-Annahmen zusammen, auf denen die Thermodynamik abgebaut ist.
Mfg
Werner Holtz
@ #16 G. Dehren
„Wolken und Wasserdampf sind sowieso die grossen weissen Flecken auf der Landkarte der Klimatologen.“
Nur für die Modellierer, weil die Bewölkungsstruktur zu fein ist, als daß man sie mit den Modellen modellieren könnte. Wie soll das gegen bei dem GFDL-Modell CMIP5 mit einer Auflösung von 2,5 * 2,02 Grad.
Ansonsten ist klar, was eine Zunahme der Bewölkung im Zuge zunehmender Luftfeuchtigkeit = höherer Wasserdampfpartialdruck = geringere Dichte für Folgen hat. Daß mit zunehmendem wasserdampfpartialdruck auch mehr nergie transportiert wird, ist auch klar. Auch das können die Modelle naturgemäß bei derart grober Auflösung auch nicht deterministisch abbilden.
#10: Werner Holtz sagt:
„Also, worin besteht ein qualitative Unterschied der Temperaturen? Eine Temperatur von 30°C sind egal wo sie diese messe, immer 30°C.“
Wenn Sie in Luft 30°C messen, ist es energetisch ein grosser Unterschied, ob diese Luft 0% oder 3% Wasserdampf enthält. Latente Wärme.
Wolken und Wasserdampf sind sowieso die grossen weissen Flecken auf der Landkarte der Klimatologen.
#3: S.Hader, Temperaturen werden nicht „addiert“, sondern gemessen.
Man kann auch indirekt darauf schließen,
wenn z.B. ganz ohne Dünger und Spritzmittel gegen Schädlinge im Mittelalter Weinanbau an der Ostsee möglich war und wieder verschwand, weil es zu kalt wurde.
Gruß
Der Autor hat recht. Wenn es um „Physik“ geht, muss man unterscheiden zwischen intensiven und extensiven „Größen“.
„Mittelwerte“ kann es nur unter Berücksichtigung extensiver Größen geben, hier also der Wärmekapazität. Und bei VERÄNDERUNG der Temperatur natürlich unter Berücksichtigung der Wärmetransportfähigkeit in der Zeit.
Eines der Kardinalfehler der „Treibhauskünstler“
ist ja gerade die Modellvorstellung eines „Gleichgewichts“ oder eines „Durchschnittswertes“ einer Temperatur.
Da sich die Erde dreht und die Energiequelle SONNE nur aus einer Richtung kommt, gibt es aber NIEMALS ein Gleichgewicht oder einen Durchschnittswert,
sondern einen PERMANENTEN Wärmetransport wegen Temperaturdifferenzen.
Und hier spielt an der Grenze zu Luft, genannt Erdoberfläche, trotz geringer Wärmekapazität die bewegte Luft (Konvektion) die größte Rolle.
Horizontaler Wärmetransport ist die Ursache für „Seeklima“ am angrenzenden Land, wobei die Transportrichtung sich ebenfalls ständig ändert, bzw. umkehrt.
Bei Strahlung wird es noch einen Tick komplizierter, da es sich hier um exponentielle Funktionen handelt.
Bei allen Vorteilen ist daher die Satelliten-Messung der „Erdoberfläche“ keine exakte Messung der Luft in 2m Höhe, wie man heute die Erdoberflächentemperatur definiert.
#12: Werner Holtz sagt: „Hier geht es um Erwärmungsraten von Modell-Werten und Messwerten, die sich dann auf die Temperaturen auswirken.“
Lieber Herr Holtz,
wie ich die Veröffentlichung verstanden habe, sind die gemessenen Ozeantemperaturen in den Datensätzen von HADCRUT4 und auch GISS Wassertemperaturen, die von Schiffen und Bojen gemessen werden, während die Modellrechnungen sich auf Lufttemperaturen in 2m Höhe beziehen. Als Laie würde man davon ausgehen, dass die Temperaturunterschiede vernachlässigbar sind. Sie sind es aber offensichtlich nicht. Die Autoren führen die unterschiedlichen Erwärmungsraten von Modell und Messung zum Teil darauf zurück dass man Äpfel mit Birnen vergleicht. Die gleiche Vorsicht ist geboten, wenn man Temperaturen der unteren Troposphäre mit den in 2m Höhe gemessenen Oberflächentemperaturen vergleicht.
#9: P. Berberich sagt:
Zitat: Dieses Problem wird auch in der Veröffentlichung ….
Aus dem Abstract: This work quantifies a systematic bias in model-observation comparisons arising from differential warming rates between sea surface temperatures and surface air temperatures over oceans.
Hier geht es um Erwärmungsraten von Modell-Werten und Messwerten, die sich dann auf die Temperaturen auswirken. Und natürlichen sind die Erwärmungsraten aufgrund der Stoffeigenschaften unterschiedlich. Trotzdem ist eine Temperatur von 30°C überall qualitativ gleichwertig (Prinzip der Kontakt-Temperaturmessung), sonst würde sich der Nullte Hauptsatz der Thermodynamik in „Luft“ auflösen.
Aber Sie können folgendes Experiment durchführen: Bringen Sie zwei Körper mit unterschiedlichen Stoffeigenschaften, aber identischer Temperatur von 30°C zusammen (zum Beispiel: Wasser und einen Stein). An der Berührungsfläche/Grenzfläche der beiden Systeme messen sie dann eine Temperatur von 30°C, denn die beiden Systeme befinden sich im thermischen Gleichgewicht (Prinzip der Kontakt-Temperaturmessung).
Strenggenommen ist die makroskopische Größe, die als (thermodyamische) Temperatur, Druck oder Dichte usw. bezeichnet wird, selbst nur ein Mittelwert.
Mfg
Werner Holtz
@ # 10 Werner Holtz
Lieber Hr. Holtz,
danke, damit haben Sie genau das gemacht, was ich schon vermutet hatte. Ihnen ist offensichtlich nicht klar, dass hier ein Grossteil der Leser und Kommentatoren über solide naturwissenschaftliche Kenntnisse verfügt. Aber, wie Sie soeben bewiesen haben, trifft dies für den einen oder anderen, der meint hier mitdiskutieren zu müssen, eben nicht zu.
Mfg
#8: Fred F. Mueller sagt:
Zitat: kleiner Tipp: Beschäftigen Sie sich mal mit den Gasgesetzen (Druck, Art der Druckänderung) und der Tatsache, dass die Atmosphäre 0 bis zu 3 % Wasserdampf enthalten kann.
Wieder so ein sinnfreies Statement.
Also, worin besteht ein qualitative Unterschied der Temperaturen? Eine Temperatur von 30°C sind egal wo sie diese messe, immer 30°C.
Damit müsste der Druck auch qualitative Unterschiede aufweisen, also ein Druck von 1bar am Nordpol ist nicht gleich zu 1bar am Äquator.
Kleiner Tipp: Beschäftigen Sie sich mal mit der Thermodynamik.
Mfg
Werner Holtz
„Allerdings ist sofort klar, dass man nicht beginnen kann, Luft und Wassertemperatur zusammenzufügen oder zu mitteln; oder Temperaturen über Land und Wasser. Das sind keine kompatiblen Medien.“
Dieses Problem wird auch in der Veröffentlichung von K. Cowtan et al (2015) mit dem Titel „Robust comparison of climate models with observations using blended land air and ocean sea surface temperatures“
näher diskutiert.
@ # 2 Werner Holtz
Lieber Hr. Holtz,
kleiner Tipp: Beschäftigen Sie sich mal mit den Gasgesetzen (Druck, Art der Druckänderung) und der Tatsache, dass die Atmosphäre 0 bis zu 3 % Wasserdampf enthalten kann.
Mfg
Herr Holtz 30°C in den Tropen empfinden Sie aber garantiert anders als 30°C hier in unseren Breiten. Und sie bewirken halt ein anderes Klima ist ein anderes.
Und das liegt schon alleine daran, dass in den Tropen die Luft nur feuchter ist als hier. Und die Luft der Tropen bewirkt dann nur mehr Wasser auf das Land als hier. Da regnet’s jeden Tag, – auch bei 30°.
@Admin, das leuchtet ein, da gebe es nur ein kleines Problem. Die Satellitendaten von der mittelalterlichen Warmzeit sind leider „verschollen“. Aber an der Stelle kann ich die NASA in Schutz nehmen, die sind nicht daran Schuld. 😉
Sehr geehrter Herr Oesch,da haben sie völlig recht und wer Lust hat herauszufinden, warum die Berechnung einer Globaltemperatur aus Thermometerdaten unfug ist, sollte die Arbeit von R. McKitrick et al. Does a Global Temperature exist? lesen.
MfG
#2: Werner Holtz sagt:
Zitat – Kommentar Admin: Sie sollten den Artikel nochmals in Ruhe und aufmerksam lesen. „Da werden Sie geholfen“
Was ist denn das für ein sinnfreies Statement.
+ Wo genau in der Thermodynamik wird von kompatiblen Medien gesprochen?
+ Wo steht in der Thermodynamik etwas, das Temperaturen Qualitätsunterscheide aufweisen?
+ Gleiche Qualitäten können gemittelt werden. Wird übrigens auch selbst die Thermodynamik durchgeführt.
Mfg
Werner Holtz
Wenn Temperaturen addieren keinen Sinn macht, woher weiß man dann eigentlich, dass es angeblich in den letzten 18 Jahre nicht wärmer geworden ist? Oder das die mittelalterliche Warmzeit wärmer als 2015 gewesen sein soll? Macht Temperaturen addieren und mitteln nur dann Sinn, wenn man damit AGW-Thesen widerlegen kann?
Hi,
Zitat: Allerdings ist sofort klar, dass man nicht beginnen kann, Luft und Wassertemperatur zusammenzufügen oder zu mitteln; oder Temperaturen über Land und Wasser. Das sind keine kompatiblen Medien.
Was sind denn kompatiblen Medien? Den Ausdruck gibt es in der Thermodynamik nicht.
Zudem ist die (thermodynamische) Temperatur selbst nur ein Mittelwert. Und seit wann gibt es qualitative Unterschiede zwischen einer (thermodynamischen) Temperatur von einem Festkörper, einer Flüssigkeit oder eines Gases. Eine Temperatur von 30°C bleiben 30°C egal welches Material es ist.
Mfg
Werner Holtz
Schon Prof. Gerlich hatte in seinen Vorträgen darauf hin gewiesen, dass eine „globale Temperaturmittelung“ physikalischer Nonsens sei. Das wurde aber nie thematisiert, stattdessen kolportieren die grün/linken Staatsmedien weiter die Botschaften der Klimakirche wie sie von Ramstorf, Latif, Schellnhuber… vorgebetet werden. So läuft das nun mal im Land der grünen Schlümpfe, da zählt nur was offiziell geglaubt werden soll und nicht was physikalisch plausibel ist.