Bild 1 (rechts). Bei Auseinandersetzungen mit „Skeptikern“ und „Leugnern“ ist ein Unfehlbarkeitsanspruch ausgesprochen praktisch (Bild: Wikimedia Creative Commons)
Obwohl der Begriff „Mathematik“ nicht allgemeingültig definiert ist, wird sie häufig als Mutter aller Wissenschaften wahrgenommen. Da mathematische Sätze als prinzipiell endgültige und allgemeingültige Wahrheiten angesehen werden, gilt Mathematik als die exakte Wissenschaft schlechthin. Kant prägte hierzu den Satz: „Ich behaupte aber, dass in jeder besonderen Naturlehre nur so viel eigentliche Wissenschaft angetroffen werden könne, als darin Mathematik anzutreffen ist“ [WIMA].
Gerade aufgrund ihres Exaktheitsanspruchs und weil viele Gebiete der modernen Mathematik selbst Wissenschaftlern anderer Disziplinen oft nur in Umrissen bekannt sind, eignet sie sich jedoch auch hervorragend als Instrument für den Betrug – sowohl an sich selbst als auch an anderen. Hoch auf dem unangreifbaren Podest absoluter Exaktheit und endgültiger Wahrheit stehend, hat derjenige, der über die besseren Mathematikkenntnisse verfügt, einen echten Machtvorteil gegenüber seinen Mitmenschen. Hiervor warnt beispielsweise auch der Hamburger Mathematikprofessor Claus Peter Ortlieb: Zahlen, so seine Erkenntnis, „sind extrem mächtig, moderne Menschen sind zahlengläubig und über Zahlen sehr leicht manipulierbar. Zahlen verkörpern schlichte Objektivität, sie verselbstständigen sich leicht und werden dadurch schnell zum Fetisch“ [ORTL].
Da Wissenschaftler eben auch nur Menschen sind, wird dies leider nur allzu häufig genutzt, um unlautere Ziele zu verfolgen. Besonders verbreitet ist dies zurzeit im Bereich der sogenannten Klimaforschung. Ebenso verbreitet wie der direkte Betrug ist allerdings auch der Selbstbetrug, denn auf praktisch allen Gebieten des realen Lebens, die sich der Mathematik bedienen, ist die beanspruchte Exaktheit nur ein Mythos. Die Folge ist, dass selbst Wissenschaftler allzu leicht an das glauben, was ein Messgerät für sie gemessen und ein Computer für sie ausgerechnet hat, und sich über Möglichkeiten und Grenzen ihrer Daten- und Zahlenwerke oft viel zu wenig Gedanken machen.
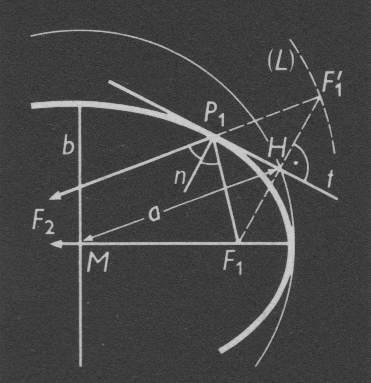
Bild 2. Mathematik, Teilgebiet analytische Geometrie. Grafische Darstellung wichtiger geometrischer Beziehungen an einer Ellipse (Grafik: H. Sieber [SIEB])
Mathematik und die Grenzen der Exaktheit
Der erste Selbstbetrug, dem auch viele Menschen mit naturwissenschaftlicher Ausbildung anheimfallen, ist die Vorstellung, dass mathematische Berechnungen per se exakt seien. Dabei trifft dies schon bei ganz einfachen Kalkulationen mithilfe der vier Grundrechenarten nicht immer zu. Schon der Bruch 1/3 hat in der Dezimalschreibweise unendlich viele Nachkommastellen. In der Praxis kann daher der Versuch, 1/3 und 1/7 zu addieren und das Ergebnis als Real- Zahl darzustellen, zu keinem wirklich exakten Ergebnis führen. Real-Zahlen sind in Computersprachen Fließkommazahlen in Dezimalschreibweise. Auch das Periodenzeichen ist nur eine Hilfskrücke, mit der man sich über diese Tatsache hinwegtröstet. Zwar wird ein echter Mathematiker angesichts derartiger Herausforderungen erst richtig zur Hochform auflaufen, wie das Beispiel der Kreiszahl Pi zeigt. Einerseits versuchten sich über die Jahrtausende hinweg zahllose Menschen – vom Mathematiker über den genialen Amateur bis hin zum Dilettanten – an der sogenannten Quadratur des Kreises, d.h. an einem Verfahren, Kreis und Quadrat irgenwie mithilfe von Zirkel und Lineal ineinander zu überführen. Andererseits gab es einen regelrechten Wettlauf zur Ermittlung derZahl Pi mit möglichst grosser Genauigkeit. Dank moderner Computer hat man hierbei inzwischen schon mehr als 10 Billionen Stellen hinter dem Komma erzielt.
Im Alltag aber wird man aus praktischen Erwägungen einen Punkt definieren, ab dem das Ergebnis als „ausreichend exakt“ akzeptiert wird. Solche Entscheidungen sind jedoch nicht mathematisch begründbar, sondern schlicht und ergreifend nur eins: Willkürlich.

Bild 3. Die möglichst genaue Berechnung der Zahl pi war für Mathematiker schon immer eine besondere Herausforderung. Inzwischen wurde sie bereits auf mehr als 10 Billionen Stellen berechnet
Mathematik als Werkzeug
Mit diesem Sündenfall hat man bereits das Gebiet der „exakten“ Mathematik verlassen und schaltet somit den ganz normalen (wenn auch oft verpönten und nicht immer zuverlässigen) gesunden Menschenverstand hinzu, der Mathematik als Werkzeug zur Lösung praktischer Probleme betrachtet. Dabei spielt es keine Rolle, ob es um einen simplen Dreisatz oder eine quantenphysikalische Aufgabenstellung in der Elementarteilchenphysik geht. Wer Alltagsprobleme mit Hilfe der Mathematik angeht, muss sich vom Ideal der Exaktheit verabschieden, muss für sich entscheiden, wie viel Aufwand er für welchen Grad an Genauigkeit der Ergebnisse seiner Berechnungen zu treiben bereit ist. In diesem Zusammenhang spielt es absolut keine Rolle, ob man einen groben Anhaltswert für eine Investitionsentscheidung oder eine hoch exakte Berechnung für die Umlaufbahn eines GPS-Satelliten benötigt. Die zu treffende Entscheidung ist in jedem Falle subjektiv und deshalb auch lediglich unter subjektiven Aspekten zu beurteilen. Bei solchen Beurteilungen kann man durchaus unterschiedlicher Meinung sein, doch sollte man den Vorwurf unzureichender Exaktheit nicht verwenden, weil er schlicht immer zutrifft. Mit diesem Argument könnte man glatt sogar einen Einstein als dummen Jungen hinstellen. Die einzig zulässige Diskussion kann daher nur darum geführt werden, welchen Grad an Nicht-Exaktheit man aus welchen Gründen für erforderlich bzw. vertretbar hält.
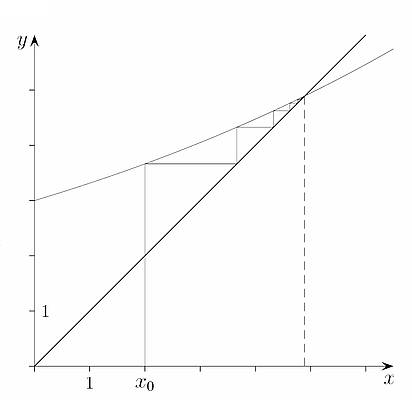
Bild 4. Grafische Darstellung einer iterativen Annäherung an den Schnittpunkt zweier Funktionen (Quelle: [SCHN])
Computer und Rechengenauigkeit
So gut wie niemand rechnet heute noch selber, man vertraut den allgegenwärtigen Taschenrechnern und Computern. Was dort herauskommt, wird so gut wie nie angezweifelt. Dabei machen sich die wenigsten Menschen klar, dass diese Systeme ungenau rechnen. Das fängt schon damit an, dass die gängigen Computer in der Regel kein Dezimalsystem verwenden, sondern intern mit einem binären Code in Exponentialdarstellung arbeiten. Um eine Dezimalzahl zu verarbeiten, wird diese zunächst in eine binäre Gleitkommazahl mit Mantisse und Exponent umgewandelt, während das Ergebnis dann wiederum zurück ins Dezimalsystem transformiert wird. Dabei geht zwangsläufig Genauigkeit verloren. Da die Länge der Mantisse begrenzt ist, sind den Ansprüchen an die Genauigkeit deutlich engere Grenzen gesetzt, als es sich der Computerlaie normalerweise vorstellt. Zudem gelten hier die Gesetze der Fehlerfortpflanzung. Vor allem bei iterativen Schleifen kommt man dann recht bald an Grenzen.
Vereinfachung statt Verkomplizierung
In vielen Bereichen der Mathematik beschäftigt man sich damit, den für die Lösung einer Aufgabe zu treibenden Aufwand zu minimieren. Dabei strebt man beispielsweise danach, Gleichungen zu vereinfachen oder den erforderlichen Rechenaufwand zu optimieren. Diese Kunst ist auch eher den Schweiβ des Edlen wert als das Gegenteil: Die Möglichkeiten, selbst einfachste Gleichung wie 1 +1 = 2 zu verkomplizieren, sind schlieβlich unendlich.
Aus den gleichen Gründen hat die Mathematik auch mit viel Kreativität Näherungsverfahren für die zahlreichen Bereiche entwickelt, in denen exakte Lösungen entweder nicht zu finden waren oder einen als nicht akzeptabel eingeschätzten Aufwand verursacht hätten. Mit dem Begriff „Näherungslösung“ wird hierbei prinzipiell anerkannt, dass darauf verzichtet wird, ein mathematisch exaktes Resultat zu fordern. Dies gilt beispielsweise für weite Gebiete der Mathematik wie die Statistik oder die polynomische Approximation, wo man von vornherein akzeptiert, dass man sich dem exakten Ergebnis nur annähert. Deshalb gibt es dort auch eigene Parameter wie das Bestimmtheitsmaβ, mit deren Hilfe beurteilt werden kann, wie nah man mit der gefundenen Lösung an die Tatsachen herangekommen ist.
Zugleich liefert dies auch die Rechtfertigung für die Vorgehensweise, bei der Berechnung realer Vorgänge z.B. in Wirtschaft und Gesellschaft – wo die verwendeten Zahlen oft sowieso mit erheblichen Unsicherheiten behaftet sind – zunächst mit vereinfachten Ansätzen zu operieren, um eine Vorstellung von den Dimensionen und Gröβenordnungen der Aufgabenstellung zu erhalten. Eine genauere Berechnung wird oft erst dann durchgeführt, wenn die Abschätzungen den Aufwand als gerechtfertigt erscheinen lassen.
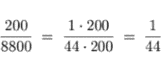
Bild 5. Eine jedem Schüler gut bekannte Aufgabenstellung: Vereinfachung von Brüchen durch Kürzen
Die Messung physikalischer Werte
Ein groβes Problem der in naturwissenschaftlichen Disziplinen angewandten Mathematik ist das oft mangelnde Verständnis der Grenzen der Messgenauigkeit. Aus Sicht des Mathematikers ist es beispielsweise wenig sinnvoll, mit acht- oder gar 15stelliger Genauigkeit zu rechnen, wenn die Eingangsgröβe selbst nur mit zwei- oder dreistelliger Genauigkeit erfasst wurde, wie dies beispielsweise bei Temperatur- oder Luftfeuchtemessungen der Fall ist. Hinzu kommen dann noch Messfehler, Driftvorgänge der Sensorik etc. Selbst bei Präzisionsmechaniken liegt die Genauigkeit, mit der Abmessungen erfasst werden, meist nur bei 4 oder 5 Stellen.
Eine wichtige Einschränkung bei der Messung vieler Gröβen wie Temperatur oder Luftfeuchtigkeit ist zudem die Tatsache, dass hier vielfach punktuell Einzelwerte erfasst werden, obwohl es sich eigentlich um komplexe, dreidimensional wie auch zeitlich veränderliche Feldgröβen handelt. Um sich eine Vorstellung von den damit verknüpften Problemen zu machen, kann man einmal alle Thermometer im Haushalt zusammentragen und diese in einem Zimmer verteilen, um dann zu versuchen, die mittlere Temperatur zu bestimmen. Selbst bei geschlossenen Fenstern und Türen sowie bei Vermeidung von direkter Sonneneinstrahlung merkt man schnell, dass nicht nur die einzelnen Thermometer teils deutliche Abweichungen aufweisen, auch die Temperatur im Raum verändert sich unaufhörlich. Dabei kann es auch zu lokalen Verschiebungen kommen, erkennbar an einer Zu- oder Abnahme der Differenzen zwischen einzelnen Messpunkten. Die Angabe einer auch nur auf zwei Stellen genauen mittleren Tagestemperatur erfordert einen erstaunlichen messtechnischen und auch rechnerischen Aufwand. Wenn man sich dann vergegenwärtigt, wie variabel sich die entsprechenden Gröβen in freier Natur darstellen, so bekommt man eine gewisse Vorstellung davon, wie schwierig die Aufgabe beispielsweise der Meteorologen des Deutschen Wetterdienstes ist, aus den Daten von wenigen 100 Messstationen in ganz Deutschland, die teils nur zu bestimmten Zeiten abgerufen werden, repräsentative Aussagen zu erzeugen [WIWD, THUE, GRAY, QUIR].

Bild 6. Sammelsurium von im Haushalt verwendeten ungeeichten Thermometern geringer Genauigkeit. Aber auch manche meteorologische Messverfahren wie die Bestimmung des flüssigen Niederschlags haben Fehler von bis zu 30%, wobei sich fast alle möglichen Meßfehler in Richtung einer negativen Abweichung vom „wahren Messwert“ auswirken 1) [WIME]
Statistik
Stochastik ist der Oberbegriff der beiden Bereiche Wahrscheinlichkeitstheorie und Statistik. Die Wahrscheinlichkeitstheorie befasst sich mit Zufallsereignissen und der Analyse von Wahrscheinlichkeiten, während Statistiker sich mit dem Sammeln, der Analyse und der Interpretation von Daten beschäftigen. Dies ist für den Umgang mit Messdaten unabdingbar, da reale Messungen stets streuen. Mit Hilfe statistischer Methoden wird daher versucht, die ermittelten Werte zu beurteilen, um zufällige Streuungen von Ausreiβern zu trennen und eventuelle systematische Fehler wie die Drift von Sensoren zu erkennen. Eine gut durchgeführte statistische Analyse von Messwerten ist für die korrekte Interpretation von Messdaten eine unschätzbare Hilfe.
Leider wird jedoch auch häufig versucht, mit Hilfe der Statistik Mängel bei der Ermittlung von Messdaten in unzulässiger Weise zu „korrigieren“ [ESCH]. Das Ergebnis ist Selbstbetrug: Wenn die zugrundeliegenden Werte nicht mit bestmöglicher Genauigkeit ermittelt wurden, ist auch die Mathematik oft damit überfordert, diese Erbsünde des Datenbestandes auszugleichen. Leider wird dies dennoch immer wieder versucht, beispielsweise bei der Interpretation von historischen Daten von Wetterstationen, die bereits seit langen Zeiträumen betrieben werden. Eines der dabei auftretenden Probleme ist der sogenannte Wärmeinseleffekt. Er tritt auf, wenn eine Station, die beispielsweise 1850 noch in freier Natur stand, heute von Beton und Bebauung umgeben ist, wodurch das gesamte Temperaturumfeld systematisch verändert wird [EIWI, WAUH]. Dadurch sind die Daten früherer Messungen nicht mehr mit heutigen Aufzeichnungen vergleichbar. Dennoch wird häufig versucht, dies durch Korrekturfunktionen zu ermöglichen, die oft selbst für Fachleute kaum nachvollziehbar sind. Die Zulässigkeit solcher Vorgehensweisen ist dementsprechend umstritten [WIME, WIMA].
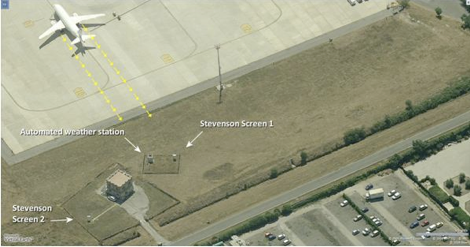
Bild 7. Von Beton und Flugzeug-Abgasstrahlen beeinflusste Wetterstation am Flughafen in Rom (Bild: [EIWI])
Missbrauch des Grundrauschens
Im Zusammenhang mit der Messung physikalischer Werte ist man heute derart an Digitalanzeigen gewöhnt, dass man sich kaum noch Gedanken darüber macht, dass diese nicht die Realität darstellen oder wo ihre Grenzen sind. Zunächst einmal basieren Messwerte in aller Regel nicht auf der zu messenden Gröβe selbst, sondern auf der Interpretation eines analogen elektrischen Signals, das von einem geeigneten Sensor erzeugt wird. Schon bei der Erzeugung wie auch bei der Verarbeitung dieses Signals können Verfälschungen auftreten, welche zu fehlerhaften Werten führen. Weitgehend unbekannt ist vielfach auch, dass analoge elektrische Signale stets ein sogenanntes Rauschen aufweisen. Dieses wird von einer Reihe physikalischer oder quantenphysikalischer Effekte hervorgerufen und führt dazu, dass das eigentliche Messsignal umso schwerer zu bestimmen ist, je weniger es sich vom Grundrauschen abhebt. Mit abnehmender Amplitude des Nutzsignals wächst der entsprechende Fehler an, bis die Werte nicht mehr als signifikant angesehen werden können. Messwerte im unteren Grenzbereich der Instrumentenempfindlichkeit weisen daher teils recht hohe prozentuale Unsicherheiten auf.
Ein solches Grundrauschen gibt es übrigens auch im Bereich der Radioaktivität, da in der Natur überall ein gewisser Mindest-Strahlungspegel herrscht. Strahlungsbelastungen, die unterhalb dieses Hintergrundwerts liegen, lassen sich daher nicht mehr von derjenigen natürlicher Quellen unterscheiden. Deshalb messen ihnen die meisten Radiologen keine Bedeutung zu. Zudem wissen sie, dass die Biologie entsprechende Anpassungen entwickelt hat: Lebende Zellen verfügen über Reparaturmechanismen, um entsprechende Schäden zu beheben.
Im Gegensatz zu diesen Erkenntnissen gibt es auch die Auffassung, dass grundsätzlich jedes Strahlungsquant schädlich sei. Anhänger dieser These rechnen Schädigungspotenziale, die bei hohen Strahlungsdosen ermittelt wurden, selbst für solche Expositionen herunter, die längst weit unterhalb des natürlichen Strahlungspegels liegen. Dieser sogenannte Linear No Threshhold (LNT)-Ansatz ist insbesondere bei Vertretern von Greenpeace und ähnlichen Organisationen sehr beliebt, weil er sich hervorragend zur Angsterzeugung eignet.
Mit dem LNT-Ansatz lieβe sich jedoch beispielsweise auch ausrechnen, wieviele Menschen jährlich durch diejenige Radioaktivität an Krebs erkranken, die in Windenergieanlagen, Solarpaneelen oder auch in Babynahrung steckt. Umfassende wissenschaftliche Untersuchungen haben die LNT-These widerlegt [RADI]. Dass man sie selbst seitens Greenpeace und Konsorten nicht so recht ernst nimmt, kann man auch daran erkennen, dass trotz der von den Medien in der Bevölkerung geschürten Strahlenangst noch immer Kureinrichtungen existieren, die Bäder- oder Luftkuren mit radioaktivem Radon anbieten. Würde die LNT-These wirklich zutreffen, dann hätte Greenpeace längst zu flammenden Protesten vor den Toren dieser Heilanstalten aufrufen müssen.
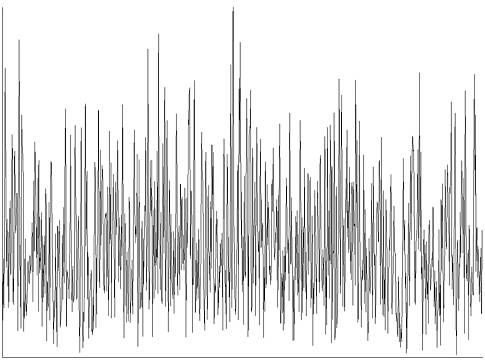
Bild 8. Das sogenannte Rauschen analoger elektrischer Signale wird durch physikalische Effekte hervorgerufen. Einmalige Signale, die kleiner sind als der Rauschpegel, sind in der Regel nicht signifikant (Grafik: Bautsch, Wikimedia Commons)
Das Tricksen mit Zeiträumen
Zu den bei Klimamodellierungen häufig angewandten Tricks gehört es, Betrachtungszeiträume so zu wählen, dass sich der gewünschte Effekt quasi „von selbst“ ergibt. Wie das funktioniert, lässt sich am Beispiel eines periodischen Signals wie z.B. einer Sinuskurve demonstrieren. Während der Sinus bei entsprechend langzeitiger Betrachtung keine Steigung aufweist, kann man durch geeignete Verkürzung wahlweise einen stark ansteigenden oder stark fallenden Scheineffekt erzeugen.

Bild 9. Die Sinusfunktion (oben) hat im Prinzip die Steigung Null. Betrachtet man jedoch Zeiträume, die kürzer sind als eine Periode, so kann man je nach Wahl der Anfangs- und Endzeitpunkte aufwärts oder abwärts zunehmende Steigungen „beweisen“ (Grafik: Viscount Monckton [EIMO])
Die Klimawissenschaft ist sich über den Zeitraum, ab dem man von „Klima“ statt von Wetter spricht, nicht einig. Die World Meteorological Organisation (WMO) beispielsweise definiert ihn auf 30 Jahre. Solche Definitionen sind nicht unbedingt „falsch“, jedoch letztlich immer willkürlich. Man könnte auch einen anderen, eher längeren Zeitraum wählen. Hinzu kommt: Die Charakterisierung erfolgt nicht durch einen einzelnen Wert, sondern durch eine Gemengelage von Mittelwerten einzelner Wetter-Elemente wie Temperatur, Druck, Feuchte, Wind etc. Klima ist deshalb (wie übrigens auch Wetter) immer ein subjektiver Summen-Akkord vieler solcher Elemente. Anders ausgedrückt: Es kann kälter, windiger und trockener werden, aber auch wärmer, windiger und feuchter etc.
In Wahrheit unterliegen klimatische Entwicklungen einer ganzen Reihe unregelmäβig schwankender Einflüsse, deren Zykluszeiten wie beim El Ninjo/ La Ninja –Effekt wenige Jahre oder, wie bei den letzten Eiszeiten, auch 100.000 und mehr Jahre betragen kann. Leider gibt es bezüglich der Zeitdauer dieser Schwankungen keine klaren, naturgesetzlich oder mathematisch beschreibbaren Regelmäβigkeiten, die man für die Ableitung von Vorhersagen nutzen könnte.
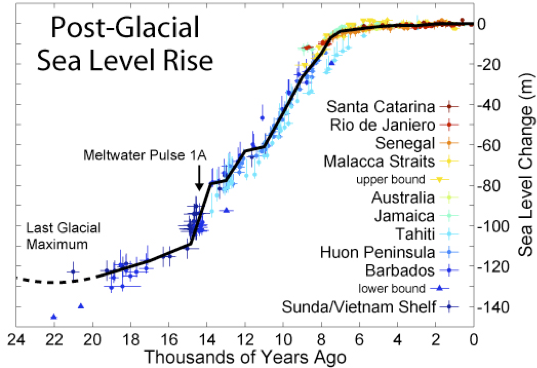
Bild 10. In den letzten rd. 20.000 Jahren ist der Meeresspiegel ohne menschliches Zutun um etwa 120 m (ca. 0,6 m pro Jahrhundert) angestiegen (Grafik: Robert A. Rohde, Wikipedia [ROHD])
So weisen Geowissenschaftler darauf hin, dass wir in den letzten ca. 2,5 Mio. Jahren eine recht ausgeprägte Zyklizität von Eis- und Warmzeiten hatten. Wer dies nicht berücksichtigt, obwohl die Tatsachen bestens dokumentiert sind, riskiert den Vorwurf, die Grundregeln wissenschaftlich korrekten Vorgehens zu missachten. Besonders beliebt sind beispielsweise Darstellungen des Meeresspiegelanstiegs, bei denen die Vorgeschichte an passender Stelle abgeschnitten wurde. Wenn man die rund 120 m, um die das Meer seit ca. 20.000 Jahren angestiegen ist, einfach ignoriert, dann kann man natürlich die aktuellen 0,2 m pro Jahrhundert als Katastrophenmeldung an den Mann bringen.
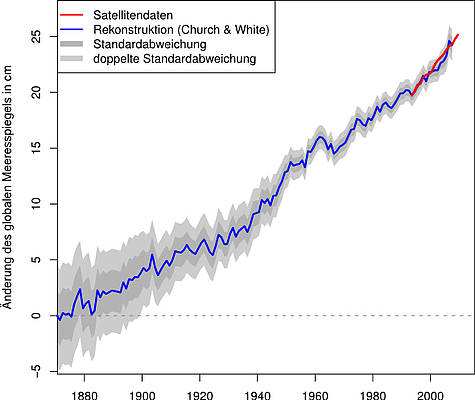
Bild 11. Betrachtet man lediglich die letzten ca. 150 Jahre, dann wirken schon Änderungen von + 25 cm Meeresspiegel bedrohlich (Grafik: El Grafo, Wikimedia commons)

Bild 12. Den Meteorologen stehen für ihre Arbeit heute auch Messdaten aus zahlreichen Satelliten zur Verfügung (Bild: NOAA)
(Klima)-Simulationen – und ihre Grenzen
Was ist eigentlich eine Computersimulation? Simulation ist der Versuch, die Realität durch – meist sehr aufwendige – mathematische Modelle in einem Computer nachzubilden. Dabei kommt es darauf an, ob das mathematische Modell die Realität auch ausreichend korrekt beschreibt, ob die Eingangswerte stimmen und ob der Rechenweg im Computer – wo meist zahlreiche iterative Schleifen durchlaufen werden – keine allzu groβen Fehler generiert. Die Ergebnisse sind selbst bei vergleichsweise einfachen Modellen oft ernüchternd. Würde Mark Twain heute leben, käme er wahrscheinlich zu dem Schluss, dass Simulation ein besonders aufwendiges Verfahren ist, um mit Hilfe eines Hochleistungscomputers schöne bunte Bildchen zu erzeugen.
Die eigentliche Herausforderung besteht darin, bei den Ergebnissen zwischen Science und Fiction zu unterscheiden, d. h. nachzuweisen, dass diese bunten Bildchen tatsächlich der Realität entsprechen. Fachleute für Simulationsberechnungen aus der industriellen Praxis, deren Ergebnisse unmittelbar mit den betrieblichen Realitäten verglichen werden können, sind bezüglich der Belastbarkeit ihrer Prognosen meist deutlich vorsichtiger als viele Klimawissenschaftler. Von solchen Industrieanwendern ist in aller Regel zu erfahren, dass exakte Voraussagen selbst bei vergleichsweise einfach strukturierten Aufgabenstellungen mit wenigen Parametern – beispielsweise Verbrennungsvorgänge in Brennkammern von Groβdieseln oder das Gieβen von Stahl in eine Kokille – nur recht begrenzt möglich sind. Bei solchen Aufgabenstellungen sind Simulationen oft hilfreich, aber nicht exakt. Sie helfen zwar dabei, Tendenzen abzuschätzen und den Versuchsaufwand zu reduzieren, Gewissheit bekommt man jedoch nur, wenn man reale Teile unter praxisüblichen Bedingungen testet. Auch Meteorologen geben zu Protokoll, dass die Genauigkeit ihrer Wettervorhersagen selbst für kurze Zeiträume bei lediglich etwa 80 bis 90 % liegt. Das muss mit der Tatsache verglichen werden, dass ein erfahrener Laie lokal auch ohne Messungen (nur mit Wind und Wolken) 70-80 % erreichen kann, während selbst die einfachst mögliche Prognose – „heute so wie gestern“ – immerhin zu etwa 65 % zutrifft [WIWD, WIME]. Vorhersagen für Zeiträume von mehr als 2-3 Tagen sind bereits mit groβen Unsicherheiten behaftet.
Bei Autoren von Simulationen, die behaupten, das Klimageschehen über Jahrzehnte oder gar Jahrhunderte vorausberechnen zu können, ist dagegen Skepsis angesagt [THUE, GRAY, ORTL]. Man mag zwar die Kunstfertigkeit bewundern, mit der dort komplizierte Gleichungssysteme mit sehr vielen sich gegenseitig beeinflussenden Einfluβgröβen zu extrem aufwendigen Programmen verknüpft werden – aber der Beweis, dass die ermittelten Ergebnisse tatsächlich der Realität entsprechen, muss noch erbracht werden. Wetterdienste, die sich auf das Abenteuer eingelassen haben, mittelfristige Vorhersagen beispielsweise für einige Monate bis zu einem Jahr zu machen, sind damit vollkommen und ohne Ausnahme auf die Nase gefallen, so die Briten mit ihrer Vorhersage milder Winter oder die Neuseeländer mit ihrer Unfähigkeit, eine starke Dürreperiode zu prognostizieren [GRAY]. Sicherlich nicht ohne Hintergedanken werden deshalb die Vorhersagezeiträume oft so groβzügig zugeschnitten, dass eine Verifizierung nur noch posthum erfolgen könnte. Eine erfreulich klare Aussage hierzu lieferte Prof. Hans von Storch vom GKSS-Forschungszentrum in Hamburg: Wir Klimaforscher können nur mögliche Szenarien anbieten; es kann also auch ganz anders kommen.“ [STOR]
Cui bono – die Kriminalfrage
Als letzte Frage ist hier noch zu klären, warum so viele und oft hochqualifizierte Menschen die Wissenschaft in solchem Umfang missbräuchlich anwenden. Darauf gibt es eine einfache Antwort, die zum Grundrepertoire jeder Kriminalistenausbildung gehört: Frage dich, wem es nützt (cui bono). Man muss sich die Tatsache vor Augen halten, dass die sogenannten Klimawissenschaften die ideologische Rechtfertigung für einen Billionen-Euro-Wirtschaftszweig liefern, der inzwischen vermutlich deutlich höhere Profite erzeugt wie beispielsweise die vielgescholtene konventionelle Stromerzeugung aus Kohle und Kernkraft. Besonderes Merkmal dieser neuen Branchen ist, dass sie nahezu ausschlieβlich davon leben, Energie viel teurer als nötig herzustellen, weil die Politik dies fördert und mit Geldern der Allgemeinheit bezahlt. Um die erforderliche ideologische Unterstützung aufrechtzuerhalten, wurde ein riesiger PR-Apparat aufgebaut, der mit vielen Millionen geschmiert wird. Und während Menschen, die sich aufgrund ihrer Fachkunde gegen diese Politik der Irreführung und Verschwendung auflehnen, in der Öffentlichkeit ständig als bezahlte Mietlinge der Kernkraft- und Fossilindustrie angeprangert werden, betreiben auf der anderen Seite PR-Agenturen, die den sogenannten EE-Industrien nahestehen, ganz kommerziell Verleumdungswebseiten wie Desmogblog, in denen der Rufmord an „Skeptikern“ und „Leugnern“ mit hoher Professionalität vollzogen wird.
Was Wissenschaftler und Hochschulprofessoren angeht, so sind diese schlicht auf Gelder angewiesen, die von der Politik dorthin gelenkt werden, wo die höchsten Prioritäten vermutet werden. Und dazu gehört schon seit Jahren alles, was irgendwie mit Etiketten wie „erneuerbar“, „klimafreundlich“, „CO2-Vermeidung“ usw. beklebt werden kann. Kein Wunder also, wenn man auch von dieser Seite fleiβig dazu beiträgt, diese Gans, die goldene Eier legt, durch „Gefälligkeitswissenschaft“ weiter am Leben zu erhalten. Wes Brot ich ess, des Lied ich sing – auch mit Hilfe der Mathematik.
Fred F. Mueller

Bild 13. In der Industrie werden Computersimulationen eingesetzt, um beispielsweise Spannungsverteilungen an Bauteilen zu ermitteln
1) Das bedeutet, dass die Niederschlagsmessungen der Wetterdienste seit dem Beginn regelmäßiger Meßreihen vor ca. 150 Jahren systematische Fehler von minus 10-30% beinhalten, je nach Meßverfahren, Region, Ort etc. Zwar ist dies den Meteorologen bewusst, aber alle Versuche zu Korrekturen, „Homogenisierungen“ usw. wurden aufgegeben, weil sie lediglich auf „Verschlimmbesserungen“ hinauslaufen [KEPU]
[EIMO] http://www.eike-klima-energie.eu/news-cache/monckton-fordert-vom-ipcc-eine-korrektur-im-ar-4/ abgerufen am 7.5.2013
[EIWI] http://www.eike-klima-energie.eu/climategate-anzeige/was-sind-temperaturmessungen-auf-grossflughaefen-wert-oder-wie-das-zdf-mit-bewusst-falschen-temperaturaussagen-die-oeffentlichkeit-taeuscht-und-die-abkuehlung-in-deutschland-verschleiert/ abgerufen am 12.5.2013
[ESCH] http://wattsupwiththat.com/2013/05/10/why-reanalysis-data-isnt-2/#more-86030 abgerufen am 11.5.2013
[GRAY] http://www.eike-klima-energie.eu/news-cache/der-weg-zurueck/ abgerufen am 15.5.2013
[KEPU] Puls, K.E.: Persönliche Mitteilung, August 2013.
[MEER] http://www.futureocean.org/static/www.futureocean.de/forschungsfelder/marine-ressourcen-u-risiken/meeresspiegelanstieg/fakten/ abgerufen am 13.5.2013
[ORTL] http://www.brandeins.de/magazin/rechnen/die-welt-laesst-sich-nicht-berechnen.html abgerufen am 14.5.2013
[QUIR] http://wattsupwiththat.com/2013/05/10/a-mean-study-of-australian-temperature/#more-86012 abgerufen am 11.5.2013
[RADI] http://radiology.rsna.org/content/251/1/13.full abgerufen am 7.5.2013
[ROHD] Robert A. Rohde, Global Warming Art, http://commons.wikimedia.org/wiki/File:Post-Glacial_Sea_Level.png abgerufen 13.5.2013
[SATE] http://www.goes.noaa.gov/index.html abgerufen am 14.5.2013
[SCHN] http://nibis.ni.schule.de/~lbs-gym/AnalysisTeil3pdf/Iteration.pdf
[SIEB] Sieber, H.: Mathematische Tafeln. E. Klett Verlag. Stuttgart.
[STOR] Der Spiegel 11/2007, S.56.
[THUE] http://www.derwettermann.de/klimaforschung-agiert-weiter-fern-jedweden-wirklichkeitsbezugs.html
[WAUH] http://wattsupwiththat.com/2011/08/16/new-paper-climatic-trends-in-major-u-s-urban-areas-quantifies-the-uhi-effect-and-the-impact-on-climate-trends/ abgerufen am 12.5.2013
[WIMA] http://de.wikipedia.org/wiki/Mathematik abgerufen am 14.5.2013
[WIME] http://de.wikipedia.org/wiki/Meteorologie#Wetterdaten abgerufen am 11.5.2013
[WISL] http://de.wikipedia.org/wiki/Meeresspiegel abgerufen am 7.5.2013
[WIWD] http://de.wikipedia.org/wiki/Wetterstation abgerufen am 5. 5. 2013

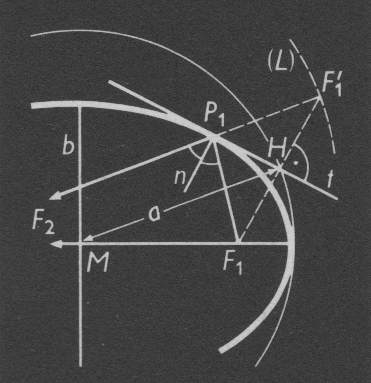















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"@ #18: Fred F. Mueller sagt am Montag, 12.08.2013, 13:49
„auch sehr stark verrauschte Signale noch interpretierbar zu machen,“
Macht jeder GPS-Empfänger.
@ #1: Hofmann,M sagt am Freitag, 09.08.2013, 11:01
„Jedoch hat der Ursprung-Mensch keine Mathematik gekannt und hat sich auch ohne Mathe das Essen und das Wasser. “
Die Anfänge der Mathematik reichenviel weiter zurück http://tinyurl.com/GrenzMat
„So konnte gezeigt werden, dass bereits Neugeborene in der Lage sind, die Kardinalität kleiner Mengen zu unterscheiden, während vorsprachliche Kleinkinder
ebenso wie höhere Tiere darüber hinaus einfache additive und subtraktive Operationen auf diesen Mengen durchführen können.“ (Bei Kormoranen reicht die Menge etwa bis 6)
Bei vielen Einzelereignissen entsteht eine höhre Qualität. Viele Stöße von Gasteilchen auf eine Wand ergeben den Druck, beschrieben durch die Gasgesetze. Viele Tage Wetter ergeben die neue Qualität Klima. Bei den Gasteilchen wird kaum jemand die Teilchenbahnen berechnen, obwohl die Stoßgesetze bekannt sid. Deswegen kann man bei einer neuen Qualität (Gasgesetze, Klima) sichere Aussagen bekommen, selbst wenn die Einzelereignisse (Teilchenstöße, Wetter) unsicher sind.
MfG
Lieber Herr Mueller,
gehen Sie mal zu http://www.wetteronline.de/wetter, suchen Sie sich einen schönen Tag und Uhrzeit aus und gucken sich die Temperaturmeßwerte an Stationen in Deutschland an. Zieht man mal die schon beschriebenen Effekten durch die Höhenlage und synoptische Strukturen wie Fronten ab, beschränkt sich der Einfluß des Lokalklimas an den Stationen auf Unterschiede von weit weniger als 5 Grad.
Wollen Sie mir jetzt erzählen, daß man das Temperaturmittel von Deutschland nun nicht auf zwei Stellen genau angeben kann? Das ist selbst für das aktuelle Temperaturmittel möglich. Monats- und Jahresmittel sind auf wenige Zehntel Grad genau möglich.
Ich kann mir Ihre Unsicherheit nur so erklären, daß Sie die (nicht operativ gemessenen) Einflüsse mikroklimatischer Effekte durch Bebauung, Vegetation, städtische Wärmeinseln etc. und die starken vertikalen Gradienten am Boden für so dominant und unheimlich ansehen, daß Sie ein Flächenmittel berechnet aus Stationsmeßwerten für nicht genau genug zur Berechnung des Temperaturtrends der flächengemittelten bodennahen Temperatur in Deutschland ansehen.
#43
„Ihren Post hätten Sie sich sparen können.“
Nöö Teufel. Ich hatte von Überheblichkeit gesprochen, danke für den prompt gelieferten Nachweis!
Sehr geehrter Herr Mueller,
„Haben Sie es nötig, zu solchen unseriösen Mitteln zu greifen?“ Ich habe eigentlich nur nachgefragt. Bzw. ich habe versucht Ihre Aussage in meinen Worten zusammenzufassen (zum besseren Verständnis).
Sie sagen also, dass man diese Fehler machen kann und zeigen diese auf. Das geht in Ordnung.
Ich hoffe, dass dies auch ein Herr Hofmann und ein Herr Paul so verstanden hat.
mfg
@ Herr Georgiev:
Ihren Post hätten Sie sich sparen können.
Lieber Herr Mueller,
ja, Die Nasa schreibt im wesentlichen dasselbe, was ich Ihnen erklaert habe. Aus diesem Grund bezieht man sich ja auch auf Temperaturanomalien, denn die sind genauer als absolute Temperaruen, weil Anomalien hoehenunempfindlicher sind als die absolute Temperatur. Fuer ersteres ist jedoch entgegen Ihrer Behauptung die Angabe von zwei Stellen vorm Komma kein Problem, bei der absoluten
Temperatur muss man sich wie gesagt aufs Bezugssystem einigen.
#37 #27
„Mussten Sie schon jemals eine Simulation machen (egal welche Fachrichtung)??“
Herr Teufel,
Ihre Frage war zwar Herrn Mueller gerichtet, da ich beruflich viel mit Simulationen zu tun habe, möchte ich stellvertretend zu Ihrer folgender Bemerkung Stellung nehmen:
„Seine Ergebnisse mit anderen Simulationsprogrammen zu verifizieren und ggf. Teile oder die gesamte Simulation noch einmal selber zu programmieren, das habe ich gelernt. Im Gegensatz zu Ihnen gehe ich davon aus, dass dies Gang und Gebe ist.“
Vergleiche mit anderen Simulationen sind nicht relevant, sondern 1. die Ergebniserwartung des Auftragsgebers und Geldgebers. Gang und Gebe ist, dass die Algorithmen so lange angepasst werden, bis die Erwartungen des Geldgebers erfüllt sind. So wie die Ergebnisse von Studien. Die Gläubigkeit, dass dort wo Menschen bewusst oder unbewusst Fehler machen, der Computer aber fehlerfrei ist, ist einfach nur lächerlich. Und 2. Der Vergleich mit der Wirklichkeit. Da bezüglich Klimasimulationen dieser erst in Jahrzehnte bzw. Jahrhunderte möglich ist, sind diese nur für den Papierkorb.
Und noch das Wichtigste: Man kann nur das naturgetreu simulieren, dessen naturwissenschaftliche Grundlagen bekannt sind. Da weder alle natürliche Klimafaktoren, noch dessen Gewichtung, gegenseitige Wechselwirkungen, natürliche Schwankungen e.t.c. exakt bekannt sind, handelt es sich bei langfristige Klimasimulationen um reine Märchen. Schon die Behauptung, dass die Simulation der Wirklichkeit entspricht beinhaltet die unendliche Überheblichkeit, die grenzenlose Komplexität der Natur erfasst und in einem Programm gesteckt zu haben. Also nicht mehr oder weniger die Überheblichkeit der Unwissenden!
@ #37 E. Teufel
Sehr geehrter Herr Teufel,
Sie schreiben: „Sie wollen mir also sagen, dass Ihr Text ein Potpourri aus im Internet zu findenden Aussagen sei?“
Nein, Herr Teufel, das ist eine Unterstellung. Ich lege halt Wert darauf, denjenigen Lesern, welche sich für die betreffende Frage interessieren, die Gelegenheit zu geben, sich selbst zu informieren.
Ich schrieb: „Diese Computergläubigkeit ist erstaunlich weit verbreitet. “ und Sie antworteten: „Und Sie unterstellen das mal pauschal allen Wissenschaftlern? Das finde ich sehr unausgereift“
Zunächst einmal habe ich nicht „pauschal allen Wissenschaftlern“ etwas unterstellt, das ist eine völlig unsachliche Verdrehung Ihrerseits, schon zum zweiten Mal. Haben Sie es nötig, zu solchen unseriösen Mitteln zu greifen?
Im Übrigen darf ich Ihnen versichern, dass es auch Wissenschaftler gibt, die dazu neigen, dem Computer zu sehr zu vertrauen. Bedenken Sie bitte auch, dass der Begriff „Wissenschaftler“ noch ein paar Disziplinen mehr umfasst als nur Programmierer oder Mathematiker. Sie dürfen gerne anderer Meinung sein, dann haben wir halt unterschiedliche Lebenserfahrungen gemacht, soll vorkommen.
Sie fragen: „Mussten Sie schon jemals eine Simulation machen (egal welche Fachrichtung)??“
Ja, auch wenn es vor vielen Jahren war und ich schon sehr lange aus dem aktiven Forschungsbetrieb ausgeschieden bin. Dafür habe ich jedoch reichlich Erfahrung im Umgang mit Menschen gesammelt, darunter auch vielen Wissenschaftlern. Das hilft mir, die Blender und die Elfenbeintürmler von den anderen zu unterscheiden.
Gruss
#38: Fred F. Mueller sagt:
am Donnerstag, 15.08.2013, 10:19
@ #30-33 Nico Baecker
Sehr geehrter Hr. Baecker, vielleicht sollten Sie mal schauen, was man bei der NASA zu Temperaturmessungen meint:
Zum Thema der bodennahen Lufttemperatur (BNL)
Es ist zu bezweifeln, dass es hierfür eine generell akzeptierte Definition gibt…. Selbst an ein und derselben Stelle kann die Temperatur nahe am Boden erhebliche Unterschiede zu der in 5 Fuss Höhe aufweisen und diese wiederum von derjenigen in 10 und 50 Fuss Höhe abweichen…Für BNL-Messungen gibt es keine Norm…bezüglich der Tagesmitteltemperatur gibt es ebenfalls keine universell akzeptierte Norm… wie soll sie gemessen werden, alle 6 Stunden, alle 2 Stunden, maschinell jede Sekunde?….an manchen Tagen können die verschiedenen Messmethoden drastisch unterschiedliche Resultate liefern…die Medien berichten über die Ablesung eines bestimmten Thermometers von einer nahegelegenen Wetterstation. Dieser Wert kann sich von der wahren BNL selbst für diesen Standort erheblich unterscheiden und hat sicherlich nichts mit der wahren regionalen BNL zu tun…Die zitierte BNL hat nur Bedeutung für die Person, welche die Wetterstation exakt zu dem Zeitpunkt besucht, an dem diese zitierte Temperatur gemessen wird, in anderen Worten, sie ist für niemanden von Bedeutung…BNL-Karten können nur mit Computerhilfe erzeugt werden…man startet das Modell mit den paar verfügbaren Messdaten und füllt den Rest mit Vermutungen (auch als Extrapolationen bezeichnet) und lässt das Modell so lange durchlaufen, bis die ursprünglichen Vermutungen keine Rolle mehr spielen, aber nicht zu lange, um zu vermeiden, dass die Ungenauigkeiten des Modells sich bemerkbar machen…
Auszugsweise übersetzt von einem Text des Goddard Space Flight Center, Sciences and Exploration Directorate, Earth Sciences Division, http://data.giss.nasa.gov/gistemp/abs_temp.html
#######################
Fred F. Müller,
Sie zitieren hier so seletkiv und sinnentstellend, dass ich erst mal eine gehörigen Portion essen muss, bevor ich so ko.zen kann, wie ich dies nach dem Lesen Ihres post machcn möchte!
@ #30-33 Nico Baecker
Sehr geehrter Hr. Baecker, vielleicht sollten Sie mal schauen, was man bei der NASA zu Temperaturmessungen meint:
Zum Thema der bodennahen Lufttemperatur (BNL)
Es ist zu bezweifeln, dass es hierfür eine generell akzeptierte Definition gibt…. Selbst an ein und derselben Stelle kann die Temperatur nahe am Boden erhebliche Unterschiede zu der in 5 Fuss Höhe aufweisen und diese wiederum von derjenigen in 10 und 50 Fuss Höhe abweichen…Für BNL-Messungen gibt es keine Norm…bezüglich der Tagesmitteltemperatur gibt es ebenfalls keine universell akzeptierte Norm… wie soll sie gemessen werden, alle 6 Stunden, alle 2 Stunden, maschinell jede Sekunde?….an manchen Tagen können die verschiedenen Messmethoden drastisch unterschiedliche Resultate liefern…die Medien berichten über die Ablesung eines bestimmten Thermometers von einer nahegelegenen Wetterstation. Dieser Wert kann sich von der wahren BNL selbst für diesen Standort erheblich unterscheiden und hat sicherlich nichts mit der wahren regionalen BNL zu tun…Die zitierte BNL hat nur Bedeutung für die Person, welche die Wetterstation exakt zu dem Zeitpunkt besucht, an dem diese zitierte Temperatur gemessen wird, in anderen Worten, sie ist für niemanden von Bedeutung…BNL-Karten können nur mit Computerhilfe erzeugt werden…man startet das Modell mit den paar verfügbaren Messdaten und füllt den Rest mit Vermutungen (auch als Extrapolationen bezeichnet) und lässt das Modell so lange durchlaufen, bis die ursprünglichen Vermutungen keine Rolle mehr spielen, aber nicht zu lange, um zu vermeiden, dass die Ungenauigkeiten des Modells sich bemerkbar machen…
Auszugsweise übersetzt von einem Text des Goddard Space Flight Center, Sciences and Exploration Directorate, Earth Sciences Division, http://data.giss.nasa.gov/gistemp/abs_temp.html
Gruss
Fred F. Mueller
Sehr geehrter Herr Müller,
„Dass es die von mir beschriebenen Fehlermöglichkeiten gibt, lässt sich im Internet leicht überprüfen, beispielsweise hier: http://www.bernd-leitenberger.de/genauigkeit-von-computern.shtml“
Sie wollen mir also sagen, dass Ihr Text ein Potpourri aus im Internet zu findenden Aussagen sei? Mir ist bewusst, was diverse Rechnerarchitekturen von Haus aus mitliefern. Aber genauso wie Sie mit Hilfe des Einmaleins auch größere Multiplikationsaufgaben (z.B 360*12) rechnen können, kann das auch der Computer. Aber genau wie Sie kann er das nicht in einem Rechenschritt. Nur der Computer hat den Vorteil, dass er unterwegs nicht irgendein Zwischenergebnis vergessen kann. Deswegen kann die Aufgabe auch recht kompliziert sein.
„Diese Computergläubigkeit ist erstaunlich weit verbreitet. “
Und Sie unterstellen das mal pauschal allen Wissenschaftlern? Das finde ich sehr unausgereift. Zumal es hier einige Leser gibt, die glauben, dass diese Fehler immer begangen werden.
Mal eine Frage: Mussten Sie schon jemals eine Simulation machen (egal welche Fachrichtung)??
mfg
#32: NicoBaecker sagt:
„Ich kann nachvollziehen, wenn der Laie nicht gleich begreift, daß bei diesem Vergleich verschiedene Dinge in einen Topf geworfen werden.
Klimaszenarien sind aber keine Wettervorhersagen. Also nicht vermischen, was nicht zu mischen ist!
Sie müssen (das gilt ganz allgemein für Ihren Artikel) sehr viel konkreter und spezifischer sein. Mit „gefühltem Verständnis“ kommt man nicht weit.“
Wodurch unterscheiden sich denn Modellen der allgemeinen Zirkulation (GCMs), mit denen die Klimaprojektionen erstellt werden, von numerischen Prognosemodellen (NWPMs)? Die Modellphysik ist im Falle von GCMs entweder aehnlich oder schlechter als die von NWPMs. Die raeumliche Aufloesung ist bei GCMs zumeist schlechter als im Falle von NWPMs.
Der grundlegende Unterschied besteht darin, dass numerische Wetterprognosen im wesentlichen auf Anfangswerte (prediction of 1st kind), und Klimaprojektionen auf Randwerte (prediction of 2nd kind) beruhen (siehe Lorenz, 1975).
Nun kann man heutzutage zwar die Bedingungen am Oberrand der Atmosphaere mit Hilfe von Satelliten brauchbar bestimmen, aber dieses erst seit ein paar Jahren. Die meisten GCMs sind bis in juengster Vergangenheit mit falschen Werten der Solarkonstanten gestartet worden.
Im Gegensatz zum Oberrand der Atmosphaere kann man die Bedingungen an der Erdoberflaeche nur mit einer inakzeptablen Genauigkeit erfassen und dementsprechend in GCMs auch nur mit unzureichender Genauigkeit berechnen. Das haengt zum einen mit der Berechnung der solaren Strahlung sowie der atmosphaerischen Gegenstrahlung ab, z.B. ob eine Wolke im Computermodell existiert oder nicht. Zum anderen koennen die Fluesse von sensibler und latenter Waerme sowieso nicht besser als mit einer relativen Genauigkeit von 15 % bis 25 % bestimmt werden. Sie koennen auch nicht durch Beobachtungen als richtig oder falsch nachgewiesen werden, denn Eddy-Kovarianzmessungen zur Bestimmung der Fluesse von sensibler und latenter Waerme werden nicht an den Stationen des meteorologischen Messnetzes routinemessig durchgefuehrt.
Klimaprojektionen sind nur die Ergebnisse der Loesung partieller Differentialgleichungen. Vom mathematisch-numerischen Standpunkt aus durchaus interessant. Vom physikalischen Standpunkt aus betrachtet, ist es ein Spekulieren mit numerischen Modellen, vielleicht die aufwaendigste und damit die duemmste Art der Spekulation.
Sehr geehrter Herr Müller,
#30:Fred F.Müller
„Sehr geehrter Herr Burowski,
Wie bereits in anderem Zusammenhang ausgeführt, sollte der Artikel darauf hinweisen, welche Fehlermöglichkeiten in Computerberechnungen versteckt lauern können. Wer diese nicht kennt oder nicht ausreichend beachtet, kann Probleme mit seinen Rechenergebnissen bekommen.“
Dann sollte man aber auch die Finger vom Programmieren lassen, zumindest, wenn man damit Geld verdienen will. All das, was Sie hier als Probleme und Fehlermöglichkeiten ansprechen, sollte ein Informatiker nach erfolgreich abgeschlossenem Studium wissen und er sollte auch die Werkzeuge kennen, wie man diese Probleme löst.
######################################
„Natürlich gibt es zu allen Problemen Ausnahmen und Sonderlösungen, aber die entsprechenden Instrumente muss man ebenso wie die zu lösenden Probleme zunächst einmal kennen, um sie richtig einsetzen zu können.“
Nein, die Steigerung der Zahlengenauigkeit durch Rechnen mit Brüchen ist allgemein bekannt; sicher gibt’s da auch schon irgendwo eine Bibliothek für die gängigen Sprachen. Auch für fast alles andere gibt es vorgefertigte Lösungen, kein Mensch schreibt heute mehr Sortieralgorithmen.
#################################
Mit Ihren Ausführungen bin ich jedoch vor allem aus folgendem Grund nicht einverstanden. Sie schreiben: „Jede reelle Zahl lässt sich in der Form eines Bruches aus ganzer Zahlen a und b mit a/b darstellen, diese Darstellung ist immer exakt“
Nach meinem Verständnis der Mathematik trifft dies nur auf die sogenannten rationalen Zahlen zu, die lediglich eine Teilmenge der reellen Zahlen bilden. Anders verhält es sich bei den irrationalen Zahlen, die auch zu den reellen Zahlen gehören.“
Da haben Sie völlig recht, exakt wäre der Begriff rationale Zahlen. Irrationale Zahlen sind mathematisch sicher hochinteressnt, nur rechnen kann man damit äußerst schwer, da sie ja unendlich lang sind. In der Realität formen wir also immer eine irrationale Zahl in eine rationale Zahl mit der gewünschten Genauigkeit um.
#################################
„Dazu zählen auch für Wissenschaftler unverzichtbare Zahl wie die Kreiszahl Pi, die Eulersche Zahl e sowie viele Wurzeln. Für sie alle gilt: Eine reelle Zahl heißt irrational, wenn sie nicht als Bruch zweier ganzer Zahlen dargestellt werden kann.“
Was machen wir jetzt mit Pi, e und Wurzel(2)?
Wie ich schon geschrieben habe, wir rechnen gurndsätzlich mit rationalen Zahlen. Nun darf man aber Pi nicht mit 22/7 darstellen, den dieser Bruch ist periodisch. Sondern wir stellen die Zahl Pi mit der gewünschten Genauigkeit als Bruch dar.
31415926535/10000000000 bei zehnsteliger Genauigkeit und 3141592653589793/1000000000000000 bei 15-stelliger Genuigkeit; analoges gilt für alle andern Konstanten mit irrationalen Zahlen.
Funktionen, deren Funktionswerte zu irrationale Ergebnissen führen können, dürfen nicht berechnet werden, sondern müssen über LookUp-Tabellen, die die Ergebnisse in der entsprechenden Genauigkeit als Bruch liefern, zur Verfügung gestellt werden.
#######################################
„Das Verständnisproblem bezüglich des Anstiegs der Funktion Sin(x) ist leicht aufzuklären. Sie müssen unterscheiden zwischen der Steigung eines Graphen in einem bestimmten Punkt (das wäre dann die Steigung der Kurventangente in diesem Punkt, und die findet man durch natürlich mithilfe der Ableitung) und der Steigung von Geraden zwischen zwei willkürlich gewählten Punkten auf einer Funktion.“
Das habe ich erstmal verstanden, finde diesen Erklärungsansatz aber recht eigenwillig. Zudem, legen Sie den Anfangspunkt Ihrer Graden in den Punkt x = 0 und tasten dann Punkt für Punkt die Sinuskurve ab und berechnen jeweils die Steigung der Geraden. Als Ergebnis erhalten Sie dann wieder eine Sinusfunktion, die mit einer Exponentialfunktion gedämpft wird und irgendwo bei x gegen unendlich den Wert 0 liefert.
#30: Hallo Herr Fred F. Mueller, ich will Sie nur etwas trösten,
da sich bei EIKE traditionell immer eine rel. fleißige Gruppe zu Wort meldet, die Sie gar nicht verstehen möchte und ihnen Aussagen unterstellt, die Sie gar nicht getroffen haben um widersprechen zu können.
Wer z.B. den Begriff „reele Zahl“ nicht kennt und trotzdem widerspricht, zeigt deutlich, dass Erkenntnis unerwünscht ist, oder gar verhindert werden soll.
mfG
Lieber Herr Mueller , #30
Die Diskussion über den Trend einer Sinusfunktion ist reichlich sophistisch. Wenn man den Verlauf einer Temperaturzeitreihe verstehen will, so läuft dies darauf hinaus, die Ursachen zu verstehen.
Lieber Herr Mueller, #25
„Prognosezuverlässigkeit auf 80-90 % selbst für kurze Zeiträume von lediglich 2-3 Tagen. Wenn man das verstanden hat, kann man sich über Menschen, die behaupten, sie könnten atmosphärische Entwicklungen für 50 bis 100 Jahre vorausberechnen, nur wundern. „
Ich kann nachvollziehen, wenn der Laie nicht gleich begreift, daß bei diesem Vergleich verschiedene Dinge in einen Topf geworfen werden.
Klimaszenarien sind aber keine Wettervorhersagen. Also nicht vermischen, was nicht zu mischen ist!
Sie müssen (das gilt ganz allgemein für Ihren Artikel) sehr viel konkreter und spezifischer sein. Mit „gefühltem Verständnis“ kommt man nicht weit.
Lieber Herr Mueller, #25
„Ihr Beispiel passt nicht. Landschaftstopographien sind in erster Näherung statisch, Temperaturfelder dagegen hoch dynamisch.“
Das Beispiel paßt grundsätzlich. Bei der Temperatur kommt nur noch hinzu, daß die Ausgangsdaten für das räumlich Feld bereits zeitlich gemittelte Meßdaten sind. Das ändert am Verfahren der räumlichen Mittelung nichts. Dafür kann genauso verfahren werden wie bei der Landschaftsvermessung.
Die zeitliche Mittelwertbildung verläuft nach einem festgelegten Verfahren. Das Monatsmittel ist das gleichgewichte Mittel der Tagesmittel. Für die Berechnung des Tagesmittels gab/gibt dafür zwar unterschiedliche Verfahren, die zu abweichenden Tagesmittelwerten führen, die anhand empirischer Korrekturformeln jedoch leicht ineinander umgerechnet werden können. Natürlich ist dies nicht ohne Fehler möglich, bei der Verarbeitung der Meßwerte muß natürlich wie allgemein in den exakten Naturwissenschaften üblich die Fehlerfortpflanzung mitgeführt werden.
„Die Wetterhütte als solche liefert nur Daten zu einem einzigen Punkt eines in Wirklichkeit räumlich wie zeitlich sehr dynamischen Temperaturfelds. Mit dem einen Punkt zu einem willkürlich festgelegten Zeitpunkt ist das Feld m.E. eben nicht ausreichend beschrieben“
Die Wetterhütte muß selbstredend einen solchen Standort haben, der repräsentativ für die Temperatur der Luftmasse der Umgebung ist. Haben Sie eine Vorstellung davon, wie groß der horizontale Korrelationsradius der Temperaturmessung einer synoptisch genutzten Wetterhütte sein muß, damit diese synoptisch nutzbar ist? Reden wir da von Metern oder zig Kilometer, hm?
Wenn man nun räumliche gemittelte Temperatur berechnet, so nimmt man diese Stationswerte und interpoliert sie mit üblichen Verfahren über die Fläche.
„egal ob Sie dafür gro?räumig einen rechnerischen „Mittelwert“ angeben können. Machen Sie doch einfach mal den Test und fahren Sie an einem schönen Sommertag abends in kurzer Kleidung mit dem Fahrrad durch eine hügelige Landschaft. Ihr Körper wird Ihnen schnell beweisen, wie heterogen das Temperaturfeld in gleichbleibender Höhe über dem Boden ist.“
Ja logisch ändert sich die Temperatur 2 m über dem Boden mit der Topographie. Das sehen Sie ja leicht in den Klimadaten von Stationen. Aber dieser Effekt ist verstanden und läßt sich korrigieren.
Etwas anderes sind die dem überlagerten schon angesprochenen mikroklimatischen Verhältnisse, die dazu führen, daß die Temperatur der Luftmasse lokale Änderungen erfährt. Und ich glaube, Sie meinen vor allem diese Effekte, die lokal sehr signifikant sein können (Waldklima, Asphaltflächen, Stadtklima, etc.), dabei spielen neben der Topographie eben auch andere Landschaftsmerkmale eine Rolle.
„“Die Angabe einer auch nur auf zwei Stellen genauen mittleren Tagestemperatur erfordert einen erstaunlichen messtechnischen und auch rechnerischen Aufwand.“ Auch da haben Sie etwas missverstanden, so etwas habe ich nicht gefordert. Eine zweistellige Angabe ist z.B. 22 °C, das ist nicht das Gleiche wie eine Angabe mit einer Genauigkeit von zwei Stellen nach dem Komma.“
Ok, da habe ich Sie in der Tat mißverstanden. Ich kann Ihre nun verstandene Meinung dennoch nicht teilen.
Wenn Sie auf eine Wetterkarte gucken, so sehen Sie, wie die aktuellen Temperaturen in einer Region an den synoptischen Stationen verteilt sind. Die Unterschiede sind wie gesagt im wesentlichen durch drei Dinge verursacht:
a) höhenbedingter Unterschied, ca. 6.5 Grad/km
b) lokal bedingte Unterschiede (mikroklimatische Besonderheiten des Standortes)
c) synoptisch bedingte Unterschiede (verschiedene Luftmassen, durch Front getrennt)
für die Wetteranalyse ist es wichtig, synoptisch repräsentative Temperaturen zu messen, also den Einfluß von c) zu extrahieren. Denn das Ziel ist ja, die Temperatur der Luftmassen zu bestimmen, denn diese sind für die Wetteranalyse bestimmend. Den Einfluß durch b) möchte man also minimieren und deshalb sucht man sich Stationsstandorte mit großen Korrelationsradien raus. Der Einfluß von a) ist leicht anhand der obigen Überschlagsformel bzw. wetterlagenabhängigen Regressionsformeln zu korrigieren und die Temperatur so – wenn nötig – auf ein einheitliches Referenzniveau zu reduzieren. Dies macht bei unserer Topographie in Deutschland aber offensichtlich nur wenige Zehntel Grad Korrektur aus, während die synoptisch notwendige Genauigkeit bei 1-3 Grad liegt.
Unabhängig davon lassen sich natürlich auf klimatischer Zeitskala betrachtet die Besonderheiten des lokalen Klimas am Standort anhand eines Vergleiches mit der Umgebung bzw. durch Feldstudien bestimmen.
Die klimatologischen Mittelwerte (monatlich, jährlich, Normalwerte, etc.) eines Standortes ergeben sich aus der Arithmetik der Meßwerte.
Die hier interessante Frage ist nun, wie sich ein räumlicher Mittelwert über die Fläche ermittelt anhand der punktweisen Verteilung synoptischer Stationen (also an besonderen Plätzen mit großem Korrelationsradius) von dem Mittel unterscheiden würde, welches aus einem unendlich dichten Meßnetz resultieren würde. Verstehe ich Sie da richtig?
Synoptische Stationen liegen z.B. nicht in zusammenhängenden Waldgebieten. Wäre das räumliche Mittel der 2m-Temperatur eines Waldgebietes signifikant anderes als das der nächstgelegenen synoptischen Station? Ja, ganz sicher! Die 2m-Temperatur an dieser Station ist sicher NICHT repräsentativ für das Waldgebiet. Das räumliche Flächenmittel aus Stationsdaten ist also sicherlich verschieden von einem Mittel, welches sich für ein unendlich dichtes Netz der 2m-Temperaturen ergäbe, denn es gibt ja noch genügend synoptisch nicht repräsentative Orte mit lokalklimatischen Besonderheiten in der Landschaft, deren Meßwerte signifikant von den aus dem synoptischen Meßnetz extrapolierten Werten abweichen.
Die einzig interessante Frage ist nun, ob dieser Unterschied relevant ist?
Wenn man nur an Trends der Temperatur interessiert ist, so nicht. Man muß nur kontrollieren, daß die einmal gegebene Repräsentativität des Stationsnetzes sich nicht signifikant verändert. Wenn man an der absoluten Temperatur interessiert ist, so ist dies (neben vielen anderen) ein Problem, wie man ja an den unterschiedlichen Angaben der absoluten globalen Flächenmittel sehen kann. Nur um das gleich klarzustellen: wir reden hier nicht um Abweichungen um zwei Stellen vorm Komma im Monats- bzw. Jahresmittel, sondern nur um mehrere Zehntel Grad. Sie können dies ja mal selber überschlagen, das Monatsflächenmittel inkl. Berücksichtigung des Mikroklimas genauer als 10 K zu bestimmen, ist keine Kunst.
@#24 Holger Burowski
Sehr geehrter Herr Burowski,
Wie bereits in anderem Zusammenhang ausgeführt, sollte der Artikel darauf hinweisen, welche Fehlermöglichkeiten in Computerberechnungen versteckt lauern können. Wer diese nicht kennt oder nicht ausreichend beachtet, kann Probleme mit seinen Rechenergebnissen bekommen. Darauf wollte ich hinweisen. Natürlich gibt es zu allen Problemen Ausnahmen und Sonderlösungen, aber die entsprechenden Instrumente muss man ebenso wie die zu lösenden Probleme zunächst einmal kennen, um sie richtig einsetzen zu können.
Mit Ihren Ausführungen bin ich jedoch vor allem aus folgendem Grund nicht einverstanden. Sie schreiben: „Jede reelle Zahl lässt sich in der Form eines Bruches aus ganzer Zahlen a und b mit a/b darstellen, diese Darstellung ist immer exakt“
Nach meinem Verständnis der Mathematik trifft dies nur auf die sogenannten rationalen Zahlen zu, die lediglich eine Teilmenge der reellen Zahlen bilden. Anders verhält es sich bei den irrationalen Zahlen, die auch zu den reellen Zahlen gehören. Dazu zählen auch für Wissenschaftler unverzichtbare Zahl wie die Kreiszahl Pi, die Eulersche Zahl e sowie viele Wurzeln. Für sie alle gilt: Eine reelle Zahl heißt irrational, wenn sie nicht als Bruch zweier ganzer Zahlen dargestellt werden kann.
Das Verständnisproblem bezüglich des Anstiegs der Funktion Sin(x) ist leicht aufzuklären. Sie müssen unterscheiden zwischen der Steigung eines Graphen in einem bestimmten Punkt (das wäre dann die Steigung der Kurventangente in diesem Punkt, und die findet man durch natürlich mithilfe der Ableitung) und der Steigung von Geraden zwischen zwei willkürlich gewählten Punkten auf einer Funktion. Die Bilder zeigen eigentlich eindeutig, was gemeint ist. Im Text habe ich auch darauf hingewiesen, dass die Aussage „Steigung = Null“ in diesem Zusammenhang nur bei entsprechend langzeitiger Betrachtung gilt, d.h. bei Betrachtung über eine ausreichend gro?e Zahl von Perioden. Für den Sonderfall ganzer Zahlen n gilt stets: Sin(0) = Sin (2n x Pi), d.h. die Gerade hat die Steigung Null. Für reelle Zahlen r >> 1 wird die Abweichung der Steigung der Geraden von Null umso kleiner, je grösser r wird. Selbst bei einer Billion Perioden ist der Wert des Sinus nie grösser als 1 oder kleiner als -1. Je grösser r, desto mehr konvergiert demnach die Steigung eines entsprechend langen Geradenstücks zwischen zwei Punkten auf der Funktion gegen Null.
Mit freundlichen Grü?en
Fred F. Mueller
Die Mathematik kann zwar berechnen, aber die Mathematik kann nicht die Zukunft bestimmen!
Die Mathematik hat weder die Kernkraft, noch das Schiefer-gas/oel voraus berechnen können. Und bei der Vorhersage der zukünftigen Klimaentwicklung ist die Vorausberechnung erst recht unmöglich. Man kann grobe Abschätzung abgeben, die dann entweder sehr kurzfristig oder auch langfristig als richtig oder falsch herausstellen werden. Um eine grobe Abschätzung über die zukünftige Klimaentwicklung zu geben, hilft es jedoch nicht sich mit dem CO2 zu beschäftigen! Der große Einflussfaktor beim Thema Klima ist und bleibt die SONNE! Die Sonne und die Sonnensystem Physik sind und bleiben zu 99% der Ausgangspunkt für unser Klima!
Wer sich mit dem CO2 in einer virtuellen Computerwelt per Mathematik dem Erdklima nähern will, der ist und bleibt in seiner virtuellen Welt gefangen. Diese mathematische Computerwelt hat weder die Sonne noch die Physik des Sonnensystems, noch die Wechselwirkungen der verschiedenen natürlichen Einflussfaktoren berücksichtig, wenn es um die kurzfristige und langfristige Entwicklung des Klima geht!
#27
Sehr geehrter Herr Mueller,
mein halbstarker Sohn ist überzeugt, die Fahreigenschaften eines Ferraris genau zu kennen, da er tausend mal (virtuell) damit gefahren ist. Er ist nicht der einzige, der sich nicht um die Unterschiede zwischen reell und virtuell Gedanken macht. Die massive Überschätzung der bunten Bilder und überhebliche Unterschätzung der Vielfalt und Komplexität der Wirklichkeit, basierend auf fehlendes Interesse und Wissen, ist in der Tat ein Massenphänomen der heutigen Internetgesellschaft. Auch hier bei EIKE.
#24
Burowski und weitere Computergläubige:
„…in ein Flugzeug zu steigen, welches per Computer konstruiert wurde oder welches per Tafelwerk, Rechenschieber…“
Die Konstruktion ohne PC wäre nicht unsicherer, nur teurer da es länger dauert, daher macht man es heute mit Computer. Der richtige Vergleich wäre: Würden Sie in ein Flugzeug steigen, dessen Pilot das erste mal im Leben fliegt und seine Ausbildung ausschließlich am Simulator gemacht hat? Und dem Wert von Klimasimulationen gerechter zu werden, müsste man hinzufügen, dass der Simulatorerfinder die Flugzeugkonstruktion nicht kennt, sondern anhand von Bilder eines Flugzeugs auf seine Eigenschaften spekuliert (Bei einer tiefgründige Analyse müsste man erkennen, dass nicht alle Klimafaktoren und dessen Gewichtung exakt kennt, daher enthalten Klimasimulationen einen reichlich Spekulationsanteil. Nein, Sie würden es nicht tun, wenn es um die eigene Haut geht, schaltet sich das Gehirn zu und entscheidet pragmatisch. Aber schöne bunte Klimasimulationen mit schaurigen Ausgang sind soooo schön….
@ #23 E. Teufel
Sehr geehrter Herr Teufel ,
Sie schreiben: „Ich kann Ihnen ganz einfach zeigen, dass auch Mantissen beliebig lang sein können. Siehe z.B. „The GNU Multiple Precision Arithmetic Library“ oder in java unter java.math.BigDecimal.“
Zunächst einmal ist anzumerken, dass ich mich bei meinem Artikel auf einfache, leicht zu erklärende Beispiele beschränkt habe, die vom Grundsatz her auch nach wie vor Gültigkeit haben. Zu vielen der von mir angeführten Punkte gibt es natürlich auch intelligente Sonderlösungen. Zu den Tugenden von Mathematikern gehört ja gerade, dass sie solche Herausforderungen gerne aufgreifen. Allerdings hat man bei Sonderlösungen zwei Probleme. Zum einen stehen einem nicht immer die nötigen Ressourcen an Zeit, Geld und Hardware zur Verfügung. Eine weitere Schwierigkeit ist, dass die Portierung von Sonderlösungen nicht immer möglich ist, und Forschung findet heute oft in Teams statt, die manchmal über die halbe Erde verteilt sind.
Dass es die von mir beschriebenen Fehlermöglichkeiten gibt, lässt sich im Internet leicht überprüfen, beispielsweise hier: http://www.bernd-leitenberger.de/genauigkeit-von-computern.shtml
Das eigentliche Problem ist jedoch nicht der Computer oder die Mathematik, sondern der Mensch. Allzu viele Menschen – auch solche mit naturwissenschaftlicher Ausbildung – kennen nämlich nicht einmal die vergleichsweise einfachen Zusammenhänge, die ich im Artikel dargelegt habe. Oder, fast noch schlimmer, sie interessieren sich nicht dafür. Diese Computergläubigkeit ist erstaunlich weit verbreitet.
Ansonsten darf ich Ihnen versichern, dass ich mir die Mühe mache, solche Artikel von Wissenschaftlern der entsprechenden Disziplinen gegenlesen zu lassen. Im vorliegenden Fall waren es ein Diplom-Mathematiker und ein Diplom-Meteorologe. Ich glaube also nicht, dass ich mit den von mir vorgestellten Beispielen allzu weit von der Realität entfernt liege.
Mit freundlichen Grü?en
Fred F. Mueller
Lieber Herr Fred F. Mueller, #22
„Sie beziehen sich vermutlich auf Alarmmeldungen des Potsdam Instituts für Klimafolgenforschung (PIK), die auch auf Wikipedia verbreitet werden. Es gibt jedoch auch seriöse Quellen, und die besagen etwas ganz anderes: „Eine neue Studie, erstellt mit den GRACE-Daten (Gravity Recovery And Climate Experiment, also Satellitendaten) zeigt, dass der Meeresspiegel während der letzten 9 Jahre mit einer Rate von nur 1,7 mm pro Jahr gestiegen ist. “
Die 3.2 mm/Jahr sind kein Forschungsergebnis des PIK, sondern der Jason Gruppe. Ob Sie dies für alarmistisch sehen, ist wissenschaftlich völlig irrelevant. Das müssen Sie nur mit Ihrer eigenen Psyche ausmachen.
Wenn Sie die GRACE studie gelesen hätten, so wüßten Sie, daß die dort genannten 1,7 mm/Jahr nur ein Teil des Gesamtrends von 3,2 mm/Jahr darstellt. In dem GRACE paper ging es nicht um den Gesamttrend.
Vergleichen mit den Trend der vergangenen 100 JAhren (Church et al) ist der gegenwärtige Trend von über 3mm/Jahr signifikant angestiegen. In der wissenschaftlichen Literatur finden Sie auch die Ursachen dafür.
@ #20 Nico Baecker
Lieber Herr Baecker,
Sie schreiben im Zusammenhang mit der Ermittlung von komplexen, zeitlich veränderlichen Temperaturfeldern: „So ist es. Aber dieses Problem hat man auch bei noch krauseren Größen der Landschaft. Nehmen wir mal die Topographie selber. Sind wir uns einig, daß man jeder noch so hügeligen Landschaft eine mittlere Höhe mit einer definierten Genauigkeit gegenüber dem Referenzniveau angeben kann? Das wäre die Mittelung über eine 2-D Fläche und entspricht mathematisch dasselbe wie die Temperaturmittelung der 2m -Temperatur.“
Ihr Beispiel passt nicht. Landschaftstopographien sind in erster Näherung statisch, Temperaturfelder dagegen hoch dynamisch.
Sie schreiben im Zusammenhang mit der Ermittlung von Temperaturfeldern: „Das kann man machen. Ist natürlich im Haus mit den variierenden mikroklimatischen Bedingungen (Wände, Heizflächen etc.) viel schwieriger als die Temperatur der Luftmasse draußen mit einer gut gelüfteten Wetterhütte zu bestimmen. Im Haus muß man erst mal die mikroklimatischen Verhältnisse vermessen. Bei der Wetterhütte sorgt schon der Austausch der Luft aufgrund des Durchzugs der Luft, für eine räumliche Mittelung.“
Da haben Sie das Beispiel komplett missverstanden. Die Wetterhütte als solche liefert nur Daten zu einem einzigen Punkt eines in Wirklichkeit räumlich wie zeitlich sehr dynamischen Temperaturfelds. Mit dem einen Punkt zu einem willkürlich festgelegten Zeitpunkt ist das Feld m.E. eben nicht ausreichend beschrieben, egal ob Sie dafür gro?räumig einen rechnerischen „Mittelwert“ angeben können. Machen Sie doch einfach mal den Test und fahren Sie an einem schönen Sommertag abends in kurzer Kleidung mit dem Fahrrad durch eine hügelige Landschaft. Ihr Körper wird Ihnen schnell beweisen, wie heterogen das Temperaturfeld in gleichbleibender Höhe über dem Boden ist.
Im Artikel steht: „Die Angabe einer auch nur auf zwei Stellen genauen mittleren Tagestemperatur erfordert einen erstaunlichen messtechnischen und auch rechnerischen Aufwand.“, worauf Sie antworteten: „Eine Genauigkeit von 0,01 °C ist operativ-meteorologisch bzw. klimatologisch nicht möglich und auch nicht nötig.“
Auch da haben Sie etwas missverstanden, so etwas habe ich nicht gefordert. Eine zweistellige Angabe ist z.B. 22 °C, das ist nicht das Gleiche wie eine Angabe mit einer Genauigkeit von zwei Stellen nach dem Komma.
Was die übrigen von Ihnen angeführten Punkte angeht: Ich will die Meteorologie nicht schlecht machen, sondern bei den Lesern Verständnis für ihre Methodik, aber auch für die damit verknüpften Problematiken wecken. Letztere sind einer der Gründe für die Begrenzungen der Prognosezuverlässigkeit auf 80-90 % selbst für kurze Zeiträume von lediglich 2-3 Tagen. Wenn man das verstanden hat, kann man sich über Menschen, die behaupten, sie könnten atmosphärische Entwicklungen für 50 bis 100 Jahre vorausberechnen, nur wundern.
Mit freundlichen Grü?en
Fred F. Mueller
Sehr geehrter Herr Müller,
das Argument, Computer würden ungenau rechnen, wird immer wieder gerne ins Feld geführt, wenn man etwas widerlegen will, aber keine so rechten Argumente findet, warum inhaltlich.
Wenn Sie vor der Wahl stünden, in ein Flugzeug zu steigen, welches per Computer konstruiert wurde oder welches per Tafelwerk, Rechenschieber und Zeichenbrett; in welches würden Sie steigen?
Es gibt zwei Arten der Zahlendarstellung von reellen Zahlen im Computer, Festkomma und Dezimalschreibweise oder Gleitkomma mit Exponenten und binäre Darstellung. Für zweitere gibt es eine Norm, die IEEE 754. Für die „Ungenauigkeit“ muss man desweiteren wissen, dass diese nicht zufällig ist, sondern Gesetzmäßigkeiten unterliegt, die in der Programmierung berücksichtigt werden kann und dass die „Ungenauigkeit“ auch nicht gleichverteilt ist, sondern dass es Zahlenbereiche gibt, in denen die „Ungenauigkeit“ größer ist und Zahlenbereiche in denen sie kleiner ist.
Ein Lösungsansatz die Genauigkeit fast unbegrenzt zu steigern, besteht im Folgenden:
Jede reelle Zahl lässt sich in der Form eines Bruches aus ganzer Zahlen a und b mit a/b darstellen, diese Darstellung ist immer exakt. Im Computer wird eine reelle Zahl also durch zwei ganze Zahlen dargestellt. Die Addition, Subtraktion und Multiplikation zweier ganzer Zahlen liefert immer ein exaktes Ergebnis; das Gleichnamigmachen für die Addition und Subtraktion ist nichts weiter als eine Multiplikation. Addition und Subtraktion sind binäre Operationen; die Multiplikation wird auf eine mehrfache Addition zurückgeführt und die Division wiederum führt man auf die Multiplikation mit dem Kehrwert zurück. Damit ist nachgewiesen, dass die vier Grundrechenarten bei dieser Zahlendarstellung immer exakte Ergebnisse liefern. Da alle höheren Rechenoperationen auf diese Operationen zurückgeführt werden, sind auch diese exakt.
Nun werden Sie sicher einwenden, aber wie bekommt man die Zahlen mit der benötigten Genauigkeit in das Programm? Indem man sie normiert, auf die benötigte/gewünschte Genauigkeit. Für eine vierstellige Genauigkeit muss der Wert b der einzulesenden Zahl 1000 sein und a entsprechend normiert werden. Die Genauigkeit ist somit nur noch von der Messgenauigkeit abhängig.
Ja, es gibt mathematische Funktionen, die durch Reihenentwicklung berechnet werden, die man irgendwo abbrechen muss. Die werden bei der Zahlendarstellung a/b an der Stelle abgebrochen, an der sie für a keine Veränderung mehr bei der benötigten Genauigkeit, dargestellt durch b, als Ergebnis liefern. Auch hier gibt es Vereinfachungen, das sind LookUp-Tabellen, in denen das Ergebnis für die entsprechende Funktion mit der Genauigkeit b für den Wert a bereits vorgegeben ist; vergleichbar mit einem Tafelwerk.
Die pauschale Aussage, Computer würden ungenau rechnen ist falsch. Wie genau ein Algorithmus zu einem Modell ist, kann erst abgeschätzt werden, wenn bekannt ist, wie(!) der Algorithmus programmiert ist.
prinzipieller Anstieg SIN(x) = 0; dieser Aussage kann ich nicht folgen, der Anstieg einer Funktion f(x) ist deren 1. Ableitung. Wenn das eine Funktion ist, dann ist das so, dann ändert sich halt der Anstieg in Abhängigkeit von x. Was es mathematisch für einen Sinn machen soll, den Durchschnitt alle Anstiegswerte zu berechnen, erschließt sich mir nicht. Nach Ihrer Lesart ist dann der prinzipelle Anstieg einer quadratischen Funktion auch 0?
Sehr geehrter Herr Müller ,
Ihr Zitat:
„Da die Länge der Mantisse begrenzt ist, sind den Ansprüchen an die Genauigkeit deutlich engere Grenzen gesetzt, als es sich der Computerlaie normalerweise vorstellt. Zudem gelten hier die Gesetze der Fehlerfortpflanzung. Vor allem bei iterativen Schleifen kommt man dann recht bald an Grenzen.“
ist leider falsch.
1. Ich kann Ihnen ganz einfach zeigen, dass auch Mantissen beliebig lang sein können. Siehe z.B. „The GNU Multiple Precision Arithmetic Library“
oder in java unter java.math.BigDecimal.
Natürlich kann dass die FPU nicht von Haus aus. Aber schon als kleiner Programmierer bin ich über das Problem gestoßen und habe mir meine eignen Routinen dazu geschrieben. Und ich war bei weitem nicht der einzige.
Heute gibt es in (ich denke) allen Programmiersprachen bereits fertige Klassen dafür. Und die werden auch genutzt. Ferner speichern sich heutige Computeralgebrasysteme die Zahlen auch als Bruch und lassen u.U. die Wurzel stehen um damit weiter rechnen zu können (siehe z.B. Maxima). Sie unterstellen hiermit Wissenschaftlern, dass Sie die vorhandenen Möglichkeiten nicht nutzen, oder Sie kennen die Möglichkeiten selber nicht.
Seine Ergebnisse mit andeen Simulationsprogrammen zu verifizieren und ggf. Teile oder die gesamte Simulation noch einmal selber zu programmieren, das habe ich gelernt. Im Gegensatz zu Ihnen gehe ich davon aus, dass dies Gang und Gebe ist.
Nur weil man bei Rot über die Ampel fahren kann, muss man es ja nicht machen.
2. An was für iterative Schleifen haben Sie denn so gedacht? Bei mir würde sich der Fehler keinesfalls fortpflanzen. Können Sie das einmal präzisieren? Nehme ich z.B. Ihr Bild 4, dann sehe ich keine Fehlerfortpflanzung. Die Verfahren um DGLs oder DGL-Systeme zu lösen kennen auch keine Fehlerfortpflanzung. Wenn meine Rechnung konvergiert, ist der von Ihnen benannte Genauigkeitsfehler kein Problem und pflanzt sich schon gar nicht fort.
@ #6 Hans Jung
Sehr geehrter Hr. Jung,
Sie schreiben zum Meeresspiegelanstieg (120 m in den letzten ca. 20.000 Jahren): „Von wegen. Das meiste passierte in den ersten Jahrtausenden nach Ende der Eiszeit“
Die von mir gezeigte Grafik dokumentiert genau dies.
Dann schrieben Sie: „In den letzten 7000 Jahren stieg er dann nur noch um 0,4mm/Jahr“
Solchen Angaben sollte man mit großem Misstrauen begegnen. Linear ist er wohl kaum verlaufen, so etwas gibt es in der Natur nur sehr selten. Ich gehe eher davon aus, dass es zu Schwankungen in beide Richtungen kam, schließlich gab es in diesem Zeitraum auch Klima-Schwankungen mit wärmeren und kälteren Perioden sowie Vorstößen und Rückzügen der Gletscher.
Was die letzten ca. 150 Jahre angeht, so entsprechen diese dem Zeitraum nach dem Ende der Kleinen Eiszeit und einem damit einhergehenden Rückgang der Gletscher. Da wäre es verwunderlich, wenn es nicht zu einem entsprechenden geringfügigen Ansteigen des Meeresspiegels gekommen wäre. Warum man daraus Alarmmeldungen ableitet, ist für mich unverständlich.
Sie schreiben letztlich: „In den letzten 20 Jahren stieg er 8-mal so schnell: 3,2mm/Jahr“.
Sie beziehen sich vermutlich auf Alarmmeldungen des Potsdam Instituts für Klimafolgenforschung (PIK), die auch auf Wikipedia verbreitet werden. Es gibt jedoch auch seriöse Quellen, und die besagen etwas ganz anderes: „Eine neue Studie, erstellt mit den GRACE-Daten (Gravity Recovery And Climate Experiment, also Satellitendaten) zeigt, dass der Meeresspiegel während der letzten 9 Jahre mit einer Rate von nur 1,7 mm pro Jahr gestiegen ist. Das ergibt ein Äquivalent von 6,7 Inches (fast 17 cm) pro Jahrhundert. Dies passt gut zu Messungen an Pegeln. Die Studie bestätigt das Sea Level Budget von NOAA 2012 (National Oceanic and Atmospheric Administration der USA, noaa.gov), dem zufolge der Meeresspiegel nur um 1,1 bis 1,3 mm pro Jahr während der vergangenen 7 Jahre von 2005 bis 2012 gestiegen ist.“ Nachzulesen hier bei EIKE unter http://preview.tinyurl.com/l3bnvfx.
Letztlich ist das Thema Meeresspiegel-Anstieg sehr komplex. Einen sehr schönen Beitrag hierzu hat Willis Eschenbach verfasst: http://preview.tinyurl.com/jwh9vbh. Ich empfehle ihn zur Lektüre. Daraus geht auch hervor, dass ein Messzeitraum von lediglich 20 Jahren bei Pegeln wegen der natürlichen Vorgänge in den Ozeanen keine ausreichend engen 95%-Vertrauensbereiche ermöglicht.
Bedenken Sie bitte auch: In den letzten mehr als 15 Jahren ist der Temperaturanstieg weltweit zum Stillstand gekommen. Es wäre doch wenig logisch, wenn der Meeresspiegel trotzdem in genau diesem Zeitraum mit nahezu doppelter Geschwindigkeit wie vorher ansteigen würde.
Mit freundlichen Grü?en
Fred F. Mueller
#19: Jochen Bäumer
Vergessen Sie mal schnell den Wert von 3,2 mm/Jahr. Dieser Wert ist darauf zurueckzufuehren, dass ab 1993 Satellitendaten verwendet wurden. Nicht alles, was Satelliten liefern, ist wirklich brauchbar.
Wenn Sie z.B. das Kap. 5 des 4. Berichts der WG1 zum IPCC von 2007 gelesen haetten, dann haetten Sie z.B. feststellen koennen, dass grosse Unsicherheiten exisitieren, die in diesem Kapitel auch nicht unterdrueckt werden. Das geht bereits daraus hervor, dass im Falle des Meerespiegelanstiegs infolge eines Schmelzens des antarktischen Eises ein Beitrag von
0,14 +/- 0,41 mm/Jahr
fuer die Zeitspanne von 1961 bis 2003 genannt wird. Das bedeutet, dass die Standardabweichung das Dreifache des Mittelwerts betraegt. Im Falle des Groenlandeises lautet der Betrag
0,05 +/- 0,12 mm/Jahr
Auch hier ist die Standardabweichung mehr als doppelt so gross wie der Mittelwert.
Bildet man die Differenz aus Beobachtung und berechneten Wert fuer diese Zeitspanne,so ergibt sich nach diesem Bericht:
Difference (Observed –Sum) 0.7 ± 0.7 mm/year.
Fuer die Zeitspanne von 1993 bis 2003 ergibt sich:
Difference (Observed –Sum) 0.3 ± 1.0 mm/year.
Damit kann man dann nicht nur einen Anstieg des Meerespiegels, sondern auch das Gegenteil „beweisen“.
Wer das Glueck hatte, beobachten zu koennen, wie Temperature und Salzgehalt im Ozean waehrend zweier Forschungskampagnen gemessen wurden, der kann nur noch darueber grinsen, wenn er die Genauigkeitsangaben liest, mit der einige die Waermefluesse im Ozean bestimmt haben wollen. Das kann man noch nicht einmal mehr mit „wishful thinking“ begruenden.
Lieber Herr Mueller,
„Eine wichtige Einschränkung bei der Messung vieler Grö?en wie Temperatur oder Luftfeuchtigkeit ist zudem die Tatsache, dass hier vielfach punktuell Einzelwerte erfasst werden, obwohl es sich eigentlich um komplexe, dreidimensional wie auch zeitlich veränderliche Feldgrö?en handelt.“
So ist es. Aber dieses Problem hat man auch bei noch krauseren Größen der Landschaft. Nehmen wir mal die Topographie selber.
Sind wir uns einig, daß man jeder noch so hügeligen Landschaft eine mittlere Höhe mit einer definierten Genauigkeit gegenüber dem Referenzniveau angeben kann? Das wäre die Mittelung über eine 2-D Fläche und entspricht mathematisch dasselbe wie die Temperaturmittelung der 2m -Temperatur.
„Um sich eine Vorstellung von den damit verknüpften Problemen zu machen, kann man einmal alle Thermometer im Haushalt zusammentragen und diese in einem Zimmer verteilen, um dann zu versuchen, die mittlere Temperatur zu bestimmen.“
Das kann man machen. Ist natürlich im Haus mit den variierenden mikroklimatischen Bedingungen (Wände, Heizflächen etc.) viel schwieriger als die Temperatur der Luftmasse draußen mit einer gut gelüfteten Wetterhütte zu bestimmen. Im Haus muß man erst mal die mikroklimatischen Verhältnisse vermessen. Bei der Wetterhütte sorgt schon der Austausch der Luft aufgrund des Durchzugs der Luft, für eine räumliche Mittelung.
„Die Angabe einer auch nur auf zwei Stellen genauen mittleren Tagestemperatur erfordert einen erstaunlichen messtechnischen und auch rechnerischen Aufwand.“
Eine Genauigkeit von 0,01 °C ist operativ-meteorologisch bzw. klimatologisch nicht möglich und auch nicht nötig.
„Wenn man sich dann vergegenwärtigt, wie variabel sich die entsprechenden Grö?en in freier Natur darstellen, so bekommt man eine gewisse Vorstellung davon, wie schwierig die Aufgabe beispielsweise der Meteorologen des Deutschen Wetterdienstes ist, aus den Daten von wenigen 100 Messstationen in ganz Deutschland, die teils nur zu bestimmten Zeiten abgerufen werden, repräsentative Aussagen zu erzeugen“
Nun, das Flächenmittel des Jahres- oder Monatsmitteltemperaturen Deutschlands ist sicherlich genauer als 0,2 °C, wie man selber nachprüfen kann, wenn man selber (fachgerecht) mißt. Gerade die Lufttemperatur in 2 m Höhe gehört (neben Luftdruck) zu den meteorologisch eher leicht zu Feldverteilungen zu interpolieren Größen. Das liegt weniger daran, daß sie leicht zu messen ist, sondern an der vergleichsweise geringen räumlichen Variabilität der Luftmassen auf synoptischer Skala. Man möge bedenken, daß für die Wetteranalyse und -vorhersage, Temperaturunterschiede von Luftmassen von 1 bis ein paar Grad synoptisch erfaßbar sein müssen, wie man leicht in Analysekarten sieht.
@Fred F. Mueller,
Sehr geehrter Herr Mueller,
„Ich weiß ja nicht, mit welchen Absichten Sie hier posten, aber Sie sollten bedenken, dass Sie riskieren, sich mit solchen Aussagen vor dem überwiegend sachkundigen Publikum dieser Internetseite der Lächerlichkeit preiszugeben.“
Ich denke, Sie setzen in erster Linie auf die in großen Teilen des hiesigen Publikums vorhandene Unbedarftheit, wenn Sie meinen, dieses mit der von Ihnen gewählten Methode hinters Licht führen zu können.
Ihre Aussage, dass der Meeresspiegel in den vergangenen 20.000 um durchschnittlich 0,6m/Jhdt. angestiegen sei, ist zwar oberflächlich betrachtet zutreffend, liefert dem Laien aber trotzdem ein grotesk falsches Bild, das Herr Jung mit seinem Posting #6 richtig gestellt hat.
Natürlich liegt Ihrerseits ein – bewusster oder unbewusster – Manipulationsversuch vor, wenn Sie bei einer derart heterogenen Entwicklung (erst enorm starker Anstieg, dann langsamerer, schließlich wieder ein zunehmender) den Eindruck erwecken wollen, ein Durchschnittswert könne eine sinnvolle Aussage darstellen, wenn 0,6m/Jhdt seit mehreren Tausend Jahren nicht mehr vorgekommen sind, wie selbst aus Ihrer Grafik problemlos abzulesen ist.
@ #14 Tritium
Sehr geehrter Tritium,
Auf meine Aussage „Einmalige Signale, die kleiner sind als der Rauschpegel, sind in der Regel nicht signifikant“ hin schrieben Sie:
„Einspruch! Tatsächlich ist die normgerechte Beurteilung der Validität von Messwerten noch weitaus restriktiver.“
Danke für den fundierten Hinweis. Im Prinzip bestätigen Sie damit zugleich meine Kritik an der LNT-Methodik und verschärfen sie sogar noch.
Neben der Frage der normgerechten Behandlung von verrauschten Signalen gibt es jedoch auch Spezialfälle. Zahlreiche Wissenschaftler haben sehr viel Flei? und mathematischen Ehrgeiz darauf verwendet, auch sehr stark verrauschte Signale noch interpretierbar zu machen, beispielsweise Bild- und Messdaten von Satelliten, die an der Grenze der Leistungsfähigkeit ihrer Sendeeinrichtungen arbeiten. Dabei gibt es teilweise erstaunliche Erfolge. Dieses Gebiet ist jedoch sehr diversifiziert und beinhaltet unterschiedliche Lösungsansätze. Darauf näher einzugehen wäre im Rahmen meines Aufsatzes nicht sinnvoll gewesen. Deshalb habe ich mich bewusst auf eine „unscharfe“, allgemein gehaltene Aussage beschränkt. Hätte ich beispielsweise die von Ihnen aufgeführten Kriterien angeführt, hätte dies auf der anderen Seite sicherlich – ebenso berechtigten – Widerspruch seitens jener Spezialisten heraufbeschworen. Ich habe somit Widerspruch zugleich erwartet und in Kauf genommen. Ich betrachte solche Diskussionen als wertvoll, denn sie vertiefen das Thema und nutzen den Teilnehmern.
Mit freundlichen Grü?en
Fred F. Mueller
Sehr geehrter Herr Mueller,
vielen Dank für Ihren erneut sehr informativen Artikel. Und für Ihre unbewusste Unterstützung. Mein Name ist zwar nicht Mark Twain, ich habe aber mehrfach sinngemäß und einmal wörtlich hier geschrieben, dass die Computersimulationen in erster Linie spannende bunte Bilder liefern.
„Die eigentliche Herausforderung besteht darin, bei den Ergebnissen zwischen Science und Fiction zu unterscheiden…“ Meine Wortwahl war in etwa: Das Ergebnis der Simulation ist abhängig vom Auge des Betrachters, ob er in der Lage ist, zwischen reelle und virtuelle Welt zu differenzieren.
„Gewissheit bekommt man jedoch nur, wenn man reale Teile unter praxisüblichen Bedingungen testet. Auch Meteorologen geben zu Protokoll, dass die Genauigkeit ihrer Wettervorhersagen…“ Meine Wortwahl war: Ergebnisse von Simulationen sind nur sinnvoll, wenn eine Schnittstelle zu Natur (reelle Welt) vorhanden ist. Je näher die simulierte Wetterprognose heranrückt, um so mehr simulierte Werte werde durch reelle (gemessene) Werte ersetzt und um so sinvoller das Ergebnis. Klimasimulationen sind ausschließlich bunte Bilder.
MfG
PG
Will der Autor mit dem Artikel nun sagen, daß man den physikalischen Wissenschaften weniger trauen kann als der Mathematik?
kann man mal konkreter werden? Sind wir uns einig, daß man fein säuberlich zwischen Angstmachen und Wissenschaft zu unterschieiden hat, und für letzteres nur die Wissenschaft zuständig ist, ersteres aber jeder Depp kann?
@ #12 Jochen Bäumer
Sehr geehrter Hr. Bäumer,
Sie schreiben zum Meeresspiegelanstieg (120 m in den letzten ca. 20.000 Jahren): „Womit bewiesen wäre, dass Fred F. Mueller genau das tut, was er der Gegenseite an Manipulation unterstellt: Er wählt den Zeitraum so, dass das von ihm gewünschte Ergebnis herauskommt“.
Ich weiß ja nicht, mit welchen Absichten Sie hier posten, aber Sie sollten bedenken, dass Sie riskieren, sich mit solchen Aussagen vor dem überwiegend sachkundigen Publikum dieser Internetseite der Lächerlichkeit preiszugeben.
Es ist eine selbst zwischen Klima-Alarmisten und ihren Gegnern, den sogenannten Skeptikern, im Prinzip weitestgehend unbestrittene Tatsache, dass der Anstieg des Meeresspiegels im Wesentlichen auf das Abschmelzen von Gletschern zurückzuführen ist. Als „Stunde null“ hierfür kann man den Zeitraum vor rund 20.000 bis 22.000 Jahren ansetzen, als die bisher letzte (von zahlreichen vorherigen) Eiszeit ihren Höhepunkt überschritten hatte. Das genau ist der aktuell allgemein anerkannte Ursprung des Koordinatensystems für die Beurteilung von Anstiegen des Meeresspiegels.
Worin also soll die von Ihnen unterstellte Manipulation bestehen?
Sie dürfen natürlich gerne anderer Meinung sein, aber dann wäre es sicherlich angebracht, Ihre Argumente hier vor einer interessierten Fachöffentlichkeit einmal darzulegen.
Mit freundlichen Grüßen
Fred F. Mueller
„Einmalige Signale, die kleiner sind als der Rauschpegel, sind in der Regel nicht signifikant“
Einspruch!
Tatsächlich ist die normgerechte Beurteilung der Validität von Messwerten noch weitaus restriktiver.
In der Qualitätsbeurteilung von Messwerten gilt:
Ein Signal muss 3 x grösser sein als das durchschnittliche Rauschen, um eine qualitative Aussage (‚Da ist etwas, aber wir wissen nicht, wie viel‘) zu machen und es muss 10 x grösser sein, um eine quantitative Aussage zu machen (‚Da sind 2 µg/l drin / Die Temperatur ist um 0,2 °C gestiegen‘).
In der Praxis heisst das: Wenn ein Thermometer eine Messungenauigkeit von 0,1 °C hat (Geräte- + Ablesefehler) kann erst ab einer Temperaturveränderung von 1,0 °C überhaupt eine Grössenaussage gemacht werden (‚Die Temperatur ist um 1°C gestiegen‘). Kleinere Änderungen dürfen nicht quantifiziert werden!
Ich bin deshalb immer wieder fasziniert von Aussagen wie ‚Die Durchschnittstemperatur ist um 0,23 °C gestiegen‘. Das würde eine langfristige Messgenauigkeit des Thermometers von
#11 Lieber Herr Paul, ich schrieb, dass die _Eignung_ eines Modells nur durch Experimente erkannt werden kann. Gemeint sind dabei wissenschaftlich begründete Experimente, welche das Ziel verfolgen, dass Modell zu widerlegen. (Bestätigungsexperimente sind logisch nicht sinnvoll.) Die _Nichteignung_ ejnes Modells kann natürlich, wie Sie bemerkt haben, auch zum Beispiel schon dadurch erkannt werden, dass es unter unzulässigen Vereinfachungen und Annahmen hergeleitet wurde.
Einige Klimamodellen dürfte so schon jeder wisenschaftliche Anspruch fehlen. Bei anderen ist es nicht so einfach, da ihre Herleitung wissenschaftlichen Ansprpüchen genügen könnte. Dann müssten aber Experimente zum Verggleich mit der Realität (und nicht mit anderen Modellen)erfolgen.
@Hans Jung,
„In den letzten rd. 20.000 Jahren ist der Meeresspiegel ohne menschliches Zutun um etwa 120 m (ca. 0,6 m pro Jahrhundert) angestiegen“
Womit bewiesen wäre, dass Fred F. Mueller genau das tut, was er der Gegenseite an Manipulation unterstellt: Er wählt den Zeitraum so, dass das von ihm gewünschte Ergebnis herauskommt.
#9: N. Koksch, es tut mir direkt leid, dass ich ihnen das gleiche vorwerfen muss, das Sie dem Autor des Beitrags vorwerfen.
„Ob ein mathematisches Modell geeignet ist, kann man nur durch Experimente erkennen: Widersprechen die experimentellen Ergebnisse den theoretischen Aussagen des Modells, so ist das Modell wohl ungeeignet.“
Ein mathematisches „richtig gerechnetes“ Modell kann auch ohne experimentelle Überprüfung als falsch erkannt werden weil, es physikalische Gesetze (Thermodynamik) missachtet,
wie z.B. dieses:
http://tinyurl.com/lrvupp
Das gilt natürlich auch für „Klimamodelle“ und die darin konstruierte Voraussagefähigkeit der Zukunft. (Indeterminismus)
mfG
@ #9 N. Koksch
Sehr geehrter Hr. Koksch,
ich bedanke mich, dass Sie mich auf einen Schreibfehler im Unterkapitel „Mathematik und die Grenzen der Exaktheit“ hinweisen. Richtig müsste es dort heißen: Das Ergebnis als Real-Zahl darzustellen. Real-Zahlen sind in Computersprachen Fließkommazahlen in Dezimalschreibweise. Die meisten Naturwissenschaftler, vor allem solche, die selbst auch Computer programmieren, dürften den Gesamtzusammenhang auch trotz des Schreibfehlers richtig verstanden haben. Mit dieser Korrektur stimmt die Aussage des Kapitels dann auch unter formalen Aspekten lückenlos.
Ich bitte den Admin, die Schreibweise entsprechend zu korrigieren.
Ansonsten kann ich Ihren Aussagen nicht so recht folgen:
Sie sagen: „Die im Artikel beschriebenen Fehler sind keine Fehler der Mathematik sondern eventuell Fehlanwendungen“
Nun, da sind wir doch völlig einer Meinung. Der ganze Artikel zielt doch darauf ab, missbräuchliche bzw. betrügerische Anwendungen der Mathematik aufzuzeigen. Von „Fehlern“ der Mathematik war nirgendwo die Rede.
Mit freundlichen Grü?en
Fred F. Mueller
Ich habe den Eindruck, dass der Autor nicht recht weiß, was Mathematik ist und nicht zwischen (mathematischen) Modell, Experimanet und Realität richtig unterscheidet.
Drollig wird es zum Beispiel bei „Schon der Bruch 1/3 hat in der Dezimalschreibweise unendlich viele Nachkommastellen. In der Praxis kann daher der Versuch, 1/3 und 1/7 zu addieren und das Ergebnis als reale Zahl darzustellen, zu keinem wirklich exakten Ergebnis führen.“ Also, was ist an 1/3+1/7=(7+3)/21=10/21 so kompliziert? (In der Realität gibt es keine Zahlen.)
Die im Artijkel beschriebenen Fehler sind keine Fehler der Mathemnatik sondern eventuell Fehlanwendungen: Ein mathematisches Modell ist nicht wahr oder falsch, sondern bestenfalls mehr oder weniger gut zur Beschreibung eines Phänomens geeignet. Ob ein mathematisches Modell geeignet ist, kann man nur durch Experimente erkennen: Widersprechen die experimentellen Ergebnisse den theoretischen Aussagen des Modells, so ist das Modell wohl ungeeignet.
Die Klima-Modelle sind von mathematischen Modellen schon weit entfernt. Ob sie geeignet sind, sind man im Vergleich mit der Realität. Wenn Klimamodelle einen Temperaturtanstieg mit steigenden CO2-Anstieg vorhersagen, dieser aber so nicht eintritt, sind die Modelle ungeeignet. Es ist aber keine falsche Mathematik, sondern eine falsche Interpretation bzw. Anwendung der Mathematik.
Gab es da nicht mal ein Land (der US-Bundesstaat Indiana), das per Gesetz den Wert von Pi auf exakt 4 festgesetzt hat?
Etwa so einfach machen es sich nun auch andere, die sich Klimaforscher nennen.
Vielen Dank, Herr Fred F. Mueller!
Mathematik ist ebenso wie die Logik KEINE Naturwissenschaft!!! Egal was Kant dazu gesagt hat.
Er irrte auch bei der Logik, die er seit Aristoteles als ewig (richtig) und abgeschlossen (falsch) betrachtete.
Man kann beides als Formalwissenschaft bezeichnen, oder als die Lehre von „richtigen“ Denken.
Etwas romantisierend darf man sie gerne auch als die „Sprache“ der Natur bezeichnen (Galilei), auch wenn heute die elektronischen Rechner wohl kaum als Naturprodukte gelten können 🙂
Aber ebensowenig, wie irgend eine andere „menschliche“ Sprache mit dem Sprecher identisch sein kann, ist Mathematik mit der Natur identisch, oder das Ergebnis einer Rechenoperation mit dem Rechner.
Die Welt der „Begriffe“ ist NICHT die Welt der realen Gegenstände. Grundsätzlich muss es also möglich sein, eine mathematische Formel auch in Worten auszudrücken.
Auch die Mathematik
widerlegt durch die fehlende positive Korrelation von CO2-Anstieg und Temperatur einen behaupteten „CO2-Treibhauseffekt“!
Auch die Mathematik widerlegt die langfristige Vorhersagbarkeit von Wetter in der behaupteten Genauigkeit (positiver Ljapunow-Exponent).
Insofern ist die CO2-Treibhaustheorie NICHT wissenschaftlich.
Politisch ist sie eine menschen- und naturfeindliche Theorie.
mfG
„In den letzten rd. 20.000 Jahren ist der Meeresspiegel ohne menschliches Zutun um etwa 120 m (ca. 0,6 m pro Jahrhundert) angestiegen“
Von wegen.
Das meiste passierte in den ersten Jahrtausenden nach Ende der Eiszeit.
In den letzten 7000 Jahren stieg er dann nur noch um 0,4mm/Jahr.
In den letzten 20 Jahren stieg er 8-mal so schnell: 3,2mm/Jahr.
Gruß
Hans Jung
Der Artikel ist eine gute Zusammenstellung der Grundprobleme der Wissenschaften, im Besonderen im vorliegenden Fall. Das kann man sich als didaktische Referenz auch als Bookmark setzen.
Übirgens: Auch die Evaoltionstheorie, im Besonderen bei der Makroevolution hat ähnliche methodische Schwächen. Wir haben häufig unerwartete Ergebnisse, die dann zurecht gebogen werden müssen, aber nicht wirklich schlüssige Erklärungen.
Es ist doch gut zu wissen dass die ganzen alarmistischen Wissenchaftler, Politiker und Aktivisten irgendwann richtig auf die Nase fallen werden und als Versager in die Geschichte eingehen werden. Nur leider kann es noch einige Jahre dauern bis es wieder eine signifikante Abkühlung gibt und bis dahin wird noch viel Schaden entstehen.
Es ist gut, das die LNT-Hypothese wieder angesprochen wird. Diese Hypothese wird seit den 1950-er Jahren von der ICRP (Internationale Strahlenschutzkommission) vertreten, sie hat sich gleichsam auf der ganzen Welt etabliert. Mit dieser Hypothese, daß jede noch so kleine Dosis unabhängig von Zeitraum eine Wirkung hat, wird die Strahlenangst erzeugt. Dazu zählt man die Becquerels, das sind GROSSE Zahlen, GROSSE Zahlen sind gut für GROSSE Angst.
Dabei ist LNT die Extrapolation eines empirisch gefundenen Zusammenhanges nach unten über ca. drei Größenordnungen. Jeder Ingenieur weiß, das ist Blödsinn.
Auf meinem Schreibtisch habe ich ein ganz normales Glas-Flüssigkeitsthermometer in stehen, es hat eine Anzeige auf Zehntel Grad. Wenn ich die Temperatur ablesen will, muß ich es in die Hand neh-men, damit ich genau genug sehe. Dann steigt die Anzeige um ein bis zwei oder drei Zehntel Grad an, ich muß ja atmen, und die IR-Strahlung meines Körpers ist auch noch da. Das zur Meßgenauigkeit bei Temperatur.
Es kommt mir oft so vor als ob diese Wissenschaftler an einem Roulette Tisch sitzten und denken das sie einen Trend erkannt/errechnet haben.
Es geht auch lange gut, aber dann passiert das was immer passiert. Das System oder Computer Model funktioniert nicht mehr.
Was macht jetzt der Wissenschaftler/Spieler? Er belügt sich selbst und auch andere. Es sei ja nur ein kleiner Fehler und nach einer kurzen Zeit wird es wieder ausgeglichen. Man wird wieder gewinnen.
Die Forscher(Spieler) rätselten über den Stillstand bei Erderwärmung. Man brauchte lange Zeit für eine Erklärung aber man fand sie in der Tiefsee, als ob die Tiefsee vorher nicht vorhanden war. Wenn die Lufttemperatur nicht mehr ansteigt, dann muß etwas anderes die Erwärmung aufnehmen. Das System sagt das es seine Erwärmung gibt und wenn das System es sagt dann muß es stimmen. Das System kann nicht falsch sein. Ergo, der Croupier muß daran schuld sein.
Solange diese Wissenschaftler spielsüchtig sind und die Realität verleugnen, werden sie Erklärungen finden, auch wenn sie noch so an den Haaren herbeigezogen sind. Spieler spielen auf Zeit und genau das selbe machen diese Wissenschafler. Was sind schon 50 oder 100 Jahre. Irgenwann wird das System wieder funktionieren.
Lieber ein Ende mit Schrecken als ein Schrecken ohne Ende ist eine schöne Aussage. Leider stellt man fest das “ein Schrecken ohne Ende” in den meisten Fällen die bevorzugte Methode ist. Man redet sich immer ein das es am Ende doch noch kommt wie man es vorausgesehen hat.
Das schöne an der Statistik ist das man (fast) alles errklären kann. Alle Glücksspiele verführen Menschen dazu zufällige Ereignisse als einen Masterplan zu sehen. Das die Klimawissenschaft sich in die Ecke von Glücksspielen begibt ist ein Problem. Wahrscheinlich ist die Spielsüchtigkeit schon so weit ausgeprägt das man ohne Therapie nicht ur Normalität zurück findet. Die einzige Therapie wäre eine Eiszeit(therapie). Je länger diese Eiszeit(therapie) ausbleibt wird die Spielsüchtigkeit weiter gehen. Ein Außenstehender hat kaum eine Chance dem Spielsüchtigen zu helfen. Da hilft auch keine Logik.
Braucht es die Mathematik, dass der Mensch auf dieser Erde leben (überleben) kann????
Die Mathematik ist ein „Muss“ für die moderene jetzt Zeit. Mathematik ist ein Bestandteil unseres Wohlstand.
Jedoch hat der Ursprung-Mensch keine Mathematik gekannt und hat sich auch ohne Mathe das Essen und das Wasser. Ein Dach über den Kopf und andere überlebenswichtige Strategien zurecht gelegt.
Dazu waren keine Berechnungen notwendig. Alleine durch das Experimentieren (Agieren und Reagieren, Versuch und Misslingen, Erfolg und Misserfolg usw.) hat der Mensch gelernt auf dieser Erde sich durch zu setzen. Die wahre Wissenschaft ist nicht die Mathematik, sondern die experimentelle „Natur-„Wissenschaft.
Bei der Energiewende werden uns zum Schluss die Gesetzmäßigkeiten der Natur (Wissenschaften) zur Umkehr vom Energiewende-Pfad zwingen.
Bei manchen Menschen/Politikern ist es mit der Vernunft und den Verstand halt nicht weit her und diese Menschen/Politiker glauben halt immr wieder daran, die Launen der Natur (Wind, Sonne) beherrschen und steuern zu können. Obwohl die Menschheit schon immer gewusst hat, dass die Natur macht was Sie will und auf den Menschen keinerlei Rücksicht nimmt. Der Vernunft und Verstand Mensch wusste dies schon längst und hat sich deswegen von der Natur unabhängig gemacht. Die Kraftwerke von Kohle, Uran und Gas waren der Erste entscheidente Schritt in unseren neuen moderenen Wohlstandsgeselslchaft dazu. Die Energiewende macht genau diesen Schritt wieder zu nichte und missachtet damit den Vernunft und Verstand des „modernen“ Menschen!