Foto rechts: MIT’s “wheel of climate” forecaster – image courtesy Donna Coveney/MIT

Ich wollte auch nachschauen, wie sich die neuen GCMs im Vergleich zu den CMIP3-Modellen geschlagen haben, die im Jahr 2003 beschrieben worden sind {2}. Die CMIP3 wurden im AR4 des IPCC verwendet. Jene Modelle erzeugten einen geschätzten Fehler von 10,1% bei der Bewölkung, was gleichbedeutend ist mit einer Ungewissheit der Wolken-Rückkopplung von ± 2,8 Watt pro m². {3} Diese Ungewissheit ist äquivalent mit ± 100% des exzessiven Antriebs durch alle von den Menschen seit 1900 in die Atmosphäre emittierten Treibhausgase. Die Ungewissheit hinsichtlich der Wolken ist für sich allein genauso groß wie die gesamte Auswirkung, die das IPCC festzustellen versucht.

Wenn wir wissen wollen, wie zuverlässig Modellprojektionen sind, die energetische Ungewissheit, d. h. wegen des Wolkenfehlers, muss dieser in die GCM-Berechnungen des zukünftigen Klimas Eingang finden. Danach sollte die Ungewissheit als Fehlerbalken dargestellt werden, die die zukünftige Lufttemperatur festlegen. Allerdings scheint die Einbeziehung einer echten physikalischen Fehlergrenze niemals zu erfolgen.

Die Klimamodellierer veröffentlichen Projektionen der Temperaturzukunft völlig ohne jede Angabe der Fehlergrenzen. Hier findet man ein Standardbeispiel, die zahlreiche GCM-Projektionen der zukünftigen Temperatur in der Arktis zeigen. Man findet keinen einzigen Fehlerbalken.

Das IPCC macht genau das Gleiche, dargestellt hier dank einer unkritischen US EPA. Die schattierten Regionen in der IPCC-SRES-Graphik beziehen sich auf die numerische Variabilität individueller GCM-Modellläufe. Sie haben nichts zu tun mit physikalischer Ungewissheit oder mit der Zuverlässigkeit der Projektionen.

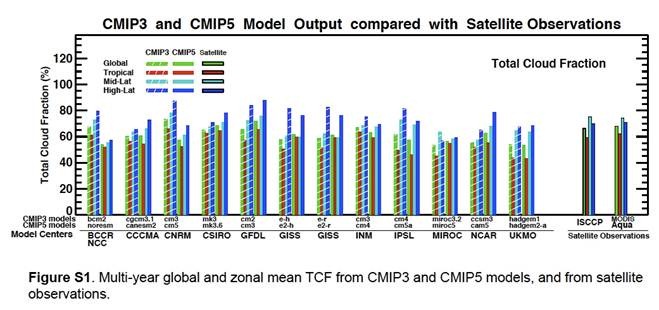
Die Abbildung S1 beim Auxiliary Material {1} [etwa: Hilfsmaterial] bei Jiang et al. fasst zusammen, wie genau die CMIP5-GCMs die globale Bewölkung in der Vergangenheit abbilden konnten. Das sieht so aus:

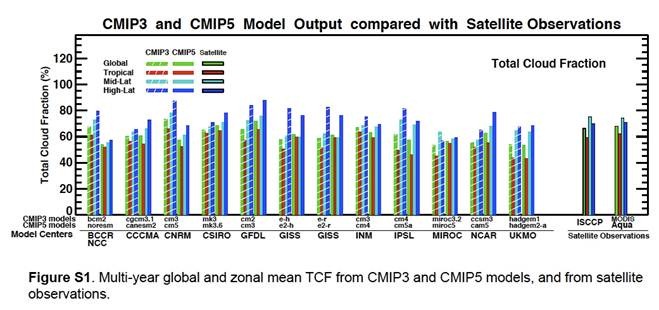
Jiang et al. sagten dazu Folgendes: „Abbildung S1 zeigt das vieljährige Mittel der TCFs [TCF = Total Cloud Fraction, etwa: der gesamte Bewölkungsanteil] global, in den  Tropen und in Mittleren Breiten aus den CMIP3 und CMIP5-Modellen sowie von den MODIS und ISCCP-Beobachtungen. Die Unterschiede zwischen MODIS und ISCCP liegen innerhalb von 3%, während die Bandbreite der Modelle bis zu 15% beträgt“.

Der Vergleich zwischen den CMIP3-Modellergebnissen mit den Ergebnissen des neuen CMIP5 lässt einen einfachen Blick auf den Fortschritt dieser Modellierung während der vergangenen 9 Jahre erkennen. Ebenso lässt sich der offizielle CMIP3-Wolkenfehler mit dem Wolkenfehler von 10% vergleichen, den ich schon früher in den Ergebnissen äquivalenter GCMs abgeschätzt habe.

Zunächst folgen hier die Tabellen der Wolkenprojektionen von CMIP3 und CMIP5 mitsamt den mit ihnen verbundenen Fehlern. Die beobachtete Bewölkung wurde aus dem Mittel der Beobachtungen von ISCCP und MODIS AQUA-Satelliten gebildet (die letzten beiden Balkenanordnungen in Abbildung S1 bei Jiang). Es ergab sich eine Wolkenbedeckung von 67,7%. Die GCM-Abkürzungen folgen den Referenzen unten.

Tabelle 1: CMIP3 GCM Globale mittlere Bewölkungsmenge und Fehlergrenzen

Table 2: CMIP5 GCM Globale mittlere Bewölkungsmenge und Fehlergrenzen

Diese Ergebnisse zeigen, dass einige Modelle zwischen 2003 und 2012 verbessert worden sind, andere nicht, und einige wurden offenbar ungenauer. Die Fehleranteile sind eindimensionale Zahlen, die aus den Fehlern in drei Dimensionen konzentriert worden sind. Die Fehleranteile bedeuten nicht, dass ein gegebenes GCM einen konstanten Bewölkungsanteil über oder unter der beobachteten Bewölkungsmenge vorhersagt. Die GCM-Bewölkungsvorhersagen schwanken rund um die beobachtete Menge in allen drei Dimensionen; die hier mehr, dort weniger Bewölkung vorhersagen {4,5}. Die GCM-Fehleranteile sind die positiven und negativen Wolkenfehler integriert über den gesamten Globus, gepresst in einzelne Zahlen. Der mittlere Fehler über alle GCMs wird aus der Wurzel der Summe der quadrierten Fehler der einzelnen GCM-Fehleranteile ermittelt. (root- mean-square = rms)

Die CMIP5-Wolkenbedeckung wurde über 25 Modelljahre gemittelt (1980 bis 2004), während CMIP3 das Mittel aus 20 Modelljahren repräsentiert (1980 bis 1999). Die mittlere Bewölkungsmenge als Mittel der GCMs wurde aus den „monatlichen Mitteln der Gitterquadrate“ [“monthly mean grid-box averages“] gebildet. Also enthielt ein 20-jähriges globales Mittel 12 x 20 monatliche Realisierungen der globalen Bewölkung, was die zufälligen Fehler [random calculational error] der GCMs um mindestens den Faktor 15 reduziert. 

Man kann daher sicher vermuten, dass die restlichen, in den Tabellen 1 und 2 gezeigten Fehler systematische GCM-Fehler hinsichtlich der Wolkenmenge repräsentieren, ähnlich dem schon früher gefundenen Bewölkungsfehler. Der mittlere systematische Fehler des Mittels der GCMs hinsichtlich der Bewölkung wurde zwischen 2003 und 2012 nicht bestimmt. Die CMIP3-Modelle ergaben im Mittel einen Fehler von 12,1%, was sich nicht signifikant von meiner Schätzung von 10,1% unterscheidet für GCMs ähnlicher Güte.

Wir können jetzt dazu übergehen, den GCM-Bewölkungsfehler in eine globale Lufttemperatur-Projektion einfließen zu lassen, um zu sehen, wie stark die Unsicherheit über die GCM-Projektionszeit wächst. Typischerweise berechnen die GCMs das zukünftige Klima stufenweise, von Monat für Monat zu Jahr für Jahr. Bei jeder Stufe werden die in der vorangehenden Periode berechneten Klimavariablen auf die nächstfolgende Periode extrapoliert. Jeder in diesen berechneten Variablen übrig gebliebene Fehler muss sich mit diesen Werten fortpflanzen. Wenn die Bewölkung durch Berechnung von Jahr zu Jahr in einer Klimaprojektion extrapoliert wird, repräsentiert der mittlere Wolkenfehler von 12,4% im CMIP5 eine Ungewissheit von ± 3,4 Watt pro m² bei der Klimaenergie {3}. Diese energetische Unsicherheit von ± 3,4 Watt pro m² muss in jede Berechnung des zukünftigen Klimas eingehen.

Klimamodelle repräsentieren begrenzte Systeme. Begrenzte Variable werden innerhalb gewisser Grenzen  gehalten, die durch die Physik des Systems festgelegt werden. Allerdings ist die systematische Unsicherheit nicht begrenzt. In einer stufenweisen Berechnung muss jeder systematische Fehler oder jede systematische Unsicherheit bei den Input-Variablen als ±sqrt(sum(per-step error)²) in die Output-Variablen einfließen. Die Unsicherheit steigt mit jeder neuen Stufe. Diese Bedingung wird in der nächsten Darstellung zusammengefasst.

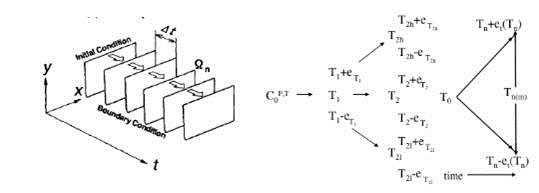
Die linke Formel illustriert die Art und Weise, mit der ein GCM stufenweise das künftige Klima projiziert {6}. Die weißen Rechtecke repräsentieren ein Klima, das sich während einer Serie von Zeitschritten weiter entwickelt. Jedes voran gegangene Klima schließt die Variablen mit ein, die sich nach Berechnung bis zum Klima der nächsten Stufe weiter entwickeln. Fehler in den Ausgangsbedingungen, Unsicherheiten in den parametrisierten Quantitäten und die Grenzen der Theorie führen allesamt zu Fehlern in projizierten Klimaten. Die Fehler in jedem voran gehenden Schritt der sich entwickelnden Klimaberechnung werden in die nächste Stufe mitgenommen.

Diese Fortpflanzung erzeugt die Zunahme des Fehlers, dargestellt in der rechten Formel, illustriert anhand der Temperatur. Die ursprünglichen Bedingungen führen zur ersten Temperaturangabe. Aber Fehler in der Berechnung erzeugen hohe und niedrige Unsicherheitsgrenzen (e_T1, etc.) bei der ersten projizierten Temperatur. Der nächste Rechenschritt erzeugt seine eigenen Fehler, die sich addieren und die hohen und niedrigen Unsicherheitsgrenzen beim nächsten Temperaturwert ausdehnen.

Wenn der Fehler systematisch ist, erscheinen ursprüngliche Unsicherheiten nicht als statistischer Fehler. Stattdessen pflanzt sich die Unsicherheit fort und erzeugt eine immer größer werdende Streuung von Unsicherheit um Klimaberechnungen nach Zeitstufen. Die Figur rechts außen fasst den Weg zusammen, auf dem der systematische Fehler als stufenweise Berechnung der Projektion mit der Zeit zunimmt.

Wenn die Unsicherheit wegen des Wachstums des systematischen Fehlers größer wird als die physikalischen Grenzen, hat die berechnete Variable keinerlei physikalische Bedeutung mehr. In der obigen Darstellung wäre die projizierte Temperatur nicht mehr bedeuten als statistisches Raten.

Hat man dies im Hinterkopf, kann sich der mittlere Fehler im CMIP5 hinsichtlich der globalen Bewölkung in eine zeitliche Temperaturprojektion hinein fortpflanzen. Dies wird die mittlere Unsicherheit der projizierten zukünftigen Temperatur infolge der Fehler zeigen, die die GCMs als Folge der Wolken-Rückkopplung machen.

Hier kommt nun der systematische Wolkenfehler im CMIP5 von 12,4% ins Spiel, der sich in jedermanns bevorzugte Temperaturprojektion fortpflanzt: Jim Hansens berühmtes Untergangsbild; das gleiche, das er in seiner Anhörung vor dem Kongress 1988 präsentierte. Die Fehlerbalken wurden berechnet mit Hilfe der Erkenntnisse meiner hoch aufgelösten GCM-Temperaturprojektions-Nachbildung, wie schon vorher detailliert beschrieben (892 kB pdf download).

Die GCM-Nachbildung zeigte, dass innerhalb der GCMs die globale Lufttemperatur lediglich eine lineare Funktion der Treibhausgase [net GHG] W/m² ist. Die Unsicherheit bei der berechneten Lufttemperatur ist dann nur eine lineare Funktion der Unsicherheit in W/m². Der mittlere GCM-Wolkenfehler pflanzte sich fort als:

„Lufttemperatur“ ist die Lufttemperatur an der Erdoberfläche in Grad Celsius. Die Lufttemperatur erhöht sich jährlich mit dem zunehmenden Antrieb durch Treibhausgase. Der „Gesamtantrieb“ ist der Antrieb in W/m² erzeugt durch CO2, Stickstoffoxide und Methan in jedem der „i“-Projektionsjahre. Der Antrieb nimmt jährlich zu mit dem Niveau der Treibhausgase. Die Gleichung ist die Standard-Fortpflanzung systematischer Fehler (eine amüsante Lektion hierzu gibt es hier (197 kb pdf)). Und jetzt, die Untergangs-Vorhersage:

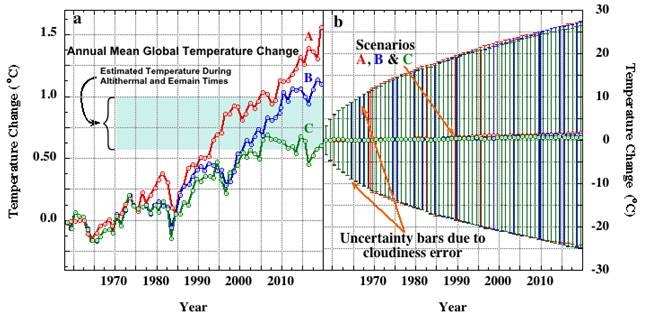
Die Abbildung erklärt sich selbst. Die Linien A, B und C in Teil „a“ sind die Projektionen der künftigen Temperatur, wie sie Jim Hansen 1988 präsentiert hatte. Teil „b“ zeigt die gleichen Linien, nur diesmal mit den Fehlerbalken aus dem mittleren systematischen Wolkenfehler von 12,4% aus dem CMIP5. Die Unsicherheit nimmt mit jedem jährlichen Schritt zu. Es kann hier mit Sicherheit angenommen werden, dass Jim Hansens GISS-Modell E von 1988 nicht die CMIP5-Standards aufwies. Daher sind die Ungenauigkeiten aus dem CMIP5-Modell die wirkliche minimale Abschätzung der Fehlerbalken um Jim Hansens Temperaturprojektionen von 1988.

Die große Unsicherheit bis zum Jahr 2020, etwa ±25°C, hat die drei Szenarien so komprimiert, dass sie alle entlang der Grundlinie zu laufen scheinen. Die Unsicherheit von etwa ±25°C bedeutet nicht, dass ich annehme, dass das Modell eine Erwärmung oder Abkühlung um 25°C zwischen den Jahren 1958 und 2020 projiziert. Stattdessen repräsentiert die Unsicherheit die Pixelgröße, die durch ein CMIP5-GCM noch aufgelöst werden kann.

Jedes Jahr wird der Pixel größer. Das bedeutet, dass die Auflösung der GCMs schlechter wird. Nach nur wenigen Jahren ist das Ergebnis eines GCM so grob, dass nichts Wichtiges mehr daraus abgeleitet werden kann. Das ist die Bedeutung der endgültigen Fehlerbalken von ±25°C. Sie bedeuten, dass die CMIP5-GCMs in 62 Jahren keine Temperaturänderung kleiner als 25°C mehr auflösen können (im Mittel).

Dem Antriebsszenario von Jim Hansen zufolge erzeugt der ±3,4°C Watt/m²-Wolkenfehler schon nach einem Jahr einen Einzelschritt-Pixel in einer Größe von ±3,4°C. Kurz gesagt, GCMs auf dem Niveau von CMIP5 sind vollständig unfähig, irgendeine Änderung der globalen Temperatur zu zeigen, die sich zu irgendeiner Zeit aufgrund des vom Menschen erzeugten CO2 ereignen kann.

Genauso war die Jim Hansen-Version von 1988 des GISS-Modells E nicht in der Lage, irgendetwas über dass zukünftige Klima vorherzusagen. Die riesigen Unsicherheitsbalken machen seine Projektionen aus dem Jahr 1988 physikalisch bedeutungslos. Darüber zu befinden, welcher der Trends die globale Anomalie am besten zeigt, ist wie eine Diskussion um Kaisers Bart. Kein Argument hat irgendeine faktische Aussagekraft.

Ähnliche physikalische Unsicherheiten sollten jede GCM-Ensemble-Projektion der globalen Temperatur umgeben. Allerdings ist die Wahrscheinlichkeit, diese im AR5 (oder in irgendeinem begutachteten Klimajournal) zu sehen, verschwindend gering.

Nichtsdestotrotz sind die CMIP5-Klimamodelle nicht in der Lage, die globale Temperatur auch nur ein Jahr im Voraus vorherzusagen. Ihre Projektionen haben keine physikalische Bedeutung und sind komplett unzuverlässig.

Wie aus der Überschrift zu diesem Artikel folgt: es gibt keinen Grund anzunehmen, dass irgendeine – ich wiederhole: irgendeine – zukünftige Klimaprojektion auf dem Niveau von CMIP5 zu finden sein wird.

Klimaprojektionen, die im IPCC-AR5 auftauchen könnten, werden völlig frei von jeder physikalischen Glaubwürdigkeit sein. Dazu beitragende Studien, die sich auf CO2 konzentrieren, sind notwendigerweise bedeutungslos. Dieses Scheitern steht im Zentrum von AGW Climate Promotions, Inc.

Zusammengefasst: jeder, der behauptet, dass das vom Menschen erzeugte CO2 dazu geführt hat, dass sich das Klima seit 1900 (oder 1950, oder 1976) erwärmt hat, setzt implizit die physikalische Verlässlichkeit von Klimamodellen voraus. Jeder, der die physikalische Verlässlichkeit von Klimamodellen ernsthaft voraussetzt, weiß buchstäblich nicht, wovon er redet. Jüngste Verkündigungen über die menschliche Schuld müssen vor diesem Hintergrund gesehen werden.

Das Urteil gegen den IPCC ist identisch: Sie wissen nicht, wovon sie reden. Glaubt irgendjemand, dass sie das davon abhalten wird, weiter zu reden?

Pat Frank PhD. San Diego.

Frank ist promovierter Chemiker,  spezialisiert in der Fehleranalyse spektroskopischer Messungen und arbeitet an der Stanford University

Andere Veröffentlichungen von Pat Frank bei EIKE z.B. hier, hier, hier und hier

References:

1. Jiang, J.H., et al., Evaluation of cloud and water vapor simulations in CMIP5 climate models using NASA “A-Train” satellite observations. J. Geophys. Res., 2012. 117, D14105.

2. Covey, C., et al., An overview of results from the Coupled Model Intercomparison Project. Global Planet. Change, 2003. 37, 103-133.

3. Stephens, G.L., Cloud Feedbacks in the Climate System: A Critical Review. J. Climate, 2005. 18, 237-273.

4. AchutaRao, K., et al., Report UCRL-TR-202550. An Appraisal of Coupled Climate Model Simulations, D. Bader, Editor. 2004, Lawrence Livermore National Laboratory: Livermore.

5. Gates, W.L., et al., An Overview of the Results of the Atmospheric Model Intercomparison Project (AMIP I). Bull. Amer. Met. Soc., 1999. 80(1), 29-55.

6. Saitoh, T.S. and S. Wakashima, An efficient time-space numerical solver for global warming, in Energy Conversion Engineering Conference and Exhibit (IECEC) 35th Intersociety. 2000, IECEC: Las Vegas. p. 1026-1031.

Climate Model Abbreviations

BCC: Beijing Climate Center, China.

CCCMA: Canadian Centre for Climate Modeling and Analysis, Canada.

CNRM: Centre National de Recherches Météorologiques, France.

CSIRO: Commonwealth Scientific and Industrial Research Organization, Queensland Australia.

GFDL: Geophysical Fluid Dynamics Laboratory, USA.

GISS: Goddard Institute for Space Studies, USA.

INM: Institute for Numerical Mathematics, Russia.

IPSL: Institut Pierre Simon Laplace, France.

MIROC: U. Tokyo/Nat. Ins. Env. Std./Japan Agency for Marine-Earth Sci.&Tech., Japan.

NCAR: National Center for Atmospheric Research, USA.

NCC: Norwegian Climate Centre, Norway.

UKMO: Met Office Hadley Centre, UK.

Link: http://wattsupwiththat.com/2012/08/23/ar5-climate-forecasts-what-to-believe/

Übersetzt von Chris Frey EIKE

Beitrag als PDF speichernBeitrag drucken