Erster Teil

Berechnung der erwarteten Klimasensitivität

Willis Eschenbach
“Klimasensitivität” ist der Name des Maßes, um wieviel sich die Erdoberfläche erwärmt bei einer gegebenen Änderung von etwas, das “Antrieb” (forcing) heißt.  Eine Änderung des Antriebs bedeutet eine Änderung im Netto des Strahlungseintrags (downwelling raditation) am oberen Rand der Atmosphäre. Darin enthalten ist die kurzwellige (solare) und die langwellige („Treibhaus“) Strahlung.
Es gibt eine interessante Studie von N. Hatzianastassiou et al. über die Strahlungsbilanz der Erde, sie heißt “Langzeit-Globalverteilung des kurzwelligen Strahlungsbudgets der Erde am oberen Rand der Atmosphäre” (Long-term global distribution of Earth’s shortwave radiation budget at the top of atmosphere). Unter anderem enthält die Studie eine Betrachtung der Albedo für jede Hemisphäre für den Zeitraum 1984-1998. Heute fiel mir auf, dass ich diese Daten zusammen mit den Solardaten der NASA benutzen könnte, um den Beobachtungs-Erwartungswert zu errechnen, bei dem Gleichgewicht bei der Klimasensitivität eintritt.
Nun kann man nicht einfach die direkte Änderung von Sonnenantrieb und Temperaturänderung betrachten, um die Langzeitsensitivität zu erhalten. So würde man nur eine sofort eintretende „unmittelbare“ Klimasensitivität erhalten. Der Grund liegt darin, dass es eine Weile dauert, bis sich die Erde erwärmt oder abkühlt. Daher wird die durch eine Verstärkung des Antriebs direkt und unmittelbar eintretende Änderung kleiner sein, als die vermutliche Änderung bis hin zum Erreichen des Gleichgewichtszustands, wenn die gleiche Antriebsänderung über einen langen Zeitraum aufrechterhalten bleibt.
Einiges geht aber dennoch. Figur 1 zeigt den Jahreszyklus der Änderungen des Sonnenantriebs und der Temperaturänderungen.

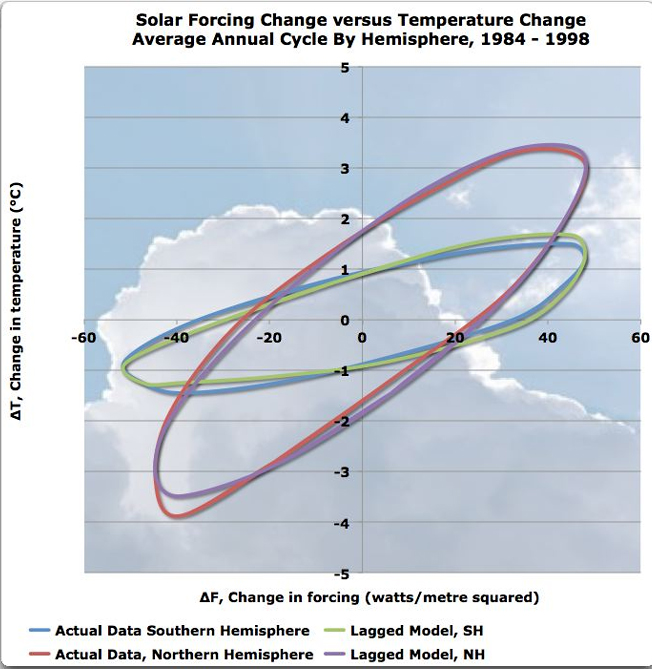
Figur 1. Lissajous Figur der Änderung des Sonnenatriebs (horizontale Achse) versus Temperaturänderung (vertikale Achse) als Jahresdurchschnitte.
[Lagged Model, … = verzögertes Modell]

Was zeigt uns Figur 1?
Ich habe angefangen mit der gemeinsamen Darstellung der Sonnendaten von der NASA (monatliche Änderung der Sonnenenergie, die auf die Erde trifft) und den Albedo-Daten. Aus dem Sonnenantrieb in [W/m2 mal (1 minus Albedo)] erhalten wir den ins System hereinkommenden Betrag der Sonnenenergie. Das ist das tatsächliche Sonnenantriebs-Netto Monat für Monat.
Dann habe ich die Änderungen in diesem Netto-Sonnenantrieb (nach Albedo Reflektionen) gegen die entsprechenden Temperaturänderungen geplottet, jeweils für die Hemisphären.
Vorab einige Bemerkungen zu diesem Plot.
Die Nordhemisphäre (NH) hat größere Temperaturschwingungen (vertikale Achse) als die Südhemisphäre (SH). Ursache sind die größeren Landmassen der NH und die größeren Wassermassen der SH … Das Meer hat eine viel größere spezifische Wärme, das Meer braucht mehr Energie zur Erwärmung als das Land.
Wir sehen das auch an der Neigung der Ovale. Die Neigung der Ovale sind Maße für die „Verzögerung“ im System. Je schwieriger es ist, eine Hemisphäre zu erwärmen oder abzukühlen, desto größer die Verzögerung, und desto flacher die Neigung.
Damit sind die roten und blauen Linien erklärt. Es sind die echten Daten für die NH und die SH.
Für ein “verzögertes Modell” habe ich das einfachste Modell benutzt. Es benutzt eine Exponentialfunktion zur Annäherung an die Verzögerung zusammen mit einer Variablen “lambda_0″. Das ist die "unmittelbare" Klimasensitivität. Das Modell bildet den Prozess ab, bei welchem ein Objekt durch einfallende Strahlung erwärmt wird. Zuerst geht die Erwärmung ziemlich rasch, mit zunehmender Zeit wird die Erwärmung immer langsamer bis sie einen Gleichgewichtszustand erreicht. Der Zeitbedarf zur Erwärmung wird von einer “Zeitkonstante” namens “tau” bestimmt. Ich benutzte folgende Formel:
                       ΔT(n+1) = λ∆F(n+1)/τ + ΔT(n) exp(-1/ τ)
wobei ∆T die Temperaturänderung ist, ∆F die Antriebsänderung, lambda (λ) die "unmittelbare" Klimasensitivität; “n” und “n + 1″ sind die Beobachtungszeiten, und tau (τ) ist die Zeitkonstante.
Ich habe Excel für die Berechnung der Werte benutzt, dazu das “Solver” Werkzeug [Anm. d. Ü: sh. Stichwort SOLVER in der Excel-Hilfe]. Es ergab sich eine bestangepaßte Kurve für die NH und die SH. Die Anpassung ist recht gut mit einem ‘Wurzel-aus-Durchschnittsquadrate-Fehler’ (RMS – Root Mean Square error) von nur 0.2°C und 0.1°C für die NH und die SH.
(Anm. d. Ü: die Excel-Tabelle kann heruntergeladen werden, Verweis siehe später!)

Und so erhalten wir unterschiedliche Zahlen für die jeweiligen lambda_0 und tau für die NH und die SH, wie folgt:

                           Hemisphäre    lambda_0     Tau (Monate)

                               NH               0.08           1.9

                               SH               0.04           2.4

Man beachte (wie zu erwarten war), dass es länger dauert, die SH zu erwärmen oder abzukühlen im Vergleich zur NH (tau ist größer für die SH). Darüberhinaus (wie ebenfalls zu erwarten war) ändert sich die SH weniger bei einem gleichen Betrag der Erwärmung.
Denken Sie bitte daran, dass lambda_0 die "unmittelbare" Klimasensitivität ist. Weil wir die Zeitkonstante kennen, können wir das zur Berechnung derjenigen Sensitivität, wo der Gleichgewichtszustand eintritt, benutzen. Ich bin sicher, dass es einen einfacheren Weg gibt, sie zu berechnen, ich habe nur die gleiche Kalkulationstabelle benutzt. Um eine Verdoppelung des CO2 zu simulieren, habe ich einen einmaligen Sprung von 3.7 W/m2 Antrieb angenommen.
Die Ergebnisse sehen so aus:

Kommentare und Kritik sind willkommen, so funktioniert die Wissenschaft. Ich veröffentliche hier meine Ideen, und Sie alle werden versuchen, Fehler zu finden.
w.
Zusatz: Die Kalkulationstabelle für die Berechnungen und zur Erzeugung des Graphen ist hier.  
Anmerkung: Ich habe auch die Änderung für den gesamten Datenbestand von 1984 bis 1998 modelliert, nicht nur die Änderungen aufgrund des Ansatzes der jährlichen Durchschnitte. (hier nicht abgebildet). Die Ergebnisse für lambda_0 und tau für die NH und die SH waren die gleichen (in Bezug auf die oben beschriebene Genauigkeit), trotz der generellen Erwärmung während jenes Zeitraums. Ich bin mir bewußt, dass die Zeitkonstante “tau”, bei nur wenigen Monaten, kürzer ist, als andere Studien gezeigt haben. Trotzdem … Ich berichte nur, was ich herausgefunden habe. Wenn ich mit einer längeren Zeitkonstante modelliere, wird die Neigung völlig falsch, viel flacher.
Während es auch möglich ist, dass es viel längere zeitliche Perioden mit Erwärmung gibt, zeigen sie sich nicht in meinen Analysen aufgrund der vorliegenden Daten. Wenn tatsächlich solche längeren Zeiträume existieren, scheinen sie nicht signifikant zu sein, um die Verzögerung zu strecken, die in meiner Analyse oben dargestellt ist. Die Einzelheiten der Langzeitanalyse (im Gegensatz zu den benutzten Durchschnitten, wie oben gezeigt) können auf dem Kalkulationsblatt zu eingesehen werden.
#############################################

Zweiter Teil

Ein langfristiger Blick auf die Klimasensitivität

Willis Eschenbach
Nach der Veröffentlichung meines obigen Beitrags, “An Observational Estimate of Climate Sensitivity“ haben zahlreiche Leser kritisiert, dass ich nur die Zyklen der jährlichen Durchschnitte betrachtet hätte. Wenn man Jahrzehnte betrachtet, sähe es anders aus und die Klimasensitivität wäre viel größer. Daher wiederhole ich meine Analyse ohne die jährlichen Durchschnitte, die ich in meinem letzten Beitrag betrachtet hatte. Figur 1 zeigt das Resultat für die nördliche Hemisphäre (NH) und die Südliche Hemisphäre (SH):

 

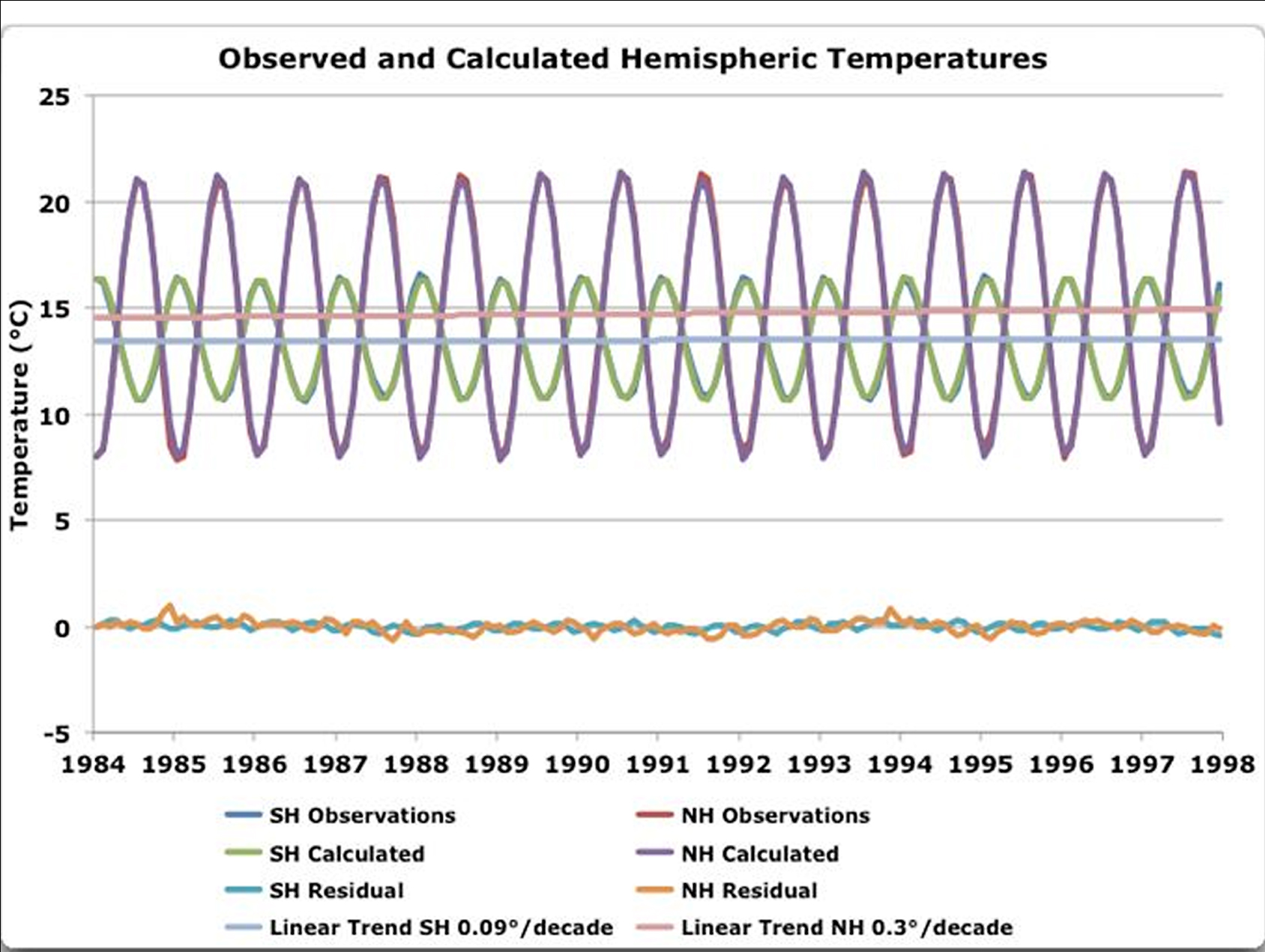
Figure 1. Temperaturen, nur auf der Grundlage der Variationen der Sonneneinstrahlung errechnet (Netto Sonnenenergie nach Albedo Reflektionen). Die Beobachtungen werden so gut durch die Berechnungen bestätigt, dass man die Linien mit den gemessenen Temperaturen nicht sieht. Sie sind hinter den Linien verborgen, die die Berechnungen abbilden. Die beiden Hemisphären haben verschiedene Zeitkonstanten (tau) und Klimasensitivitäten (lambda). Für die NH beträgt die Zeitkonstante 1.9 Monate und die Klimasensitivität 0.30°C bei einer Verdoppelung des CO2. Die entsprechenden Werte für die SH betragen 2.4 Monate und 0.14°C bei einer Verdoppelung des CO2. [… Residual = Rest]

Ich habe anhand des gleichen Verzögerungs-Modells gerechnet, das ich in meinem vorgehenden Beitrag erwähnte, aber ich habe nun die tatsächlichen Daten benutzt, anstelle der Durchschnitte. Ich verweise daher auf meinen vorgehenden Beitrag und das beigefügte Kalkulationsblatt mit den Einzelheiten zur Berechnung. Und jetzt gibt es einiges Interessantes bei dieser Grafik.
Erstens, die von mir im vorgehenden Beitrag benutzten Klimasensitivitäten eignen sich vorzüglich, um die Temperaturänderungen über ein-einhalb Jahrzehnte zu berechen, wenn auch die mit meinen Berechnungen nicht einverstandenen Leser anderer Meinung sind. In dem von der Aufzeichnung überdeckten Zeitraum stieg die NH-Temperatur um 0.4°C an, vom Modell ganz exakt so berechnet. Auf der SH gab es kaum einen Anstieg, auch das wurde vom Modell genau so berechnet.

Zweitens, nur die Sonne und die Albedo wurden benötigt, um diese Berechnungen durchzuführen. Ich brauchte keine Aerosole, vulkanischen Antriebe, Methan, CO2, Ruß, indirekten Aerosol-Effekt, Bodennutzung, Schnee- oder Eis-Albedo, und auch nichts von all dem übrigen Zeug, von dem die Modellierer behaupten, es steuere die Temperatur. Sonnenlicht und Albedo scheinen notwendige und hinreichende Variablen zu sein, um die Temperaturänderungen über den betrachteten Zeitraum zu erklären.

Drittens, die Treibhausgase werden gemeinhin als “gut durchmischt” angesehen, daher wurde ein Reihe von Erklärungen versucht, um die Unterschiede in den Trends der Temperaturen für die beiden Hemisphären zu erklären … aber allein mit der Sonne und der Albedo können die unterschiedlichen Trends sehr gut erklärt werden.
Viertens, es gibt keinen signifikanten Trend in den Resten aus Errechnetem minus Messwerten weder für die NH noch für die SH.
Fünftens, ich sage schon seit vielen Jahren, dass das Klima auf Störungen und Änderungen bei den Antrieben reagiert, indem es gegensteuert. So meine ich beispielsweise, dass die Auswirkung von Vulkanausbrüchen auf das Klima in den Klimamodellen stark überschätzt wird. Es sind die Albedoänderungen, die die Dinge zurück ins Gleichgewicht bringen.
Wie haben Glück, dass unser Datenbestand mit dem Pinatubo-Ausbruch einen der stärksten Vulkanausbrüche unserer Zeit enthält … kann man ihn aus der in Figur 1 gezeigten Aufzeichnung herausnehmen? Nein, das geht nicht und zwar aus folgendem Grund: die Wolken reagieren auf eine derartige Störung sofort wie ein Thermostat.
Sechstens, wenn es über jahrzehntelange Perioden eine längere Zeitkonstante gäbe (tau), oder eine größere Klimasensitivität (lambda), dann würde sich das in den Resten für die NH zeigen, aber nicht in den Resten für die SH. Dies deswegen, weil es bei der NH einen Trend gibt, und bei der SH grundsätzlich keinen. Aber die Berechnungen mit den gegebenen Zeitkonstanten und Sensitivitäten konnten beide Hemisphären sehr genau abdecken. Der Fehler der Wurzel-aus-den-Quadratdurchschnitten (Root Mean Square – RMS error) bei den Resten beträgt nur ein paar Zentel eines Prozents.

Also, Leute, das ist Alles, machen Sie sich drüber her … aber denken Sie bitte daran: Es ist Wissenschaft und die Spielregel ist, dass die wissenschaftliche Erkenntnis selbst angegriffen werden soll, nicht der Wissenschaftler als Mensch.

Denken Sie bitte auch daran, dass es nutzlos ist, meine Ergebnisse als einen „Witz“ oder als „Unsinn“ zu bezeichnen. Die Rechenergebnisse passen extrem gut zu den beobachteten Messwerten. Wenn es Ihnen nicht gefällt, müssen Sie die Fehler suchen und finden, und dann die Fehler in meinen Daten, in meiner Logik oder in meiner Mathematik aufzeigen.
Mit freundlichen Grüßen
w.
PS – Man hat mir häufig gesagt, so als ob keine weitere Diskussion möglich wäre, dass niemand jemals eine Modell erzeugt hätte, wo der Temperaturanstieg ohne Einbezug anthropogener Beiträge von CO2 und dergleichen hätte erklärt werden können. Nun, dieses Modell hier erklärt einen Anstieg von 0.5°C/pro Jahrzehnt in den 1980er bis 1990ern, genau den Anstieg, über den man sich Sorgen macht, und das ohne anthropogenen Beitrag.
[Anmerkung: Ich danke Stephen Rasey für seinen aufmerksamen Hinweis, dass meine ursprüngliche Trend-Berechnung wegen Endpunkt-Effekten leicht abwich. Ich habe daraufhin die Grafik und die darauf bezogenen Trend-Verweise berichtigt. Das hat keine Bedeutung für die Berechnungen oder für meine Schlussfolgerungen. -w.]
#######################################################

Original zum ersten Teil: „An Observational Estimate of Climate Sensitivity“

Original zum zweiten Teil: "A Longer Look at Climate Sensitivity"

Willis Eschenbach

 

Übersetzung: Helmut Jäger, EIKE