Signifikanz
Betrachten Sie den Verlauf der globalen Temperatur in Abbildung 1, die die Daten der NASA verwendet. Zunächst könnte es offensichtlich scheinen, dass der Graph eine Zunahme der Temperatur anzeigt. Tatsächlich sieht die Geschichte etwas anders aus, wie wir jetzt sehen werden.
Abbildung 1 rechts: Zeitreihe der globalen Mitteltemperatur.
Stellen Sie sich vor, Sie werfen zehn mal eine Münze. Falls jedes Mal der Kopf oben liegt, würden wir einen signifikanten Beweis dafür haben, dass die Münze keine richtige Münze ist. Stellen Sie sich nun vor, die Münze wird nur dreimal geworfen. Falls jetzt wieder dreimal der Kopf oben liegt, würden wir keinen signifikanten Beweis für die Fehlerhaftigkeit der Münze haben: Dreimal Kopf kann jederzeit zufällig vorkommen.
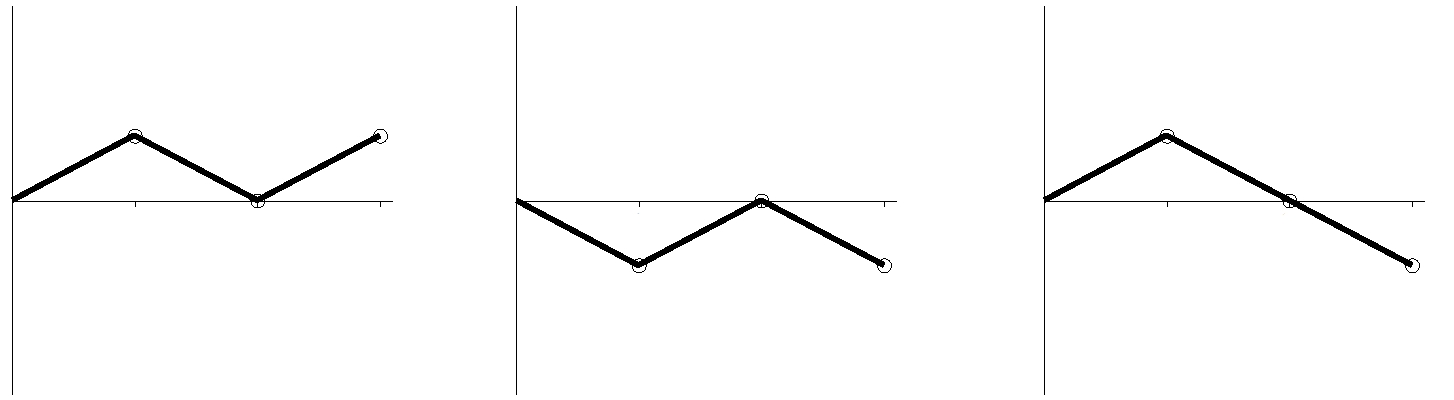
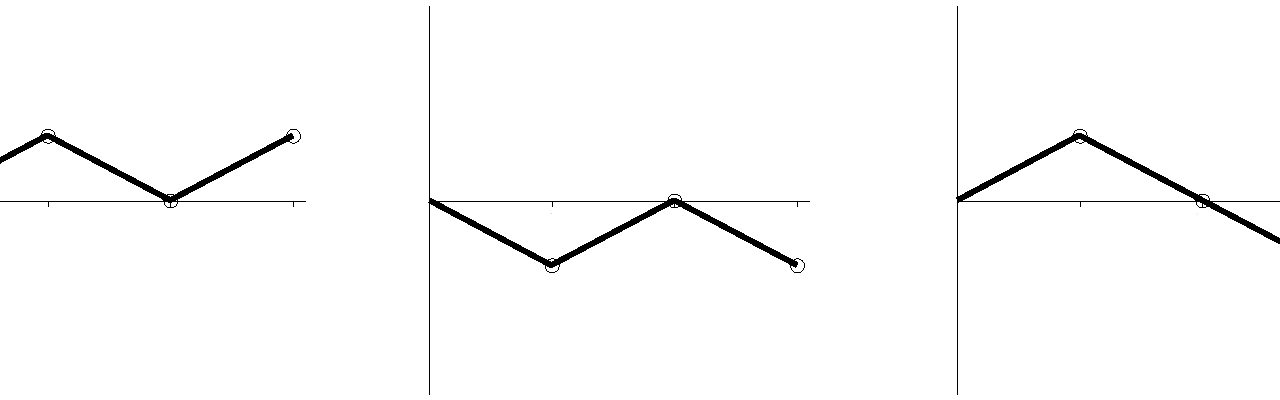
Abbildung 2: Münzwürfe: K, Z, K (links); Z, K, Z (Mitte); K, Z, Z (rechts)*
*head and tail [H, T] ist das typische entweder-oder im englischen Sprachraum, wenn es um das Losen mit Münzen geht. Hier wird dafür die gängige deutsche Bezeichnung Kopf und Zahl (K, Z) verwendet. A. d. Übers.]
In Abbildung 2 besteht jeder Graph aus drei Teilen: jedes Segment steht für je drei Münzwürfe. Falls die Münze Kopf zeigt, zeigt der Graph aufwärts, zeigt sie Zahl, zeigt er abwärts. In Abbildung 2 zeigt der Graph links Kopf, Zahl, Kopf; der mittlere Zahl, Kopf, Zahl und der rechte Kopf, Zahl, Zahl.
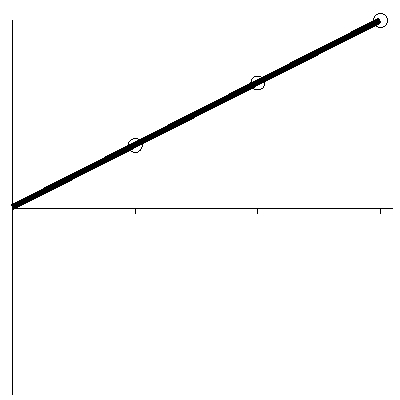
Abbildung 3: Münzwürfe: K, K, K
Betrachten Sie jetzt Abbildung 3. Auf den ersten Blick könnte es so aussehen, als ob der Graph eine Zunahme zeigt. Dieser Graph illustriert jedoch Kopf, Kopf, Kopf. Dreimal Kopf ist kein signifikanter Beweis für etwas anderes als Zufall. Ein Statistiker würde sagen, dass, obwohl Abbildung 3 eine Zunahme zeigt, diese Zunahme „nicht signifikant“ ist.
Nehmen Sie jetzt an, dass wir an Stelle der Münzen einen normalen sechsseitigen Würfel werfen. Zeigt sich die 1, wird eine abwärts führende Linie gezeichnet, bei einer 6 eine aufwärts führende Linie. Sollten die 2, 3, 4 oder 5 geworfen werden, wird eine Linie waagerecht gezeichnet. Wir werfen jeden Würfel dreimal. Beispiele zeigt Abbildung 4.
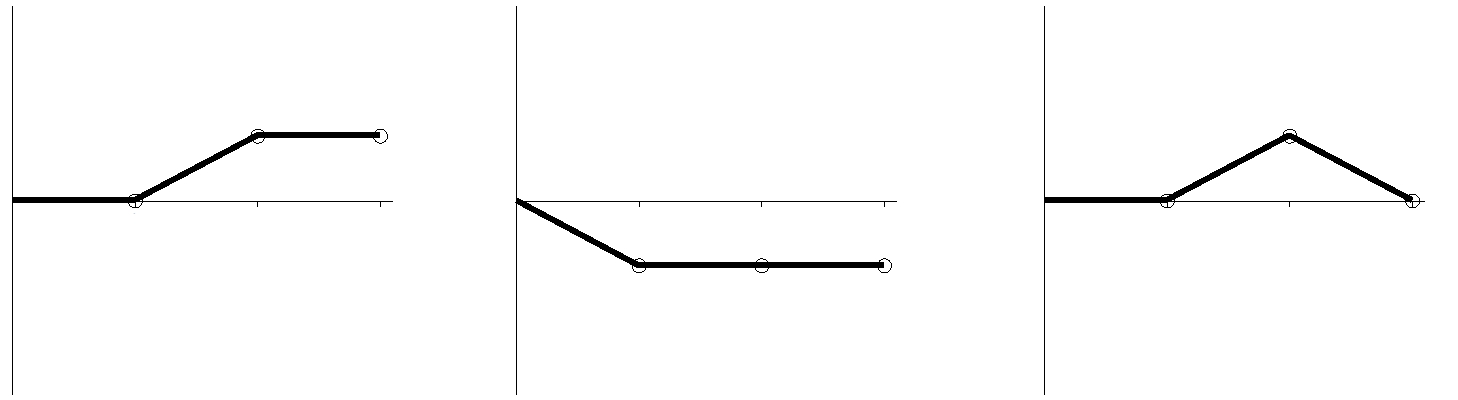
Abbildung 4: gewürfelte Ziffern 3, 6, 3 (links); 1, 5, 2 (Mitte); 4, 6, 1 (rechts)
Als nächstes betrachte man Abbildung 5, die dreimal eine 6 gewürfelt repräsentiert. Dieses Ergebnis würde zufällig nur einmal in 216 Fällen auftreten und stellt so einen signifikanten Beweis dar, dass der Würfel nicht normal rollt. Das heißt, die Zunahme in Abbildung 5 ist signifikant.
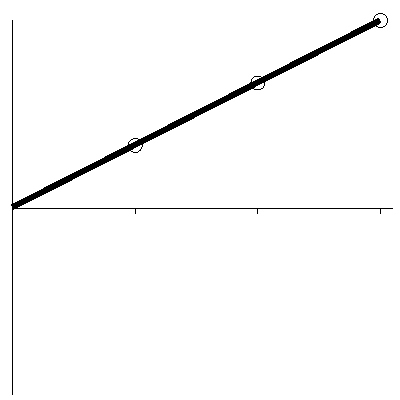
Abbildung 5: gewürfelt 6, 6, 6
Die Abbildungen 3 und 5 sehen identisch aus. In Abbildung 3 ist die Zunahme nicht signifikant, und in Abbildung 5 ist sie es. Diese Beispiele verdeutlichen, dass wir nicht durch bloßes Betrachten bestimmen können, ob eine Linie eine signifikante Zunahme zeigt. Vielmehr müssen wir etwas über den Prozess wissen, der zur Erstellung der Linie geführt hat. In der Praxis kann dieser Prozess sehr kompliziert sein, was die Abschätzung schwierig macht.
Betrachten Sie nochmals den Graph in Abbildung 1 oben rechts. Wir können nicht durch bloßes Anschauen des Graphen sagen, ob die globale Temperatur signifikant zunimmt. Mehr noch, der Prozess zur Erzeugung dieses Graphen – das Klimasystem der Erde – ist extrem kompliziert. Folglich wird es schwierig zu beurteilen sein, ob es eine signifikante Zunahme gibt oder nicht.
Zeitreihen
Dies führt uns zum statistischen Konzept einer Zeitreihe. Eine Zeitreihe ist jede Reihe von Messungen in bestimmten regelmäßigen Zeitabständen. Beispiele sind Folgende: Die Preise der Börse in New York bei Handelsschluss an jedem Tag, die tägliche Höchsttemperatur in London, die jährliche Menge der Weizenernte in Kanada. Ein weiteres Beispiel ist die mittlere globale Temperatur eines jeden Jahres.
In der Analyse einer Zeitreihe lautet eine der grundlegenden Fragen, wie man abschätzen kann, ob sich eine gegebene Reihe signifikant aufwärts (oder abwärts) bewegt. Die Mathematik einer Zeitreihenanalyse stellt uns einige Methoden zur Beantwortung dieser Frage zur Verfügung. Als erstes müssen wir zusammentragen, was wir über die Zeitreihe wissen. Zum Beispiel können wir feststellen, dass die Reihe immer dann einen Schritt nach oben macht, wenn eine bestimmte Münze Kopf zeigt, und dass die Reihe drei Schritte nach oben enthält, wie in Abbildung 3. Als nächstes müssen wir einige Berechnungen auf der Basis dessen, was wir festgestellt haben, durchführen. Zum Beispiel, wir berechnen die Wahrscheinlichkeit, dass eine Münze drei mal hintereinander Kopf zeigt, mit ½ × ½ × ½ = ?, d. h. es ergibt sich eine Wahrscheinlichkeit des Eintreffens von 12,5%. Daraus schließen wir, dass die drei Schritte nach oben in der Reihe der Münzwürfe gut und gerne als Zufall betrachtet werden – und folglich, dass die Zunahme in Abbildung 3 nicht signifikant ist.
Ganz ähnlich müssen wir, um festzustellen, ob die globale Temperatur signifikant zunimmt, zunächst festlegen, was wir über die Temperaturreihe wissen. Was wissen wir über die Reihe? Unglücklicherweise nicht genug, um eine brauchbare Zeitreihenanalyse durchzuführen. Also müssen wir über die Reihe einige Hypothesen machen und unsere Analyse dann auf der Basis dieser Hypothesen durchführen. Dies wird von den Zeitreihenanalysten vorgeschlagen. Solange die Hypothesen sinnvoll sind, können wir zuversichtlich sein, dass die Schlussfolgerungen aus unserer Analyse vernünftig sind.
Die IPCC-Hypothese
Die grundlegende Institution, wenn es um die globale Erwärmung geht, ist das IPCC. Der jüngste Bericht des IPCC zur wissenschaftlichen Basis der globalen Erwärmung wurde 2007 veröffentlicht. In Kapitel 3 werden Überlegungen zur globalen Temperaturreihe wie in Abbildung 1 angestellt. Die wesentliche Schlussfolgerung dieses Kapitels lautet, dass die Zunahme der globalen Temperatur extrem signifikant ist.
Um diese Schlussfolgerung zu ziehen, musste das IPCC eine Annahme über die Reihe der globalen Temperatur machen. Diese Annahme ist als „AR1“-Annahme bekannt (aus dem statistischen Konzept der „Autoregression erster Ordnung“). Die Annahme lautet neben Anderem, dass nur der gegenwärtige Wert in einer Zeitreihe eine direkte Auswirkung auf den nächsten Wert hat. Für die globale Temperaturreihe bedeutet dies, dass die Temperatur dieses Jahres Auswirkung auf die Temperatur des nächsten Jahres hat, nicht aber die Temperatur der Jahre zuvor. Zum Beispiel, falls die letzten Jahre extrem kalt waren, würde dies keine Auswirkungen auf die Wahrscheinlichkeit haben, dass es im nächsten Jahr kälter als im Mittel zu erwarten sein wird. Also scheint die vom IPCC gemachte Annahme intuitiv nicht plausibel zu sein.
Es gibt Standardchecks, um (teilweise) zu testen, ob eine Zeitreihe zu einer gegebenen statistischen Annahme passt. Ist dies nicht der Fall, müssen alle Schlussfolgerungen, die auf dieser Annahme basieren, als unbegründet betrachtet werden. Zum Beispiel, wenn die Signifikanz der Zunahme in Abbildung 5 aufgrund der Annahme berechnet worden wäre, dass die Wahrscheinlichkeit der Aufwärtsbewegung eins zu zwei anstatt eins zu sechs betragen würde, würde dies zu einer unrichtigen Schlussfolgerung führen. Im Kapitel des IPCC fehlt jedoch jeder Hinweis, dass solche Checks durchgeführt worden waren.
Mit anderen Worten, die Hypothese des IPCC besteht einfach aus einer Ankündigung. Von der Wissenschaft nimmt man an, dass sie auf Beweisen und Logik basiert. Dass das IPCC keinerlei Beweise oder Logik präsentiert, die seine Hypothese untermauern, ist eine ernste Verletzung grundlegender wissenschaftlicher Prinzipien.
Mehr noch, Standardchecks zeigen, dass die globale Temperaturreihe nicht mit der Hypothese des IPCC konform geht; ein solcher Check wird in einer separaten Sektion unten beschrieben. Folglich basiert die Behauptung, dass die Zunahme der Temperatur signifikant ist – immerhin die grundlegende Schlussfolgerung eines zentralen Kapitels des IPCC-Berichtes – auf einer untragbaren Hypothese. Allgemeiner, Das IPCC ist damit gescheitert, zu zeigen, dass die globale Temperatur signifikant steigt! [Hervorhebung im Original]
Diese Probleme sind auch nicht nur auf das IPCC beschränkt. Das Climate Change Science Program (CCSP) der USA, welches den Kongress berät, veröffentlichte seinen Bericht über Temperaturänderungen im Jahre 2006. Dieser Bericht beruft sich auf die gleiche unmögliche Hypothese wie im Kapitel des IPCC-Berichtes.
Nichts hiervon ist Meinung. All dies sind nicht diskutierbare Tatsachen. Und es gilt für jede Erwärmung – ob nun verursacht von der Natur oder vom Menschen. Solange keine Forschungen durchgeführt werden, eine angemessene Hypothese zu finden, kann keine Schlussfolgerung über die Signifikanz von Temperaturänderungen gezogen werden.
Mr. Keenan führte früher mathematische Forschungen und solche über den Finanzhandel an der Wall Street und in London; seit 1995 forscht er unabhängig, Er unterstützt den Umweltschutz und die Energiesicherheit.
Eine unmögliche Hypothese
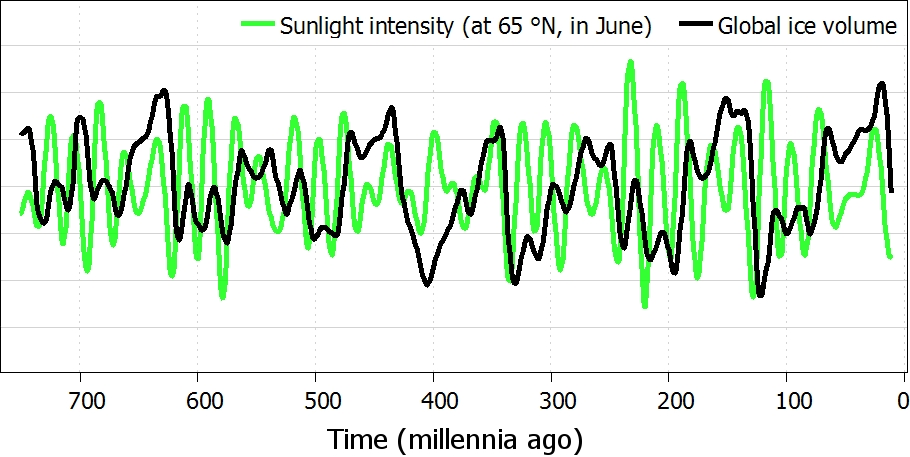
Abbildung 6: Intensität des Sonnenlichts (invers) und globale Eismenge.
Änderungen
Viele Jahrtausende lang waren die wichtigsten Fluktuationen im Klima der Erde durch die Eiszeiten bestimmt. Die Eiszeiten werden durch natürliche Variationen des Erdorbits um die Sonne hervorgerufen. Jene Variationen des Orbits verändern die Intensität des sommerlichen Sonnenlichts. Einige relevante Daten zeigt Abbildung 6: die schwarze Linie repräsentiert die Menge des globalen Eises, und die grüne Linie repräsentiert die Intensität des Sonnenlichts in der Nordhemisphäre (wo die Auswirkungen am größten sind). Man beachte, dass die Ähnlichkeit zwischen beiden Linien nur sehr schwach ist.
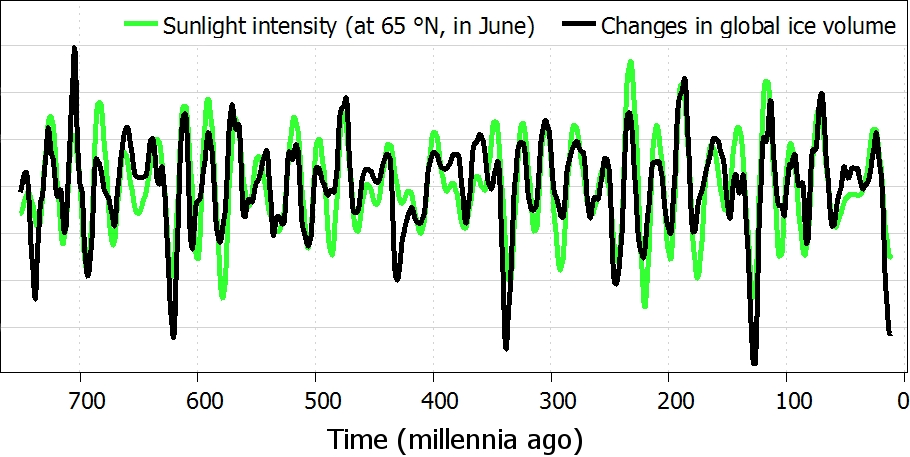
Abbildung 7: Intensität des Sonnenlichts (invers) und Veränderungen der globalen Eismenge
Warum ist die Ähnlichkeit so schwach? Um zu verstehen, was hier vor sich geht, müssen wir die Veränderungen der globalen Eismenge betrachten. Zum Beispiel, falls die Eismenge zu verschiedenen Zeiten 17, 15, 14, 19, … beträgt, und wenn man davon die jeweils folgenden Mengen subtrahiert; 2, 1, -5, … Die schwarze Linie in Abbildung 7 zeigt die Veränderungen der Eismenge, während die grüne Linie wie zuvor die Intensität des sommerlichen Sonnenlichts zeigt. Jetzt ist die Ähnlichkeit beider Linien groß. Dies ist ein ausgezeichneter Beweis dafür, dass die Eiszeiten durch orbitale Variationen verursacht wurden (dafür gibt es auch noch andere Beweise).
Ein Zusammenhang zwischen Eiszeiten und orbitalen Variationen wurde erstmals 1920 ins Spiel gebracht, und zwar durch den serbischen Astrophysiker Milutin Milankovitch. Um diesen Vorschlag zu untersuchen, sind Daten über die Eismenge in vergangenen Millenien unabdingbar; diese Daten wurden 1976 verfügbar. Und doch dauerte es bis zum Jahr 2006, bis Wissenschaftler die Veränderungen der Eismenge betrachteten. Mit anderen Worten, die Wissenschaftler brauchten 30 Jahre Denkzeit, um die erforderliche Subtraktion durchzuführen, um die schwarze Linie in Abbildung 7 zu erhalten. Während dieser drei Dekaden analysierten die Wissenschaftler den Vorschlag von Milankovitch auf der Basis von Kurven wie in Abbildung 6, und sie überdachten eine Palette von Gedanken, um zu versuchen, die schwach ausgeprägte Similarität zwischen den beiden Linien zu erklären.
Alternative Hypothesen
Dieses Vorgehen warf eine Frage auf: In Bezug auf die globale Temperatur, was passiert, wenn wir die Änderungen analysieren anstatt die Temperaturen selbst? Es stellt sich heraus, dass es dann eine offensichtliche Alternative zu den Hypothesen des IPCC gibt. Wie gut ist diese neue Hypothese im Vergleich zu der des IPCC? Eine allgemein übliche Methode, Hypothesen zu vergleichen, ist die Durchführung eines Verfahrens, das die Statistiker „AICc“ nennen (Akaike Information Criterion with correction). Diese Methode zeigt, dass die Alternative so viel besser ist als die des IPCC, dass wir daraus folgern, dass die Hypothese des IPCC untragbar ist. Das heißt, das IPCC machte den gleichen Fehler wie diejenigen Wissenschaftler, die 30 Jahre lang versuchten, den Vorschlag von Milankovitch zu verifizieren: Sie betrachteten nicht die Veränderungen in einer Reihe.
Mit der alternativen Hypothese ist die Zunahme der globalen Temperatur nicht signifikant. Wir wissen jedoch nicht, ob die alternative Hypothese selbst vernünftig ist – vielleicht gibt es noch bessere Hypothesen. Die Abschätzung, wie viel Gültigkeit die alternative Hypothese hat, sind Studien vonnöten. Es gab Studien, die alternative Hypothesen untersuchten und damit unterschiedliche Schlussfolgerungen über die Daten zogen. Der IPCC-Bericht erwähnt solche Studien, jedoch ohne anzuerkennen, dass die Stichhaltigkeit auf der Auswahl der Hypothese beruht – oder dass die Auswahl schwierige Forschungen erforderlich macht.
Link: http://www.informath.org/media/a42.htm
Anmerkungen
Was das IPCC-Kapitel über die globale Temperaturzunahme sagt
Der Zustandsbericht des IPCC aus dem Jahr 2007 enthält ein Kapitel mit der Überschrift: “Observations: surface and atmospheric climate change” [etwa: Oberfläche und atmosphärische Klimaänderung] (darin bezieht sich „Oberfläche“ auf die Erdoberfläche, d. h. wo Menschen wohnen). Dieses Kapitel präsentiert die globalen Temperaturmessungen, dargestellt in Abbildung 1. Die Hauptschlussfolgerung dieses Kapitels steht gleich fett gedruckt im ersten Satz. Sie lautet: „die globale mittlere Temperatur an der Erdoberfläche ist um 0,74°C ± 0,18°C gestiegen, wenn man sie mit einem linearen Trend über die letzten 100 Jahre abschätzt (1906 bis 2005)“. (Hier bedeutet “0.74°C ± 0.18°C”, dass das IPCC zu 90% sicher ist, dass der Temperaturanstieg in einem Bereich zwischen 0,56°C und 0,92°C pro Jahrhundert liegt). Ein Trend, der mit so großer Sicherheit so hoch über der Nulllinie liegt, ist extrem signifikant.
Eine NON- AR1– Hypothese die im IPCC-Kapitel verworfen wird
Im Jahre 2005 haben zwei Wissenschaftler im U.S. Geological Survey, T. A. Cohn und H. F. Lins einen Forschungsartikel veröffentlicht, der eine andere Hypothese als die AR1-Hypothese untersuchte. Dem Artikel zufolge lässt sich sagen, falls diese andere Hypothese gültig ist, ist die Zunahme der globalen Temperatur nicht signifikant. Der Artikel von Cohn & Lins wird im IPCC-Kapitel erwähnt, aber nur in einem einzigen Absatz in einem Anhang (§3.A). In dem Absatz wird anerkannt, dass „die statistische Signifikanz der … Trends des AR1 überschätzt worden sein könnten“. Dann wird behauptet, dass andere Hypothesen als die mit AR1 berechneten nicht übernommen werden sollten, weil „die Ergebnisse von den benutzten (Hypothesen) abhängen, und komplexere (Hypothesen) nicht so transparent sind, und es mangelt ihnen oft an physikalischem Realismus“. Der erste Teil, dass die Ergebnisse von den gewählten Hypothesen abhängen, ist korrekt, aber offensichtlich kein Grund, sich auf AR1 zu verlassen. Der zweite Teil hinsichtlich komplexerer Hypothesen könnte in einigen Fällen zutreffen (abhängig davon, welche Hypothese man verwendet). Der dritte Teil hinsichtlich der physikalischen Realität ist eine wichtige Sache. Eine Hypothese ist physikalisch realistisch, wenn sie mit unserem Verständnis über das Wirken physikalischer Vorgänge übereinstimmt. Hier folgt ein Beispiel einer unrealistischen Hypothese: nämlich die Hypothese, dass sich eine geworfene Münze immer auf und ab in einer perfekten geraden Linie durch die Luft bewegt. Der IPCC-Bericht stellt keine Betrachtung darüber an, ob seine Hypothese physikalisch realistisch ist: dies ist ein Manko des Berichtes. Die Angelegenheit wurde jedoch in einem Forschungspapier 2008 mit den Mitautoren G. A. Schmidt (NASA-Klimatologe) und dem führenden Alarmisten M. E. Mann betrachtet (beide Hauptbefürworter der globalen Erwärmung). In dem Papier finden sich starke Argumente, dass das AR1 physikalisch unrealistisch ist und dass irgendeine andere Hypothese verwendet werden muss. Dies bedeutet, dass die Behauptung des IPCC im Anhang, andere auf physikalischem Realismus beruhende Hypothesen zu vermeiden, schwer in die Irre führt.
Ob die Hypothese von Cohn & Lins angemessen ist, ist unbekannt (obwohl sie 2007 einige Unterstützung von Koutsoyiannis & Montanan erhalten hat). Das IPCc nennt jedoch höchst dubiose Gründe dafür, jene Hypothese zurückzuweisen.
Andere Hypothesen, die im IPCC-Bericht erwähnt werden
Einige andere Hypothesen als die in AR1 werden kurz in einem späteren Kapitel des IPCC-Berichtes erwähnt, in §9.4.1. Die entscheidende Frage jedoch – welche Hypothese man auch immer verwendet, sie muss gerechtfertigt sein – wird nicht angesprochen. Dass die Signifikanz mit einigen Hypothesen verschwinden kann, wird nicht angedeutet.
Was das Wissenschaftsprogramm der Klimaänderung (CCSP) zur Hypothese im AR1 sagt
Der CCSP-Bericht behauptet, dass AR1 „eine Hypothese enthält, die eine gute Näherung für die meisten Klimadaten darstellt”. Die Behauptung wird ohne jeden Beweis, Argumentation oder Verweise auf andere Arbeiten erhoben. Tatsächlich werden Methoden, die Behauptung zu testen – und welche beweisen, dass die Behauptung falsch ist – schon in Einführungskursen über Zeitreihen gelehrt: siehe die Bibliographie.
[Die folgenden Details stellen eine technische Beschreibung dar und werden daher nicht mit übersetzt. Im Original sind dazu auch zahlreiche Links anzuklicken. A. d. Übers.]
Douglas J. Keenan
Keenan betrieb früher mathematische Forschung für den Finanzmarkt an der Wallstreet und in der City of London. Seit 1995 arbeitet er unabhängig. Er unterstützt Umweltbwegungen und Energiesicherheit
Übersetzt von Chris Frey für EIKE
Link: http://www.informath.org/media/a41/b8.pdf
Einige statistische Details (nicht übersetzt)
The annual global temperature data was downloaded via http://data.giss.nasa.gov/gistemp/ on 2010-11-17. The available data was for years 1881–2009. It is given as differences from the mean, in hundredths °C. (The mean used in Figure 1 is from NASA’s Earth Fact Sheet; the accuracy of that mean is irrelevant for the analysis herein.)
The IPCC and the CCSP use slightly different methods to fit a straight line to the temperature data. The CCSP uses ordinary least squares, and then finds approximate confidence intervals assuming that the residuals conform to AR(1). The IPCC uses generalized least squares and REML, assuming AR(1). The difference between the two methods is negligible; using ML instead of REML also makes negligible difference: see the R session below.
> # Assign the annual global temperature data (source: NASA)
> gistemp<- ts(c(-21, -26, -27, -32, -32, -29, -36, -27, -17, –
39, -28, -32, -33, -33, -25, -14, -11, -26, -16, -8, -15, -25, –
30, -35, -24, -19, -39, -33, -35, -33, -34, -32, -30, -15, -10, –
30, -39, -33, -20, -19, -15, -26, -22, -22, -17, -2, -15, -13, –
26, -8, -2, -8, -19, -7, -12, -5, 7, 10, 1, 4, 10, 3, 9, 19, 6, –
5, 0, -4, -7, -16, -4, 3, 11, -10, -10, -17, 8, 8, 6, -1, 7, 4,
8, -21, -11, -3, -1, -4, 8, 3, -10, 0, 14, -8, -5, -16, 12, 1, 8,
19, 26, 4, 25, 9, 4, 12, 27, 31, 19, 36, 35, 13, 13, 23, 37, 29,
39, 56, 32, 33, 47, 56, 55, 48, 63, 55, 58, 44, 57), start=1881)
> # Show that the three methods give essentially the same result
> library(nlme) # nlme contains gls
> ols<- lm(gistemp ~ time(gistemp)); coefficients(ols)
(Intercept) time(gistemp)
-1134.0286319 0.5820159
> gls.REML<- gls(gistemp ~ time(gistemp), cor=corARMA(p=1,q=0), method="REML"); coefficients(gls.REML)
(Intercept) time(gistemp)
-1137.7531478 0.5842142
> gls.ML<- gls(gistemp ~ time(gistemp), cor=corARMA(p=1,q=0),
method="ML"); coefficients(gls.ML)
(Intercept) time(gistemp)
-1137.362997 0.583983
> phi<- coefficients(arima(resid(ols), order=c(1,0,0),
include.mean=FALSE))[1] # for the CCSP confint approximation
> ci.ccsp<- coefficients(ols)[2] + sqrt((1+phi)/(1-phi))*
(coefficients(ols)[2] – confint(ols)[c(4,2)])
> ci.ccsp; confint(gls.REML)[c(2,4)]; confint(gls.ML)[c(2,4)]
[1] 0.4612661 0.7027656
[1] 0.4596008 0.7088276
[1] 0.4677889 0.7001771
> # Check AICc of IPCC/CCSP model and driftless ARIMA(3,1,0)
> calcAICc<- function(aicx,n,k) aicx+(2*k*(k+1))/(n-(k+1))
> arima310z<- arima(gistemp, order=c(3,1,0)) # uses drift zero
> calcAICc(AIC(gls.ML), length(gistemp), 1+0+3)
[1] 964.7413
> calcAICc(AIC(arima310z), length(gistemp), 3+0+1)
[1] 951.0372
> exp((951.0372-964.7413)/2)
[1] 0.001057286
Bibliography [annotated]
Burnham K.P., Anderson D.R. (2002), Model Selection and Multimodel Inference (Springer). [The standard reference for AIC (Akaike Information Criterion) and similar; strongly recommends AICc; §2.6 and §8.6 discuss how to interpret differences in AICc values.]
Cohn T.A., Lins H.F. (2005), “Nature’s style: naturally trendy”, Geophysical Research Letters, 32, L23402; doi:10.1029/2005GL024476. [Dismissed by Trenberth et al.]
Cowpertwait P.S.P., Metcalfe A.V. (2009), Introductory Time Series with R (Springer). [Presents what its title says; §4.6.3 gives argumentation for using AR4 without a trend for global temperature measurements; see also Shumway & Stoffer.]
Foster G., Annan J.D., Schmidt G.A., Mann M.E. (2008), “Comment on "Heat capacity, time constant, and sensitivity of Earth’s climate system" by S. E. Schwartz”, Journal of Geophysical Research, 113, D15102; doi:10.1029/2007JD009373. [A research paper by some leading global-warming scientists, arguing against AR1 for global temperatures.]
Koutsoyiannis D., Montanari A. (2007), “Statistical analysis of hydroclimatic time series”, Water Resources Research, 43, W05429, doi:10.1029/2006WR005592. [One of the few research articles that discusses non-AR assumptions (see also Cohn & Lins).]
NASA (2010), GISS Surface Temperature Analysis, http://data.giss.nasa.gov/gistemp/. [Has the annual global temperature measurements used herein: see section “Statistical details”.]
R Development Core Team (2010), R: A Language and Environment for Statistical Computing (Vienna: R Foundation for Statistical Computing). [R is standard statistical software, used in the section “Statistical details”; it is free, via www.R-project.org.]
Roe G. (2006), “In defense of Milankovitch”, Geophysical Research Letters, 33, L24703; doi:10.1029/2006GL027817. [The first research paper to present a proper elucidation of the link between ice ages and orbital cycles; source of Figures 6 and 7.]
Shumway R.H., Stoffer D.S. (2011), Time Series and Its Applications—With R Examples (Springer). [An introductory text, more advanced than that of Cowpertwait & Metcalfe; Example 2.5 argues that it is better to consider changes in global temperatures than to use a linear trend; set problems 3.33 and 5.3 elaborate on that.]
Trenberth K.E., Jones P.D., Ambenje P., Bojariu R., Easterling D., Klein Tank A., Parker D., Rahimzadeh F., Renwick J.A., Rusticucci M., Soden B., Zhai P. (2007), “Observations: surface and atmospheric climate change”, Climate Change 2007: The Physical ScienceBasis (editors—Solomon)
S., Qin D., Manning M., Chen Z., Marquis M., Averyt K.B., Tignor M., Miller H.L.) Chapter 3 (Cambridge University Press). [The chapter of the Fourth Assessment Report by the IPCC that treats surface climate; this is the chapter that is the source for the IPCC (2007) claim that global temperatures are increasing at 0.74°C ± 0.18°C per century; Appendix A describes statistical methods.]
Wigley T.M.L. (2006), “Statistical issues regarding trends”, Temperature Trends in the Lower Atmosphere (editors—Karl T.R., Hassol S.J., Miller C.D., Murray W.L.) Appendix A (Washington D.C.: U.S. Climate Change Science Program). [Describes the statistical method used for the CCSP trend analysis.]
Acknowledgements
For discussions on drafts, I thank David R. Anderson, David L. Banks, David Henderson,
Olavi Kärner, Demetris Koutsoyiannis, Richard S. Lindzen, A.W. Montford, and Gerard Roe.
—Douglas J. Keenan
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"@26 Lotte Bruch:
Gute Frau, welche Parodie ?? Sie sind wohl eine Witzboldin.
Lieber Herr Weiss,
Ihre Parodie ist herzerfrischend und wirkt manchmal wirklich echt. Respekt.
Beste Grüße Lotte
@24 Bäcker: in Ihrem Beitrag ist fast jedes Wort Blödsinn, und dass Sie jemandes Kenntnisse in welchem Gebiet auch immer, ohne diesen Jemand auch nur im Geringsten zu kennen, meinen in diesem Tonfall qualifizieren zu können, beweist einmal mehr Ihre Präpotenz und geistige Kleinmütigkeit.
Indem ich Ihre AGW Kirche angreife, fällt Ihnen anscheinend nichts Besseres ein, als unadequat reagieren zu müssen: zu Sachlichkeit sind Sie unfähig und Ihr Diskussionsstil besteht darin, wie rechthaberische Kleinkindern zu kaifen und um jeden Preis das letzte Wort haben zu müssen. Aber Sie machen sich immer mehr zum Narren.
Werden Sie eigentlich für die Anzahl Wörter, die Sie hier pro Tag herumschmieren, bezahlt ???
Weiss, #23
Sparen Sie sich die ad hominem Eskapaden.
M.a.W. Sie verfügen nicht über die nötigen fachlichen Kenntnisse, auch wenn es nur Schulkenntnisse wären (meines Wissens gehört die Berechnung der Konfidenzintervalle eines linearen Trends nicht zum Statistikschulstoff, aber da Sie nicht wissen, was man braucht, wissen Sie das nicht)
„Was bilden Sie sich eigentlich ein, hier Rechenaufgaben anderen Diskutanten stellen zu wollen. “
Sie wollten doch wissenschaft, das gehört dazu. Ich will Sie ja nicht prüfen, sondern Sie wollen mich durch wissenschaftliche Argumente überzeugen, dass ich unrecht habe!
@22: Oberlehrer, Forentroll Bäcker:
Ihre Schulphysikkenntnisse braucht hier gar niemand. Und dass Sie von eigenen pseudo-„wissenschaftlichen“ Leistungen (wahrscheinlich langweilige x-fache Wiederholungen von Lichtgeschwindigkeitsmessungen, NATO Forschung ohne jeden Bezug zu wissenschaftlichem Erkenntnisgewinn, etc.) angewidert – hier eine lohnendere und Sie offenbar befriedigendere Beschäftigung suchen (aber eben, schon wieder nichts Wissenschaftliches, ist ja eh alles Gequatsche, was Sie hier leisten, ansonsten würden Sie ja stolz Ihre Originalbeiträge in anerkannten Journals als tinurl Links präsentieren: können Sie ja nicht, deswegen die frustrierte Überreaktion eines offenbar Zu-Kurz-Gekommenen) ist zwar verständlich, aber trotzdem sehr entbehrlich.
Was bilden Sie sich eigentlich ein, hier Rechenaufgaben anderen Diskutanten stellen zu wollen. Pfeifen Sie schon aus dem letzten Loch, weil Ihre Verzweiflung ob Ihres verlogenen wissenschaftlichen Weltbildes zu gross ist, und Sie spüren, dass Ihre Felle davonschimmen. Die Götzendämmerung des Einsturzes des Weltbilds der AGW-Kirche steht bevor: die Aufklärungsarbeit über die Machenschaften der noblen „Wissenschaftler“, die im Namen von Politik und Geld die Wahrheit beugen und den Steuerzahler betrügen, geht immer heftiger und schneller weiter (ähnlich den Aufklärungen über gefälschte Dissertationen) und wird die Wahrheit den Steuerzahlern bald unmissverständlichh präsentieren.
Sie sind sich sicher bewusst, dass jeder Schwachsinn, den Sie im Internet irgendwo schreiben auf ewig nachweisbar bleibt. Bei etwas mehr Selbstkritik würden Sie viel vorsichtiger sein mit Ihrem Geschreibsel bei Ihrer vorurteilslosen (da in Lohnarbeit ???) Parteinahme zugunsten des grössten Wissemnschaftsbetrugs, den die Menschheit bis dato gesehen hat.
Aber machen Sie nur weiter so …
Herr Weiss,
Sie muessen natuerlich noch wissen, dass Keenan Verwirrung stiftet mit seiner Behauptung, dass die Temperaturen der Reihe aus einem AR(1)Modell stammten, aber sie stammen aus keinem stastischen Modell, sondern aus Messwerten. Diese haben aufgrund der Klimaeigenschaften ein persistenzverhalten (dies wird ja bei der Trendberechnung von Bunde et al. vorher rausgerechnet). Aber dies Eigenschaft wird nicht modelliert, sondern ist Eigenschaft der Daten. Wie man im IPCC appendix 3B nachlesen kann, den Keenan eben kritisiert, modelliert der IPCC die Fehlerkorrelation in den Temperaturen nach dem Modell. Diesen entscheidenden Unterschied unterschlaegt Keenan einfach. In seinem Program aber ist es korrekt unterschieden. Dies ist doch seltsam, oder?
Herr Weiss,
Sie wollen wissenschaftlich diskutieren, kontern aber nur mit ad hominem Argumenten. Wie waere es, wenn Sie mal Ihre Statstikkenntnisse unter Beweis stellen und ausrechnen, welche Signifikanzgrenten die GISS Temperturreihe hat, hm? Bekommen Sie das hin, oder sind Sie nicht besser als Sie es vom IPCC denken?
Entschuldigung Herr Weiss, von Pfeifen schreibt Keenan nichts.
Verstehen Sie nicht, dass Keenans Kritik darin besteht, dass der IPCC die Ergebnisse aller denkbaren Fehlerkorrelationsmodelle nicht dargestellt hat und sich stattdessen ohne Begruendung auf nur eines festlegte?
Wie Keenans Untersuchung aber zeigt, fuehren andere Fehlerkorrelationsmodelle zu im Rahmen der Signifikanzgrenzen identischen Ergebnissen fuer den linearen Trend.
Keenans Ergebnis ist eine nette Ergaenzung, deren Ergebnis offensichtlich wenig ueberrascht, denn das unterschiedliche Fehlerkorrelationsmodelle wenig am linearen Trend ruetteln koennen, kann man der Temperturkurve ja schon mit blossem Auge ansehen.
@18 Bäcker sehr schwach:
Und dass der überragende Hauptpunkt, d.h. der wesentliche Inhalt, von Keenan’s Arbeit darin bestand zu zeigen, dass die IPCC „Forscher“ regelrechte Pfeifen in wissenschaftlicher Statistik sind und es nicht einmal verstehen, verschiedene Hypothesen gegeneinander zu testen, ist Ihnen entgangen?? Dazu fällt Ihnen nichts ein ??
Im Gegenteil – nach typsch Bäcker’scher Manier (die jeder echten wissenschaftlichen Diskussionkultur Hohn spricht) – suchen Sie sich gezielt jene Items heraus, die Ihnen in Ihren Kram passen, und seien Sie im Gesamtzusammenhang der Darstellung des Autors noch so nebensächlich, um dann Ihrer präformierten „hidden agenda“ in Ihrem Hirn wieder zu folgen, die immer nur einem Schema folgt:
1) IPCC hat recht
2) AGW ist richtig
3) Ich weiss Alles, bin der Grösste und habe niemals einen Irrtum oder ein Defizit meinerseits einzugestehen.
Was ist also Ihr Standpunkt zum Kerninhalt von Keenan’s Artikel, wonach die IPCC „Wissenschaftler“ Statistikpfeifen sind. Wenn er nämlich recht hat, können Sie die IPCC Berichte rauchen …
Vorsicht! Der CO-2 Baecker arbeitet wieder mit der Nebelkerze. Keenan nennt den gleichen Trend „nicht signifikant“ und begründet das. Der Herr Baecker verschweigt das in typischer Politikermanier, weil er sich gegen die Begründung sachlich nicht wehren kann. Also tut er so als ob der gefundene Trend schon deswegen signifikant wäre, weil er im IPCC Report steht. Das bestreitet Keenan. Das ist der Punkt. Der Rest ist wieder bewusste Irreführung durch unsere Desinformanten.
Michael Weber
Herr Weiss, #17
bleiben Sie bitte bei Keenans Beiträgen.
Wie Sie im Artikel oben im Progrmmcode sehen können, kommt er zum gleichen Trend wie IPCC und CCSP.
@Bäcker, Fischer: Ihre Beiträge zeigen einmal mehr, dass Sie beide offenbar unbelehrbar sind hinsichtlich der Einsicht in Ihre eigene unwissenschaftliche Denk- und Diskussionsweise.
In präpotentem, von Ihnen irrigerweise als besserwisserisch gemeintem Stil setzen Sie sich permanent über Ihnen missliebige Argumente hinweg und verwedeln jede sachbezogene Argumentation vor dem Hintergrund Ihres Glaubensbekenntnisses, das folgenden Geboten folgt:
1) das IPCC hat immer recht
2) 1 – 2 ppm droht uns mit dem Ertrinkungs- oder Erhitzungstod (in einigen Tausend Jahren)
3) Die Computerspiele GCMs geben die uneingeschränkte zukünftige Wahrheit über Meeresspiegel und Globaltemperatur an
4) Wir sind die Grössten und wissen alles
5) Wir massen uns eine permanent präpotente, besserwisserische Haltung allen „Klimaleugnern“ (O-Ton Leggewie) gegenüber an
6) Wir können die behauptete grosse Wasserdampfrückkopplung nicht beweisen, aber ist ja wurscht …
Auf der Webpage von EIKE sind Sie definitv fehl am Platze, da Sie gezielte Desinformation betreiben und auch dem hier im Durchschnitt üblichen intellektuellen Niveau und der Wahrheitsliebe nicht genügen.
Keenan bestätigt also, dass die linearen Trends im AR4 eine signifikante Erwärmung über 100 Jahre auch bei vom IPCC abweichenden Trendanalysen zeigen.
Keenan schreibt in http://www.informath.org/media/a41/b8.pdf
“Show that the three methods give essentially the same result ….Herein, the IPCC/CCSP model is compared, via AICc, to a driftless ARIMA(3,1,0) model.”
Herr Limburg,
ich gab nur Zahlen auf dem obigen Artikel wieder.
Ich habe den autoregressiven Prozeß letztens in Formeln hier dargestellt:
http://preview.tinyurl.com/3s5o3fx
Eine Einführung zum Thema Zeitreihenanalyse, in dt.: Schlittgen, Streitberg: Zeitreihenanalyse, R. Oldenbourg Verlag, aus der Reihe Lehr- und Handbücher der Statistik
Danke an Herrn Weiss für die messerscharfe Beurteilung unter #12!
Übrigens habe ich trotz mäßiger Statistikkenntnisse die Ausführungen Keenans genau so verstanden, wie Sie es unter #9 dankenswert klar beschrieben haben.
Anfangs dachte ich auch, dass es den „Spielwiesen-Schreibern“ um wissenschaftlichen Diskurs ginge. Aber nach ein/zwei Repliken wusste ich, dass sie genau das nicht wollten.
Noch bezeichnender und regelrecht unerträglich ist allerdings ihre Unfähigkeit zu vernünftigen Gegenargumenten bei Themen, bei denen Lebenserfahrung und/oder ökonomisches bzw. ingenieurtechnisches Fachwissen notwendig wären.
Befähigt scheinen sie lediglich auf dem Gebiet der Rabulistik.
Herr Weiss,
Sie arbeiten eben so hart daran, nicht ernstgenommen zu werden, dass ich nicht für die Folgen verantwortlich bin.
Ihr Beitrag zeigt im Unterschied von #1,#2 und #10, dass Sie nichts von Statistik wissen. Gleichzeitig meinen Sie aber zu wissen, dass meine Person und die Klimaforscher absolute Nullen sind, während Keenan ein Topstatistiker ist. Und jetzt verlangen Sie, dass ich ernst bleibe, sorry, aber das ist zu viel verlangt 😉
@11: Herr Fischer, Sie betrachten die Diskussion hier als Spiel und nehmen gar nichts ernst, was Ihnen nicht in den Kram passt. Das ist schon reichlich primitiv.
Sie kapieren offenbar wirklich nicht, was ein anständiger wissenschaftlicher Diskurs ist: dazu gehört der Eigenzweifel, den Sie anscheinend nicht kennen. Insofern sind Sie hier auf diesem Forum vollständig fehl am Platz. Ihre Erwiderung auf meinen Beitrag hätte sich – um ernst genommen werden zu können – auf die Substanz der Vorwürfe an die statistische Unterbelichtetheit wichtiger Aussagen der IPCC Assessement Reports durch Herrn Keenan beziehen sollen. Stattdessen verwedeln Sie – wie bei Ihnen üblich – das Thema in einer Weise, die dem intellektuellen Gehalt der Kritik von Herrn Keenan Hohn spricht. Schämen Sie sich bitte für diese perfide charakterliche Haltung. Es geht Ihnen – im typisch primitiven Politikdiskutierstil – nur um eigene Rechthaberei und narzistische Selbstbefriedigung, aber keineswegs um wissenschaftlichen Erkenntnisgewinn und die Wahrheit.
@ K. Keller
Vielen Dank, jetzt habe ich es verstanden, was der Autor will.
@ weiss
Lassen Sie mich ihren Beitrag kurz zusammenfassen: Sie hatten einfach sagen können, dass Sie es auch nicht verstanden haben.
„HERR KEENAN SAGT (mit Recht natürlich), DASS IHRE „WELTKLASSE“ FORSCHER DES IPCC IN SACHEN WISSENSCHAFTLICHER STATISTIK LAUSIGFE PFEIFEN SIND, DIE NICHT EINMAL GRUNDBEGRIFEE WISSENSCHAFTLICH-STATISTISCHEN ARBEITENS GENÜGEND KENNEN UND NULLHYPOTHESEN KORREKT UNTERSUCHEN KÖNNEN.“
So, wirklich? Wer schreit, hat unrecht 😉
Hinweise eines Statistikers:
Die Fragestellung ist, ob die Zeitreihe bei Wegrechnen eines linearen Trends nur noch zufällig schwankt. Könnte das gezeigt werden, wäre der lineare Trend als deterministische Komponente bestätigt.
Diese Betrachtung unterstellt, dass der die Zeitreihe x(t) generierende Prozess durch
x(t) = trend + rho * x(t-1)
gegeben ist, d.h. durch einen „auto-regressiven Prosess erster Ordnung“, kurz AR(1).
Ein Ansatz zum Test auf einen deterministischen Trend besteht nun darin, die „ersten Differenzen“, also z(t) = x(t) – x(t-1) daraufhin zu testen, ob sie „AR(0)“ sind.
Locker gesprochen ist das der Fall, wenn der Regressionswert für rho nicht von 1 unterschieden werden kann. Dann gilt der deterministische Trend als bestätigt, d.h. z(t) (die Residuen) sind ein reiner Random Walk.
So weit, so gut. Allerdings weis jeder, der hier schon mal tiefer eingestiegen ist, dass die notwendigen Bedingungen für einen mathematisch sauberen Signifikanztest in der Realität so gut wie unerfüllbar sind! Diese Tests („Unit-Root-Tests“) leiden unter einer sehr geringen Trennschärfe und erfordern schon theoretisch enorm lange Stichprobenzeiträume und eine sehr genaue Messung des physikalischen Prozesses.
Der mathematische Statistiker kann hier nur darauf hinweisen, dass die theoretischen Voraussetzungen für die praktische Anwendbarkeit solcher Tests im Rahmen der kurzen und bekanntermaßen enorm fehlerhaften „Meßreihen“ schlicht nicht gegeben sind!
(Hier ist nicht der Ort, um das weiter auszuführen; es sei nur gesagt, dass es weitere Ansätze zur Konstruktion solcher Tests gibt; auch kann hier nicht auf die subtilen, aber sehr bedeutsamen Fragen eingegangen werden, welche Hypothese überhaupt gegen welche Alternativhypothese getestet werden muss!
Die Literatur hat im Übrigen in den letzten Jahrzehnten sehr umfangreich große Klassen unterschiedlicher möglicher „generierender Prozesse“ und die mit ihnen verbundenen Schätz- und Testverfahren untersucht!)
@Bäcker, Fischer, Adeno: „Weltklasse IPCC versteht nichts von Statistik“
Herr Adeno, Herr Fischer: haben Sie denn wirklich nicht bemerkt, dass Herr Douglas J. Keenan in seinem Artikel versucht hat, Ihnen – als von wissenschaftlicher Statistik offenbar völlig unbedarften Laien – die einfachsten statistischen Begriffe wie zum Beispiel „Signifkanz“ zu erklären, damit Sie dann auch seine Kritik am wissenschaftlichen Gehalt der Assessment Reports des IPCC verstehen können.
Wenn Herr Adeno sagt „… denn die beruhen doch wohl weniger auf Münzwürfen als auf physikalische Mechanismen und Energiebilanzen. Welche Mechanismen da genau welche Rolle spielen mag ja im Detail noch unklar sein. …“ gibt er sogleich zu erkennen, dass er die Erklärungen und die pädagogischen Ziele von Herrn Keenan überhaupt nicht verstanden hat (oder verstehen wollte ?).
Herrn Fischer möchte ich an dieser Stelle keine Vorwürfe machen, wenn er sagt „Wenn es Sie tröstet, dann gestehe auch ich, dem Autor nicht ganz folgen zu können.“ Das ist wenigstens ehrlich, wenngleich auch enttäuschend, dachte ich doch, dass Herr Fischer mehr vom wesentlichen Rüstzeug wissenschaftlicher Arbeit versteht: den statistischen Grundbegriffen und Methoden, sowie deren korrekter Anwendung bei der Analyse und Bewertung quantitativer wissenschaftlicher Resultate.
Herrn Bäcker’s Bemerkungen in #1 und #2 zu Übersetzungsfehlern, die das Wesentliche des Inhalt des Keenan’schen Artikels überhaupt nicht tangieren, haben mich insofern enttäuscht, als auch Herr Bäcker zum brisanten Inhalt des Artikels von Herrn Keenan, der einen AGW Anhänger maximal irritieren müsste, überhaupt nicht Stellung bezieht – entgegen der sonst bei Herrn Bäcker üblichen sofortigen Gegenrede (fundiert oder nicht).
Ja, meine Herren AGW Fans (Aviso, Bäcker, Fischer), haben Sie denn die Kritik von Herrn Keenan an der wissenschaftlichen Qualität des IPCC wirklich nicht verstanden ?? Dann also hier nochmals in Klarschrift, was Herr Keenan Ihnen – offenbar erfolglos – sagen wollte:
HERR KEENAN SAGT (mit Recht natürlich), DASS IHRE „WELTKLASSE“ FORSCHER DES IPCC IN SACHEN WISSENSCHAFTLICHER STATISTIK LAUSIGFE PFEIFEN SIND, DIE NICHT EINMAL GRUNDBEGRIFEE WISSENSCHAFTLICH-STATISTISCHEN ARBEITENS GENÜGEND KENNEN UND NULLHYPOTHESEN KORREKT UNTERSUCHEN KÖNNEN.
Herr Keenan legt methodisch völlig zwingend dar, dass die Hauptaussagen des IPCC von einem signifikanten Temperaturanstieg (auf der Basis der globalen Mittelwertstenmperaturen in Abb. 1 des Artikels) wissenschaftlich-statistisch, methodisch ungenügend und daher ungerechtfertigter Weise vom IPCC als „signifikant“ bezeichnet worden sind.
Wenn Sie das nicht verstehen, sollten Sie sich wenigstens ein Minimalrüstzeug an statistischem Wissen zulegen, um die wissenschaftlich vollkommen korrekte Kritik von Herrn Keenan überhaupt zu verstehen, geschweige denn zu kommentieren oder kritisieren zu können (man muss wissen, ob man kompetent ist, zu einem Sachverhalt Stellung nehmen zu können: dies gehört zu den einfacheren Aufgaben von Menschen, die als intelligent wahrgenommen werden wollen).
Noch ein Zweites: selbst wenn der Temperaturanstieg in Abb. 1 als „signifikant“ einzustufen wäre, hiesse dies noch lange nicht, dass dieser von Ihrem geliebten anthropogenen 1 bis 2 ppm CO2 stammt, da ja mindestens fünf – bei weitem – wichtigere Faktoren dafür viel, viel eher in Frage kommen:
– Sonne
– Wolken
– Vulkane
– Wasserdampf
– natürliches CO2
– vielleicht ein weiterer, noch unbekannter Faktor X
– …..
– vielleicht ein weiterer, noch unbekannter Faktor Z
– 1 bis 2 ppm anthropogenes CO2
HÖREN SIE AUF MIT IHREN LEBENSLÜGEN VOM BÖSEN MENSCHLICHEN CO2 UND NÜTZEN SIE IHRE LEBENSZEIT FÜR POSITIVERE DINGE ALS FÜR DIESEN BLANKEN UNSINN !!!
Übrigens habe ich nicht die geringste Hoffnung, dass „Weltklasse“-Geister wie Schellnhuber, Rahmstorf und der überragende „Klimaforscher“ Leggewie (ein Professor für Ökonomie und Mitglied des WBGU, der sich permanent erfrecht, echte Wissenschaftler, die seinen CO2-Wahnsinn nicht als Wahrheit anerkennen, als „notorische Klimaleugner“ zu verhöhnen) die einfachen, pädagogischen Ausführungen in Statistik von Herrn Keenan folgen zu können: da reicht der Intellekt vielleicht nicht …
Herr Fischer,
googeln Sie mal nach Sally Clark und Lucia de Berk , die sind mit Ihrer Mathematik als Mörderinnen verurteilt worden, wären sie an einen guten Statistiker gekommen, wären sie nicht mal angeklagt worden.
Hallo Herr Becker in #2,
danke für die Belehrungen. Akzeptiert! Zumal Sie sie – bis auf den ersten Satz – recht sachlich vortragen. Nur eines: Ich führe niemanden in die Irre! Das hieße nämlich, dass Sie mir unterstellen, ich übersetze absichtlich falsch! Hoffentlich haben Sie noch nie jemanden in die Irre geführt!
In dieser Hinsicht danke ich Herrn Fischer in #6 für seine Bemerkung, dass er dem Autor auch nicht ganz folgen konnte.
Chris Frey
Herr Demmig,
Wenn es Sie tröstet, dann gestehe auch ich, dem Autor nicht ganz folgen zu können.
Wenn er untersuchen möchte, ob der Temperaturanstieg zufällig ist oder nicht, dann muss er nichts über die Ursache wissen. Er muss nicht einmal wissen, dass es sich um Temperaturdaten handelt. Er muss nur eine lineare Regression durchführen und den Fehler betrachten, fertig.
Darauf haben wir alle gewartet, die nicht spezialisierte Fachwissenschaftler sind. Summa cum laude!!
Sind Temperaturen signifikant? Ich meine schon, denn die beruhen doch wohl weniger auf Münzwürfen als auf physikalische Mechanismen und Energiebilanzen. Welche Mechanismen da genau welche Rolle spielen mag ja im Detail noch unklar sein.
Um ehrlich zu sein, die deutschen Wörter habe ich lesen können, der Inhalt ist jedoch beim ersten Durchlesen für mich nicht klar, ich bin wohl die falsche Zielgruppe.
In der Diskussion mit unbedarften Allesgläubigern habe ich mit ein paar allgemeinen Denkanstößen eher Erfolg. Ausdrücklich betone ich, dass ich keinen von etwas anderem überzeugen will und auch nicht kann. Und wenn Sie denn überzeugt sind, das Richtige zu glauben / zu wissen, so macht es wohl nichts aus ein paar Dinge zu äußern, die mir unklar wären:
• Das Co2 Molekül ist ein wesentlich schweres Molekül als die Luft, wieso soll sich das in den höheren Luftschichten versammeln und dort halten können um wie ein Spiegel zu wirken?
• Wieso soll eine „Gegenstrahlung“ zur wärmeren Erde hin strahlen anstatt in den kalten Weltraum?
• Wieso ist es tagsüber in der Sonne so warm und nachts wird es bei klarem Himmel so kalt. Bei Wolkenbedeckung ist zwar auch nicht schön, aber wärmer, wenn doch Co2 die Wärmestrahlen zurückwerfen soll?
• Warum ist in den Perioden mit Folgen von Eiszeiten und Warmzeiten die Temperatur überhaupt wieder zurückgependelt, wenn es doch einen Kipppunkt gibt?
• Wieso sollen bei den jährlichen Schwankungen des Co2 Gehaltes um gut 1,5%, die anteiligen 3% anthropogenen Anteile überhaupt etwas bewirken?
http://tinyurl.com/27eq88
• Warum findet man Gegenstände von regen Verkehr über die Alpen, die das Eis freigibt (u.a. Ötzi), wenn es dort erst in unserer Zeit zur Gletscherschmelze gekommen sein soll?
• Wenn es wärmer wird, verdunstet auch mehr Wasser, dann müsste doch auch die Wolkenbildung wieder zunehmen? Und wenn es über den Alpen schneit, nehmen dann die Eisflächen wieder zu?
• Warum sind in der Antarktis und in der Arktis immer noch viel Eis – seit 1973 / 74? (Siehe ICECAP in der Eike-Linkliste, rechte Spalten, Uni Bremen)
• Wieso soll wärmer werden schädlich sein, wenn wir 1850 gerade die kleine Eiszeit hinter uns hatten, und zuletzt 1973 /74 vor einer neuen Eiszeit gewarnt wurde?
• Wieso nehmen die Wüsten ab?
• Wie viel Menschen können durch den erhöhten Co2 Gesamtgehalt durch zusätzliches Pflanzenwachstum ernährt werden? 50t oder 120t oder mehr?
Herr Frey,
hier noch zwei Übersetzungsfehler:
Den ersten hatte ich schon oben erwähnt, hier nochmal deutlicher:
Ihr Deutsch.: “ Im Jahre 2005 haben zwei Wissenschaftler im U.S. Geological Survey, T. A. Cohn und H. F. Lins einen Forschungsartikel veröffentlicht, der eine andere Hypothese als im Zustandsbericht 1 (AR1) untersucht hatte. „
Original-Englisch Keenan: “ In 2005, two scientists at the U.S. Geological Survey, T.A. Cohn and H.F. Lins, published a research article that considers an assumption other than AR1.”
Sie haben AR1 als FIR betrachtet. Keenan meint damit aber nicht die assessments reports des IPCC, sondern eine Autoregression 1. Ordnung. Den Fehler ziehen Sie im Folgenden so durch.
Hier der zweite (auch mathematischer Natur):
Ihr Deutsch.: „Die Hypothese lautet neben Anderem, dass nur der gegenwärtige Wert in einer Zeitreihe eine direkte Auswirkung auf den nächsten Wert hat. Für die globale Temperaturreihe bedeutet dies, dass die Temperatur des vorigen Jahres keine Auswirkung auf die Temperatur des nächsten Jahres hat.“
Original-Englisch Keenan: “The assumption implies, among other things, that only the current value in a time series has a direct effect on the next value. For the global temperature series, it means that this year’s temperature affects next year’s, but temperatures in previous years do not. “
Herr Frey,
Sie führen die Leser mit Ihren Übersetzungsfehlern in die Irre!
Ihr Deutsch.: “Eine Hypothese, die nicht im AR1 enthalten ist und im IPCC-Kapitel verworfen wird“
Original-Englisch Keenan: “A non-AR1 assumption dismissed by the IPCC chapter”
Mit AR1 (siehe Keenan und die mathematische Literatur über Zeitreihenanalyse) ist ein autoregressiver Prozeß 1. Ordnung gemeint. Dies bezieht sich hier auf die Analysemethode zur Berechnung des linearen Trends im IPCC AR4 report (AR4 steht für fourth assessement report des IPCC, nach FI(first)R, S(second)AR und T(third)AR).