Einführung der Redaktion
Die Venus gibt nach wie vor jede Menge Rätsel auf. Eines davon ist die hohe Temperatur der Atmosphäre, bei gleichzeitig extrem hohem Druck und zu fast 100 % aus CO2 bestehend. Daher benutzen Treibhausanhänger wie Harald Lesch diesen Umstand gern als Beleg für einen starken Treibhauseffekt, der – ggf. wenn wir nicht schnell und stark gegensteuerten – auch unsere Erde heimsuchen könnte. Besonnenere Zeitgenossen, wie der Ingenieur Fleischmann versuchten die hohe Venustemperatur mit dem adiabatisch- konvektiven Effekt zu erklären (hier und hier), und können damit die gemessene Temperatur von im Schnitt 464 °C erstaunlich gut berechnen. Doch bleibt die Frage ungeklärt, woher denn die Energie stammt, die durch den adiabatisch- konvektiven Kreislauf verteilt wird. Fleischmann hält sich dazu bedeckt, zitiert aber die Autoren Limaye et al 2017 mit „its atmosphere is heated from the top“, die Atmosphäre wird von oben beheizt“
Unser Autor Uli Weber, glaubt ausnahmsweise mal WIKIPEDIA, und übernimmt dessen Aussage, dass die Venusoberfläche „grau“ glühe. Die Energie stammt nach dieser Hypothese also überwiegend aus dem Planeten Innern. Lesen Sie selbst.
Uli Weber
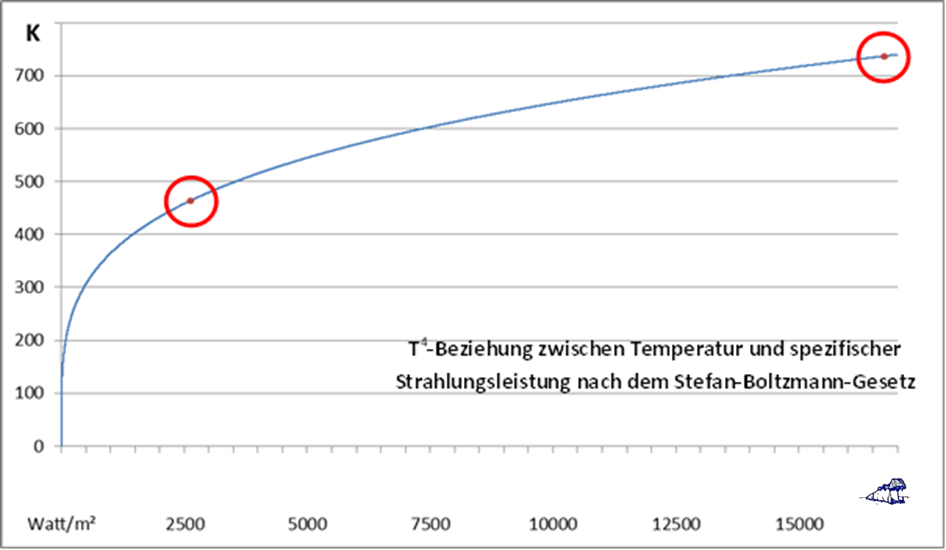Abbildung 1: Die rechnerische hemisphärische Maximaltemperatur ohne Albedo (464K, roter Punkt links) und die gemessene Temperatur (464°C oder 737K, roter Punkt rechts) auf der Venus.
Blaue Kurve: Die T4-Funktion des Stefan-Boltzmann-Gesetzes
Die Temperatur auf der Venus ist das Paradebeispiel für einen sogenannten „natürlichen atmosphärischen Treibhauseffekt“, weil diese nicht allein von der Sonneneinstrahlung verursacht werden kann. Die Temperatur auf der Venus wird nämlich mit 464°C angegeben, und die Solarkonstante Sv wird dort wegen der geringeren Entfernung zur Sonne in unterschiedlichen Quellen mit Werten zwischen 2601 und 2623 W/m² beziffert. Eine Rückrechnung mit meinem hemisphärischen S-B-Ansatz über das Stefan-Boltzmann-Gesetz ergibt nun für die solare Einstrahlung aus dieser Solarkonstanten (hier: Sv=2623 W/m²) eine Maximaltemperatur ohne Albedo von 464 Kelvin (Abbildung 1):
Es wird sofort deutlich, dass zwischen der maximal möglichen hemisphärischen und der tatsächlich gemessenen Temperatur auf der Venus eine Differenz von genau 273 Grad besteht, die exakt die Differenz zwischen der Celsius- und der Kelvin-Temperaturskala ausmacht. Gegenüber der in Abbildung 1 dargestellten hemisphärischen Maximaltemperatur von 464 Kelvin durch die solare Einstrahlung wird dagegen die sogenannte Schwarzkörpertemperatur der Venus von der NASA unter Einbeziehung von deren sphärischer Albedo von 0,77 mit 226,6 Kelvin angegeben. Daraus ließe sich für die Venus wiederum ein sogenannter „natürlicher atmosphärischer Treibhauseffekt“ von etwa 510 Grad gegenüber der gemessenen Temperatur konstruieren.
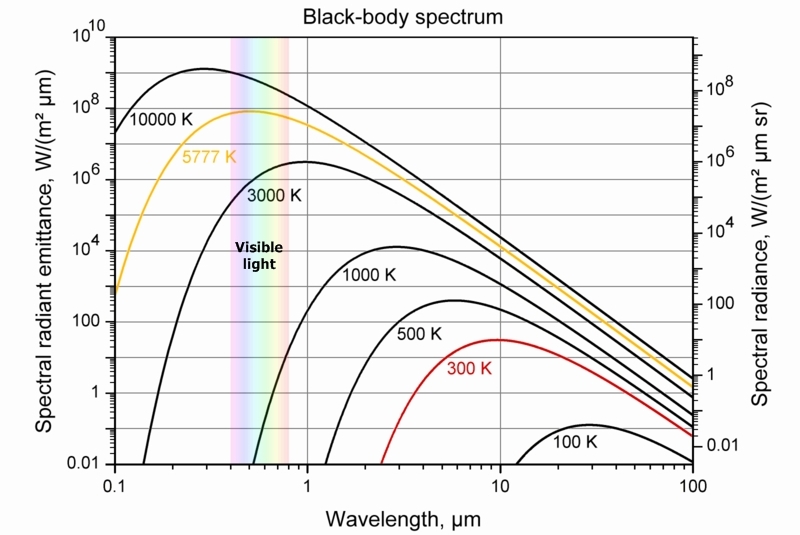Abbildung 2: Die Schwarzkörperspektren für unterschiedliche Temperaturen (NASA aus Sekundärquelle)
Schauen wir jetzt ganz einmal genau hin: Eine Temperatur von 464°C (=737K) entspricht nach dem Stefan-Boltzmann-Gesetz einer spezifischen Strahlungsleistung von 16.742 W/m², also mehr als dem 6-fachen der Solarkonstanten von 2623 W/m² auf der Venus. Die zugehörigen Schwarzkörperspektren dieser Temperaturen können anhand der nachfolgenden Grafik abgeschätzt werden (Abbildung 2):
Das Spektrum von 226,6 Kelvin liegt unterhalb des Spektrums von 300K, das Spektrum von 464 Kelvin knapp unterhalb von 500K. Und das Spektrum von 736,6 Kelvin liegt unterhalb vom 1000K-Spektrum. Damit aber liegt das Maximum der gemessenen Venustemperatur in einem Bereich, in dem deren solar indiziertes Schwarzkörperspektrum von 226,6 Kelvin bereits auf null geht. Wo soll nun also die erforderliche spezifische Strahlungsleistung für die gemessene Temperatur von 464°C herkommen? Es gibt hier doch überhaupt keine spektrale Überschneidung und damit keine primäre spezifische solare Strahlungsleistung, die zum Strahlungsmaximum der gemessenen Venustemperatur beitragen könnte.
Nach den Gesetzen der Thermodynamik (kein Perpetuum Mobile der 1. und 2. Art) ist daher die gemessene Venustemperatur nicht mehr durch die Sonneneinstrahlung zu erklären, sondern muss andere Ursachen haben. Denn die erforderliche 6-fache spezifische Strahlungsleistung für die gemessene Venustemperatur gegenüber der Solarkonstante muss ja irgendwo herkommen/erzeugt werden. Nachfolgend stelle ich spontan drei Lösungen zur Diskussion:
- Die NASA hat die Skalen für „Grad Celsius“ und „Kelvin“ vertauscht.
- Die HS der Thermodynamik sind falsch, und damit auch mein hemisphärisches S-B-Modell.
- Es existiert auf der Venus ein CO2-Treibhauseffekt von etwa 510 Grad.
Alle drei Lösungen fallen aus:
- Es ist ziemlich unwahrscheinlich, dass sich die NASA bei der Temperaturskala (°C/K) über Jahre hinweg geirrt haben könnte. (=> 1=unwahr)
- Weiterhin wäre es physikalisch völlig absurd, wenn auf der Venus die Hauptsätze der Thermodynamik nicht gelten würden. (=> 2=unwahr)
- Und ein sich selbst erhaltender Treibhauseffekt von etwa 510 Grad auf der Venus wäre ohne die zusätzliche Zufuhr einer etwa sechsfach größeren spezifischen Strahlungsleistung als die Solarkonstante physikalisch unmöglich, sonst hätten wir alle inzwischen völlig brennstoff-freie CO2-Öfen – und Herr Putin das Nachsehen…. (=> 3=unwahr)
Wikipedia sagt nun über die Venus-Oberfläche, Zitat: „Der Boden der Venus ist ständig grauglühend, für das menschliche Auge wäre das aber nur während der Nacht und nur schwach wahrnehmbar. Aufgrund der sehr hohen Temperaturen gibt es keine Gewässer. Das Relief wird hauptsächlich von sanft gewellten Ebenen beherrscht…“
Und, ebenfalls nach Wikipedia, hat die „farblose Grauglut“ eine Temperatur von etwa 400°C und ist nur im Dunkeln wahrnehmbar; bei 525°C beginnt dann die sichtbare Rotglut. Für die durchschnittlich gemessene Oberflächentemperatur von 464°C besteht zwischen beiden also ausreichend unsichtbarer Spielraum; Lavaausbrüche können mit 650°C bis 1260°C sogar noch wesentlich heißer ausfallen.
Mit der heißen Venus-Oberfläche haben wir also die Quelle für die hohen Temperaturen gefunden.
Nach den Hauptsätzen der Thermodynamik kann eine Erwärmung der Oberfläche durch eine heiße Atmosphäre ausgeschlossen werden, weil es sich dabei um ein Perpetuum Mobile handeln würde. Eine adiabatisch erhitzte Venusatmosphäre könnte nämlich ihre Wärme nicht an die Oberfläche abgeben und gleichzeitig aufgrund ihrer hohen Temperatur und geringeren Dichte erneut in der Troposphäre aufsteigen. Um es barrierefrei auszudrücken, man kann entweder die Kuh schlachten oder ihre Milch trinken – aber nicht beides gleichzeitig. Vielmehr würde sich in der bodennahen Atmosphäre sofort eine kältere (und damit dichtere) Sperrschicht ausbilden, die einen solchen Prozess blockieren würde.
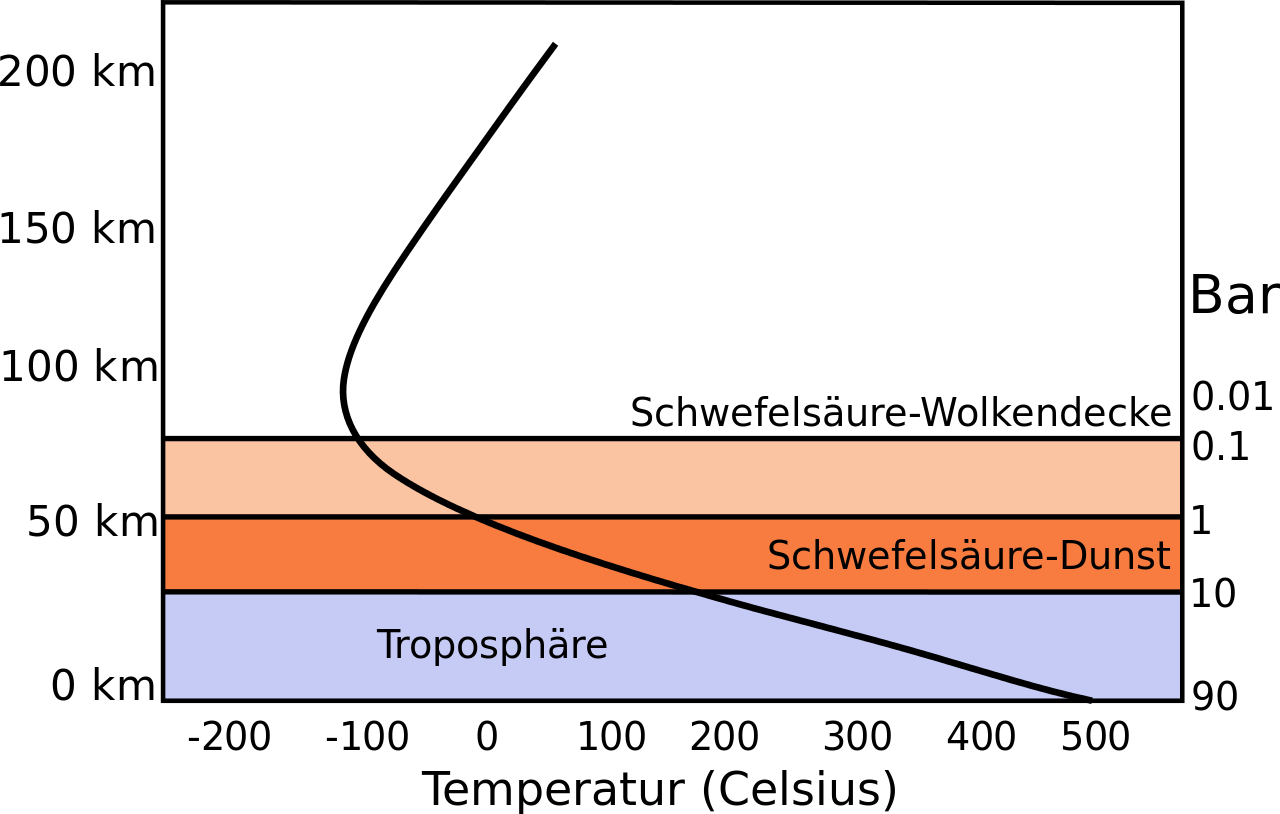
Abbildung 3: Der Temperatur- und Druckverlauf in der Venus-Atmosphäre
Quelle Wikipedia: Venusatmosphere.svg, Alexparent derivative work: Anaximander, gemeinfrei
Abbildung 3 macht deutlich, dass die Hitze direkt von der Venus-Oberfläche kommt:
Wie Abbildung 3 verdeutlicht, hat die Venustemperatur also gar nichts mit der hemisphärischen solaren Einstrahlung zu tun. Vielmehr ruht die Venus-Atmosphäre auf der heißen Planetenoberfläche wie auf einer heißen Herdplatte und bezieht die notwendige Energie für die gemessenen Temperaturen von dort wie ein brodelnder Topf.
Ein CO2-Treibhauseffekt von etwa 510 Grad ist daher auf der Venus mit Sicherheit auszuschließen.
Und damit wäre auch der fehlende Temperaturunterschied (NASA) auf der Venus zwischen der Tag- und Nachtseite (Tageslänge = 243 Erdentage) geklärt, denn der heißen Venusoberfläche ist die Tageszeit ziemlich egal, und die Sonne spielt bei einer Albedo von 0,77 praktisch keine Rolle für die Temperaturgenese. Anders ist es bei der Abkühlung. Hier scheint die solare Einstrahlung in Summe auszureichen, um die Abkühlung der Venus soweit zu reduzieren, dass diese über den bisherigen Beobachtungszeitraum hinweg nicht auffällig niedriger geworden ist.
Ganz anders sieht beispielsweise die (mond-)tägliche Schwankungsbreite auf unserem erkalteten Erd-Mond mit einer Tageslänge von etwa 29,5 Erdentagen aus. In der, gegenüber der Venusnacht, wesentlich kürzeren Mondnacht kühlt die Mondoberfläche nämlich auf bis zu -200°C ab, entsprechend einem S-B-Äquivalent von etwa 2W/m². Auf unserem Mond ist daher die solare Einstrahlung entscheidend für die Temperaturgenese:
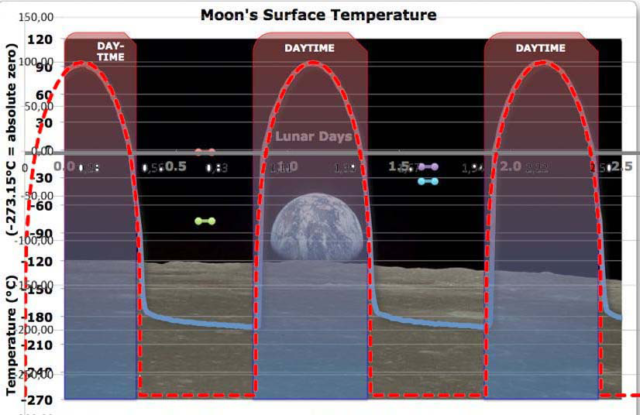Abbildung 4: Oberflächentemperatur auf dem Mond (aus meinem EIKE-Artikel „Beweist die Temperatur des Mondes den hemisphaerischen Stefan-Boltzmann-Ansatz?“
Blau: Die gemessene Temperatur am Landeplatz von Apollo 15 (@ 26°7′55,99″ N 3°38′1,9″ E)
Original aus einem Artikel auf EIKE, Primärquelle WUWT (W. Eschenbach)
Rot: Hemisphärisch ohne Ekliptik berechnete Temperatur am Landeplatz von Apollo 15 durch die Sonneneinstrahlung (U. Weber)
Eckwerte der Berechnung: Solarkonstante=1.367 [W/m²], Albedo=0,11, maximal temperaturwirksame Solarstrahlung bei 26,125° geogr. Breite=1.092 [W/m²]
Das hemisphärisch berechnete S-B-Temperaturäquivalent liefert lediglich für die sonnenbeschienene Tagseite des Mondes korrekte Ergebnisse, die Temperaturen auf der Nachseite des Mondes ergeben aufgrund der bei diesem Modell fehlenden Sonneneinstrahlung und Wärmespeicherung grundsätzlich 0 Kelvin. Williams et al. (2017) stützen nun aber ausdrücklich diesen hemisphärischen S-B-Ansatz für die Tagseite des Mondes, Zitat mit Hervorhebungen:
„The lunar regolith is highly insulating due to its low density and thermal conductivity (Linsky, 1966, Cremers and Birkebak, 1971, Keihm and Langseth, 1973) and therefore heat flow into the subsurface during the day is small compared to the incident solar flux (Vasavada et al., 1999, 2012). Daytime temperatures can therefore be approximated from the balance of incoming solar flux and outgoing thermal emission: …”
Der Google-Übersetzer: „Der Mondregolith ist aufgrund seiner geringen Dichte und Wärmeleitfähigkeit hochisolierend (Linsky, 1966, Cremers und Birkebak, 1971, Keihm und Langseth, 1973) und daher ist der Wärmefluss in den Untergrund während des Tages im Vergleich zum einfallenden Sonnenfluss gering (Vasavada et al., 1999, 2012). Die Tagestemperaturen können daher aus dem Gleichgewicht des einfallenden Sonnenflusses und der ausgehenden Wärmeabgabe angenähert werden: …“
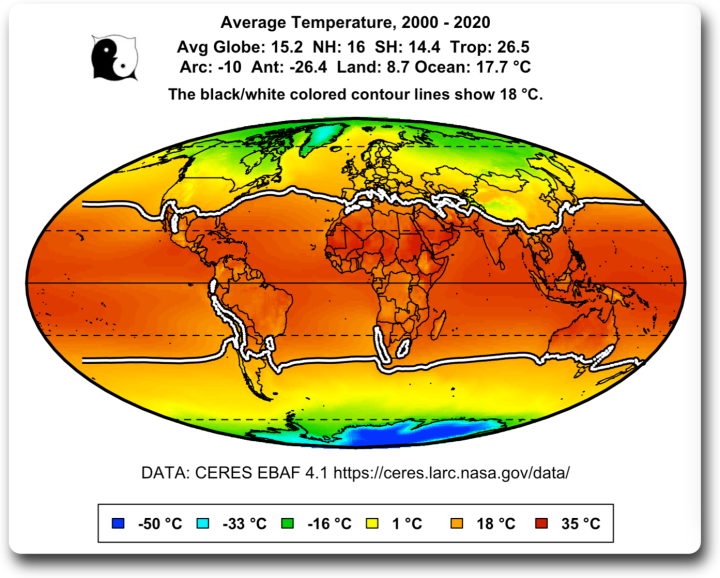Abbildung 5: Durchschnittstemperatur für die Jahre 2000 – 2020 von Willis Eschenbach auf EIKE
Auf dem Erdmond – und auch auf unserer Erde – ist die Temperaturgenese also eindeutig exogen, nämlich von der Sonneneinstrahlung bestimmt, während sie dagegen auf der Venus endogen ist, d.h. die Temperatur wird von der eigenen heißen Oberfläche erzeugt. Unsere Erde besitzt nun glücklicherweise erhebliche Wärmespeicher in Form ihrer kombinierten Luft-Wasser-Heizung (Atmosphäre und Ozeane), die ein mondähnliches Absinken der Nachttemperaturen sicher verhindern. Nur zur Erinnerung nachfolgend die Durchschnittswerte der globalen Temperatur in Abbildung 5.
Die schwarz-weiße Linie in Abbildung 5 begrenzt den 18°C-Temperaturbereich um den Äquator, der sich weit hinaus über die Wendekreise erstreckt. Das Meer mit einer Durchschnittstemperatur von 17,7°C bedeckt ca. 2/3 der Erdoberfläche und wirkt im Verbund mit der Atmosphäre der Nachtabkühlung der Landmassen sehr erfolgreich entgegen.
Ein sogenannter „natürlicher atmosphärischer Treibhauseffekt“ ist eine klimawissenschaftliche Schimäre, die sich zwangsläufig aus einer fehlerhaften Faktor4-Tag=Nacht-Inversion des Stefan-Boltzmann-Gesetzes herleitet.
Anhang: Auseinandersetzung mit dem konvektiv-adiabatischen Modell
Herr Dr.-Ing. Bernd Fleischmann hatte das konvektiv-adiabatische Model auf der 14. Internationalen EIKE-Klima- und Energiekonferenz (IKEK-14) am 12. und 13. November 2021 in Gera unter dem Titel „Die Berechnung absoluter Temperaturen mit dem konvektiv-adiabatischen Model“ vorgestellt. Aus der zugehörigen Foliensammlung habe ich nachfolgend einige Kernaussagen („kursiv“ dargestellt) zusammengetragen und kritisch diskutiert:
Generelle Aussage (Folie 12): “Robinson und Catling (NASA Astrobiology Institute’s Virtual Planetary Laboratory) „Common 0.1 bar tropopause in thick atmospheres set by pressure-dependent infrared transparency” nature geoscience letters, 2013
In allen untersuchten Planeten (Erde, Titan, Jupiter, Saturn, Uranus und Neptun) separiert die Tropopause eine Stratosphäre mit einem Temperaturprofil, das durch die Absorption der Sonnenstrahlung kontrolliert ist, von einer Region darunter, die durch Konvektion, Wetter und Wolken charakterisiert ist.
Mit dem Strahlungsgleichgewicht an der Wolkendecke und dem konvektiv-adiabatischen Modell können die Temperaturen unterhalb der Tropopause für alle Planeten berechnet werden.“
Für die Venus ergeben sich folgende Aussagen (Folien 13 und 15):
„Die geschlossene Wolkendecke, die dichte Atmosphäre und die hohen Wolkengeschwindigkeiten von mehr als 350 km/h sorgen dafür, dass die Temperaturen sehr ausgeglichen sind. Wir verteilen also die eintreffende Sonnenstrahlung gleichmäßig über die Venus und ziehen die Reflexion (77 %) ab.“
WIDERSPRUCH 1: Auch Wolkengeschwindigkeiten von mehr als 350 km/h können den Energietransport durch Strahlung nicht zeitnah ausgleichen.
„Ieff = Smax (1 – 0,77) ・ (1 – 0,01) ・ 0,98 / 4 = 145 W/m² “
WIDERSPRUCH 2: Ieff leitet sich offensichtlich aus einem Faktor4-Tag=Nacht-Ansatz her. Entscheidend für die Temperatur ist aber die korrekte Berechnung der hemisphärisch einfallenden Sonnenstrahlung.
„T1 = (Ieff /(ε σ))1/4 = 225 K
Um die Adiabatengleichung von Poisson anwenden zu können, benötigen wir den Isentropenexponenten γ der Venusatmosphäre. Bei 96,5 % CO2 und 3,5 % N2 ergibt sich ein Wert von γ = 1,3. Um Phasenübergange in der Atmosphäre zu berücksichtigen, verwenden wir den Korrekturfaktor k = 0,8 für den Exponenten, weil es die NASA seit Carl Sagan auch so macht.
T1/ T0 = (p1 / p0) k(γ-1)/γ “
WIDERSPRUCH 3: Die konkreten Zahlenangaben zu p1 und p2 fehlen hier. Wenn wir als p1 einmal den weiter oben zitierten Wert von 0,1 bar für die Tropopause annehmen, fehlt trotzdem noch der Zahlenwert p0 für die Oberfläche. Erst später wird auf der Folie 17, „Temperatur der Venus mit Erdatmosphäre“, der Druck auf der Venusoberfläche mit 92 bar angegeben.
„Jetzt haben wir alles, um T0 , die Temperatur auf der Venusoberfläche zu berechnen. Das Ergebnis:
T0 = 736 K = 463 °C “
WIDERSPRUCH 4: Mit den rekonstruierten Werten für p1 und p2 ergibt sich für die Venus eine Oberflächentemperatur von 793 Kelvin. Es ist jedoch durchaus möglich, dass Dr.-Ing. Fleischmann mit einem abweichenden p1 und/oder p0 gerechnet haben könnte, weil beide dort nicht explizit angegeben worden sind.
Zitat aus Limaye et al. (2017) – Folie 14: „its [Venus’] atmosphere is heated from the top“,
die Venus-Atmosphäre wird von oben beheizt.
Das Gleiche gilt für alle anderen Planeten mit dichter Wolkendecke. “
WIDERSPRUCH 5: Eine konvektive „Deckenheizung“ für die erdähnlichen Planeten macht gravitativ überhaupt keinen Sinn, da ist eine Fußbodenheizung schon sehr viel konvektiver…
Und für die Erde sind folgende Aussagen belegt (Folien 20 bis 22):
„Ieff = Smax ・ (1 – 0,04) ・ (1 – 0,02) ・ (1 – 0,06) / π = 383 W/m² “
WIDERSPRUCH 6: Gleichgültig, ob der Devisor „Pi“ den Raumwinkel darstellen soll, oder ob es sich um einen Schreibfehler zulasten des „Faktors 4“ handelt, beides trifft nicht auf die hemisphärische solare Einstrahlung hier auf der Erde zu.
„Die Wolken reflektieren etwa 34 % der Sonnenstrahlung (Messung des Deep Space Climate Observatory). Für die Absorption in den Wolken nehmen wir an, dass sie der gemessenen Emissivitat von 90 % entspricht („Ice water content vertical profiles of high-level clouds classification and impact on radiative fluxes, Feofilov et al. 2015), dann ist die Intensität
IWolken = 228 W/m2
T Wolken = (IWolken / (ε σ))1/4 = 252 K = -21 °C
TBoden = TWolken – hW ・ dT/dh = 252 K + 5,8 ・ 8,4 K = 300 K = 27 °C “
WIDERSPRUCH 7: Durch die Benutzung der beiden fremd vorgegebenen Werte für die Wolkenhöhe [hW] und den Gradienten [dT/dh] reicht bei dieser Berechnung eine einzige Temperatur, T1 oder T0 , völlig aus, um die jeweils andere Temperatur bestimmen zu können. Von der Erdoberfläche aus gerechnet kommt das hemisphärische S-B-Modell über die barometrische Höhenformel mit einem Gradienten von [-6,5°C/1000m] zu vergleichbaren Ergebnissen:
Das hemisphärische Modell berechnet den tagseitigen Temperaturdurchschnitt zu 15°C. Mit einem Gradienten von [-6,5°C/1000m] ergibt sich für die sogenannte Abstrahlungshöhe von ca. 5.000m:
15°C * 5.000m * (-6,5°C/1.000m) = -17,5°C
Und -18°C entsprechen der vorgeblichen globalen Abstrahlungstemperatur der Erde.
ERGO: Die Berechnungen für die Oberflächentemperaturen von Venus und Erde nach dem konvektiv-adiabatischen Modell leiten sich aus einer Art Faktor4-Tag=Nacht-Ansatz für die hemisphärische solare Einstrahlung her. Die Berechnungen für die Erde basieren auf der barometrischen Höhenformel; bestimmend für das rechnerische Ergebnis auf der Venusoberfläche ist ein frei gewählter Korrekturfaktor für den Exponenten, der einen bestimmenden Einfluss auf das Endergebnis ausübt. Willkürlich festgelegte Parameter können aber zu fehlerhaften Ergebnissen führen, oder auch umgekehrt ein gewünschtes Ergebnis erzeugen. Hierfür würde beim konvektiv-adiabatischen Modell für die Venus allein schon der Korrekturfaktor „k“ ausreichen, wie die nachfolgende Abbildung beweist:
Abbildung: Oberflächentemperatur T0 [K] als Funktion des Korrekturfaktors „k“
Eine Varianz des Korrekturfaktors „k“ zwischen 0,5 und 1,0 lässt die Oberflächentemperatur der Venus zwischen ca. 500 K und 1.100 K schwanken und steht damit in diametralem Gegensatz zu der vorgeblichen Rechengenauigkeit von einem Grad (Folie 15). Von daher reicht die Begründung für den benutzten Zahlenwert des entscheidenden Parameters von exakt „k=0,8“ nicht aus, nur, Zitat, „…weil es die NASA seit Carl Sagan auch so macht“. Es ist nämlich nicht auszuschließen, dass dieser Korrekturparameter durch ein gezieltes „Back-Engineering“ zustande gekommen sein könnte.
Der Mathematiker John von Neumann soll einmal gesagt haben, Zitat: „Mit vier freien Parametern zeichne ich einen Elefanten. Mit fünf freien Parametern lasse ich ihn mit dem Rüssel wackeln.“
Nach Wikipedia sagt Ockhams Rasiermesser vereinfacht Folgendes aus, Zitat: „
- Von mehreren möglichen hinreichenden Erklärungen für ein und denselben Sachverhalt ist die einfachste Theorie allen anderen vorzuziehen.
- Eine Theorie ist einfach, wenn sie möglichst wenige Variablen und Hypothesen enthält und wenn diese in klaren logischen Beziehungen zueinander stehen, aus denen der zu erklärende Sachverhalt logisch folgt.“
Das konvektiv-adiabatische Modell kann die Temperaturen der erdähnlichen Planeten offensichtlich nicht aus sich selbst heraus erklären, sondern benötigt reale Meßwerte (Luftdruck, Wolkenhöhe, Temperaturgradient) sowie einen nicht konkret begründeten Korrekturfaktor für die Kondensation. Darüber hinaus geht es von einem gravitativ unmöglichen konvektiven Antrieb „von oben“ aus. Meine hemisphärischen Berechnungen für die Erde kommen dagegen ohne jedwede Korrekturfaktoren aus und sind hier für die Tagseite und hier für die Nachtseite zu finden.
Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Schon in der Einleitung ist ein grober Fehler. Es sind 96% CO2 in der Atmosphäre. Das sind zwar für jeden viele Anwendungen tatsächlich „fast 100%“ aber bei einer Zusammensetzung, die, zumindest hier auf der Erde bei einer Erhöhung um 0,02% 1K Temperaturunterschied ausmacht nicht zu vernachlässigen. Würde man das linear Hochrechnen wären das bei 4% 200K was eine ordentliche Menge ist.
Das ist aber mal wieder typisch EIKE. Aber das ist auch gut, dass solche Fehler schon in den ersten Sätzen stehen, dann braucht man sich den Rest gar nicht durchlesen um festzustellen, dass das alles an den Haaren herbeigezogen ist und falsche Schlüsse gezogen werden. Wäre das nämlich nicht so, würde man solche Artikel eher in der Nature oder anderen wissenschaftlichen Publikationen lesen.
Die Venus ist ein schönes Beispiel dafür, was die wenige Sonnenenergie, die auf den Boden dringt in einer CO2 reichen Atmosphäre anrichten können.
Es ist gut das sie hier nicht gelesen haben. Der Wissenszuwachs ist immens, wenn sie schon alles wissen.
Steht in der Literatur auch drin welche Aenderung eintritt, wenn aus Versehen die Venus 100 % CO2 haette?
Warum hat der Mars solch einen immens kleinen Effekt, obwohl der auch nicht ganz 100 % CO2 in der Atmosphaere auszuweisen hat?
Bitte machen sie weiter und lesen sie nichts, das ihnen nicht gefaellt. Und wichtig ist, das sie gut dokumentieren, das man ohne zu Ende zu Lesen immer noch kommentieren kann.
Ich bedanke mich bei der EIKE-Redaktion für die Veröffentlichung meines Venus-Beitrags sowie bei den betreffenden Kommentatoren für positive und konstruktive Kommentare.
Zum Kommentar von G. Wedekind am 6. April 2022 um 9:26: Wenn man diesem exogenen hemisphärischen Ansatz folgt, müsste sich auf der Venus aufgrund der Tageslänge eigentlich eine Tag#Nacht-Struktur ausbilden – darüber ist mir nichts bekannt.
Zum Kommentar von Udo Wehmann am 5. April 2022 um 12:23, Zitat aus dem Abstract von Robert Ian Holmes (2017): „The formula used is the molar version of the ideal gas law. It is here demonstrated that the information contained in just these three gas parameters alone is an extremely accurate predictor of atmospheric temperatures on planets with atmospheres >10kPa. This indicates that all information on the effective plus the residual near-surface atmospheric temperature on planetary bodies with thick atmospheres, is automatically ‘baked-in’ to the three mentioned gas parameters.”
(Der Google-Übersetzer sagt [mit meiner Korrektur]: Die verwendete Formel ist die molare Version des idealen Gasgesetzes. Hier wird gezeigt, dass allein die in diesen drei Gasparametern enthaltenen Informationen ein äußerst genauer Indikator für atmosphärische Temperaturen auf Planeten mit Atmosphären >10 kPa sind. Dies deutet darauf hin, dass alle Informationen über die effektive plus die verbleibende oberflächennahe Atmosphärentemperatur auf planetaren Körpern mit dicken Atmosphären automatisch in die drei genannten Gasparameter „eingebacken“ werden [sind].)
Wie immer eine solche „Einback-Automatik“ zu globalen Mittelwerten gekommen sein mag: Es ging hier gar nicht um Zahlenwerte, sondern um die Identifizierung der temperaturbestimmenden (endogenen) Energiequelle auf der Venus.
Zum Kommentar von Thomas Heinemann am 6. April 2022 um 7:26: Offenbar propagiert der Kommentator ein Perpetuum Mobile und hat das Wiensche Verschiebungsgesetz nicht verstanden …
Die sog. „Abstrahlhöhe“ ist eine virtuelle Höhe, nämlich jene, die leistungsmäßig der Temperatur der falsch berechneten „mittleren Zustrahlung“ entspricht. Auf der Erde ist das angeblich etwa in 6 km Höhe anzutreffen. Nur dort strahlt nichts, die Temperatur dort ist Resultat des hydrostatischen Luftdrucks. Analoges gilt für die Venus.
Breitbandige Strahlung stammt immer von der Oberfläche, Bandenstrahlung immer von Gasen. Bei Breitbandstrahlung kann man anhand der Wellenlänge des spektralen Maximums die Abstrahltemperatur ermitteln. Bei Gasen ist es schwierig, weil die zumeist rel. homogen in allen Höhen und damit Temperaturen verteilt sind. Die Stärke der Gasstrahlung hängt proportional von der Leistung der Oberflächenstrahlung bei der jeweiligen Bandenwellenlänge ab und bewegt sich grob bei 50% dieser Abstrahlung, weil die anderen 50% zurückgestrahlt werden, allerdings ohne die Oberfläche wärmer machen zu können, als sie ist.
Die einzige physikalische Bilanzschicht, die ein Planet hat, ist seine Oberfläche.
Kühne Behauptung von Ihnen. Ohne Beweis allerdings wertlos
ist zwar offensichtlich falsch, aber wenn Sie meinen, sollten Sie ja die Bilanz dieser Schicht zumindest im Detsil auch aufstellen können.
Eine Verschwörungstheorie:
https://www.youtube.com/watch?v=6a27RlwpUGM
Welches Landegerät soll eigentlich fast 400°C aushalten???
Nachdem und über den Mond unglaublicher Unfug erzählt wird (Kennt jemand vergleichbar gute Aufnahmen der Apollo-Landeplätze, wie von Lunokhod 2? Wer kennt die wahre Auflösung des LRO?), warum dann über die anderen Planeten?
@Weber
Was jetzt noch fehlt ist eine Temperaturberechnung von Ihnen für den Mars. Der übrigens auch einen Treibhauseffekt hat. Auch dort ist der Boden wärmer als die Wärmeabstralung ins All. Oder Strahlungstemperatur. Bin auf Ihre Theorie gespannt, wie das da kommt.
Noch zum planetaren Treibhaueffekt. Alle festen Planeten und Monde, die eine Atmosphäre haben, haben in dieser udR auch infrarotaktive Treibhausgase. D.h. die Oberfläche erwärmt sich durch die Sonneneinstrahlung und die Atmosphäre lässt die Wärme im Infraroten durch die Treibhausgase nicht mehr ungehindert raus. Dadurch wird es unten wärmer, bis sich ein Gleichgewicht zwischen Sonneneinstrahlung und Wärmeaustrahlung des Planeten ergibt. Bei der Erde wird im Mittel aus ca. 5 km Höhe abgestrahlt, bei der Venus aus etwa 60 km Höhe. Alles seit Jahrzehnten durch Messungen von Satelliten und Sonden gut belegt.
Auf der Tagseite der Venus ist es übrigens taghell und auf der Nachtseite dunkel. Und die Venus ist der zweitnächste Planet zur Sonne.
Merkur, der nächste Planet zur Sonne hat übrigens sogut wie keine Atmosphäre und auch keinen erwärmenden THE. Genau wie unser Mond.
Die mittlere Abstrahlungshöhe, bei der die Wärme ins All abgesrahlt wird liegt bei der Venus zwischen 50-100 km Höhe und bei der Erde bei 5 km Höhe. Das zeigt wie wenig Wärme die Venusatmosphäre von der heißen Oberfläche durchlässt. Eigentlich ganz einfach. Die beiden Abstrahlungsspektren, vom Boden und aus der oberen Atmosphäre der Venus ins All kann man auftragen und schon sieht man, wo die Wärme bleibt.
Ich wuerde sagen es „reflektiert“ eigentlich nur, das die Venus eine dickere Atmosphaere mit mehr Masse hat.
Hier wird ja richtig heiß diskutiert!! Herrlich!
Herr Dietze:
„Herr Limburg, natülich gibt es auch Konvektion, aber da vertikale Luftbewegunge
n relativ selten zu beobachten sind …“
Es gibt auch in Erdatmosphäre sehr heftige Vertikalbewegungen. Die Wolken selber bewegen sich zwar nicht auf und ab, aber sie sind nun mal keine festen Gebilde. Die Luft strömt durch Cumuluswolken teilweise sehr heftig nach oben (und sinkt außerhalb der Wolke wieder ab). Fliegen Sie nur mal durch eine Gewitterwolke – besser nicht. So um die 40 m/s Aufwind sind da keine Seltenheit. Flugzeuge haben deswegen ein Wetterradar, um diese Orte zu vermeiden.
Admin:
Sie haben recht, der Temperaturgradient folgt (mehr oder weniger) der Adiabatengleichung wie in einer Luftpumpe: Sinkt Luft ab, dann kommt sie in Bereiche höheren Luftdruckes, wird komprimiert und heizt sich auf. Die Schicht, wo die Wärme per Strahlung an die Weltraumbedingungen ankoppeln muß, ist die Wolkenoberfläche, und die ist bei der Venus sehr hoch. Dort ergibt sich ein Temperatur-Druckzustand u.a. aus dieser Kopplungsbedingung. Und ab da wird es nach unten immer heißer. Der Boden nimmt halt die Temperatur an, die sich an ihm durch Strahlungs- und Wärmeleitungsbedingungen ergibt. Eine Aufheizung der Venus von innen hat damit nichts zu tun.
Michael Krüger:
„Ein Venustag/ -nacht dauert zudem fast 4 Monate. Die Nachtseite ist aber auch kichendheiss da die Wärme nun mal schlecht durch die Atmosphäre ins All abgestrahlt werden kann.“
Es ist eher so, daß die Venus nur eine sehr geringe Rotation hat und deswegen praktisch keine Coriolisbeschleunigung aufweist. Aus diesem Grunde baut sie in der Atmosphäre nur eine einzige Zirkulationszelle (Headley-Zelle) auf, und der Austausch der Luft zwischen Äquator und Pol geht sehr effektiv vonstatten. Dieser Effekt, zusammen mit der Wärmeträgheit der dichten Atmosphäre gleicht die Temperaturen auf der gesamten Venus erstaunlich effektiv aus.
Bei der Erde mit ihrer sehr viel höheren Rotationsgeschwindigkeit ist das völlig anders: In ihrer Atmosphäre existieren im Mittel mehrere Zellen (Headley-Zelle, Ferrelzelle und Polarzelle). Diese halten die Luft in ihren Breite mehr oder weniger fest und behindern den Luftaustausch zwischen Äquator und Polen.
Übrigens ist es auf der Venus entgegen der früher geäußerten Auffassung gar nicht so dunkel. Nach den Messungen der Venera-Sonden entsprechen die Sichtbedingungen am Venusmittag in etwa denen an einem leicht bewölkten irdischen Junitag in mittleren Breiten.
MfG
G.Wedekind
„Es ist eher so, daß die Venus nur eine sehr geringe Rotation hat und deswegen praktisch keine Coriolisbeschleunigung aufweist. Aus diesem Grunde baut sie in der Atmosphäre nur eine einzige Zirkulationszelle (Headley-Zelle) auf, und der Austausch der Luft zwischen Äquator und Pol geht sehr effektiv vonstatten. Dieser Effekt, zusammen mit der Wärmeträgheit der dichten Atmosphäre gleicht die Temperaturen auf der gesamten Venus erstaunlich effektiv aus.“
Interessanter Punkt!
Der Autor hat die Grundprinzipien nicht verstanden. Die solare Einstrahlung muß mit der thermischen Abstrahlung spektral keinen Überlapp haben.
Die beiden Strahlungen haben ja gar nichts miteinander zu tun.
Die solare wird absorbiert, dazu ist der Absorptionsgrad des Planeten im solaren Spektralbereich wichtig, die thermischen Abstrahlung stellt sich mit der Temperatur und dem Absortionsgrad im entsprechenden Spektralbereich dieser Strahlung ein.
Die hohen Bodentemperaturen liegen an der sehr schweren Atmosphäre und weniger an einem Treibhauseffekt. Diese entspricht massenmäßig einem irdischen Ozean von 1300 Metern Tiefe. Dadurch ist die bei Atmosphärenphysikern bekannte sogenannte „Emissionshöhe“ mit 61 km sehr groß. (Bei der Erde liegt sie bei 5 km.). In ihr, im oberen Bereich der Wolkendecke, herrscht eine Temperatur von ca. -13 C und ein Druck von 0.2 bar, also fast irdische Verhältnisse. Dort wird die Leistung der Atmosphäre als Wärme wieder abgestrahlt und entspricht der einfallenden Leistung der Sonnenstrahlung, Albedo berücksichtigt.
Der Temperaturgradient über der Höhe h darunter, dT/dh, hängt direkt am Druckgefälle dp/dh, und wird in hohem Maße wie auch bei der Erdatmosphäre durch die atmosphärische Konvektion in der Atmosphäre bestimmt. Bei einer CO2-Atmosphäre beträgt er etwa (dT/dh = 0.14 dp/dh), was bedeutet, daß bei der großen Emissionshöhe die Bodentemperatur gar nicht anders kann als sehr hoch zu sein.
Treibhauseffekt:
Bei der Erdatmosphäre mit ca 300 K liegt das Strahlungsmaximum nach Stefan-Boltzmann bei etwa 10 Mikrometern. Dadurch hat die CO2-Linie, die bei 15 Mikrometern liegt, eine starke Auswirkung. Bei der heißen Venusatmosphäre ist das Strahlungsmaximum bei etwa 4 Mikrometern, und hier spielt der Wasserdampf eine wesentlich größere Rolle. Der Treibhauseffekt, der neben der Konvektion ebenfalls einen Einfluß hat, wird dadurch stark vom Wasserdampf (immerhin ca 0.14 Volumen-%) bestimmt. Einen Treibhauseffekt durch CO2 gibt es durchaus und heizt natürlich den Boden auf. Diese Wärme wird aber durch die Konvektion wieder nach oben bis zur Emissionshöhe getragen und dort abgestrahlt. So ergibt sich ein Kreislauf der Leistungen.
Der Einfluß der Konvektion auf den Wärmehaushalt einer Atmosphäre ist extrem, sobald sich der Temperaturgradient dem Stabilitätsrand nähert, und das ist sowohl bei der Erde als auch der Venus der Fall. Dieser Einfluß, der einen sehr großen Bypass zur Strahlungsbilanz der Atmosphäre darstellt, wird leider häufig in der Diskussion weggelassen.
MfG
G.Wedekind
Herr Wedekind,
insofern sehe ich es wie sie, aber die Aussage:
Halte ich fuer ungluecklich und falsch. Jedwede Strahlung die schwaecher als die Abstrahlung ist, fuehrt nicht zu einem Heizeffekt, sonder verringert nur die Waermeabgabe.
Was sie beschreiben ist der Strahlung und Konvektionsgleichgewicht. Das sollte man so formulieren: Die Waerme die nicht durch Strahlung transportiert wird, wird durch Konvektion transportiert. Da es sich um ein Gleichgewicht handelt, gibt es auch hier keinen Ueberschuss, der zu einer Erwaermung oder Erhitzung fuehren kann.
mfg Werner Schulz
„Einen Treibhauseffekt durch CO2 gibt es durchaus und heizt natürlich den Boden auf.“
Co2 heizt gar nichts auf, es sei denn die Atmosphäre ist wärmer als der Boden und die Abstrahlung wird nicht durch Abregung durch Stoß verhindert
=> Die Energie stammt nach dieser Hypothese also überwiegend aus dem Inneren des Planeten. Ein CO2-Treibhauseffekt von etwa 510 Grad ist daher auf der Venus mit Sicherheit auszuschließen. Ein sogenannter „natürlicher atmosphärischer Treibhauseffekt“ ist eine klimawissenschaftliche Schimäre, die sich zwangsläufig aus einer fehlerhaften Faktor4-Tag=Nacht-Inversion des Stefan-Boltzmann-Gesetzes herleitet.
Herr Weber, Ähnliches bezüglich der Energie gilt dann auch für die Erde, bloß dass hier aus dem Inneren nur 50 mW/m² kommen. Aber wie dumm, dass ohne Treibhauseffekt der globale solare Temperaturmittelwert des Erdbodens (mit Albedo sowie Speicherung über Tag/Nacht und über alle Breitenkreise gerechnet) nur -21 statt +15 Grad beträgt. Und damit hätten wir des Pudels Kern:
Die Treibhauswärme am Boden braucht zusätzliche Energie. Und bei der Erde kann die „kältere“ Gegenstrahlung diese wegen des 2.HS vermeintlich nicht an den wärmeren Boden liefern – und natürlich liefert auch die Solarstrahlung nicht mehr Energie. Also gibt es garkeinen Treibhauseffekt und Sie konnten bei EIKE zum 33. Mal wieder Verwirrung stiften.
Oder entsteht die höhere Bodentemperatur vielleicht doch so dass sich die 150 W/m² der Gegenstrahlung gemäß Energieerhaltungssatz am Boden zur Solarstrahlung addieren und so dessen Temperatur um 33 Grad erhöhen??
Die Antwoort ist ganz klar nein!
Die Strahlung addiert sich nicht. Es gibt keine Erwaermung durch Rueckstrahlung.
Es gibt nur eine Isolierwirkung, die dazu fuehrt das die Waerme aus dem Erdinneren nicht so schnell verloren geht. Dieser Prozess ist bei Venus und Erde und allen anderen Planeten gleich.
Die Erde hat einen heissen Erdkern und einen Temperaturgradienten in der Erdkruste. Falls sie den mit Strahlung erklaeren koennen, glaube ich ihnen auch ihre alternative Physik.
Ansonsten ist die Venus da oben schon ganz gut erklaert.
Herr Schulz, Ihr Argument welches auf interner Heizung und Isolierung wegen geringer Wärmeleitung der Erdatmosphäre beruht, können Sie vergessen. Die 50 mW/m² sind gegen die IR-Emission des Bodens von 390 W/m² vernachlässigbar, die bei 15 Grad (im Strahlungsmodell) durch 240+150 W/m² an absorbierter Zu- sowie Abstrahlung nach S-B entstehen. Und der reale Effekt bei jeder CO2-Verdoppelung beträgt am Boden (all inclusive) etwa +0,6 Grad – und zwar dadurch dass die IR-Absorption zunimmt und die Gegenstrahlung etwa um 3,3 W/m² ansteigt.
Herr Dietze,
offensichtlich kennen sie den Unterschied zwischen Waermeinhalt und Waermestrom nicht.
Ich kann bei entsprechender Isolierung Gestein mit 50 W/m2 schmelzen!
Als anschauliches Beispiel biete ich ihnen die unzaehligen Magmakammern an, die sich auf der Erde verteilen. Ganz angesehen vom heissen Erdkern.
Durch welche Strahlung wird der Erdkern so heiss?
Herr Schulz, natürlich kann im Erdinneren bei entsprechend dicker Isolierung Gestein mit 50 W/m2 schmelzen. Aber nicht dann wenn Ihrem Gestein 240 W/m² solar und 150 W/m² zugestrahlt wird und es 390 W/m² abstrahlt. Hören Sie auf mit solchen unsinnigen Beispielen! Unsere Atmosphäre ist strahlungsdurchlässig und daher trotz sehr geringer Wärmeleitung keine dicke Isolierschicht. Sie wissen ja, wie schnell es nachts bei klarem Himmel kalt wird, wenn die Gegenstrahlung der Wolken fehlt.
Herr Dietze,
ich weiss auch das der Weinkeller sich nicht um die Sonneneinstrahlung kuemmert. Er hat sogar eine sehr gleichmaessige Temperatur. Errinnert ein wenig an die Venus. Denken sie sich einfach eine etwas tiefere Stelle der Erdkruste, wo mehr Isolation darueber liegt. Die ist auch waermer!
Wie werden die Temperaturen in der Erdkruste bestimmt? Sehen sie Strahlung in der Erdkruste als die Hauptform der Wearmeuebertragung an?
Ansonsten werfen sie mehr Fragen auf als sie beanworten koennen.
Isoliert die Atmosphaere nicht? Sie wissen schon das eine Flaeche keine Waerme halten kann? Der Erdkoerper ist durch die Atmosphaere isoliert oder nicht? Das ist doch was sie uns mit der ‚Gegenstrahlung“ verklickern wollen. Stimmt also das Gleichnis mit dem Pullover von Frau Kosch nicht? Stimmt es nicht, das die Gegenstrahlung die Strahlungkuehlung verringert?
Wie wuerde die Atmosphaere funktionoeren, wenn sie einen exklusiv gute Waermeleitfaehigkeit haette?
Bitte um ihre Ausfuehrungen!
@Peter Dietze am 7. April 2022 um 13:01
Na, was ist denn das jetzt? „Gegenstrahlung“ der Wolken??? Gibt es die bei Ihnen nicht nur beim phösen CO2? Oder ist es doch nur der Pullover von Frau Kosch, den Sie eigentlich gemeint haben?
Richtig, Herr Dietze, genauso heize ich mein Haus: Wenn mein Haus 16°C hat und draußen sind es 8°C, mache ich alle Fenster und Türen auf. Dann gelangt die Wärme nach draußen zu den Treibhausgasen und diese strahlen jeweils die Hälfte vom Haus weg und die andere Hälfte ins Haus hinein. Die Hälfte, die ins Haus hineinstrahlt, addiert sich nun mit der Strahlung der 16°C warmen Heizung zu angenehmen +20°C. Putins Gas brauche ich nicht mehr.
„Putins Gas brauche ich nicht mehr.“
So ist das!
Ein richtiger Ingenieur nimmt die Physik als Basis und schafft einen Nutzen damit.
Mit der alten Physik hätte das nicht funktioniert, aber zum Glück gibt es ja gerade zum richtigen Zeitpunkt die Treibhausphysik
@Weber
Tragen Sie doch einfach mal die Schwarzkörper-Wärmeabstrahlungskurve bei 465 Grad, entsprechend der Venus Oberflächentemperatur auf und legen darüber das Wärmeabstrahlungsdpektrum der Venus ins All. Dann sehen Sie direkt, welche Wärmeabstrahlung die Treibhausgase zurückhalten. Die Sonne erwärmt die Venus und die Wärme wird sie duch die Treibhausgase in der Atmosphäre schlecht wieder ins All los. Daher ist es dort dort so heiß, auch auf der Nachtseite.
Herr Krueger,
wie erwaermt die Sonne die Venus?
Durch indirektes Anstrahlen oder weil etwas sichtbares Licht auf die Oberflaeche faellt?
Die Tatsache das es keine Tag und Nachtunterschiede bei den Temperaturen gibt, bezeugt doch, das dem nicht so ist. Sehen sie das jetzt anders oder Kwass?
Es gibt etliche Bilder von Venussonden auf deren Oberfläche. Dort ist es taghell. Zudem wird Sonnenlicht in der Atmosphäre absorbiert. Und die Venus ist der zweitnächste Planet an der Sonne.
Nun das beantwortet die Frage nicht.
Aber mal was anderes, ist es in der Nacht auf der Venus dunkel?
Zur Frage der Venus-Temperatur gibt es eine interessante Studie (Holmes, Fed. Univ. Australia, 2017), in der die Temperaturen der Planeten mit der idealen Gasgleichung berechnet werden. Mit diesen Daten von Erde und Venus
Erde Venus
Druck (kPa) 101 9200
Dichte (kg/m3) 1.225 65
molare Masse (gm/Mol) 28.97 43.45
berechnet er 288 K und 740 K für Erde und Venus. Auch die Daten anderer Planeten werden gut wiedergegeben. Man braucht also die Umwege über Stefan-Boltzmann und einen möglichen Treibhauseffekt gar nicht, um die Unterschiede zu erklären.
Herr Wehmann, wenn Sie den Unsinn glauben dass Luftdruck Wärme erzeugt und die Temperatur aus der adabatischen Gasgleichung berechnet werden kann, dann legen Sie sich doch zum Heizen ein paar Pressluftflaschen in die Wohnung. Tatsache ist dass bei einer transparenten N2-Atmosphäre die Bodentemperatur -18 Grad betrüge und die gesamte Atmosphäre dieselbe Temperatur hätte, es also mangels Treibhauseffekt auch keinen gravitationsbedingten T-Gradienten gäbe. Wir hätten keine Gegenstrahlung, und so könnte der Boden auch nicht mehr als 240 W/m² abstrahlen – sonst hätten wir ja ein Energie erzeugendes Perpetuum Mobile.
Dazu James Clerk Maxwell: Aus seinem Buch „Theory of Heat“ von 1871:
Ø Gravitation hat in einer ruhenden Gassäule keinen Einfluss auf das thermische Gleichgewicht.
Ø Das ist jedoch keinesfalls anwendbar auf die Atmosphäre, in der die Sonnenstrahlung das thermische Gleichgewicht stört und ständig Luftmassen von einer Höhe auf eine andere gehoben werden.
Ø Dadurch besteht ein konvektives Gleichgewicht der Wärme, in dem nicht mehr die Temperatur konstant ist, sondern die Energie (Höhenenergie plus kinetische Energie).
Ø Der Temperaturgradient folgt aus der Adiabatengleichung
Ø Der Energieerhaltungssatz bedeutet in der Atmosphäre, dass Luftmassen, die nach oben steigen, an potenieller Energie gewinnen und an kinetischer Energie verlieren.
Ø Das gilt analog für absinkende LuDmassen.
Ø Es muss noch ergänzt werden um die Energieumwandlung durch Phasenübergänge in
einer feuchten Atmosphäre und StrahlungsabsorpEon und –Emission.
Herr Limburg, natülich gibt es auch Konvektion, aber da vertikale Luftbewegungen relativ selten zu beobachten sind (in der Regel bewegen sich Wolken nicht auf und ab), habe ich statischen Luftdruck betrachtet, wie er ja auch in die adiabatische Gasgleichung eingeht.
Natürlich könnte man sich auch bei einer N2-Atmosphäre grosse Luftpakete vorstellen, die durch einen Paternoster schnell auf und ab bewegt werden. Dann hätte man am Boden natürlich auch ohne Gegenstrahlung eine erhöhte Temperatur.
Der Boden würde dann mehr als 240 W/m² abstrahlen, aber solar nur 240 W/m² erhalten. Da es kein Energie erzeugendes Perpetuum Mobile gibt, müsste die Differenz vom Antrieb des Paternosters geleistet werden. Da hierfür keine zusätzliche Energiequelle vorhanden ist, kann der Boden nur -18 Grad annehmen.
Fazit: Erhöhte Temperatur des Erdbodens kann nur durch Gegenstrahlung verursacht sein – und selbstverständlich addieren sich W/m². Sonst würde man z.B. im Solarkraftwerk Almeria auch nicht etwa tausend Spiegel auf den Absorberturm richten um gemäss T^4 = Summe_S/Sigma eine hohe Temperatur zu erreichen.
Falsch,
wie immer hoeren sie nicht zu, lesen sie nicht mit und rattern die Propaganda vom IPCC runter.
Die Atmosphaerische Strahlung verringert nur den Waermeverlust, fuegt aber keine Waerme hinzu. Genau so wie die geringe Waermeleitfaehigkeit der Luft den Waermeverlust durch Waermeleitung verhindert. Was hindert sie daran die geringe Waermeleitfaehigkeit und super Isoliereigenschaft von der Luft als Grund fuer die Erwaermung zu postulieren?
Beide haben die gleiche Wirkung, aber sie denken das die Strahlung die Erwaermung macht? Das bezeugt eigentlich nur, das sie die wirkliche Mechanik, wie eine Isolierung funktioniert und wie man diese thermodynamisch berechnet, nicht verstanden haben.
„Ø Gravitation hat in einer ruhenden Gassäule keinen Einfluss auf das thermische Gleichgewicht.“
Da kann ich dem ollen Maxwell nicht zustimmen.
In jeder Gassäule in einem Schwerefeld existieren kinetische und potentielle Energie, die sich gegenseitig substituieren.
Sie müssen die ganze Begründung lesen. Eben weil die Gassäule in einem Schwerefeld – ohne äußere Grenzen- nie ruhen kann, stellt sich nicht ein thermisches Gleichgewicht ein, sonder ein adiatbatisch-konvektives.
Das sagt Maxwell ein wenig später aus o.a. Gründen.
In jeder Gassäule in einem Schwerefeld existieren kinetische und potentielle Energie, die sich gegenseitig substituieren.
„Eben weil die Gassäule in einem Schwerefeld – ohne äußere Grenzen- nie ruhen kann,…“
Wieso sollte dies nicht möglich sein???
-Planetenoberfläche mit vergleichmäßigter Energiezufuhr aus Planeteninneren und/oder von extern
-IR-inaktive Atmosphäre
Es stellt sich am Boden eine Atmosphärentemperatur gemäß der Bodentemperatur ein, der Temperaturgradient folgt den Regeln der Isentropie bzw. der barometrischen Höhengleichung,
Ist T= 0°K, fällt die Gassäule in sich zusammen, d.h. das Das kondensiert an der Oberfläche aus.
MfG
Der Jupiter enthalt kaum Spurengase, sondern besteht zu etwa 90% aus H2 und zu 10% aus He. Dennoch wird es – aufgrund des zunehmenden Drucks – von außen nach innen immer wärmer. Das alles wurde am 7. Dezember 1995 gemessen, nämlich mit einer Kapsel bei der Galileo-Mission. Also, Herr Dietze, das Märchen mit der isothermen Atmosphäre ohne so-genannte „Treibhausgase“ können Sie vergessen. Genauso ein Unsinn sind die angeblichen-18°C für eine Erde ohne Atmosphäre bzw. eine reine N2-Atmosphäre.
Es gibt auch andere Arbeiten die in diese Richtung zeigen.
So haben Ned Nikolov and Karl Zeller diese Beziehung dargestellt.
Was man dem Aufschrei der Reifendruckpropaganden entgegenstellen sollte, ist, das nicht der Druck selber die Temperatur erzeugt, sondern, das der Druck nur ein perfektes Mass der Dicke der Isolation ist.
mfg Werner
Die Temperatur der Atmosphäre ist durch die Polytropengleichung durch Konvektion alleine selbstverständlich nicht bestimmt. Wer das behauptet, täuscht. Denn wie man an der Gleichung sehen kann, benötigt man die Temperatur an wenigstens einem Höhenpunkt, um den gesamten Temperaturverlauf zu bestimmen. Wenn das nun nicht die Temperatur am Boden ist, so verwenden die Leute eben eine andere Temperatur. Aber diese stammt aus Beobachtungsdaten und ist nicht modellmäßig durch die Konvektion bestimmbar, sondern wird durch die Strahlungsbilanz determiniert.
Aber der Gradient ist! Sollte ihnen klar sein!
Richtig! Und eine Temperatur kennt man, wenn man annimmt, das die Erde im Gleichgewicht nur soviel Waerme abgeben muss, wie sie von der Sonne erhaelt, und vielleicht noch so viel, wie sie im Inneren produziert, damit die Bilanz ausgeglichen ist.
So und dreimal duerfen sie raten, welche Temperatur damit bestimmt ist. Genau die Abstrahltemperatur unter Beruecksichtigung des Emissionskoeffizienten. Am Einfachsten kann man das bestimmen, wenn man die Atmosphaere als grauen Strahler nimmt, da man dann nicht mit Wellenlaengen und unterschiedlichen Abstrahlungsorten rumhantieren muss.
In der Annahme koennte man sagen Wolken, Staub, Wasserdampf, CO2 und Aerosole geben der Atmosphaere graue Eigenschaften? Jetzt muss man nur noch die Bedingungen rausfinden, die gegeben sein muessen, um den Abstrahlungsort und seine Hoehe zu definieren.
Herr Heinemann, welcher Druck oder Partialdruck bestimmt die Tropopause? Welche andere Bedingung koennen sie angeben, die fuer die Abstrahlung ins All gegeben sein muessen?
Die Polytrophen Gleichung ist gut, um den Waermedurchgang durch die Atmosphaere zu bestimmen. Die Dicke der Atmsophaere bestimmt, wie gut die Isolierung ist.
Alle anderen Temperaturen sind bestimmbar und mit der Realitaet vergleichbar.
Jetzt Sie Herr Heinemann!
Und da diese nicht am Boden, sondern oberhalb der Troposphäre erreicht wird, ist es am Boden wärmer als ohne Treibhausgase. Das ist der THE.
Wer?
Danke für den sehr guten Artikel. Die Venus ist geradezu ein Paradebeispiel, dass es keinen CO2-THE gibt. Die Sonnenstrahlen erreichen aufgrund der Atmosphärendichte überhaupt keinen Venusboden und können nichts aufheizen. Auf der Tagseite ist es nur unwesentlich heller wie auf der Nachtseite, also fast dunkel. 2.) Auf der Nachtseite ist die Bodentemperatur trotzdem ähnlich hoch wie auf der Tagseite.
So ist das! Bei der dicken Isolierung wo die Waerme von aussen nicht bis nach innen durchdringt, stellen sich die Temperaturen entsprechend dem Waermedurchgang durch die Isolierung ein. Am Oberrand wird die aus der Sonne gewonnene und die abfliessende Waerme aus dem Venusinneren abgegeben und bestimmt die Abstrahlungstemperatur am Abstrahlunghorizont, unter Beruecksichtigung der Strahlungseigenschaften.
Die Strahlung von CO2 spielt keine Rolle.
Eine Hauswand bei gleicher Oberflaechenbeschaffenheit und demnach Strahlungseigenschaften, strahlt auch entsprechend ihrer Temperatur in den Raum zurueck und an der Aussenseite entsprechend der Waermemenge die durch die Wand geht. Massgeblich fuer die Temperaturen ist die Dicke der Wand, da eine Dicke Wand an der Aussenseite die gleiche Temperatur hat wie die duenne Wand, aber im inneren erzeugt die dicke Wand hoehere Temperaturen. Aber nicht weil sie „zurueckstrahlt“ sondern weil sie eine Waermewiderstand hat.
Luft und Gase sind schlechte Waermeleiter. Dieses beiflusst den Waermewiderstand der Atmosphaere. Wieviel? Das kann Frau Kosch sicherlich erklaeren. Es ist ihr Pullover!
H. Schulz,
warum wird es es in einem Glashaus aus Wärmeschutzverglasung mit einem Wärmedurchgangskoeffizient 0,7 W/(m²K) bei Sonneneinstrahlung innerhalb kurzer Zeit unerträglich warm, während sich bei einem Haus aus Styropor mit gleichem Wärmedurchgangskoeffizient die Temperatur nur sehr langsam verändert?
Silke Kosch
„warum wird es es in einem Glashaus aus Wärmeschutzverglasung mit einem Wärmedurchgangskoeffizient 0,7 W/(m²K) bei Sonneneinstrahlung innerhalb kurzer Zeit unerträglich warm, während sich bei einem Haus aus Styropor mit gleichem Wärmedurchgangskoeffizient die Temperatur nur sehr langsam verändert?“
Oh Herr…
„Oh Herr“ …. habe ich auch gedacht, als ich den Beitrag von H. Schulz gelesen habe. Irgendwie fehlt da so jedes Verständnis für Systeme, wo Sonnenlicht gut eindringen kann, die abgehende Wärmestrahlung aber schlecht wieder raus und dadurch eine zusätzliche Erwärmung erfolgt … und alles im Einklang mit dem 2. HS der Thermodynamik.
Silke Kosch
„„Oh Herr“ …. habe ich auch gedacht, als ich den Beitrag von H. Schulz gelesen habe. Irgendwie fehlt da so jedes Verständnis für Systeme, wo Sonnenlicht gut eindringen kann, die abgehende Wärmestrahlung aber schlecht wieder raus und dadurch eine zusätzliche Erwärmung erfolgt … und alles im Einklang mit dem 2. HS der Thermodynamik.“
Wie kann man blos so komplett verpeilt sein?
Denken Sie mal über Konvektion nach oder lesen Sie mal G/T, da wird es gut erklärt
Frau Kosch,
beantworten sie bitte ihre eigene Frage.
Es hilft sich das selber vorzustellen.
Frage an sie: Warum wollen sie das wissen? Und wissen sie es?
Entschuldigung dass ich versucht habe Sie zu animieren, Ihre etwas weltfremde und wenig physikalische Beschreibung vom Energiedurchgang durch „dicke und dünne“ Wände zu überdenken. Grundschulkinder sind da deutlich weiter als Sie.
Nichts für ungut.
Silke Kosch
Was wollen sie eigentlich sagen?
Isoliert eine dicke Wand aus dem selben Material nicht besser als eine duenne?
Es ist wahrscheinlich richtig: Kinder verstehen das besser.
Das Problem sehe ich bei Leuten, die in Abwesenheit von thermodynamischen Grundwissens, sich eine Meinung bilden und diese dann ohne Selbstreflektion verteidigen. Da kommen dann manchmal oder meistens keine Argumente sondern wilde Anschuldigungen.
Falls sie es nicht mitbekommen haben kaufe ich ihnen den Pullover ab, aber nicht ihre Beschreibung wie dieser funktioniert.
Tauschen sie Wand mit Pullover. Die gleiche Sache, aber eine Isolierung fuehrt nunmal der geheizten Seite keine Waerme zu. Da liegen sie falsch.
Bitte tauschen sie ihre Anmassung mit Bildung aus, dann koennen sie ordentlich Argumentieren und stellen sich und ihre Persoehnlichkeit nicht so blos.
@silke Kosch am 6. April 2022 um 11:35
Äußerste Vorsicht mit solchen laienhaften Aussagen, Sie scheinen das „Lichtenfelser Experiment“ nicht zu kennen ;-)))
Aber bei Ihnen wärmt ja auch die Jacke ……
„… eine Isolierung fuehrt nunmal der geheizten Seite keine Waerme zu“
H. Schulz,
wenn Sie auf solchem Unsinn bestehen, werden Sie nie aus Ihrer Froschperspektive heraus kommen.
Ein lebender menschlicher Körper hat je in einem beheizten Raum unbedeckt eine Oberflächentemperatur von vielleicht 28°C. Mit Kleidung steigt diese Temperatur auf etwa 35°C an. Das kann man messen. Das kann man spüren. Und wenn man ganz fleißig ist, kann man es auch rechnen.
Wenn Sie weiter darauf bestehen, dass es nicht die Dämmung bzw. nicht die Kleidung ist, die der beheizten Seite Wärme zuführt, dann werden Sie Physik und Menschen, die auf physikalische Gegebenheiten aufmerksam machen, weiterhin als anmaßend empfinden.
Sie verstehen die Welt nicht (mehr) und mit Ihrer Verweigerung, Physik zu akzeptieren, haben Sie auch keine Chance, Sie zu verstehen.
Silke Kosch
„Ein lebender menschlicher Körper hat je in einem beheizten Raum unbedeckt eine Oberflächentemperatur von vielleicht 28°C. Mit Kleidung steigt diese Temperatur auf etwa 35°C an. Das kann man messen. Das kann man spüren. Und wenn man ganz fleißig ist, kann man es auch rechnen.
Wenn Sie weiter darauf bestehen, dass es nicht die Dämmung bzw. nicht die Kleidung ist, die der beheizten Seite Wärme zuführt, dann werden Sie Physik und Menschen, die auf physikalische Gegebenheiten aufmerksam machen, weiterhin als anmaßend empfinden.
Sie verstehen die Welt nicht (mehr) und mit Ihrer Verweigerung, Physik zu akzeptieren, haben Sie auch keine Chance, Sie zu verstehen.“
Hm…
-Impfbedingte Durchblutungsstörungen in der CPU?
-Beweisaufnahme im Rahmen eines Verfahrens gegen eines der „Kultusministürien“ in Blödland wegen Bildungsvorenthalt?
-Bewerbungschreiben für ein Ministeramt im Berliner Marionettenkabinett?
-Nur „zur“ Schule gegangen aber nicht „in“ die Schule?
Wirklich schwer zu sagen…
Frau Kosch,
stellen sie das Essen ein oder versuchen sie eine Waermflasche unter einem Pullover zu erhitzen.
Beides sind Hinweise darauf wo sie falsch liegen.
mfg Werner
Frau Kosch, Wärmeübergang und Wärmeübertragung sind nicht das Gleiche. Deshalb hält Ihr Pullover nur warm und wärmt nicht. Ob die Hauswand dick oder dünn ist, ist wurscht. Die Temperaturdifferenz bleibt immer gleich.
Wir sind uns also einig:
Ein lebender Körper wird unter Kleidung wärmer als ohne diese Kleidung.
Ein lebender Körper unter einer dünnen Folie (Rettungsfolie) wird wärmer als ohne diese Folie.
Ein toter Körper kühlt aus, unter Kleidung oder unter einer Rettungsfolie langsamer.
Ein Stein in der Sonne erreicht eine höhere Temperatur, wenn er unter eine Folie (Rettungsfolie) gelegt wird.
Ein Stein in Dunkelheit kühlt aus, unter einer Folie langsamer.
Ein Planet, der konstant von einer Sonne beschienen wird und wo alle anderen Randbedingungen gleich bleiben, hat eine konstante Oberflächentemperatur.
Ein Planet ohne Sonne kühlt aus.
Wir sind uns nicht einig:
Die Erdoberfläche auf einem von einer Sonne beschienenen Planeten mit Treibhausgasen in der Atmosphäre ist wärmer, als ohne diese Treibhausgase.
Ein Planet ohne Sonne kühlt aus, mit Treibhausgasen langsamer.
Habe ich das so richtig wieder gegeben?
Silke Kosch
@silke KOsch am 9. April 2022 um 15:35
Peter Hanass hat Ihr Geschwurbel ja schon ein wenig zu ordnen versucht, was bei Ihnen aber wohl nicht fruchten wird, weil Ihnen grundlegende physikalische Umstände nicht geläufig sind.
Nur mal zu Ihrer (spiegelnden) Rettungsfolie (die sich völlig anders verhält als eine durchsichtige Folie!!!): Da macht es einen großen Unterschied, ob ein Luftpolster zum Körper besteht oder die Folie auf der Haut / Kleidung anliegt, ebenso wie bei Ihrem Stein. Können Sie das begreifen? Kennen Sie die Unterschiede zwischen Wärmestrahlung, Wärmeleitung, Konvektion? Ihrem Gewurbel nach zu urteilen, nicht so recht …..
H. Tengler,
in diesem Blog gibt Kommentare und sogar Artikel in denen behauptet wird, dass ein Treibhauseffekt nicht möglich ist, weil der dem 2. HS der Thermodynamik widerspricht. Denjenigen, die solch einen Unsinn verbreiten, bin ich mit meinen Physikkenntnissen (wie gut oder schlecht die immer sein mögen) weit überlegen.
Silke Kosch
Wie können Sie die Strassersche Strahlenkanone in Frage stellen?
Sehr geehrter Herr Tengler,
ich bewundere Ihre fast unendliche Geduld:
Meine Interpretation für:
„in diesem Blog gibt Kommentare und sogar Artikel in denen behauptet wird, dass ein Treibhauseffekt nicht möglich ist, weil der dem 2. HS der Thermodynamik widerspricht. Denjenigen, die solch einen Unsinn verbreiten, bin ich mit meinen Physikkenntnissen (wie gut oder schlecht die immer sein mögen) weit überlegen.“
ist:
„in diesem Blog gibt Kommentare und sogar Artikel in denen behauptet wird, dass ein „Großes Einmaleins“ nicht möglich ist, „wenn“ es dem „Kleinen Einmaleins“ widerspricht. Denjenigen, die solch einen Unsinn verbreiten, bin ich mit meinen „Mathematikkenntnissen“ (wie gut oder schlecht die immer sein mögen) weit überlegen.
Schönen, geruhsamen Palmsonntag noch
@silke Kosch am 10. April 2022 um 16:10
Leider plappern Sie nur das „Mainstreamgewäsch“ nach und sind auf Ihre marginalen Physikkenntnisse und vor allem auf Ihre grüne Ideologie mächtig stolz ….
Fachlich kann man sich nur austauschen, wenn die benutzte Terminologie dafür sorgt, dass alle Seiten wissen, worum es geht. DA hapert es bei Ihnen mächtig und führt anscheinend insbesondere bei Ihnen zu völlig falschen Schlüssen, die zwar in Ihre Ideologie passen, aber mit Physik nix mehr zu tun haben. Da gehört für mich der Begriff „THE“ dazu. WO haben wir in der Atmosphäre ein „Treibhaus“?????? Wissen SIE überhaupt, was das ist? Hatten Sie schon mal damit zu tun? Anscheinend nicht ….. ;-))), sorry ….., SIE blamieren sich mit jedem „Beitrag“ aus Ihrer Tastatur ….
Die Antwort ist:
Weil die Sonne mit einer Temperatur von 5700 K heizt und die Heizkoerper mit irgendwas um die 30 Grad.
Sie koennen die Heizzeit verkuerzen wenn sie mit direkter Flamme im Styroporhaus rumhantieren.
„Nach den Hauptsätzen der Thermodynamik kann eine Erwärmung der Oberfläche durch eine heiße Atmosphäre ausgeschlossen werden, weil es sich dabei um ein Perpetuum Mobile handeln würde.“
Oh, das ist jetzt was Neues. Hier wird ja gerne schon einmal geglaubt, dass auf der Erde eine gegenüber der Erdoberfläche kalte Atmosphäre die Erde nicht erwärmen kann jetzt wird auch noch ausgeschlossen, dass auf der Venus die Oberfläche selbst durch die heiße Atmosphäre nicht erwärmt werden kann.
Es ist aber auch ein Dilemma, wenn man einmal die Pfade der Physik verlassen hat und nun die Welt in Unlogik zerfällt. Pullover wärmen nicht mehr, die Durchschnittstemperatur der Erde kann nicht mehr erklärt werden und man sieht den Wald vor lauter Bäumen nicht. Zum Glück hatten schon unsere Altvorderen das gleiche Problem schon vor über 100 Jahren. Die Erde war wärmer als es sich aus der Sonneneinstrahlung ableiten ließ. Warum ist die Erde so warm, wie sie ist? Das Problem war gelöst, als erkannt wurde, dass infrarotaktive Bestandteile in der Atmosphäre eine Gegenstrahlung erzeugen, die die Erde rund 30°C wärmer macht als ohne diesen Treibhauseffekt.
Worin liegt der Sinn, immer wieder die gleichen Fragen zu stellen, die sich nur daraus ergeben, dass man grundsätzliche physikalische Vorgänge ignoriert?
Silke Kosch
So einfach kann das sein. Und weil die Thermodynamik auch noch von jedem verstanden wird, brauchen wir auch keine Ingenieure mehr, um unsere Energieversorgung zu sichern oder einfach mal nur ne Bruecke zu bauen.
Kurze Frage dann noch, wenn 300 W/m2 in die eine Richtung strahlt und 370 W/m2 in die entgegengesetzte, wird dann genau so viel Waerme uebertragen, wie als wenn 350 W/m2 in die eine Richtung geht und 420 W/m2 in die andere?
Ich frage mich woher die Atmosphaere weiss, wieviel sie strahlen muss, da sie ja gar nicht weiss wie warm sie sein muss.
Frau Kosch,
wie ist ihre Antwort bitte?
,“als erkannt wurde,“ Wirklich? Wirklich erkannt?
Hier muss ich Ihnen beipflichten – ist das jetzt auf Ihrem eigenen „Mist“ gewachsen?
Was das zusätzliche anthropogene CO2 in Verbindung mit einer komplexen Troposphäre genau bewirkt, ist eine ganz andere Frage – mit hoher Wahrscheinlichkeit aber deutlich weniger, als es uns Alarmforscher erzählen.
@silke KOsch
Ein lebender Körper wird unter Kleidung wärmer als ohne diese Kleidung.
Nein. Sollte es bei Ihnen so sein, tun Sie mir leid – immer im Fieber.
Ein lebender Körper unter einer dünnen Folie (Rettungsfolie) wird wärmer als ohne diese Folie.
Nein
Ein toter Körper kühlt aus, unter Kleidung oder unter einer Rettungsfolie langsamer.
Nur, wenn TToter >TU.
Ein Stein in der Sonne erreicht eine höhere Temperatur, wenn er unter eine Folie (Rettungsfolie) gelegt wird.
Nein
Ein Stein in Dunkelheit kühlt aus, unter einer Folie langsamer.
Nur, wenn TStein >TU. Dunkelheit ist nicht erforderlich.
Ein Planet, der konstant von einer Sonne beschienen wird und wo alle anderen Randbedingungen gleich bleiben, hat eine konstante Oberflächentemperatur.
Einen Planeten mit mit unveränderlichen Randbedingungen wird es wohl auch nicht geben.
Ein Planet ohne Sonne kühlt aus.
s.w.u.
„Die Erdoberfläche auf einem von einer Sonne beschienenen Planeten mit Treibhausgasen in der Atmosphäre ist wärmer, als ohne diese Treibhausgase.“
Es gibt keine Treibhausgase
„Ein Planet ohne Sonne kühlt aus, mit Treibhausgasen langsamer.“
Einen Paneten ohne Sonne gibt es wahrscheinlich nicht
Hier die Wärmeabstrahlungsspektren von Erde, Mars und Venus.
https://www.directupload.net/file/d/6509/2uw6q2vf_png.htm
Venus lässt da wo CO2 stark absorbiert halt ganz wenig Wärme durch die Atmosphäre raus.
Ein Venustag/ -nacht dauert zudem fast 4 Monate. Die Nachtseite ist aber auch kichendheiss da die Wärme nun mal schlecht durch die Atmosphäre ins All abgestrahlt werden kann. Eigentlich ganz einfache Physik.